近年来,我国高速铁路网逐渐向沿海区域扩张,越来越多的跨海高铁桥梁被修建,近期开通的首条350 km/h跨海高铁线路更是给列车运营安全及跨海高铁桥梁建设带来了新的挑战。不同于陆地桥梁及跨江跨河桥梁,跨海桥梁水文条件及建设条件更复杂。考虑到深水建设条件及更高的通航要求标准,往往需采用刚度较低、阻尼较小的大跨径桥式方案,因而,海洋环境中强风、巨浪所激发的结构响应不可忽视。目前,一些研究者对风、浪荷载作用下跨海桥梁的动力响应进行了研究,如:房忱等[1]以某跨海桥梁为研究背景,分析了不同风、浪、流的JCSS荷载组合作用对跨海桥梁主梁的动力响应,发现采用规则波对波浪进行模拟时,结构响应会被低估;张天昊[2]通过构造风-浪联合功率谱矩阵并自行定义风、浪之间的相关系数,分析了不同相关系数下跨海斜拉桥的动力响应。一些研究者对风、浪荷载作用于车-桥耦合系统的动力响应进行了研究,如:李永乐等[3]在风-车-桥耦合振动体系的基础上,将波浪荷载作为外部荷载输入耦合体系中,计算了风浪作用下的列车与桥梁响应;刘高等[4]基于大系统的思想,建立了车-桥-风浪流耦合动力系统,对风浪流耦合作用下车辆与桥梁的响应进行了分析;FANG等[5]通过观测数据,拟合了1条描述风速和波高的经验曲线,并对风浪作用下的列车-桥梁耦合振动响应进行了分析。但他们均未合理考虑相干风浪之间的联合概率分布。崔圣爱等[6-7]基于Copula分布建立了风浪之间的联合概率模型,对不同重现期风浪作用下的车桥耦合振动响应进行了分析,但其忽视了风、浪时程的随机性。目前,研究中考虑风浪相关性及风、浪随机特性的高速列车-跨海桥梁耦合振动分析很少。
本文基于耿贝尔逻辑模型建立年极值平均风速-有效波高两变量联合分布概率模型,并基于功率谱法生成脉动风风速及随机波波面时程。以某跨海高铁双塔斜拉桥为背景,建立桥梁有限元模型,并考虑梁轨连接关系与轮轨接触关系,考虑轨道不平顺,建立考虑风浪相关性及风、浪随机特性的车-轨-桥耦合模型。分别对单独波浪、单独风、相干风浪联合作用下高速列车通过跨海斜拉桥时的空间振动进行分析,研究有效波高、桥位处水深、风速对车桥动力响应的影响特征,以便为高速列车-跨海桥梁耦合振动分析提供参考。
1 考虑风浪相关性影响的车-轨-桥耦合模型
1.1 风-浪联合概率模型
对于水文和气象条件复杂的海洋环境,风浪之间存在着较强相关性。对跨海桥梁车-轨-桥耦合振动进行分析时,采用合适的联合概率模型合理考虑风浪之间的相关性十分重要。耿贝尔逻辑模型计算过程简洁,使用方便,能合理地描述海洋环境中年极值平均风速和有效波高的联合概率分布[8]。
耿贝尔逻辑模型以标准耿贝尔分布为边缘分布,令U为不同时刻在10 m高度处10 min的平均风速集合,H为对应时刻的有效波高集合,u、h分别为平均风速U、有效波高H集合中的某个元素,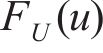
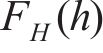
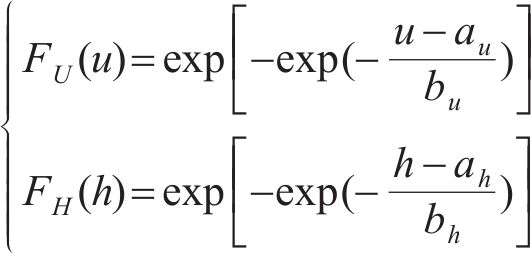
式中: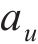
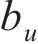
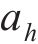
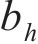
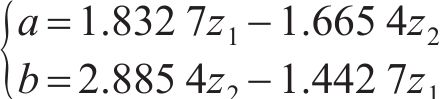
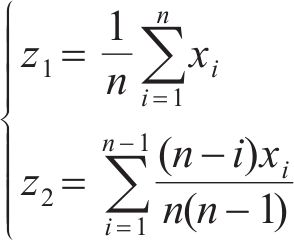
式中:n为样本容量,样本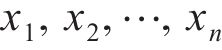
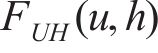
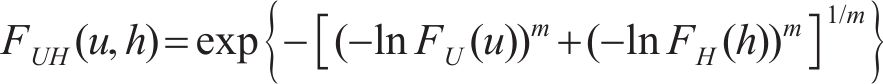
式中:m表示平均风速U和有效波高H之间的相关性,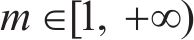
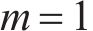
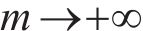
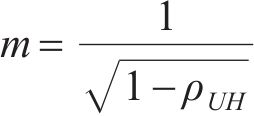
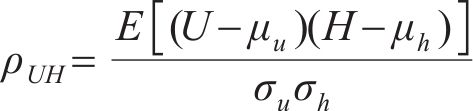
式中: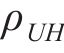
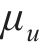
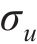
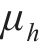
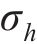
考虑到当风速较大时列车将停止运行,在对风浪联合作用下的车桥振动进行分析时,需要先确定平均风速,再选取相应的有效波高进行组合。而对某一确定平均风速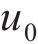
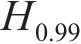
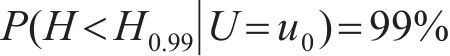
1.2 脉动风及随机波模拟方法
脉动风及随机波的频谱特性可由各自的功率谱密度函数表示。对于海洋风场,其脉动风能量相较于陆地风场在频域上有明显的向低频偏移趋势[2],故研究中通常采用Ochi谱来描述其功率谱密度。功率谱密度函数表达式为
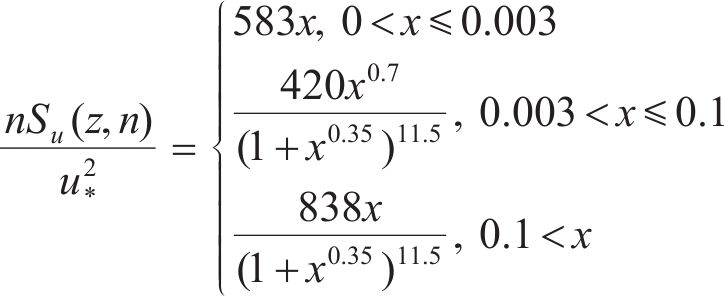
式中: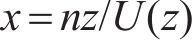
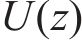
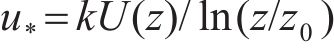
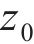
对脉动风场中的多个风速模拟点进行模拟时,空间内任意两点的脉动风速在空间上存在相关性,本文采用Davenport相干函数描述两点间脉动风速的空间相关性,如式(9)所示。
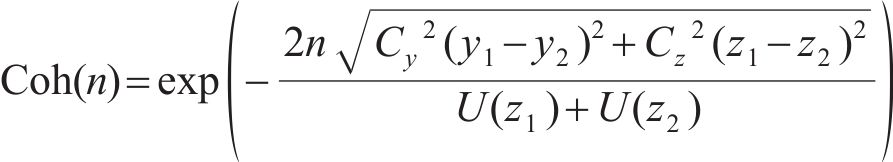
式中: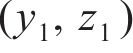
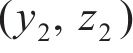
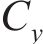
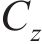
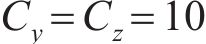
常用的随机波谱为Goda修正的Jonswap谱,则对波面时程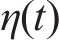
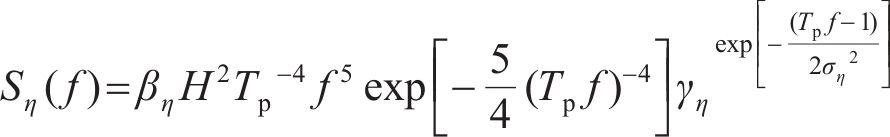
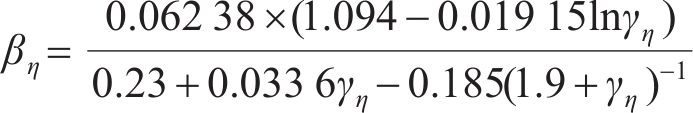
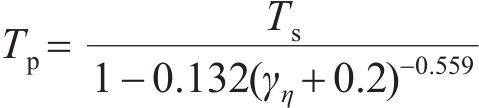
式中: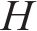
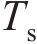
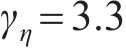
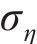
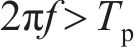
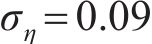
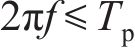
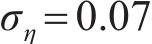
确定平均风速、有效波高后,脉动风及随机波各自的功率谱密度函数将随之确定。本文所确定的平均风速及有效波高之间存在一定相关性,故所模拟的脉动风及随机波之间也存在一定相关性。可采用谱解法由功率谱密度函数对脉动风及随机波进行模拟,以脉动风速时程为例,模拟基本步骤如下。
1) 根据所拟定风速模拟点的数目,构造待计算结构的节点功率谱矩阵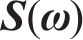
2) 对节点功率谱矩阵进行Cholesky分解,得到一个下三角阵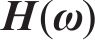
3) 使用谐波合成法对脉动风速时程进行计算,其计算公式为:
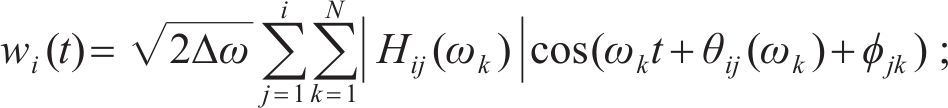
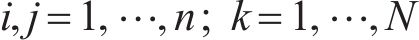
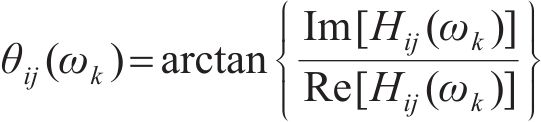
式中: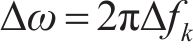
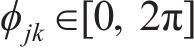
1.3 风、浪荷载计算方法
依据所生成的具有相关性的脉动风及随机波计算结构所受到的具有相关性的风、浪荷载时程。
作用在结构上的风荷载可分为两部分:一部分是由平均风引起的静风力;另一部分是由脉动风引起的抖振力。每一部分力又可分为阻力、升力和力矩。作用在结构单位长度上的静风力可由式(15)~(17)计算。
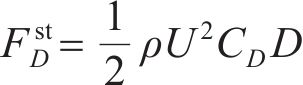
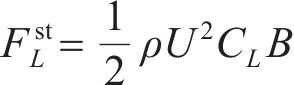
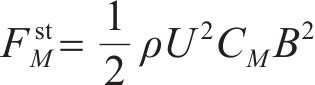
式中:ρ为空气密度;U为平均风速;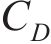
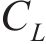
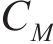
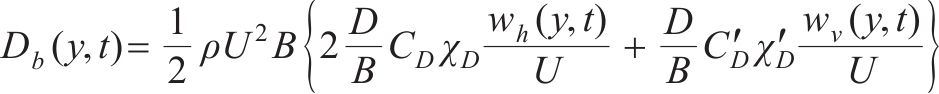
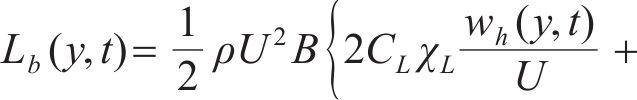
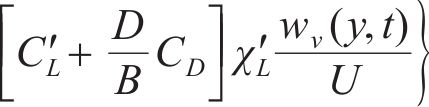
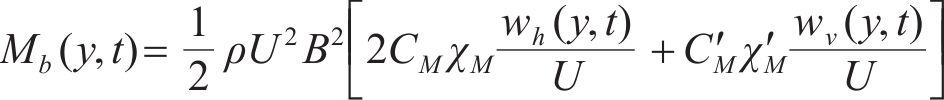
式中: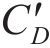
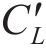
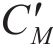
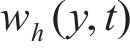
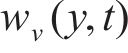
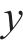
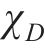
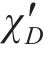
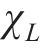
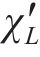
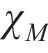
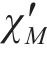
随机波可认为是若干个不同频率、振幅、相位的规则波的组合,则随机波波浪力的计算可拆分为这些规则波波浪力之和[13]。对第i个规则波成分波浪力的计算可分为小尺度结构计算和大尺度结构计算。对于结构尺寸与波长之比小于0.2的小尺度结构,其波浪力主要采用Morison方程计算。将波浪力视为波浪速度引起的阻力和水体加速度引起的惯性力之和[14-15],则作用在小尺度结构单位长度上的波浪力可以由式(21)~(23)计算[11]。
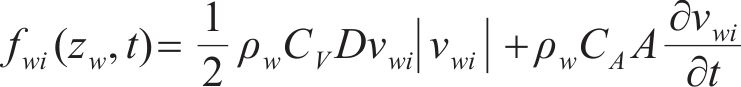
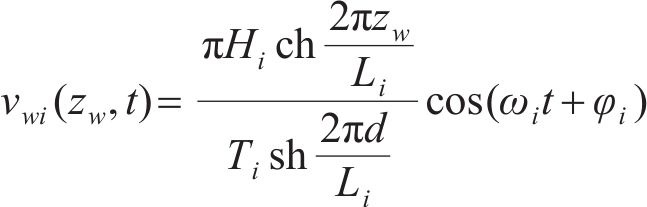
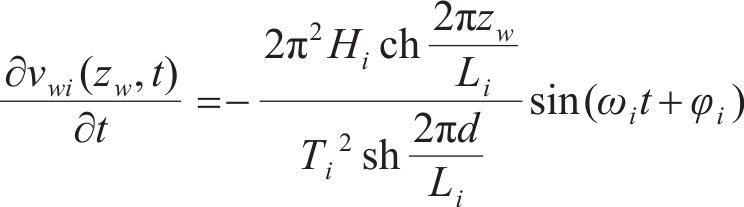
式中: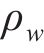
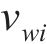
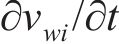
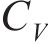

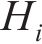
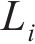
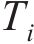
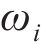
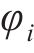
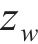
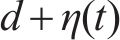
对大尺度结构,需采用绕射理论对波浪力进行计算。当大尺度结构截面为矩形时,第i个规则波成分作用在单位高度矩形柱体上的波浪力可由式(24)计算[16]。
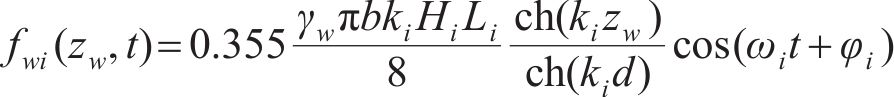
式中: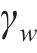
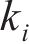
1.4 车-轨-桥耦合模型
采用ANSYS和SIMPACK联合仿真建立车-轨-桥耦合模型。首先,在ANSYS中建立桥梁及轨道有限元模型。将轨道视为若干点支撑的欧拉梁,采用空间梁单元模拟并通过扣件连接于主梁上,采用并联弹簧阻尼单元模拟扣件对梁轨之间的约束关系。在SIMPACK中建立车辆多体动力学模型。将单节列车模型简化为由1个车体、2个转向架和4个轮对组成的多刚体模型,每个刚体考虑伸缩、横摆、浮沉、侧滚、点头、摇头共6个自由度,模型共42个自由度,并将一系悬挂和二系悬挂视为并联的弹簧阻尼[17]。轮轨相互作用考虑轮轨几何接触关系、轮轨法向力和轮轨蠕滑力,其中,轮轨法向力采用Hertz弹性理论[18]计算;轮轨蠕滑力采用Kalker简化理论[19]进行计算。
将ANSYS建立的桥梁及轨道有限元模型通过SIMPACK所预留的程序接口转化为柔性体模型导入SIMPACK中,在主梁和桥塔上每隔一定距离建立固定的标记点(marker),在列车质心位置建立随之运动的移动标记点,通过力元在标记点上施加荷载[20],再通过定义轮轨相互作用和梁轨约束关系将列车、轨道、桥梁进行组装,即组成车-轨-桥整体耦合模型。
2 工程背景及计算条件
2.1 工程概况
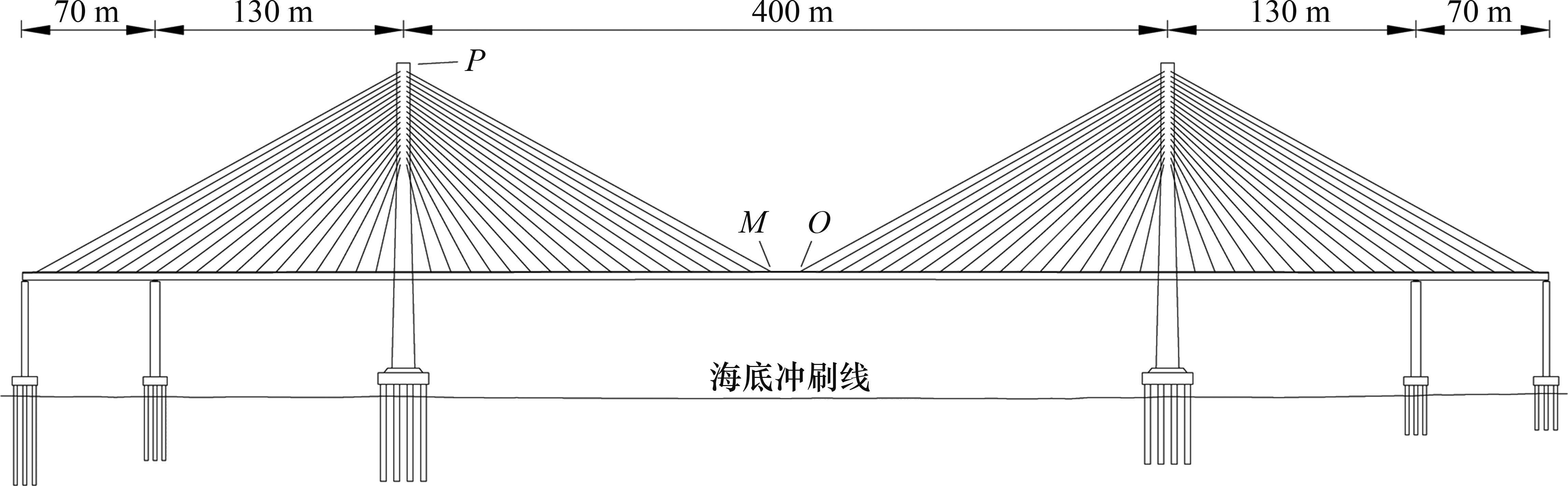
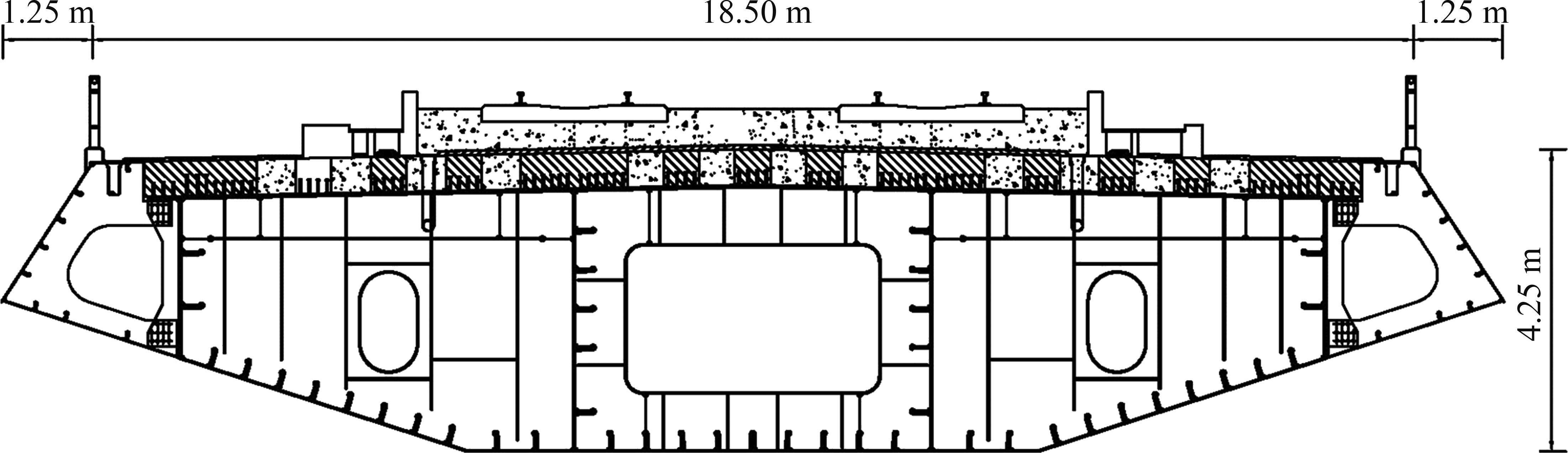
以我国某跨海高铁双塔双索面斜拉桥为例,其主桥跨径布置为(70+130+400+130+70) m,主桥两侧设有辅助墩,塔梁间纵向设置阻尼器,阻尼器具体位置见文献[17],总体立面布置如图1所示。图1中,M、O、P为选取的3个桥梁脉动风速模拟点。主梁采用混凝土桥面板+槽型钢箱梁的钢-混组合梁形式,梁高为4.25 m,梁宽为21.00 m。主梁横截面图如图2所示。桥塔为曲线混凝土H型索塔,塔底以上桥塔全高为160.254 m。全桥共72对斜拉索,采用双索面体系,扇形布置。
桥梁有限元分析模型中主梁、桥塔、桥墩均采用空间梁单元进行模拟,斜拉索采用空间杆单元模拟并依据Ernst公式对拉索弹性模量进行修正,塔梁间纵向阻尼器采用弹簧-阻尼单元进行模拟。对有限元模型进行模态分析可得结构前8阶自振频率及振型形状如表1所示。
| 振型阶次 | 自振频率/Hz | 振型形状 |
|---|---|---|
| 1 | 0.260 | 主梁一阶横弯 |
| 2 | 0.278 | 主梁纵飘 |
| 3 | 0.334 | 桥塔一阶横弯 |
| 4 | 0.348 | 桥塔二阶横弯 |
| 5 | 0.414 | 主梁一阶竖弯 |
| 6 | 0.559 | 主梁二阶竖弯 |
| 7 | 0.773 | 主梁二阶横弯 |
| 8 | 0.822 | 主梁三阶竖弯 |
2.2 车辆及轨道模型参数
模型中车辆采用8节编组模型,编组为(1拖 车+6动车+1拖车),各节车辆刚度、质量、阻尼及几何参数见文献[21]。钢轨采用标准60 kg/m轨,轨距取标准1 435 mm,轨道不平顺采用德国低干扰谱进行模拟,考虑轨道高低不平顺、方向不平顺和水平不平顺。钢轨扣件间距为0.6 m,横向及竖向刚度分别取60 MN/m和120 MN/m,横向及竖向阻尼分别取120 (kN∙s)/m和150 (kN∙s)/m。
2.3 考虑风浪相关性的风、浪荷载计算
依据国家海洋科学数据中心1999—2022年风浪同步观测数据,筛选出年极值平均风速及对应时刻有效波高的子样后,建立平均风速和有效波高两变量联合概率模型。其中,平均风速和有效波高的位置参数分别为21.941 2、2.877 1,尺度参数分别为5.955 5、1.574 3,平均风速和有效波高之间相关性参数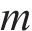
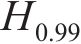
采用脉动风及随机波模拟方法进行模拟,对桥塔及主梁共布设104个风速模拟点,其中主梁72个,位于斜拉索与主梁连接处;桥塔2×16个。风速模拟点之间任意点的脉动风速可由相邻2个模拟点的脉动风速进行线性内插求得[22]。地表粗糙高度z0=0.01 m,频率范围取(0,1) Hz,划分为N=210段。其中,各风速模拟点因距静水面距离z不同,其平均风速则按式(25)计算。
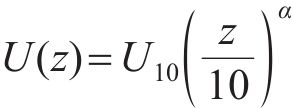
式中: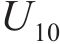
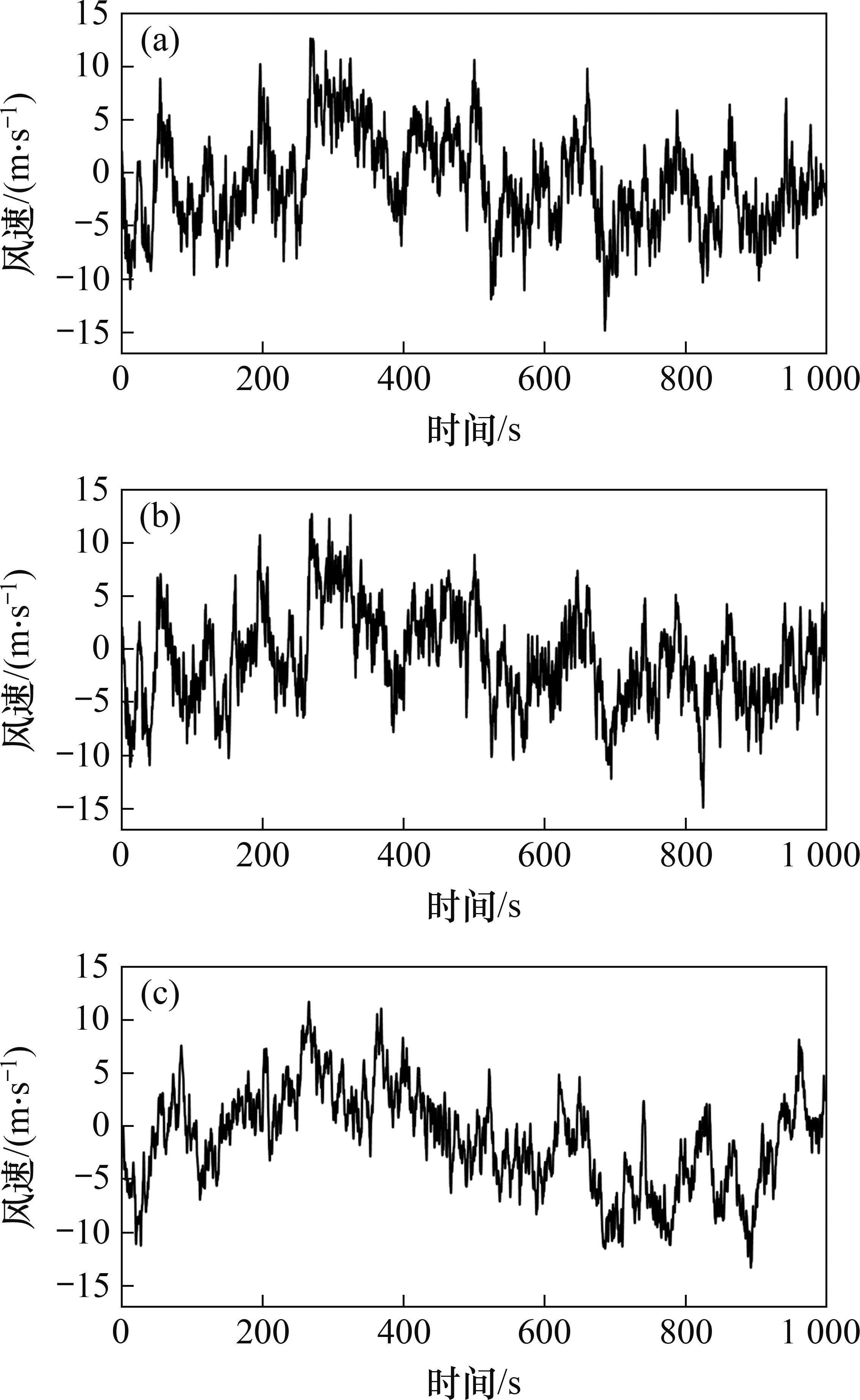
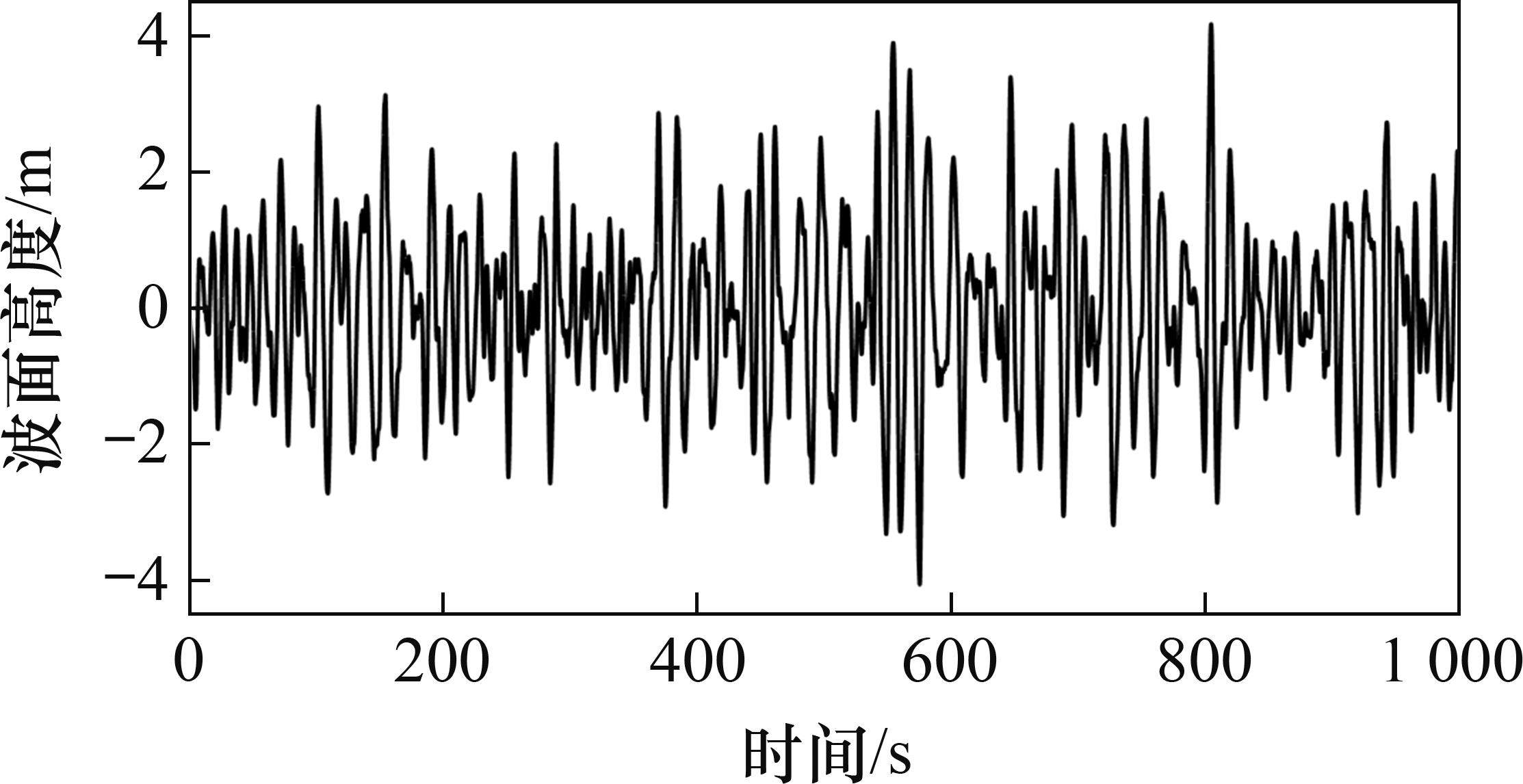
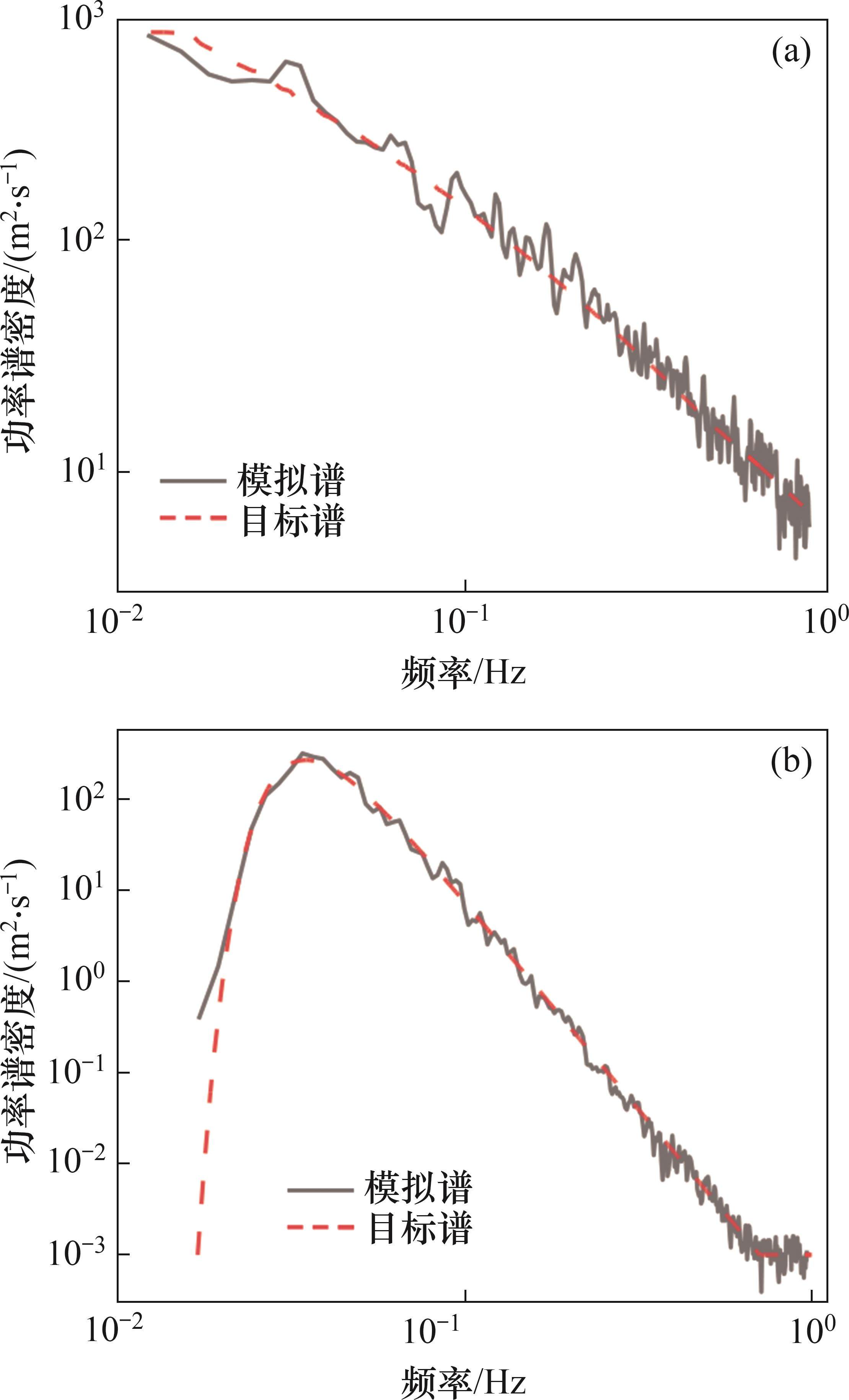
图1中,M、O为距主跨跨中最近的2个风速模拟点,P为左桥塔塔顶处的风速模拟点。模拟平均风速为25 m/s时M、O、P的脉动风速时程曲线如图4所示,有效波高为6 m时桥位处的波面时程曲线如图5所示。对所生成的脉动风速时程及波面时程进行功率谱分析并与目标谱对比,如图6所示。从图6可见:模拟谱与目标谱两者吻合良好,表明所生成的脉动风及随机波满足要求。
列车过桥会使列车所在位置主梁梁段的气动外形发生改变,列车行车位置不同也使得气动外形产生不同的变化,因此,采用CFD对列车位于不同行车位置处时的车、桥气动特性进行分析。当侧风来流方向为从左向右时,令阻力水平向右,升力竖直向上,力矩逆时针方向为正,计算得各个工况下车、桥的气动三分力系数如表2所示。对于桥塔仅考虑阻力系数,其取值为2.0[23]。依据所模拟的脉动风风速时程及随机波波面时程,计算作用在车桥系统上的风、浪荷载时程。
| 类型 | 阻力系数 | 升力系数 | 力矩系数 |
|---|---|---|---|
| 仅主梁 | 0.222 | -0.461 | 0.021 |
| 仅车 | 1.210 | 0.360 | 0.062 |
| 迎风侧行车 | 0.583 | 0.979 | 0.118 |
| 迎风侧行车主梁 | 0.404 | -0.741 | 0.175 |
| 背风侧行车 | 0.396 | 0.892 | 0.031 |
| 背风侧行车 | 0.320 | -1.206 | 0.186 |
3 结果分析
3.1 单独波浪作用下车-轨-桥系统动力响应分析
为研究单独波浪对高速列车通过跨海斜拉桥运行安全性舒适性的影响,对仅考虑波浪作用下的车桥空间振动进行分析,研究有效波高、桥位处水深等参数对车-轨-桥动力响应的影响。
3.1.1 有效波高的影响
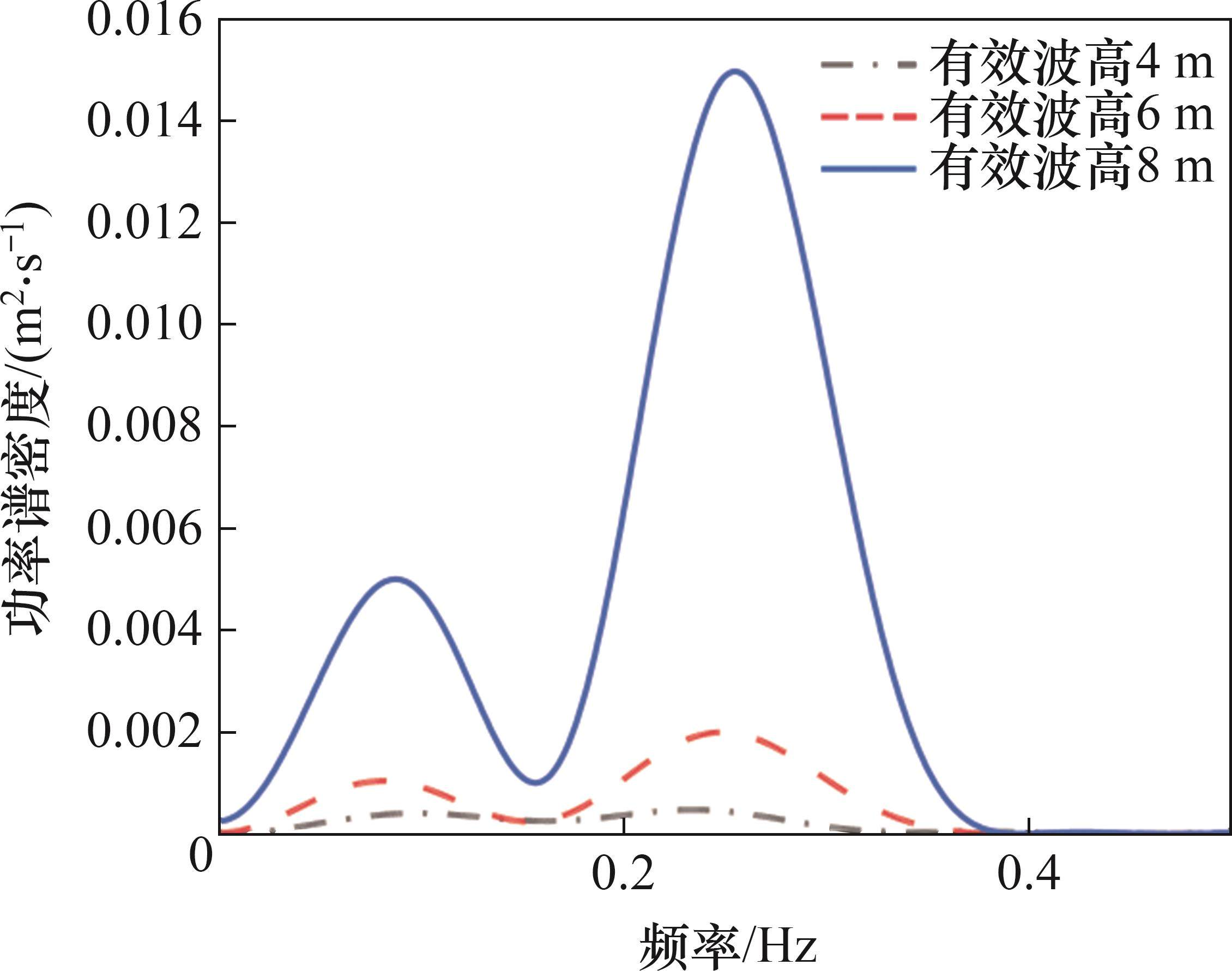
为研究有效波高对车-轨-桥系统动力响应的影响,选定车速为300 km/h,静水面水深为40 m,分别对无波浪(0 m)及4、6、8 m有效波高作用下高速列车通过跨海斜拉桥时的空间振动进行计算分析,4、6、8 m有效波高所对应的有效波周期分别为8.7、10.6、12.1 s。列车、桥梁最大动力响应计算结果见图7。选取主梁跨中横向位移时程进一步进行功率谱分析,结果如图8所示。从图7和 图8可以看出:
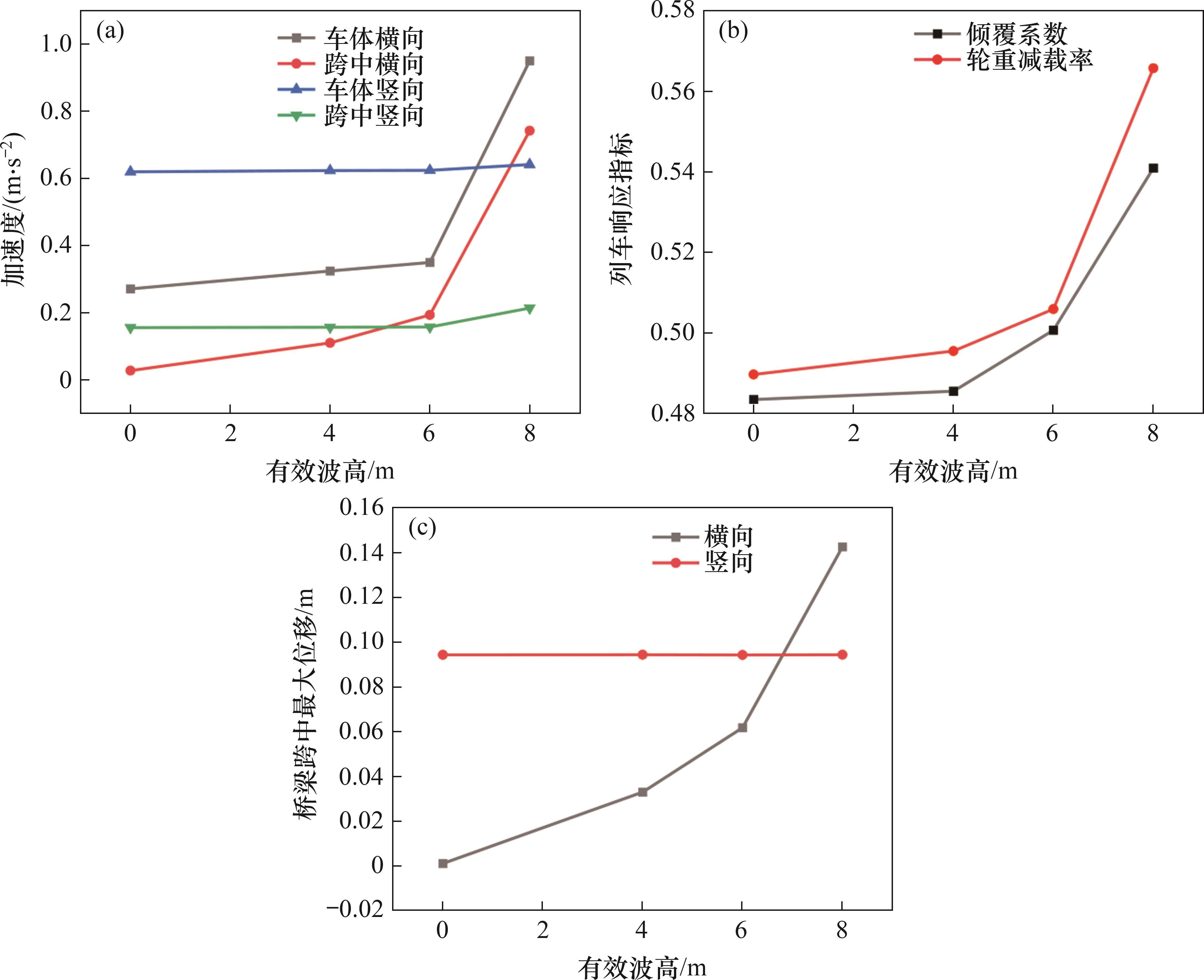
1) 随着有效波高增大,车桥动力响应有所增大,其中,主梁跨中横向位移、横向振动加速度、列车横向加速度、轮重减载率、倾覆系数等增长显著,而主梁跨中竖向振动加速度、列车竖向振动加速度、主梁跨中竖向位移增幅较小。由于波浪荷载为横桥向作用,桥塔产生横向弯曲,主要使主梁产生横向振动。
2) 当有效波高由6 m增大至8 m时,车体及主梁跨中的横向加速度陡增,列车倾覆系数和轮重减载率与无波浪作用时相比分别增大11.9%和15.5%。波浪作用于桥梁下部结构,当有效波高增大时,桥梁所受波浪荷载将呈指数增大,主梁动力响应增幅将越来越大,这表明当波浪荷载较大时,较大的桥梁响应可能对列车运行安全产生较大影响。
3) 主梁跨中横向位移时程主要包含2个频率成分(波浪频率、主梁一阶横弯频率),当有效波高较小时,功率谱密度两峰峰值相近;随着有效波高增大,两峰峰值均有所增大,但主梁一阶横弯频率对应频率成分增长更快,这是有效波高增加导致波浪成分向高频偏移引起的。
3.1.2 桥位处水深的影响
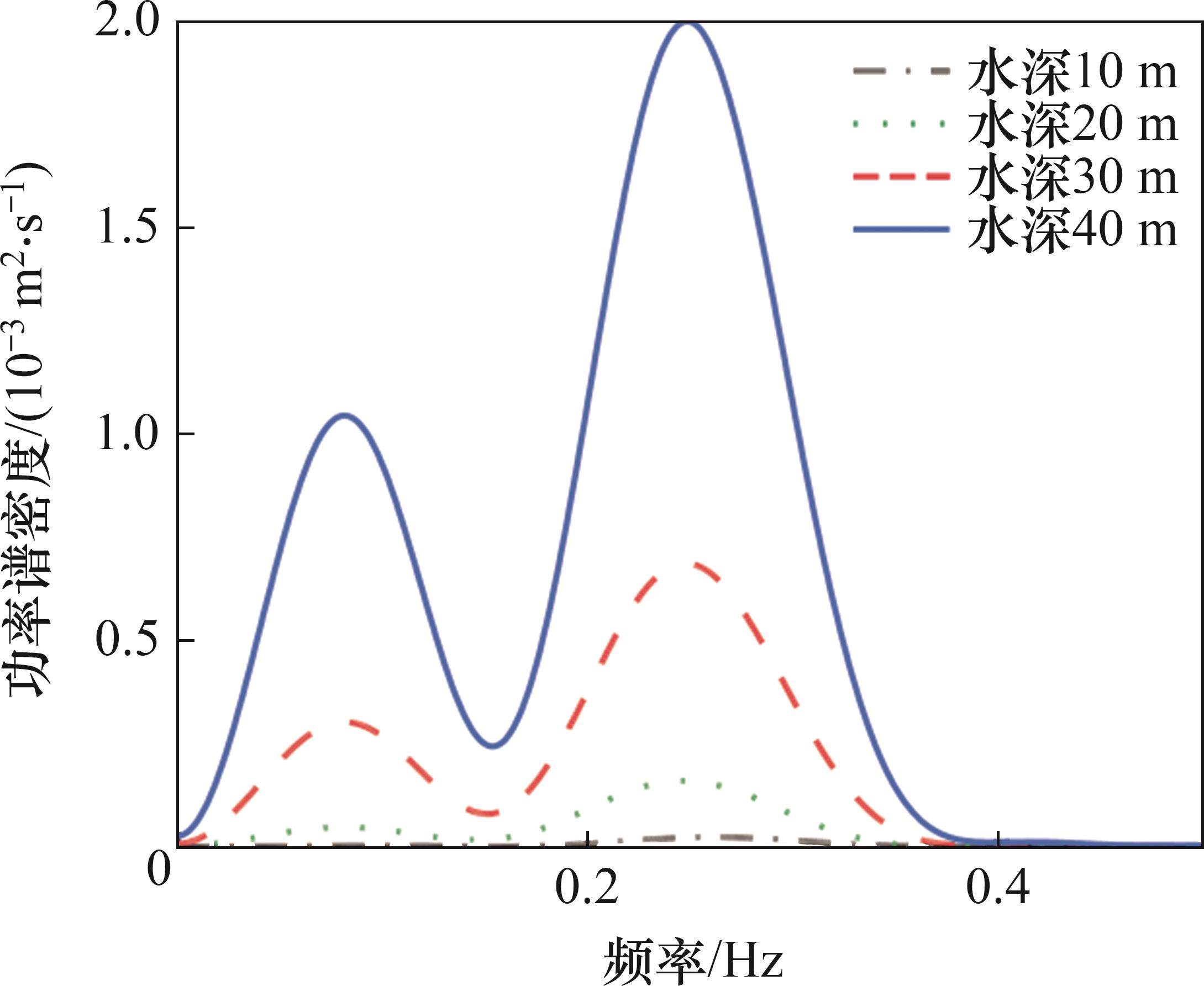
由于波浪仅作用于波面以下的桥梁结构上,为研究波浪作用下桥位处水深对车-轨-桥耦合系统动力响应的影响,选定车速为300 km/h,有效波高为6 m,分别在无波浪(0 m)及10、20、30、40 m水深时对高速列车通过跨海斜拉桥时的空间振动进行计算分析。列车、桥梁最大动力响应计算结果见图9。选取主梁跨中横向位移时程进一步进行功率谱分析,结果如图10所示。从图9和图10可以看出:
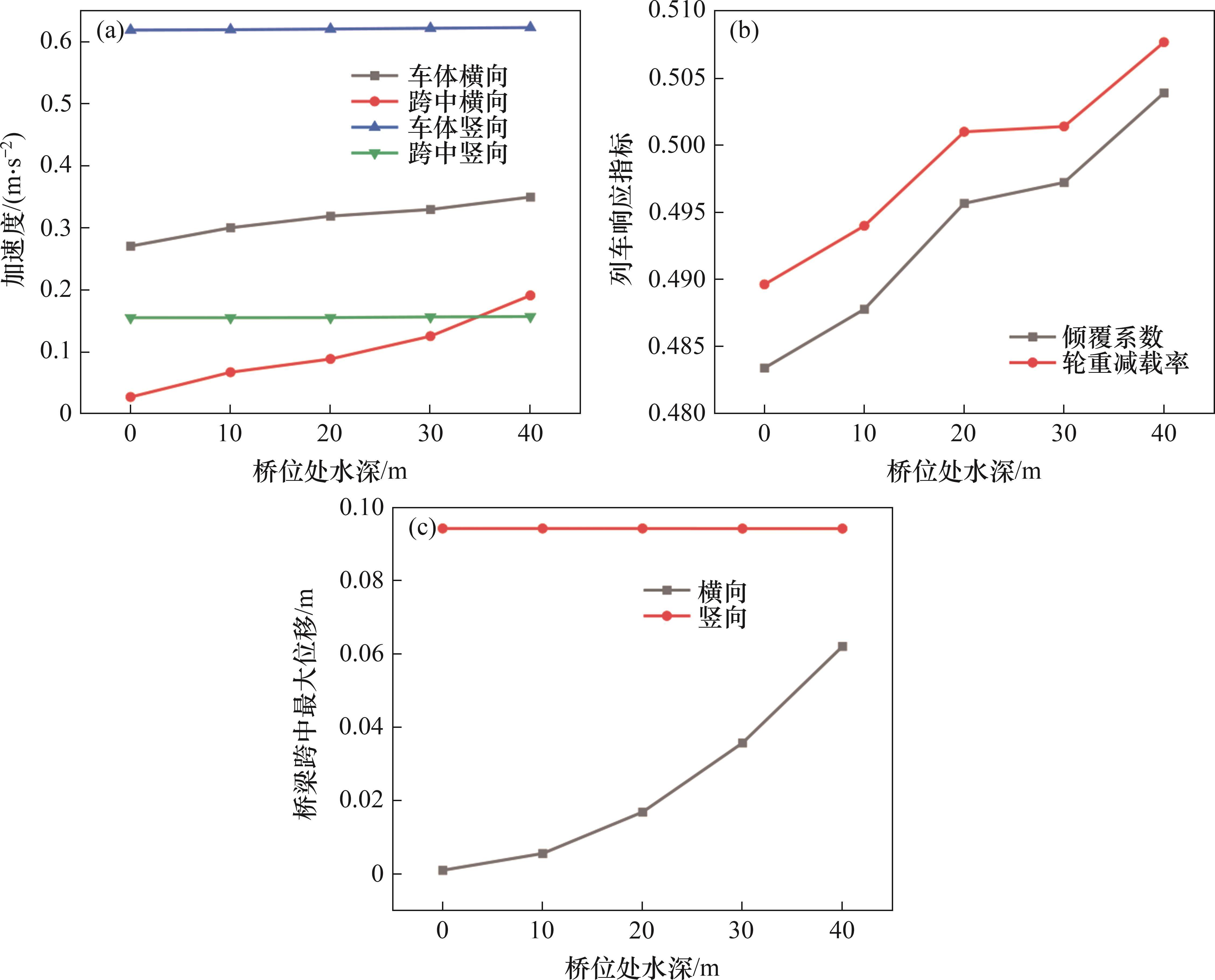
1) 随着水深增大,主梁跨中横向位移、横向振动加速度、列车横向加速度、轮重减载率、倾覆系数等有一定程度增大,但主梁跨中竖向振动加速度、列车竖向振动加速度、主梁跨中竖向位移变化不大。
2) 主梁跨中横向位移时程依然主要包含2个频率成分(波浪频率、主梁一阶横弯频率)。随着水深增大,跨中位移时程中波浪频率对应频率成分与主梁一阶横弯频率对应频率成分的比例基本保持不变,这是由于水深增加对波浪频率成分几乎无影响。
3.2 单独风作用下车-轨-桥系统动力响应分析
为研究单独风作用对车-轨-桥耦合系统动力响应的影响,选定车速为300 km/h,水深为40 m,分别对0、15、20和25 m/s风速下车-轨-桥耦合系统的动力响应进行计算分析。列车、桥梁的最大动力响应结果见表3。从表3可以看出:
| 平均风速/(m·s-1) | 行车 位置 | 脱轨系数 | 倾覆系数 | 轮重减载率 | 列车横向加速度/(m·s-2) | 列车竖向加速度/(m·s-2) | 主梁跨中横向位移/mm | 主梁跨中横向加速度/(m·s-2) | 主梁跨中竖向加速度/(m·s-2) |
|---|---|---|---|---|---|---|---|---|---|
| 0 | — | 0.18 | 0.48 | 0.49 | 0.27 | 0.62 | 0.0 | 0.03 | 0.15 |
| 15 | 迎风侧 | 0.20 | 0.42 | 0.55 | 0.29 | 0.63 | 2.5 | 0.03 | 0.15 |
| 背风侧 | 0.20 | 0.42 | 0.55 | 0.27 | 0.62 | 2.7 | 0.03 | 0.16 | |
| 20 | 迎风侧 | 0.28 | 0.48 | 0.63 | 0.37 | 0.71 | 8.0 | 0.04 | 0.16 |
| 背风侧 | 0.26 | 0.50 | 0.64 | 0.33 | 0.69 | 7.1 | 0.03 | 0.16 | |
| 25 | 迎风侧 | 0.28 | 0.64 | 0.79 | 0.52 | 0.74 | 11.7 | 0.03 | 0.17 |
| 背风侧 | 0.25 | 0.62 | 0.75 | 0.47 | 0.67 | 9.9 | 0.04 | 0.20 |
1) 随着风速增大,列车与桥梁响应均有所增大,且增幅也随着风速的增大而增大。车桥系统所受静风力与风速平方成正比,故随着风速增大,列车与桥梁的动力响应受风荷载的影响更为显著。
2) 当列车分别位于迎风侧或背风侧线路行驶时,由于列车在桥面横向位置不同,对车桥系统三分力系数影响较大,同时,考虑脉动风速及轨道不平顺存在随机性,车桥动力响应最大值有时会出现在迎风侧行车时,有时会出现在背风侧行车时。因此,对车桥振动进行分析时,应考虑列车行车线路对车桥动力响应的影响。
3.3 相干风浪联合作用下车-轨-桥系统动力响应分析
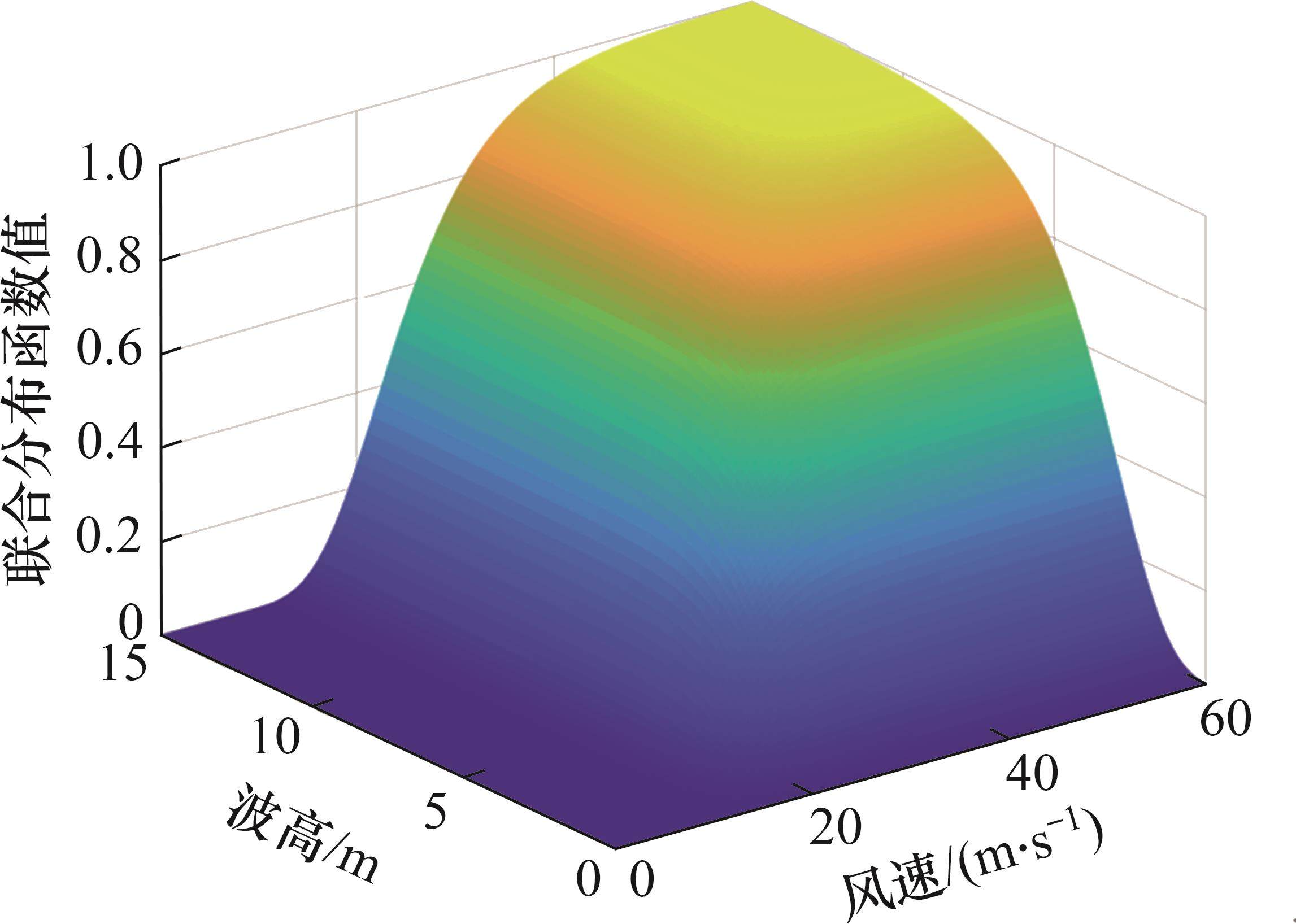
为研究考虑风浪相关性后相干风浪联合作用对车-轨-桥耦合系统动力响应的影响,选定车速为300 km/h,水深为40 m,将15、20、25 m/s的风速与其各自对应的H0.99进行组合,对相干风浪联合作用下的车-轨-桥耦合系统动力响应进行计算分析。列车、桥梁的最大动力响应结果见表4。从表4可以看出:考虑相干风浪联合作用后,除列车竖向振动加速度保持基本不变外,列车和桥梁其他响应均有所增大,且随着风速的增大,动力响应的增长幅度更加明显。其中,当风速为25 m/s时,在相干风浪联合作用下,列车的最大轮重减载率为0.89,已超出安全限值标准0.80。若不考虑风浪相关性,采用百年一遇的有效波高与各风速直接组合,对风浪联合作用下车轨桥系统动力响应进行分析,则列车、桥梁的动力响应明显被高估。为更真实地模拟风浪联合作用对车桥动力响应的影响,在选取风速与波高进行动力响应分析时应考虑风浪之间相关性。
| 平均风速/(m·s-1) | 行车 位置 | 脱轨系数 | 倾覆系数 | 轮重减载率 | 列车横向加速度/(m·s-2) | 列车竖向加速度/(m·s-2) | 桥梁跨中横向位移/mm | 桥梁跨中横向加速度/(m·s-2) | 桥梁跨中竖向加速度/(m·s-2) |
|---|---|---|---|---|---|---|---|---|---|
| 15 | 迎风侧 | 0.21 | 0.45 | 0.56 | 0.36 | 0.63 | 64.3 | 0.18 | 0.16 |
| 背风侧 | 0.20 | 0.45 | 0.56 | 0.35 | 0.62 | 64.5 | 0.18 | 0.17 | |
| 20 | 迎风侧 | 0.28 | 0.49 | 0.63 | 0.41 | 0.71 | 66.7 | 0.19 | 0.16 |
| 背风侧 | 0.26 | 0.52 | 0.66 | 0.38 | 0.70 | 66.0 | 0.19 | 0.16 | |
| 25 | 迎风侧 | 0.36 | 0.70 | 0.89 | 1.33 | 0.73 | 151.4 | 0.80 | 0.20 |
| 背风侧 | 0.31 | 0.67 | 0.84 | 1.30 | 0.67 | 150.5 | 0.80 | 0.22 |
4 结论
1) 波浪力为横向作用力,主要影响列车和桥梁的横向动力响应,对竖向动力响应的影响较小。
2) 随着有效波高及桥位处水深增大,波浪作用致使列车和桥梁动力响应随之增大,且增幅也越来越高。当波高较大时,有效波高是影响车桥系统动力响应的主要因素;当波高较低时,桥位处水深及有效波高对车桥动力响应的影响相当。
3) 在波浪作用下,主梁跨中横向位移时程主要包含波浪频率和主梁一阶横弯频率两个频率成分,随着有效波高增大,主梁一阶横弯频率成分占比越来越大,桥位处水深对两频率成分所占比例的影响很小。
4) 随着平均风速增大,列车与桥梁动力响应有所增大。当列车行车线路位于桥面不同横向位置时,车桥系统三分力系数影响较大。考虑脉动风速及轨道不平顺存在随机性,车桥动力响应最大值有时会出现在迎风侧行车时,有时会出现在背风侧行车时,因此,对车桥振动进行分析时,应考虑列车行车线路对车桥动力响应的影响。
5) 与单独风作用相比,考虑风浪联合作用后,车桥系统动力响应明显增大。为更真实模拟风浪联合作用对车桥动力响应的影响,在选取风速与波高进行动力响应分析时,应考虑风浪之间的相关性。
蔡宝锋, 谌启发, 郭文华, 等. 考虑风浪相关性影响的高速列车-轨道-跨海斜拉桥时变系统动力响应分析[J]. 中南大学学报(自然科学版), 2025, 56(2): 598-609.
CAI Baofeng, CHEN Qifa, GUO Wenhua, et al. Dynamic response analysis of time-varying system of high-speed train-track-sea-crossing cable-stayed bridge under the action of related wind and wave[J]. Journal of Central South University(Science and Technology), 2025, 56(2): 598-609.

