斜拉桥是大跨桥梁常用桥型。对300~500 m中等跨度斜拉桥,双索面能有效约束主梁扭转,因此即使采用开口截面主梁,比如Π形截面双边钢板梁或双边钢箱梁,斜拉桥也具有较大的扭转刚度。Π形开口截面钢-混组合主梁能充分发挥钢和混凝土材料各自的优点,使得桥梁结构受力合理、施工方便和经济性好。因此,国内外很多斜拉桥采用了这种主梁形式。与流线化特征较好的扁平闭口箱梁相比,Π型开口截面是一种极其典型的钝体截面,流动在主梁迎风侧的上缘和下缘分离,两边梁之间的区域为大的回流区,且流动还可能在主梁的后缘上方和下方再次分离,形成桥梁断面周围极为复杂的流动分离场和涡系作用。通常情况下,气流流经结构后形成的旋涡脱落频率满足如下关系式:
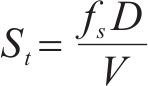
式中: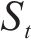
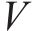
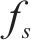
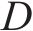
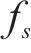
需指出,对采用Π形开口截面主梁的斜拉桥,其抗风往往是此类桥梁设计的关键之一[6],因此,国内外学者开展了大量研究。SAKAI等[7]的风洞试验表明在边主梁断面最外侧布设水平分流板(Tip plate)能改善此类主梁的颤振和涡振性能,机理是分流板能明显抑制主梁前缘的流动分离。KUBO等[8]的风洞试验研究有无桥面栏杆的双边工字钢主梁的涡振稳定性,发现将两侧工字钢纵梁横桥向相互靠近,增大桥面板悬挑长度,可明显降低涡振幅值,但这种布置不一定有利于索梁传力。MURAKAMI等[9]对比了双边工字钢主梁底部布设2种高度纵隔板的涡振性能,发现纵隔板高度大的主梁抗涡振性能改善,作用类似于下稳定板。张天翼等[10]的风洞试验尝试了12种气动措施以抑制盐坪坝长江大桥双边箱主梁的涡振,并在边箱外侧下方安装三角形风嘴并组合防撞栏封闭的方案抑制涡振。贺耀北等[11]发现封闭中央防撞栏的涡振抑制效果不明显,而上中央稳定板高度要达2.5 m以上才能抑制涡振;但如主梁上下各设一道稳定板加人行栏杆局部封闭,能明显抑振主梁涡振。王峰等[12]发现倒L型导流板能改善Π型断面涡振性能,并研究了倒L型导流板尺寸变化对涡振的抑制。WANG等[13]研究了主梁发生弯扭耦合时的涡振特性,并给出了相应的抑振措施。黄林等[14]对发生显著涡振的Π型叠合主梁,分别试验了中央稳定板、工字梁下缘外侧设置的外倾导流板,以及二者组合对涡振的控制,发现导流板对涡振有显著影响,如组合中央稳定板能较好地抑制主梁涡振。董佳慧等[15]研究了不同气动措施对Π型钢-混组合梁斜拉桥涡振的抑制作用,表明整流罩与下中央稳定板的组合能显著降低竖弯和扭转涡振振幅。刘志文等[16]通过改变稳定板和裙板的组合来控制Π型截面主梁的涡振。李春光等[17]的风洞试验表明风嘴和稳定板均可抑制涡振。宋玉冰等[18]研究了宽幅Π型桥梁断面的涡振特性和抑制气动措施,表明倒L形裙板均能显著抑制竖向和扭转涡振。李震等[2]的风洞试验研究了Π型开口截面斜拉桥的涡振性能,并测试了下稳定板、导流板和变化检修车轨道位置等典型气动措施的抑振效果,表明安装下稳定板可有效抑制竖弯涡振,如组合导流板可进一步提高涡振抑制能力。雷伟等[19]开展了主跨520 m的Π型双边工字梁钢混组合主梁斜拉桥1∶25的大比例节段模型试验,尝试了工字梁下翼缘外侧不同长度和倾角的导流板的涡振抑制作用,发现与水平面成35°的1.5 m长导流板,能有效抑制桥梁的竖弯和扭转涡振,实际上该导流板导流机理与风嘴类似。现有研究虽开展了不少开口截面主梁的涡振研究,但这些涡振抑制气动措施对此类桥梁颤振稳定性和气动力的影响报道较少,且与常规斜拉桥相比,本文中桥梁为独塔部分地锚式斜拉桥,跨度大,结构极为复杂。为保证该大桥抗风安全,有必要对其开展风洞试验研究,通过风洞试验研究气动措施以有效抑制其涡振,并评估这些气动措施对桥梁气动特性和颤振稳定性的影响。
1 工程概况
某大桥为独塔部分地锚式混合主梁斜拉桥,主跨和边跨跨度分别为340 m和139 m。主跨采用Π型开口截面双边钢箱钢-混组合主梁,其中边箱宽2 m、高3.5 m,通过纵桥向间距2 m的钢横梁和边钢箱上翼缘上布置剪力钉,与26 cm厚混凝土桥面板组合形成钢-混组合主梁,上铺10 cm沥青混凝土铺装,主梁全宽29.5 m,梁高3.5 m。边跨主梁为预应力混凝土Π型双边主肋截面,如图1所示。索塔横桥向为H形,布设空间双索面,主跨和边跨各布置27对拉索,其中主跨斜拉索梁端锚固间距12 m,由边箱外腹板上伸与锚拉板相连。边跨岸侧16对斜拉索锚固在地锚桥台上,间距2.3 m,索塔侧11根斜拉索锚固在混凝土主梁的齿块上,纵向锚固间距8 m,形成斜拉索部分地锚结构。在索塔顺桥向中心线处设置2根竖直0号拉索支承主梁。斜拉索采用强度等级为1 860 MPa的预制高强平行钢丝。桥面布置SAM级的中央防撞栏和HA级的路侧防撞栏,并在检修道外侧布置护栏。
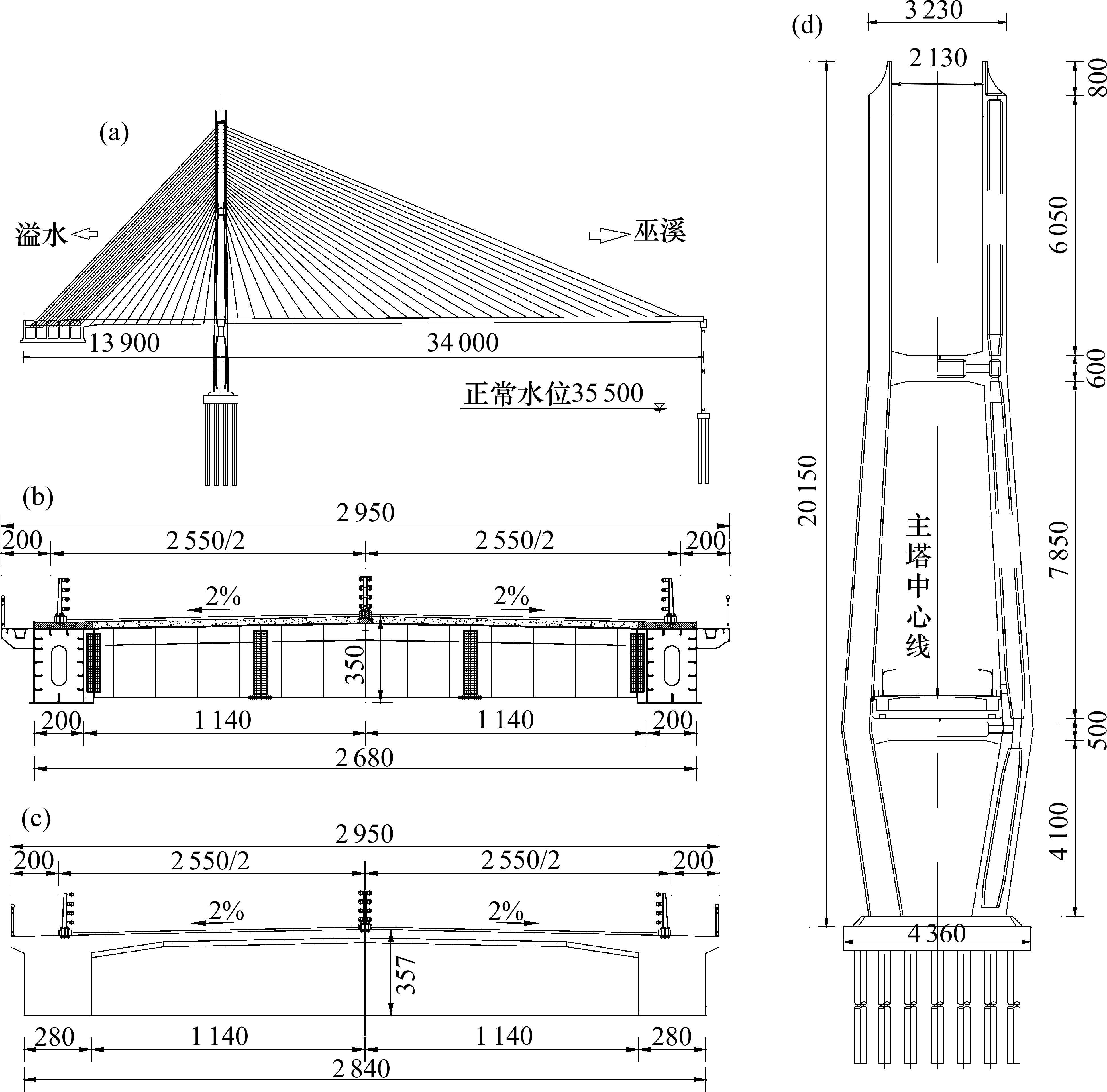
根据全国基本风速分布图[20],100年重现期桥位基本风速为26 m/s,桥址处为B类地貌,抗风风险区域等级为R2。在成桥状态,由规范[20]计算得到主梁基准高度处设计基准风速为35.7 m/s。
2 节段模型设计
2.1 全桥动力特性分析
大跨桥梁涡振和颤振等风洞测振试验需要制作节段模型。节段模型需模拟实际桥梁的动力特性,因此全桥动力特性分析是获得桥梁振动频率和模态,进而开展节段模型测振试验的基础。本文采用大型有限元分析软件ANSYS建立大桥空间有限元模型。主梁采用单主梁模式,并处理为桥中线处的单根脊梁和水平向垂直该主梁的横鱼骨,主梁、横鱼骨均用Beam188三维梁单元模拟。主梁轴向刚度、弯曲刚度、扭转刚度和剪切刚度均集中到脊梁上,因主梁为钢-混组合梁,根据抗弯刚度等效将混凝土桥面板等效为等宽的一定厚度的钢板;又因开口截面的约束扭转刚度不可忽略,为此计算了等效截面的抗弯刚度、自由扭转和约束扭转刚度,并将自由扭转和约束扭转刚度之和视为截面扭转刚度。脊梁每个节点通过与脊梁垂直的2根刚臂横鱼骨与索单元相连。主梁一期和二期恒载分配到脊梁单元的两端节点上,通过集中质量单元(Mass21)来模拟其平动质量和转动惯量。另外,主塔采用Beam4梁单元模拟;斜拉索采用Link10单元模拟,并考虑垂度效应的影响通过Ernst公式修正斜拉索的弹性模量。不考虑桩土相互作用,即塔底、墩底和承台底均为固结,索塔与主梁处横向抗风支座、过渡墩与主梁连接处单向支座、横向支座均采用Combin14单元模拟。动力特性计算了大桥前40阶振型,表1给出了大桥前4阶模态的频率和振型;可见第1阶模态为主跨主梁1阶正对称竖弯,频率0.3 Hz;主梁第1阶扭转模态是全桥第4阶模态,呈正对称,频率0.526 Hz,明显高于第1阶竖弯频率,对应的扭弯频率比为1.75,说明主梁即使采用开口截面,其抗扭刚度也明显高于竖弯刚度,这表明空间双索面为主梁提供了强大的抗扭刚度。主梁振动主导的模态表现为主跨的明显振动,表明边跨PC主梁刚度大,且未见索塔的顺桥向振动,表明地锚桥台通过背索有效地锚固了索塔。与涡振和颤振相关的第1阶竖弯和第1阶扭转模态如图2所示。
模态 序号 | 频率/ Hz | 振型 | 模态质量 | |||
|---|---|---|---|---|---|---|
| mx/(t∙m-1) | my/(t∙m-1) | mz/(t∙m-1) | Jx(t∙m2∙m-1) | |||
| 1 | 0.300 | 主跨主梁1阶正对称竖弯 | 1.99×105 | 4.83×101 | 2.82×1013 | 1.47×1017 |
| 2 | 0.413 | 索塔塔柱同向横弯 | 3.09×1017 | 6.75×1012 | 2.66×102 | 8.46×106 |
| 3 | 0.507 | 主跨主梁1阶反对称竖弯 | 4.15×106 | 4.84×101 | 1.08×1012 | 3.17×1014 |
| 4 | 0.526 | 主跨主梁1阶正对称扭转 | 1.76×1017 | 1.46×1012 | 1.08×103 | 4.25×103 |
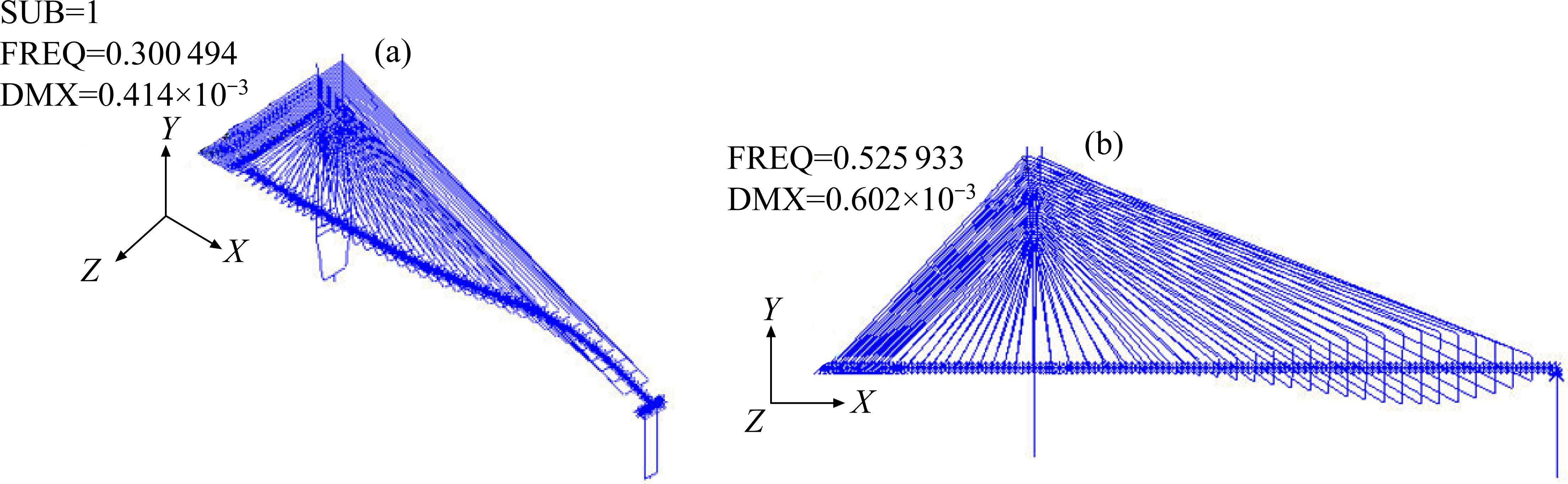
2.2 节段模型设计
桥梁节段模型涡振试验需模拟竖向和扭转2个自由度的振动特性,且需严格模拟其气动外形、涡振相关模态的广义质量和频率特性。表1给出了前4阶模态对应的模态质量。根据实桥主梁断面尺寸、风洞试验段尺寸(宽5.7 m、高2 m)和试验其他考虑,涡振试验节段模型缩尺比为1∶50,对应节段模型长、宽和高分别为1.6,0.59和0.07 m,因节段模型长宽比大于2.5,满足节段模型风洞试验对模型长宽比的要求,且因风洞试验段尺寸大,在±5°风攻角范围对应的模型堵塞度少于1%,试验结果无需堵塞度修正。主梁模型为刚体,由铝合金骨架保证刚性,轻质木板外表模拟主梁外形,防撞栏及栏杆用ABS塑料板雕刻制成,模型两端设置端板以维持模型端部的二元流特性。
根据模型缩尺比和相似率,计算得到节段模型单位长度等效质量为19.34 kg/m,等效质量惯性矩为0.68 kg∙m2/m,并确定涡振试验和颤振试验的风速比分别为1∶3和1∶5,结合模型缩尺比,计算得到模型的涡振第1阶竖弯和第1阶扭转频率分别为5 Hz和8.77 Hz,模型的颤振第1阶竖弯和第1阶扭转频率分别为3 Hz和5.26 Hz。节段模型由8根弹簧悬挂于汕头大学边界层风洞试验段内,通过调节弹簧刚度和力臂调整节段模型的竖弯刚度和扭转刚度,并组合节段模型质量和质量惯性矩调整实现节段模型目标频率。通过布置在弹簧中部的钢丝圈和电工胶带调节节段模型系统的阻尼,如图3所示。节段模型响应由数据采集仪采集4个激光位移计响应,激光位移计对称布置在节段模型的两端和上下游侧,系统采样频率200 Hz,采样时长60 s。

3 原主梁涡振及其气动改进试验
本桥为混合主梁,从动力特性分析可知,大桥第1阶竖弯和扭转模态是主跨主梁主导的振动,根据规范[20],阻尼比可取1%,为此,调节节段模型及悬挂系统的竖弯和扭转阻尼比,使其均为1%。由规范[20]计算的实桥竖向涡振位移限值为
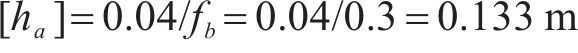
而规范扭转涡振位移限值为
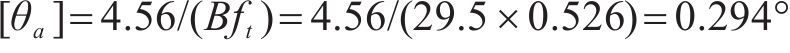
3.1 原主梁断面
针对原设计主梁标准断面(后简称原主梁断面),开展了风攻角±3°范围的涡振试验,结果如图4所示。可见实桥风速低于10.0 m/s,未见主梁涡振,但风速增大到12.0 m/s,节段模型在竖向出现明显振动,并随风速增大振动越趋明显,在15.0 m/s达到峰值0.2 m,明显高于规范竖弯涡振限值。此时以模型宽度为特征尺度根据式(1)计算得到的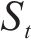
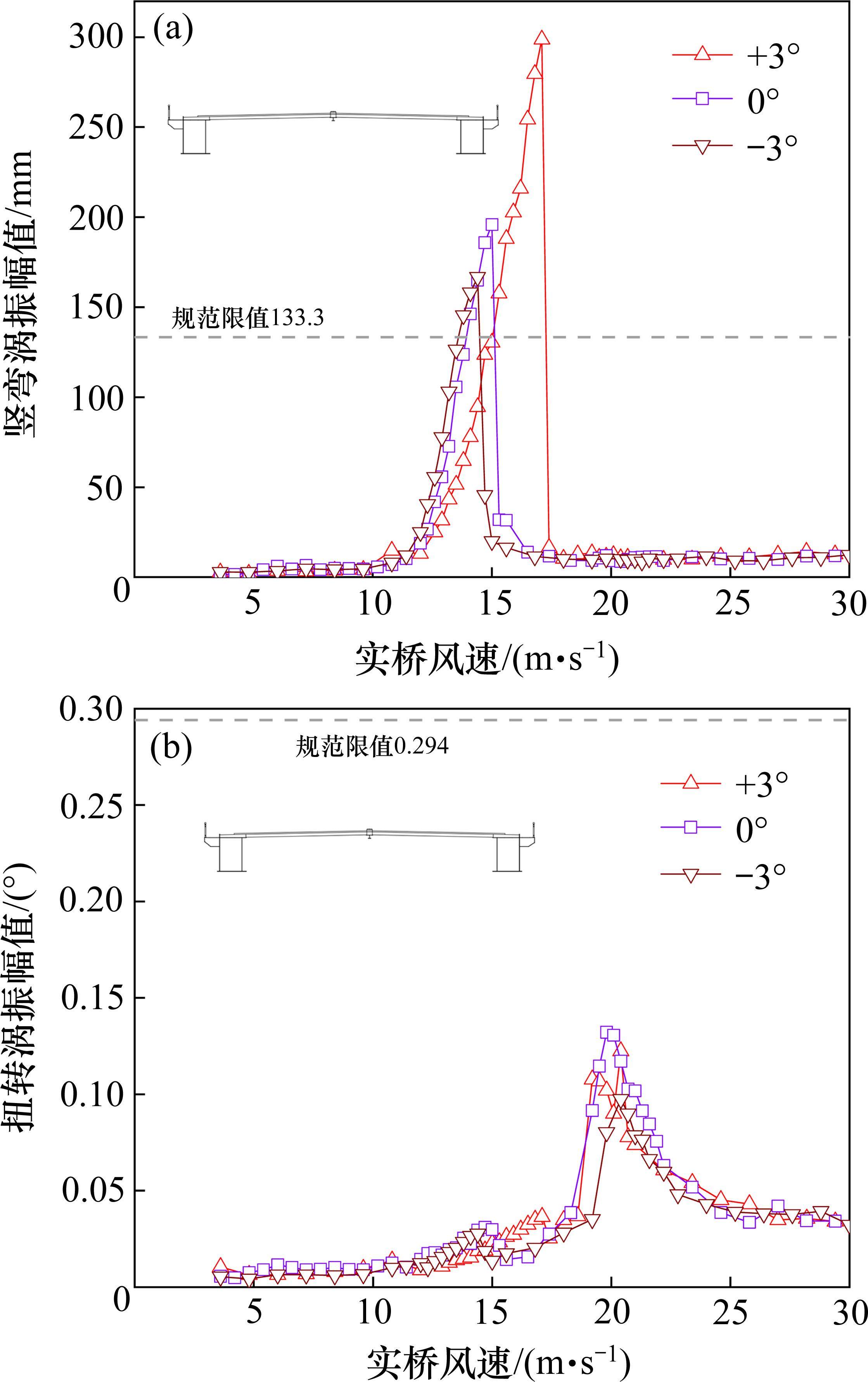
如风速再增大,竖向涡振振幅快速减小,并在大于16.0 m/s风速后竖弯涡振消失。当风速增大到17.0 m/s后,出现了明显的扭转涡振,并在19.8 m/s风速后达到峰值0.13°,但该峰值低于规范限值。此时以模型宽度为特征尺度根据式(1)计算得到的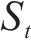
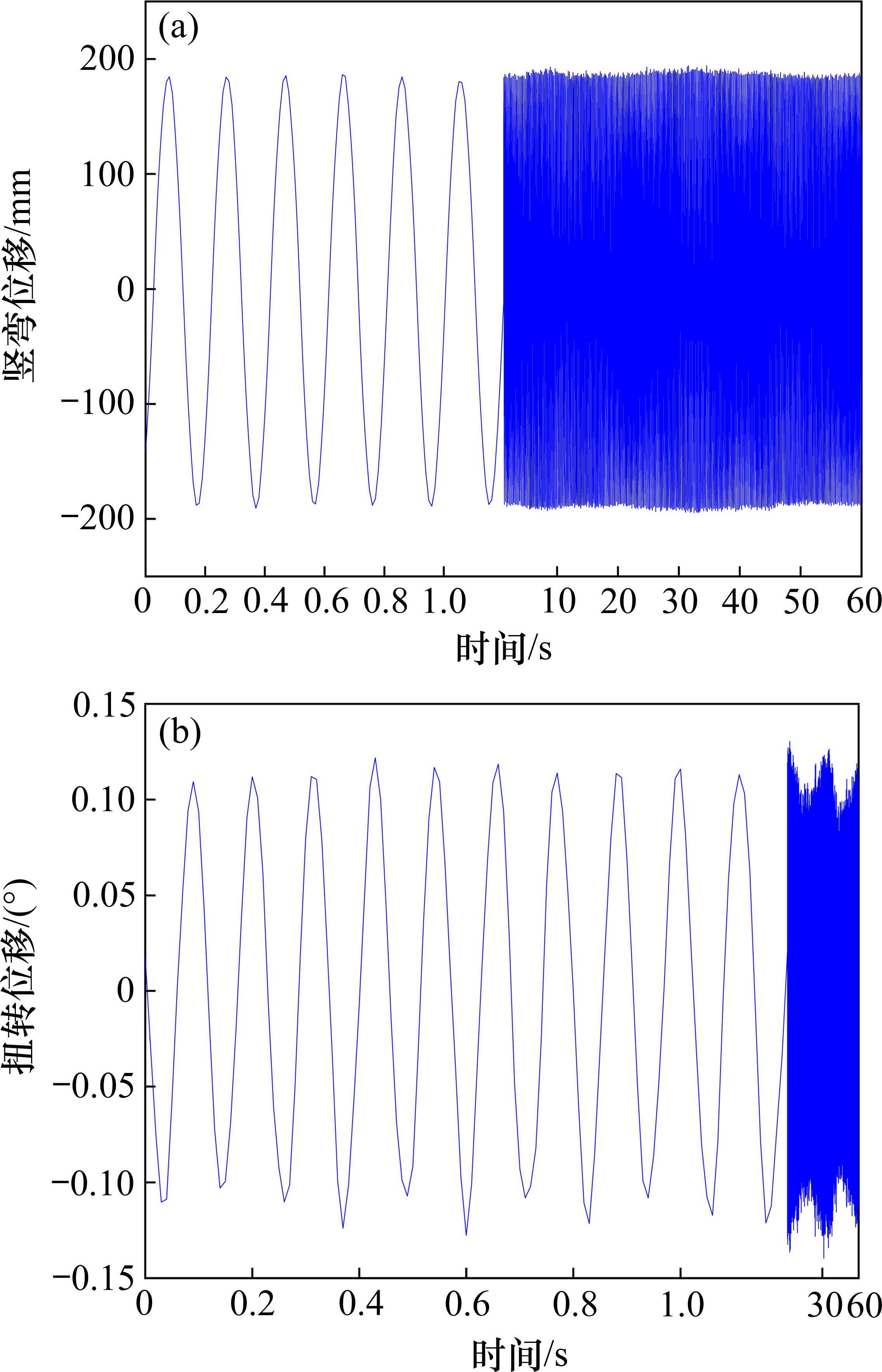
风攻角-3°,实桥风速12~15.6 m/s范围内可见竖弯涡振,在风速19.8~22.8 m/s范围内可见扭转涡振,虽扭转涡振幅值在规范限值内,但竖弯涡振幅值超出规范要求。另外,风攻角+3°,实桥风速12.6~17.4 m/s范围内可见明显的竖弯涡振,风速19.2~21 m/s范围内可见扭转涡振,同样,虽然扭转涡振幅值没有超出规范限值,但竖弯涡振幅值大大超出规范要求。
从风攻角±3°范围内的涡振试验来看,在实桥设计风速范围内,原主梁断面均发生了明显的竖弯和扭转涡振,且竖弯涡振幅值明显超出规范要求。基于这一考虑,本文没有开展原主梁更大风攻角下的涡振试验。从桥梁抗风安全的角度,需采取措施抑制桥梁涡振,本文尝试多种气动措施来消除或减小桥梁涡振幅值,使其满足规范对桥梁抗涡振的要求。
3.2 增设下稳定板
为改善原主梁断面的涡振性能,本文在原主梁断面下方设置下稳定板,为便于桥梁检修车通行,稳定板高度与横梁等高,横桥向布置见图6(a),横梁腹板上的竖向加劲肋同时充当下稳定板的节点板,通过普通螺栓固定下稳定板。
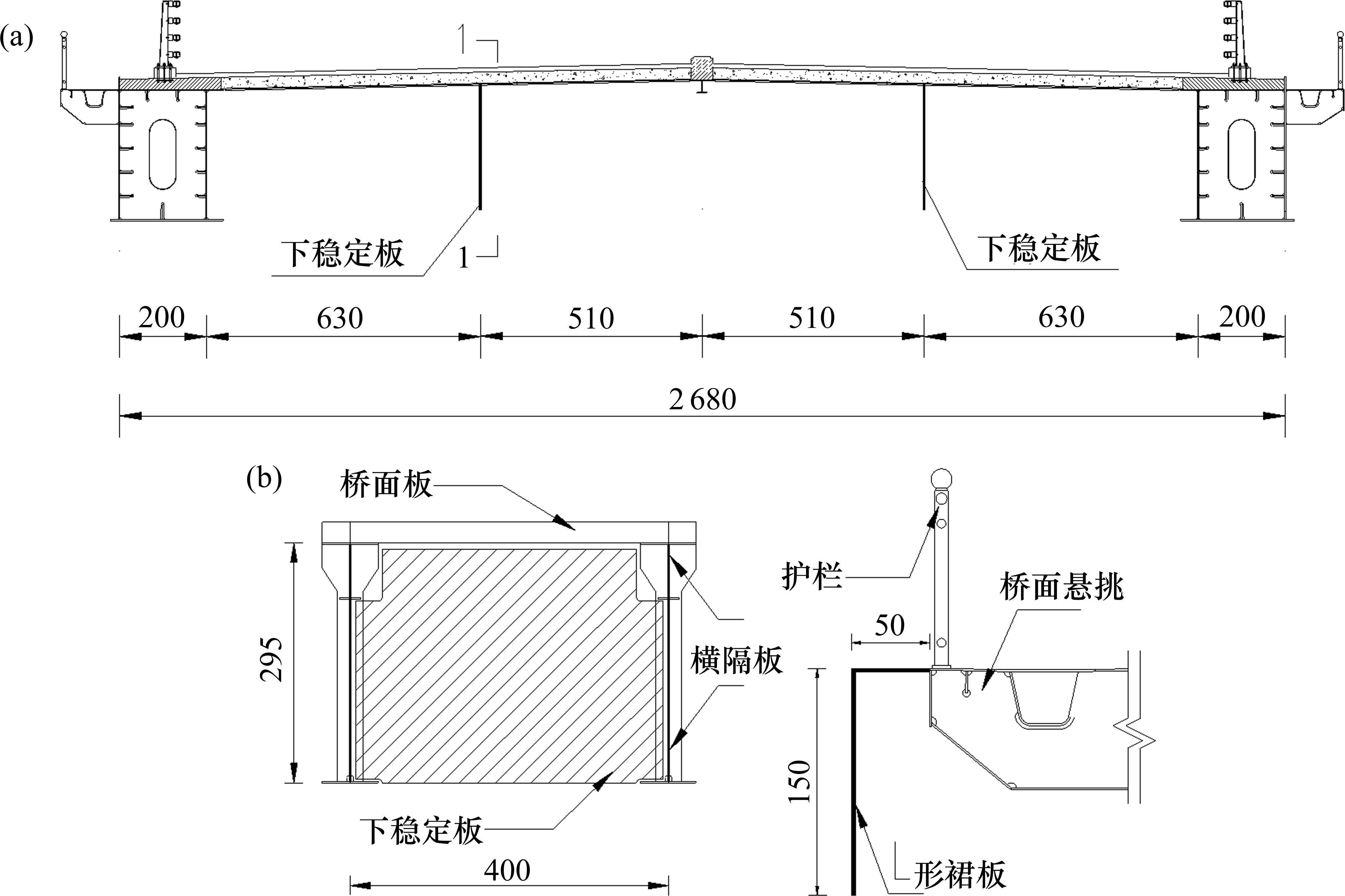
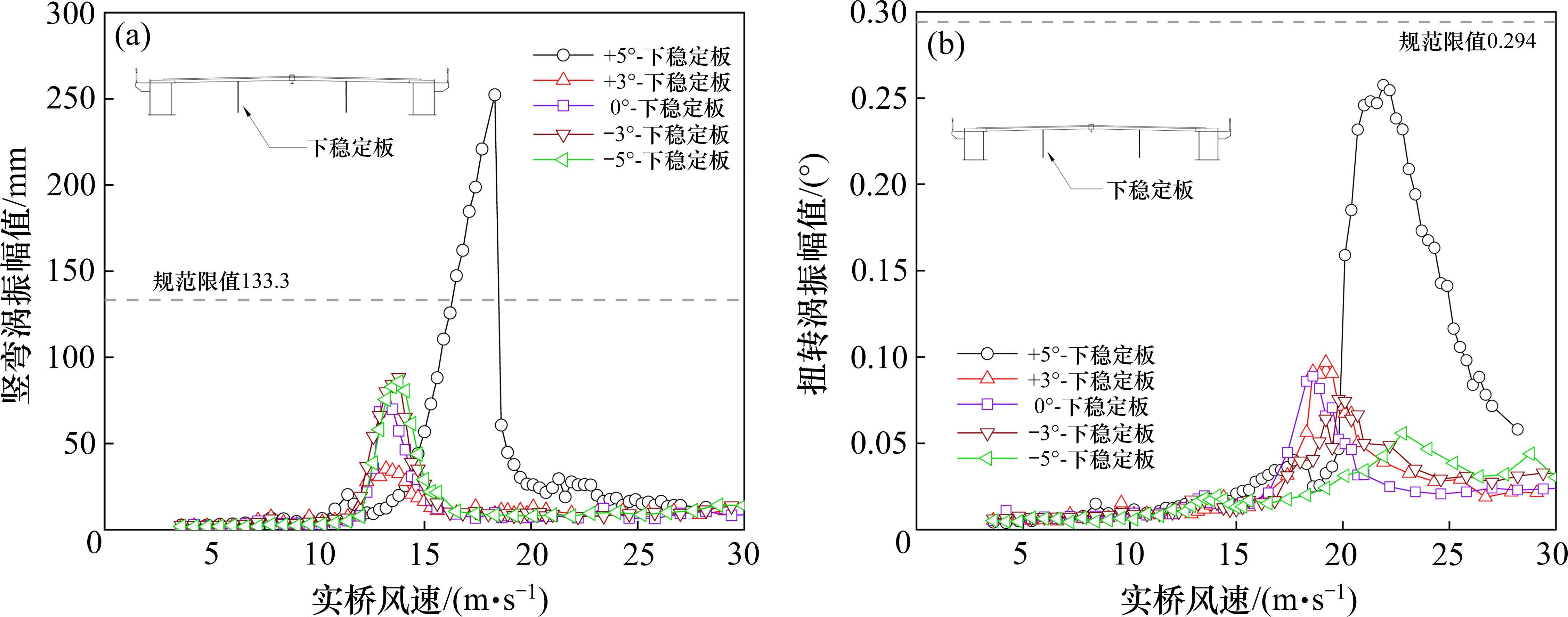
对比原主梁断面,可见±3°风攻角范围内,增设下稳定板并不改变竖弯和扭转涡振区间,但能显著降低竖弯涡振幅值,使其明显低于规范限值,也能一定程度降低扭转涡振幅值。李春光等[17]通过CFD分析认为,下稳定板分隔了上下游边梁之间的空间,与原设计断面相比,减小了上下游边梁之间形成的漩涡尺度和强度,从而降低了涡激力。可见,通过在主梁下方增设下稳定板,使得±3°风攻角范围内桥梁涡振满足规范要求。本文还对其开展了5°和-5°风攻角时的涡振性能试验。可见,-5°风攻角下桥梁涡振满足规范限值要求,但5°风攻角时带下稳定板的主梁竖弯涡振幅值明显高于规范限值,扭转涡振幅值接近规范限值。可见仅采用下稳定板不能满足桥梁在大风攻角下的抗涡振的要求(如桥梁迎风向有山坡的特殊桥址风环境,易形成大风攻角),需要尝试其他气动措施或再组合其他气动措施,以有效抑制桥梁涡振。
3.3 增设倒L形裙板
风洞试验也尝试了在桥面检修道外侧悬挑端增设倒L形裙板,实桥倒L形裙板长边和短边分别长1.5 m和0.5 m,短边端部与悬挑端连接,长边朝下,布置如图6(c)所示。
图8给出了不同风攻角下增设下稳定板的试验结果。可见±3°风攻角范围内,增设倒L形裙板能一定范围提高竖弯和扭转涡振风速区间。与下稳定板类似,能显著降低竖弯涡振幅值,使其明显低于规范限值,也能一定程度降低扭转涡振幅值。可见,增设倒L形裙板能使±3°风攻角范围内桥梁涡振满足规范要求。因主梁负攻角涡振性能优于正风攻角,因此本文仅给出5°风攻角下的实验结果。可见,与下稳定板类似,竖弯涡振幅值明显高于规范限值,扭转涡振也明显,幅值接近规范限值,且涡振区间对应风速提高。
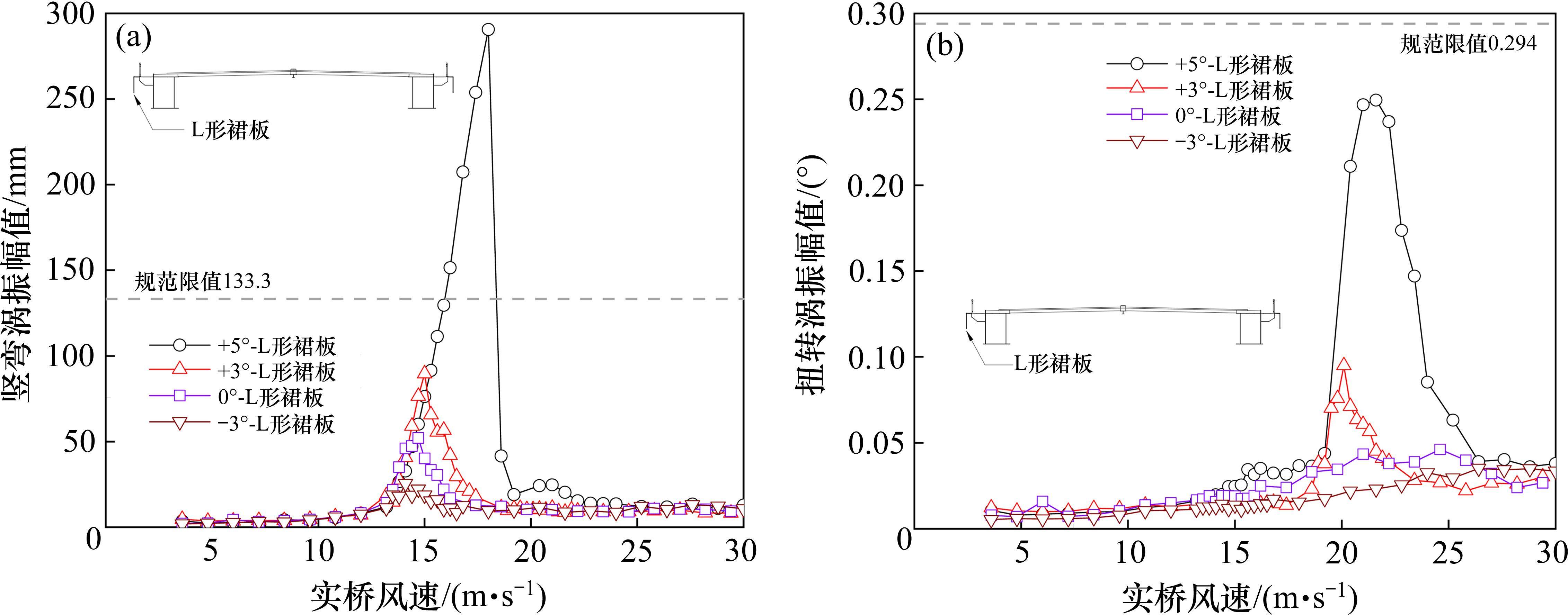
3.4 同时增设下稳定板和倒L形裙板
因+5°风攻角下单独施加上述2种气动措施中的一种,其涡振抑制效果不佳,本文尝试了同时增设下稳定板和倒L形裙板,风洞试验结果如图9所示。与单独一种气动措施相比,同时增设下稳定板和倒L形裙板能显著降低竖弯和扭转涡振幅值,使5°风攻角下的涡振幅值明显低于规范值,特别是竖弯。因此下稳定板组合倒L形裙板能显著改善大风攻角下的此类主梁涡振性能。
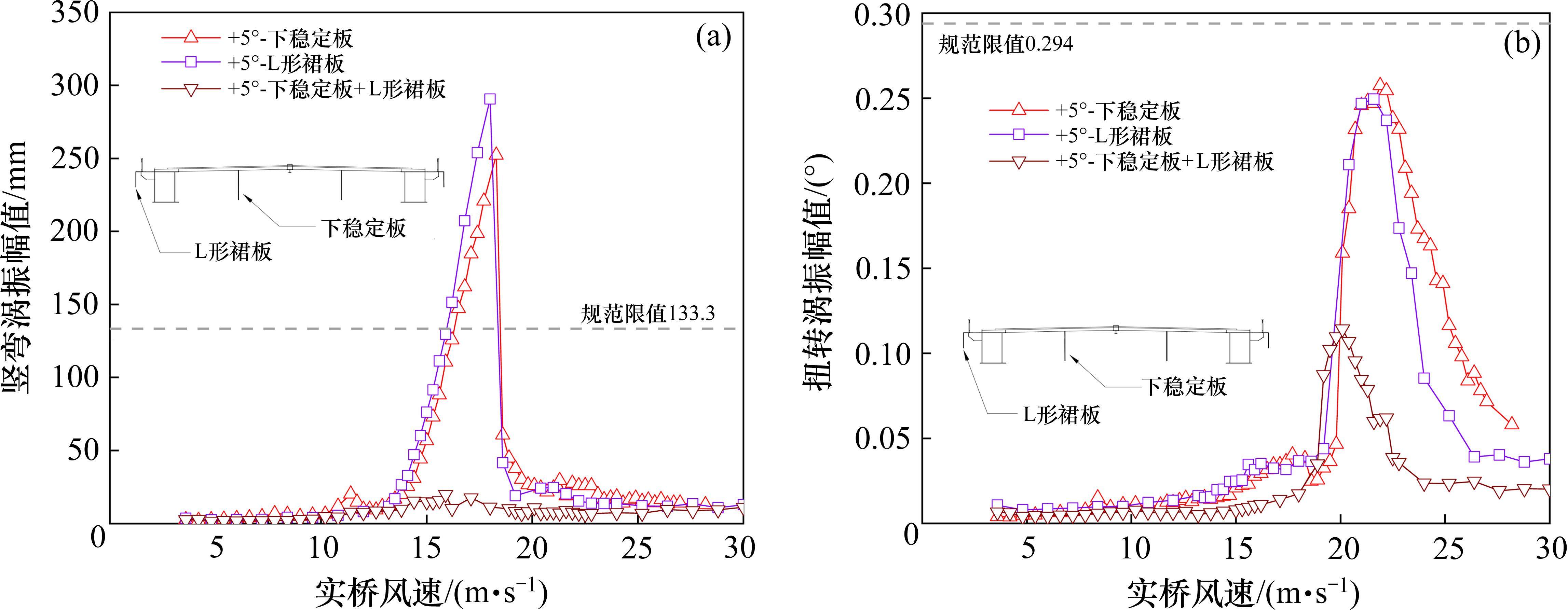
4 气动改进主梁颤振稳定性、气动力和抑振机理
4.1 颤振稳定性
经涡振气动措施改善的主梁,如应用于大桥,其颤振稳定性是桥梁抗风的另一个重要考虑,因此,需评价其颤振稳定性。为此,本文开展了原设计断面、增设下稳定板、增设倒L形裙板、同时增设下稳定板和倒L形裙板的桥梁颤振节段模型试验。根据桥址风参数和规范确定的大桥颤振临界风速为53.4 m/s。
选取大桥第1阶正对称竖弯和第1阶正对称扭转,扭弯频率比为1.75,沿用涡振试验节段模型,取风速比1∶5,得到节段模型频率比为10∶1,根据相似关系确定的节段模型竖弯和扭转频率,以及质量或质量惯性矩分别为3 Hz和5.26 Hz、19.34 kg/m和0.68 (kg∙m2)/m。颤振试验节段模型由8根不同于涡振试验的弹簧悬挂于风洞内,其他试验布置和数据采集与涡振试验相同。颤振试验在均匀流场中进行,风攻角分别为0°、±3°和±5°,节段模型竖弯和扭转阻尼比1%。不同工况的试验结果如表2所示。
| 主梁断面 | 风攻角/(°) | 颤振风速/ (m∙s-1) | 是否 发生 颤振 | |
|---|---|---|---|---|
| 试验值 | 检验值 | |||
| 原主梁断面 | -3、0和3 | >60 | 53.4 | 否 |
| 增设下稳定板 | -5、-3、0、3、5 | >60 | 否 | |
| 增设倒L形裙板 | -3、0和3 | >60 | 否 | |
| 同时增设下稳定板+倒L形裙板 | -5、-3、0、3、5 | >60 | 否 | |
可见,原主梁和增设气动措施的3种主梁,在试验风攻角范围内,颤振临界风速均明显高于颤振检验风速,因此,增设抑制桥梁涡振气动措施,并不影响桥梁的颤振稳定性,也即本文对原设计断面涡振的气动改进是有效且可行的。图10给出了-3°~3°风攻角下增设倒L形裙板,其主梁竖弯和扭转振动幅值随来流风速增大的曲线,可见响应整体趋势是随着风速的提高而增大,在较低风速下有涡振,这与前述涡振试验一致。图10(b)在40~60 m/s风速下扭转振幅随风速先增大后减小,可能是主梁发生了高风速扭转涡振,但此时风速已明显高于主梁设计风速,可不考虑。
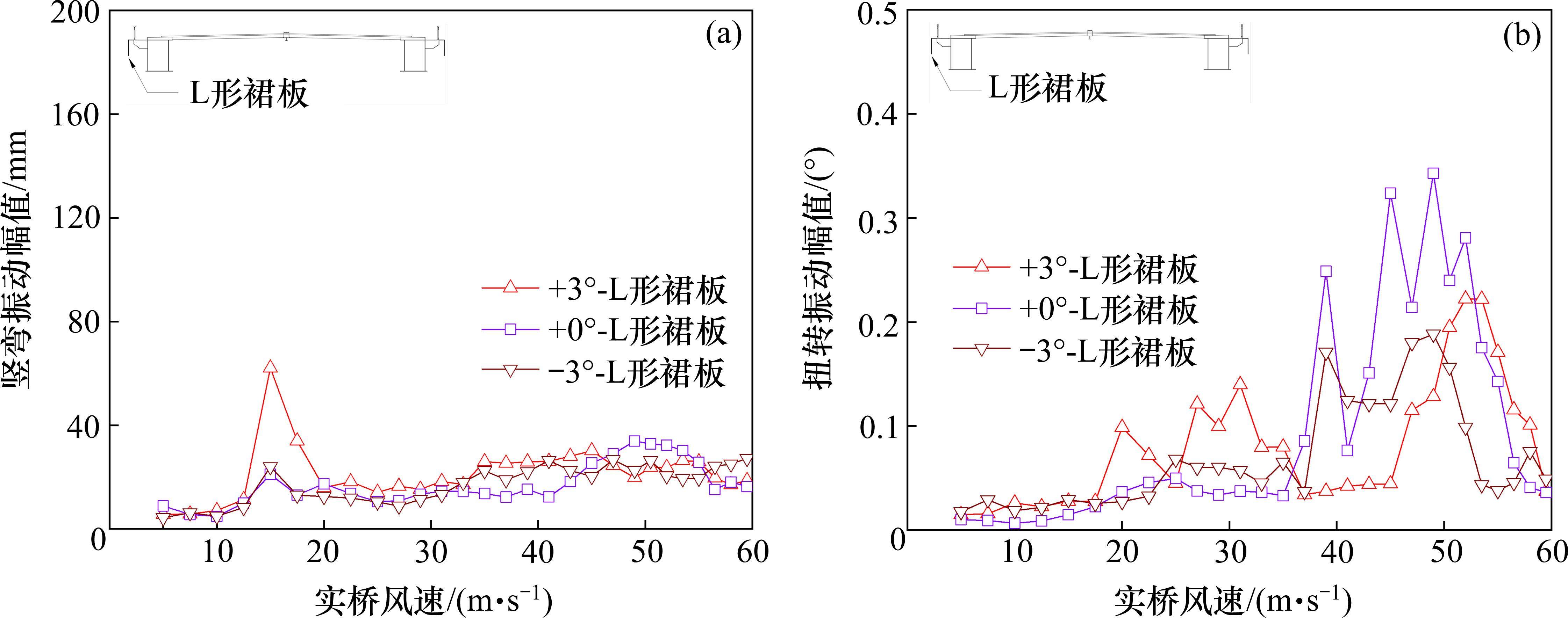
4.2 主梁三分力与抑振机理
直立的主梁模型通过底座固定在安放有六分量高精度天平的风洞转盘上(图11),测定试验风速下,主梁断面在-10°~+10°范围内的三分力,并根据式(4)~(6)获得主梁风轴坐标系下的阻力、升力和扭矩系数。
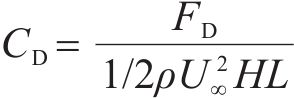
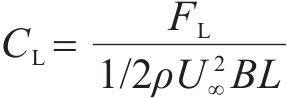
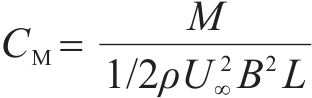
式中: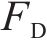
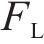
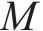
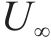
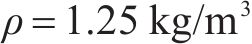
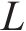
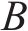


图12给出了原主梁断面,及其增设下稳定板、增设倒L形裙板、同时增设下稳定板和倒L形裙板后的三分力系数随来流攻角的变化。可见,随着风攻角的增大,阻力系数均先减小再增大,呈马鞍形,最小值在0~2°,原主梁断面0°风攻角下约为1.6。需指出,增设下稳定板基本不改变原主梁阻力系数,但增设倒L形裙板明显减小原主梁断面阻力系数,0°风攻角下约为1.2,降幅达25%,阻力降幅负风攻角下明显大于正攻角,如图12(a)所示,这说明,增设倒L形裙板能流线化Π形双边箱开口截面主梁的气动外形。
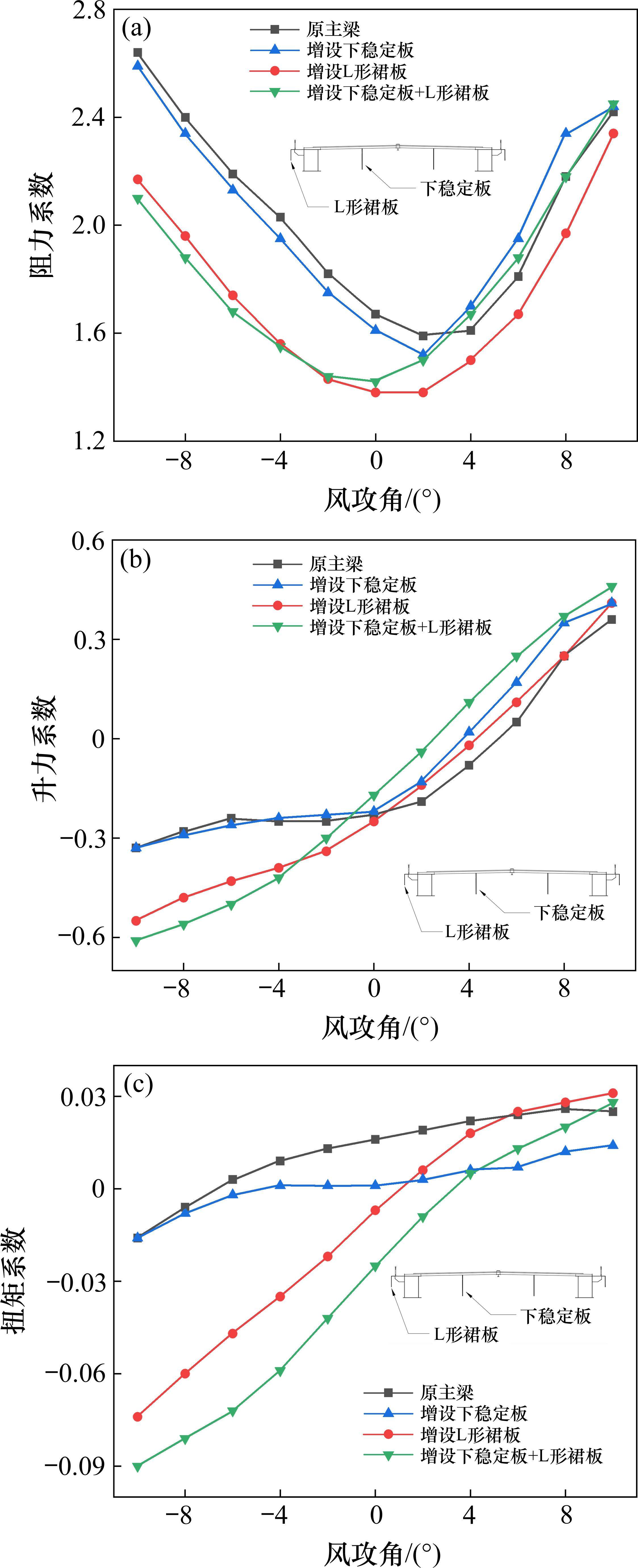
从图12(b)可见,增设下稳定板并不显著改变原主梁断面的升力系数,但在负攻角下,增设倒L形裙板显著增大与恒载同向的升力,因此,增设倒L形裙板应能改善主梁的静风稳定性。另外,升力系数均随风攻角的增大而增大,但增设倒L形裙板的主梁增长明显,也即具有较大的升力线斜率。因升力系数斜率与竖弯振动的阻尼有关[21],升力系数斜率越大,越能提供大的竖弯振动阻尼,也即增大竖弯方向的气动稳定性,这可能是倒L形裙板能显著降低竖弯涡振的原因。带下稳定板的主梁,负攻角升力线斜率与原主梁同,但正攻角稍大于主梁,这也是下稳定板为何能降低竖弯涡振的原因。
图12(c)是扭矩系数随风攻角的变化曲线,可见增设气动措施能减小扭矩系数,也即减小迎风侧主梁抬头的扭矩,特别是负攻角下会明显增大迎风侧主梁低头的扭矩,这也将提高桥梁的静风稳定性,增设倒L形裙板后上述特征越加明显。另外,增设倒L形裙板将明显增大扭矩系数斜率,因扭矩系数斜率与扭转运动的阻尼有关[21],该斜率越大,能提供更大的扭转振动气动阻尼,也即增大扭转方向的气动稳定性,这可能是倒L形裙板能显著降低扭转涡振的原因。
上述基于气动三分力系数的分析,解释了增设下稳定板或同时增设下稳定板和倒L形裙板,能改善主梁涡振性能的机理。
5 结论
1) 动力特性分析表明,大桥主梁振动主导的模态表现为主跨的明显振动,表明边跨PC主梁刚度明显大于主跨;未见索塔的顺桥向振动,表明该部分地锚式斜拉桥的地锚桥台通过背索有效地锚固了索塔。
2) 在实桥常遇风速范围和±3°风攻角内,原设计主梁断面在竖弯和扭转方向均发生了涡振,竖弯涡振幅值均大于规范限值;增设下稳定板或倒L形裙板,能显著降低竖弯涡振幅值,也能一定程度降低扭转涡振幅值,使得±3°风攻角内桥梁涡振满足规范要求;但±5°风攻角下仅增设一种气动措施,竖弯涡振幅值明显高于规范限值,扭转涡振也很大;如同时增设下稳定板和倒L形裙板,能显著降低涡振幅值至规范限值以下。
3) 原主梁断面在±3°风攻角内有足够的颤振稳定性;增设用于抑制涡振的下稳定板和倒L形裙板的主梁,颤振临界风速均明显高于颤振检验风速,也即增设气动措施仍能保证大桥有足够的颤振稳定性。
4) 增设下稳定板基本不改变原主梁的阻力系数,但增设倒L形裙板明显减小原主梁断面阻力系数,且负风攻角下阻力降幅明显大于正攻角,表明倒L形裙板能流线化Π形截面主梁气动外形,改善主梁的静风稳定性。
5) 增设倒L形裙板将明显增大升力和扭矩系数曲线的斜率,也即增大了竖弯和扭转运动相关的气动阻尼,因而能显著降低竖弯和扭转涡振,从而改善桥梁的抗涡振性能。
本文研究能为大桥抗涡振设计提供依据,也能为同类桥梁抗风研究提供参考;相关的涡振抑制机理分析,可在未来通过其他同类桥梁的涡振研究进一步证实。
祝志文,刘桂荣,沈焯悦等.独塔部分地锚斜拉桥涡振气动抑振措施与气动影响研究[J].铁道科学与工程学报,2025,22(02):757-769.
ZHU Zhiwen,LIU Guirong,SHEN Zhuoyue,et al.Mitigation countermeasure on VIV and its effects on aerodynamics of partial gravity-anchored cable-stayed bridge with a single tower[J].Journal of Railway Science and Engineering,2025,22(02):757-769.

