与其他形式的结构相比,薄壁箱梁结构具有重量轻、抗弯抗扭性能好、材料利用充分等特点,因此,在工程实践中得到了广泛的应用[1]。弯曲荷载作用下,剪力流不均匀分布会导致箱形截面翼缘板翘曲应力不均匀分布,即剪力滞后现象[2]。箱梁的剪力滞效应会降低箱梁的面内刚度,导致挠度变形增大[3-4]。近年来,随着公路交通需求的增加,箱梁横向宽度不断增大,单箱双室的断面形式备受关注。因此,剪力滞效应对单箱双室薄壁箱梁力学性能的影响是当前亟需解决的课题之一。针对箱形截面剪力滞效应研究,国内外学者做了大量基础性工作,取得了阶段性成果,其中以REISSNER[2]、DEZI[5]、LUO等[6-7]、ZHANG等[8-10]为代表应用能量变分法求解箱形截面剪力滞效应,推动了剪力滞效应理论力学研究。为提高箱形截面剪力滞效应的预测精度,完善剪力滞效应理论分析方法,在理论分析过程中引入了纵向翘曲位移函数修正:1) 纵向翘曲位移横向分布函数选取,如:二次抛物线[2, 5, 8-10]、三次抛物线[6-7, 11]、余弦函数[12-14]、悬链线[15]等;2) 纵向翘曲位移滞后函数修正系数[3-4, 8-10, 12-14];3) 内力平衡因子修正[8-10, 12-14];4) 腹板剪切变形对曲率修正[4, 13-14]。尽管对箱形截面纵向翘曲位移函数引入了诸多修正项,LUO等[7-10, 16-17]研究结果表明,箱形截面悬臂板理论应力值明显高于实际应力值,且理论方法对顶、底板应力预测偏差较大。导致应力偏差存在的主要原因有:1) 纵向翘曲位移横向分布函数选取方面缺乏理论依据及合理性论证;2) 纵向翘曲位移滞后函数修正系数未考虑箱形截面翼缘板边界条件的差异。张元海等[9]通过试算确定悬臂板边界约束修正系数,缺乏理论依据。LI等[14]基于提出的假设,设计了悬臂板修正系数计算程序。然而,上述研究主要针对单箱单室薄壁箱形截面,对单箱双室薄壁箱形截面剪力滞效应的研究相对匮乏。姚浩等[18-19]应用能量变分法求解单箱多室薄壁箱梁剪力滞效应时,以腹板间距一半作为弯曲剪力流零点的做法与实际剪力流分布不符。需要指出的是,剪力滞效应理论分析,单箱多室与单箱单室箱梁的区别不仅仅是箱室的增加,还涉及到翼缘板翘曲位移函数的构建、翼缘板宽的划分和纵向翘曲位移滞后函数的关系等。本文通过合理的假定与简化,采用理论分析方法研究单箱双室薄壁箱梁剪力滞效应,揭示其力学机理。通过弯曲剪力流零点分布确定翼缘板宽度划分原则,考虑剪切变形对曲率影响,引入内力平衡因子,利用纵向翘曲位移横向分布连续性,对翼缘板纵向翘曲位移函数进行修正;提出初始剪切转角概念,确定纵向翘曲位移滞后函数的关系,推导纵向翘曲位移横向分布函数合理形式。基于能量变分原理,建立单箱双室薄壁箱梁剪力滞效应控制微分方程。以单箱双室薄壁简支箱梁作用均布荷载为例,建立ABAQUS有限元数值模型,选取跨中截面应力和腹板挠度变形为分析对象,比较本文理论分析方法解析解与有限元模型数值解,验证本文所提理论的正确性。
1 纵向翘曲位移函数的构造
1.1 基本假设
本文研究对象为单箱双室薄壁结构,因此剪力滞效应理论研究主要基于以下假设:
1) 法向应变和面内剪切应变沿壁厚方向均匀分布;
2) 忽略翼缘板板平面外的剪切变形、横向变形影响;
3) 弹性范围内,应力-应变关系符合胡克定律。
1.2 纵向翘曲位移
图1所示单箱双室薄壁箱梁截面由顶板、底板、悬臂板及腹板组成,全局坐标系原点O位于截面形心处,y轴与z轴为形心主轴,x轴沿梁轴线方向,翼缘板局部坐标系详见图1。
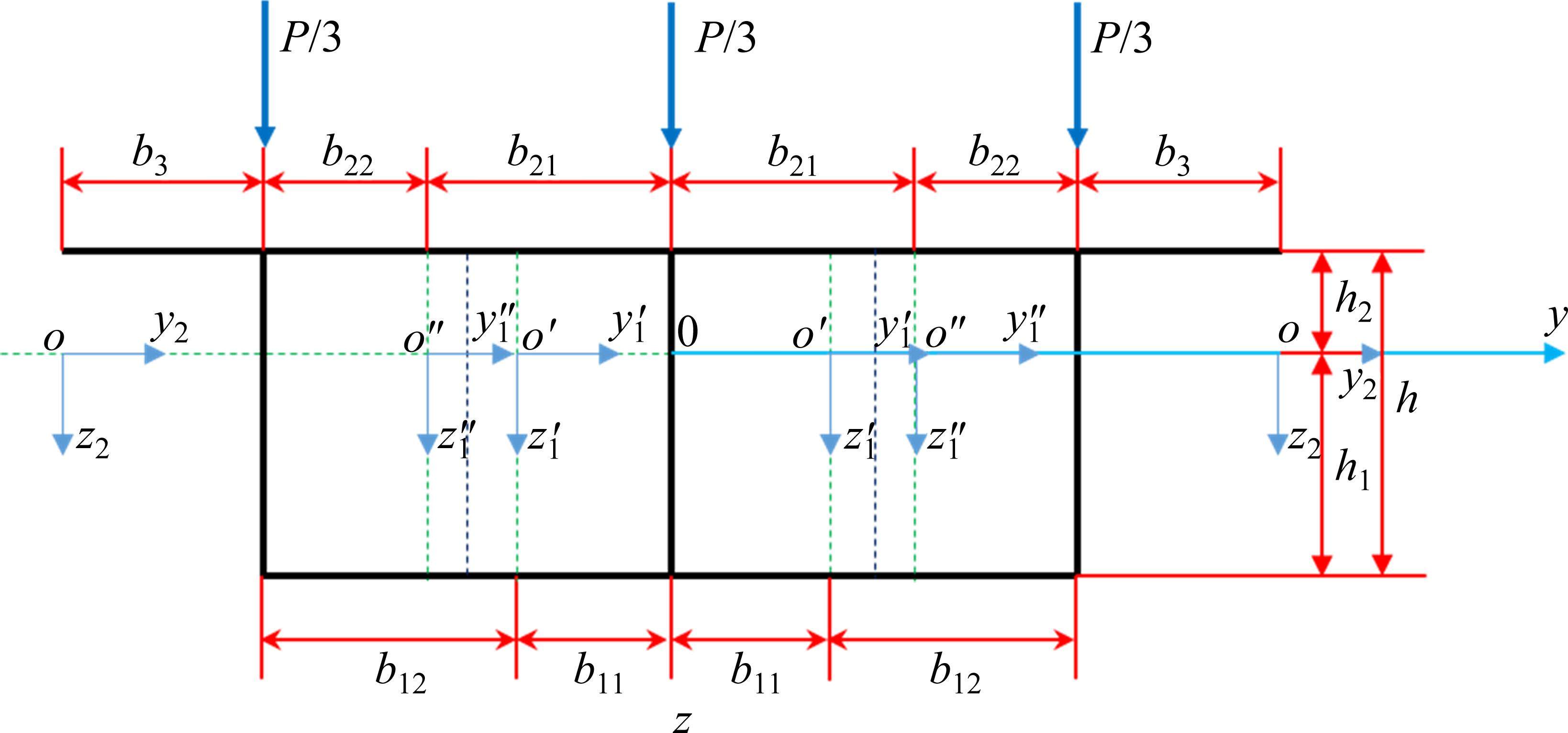
根据剪力滞效应产生机理[2, 8, 14],薄壁箱梁翼缘板纵向翘曲位移主要受剪力流不均匀分布和弯曲曲率影响,其函数表达式可表述为[13-14]:
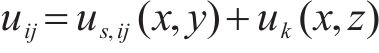
箱形截面翼缘板剪力流不均匀分布引起的纵向翘曲位移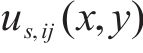
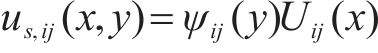
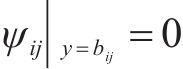
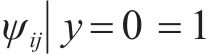
式中: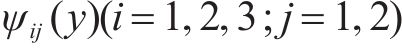
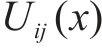
考虑腹板剪切变形对曲率的影响,纵向翘曲位移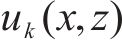
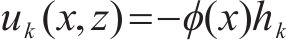
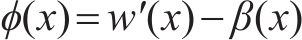
式中: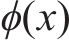
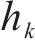
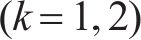
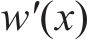
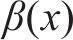
1.3 弯曲剪力流零点位置确定
薄壁箱形截面的剪力滞效应主要是由弯曲剪力流不均匀分布造成的。因此,确定薄壁箱形截面剪力流分布是研究单箱双室剪力滞效应的关键。
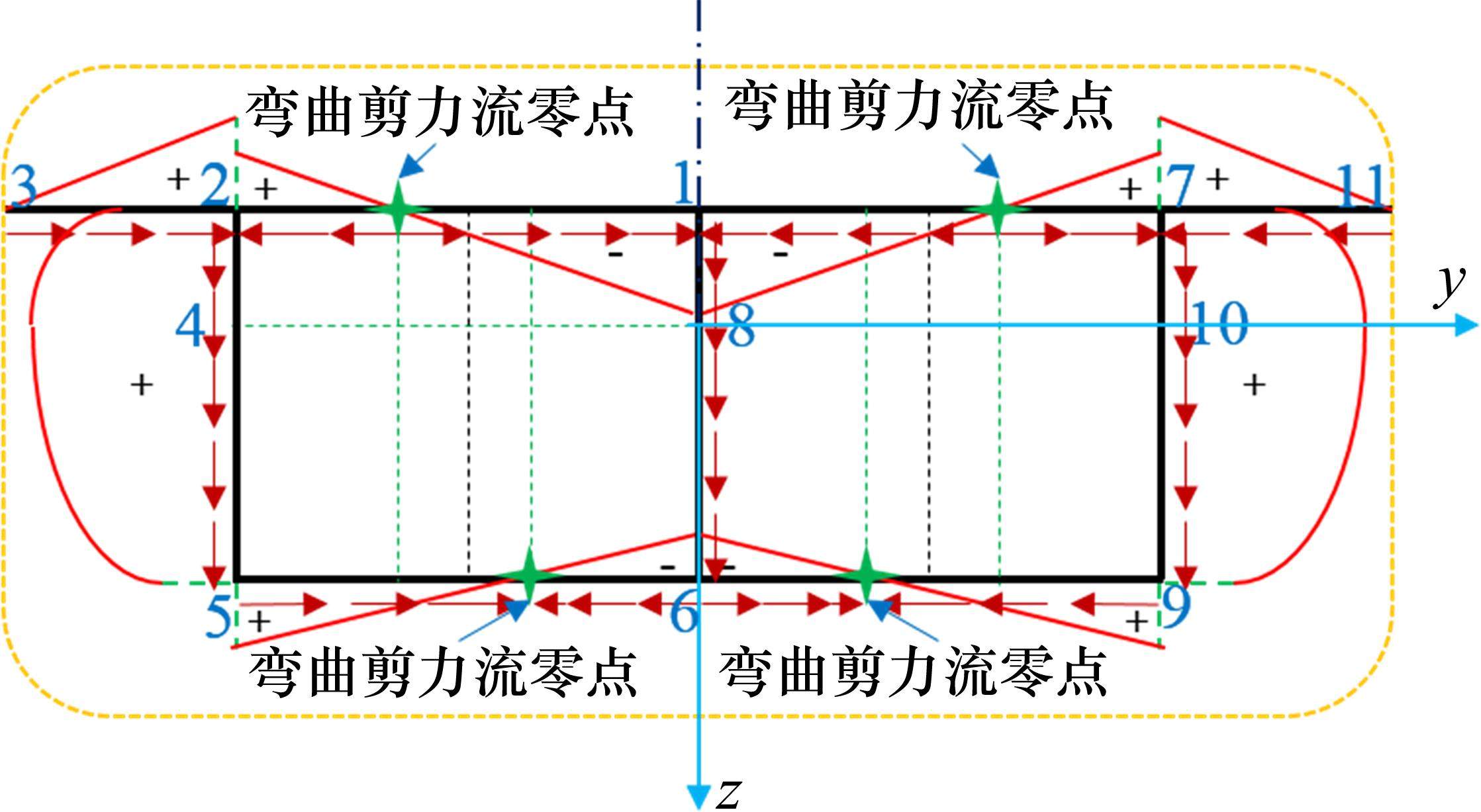
在节点1与节点7位置虚立开口(如图2所示),利用微元体平衡原理,建立开口截面剪力流,箱室左、右侧分别虚设封闭剪力流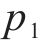
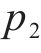
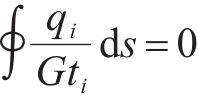
分别就左室与右室建立如下公式,求解封闭剪力流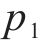
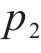
左室:
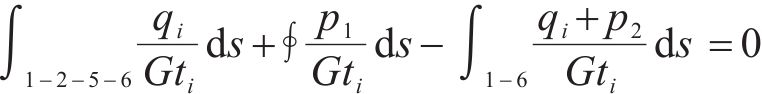
右室:
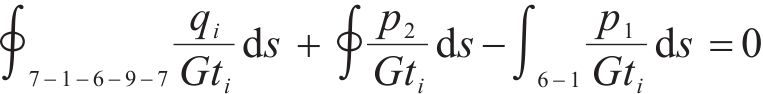
由单箱双室弯曲剪力流的零点分布可确定各翼缘板宽度bij(i=1, 2, 3; j=1, 2)(如图1所示)。因此,单箱双室箱梁剪力滞效应研究不能按文献[18-19]做法:取顶、底翼缘板腹板间距一半建立分布函数表达式。
弹性范围内,图2所示弯曲剪力流零点处的剪应变应为0,即
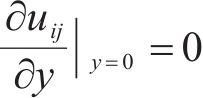
亦可写成:
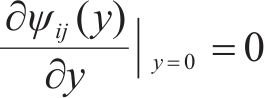
由于剪力滞效应所产生纵向翘曲位移差是由剪力流不均匀分布造成的,则各翼缘板块的纵向翘曲位移差可由剪力流表示
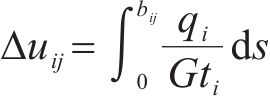
由式(8)可知,各翼缘板块的翘曲位移差值受荷载、材料条件影响,而各翼缘板块间翘曲位移差的相对关系不受荷载、材料条件影响,仅与截面参数有关。因此
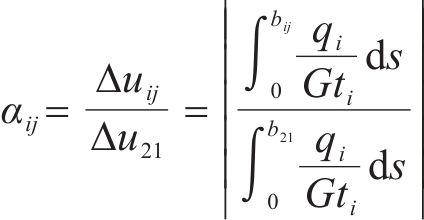
结合式(2),令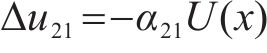
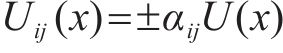
式中: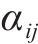
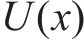
1.4 纵向翘曲位移函数连续性修正
为保证所设各翼缘板翘曲位移函数的正确性,现就翘曲位移函数的连续性进行考察。
上翼缘板:
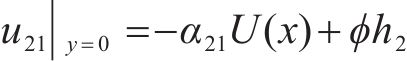
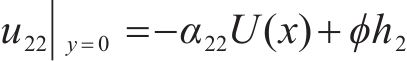
由于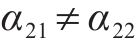
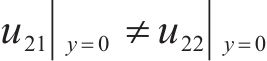
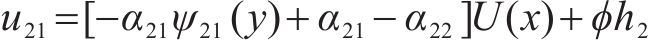
同理,下翼缘板:
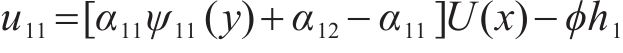
考虑剪力滞效应后,箱型截面上的内力不应发生改变,这就要求考虑剪力滞效应影响的翘曲应力在箱形截面上满足自平衡条件[8, 14],即
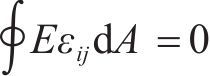
文中关于纵向翘曲位移横向分布函数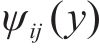
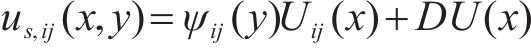
其中:
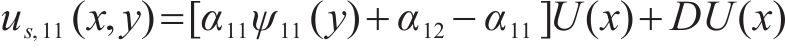
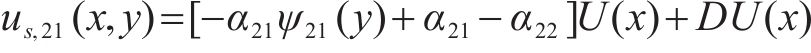
2 初始剪切转角对纵向翘曲位移函数的影响
2.1 初始剪切转角概念引入
由图2、式(7)知,在悬臂板端部,弯曲剪力流为0,相应地纵向翘曲位移函数沿横桥向的一阶导也为0。实际上,由于悬臂板端部为自由端,其对相邻板块的约束能力忽略不计。因此,在悬臂板端部,纵向翘曲位移函数沿横桥向的一阶导并不为0,而应存在一个角度——初始剪切转角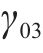
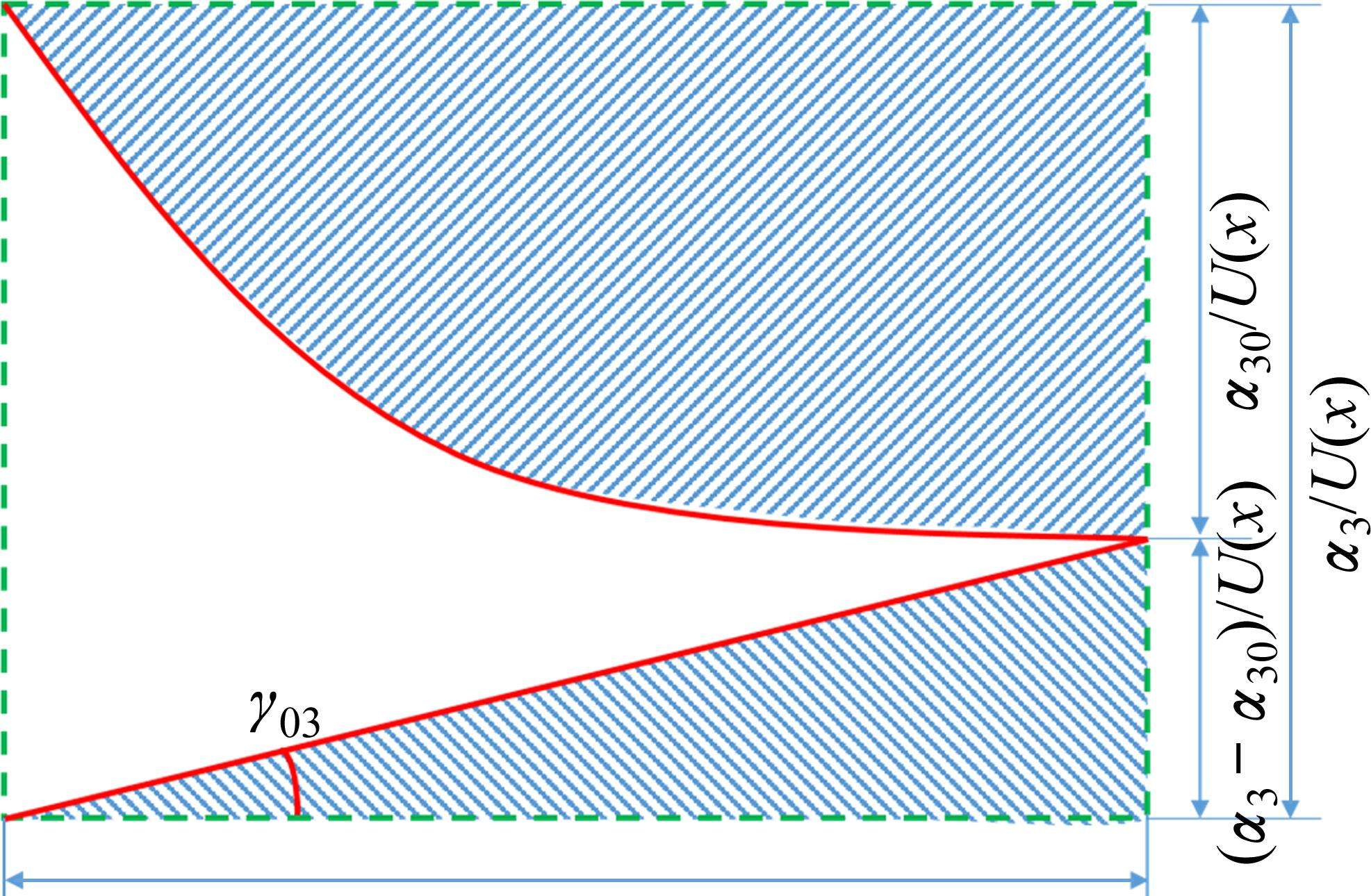
根据式(9),令
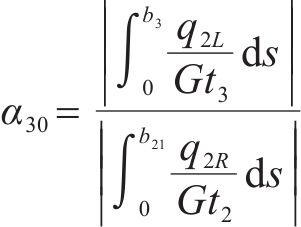
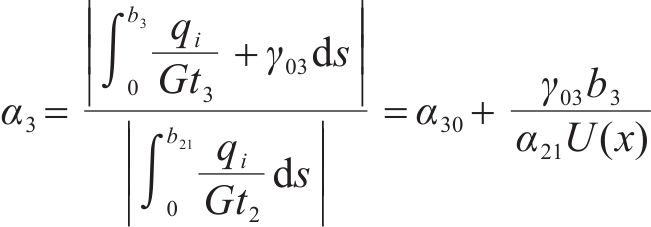
初始剪切转角对悬臂板纵向翘曲位移的附加修正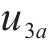
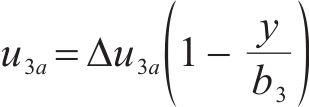
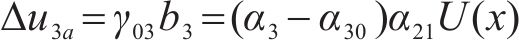
2.2 纵向翘曲位移横向分布函数ψij的选取
考虑到初始剪切转角γ03与悬臂板端部边界条件和剪力流的分布有关,无法直接确定其数值,可先确定系数α3,通过式(18)反向求解初始剪切转角γ03对悬臂板纵向翘曲位移的影响。
悬臂板纵向翘曲位移函数由截面弯曲、剪力流不均匀分布和附加位移构成,悬臂板各微元体必然无法满足应力平衡条件,而在悬臂板与腹板交接处,纵向翘曲位移横向分布函数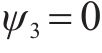
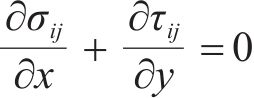
根据假定3,式(20)可写成:
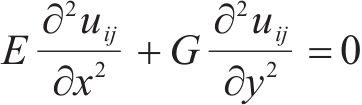
将式(1)、式(3(a))和式(15)代入式(21),可得:
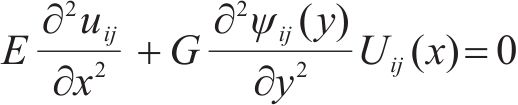
当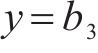
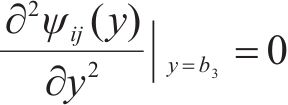
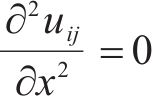
由式(2(b))、式(2(c))、式(7)和式(23(a))可确定纵向翘曲位移横向分布函数ψij(y):
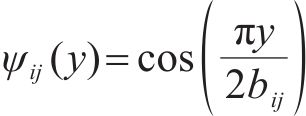
或
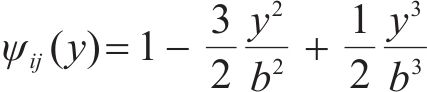
本文纵向翘曲位移横向分布函数ψij(y)均基于式(24)开展。
由式(23(b))可知,以系数α3为变量,当悬臂板和腹板交接处的应变取极值时,确定系数α3数值。
2.3 悬臂板翘曲应力修正
由式(18)可知,系数α3考虑了初始剪切转角γ03的影响,需将初始剪切转角从纵向翘曲位移中分离出来,从而反映悬臂板的真实应力情况。
由式(15)知,悬臂板纵向翘曲位移最大差值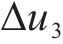
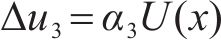
根据胡克定律,悬臂板纵向翘曲应力最大差值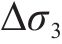
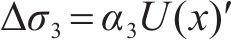
由式(19)可知,初始剪切转角引起的悬臂板纵向翘曲应力最大差值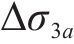
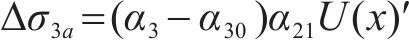
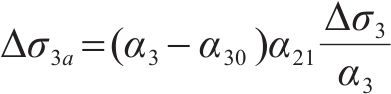
剪力流不均匀分布引起的悬臂板纵向翘曲应力最大差值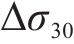
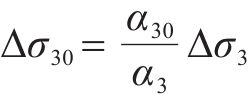
修正后的悬臂板纵向翘曲应力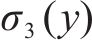
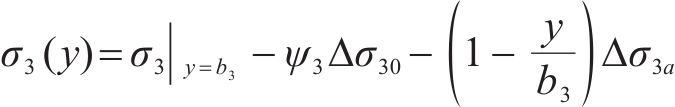
3 基于极小势能原理的控制微分方程推导
根据最小势能原理,当体系处于稳定平衡状态时,体系的总势能取极值,即体系总势能的一阶变分为0:
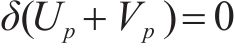
式中: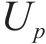
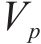
体系总形变势能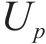
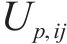
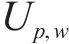
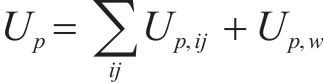
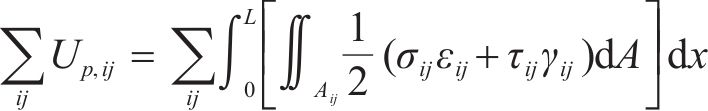
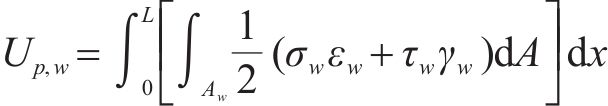
式中:
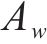
外力势能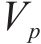
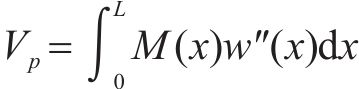
将式(33)和(34)代入式(32),根据变分原理,可得到以箱梁竖向挠度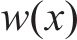
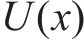
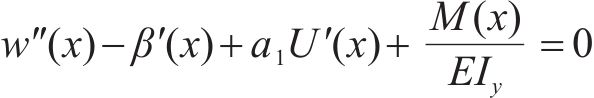
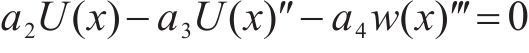
以及自然边界条件:
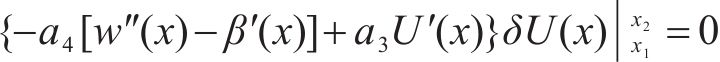
式中:
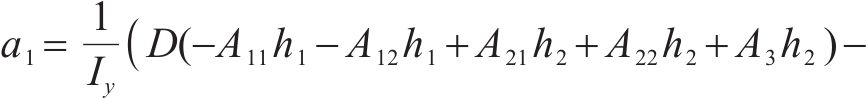
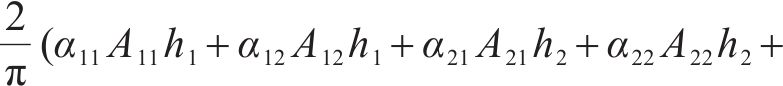
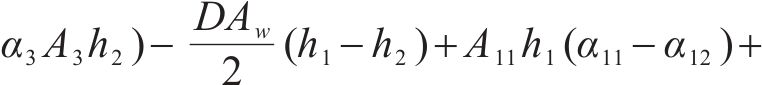
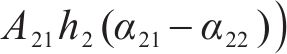
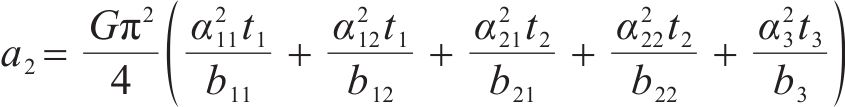
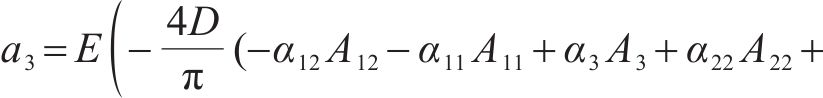
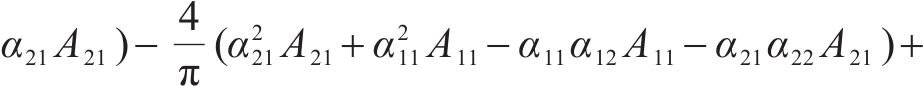
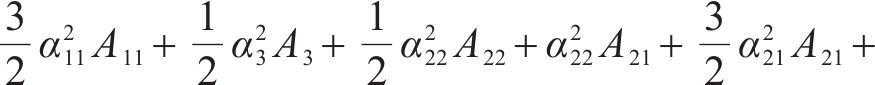
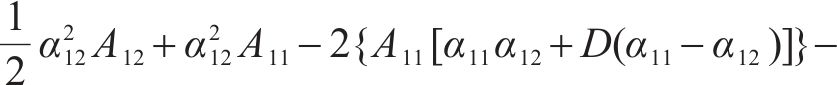
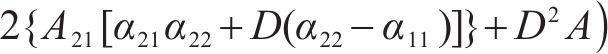
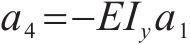
式中: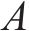
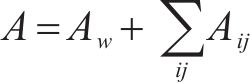
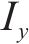
对式(35(a))和式(35(b))解耦,并令
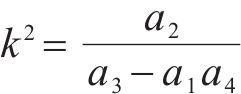
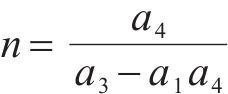
可得
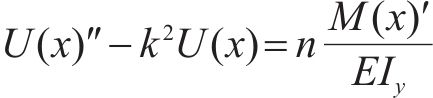
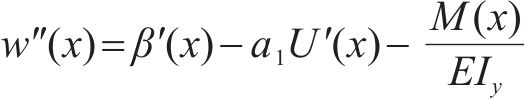
式(36(a))~(36(b))微分方程边界条件:
固定端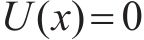
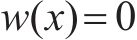
铰接端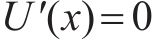
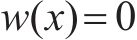
自由端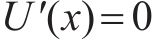
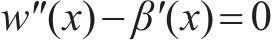
4 算例验证
4.1 算例介绍
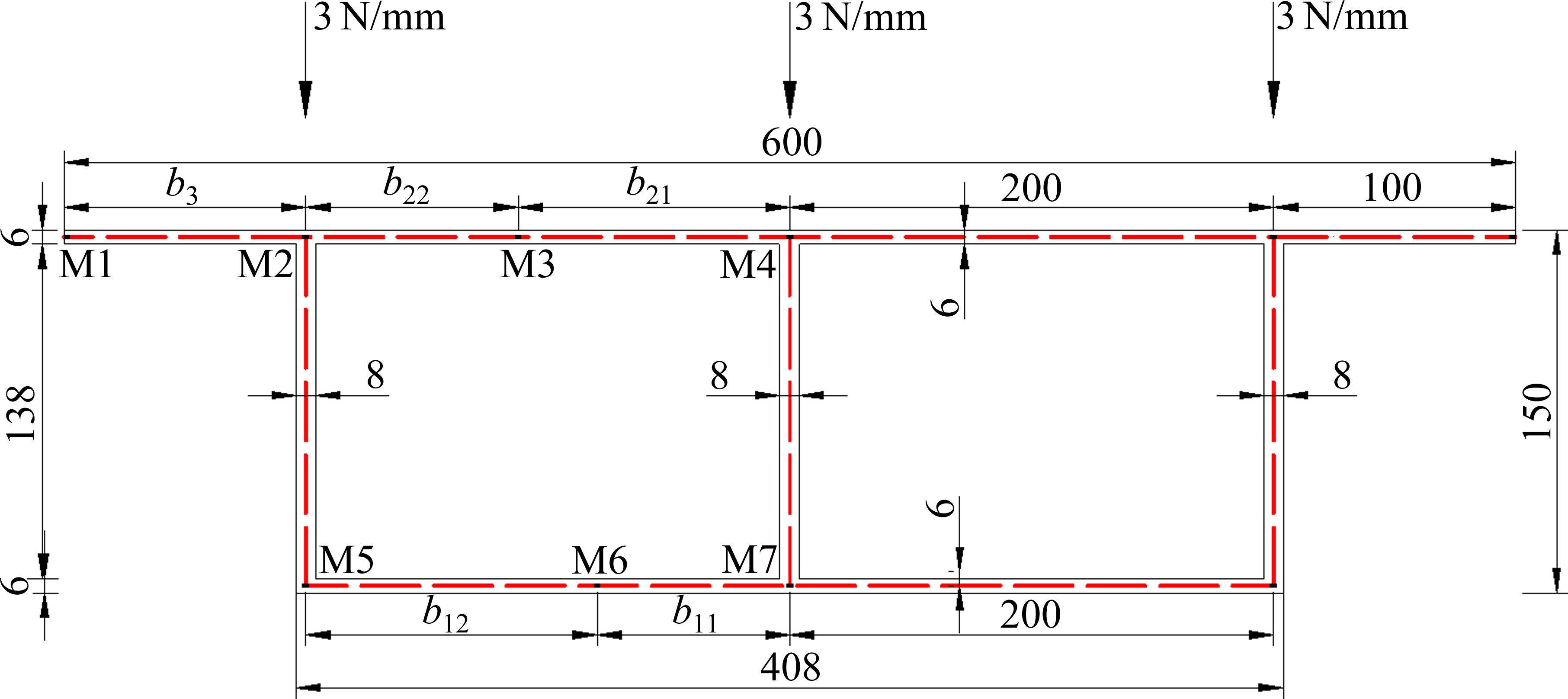
为验证本文单箱双室薄壁箱梁剪力滞效应所提理论分析的正确性,选取如图4所示的单箱双室薄壁简支箱梁算例进行分析。梁长900 mm,均布荷载集度q=9 N/mm平均作用于箱梁腹板处以消除截面局部扭转、畸变以及顶板横向弯曲的附加影响[18]。材料的弹性模量和剪切模量分别是E=3 000 MPa,G=1 083 MPa;泊松比μ=0.385。
4.2 有限元模型
由于缺少单箱双室薄壁箱梁剪力滞效应计算的相关文献,本文主要通过与ABAQUS有限元计算结果对比来验证单箱双室薄壁箱梁剪力滞效应理论分析的计算精度。
采用ABAQUS进行有限元建模,薄壁箱梁采用八节点六面体线性非协调模式单元(C3D8I),该单元不仅克服了线性完全积分单元中的剪切自锁问题,而且在厚度方向只需划分很少的单元,可以取得与二次单元相当的结果精度,计算成本明显降低[21]。各翼缘板网格大小为3 mm×3 mm×3 mm,腹板网格大小为4 mm×3 mm×3mm;有限元模型如图5所示,考虑到实体单元结点3自由度,边界条件施加仅约束两侧竖向位移和一侧横向位移。计算中应力结果提取各翼缘板厚度中面位置处,挠度提取悬臂板与(中、边)腹板交接处。
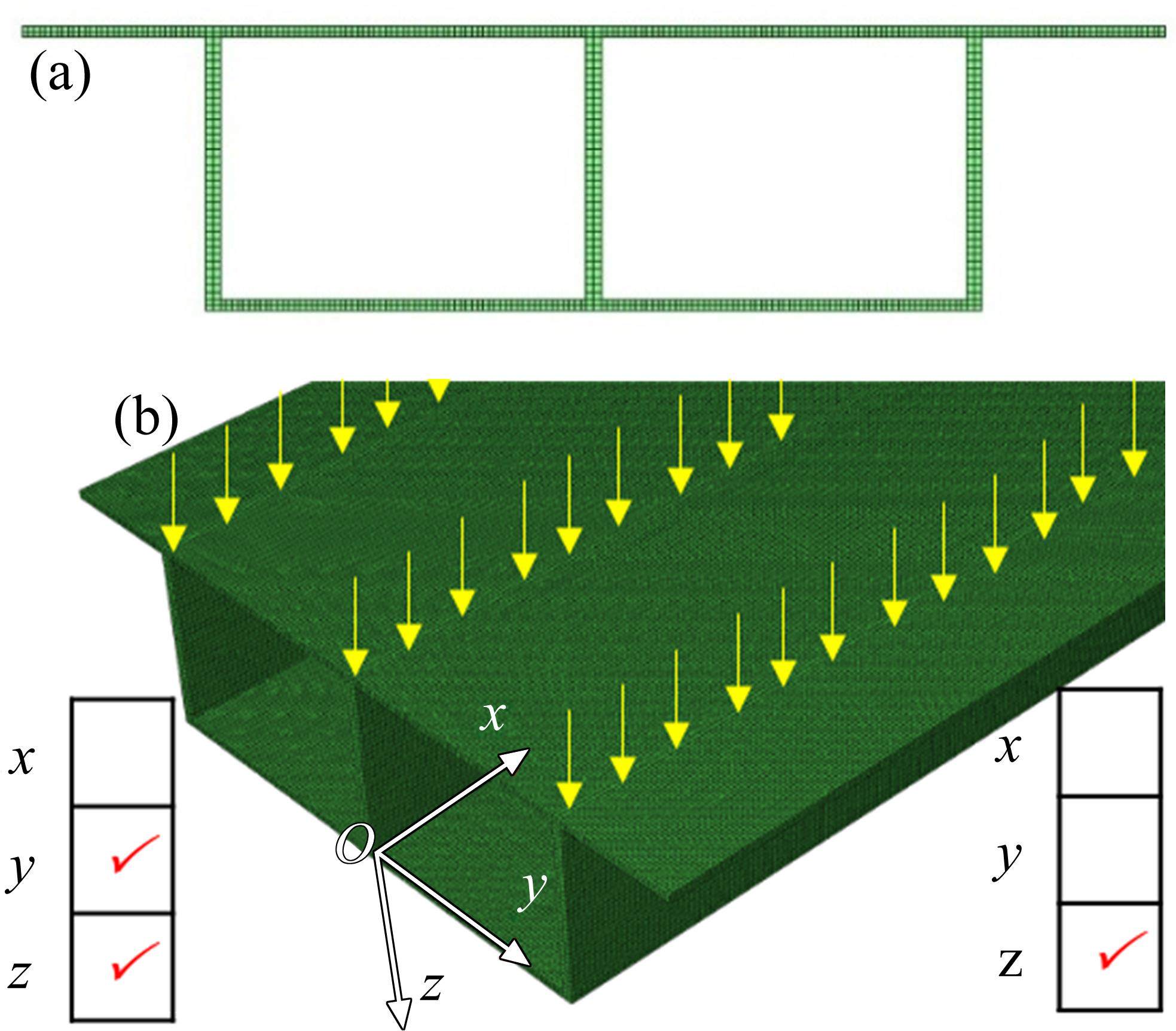
4.3 弯曲剪力流零点验证
采用式(4)~式(5)计算图4所示截面的弯曲剪力流,得到理论公式计算下的弯曲剪力流零点位置列于表1。根据式(6),提取有限元纵向应力极值点位置,列于表1。
| 翼缘板块划分bij | 理论值/mm | 有限元值/mm | 误差(理论值-有限元值)/有限元值×100 |
|---|---|---|---|
| b11 | 75.87 | 74.5 | 1.8 |
| b12 | 124.13 | 125.5 | -1.1 |
| b21 | 111.88 | 112 | -0.1 |
| b22 | 88.12 | 88 | 0.1 |
由表1可知,通过理论分析方法得到的弯曲剪力流零点位置与有限元计算值偏差较小,误差在2%以内;顶、底翼缘板剪力流零点位置均偏离腹板一半位置;表明单箱双室薄壁箱梁剪力滞效应分析中,理论分析弯曲剪力流零点方法对顶、底翼缘板宽划分具有较高的精度,而传统取腹板间距一半的方法不再适应。
4.4 应力验证
图6所示为均布荷载作用下单箱双室薄壁简支箱梁跨中截面顶板中面纵向翘曲应力分布图。
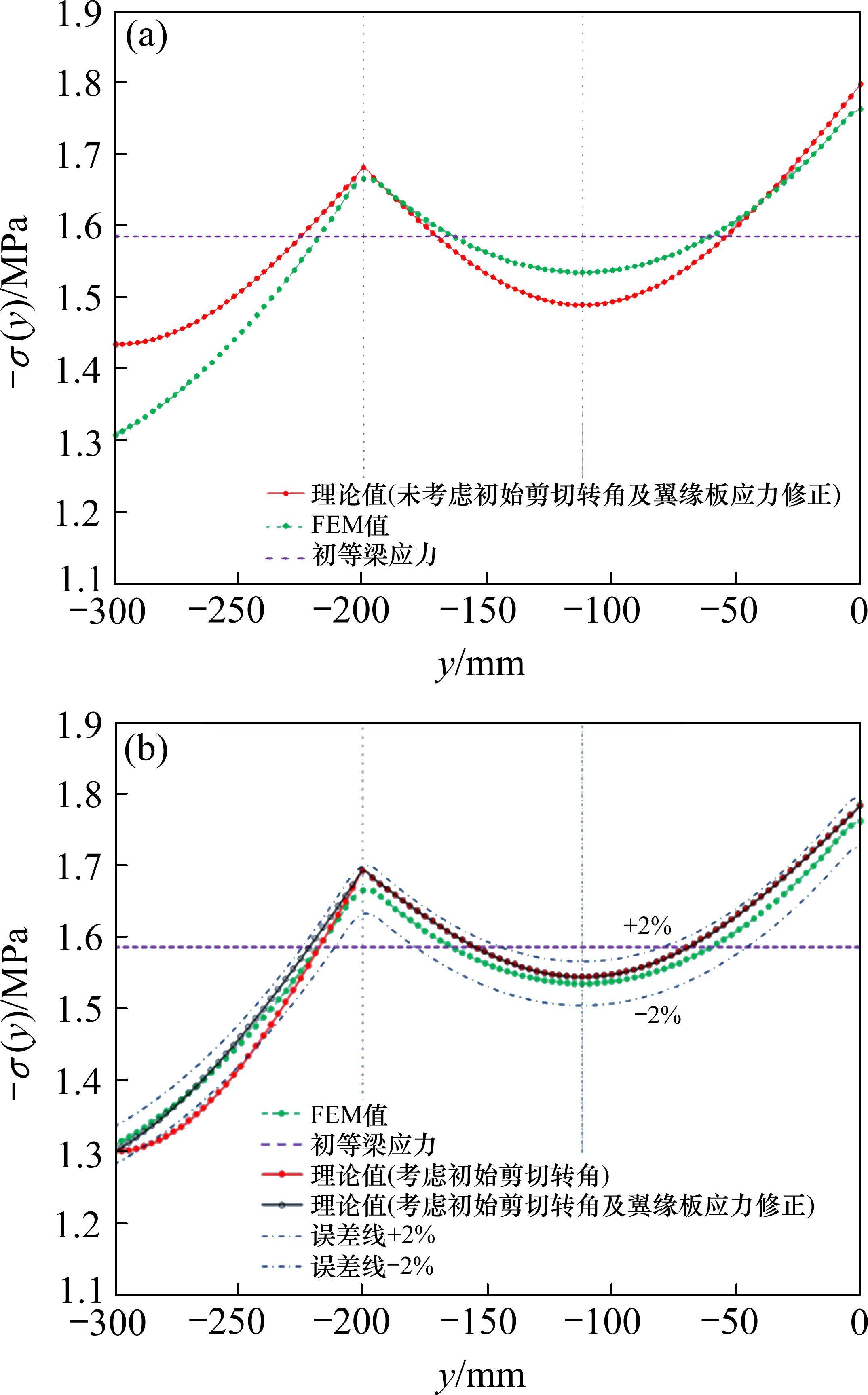
由图6(a)可见,本文理论分析方法(未考虑初始剪切转角)得到的应力值与有限元计算值偏差明显——悬臂板预测应力偏大,而顶板应力偏小。图6(b)中,本文理论分析方法(考虑初始剪切转角未考虑翼缘板应力修正)对顶板沿横向应力分布具有较高预测精度,而对悬臂板沿横向应力分布,则出现了“镰刀”形状偏差,这是由于悬臂板中考虑了初始剪切转角的影响,并默认其对纵向翘曲位移的影响与剪力流不均匀分布产生的翘曲变形一致。因此需要按式(31)对悬臂板应力进行修正,分离出初始剪切转角对悬臂板纵向翘曲应力的影响。本文理论分析方法(考虑初始剪切转角及翼缘板应力修正)不仅对顶板沿横向应力分布具有较高预测精度,而且对悬臂板沿横向应力分布也具有很高预测精度。
图7绘制了均布荷载作用下单箱双室薄壁简支箱梁跨中截面底板中面纵向翘曲应力分布图。
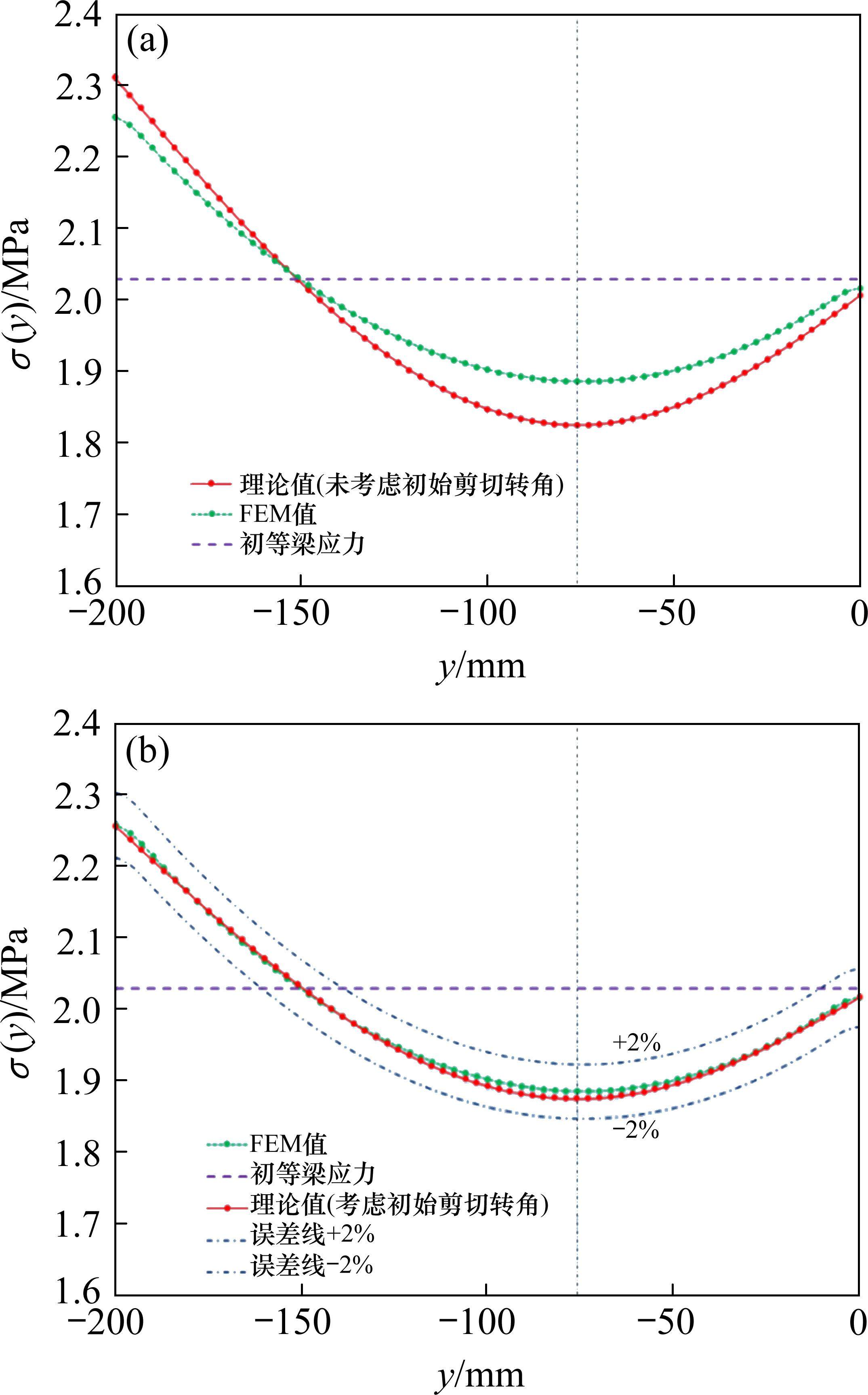
由图7可知,本文理论分析方法(未考虑初始剪切转角)得到的应力值与有限元计算值偏差明显,这是由于悬臂板未考虑初始剪切转角影响,在应用势能原理时,为满足内力平衡,顶、底板的应力分布必然与实际情况产生较大偏差,而本文理论分析方法(考虑初始剪切转角)对底板沿横向应力分布具有较高预测精度,与有限元计算值几乎重合。
表2、表3分别列出了均布荷载作用下单箱双室薄壁箱梁跨中截面、1/4截面(如图4所示)各计算点M1~M7的有限元应力计算值、未考虑初始剪切转角影响的理论应力值和考虑初始剪切转角影响的理论应力值。
| 计算点 | FEM/MPa | THY1/MPa | THY2/MPa | 误差1/% | 误差2/% |
|---|---|---|---|---|---|
| M1 | -1.31 | -1.44 | -1.30 | 9.61 | -0.68 |
| M2 | -1.67 | -1.68 | -1.69 | 0.90 | 1.62 |
| M3 | -1.54 | -1.49 | -1.54 | -2.94 | 0.59 |
| M4 | -1.76 | -1.80 | -1.78 | 2.02 | 1.24 |
| M5 | 2.26 | 2.31 | 2.26 | 2.49 | -0.06 |
| M6 | 1.89 | 1.83 | 1.88 | -3.23 | -0.55 |
| M7 | 2.02 | 2.01 | 2.02 | -0.46 | 0.05 |
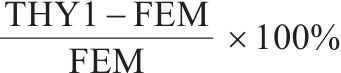
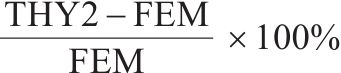
| 计算点 | FEM/MPa | THY1/MPa | THY2/MPa | 误差1/% | 误差2/% |
|---|---|---|---|---|---|
| M1 | -0.93 | -1.02 | -0.93 | 9.92 | 0.48 |
| M2 | -1.29 | -1.30 | -1.30 | 0.60 | 0.23 |
| M3 | -1.13 | -1.08 | -1.12 | -3.25 | -0.01 |
| M4 | -1.33 | -1.35 | -1.34 | 2.27 | 0.01 |
| M5 | 1.88 | 1.94 | 1.89 | 2.21 | 0.24 |
| M6 | 1.30 | 1.27 | 1.29 | -3.17 | -0.27 |
| M7 | 1.45 | 1.44 | 1.45 | -0.50 | 0.03 |
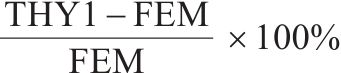
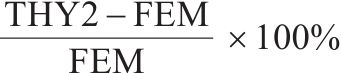
从表2、表3可以看出,与有限元数值解相比,本文考虑初始剪切转角影响的理论应力值较未考虑初始剪切转角影响的理论应力值,能显著降低各测点的应力误差,尤其对悬臂板端部M1计算点,误差从10%降低到1%以内,且计算点M1~M7的所有应力误差均降低至2%以内。结合图6、图7所绘有限元数值解误差线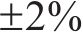
4.5 挠度验证
为进一步验证本文所提理论分析的正确性,利用式(36(b))及边界条件计算如图4所示均布荷载作用下单箱双室薄壁简支箱梁沿跨方向挠度分布。图8所示为边、中腹板(M2、M4)有限元值与理论值(未考虑初始剪切转角和考虑初始剪切转角)2种情况的对比。
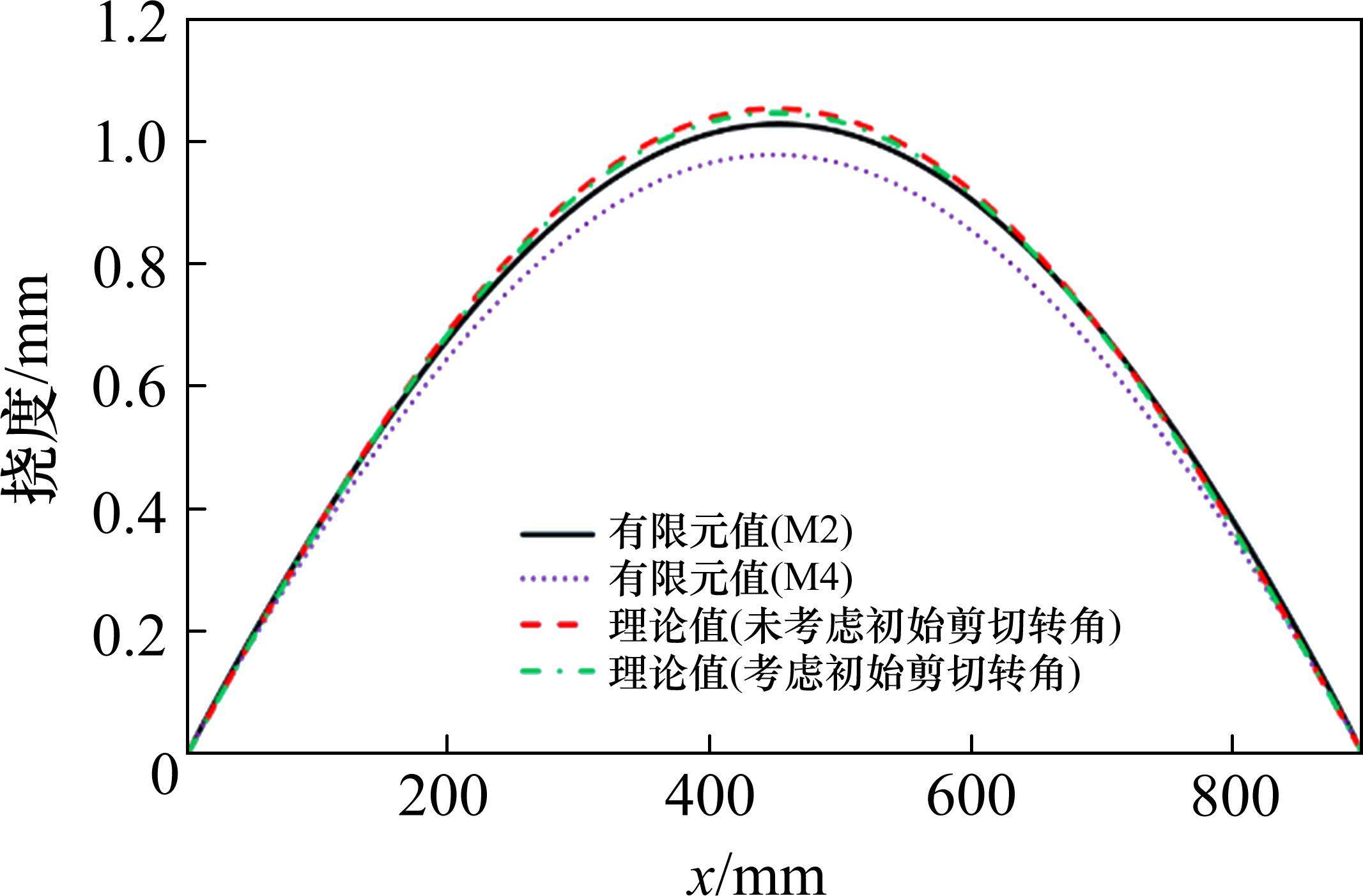
图8可以看出均布荷载作用下单箱双室薄壁简支箱梁边腹板(M2)竖向挠度明显大于中腹板(M4)竖向挠度;本文理论分析方法得到的解析解对边腹板(M2)沿梁轴向挠度分布具有较高的预测精度,且理论分析中,考虑初始剪切转角与未考虑初始剪切转角影响下的挠度曲线几乎重合,表明初始剪切转角对梁轴向挠度分布影响较小。
表4为均布荷载作用下单箱双室薄壁简支箱梁跨中挠度解析解与有限元值的比较。
| 计算方法 | 边腹板(M2) | 中腹板(M4) |
|---|---|---|
| FEM/mm | 1.030 | 0.979 |
| THY1/mm | 1.056 | 1.056 |
| THY2/mm | 1.049 | 1.049 |
| 误差1/% | 2.49 | 7.78 |
| 误差2/% | 1.84 | 7.10 |
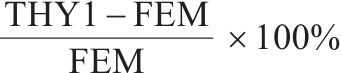
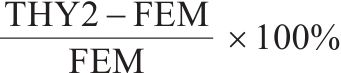
由表4可见,与有限元数值解相比,边腹板考虑初始剪切转角影响较未考虑初始剪切转角影响的挠度值误差降低了0.65%,而中腹板降低了0.68%;边、中腹板处,本文理论分析解(考虑初始剪切转角)与有限元数值解的误差分别为1.84%、7.10%,理论分析中应以边腹板挠度作为变形基准。
5 结论
1) 通过弯曲剪力流零点和有限元纵向应力极值点位置比较,2种方法所确定的翼缘板宽度误差在2%左右,表明理论分析弯曲剪力流零点对单箱双室薄壁箱梁剪力滞效应翼缘板宽度划分具有一定的参考意义。
2) 对比均布荷载作用下单箱双室薄壁箱梁跨中截面理论应力解析值与有限元计算值,未考虑初始剪切转角影响应力最大误差为9.61%,考虑初始剪切转角影响应力最大误差为1.62%,表明本文考虑初始剪切转角影响的理论分析方法对单箱双室薄壁箱梁应力预测具有较高的精度。
3) 通过对均布荷载作用下单箱双室薄壁箱梁沿跨方向理论挠度解析值与有限元计算结果的比较,可以发现,初始剪切转角影响对理论挠度解析解影响较小,边腹板挠度明显大于中腹板挠度,本文理论分析方法可以准确预测边腹板挠度变形,且最大误差为1.84%。
郭向荣,张文格,崔睿博等.基于修正翘曲位移函数的单箱双室薄壁箱梁剪力滞效应分析[J].铁道科学与工程学报,2024,21(12):5117-5127.
GUO Xiangrong,ZHANG Wenge,CUI Ruibo,et al.Analysis on shear lag effect in thin-walled box girder with single-box two-cell based on modified warping displacement function[J].Journal of Railway Science and Engineering,2024,21(12):5117-5127.

