铁路工程建设项目物资保障非常重要,尤其是一些复杂艰险地区,如川藏铁路工程建设项目,所需物资运距远、运量大、风险高,为项目实施带来了更多的不确定性[1]。在铁路施工项目中,水泥作为重要的建筑材料,其库存管理对工程进展至关重要。铁路施工项目大多数会配套建设混凝土搅拌站,存储在搅拌站筒仓中的水泥库存控制十分重要,库存过低会造成供应中断,影响施工进度,库存过高,水泥可能会因长时间存放而过期失效。水泥在存储时还需要考虑其批次限制,不同批次的水泥不能存储在同一筒形仓库中。水泥的库存模型有别于其他物资,筒仓存储及批次限制的特点,使得其库存变化不是连续型而是离散型。这些多种因素叠加对水泥的库存管理及控制带来更大的挑战,一般的通用库存控制策略无法完全适用于水泥。因此,本文从水泥的特质出发,研究水泥在铁路施工项目中的库存模型,以提高工程建设的保障水平。水泥库存控制理论的基础是随机库存模型,而连续检查策略和周期性检查策略是随机型库存模型的2种库存控制策略。一般在制定库存控制策略研究时,往往将周期检查和周期采购相结合,将连续检查和连续采购相结合[2-4]。PRAK等[5]研究了将周期检查和连续采购相结合的模式,为本文研究水泥库存控制策略带来一定启发。在实际应用中,库存控制策略需要依赖于具体的应用场景进行选择,许多学者也对基础的库存控制策略进行了改进。ROSSI等[6]研究了在订单容量限制下的随机库存决策问题,提出改进的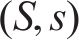
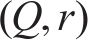
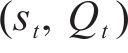
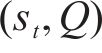
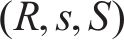
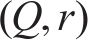
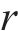
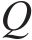
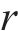
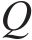
1 订货箱数不可变的等箱法模型构建
本文依此构建订货箱数不可变的双等箱模型和多等箱模型,并在其基础上构建订货箱数可变的多等箱模型,表1为2类模型的参数设置,在本节中首先构建订货箱数不可变的等箱法模型。
| 参数含义 | 符号 | 参数含义 | 符号 |
|---|---|---|---|
| 单个箱的容量 | 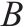 | 平均最低库存量 | 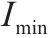 |
| 双等箱模型单个水泥筒仓的容量 | 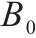 | 平均库存量 | 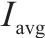 |
| 多等箱模型单个水泥筒仓的容量 | 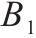 | 水泥筒仓的批量 | 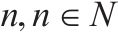 |
| 采用连续检查的多等箱法水泥筒仓容量 | 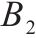 | 检查周期 | 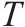 |
| 采用周期检查的多等箱法水泥筒仓容量 | 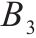 | 最优检查周期 | 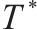 |
| 日平均需求量 | 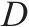 | 水泥罐车容量倍数系数 |  |
| 单位库存每日存储成本 | 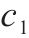 | 水泥罐车载重量 | V |
| 单次采购成本 | 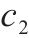 | 多等箱模型每日总成本 | 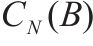 |
| 采购提前期 | 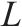 | 多等箱模型的经济订货批量 | 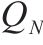 |
| 安全库存量 | 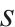 | 采用连续检查的多等箱法每日总成本 | 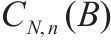 |
正态分布的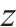 | 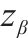 | 采用连续检查的多等箱法经济订货批量 | 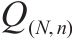 |
| 日平均需求标准差 | 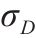 | 采用周期检查的多等箱法每日总成本 | 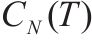 |
| 采购提前期标准差 | 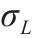 | 双箱模型的库存总成本 | 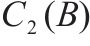 |
| 平均最高库存量 | 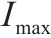 | 双箱模型的经济订货批量 | 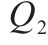 |
1.1 双等箱模型
双等箱系统,顾名思义就是使双箱系统分割出的两部分库存量相等。双等箱系统通常一部分库存为工作仓,另一部分库存为储存仓。对于水泥物资而言,无法对使用一半的筒仓进行补货,只有当一个筒仓水泥全部用完后,才能补货,筒仓大小不一致会带来更高的人工成本。在实际问题中如图1所示,每个圆柱体代表一个筒仓,总共有2个批次,每个批次有1个筒仓,一个批次的水泥量为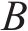
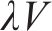
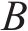
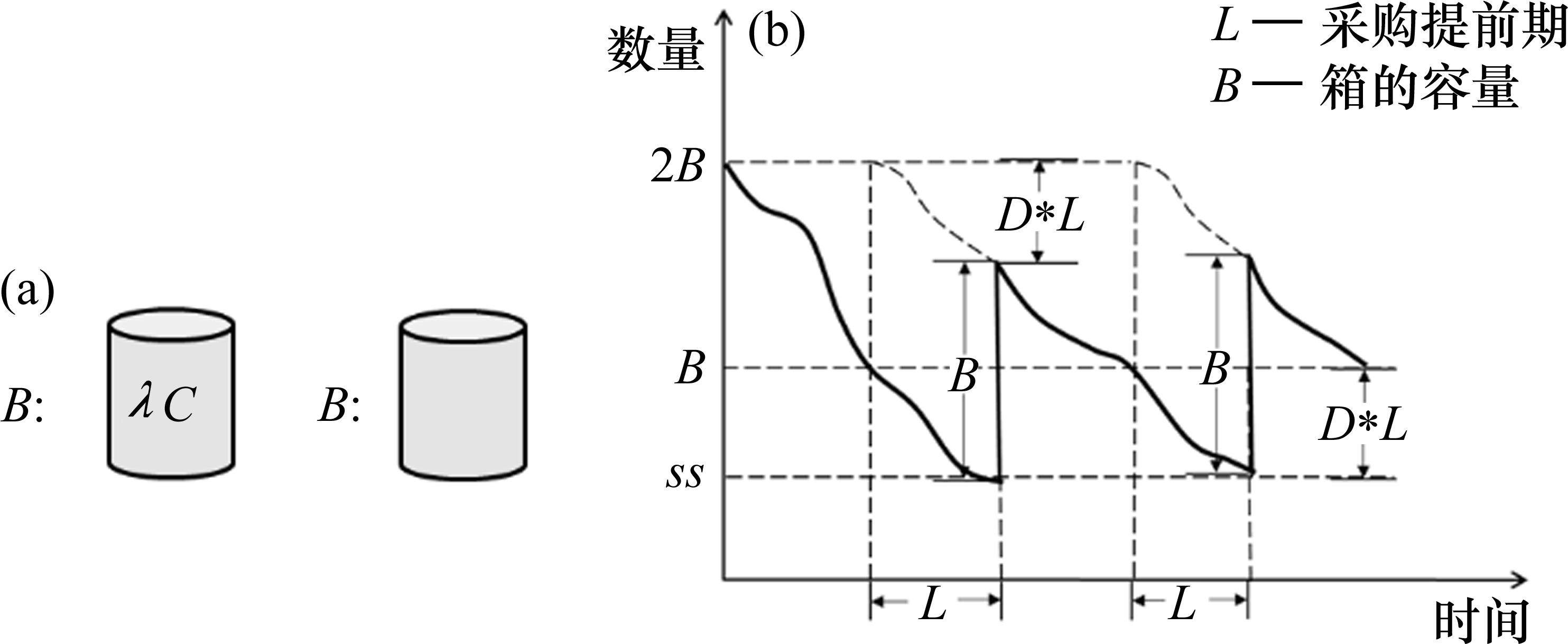
双等箱系统订购数量和重新订购点是相同的,当水泥运达时,理想情况下新到达的批次水泥正好补充库存。该模型的示意图如图1(a)。
在双等箱系统中,再订货点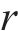
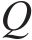
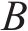
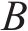
在第1个周期后的双箱模型达到稳定状态,如图1(b)所示,考虑在稳定状态下,当采购提前期为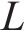
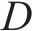
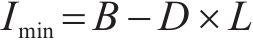
假设提前期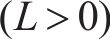
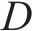
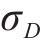
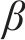
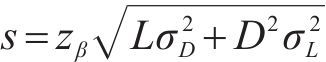
这是处理需求和采购提前期不确定的情况下最基础的方法,具体可查阅文献[22-23]。在模型中要满足最低库存水平大于安全库存,则有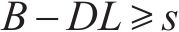

从图1(b)可知,最高库存为
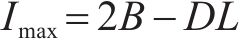
可以得出平均库存量为
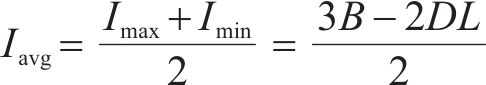
如果缺货损失很小,不考虑缺货情况,库存总成本主要由两部分构成,即库存持有成本和采购成本,因此库存总成本为
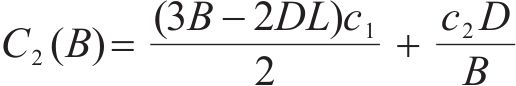
其中,等式右边第1项是库存持有成本,第2项是采购成本。求式(5)1阶导的零点,可以得到双等箱模型的最优订货批量,用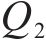
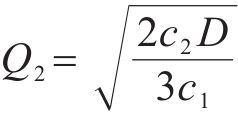
已知库存总成本函数是一个关于容量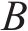
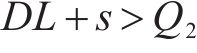
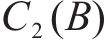

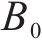
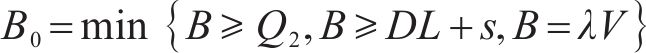
在双等箱模型中,单批次采购量等于单个水泥筒仓的容量等于单个箱的容量,在实际应用中,为方便储存,可以使用多个小型筒仓代替大型筒仓,这一点在3.5节中加以考虑。
1.2 多等箱模型
多等箱模型是将水泥库存分为
图2(a)为多等箱示意图,其中最大总库存量为

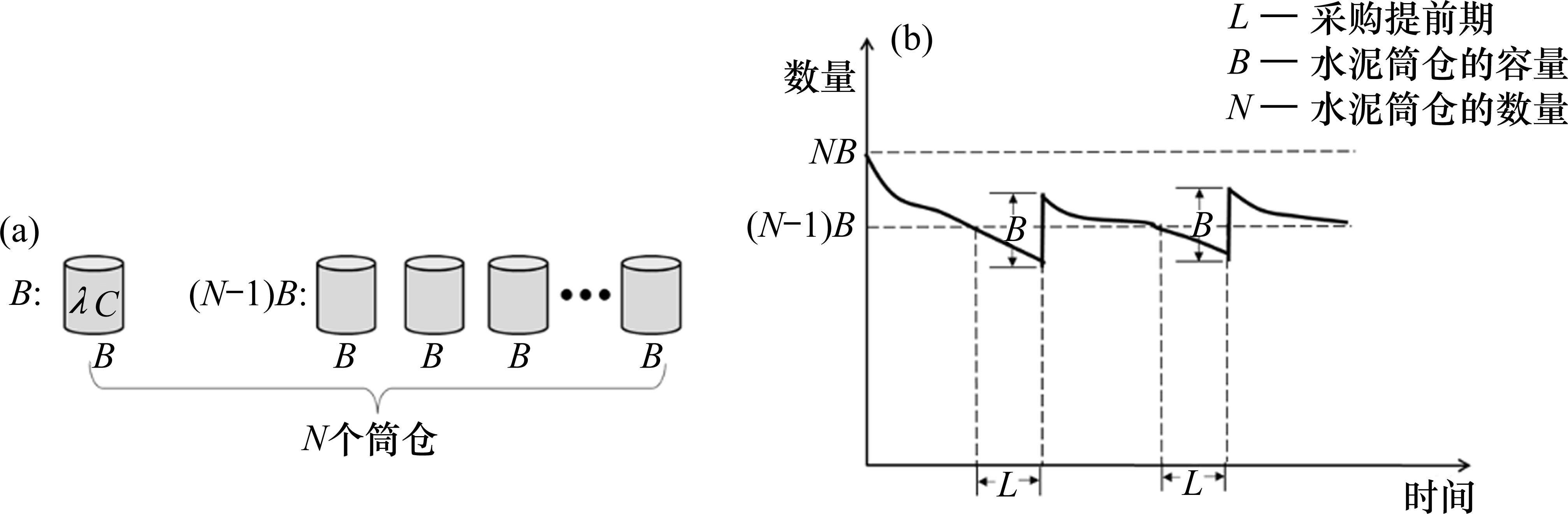
该模型同样只考虑存储成本和采购成本。
如图2(b)所示,第1个周期后的多等箱模型达到稳定状态。在稳定状态下,可以对该模型进行分析。
最低库存为
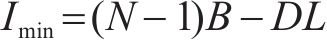
同双等箱模型,为了保证适当的客户服务水平(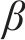
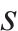
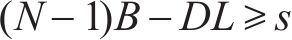
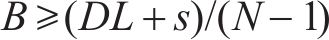
最高库存为
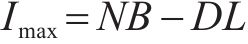
因此,可以得出平均库存量为
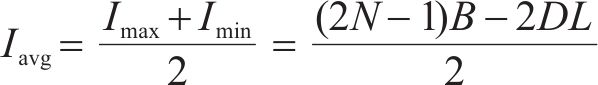
同样不考虑缺货的情况,库存总成本由库存持有成本和采购成本构成,可得到库存总成本为
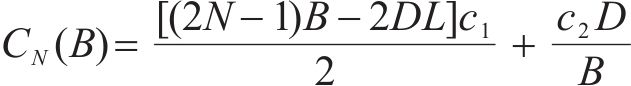
对式(11)1阶求导,并令导数为0,可以得到多等箱模型的最优订货批量,多等箱模型的最优订货批量为
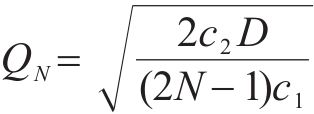
同样,考虑水泥的筒仓容量应为水泥罐车容量的正整数倍,用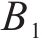
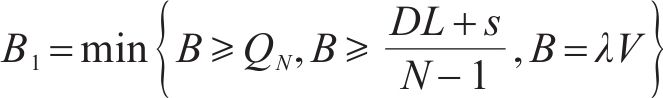
2 订货箱数可变的多等箱优化模型构建
2.1 采用连续检查库存控制策略的多等箱模型
采用连续检查库存控制策略的多等箱模型是在多等箱模式的基础上,考虑当实施多等箱系统时,对库存状态进行连续检查,当消耗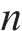
图3(a)为采用连续检查库存控制策略的多等箱示意图,其中最大总库存量为

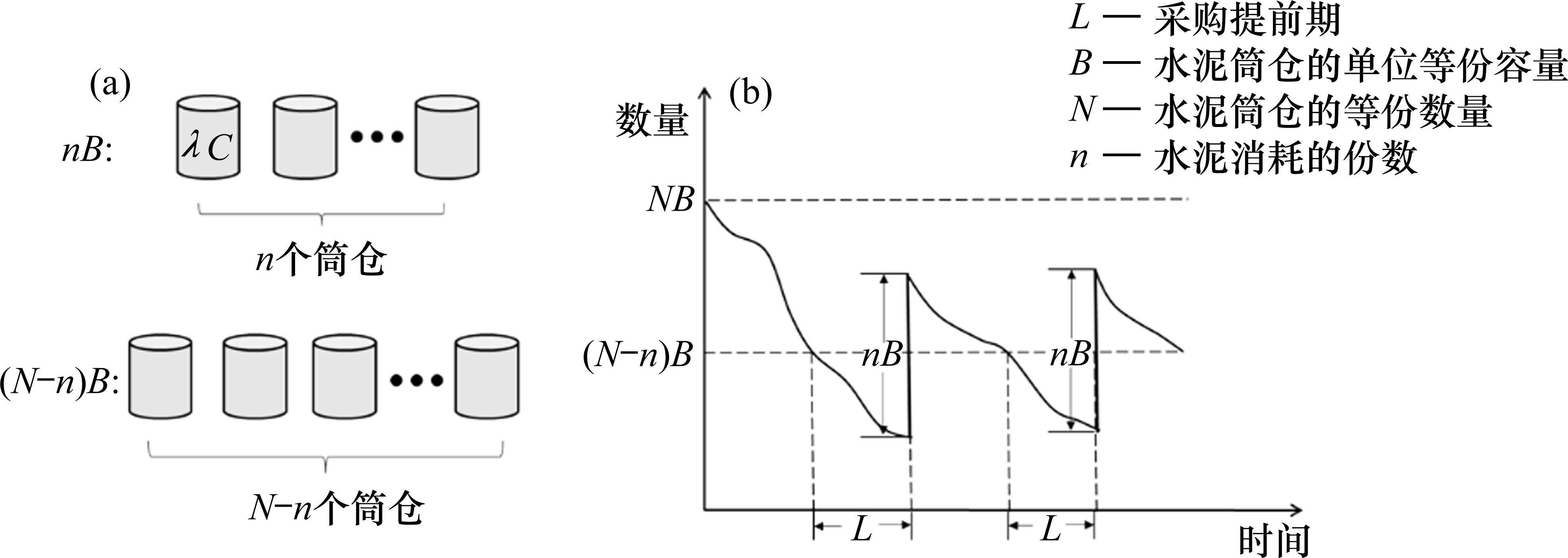
如图3(b)中所示,库存消耗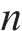
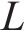
最低库存为
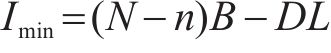
最低库存水平应大于安全库存,也就是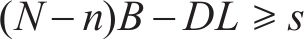
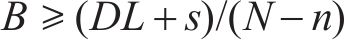
最高库存为
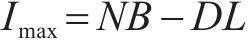
因此,可以得出平均库存为
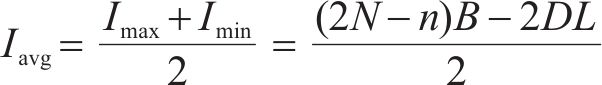
同样,不考虑缺货,库存总成本仅考虑库存持有成本和采购成本,库存总成本为
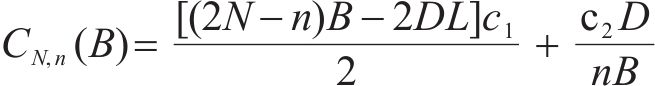
求式(17)1阶导的零点,可以得到采用连续检查的多等箱优化模型的最优订货批量,多等箱优化模型的最优订货批量为
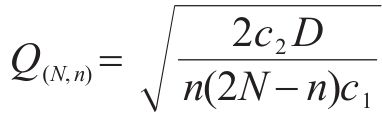
用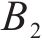
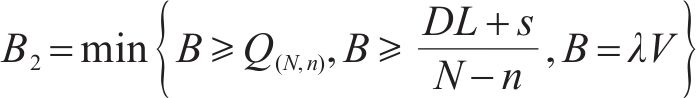
在采用连续检查库存控制策略的多等箱模型中,单批次采购量等于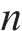
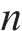
2.2 采用周期检查库存控制策略的多等箱模型
采用周期检查库存控制策略的多等箱模型是通过设定采购周期和最高库存量,从而达到库存控制的目的。周期检查的库存策略在某些情形下,相比连续检查库存策略更为适用,该模型示意图如图4。
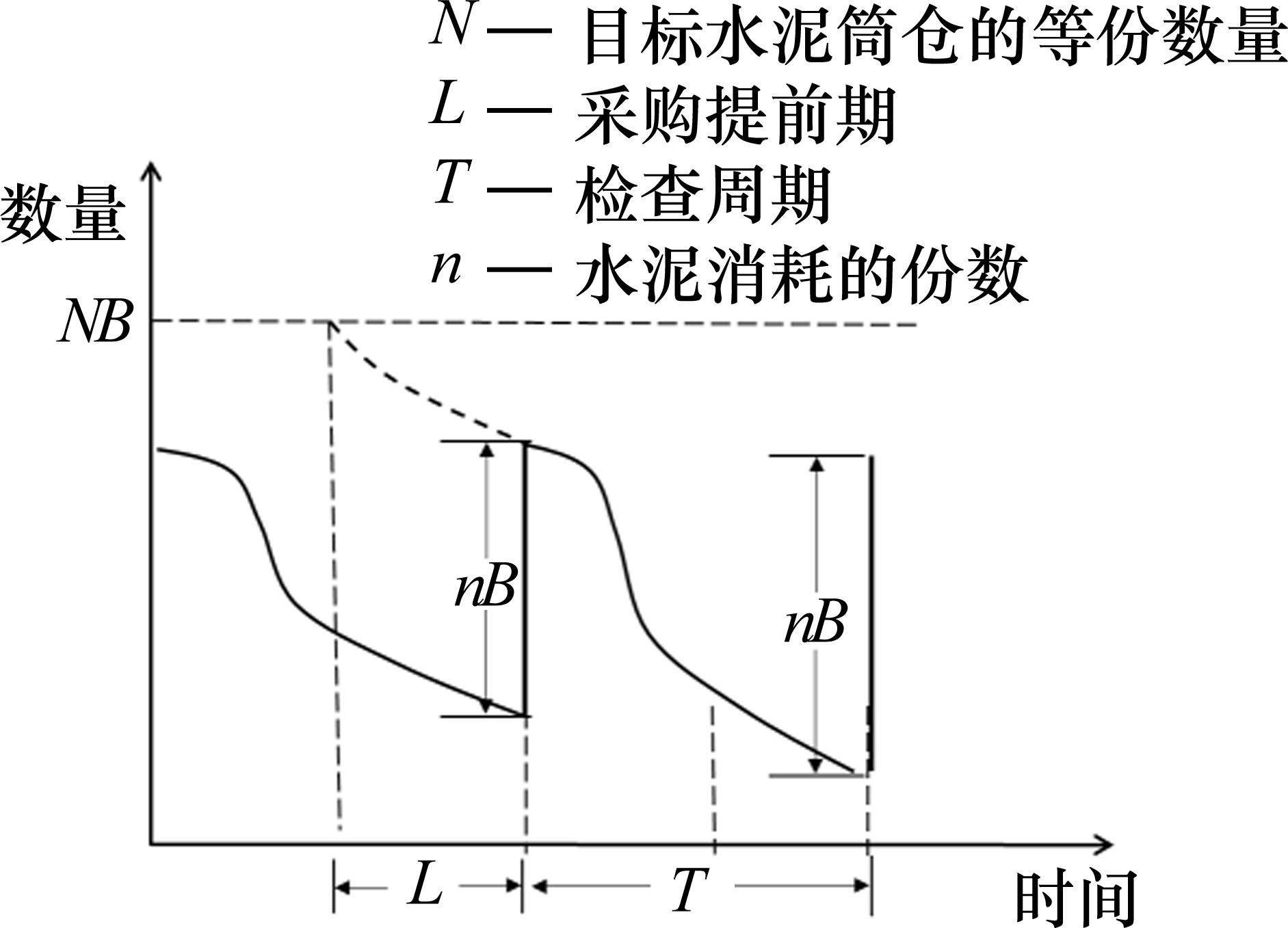
在该模型中,每个水泥筒仓容量为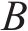

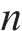
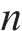
最高库存为
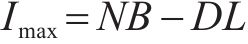
最低库存为
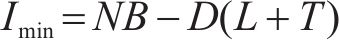
同样,安全库存如式(2),有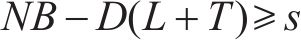
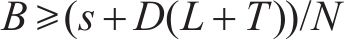
则平均库存应为
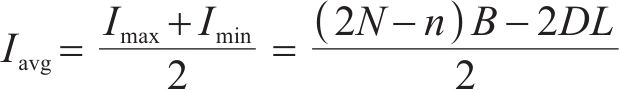
该模型中同样不考虑缺货成本,库存总成本由库存持有成本和采购成本构成,则库存总成本为
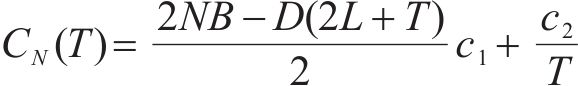
该模型的理想目标库存水平为
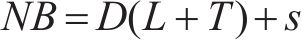
将式(24)代入式(23)求1阶导为0,得到该模型的最优采购周期为
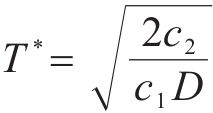
用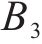
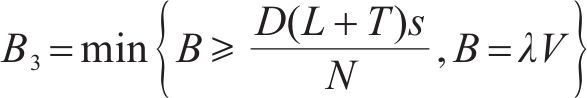
2.3 模型差异
在模型构建上双等箱模型和多等箱模型都是采用连续检查策略。采用连续检查策略的多等箱模型以及采用周期检查策略的多等箱模型是对多等箱模型的改进模型。几个模型的差别详见表2。
| 检查策略 | 最优筒仓容量 | 最大总库存量 | 单次订货批量 | |
|---|---|---|---|---|
| 双等箱模型 | 连续检查 | 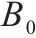 | 2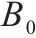 | 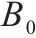 |
| 多等箱模型 | 连续检查 | 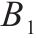 | 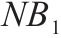 | 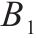 |
| 采用连续检查策略的多等箱模型 | 连续检查 | 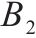 | 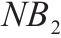 | 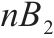 |
| 采用周期检查策略的多等箱模型 | 周期检查 | 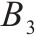 | 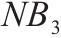 | 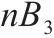 |
3 水泥等箱法模型算例求解及结果分析
3.1 数据准备
本文调研某一铁路工程建设项目工段,根据调研数据对水泥等箱法库存模型求解及分析。此项目日平均水泥需求为322.16 t,日均需求标准差约为86.20 t,水泥的正常运输时间为2 d,但在某些偏远地区道路运输时有中断,运输时间可能会达到4 d,设定采购提前期平均值为3 d,采购提前期的标准差为1 d,需求满足率为95%,则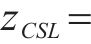
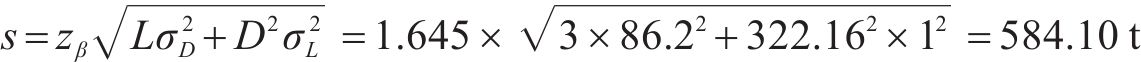
水泥库存控制的单位采购成本主要是运输价格、人工费用等多项费用构成,单位存储成本主要是筒仓的运营成本。水泥罐车一车可以装6~18 m3水泥,以8 m3为主,水泥的密度按照3.1 t/m3,通过计算得到水泥罐车的装载量为24.3 t。模型参数详见表3。
| 符号 | 参数说明 | 参数值 |
|---|---|---|
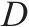 | 日平均需求量 | 322.16 |
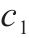 | 单位库存每日存储成本 | 0.5 |
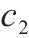 | 单次采购成本 | 5 000 |
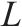 | 平均采购提前期 | 3 |
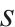 | 安全库存量 | 584.10 |
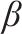 | 需求满足率 | 0.95 |
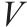 | 水泥罐车可承载重量 | 24.3 |
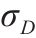 | 日需求量的标准差 | 86.20 |
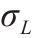 | 采购提前期的标准差 | 1 |
3.2 算例求解结果
1)双等箱模型
首先,按照上述参数,可以得到水泥双等箱模型单个筒仓容量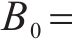
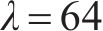
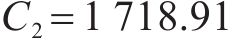
2) 多等箱模型
对于多等箱模型,先对不同的水泥筒仓数量
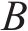
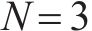
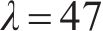
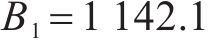

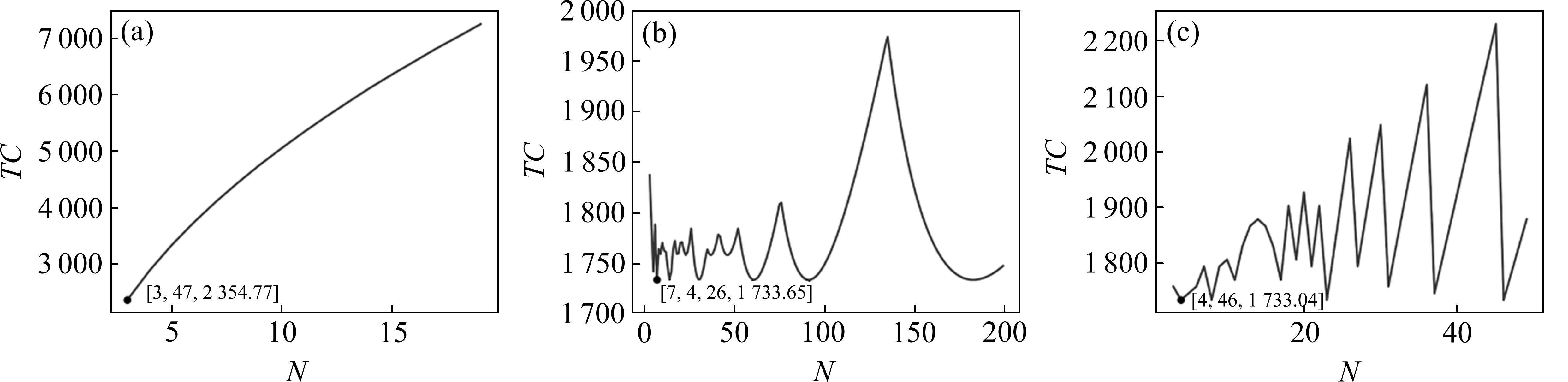
3) 采用连续检查库存控制策略的多等箱模型
对于采用连续检查库存控制策略的多等箱模型,具体求解步骤与多等箱模型相似。如图5(b)为采用连续检查库存控制策略的多等箱模型的库存总成本变化曲线,从该图中可以得到在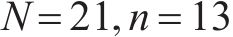
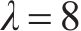
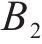


4) 采用周期检查库存控制策略的多等箱模型求解
针对采用周期检查库存控制策略的多等箱模型,可以发现求得的最优检查周期与水泥筒仓数量
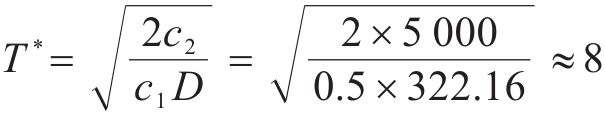
求解方式同采用连续检查的多等箱模型,如图5(c)所示为采用周期检查策略的多等箱模型的库存成本曲线,可以发现该模型同样存在多个极值,最低成本为1 562.94元,此时最优水泥筒仓数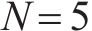
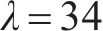
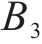
3.3 模型算例结果分析
一些铁路工程建设项目的水泥库存控制采用双箱法,以双箱为比较基准,对比不同模型的优化效果。多等箱模型在大批量订货,且需求不稳定的情况下并不适用,优化后的多等箱模型相比于双等箱模型对于铁路施工项目的成本管控有较大的增益,水泥库存成本降低比率可达9.07%,采用连续检查和周期检查策略的多等箱模型对成本的优化差异不大。分析双等箱、多等箱以及采用连续检查策略的多等箱模型主要的差别,设最大水泥筒仓数量
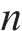
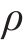
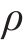
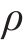
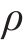
3.4 灵敏度分析
1) 水泥罐车容量
将水泥罐车容量按GB/T 5059中规定,取额定装载量中25、30、35、40以及45 t,可得到如表5所示结果。可以发现,水泥罐车容量对于不同库存模型的影响较小,对于库存策略的选择存在一定程度的影响,从结果上分析,在当前参数设定下,越大的水泥罐车装载量越易使周期检查所求得的目标库存
| 库存模型 | 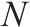 | 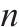 |  | 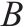 | 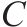 | 优化程度/% |
|---|---|---|---|---|---|---|
| 双等箱模型 | 2 | 1 | 64 | 1 555.20 | 1 718.91 | — |
| 多等箱模型 | 3 | 1 | 47 | 1 142.1 | 2 354.77 | 36.99 |
| 采用连续检查策略的多等箱模型 | 21 | 13 | 8 | 194.4 | 1 563.55 | -9.04 |
| 采用周期检查策略的多等箱模型 | 5 | — | 34 | 826.2 | 1 562.94 | -9.07 |
| 库存模型 | 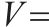 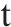 | 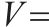  | 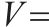 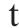 | 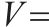 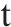 | 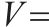 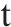 |
|---|---|---|---|---|---|
| 双等箱模型 | 1 721 | 1 719 | 1 721 | 1 719 | 1 721 |
| 多等箱模型 | 2 355 | 2 355 | 2 355 | 2 355 | 2 356 |
| 采用连续检查策略的多等箱模型 | 1 573 | 1 566 | 1 573 | 1 566 | 1 573 |
| 采用周期检查策略的多等箱模型 | 1 567 | 1 567 | 1 564 | 1 597 | 1 564 |
2) 需求和采购提前期
用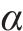
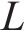
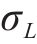
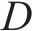
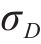
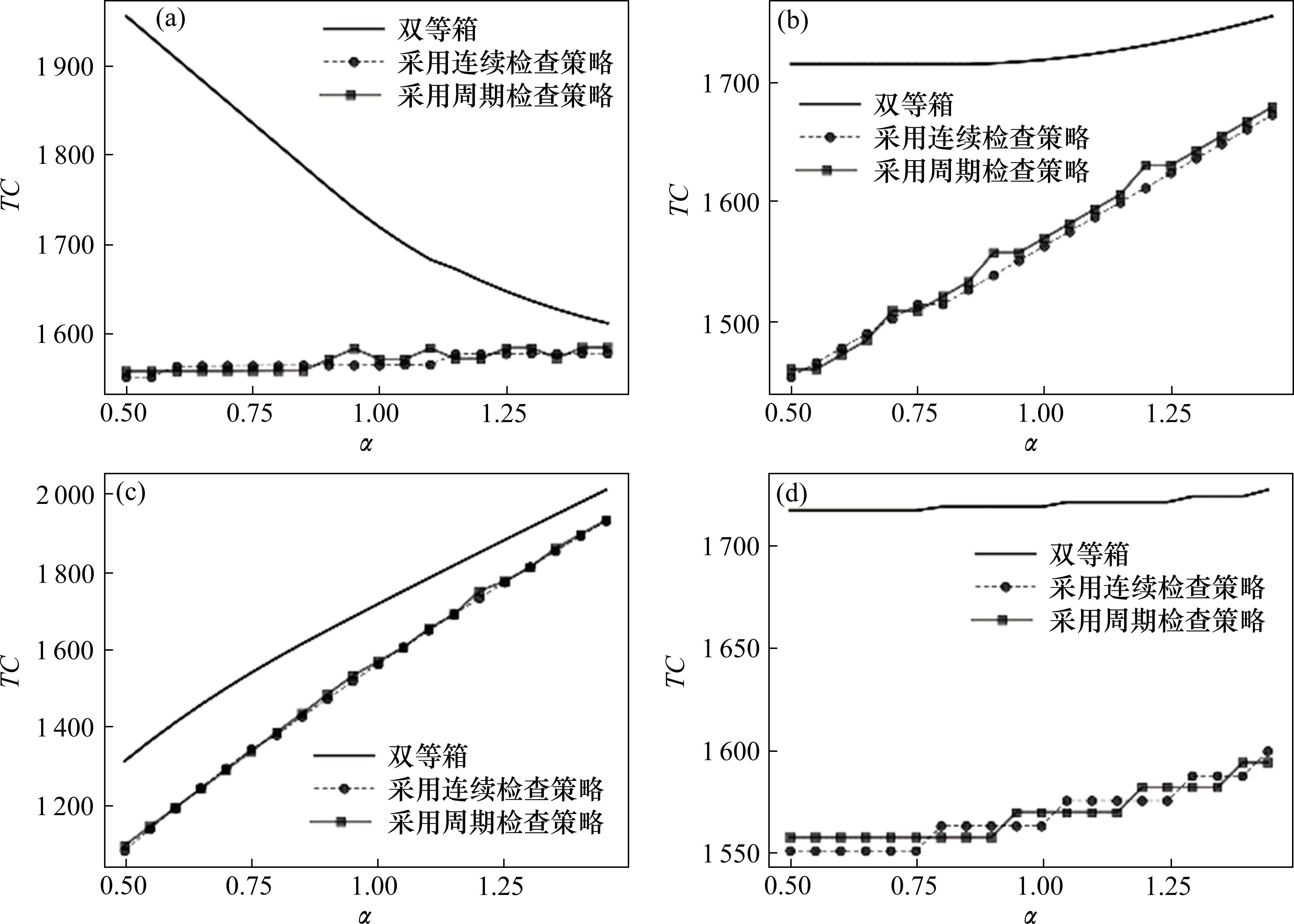
从结果中可以看出,采购提前期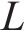
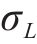
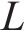
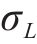
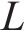
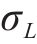
需求量标准差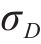
3.5 筒仓储备数量仿真模拟分析
在实际的生产过程中,由于需求量以及提前期的波动,水泥筒仓可能会出现准备过多或者准备不足的情况。水泥罐车到达时,需要立即卸货,因此需要对水泥筒仓的储备数量进行进一步的研究。
1) 仿真逻辑
该节中,通过仿真程序实现对铁路施工现场水泥库存变化的模拟,记录每日水泥库存量,从而获得水泥筒仓使用量,为避免水泥到达时无法存储的情况,水泥筒仓最优储备量应为水泥筒仓使用量的最大值。当前筒仓满足率即为当前水泥筒仓储备量占最优筒仓储备量的百分比。最优储备量水泥筒仓利用率即为水泥平均每日库存量占最优水泥筒仓储备容量的百分比。当前水泥筒仓利用率即为水泥平均每日库存量占当前筒仓储备容量的百分比。依据表3中的参数设定以及表4中的水泥筒仓数量和容量对水泥筒仓储备数量进行仿真。
2) 仿真结果
重复实验1 000次,最终结果如表6所示。双等箱库存控制策略在实际的运作中,常常将多个相同大小的水泥筒仓分为2等份,一部分作为储存仓,一部分作为订购仓,在仿真中考虑这一点,由于设定水泥筒仓容量只能为整数倍的水泥罐车容量,在需求满足率为0.95的情况下,考虑共使用2、4、8和16个水泥筒仓对项目库存成本、管理效率和服务水平的影响。从结果中可以发现,对于双等箱模型而言,水泥筒仓数量越多,水泥筒仓的满足率越高,当前筒仓利用率越低。但在水泥筒仓理论储备量
| 库存模型 | 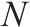 | 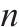 | 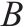 |  | 最优筒仓储备量 | 当前筒仓满足率/% | 最优储备量筒仓利用率/% | 当前筒仓利用率/% | |
|---|---|---|---|---|---|---|---|---|---|
需求满 足率=0.95 | 双等箱模型 | 2 | 1 | 1 555.20 | 64 | 3 | 66.7 | 53.08 | 79.64 |
| 4 | 2 | 777.6 | 32 | 5 | 80 | 53.54 | 66.87 | ||
| 8 | 4 | 388.8 | 16 | 10 | 80 | 48.49 | 60.66 | ||
| 16 | 8 | 194.40 | 8 | 20 | 80 | 46.00 | 57.47 | ||
| 采用连续检查策略的多等箱模型 | 21 | 13 | 194.40 | 8 | 21 | 100 | 55.33 | 55.33 | |
| 采用周期检查策略的多等箱模型 | 5 | — | 826.20 | 34 | 5 | 100 | 52.63 | 52.63 | |
需求满 足率=0.99 | 双等箱模型 | 2 | 1 | 1 895.40 | 78 | 3 | 66.7 | 55.17 | 82.80 |
| 4 | 2 | 947.7 | 39 | 5 | 80 | 56.22 | 70.29 | ||
| 12 | 6 | 315.9 | 13 | 14 | 85.7 | 53.06 | 61.95 | ||
| 采用连续检查策略的多等箱模型 | 7 | 4 | 631.8 | 26 | 7 | 100 | 63.63 | 63.63 | |
| 采用周期检查策略的多等箱模型 | 4 | — | 1 117.8 | 46 | 4 | 100 | 59.11 | 59.11 |
而采用连续检查和采用周期检查策略的多等箱模型筒仓满足率均为100%,也就是说,在采用周期检查和连续检查策略的多等箱模型中,不需要额外储备水泥筒仓,从而减少资金占用,且在需求满足率为0.95和0.99这2种情况下,采用连续检查策略的多等箱模型水泥筒仓最优储备量下的利用率均为最大,分别为55.33%和63.63%。筒仓满足率与筒仓利用率是相背相反的2个指标,筒仓满足率高则会带来筒仓利用率的下降,筒仓满足率低,则会带来筒仓利用率的上升。需求满足率的增高会带来水泥储备量的增加,从而带来更高的库存成本,追求更高服务水平的同时,需要权衡库存成本和资源利用效率。对于该问题背景下,需求满足率为0.99相比于0.95降低了多等箱优化模型的最优筒仓量
4 结论
1) 针对水泥库存控制中的批次限制和筒仓的整数库存特性,分别建立订货箱数不可变的双等箱模型和多等箱模型,并针对其订货箱数不可变的特点进行优化,构建了订货箱数可变的多等箱模型。通过对比,本文发现多等箱库存优化模型对于水泥库存控制这种大批量订货的物资更为适用。
2) 本文还考虑了水泥筒仓的容量与水泥运输罐车的整数关系,水泥罐车容量倍数系数的加入使库存成本曲线随着水泥筒仓数量的增加呈现非常规变动,存在多个峰值,难以通过理论推导。水泥罐车装载量的变化对于不同库存模型的成本影响较小,但是越大的水泥罐车装载量越易使周期检查所求得的目标库存远离最优值,由此连续检查策略在水泥罐车装载量较大的情况下更为适用。
3) 仿真结果表明,在采用周期检查和连续检查策略的多等箱模型中,不会由于水泥筒仓的额外储备造成资金占用,且采用连续检查策略的水泥筒仓的利用率也略有提高。筒仓满足率与筒仓利用率、需求满足率与库存成本是相背相反的2个指标,在进行决策时应该权衡,追求更高服务水平的同时,需要权衡库存成本和资源利用效率。在水泥拌合站设计时,可以采用容量较小、数量较多的筒仓,并使水泥筒仓和水泥罐车成整数倍数关系,这样筒仓利用率会比较高,在一定程度上降低库存成本。
研究不仅局限于水泥物资,其提出的等箱系统库存控制策略选择对其他罐体存储的物资同样具有借鉴意义。在后续的工作中,应结合具体应用情况对不同的库存控制模型进行选择。
谭雪,鲁晓春,倪铮.基于批次管理的铁路施工水泥库存控制研究[J].铁道科学与工程学报,2025,22(01):392-403.
TAN Xue,LU Xiaochun,NI Zheng.Research on batch management-based inventory control of cement in railway construction[J].Journal of Railway Science and Engineering,2025,22(01):392-403.

