铁路上常常使用大型养路机械(简称大机)来进行线路的养护维修作业。大机施工作业具有重复性和线性的特点,可以利用多个机组(工作队)共同完成维修作业来提高维修速率,以满足不断增长的维修需求,适合使用线性调度技术[1]中能够处理多工作队情形的平衡线法(line of balance,LOB)进行求解[2-6]。TANG等[7]提出一种基于LOB的资源均衡调度优化模型,能够直观展示多工作队的施工进展情况,便于项目进度管理和控制。DAMCI等[8]在LOB方法中设计了自然节奏和最佳工作队规模,以确保工作队的闲置时间最小。项目调度的两大目标是工期优化[9]和资源优化[10],许多研究者对重复性项目的工期和资源进行了研究。ZHANG等[11]在满足总工期的情况下进行资源优化配置。HYARI等[12]提了一种工期的多目标优化模型,并利用多目标遗传算法进行求解。LONG等[13]设计了改进的遗传算法能够对工期最优或者成本最优进行搜索优化。EI-RAYES等[14]提出了时间-费用-质量三者的优化模型。资源均衡虽然被大多数研究者关注[15-16],但有些研究没有将每日资源使用量峰值作为约束条件,可能会导致资源闲置[17],有些研究没有使用LOB方法,只采用单一的施工方式和单一的施工人员进行作业[18]。因此,本文构建基于LOB的大机施工调度工期最短-资源均衡双目标模型,并且引入自然节奏和最佳工作队规模,以及将每日资源使用量峰值作为约束条件,旨在同时实现工期和资源的优化。研究人员以往常采用线性规划、整数规划和分支定界法等精确算法对模型进行求解,但此类算法耗时且建模相对困难,一般只能得到小规模问题的最优解,但难以求解大规模问题。后来研究者开始尝试使用遗传算法[19]、模拟退火算法[20]、蚁群算法[21]等启发式算法[22-23],虽然可行解的求解速度较快,但是解决方案的质量难以保证且缺乏约束的通用处理方法。近年来,约束规划(constraint programming,CP)方法逐渐发展,适合于算法解决组合问题以及具有大量变量和约束条件且收敛速度缓慢的约束满足问题[24]。LIU等[25]采用CP进行优化取得了较启发式更优的结果。因此,本研究采用CP方法,并改进其搜索策略,提高搜索效率,解决基于LOB的大机施工调度的工期最短-资源均衡优化问题。
1 基于LOB的大型养路机械施工调度
大机类型一般有捣固车[26]、清筛机、配砟整形车、动力稳定车、钢轨打磨车[27]等,常通过机组的形式开展作业,即将多台不同类型的机械组合完成作业。大机作业包括捣固、打磨、清筛等若干作业,捣固作业是4 km/d,打磨作业是10 km/d,清筛作业是1 km/d[28]。活动是指大机的某个作业,如捣固作业即为一个活动。LOB方法是将一个活动按照空间距离分解成多个相同的单元,同一个活动中各个单元的持续时间(单元的开始时间到结束时间)相等,比如将20 km的大机捣固作业划分成5个单元,那么每4 km的大机活动就可以认为是一个单元,规定一个单元只能由一个工作队独立完成,这里工作队就是指大机机组。如图1所示,LOB图中的每一个斜柱代表相对应的一个活动,斜柱的边界是活动的开始时间和结束时间,斜柱的宽度是单元持续时间,缓冲时间是不同活动之间应对不可预测情况需要的额外时间。只要在每个活动中保持最佳工作队规模(每个大机机组的机械数量和相应的工人数量),即每个活动所有单元的施工速率保持一致,则每个单元的持续时间是相同的。建立LOB计划的第1步是估算一个单元所需的工时并计算出一个单元持续时间,确定最佳的工作队规模和每个活动的每日工作时间。第2步是确定一个活动各个单元的开始和结束时间。
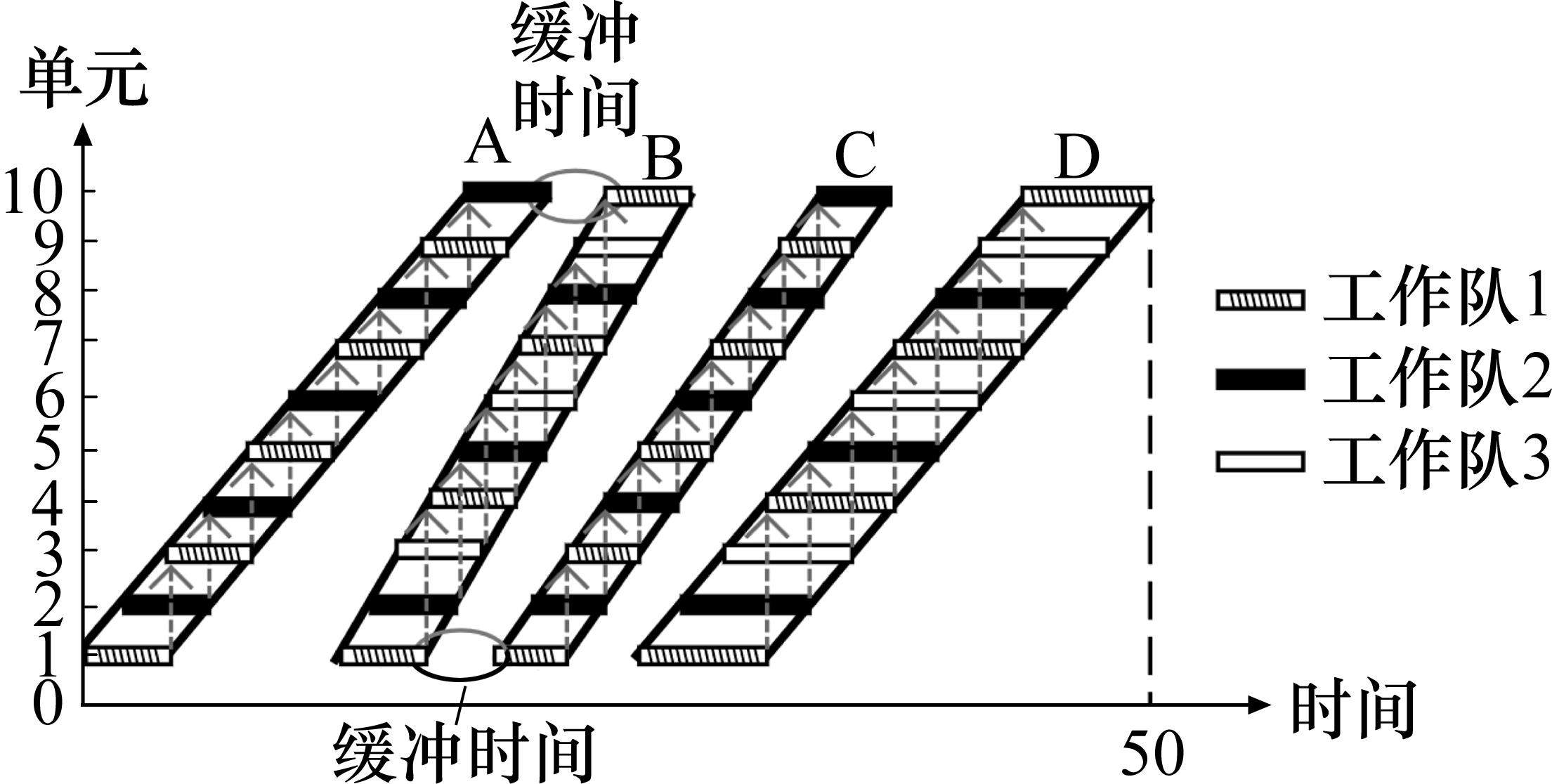
“自然节奏”是指必须使用最佳工作队规模提高施工速率,且要求同一个工作队从一个单元移动到下一个单元时不能产生空闲时间,随着工作队数量增多,施工速率也会随之变高(斜线变陡)。如图1所示,活动A中工作队1只有完成单元1的作业后才能进行单元3的作业,工作队1没有闲置(没有空闲时间)。而活动B中可以在单元1的作业未完成时直接由工作队3开始单元3的作业,因此活动B的施工速率比活动A有所提高。活动C和活动A、活动D和活动B的工作队数量一样,但是单元持续时间不一样,活动C的斜率高于活动A,活动D的斜率低于活动B。“自然节奏”原则允许在不违反活动优先级的前提下,通过调整活动的工作队数量,改变活动中不同单元的开始时间。“自然节奏”原则因在实际中很难实现,从而被大多数线性调度问题的研究者忽视,但可以通过很容易获取并记录的已经完成项目的活动开始和结束时间、工作队规模和每日工作时间的信息,估计不同活动的最佳工作队规模。获取活动名称、单元数量、缓冲时间、最佳工作队规模、每日工作时间、工作队数量以及一个单元所需的施工时间等必要信息后,一个活动每单元的持续时间等于其所需施工时间除以最佳工作队规模的每日工作时间。每个活动的施工速率是由单元持续时间和工作队数量计算的,且限制为自然节奏的倍数[29]。在计算活动的单元持续时间和施工速率后,计算每个单元的开始和完成时间。一旦建立了所有活动的单元开始时间和结束时间,并且设置优先级关系,就可以绘制出一个活动只使用一个工作队完成各单元工作的初始LOB图。如果初始LOB图确定的最终计划时间超出指定的工期,可以通过分配更多的工作队来加快施工。根据TOKDEMIR等[30]的建议,将所有活动按照每个单元的持续时间降序进行排列,并为其中单元持续时间较长的活动分配更多的工作队来提高施工速率,当计划时间等于或小于指定的工期时,进程停止。在建立了LOB图后,绘制每个资源的资源直方图。
2 基于LOB的工期最短-资源均衡双目标模型建立
2.1 模型建立
1) 符号说明
模型的符号说明如表1所示。
| 符号 | 说明 | 符号 | 说明 |
|---|---|---|---|
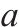 | 所涉及的活动数量 | 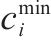 | 第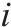 |
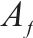 | 第1个活动 | 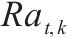 | 第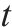 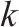 |
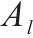 | 最后一个活动 | 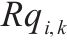 | 分配给第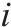 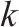 |
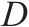 | 总工期 | 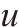 | 一个活动包含的单元数量 |
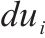 | 第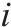 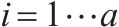 | 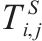 | 第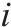 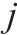 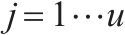 |
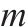 | 资源的类型数量 | 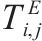 | 第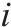 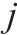 |
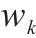 | 第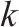 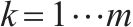 | 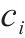 | 活动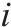 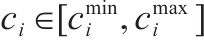 |
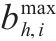 | 第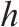 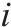 | 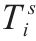 | 活动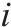 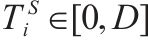 |
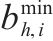 | 第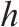 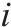 | 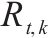 | 表示第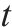 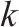 |
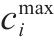 | 可用于第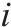 | 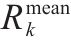 | 第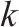 |
2) 决策变量
模型的决策变量是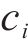
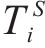
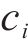
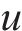
3) 目标函数
① 最小工期:保证所需总工期最短。
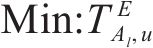
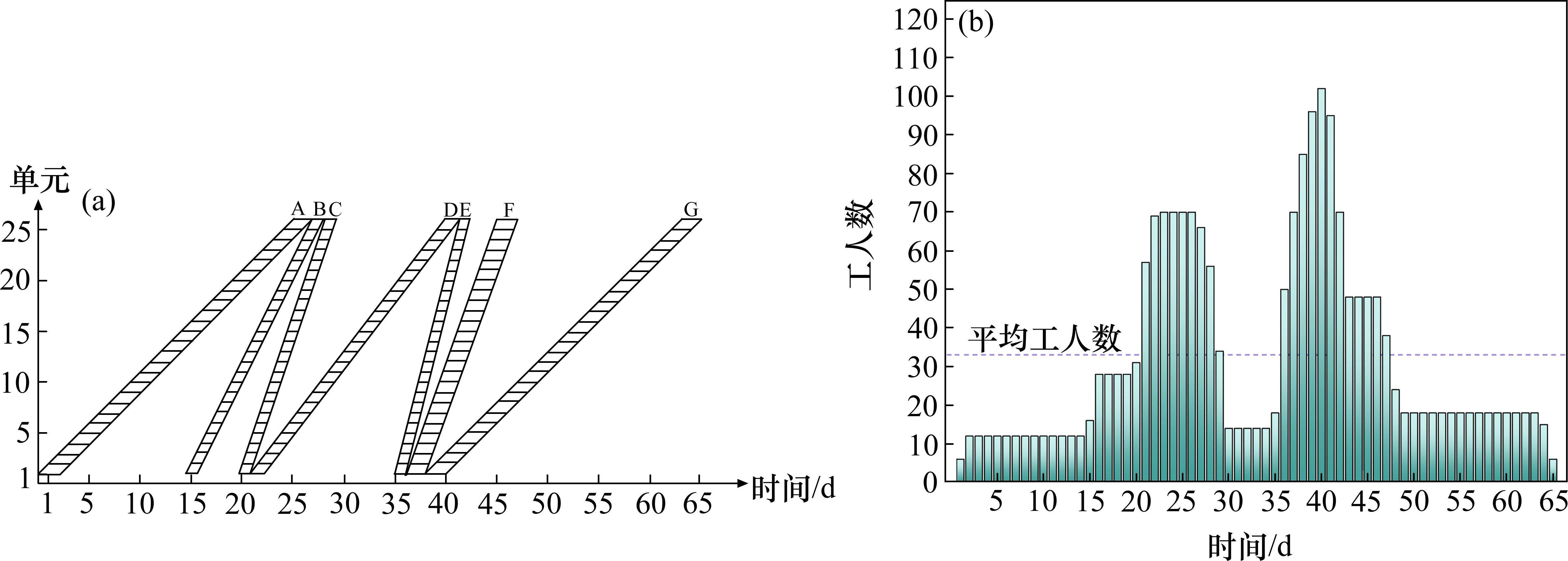
② 资源均衡:所有资源类型的每天资源使用量和平均日使用量之差的绝对值之和最小。
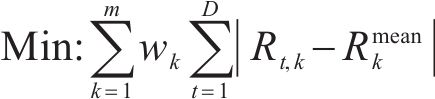
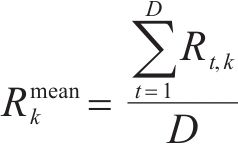
4) 约束条件
① 工期约束:
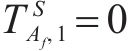
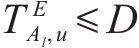
② 工作队连续性约束:
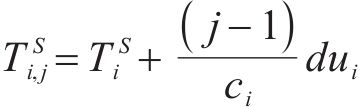
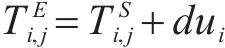
③ 缓冲区约束:
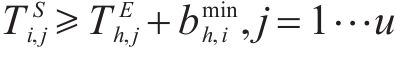
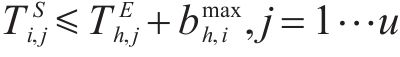
④ 时间依赖性约束:指活动的每个单元必须在前一个活动的同一单元完成后执行。
时间依赖性约束可以用同时存在2个活动之间的最小/最大缓冲区来代替。如图2(a)所示,最小缓冲区设置为0,活动B和C的速率允许在最大缓冲区内(阴影区域)变化,且可以与它的前一个活动速率不相同,因此可以实现活动B和C的自然节奏,不产生空闲时间。
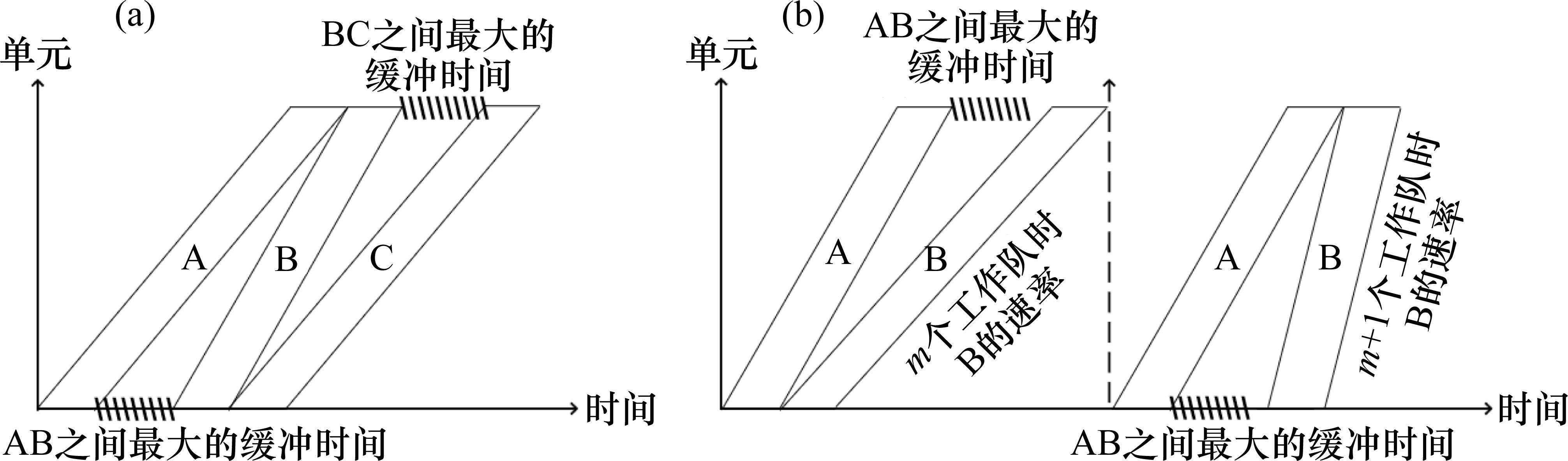
但是工作队数量的整数特征会导致速率离散而非连续,可能存在改变工作队数量却不能够满足时间依赖性约束的最小/最大缓冲区情形。如图2(b)所示,活动B有m个工作队,此时最后一个单元违反了最大缓冲约束。如果增加一个工作队,此时第1个单元又违反了最大缓冲约束。这种情形下就必须引入一个空闲时间(图3活动C中的工作队闲置时间),改变缓冲区的大小,使速率保持在m个工作队和m+1个工作队的速率之间,以满足时间依赖性约束。
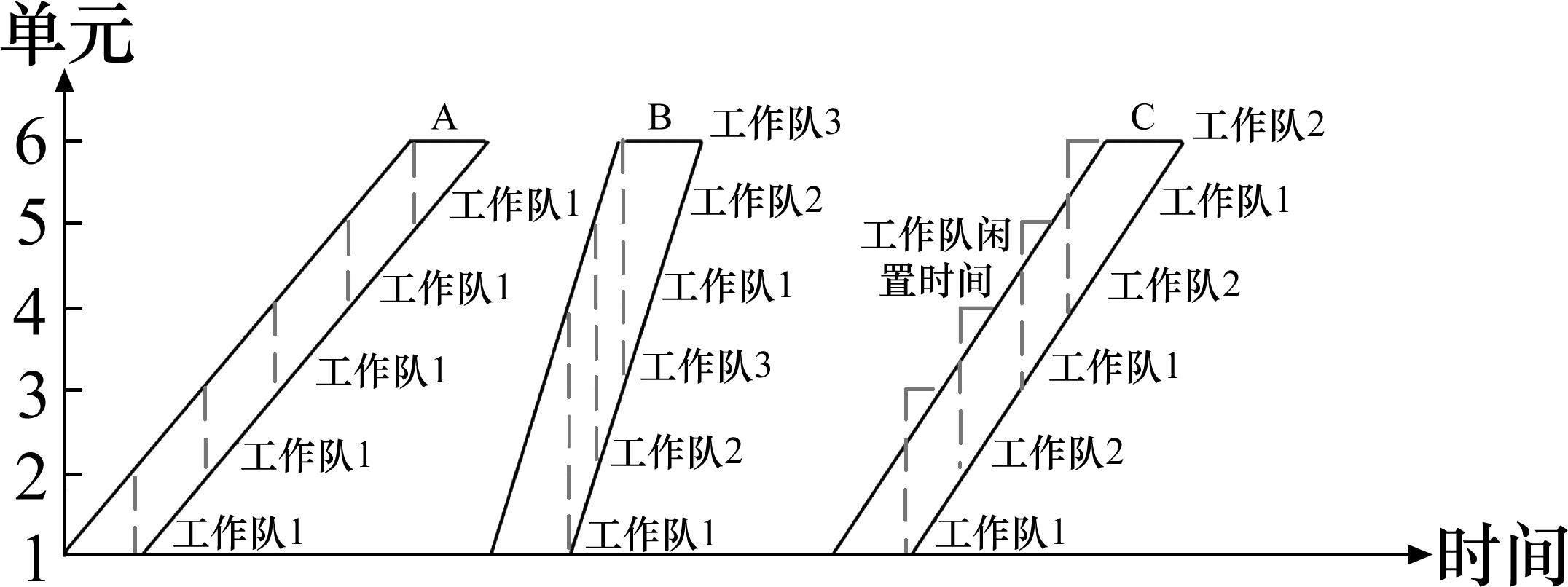
对此,首先限制分配给活动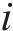
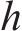
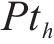
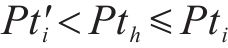
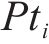
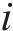
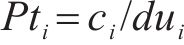
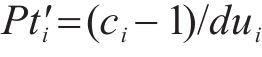
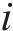
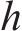
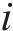
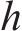
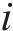
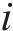
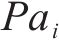
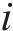
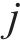
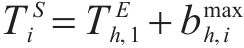
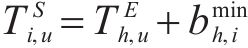
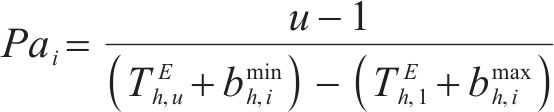
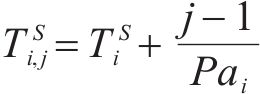
⑤ 工作队可用性约束:通过设置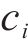
⑥ 资源约束:第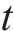
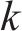
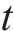
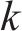
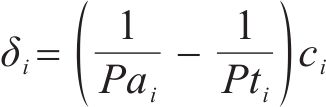
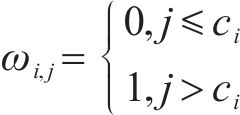
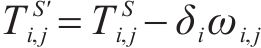
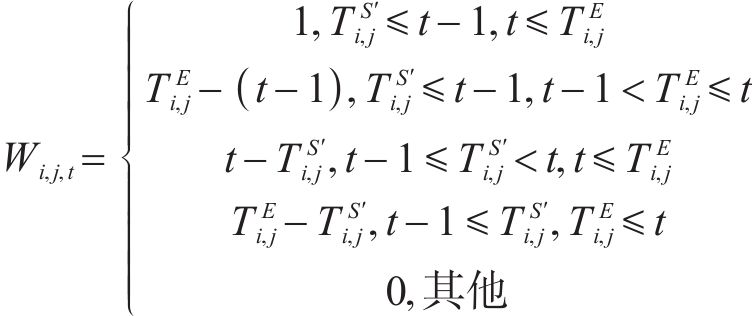
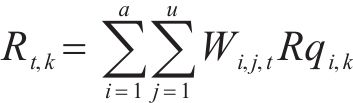
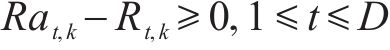
其中,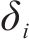
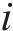
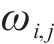
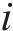
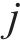
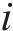
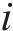
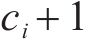
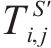
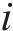
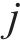
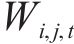
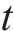
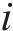
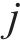
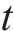
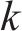
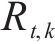
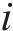
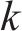
2.2 多目标优化
提高最优资源均衡优化目标的水平有助于提高项目整体资源利用率,进而降低总成本。然而,通常情况下,总成本的降低可能会导致项目总工期的增加。因此,资源均衡和工期最短之间存在着冲突。本文通过线性加权法,对多目标优化问题中的各个目标归一化后赋予适当的权重,即工期权重系数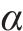
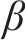
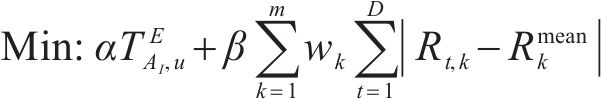
3 基于改进约束规划的求解方法
3.1 基于随机重启的约束规划改进
约束编程(CP)是一种有效解决和优化调度问题的方法,特别适用于具有非线性约束、逻辑语句或非凸解空间特征的问题。其声明性逻辑语言和约束表示能力使其在处理现实世界复杂性方面表现出色。CP利用搜索策略和约束规划机制解决约束满足问题,通过逐步为变量寻找值并减少搜索空间来提高搜索效率。常见的搜索算法包括生成-测试法和回溯搜索,但效率较低[18]。为改善搜索效率,引入随机重启策略,周期性地随机重置搜索状态,以增加搜索多样性,提高发现更优解的可能性。随机重启策略步骤:1) 初始化当前解和最优解;2) 在每次迭代过程中,寻找当前解周围的邻域,采用相应的策略选择新解;3) 一旦新解比当前解更优,就更新当前解,并且在必要情况下会更新最优解;4) 如果迭代次数达到了重启间隔,则进行随机重启,重新形成初始解,并且重置迭代计数器;5) 重复执行步骤2至4,直到满足终止条件。
3.2 模型对比验证
根据DAMCI基于LOB的资源均衡研究[10],项目共分为26个单元,每单元需进行7项活动,总工期65 d。资源类型只考虑人力资源,即工人数量。活动信息如表2所示。项目没有进行优化前的初始LOB图和初始资源直方图如图4所示,最大工人数102,最小工人数为6,平均工人数为33,对于初始资源直方图,资源日常使用和平均使用之差的绝对值之和为1 404。
| 活动 | 单元所需时间/h | 最佳工作队规模/人 | 每日工作时间/h | 单元持续时间/d | 工作队数量 | 实际速率/(km∙d-1) |
|---|---|---|---|---|---|---|
| A | 96 | 6 | 8 | 2 | 2 | 1 |
| B | 64 | 8 | 8 | 1 | 2 | 2 |
| C | 80 | 10 | 8 | 1 | 3 | 3 |
| D | 84 | 7 | 8 | 1.5 | 2 | 1.33 |
| E | 80 | 10 | 8 | 1 | 4 | 4 |
| F | 96 | 6 | 8 | 2 | 5 | 2.5 |
| G | 144 | 9 | 8 | 2 | 2 | 1 |
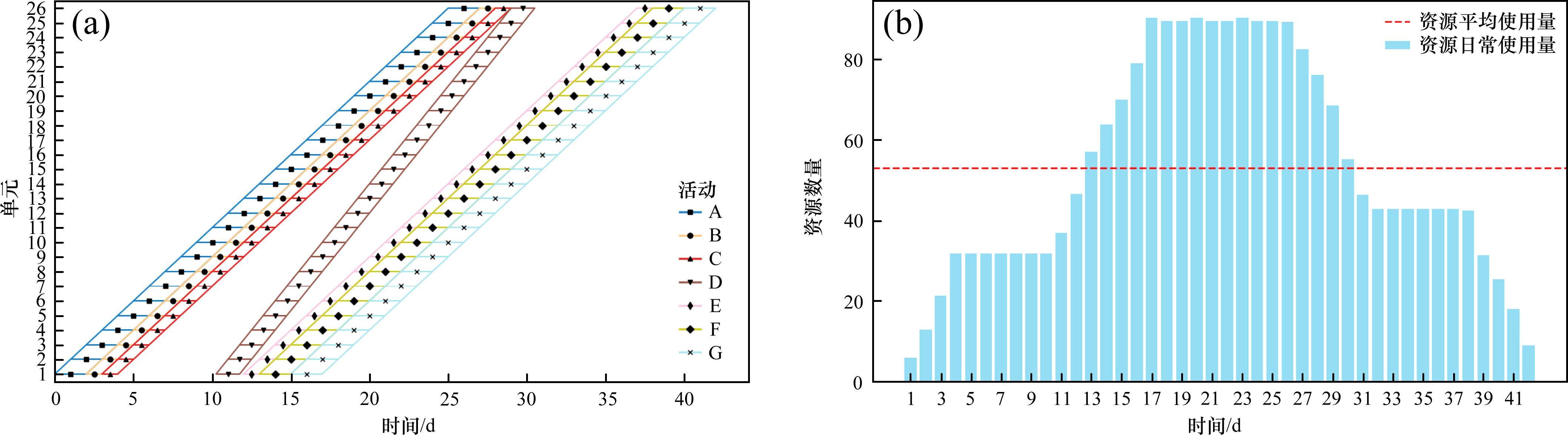
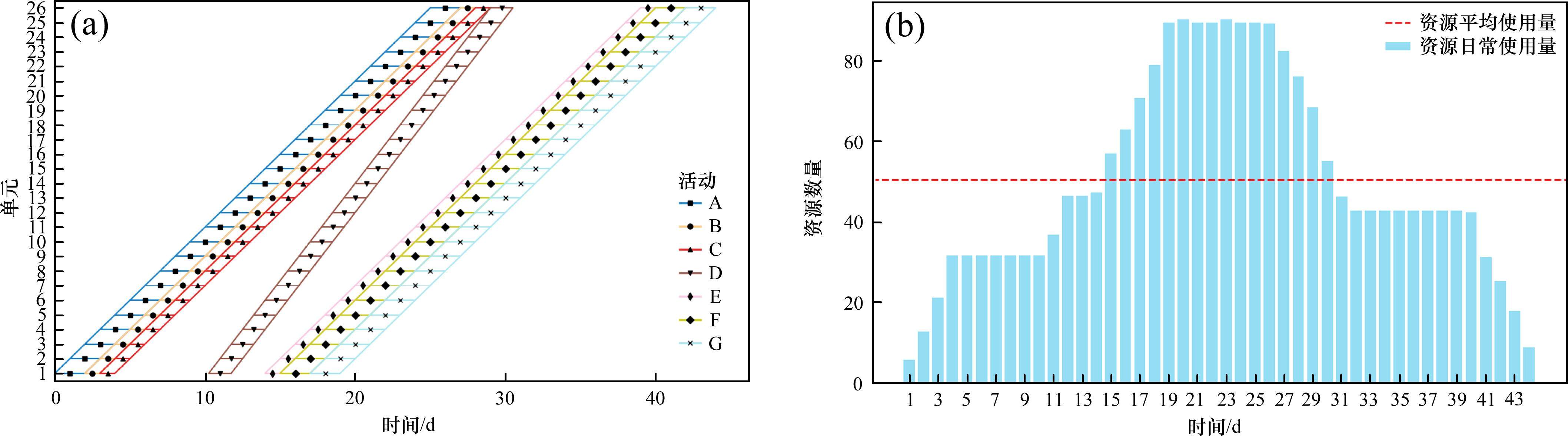
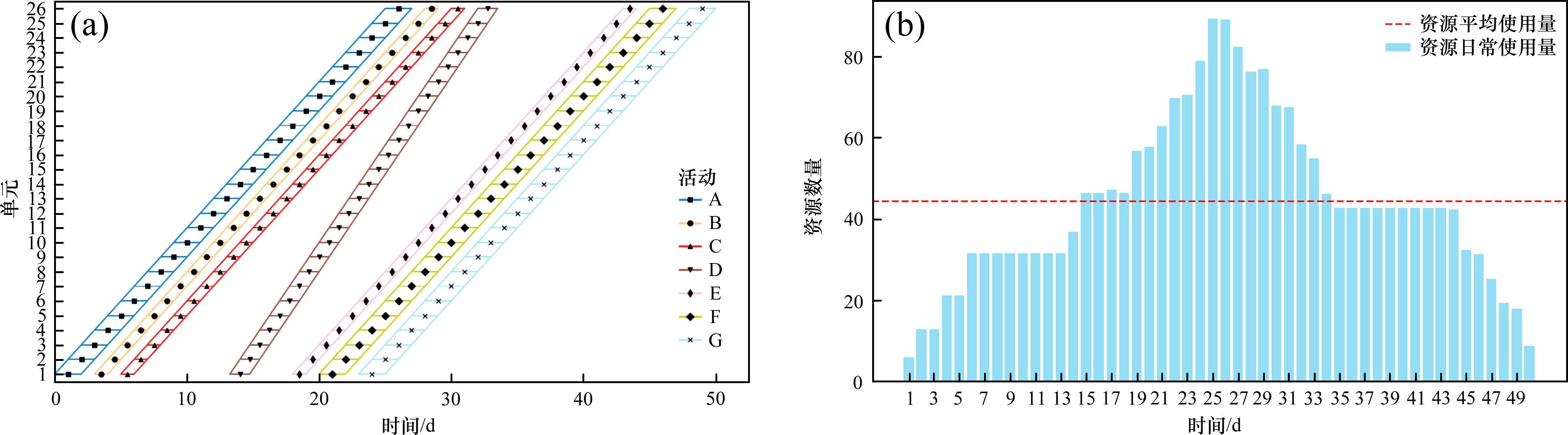
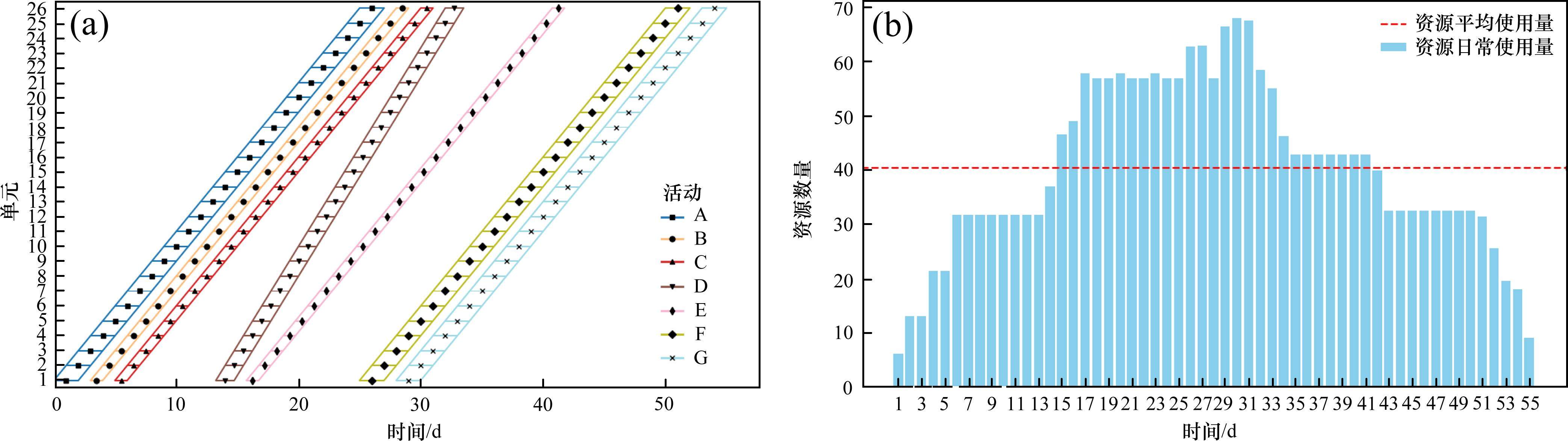
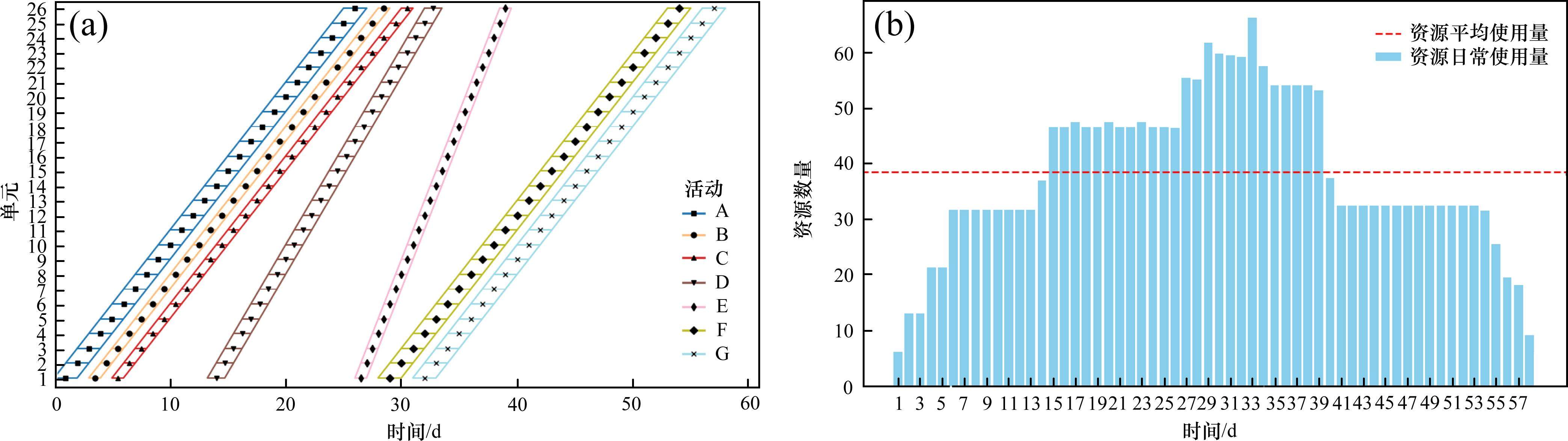
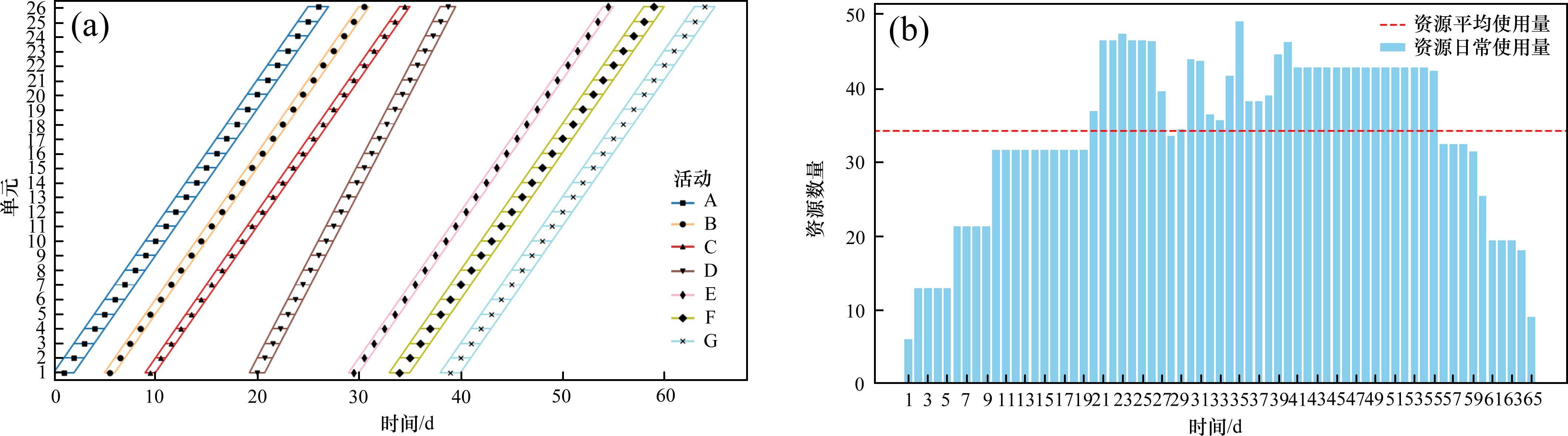
通过改变工期最优和资源均衡的权重系数,权衡工期最优和资源均衡。因该工期的范围为0~65,资源日常使用和平均使用之差的绝对值之和范围为0~1 404,通过归一化后与权重系数相乘求最小化。不同权重系数下的优化结果如表3所示,相应的LOB图和资源直方图如图5~10。β从0到1的过程中,资源均衡的效果逐渐增强,资源波动逐渐减小,优化后的最大工人数均明显小于原始的最大工人数102,资源日常使用和平均使用之差绝对值之和也明显小于原始的1 404,在资源均衡这一目标上有明显优越性。当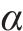
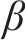
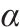 | 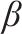 | 工期/d | 资源日常使用和平均使用之差的绝对值之和 | 目标函数值 | 最大工人数 | 最小工人数 | 平均工人数 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 42 | 989 | 0.646 | 89 | 6 | 53 |
| 0.8 | 0.2 | 44 | 919 | 0.672 | 89 | 6 | 50 |
| 0.6 | 0.4 | 50 | 809 | 0.692 | 89 | 6 | 44 |
| 0.4 | 0.6 | 55 | 727 | 0.681 | 67 | 6 | 40 |
| 0.2 | 0.8 | 58 | 685 | 0.649 | 67 | 6 | 38 |
| 0 | 1 | 65 | 585 | 0.416 | 48 | 6 | 34 |
4 案例分析
本研究采用一个43 km的铁路线路集中修进行案例分析,共有换轨大修、大机清筛、大机捣固、钢轨预打磨4个活动,各自的实际施工速率为2.40、1.20、4.00和5.00 km/d,共有40 d[31]。清筛机组配置2台清筛车、3台捣固车、1台配砟车、1台稳定车,维修捣固机组配置2台捣固车、1台稳定车、1台配砟车,打磨钢轨配置1台打磨列车,换轨大修机组配置1台大修列车、1台捣固车、1台配砟车[32]。每1 km公里为一个单元,其最小缓冲时间、工作队数量取值范围、施工速率等活动信息如表4。
实际施工调度计划如表5所示,根据数据绘制的LOB图如图11所示,能直观展示施工进度。
| 活动代号 | 活动名称 | 工作队数量 | 开始时间/d | 结束时间/d | 工期/d |
|---|---|---|---|---|---|
| A | 换轨大修 | 1 | 0 | 18 | 18 |
| B | 大机清筛 | 1 | 1 | 37 | 36 |
| C | 大机捣固 | 1 | 28 | 39 | 11 |
| D | 钢轨预打磨 | 1 | 31 | 40 | 9 |
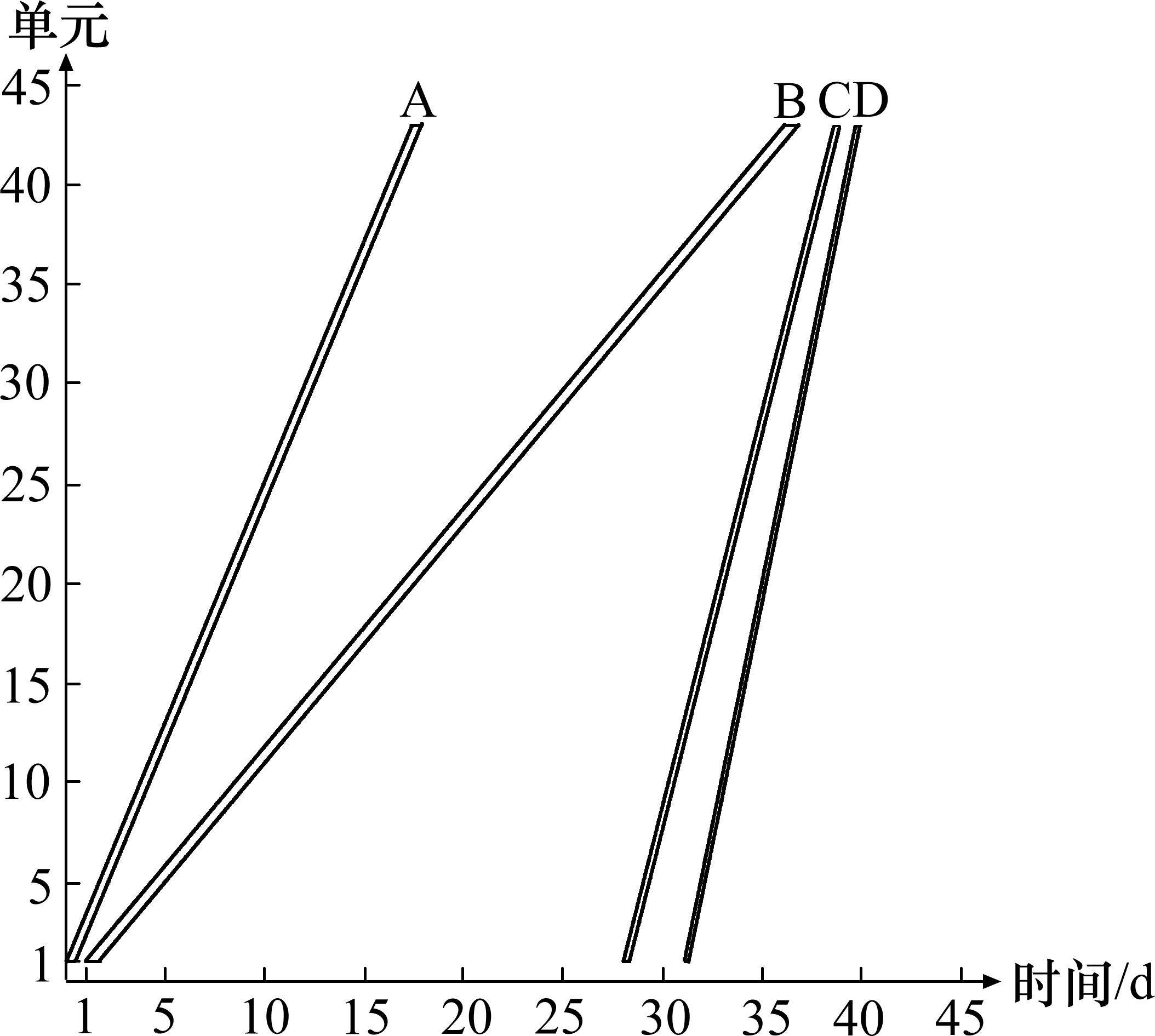
在表5的基础上,通过多目标优化模型对该集中修施工调度计划进行了优化,优化后的施工调度计划如表6所示。在3.2节,工期和资源均衡的权重系数各为0.4和0.6时,结果较符合实际,因此采用0.4的工期权重系数和0.6的资源均衡权重系数。因篇幅限制,简化人力资源和机械资源之间的差异,将人力资源和机械资源的权重设为0.5和0.5。优化后的LOB图如图12所示,工期从40 d变成23 d,工期缩短17 d。人力和机械资源直方图如图13和图14所示,人力和机械资源均波动较小,资源日常使用和平均使用之差的绝对值之和为635,该优化模型对大型养路机械施工调度在工期优化和资源均衡目标中具有明显的优越性,有良好的实际应用价值。
| 活动 | A | B | C | D |
|---|---|---|---|---|
| 一个单元所需的工作时间/h | 1.25 | 2.50 | 0.71 | 0.60 |
| 最佳工作队的工人数量/人 | 65 | 60 | 50 | 10 |
| 最佳工作队的机械数量/台 | 3 | 7 | 4 | 1 |
| 每日工作时间/h | 3 | 3 | 3 | 3 |
| 单元持续时间/d | 0.41 | 0.83 | 0.24 | 0.20 |
| 施工速率/(km∙d-1) | 2.40 | 1.20 | 4.20 | 5.00 |
| 开始时间/d | 0 | 1.4 | 10.6 | 18.6 |
| 工作队数量/个 | 2 | 2 | 1 | 2 |
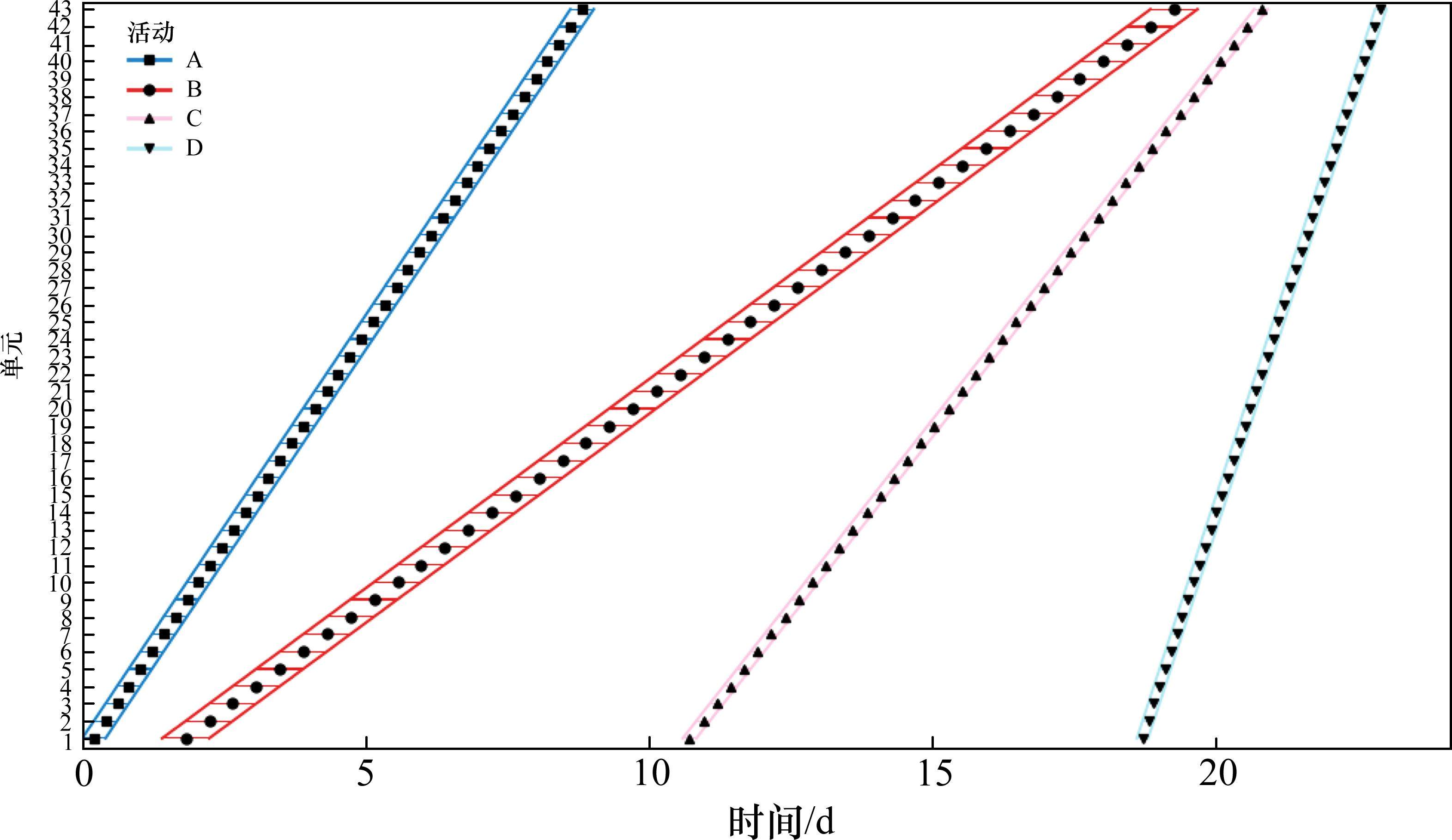
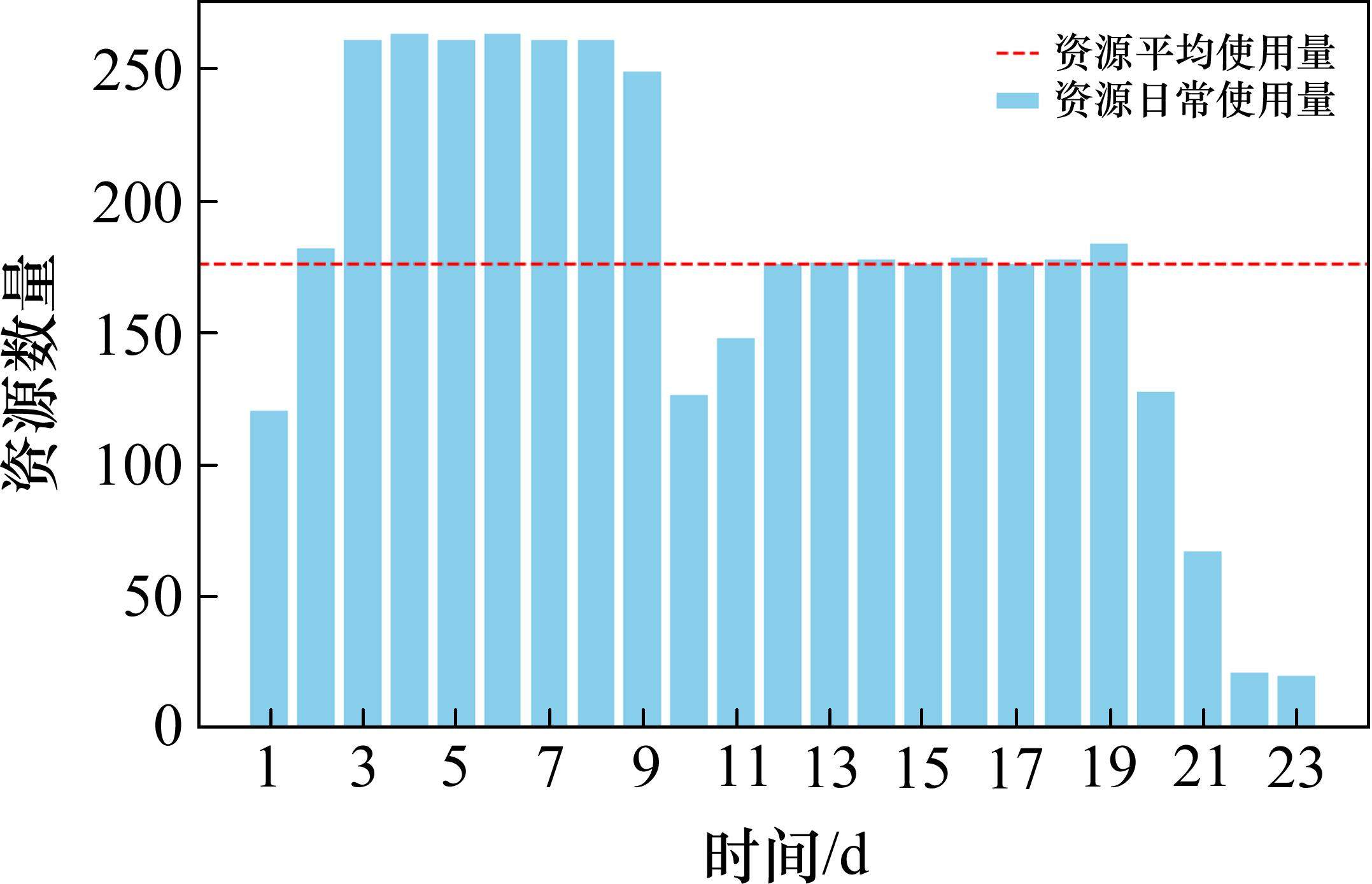
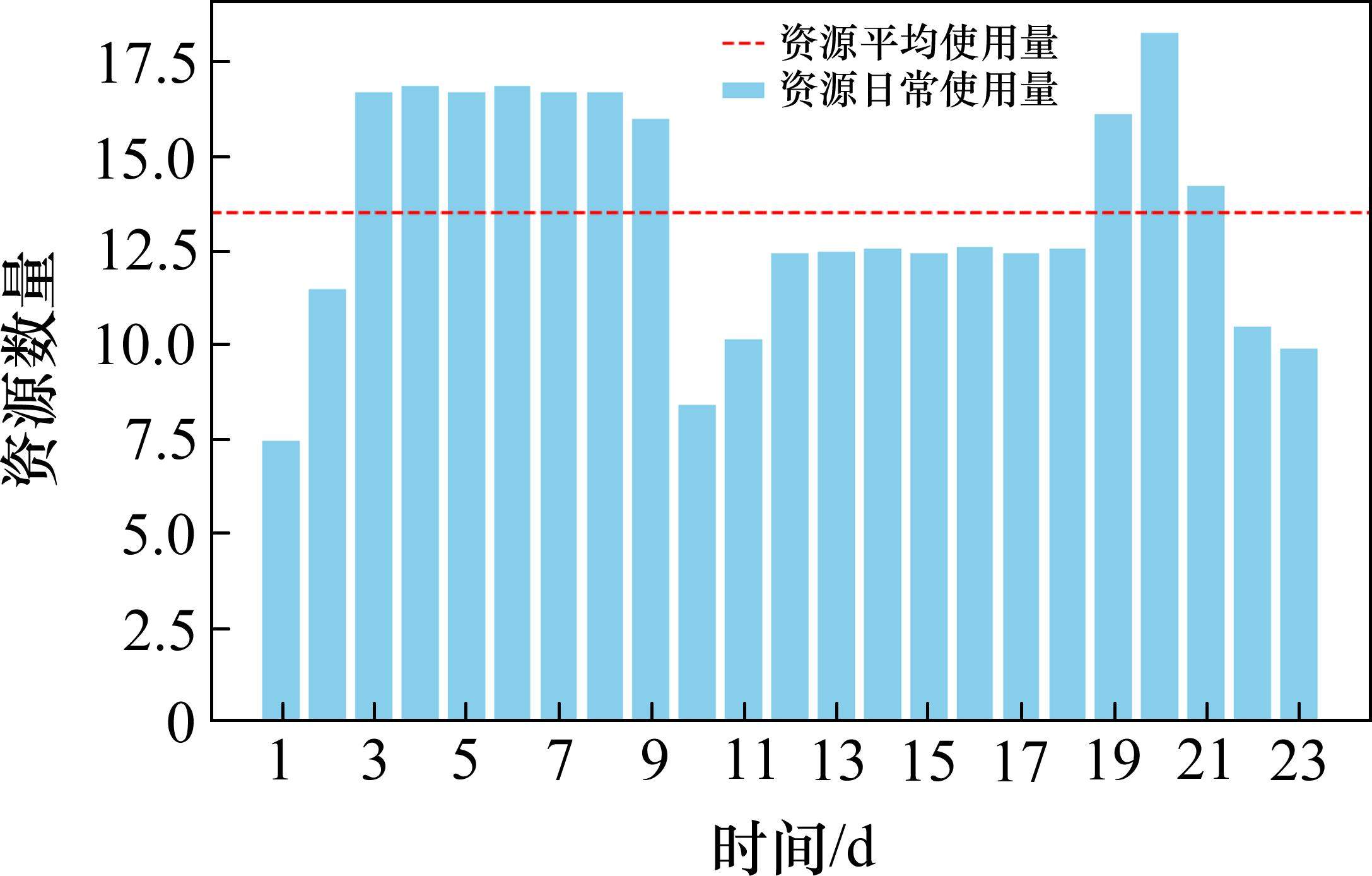
5 结论
1) 基于LOB的工期最短-资源均衡优化模型实现了工期的显著缩短和资源的合理利用,并直观展示多工作队的施工进展情况,对大型养路机械施工调度研究具有重要意义。
2) 采用改进的约束规划算法,引入随机重启策略,提高了求解效率,有效避免了局部最优解和搜索空间局限性问题,为工程实践提供了可行的解决方案。
3) 通过大型养路机械施工调度的2个案例验证本文算法,当工期优化效果逐渐降低时,资源均衡效果逐渐增强,验证了模型的有效性和优越性。优化后的大型养路机械施工调度计划优于原始方案,工期从40 d变为23 d,缩短了17 d,人力资源和机械资源波动均较小,资源利用效率得到了明显提升,证明了本研究模型具有良好的理论与实际应用价值。
邱实,杨波波,王劲等.基于LOB的大型养路机械施工调度工期最短-资源均衡优化[J].铁道科学与工程学报,2025,22(01):381-391.
QIU Shi,YANG Bobo,WANG Jin,et al.Shortest duration and resource balance optimization of heavy-duty railway maintenance machinery construction scheduling based on LOB[J].Journal of Railway Science and Engineering,2025,22(01):381-391.

