我国高速铁路已经迈入网络化运营时代,其路网规模之广、行车密度之大、运输组织过程之复杂决定了列车运行过程极易受到突发事件影响而偏离既定运行计划。既有列车运行调整研究侧重线网层面采取更改列车运行顺序、调整停站等策略来恢复列车运行秩序[1-2]。而行车扰动也会导致车站节点范围内的接发列车作业出现冲突,当到发线运用计划难以满足作业需求就会产生“机外停车”现象,进而造成延误传播。因此,制定合理的到发线运用调整方案对于尽快恢复列车运行秩序、提升高铁系统韧性具有重要意义。到发线运用是铁路行车组织中的经典问题,既有研究主要包含2类,一是到发线运用方案编制问题。部分学者从压缩追踪间隔时间[3]、提升车站通过能力[4]、优化车底折返运用[5]、改善乘客换乘[6]等角度研究了到发线运用计划编制问题。任禹谋等[7]提出在高峰时段以到发线利用均衡及连续占用间隔时间最大为目标编制到发线运用方案,提升车站的晚点吸收能力。ZHANG等[8]提出区间-咽喉区-到发线三段式列车运行图编制框架,以列车运行总费用最小为目标协同编制列车运行图和多车站到发线运用方案。CAPRARA等[9]从算法层面将所提出的混合整数非线性规划松弛为线性规划进行求解,求解结果优于广泛使用的简单启发式算法。二是到发线运用方案调整问题。到发线运用方案编制问题是按照列车图定时刻为其合理分配到发线,而当这一要求放松时,就变成了到发线运用方案调整问题,其目的是在发生扰动后迅速疏解冲突、吸收冲击,最大程度地减小延误传播范围[10-12]。张英贵等[13]将该问题抽象成一类新型复合排序问题,协同调整相邻车站的到发线运用方案。ZHANG等[14]基于站台、轨道的离散化时空资源准确描述列车间冲突,高效求解行车扰动后的到发线运用调整方案。ZHANG等[15-16]进一步考虑局部网络范围内车站作业计划协同调整,设计基于ADMM的算法以保证求解大规模问题的时效性。上述研究均以进路为最小单位建立优化模型,忽略了进路中的轨道电路细节。LU等[17]通过预处理各进路对的冲突度以降低计算复杂性并适应多种不同的联锁机制,对多目标函数的处理导致求解结果依赖于惩罚因子取值与具体的延误场景,但文中并未对其进行详细的讨论分析。CORMAN等[18]则针对扰动类型、持续时间不确定场景,基于随机规划方法进行建模求解,但其忽略了咽喉区可能产生的冲突。综上,大部分既有研究考虑的要素较为粗放,对列车在站内疏解冲突过程刻画不够细致,LU等[17]探究了不同联锁机制下的晚点恢复能力,但弱化了到发线运用方案调整对车站客运服务秩序的影响。为此,本文重点关注行车扰动下列车在站内的冲突疏解过程,以接发车进路采用“一次办理,分段解锁”制式为前提条件,精细刻画列车占用站内固定设备资源全过程(细化至轨道电路),面向行车秩序尽快恢复与车站客运服务秩序稳定的双重需求,建立行车扰动场景下的车站到发线运用方案调整方法,以提升车站“节点”的扰动恢复能力。
1 问题描述
1.1 进路分段解锁
列车进路是指列车到达、出发或通过所需占用的一段站内线路。不同类型列车在车站的作业内容和走行过程描述见表1,在不考虑跨线立折方式的前提下,所有类型列车的过站径路均可抽象为“接车进路-股道-发车进路”。
| 列车类型 | 作业内容 | 走行径路 |
|---|---|---|
| 不停站通过列车 | 通过作业 | 接车进路-正线-发车进路 |
| 停站通过列车 | 接车作业、发车作业 | 接车进路-到发线-发车进路 |
| 始发列车 | 出段作业、发车作业 | |
| 终到列车 | 接车作业、入段作业 | |
| 本线立折列车 | 接车作业、发车作业 |
进路分段解锁是指列车出清进路中某一轨道电路后延时几秒即可解锁[19],相比一次解锁条件下的车站作业效率更高。在进路分段解锁条件下,资源粒度进一步细化,列车在站全过程可表述为对轨道电路资源的序列化占用、释放。首先定义如下符号对车站进行刻画: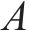
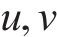


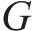
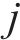
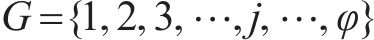
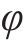
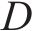
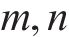

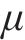
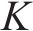

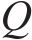
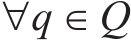


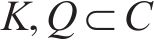
结合图1对列车在站全过程进行描述。
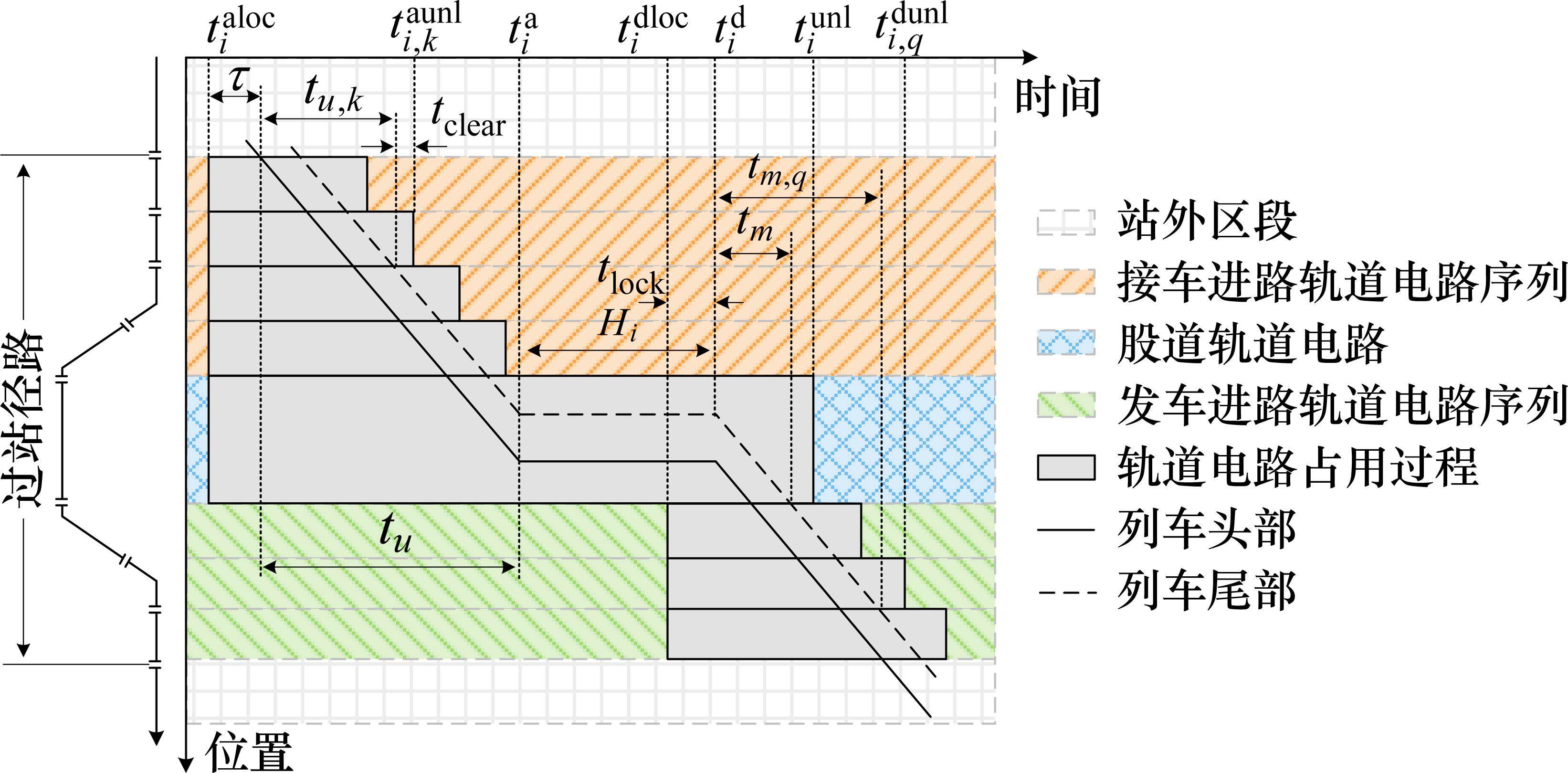
假设存在列车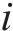
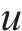
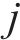
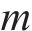
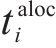
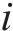
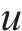
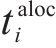


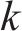
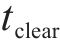
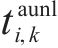
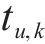
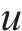
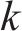
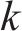
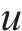
列车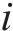
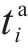
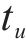
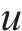
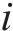
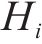
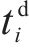
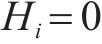
定义在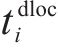
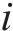
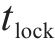
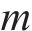
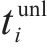
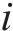
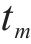
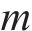
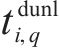
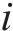
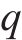
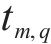
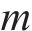
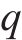
1.2 到发线运用调整
为方便问题描述,以图2为例说明到发线运用调整过程。
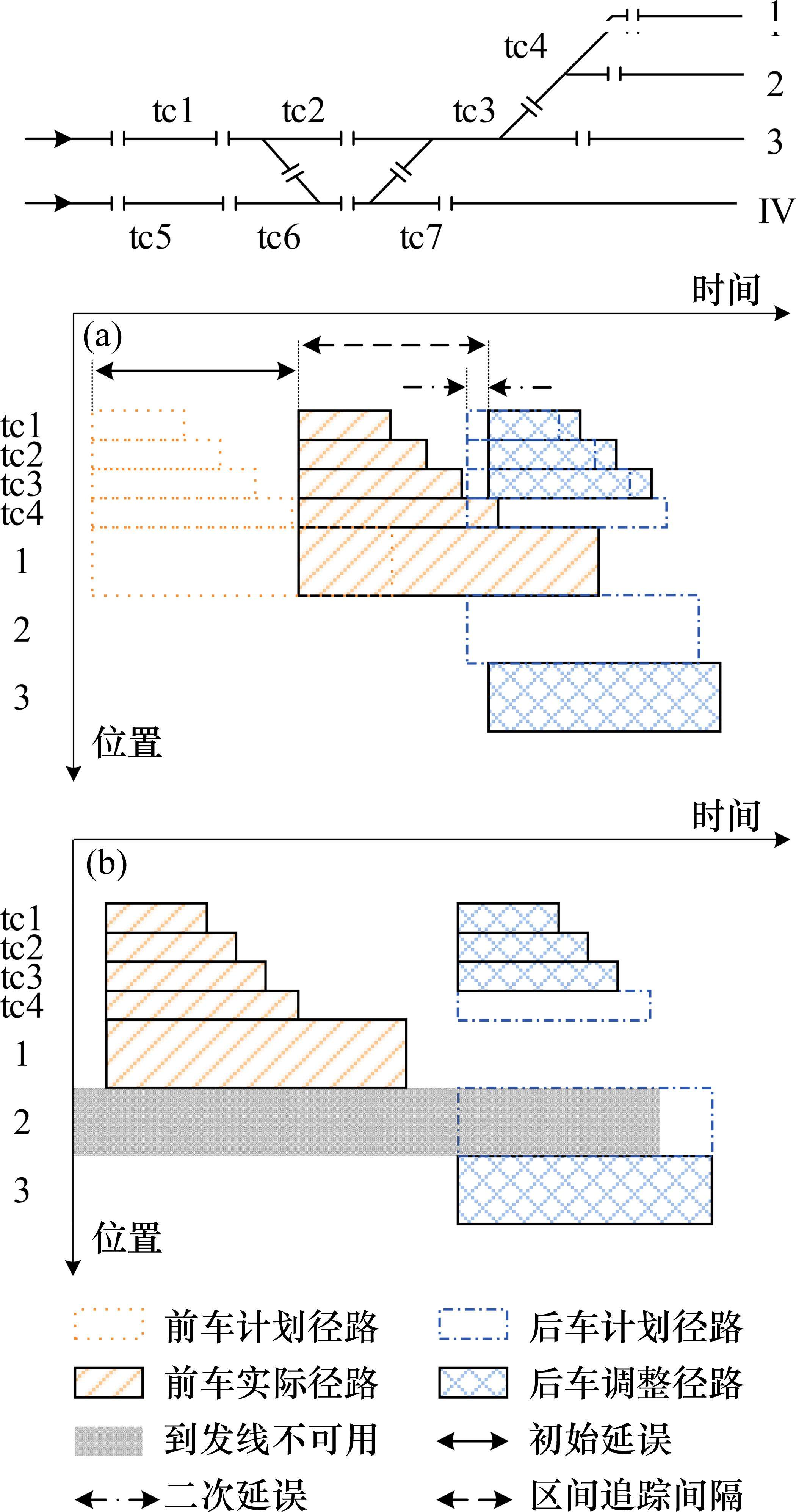
1) 原计划2车先后接入1道和2道且互不干扰,假设实际中前车在区间发生延误,此时调整后车接入3道,则可有效控制延误传播,否则需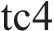
2) 假设实际中2道因临时出现故障或更早停靠2道的列车未能按计划发出而不可占用,调整后车停靠3道或1道均可以避免延误,如图2(b)所示。
我国高速铁路枢纽车站通常衔接多条高铁线路,站场结构复杂且高峰期列车到发密集,当列车运行受到扰动后极有可能与后续列车在咽喉区或到发线产生冲突,导致延误增强传播。从列车运行角度出发,发生扰动后应及时调整车站到发线运用方案以吸收冲击,尽快恢复按图行车;而从车站秩序角度出发,应尽可能少地改变到发线运用方案以保障车站旅客乘降作业的稳定。因为大型客站通常配备有多个检票口对应不同站台,旅客会根据所乘车次对应的检票口就近候车,过多调整到发线运用方案会导致大量旅客临近发车时刻在站内移动,存在安全隐患。为此,本研究的核心思想是:发生行车扰动后合理调整到发线运用方案,在兼顾旅客乘降作业秩序稳定的同时最大限度地降低列车总延误。
2 到发线运用方案调整模型
2.1 假设及符号定义
基于以下假设建立到发线运用方案调整模型。
1) 进路采用“一次办理,分段解锁”制式;
2) 扰动场景、持续时间已知;
3) 立折列车采用本线折返方式,不考虑跨线折返。
除问题描述部分定义的符号外,模型其他相关参数及变量定义见表2和表3。
| 符号 | 说明 |
|---|---|
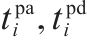 | 列车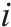 |
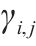 | 原方案中列车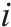 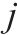 |
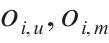 | 列车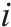 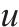 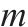 |
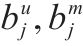 | 接车进路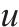 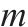 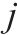 |
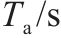 | 到发线安全使用间隔 |
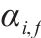 | 列车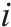 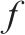 |
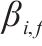 | 列车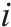 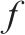 |
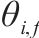 | 列车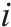 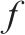 |
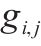 | 列车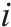 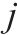 |
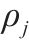 | 到发线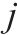 |
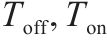 | 到发线不可用起止时刻 |
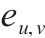 | 接车进路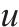 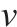 |
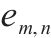 | 发车进路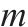 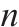 |
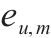 | 接车进路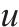 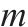 |
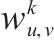 | 轨道电路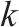 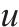 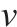 |
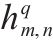 | 轨道电路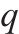 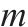 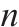 |
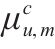 | 轨道电路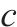 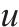 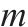 |
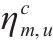 | 轨道电路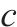 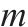 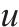 |
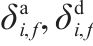 | 列车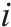 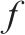 |
 | 区间运行追踪间隔,一般取180 s |
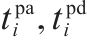 | 列车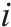 |
| 符号 | 说明 |
|---|---|
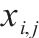 | 列车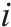 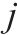 |
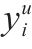 | 列车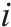 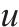 |
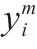 | 列车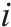 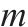 |
2.2 模型构建
从列车运行角度,应尽量减少列车实际到发时刻与计划时刻的偏差;从车站秩序角度,应尽可能少地改变既有到发线运用方案以维持稳定。为此,模型优化目标由2个部分组成:目标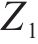
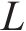
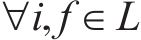
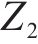
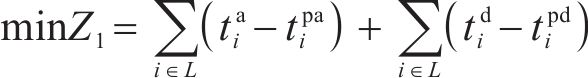

根据列车在实际车站范围内走行的限制和到发线运用规则建立以下约束。
1) 到发线与进路选择唯一性约束。式(3)~式(5)表示任意列车在站内只能占用一条到发线、接车进路与发车进路。
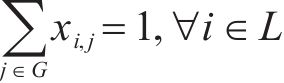
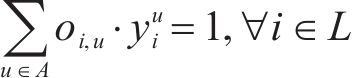
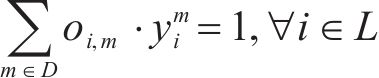
2) 到发线与进路连通性约束。式(6)和式(7)表示列车所选择到发线与接车进路、发车进路需满足车站站场布局,接、发车进路确定,则到发线唯一确定。
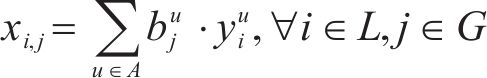
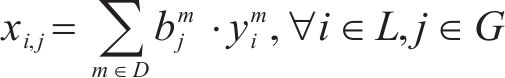
3) 到发线占用冲突疏解约束。
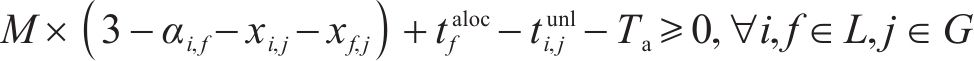
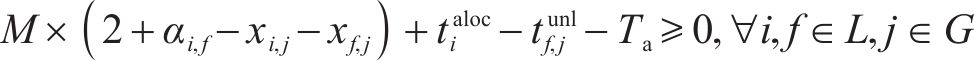
式中: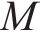
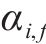
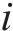
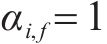
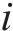
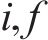
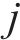
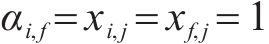
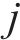
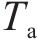
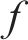
4) 进路占用冲突疏解约束。式(10)和式(11)表示接车进路之间冲突疏解约束;式(12)和式(13)表示发车进路间冲突疏解约束,包括折返发车与正向发车进路冲突疏解;式(14)和式(15)表示折返发车进路与接车进路冲突疏解约束。进路分段解锁条件下,前车出清2条进路冲突的最后一个轨道电路即可为后车办理进路,其中最后一个轨道电路对于2接车进路为最靠近车站中心的轨道电路,两发车进路为最远离车站中心的轨道电路,接车进路与发车进路之间则取决于两车到发的先后顺序。
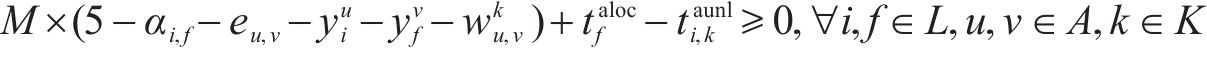
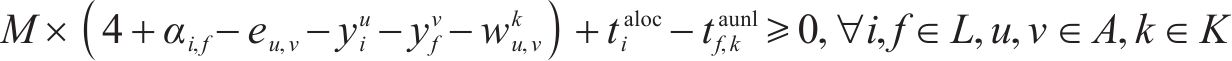
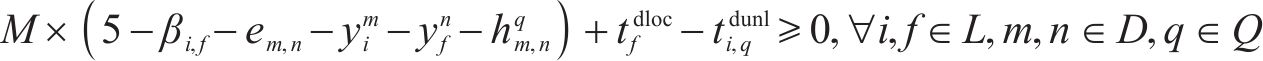
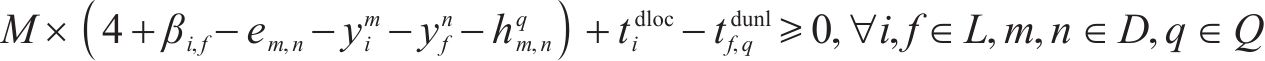
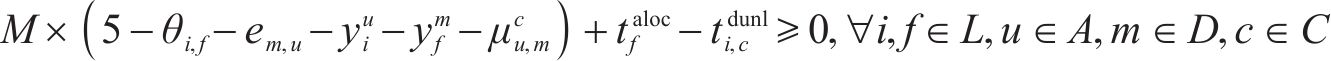
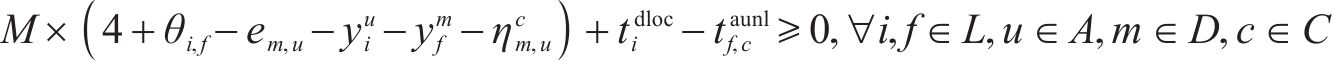
5) 到发线不可用约束。式(16)和式(17)表示到发线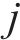
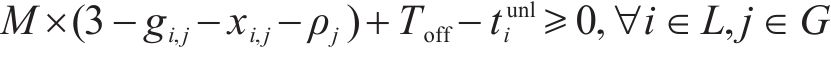
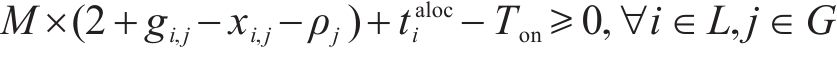
6) 列车站内走行过程约束。根据前文对列车占用车站资源过程的描述得到如下约束:
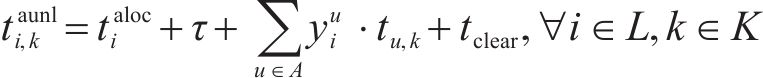

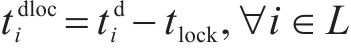
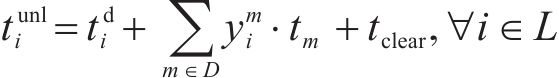
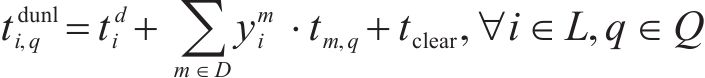
7) 区间运行追踪间隔约束。式(23)用列车进路锁闭时间之差表示列车在区间不能发生越行并满足区间运行追踪间隔要求,当且仅当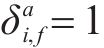
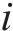
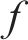
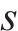
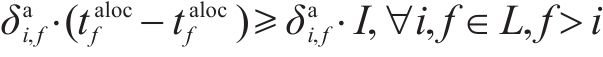
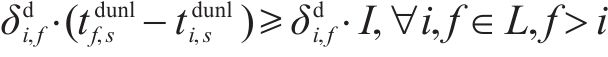
8) 最小停站时间约束。式(25)表示列车需满足图定停站时间以保证换乘衔接顺利进行;式(26)和式(27)表示实际的到发时刻不得早于图定到发时刻,即列车不允许早发早到破坏潜在的旅客换乘衔接关系,同时可以保证目标函数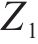
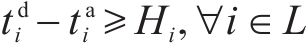
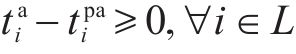
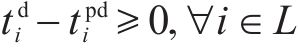
2.3 求解算法
所构建模型为混合整数线性规划模型,可使用商业求解器内置的分支定界算法进行精确求解。此外,采用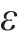
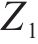
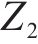
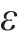
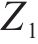
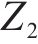
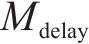
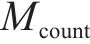
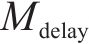
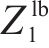
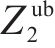
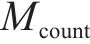
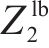
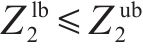
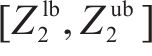
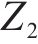
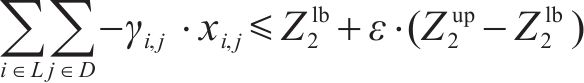
式中: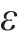
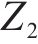
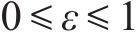
将式(28)加入模型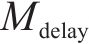
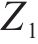
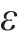
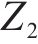
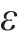
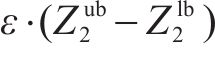
3 案例分析
3.1 基本信息
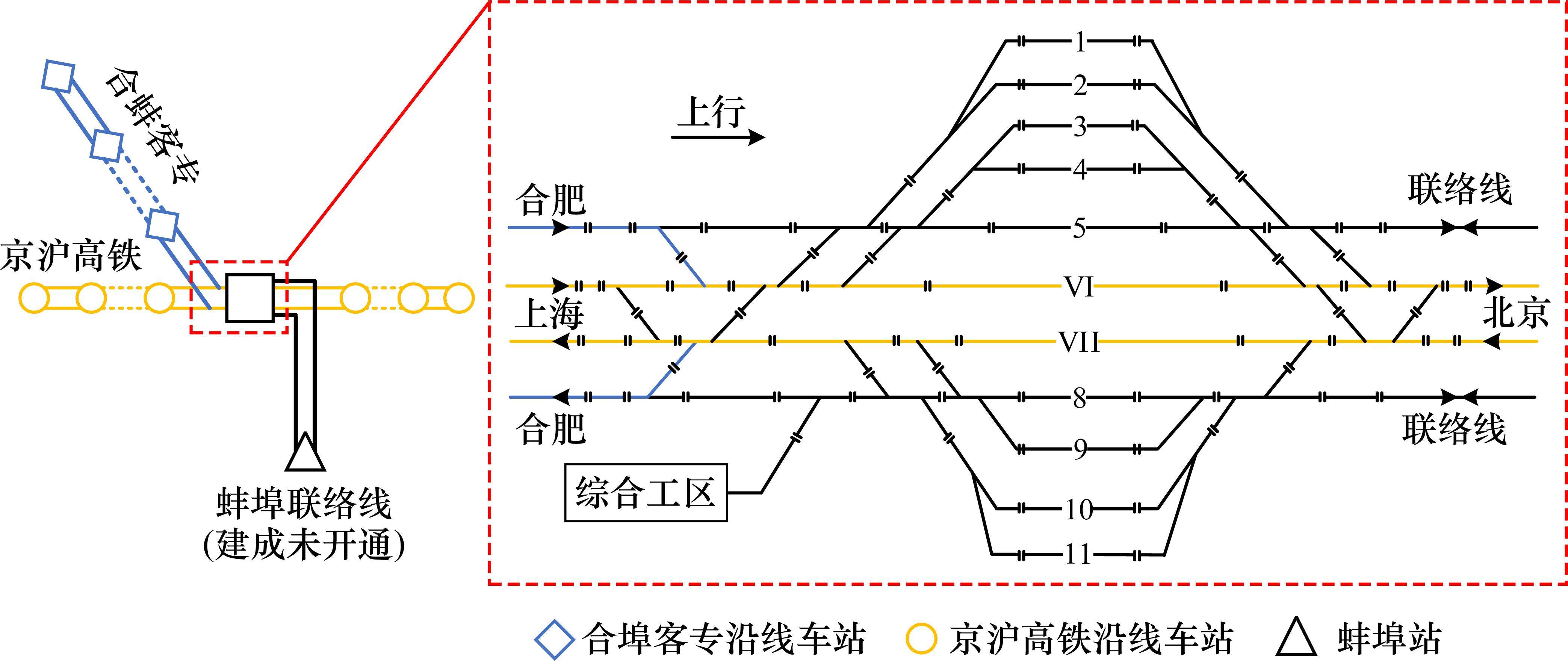
选取“徐蚌瓶颈”中的蚌埠南站为对象进行案例分析,车站平面图见图3。蚌埠南站是京沪高铁与合蚌客专交汇的枢纽站(合蚌客专在站前汇入京沪高铁),衔接上海、合肥、北京、蚌埠站4个方向,设有2条正线、9条到发线、41个轨道电路,各轨道电路占用时间取值由列车长度、列车走行速度及轨道电路长度等因素综合确定。考虑到《铁路技术管理规程》[20]中对车站股道固定运用的要求,假设蚌埠南站上行场的1、2道固定为合蚌客专线路使用,3~5道固定为京沪线上的列车使用,扰动发生后调整到发线运用方案也需要遵从此约束,下行方向亦然。根据历史某年春运期间计划运行图,车站17:00—19:00内上下行合计接发38列列车,其中停站通过列车29列、不停站通过列车8列、立折列车1列。限于篇幅,表4仅列出上行方向列车的计划时刻表和到发线运用方案。
| 车次 | 列车类型 | 到时 | 发时 | 接车方向 | 发车方向 | 计划股道 |
|---|---|---|---|---|---|---|
| G52 | 停站通过 | 17:02:00 | 17:04:00 | 上海 | 北京 | 3 |
| G9270/G9269 | 立折 | 17:06:00 | 17:34:00 | 上海 | 上海 | 5 |
| G7780 | 停站通过 | 17:09:00 | 17:15:00 | 上海 | 北京 | 4 |
| G2566 | 停站通过 | 17:13:00 | 17:19:00 | 合肥 | 北京 | 2 |
| G270 | 停站通过 | 17:18:00 | 17:24:00 | 合肥 | 北京 | 1 |
| G146 | 停站通过 | 17:28:00 | 17:30:00 | 上海 | 北京 | 3 |
| G442 | 停站通过 | 17:32:00 | 17:34:00 | 上海 | 北京 | 4 |
| G304 | 停站通过 | 17:33:00 | 17:38:00 | 合肥 | 北京 | 2 |
| G22 | 不停站通过 | 17:43:00 | 17:43:00 | 上海 | 北京 | VI |
| G60 | 停站通过 | 17:48:00 | 17:50:00 | 上海 | 北京 | 5 |
| G1742 | 停站通过 | 17:55:00 | 18:00:00 | 合肥 | 北京 | 1 |
| G148 | 不停站通过 | 17:56:00 | 17:56:00 | 上海 | 北京 | VI |
| G1822 | 停站通过 | 18:05:00 | 18:12:00 | 上海 | 北京 | 5 |
| G150 | 不停站通过 | 18:09:00 | 18:09:00 | 上海 | 北京 | VI |
| G356 | 停站通过 | 18:14:00 | 18:16:00 | 合肥 | 北京 | 2 |
| G152 | 停站通过 | 18:17:00 | 18:19:00 | 上海 | 北京 | 5 |
| G7290 | 停站通过 | 18:26:00 | 18:28:00 | 上海 | 北京 | 5 |
| G1898 | 停站通过 | 18:33:00 | 18:35:00 | 合肥 | 北京 | 2 |
| G24 | 不停站通过 | 18:43:00 | 18:43:00 | 上海 | 北京 | VI |
| G2568 | 停站通过 | 18:55:00 | 18:58:00 | 合肥 | 北京 | 2 |
按照区间延误、到发线故障2种类型随机设定5个行车扰动场景,见表5。其中初始延误时长表示列车晚点的最小值,如场景5同时存在2种耦合扰动,G60在区间初始延误时长为10 min代表其可能的最早到达时间为17:58:00,如果8道故障导致前序其他列车与其产生冲突,则其延误不只10 min;到发线在故障时段内不可被占用,如10道于18:00:00开始临时维修,停止办理列车接发作业,直至18:30:00恢复。
| 扰动场景 | 扰动类型 | 初始延误车次 | 故障到发线 | 初始延误时长/故障时段 |
|---|---|---|---|---|
| 1 | 区间延误 | G419 | — | 20 min |
| 2 | 区间延误 | G7780/G141 | — | 5 min/5 min |
| 3 | 到发线故障 | — | 10 | 18:00:00—18:30:00 |
| 4 | 到发线故障 | — | 2 | 17:30:00—18:50:00 |
| 5 | 区间延误且到发线故障 | G60 | 8 | 10 min/17:15:00—18:15:00 |
3.2 结果分析
为验证模型的有效性和实用性,设置不同调整目标进行结果对比。目标1:到发线运用方案改变数量最小化;目标2:列车总延误时间最小化,即以列车为中心进行调整;目标3:以到发线运用方案改变数量、列车总延误时间双方面最小化为目标,主目标为最小化延误时间,
表6给出各扰动场景下采用不同调整目标的对比结果。可以看出,目标1下优化结果是发生扰动后不进行任何调整,仍执行计划到发线运用方案,受影响列车需要在区间降速运行甚至机外停车,会导致延误持续向后传播,影响局部路网的稳定性产生蝴蝶效应;相较于不进行任何调整的结果,目标2下优化结果可以实现列车总延误最小化,针对包含到发线故障的扰动场景3、4、5,优化效果更为明显,总延误降幅均超过92%,场景4下可以找到完全避免延误的到发线运用调整方案;目标3考虑列车运行与车站作业秩序两方面因素,相较于目标2结果,仅需较少改变到发线运用方案即可实现列车延误的显著下降,如针对场景5,调整3列车的到发线运用方案即可实现延误降低89%。各场景在不同目标下具体的调整方案见表7,为简化描述,每一个测试案例都由一个字符串表明,如“S1O2”即代表“扰动场景1、目标2”,以此类推。值得说明的是,目标1下所有场景的调整方案与计划方案保持一致,以“SNO1”代表。
扰动 场景 | 目标1 | 目标2 | 目标3 | |||||
|---|---|---|---|---|---|---|---|---|
总延误/ min | 到发线运用方案改变数量 | 总延误/ min | 总延误时间下降比例/% | 到发线运用方案改变数量 | 总延误/min | 总延误时间下降比例/% | 到发线运用方案改变数量 | |
| 1 | 176.25 | 0 | 146.65 | 16 | 2 | 150.75 | 14 | 1 |
| 2 | 39.77 | 0 | 33.77 | 15 | 5 | 34.88 | 12 | 2 |
| 3 | 53.15 | 0 | 4.10 | 92 | 2 | 12.73 | 76 | 1 |
| 4 | 1 430.22 | 0 | 0 | 100 | 5 | 4.10 | 99 | 3 |
| 5 | 1 966.60 | 0 | 42.33 | 98 | 6 | 213.08 | 89 | 3 |
| 测试案例 | 上行方向 | 下行方向 |
|---|---|---|
| SNO1 | {3, 5, 4, 2, 1, 3, 4, 2, VI, 5, 1, VI, 5, VI, 2, 5, 5, 2, VI, 2} | {VII, 9, 8, 9, 8, 10, 8, VII, 8, 9, 8, VII, 10, 10, 8, VII, 11, 8} |
| S1O2 | {3, 5, 4, 2, 1, 3, 4, 2, VI, 5, 1, VI, 5, VI, 2, 5, 5, 2, VI, 2} | {VII, 9, 8, 9, 8, 10, 9, VII, 8, 9, 8, VII, 11, 10, 8, VII, 11, 8} |
| S1O3 | {3, 5, 4, 2, 1, 3, 4, 2, VI, 5, 1, VI, 5, VI, 2, 5, 5, 2, VI, 2} | {VII, 9, 8, 9, 8, 10, 9, VII, 8, 9, 8, VII, 10, 10, 8, VII, 11, 8} |
| S2O2 | {3, 4, 5, 2, 1, 3, 5, 2, VI, 5, 1, VI, 5, VI, 2, 3, 5, 2, VI, 2} | {VII, 9, 8, 9, 8, 10, 8, VII, 8, 9, 8, VII, 10, 11, 8, VII, 11, 8} |
| S2O3 | {3, 5, 4, 2, 1, 3, 4, 2, VI, 5, 1, VI, 5, VI, 2, 3, 5, 2, VI, 2} | {VII, 9, 8, 9, 8, 10, 8, VII, 8, 9, 8, VII, 10, 11, 8, VII, 11, 8} |
| S3O2 | {3, 5, 4, 2, 1, 3, 4, 2, VI, 5, 1, VI, 5, VI, 2, 5, 5, 2, VI, 2} | {VII, 9, 8, 9, 8, 10, 8, VII, 8, 9, 8, VII, 11, 11, 8, VII, 11, 8} |
| S3O3 | {3, 5, 4, 2, 1, 3, 4, 2, VI, 5, 1, VI, 5, VI, 2, 5, 5, 2, VI, 2} | {VII, 9, 8, 9, 8, 10, 8, VII, 8, 9, 8, VII, 11, 10, 8, VII, 11, 8} |
| S4O2 | {3, 5, 4, 2, 1, 3, 5, 1, VI, 5, 1, VI, 5, VI, 1, 5, 5, 1, VI, 2} | {VII, 9, 8, 9, 8, 10, 8, VII, 8, 9, 8, VII, 10, 11, 8, VII, 11, 8} |
| S4O3 | {3, 5, 4, 2, 1, 3, 4, 1, VI, 5, 1, VI, 5, VI, 1, 5, 5, 1, VI, 2} | {VII, 9, 8, 9, 8, 10, 8, VII, 8, 9, 8, VII, 10, 10, 8, VII, 11, 8} |
| S5O2 | {3, 5, 4, 2, 1, 3, 4, 2, VI, 5, 1, VI, 5, VI, 2, 5, 5, 2, VI, 2} | {VII, 9, 9, 9, 9, 10, 9, VII, 9, 9, 9, VII, 10, 11, 8, VII, 11, 8} |
| S5O3 | {3, 5, 4, 2, 1, 3, 4, 2, VI, 5, 1, VI, 5, VI, 2, 5, 5, 2, VI, 2} | {VII, 9, 9, 9, 9, 10, 9, VII, 8, 9, 8, VII, 10, 10, 8, VII, 11, 8} |
图4为扰动场景5下不同
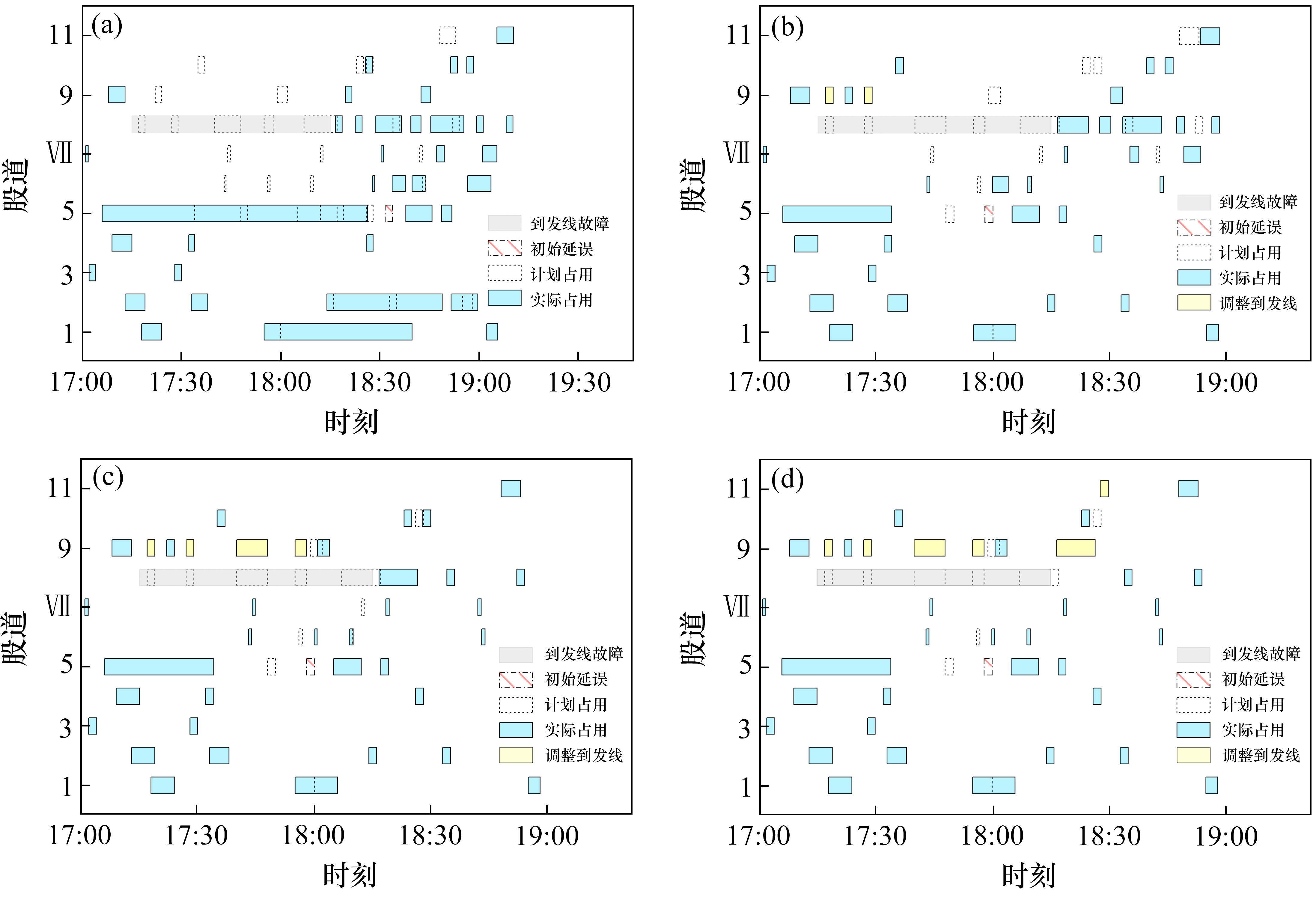
3.3 联锁机制对比
前文已经证明了进路分段解锁条件下调整到发线运用方案可以有效吸收列车延误,因此本节重点关注不同联锁机制对车站作业调整的影响,并主要针对包含区间延误的场景进行分析。为丰富场景多样性,在延误场景2的基础上将G7780和G141的延误时间均设置为10 min,定义为延误场景6。值得说明的是,本节重点讨论不同联锁机制的性能,因此仅考虑目标函数
基于文献[10]中进路一次解锁条件下的到发线运用方案调整模型,分别对场景1、2、5、6进行求解,得到各车次延误时间大小如图5(a)所示,通过气泡的直径表示。与图5(b)所示的分段解锁结果对比,一次解锁条件下各场景受延误列车数量更多、总体延误更大,如场景5分段解锁条件下延误列车数量为3列,一次解锁条件下延误数量为8列,并且一次解锁条件下的单车最大延误也显著大于分段解锁条件下的单车最大延误。整体来看,进路一次办理,一次解锁机制在实际中行车高峰期表现更差,既不利于压缩追踪间隔也不利于晚点恢复,进一步验证了本文研究分段解锁条件下到发线运用方案调整的必要性。
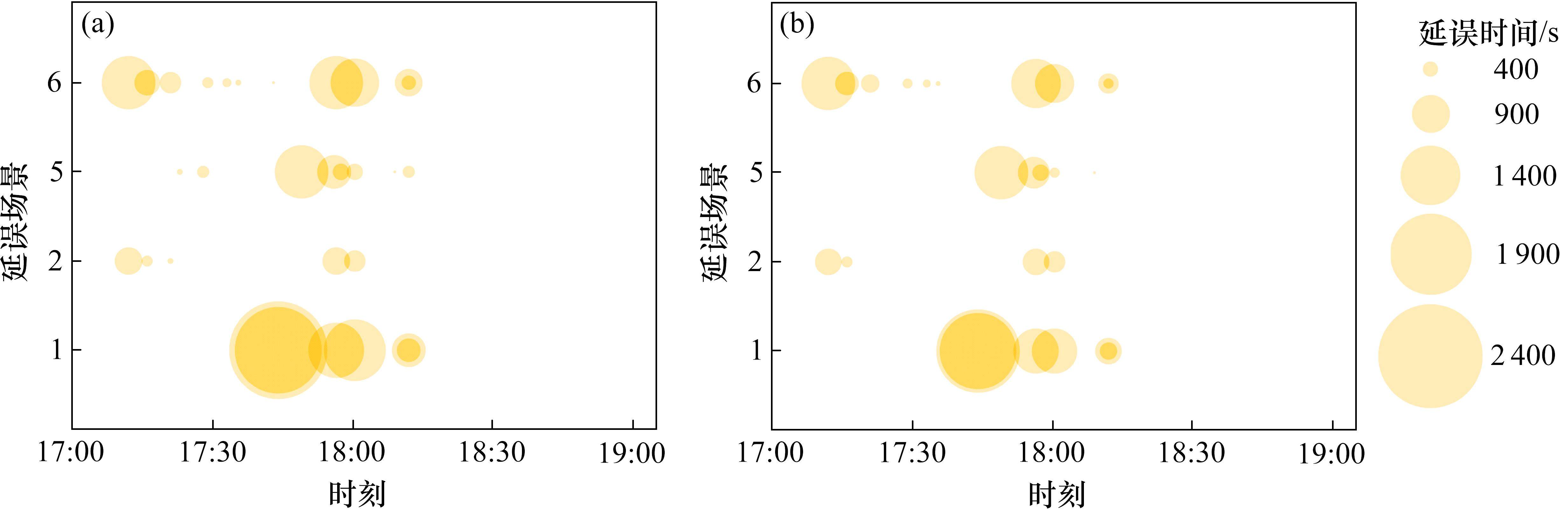
3.4 调整策略对比
本节进一步考虑到发线灵活运用的调整策略对列车运行与车站作业计划的影响。此外,压缩停站时间也是列车晚点恢复的重要措施。设置4种不同的调整策略,见表8。仍以扰动场景5为例进行求解,得到Pareto曲线,见图6。
| 序号 | 优化目标 | 具体策略 | ||
|---|---|---|---|---|
| 总延误时间最小 | 到发线改变数量最小 | 到发线灵活使用 | 压缩停站时间 | |
| 策略1 | √ | √ | × | × |
| 策略2 | √ | √ | √ | × |
| 策略3 | √ | √ | × | √ |
| 策略4 | √ | √ | √ | √ |
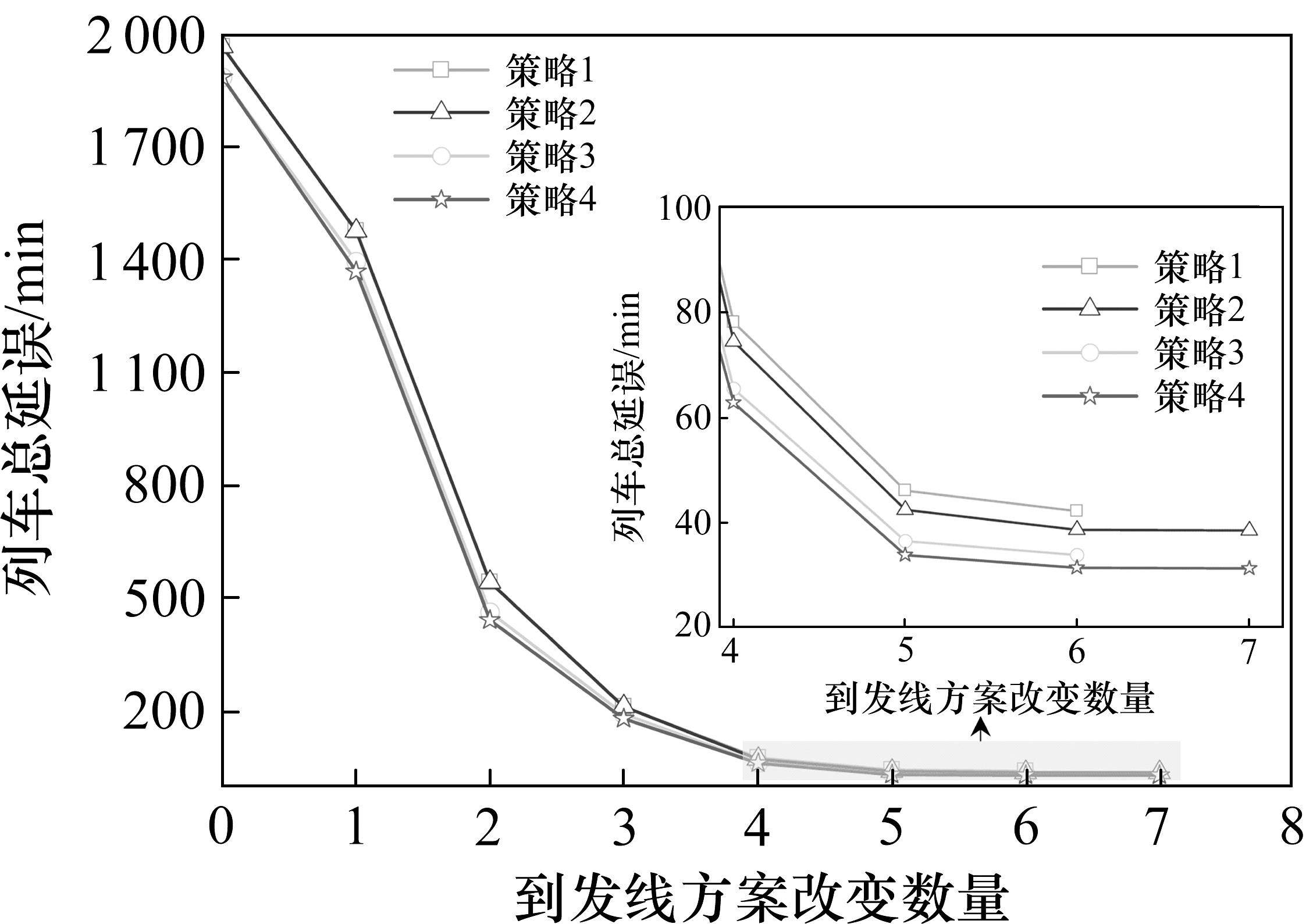
图6可以看出,策略1整体延误最大,说明到发线灵活使用与停站时间可调整策略均能进一步降低延误;策略3与策略4明显优于策略1与策略2,即在到发线方案改变数量固定的前提下,停站时间是否可压缩相较于到发线是否灵活使用对于降低列车延误更为关键;在其他策略相同的前提下允许压缩停站时间可以进一步降低延误约10%,但是压缩停站时间可能会破坏潜在的接续换乘关系,导致旅客无法顺利换乘,实际中需权衡旅客接续换乘与晚点恢复的关系进行决策。
4 结论
1) 以车站进路分段解锁为前提条件,精细描述列车对车站内固定设备资源的占用过程,在此基础上提出行车扰动条件下的车站到发线运用方案调整模型,该方法具有良好的实用性与时效性,能够为车站接发车作业的调整提供技术支持。
2) 以蚌埠南站为对象进行实证研究,多种扰动场景下的优化结果表明,所构建调整方法可适用于多种不同类型的扰动场景,在兼顾车站作业秩序稳定的同时平均降低延误约60%,针对到发线故障扰动类型则能够实现延误降低76%以上。
3) 对比不同调整策略对降低延误的效果,认为多种策略结合能够进一步降低列车总延误约10%,建议实践中优先考虑压缩列车停站时间的调整策略,其次为到发线不固定车场使用。
张伯男,姚向明,赵鹏等.分段解锁下高速铁路车站到发线运用方案调整研究[J].铁道科学与工程学报,2025,22(04):1432-1443.
ZHANG Bonan,YAO Xiangming,ZHAO Peng,et al.Train platform scheme rescheduling in high-speed railway station with route-lock sectional-release mechanism[J].Journal of Railway Science and Engineering,2025,22(04):1432-1443.

