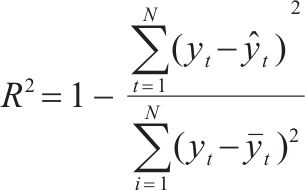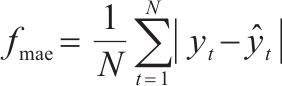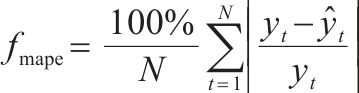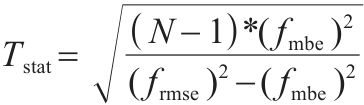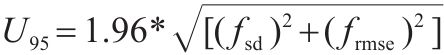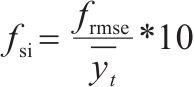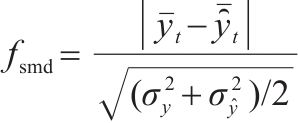列车荷载作用下,高速铁路路基会产生不可恢复的永久变形[1]。而过量的永久变形易导致路基不均匀下沉或沉降超限病害,严重威胁高速列车运行安全[2],因此高速铁路对路基永久变形有严格的限制[3]。若能通过预测手段掌握高速铁路路基变形发展,对于变形病害控制与运营管理意义重大。路基累积变形预测模型是获取高速铁路路基长期变形发展的重要手段。目前,路基累积变形预测模型主要包括经验方法、数值模拟方法、统计分析方法和机器学习方法4个种类。经验方法基于试验结果来建立预测路基累积变形的数学方程[4],具有无法量化非线性问题的弊端;数值模拟方法可考虑多种模拟条件[5]、统计分析方法基于饱和土理论或变形规律建立数学模型[6],但均具有内部参数设置困难、过于依赖假设的弊端[7]。相比之下,机器学习方法具有非线性映射、自适应学习、高预测精度等优势[8],逐渐被推广应用于累积变形预测。例如,CHEN等[9-11]的研究均证明了机器学习方法在路基累积变形预测上的适用性,也推动机器学习方法在高速铁路工程中的应用。通常,机器学习方法需要较大的训练样本支撑,而高速铁路速度快、客运任务重且具有封闭性[12],因此实际工程中可能面临不充足训练数据的问题,这对于预测模型的时间分布外泛化性能提出更高要求。而在传统机器学习路基累积变形预测模型中,训练集和测试集(用于测试模型预测精度)是按照时间顺序从数据集中划分的,通常各自占比70%与30%[13]或80%与20%[14]。这一方式使得训练集和测试集在时间上具有相似的分布,因此所得预测模型虽然在测试集上表现较好,但往往只有分布内的泛化能力,存在时间分布外泛化性差的弊端。近年来,研究者发现工程中的基础理论可为解决机器学习预测模型的时间分布外泛化问题提供支撑。其中,最具代表性的是RAISSI等[15]提出的物理信息神经网络(physical information neural network, PINN)。PINN通常将特定领域的物理信息作为约束条件纳入损失函数,可提高机器学习模型的分布外泛化性[16],该方法已广泛应用于力学[17]、医学[18]、工程[19]等多个领域。然而,由于高速铁路路基累积变形的影响因素众多,因此较难找到一个能够支撑机器学习建模的物理方程。对比而言,经验信息简要总结了高速铁路路基累积变形这一复杂的发展过程,且经过长期试验与工程实例的验证[20];虽然不如物理信息那样精确,但在一定程度上也能揭示路基累积变形的发展趋势和潜在规律[21]。故在物理信息无法快速获取和有效量化的条件下,经验信息相对而言更适合作为机器学习路基累积变形预测模型中的约束条件。因此,如何利用高速铁路工程领域已有的经验知识,构造具有时间分布外泛化性的路基累积变形预测模型是一个值得探索的问题。综上,提出一种基于经验约束神经网络(empiricism-constrained neural network, ECNN)的高速铁路路基累积变形预测方法。首先,构建路基累积变形预测数据集,并划分为训练集和测试集;其次,基于训练集建立神经网络模型,综合预测精度与误差、预测不确定性2个层次结果确定最优神经网络预测模型;最后,利用最优神经网络模型驱动路基累积变形的数据信息,并以损失函数修正的方式嵌入累积塑性应变关系曲线(经验信息),实现对最优神经网络模型参数和损失函数的约束,完成ECNN模型构建。借助杭绍台高速铁路的路基试验段验证了所提方法的有效性。
1 基于经验约束神经网络的高速铁路路基累积变形预测方法
1.1 神经网络算法
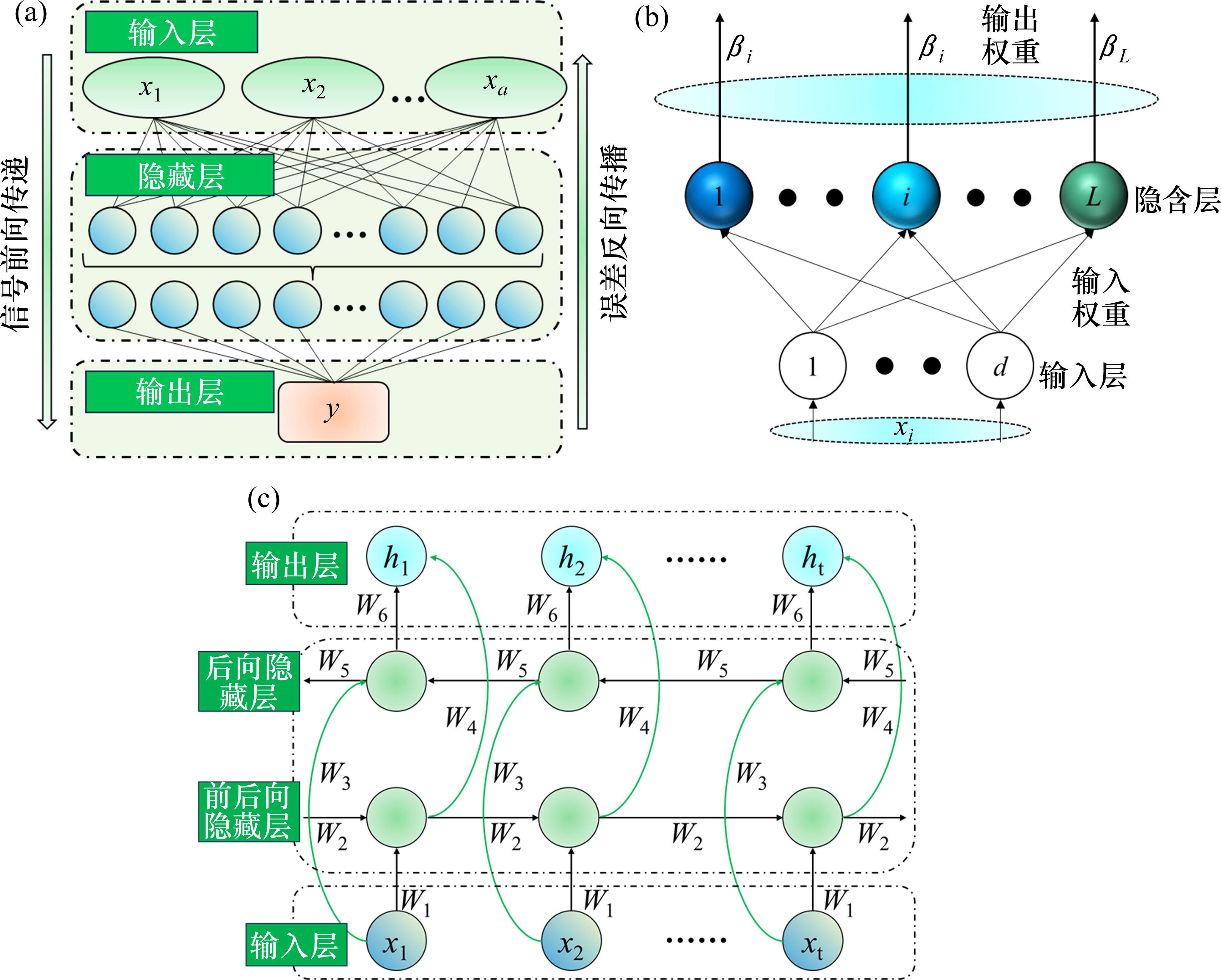
如图1所示,采用反向传播(back propagation, BP)、极限学习机(extreme learning machine, ELM)、双向门控循环单元(bidirectional gate recurrent unit, Bi-GRU)这3种典型的神经网络算法(属于机器学习算法)对高速铁路路基累积变形进行预测。BP是一种基于梯度下降的神经网络,其核心在于计算网络输出层与真实值之间的误差,并不断调整网络参数使得总误差最小;ELM是一种无需迭代即可计算输出权重的前馈神经网络,具有训练速度快、计算效率高等优势;Bi-GRU是从循环神经网络发展而来的一种变体,其结合了双向循环神经网络的鲁棒性和门控循环单元(GRU)的长序列处理能力[22],可高效地处理路基累积变形数据。
1.2 累积塑性应变关系曲线
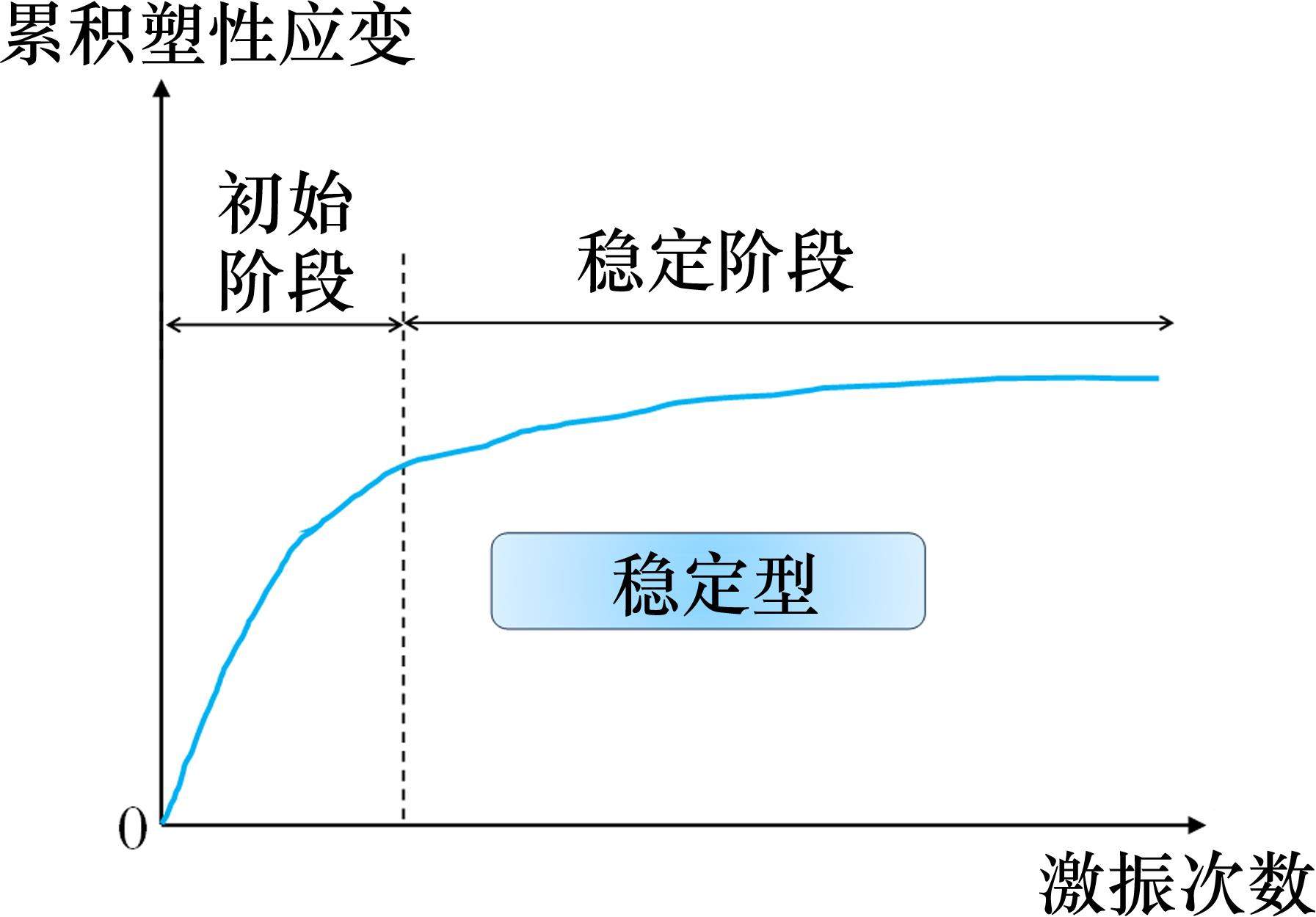
基于经验约束神经网络(empiricism-constrained neural network, ECNN)的高速铁路路基累积变形预测方法利用经验信息来提高神经网络模型的时间分布外泛化性。经验信息应从一般的经验理论中提取,这些经验理论可从试验或真实运营条件中得到。通常,高速铁路路基在列车循环荷载作用下,累积变形逐渐发展,累积塑性应变随振次增长[20]。在各种累积塑性应变关系曲线中,稳定型增长曲线模型适合于这一目的,因为在高速铁路实际工程中,稳定型累积塑性应变曲线最为常见[20],最具普适性。如图2所示,稳定型累积塑性应变曲线的增长过程可归纳为2个阶段:1) 初始快速增长阶段,即加载初期,应变增加快;2) 后期稳定阶段,即加载后期,应变的增长速率减缓或停滞,最终应变趋于稳定。
1.3 基于经验约束神经网络的高速铁路路基累积变形预测模型
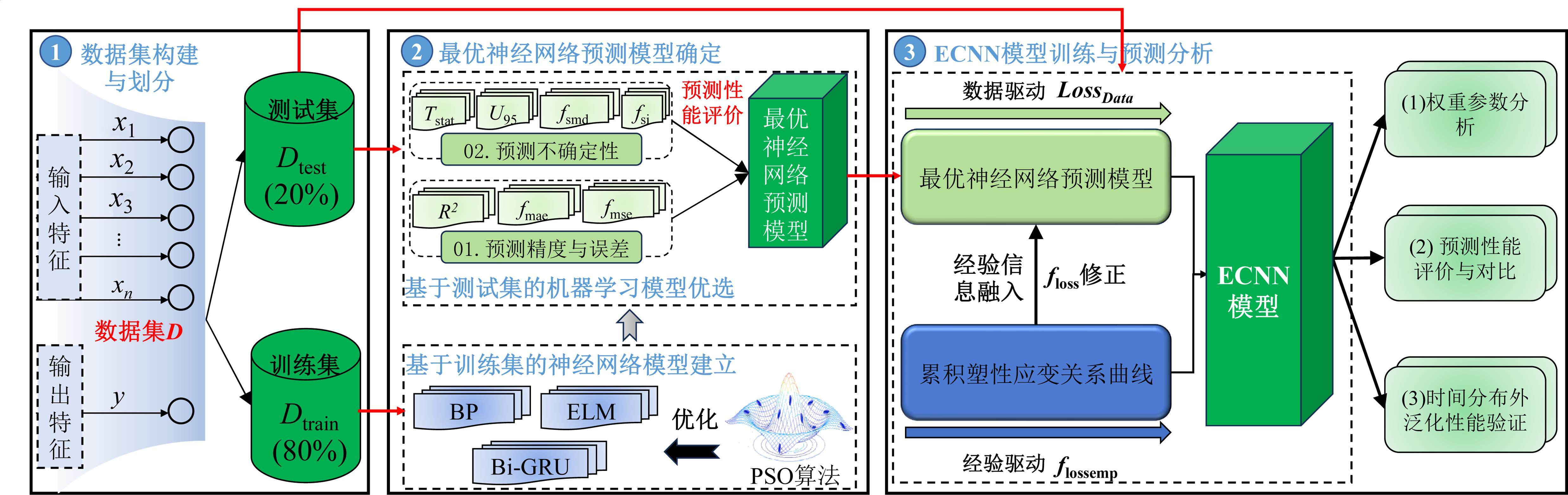
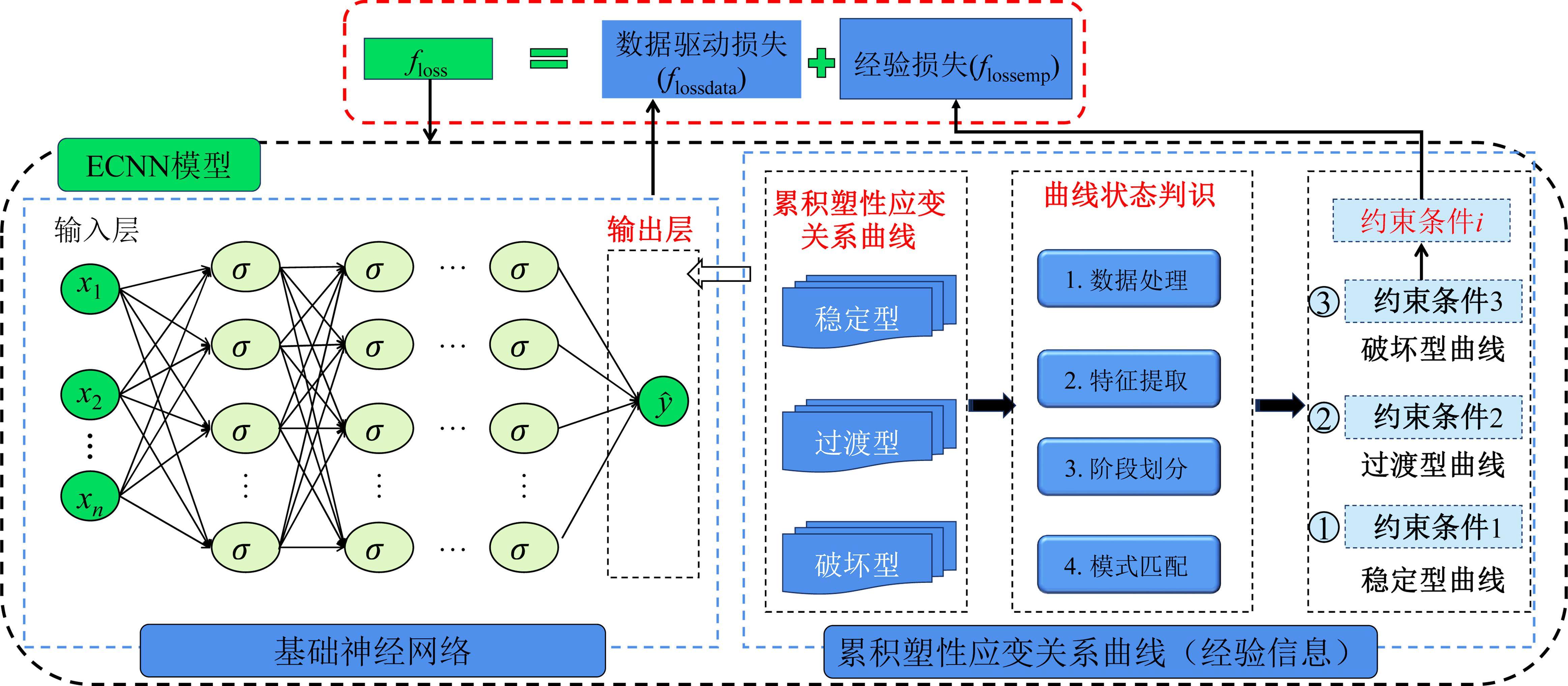
融合神经网络算法和累积塑性应变关系曲线,建立一种基于ECNN的高速铁路路基累积变形预测模型。首先,构建路基累积变形预测数据集,并划分数据集为训练集和测试集;其次,基于训练集建立神经网络模型,通过预测精度与误差、预测不确定性2个层次评价预测性能,从而确定最优神经网络预测模型;最后,利用最优神经网络模型驱动累积变形的数据信息,并以损失函数修正的方式嵌入累积塑性应变曲线,融入经验信息并实现对最优神经网络模型参数和损失函数的约束,完成ECNN模型构建。该模型的详细建立流程如图3所示,主要包括如下3个步骤。
步骤1:数据集构建与划分
基于工程现场或室内试验数据驱动,构建路基累积变形预测数据集D。按照8:2的比例将D划分为训练集Dtrain和测试集Dtest,训练集用于神经网络模型建立,测试集用于选择最优神经网络预测模型。
步骤2:最优神经网络预测模型确定
1) 基于训练集的神经网络模型建立
采用BP、ELM和Bi-GRU这3种典型的神经网络模型对高速铁路路基累积变形进行预测。在这3种典型的神经网络模型中,存在多种超参数,包括学习率、神经元个数、训练迭代次数等。为保障其预测精度,有必要寻找最优的超参数,故将训练集输入神经网络模型后,引入PSO算法[23]优化其超参数。
2) 基于测试集的神经网络模型优选
为确定最优的神经网络模型,得到在测试集上的预测结果后,通过预测精度与误差、预测不确定性2个层次评价预测性能,如表1所示。其中,使用拟合优度(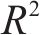
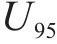
步骤3:ECNN模型训练与预测分析
1) ECNN模型训练
ECNN模型的网络结构如图4(a)所示。该模型的floss函数主要由数据驱动损失项和经验损失项2个部分组成。第1部分是基于最优神经网络模型所得的路基累积变形预测结果与实测路基累积变形值之间的偏差,记为flossdata,常采用均方误差fmse进行计算:
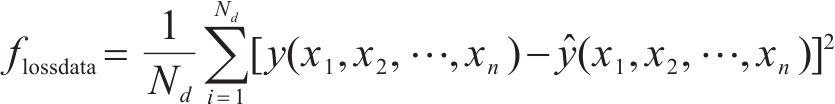
式中: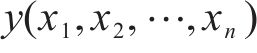
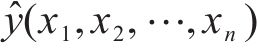
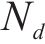
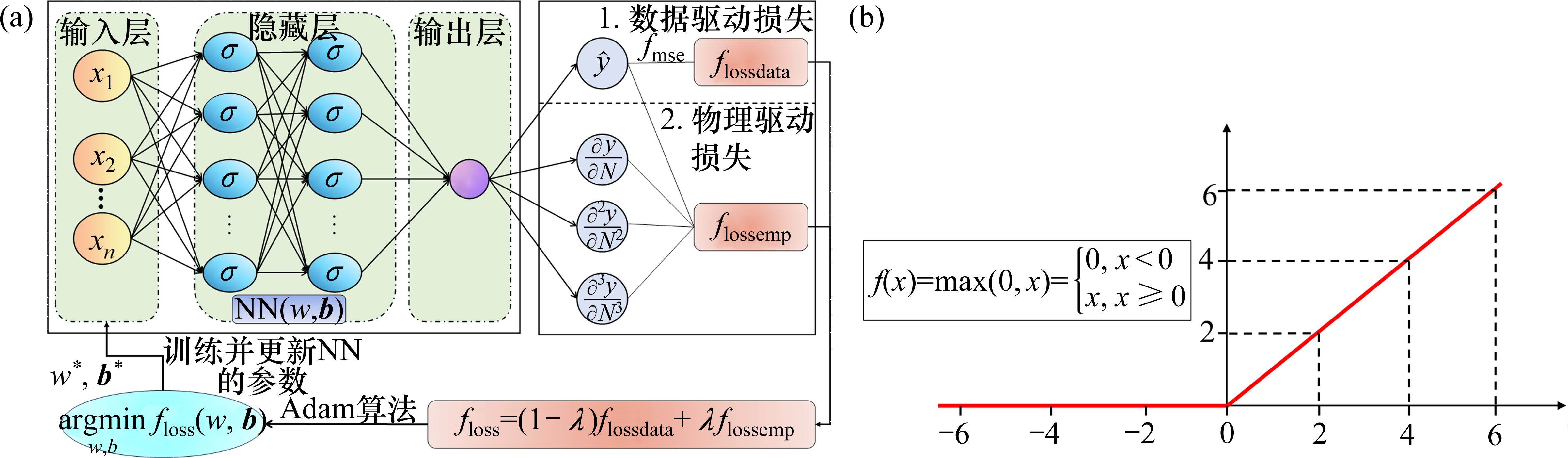
第2部分是从稳定型累积塑性应变关系曲线中提取得到经验损失项flossemp,将其作为最优神经网络模型的约束。为符合稳定型累积塑性应变关系曲线的变化模式,路基累积变形应满足如下5个约束条件:
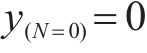
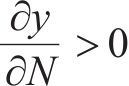
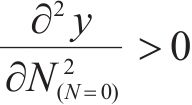
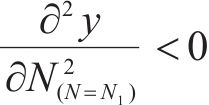
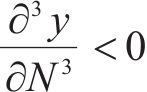
式中:路基累积变形的初始点应为0,故应满足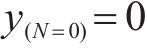
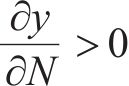
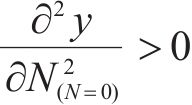
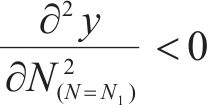
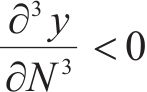
为确定加载初期与加载后期的分界点N1,利用文献调研手段,对国内外高速铁路路基累积变形领域的现场激振试验进行了总结,具体如表2所示。分析可知,现场总体激振次数绝大部分在200万次~300万次之间。当填料为AB组填料时,路基累积变形趋于稳定的激振次数在70万次~100万次之间;当填料为特殊土或改良土时,路基累积变形趋于稳定的激振次数在50万次~140万次之间。考虑各自范围的上限,可将100万次取为AB组填料条件下加载初期和加载后期的分界点,将140万次取为特殊土或改良土条件下加载初期和加载后期的分界点。
为满足上述5个约束条件,构建经验损失项flossemp如下:
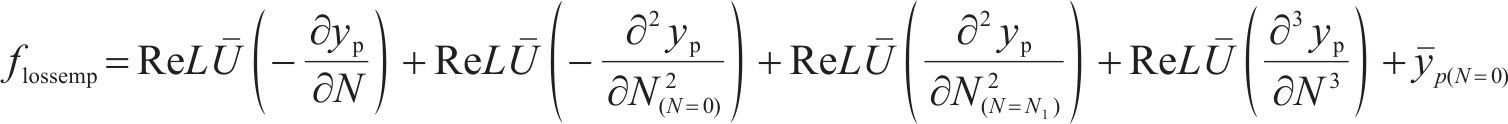
式中: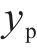
将经验损失项flossemp与数据驱动损失项flossdata加权求和,可得到损失函数:
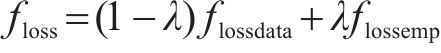
式中:λ为权重参数,决定了flossemp在损失函数中的占比,对于floss值的控制尤为重要。为实现训练充分的目的,在损失函数计算过程中采用梯度迭代优化算法以最小化floss值,并同步更新神经网络的权重参数w和偏置向量b:
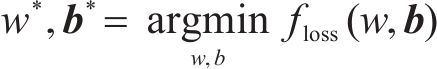
式中: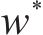
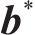
2) ECNN模型预测分析
完成ECNN模型训练后,分别从权重参数分析、预测性能评价与对比、时间分布外泛化性能验证3个方面分析ECNN模型的预测结果。
① 权重参数分析
从0到0.9,间隔0.1,分别设置不同的权重参数λ。输出在训练集上稳定后的损失值以及在测试集上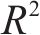
② 预测性能评价与对比
在最佳权重参数λ下,输出ECNN模型在测试集上的预测结果,从预测精度与误差、预测不确定性2个层次对比ECNN模型与最优神经网络预测模型的预测性能。
③ 时间分布外泛化性能验证
在最佳权重参数λ下,采用时间序列交叉验证(Time Series Cross-Validation, TSCV)对ECNN模型的时间分布外泛化性能进行验证。如图5所示,该方法保留时间序列顺序将数据集分为10组,每组的数据量占数据集D的10%,根据训练集和测试集的数据占比不同,得到了9种划分类型。以第1种(第1折)为例,采用数据集D的前10%作为训练集,剩余90%的数据作为测试集进行预测分析;其余划分类型中,每次将训练集占比向后扩充10%,对应测试集减少10%。

2 案例分析
2.1 试验概况
2.1.1 工程概况
如图6(a)所示,依托工点位于浙江省杭绍台高速铁路沿线里程DK86+130~DK86+160的路基试验段。在路基填筑完成后,借助大型激振器快速模拟高速列车循环荷载,激振试验的主要技术参数设置为:通过调节激振频率并结合基床表层动土压力盒反馈值的方式,确定激振频率为15 Hz。激振次数取为150万次~200万次时可满足高速铁路路基表面荷载的模拟要求[28],本研究中取为200万次。为监测循环荷载作用下的路基累积变形值,在加载板的对角上布设测点C-1和C-2,如图6(b)所示。
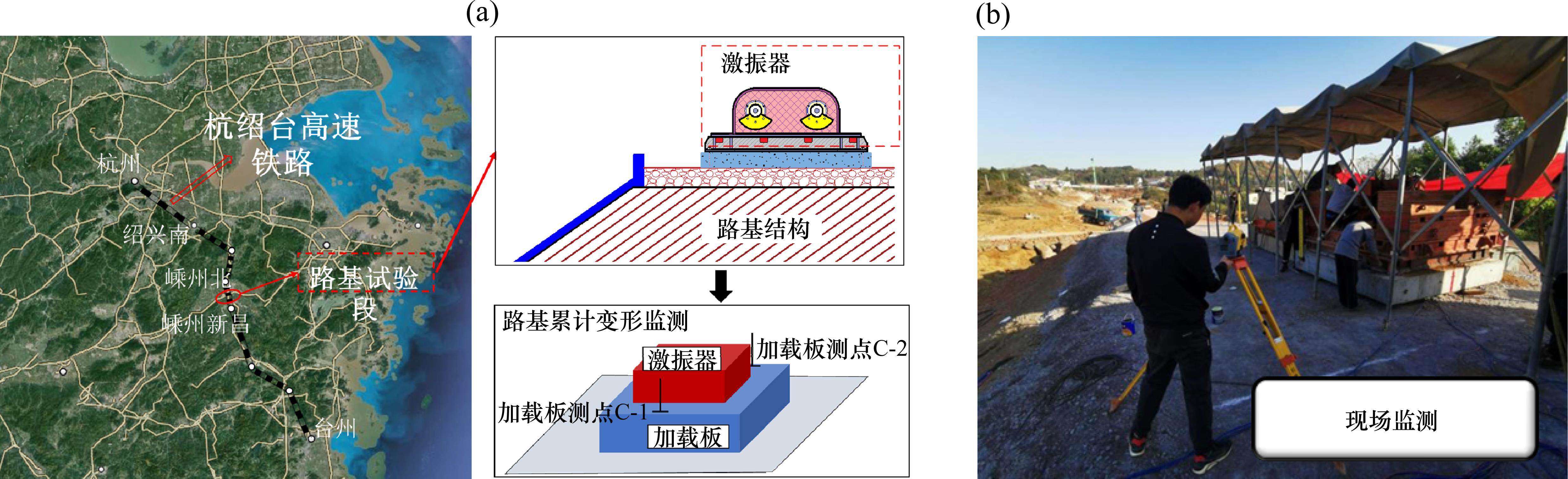
2.1.2 路基累积变形监测结果
绘制激振试验过程中的路基累积变形规律如图7所示。分析可知,路基累积变形速率逐渐缓慢最后趋于稳定状态,这说明路基动应力小于其临界动应力,路基累积变形得到有效控制。当激振次数达到90万次,路基累积变形速率减小,逐渐趋于稳定,故N1应大于或等于90。由于本研究所依托工点的填料类型为AB组填料,将N1取为100。当激振次数达到200万次,加载板下路基累积变形为3.26 mm,说明高速列车循环荷载作用下路基压缩变形量相对较小,路基结构的动变形满足稳定需求。综上可判定该试验所得的路基累积变形符合稳定型曲线规律,并以C-1测点的数据作为数据集,开展后续的预测分析。
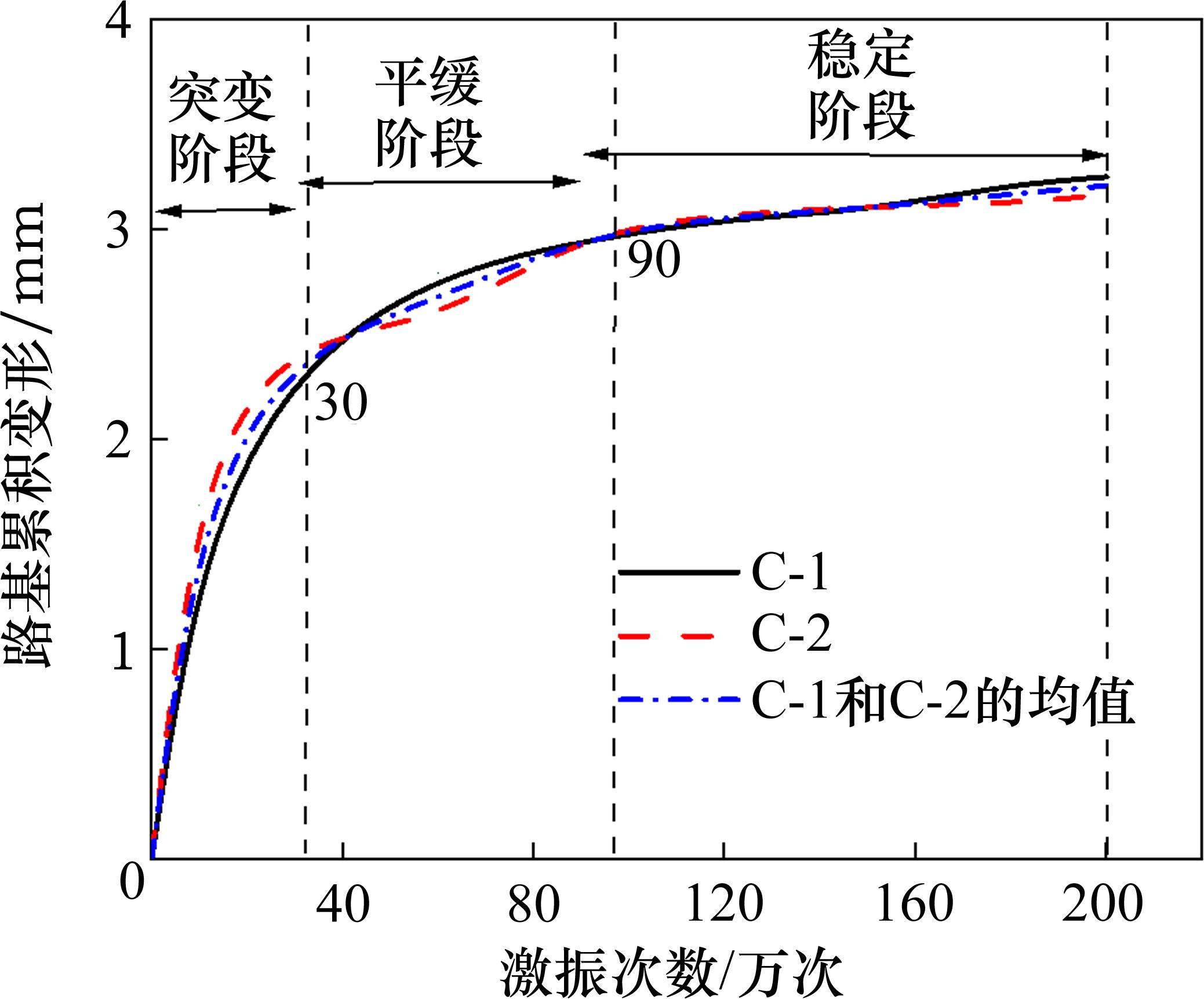
2.2 最优神经网络模型确定
2.2.1 PSO参数优化结果
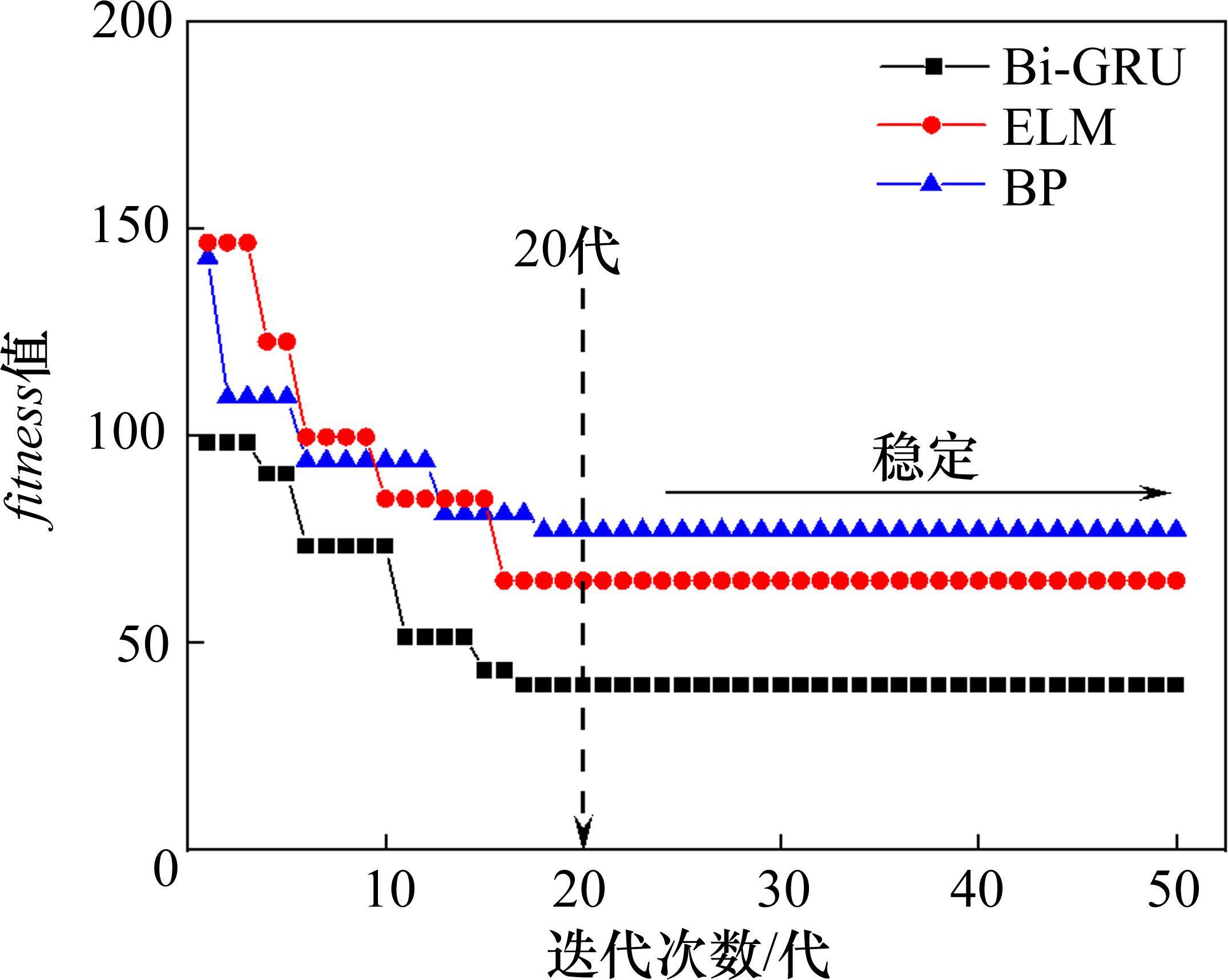
PSO算法优化各神经网络模型超参数过程中的适应度值变化规律如图8所示。分析可知,通过PSO算法的迭代优化,各模型的适应度显著降低,并均在20代之前趋于稳定。其中,Bi-GRU模型的适应度最低,一定程度上说明该模型更具优势。迭代完成后,将各神经网络模型的最优超参数保存后再次输入模型中,执行后续的最优神经网络模型优选操作。
2.2.2 最优神经网络模型优选结果
1) 预测精度与误差使用3个预测精度与误差评价指标对预测结果进行评估,总结计算结果于表3。各模型对路基累积变形都具有较强的预测能力,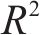
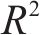
| 模型种类 | R2 | fmae/mm | fmape/% |
|---|---|---|---|
| Bi-GRU | 0.972 59 | 0.005 32 | 0.167 56 |
| ELM | 0.954 13 | 0.006 98 | 0.216 81 |
| BP | 0.927 20 | 0.008 79 | 0.273 13 |
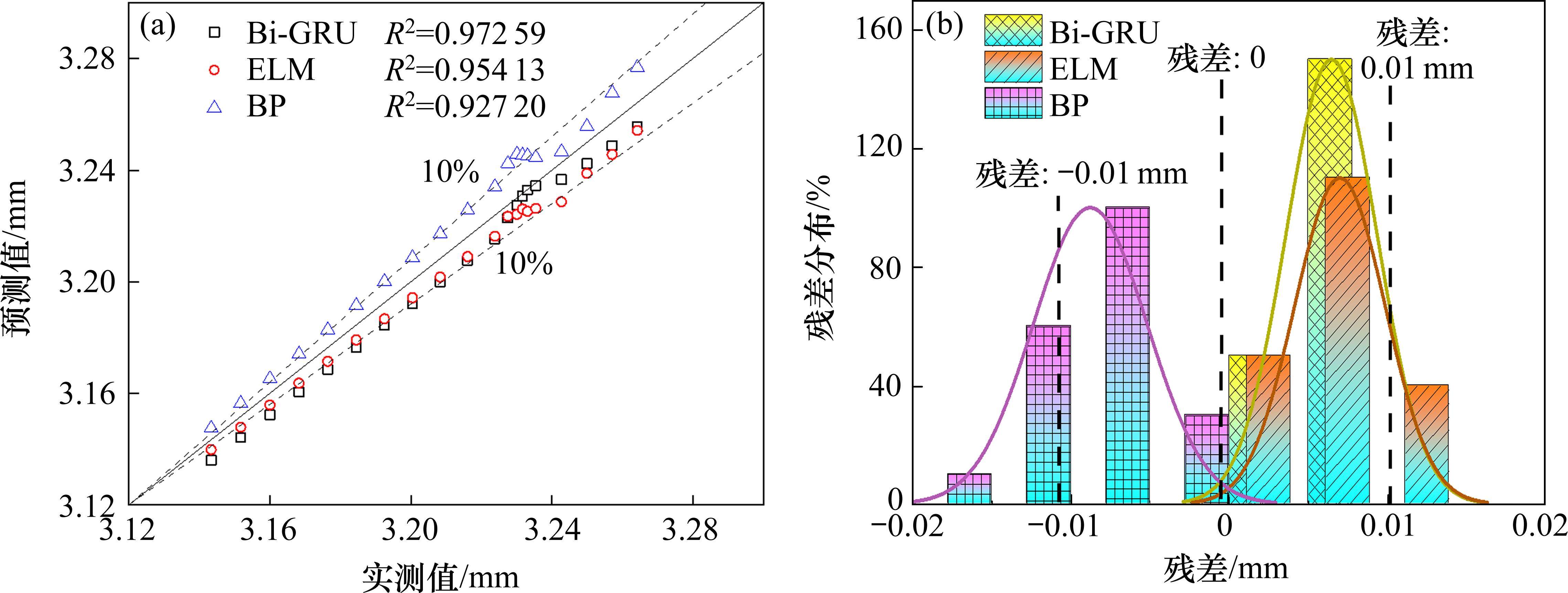
绘制路基累积变形预测值与实测值对比散点图如图9(a)所示,图中的数据点越集中于45°中轴线则预测效果越好。分析可知,3种神经网络模型的预测效果均较好,基本上聚集在45°中轴线附近,且绝大多数点集中在10%的误差线内。为分析各模型预测值与实测值之间的误差,绘制残差分布如图9(b)所示。发现各预测模型的残差整体较小,主要集中在-0.02~0.02 mm。而Bi-GRU模型最聚集于0 mm处,其次分别是ELM模型和BP模型。为更好地区别出最优神经网络预测模型,需借助预测结果的不确定性分析来综合评定。
2) 预测不确定性计算得到预测的不确定性分析结果如表4所示。对比各模型的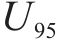
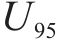
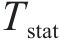
| 模型种类 | U95/mm | Tstat | fsmd/mm | fsi |
|---|---|---|---|---|
| Bi-GRU | 0.014 85 | 10.019 58 | 0.181 09 | 0.021 92 |
| ELM | 0.015 82 | 10.889 49 | 0.204 83 | 0.023 43 |
| BP | 0.019 68 | 10.917 51 | 0.242 34 | 0.029 38 |
2.3 ECNN模型预测结果分析
2.3.1 权重参数λ分析结果
计算不同权重参数下ECNN模型在训练集的最终损失以及在测试集上的评价结果如表5所示,其中最优评价结果以粗体标出。分析可知,训练集的最终损失floss随着λ的增大而减小,表明权重参数的增大可以增加ECNN模型对于路基累积变形的拟合能力。相比之下,测试集上的评价结果是非单调的,当λ为0.3时,预测精度指标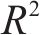
| 权重λ | flossdata | flossemp | floss | R2 | fmae/mm | fmape/% |
|---|---|---|---|---|---|---|
| 0 | 0.000 73 | 0.000 20 | 0.000 73 | 0.972 59 | 0.005 32 | 0.167 56 |
| 0.1 | 0.000 73 | 0.000 20 | 0.000 67 | 0.974 65 | 0.005 13 | 0.160 21 |
| 0.2 | 0.000 73 | 0.000 19 | 0.000 62 | 0.981 06 | 0.004 52 | 0.141 28 |
| 0.3 | 0.000 72 | 0.000 20 | 0.000 56 | 0.989 03 | 0.003 49 | 0.109 03 |
| 0.4 | 0.000 73 | 0.000 20 | 0.000 51 | 0.963 21 | 0.006 13 | 0.191 46 |
| 0.5 | 0.000 73 | 0.000 20 | 0.000 47 | 0.971 70 | 0.005 39 | 0.168 18 |
| 0.6 | 0.000 74 | 0.000 20 | 0.000 42 | 0.937 04 | 0.008 38 | 0.261 44 |
| 0.7 | 0.000 73 | 0.000 20 | 0.000 36 | 0.959 12 | 0.006 53 | 0.203 71 |
| 0.8 | 0.000 75 | 0.000 19 | 0.000 31 | 0.922 85 | 0.009 39 | 0.292 60 |
| 0.9 | 0.000 73 | 0.000 21 | 0.000 26 | 0.959 88 | 0.006 45 | 0.201 33 |
2.3.2 预测性能评价与对比
绘制Bi-GRU模型与ECNN模型的全局分布对比如图10所示,图中的柱子表示在特定激振次数下的绝对误差,越高则表示误差越大。易知,Bi-GRU模型与ECNN模型均能反映实测路基累积变形值的走势,对比而言ECNN模型更为贴合。ECNN模型的绝对误差柱子高度约为Bi-GRU模型的一半,fmae仅为0.003 49 mm,改善了34.40%,表明ECNN模型在误差控制方面更优。
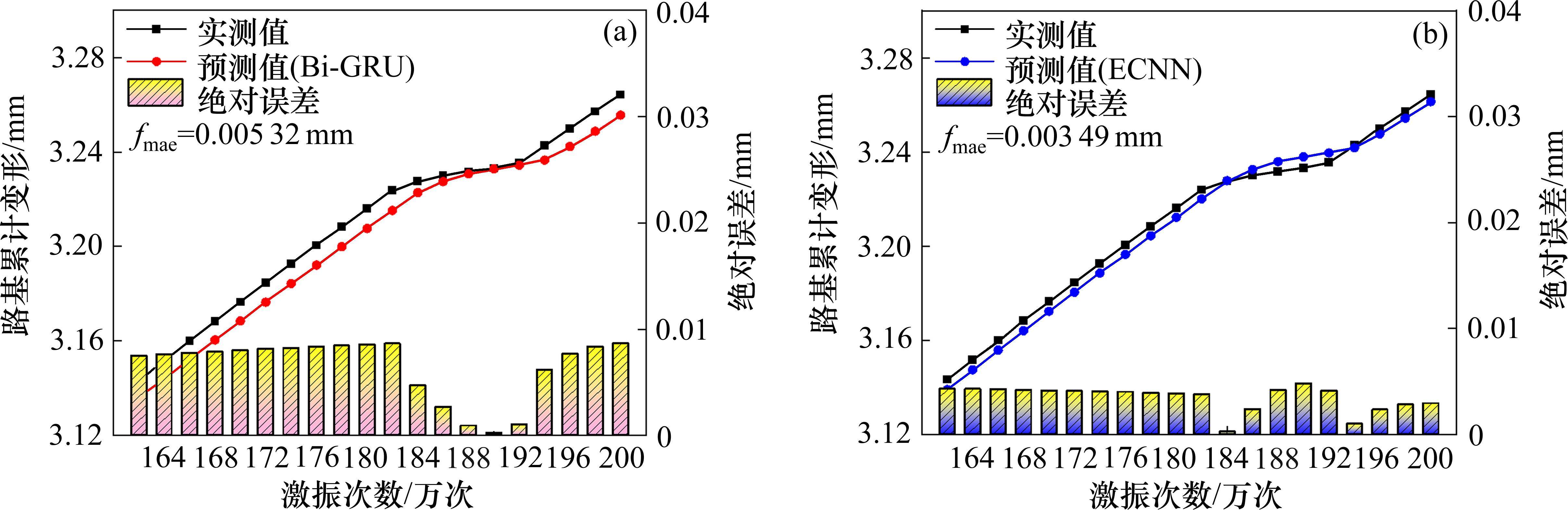
计算Bi-GRU与ECNN模型的预测性能对比结果如表6所示。由预测精度与误差层次可知,ECNN模型在预测精度指标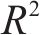
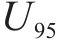
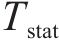
| 评价层次 | 评价指标 | Bi-GRU | ECNN |
|---|---|---|---|
| 预测精度与误差 | R2 | 0.972 59 | 0.989 03 |
| fmae/mm | 0.005 32 | 0.003 49 | |
| fmape/% | 0.167 56 | 0.109 03 | |
| 预测不确定性 | U95 | 0.015 6 | 0.009 48 |
| Tstat | 10.019 58 | 2.656 31 | |
| fsmd | 0.181 09 | 0.053 17 | |
| fsi | 0.021 92 | 0.011 46 |
2.3.3 时间分布外泛化性能验证
采用TSCV方法测试并对比了Bi-GRU模型与ECNN模型的时间分布外泛化性能,得到不同的训练集长度下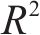
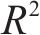
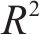
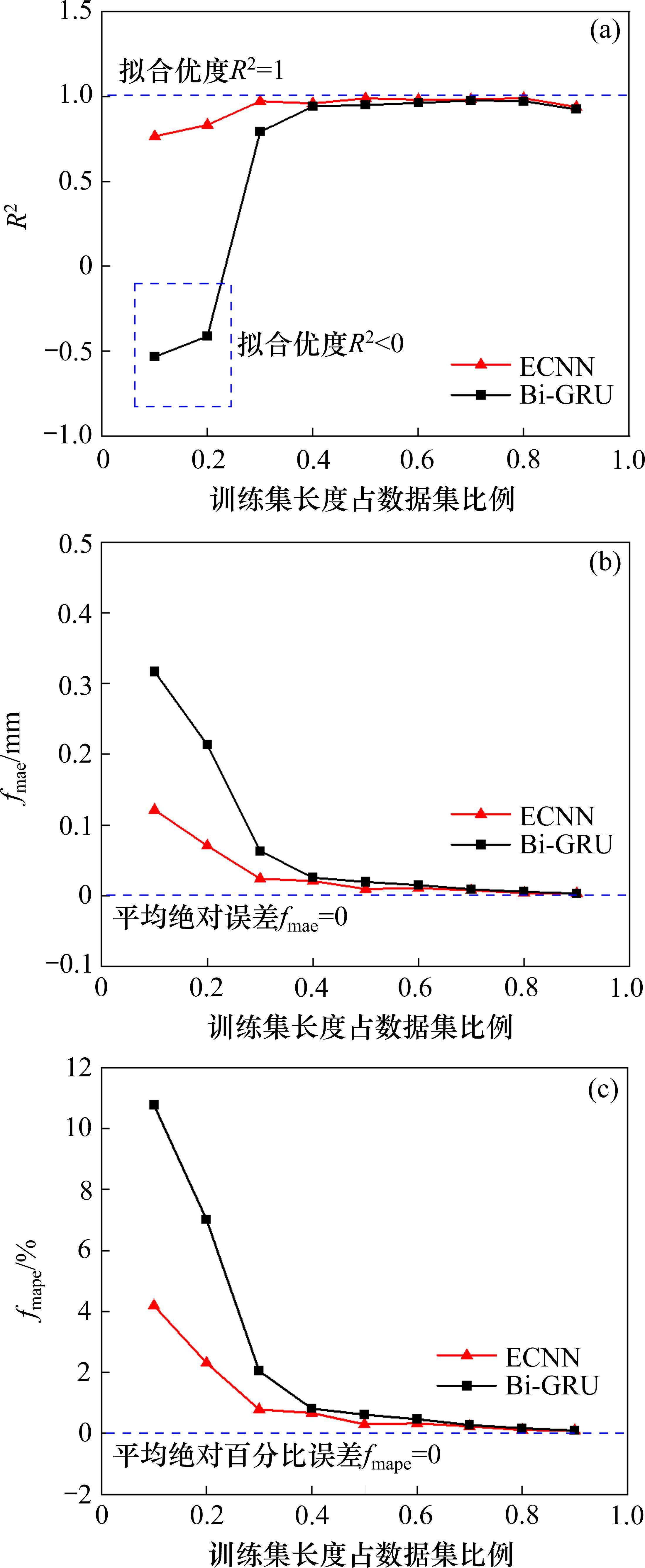
综上,当训练集覆盖的时间跨度较大时,Bi-GRU模型与ECNN模型均能较好地做出预测,因为稳定型曲线的路基累积变形最终会趋于平缓。而当训练集覆盖的时间跨度较小时,纯数据驱动的Bi-GRU模型完全失去预测能力,具有经验约束的ECNN模型表现更好。因此,当训练集覆盖的时间跨度较小时,ECNN模型可有效提高累积变形的预测精度。
3 讨论
3.1 ECNN模型长期预测分析
短期预测方法由于预测精度较高,目前在路基沉降预测、累积变形预测中得到广泛应用[38],而面向工程应用时,长期预测往往更有意义。为验证ECNN模型的长期预测性能,将测试集上的第1组时序样本输入,并采用滚动预测方法[11]对测试集上的路基累计变形进行预测分析。得到测试集上的长期预测结果后,采用fmae和fmape评估其预测误差。绘制ECNN模型在测试集上的长期预测结果如图12(a)所示,并对比图10(b)中的短期预测结果。整体分析可知,ECNN模型的长期预测性能低于其短期预测性能,长期预测误差指标fmae和fmape分别为0.009 01 mm、0.280 20%,但长期预测下的预测曲线与实测曲线的整体趋势较为贴合。进一步分析发现,在ECNN模型的长期预测过程中,ECNN模型对于前5个预测时间步的预测误差控制较好,绝对误差均低于0.01 mm;但随着预测时间步数的增加,预测误差逐渐增加,这主要由于每一步的预测都依赖于前一步的预测结果,导致了长期预测过程中的误差累积效应[39],进而影响整体预测精度。
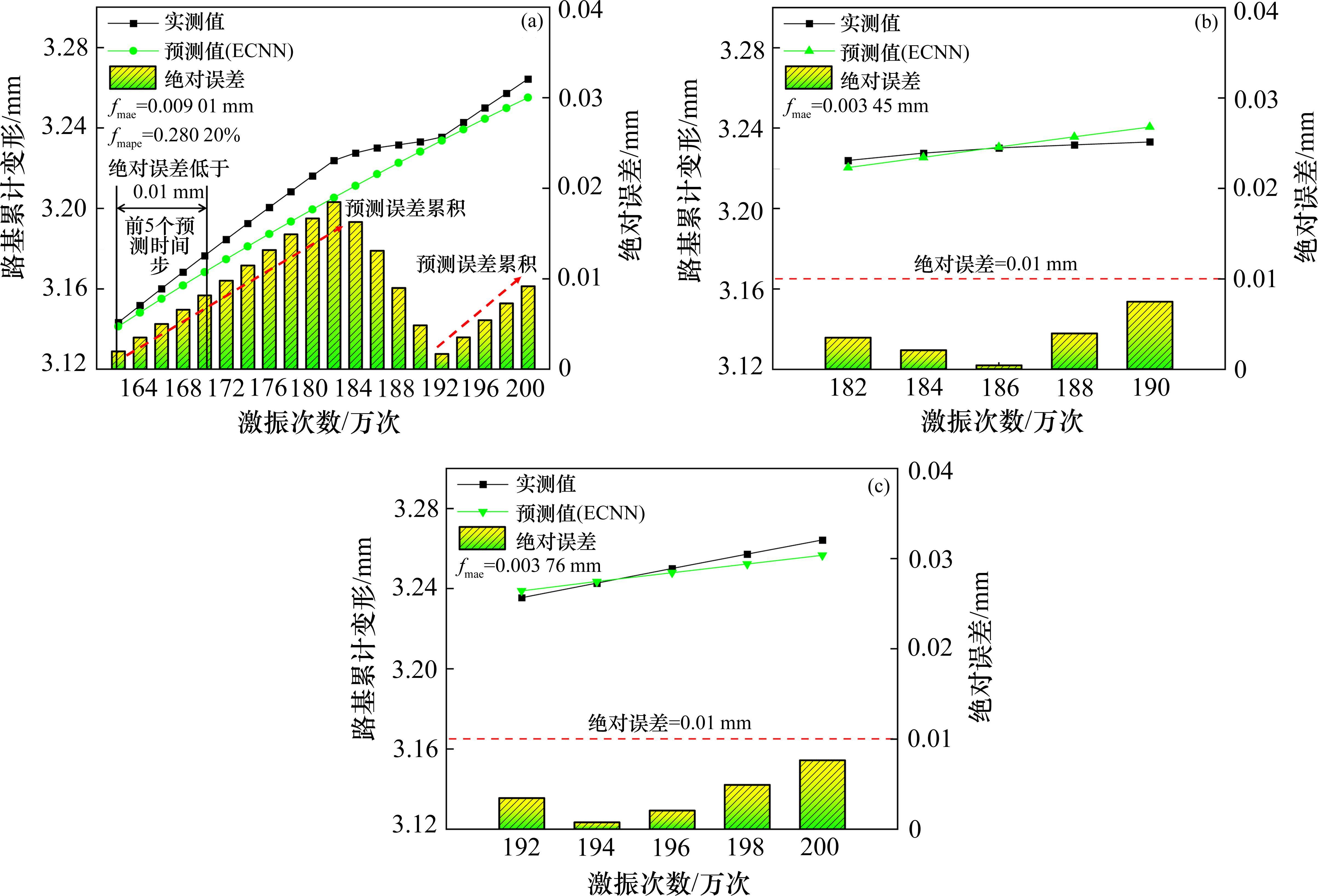
为验证ECNN模型对于路基累积变形突变点的适应能力,将突变点1和突变点2最近的一组时序样本输入,同样采用滚动预测的方法,向后预测5个时间步,绘制其结果如图12(b)和图12(c)所示。分析可知,2个突变点往后的短期预测误差较小,绝对误差均低于0.01 mm,fmae分别为0.003 45 mm和0.003 76 mm,一定程度上证明了ECNN模型在短期预测中对于突变点或拐点处预测误差的控制能力。
综上可知,短期预测与长期预测存在这样的关系,即短期预测性能优于长期预测,而高精度、高泛化的短期预测手段是长期预测的前提。建议以短期预测为主、长期预测为辅的方式开展路基累积变形的分析工作,以提供有效的预测结果。
3.2 ECNN模型未来研究展望
本研究融合神经网络算法和累积塑性应变关系曲线建立一种基于经验约束神经网络的高速铁路路基累计变形预测模型,有效提升了纯数据驱动模型的预测精度以及分布外泛化性能。但为进一步提升其工程意义和实用价值,为路基工程的灾害预测、预警提供理论支撑。未来的工作主要从如下2个方面展开。
1) 考虑模型参数动态更新的ECNN预测模型
为改善长期预测过程中的预测误差累积问题,有必要在既有ECNN模型的基础上考虑模型参数的动态更新。完成ECNN模型的训练后,在测试集或实际部署环境中进行滚动预测。在每一个预测时间步上计算其绝对误差,并与0.01 mm对比;如果在第i个时间步上的绝对误差小于0.01 mm,则继续预测直到满足条件;相反,则停止滚动预测并将其之前的时间步上所有预测值添加到输入序列中,并重新训练模型,然后从第i个时间步继续预测。
2) 考虑路基变形状态判识的ECNN预测模型
本研究的主要目标是提出一种基于经验约束神经网络的高速铁路路基累积变形预测方法,并验证该方法的基本框架和可行性。由于稳定型累积变形是高速铁路路基变形的主要形式之一,且最为常见和最具普适性,故首先选择了稳定型累积塑性应变曲线进行深入研究。与此同时,在构建ECNN模型时,需要一定的数据作为训练样本。由于稳定型累积变形数据相对较为丰富和易于获取,且具有较高的代表性,因此将该类型的数据作为研究基础,并依托工程案例开展分析。
参考TONG等[40]、管凌霄等[41]的研究成果,路基累积变形发展具有3种典型的形式,即稳定型、过渡型和破坏型。为进一步提升ECNN模型的实用性和推广应用价值,有必要提出一种考虑路基变形状态判识的ECNN预测模型,具体如图13所示。基于工程现场或试验获得高速铁路路基累积变形数据后,首先对曲线状态进行判识,以识别曲线类型;然后针对具体的曲线类型,例如稳定型、过渡型或破坏型,得到对应的经验信息约束条件,并以损失函数修正的方式嵌入到神经网络模型中;最后完成考虑路基变形状态判识的ECNN模型构建。
4 结论
1) 所提基于经验约束神经网络的高速铁路路基累积变形预测方法包括最优神经网络预测模型确定、ECNN模型训练与预测分析2个部分。前者具有神经网络预测模型评价与优选功能,后者可构造具有时间分布外泛化性的高速铁路路基累积变形预测模型。
2) Bi-GRU模型的拟合优度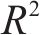
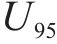
3) 相较于Bi-GRU模型,ECNN模型在预测精度与误差、预测不确定性2个层次均更优,表明考虑累积塑性应变关系(经验信息)约束的ECNN模型具备更强的预测性能。
4) 采用时间序列交叉验证方法,证实ECNN模型相较于Bi-GRU模型具有优异的时间分布外泛化性能,当训练集覆盖的时间跨度较小时,可有效提高累积变形的预测精度。ECNN模型短期预测性能优于长期预测,而高精度、高泛化的短期预测手段是长期预测的前提。为进一步提升其工程意义,未来研究工作建议考虑模型参数动态更新和路基变形状态判识。
邓志兴,徐林荣,李永威等.基于经验约束神经网络的高速铁路路基累积变形预测研究[J].铁道科学与工程学报,2025,22(02):469-484.
DENG Zhixing,XU Linrong,LI Yongwei,et al.Research on subgrade cumulative deformation prediction of high-speed railway based on empiricism-constrained neural network[J].Journal of Railway Science and Engineering,2025,22(02):469-484.