永磁同步电机因其功率密度高、可靠性好等特点被广泛应用于交通领域[1]。开绕组永磁同步牵引电机(Open-winding permanent magnet synchronous traction motors,OW-PMSTM)由2个逆变器供电,电压增加2倍,电机调速范围拓宽。共母线OW-PMSTM系统只需1个直流电源,结构简单,成本低,应用广泛[2-3]。然而,这种电机传动系统由于零轴回路存在,逆变器产生的零轴电流会造成三相电流严重畸变和6倍频转矩脉动,降低系统控制性能。为抑制零轴电流和转矩脉动,年珩等[2-3]通过增加零轴电流闭环调节回路,抑制了零轴电流,减小了电流纹波,但系统复杂度也随之增加。孙丹等[4]重构19个电压矢量,扩大了备选矢量范围,抑制了转矩脉动,但忽略了三次谐波反电动势对系统的影响。AN等[5]通过新型SVPWM调制,对零轴电压进行实时控制,抑制了零轴电流,降低了转矩脉动,但未考虑dq轴电流分量误差增加的转矩脉动。为简化控制系统结构,增强系统动态响应速度,LIU等[6-8]引入模型预测控制,建立电机控制系统,对零轴电流进行模型预测控制,简化系统结构,缩短计算时间,抑制了零轴电流。但是,模型预测控制的代价函数中权重系数整定难度较大,且开关频率较高,对电机参数依赖性高。YUAN等[9]设计出一种自适应滑模观测器观测补偿零轴电流,抑制转矩脉动,但q轴电流误差仍会增加转矩脉动。SUN等[10]为降低开关频率和抑制零轴电流,建立新的矢量查找表,根据传统直接转矩控制策略中的转矩和磁通量选择一个矢量,基于零轴电流控制选择另一个矢量。高锋阳等[11]对共母线开绕组永磁同步牵引电机设计了带有开关频率代价函数的自抗扰级联模型预测电流控制(Cascade Model Predictive Current Control,CMPCC)策略降低开关频率,但系统仍存在较高的开关频率。为降低模型预测控制对电机参数依赖性,减小调速超调,姚绪梁等[12]提出一种级联模型参考自适应方法;刘成等[13]将扩张状态观测器改进为通用积分型扩张状态观测器;TÜRKER等[14-18]为降低模型预测控制对电机传动系统参数的依赖性,分别在无差拍模型预测控制中引入离散积分项、在线参数辨识器、级联线性与非线性自抗扰控制器和设计自适应律,提高系统鲁棒性;张立伟等[19]为减小参数辨识器稳态误差设计了Adaline辨识器,提升了参数辨识的准确度;王静等[20-22]分别引入无功转矩、增加代价函数和几何法,避免了权重系数整定。但是,参数辨识和避免权重系数整定策略不适用OW-PMSTM控制系统。基于以上分析可知,现有对共母线OW-PMSTM控制方法存在系统复杂度较高、转矩脉动大、三次谐波反电动势影响控制系统性能、优化价值函数中权重系数整定难度大、开关频率高的问题。针对共母线OW-PMSTM系统存在零轴电流、转矩脉动大、开关频率高和模型预测控制依赖电机参数问题,提出一种基于变步长Adaline改进可调参数级联模型预测电流控制策略。剔除造成开关频率和零序电流较高的小矢量,分别对dq轴电流和零轴电流进行分级寻优,对各目标分级优化,避免权重系数整定,并改进PI控制器和设计Adaline参数辨识器,抑制转矩脉动和零轴电流,降低开关频率和减小调速超调,提升控制系统鲁棒性,对系统的控制性能有明显的提升作用。研究结果为进一步对共母线开绕组永磁同步牵引电机传动系统应用于机车牵引提供参考。
1 共直流母线OW-PMSTM系统
1.1 共直流母线OW-PMSTM数学模型
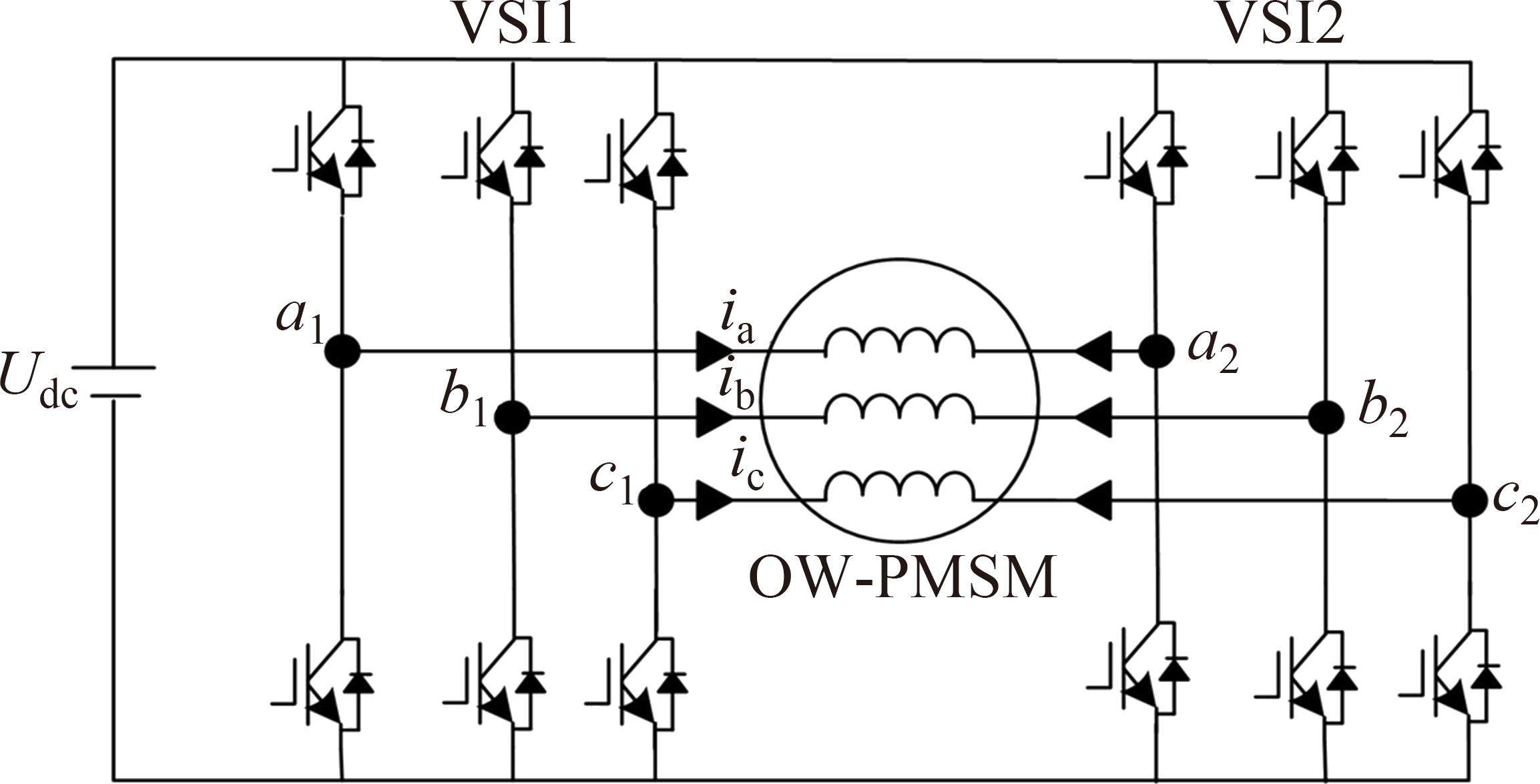
图1为共母线OW-PMSTM系统结构,2个逆变器与同一直流电源相连,电机三相绕组分别接逆变器三相桥臂。共母线OW-PMSTM系统dq0坐标系下数学模型为:
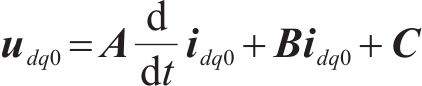
式中: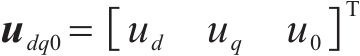
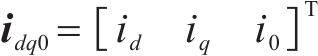
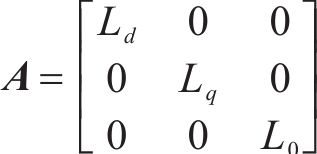
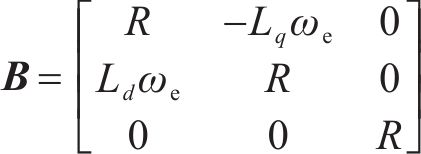
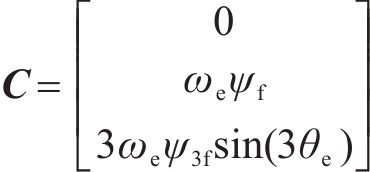
1.2 共母线OW-PMSTM系统电压矢量与电流预测
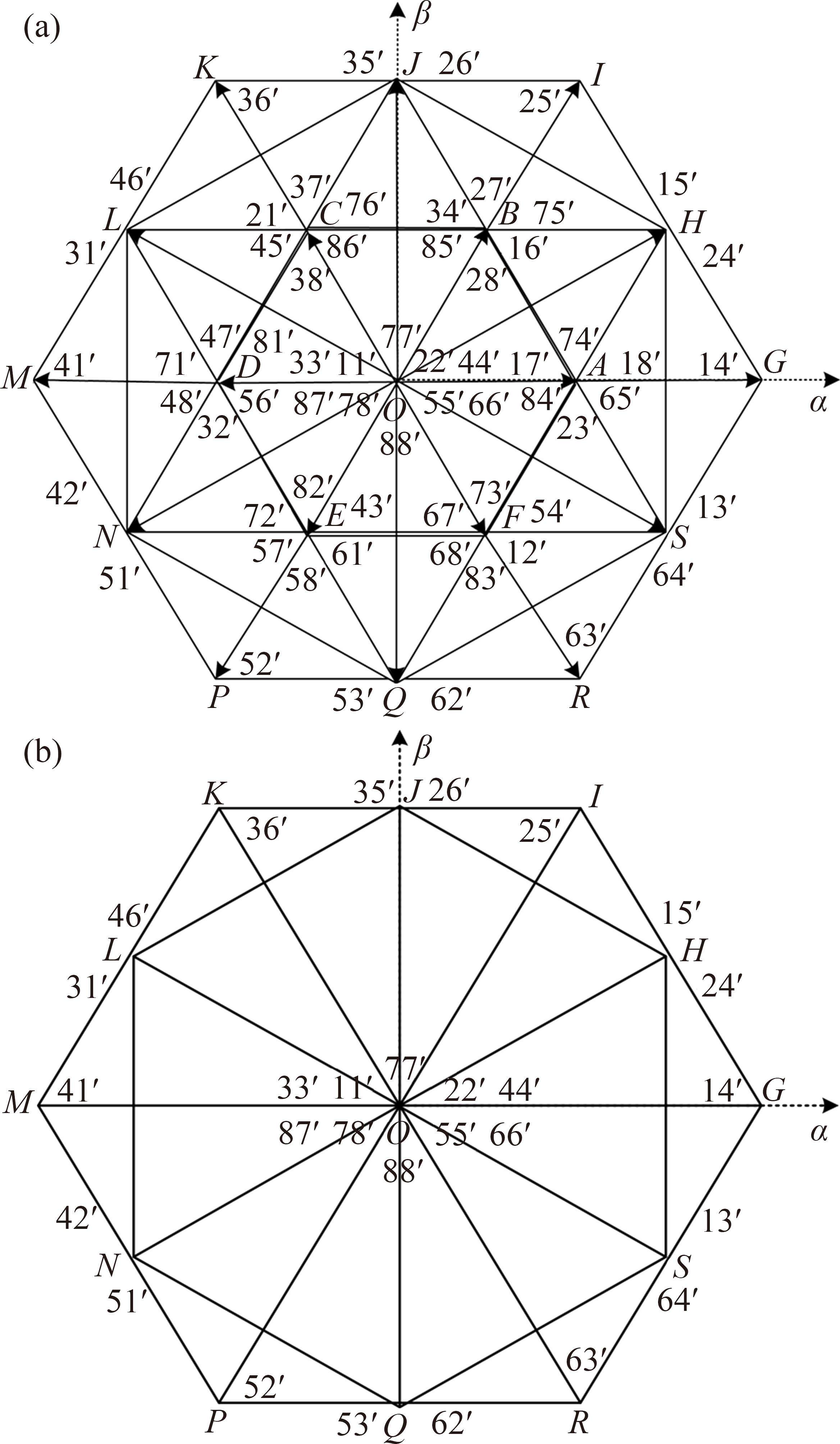
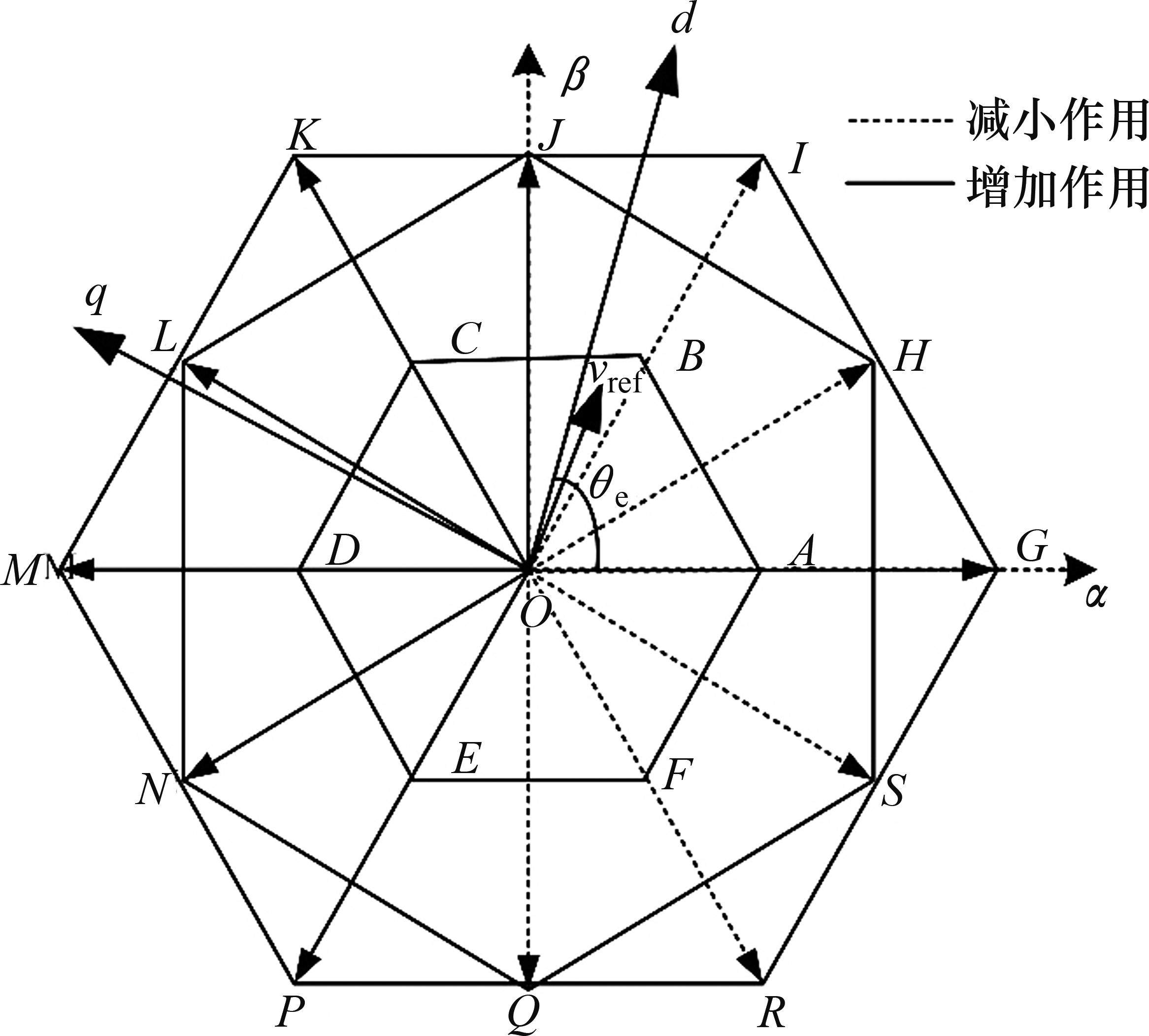
共母线OW-PMSTM系统,其电压矢量由2个两电平逆变器产生,每个逆变器有8种开关状态。共母线OW-PMSTM系统有64种开关状态,27种电压矢量,有-Udc、-2/3Udc、-1/3Udc、0、1/3Udc、2/3Udc、Udc这7种不同零轴电压。在αβ平面有19种矢量,有大、中、小矢量各6种,零矢量1种。而小矢量有6个开关状态,中矢量有2个开关状态,零矢量有10个开关状态。如图2(a)所示,A,B、C、D、E、F电压矢量为小矢量,H、J、L、N、Q、S电压矢量为中矢量,G、I、K、M、P、R为大矢量。
将式(1)离散化得到电流预测方程为:
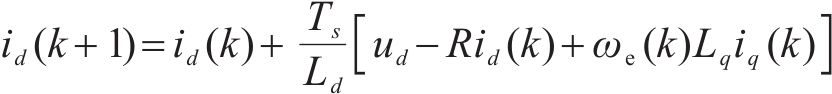
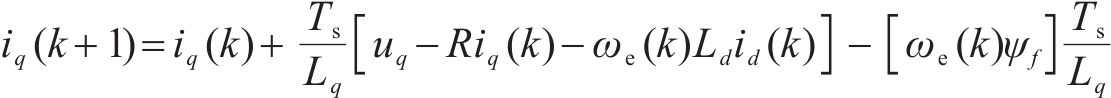
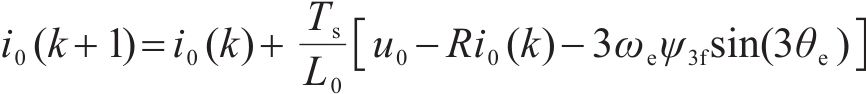
式中:id(q)(k+1)为k+1时刻d(q)轴电流;id(q)(k)为k时刻d(q)轴电流;Ts为采样周期。
2 变步长Adaline参数改进可调级联模型预测电流控制
2.1 级联模型预测电流控制
文献[11]采用第1个有效电压矢量使q轴电流增加,第2个有效电压矢量和零矢量使q轴电流减小的电压矢量组合原则。同时,对各电压矢量分级预测控制,其矢量选择和作用时间分配设计如式(5)~式(27)所示。
有效电压矢量与零电压矢量作用的d轴电流变化率分别为:
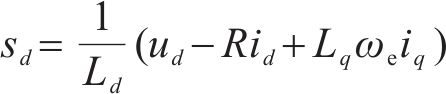
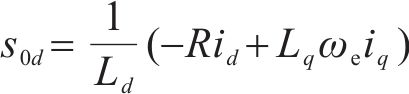
有效电压矢量与零电压矢量q轴电流变化率分别为:
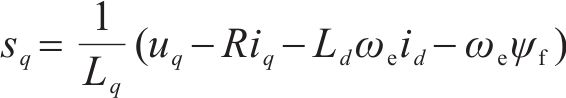

下一时刻电流为:
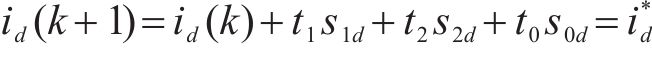
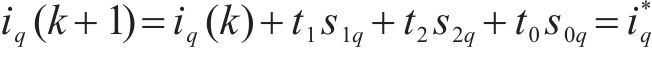
式中: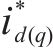
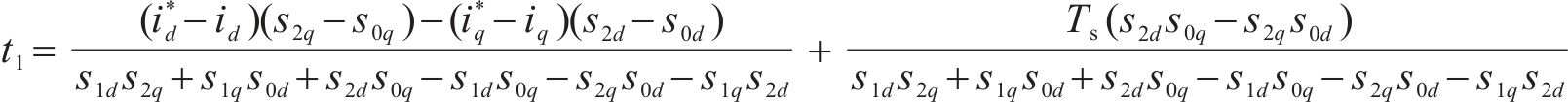
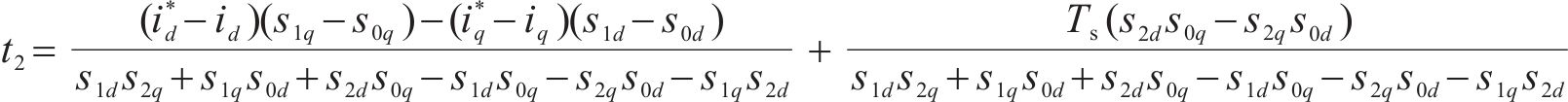
联合式(2)~式(4)、式(9)和式(10)可得在k+t1时刻和k+1时刻dq轴电流为:
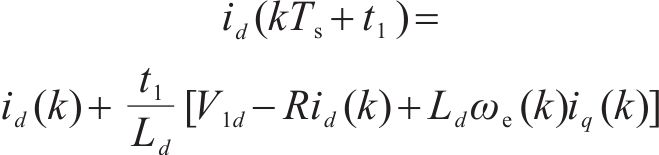
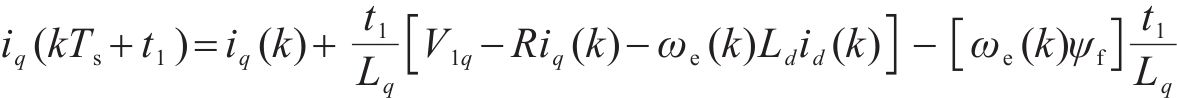
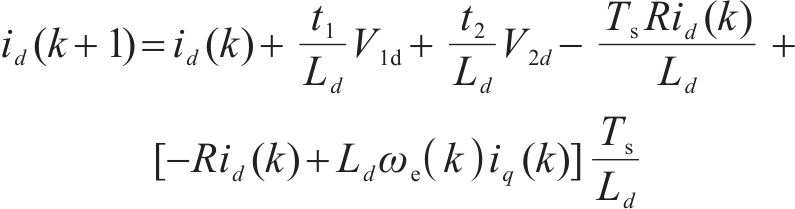
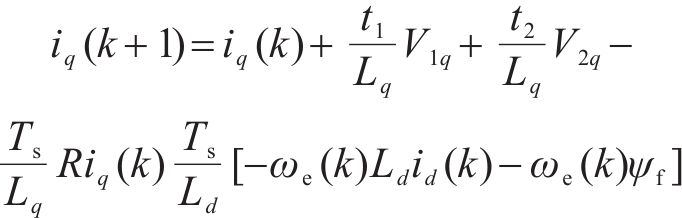
式中:Vxd(q)(x=1,2)为第1、第2矢量d(q)轴电压分量。
第1级优化价值函数为:
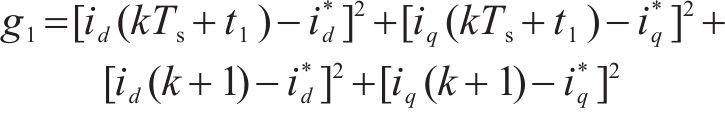
由式(17)确定dq轴2个最优矢量后,还需对零轴电流进行抑制。小矢量有2种不同的零轴电压,由式(2)~式(4)可知,kTs+t1和kTs+t1+t2时刻零轴电流为:
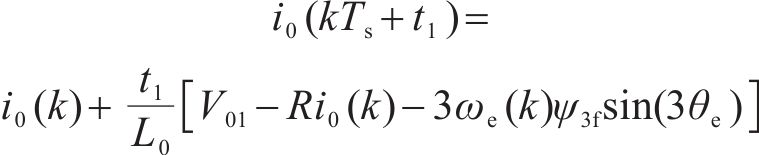
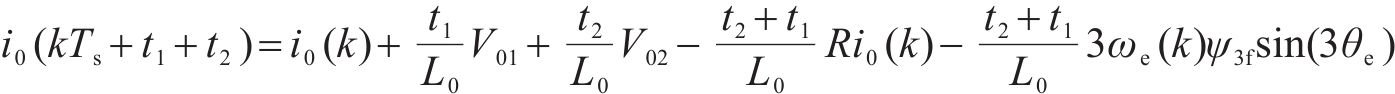
式中:L0为零轴电感。
第2级优化价值函数为:
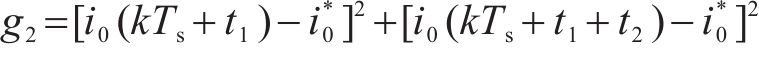
式中:i0*为零轴电流参考值。
零矢量有u0=0、u0=Udc和u0=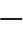
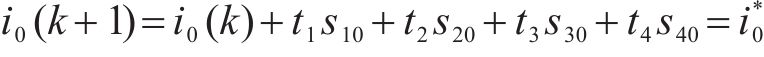
由于Ts=t1+t2+t3+t4,则t3为:
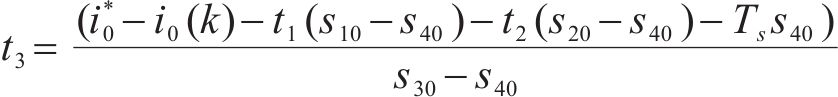
式中:t3为零轴电压非零的零矢量作用时间;t4为零轴电压为0的零矢量作用时间;s10、s20、s30、s40分别为各矢量作用时,零轴电流变化率。
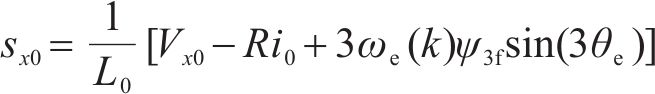
式中:x=1,2,3,4;Vx0为各矢量零轴分量。
零轴电压为0的零矢量作用时间t4为:
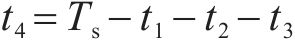
则k+1时刻零轴电流为:
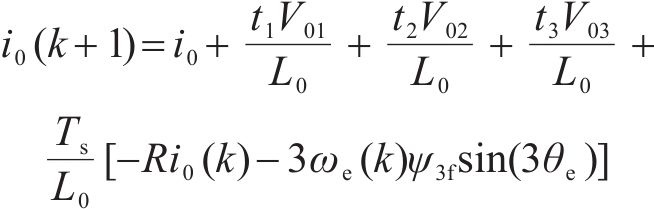
式中:V03为零矢量的零轴电压。
第3级优化价值函数为:
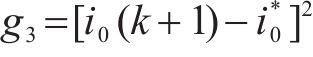
由于零矢量、小矢量和中矢量有多种开关状态,可以优化开关频率。
第4级优化价值函数为:
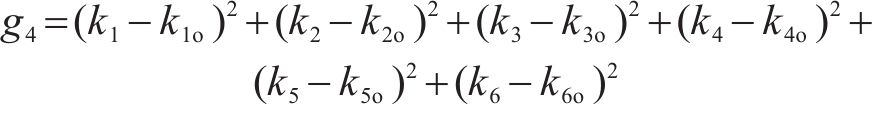
式中:kx(x=1,2,3,4,5,6)为待优化开关状态;kxo(x=1,2,3,4,5,6)为当前开关状态。
2.2 改进三矢量级联模型预测控制
2.1节所介绍的三矢量级联模型预测控制主要对18种有效电压矢量和零电压矢量进行分组再组合寻优,从而抑制零轴电流和转矩脉动,之后再对开关频率进行优化。然而,三矢量级联模型预测控制仍然使电机传动系统存在较高的开关频率和寻优次数。
由图2(a)可知,当级联模型预测控制第1级选择大矢量或中矢量与小矢量组合时,由于小矢量存在较高的零轴电压和开关切换频率,造成系统零轴电流和开关频率较高。以图3中的参考电压矢量为例,选择小矢量B和中矢量J合成电压矢量Vref最多需要进行3次开关变换,最少需要1次开关变换,合成电压矢量零轴电压最大幅值为2/3Udc,零轴电压最小幅值为1/3Udc。而选择大矢量I和J合成有效电压矢量Vref时,开关频率只需要变换一次,合成零轴电压矢量幅值为1/3Udc。综上所述,小矢量参与电压矢量合成造成了系统开关频率和零轴电压较高。所以将小矢量从候选电压矢量集中剔除,所得由大矢量和中矢量组成的矢量分布如图2(b)所示,其所构成的36种电压矢量组合,极大降低了模型预测控制的寻优次数,保证了改进级联模型预测控制能达到系统的最大调制范围。大矢量、中矢量和小矢量虽电压幅值不同,带有的能量也不相同,但在级联模型预测控制中对电压矢量作用时间精确分配,保证了合成参考电压矢量的各电压矢量带有相同的能量。所提策略降低了开关频率,使得逆变器开关损耗更小。
2.3 Adaline改进PI控制器与参数辨识器
针对速度外环ADRC控制器兼顾调速快速性与超调,但其参数复杂整定难度大的问题,引入变步长自适应线性神经网络(Adaptive linear neural network,Adaline)。改进PI控制器是PI控制器利用电机转速与参考转速之差消除控制系统转速控制误差的原理,与变步长Adaline结合,通过特殊功能的比例积分系数自整定环节对调速超调进行抑制。
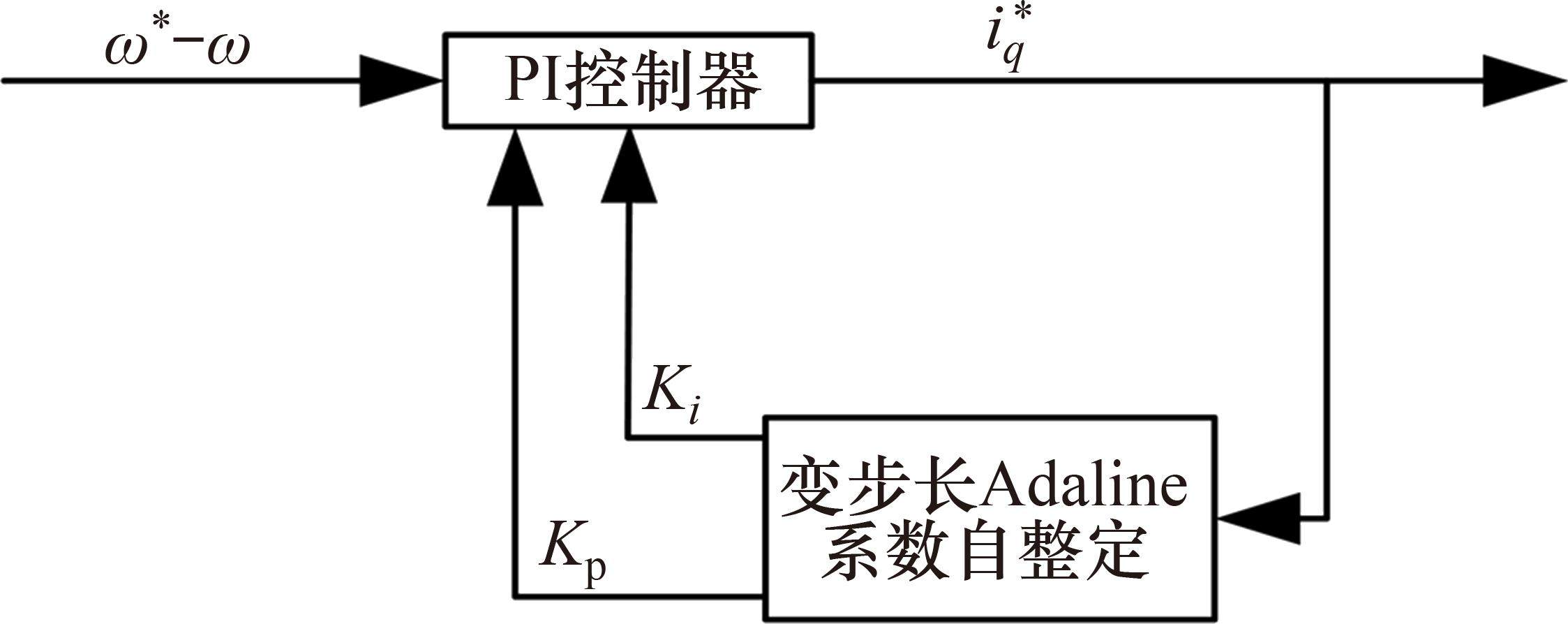
改进PI控制器由传统PI控制器比例积分环节和变步长Adaline系数自整定组成,其控制框图如图4所示。OW-PMSTM系统改进PI控制器变步长Adaline系数自整定环节设计如下所示。
电机转速状态方程为:
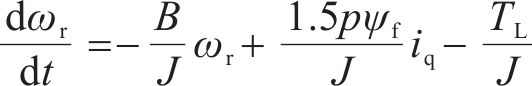
式中:ωr为转速;B为摩擦因数;J为转动惯量;TL为负载转矩。
对式(28)离散整理得到q轴参考电流目标值为:
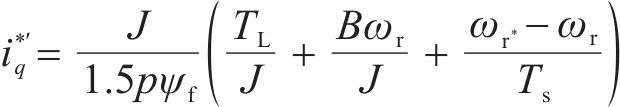
式中:ω*为给定转速。
由文献[19]可知,变步长Adaline具有收敛速度快、稳态误差小的优点。构建自整定器步长与瞬时误差二次方函数关系,实现了神经网络步长实时变化以达到减小稳态误差目的。改进PI控制设计为:
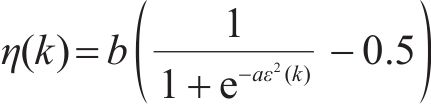
式中:η为计算步长。由文献[19]可知,为使Adaline网络收敛,计算步长η需满足的条件为:
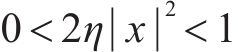
式中:x为电机输出转速与给定转速的差值。
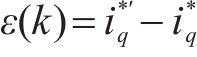
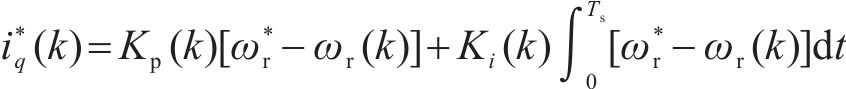
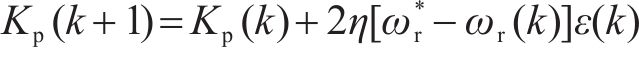
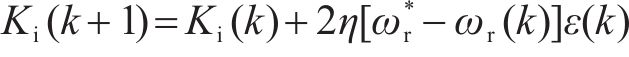
式中:ε为参考电流误差;Kp为比例系数;Ki为积分系数;a、b为调节系数。
改进PI控制器通过变步长Adaline,将参考电流误差不断迭代更新,并通过调节Kp和Ki达到兼顾调速快速性与超调抑制目的。
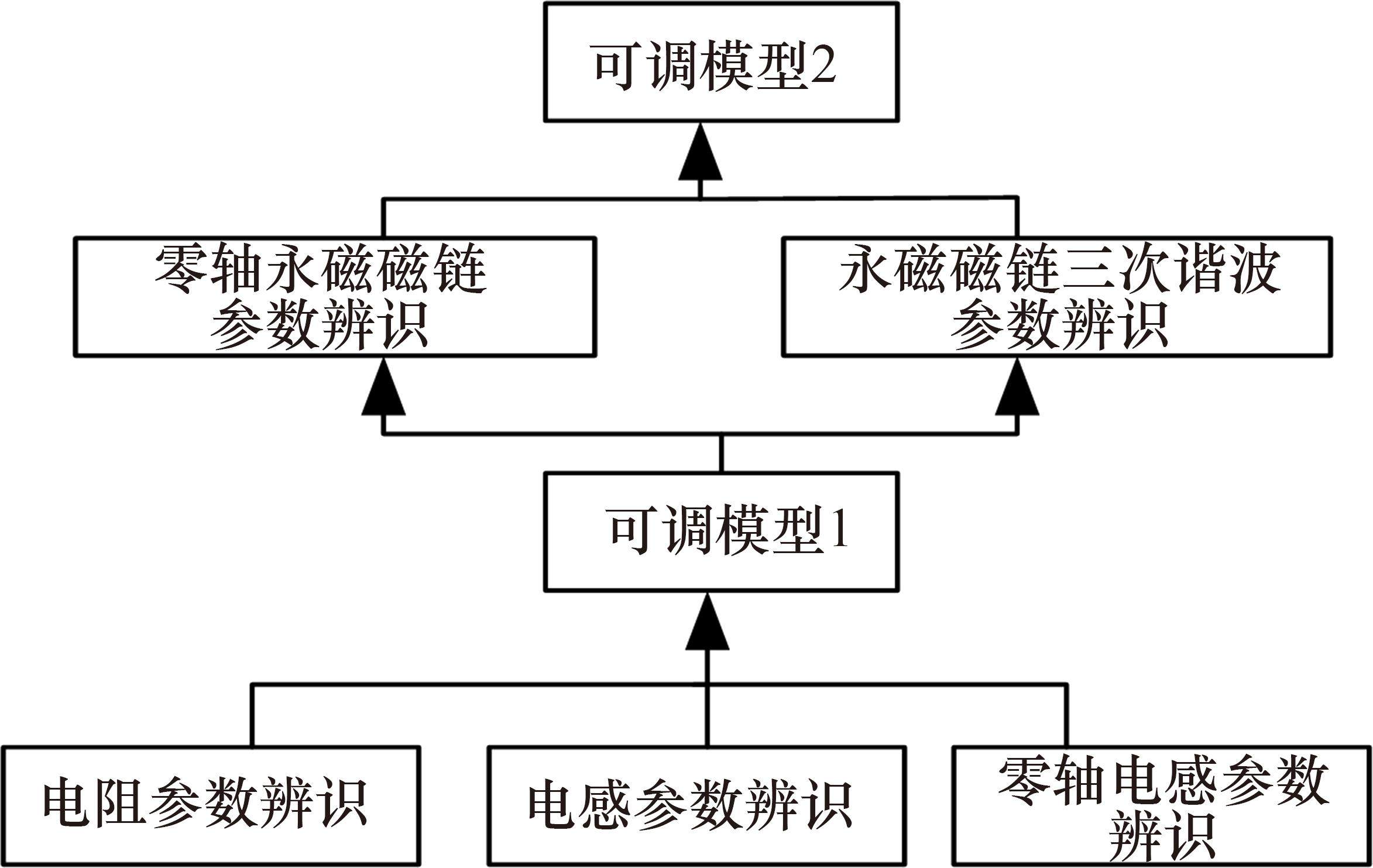
变步长Adaline参数辨识器则可以通过电机状态方程设计合适的辨识模型,对OW-PMSTM定子电阻、电感、永磁磁链、零轴电感和永磁磁链三次谐波进行准确辨识,对级联模型预测控制模型实时更新,提高系统的鲁棒性。由式(1)可知对电机5种参数进行在线辨识存在欠秩问题,结合文献[17]所提策略与式(1),得到电机机械时间常数远大于电气时间常数,电感与电阻在单个周期内对电机预测控制影响较大。因此,可以设计电机参数分步辨识。首先根据电机铭牌参数对电机定子电阻、电感和零轴电感进行辨识,得到调节模型1;然后通过调节模型1再辨识永磁磁链和永磁磁链三次谐波,对电机参数完成一次完整更新,不断更新辨识参数提升电机控制系统鲁棒性,其辨识框图如图5所示。联立式(1)与式(30)设计参数辨识模型如下。
电阻参数辨识:
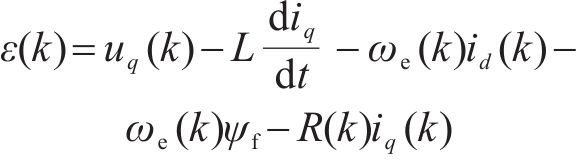
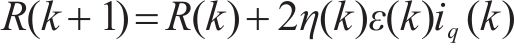
电感参数辨识:
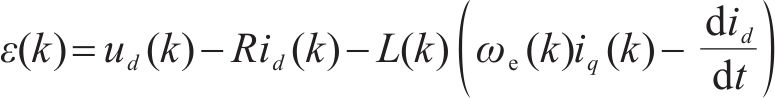
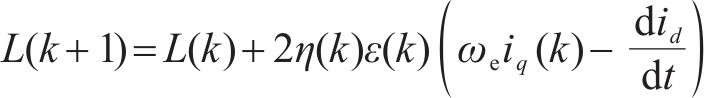
永磁磁链参数辨识:
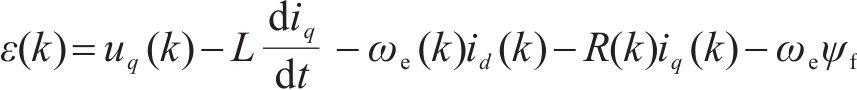
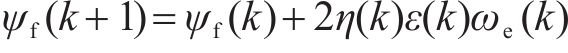
零轴电感参数辨识:
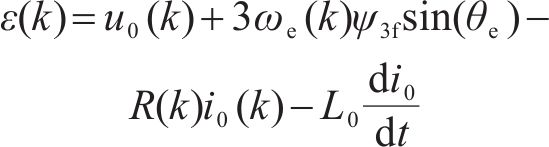
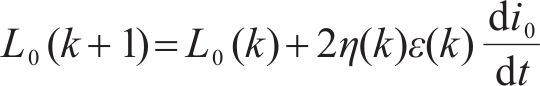
永磁磁链三次谐波:
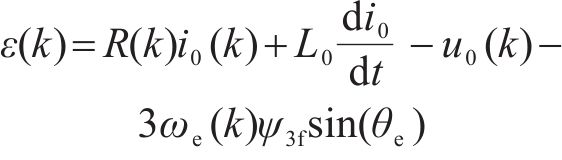
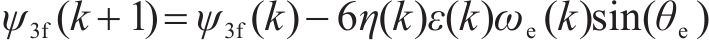
由式(30)、式(31)和式(36)~式(45)可知,上述设计的参数辨识器中电阻辨识器的Adaline输入x为q轴电流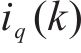
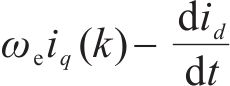
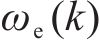
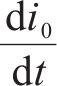
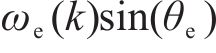
3 仿真测试分析
Adaline_PI控制器共母线OW-PMSTM参数可调改进级联模型预测电流控制策略采用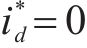
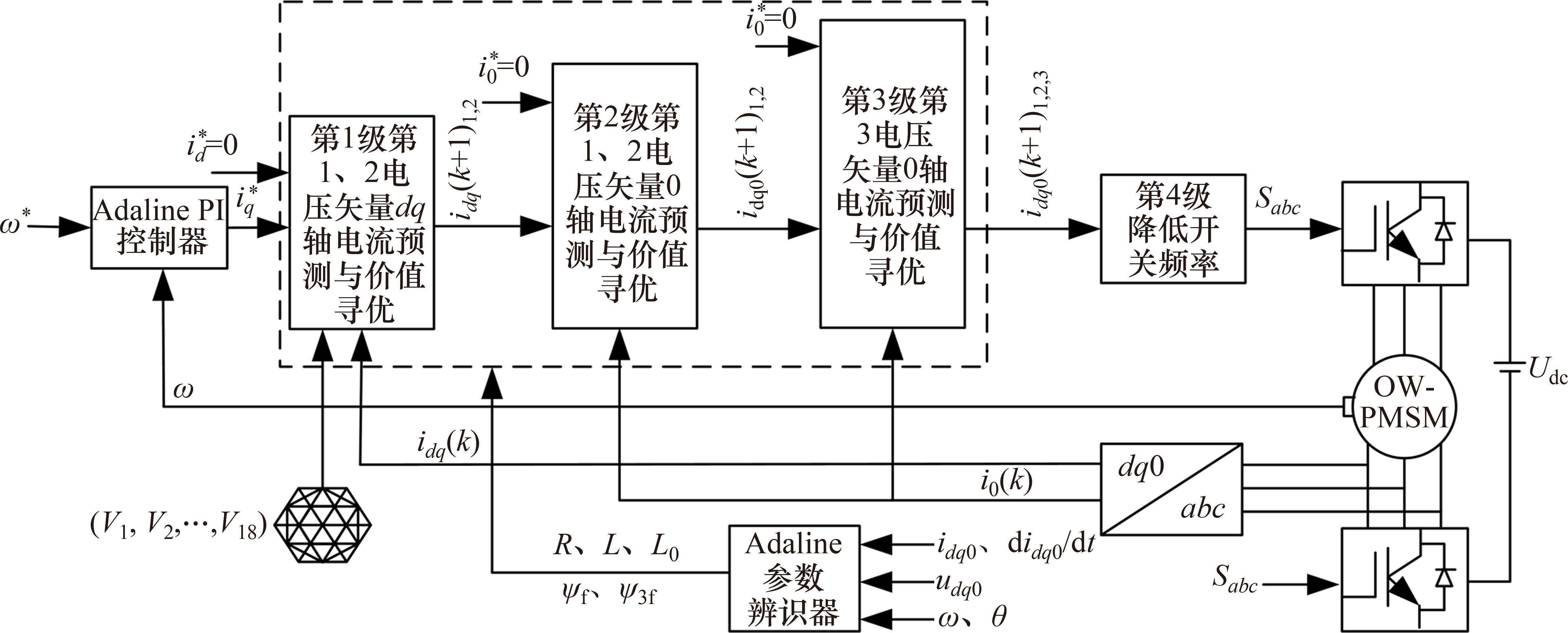
| 参数 | 数值 | 参数 | 数值 |
|---|---|---|---|
| 极对数np | 2 | 永磁磁链3次谐波分量ψ3f/Wb | 0.005 915 2 |
| 绕组内阻R/Ω | 1.8 | 转动惯量J/(kg·m2) | 0.000 31 |
| 额定转速n/(r∙min-1) | 2 000 | 摩擦因数B | 0.006 |
| 绕组电感Ld,Lq/mH | 6.6 | 转动惯量J/(kg·m2) | 0.000 31 |
| 零轴电感L0/mH | 4.97 | 摩擦因数B | 0.006 |
| 永磁磁链ψf/Wb | 0.240 4 |

3.1 稳态测试验证
将CMPCC策略与改进CMPCC策略在转速为800 r/min和2 000 r/min,额定负载(4 N∙m)工况下进行测试,可得测试结果如图8、图9所示。图8为2种方法在800 r/min额定转矩(4 N∙m)工况下测试结果。由图8(a)和图8(d)可知,改进CMPCC方法将转矩脉动从CMPCC方法产生0.075 8 N∙m降低到0.045 7 N∙m。为验证所提改进CMPCC策略对零轴电流的抑制效果,将2种策略稳态工况下零轴电流进行对比。如图8(b)和图8(e)所示,零轴电流波动和最大波动幅值分别从0.096 1 A和0.493 A降低到0.055 9 A和0.166 9 A。为进一步验证所提策略对电机电流质量有一定提高,对2种策略低速工况下电机a相电流进行傅里叶分解得到图8(c)和图8(f),比较2组图可知,THD值从4.21%降低到3.59%。
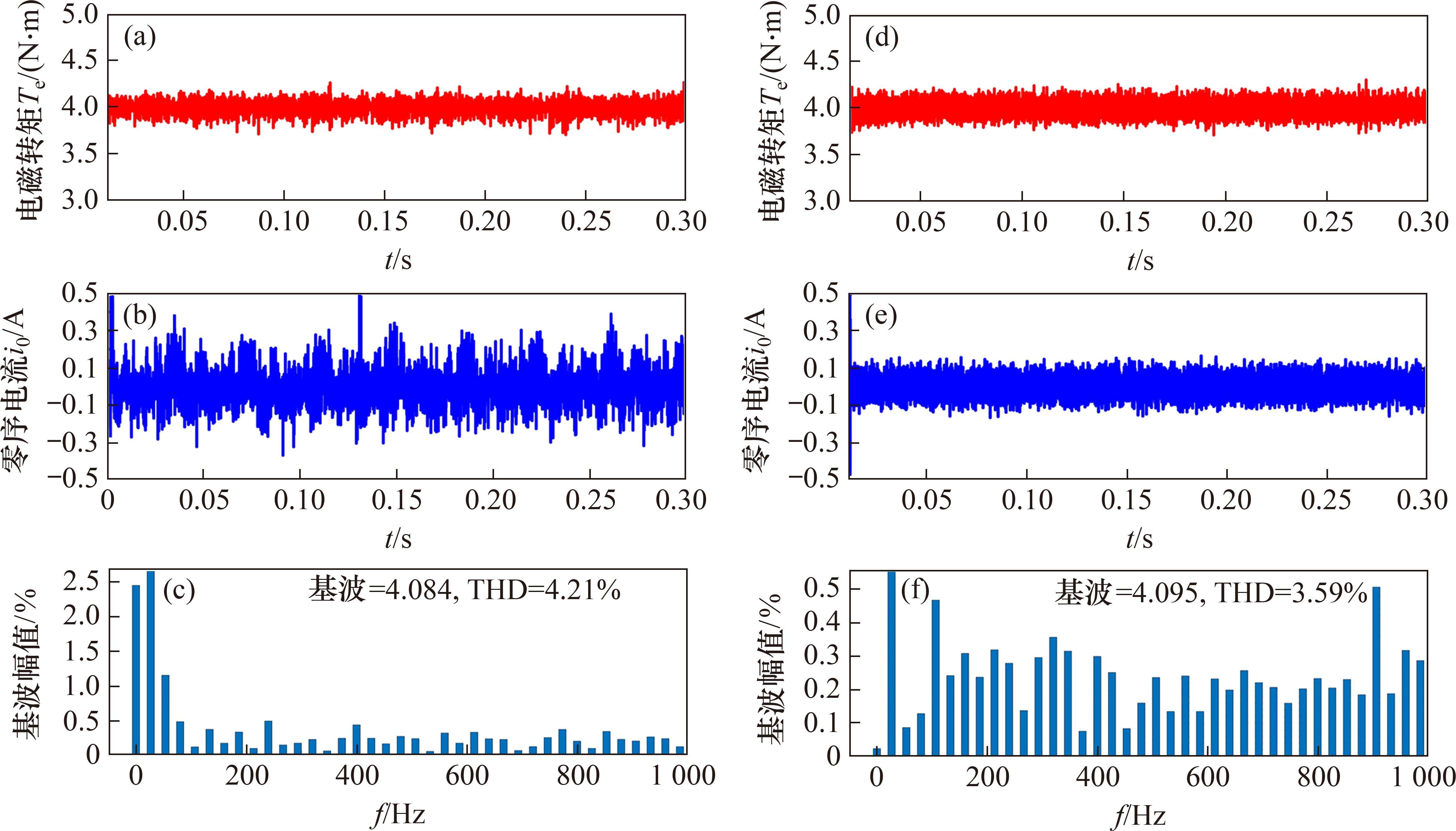
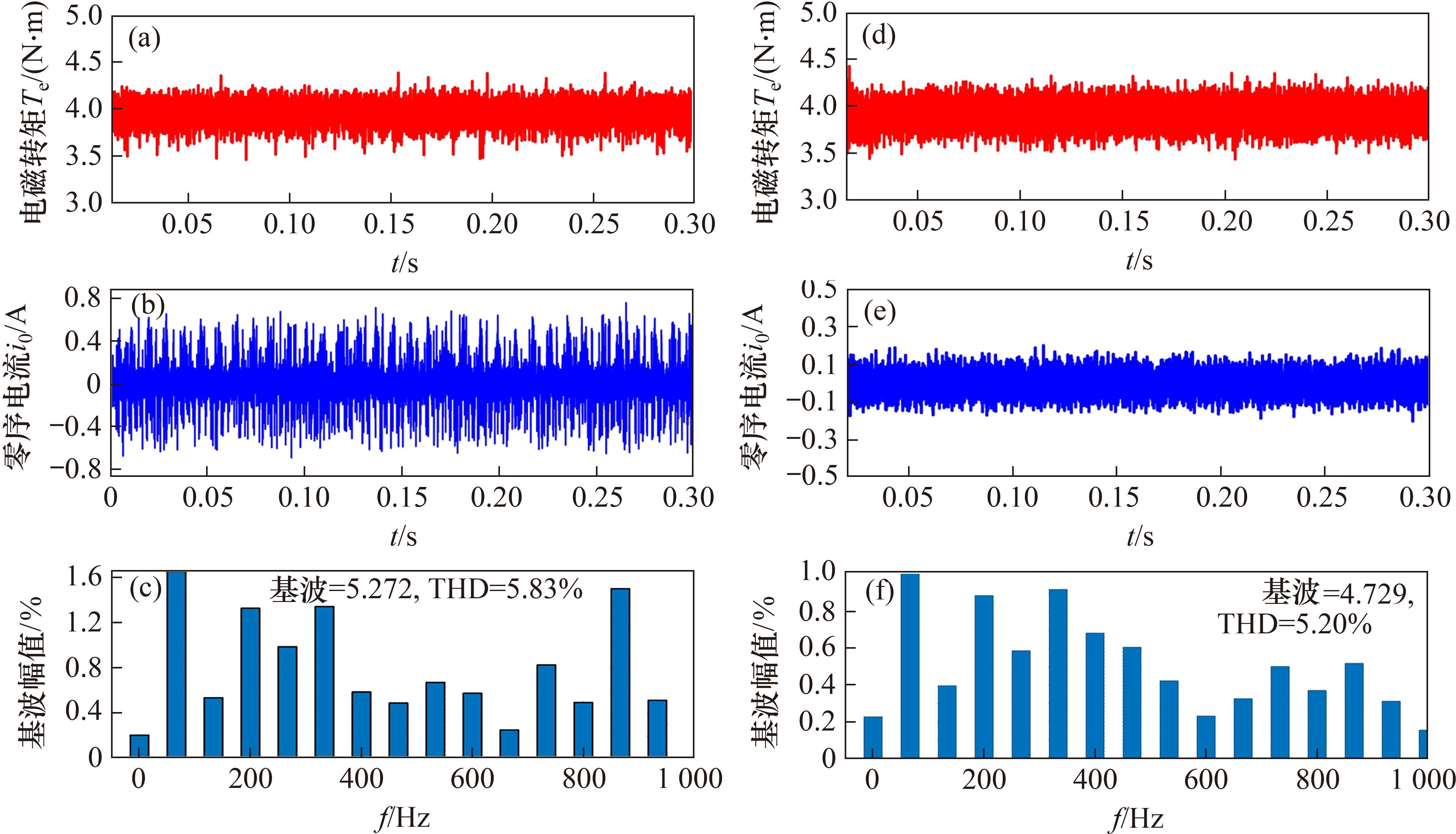
图9为2种方法在2 000 r/min额定转矩(4 N∙m)工况下仿真。稳态时,由图9(a)和图9(d)可知,改进CMPCC方法将转矩脉动从CMPCC方法产生0.137 N∙m降低到0.062 3 N∙m。将2种策略稳态工况下零轴电流进行对比,如图9(b)和图9(e)所示,零轴电流波动和最大波动幅值分别从0.176 A和0.733 A降低到0.061 A和0.171 A。
采样2种策略高速工况下电机a相电流傅里叶分解得到图9(c)和图9(f)。比较2组图可知,THD值从5.83%降低到5.2%。
3.2 动态测试验证
图10为ADRC_CMPCC与Adaline_PI改进CMPCC策略在额定转速(2 000 r/min)下,电机转矩在0.1 s从4 N∙m降低到1 N∙m,在0.2 s从1 N∙m升高到4 N∙m动态对比。
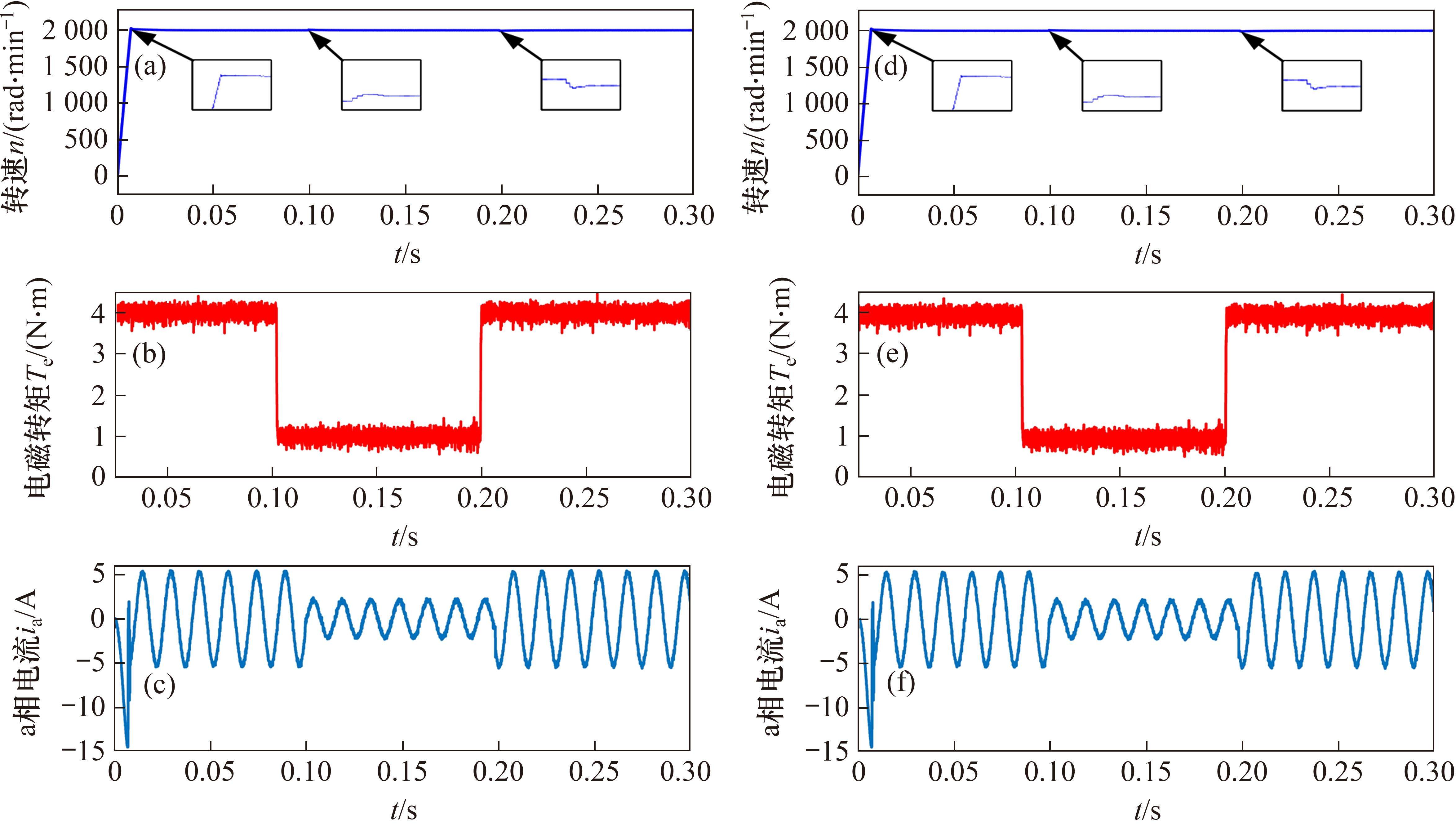
由图10(a)和图10(d)比较可知,2种策略在负载转矩突变时,都能在0.02 s内恢复到额定转速,它们具有相同的动态响应速度,并且转速外环采用ADRC控制器和变步长Adaline_PI控制器均能对电机调速超调有很好的抑制作用。电机控制系统输出的动态电磁转矩脉动如图10(b)和图10(f)所示。从图中可以得出Adaline_PI改进CMPCC策略在不失去快速动态响应的条件下,转矩脉动降低了0.074 7 N∙m。为比较2种策略下三相电流畸变情况,以a相为例仿真得到a相电流波形图,如图10(c)和图10(f)所示。所提策略总谐波畸变率降低了10.3%。
3.3 开关频率优化与参数辨识验证
图11为改进CMPCC开关频率优化和CMPCC方法在不同转速下开关频率优化以及未优化开关频率仿真结果对比,可以得出改进CMPCC经过矢量开关冗余优化的开关频率比CMPCC经优化的开关频率降低了45.4%,比CMPCC未经优化的开关频率降低了70.3%。
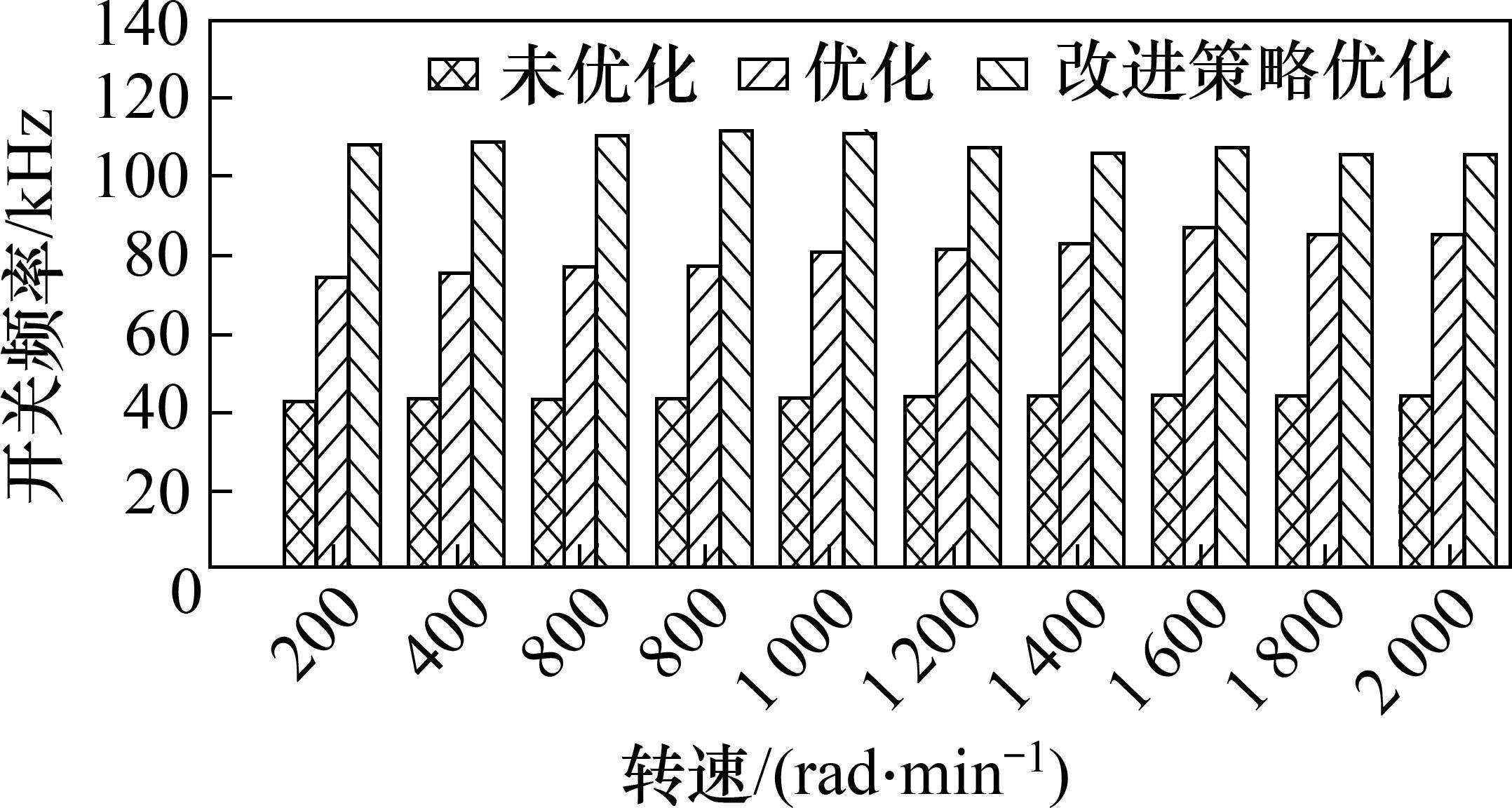
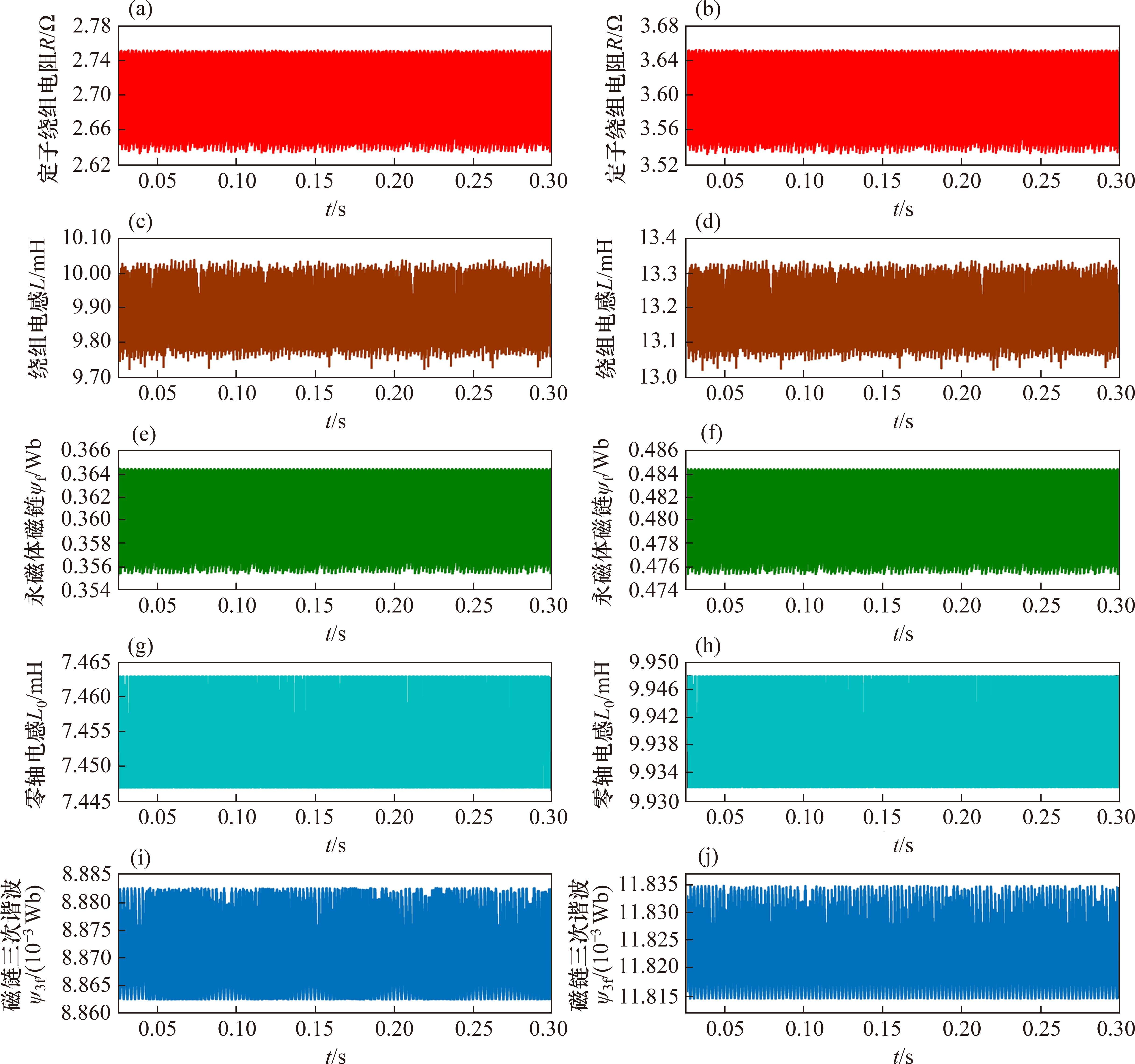
图12为变步长Adaline参数辨识器对电机参数辨识结果,图12(a)、图12(c)、图12(e)、图12(g)、图12(i)为转速1 500 r/min参数变化为1.5倍标识值时,辨识器对定子电阻最大辨识误差为2.59%,绕组电感最大辨识误差为1.81%,永磁磁链最大辨识误差为1.39%,零轴电感最大辨识误差为1.21%,磁链三次谐波最大辨识误差为0.91%。图12(b)、图12(d)、图12(f)、图12(h)、图12(j)为转速2 000 r/min参数变化为2倍标识值时,辨识器对定子电阻最大辨识误差为1.94%,绕组电感最大辨识误差为1.44%,永磁磁链最大辨识误差为1.04%,零轴电感最大辨识误差为0.905%,磁链三次谐波最大辨识误差为0.85%。参数辨识测试结果验证了设计的Adaline辨识器对电机参数准确辨识,提高了系统鲁棒性。
4 结论
1) 改进级联模型预测控制剔除了造成高开关频率和零轴电流的小矢量,根据零轴电流和q轴电流作为转矩脉动的主要影响因素实现分级优化,降低了零轴电流波动、转矩脉动和寻优次数,优化了脉动开关频率,不需要额外增加零轴电流控制回路。
2) 通过变步长Adaline对PI控制器参数实时更新,减小了调速中超调对控制系统影响。
3) 系统对电机多目标优化和参数辨识采用了分级和分步策略,避免了代价函数权重系数整定和参数辨识欠秩问题,简化了系统建立难度,提高了模型预测控制精度。
半实物仿真测试验证了Adaline_PI控制器共母线OW-PMSTM参数可调改进级联模型预测电流控制在稳态、动态和参数失配工况下对电机具有较好的控制效果,提升了电机系统控制性能。在所提策略开展共母线OW-PMSTM实物实验时,电机系统存在采样误差、系统外部干扰、电机非理想状态和系统噪声等问题,影响电机控制性能。因此,需要进一步优化电机系统的Adaline调节参数以达到参数准确辨识和对实际系统精确控制,实现所提策略在实际系统中对电机的高效控制。
高锋阳,吴银波,徐昊等.共母线开绕组永磁同步牵引电机改进级联模型预测控制[J].铁道科学与工程学报,2025,22(03):1254-1265.
GAO Fengyang,WU Yinbo,XU Hao,et al.Common bus bar open winding permanent magnet synchronous traction motor improved cascade model predictive control[J].Journal of Railway Science and Engineering,2025,22(03):1254-1265.

