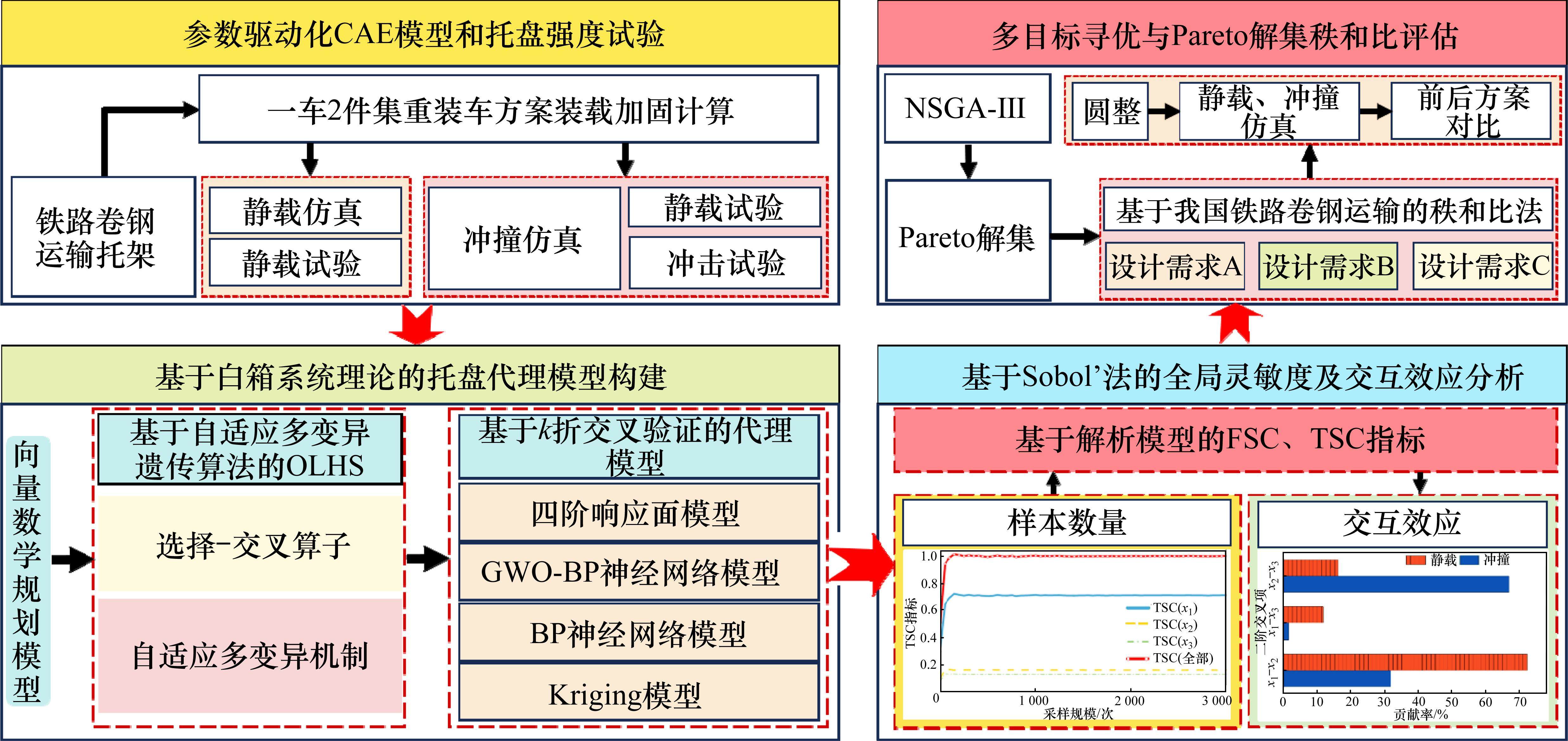
我国区域经济发展、资源分布和工业布局不均衡,导致近年来国内卷钢市场呈现“北材南运”现象,铁路中长途卷钢运量逐年增大。铁路卷钢运输托架(以下简称托架)是用于装载、固定、运输卷钢的重要载具。目前,国内铁路优先采用敞车、平集两用车刚性连接托架,卧装运输卷钢[1]。因此,科学设计、改进托架对铁路卷状货物运输具有重要的现实意义和工程应用价值。近年来,国内学者通过仿真、强度试验的组合方式,设计、改进了多款托架,确保满足铁路安全运输需求,即托架静载、冲撞工况应力必须低于规范要求的不同工况材料许用应力[2]。刘晓华[3]对RUL-C1型卷钢托架进行静载、冲撞仿真和强度试验,对比静载仿真与实测应力、冲撞仿真与合成应力,根据工程经验对薄弱部补强后,再进行强度试验,通过反复试验,确保托架安全可靠。韩立东[4]对DD-3P型卷钢托架进行静载、冲撞仿真和强度试验,通过经验结合理论计算的方法改进托架。王晨[5]设计了一款35 t敞顶箱卷钢托架,通过静载、冲撞仿真和强度试验检验托架各工况应力,结合经验,对薄弱处补强。袁舜等[6]设计了一款可折叠、适用敞车、平集车的卷钢托架,静载、冲撞仿真初步验证了托架安全可靠。然而,这些研究均严重依赖个人经验和强度试验,对设计人员要求高、周期长、试验资源浪费严重、成本高昂。随着数值拟合理论及智能算法不断发展,在工程问题中引入代理模型、利用智能算法寻优逐渐成为研究热点。以支持向量机(SVM)、径向基函数(RBF)、BP神经网络、启发式算法混合BP神经网络等为代表的代理模型广泛应用于各个领域[7-10]。然而,上述代理模型属于黑箱模型,可解释性差、透明度低、无法直观理解内部机制,不易被现场理解接受,导致实际应用受限。不同于以上代理模型,基于白箱系统理论的响应面代理模型,克服了上述缺点。HAN等[11]以雷诺数、扭曲比、间隙比为参数,传热比、摩擦因数比为响应,建立了波纹管传热性能响应面模型,定量化各参数与响应之间的联系。然而,2阶响应面模型存在拟合精度低、误差大等问题。例如,高广军等[12]以行李架比吸能、位移等为响应,以螺栓预紧力、拉杆厚度等为变量,建立了动车组行李架耐撞性1~4阶响应面模型,发现4阶响应面精度明显高于低阶响应面,满足工程需要。邬斌扬等[13]以不同注塑参数为输入,以最大锁模力、隔片收缩率为响应,建立了抑爆球注塑质量2~4阶响应面,发现4阶响应面精度最高,可以快速为一线人员提供可靠的参考值。可见,高阶响应面模型在满足计算精度的同时,还将工程问题中复杂非线性隐式关系转化为显式函数,快速为设计人员提供可靠参考值,大幅降低技术门槛,具有简单实用、直观透明、可操作性强等特点,更容易被现场理解、接受。然而,高阶响应面模型在铁路卷钢托架设计、改进等研究领域尚未见相关报道。基于上述分析,本文提出基于4阶响应面模型的托架多目标优化方法,在满足计算精度的同时,还能快速为设计人员提供参考值,大幅降低技术门槛,简单实用、可操作性强,更容易被现场理解、接受,有望为托架设计、改进等研究领域提供关键技术支撑及新思路。图1是优化流程。
1 托架CAE仿真和实物强度试验
1.1 托架及装载加固计算
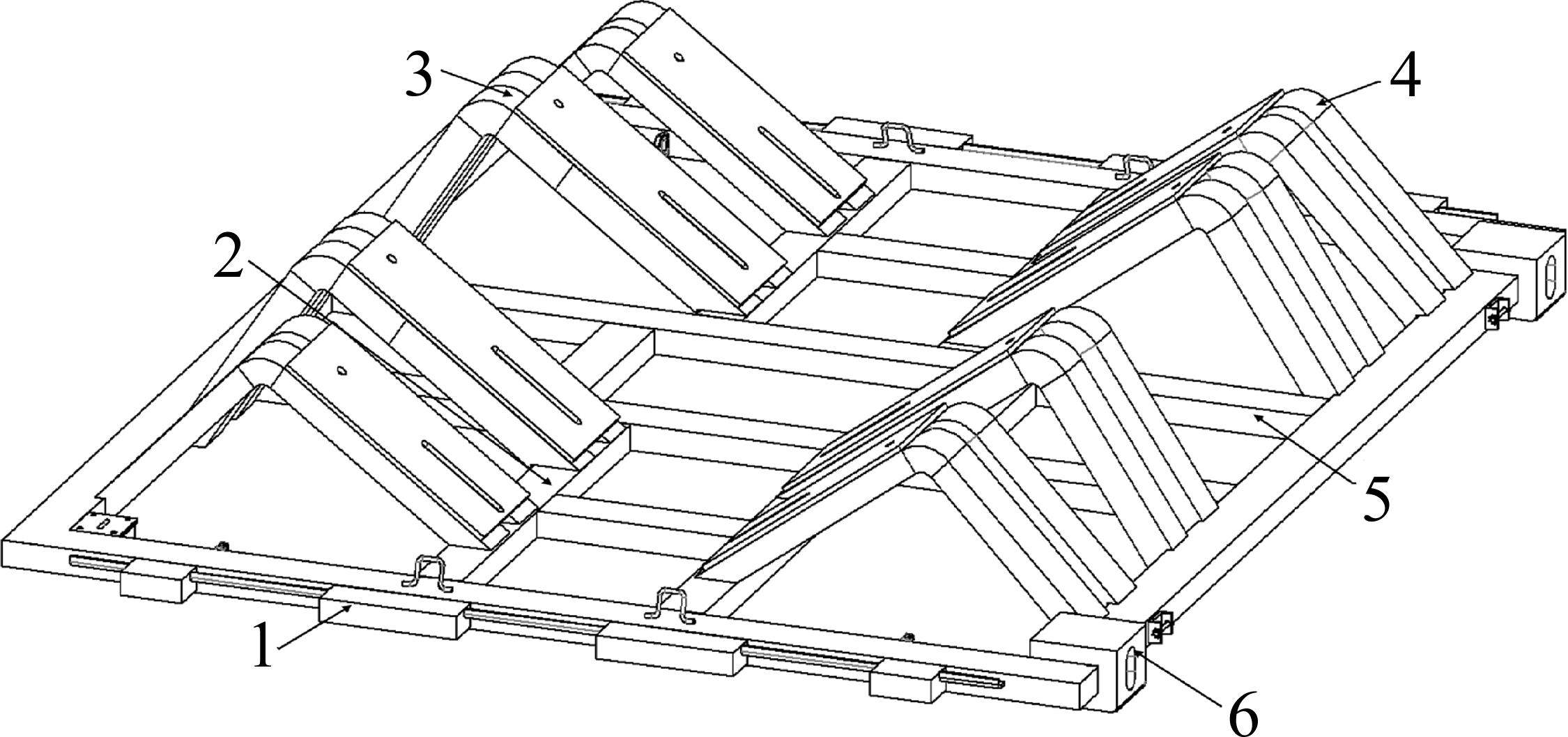
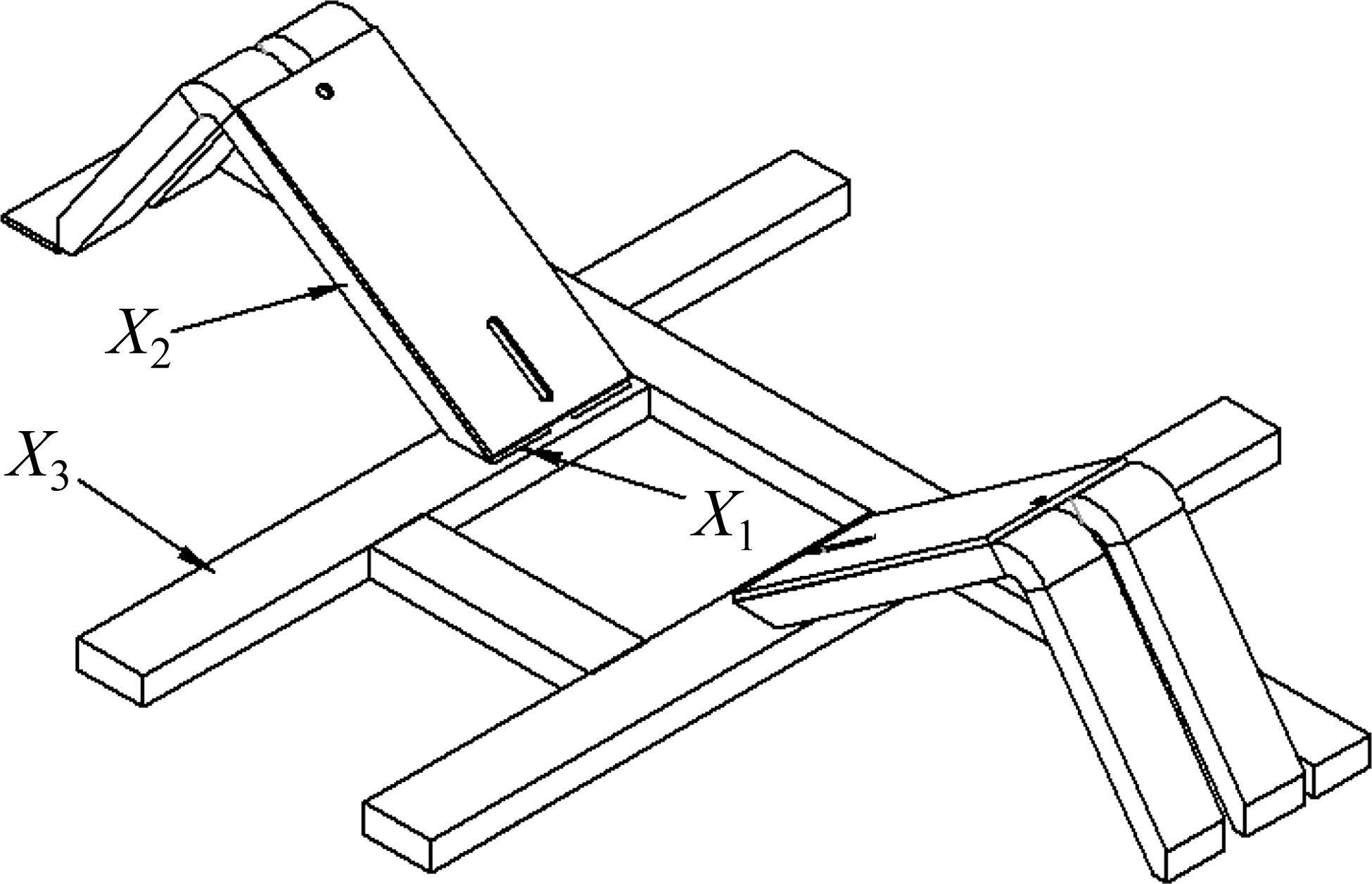
现役货车中,敞车、平集两用车约54.1万辆、7.4万辆,共占全路运用车保有量71.57%[14]。因此,选取适用车型为敞车、平集车的RTKD-1P款托架进行优化。托架自重511 kg,最大载重34.4 t,适用货物卷径1 000~2 200 mm、板宽890~2 290 mm,主体材料是Q700,结构见图2。
根据《铁路货物装载加固定型方案》,选择集重方案070306作为不利装车工况,见图3[1]。按照《铁路货物装载加固规则》计算,见表1[15]。

| 纵向惯性力/kN | 垂向惯性力/kN | 横向惯性力/kN | 横向摩擦力/kN | 纵向摩擦力/kN |
|---|---|---|---|---|
| 475.0 | 179.20 | 129.36 | 30.58 | 97.02 |
1.2 托架CAE仿真
采用SolidWorks和Ansys Workbench协同仿真技术,略去可能导致应力集中的细节,适当简化托架。添加Q700材料属性(弹性模量是2.06×105 MPa,屈服强度是650 MPa,密度是7 850 kg/m3)。通过四面体和六面体网格共节点的划分方式,提高网格质量,确保边角过度细腻平滑,网格质量是0.88。最终,划分节点数是201 156,单元数是65 689。
静载工况,敞车保持静止或匀速,托架仅受卷钢重力[16-17]。其中,斜支撑倾斜角度是34°,卷钢件重33 t,因此单侧斜支撑所受压力是97.53 kN。施加载荷,最大应力值出现在卷钢与斜支撑接触面处,是178.81 MPa,见图4(a)。最大变形是0.45 mm。其余部分受力、变形小,忽略不计。
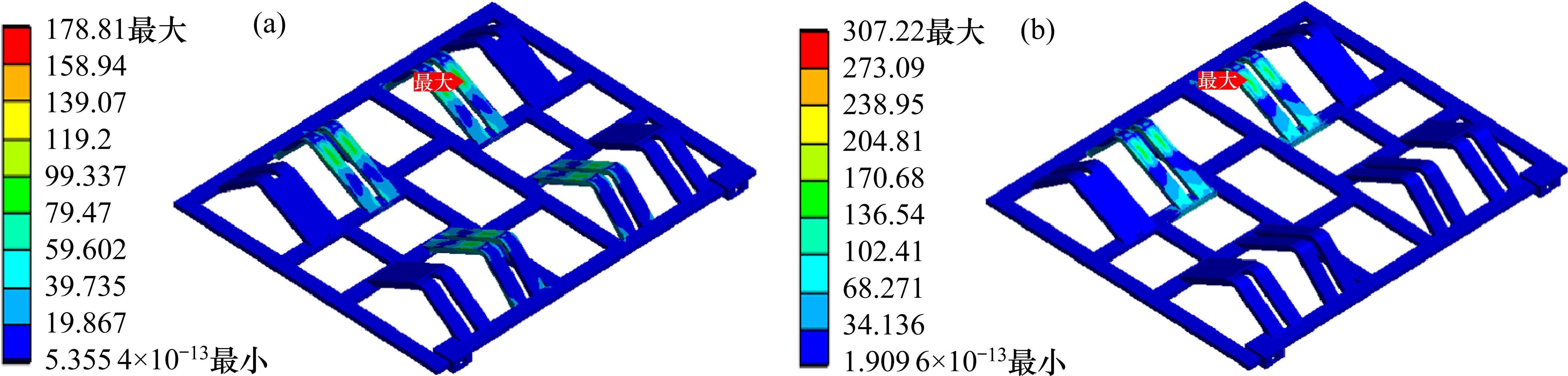
动载工况,敞车处于启动、加速、制动等非匀速状态或调车作业,以调车冲撞最不利[16-19]。该工况下,卷钢受方向平行于敞车车地板且和冲击反向的纵向惯性力作用,同时还受方向向下的垂向力作用。结合表1,在托架靠近冲击端侧的两对斜支撑接触面上,施加上述载荷。最大应力值出现在靠近冲击端侧的斜支撑与货物接触面位置上方,为307.22 MPa,见图4(b)。最大变形为0.69 mm。
1.3 托架强度试验
强度试验包括静载、冲击试验[2, 19]。其中,静载试验采集货车在静止或匀速状态下,托架各测点的应力值。冲击试验是采集在该工况下,托架相较于静载时增加的应力值,再与静载值合成最终工作应力,作为冲撞应力[2, 16, 19]。对比静载、冲撞仿真与强度试验,检验仿真是否可靠。结合仿真,根据现场条件和经验,选取12个测点,试验现场见图5。

1.3.1 静载试验
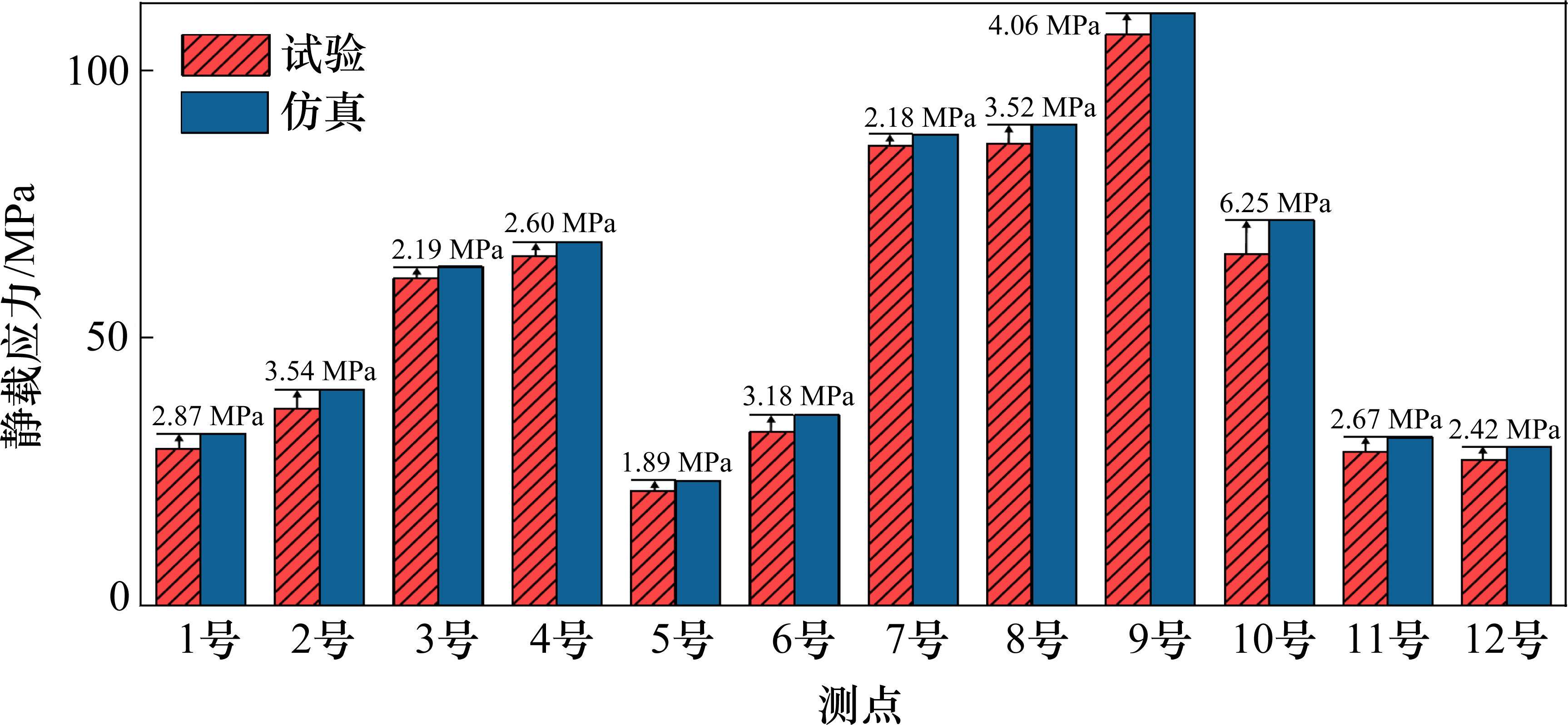
33 t卷钢一件;JMtest3815静态检测系统,系统精度是±0.2%Fs±1 με,用于测试采集分析应变;单向箔应变计,灵敏系数2.12±1%,标称电阻(Ω)120±0.1;静态电阻应变仪,用于检测测点应变。1次预加载后,进行3次正式加载,每次持续时间2 min,记录各测点应力。为减小偶然误差,3次数据均值处理,作为各个测点实际静载应力值。静载仿真与试验对比,见图6。由图6可知,仿真与检测值吻合度高。具体来说,误差最大在10号测点,是6.52 MPa;最小在5号测点,是1.89 MPa。这是因为试验场地,硬化地面不完全平整导致。
1.3.2 冲击试验
冲击试验是模拟铁路调车作业,以一辆载重70 t的冲击重车连续向停在平直线路上处于非制动状态的试验车进行单端冲撞[2, 16, 19]。试验过程中,先以3 km/h速度预先冲击,观察卷钢与托架状态。确定无异常后,冲击速度逐渐提高1 km/h,每个速度区间冲击次数不少于3次。选用DF7G内燃机车、满载C70E冲击车1辆、按照上述集重方案装载的C70试验车1辆、33 t卷钢2件、托架2个、坡度少于1/5‰且长度大于100 m的直线线路、铁鞋2对、JMtest3839动态测试仪及JMtestDASP测试系统用于检测动态应变、BE120-3AA应变计若干。本次试验,共冲击19次,速度范围在4.2~8.3 km/h。
1.3.3 冲撞应力
现行《铁路货物装载加固规则》,纵向惯性力计算公式是在冲击速度5 km/h工况下,作用于货物的惯性力值的线性拟合[17]。因此,选取5 km/h级的3次测试值,均值处理作为冲击应力值。根据静载、冲击应力,合成冲撞应力。比较仿真与实测数据,检验仿真是否可靠,对比见图7。
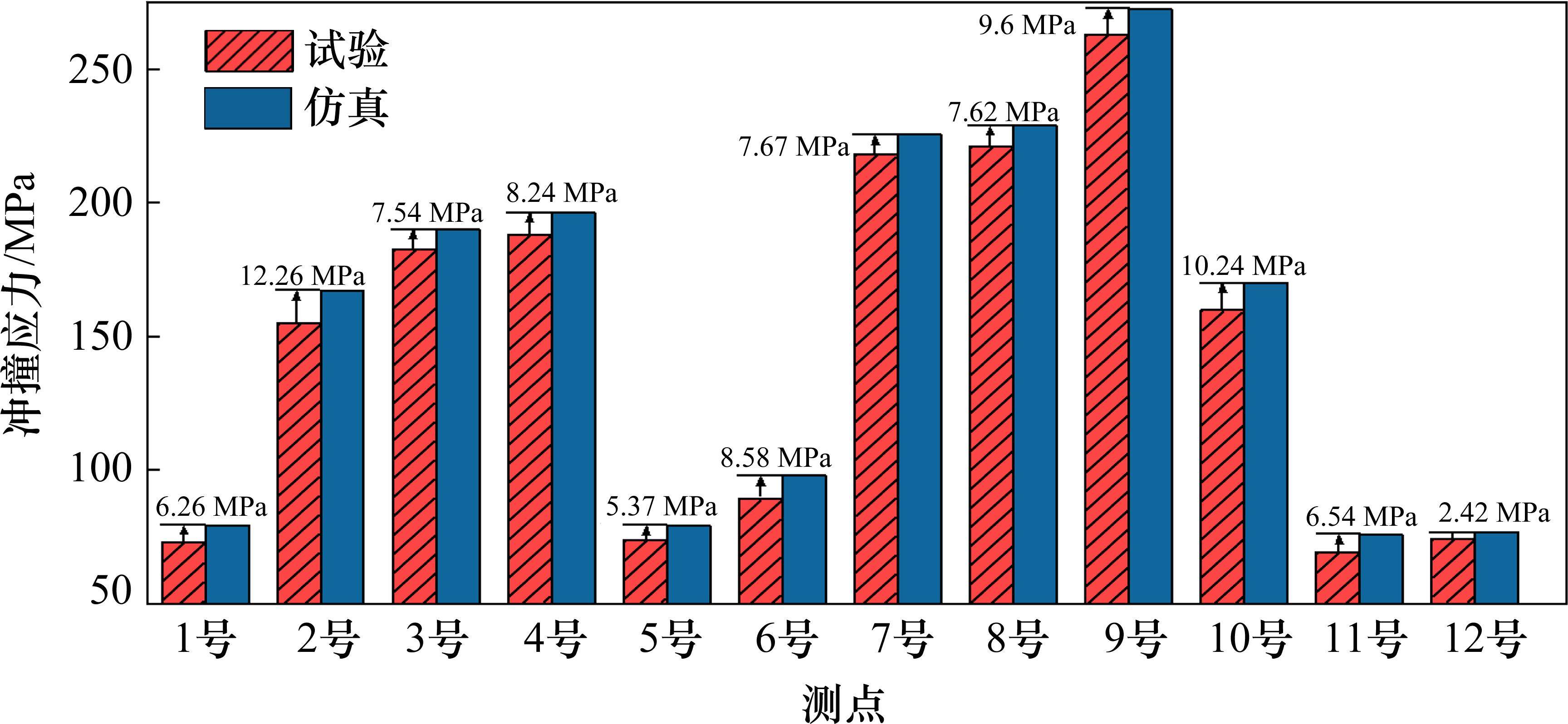
由图7可知,仿真分析与检测结果吻合度高。具体来说,误差最大在2号测点,为12.26 MPa;最小在12号测点,为2.42 MPa。这是因为试验车车地板不平整导致。此外,无论托架冲撞仿真或者试验,应力分布趋势一致,即无论哪种分析方式,只有冲击端侧的斜支撑应力分布显著,剩余部分并不明显。
托架CAE仿真与强度试验基本一致,证明仿真准确可靠,为构建代理模型提供基础。
2 托架高阶响应面模型
2.1 托架多目标向量数学规划模型
根据仿真和实测,选择斜支撑长边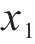
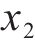
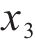
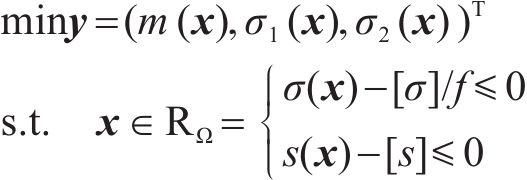
式中: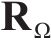
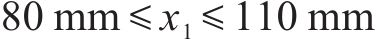
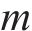
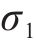
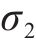
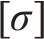
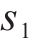

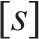
2.2 取样方法
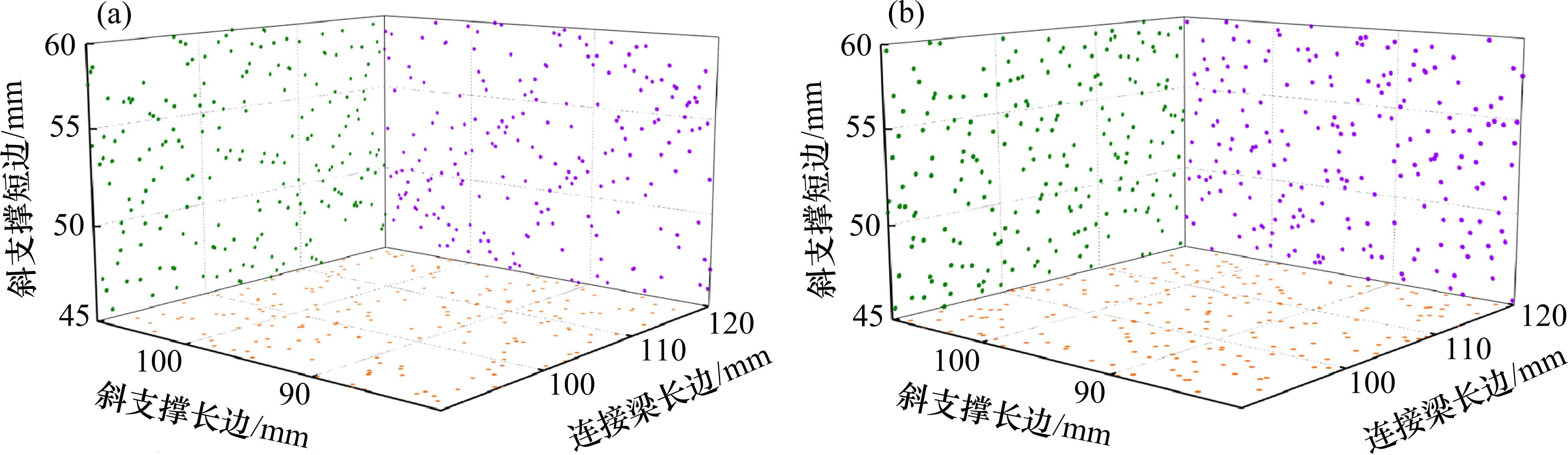
为防止子空间样本点过于稀疏或者集中而无法反映高维空间特性[20-21],本文采用AE势能准则和自适应遗传算法组合优化的最优拉丁超立方取样方法(OLHS),实现最大化填充。
2.2.1 优化准则
AE势能准则是指将参数空间类比为由单位质量粒子构成的物理系统,粒子间存在斥力造成系统势能不断变化,直至整体势能最小,则认为填充效果最佳。粒子间的斥力与距离平方成反比,势能函数见式(2)。
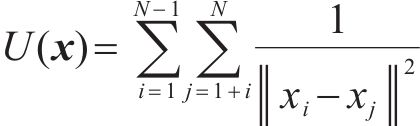
式中: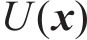
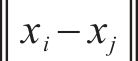
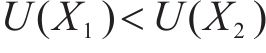
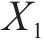
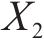
2.2.2 优化流程
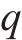
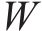
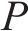
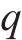
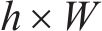
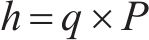
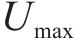
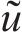
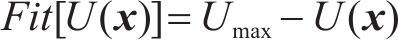
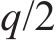
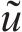
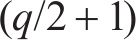
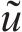
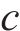
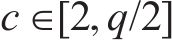
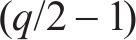
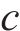
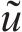
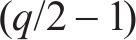
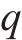
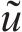
式中: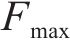
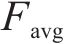
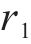
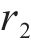
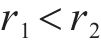
2.2.3 取样试验
设定初始种群数量为60,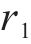
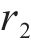
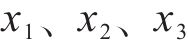
2.3 响应面模型
响应面模型是对实物试验数据或数值模拟数据进行显化拟合,得到响应和约束关于参数的函数近似表达式的方法[22-23]。该方法原理简单、使用方便、无需经过复杂的推导,广泛用于实际工程优化问题。响应面模型显示表达式,见式(5)。
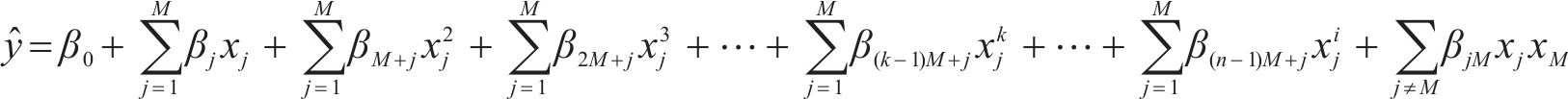
式中: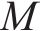
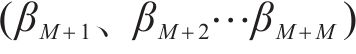
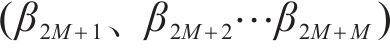
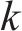
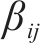

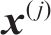
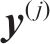
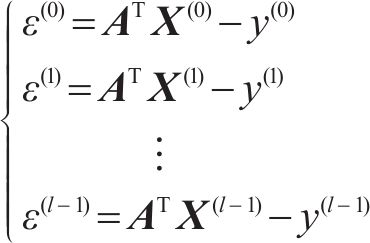
式中: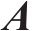
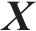
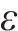
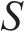
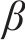
2.4 k折交叉验证
k折交叉验证是一种最大程度利用样本点评估模型的方法[24]。该方法将部分样本作为测试集,剩余随机划分成k份相同容量的互斥子集,将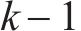
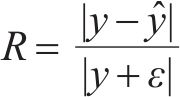
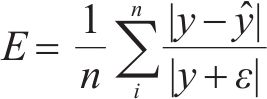
式中: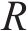
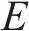
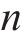
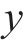
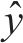
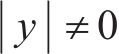
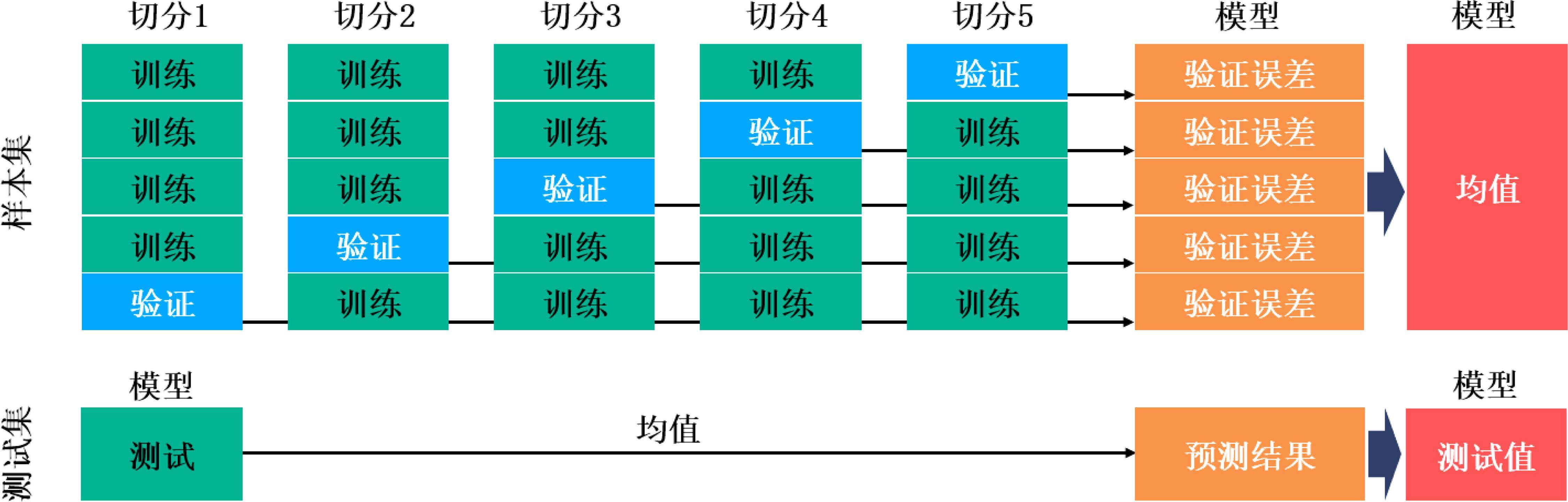
采用10折交叉验证评价代理模型。随机划分200组样本点,其中50组测试集,剩余150组随机划分为10份互斥子集,每份15组,依次轮换10次,计算不同模型关于各响应均值误差及测试误差,见图12。
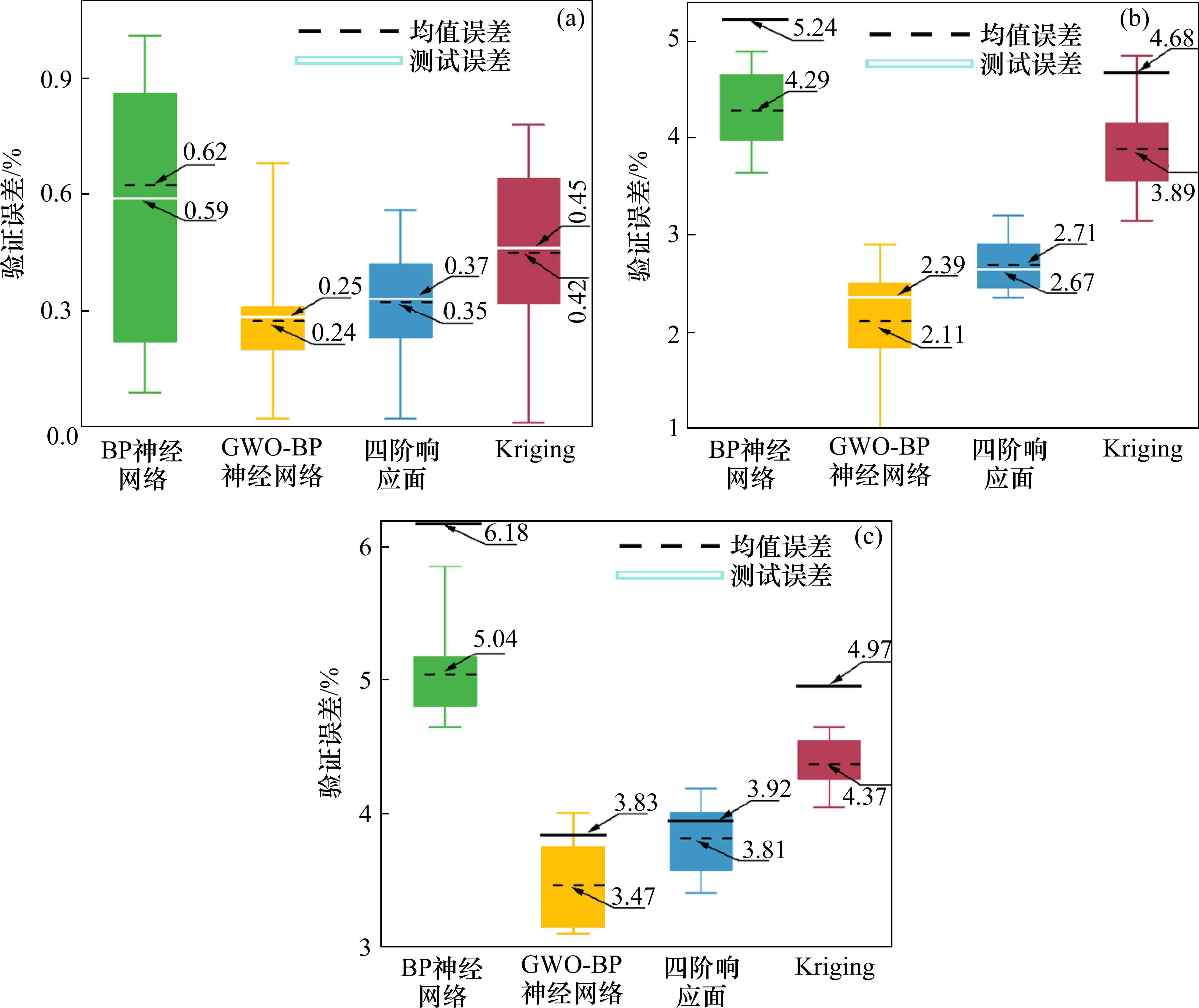
由图12(a)可知,各代理模型关于质量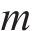
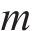
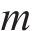
由图12(b)可知,不同代理模型关于应力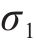
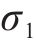
由图12(c)可知,GWO-BP神经网络、4阶响应面模型关于应力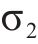
因此,无论对于非线性程度高,或线性程度高的响应,GWO-BP神经网络、4阶响应面模型拟合效果均表现良好,精度都满足实际工程需要。然而,不同于GWO-BP,基于白箱系统理论的4阶响应面模型不需要一线设计者具有较高的算法理论和素养,可快速为设计者提供可靠的参考值,凭借简单实用、直观透明、操作性强等特点,更容易被现场理解、接受。因此,优先选择4阶响应面代替仿真进行工程优化。
3 基于Sobol法的全局灵敏度及交互效应分析
Sobol法是一种基于方差的全局灵敏度分析方法,核心思想是任意模型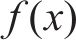
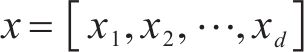

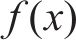
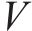
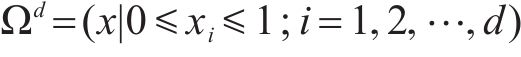
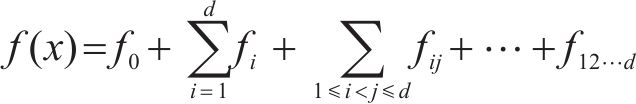
其中,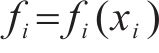
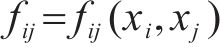
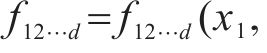
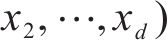
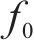
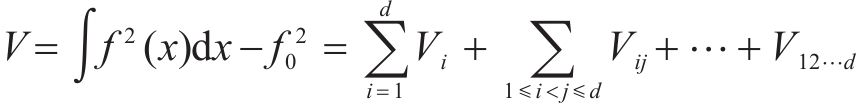
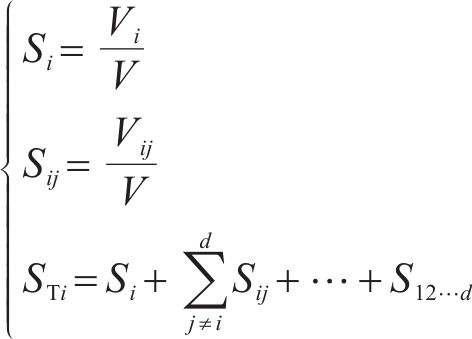
其中,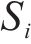
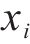

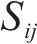
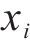
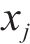


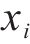
采用Sobol法进行灵敏度分析,确定采样规模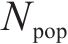
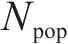
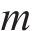
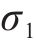
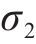
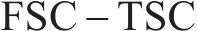
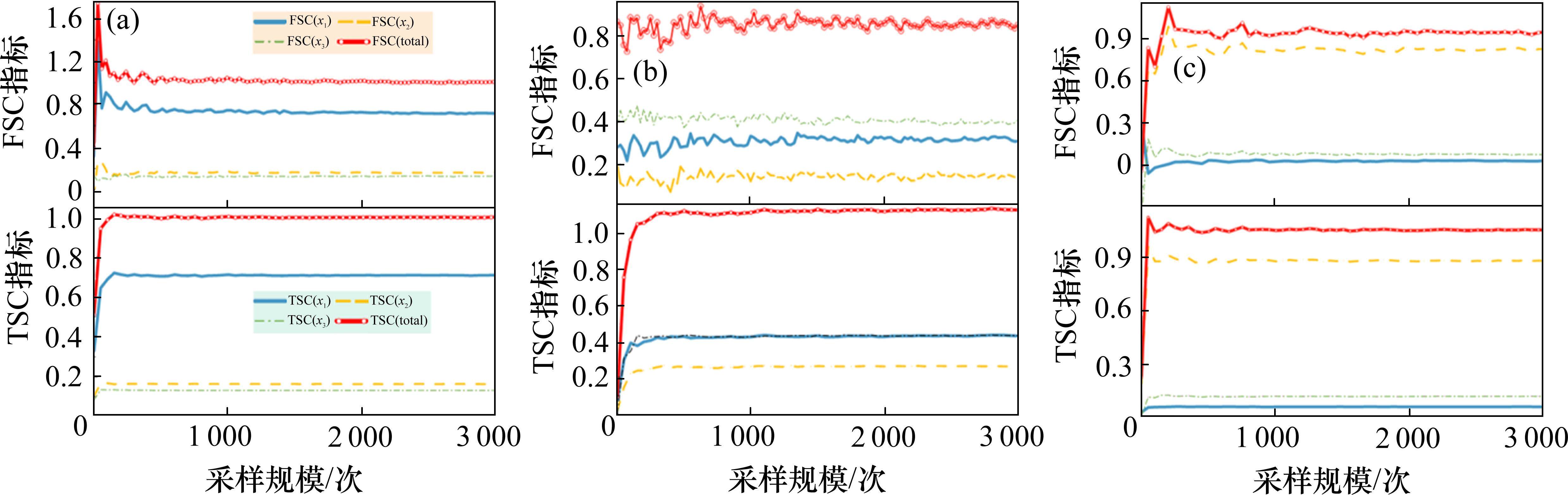
由图13可知,各响应在采样规模达到1 500时,灵敏度均趋于稳定,不再随采样规模增加而发生明显变化。其中,质量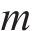
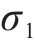
本文输入3项,设置采样规模5 000,创建5 000*3矩阵,评估测试,计算得到关于响应的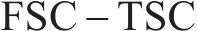
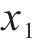
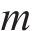

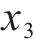

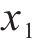

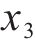
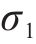

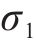
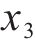
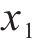
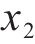

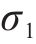
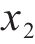
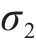

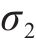
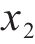

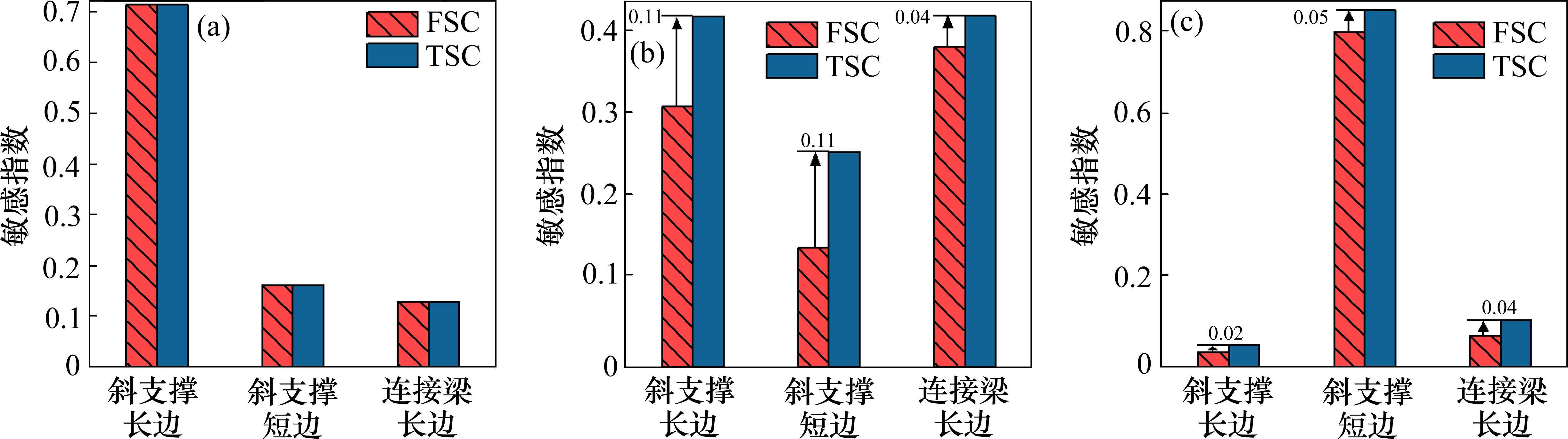
为了进一步分析不同参数间的耦合关系,需要计算

| 交叉项 | 静载应力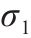 | 冲撞应力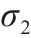 |
|---|---|---|
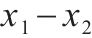 | 0.098 | 0.017 |
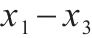 | 0.016 | 0.001 |
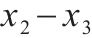 | 0.022 | 0.036 |

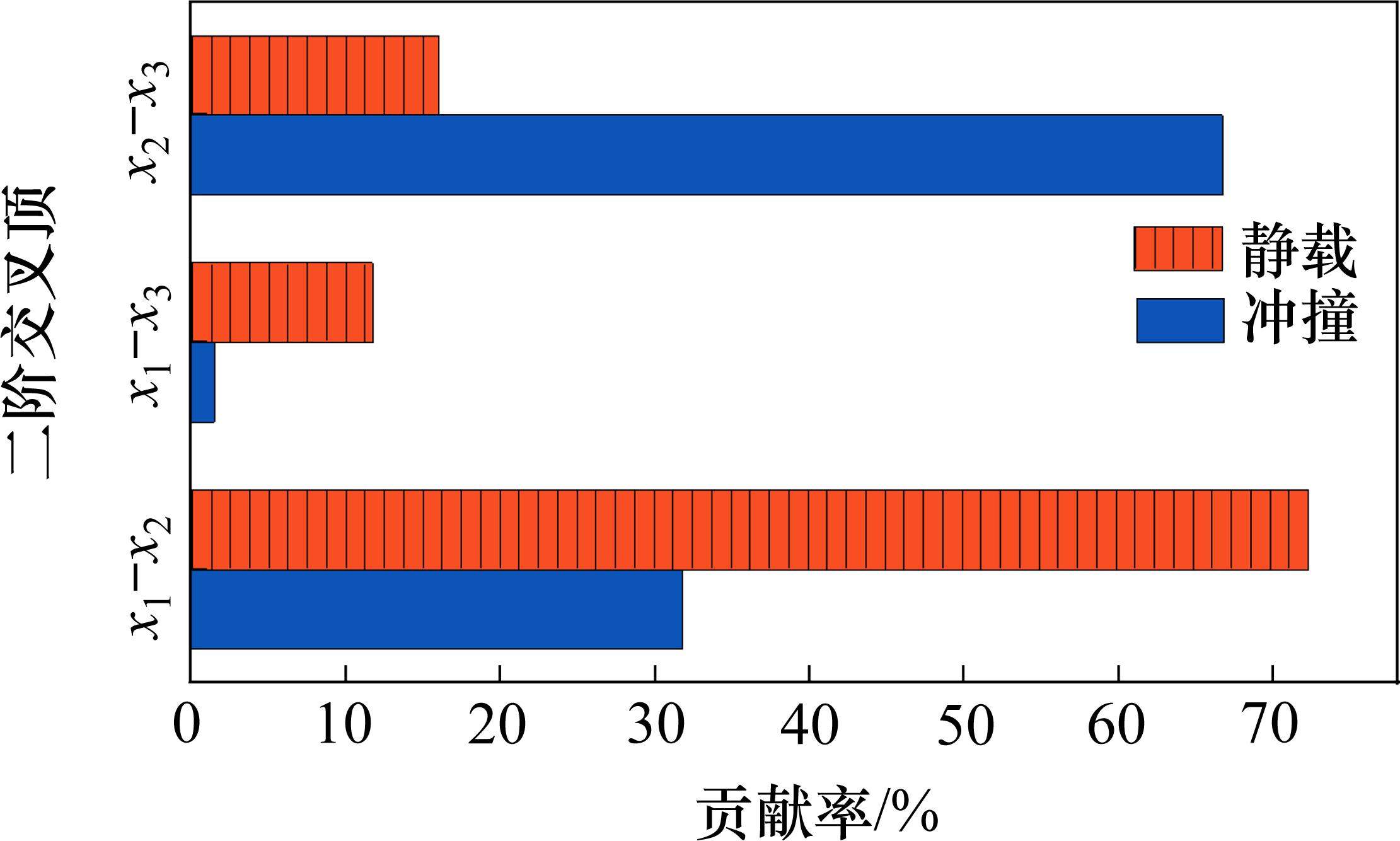
由表2和图15可知,对于静载应力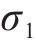
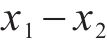
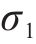
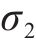
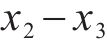
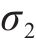
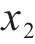
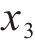
4 托架多目标寻优及秩和比评价
4.1 第3代非支配排序遗传算法
求解多目标优化问题,NSGA-II算法最常见。然而,该算法解决双目标问题效果良好,但解决3个及以上目标问题时,解的多样性不佳,因此,DEB等提出了NSGA-III算法[28]。该算法具有以下优势:
1) NSGA-III算法改变了选择机制,舍弃了NSGA-II算法拥挤距离排序,引入了参考点机制,避免了由于维度增加导致计算量指数增长的问题。因此,可有效处理具有复杂多样性的多目标优化问题。
2) NSGA-III算法采用了快速非支配排序、高效选择策略。这极大提高了算法计算效率和搜索速度。
4.2 Pareto解集
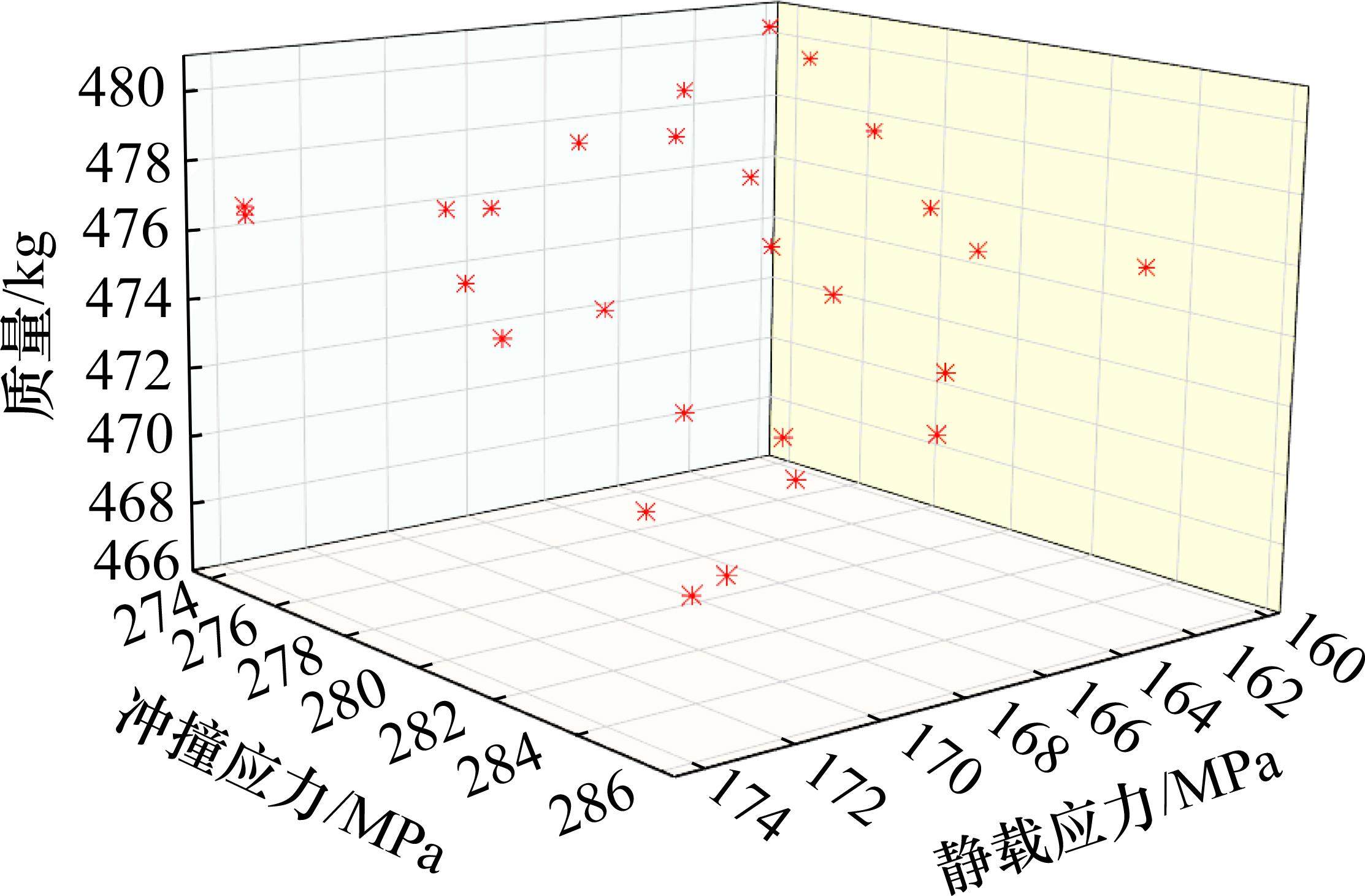
考虑到NSGA-III算法的优越性,本文采用该算法求解托架多目标寻优问题。其中,种群大小是100,最大迭代次数5 000次,获得Pareto解集,分布见图16。从图16可知,Pareto解均满足铁路货运安全需求,并且质量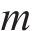
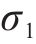
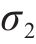
4.3 考虑铁路卷钢运输的秩和比评价
考虑到设计人员对各响应偏好不同,本文利用秩和比法赋予质量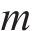
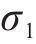
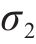
| 方案 | 权重矩阵 | 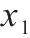 | 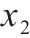 | 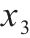 | 质量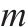 | 应力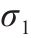 | 应力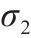 |
|---|---|---|---|---|---|---|---|
| 1 | 0.33,0.33,0.34 | 85.72 | 55.48 | 100.88 | 443.44 | 170.52 | 271.37 |
| 2 | 0.55,0.15,0.30 | 85.00 | 52.52 | 97.11 | 421.69 | 184.21 | 305.43 |
| 3 | 0.15,0.55,0.30 | 88.12 | 58.52 | 120.00 | 519.30 | 156.44 | 226.83 |
| 4 | 0.15,0.30,0.55 | 85.52 | 57.44 | 103.47 | 459.27 | 167.22 | 262.51 |
仿真分析中,优化前后结果见表4。由表4可知,托架各响应优化效果显著。具体来说,与初始方案比较,圆整方案托架质量降低9.89%,斜支撑静载、冲撞最大应力分别降低6.79%、14.36%。此外,圆整方案托架不同工况应力均小于规范规定的材料不同工况许用应力,符合铁路安全运输需求[2, 19]。因此,验证了文章提出的基于高阶响应面模型的托架多目标优化方法可行有效。
| 名称 | 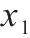 | 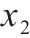 | 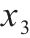 | 质量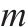 | 静载应力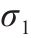 | 冲撞应力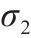 |
|---|---|---|---|---|---|---|
| 初始方案 | 100.0 | 50 | 110 | 511 | 178.81 | 307.22 |
| 圆整方案 | 86 | 57 | 104 | 460.45 | 166.67 | 263.11 |
5 结论
1) 对托架进行仿真和强度试验,二者误差均低于10%,验证仿真可行有效,可准确反映托架应力分布。
2) 采用基于AE势能准则和自适应遗传算法组合优化的最优拉丁超立方取样方法,提高了样本点集空间填充度,系统最小势能是0.41。创建含交叉项的4阶响应面模型,将托架优化问题中复杂的非线性隐式关系显式化表达。通过k折交叉验证,发现高阶响应面误差低于4.5%,精度满足工程需要,可为设计人员快速提供参考值,这大幅降低了技术门槛,简单实用、精准度高、可操作性强,更容易被现场理解、接受。
3) 采用Sobol法量化各参数对不同响应的影响,发现参数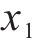
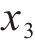
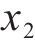
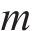
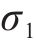
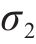

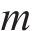
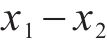
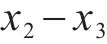
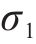
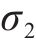
4) 根据我国铁路卷钢运输特点,采用秩和比法赋予权重矩阵,获得不同设计偏好下的最优方案。选择方案4作为最优设计,与原方案相比,托架质量降低了9.89%,2个工况应力降低了6.79%、14.36%。
5) 优化后的托架满足铁路安全运输需求,验证了本文提出的方法可行有效,能够为同类型托架设计、改进研究提供了理论依据和工程参考。
Prediction of geological characteristics from shield operational parameters by integrating grid search and k-fold cross validation into stacking classification algorithm
[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2022, 14(4): 1292-1303.潘帅,袁舜,周宝宪等.基于高阶响应面和NSGA-III的卷钢托架多目标优化[J].铁道科学与工程学报,2025,22(03):1266-1278.
PAN Shuai,YUAN Shun,ZHOU Baoxian,et al.Multi-objective optimization of coil steel pallet based on high-order response surface and NSGA-III[J].Journal of Railway Science and Engineering,2025,22(03):1266-1278.

