转向架焊接构架作为高速动车组的关键承载部件,承担着载荷传递、车轴定位和组装基准等重要功能,其可靠的结构强度是确保高速动车组安全运营的基础[1]。在转向架构架的设计和生产过程中,由于没有充分考虑整体焊缝布局和焊缝的抗疲劳能力等因素,使得焊缝的主要承力位置在频繁的服役过程中逐渐出现疲劳断裂等问题,疲劳强度问题逐步显现。因此,需要通过可靠的疲劳损伤分析方法,预测构架的疲劳状态,从而强化构架的服役安全性[2]。疲劳破坏是材料在循环载荷作用下损伤累积、性能退化,最终导致断裂的一种失效形式[3]。可靠的疲劳损伤分析方法可以通过预测结构的疲劳状态来强化结构的服役安全性。损伤累积思想[4]的提出,使得疲劳寿命分析可以通过分析疲劳累积损伤实现,并可根据损伤的演化规律分为线性和非线性两大类。基于线性累积损伤的Palmgren-Miner模型[5]认为疲劳损伤累积不依赖于加载历史,在多级载荷加载作用下发生线性累积。该模型形式简单,原理易懂,广泛应用于轨道车辆转向架关键结构的疲劳损伤分析:杨广雪等[6]以标准动车组齿轮箱为研究对象,基于Palmgren-Miner模型得出不同应力等级对齿轮箱疲劳损伤的贡献量。赵彬娜等[7]以转向架悬伸部件为研究对象,基于Palmgren-Miner模型分析了随机振动下的疲劳损伤。顾明[8]以转向架构架为研究对象,基于Palmgren-Miner模型进行疲劳损伤分析和服役寿命预测。然而各级应力下的疲劳损伤并非独立而是相互影响,线性累积损伤模型简化了疲劳失效过程的机理,难以给出有效预测[9]。为弥补线性累积损伤模型的不足,有效追踪疲劳损伤的非线性累积过程,对非线性累积损伤模型展开了研究。MARCO等[10]最先提出将损伤力学与疲劳累积损伤理论结合的观点,提出了Marco-Starkey非线性累积损伤模型。Manson-Halford模型(M-H)[11]是基于Marco-Starkey模型和裂纹扩展提出的基于经验公式的非线性累积损伤模型,由于考虑了损伤累积与循环比之间的非线性关系,在工程实践中得到广泛应用。薛齐文等[12]应用M-H模型分析了焊接接头的疲劳损伤特性,并与Palmgren-Miner模型进行对比,结果表明M-H模型可用于工程设计中结构的疲劳寿命预测。在多级加载疲劳损伤分析中,载荷的影响表现为加载顺序影响和既有载荷间的相互作用影响[13]。M-H模型能够较好地描述载荷加载顺序的影响,但并未考虑载荷间的相互作用。为保证预测精度,众多学者对M-H模型进行改进:YUAN等[14-15]引入前后载荷比的最小值,通过2级载荷实验数据对比表明预测值相较传统模型有较好的吻合度,并未验证3级及以上加载等级的精确性。为考虑金属材料在线性递增载荷作用下的Coaxing效应[16],YUE等[17]引入等效应力并选用TC11,Ti-6Al-4V和DZ22这3种材料验证了改进模型的精确性。高月华等[18]利用前后载荷比的e次方提高改进模型的预测精度,但过分强调了材料受递增载荷引起的Coaxing效应,而忽略了受递减载荷引起的损伤加深。HAGHGOUEI等[19]采用加载循环次数的对数关系修正模型,并通过预测岩石的疲劳寿命验证改进模型的合理性,由于研究材料的特殊性,该模型对于金属材料并不适用。GAO等[20]综合考虑载荷比与疲劳寿命比的关系,得到目前预测精度较好的模型。在疲劳损伤累积过程中,材料的力学性能随着加载次数的增加而逐渐退化,现有的M-H模型都不能很好地解释这一现象,从而使得预测值与实际值仍存在较大偏差。为提高模型的预测精度并扩展模型的应用范围,将生物学中有机物生态质量的损耗[21]类比于材料力学性能的退化,通过引入考虑材料力学特征指标和结构尺寸参数的力学性能退化率,提出新的M-H模型。在单一疲劳损伤的分析与计算方法中,结合材料S-N曲线的名义应力法作为最简单有效的方法,在转向架焊接构架的损伤分析与寿命预测方面应用广泛[22]。随着焊接接头的分级逐渐严格,实际焊接结构与S-N曲线的不匹配性逐渐凸显,使得名义应力法的应用存在局限性。为此,DONG[23]提出等效结构应力法,并结合大量焊接接头的疲劳实验数据,拟合出主S-N曲线,使得焊接接头的疲劳损伤分析结果更加真实可靠。陈宏烨等[24]基于等效结构应力法和名义应力法同时分析转向架焊接构架的疲劳损伤,验证了等效结构应力法的可靠性,并表明该方法可以应用于转向架焊接构架的疲劳损伤分析与寿命预测。本文针对转向架焊接构架承受多级变幅载荷的疲劳损伤问题,建立转向架焊接构架有限元模型,并对构架施加多级变幅疲劳载荷,基于等效结构应力法计算构架单级疲劳损伤值,并应用改进的M-H模型分析构架多级疲劳累积损伤,从而验证构架的结构强度满足服役要求,进一步表明改进的M-H模型能够应用于轨道车辆关键结构的疲劳累积损伤分析。
1 改进M-H模型的提出
1.1 传统M-H模型
M-H非线性累积损伤模型以结构能承受的最大裂纹长度累积量来表示结构的累积损伤量D:
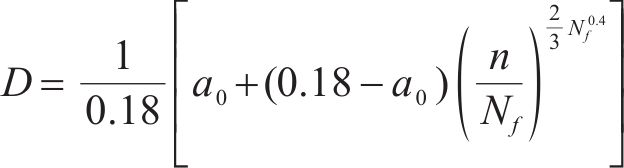
式中:n为加载循环次数;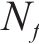

图1给出了2级加载下的疲劳损伤路径,即材料先以应力幅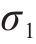
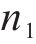
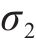
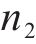
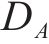
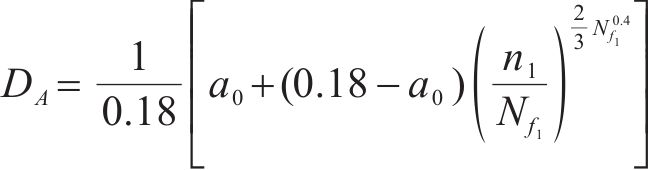
式中:Nf1为造成材料失效的总循环次数。
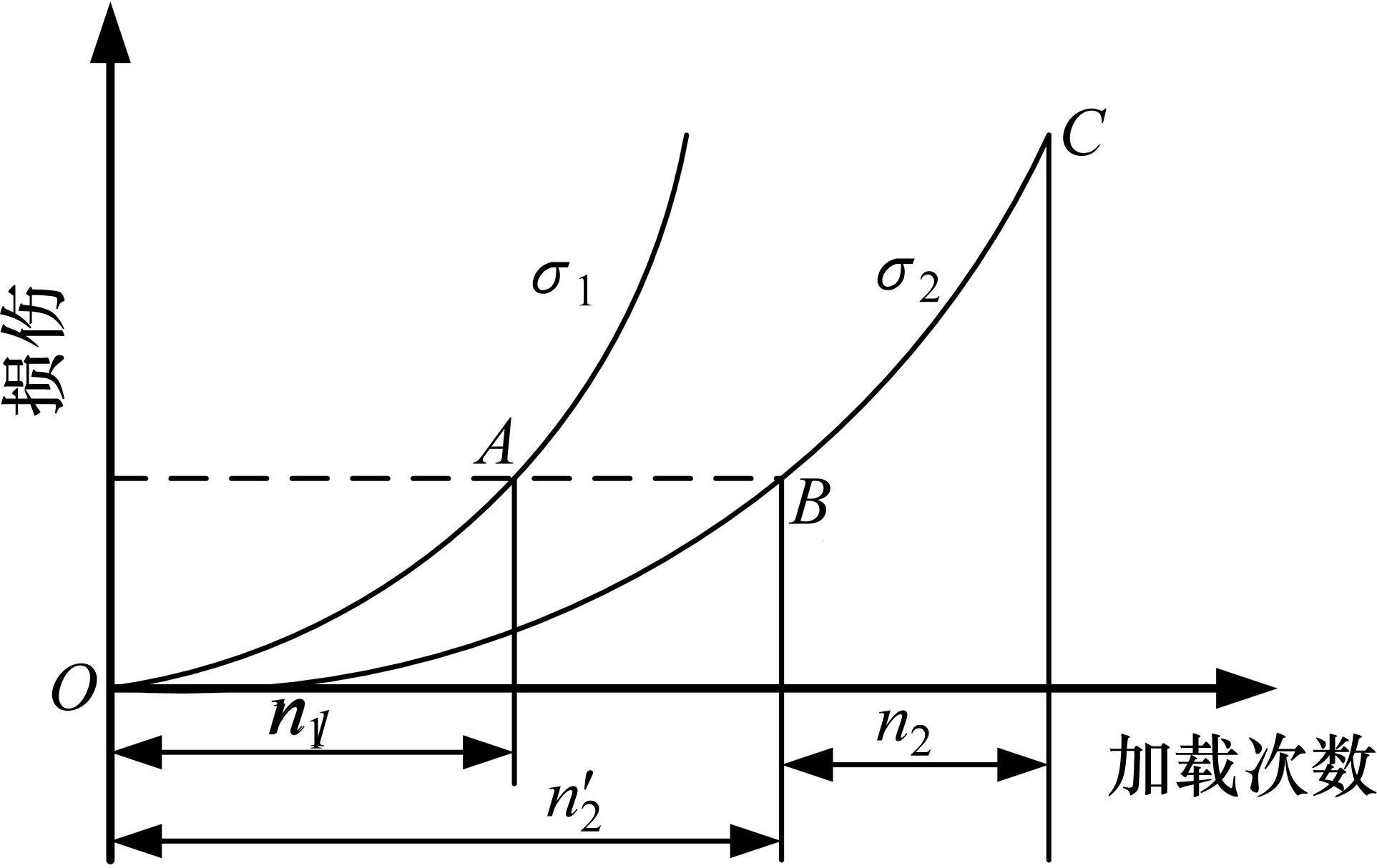
应用等效疲劳损伤的概念,将材料的损伤累积从A扩展到B,B点处的损伤累积为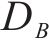
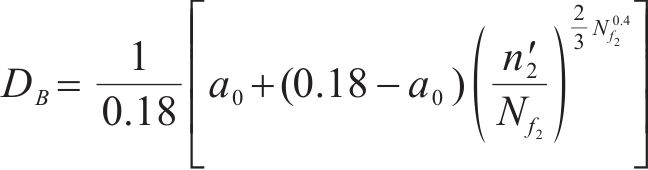
式中,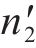
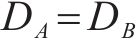
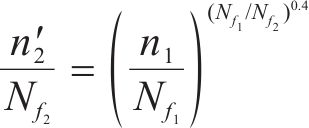
在2级荷载下,材料的损伤累积沿着从B点到C点的损伤曲线进行,其中C点处的损伤累积DC为
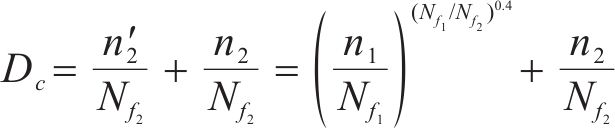
基于累积损伤准则,将公式(5)推广到一般情况,可以得到多级载荷下的疲劳累积损伤准则为
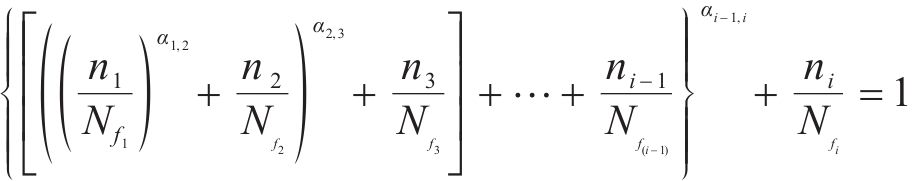
式中: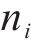
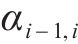
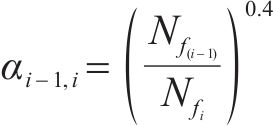
当寿命比特征参数为1时,M-H非线性损伤累积模型将退化为Palmgren-Miner线性损伤累积模型。因此,寿命比特征参数在表征非线性损伤方面作用显著,M-H模型的改进也是对寿命比特征参数的改进。
1.2 改进M-H模型
在生物学中有机物的分解通常表示为关于时间的指数函数[25],即
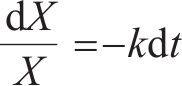
式中: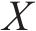
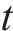
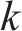
ROVIRA等[26]将式(8)中的瞬时分解率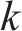
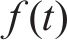
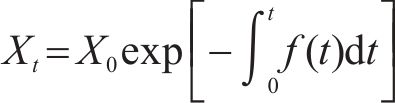
式中: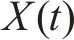
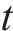
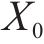
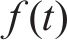
同时认为瞬时分解率遵循指数定律,因此令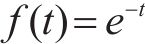
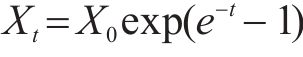
LI等[27]认为有机物的分解具有先快后慢的趋势,因此采用双指数函数来表征有机物的分解过程,即
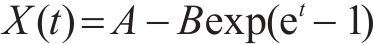
式中: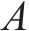
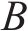
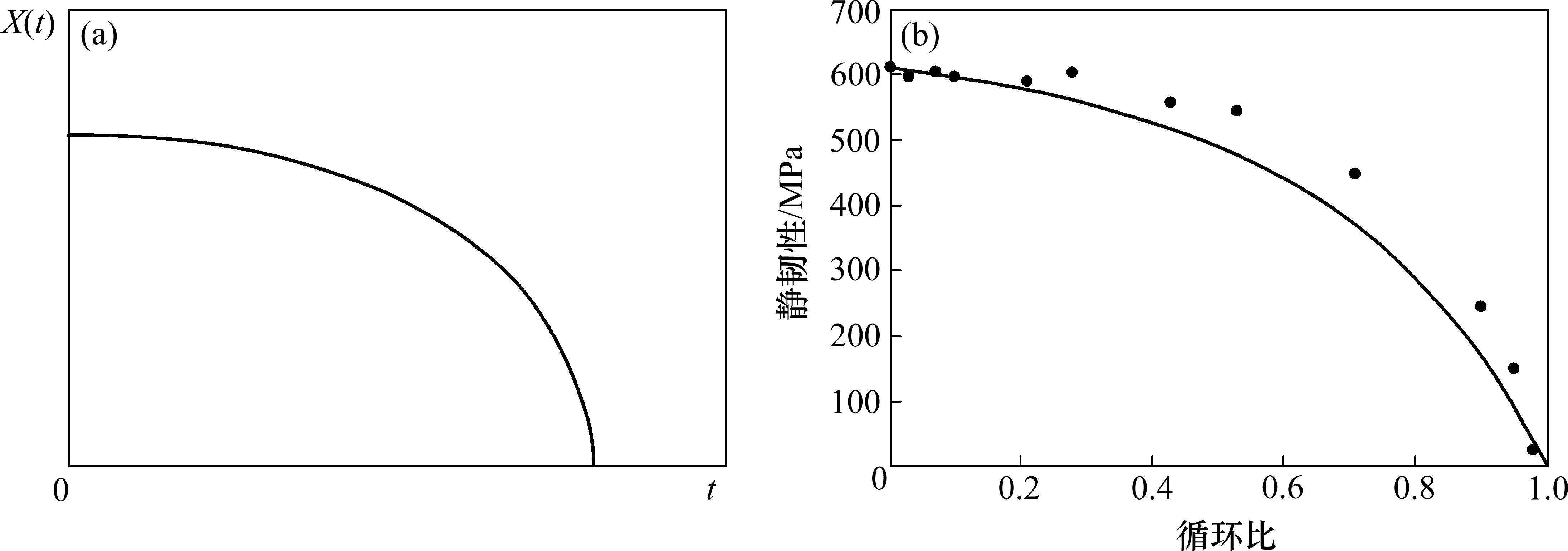
如图2所示,图2(a)为描述有机物随时间的分解公式(11),图2(b)为基于C35材料在加载状态下静韧性实验数据[28]的拟合,由此可知2个图所表示趋势相似,可以进行类比。因此将公式(11)中的变量t替换为n/Nf可得
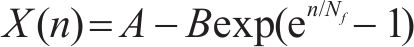
因此不同材料的力学性能退化率为
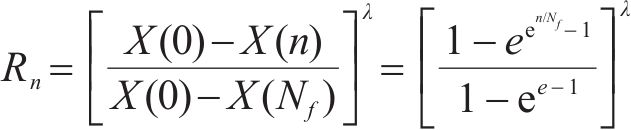
式中:λ为考虑不同材料力学性能的特征参数,研究表明,材料的抗拉强度、屈服强度和断裂韧度等力学指标均影响材料的疲劳损伤[29],因此可根据公式(14)计算。
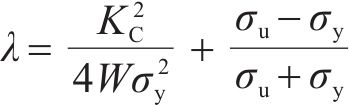
式中: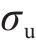
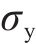
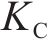
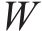
基于GAO提出的改进模型,将载荷比引入力学性能退化率,将生物学中有机物的生态质量损耗类比于材料力学性能的退化从而表征材料力学特性和结构尺寸对疲劳寿命的影响,则新的寿命比特征参数为
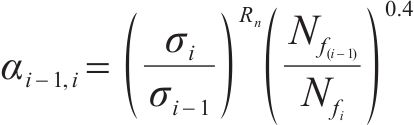
由于提出以指数形式引入力学性能退化率,因此对其合理性和准确性进行验证。选取C35[30]材料试样、C45[31]材料试样和Al-2024-T42[32]材料试样的2级加载实验数据,通过设置不同的指数数值进行疲劳损伤预测,如图3所示,当指数取值在1~1.5的范围时,预测的平均误差能够位于较小值的范围内。图中方框中范围则表明,基于力学性能退化率所得的数据点的指数值均在1~1.5的范围内,同时各数据点的单点预测误差均低于50%,超过半数的数据点预测误差低于25%,从而说明以指数形式引入力学性能退化率具备一定的预测精确性。
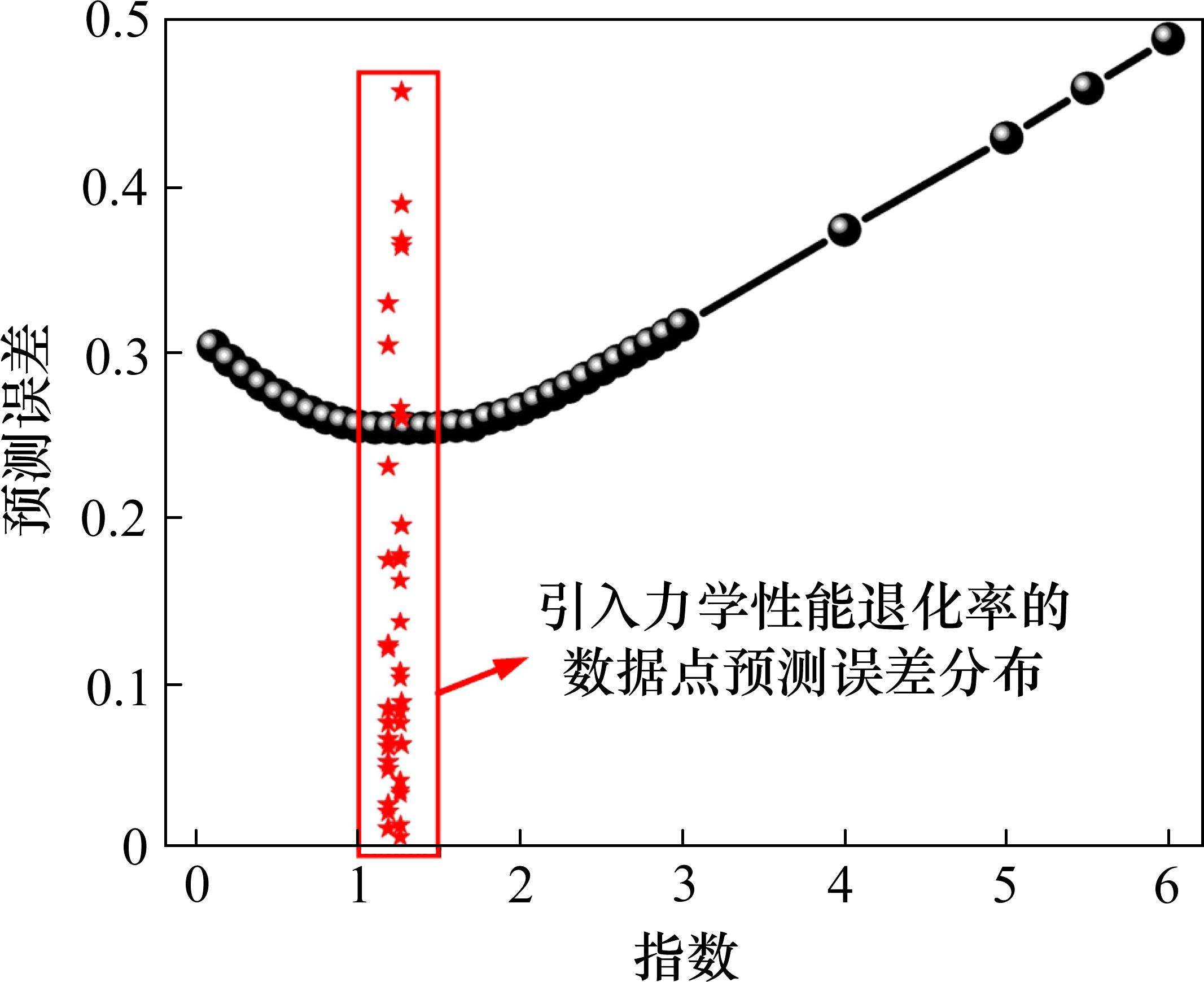
2 改进M-H模型的验证
由于UIC615-4标准[33]中规定的疲劳试验加载仅到3级,且为低高加载,因此以2级高低和低高加载以及3级低高加载为例,分别选取C35[30]材料试样的2级加载(与上文所选数据不同)和Q235[20]材料试样的3级加载疲劳实验值。由于实验数据仅给出了试样单级的损伤度实验值,因此为了体现与实验值的直接比较,并借鉴该领域现有研究方式,将最高级损伤度的预测值与实验值以及相对预测误差整理如表1所示,与Palmgren-Miner模型和传统M-H模型的预测值相比,改进M-H模型的预测值均更加接近实验值。
| 损伤度实验值 | 损伤度预测值 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1级 | 2级 | 3级 | Miner | M-H | 改进M-H | ||||
| 最高级损伤度 | 预测误差/% | 最高级损伤度 | 预测误差/% | 最高级损伤度 | 预测误差/% | ||||
| C35二级高低加载:σ1=353 MPa, σ2=275 MPa | |||||||||
| 0.1 | 0.458 | 0.9 | -97 | 0.55 | -19 | 0.41 | 10 | ||
| 0.2 | 0.281 | 0.75 | -167 | 0.38 | -34 | 0.30 | -7 | ||
| 0.5 | 0.109 | 0.5 | -359 | 0.21 | -94 | 0.15 | -28 | ||
| 0.75 | 0.054 | 0.25 | -363 | 0.09 | -74 | 0.06 | -10 | ||
| C35二级低高加载:σ1=294 MPa, σ2=334 MPa | |||||||||
| 0.1 | 1.06 | 0.9 | 15 | 0.98 | 8 | 0.99 | 7 | ||
| 0.25 | 0.96 | 0.75 | 22 | 0.90 | 6 | 0.94 | 2 | ||
| 0.5 | 0.78 | 0.5 | 36 | 0.69 | 12 | 0.76 | 3 | ||
| Q235三级低高加载:σ1=23.3 MPa, σ2=25.1 MPa, σ3=26 MPa | |||||||||
| 0.136 | 0.684 | 0.356 | 0.51 | 43 | 0.23 | 35 | 0.31 | 13 | |
| Q235三级低高加载:σ1=38 MPa, σ2=40 MPa, σ3=42 MPa | |||||||||
| 0.371 | 0.463 | 0.353 | 0.17 | 52 | 0.21 | 41 | 0.23 | 36 | |
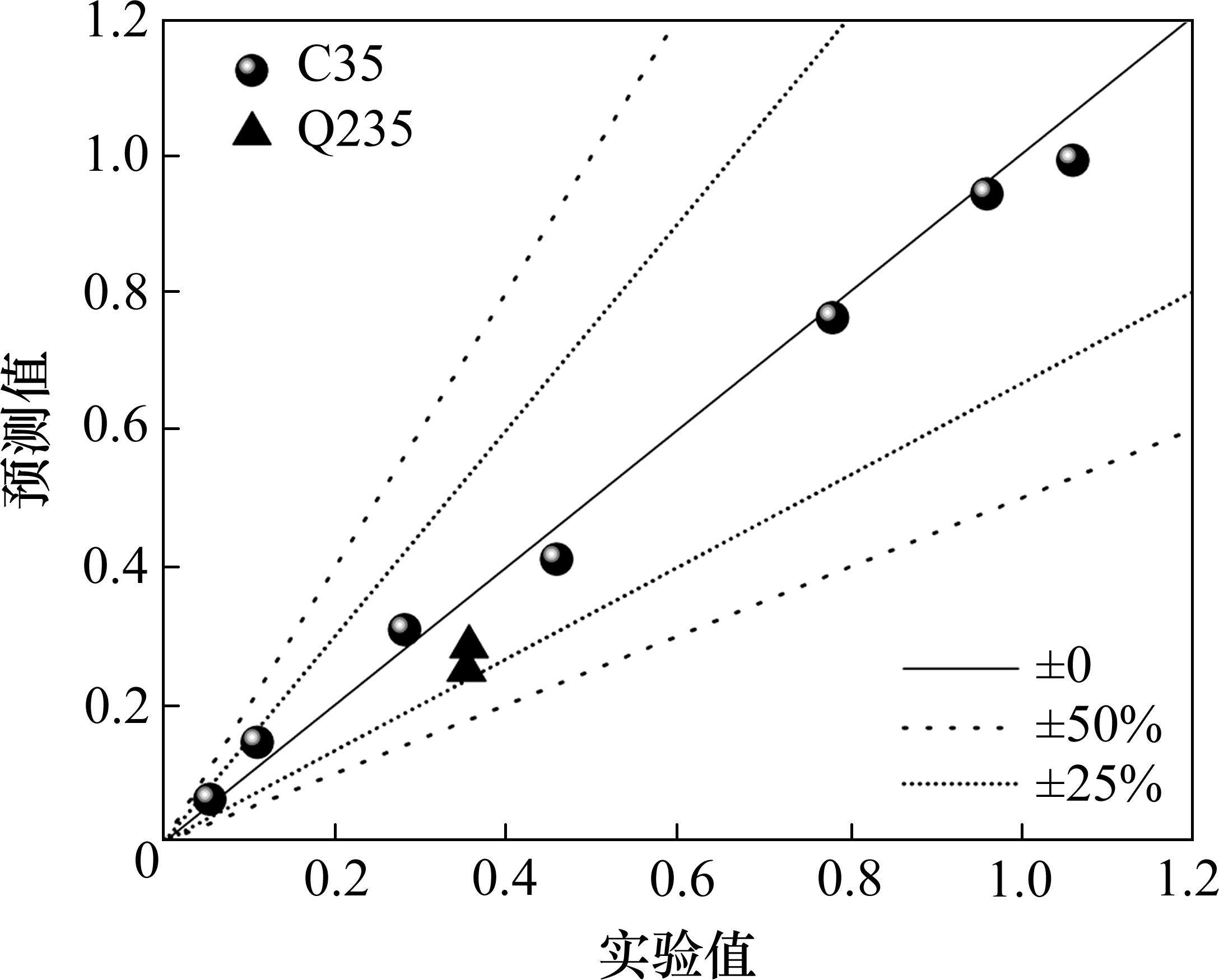
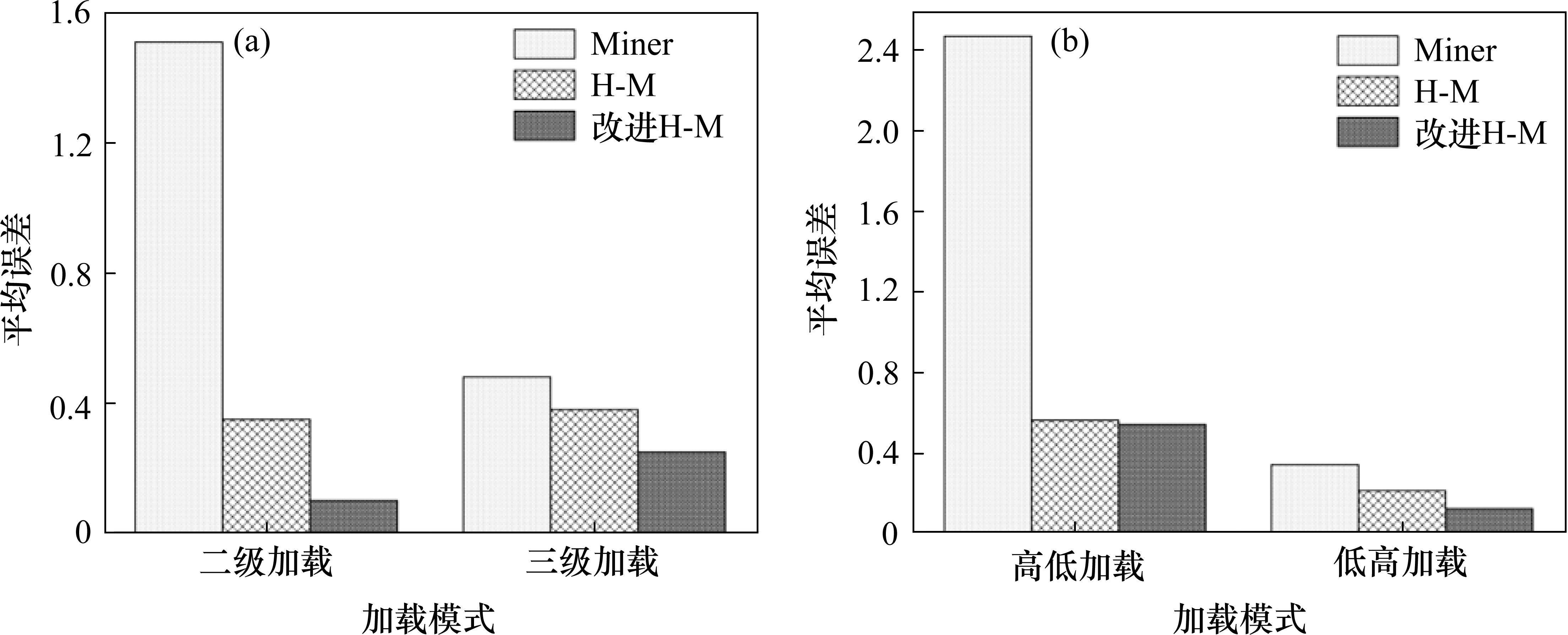
如图4所示,基于改进M-H模型预测的疲劳损伤比均在±50%的允许预测误差范围内,并且大部分能够满足±25%的良好预测误差。对于不同加载模式的预测误差,对表1中相关的预测误差取平均值进行进一步分析对比,如图5所示,改进M-H模型的平均误差明显降低,并且针对低高加载模式,与传统M-H模型相比,改进模型的预测误差降幅更加明显,在此种加载模式下,改进的M-H模型具备更好的预测精度,因此针对转向架构架承受的UIC615-4标准中提供的3级低高加载模式,改进M-H模型能够对该结构进行有效疲劳损伤分析。
3 转向架构架疲劳损伤分析
3.1 疲劳载荷工况
UIC615-4标准规定的疲劳试验载荷主要包括横向载荷和垂向载荷。垂向载荷包括动态、静态和准静态3部分,由于静态部分不会造成应力的明显变化,从而不考虑。横向载荷包括动态和准静态2个部分。疲劳实验主要分为3个阶段,分别以1、1.2和1.4倍的应力对应循环6×106、2×106和2×106次,具体加载信息见表2。
| 工况序号 | 描述 | 载荷数值 | |||||
|---|---|---|---|---|---|---|---|
| 6×106加载/kN | 2×106加载/kN | 2×106加载/kN | |||||
| 1 | 准静态 | 垂向 | 22.47 | 垂向 | 26.96 | 垂向 | 31.46 |
| 横向 | 64.87 | 横向 | 77.84 | 横向 | 90.82 | ||
| 2 | 动态 | 垂向 | 112.33 | 垂向 | 134.80 | 垂向 | 157.26 |
| 横向 | 64.87 | 横向 | 77.84 | 横向 | 90.82 | ||
3.2 疲劳损伤分析
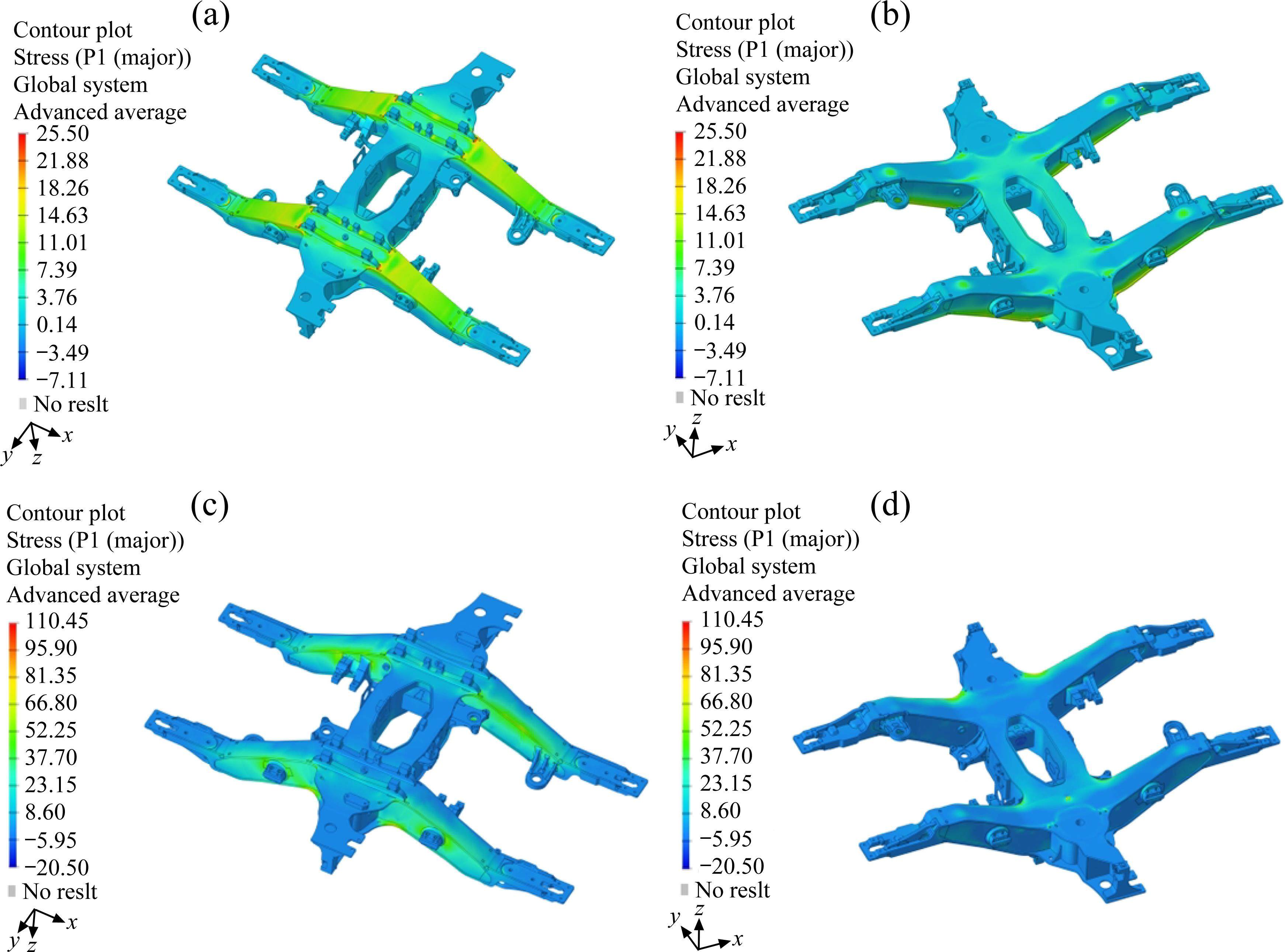
计算各工况各阶段应力,由于各工况第1阶段对构架的疲劳损伤贡献最大,因此根据各工况第1阶段的应力计算结果(应力云图如图6所示),选取应力较大位置处的典型焊缝进行疲劳损伤分析,如图7所示。
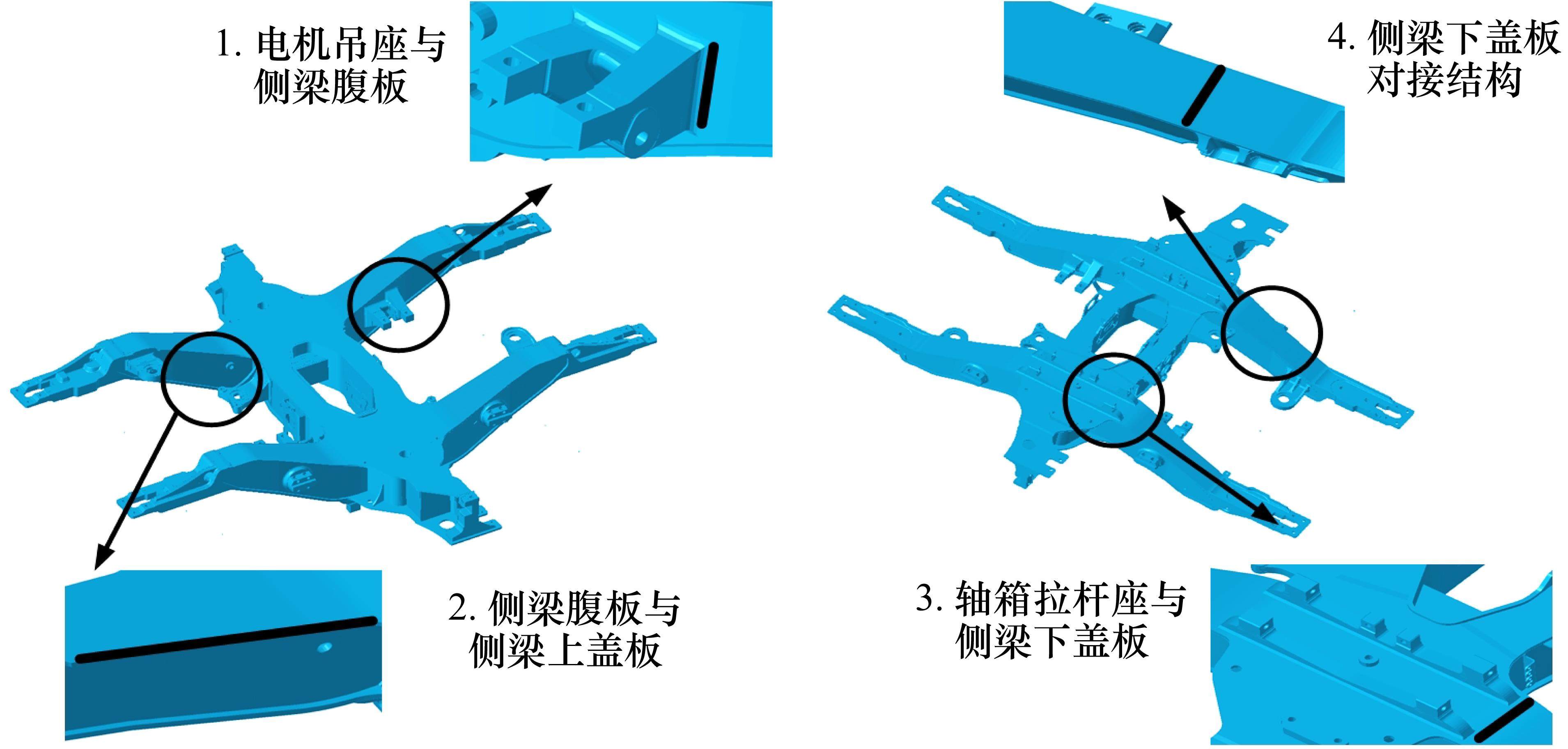
单级加载疲劳损伤采用等效结构应力法分析。等效结构应力法采用网格不敏感的结构应力与断裂力学理论相结合,并得出主S-N曲线方程,可以克服名义应力的局限性,从而有效预测焊接结构的疲劳寿命。应用基于等效结构应力分析法原理自主研发的Weld Fatigue软件,提取单级加载下图7中各评估焊缝的结构应力与等效结构应力,如图8所示(以最大工况2工况第1阶段加载为例),并基于98%可靠度的确定概率的主S-N曲线,计算评估焊缝单级加载下的疲劳寿命,如图9所示(以最大工况第2工况第1阶段为例)选取各评估焊缝疲劳寿命最小值点,即疲劳损伤最大值点。
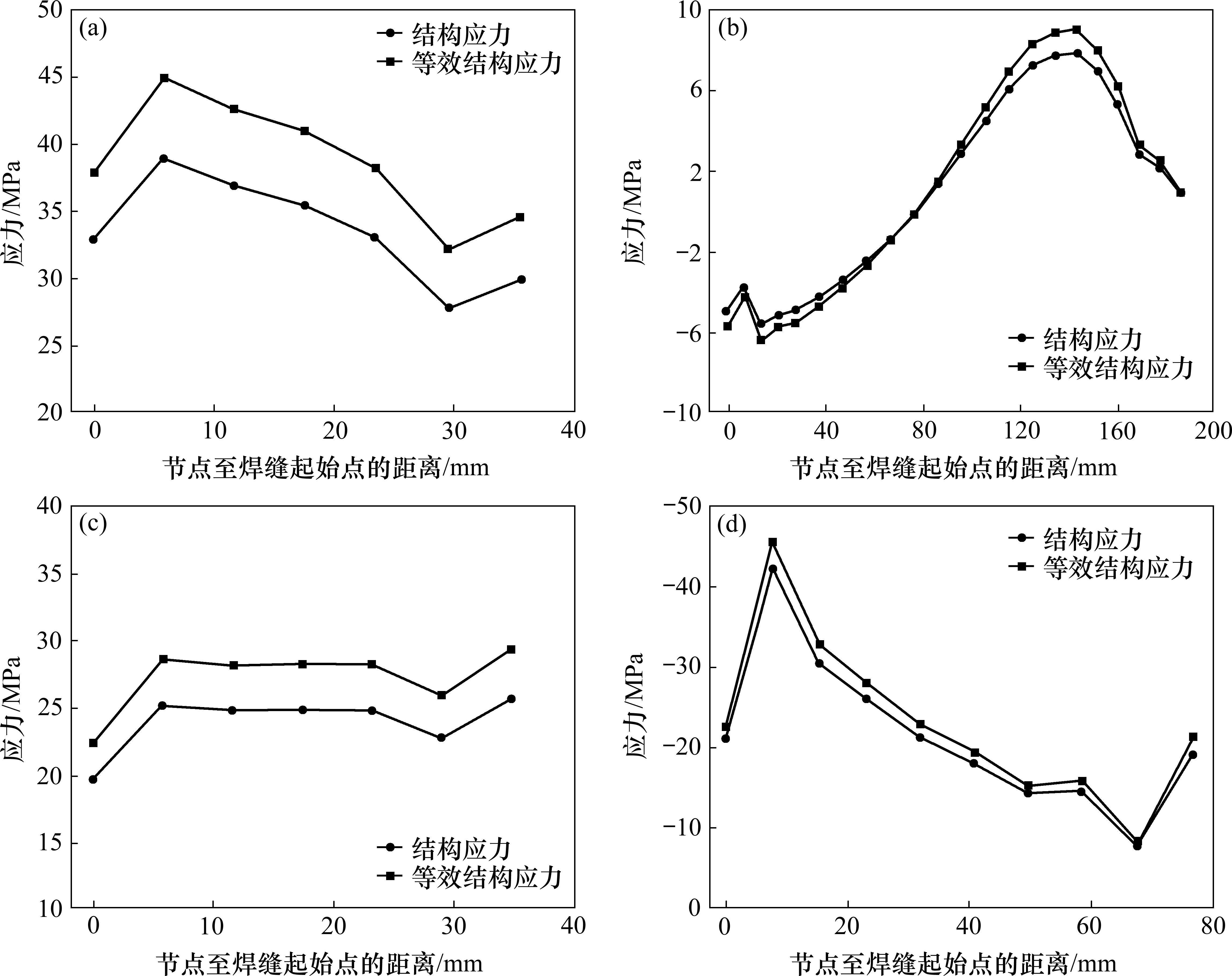
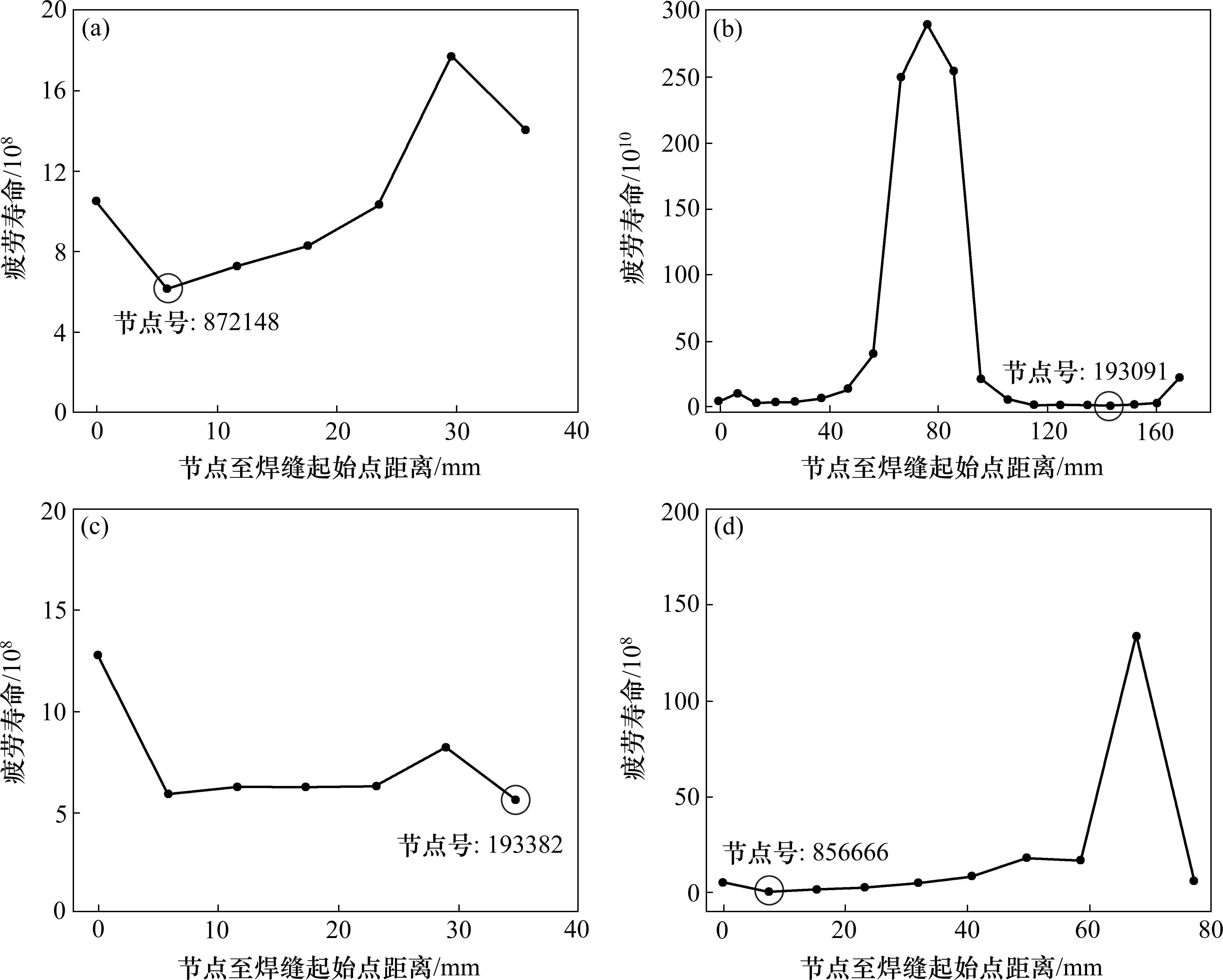
与试样多级加载实验不同,在工程实际中,对于结构疲劳损伤的分析主要是针对结构在承受多级载荷下的疲劳累积损伤数值进行分析,因此分别基于Miner、传统M-H和改进M-H计算疲劳累积损伤,整理如表3所示。综合对比分析表1和表3,对于多级加载单级损伤度的预测,Miner线性累积损伤模型相比M-H非线性累积损伤模型存在较大预测差异,而对于多级加载累积损伤的预测,Miner线性累积损伤模型与改进的M-H非线性累积损伤模型预测值较为接近,传统的M-H模型与二者之间存在较大差异。
| 焊缝编号 | 节点号 | 改进M-H模型 的阶段损伤 | 累积损伤 | ||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | Miner | M-H | 改进M-H | ||
| 1 | 872148 | 0.12 | 0.06 | 0.09 | 0.27 | 0.76 | 0.36 |
| 2 | 193091 | 0.15 | 0.06 | 0.08 | 0.29 | 0.72 | 0.38 |
| 3 | 193382 | 0.07 | 0.02 | 0.06 | 0.15 | 0.77 | 0.20 |
| 4 | 856666 | 0.1 | 0.05 | 0.06 | 0.21 | 0.64 | 0.40 |
4 结果与讨论
分析表3可知,各焊缝最大损伤累积值均小于1,该转向架构架疲劳强度符合要求。其中,焊缝2和焊缝4为构架板材与板材之间的焊缝,疲劳累积损伤值较小。相对而言,焊缝1和焊缝3为吊座与板材之间的焊缝,疲劳累积损伤值较大,在承受多级变幅载荷时表现出较弱的抗疲劳性能。究其原因:吊座与板材之间通常采用角焊缝连接,焊接部位存在较大的应力集中。当承受多级变幅载荷时,应力集中部位的应力幅值较大,导致疲劳裂纹更容易萌生和扩展。并且吊座与板材之间的焊接位置通常位于板材边缘或拐角处,焊接质量难以控制,容易出现缺陷,如气孔、裂纹、未焊透等,这些缺陷会导致焊接部位的强度降低,抗疲劳性能下降。此外,吊座与板材之间通常采用不同的材料,2种材料机械性能的差异会导致焊接部位的强度和抗疲劳性能不匹配,更容易出现疲劳损伤。
比较基于3种模型计算的疲劳累积损伤结果:其中基于改进M-H模型的计算结果高于基于Miner模型的计算结果,但低于基于传统M-H模型的计算结果。进一步分析可知,对于多级加载的非线性疲劳累积损伤问题,应用基于线性疲劳累积损伤理论的Miner模型本身就存在不准确性,而基于非线性疲劳累积损伤理论的M-H模型考虑到了载荷之间的顺序效应和相互作用效应,使得整体预测结果偏为保守。但传统的M-H模型由于未进一步细化考虑材料的自身性能对于多级加载疲劳损伤的贡献,预测结果较为笼统,为保证结构的安全性,容易损伤较多的设计安全裕量。新改进的M-H模型,充分考虑到了材料力学指标与结构尺寸参数对疲劳损伤的影响,与Miner模型和传统M-H模型相比,预测结果相对合理精确,且并未损伤较多设计安全裕量。同时,表3所示3种模型的疲劳累积损伤预测差异与表1所示的单级损伤不同,对于工程实际应用中所研究的疲劳累积损伤,基于改进的M-H模型和Miner模型所得的疲劳累积损伤值相对接近,这也进一步说明了各模型应用的局限性。从理论和实验的角度,试样多级加载的疲劳实验数据验证了改进M-H模型对单级疲劳损伤预测的精确性,但在考虑疲劳累积损伤的工程实际应用中,改进的M-H模型与Miner模型分析值并无较大差别,这也是Miner模型在无较严格预测精度要求下最为常用的原因。
如前所述,改进的M-H模型引入了材料结构尺寸参数和力学性能指标,因此改进的M-H模型可以考虑这些因素对结构疲劳寿命的影响。图10通过当只有一个参数变化而其余参数固定时的疲劳寿命变化来详细说明上述因素的影响。由图10可知,疲劳寿命随结构尺寸和屈服强度的增大而减小,随抗拉强度和断裂韧性的增大而增大,符合常规理论逻辑,表明该模型引入的参数的影响较为合理,并且这些结果将有助于结构的抗疲劳设计,因此,该模型可以为设计人员在进行结构设计时提供更多的信息。对于高速动车组转向架构架而言,设计人员通过调整板厚或者更改材料,从而提升结构的抗疲劳性能。
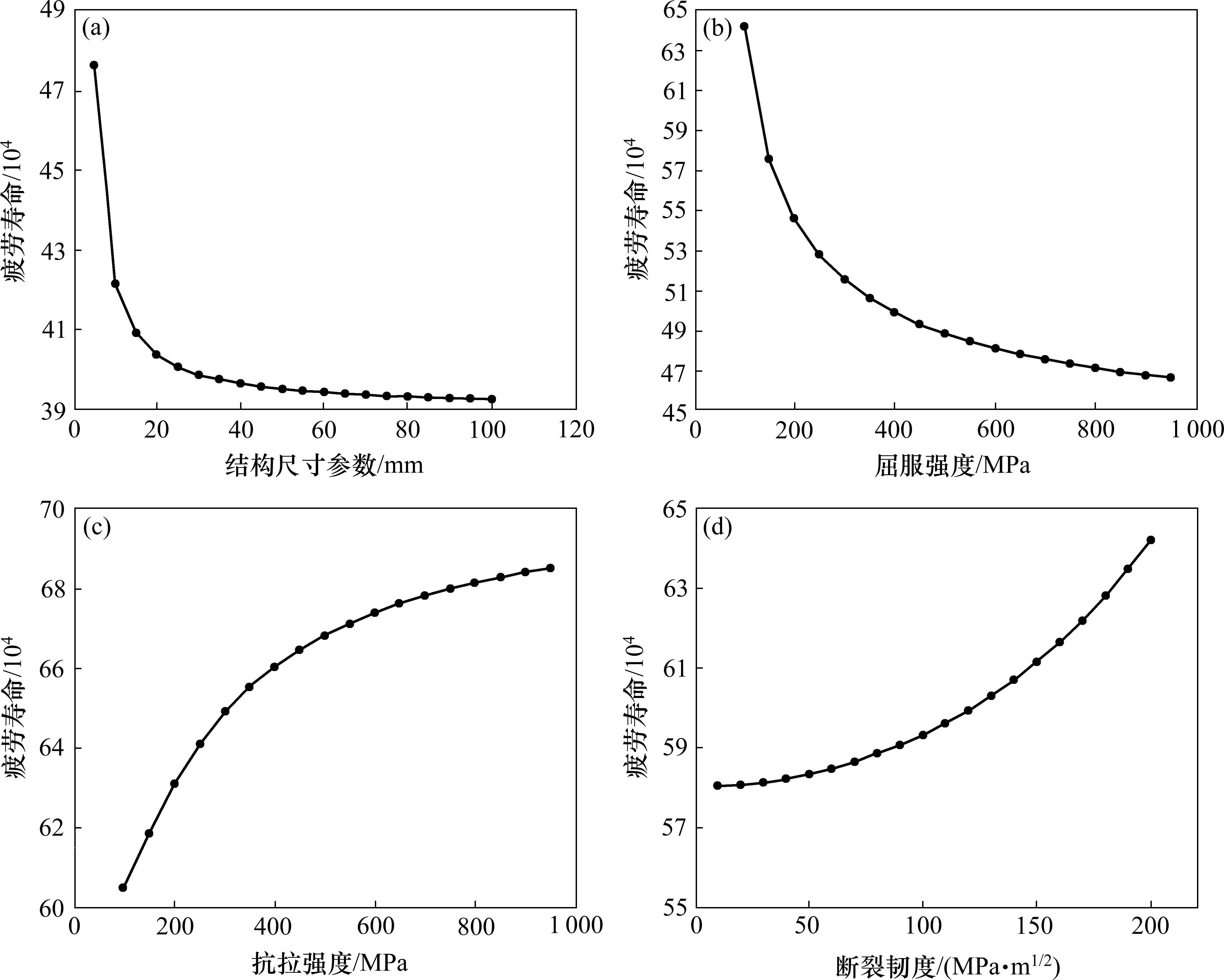
5 结论
1) 将生物学中有机物的生态质量损耗类比于材料力学性能的退化,充分考虑了结构尺寸参数和力学性能的影响,因此将该新模型应用于工程结构疲劳寿命预测时可以提供更多的信息,从而使得现在的模型比以前的模型更有优势。同时基于标准试样的多级加载实验数据,验证了改进M-H模型预测的精确性。
2) 基于3种模型仿真分析了某转向架构架多级加载下的疲劳损伤,表明构架结构疲劳强度符合要求,同时分析结果体现了3种模型的适用性,因此在工程实际应用中,若无高精度要求,改进的M-H模型与Miner模型预测效果并无较大差别。但由于构架结构较为庞大,缺少实际疲劳实验数据进一步支撑仿真结果的正确性。
唐毓晗,王悦东,郭涛.基于改进M-H模型的转向架构架疲劳损伤分析[J].铁道科学与工程学报,2025,22(03):1279-1290.
TANG Yuhan,WANG Yuedong,GUO Tao.Fatigue damage analysis of bogie frame based on improved M-H model[J].Journal of Railway Science and Engineering,2025,22(03):1279-1290.

