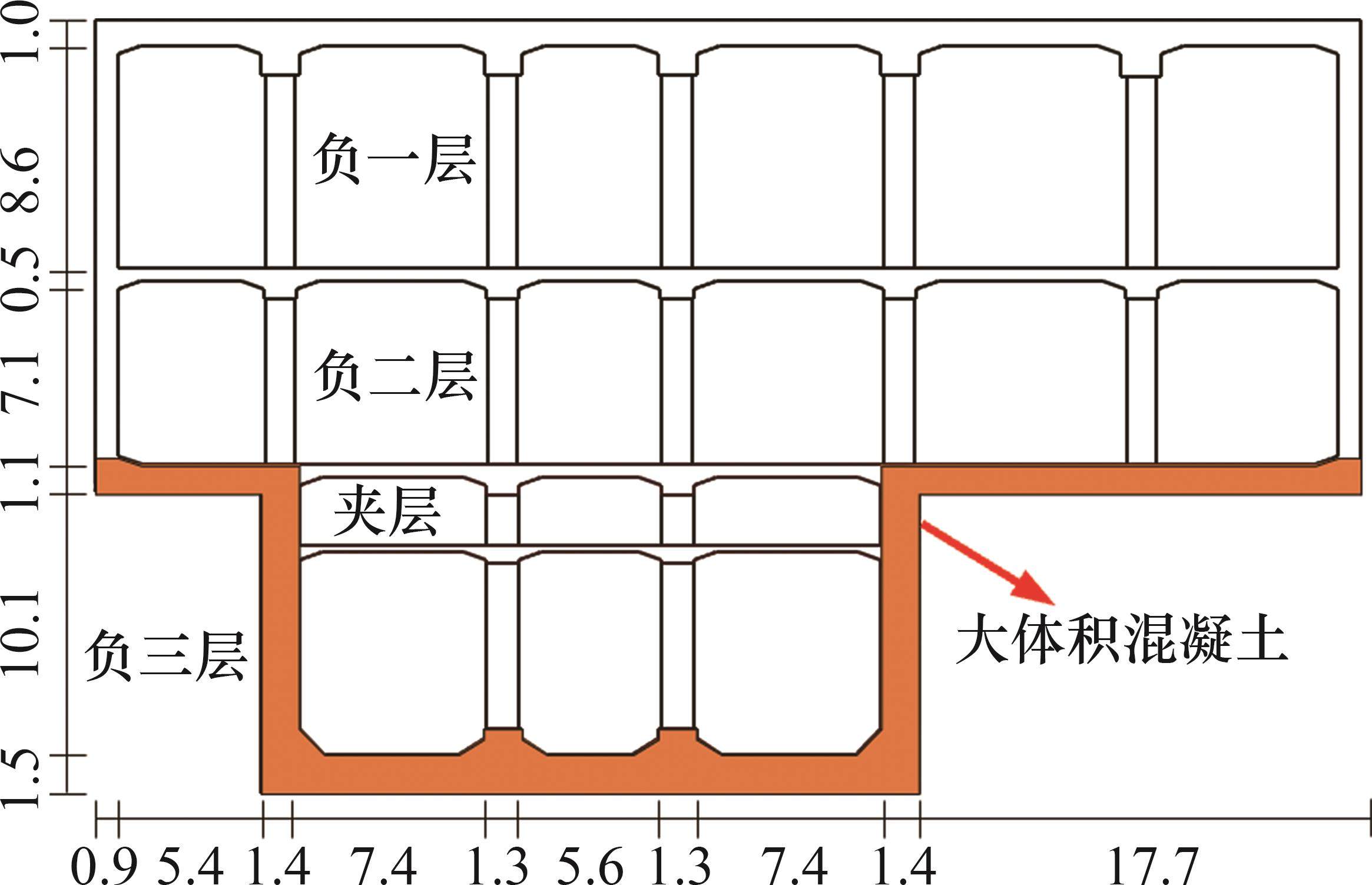
深圳地铁大运站主体结构为地下4层单岛双线式车站,车站为框架结构,采用明挖顺作法施工。车站全长295.78 m,划分为16个浇筑段,依次编号为1~16号,每段长度约为18 m。车站标准段横断面如图1所示,其中,负一层与负二层为一级基坑,宽度为50 m;负三层为二级基坑,宽度为 26 m;负三层底板与侧墙的厚度分别为1.5 m和1.4 m,负三层底板与侧墙均属于大体积混凝土[1-2]。大体积混凝土施工中会释放大量水化热,导致内表温差较大,容易引发表面温度裂缝,进而可能发展为贯穿裂缝,导致车站出现渗漏水等病害,对车站结构的耐久性和稳定性均会产生影响[3-6]。因此,对车站结构进行浇筑时,如何有效控制混凝土施工期的温度,以降低内部温度、减小温度应力、降低开裂风险,是一个亟待解决的问题。
众多学者对大体积混凝土温度裂缝控制技术优化进行了研究。于冬等[7]运用ANSYS有限元模拟大体积混凝土基床结构施工过程,发现随着入模温度升高,温度应力增大。谢祥明等[8]针对高温气候地区混凝土重力坝坝体容易产生温度裂缝的问题,提出采用表面保温与冷却管降温措施能,以有效降低表面温度应力。刘新辉等[9]结合某大体积混凝土桥梁承台,通过数值模拟发现混凝土入模温度、冷却水管间距、冷却管进水温度对承台内部的降温效果影响显著。李志鹏等[10]结合大体积混凝土温度场解析解与数值分析,得出采用降低入模温度、减小热交换系数等措施能减小混凝土内部的自约束应力。SAEED等[11]对施工现场的大体积混凝土温度场与应力场进行了数值模拟,准确预测了混凝土结构的温度应力与裂缝分布情况。目前,大多数研究集中于单因素变化对大体积混凝土温度场与应力场的影响,而忽略了各影响因素之间交互作用对温度裂缝的影响,这样优化的结果往往过于保守,容易造成资源浪费,增加温控成本。近年来,有学者采用响应面法研究了因变量(响应值)与多个自变量之间相互作用的影响,解决了工程中的优化问题。徐征杰等[12]针对某地铁盾构区间强风化花岗岩地层的膨润土改良问题,通过构建响应面-满意度函数确定了在不同盾构推进速度下的最优改良参数。许世展等[13]将桥梁的节段参数作为待修正参数,建立了待修正参数与目标参数之间的响应面函数,并结合目标参数的现场实测数据动态优化待修正参数。成棣等[14]针对车轮踏面优化问题,探讨了多项式与高斯径向基函数两种响应面法的应用,发现优化后的车轮踏面磨耗指数显著降低,说明了响应面法的适用性。REN等[15]将响应面法应用于结构动力学中,通过仿真数据构建多项式响应面模型,并结合实测数据验证了模型的准确性。
本文以深圳大运站主体结构为研究对象,采用响应面法研究多因素交互作用对大体积混凝土温度裂缝的影响,合理设计数值模拟试验,拟合出优化目标参数与各影响因素的多元回归模型,在响应面函数的基础上,构建目标优化函数,结合粒子群优化算法求解全局最优解,确定温度裂缝的最优参数取值,以便为大体积混凝土温度裂缝控制技术的优化设计提供参考。
1 大体积混凝土车站热-力耦合模型
1.1 工程概况
深圳地铁大运站主体结构采用C35混凝土,抗渗等级为P12,混凝土中水泥、粉煤灰、水、砂、碎石、外加剂质量比为305꞉90꞉150꞉751꞉1 030꞉8.69,采用P·O42.5普通硅酸盐水泥和Ⅱ级粉煤灰。在对车站施工时,在大体积混凝土内部均匀预埋冷却管,用于降低混凝土内部的高温。对底板施工时,采用分层浇筑,每层厚度为40 cm,浇筑完成后,冷却管通水开始工作;对侧墙同样采用分层浇筑,每层高度为40~50 cm,在初凝之前浇筑下一层,并以不超过1.5 m/h的浇筑速度进行。
1.2 模型建立
选取图1中的大体积混凝土、夹层与立柱为隔离体,建立车站标准段的热-力耦合分析模型,如图2所示。底板与地基接触,接触界面采用固结边界;侧墙在靠近围岩一侧为临空面,侧墙浇筑完成1 d后采用C25混凝土填充临空面。考虑车站已浇筑段对本模型(现浇筑段)的约束,在车站模型纵向方向上的一侧设置法向约束,如图2(a)所示。
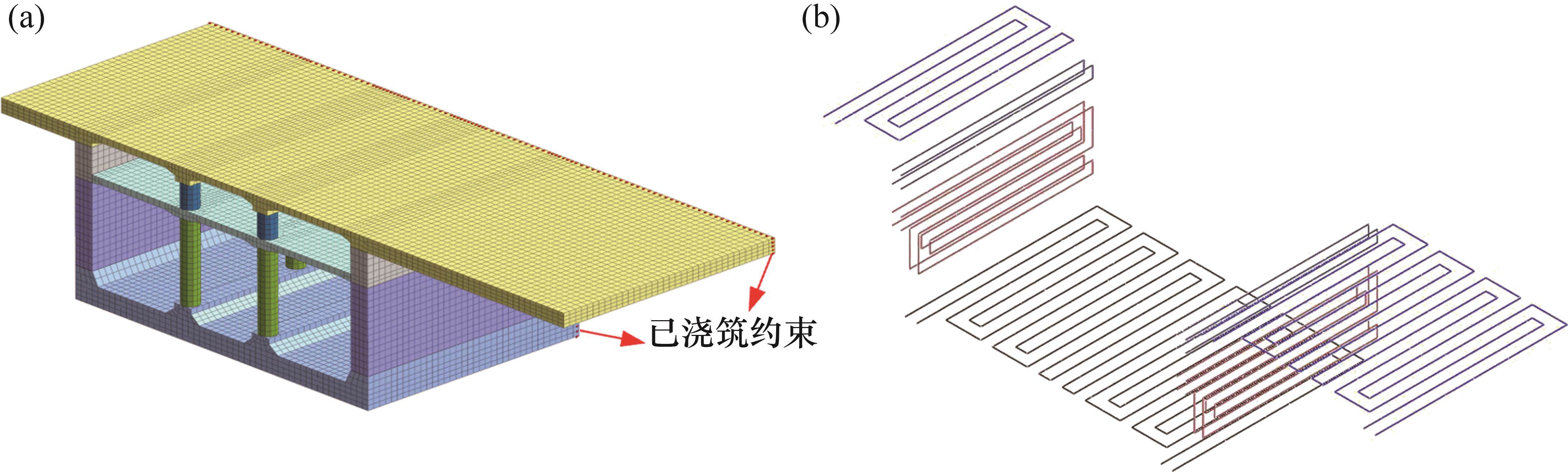
车站底板与侧墙采用分层浇筑,新旧混凝土交界面的热对流系数随着施工阶段的进行不断发生变化,在浇筑第二层之前,第一层混凝土顶面与空气发生热对流;第二层浇筑后,第一层顶面与空气的热对流消失,其他面的热交换保持不变。车站底板与侧墙在浇筑过程中,采用厚度为6 mm的钢板支护,浇筑完成3 d后拆模,拆模后采用喷淋洒水养护,拆模前后的热对流系数βs通过式(1)计算。将结构与地基、围岩或已浇筑段的接触界面定义为固结面,结构与空气接触界面定义为自由面,对2种界面的热对流系数分开赋值。根据现场施工方案,将模型的施工阶段设计为:对负三层底板作业10 d,对负三层(不包括夹层)侧墙与立柱作业15 d,对夹层侧墙与立柱作业6 d,对负二层底板作业10 d。在大体积混凝土区域,采用管单元模拟大体积混凝土区域中均匀布置的冷却管,将管单元节点与混凝土节点耦合,实现混凝土与冷却管之间的热传导。数值模型的计算参数取值见表1,混凝土的导热系数和比热容等参数由现场配合比计算得到,其余参数由现场施工方案与规范[1]确定。
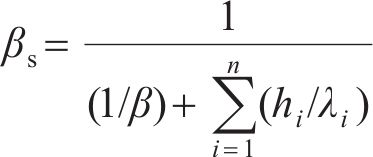
式中:β为最外层保温层在空气中的放热系数;hi为第i层保温层的厚度;n为保温层层数;λi为第i层保温层的导热系数。β与环境风速有关,车站处平均风速为1.0 m/s,经计算所得。自由面在拆模前后的热对流系数如表1所示。
| 参数 | 取值 |
|---|---|
| 导热系数/[kJ·(h·m·℃)-1] | 9.18 |
| 比热容/[kJ·(kg·℃)-1] | 0.93 |
| 28 d抗拉强度/MPa | 2.2 |
| 弹性模量/MPa | 34.5 |
| 环境温度/℃ | 30.0 |
| 拆模前自由面热对流系数/[kJ·(m2·h·℃)-1] | 38.6 |
| 拆模后自由面热对流系数/[kJ·(m2·h·℃)-1] | 18.5 |
| 入模温度/℃ | 23 |
| 冷却管间距/m | 1.0 |
| 冷却管进水温度/℃ | 25 |
| 冷却管水流量/(m3·h-1) | 1.2 |
| 环境风速/(m·s-1) | 1.0 |
| 固结面热对流系数/[kJ·(m2·h·℃)-1] | 13.5 |
1.3 模型验证
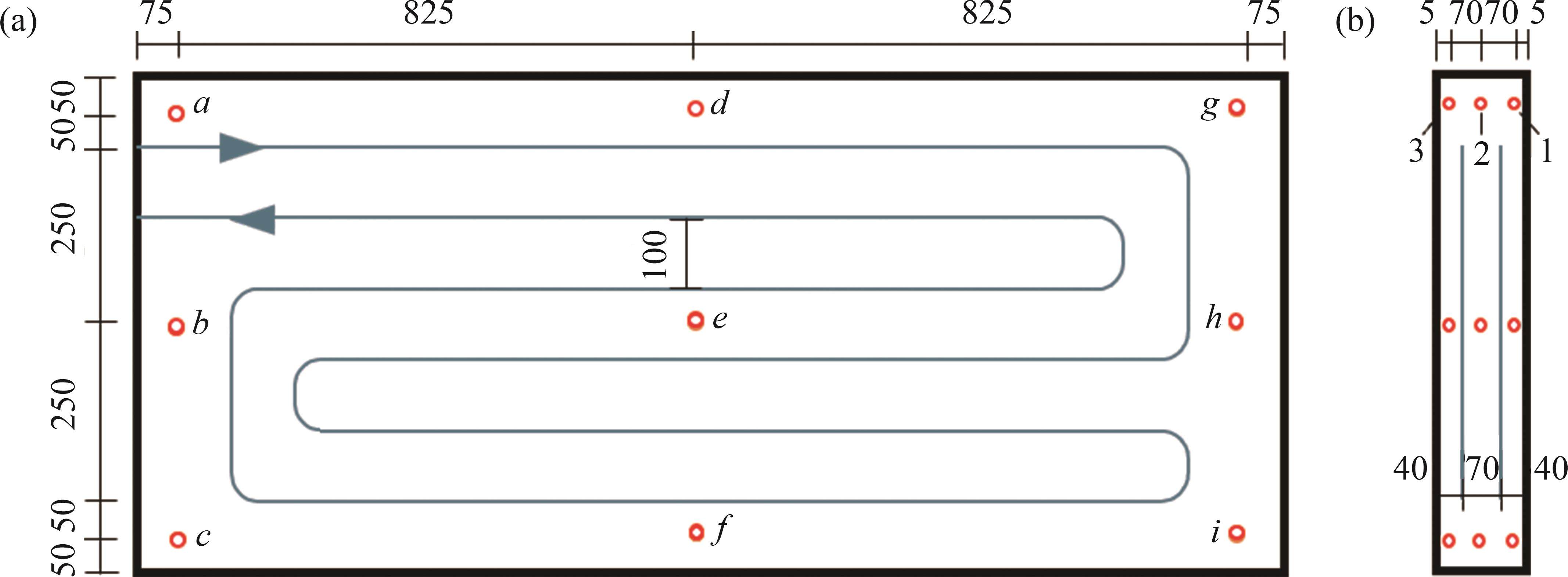
为验证数值模型的准确性,在第8号浇筑段的侧墙混凝土内部布置温度测点,负三层侧墙的温度测点布置如图3所示。编号依次为a~i。在侧墙厚度方向等间距布置3个温度探头,自由面至围岩面的编号依次为1、2、3。这里选取负三层侧墙中心测点e的温度数据进行分析,通过对比分析该点的现场实测结果与数值计算结果,验证计算模型的可靠性。侧墙浇筑前10 d测点e的温度变化模拟结果与实测结果见图4。
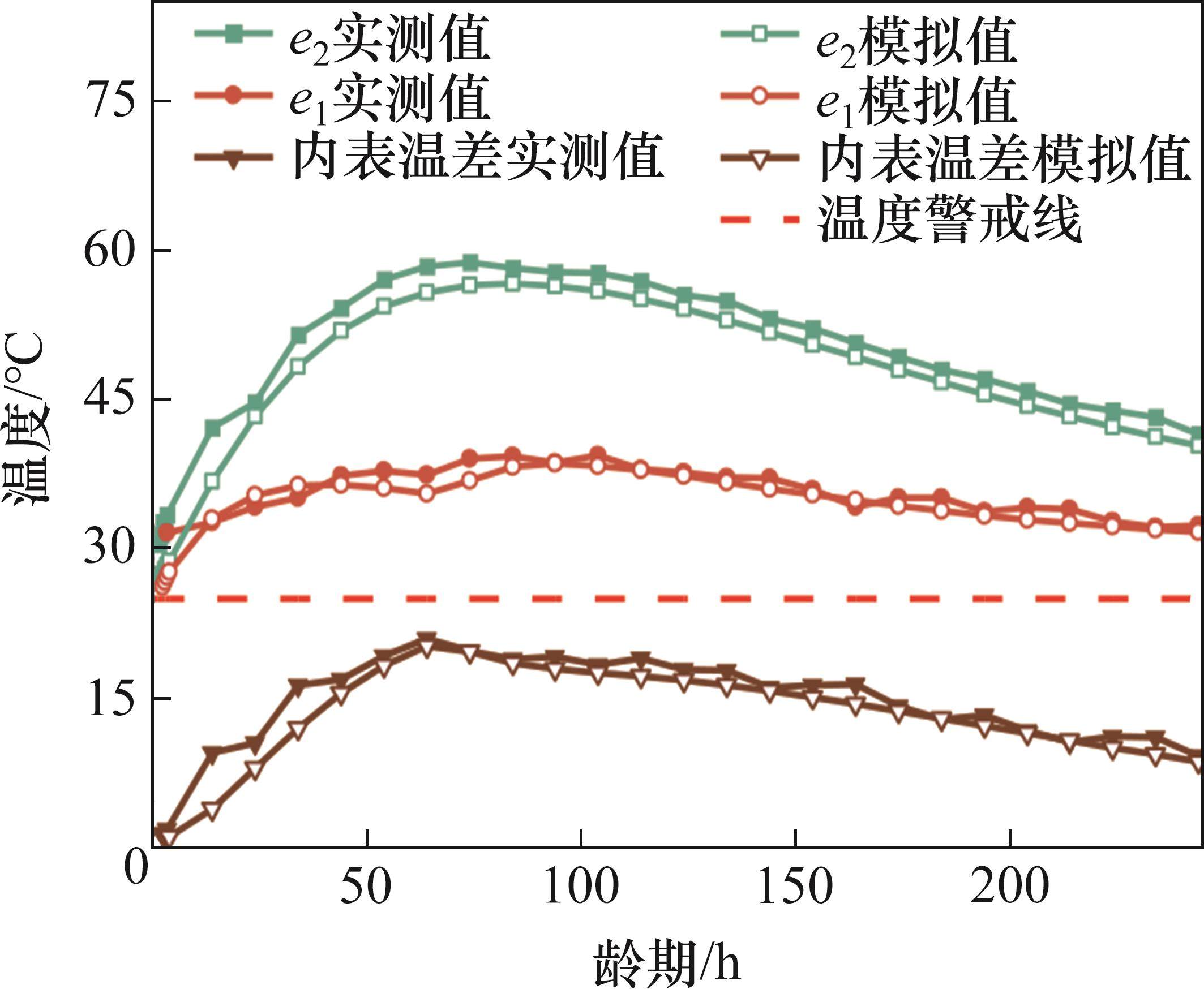
由图4可知:数值模拟得到的测点e的温度时程曲线与现场实测数据变化趋势基本一致,但在浇筑早期(前3 d)混凝土的温度差异较大。这是由于在施工方案中,侧墙混凝土计划采用分层浇筑,在下层混凝土初凝之前浇筑下一层,而现场施工人员过早地浇筑,导致水泥水化热在内部集聚,因此,中心温度的实测结果略大于数值模拟结果,但曲线的温度峰值与变化趋势基本一致,中心温度峰值相差2.3 ℃,相对误差为3.9%。综上可见,本文建立的大体积混凝土车站数值模型的计算精度较高[6],可用于后续建立响应面模型。
2 温度裂缝控制的响应面模型
2.1 响应面法原理
响应面法通过构建简单的近似函数,以代替无法显示表达的复杂状态方程,设置合理的参数与多次迭代,一般满足实际工程精度,具有高效、易收敛和降噪能力强的特点,常用于解决工程中的优化问题。在应用响应面法时,首先,确定近似函数的表达形式;然后,通过统计学原理设计试验,即在样本空间内选取足够多的样本点,最后使用最小二乘法对试验数据进行拟合,从而确定响应值与变量之间的近似函数,得到响应面模型。
在工程实践中,响应面函数通常采用二次多项式形式,其表达式为
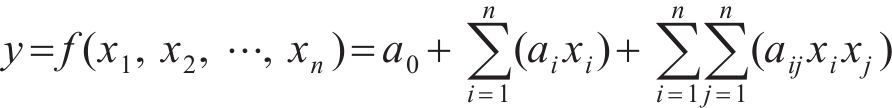
式中:xi为设计变量;a0、ai和aij分别为常数项、一次项和二次项待定系数,这些系数需通过试验样本数据确定;n为设计变量个数。
为了确定待定系数,需要进行m次试验,其中m≥(n+1)(n+2)/2,n为设计变量的个数。每次试验的变量取值不同,得到各样本点对应的响应值y(i)(i=0,1,…,m-1),函数中的待定系数向量A可由下式计算:
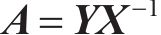
其中:Y为响应面函数预测向量;X为优化参数矩阵;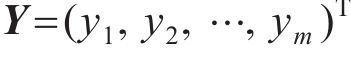
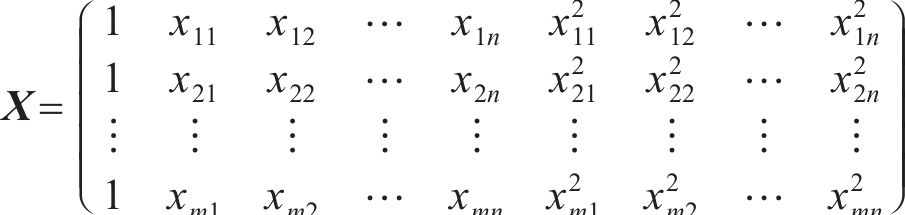
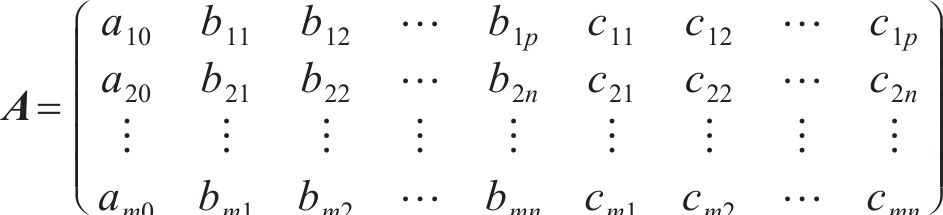
2.2 响应面模型建立与可靠性分析
2.2.1 设计参数优化和优化目标参数选取
车站结构大体积混凝土在施工期释放大量的水化热,是引起温度裂缝产生的主要原因。影响水化热的因素有很多,参考文献[16-20],本文选取施工养护过程中的混凝土入模温度x1、养护温度x2和冷却管进水温度x3这3个关键因素作为优化设计参数,参数的初始值分别为:x1,0=18 ℃,x2,0=30 ℃,x3,0=25 ℃。充分考虑大体积混凝土施工养护过程的规范设计要求和实际情况,优化参数x1、x2和x3的上下限取值分别为[13,23]、[25,35]和[15,35] ℃。在保证大体积混凝土结构温度场与应力场满足要求的同时,还应考虑开裂风险较高的区域,因此,选取混凝土内表温差峰值y1、应力安全系数y2及结构破坏占比y3作为车站大体积混凝土温度裂缝控制的优化目标参数。
应力安全系数y2的定义为混凝土施工期抗拉强度与表面最大温度应力的比值,若y2<1,则结构发生开裂,若y2≥1,则结构处于安全状态。y2的计算过程如下:确定混凝土表面最大温度应力出现的龄期,根据施工期抗拉强度计算式(4),计算该龄期下的抗拉强度,对比抗拉强度与最大应力得到应力安全系数。结构破坏占比y3的定义为产生开裂的单元数量占模型总单元数量的百分比,取值范围为[0,1],当y3<0时,令y3=0,当y3>1时,令y3=1。
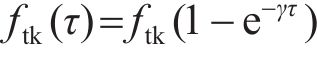
式中: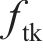
2.2.2 响应面函数建立
上述温度裂缝控制优化目标参数均有3个设计参数,其响应面函数的形式为
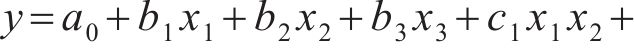
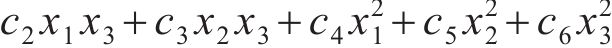
为确定待定参数,并确保函数的精确性,响应面法通常采用的试验设计方法有CCD(central composite design)和BBD(box-Behnken design)。在设计参数相同的情况下,BBD具有旋转性近似、试验工况少和成本低等优点,故在温度裂缝措施优化中采用BBD设计方法,试验设计与模拟结果见表2。
| 试验组编号 | x1/℃ | x2/℃ | x3/℃ | y1/℃ | y2 | y3/% |
|---|---|---|---|---|---|---|
| 1 | 18 | 30 | 25 | 20.22 | 1.00 | 0.12 |
| 2 | 18 | 30 | 25 | 20.90 | 0.99 | 0.16 |
| 3 | 23 | 30 | 35 | 23.71 | 0.89 | 1.21 |
| 4 | 18 | 25 | 35 | 24.21 | 0.85 | 1.64 |
| 5 | 18 | 35 | 35 | 19.30 | 0.98 | 0.25 |
| 6 | 13 | 30 | 35 | 19.90 | 0.98 | 0.26 |
| 7 | 18 | 30 | 25 | 20.90 | 1.00 | 0.08 |
| 8 | 23 | 35 | 25 | 19.91 | 1.05 | 0 |
| 9 | 18 | 35 | 15 | 17.77 | 1.20 | 0 |
| 10 | 13 | 30 | 15 | 17.01 | 1.13 | 0 |
| 11 | 23 | 25 | 25 | 25.83 | 0.91 | 1.04 |
| 12 | 13 | 25 | 25 | 21.50 | 0.99 | 0.17 |
| 13 | 18 | 25 | 15 | 22.51 | 1.01 | 0 |
| 14 | 18 | 30 | 25 | 20.90 | 1.00 | 0.08 |
| 15 | 23 | 30 | 15 | 22.20 | 1.06 | 0 |
| 16 | 13 | 35 | 25 | 15.88 | 1.12 | 0 |
| 17 | 18 | 30 | 25 | 20.90 | 0.99 | 0.21 |
通过对表2中的计算结果进行统计分析与多元回归拟合,得到车站大体积混凝土内表温差峰值y1、应力安全系数y2及结构破坏占比y3这3个响应面函数待定系数的取值,见表3。得到的响应面函数可选择3个因素的任一因素,并获得对应条件下的优化目标结果,以便于对不同水平条件下单一因素或多因素交互作用下的影响规律进行分析。
| 响应面函数 | a0 | b1 | b2 | b3 | c1 | c2 | c3 | c4 | c5 | c6 |
|---|---|---|---|---|---|---|---|---|---|---|
| y1 | 20.763 | 2.170 | -2.649 | 0.955 | -0.072 | -0.345 | -0.042 | -0.111 | 0.128 | 0.053 |
| y2 | 0.995 | -0.040 | 0.072 | -0.087 | 0.004 | -0.005 | -0.013 | 0.014 | 0.007 | 0.009 |
| y3 | 0.130 | 0.228 | -0.325 | 0.420 | -0.218 | 0.238 | -0.348 | 0.034 | 0.139 | 0.204 |
对优化目标的响应面模型进行方差分析,得到模型的F、P、决定系数R2与变异系数CV等,见表4。同时,分别将车站大体积混凝土内表温差峰值、应力安全系数及结构破坏占比的数值试验结果(即,模拟值)作为横坐标、响应面模型的预测值作为纵坐标绘制散点图,结果如图5所示。
| 方差来源 | 平方和 | 方差 | F | P | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| y1 | y2 | y3 | y1 | y2 | y3 | y1 | y2 | y3 | y1 | y2 | y3 | |
| 失拟项 | 0.673 | 6×10-4 | 0.027 | 0.224 | 2×10-4 | 0.009 | 2.456 | 5.470 | 2.890 | 0.203 | 0.067 | 0.166 |
| 回归模型 | 101.724 | 0.118 | 3.850 | 11.303 | 0.118 | 3.850 | 76.202 | 131.230 | 76.180 | <10-4 | <10-4 | <10-4 |
| x1 | 37.665 | 0.013 | 0.414 | 37.665 | 0.013 | 0.414 | 253.935 | 126.190 | 73.750 | <10-4 | <10-4 | <10-4 |
| x2 | 56.131 | 0.042 | 0.845 | 56.131 | 0.042 | 0.845 | 378.436 | 420.210 | 150.510 | <10-4 | <10-4 | <10-4 |
| x3 | 7.295 | 0.061 | 1.410 | 7.295 | 0.061 | 1.410 | 49.183 | 611.160 | 251.360 | 2×10-4 | <10-4 | <10-4 |
| x1x2 | 0.021 | 10-4 | 0.189 | 0.021 | 10-4 | 0.189 | 0.139 | 0.683 | 33.700 | 0.720 | 0.436 | 0.001 |
| x1x3 | 0.477 | 10-4 | 0.226 | 0.477 | 10-4 | 0.226 | 3.217 | 1.030 | 40.190 | 0.116 | 0.345 | 4×10-4 |
| x2x3 | 0.007 | 7×10-4 | 0.483 | 0.007 | 7×10-4 | 0.483 | 0.048 | 6.880 | 86.030 | 0.833 | 0.034 | <10-4 |
| x12 | 0.052 | 8×10-4 | 0.005 | 0.052 | 8×10-4 | 0.005 | 0.352 | 7.630 | 0.854 | 0.571 | 0.028 | 0.386 |
| x22 | 0.069 | 2×10-4 | 0.081 | 0.069 | 2×10-4 | 0.081 | 0.467 | 2.140 | 14.440 | 0.516 | 0.187 | 0.007 |
| x32 | 0.012 | 4×10-4 | 0.175 | 0.012 | 4×10-4 | 0.175 | 0.080 | 3.690 | 31.130 | 0.785 | 0.096 | 0.001 |
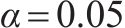
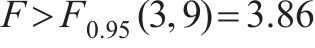
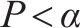
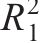
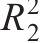
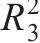
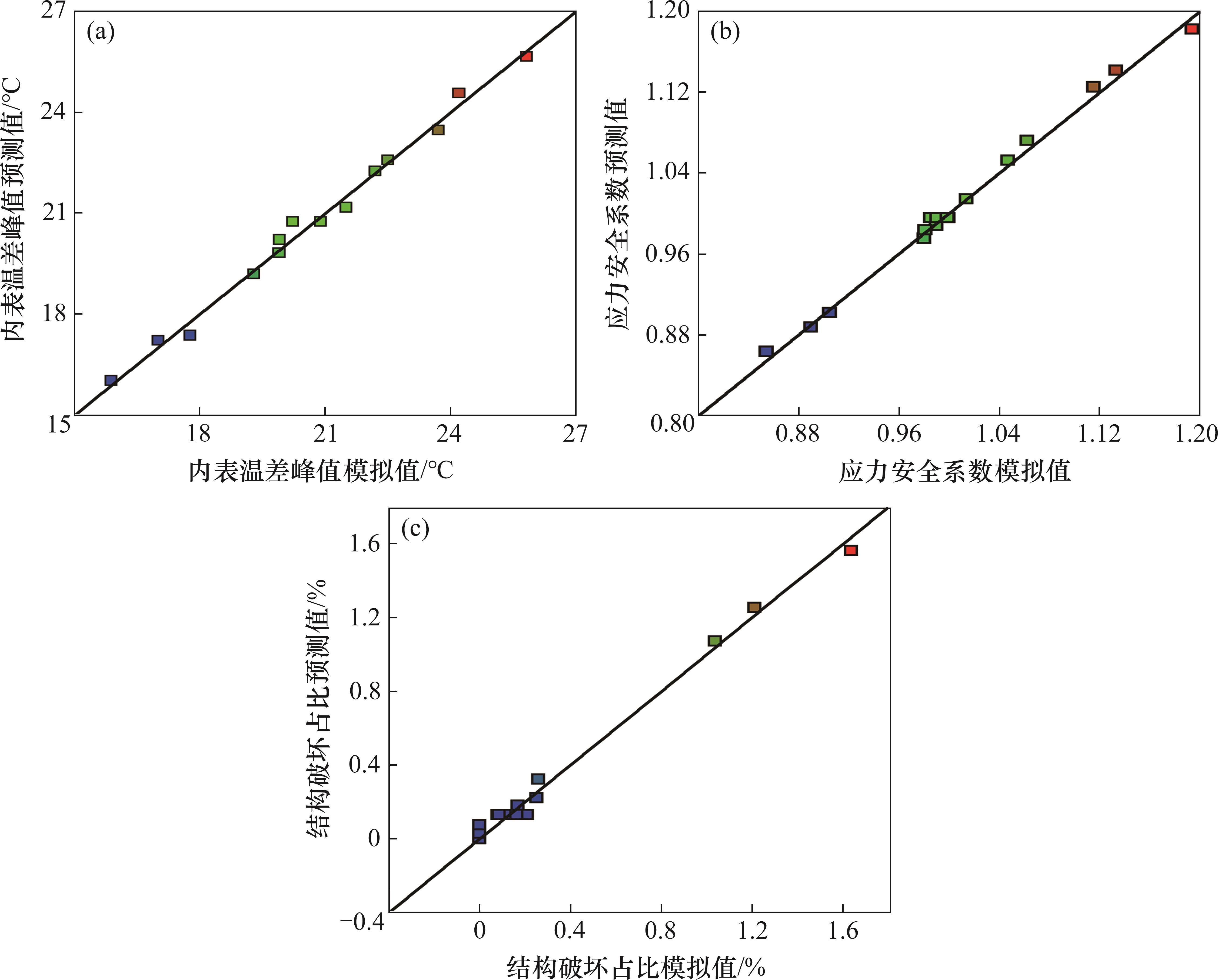
由表4可见:3个优化目标参数的响应面回归模型的F均大于3.86,且P均小于10-4,模型失拟项的P均大于0.05,失拟项不显著,3个模型决定系数R2分别为0.990、0.994和0.990,均接近1,说明各响应面模型的回归效果显著。由图5可知:混凝土的内表温差峰值、应力安全系数与破坏占比的响应面函数预测值与模拟值散点均分布在y=x直线附近,表明回归模型的拟合度较高,能够很好地反映待优化参数与优化目标参数之间的关系,可用于后续的优化计算。
从表4可见:3个优化目标参数不仅受入模温度、养护温度与进水温度中单一因素的影响,而且受双因素的交互作用影响。对于混凝土内表温差峰值,入模温度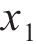
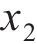
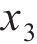
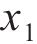
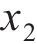
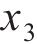
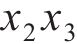
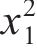
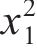
3 影响因素分析
3.1 单因素分析
响应面法的优点在于可在各因素的变化范围内选取任一水平对响应值的影响结果进行准确预测。为此,对每个因素在其变化范围内选取等间距的5个值,分析单一水平入模温度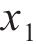
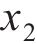
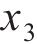
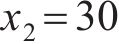
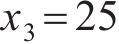
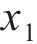
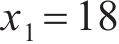
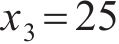
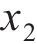
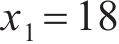
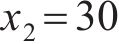
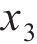
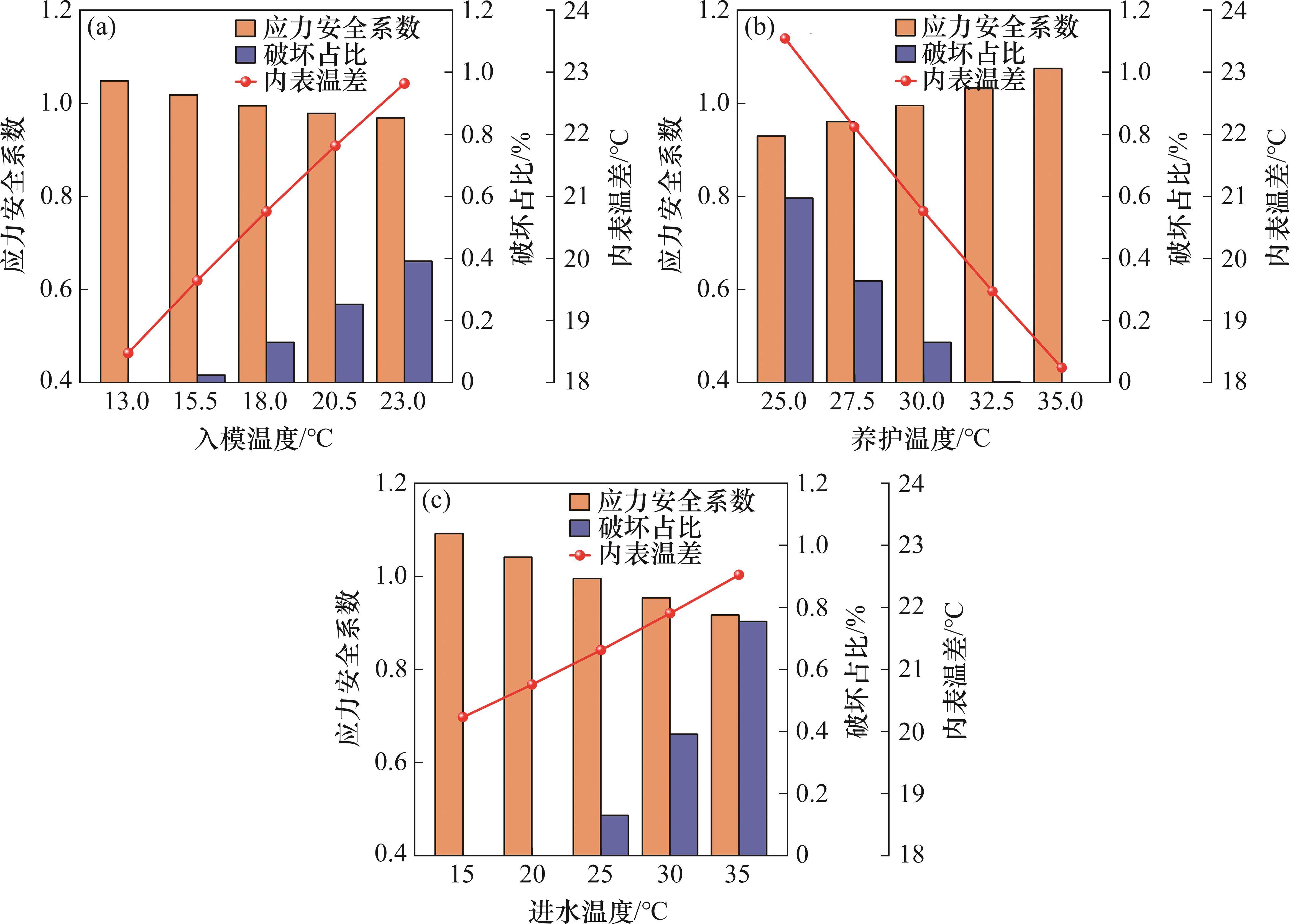
由图6(a)可知:随着入模温度提高,混凝土内表温差峰值与结构破坏占比基本上呈线性增大,应力安全系数不断降低;当混凝土入模温度升高10 ℃时,内表温差峰值增大4.34 ℃,结构破坏占比增大0.39%,应力安全系数减小0.08。这说明入模温度对混凝土内表温差与温度应力的影响较大,降低入模温度可有效降低混凝土开裂风险,如在混凝土拌合过程中加冰(冰水)降温。
由图6(b)可知:当养护温度从25 ℃升高至35 ℃时,混凝土内表温差峰值降低5.30 ℃,结构破坏占比减小0.59%,应力安全系数增大0.14,说明增大养护温度可有效减少混凝土产生的温度裂缝;当养护温度不低于32.5℃时,混凝土结构不发生破坏,在施工过程中,可对混凝土表面进行覆盖保温处理。
由图6(c)可知:当冷却管进水温度升高20 ℃时,内表温差峰值增大1.91 ℃,结构破坏占比增大0.75%,应力安全系数减小0.17,相较于前2种温控措施,进水温度对内表温差的影响较小。当进水温度控制在20 ℃以下时,应力安全系数大于1,结构不发生破坏。
3.2 因素交互作用分析
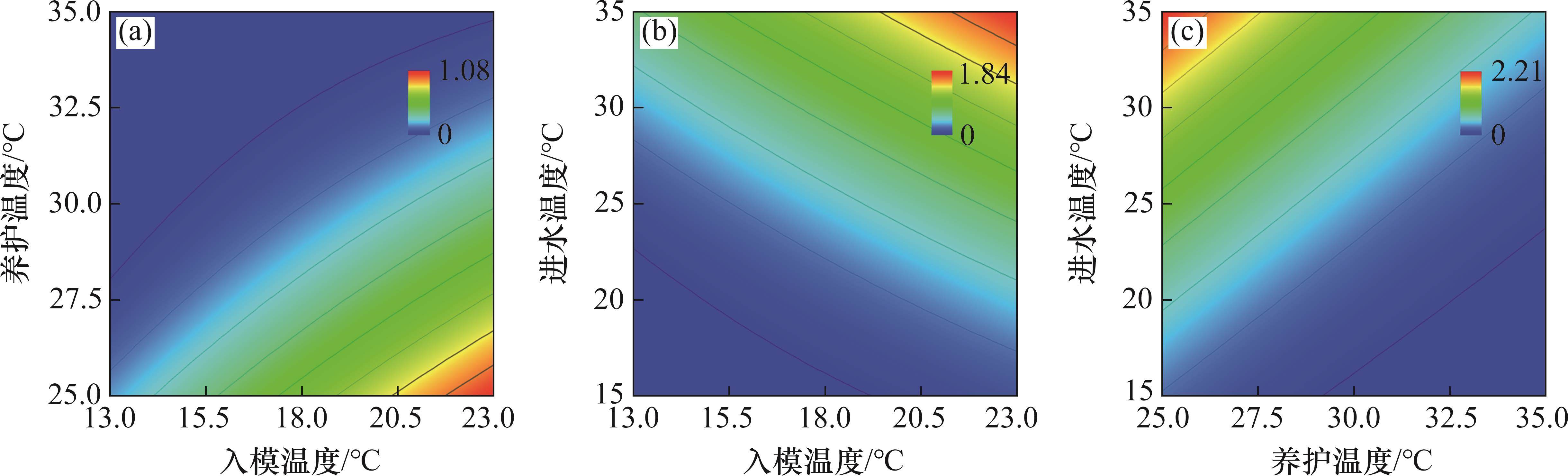
入模温度x1、养护温度x2与进水温度x3之间的两两交互作用对内表温差峰值、应力安全系数与结构破坏占比的影响分别如图7、图8和图9所示。
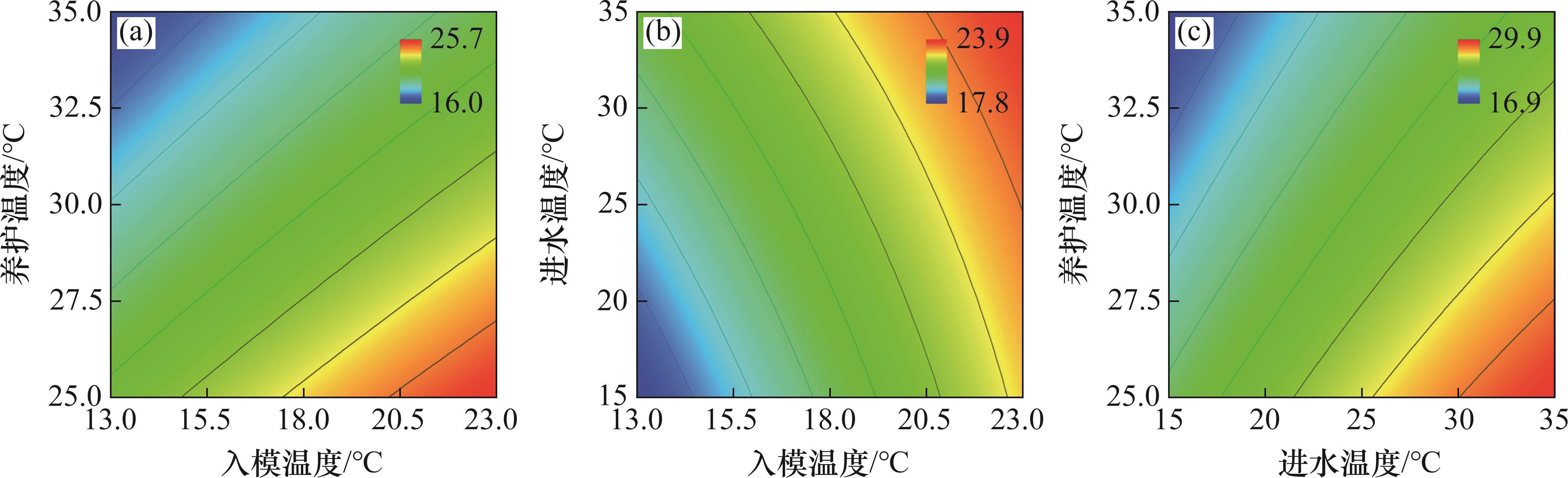
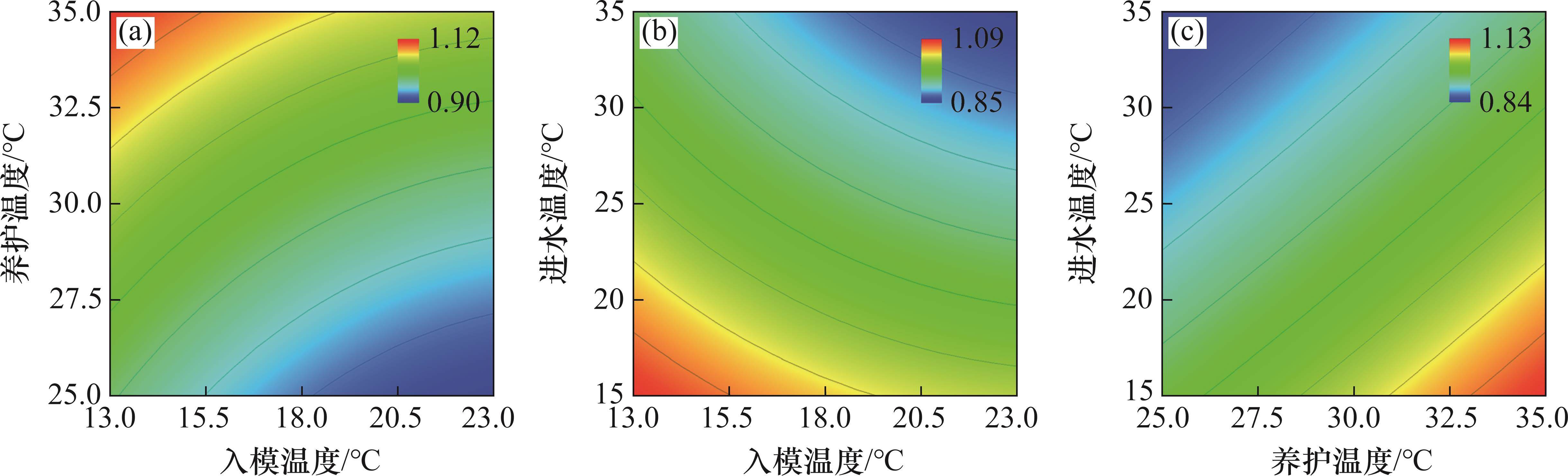
根据方差分析结果可知:单一因素对内表温差峰值影响的显著性由大至小分别为x2、x1与x3,交互作用的影响由大至小分别为x1x3、x1x2和x2x3。因素交互作用对内表温差峰值的作用效果如图7(a)~(c)所示。从图7(a)~(c)可见:在x1x2交互作用下,当养护温度x2为25~35 ℃时,内表温差峰值与x1呈正相关关系;在x1x3交互作用下,内表温差峰值随x1x2增大而增大;当入模温度x1较低时,进水温度x3对内表温差峰值的影响作用较大,当x1=23 ℃,x2=35 ℃时,内表温差峰值达到最大值23.9 ℃;在x2x3交互作用下,内表温差峰值随x2增大而减小,随x3增大而增大,与x1x2的作用效果类似。
图8(a)~(c)所示为安全应力系数随各因素的变化规律等高线图。从图8(a)可见:安全应力系数随养护温度x2的增大而增大;在入模温度x1不变的情况下,随着x2增大,x1x2的交互作用促进了安全应力系数增大;当x2=35 ℃时,x1最低水平下的安全应力系数比x1最高水平时高6.67%,这是因为入模温度降低,即混凝土初始温度降低,水化热温升的最高温度减小,内表温差减小,从而减小了混凝土表面的温度应力,增大了应力安全系数。从图8(b)可见:安全应力系数与x1x3呈负相关关系,即入模温度x1越小或进水温度x3越小,应力安全系数越大。x2x3交互作用对安全应力系数的影响不显著。
对比图9(a)~(c)及图7(a)~(c)可知:结构破坏占比随各因素的变化规律与内表温差峰值随各因素的变化规律类似。由图9(a)可知:固定进水温度 x3=25 ℃,当养护温度x2=28.3 ℃,入模温度x1=13 ℃时,结构破坏占比开始小于0,即不发生破坏;当x2控制在最高水平,x1在变化范围内任意取值时,结构均不开裂。由图9(b)可知:固定x2=30 ℃,当冷却管进水温度高于25℃时,入模温度对结构破坏占比的影响程度增大;随着进水温度x3与入模温度x1逐渐增大,结构发生破坏的速率增大。由图9(c)可知:保持x1=18 ℃恒定,当x3=25 ℃时,进水温度x2对结构破坏占比的影响效果较大;相较于其他因素作用,在x2x3交互作用下,结构破坏占比的程度更加明显。
4 车站温度裂缝控制技术优化
4.1 目标优化函数
在处理多目标优化问题[21-22]时,由于各个子优化目标之间相互冲突,使得所有优化目标参数难以都得到最优解。为解决这一问题,本文基于响应面法求得的3个优化目标参数的响应面函数,在确保混凝土应力安全系数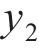
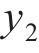
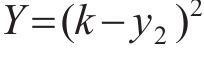
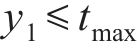
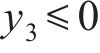
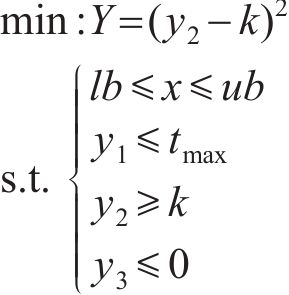
其中:x为待优化参数的变量;lb和ub分别为参数的下限和上限约束;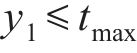
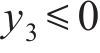
4.2 基于粒子群算法的参数优化
4.2.1 算法原理
粒子群算法的基本思想围绕“群体”与“进化”展开,将粒子假定为没有质量和体积的点,这些点以一定的速度在空间内飞行搜索,并根据个体与群体的飞行经验来调整自身的位置和速度。粒子群算法的进化方程为:
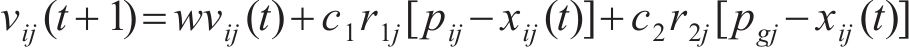
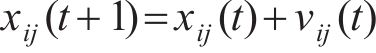
式中:i为粒子编号;j为粒子所在的空间维数;t为粒子迭代次数;vij为粒子速度;xij为粒子位置(即,待优化参数的大小);pij为粒子i在第j维的最优位置;pgj为全部粒子在第j维空间的最优位置;w为惯性权重;c1和c2分别为粒子个体与群体的学习因子,取值范围为1~2.5[23];r1j和r2j为取值在 0~1之间相互独立的随机数。
采用动态递减的惯性权重与动态的学习因子(c1逐渐递减、c2逐渐递增)的方法,能够实现增强权衡全局搜索与局部搜索的能力,并提高算法的收敛速率。
惯性权重的动态递减表达式为
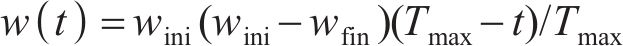
式中:wini、wfin分别为惯性权重的初始值与最终值;t为当前迭代次数;Tmax为总迭代次数。
粒子个体与群体学习因子的动态表达式分别为:
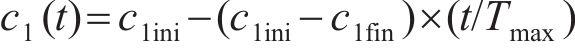
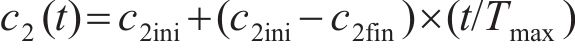
式中:c1ini、c1fin分别为个体学习因子的初始值和最终值;c2ini、c2fin分别为群体学习因子的初始值和最终值。
4.2.2 参数优化结果
根据粒子群优化算法的基本原理,利用MATLAB软件编写相关优化程序进行寻优分析,设置算法中的相关参数,如取粒子数目为100,粒子个体学习因子的初始值c1ini和最终值c1fin分别为0.8和0.2,粒子群体学习因子的初始值c2ini和最终值c2fin分别为0.2和0.9,惯性权重的初始值wini与最终值wfin分别为0.8和0.4,总迭代次数Tmax为500,入模温度x1,养护温度x2和冷却管进水温度x3的取值范围分别为[13,23]、[25,35]和[15,35] ℃。优化前后大体积混凝土的各响应面函数值如表5所示。
| 优化顺序 | x1/℃ | x2/℃ | x3/℃ | y1/℃ | y2 | y3/% |
|---|---|---|---|---|---|---|
| 差值 | -4.8 | 1.2 | -9.2 | -4.05 | 0.16 | -0.21 |
| 优化后 | 13.2 | 31.2 | 15.8 | 16.85 | 1.15 | 0.00 |
| 优化前 | 18.0 | 30.0 | 25.0 | 20.90 | 0.99 | 0.21 |
从表5可见:当入模温度为13.2 ℃(降低4.8 ℃),养护温度为31.2 ℃(升高1.2 ℃),冷却管进水温度为15.8 ℃(降低9.2 ℃)时,可保证大体积混凝土不发生开裂,优化结果与实际结果相符。减小混凝土的入模温度可有效降低温升过程的初始温度,从而降低混凝土水化反应所引起的最高温度。相较于混凝土内部温度,表面温度更容易受养护温度变化的影响,提高养护温度会显著升高表面温度,从而减小混凝土内表温差。此外,通过降低冷却管进水温度,可加强冷却水与混凝土内部高温区的热交换,使冷却水更有效地带走热量,降低内部温度,削减温度峰值。
由表5可知:优化后车站地铁大体积混凝土的内表温差峰值由20.90 ℃降低为16.85 ℃,减小了19.4%;应力安全系数由0.99增大为1.15,增大了16.2%,满足规范要求;结构开裂部分的破坏占比由0.21%降低为0,开裂风险降为零。分析结果表明,采用升高养护温度、降低入模温度和进水温度等措施,可有效减小内表温差与表面温度应力,降低混凝土开裂风险。
4.2.3 参数优化验证
将优化后的设计参数代入数值模型重新计算,将数值计算结果与算法优化结果对比分析,内表温差峰值、应力安全系数与结构破坏占比对比结果见表6。
| 方法 | y1/℃ | y2 | y3/% |
|---|---|---|---|
| 相对误差/% | 2.00 | 0.521 | 0 |
| 数值模拟 | 16.52 | 1.146 | 0 |
| 算法计算 | 16.85 | 1.152 | 0 |
从表6可以看出,优化后的参数模拟结果与算法计算结果基本一致,相对误差在3%以内[24],从而验证了算法优化的正确性与可行性。
4.3 不同养护温度下的控制措施
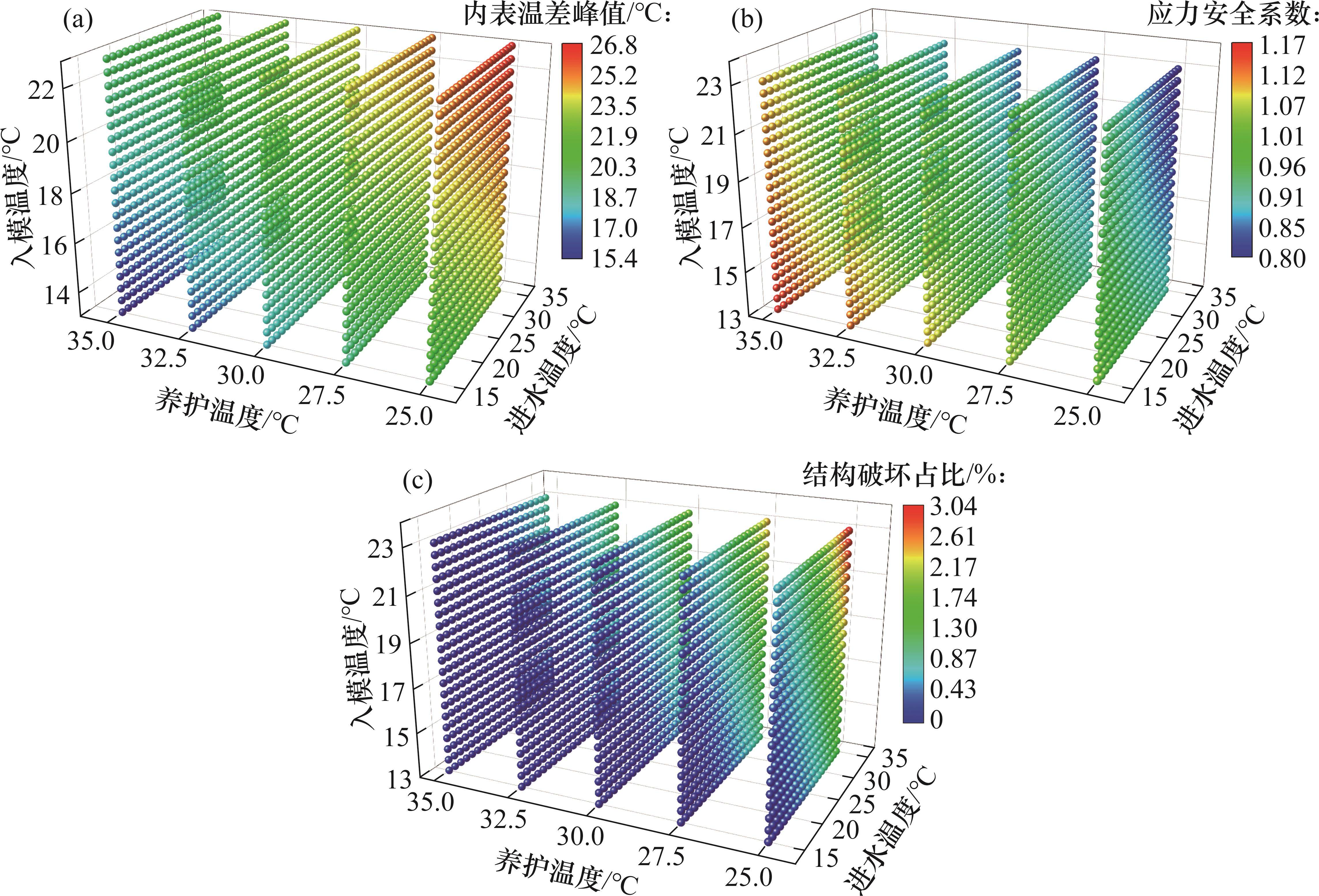
在施工现场,大体积混凝土表面的养护温度通常随所在地区的气候温度变化而变化且不易于控制,因此,针对不同气候条件下的养护温度,可控制混凝土的入模温度与冷却管的进水温度,降低混凝土开裂风险,结果如图10和表7所示。
| 养护温度/℃ | 入模温度/℃ | 进水温度/℃ | 内表温差/℃ | 应力安全系数 | 破坏占比/% |
|---|---|---|---|---|---|
| 35.00 | 21.4 | 16.7 | 19.12 | 1.15 | 0 |
| 32.50 | 14.6 | 17.2 | 17.08 | 1.14 | 0 |
| 30.00 | 13.3 | 15.5 | 17.46 | 1.13 | 0 |
| 27.50 | 13.0 | 15.0 | 18.53 | 1.11 | 0 |
| 25.00 | 12.6 | 14.7 | 19.61 | 1.08 | 0 |
由图10可知:当养护温度高于30 ℃时,降低入模温度与进水温度可提高应力安全系数,降低结构破坏占比,确保混凝土不发生开裂;但当养护温度处于较低值时,调节入模温度与进水温度虽然能增大应力安全系数,但难以将应力安全系数降低至规范值。从表7可知:随着养护温度降低,应适当降低混凝土的入模温度或冷却管的进水温度;当养护温度降低10.0 ℃时,入模温度降低8.8 ℃,进水温度降低2.0 ℃,尽管采取了降低入模温度与进水温度的措施,混凝土的应力安全系数仍然逐渐减小。综上所述,在外界温度剧烈下降的情况下,一方面,可降低入模温度与进水温度,增大应力安全系数;另一方面,需采取其他温控措施,如采用覆盖保温材料、增加保温层厚度、延长养护时间、控制混凝土振捣质量等[25]。
5 结论
1) 根据响应面设计的试验结果,确定内表温差峰值、应力安全系数和结构破坏占比与入模温度、养护温度和进水温度之间的回归关系,响应面模型的决定系数R2分别为0.990、0.994和0.990。借助响应面模型预测响应值随设计参数的变化,其预测值与模拟值的散点均分布在y=x直线附近,模型预测精度较高。
2) 单一因素一次项对内表温差峰值、应力安全系数和结构破坏占比的影响显著性极强,入模温度与进水温度的交互作用对内表温差峰值影响较大,养护温度与进水温度的交互作用对应力安全系数的影响显著,结构破坏占比受3个因素之间两两交互作用的影响均显著。
3) 采用构建的优化设计方法,确定了车站大体积混凝土温度裂缝的具体控制参数:入模温度为13.2 ℃,养护温度为31.2 ℃,冷却管进水温度为15.8 ℃。采用该组参数,车站混凝土内表温差峰值降低19.4%,应力安全系数增大16.2%,结构各部位均未出现开裂现象,取得较好的温控效果。
4) 在大体积混凝土施工养护过程中,养护温度对混凝土开裂的影响较大,且不易控制,当养护温度随外界温度剧烈下降时,应降低入模温度与进水温度,并采取其他温控措施预防混凝土开裂。
康瑞强, 施成华, 孙晓贺, 等. 基于响应面-粒子群算法的大体积混凝土温度裂缝控制方法[J]. 中南大学学报(自然科学版), 2024, 55(12): 4505-4518.
KANG Ruiqiang, SHI Chenghua, SUN Xiaohe, et al. Method for controlling temperature cracks in mass concrete based on response surface and particle swarm algorithm[J]. Journal of Central South University(Science and Technology), 2024, 55(12): 4505-4518.

