水轮机作为水力发电最重要的流体机械,其水力性能直接影响水电开发效益。为充分保证水力性能,有必要对水轮机周围流场进行精细化数值模拟。传统水轮机大多安装在水电站内,通过拦河筑坝或引水产生的水流势能发电[1],对水流势能进行数值模拟时需重点考虑叶轮旋转过程中复杂形体动边界。近年来,潮流能水轮机等[2]直接利用水流动能发电的水轮机日益受到关注。不同于传统水轮机,这类水轮机往往直接安装在河流或海洋中[3-4],其叶轮旋转会引起自由液面波动,自由液面波动亦会影响叶轮性能。自由液面与水轮机的相互作用过程涉及湍流与自由液面的非定常、非线性相互作用。周围流场十分复杂[5-6],故有必要针对性地研究自由液面条件下水轮机周围流场的非定常特性。因此,在水轮机数值模拟中,除了需考虑复杂形体动边界外,还应重点考虑自由液面的精确求解。
现有的自由液面求解方法包括水平集(level-set,LS)法和流体体积(volume-of-fluid,VOF)法。水平集法是OSHER等[7]提出的一种通过符号距离函数(LS函数)隐式表示自由液面的方法。该方法可以准确捕捉到界面的变形,但在经过一段时间迭代后,LS函数的梯度和等值线均无法保持稳定,以致其不再具备距离函数的性质,导致该方法难以保证守恒[8]。流体体积法由HIRT等[9]提出,主要通过VOF法确定自由液面所在位置。该方法具有守恒性强的优点,但确定的界面往往不连续,直接离散其控制方程会导致界面受破坏[10]。针对上述问题,本文将LS法和VOF法相结合,提出耦合水平集流体体积法(coupled level-set and volume-of-fluid,CLSVOF)精确求解自由液面,可以在准确捕捉界面形状的同时保证质量守恒。
对于动边界的处理问题,常用的方法有动网格法和浸入边界法(immersed boundary method,IBM)[11]。ANSYS FLUENT等商用CFD软件中一般采用动网格法,该方法需采用适应固体表面形状的贴体网格,对于复杂形体边界附近的网格划分难度较大,且当边界不断移动时,在各时间步都需要重新划分网格,大大降低了计算效率,对于水轮机旋转问题往往计算量过大。另外,动网格法在求解复杂三维、大位移动边界流动问题时,极易在网格重构过程中计算出错。浸入边界法由PESKIN[12]提出,最初用于模拟心血管中血液流动。近年来,该方法受到越来越多研究者关注,其应用逐渐扩展到鱼类运动、昆虫飞行等多个领域[13]。浸入边界法采用固定笛卡尔网格等独立于固体表面形状的网格,将固体作为移动边界。固体对流体的作用则通过在Navier-Stokes方程右端施加附加力,以使边界附近网格点满足相应的边界条件体现[14-15]。因此,浸入边界法具有无需网格重构的优势,尤其适合处理复杂形体动边界问题,且该方法可以有效地实现动网格法难以处理的包含大位移运动边界的流动问题。但浸入边界法需通过自主编程实现,在流体机械数值模拟中应用相对较少。
鉴于此,本文作者提出耦合水平集流体体积法以精确求解自由液面,并基于IBM提出一种适用于任意复杂形体动边界的界面追踪方法以求解动边界。通过自编程构建高精度CFD求解方法,以针对河流动能利用自主研发的河岸水轮机[16]为研究对象,对其与自由液面的相互作用过程进行大涡模拟,求解得到不同安装高度下流场的精细化模拟结果,以揭示自由液面对河岸水轮机尾迹特征的影响规律。
1 CFD求解方法
1.1 自由液面求解
1.1.1 水平集法
水平集法的基本思想是将水和空气的交界面定义为零水平集,即当网格点处LS函数的值为0时,就表示该点位于两相界面上。该方法的优点是能在固定笛卡尔网格上对界面曲率和法线进行准确的数值计算,且容易捕捉界面形状的变化。但该方法的缺点在于无法保证流体的质量守恒。
LS函数为一个到两相界面的标准距离函数。对空间任意网格点P,LS函数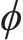

式中:d为空间点到两相界面的距离。
在计算水平集函数时,界面法向向量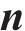
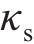
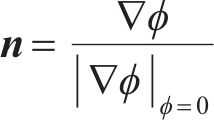
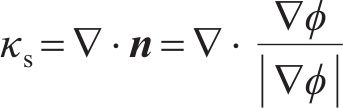
式中: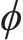
水平集函数的对流控制方程如下:
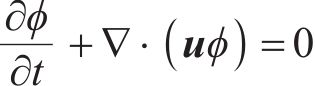
式中: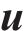
在界面上满足LS函数的控制方程,当界面移动时,界面上网格点的速度是准确的。但在距离界面较远的位置,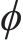
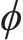
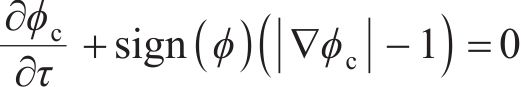
判断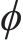
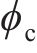
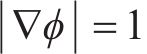

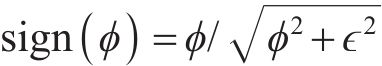
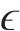
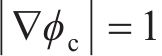
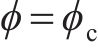
1.1.2 流体体积法
流体体积法采用固定的欧拉网格,在各时间步计算计算域网格内水的体积分数函数F。当其值为0~1时,表明网格单元中存在两相界面,即得到该时间步下的网格内的两相界面。之后再根据流场信息确定下个时间步的界面所在位置,获得各网格内的流体质量和动量的变化情况,即得到了整个流场信息。
VOF法可以精确地保持流体各相的质量守恒。但当流体移动时,该方法难以捕捉界面的变化,其模拟出的两相界面不连续,因此,需要通过重构的方式得到自由液面。可以采用分段线性界面构造(piecelinear interface construction,PLIC)的算法对F进行重构,该方法在每个网格单元中采用线性平面段(二维问题中为线性线段)来构造界面,来保证其求解精度。VOF法的优点是可以保持质量守恒,却不能直接表征两相界面的曲率。
网格单元中水的体积分数F定义为

式中: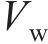
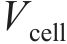
VOF函数的控制方程如下:
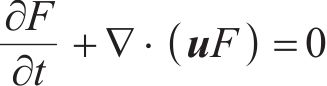
1.1.3 耦合水平集流体体积法
单独采用VOF法或LS法较难精确捕捉自由液面的变化过程,较难深入研究其对水轮机尾迹特征的影响,为更真实地反映自由液面的变化规律,本文将2种方法结合,得到CLSVOF法。CLSVOF法同时解决了LS法守恒性差以及VOF法界面精度不够高的问题,并结合了这2种方法的优点,是一种守恒性更强、界面光滑性更好的自由液面求解方法,界面示意图如图1所示。该方法的基本思想是通过LS函数来获得两相界面的法线方向即界面的方向,并通过VOF函数在保证质量守恒的同时确定出界面的位置。
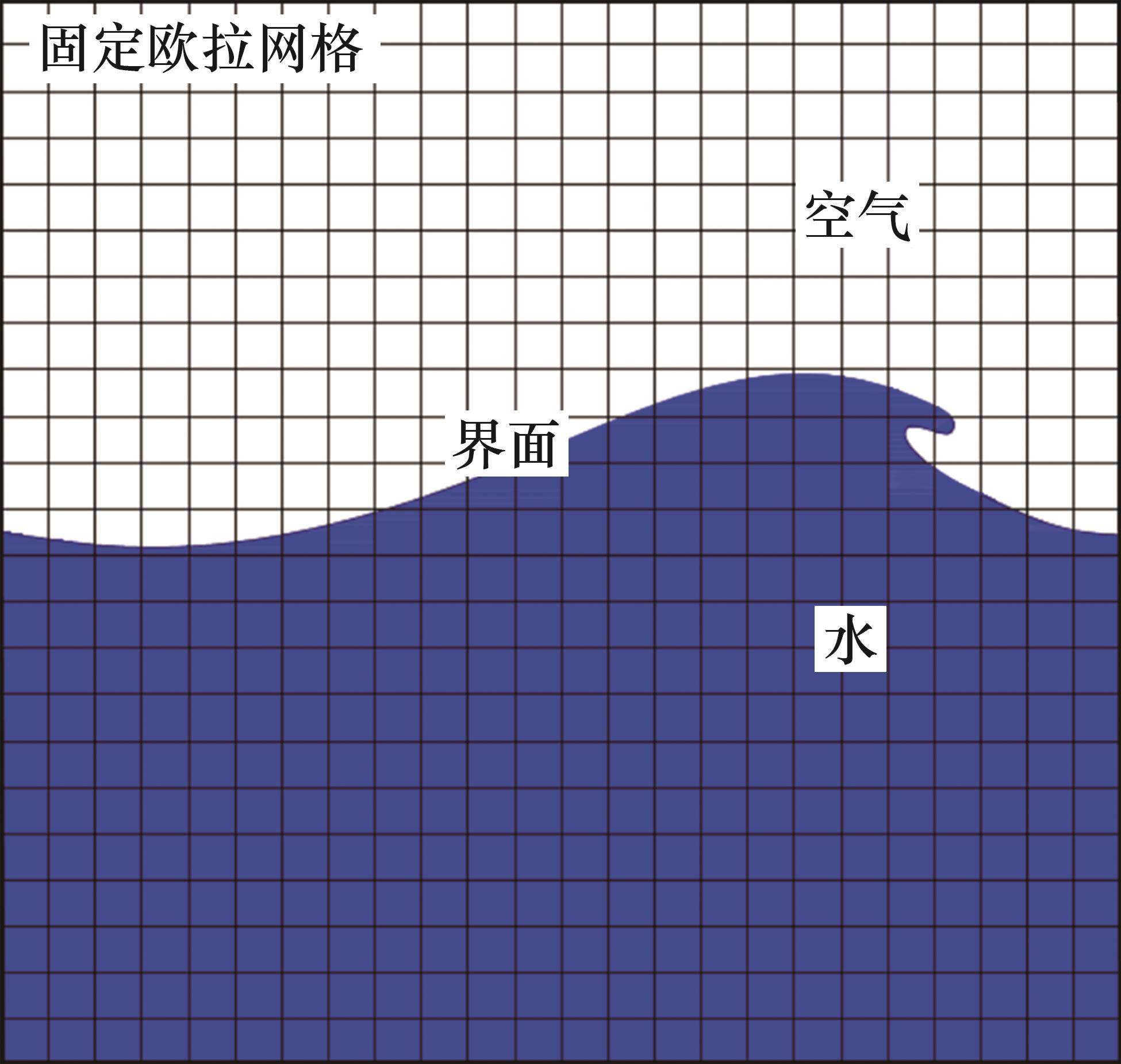
密度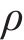
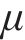
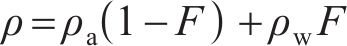
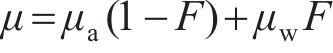
式中:ρa和ρw分别为空气和水的密度;μa和μw分别为空气和水的黏度。
图2所示为CLSVOF方法的求解流程图,求解步骤如下。
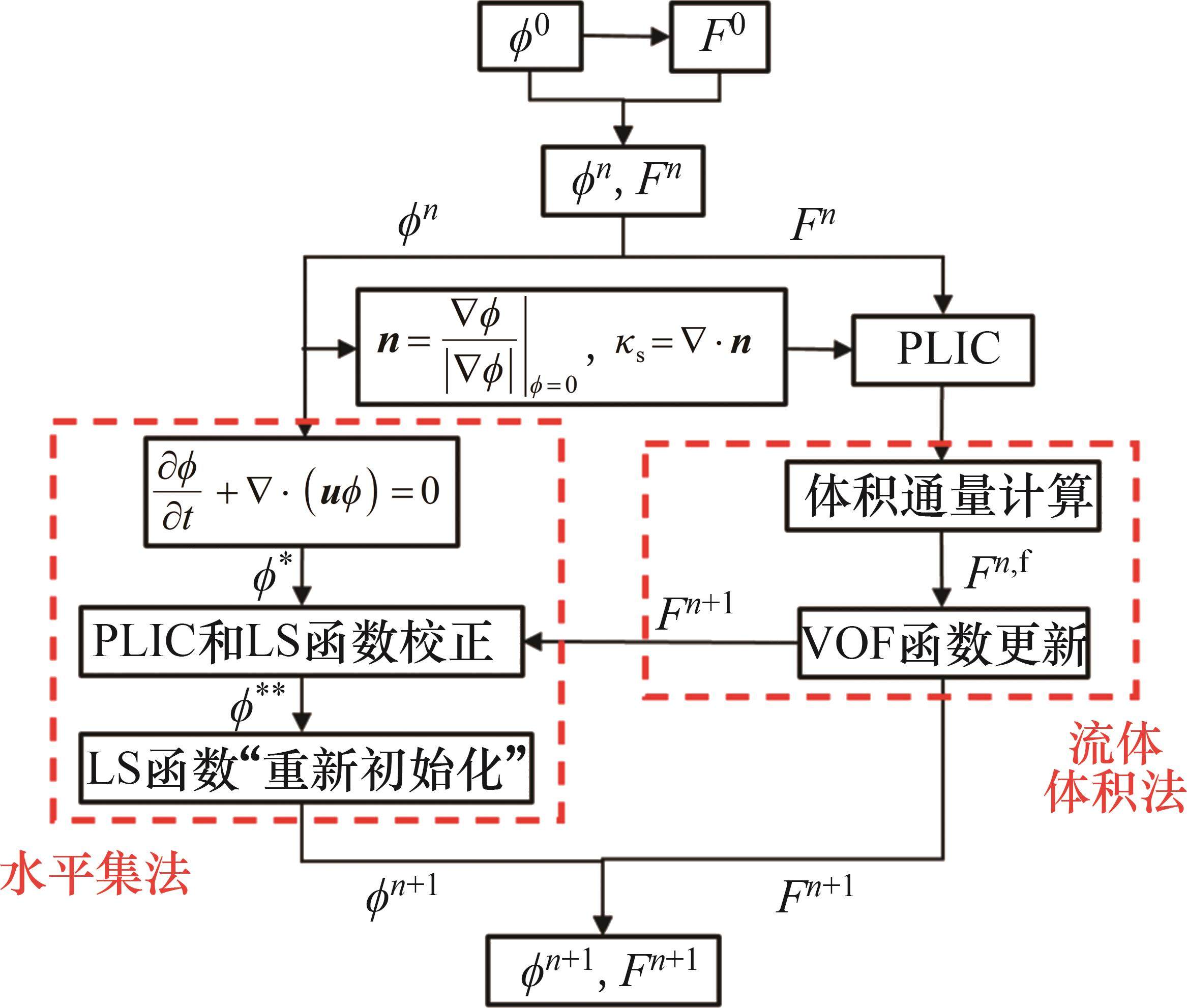
1) 据模拟的初始状态给出LS函数和VOF函数的初值。据界面法线,得到初始的LS函数。计算基于LS函数的体积分数,利用LS函数构造界面,得到基于界面位置的VOF函数初值。
2) 构造两相界面。通过界面的位置对LS函数和VOF函数进行更新。并基于LS函数来获取界面的法线方向,而后利用VOF函数确定界面位置,并保证质量守恒。
3) 求解LS函数和VOF函数的控制方程,更新LS函数值和VOF函数值。
4) 利用 PLIC算法重新构造界面,并对LS函数进行修正。更新LS函数和VOF函数后,界面发生变化,需要对界面进行重构。重构界面后,重新计算点到界面的距离,将其作为一个新的LS函数,并更新界面附近的LS函数。
综上所述,采用CLSVOF法捕捉两相界面时,通过求解LS函数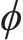
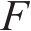
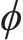
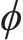
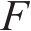
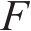
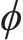
1.2 运动固体边界求解
本算法中,采用基于水平集函数的浸入边界法对运动固体边界的求解,流场计算域采用固定背景笛卡尔网格,固体则被当作移动边界。IBM通过计算网格点到浸入边界之间的距离(LS函数值),将计算域中的网格点分成流体点、固体点以及IB点,并完成流体域中各网格点的流场及压力场的求解。
本文研究对象为河岸水轮机试验装置及水轮机转轮模型,如图3所示。由于河岸侧壁及半圆柱形空腔结构模型构造简单,可以通过直接计算其LS函数表达式得到。而对于几何结构相对复杂且三维旋转的水轮机,本文提出了一种适用于任意复杂形体动边界的固体界面追踪方法,算法步骤如下:1) 将固体边界离散为非结构化三角形网格;2) 计算空间网格点到离散的三角形网格的距离,其中,距离最小值即为该网格点到固体界面的距离,即LS函数的绝对值;3) 采用射线法通过判断网格点与固体边界的位置关系来确定LS函数的符号,结合步骤2) 即可得到复杂形体的LS函数;4) 求解类似于三维旋转水轮机的运动边界,可以根据边界的运动信息将网格点进行相应的反向运动,通过插值得到每一时刻的LS函数,无须在各时间步重复进行LS函数计算,可极大减少计算时间。

数值计算的控制方程为量纲为一的不可压缩的连续性方程和Navier-Stokes动量方程:
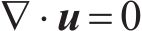
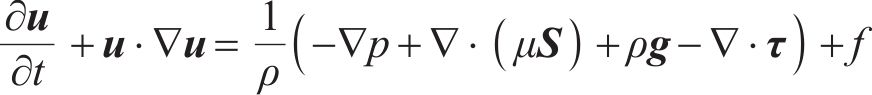
式中: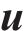
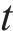
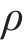
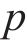
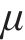
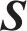
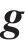
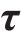
1.3 数值离散格式
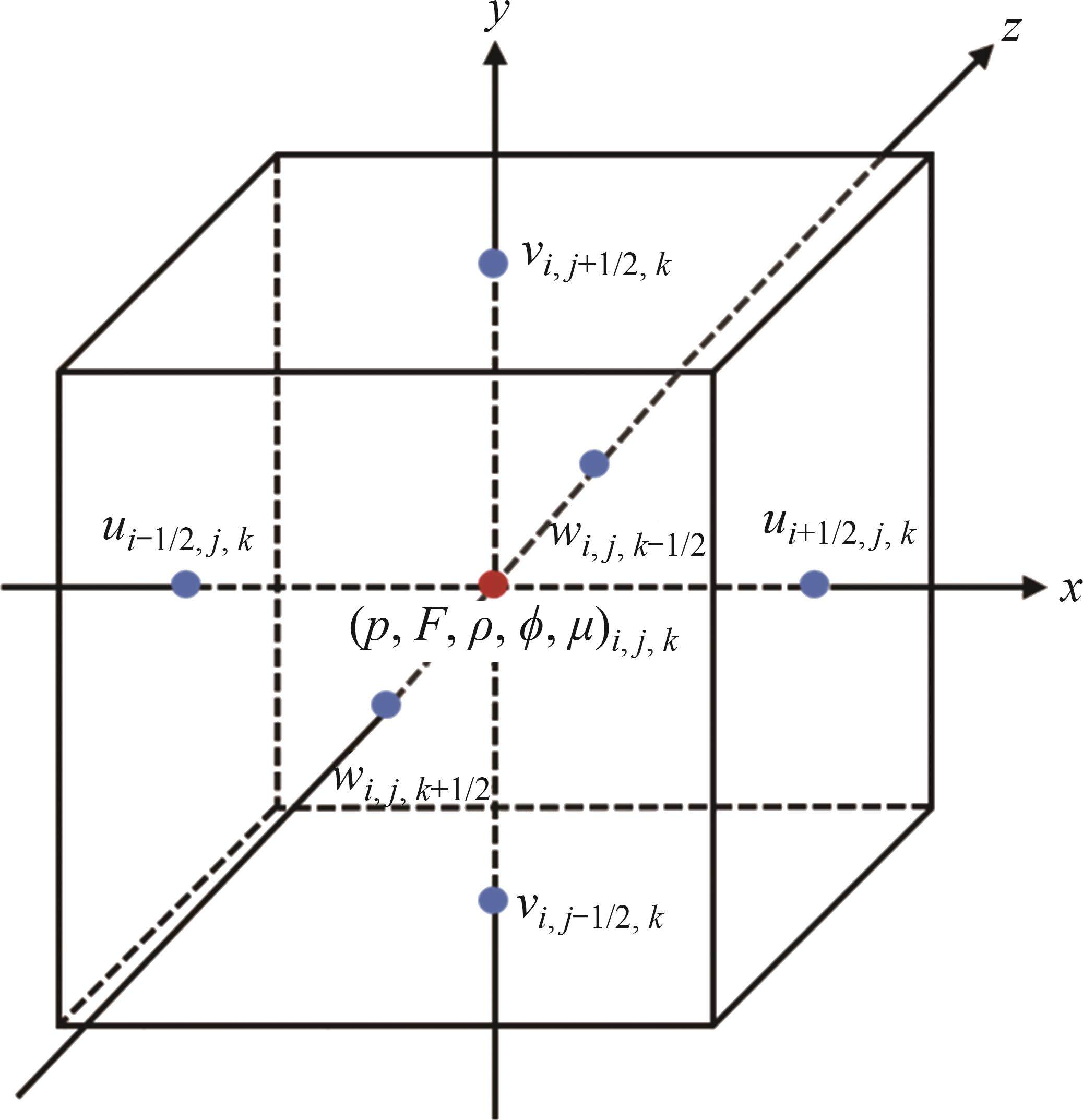
采用有限差分法并基于交错网格对控制方程进行空间离散。直角坐标下的交错笛卡尔网格示意图如图4所示,x、y和z方向上的速度分量u、v和w均位于六面体网面的中心,其余的如压强、密度、动力黏度等变量均位于六面体网格的体心。网格体心记作(i,j,k)。
时间推进采用二阶龙格库塔(second-order Runge-Kutta, RK2)法。将投影法与RK2法的每一个步骤相结合以满足无散度条件。时间步长采用基于CFL数计算的动态时间步长。利用科学计算工具包(PETSc)求解泊松方程,采用信息传递接口(MPI)库进行并行计算。
2 算例验证
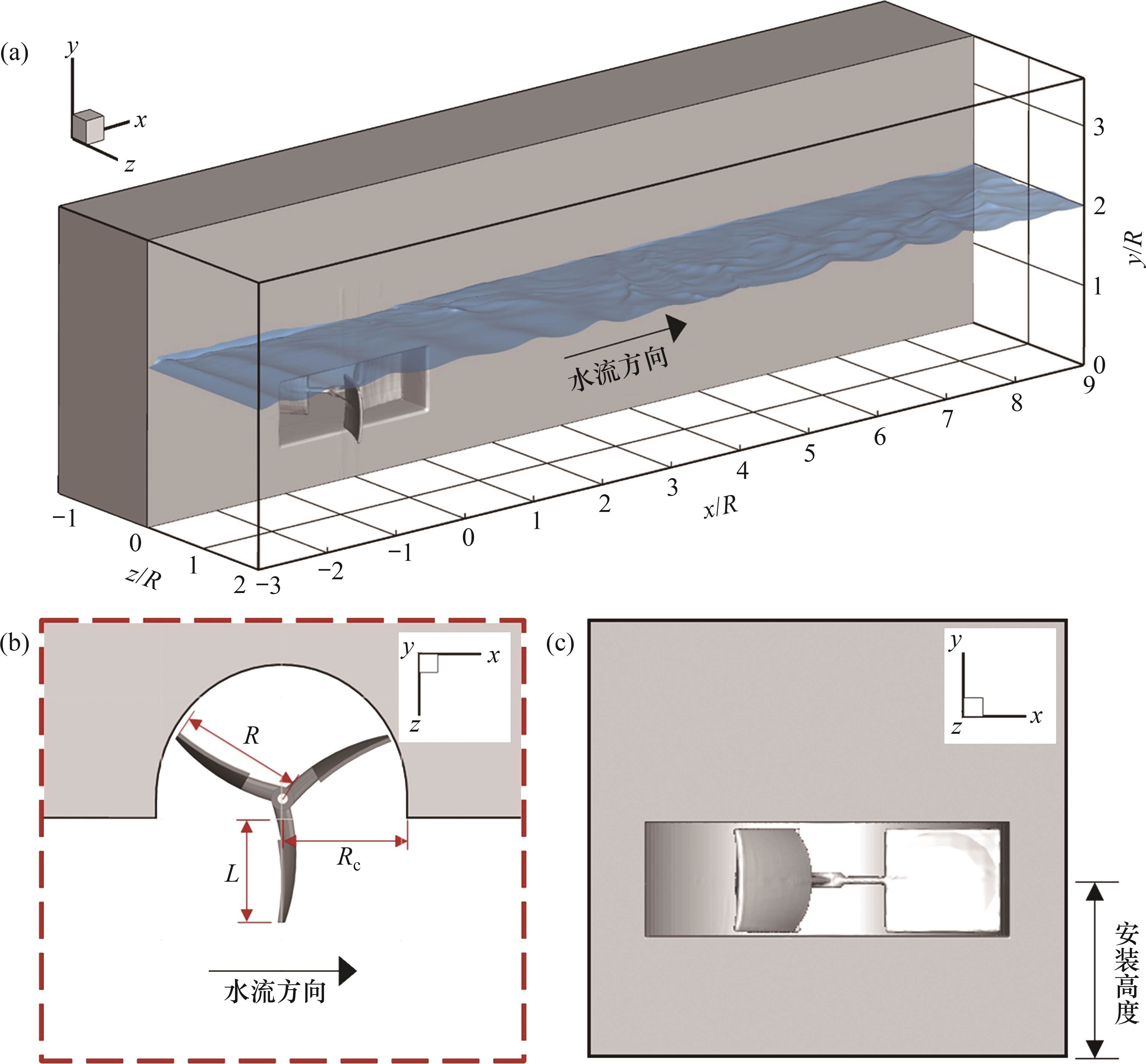
采用本文提出的数值方法对自主研发的河岸水轮机进行大涡模拟,并通过模型试验加以验证,如图3所示。该水轮机为垂直轴阻力型水轮机,安装在河岸侧壁的半圆柱形转轮室中。水轮机和转轮室的半径分别为R=0.15 m和Rc=0.155 m。采用扭矩传感器测量不同叶尖速比下水轮机的扭矩,模型试验相关细节见文献[17]。数值模拟中计算域设置如图5所示,模型尺寸参数参照模型试验 (图3)设置,整个计算域流向(x方向)长度、垂向 (y方向)深度和展向(z方向)宽度分别设置为12R、3.6R和3.6R。展向上水轮机的叶片与水流的最大接触长度L=0.11 m。由于水轮机尾迹只在槽道的一侧发展,因此,将展向的流体计算域减小到半槽道宽度(2R=0.3 m)以减少计算资源,水轮机中心的位置坐标为x=0,z=-0.27R=-0.04 m。
在来流速度U=0.44 m/s及不同叶尖速比(
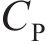
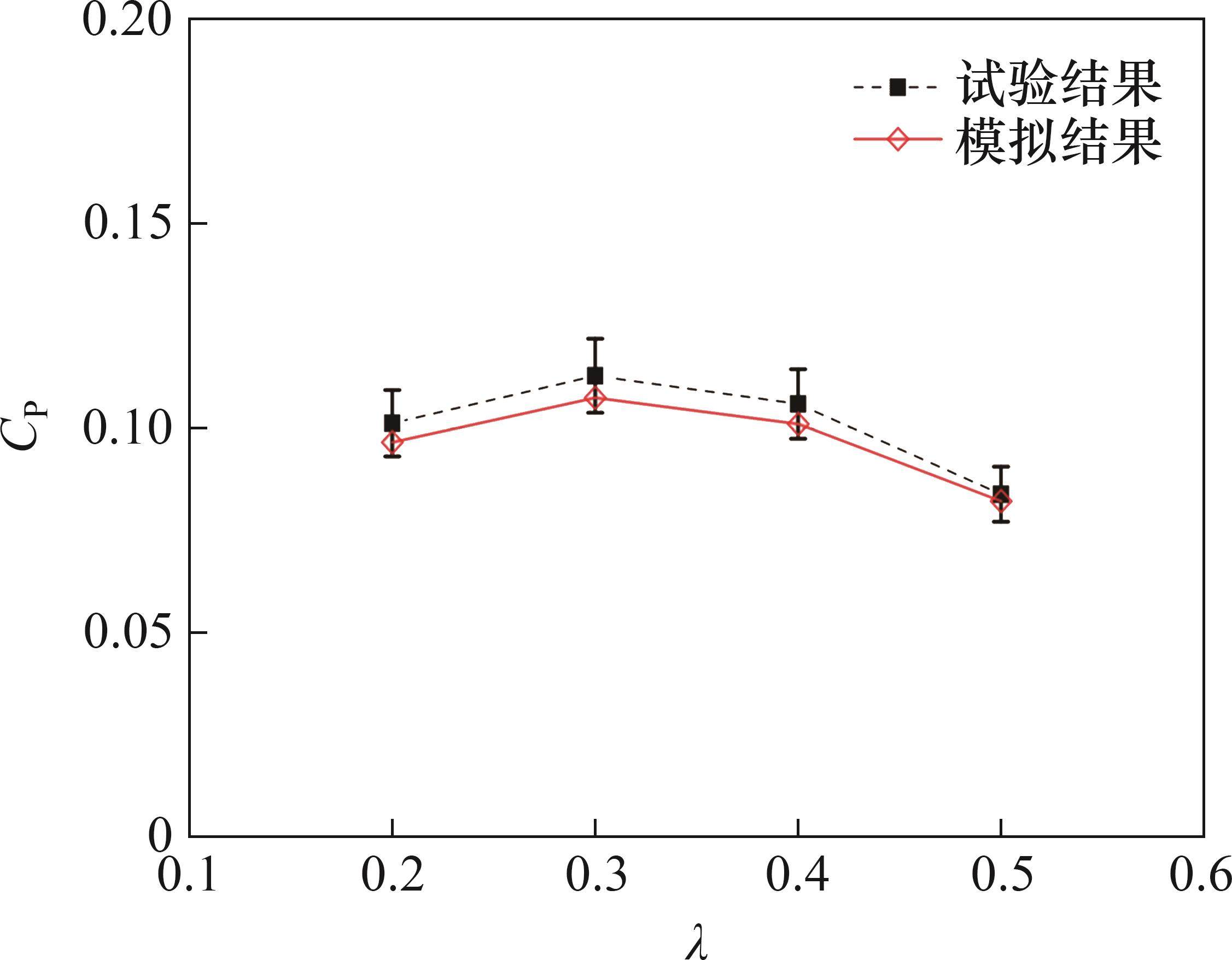
为了研究自由液面对河岸水轮机尾迹特征的影响,在模拟参数一致的前提下,设置3种计算工况,对应河岸水轮机中心沿垂向中心的安装高度分别为0.20、0.15和0.10 m,3种工况下水轮机沿 y方向的值分别为0.20、0.15和0.10 m,见图5(c)。
3 三维流场分析
3.1 各横截面上流场特征
3.1.1 x-y截面
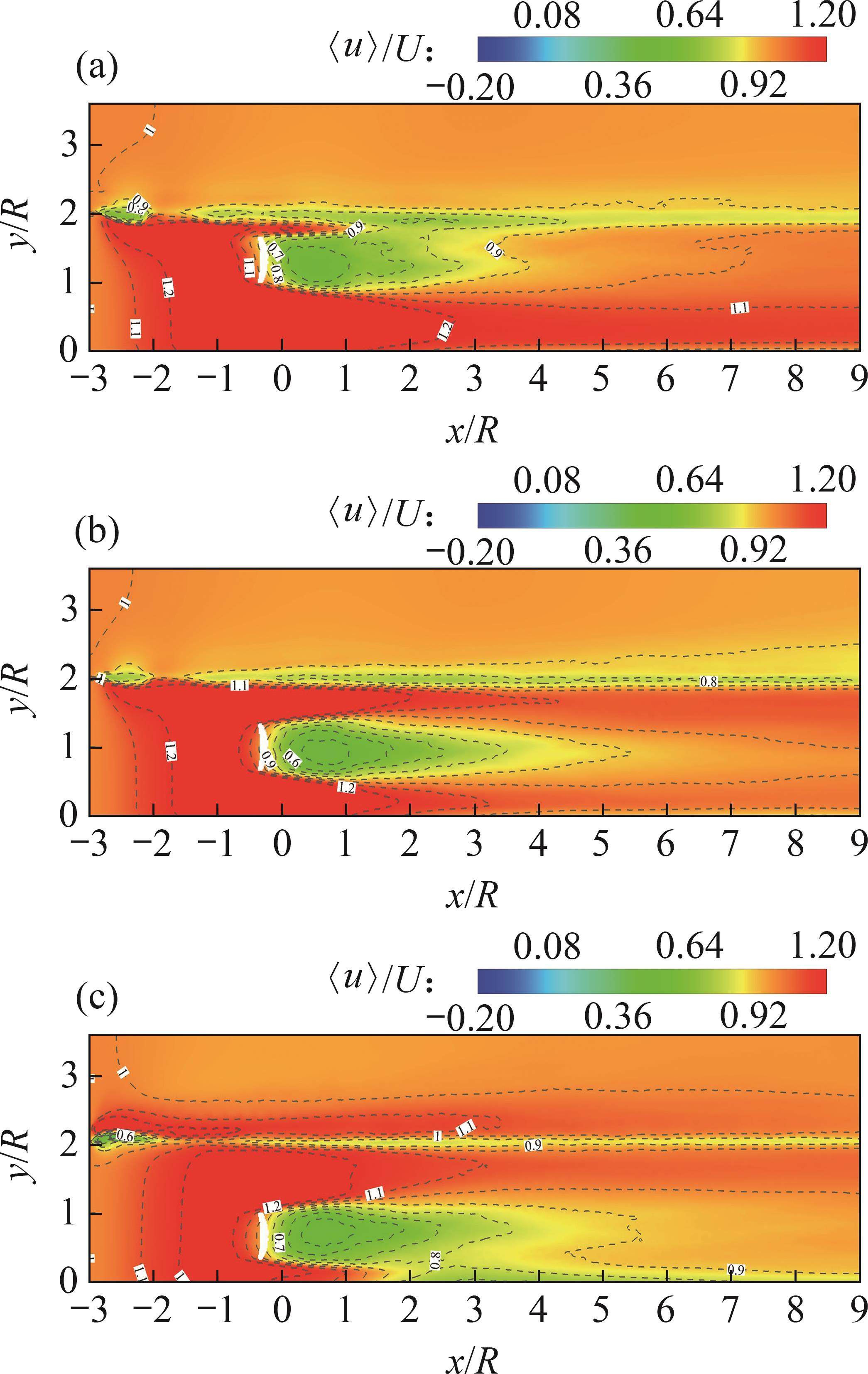
图7所示为侧壁附近的x-y横截面上河岸水轮机的流向速度(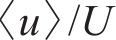
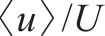
3.1.2 y-z横截面
图8所示为不同安装高度的河岸水轮机在下游y-z截面的流向速度(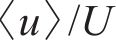
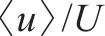
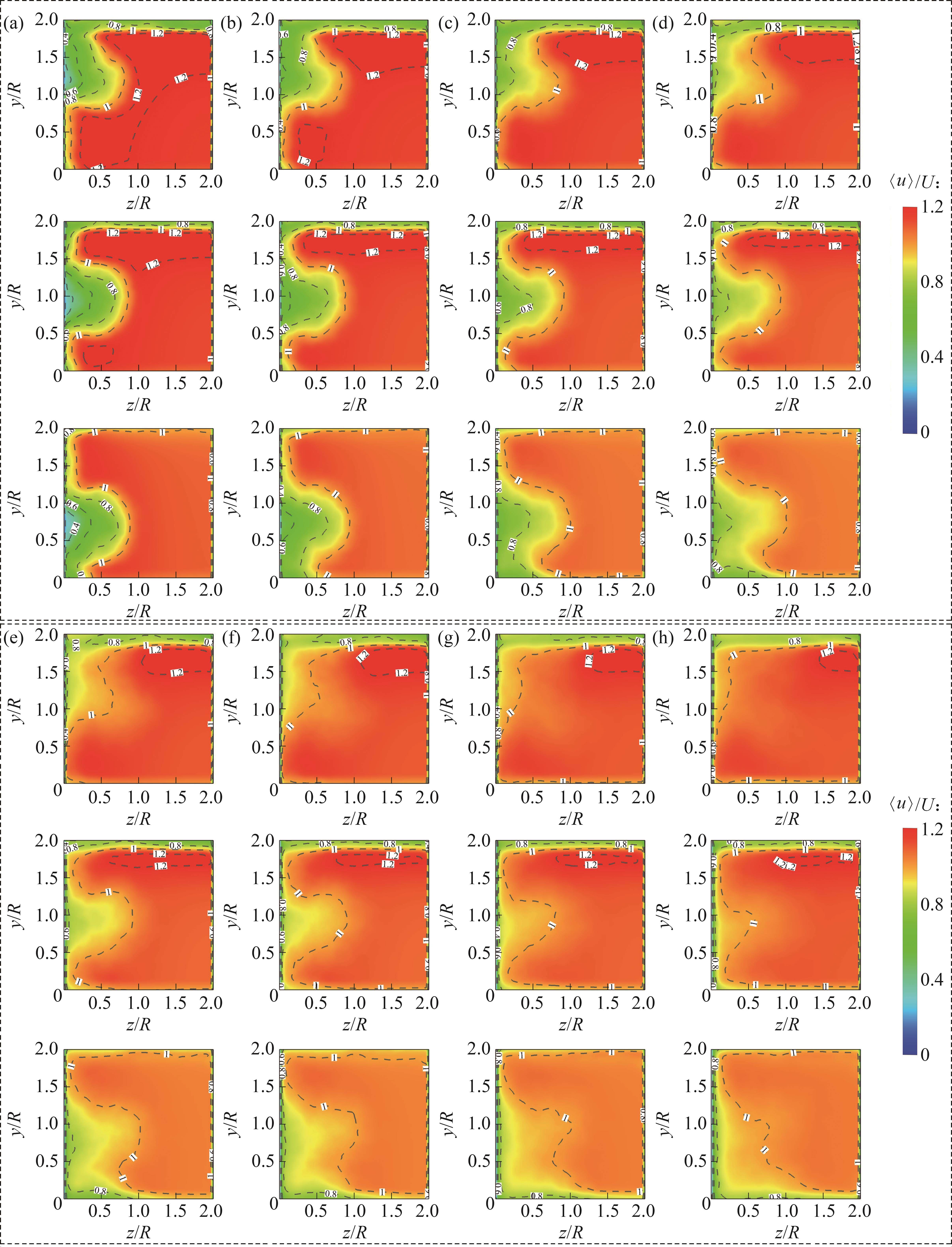
3.1.3 x-z截面
图9所示为不同安装高度位置的河岸水轮机中心所在平面(x-z截面)流向速度(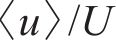
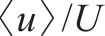
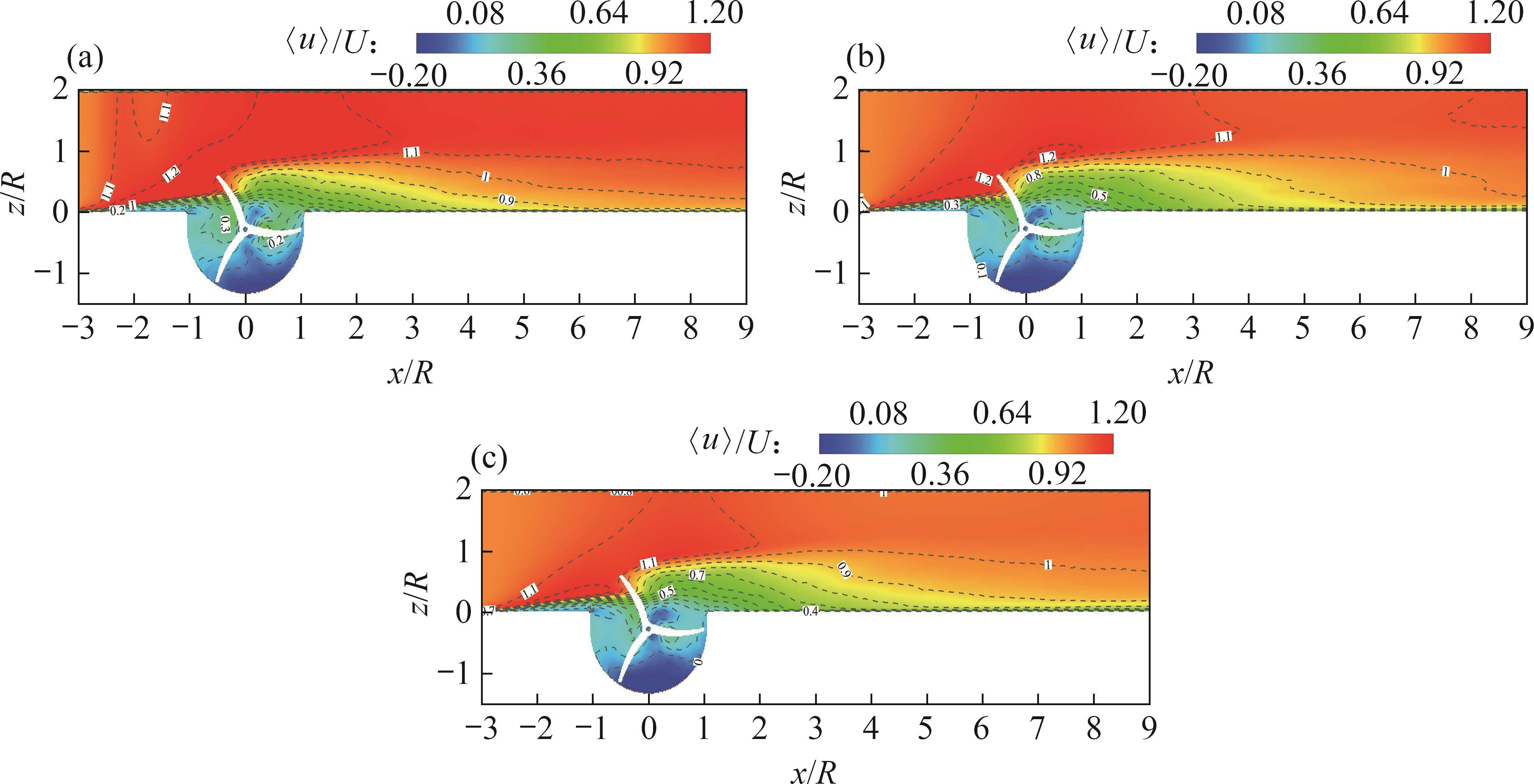
3.2 尾流沿展向分布特征
图10所示为安装高度不同时,河岸水轮机尾流区的流向速度沿展向的分布对比。由图10可知:水轮机安装在y=0.20 m位置的尾流流向速度比安装在y=0.15 m和y=0.10 m位置时的尾流速度更大,且在该位置时,流向速度恢复得更快,大致在x=7L处恢复至来流速度,而将水轮机安装在另外2个更靠近水槽底部的位置时,流向速度大概在x=9L处恢复至来流速度。同时,当水轮机安装水面中心高度位置更靠近底部位置时,流向速度的分布较为接近。该结果与图7、图8和9所示结果相吻合。
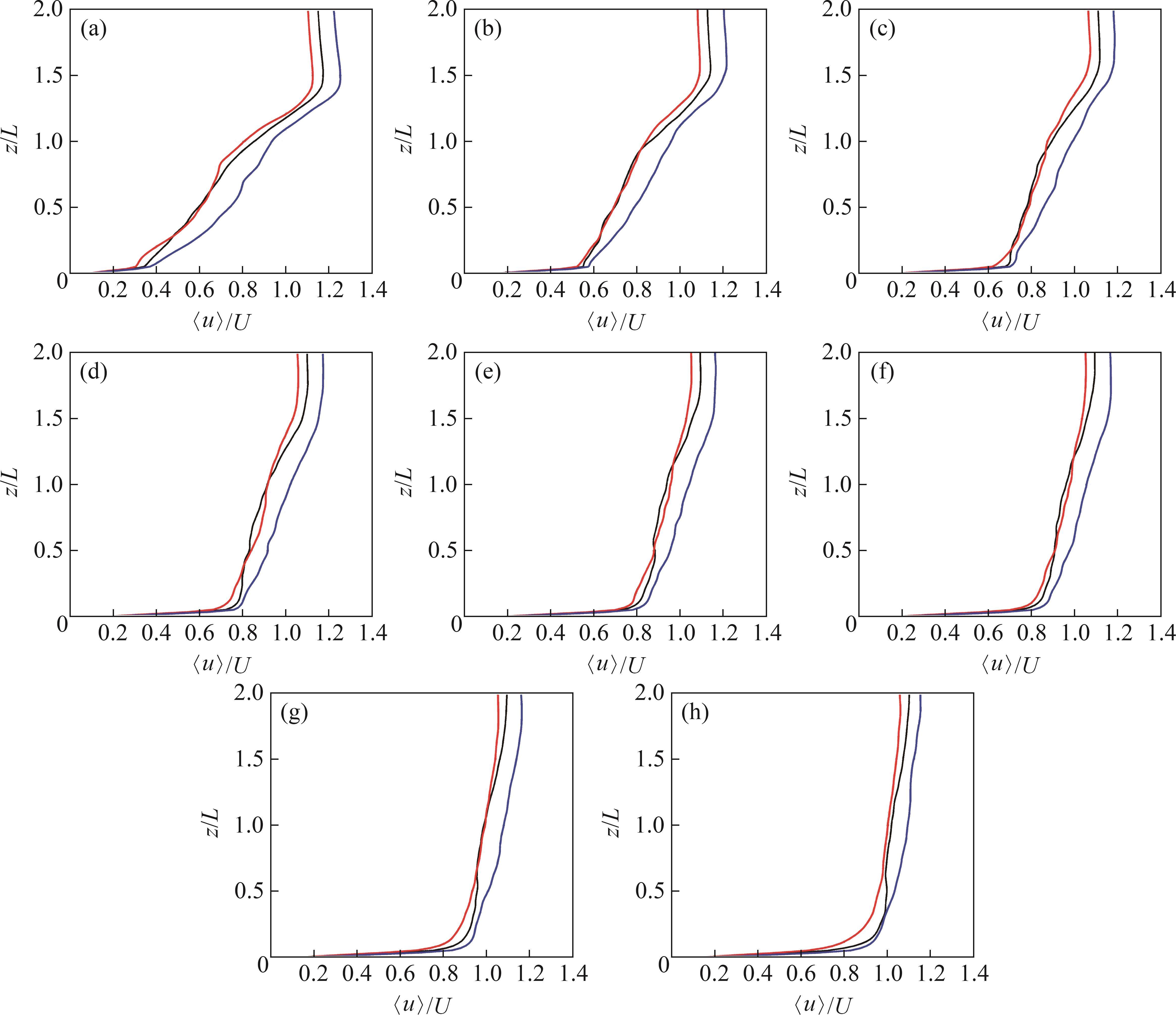
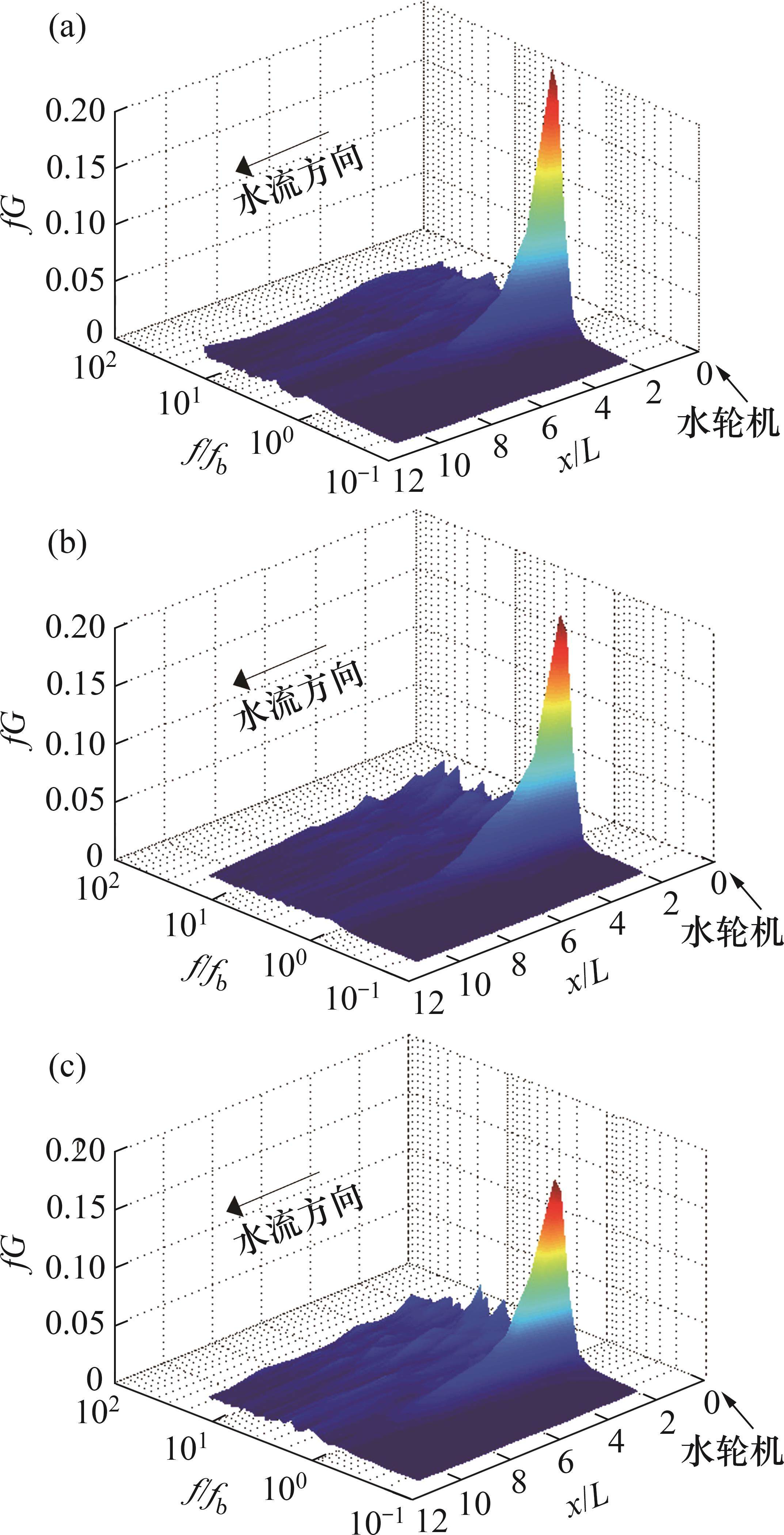
为对比不同安装位置下水轮机尾流区的湍流不稳定性,对3种工况下尾流区不同位置的瞬时流向速度分别进行预乘谱分析。对流向速度的自相关函数进行傅里叶变换得到功率谱密度函数G,乘以对应频率即得到预乘谱(fG),其主要用于检测引起大量湍流动能的主频,并沿流向追踪其能量衰减。图11所示为流向速度的预乘谱对比,其中,fb为叶片通过频率。由图11可知:在3种工况下,预乘谱对应的峰值在f/fb=1处,这表明水轮机尾流中包含一种周期性的波动流,其波动频率与fb相同;在3种工况下,尾流区叶片的通过频率位置分别在距离水轮机7L、9L和9L处出现显著的能量峰值,且安装在更靠近自由液面位置时,能量峰值更小,这同样表明水轮机安装离自由液面越近,尾流恢复速度越快。
4 结论
1) 当转轮安装在靠近自由液面位置时,迎流叶片后方的速度亏损区域向自由液面扩展,尾迹沿纵向的分布向自由液面偏斜,流向速度恢复到来流速度的位置约在距离水轮机中心7L处;在此工况下,尾流区的流向速度更大,尾流恢复更快,减流效果更弱,自由液面的波动也更为剧烈。
2) 当转轮安装在水深中部时,尾迹沿纵向大致呈对称分布,迎流叶片后方的速度减小区域类似于叶片投影形状(矩形),流向速度恢复到来流速度的位置在距离水轮机中心9L处。
3) 当转轮安装靠近河床底部的位置时,迎流叶片后方的速度亏损区域向底部扩展,尾迹沿纵向也不呈对称分布;在此工况下,流向速度与安装在水深中部时的流向速度较接近,且流向速度恢复到来流速度的位置也相同,这表明自由液面对河岸水轮机尾流产生的影响比对水槽底部产生的影响更大。
高瑾瑾, 杨帆, 郑源, 等. 自由液面条件下河岸水轮机尾迹特征[J]. 中南大学学报(自然科学版), 2024, 55(12): 4687-4697.
GAO Jinjin, YANG Fan, ZHENG Yuan, et al. Wake characteristics of a bank-embedded hydrokinetic turbine in free surface flow[J]. Journal of Central South University(Science and Technology), 2024, 55(12): 4687-4697.

