安全是交通运输永恒的主题。随着交通运输行业的加速发展[1-6],对碰撞防护系统的性能提出了更高的要求。防护系统不仅承受高能量的冲击[7-10],而且在诸如海洋船舶、铁路/公路桥梁等领域应用时,还面临化学腐蚀、磨损、疲劳等问题[11-14],研究新一代的碰撞防护结构显得尤为迫切。
在探索高效碰撞防护材料过程中,超高性能混凝土(UHPC)因具有优异的力学性能而成为研究热点,其不仅具有高强度和高韧性,而且具有很强的耐腐蚀、高耐久和抗疲劳等性能[15-16],但自身的吸能能力较弱。本文结合金属蜂窝结构的高吸能与轻量化特性[17-18],提出一种新型UHPC-蜂窝复合结构,有望实现其与UHPC性能的协同优化与增强,发挥更强的防护能力。
该复合结构在抵御高能量撞击方面具有巨大潜力,同时具有较强的服役耐久性。但目前关于该类结构的抗冲击特性研究未见报道,面向大尺寸工程应用、局部受载条件下的蜂窝等效数值模拟方法研究缺乏。为此,本文设计一种UHPC-蜂窝复合结构,开展局部冲击特性研究与阻抗优化设计,以便为该结构的抗冲击能力提升提供思路和设计指导。
1 复合结构有限元模型与验证
这里开展UHPC-蜂窝复合结构设计,并建立LS-DYNA有限元模型。开展蜂窝实体等效数值模拟方法研究,并基于UHPC-蜂窝复合结构平面及弧面压缩准静态试验对仿真模型进行验证。
1.1 复合结构几何构型及有限元模型
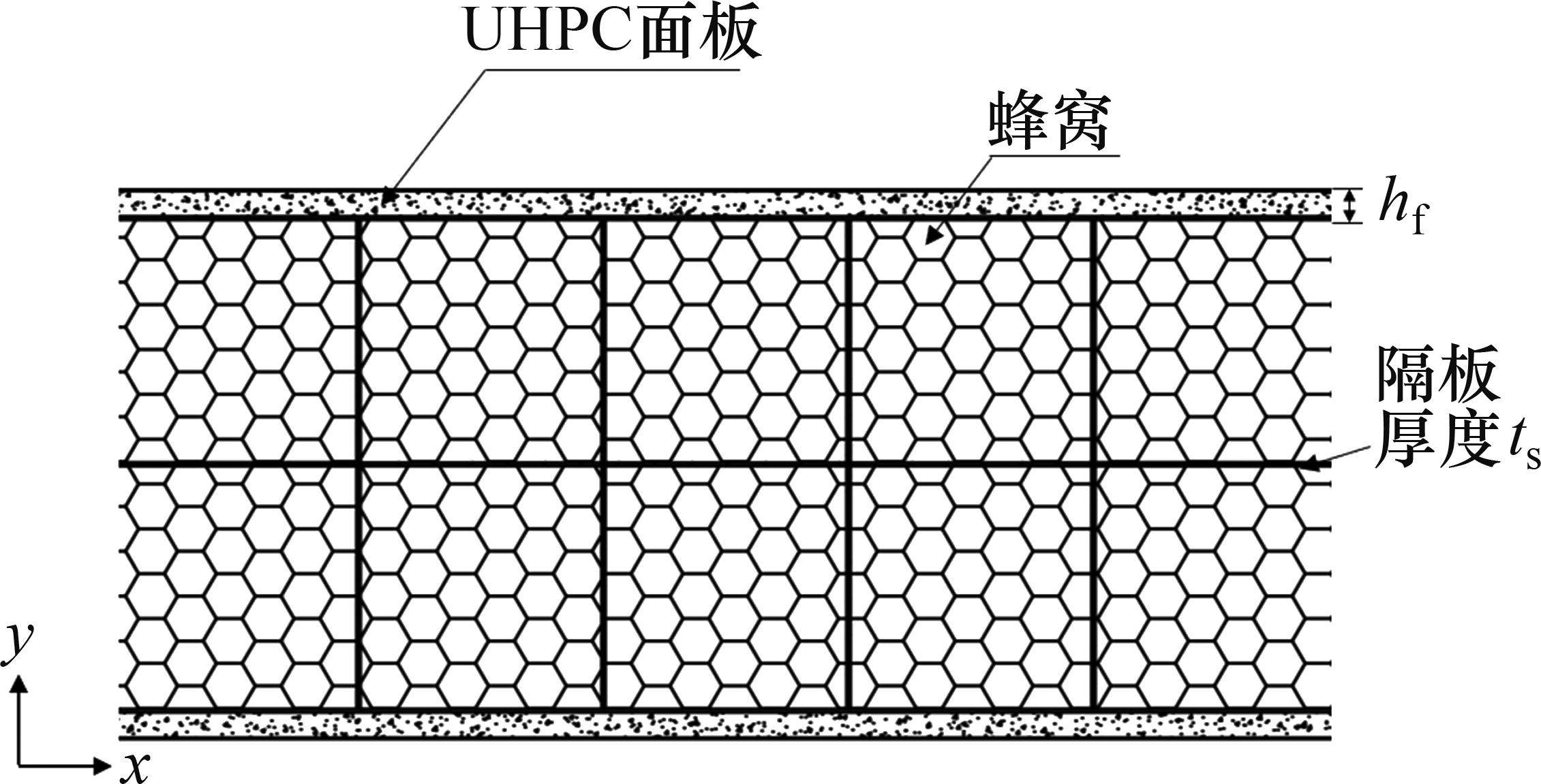
复合结构几何构型示意图如图1所示。该结构由2层厚度为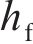
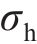
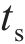
基于LS-DYNA建立的有限元模型如图2所示,其中,锤头、UHPC面板、蜂窝采用SOLID单元建模,隔板采用SHELL单元进行建模。水平与纵向隔板以共节点方式连接,水平隔板与蜂窝通过TIE_SURFACE_TO_SURFACE模拟胶接,其余各部件间的接触通过定义CONTACT_AUTOMATIC_SURFACE_TO_SURFACE关键字进行模拟。设置动摩擦因数为0.15,静摩擦因数为0.20[3],结构底部设置固定约束。采用精细的均匀网格划分各部件,以更好地模拟冲击下的大变形,UHPC面板网格尺寸为4 mm(沿厚度方向设置4层),蜂窝与格栅网格尺寸为5 mm。荷载设置方法如下:以MASS_PART关键字定义锤头总质量为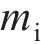
采用CSCM本构模型来描述混凝土的屈服和流动,屈服面本构方程如下:
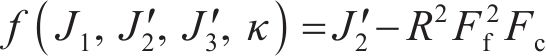
其中: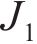
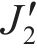
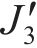
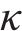
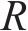
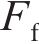

| 实验次数 | 弹性模量/GPa | 抗压强度/MPa | 抗拉强度/MPa |
|---|---|---|---|
| 1 | 46.30 | 158.6 | 7.28 |
| 2 | 47.42 | 169.9 | 7.77 |
| 3 | 46.44 | 156.4 | 7.91 |
| 实验次数 | 峰值应力/MPa | 峰值应变/‰ | 应变率/s-1 | 动态增强系数 |
|---|---|---|---|---|
| 1 | 37.8 | 0.3 | 101 | 2.02 |
| 2 | 29.2 | 0.5 | 92 | 1.70 |
| 3 | 22.5 | 0.3 | 73 | 1.31 |
隔板材料为Q235,密度为7 850 kg/m3,弹性模量为210 GPa,屈服强度为235 MPa,泊松比为0.3。通过Cowper-Symonds方程来描述其黏塑性行为:
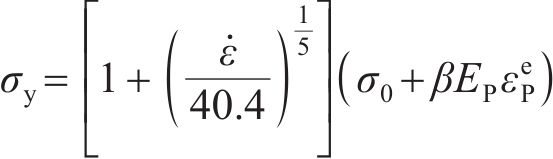
其中: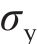
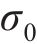
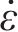
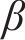
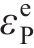
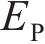
1.2 蜂窝实体等效本构模型
1.2.1 蜂窝实体等效屈服面
蜂窝作为一种周期性薄壁结构,胞元边长通常为毫米级[18]。对于大尺度的场景,采用壳单元精细化建模会造成网格数激增,计算效率很低。LS-DYNA显动力学软件提供了一种可用实体单元等效模拟蜂窝各向异性行为的MAT_126材料模型,能有效减小计算时间。
目前,应用该材料模型集中于单轴压缩工况的研究[19],针对船桥碰撞这类涉及蜂窝压剪混合受载的局部冲击问题,材料本构的设置方法与适用性有待进一步研究。为此,首先设置实体蜂窝的密度,蜂窝的等效密度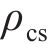
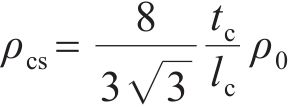
其中: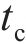
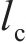
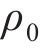
该模型可采用3个屈服面来表达,其中,第一屈服面需要分别定义所有法向应力和剪切应力,可通过试验测得,这些参数在求解过程中是完全解耦的。
在MAT_126本构中,激活第二屈服面需定义蜂窝等效屈服强度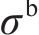
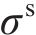
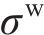
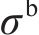

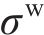
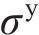
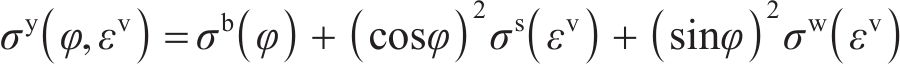
其中: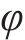
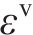
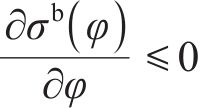
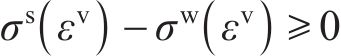
压缩强度为1.1 MPa的蜂窝在面外方向单轴加载下的应力-应变曲线如图3所示。采用预压工艺减小了初始峰值力。单个蜂窝块的长×宽×高为150 mm×150 mm×150 mm,蜂窝胞元边长为4 mm,壁厚为0.062 mm。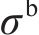
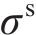
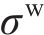
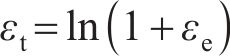
其中:
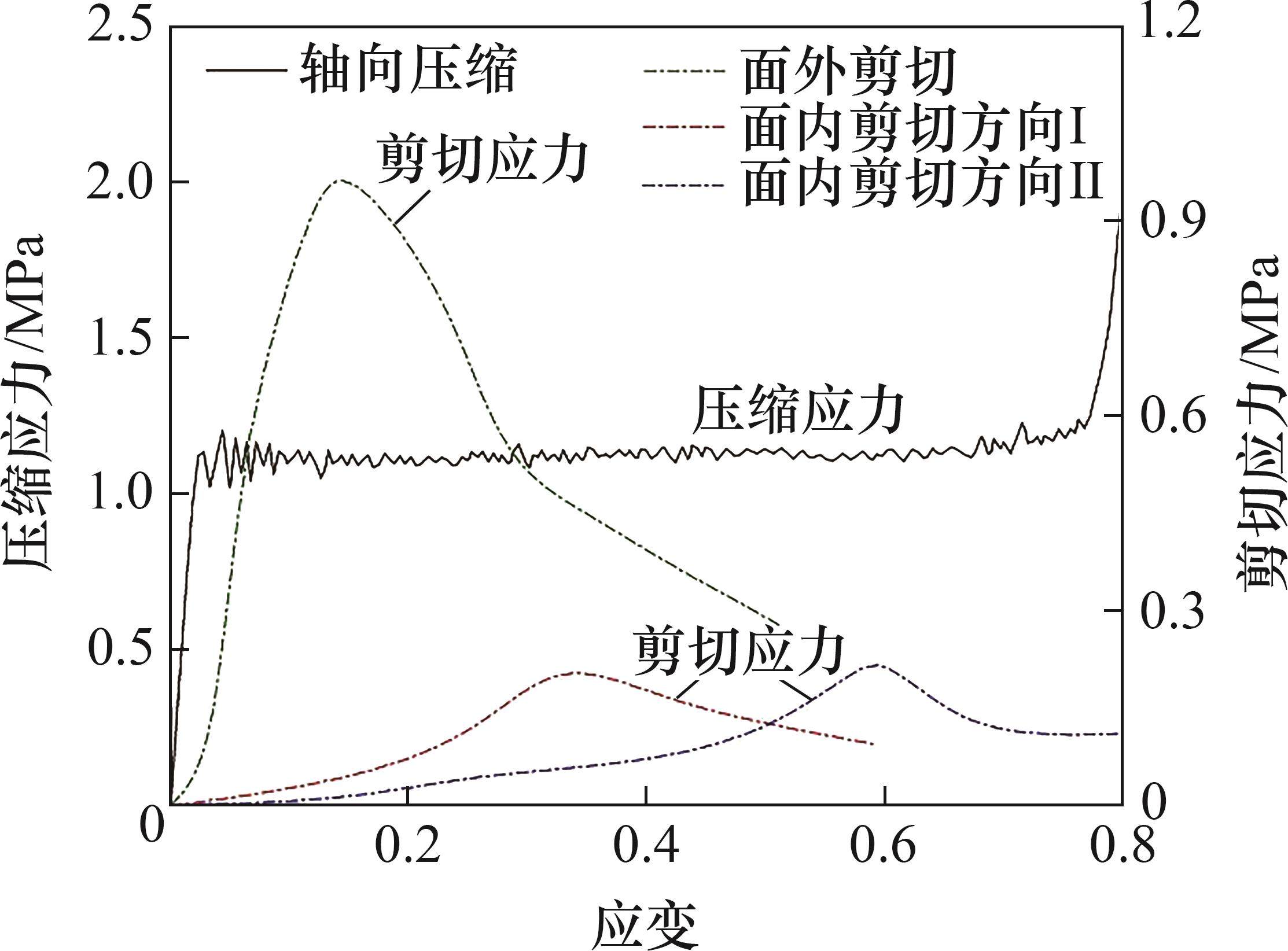
需分别定义LCAB、LCBC、LCCA这3条损伤曲线,以表征蜂窝的各向剪切行为。曲线的自变量为应变,因变量为剪切应力系数。在模拟中,应力会在每个时间步长随损伤值逐步更新。未损伤时,剪切应力系数记作1,损伤后,剪切应力系数定义为(0,1)区间的值。可根据图3中剪切曲线确定。
在激活第二屈服面时,为避免结构由于剪切抗性低、在小应力作用下出现严重的剪切畸变等情况,需要引入第三屈服面,在不影响单轴性能的情况下,进一步规定材料的静水强度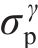
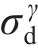
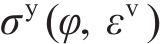
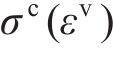
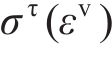
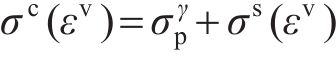
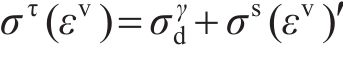
1.2.2 蜂窝实体等效方法验证
设计如图4和图5所示的蜂窝压缩试验,用于验证实体等效模型的模拟结果,并对激活和未激活第二、第三屈服面两种情况均进行对比分析。在单元类型的选择上,参考LS-DYNA手册,选取全积分单元和非线性弹簧单元两种。试验基于INSTRON 1342试验机开展,分别用于验证蜂窝的单轴压缩与局部受载下的压剪混合行为。平面锤头是为长×宽150 mm×150 mm的方形,弧面锤头是半径为75 mm的半圆构型。在2组试验中,锤头均以5 mm/min匀速压缩。蜂窝块结构与材料参数与1.2.1节中的一致。


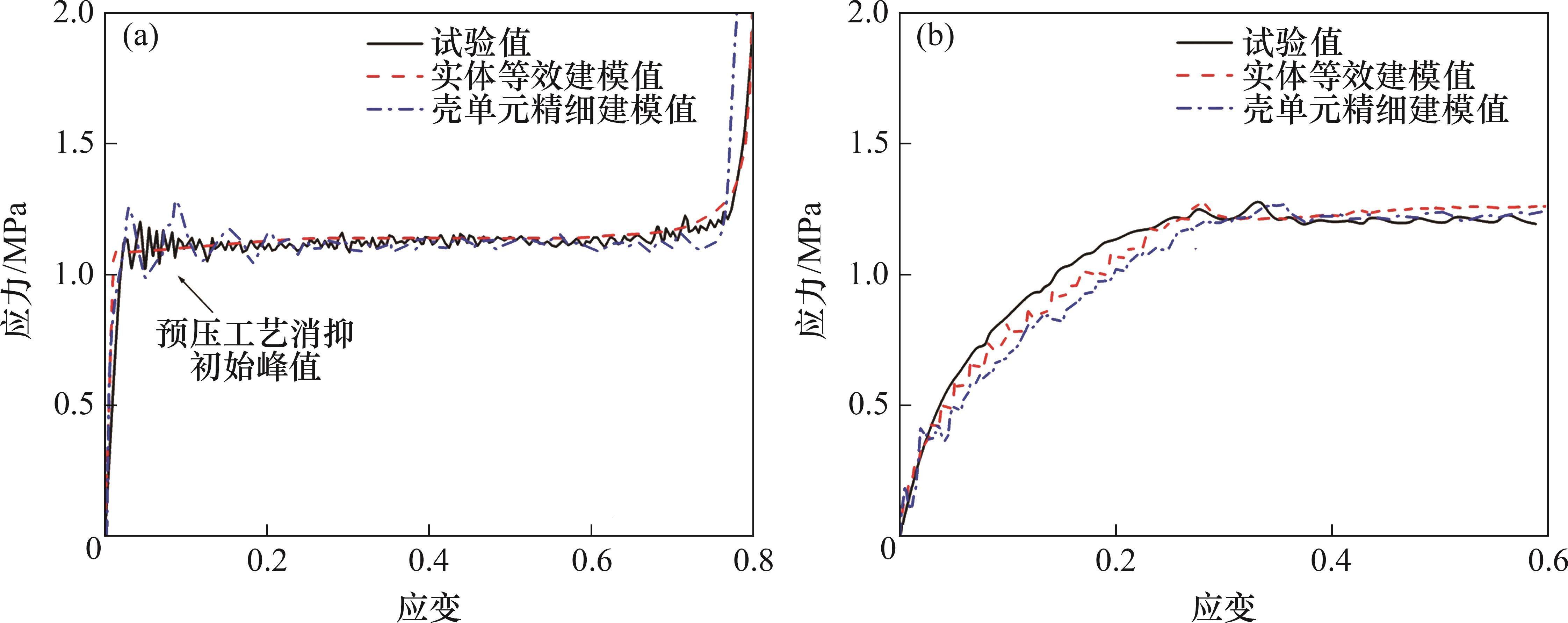
从图4可见:在单轴压缩下,本构屈服面模型和单元类型均能得到较好的模拟结果;在弧面锤头荷载下,蜂窝不仅受到沿轴向传递的力,而且受到剪切作用和面内的侧向荷载,在这种复杂应力耦合作用下,采用非线性弹簧单元的蜂窝无法在仿真中反映出合理剪切抗力,产生了明显的单元畸变;采用不激活第二和第三屈服面的设置方法,蜂窝在非轴向荷载下出现了整体向外扩张的现象。上述结果均与试验中的变形结果不符。总体而言,全积分单元与激活第二和第三屈服面结合的建模方法具有最优适应性,无论是在单轴荷载下还是在弧面复合荷载下,所得结果均与试验结果高度吻合。
应力-应变曲线试验结果与数值模拟结果如 图6所示。为确保可比性,硬件设备以及所采用的CPU线程数均保持一致。结果表明,采用实体等效模拟方法所得应力曲线不仅与试验的应力曲线吻合度较高,而且可大幅度减小计算时间,相比于壳单元精细建模,计算时间减小了72.75%。在本文后续研究中,对蜂窝均按该方法进行实体建模。
1.3 复合结构落锤冲击试验与验证
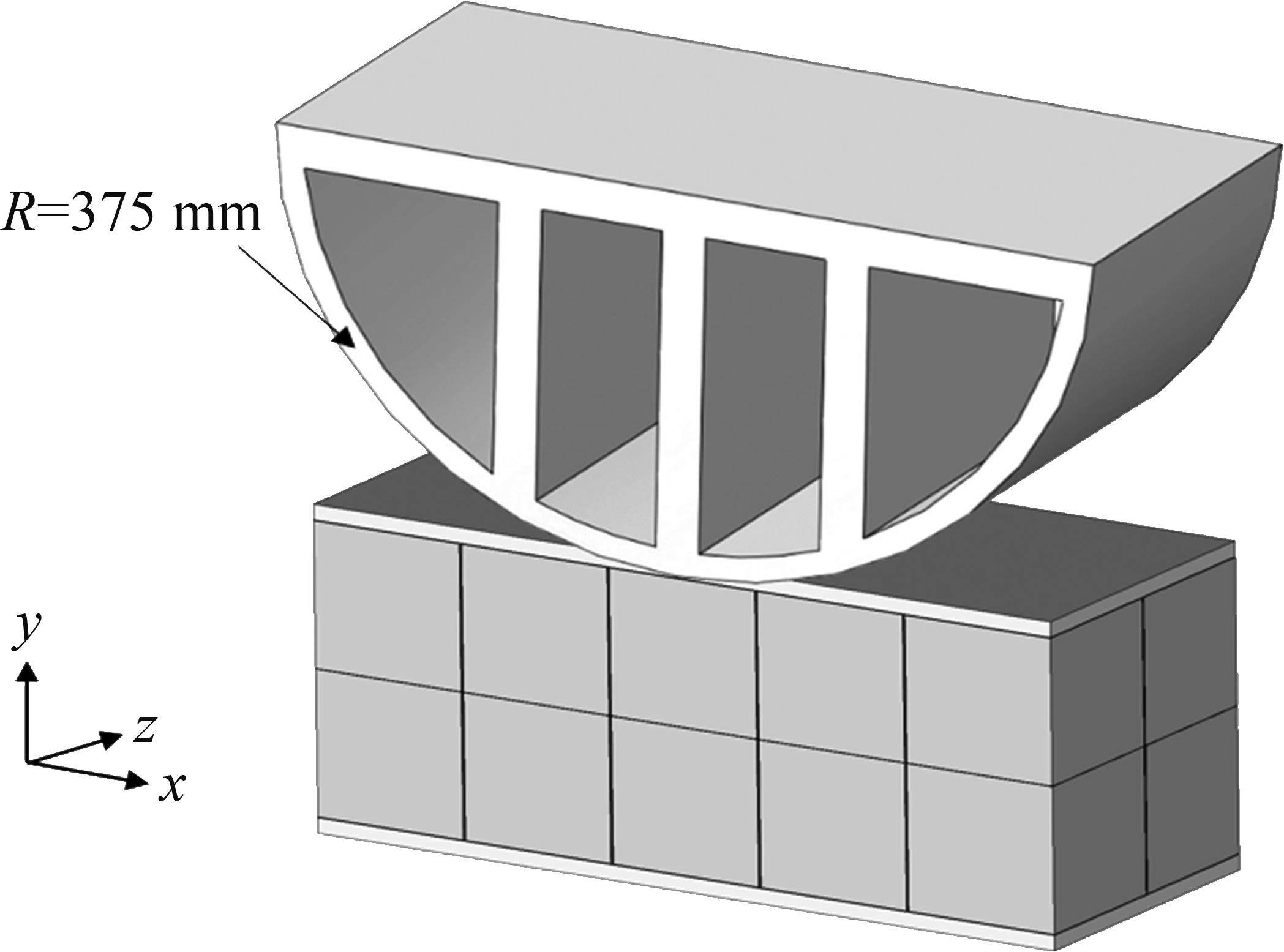
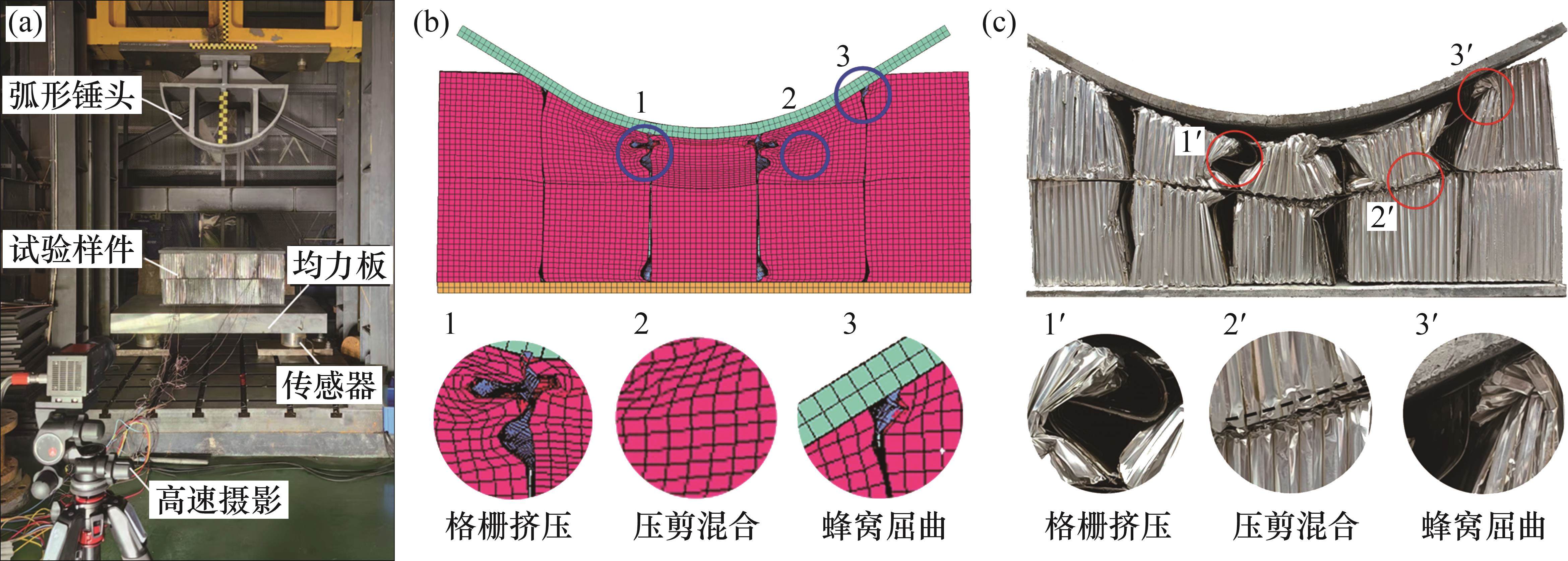
基于中南大学高能级落锤试验平台,开展UHPC-蜂窝复合结构冲击试验。试验实物图如图 7(a)所示,锤头呈半圆弧构型,半径为375 mm,质量为1.6 t。试验时,锤头距试样上表面抬升高度为80 mm,对应撞击初速度为3.5 m/s。试样总长×宽×高为750 mm×300 mm×332 mm,试样上下UHPC板厚度为16 mm,蜂窝面外压缩强度为 0.5 MPa,格栅厚度为0.2 mm。试样横向置于均力板上,均力板底部沿试样对称设置2个200 t量程力传感器,通过高速摄影装置采集复合结构冲击变形响应模式。
基于LS-DYNA开展显式动力学仿真计算,荷载与边界条件定义方法与1.1节中的相同,设置冲击初速度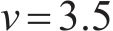
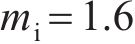
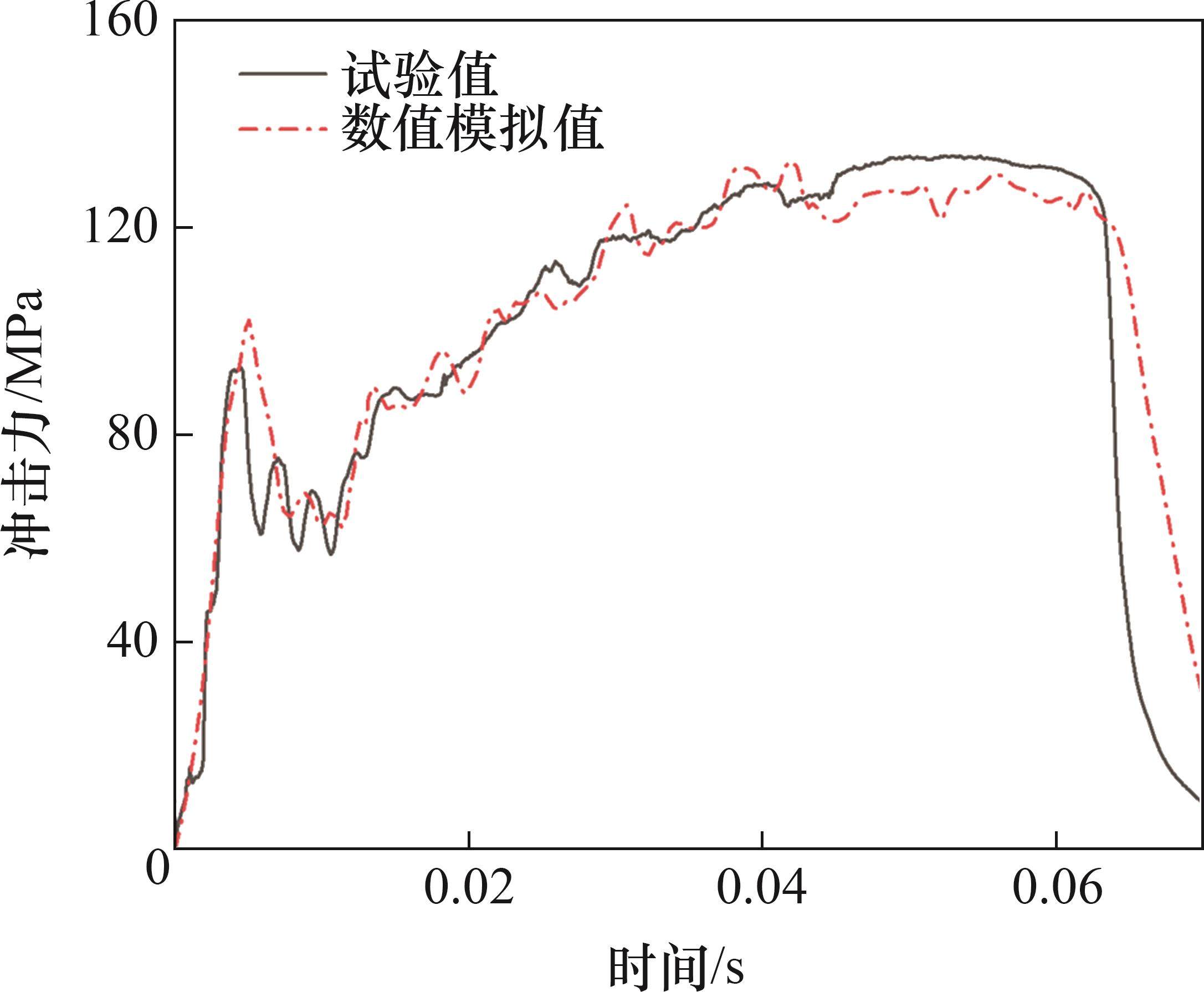
试验与仿真所得的冲击力-时间曲线对比见 图8。从图8可见:在冲击初期出现1个初始峰值;由于格栅的屈曲,曲线呈现振荡形状;弧面构型锤头在冲击过程中与样件的接触面积不断增大,使得撞击力随之提升,并逐渐达到最大峰值;最后,由于样件的速度减小,锤头回弹并迅速卸载。结果表明:冲击力试验曲线与仿真曲线高度吻合,其中,撞击初始峰值力相对误差为7.8%,最大峰值力的相对误差为6.4%,撞击响应时间的相对误差为7.0%。
2 复合结构局部冲击响应特性
基于拉丁超立方采样的数值模拟结果,利用Spearman秩相关系数[20]评估结构几何参数与冲击特性间的非线性关联性。运用高斯过程回归方法建模,进一步探究几何参数对关键性能指标的影响,以便为结构设计的优化提供定量依据。
2.1 冲击响应与能量分配关系
在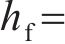
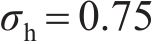
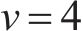
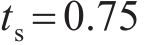
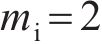
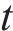
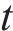
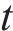
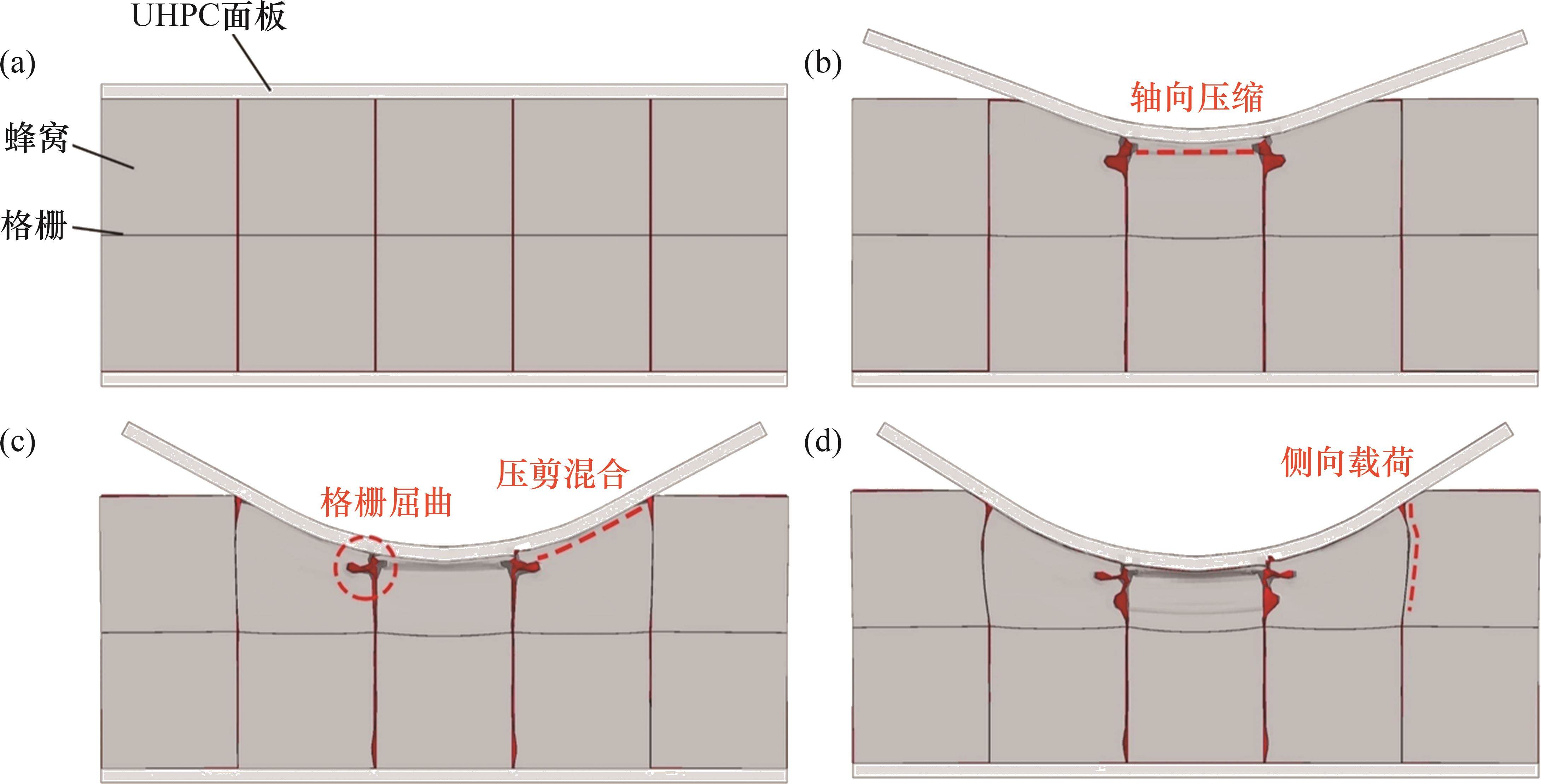
图10(a)所示为整个冲击响应历程的力-位移曲线,可反映响应模式的时空依赖性以及各个部件在碰撞吸能中的贡献。从图10(a)可见:在冲击响应第一阶段,由于锤头与复合结构的接触区域较小,变形集中在中心附近;冲击力随隔板的屈曲而呈现波形变化;随着冲击位移逐步增加,变形区域不断扩大,与之相应的冲击力也逐渐升高;同时,曲线在第二阶段末期出现最大峰值,反映了结构的吸能效率最高。
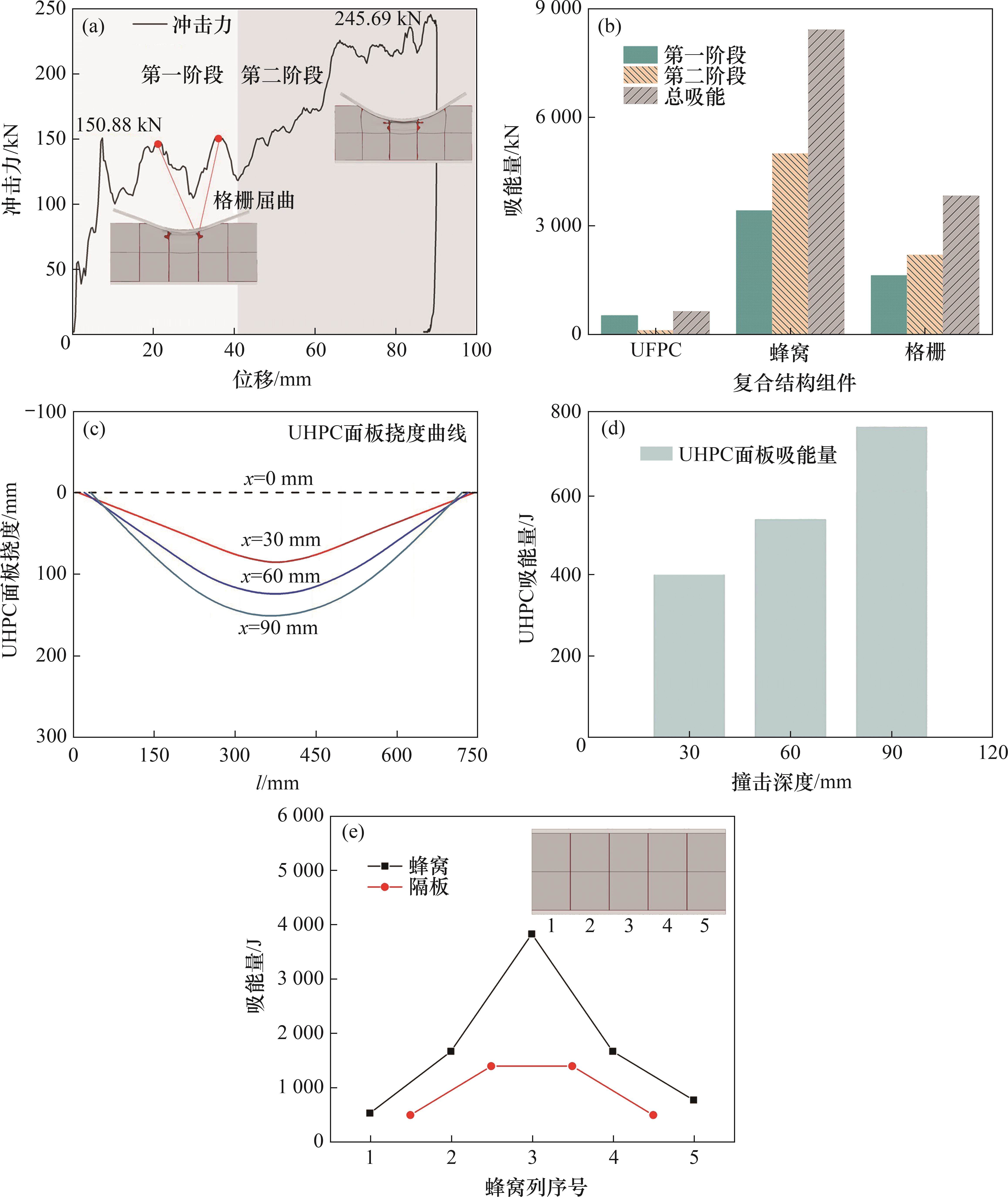
不同组件的吸能能力与时序性如图10(b)所示。从图10(b)可见UHPC的吸能主要集中于第一阶段。图10(c)中的挠度-位移曲线和图10(d)中的吸能量-位移图进一步阐释了这一现象,其中,x为锤头位移, 
蜂窝与隔板在整个冲击历程中的吸能量均显著高于UHPC,且第二阶段的吸能量大于第一阶段,说明塑性区域的扩展强化了芯层的吸能能力。同时,蜂窝作为复合结构主要吸能单元,对总吸能量的贡献率达52.36%。蜂窝与隔板的吸能贡献与空间位置的关系见图10(e)。从图10(e)可见:蜂窝被划分为5列,从左至右用自然数标记,位于蜂窝之间的隔板相应划分为4部分;芯层的吸能量随空间位置呈现正态分布。由于存在最高的压缩量以及面外的单轴压缩主导变形模式,仅中心一列的蜂窝吸能量贡献了全蜂窝46.37%的吸能量;中心两侧的两列蜂窝处于压剪混合与面内凹陷的复杂受载状态,贡献了40.57%的吸能量。类似地,处于冲击中心位置的隔板产生了更多的塑性吸能量,占比为73.68%。表明在局部受载情况下,塑性波由撞击中心向外传播,芯层的吸能效果由中心向两侧递减。
2.2 结构参数-冲击特性关联性研究
2.2.1 Spearman秩相关系数分析
选取UHPC厚度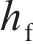
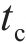
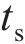
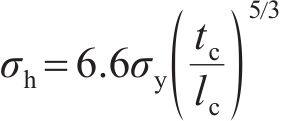
其中: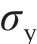
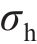
| 序号 | 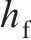 | 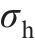 | 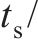 | 序号 | 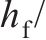 | 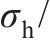 | 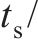 |
|---|---|---|---|---|---|---|---|
| 1 | 12.50 | 0.94 | 0.64 | 11 | 13.29 | 0.65 | 0.62 |
| 2 | 17.40 | 0.54 | 0.66 | 12 | 12.40 | 0.51 | 0.88 |
| 3 | 16.74 | 0.69 | 0.54 | 13 | 18.49 | 0.78 | 0.84 |
| 4 | 10.26 | 0.6 | 0.86 | 14 | 18.94 | 0.99 | 0.91 |
| 5 | 14.56 | 0.73 | 0.94 | 15 | 14.60 | 0.58 | 0.58 |
| 6 | 16.36 | 0.76 | 0.81 | 16 | 14.01 | 0.57 | 0.75 |
| 7 | 10.83 | 0.64 | 0.50 | 17 | 15.72 | 0.96 | 0.57 |
| 8 | 11.58 | 0.85 | 0.98 | 18 | 19.02 | 0.70 | 0.95 |
| 9 | 17.77 | 0.83 | 0.78 | 19 | 13.73 | 0.91 | 0.72 |
| 10 | 19.97 | 0.81 | 0.70 | 20 | 11.47 | 0.88 | 0.69 |
利用Spearman秩相关系数[20]评估UHPC-蜂窝复合结构设计参数与其冲击性能指标之间的非线性关联性。关键冲击特性指标如下。
1) 初始峰值力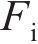
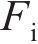
2) 冲击响应过程中的最大峰值力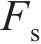
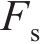
3) 撞击深度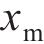
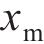
Spearman秩相关系数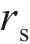
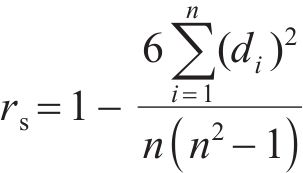
其中: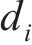
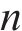
| 输入变量 | 输出变量 | 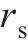 | p |
|---|---|---|---|
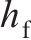 | 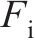 | 0.660 | 0.001 53 |
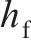 | 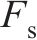 | 0.269 | 0.251 00 |
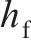 | 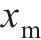 | -0.163 | 0.489 00 |
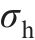 | 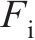 | 0.624 | 0.003 27 |
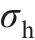 | 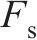 | 0.911 | 2.330 00×10-8 |
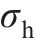 | 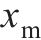 | -0.924 | 5.530 00×10-9 |
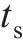 | 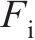 | 0.592 | 0.005 91 |
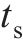 | 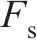 | 0.294 | 0.207 00 |
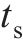 | 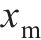 | -0.315 | 0.174 00 |
从表4可见: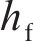
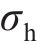
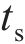
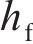
2.2.2 结构几何参数-冲击特性相关性
为进一步直观展示结构参数对冲击特性的影响,采用高斯过程回归模型作为建模工具,建立多维非线性的代理模型。高斯过程作为一种贝叶斯非参数统计方法,它能够预测连续的输出变量,并且给出预测的不确定性。
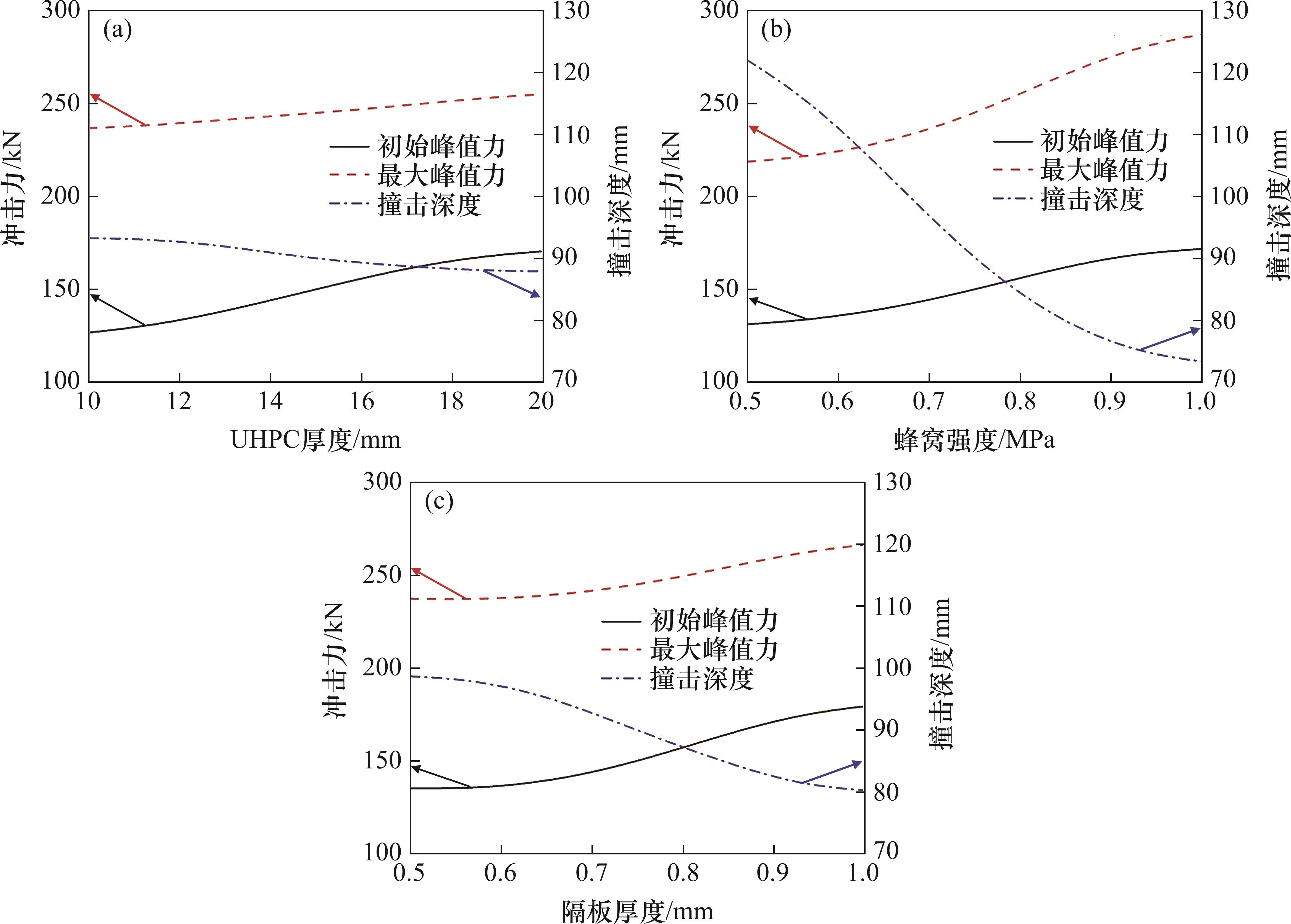
基于代理模型进一步分析结构参数-冲击特性相关性,结构参数作为自变量输入,自变量区间与2.2.1节中的一致,为UHPC厚度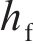
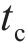
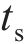
3 复合结构冲击抗性优化设计
3.1 参数优化方法
以UHPC厚度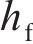
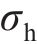
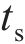
为实现结构的耐撞性与冲击阻抗提升,提出如下优化策略:最小化撞击深度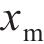
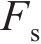
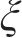
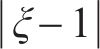
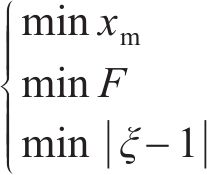
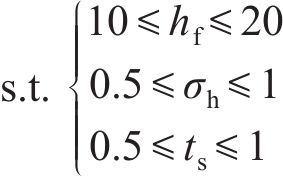
对于每一代种群中的每个个体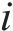
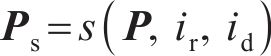
其中: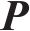
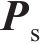
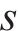
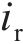
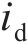
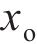
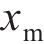
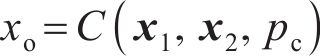
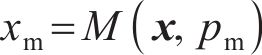
其中:

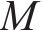


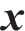
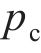
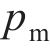
3.2 优化结果分析
在多目标优化过程中,可计算得到一系列支配解和非支配解[21]。Pareto是前沿由中互不支配的解构成的集合。在目标函数空间中,前沿解是在一个目标上改进的同时不会在另一个目标上劣化的解,因此,这些解被认为是最优的。在前沿解集中,采用一种基于最短归一化距离的方法得到最佳的权衡的平衡解:
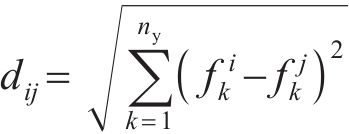
其中: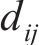
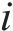
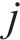
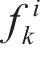
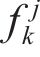
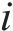
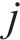
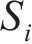
其中:
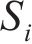
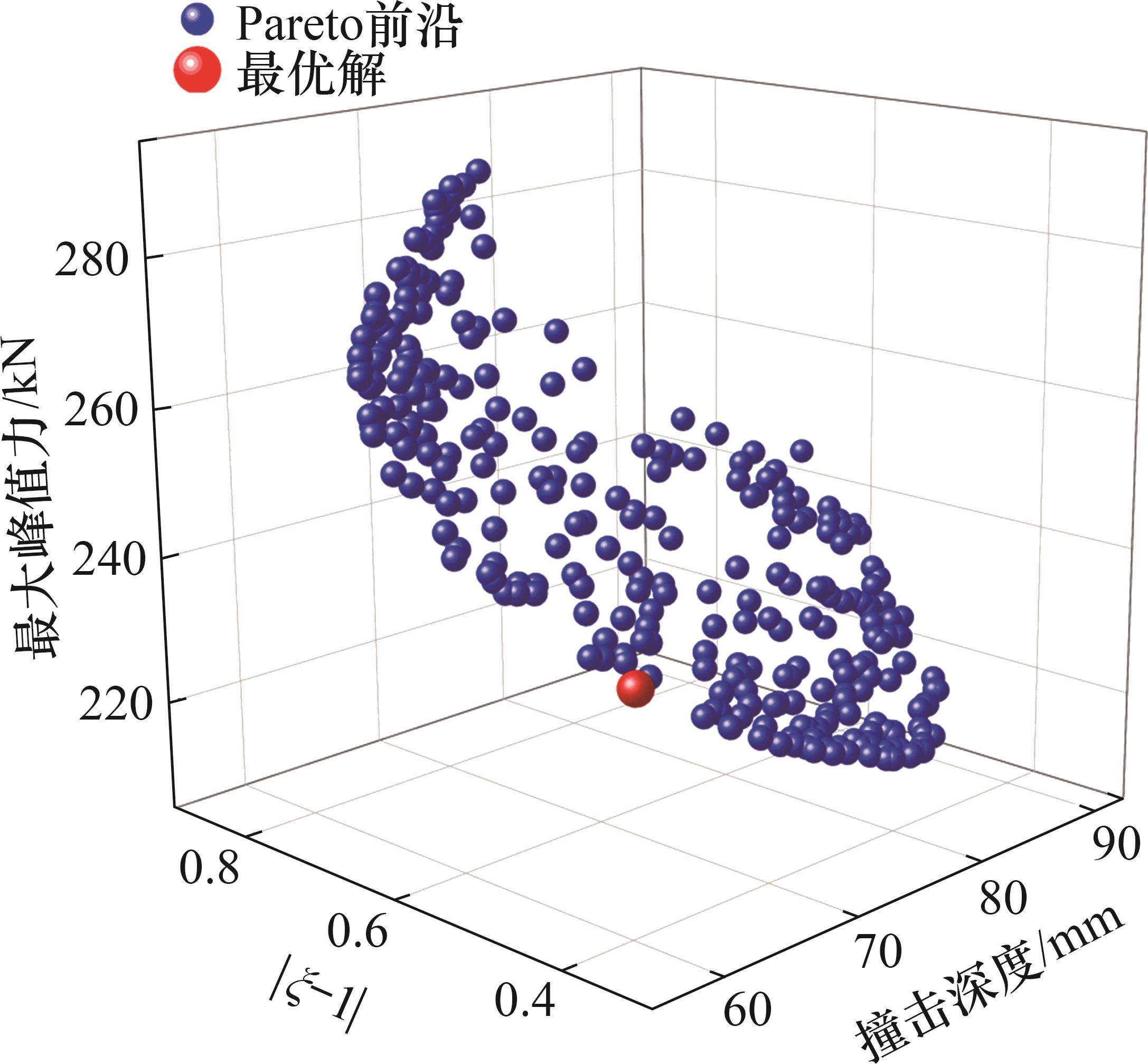
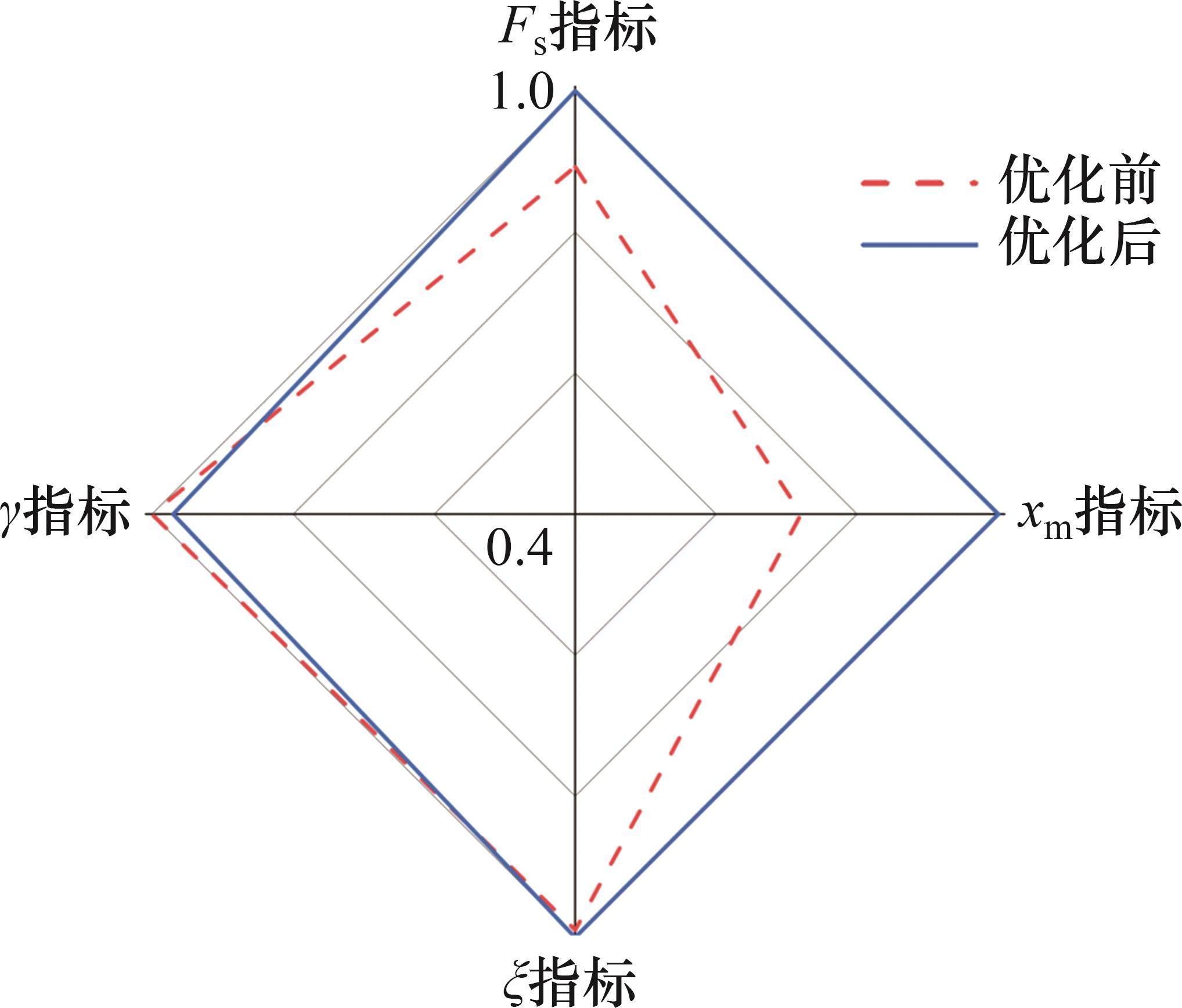
对所设计结构,优化得到的最优结构参数取值如下:UHPC面板厚度为12.40 mm,蜂窝强度为0.84 MPa,格栅壁厚为0.81 mm。计算上述最优解的数值模拟结果,并与优化预测结果进行对比,结果如表5所示。从表5可见:多目标优化结果与数值仿真结果具有较高的吻合度,且采用较小厚度的UHPC与较高强度的蜂窝进行匹配,能得到更优的冲击特性。以雷达图的形式对比优化前后的结构(优化前结构参数与2.1节中的一致)在关键指标上的表现,除
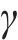
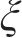
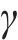
| 方法 | 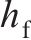 | 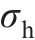 | 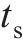 | 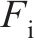 | 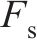 | 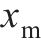 |
|---|---|---|---|---|---|---|
| 相对误差/% | 0 | 0 | 0 | -4.89 | +2.93 | +4.50 |
| 优化预测 | 12.40 | 0.84 | 0.81 | 117.54 | 225.25 | 68.84 |
| 数值模拟 | 12.40 | 0.84 | 0.81 | 111.79 | 231.84 | 71.94 |
4 结论
1) 开展蜂窝实体等效模拟研究,基于各向压缩、剪切试验确定了本构参数。激活第二和第三屈服面的全积分单元模型的模拟结果与试验吻合度最高,结合蜂窝平面与弧面压缩试验与复合结构落锤冲击试验,证明该等效方法具有高精度,且能大幅度缩减计算时间。
2) 复合结构的冲击响应模式与能量分配具有时序与空间性。UHPC面板表现为大挠度屈曲,其塑性变形与吸能集中于冲击前期与中期;芯层塑性区域随冲击位移的增加而扩展,中心的蜂窝以轴向压缩为主导,两侧的蜂窝呈压剪混合和面内凹痕的复杂耦合模式,芯层吸能量随空间呈正态分布。
3) 在所设计的复合结构中,UHPC厚度对初始峰值力有重要影响,但对最大峰值力和撞深的影响程度较小。芯层中,蜂窝作为能量吸收的主导因素,对最大峰值力和撞深的影响最显著,隔板与初始峰值力的相关性更大。
4) 基于遗传算法开展了冲击阻抗增强多目标优化。对于所设计结构,优化后最大峰值力下降8.32%,撞击深度减小23.51%。
雷紫平, 刘杰夫, 邸昊, 等. UHPC-蜂窝复合结构局部冲击特性及阻抗优化[J]. 中南大学学报(自然科学版), 2024, 55(12): 4698-4710.
LEI Ziping, LIU Jiefu, DI Hao, et al. Local impact characteristics and resistance optimization of UHPC-honeycomb sandwich structures[J]. Journal of Central South University(Science and Technology), 2024, 55(12): 4698-4710.

