随着社会进步,铁路技术不断提升,高速铁路的安全性日益提高;而随着车速不断提高,在急剧不平顺等跳轨诱因作用下,高速车辆极易出现跳轨现象,车轮将失去钢轨对其约束,在不利荷载作用下,存在跳轨脱轨的安全隐患。因此,研究高速车辆跳轨的动力行为具有重要理论与现实意义。
目前,关于车辆跳轨全过程研究尚处于初级阶段。对车辆-轨道系统动力学的研究大多是在假定轮轨密贴条件下进行的,只有少数考虑了轮轨分离(或称跳轨)状态。FRÝBA等[1]研究了车轮跳轨现象,分析了二轴车辆跳离钢轨的车桥振动问题,指出了考虑跳轨现象的必要性。LEE等[2-3]研究了单个车轮跳离钢轨的车桥振动问题。LIU等[4-5]研究了车辆在桥梁上的跳轨问题。STÂNCIOIU等[6-7]研究了单轴及两轴车辆模型在简支梁上的跳轨问题。CHENG等[8]研究了单个轮对跳离钢轨的车桥振动问题,并提出了轮轨冲击作用算法。樊建平等[9]利用此算法,进行了跳车冲击力作用下的单轴行车简支梁的数值分析。BAEZA等[10]研究了单轴车辆在简支桁梁上的跳轨问题。翟婉明[11]建立了单轮对-轨道相互作用模型,对单轮对爬轨和跳轨这2种工况下的脱轨行为进行了计算分析。娄平[12]研究了二轴车辆跳离桥梁结构的振动问题。曾京等[13-14]分析了轮对横向冲击对车轮跳轨的影响规律。肖新标等[15-16]研究了复杂环境状态下的轮轨分离现象,建立了判断轮轨是否分离的指标。孙丽霞等[17]研究了车辆蛇形运动对于跳轨脱轨的影响。通过对比分析,发现FRÝBA等[1-6]没有考虑轨道振动及轮轨冲击作用;文献[7-10]虽然考虑了轮轨冲击作用,但没有考虑轨道振动;翟婉明等[11-12]虽然考虑了轨道振动,但在轮轨再次密贴时,没有考虑轮轨冲击作用;曾京等[13-17]主要考虑了轮轨横向振动对跳轨脱轨的影响。
针对上述国内外研究的不足,向俊等[18-19]针对提速及高速有砟轨道,提出了一种铁道车辆车轮跳轨全过程的计算方法,可以反映车辆在有砟轨道上跳轨全过程的完整信息,但尚不能模拟高速车辆在无砟轨道上的跳轨全过程行为及跳轨规律。为此,本文拟建立高速车辆在无砟轨道上的跳轨全过程计算模型并自编程序,在跳轨诱因作用下,实现高速车辆跳轨全过程计算,在此基础上,分析高速车辆的跳轨规律,以便为高速铁路维修规则提供参考。
1 计算模型的建立及程序编制
分别建立高速车辆及无砟轨道振动分析模型及方程。以轮轨相互作用力为纽带,考虑高速车辆在无砟轨道上的车轮跳轨全过程,包含轮轨正常密贴、轮轨分离、轮轨冲击、轮轨正常密贴共4个阶段,基于Wilson-θ法求解车-轨系统振动方程,采用FORTRAN语言编制相应计算程序。
1.1 高速车辆竖向振动分析模型
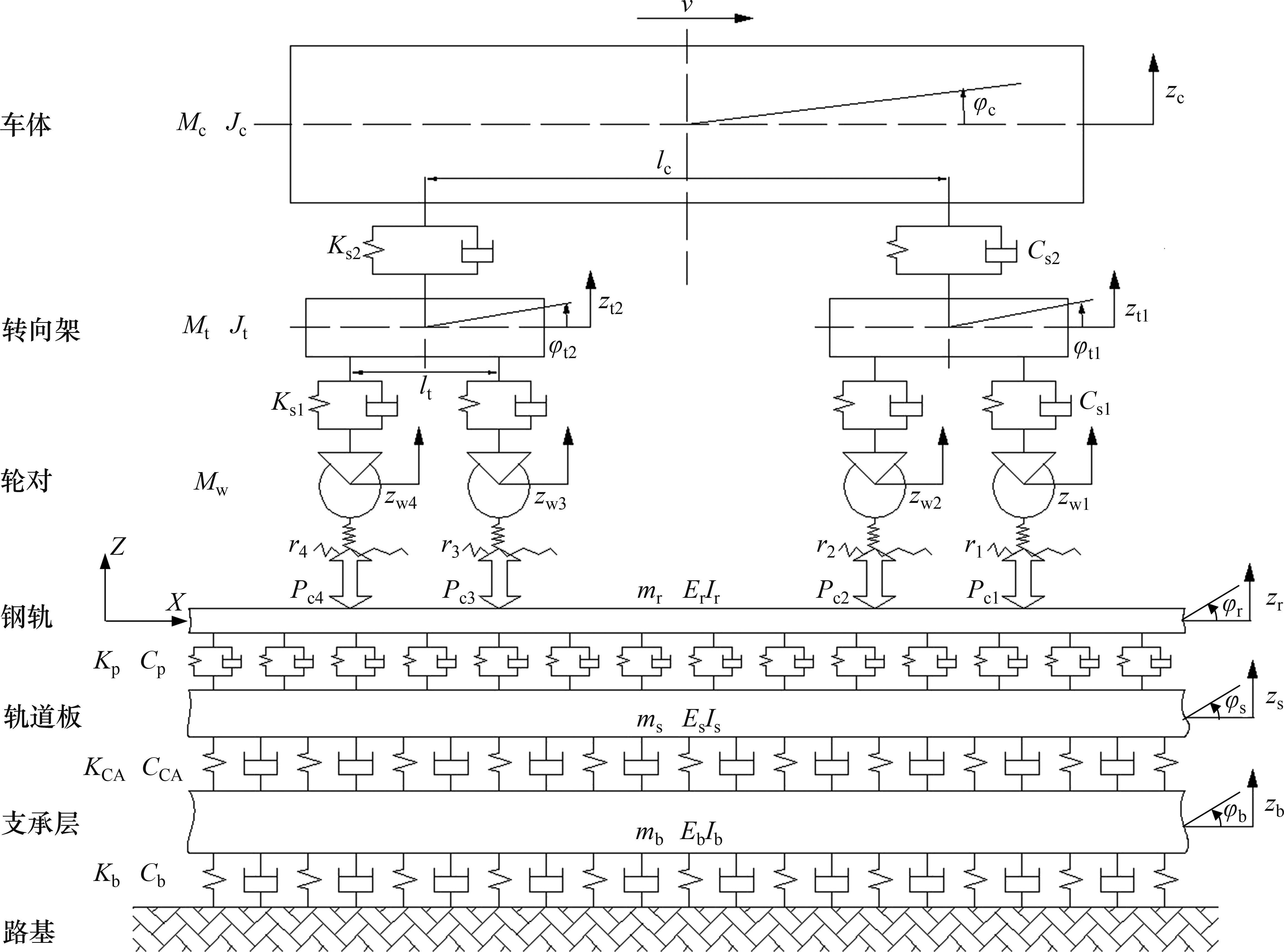
整节车辆-无砟轨道系统竖向振动分析模型见图1。目前,关于车辆竖向振动分析模型,一般模拟为车体、前后转向架及4个轮对的多刚体系统,且以10个自由度(即车体转角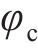
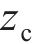
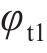
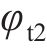
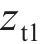
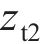
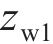
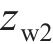
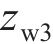
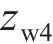
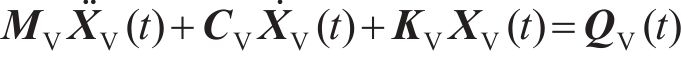
式中: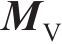

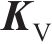
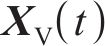
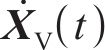
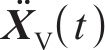
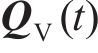
| 参数 | 取值 |
|---|---|
车体质量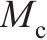 | 40 000 |
构架质量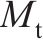 | 3 200 |
轮对质量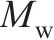 | 2 400 |
车体点头惯量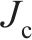 | 5.47×105 |
构架点头惯量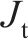 | 6 800 |
一系弹簧刚度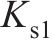 | 2.08×106 |
二系弹簧刚度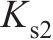 | 0.8×106 |
一系阻尼系数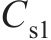 | 1.0×105 |
二系阻尼系数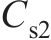 | 1.2×105 |
固定轴距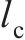 | 17.375 |
构架中心距离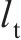 | 2.5 |
车轮半径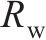 | 0.43 |
1.2 无砟轨道竖向振动分析模型
将无砟轨道视为三层叠合梁,路基不参与振动,只是考虑其顶面支撑刚度及阻尼的影响,基于有限元法建立的板式无砟轨道竖向振动分析模型如图1所示。将相邻2个扣件之间的轨道划分为1个单元,在每一单元中,又将钢轨视为离散黏弹性点支撑的二维梁单元,轨道板和支承层分别视为连续黏弹性支承的二维梁单元,忽略各个梁单元的轴向变形,只考虑节点的竖向位移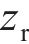
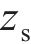
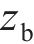
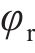
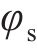
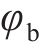
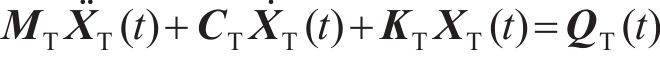
式中: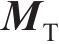

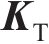
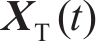
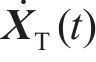
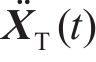
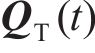
| 路基类型 | 参数 | 取值 |
|---|---|---|
| 钢轨 | 单位质量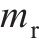 | 60 |
弹性模量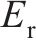 | 2.1×1011 | |
惯性矩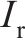 | 3.217×10-5 | |
| 轨道板 | 单位质量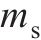 | 1275 |
弹性模量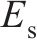 | 3.5×1010 | |
惯性矩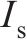 | 6.7×10-4 | |
| 混凝土支承层 | 单位质量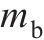 | 2213 |
弹性模量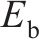 | 3.3×1010 | |
惯性矩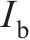 | 1.7×10-3 | |
| 扣件和垫板 | 刚度系数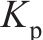 | 6×107 |
阻尼系数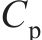 | 4.77×104 | |
间距 | 0.625 | |
| 水泥乳化沥青砂浆 | 刚度系数 | 1.25×109 |
阻尼系数 | 8.3×104 | |
| 路基 | 刚度系数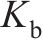 | 6×107 |
阻尼系数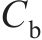 | 9×104 |
1.3 轮轨相互作用力模型
向俊等[18]针对铁道车辆受某跳轨诱因的情况,提出了车轮跳轨全过程可划分为4个阶段(如图2所示):轮轨正常密贴、轮轨分离、轮轨冲击和轮轨再次正常密贴。当列车正常行驶期间(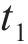
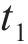
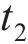
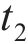
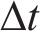
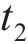
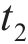
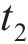
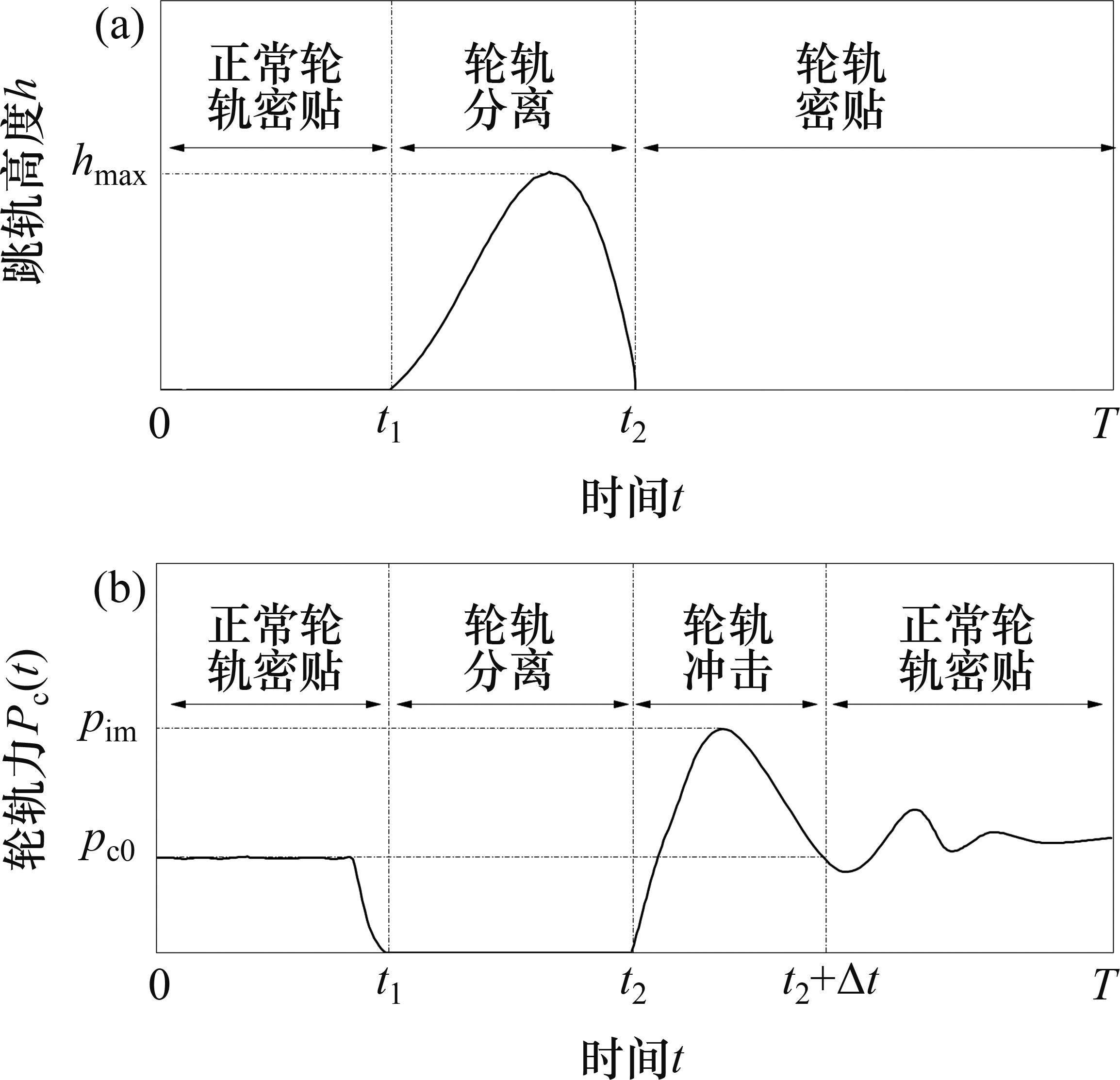
1.3.1 密贴与分离阶段轮轨力表达式
在正常密贴阶段,轮轨力一般采用Hertz非线性接触理论来计算;分离时,轮轨力则为零。
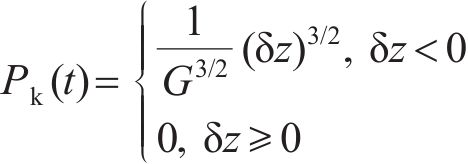
式中:G为轮轨接触挠度系数;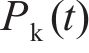
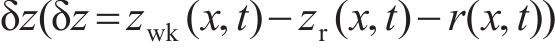
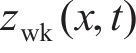
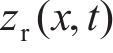
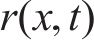
1.3.2 冲击阶段轮轨力表达式
如图2所示,在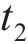
第一步:假设冲击阶段轮轨力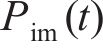
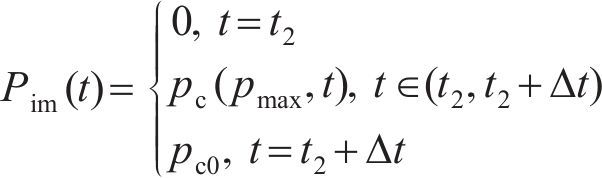
式中: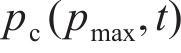
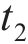
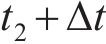
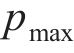
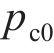
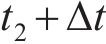
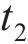
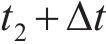
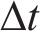
第二步:假设函数形式为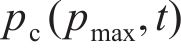
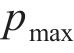
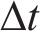
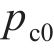
第三步:根据冲击结束时轮轨相对速度差,假设最小化目标函数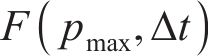
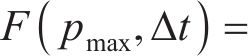
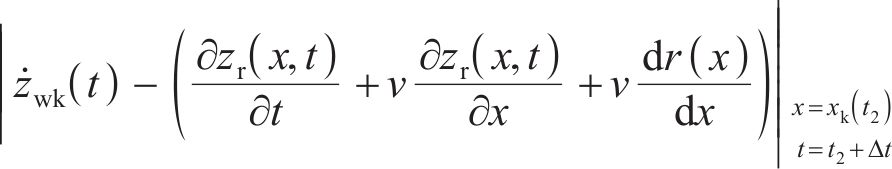
式中: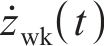
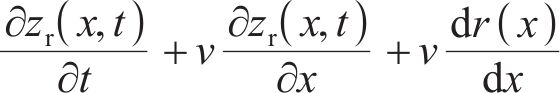
第四步:根据轮轨冲击结束时轮轨相对位移、轮轨相对速度及轮轨力的特征,分别建立式(6)~(12)所示约束条件(其中,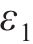
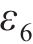
1) 轮轨相对位移的约束条件:
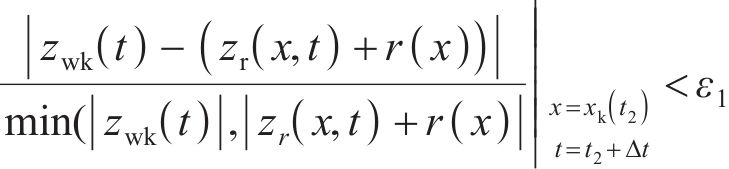
当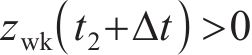
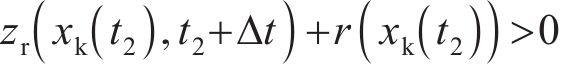
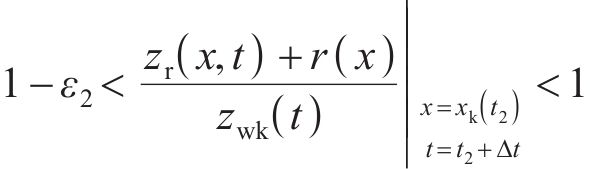
当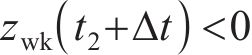
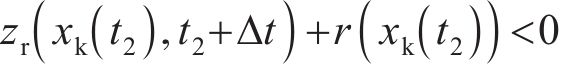
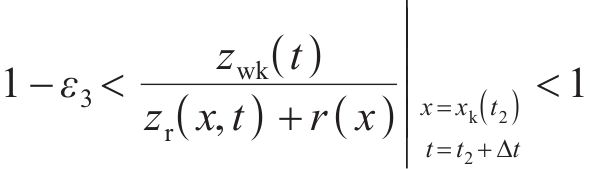
当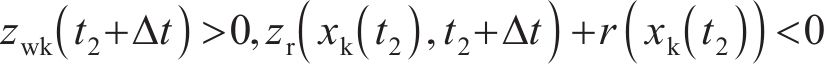
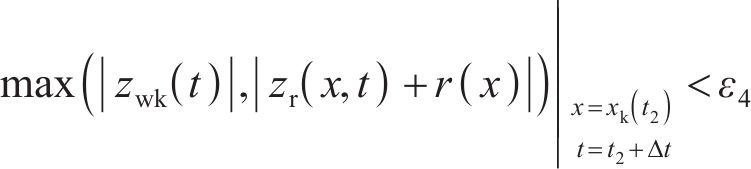
2) 轮轨相对速度的约束条件:
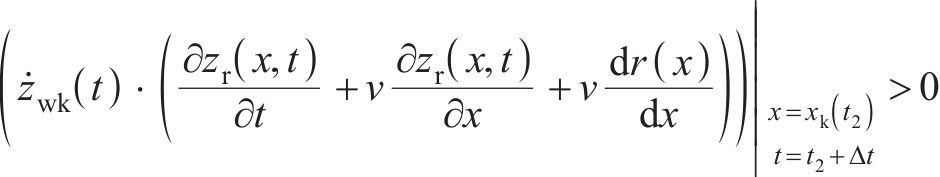
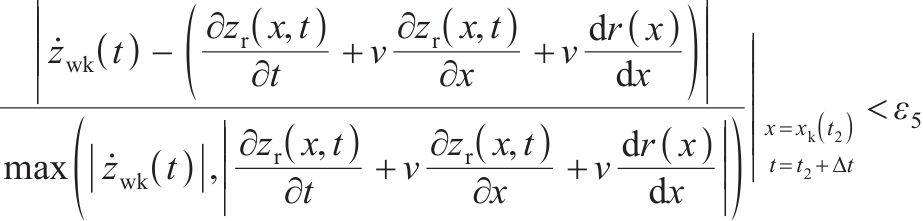
3) 轮轨力的约束条件:
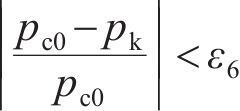
第五步:迭代循环寻找使目标函数达到最小值且满足所有约束条件的控制变量,即可确定冲击阶段轮轨接触力表达式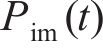
1.4 程序编制
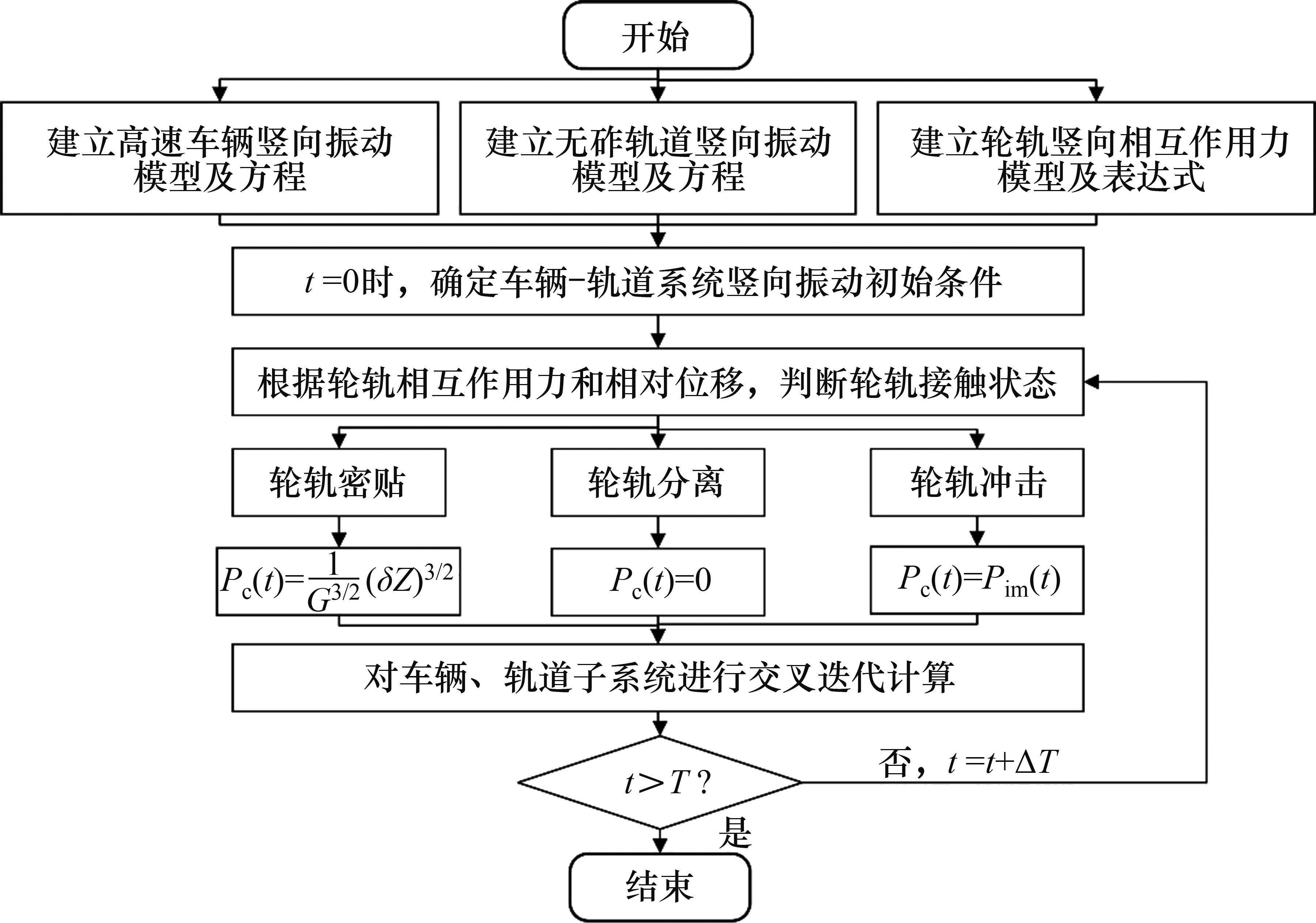
根据式(1)、(2)及1.3节的表达式,基于Wilson-θ法,对车辆、轨道子系统进行交叉迭代计算,采用Fortran语言编制高速车辆在无砟轨道上的跳轨全过程计算程序HRVJS。程序编制计算流程如图3所示,其中,T表示计算总时长,ΔT表示计算步长。程序HRVJS主要功能如下:1) 能够完整描述高速车辆在无砟轨道上的车轮跳轨全过程,并主要反映跳轨高度、跳轨时长、冲击力峰值、冲击力时长、钢轨最大加速度等核心指标;2) 能够分析跳轨诱因对车辆跳轨全过程的影响规律;3) 能够反映通常轮轨正常密贴状态下的车辆-轨道系统竖向振动响应;4) 为进一步研究跳轨脱轨机理乃至车辆跳轨控制奠定了良好基础。
2 初步验证
鉴于实际的高速车辆乃至高速列车的车轮跳轨试验数据难以获得,而关于高速车辆在无砟轨道上的跳轨全过程计算又鲜见报道,本文主要从如下3个方面对上述计算模型及程序进行间接校验,以便为后续规律性分析提供依据:1) 对轮轨密贴状态下的车-轨系统竖向振动响应进行对比分析;2) 对1个实例进行分析,实现高速车辆在无砟轨道上的车轮跳轨全过程计算;3) 对是否考虑轮轨冲击作用的影响程度进行对比分析。
2.1 轮轨密贴状态下的车-轨系统竖向振动响应对比分析
罗震[21]分别计算了CRH2型高速车辆以200、210、220 km/h在CRTS Ⅰ型板式无砟轨道上运行时的车-轨系统振动响应,并与遂渝线动力学试验结果进行比较,见表3。在整个计算过程中,发现轮轨力均大于零,说明车辆在运行过程中未出现跳轨现象。本文采用与文献[21]相同的计算参数及工况,所得计算结果见表3。从表3可见本文计算结果与文献[21]的计算结果及现场试验结果基本一致,说明上述计算模型及程序在反映轮轨密贴状态下的车-轨系统竖向振动响应方面具有可靠性。
2.2 高速车辆在无砟轨道上的车轮跳轨全过程计算
利用本文建立的高速车辆模型、无砟轨道模型、轮轨力模型以及所编制的计算程序HRVJS,对高速车辆在无砟轨道上的车轮跳轨全过程进行计算。具体采用参数及工况如下:结合我国高速铁路实际最高运行速度,车速v=350 km/h;实际车辆以CRH3型高速车辆为例,模型参数见表1;轨道以CRTSⅡ型板式无砟轨道为例,模型参数参见表2;轮轨力模型参见1.3节,其中冲击力函数假定如下:
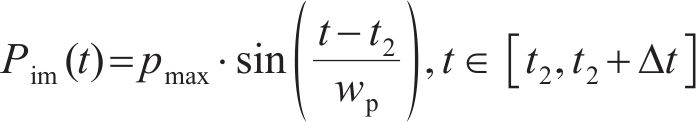
式中: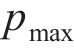
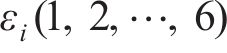
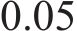
跳轨诱因仅考虑了一个急剧不平顺,设置于轨道计算长度(L=375 m)的中间L/2处,具体为1个凹形单波余弦型轨面不平顺函数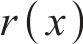
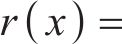
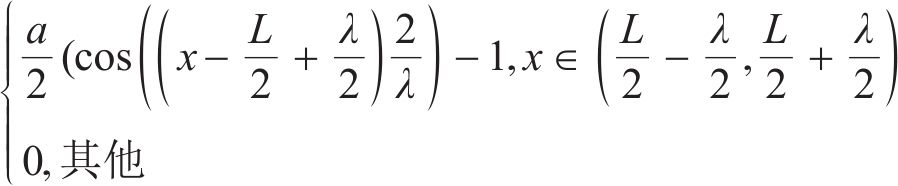
图4所示为高速车辆在无砟轨道上的车轮跳轨全过程时程曲线。图4中,T为总计算时长;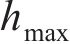
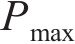
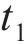
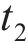
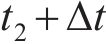
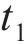
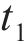
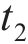
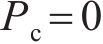
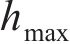
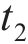
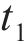
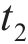
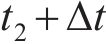
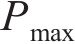
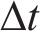
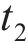
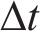
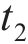
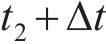
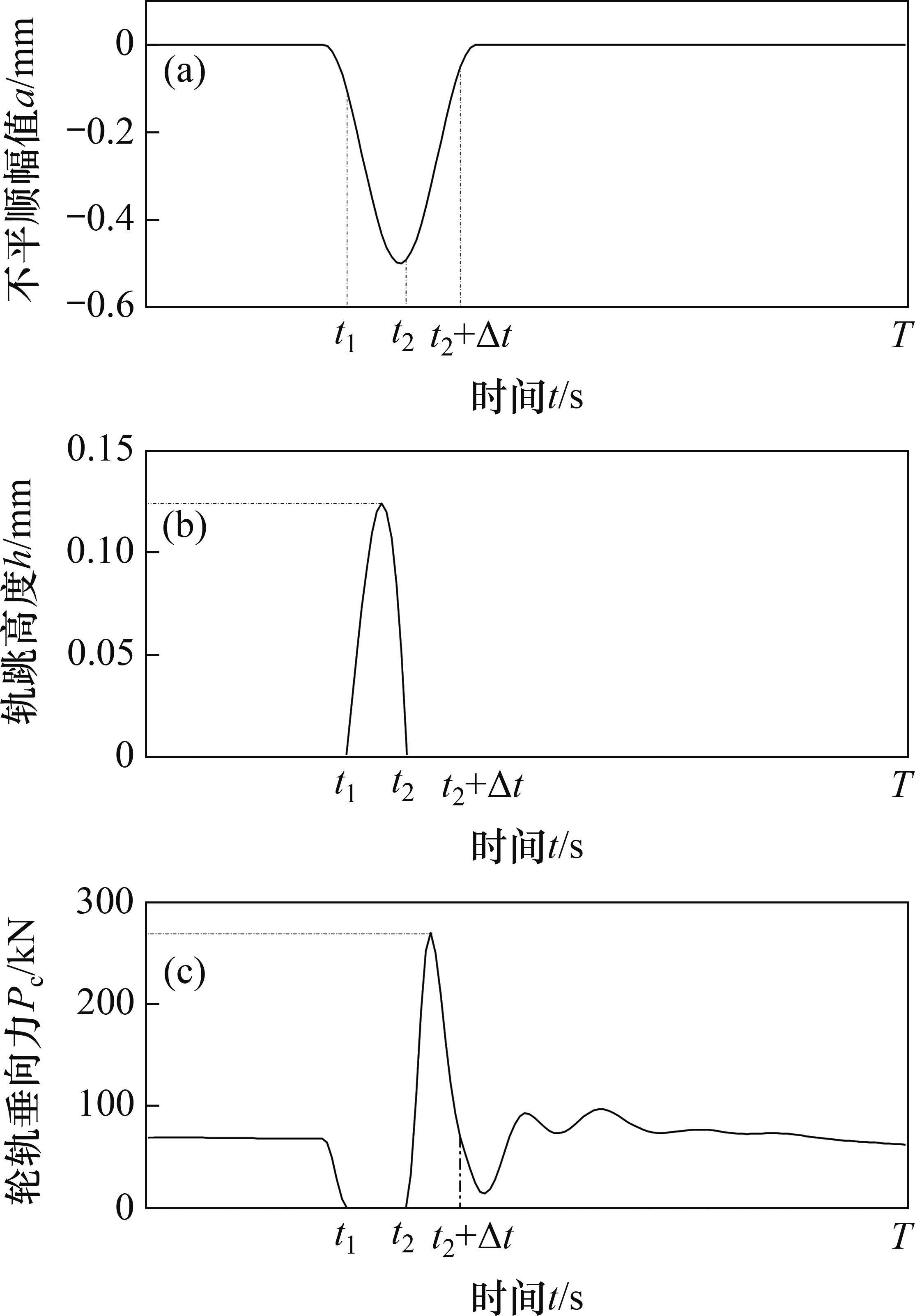
2.3 是否考虑轮轨冲击作用的比较
车轮跳轨全过程计算的关键在于是否考虑了轮轨冲击作用。为此,分别计算是否考虑轮轨冲击作用的车-轨系统振动响应。
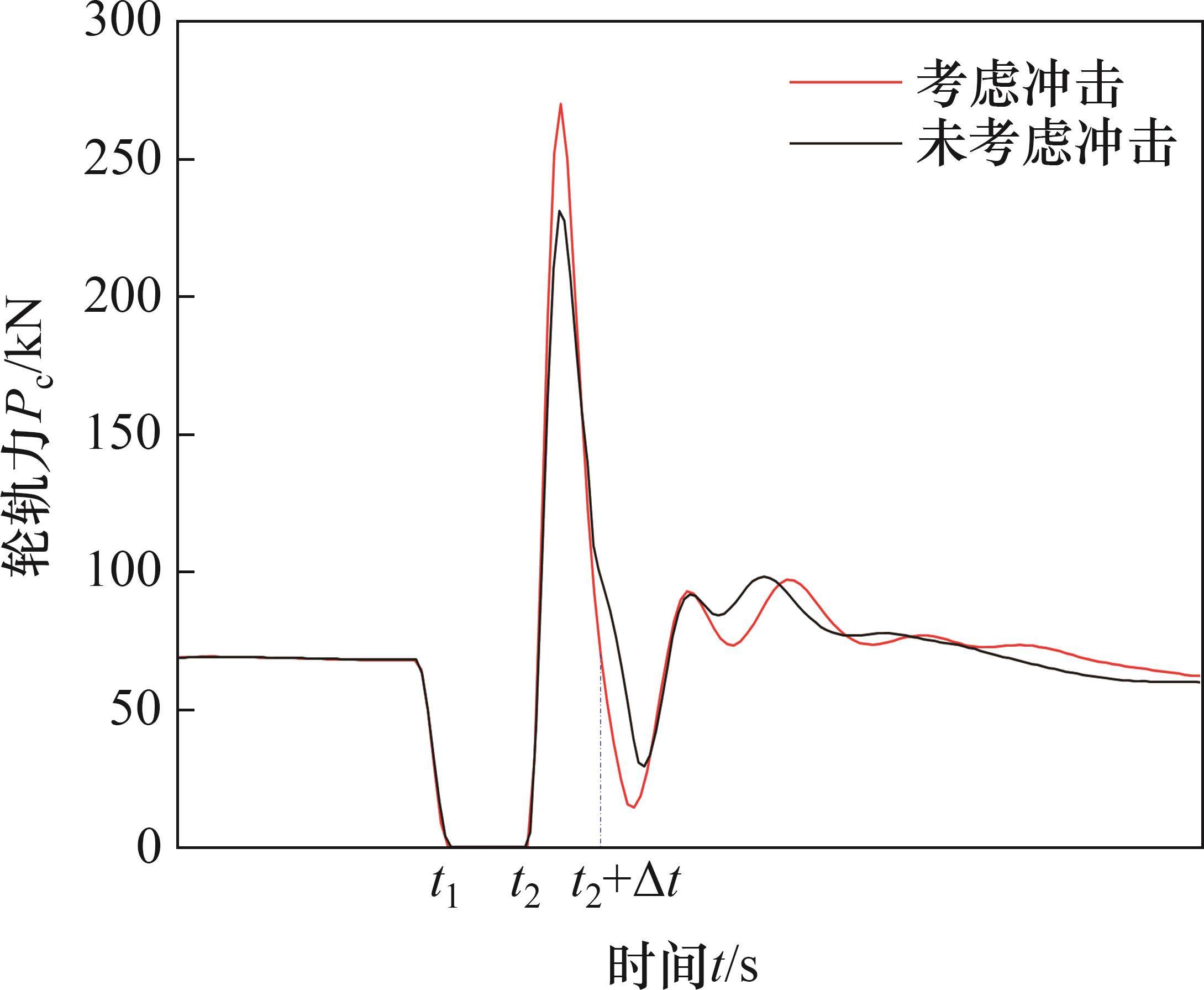
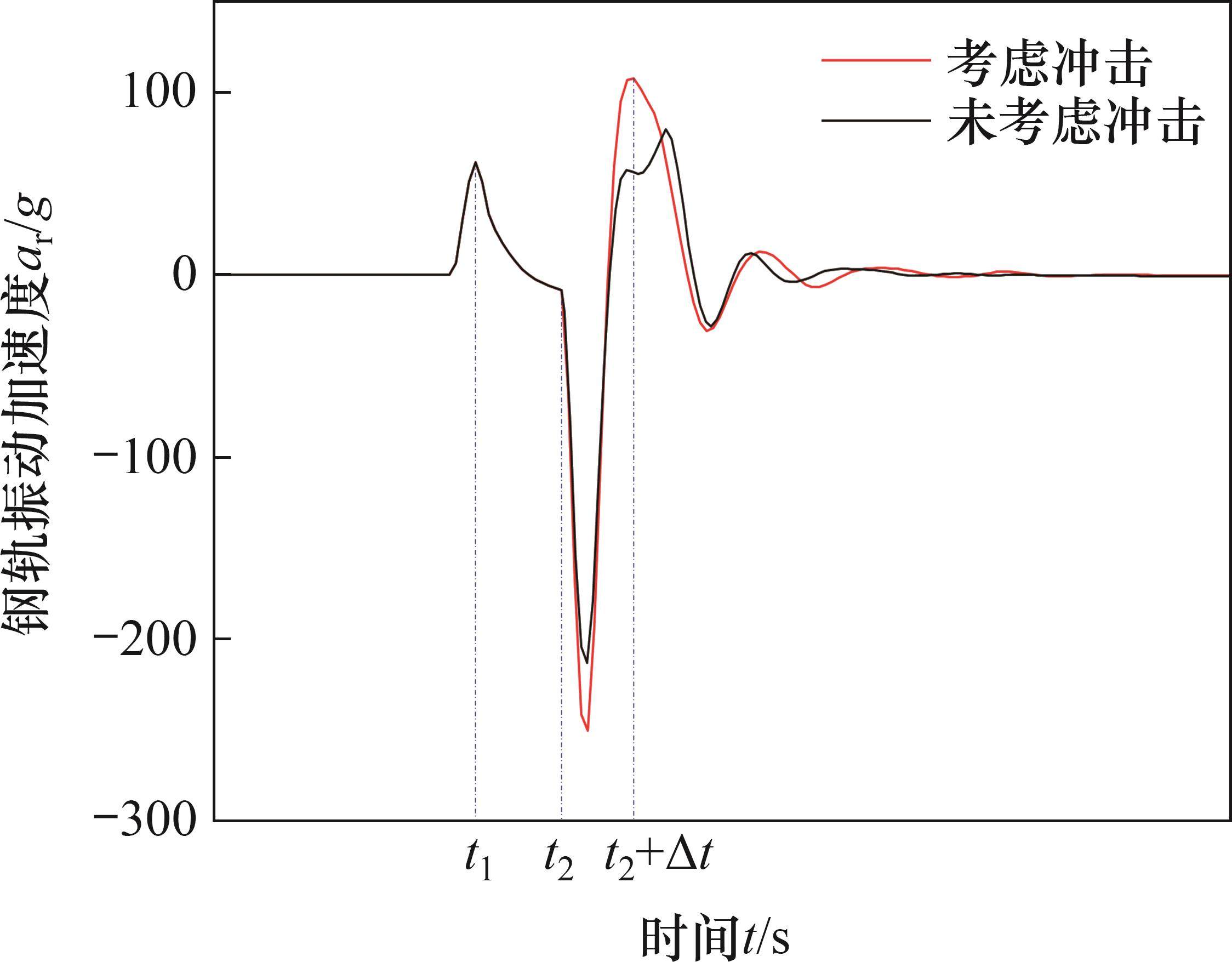
考虑轮轨冲击作用的计算直接采用2.2节的中的计算式。在不考虑轮轨冲击作用的计算中,仅考虑轮轨正常密贴、轮轨跳轨及轮轨正常密贴这3个阶段,换言之,仅使用式(3)表示轮轨相互作用力模型及表达式,其他计算条件与2.2节中的相同。比较时,重点考察轮轨力及钢轨加速度这2个指标的时程曲线,其计算结果分别如图5及图6所示。图5及图6在波形的变化趋势上有相似之处,但由图5可见,考虑冲击作用的最大轮轨力为 270 kN,不考虑冲击作用的最大轮轨力为231 kN,两者相差39 kN。从图6可见,考虑冲击作用的最大钢轨加速度为250.306g(1g=9.8 m/s2),不考虑冲击作用的最大钢轨加速度为212.939g,两者相差37.367g。这表明考虑轮轨冲击作用的计算结果要远大于不考虑轮轨冲击作用的计算结果,且这2个指标将直接影响车辆及轨道结构的振动特性。
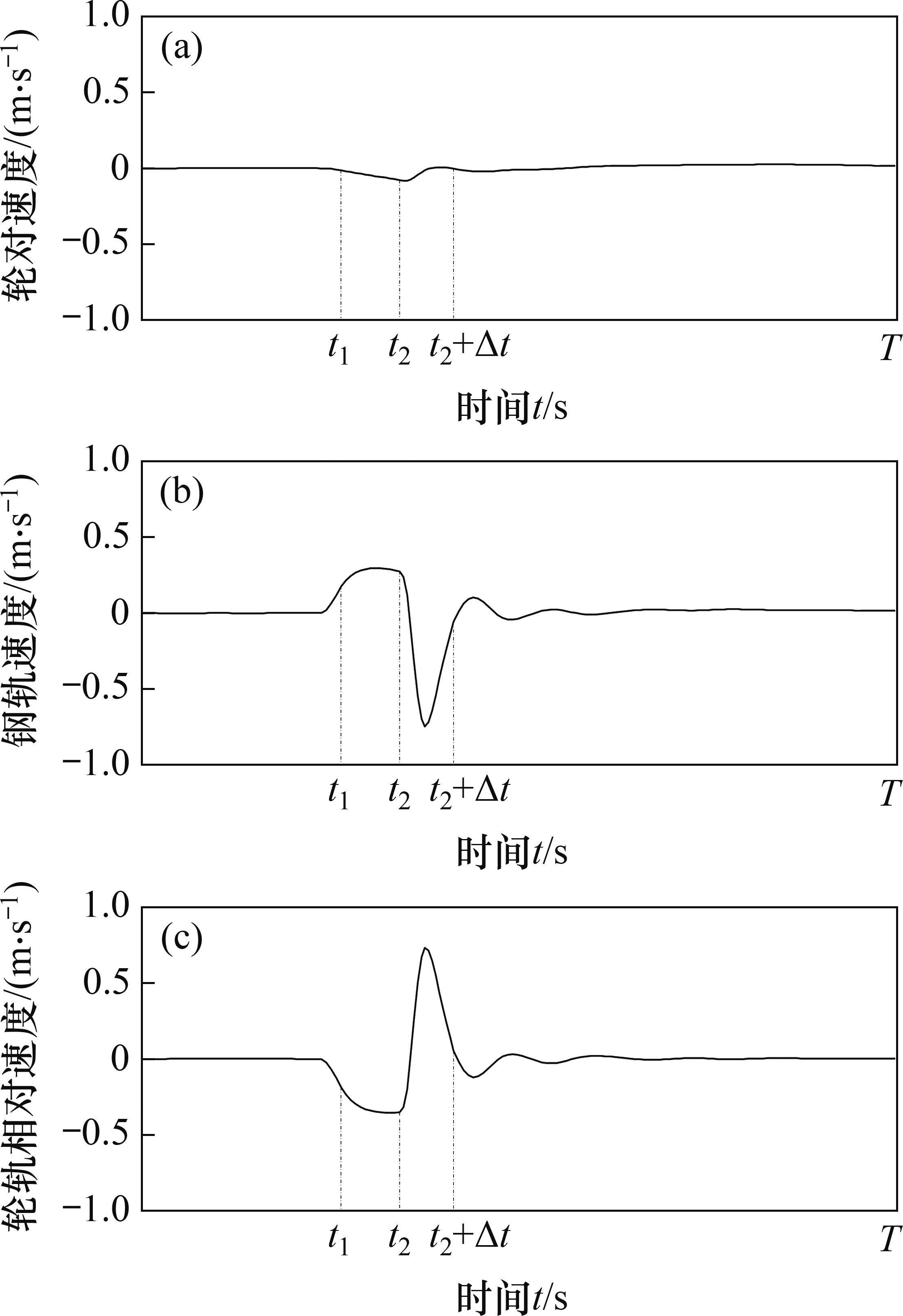
轮对速度、钢轨速度及轮轨相对速度时程曲线见图7。从图7(c)可见:轮轨之间出现了相对速度差的现象,特别地,在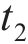
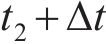
3 轨面急剧不平顺对高速车辆跳轨的影响分析
研究结果与经验表明,轨道竖向几何不平顺将直接引起车辆-轨道系统竖向振动,且随着不平顺波长缩短、波幅增大,引起的振动响应越大,甚至会导致轮轨分离(也称车轮跳轨,而对于波长越短的不平顺,一般称为轨道急剧不平顺)。本文重点讨论轨面急剧不平顺对高速车辆跳轨的影响规律,同时,从高速车辆跳轨控制功能方面,对高速铁路钢轨表面质量缺陷深度容许偏差及钢轨焊缝平直度要求[22]进行评估。
利用计算程序HRVJS,考虑CRH3型高速车辆以350 km/h速度在CRTSⅡ型板式无砟轨道上的实际运营情况,有关车辆及轨道参数取值分别见表1与表2。轨面急剧不平顺采用式(14)描述,分别以《高速铁路线路维修规则》[22]中的钢轨表面质量缺陷深度(代表凹形不平顺)及焊接后钢轨表面平直度(代表凸形不平顺)为例,式(14)中的不平顺幅值r若取正值,则表示凸形,若取负值,则表示凹形。根据文献[23-25],高速铁路的轨面急剧不平顺波长一般大于100 mm,而波长小于100 mm的短波 不平顺主要发生于重载铁路钢轨磨耗区。因此,本文考虑的轨面急剧不平顺波长范围λ=0.15~1.0 m,波幅范围a=0~2.0 mm。
3.1 凹形不平顺的影响
当波幅a=0.5 mm、波长λ=0.15~1.0 m时,凹形不平顺波长对高速车辆跳轨的影响规律如图8所示。从图8(a)可见:当0.15≤λ≤0.4 m时,随着λ减小,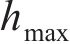
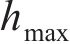
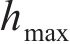
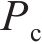
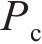
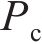
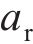
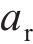
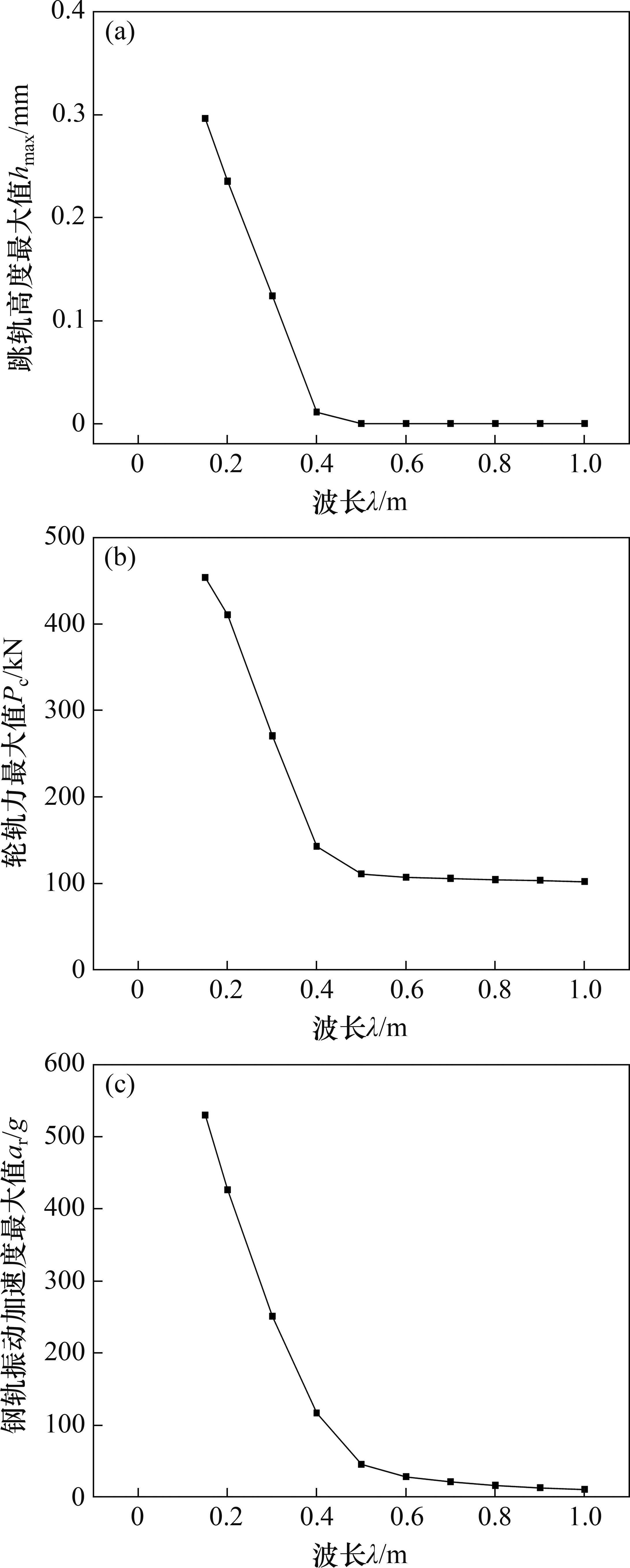
当波长λ=1.0 m、波幅a=0~2.0 mm时,凹形不平顺波幅对高速车辆跳轨的影响规律如图9所示,从图9(a)可见:当a>1.0 mm时,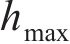
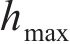
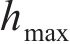
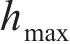
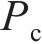
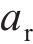
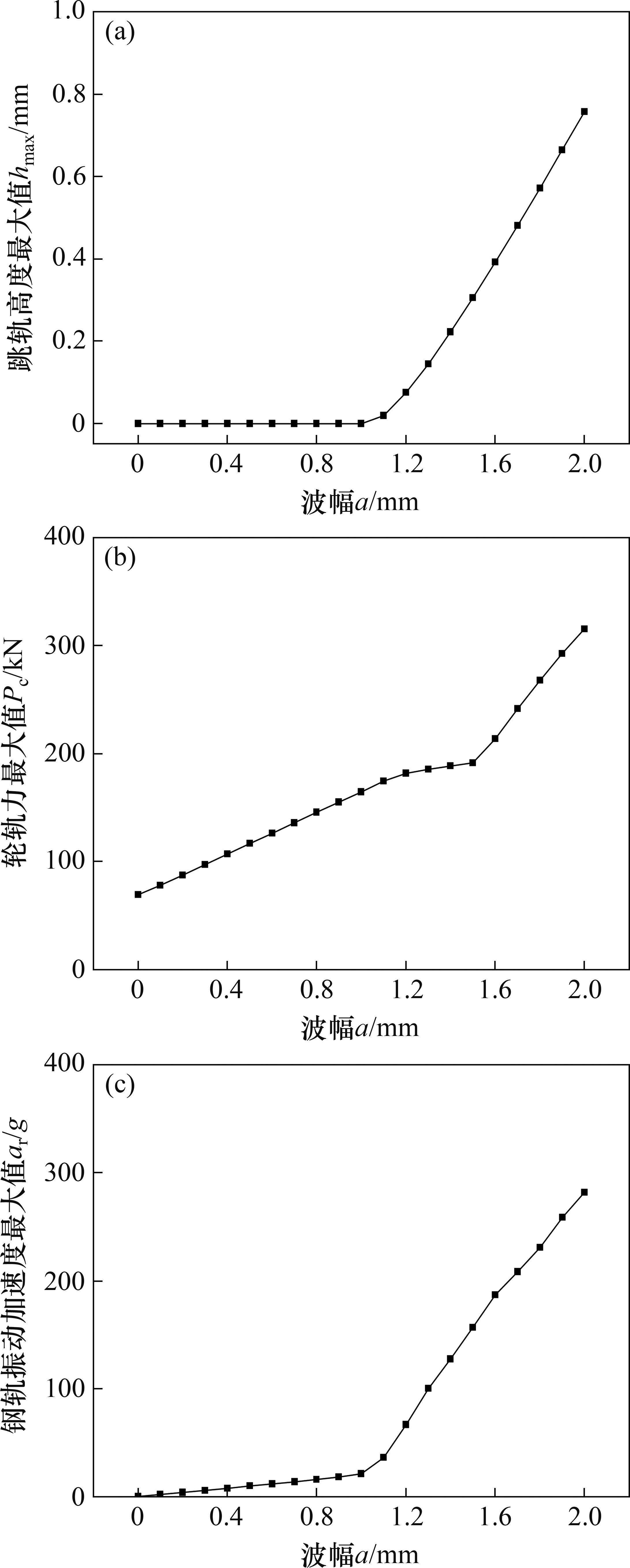
在《高速铁路线路维修规则》[22]中,规定钢轨表面质量缺陷深度的偏差管理值最小不超过 0.3 mm,最大不超过0.5 m,而对波长未明确规定。由图9(a)可见,参照焊接后钢轨表面平直度波长采用1.0 m的管理标准,要使车辆出现跳轨,必须使a>1.0 mm;当波幅a=0.5 mm时,跳轨高度最大值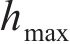
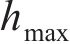
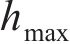
3.2 凸形不平顺的影响
当波幅a=0.30 mm、波长λ=0.15~1.00 m时,凸形不平顺波长对高速车辆跳轨的影响规律如图10所示。从图10(a)可见:当0.15≤λ<0.30 m时,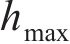
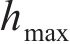
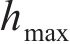
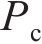
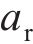
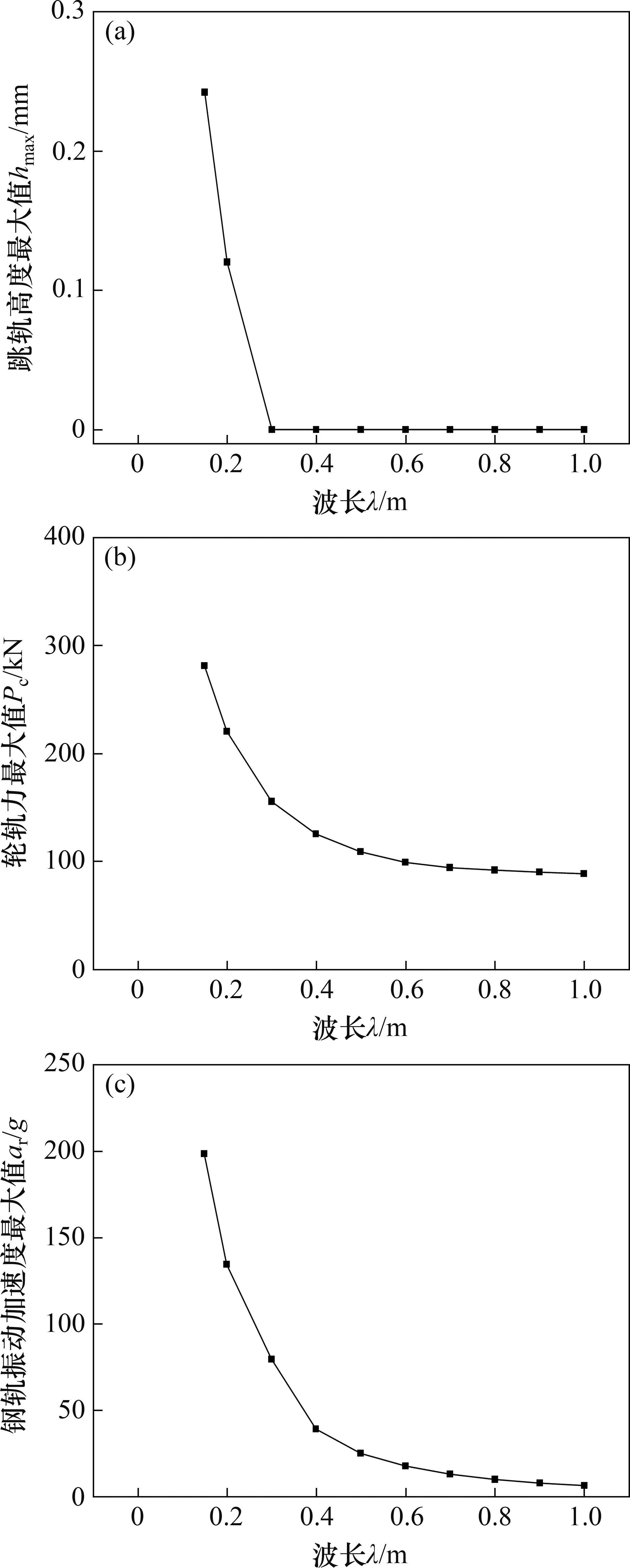
当波长λ=1.0 m、波幅a=0~2.0 mm时,凸形不平顺波幅对高速车辆跳轨的影响规律如图11所示。从图11(a)可见:当a>0.8 mm时,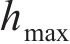
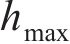
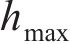
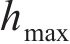
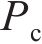
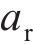
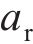
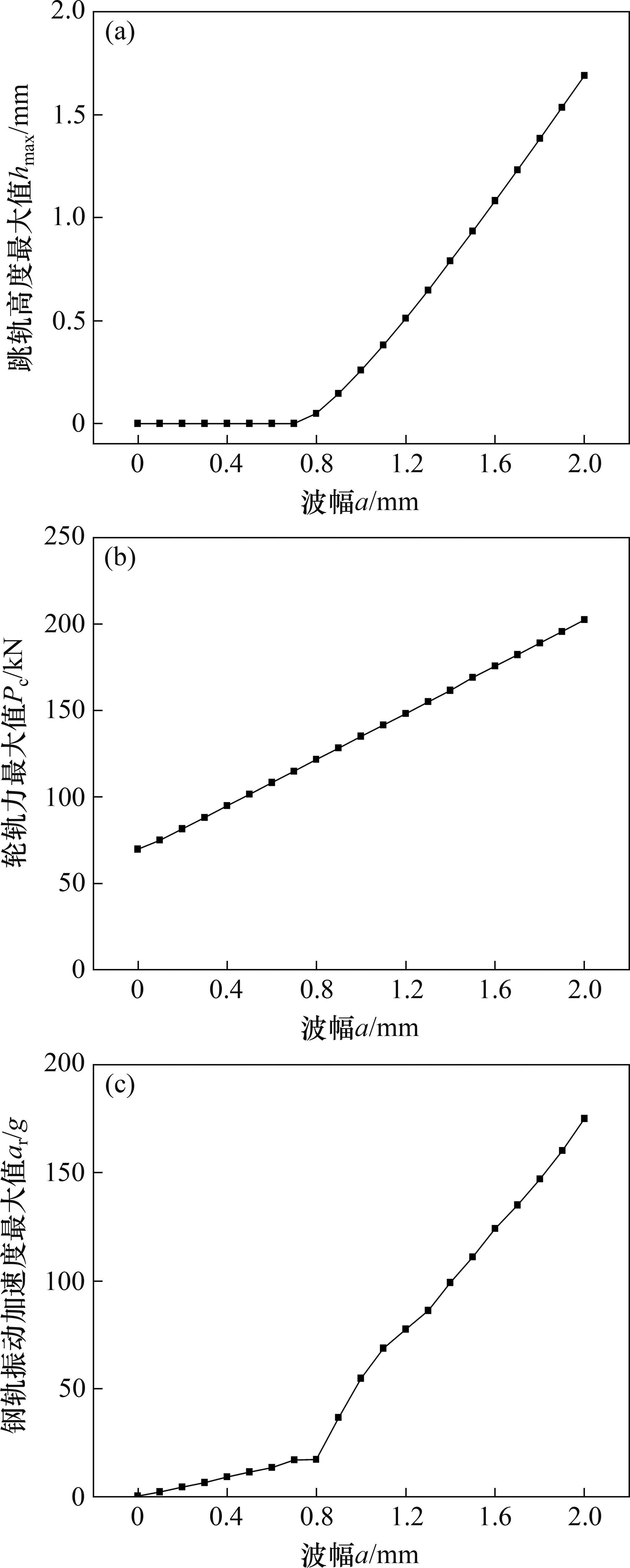
在《高速铁路线路维修规则》[22]中,有关焊接后钢轨表面平直度管理值规定为:最大波幅值不超过0.3 mm,且波长为1.0 m。从图11(a)可见,当波长λ=1.0 m、波幅a=0.3 mm时,跳轨高度最大值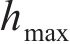
4 结论
1) 本文建立的模型及编制的程序能够完整地描述高速车辆跳轨的动力学轮轨密贴—轮轨分离—轮轨冲击—轮轨再次密贴全过程,并能全面反映高速车辆跳轨的特征指标如跳轨高度、跳轨时间、轮轨冲击力、冲击作用下的钢轨加速度和速度及位移等。
2) 当CRH3型高速车辆以350 km/h在CRTS Ⅱ型板式无砟轨道上运行时,在轨面急剧不平顺作用下,高速车辆一旦出现跳轨现象,将随着不平顺波长减小,跳轨程度加剧;随着不平顺波幅增大,跳轨程度也加剧。
3)《高速铁路线路维修规则》中有关焊接后钢轨表面平直度管理值不但能够保证高速车辆不跳轨,而且距离跳轨尚有57%的安全余量;另外,要使《高速铁路线路维修规则》中有关钢轨表面质量缺陷深度管理值具有高速车辆跳轨控制功能,建议增加与深度配套的长度指标管理值。具体建议值有待进一步研究。
向俊, 梁洁林, 龚凯, 等. 高速铁路无砟轨道车辆跳轨全过程计算[J]. 中南大学学报(自然科学版), 2024, 55(12): 4711-4722.
XIANG Jun, LIANG Jielin, GONG Kai, et al. Calculation of the whole process of vehicle jumping off ballastless track of high-speed railway[J]. Journal of Central South University(Science and Technology), 2024, 55(12): 4711-4722.

