铁路有砟道床由一定级配的碎石道砟组成,道砟颗粒嵌挤形成的多孔隙结构可以保障碎石道床良好的弹性及渗透性。ROSA等[1]发现在相同的运营条件下,道砟级配会影响道床的耐久性,当道床中的孔隙被小粒径脏污颗粒填满时,就会引发道床排水不畅、基床翻浆等病害,进而缩短道砟的服役寿命[2]。此外,在不同线路运营条件、不同线下基础条件下,道砟的级配也应有所不同,例如北美铁路主要以重载为主,但规范中[3]规定了5种级配以适应不同的线路条件。我国TB 2104.2—2018[4]中仅有特级、一级2种级配,而在有砟道床清筛换砟时,采用孔隙较小的宽级配道砟相比于标准中的窄级配特级道砟更有利于道床的稳定,且服役寿命更长。GUO等[5]也发现道砟颗粒特性与耐磨耗性能存在较强的关联。综合而言,现有道砟级配难以满足我国复杂运营条件对于道砟级配的多元化需求,亟需对此进行研究。
铁路道砟级配设计不同于其他碎石集料级配设计,需要同时考虑承载力需求以及较大的孔隙率以满足道床渗透性需求。但当道砟颗粒间的孔隙过大时,又会导致颗粒嵌挤不密实,道床在循环荷载作用下易发生不均匀沉降的问题。因此,如何使道床内部孔隙均匀、结构整体孔隙率合理,也成为了道砟级配设计时需要重点考虑的因素。传统土工试验中的灌水法等方法误差较大,且无法考虑道砟颗粒随机复杂外形的影响,从而难以用于分析不同道砟级配的细观孔隙结构特征。可见,对道砟孔隙的细观空间分布规律的解析是铁路道砟级配设计中的难点。为解决这一难题,国内外学者采用离散元法[6]进行了研究,孙珊珊等[7]采用扩展多面体对道砟在循环荷载下的力学行为进行了研究,但尚未从细观角度分析道砟级配的孔隙特征,BIAN等[8]通过离散元法对不同级配的道砟试样的力学特征进行了研究,并认为均匀的级配具有较大的孔隙,但尚未开展道砟孔隙随高度的分布关系的研究。D'ANGELO等[9]发现道砟的孔隙分布对于外加材料固化道床产生了重要影响,决定了成型后轨道结构的力学行为。DELGADO等[10]发现采用缩尺级配的钢渣道砟相比于传统道砟具有更好的力学性能。KAMANI等[11]认为颗粒形态是影响道砟耐破碎性能的重要因素。
综合而言,国内外学者对于不同级配道砟颗粒孔隙特征及空间分布规律的研究分析较少。此外,由于道砟在工程实际中属于分层密实的结构,在列车荷载下又呈现出上部受压的特点,其孔隙率随高度的分布往往不同,既有研究均未能对道砟集料孔隙随试样高度变化进行精准分析,导致不同级配道砟集料孔隙率难以精确量化。我国规范中道砟级配设计曲线缺乏多样性。
尽管目前对于铁路道砟孔隙空间分布特征的研究有限,但近年来,在工程材料组构解析方面,国内外学者尝试采用X-Ray CT等技术开展了大量研究工作。MASAD等[12]采用CT扫描研究了不同压实方法对沥青混凝土试样孔隙分布的影响。LOEFFLER等[13]从准三维角度提出了一种能提升CT扫描混凝土试样裂缝特征的分析方法,但仅能对小孔隙的特征进行分析。秦武等[14]通过图像识别的方法针对长×宽为100 mm×100 mm混凝土试样进行了图像分析,并在此基础上建立了有限元模型,分析了骨料分布对混凝土破坏的影响。汪海年等[15]通过X-Ray CT技术对沥青混合料扫描结果的影响因素进行了研究,认为图像质量会随试样尺寸增大而下降。张蕾等[16]通过工业CT扫描技术研究了不同级配水泥的裂纹扩展规律,认为混合料的孔隙特征值随4.75 mm以下细颗粒的含量增大而呈现出先减小后增大的趋势。
综上所述,CT、图像识别等手段可较好地实现沥青、混凝土等小粒径骨料工程材料的组构分析。但由于道砟颗粒外形的随机性以及大粒径道砟颗粒所形成的尺度效应,传统的CT扫描、图像分析手段难以适用于道砟集料细观空间结构特征的分析。基于X射线的CT研究手段成本较高,探索新的数值分析方法以实现颗粒集料细观特征的组构解析具有重要的意义[17]。本文提出一套基于离散单元法与图像识别技术相融合的道砟骨料空间孔隙率精细化解析方法。通过自编图像识别算法,实现基于图像的试样层间孔隙率精确解析,并结合离散元理论分析结果,研究不同级配道砟孔隙率与力学性能的关系。
1 道砟孔隙率测量及离散元模型建立
1.1 道砟级配设计及基于灌水法的孔隙率测量
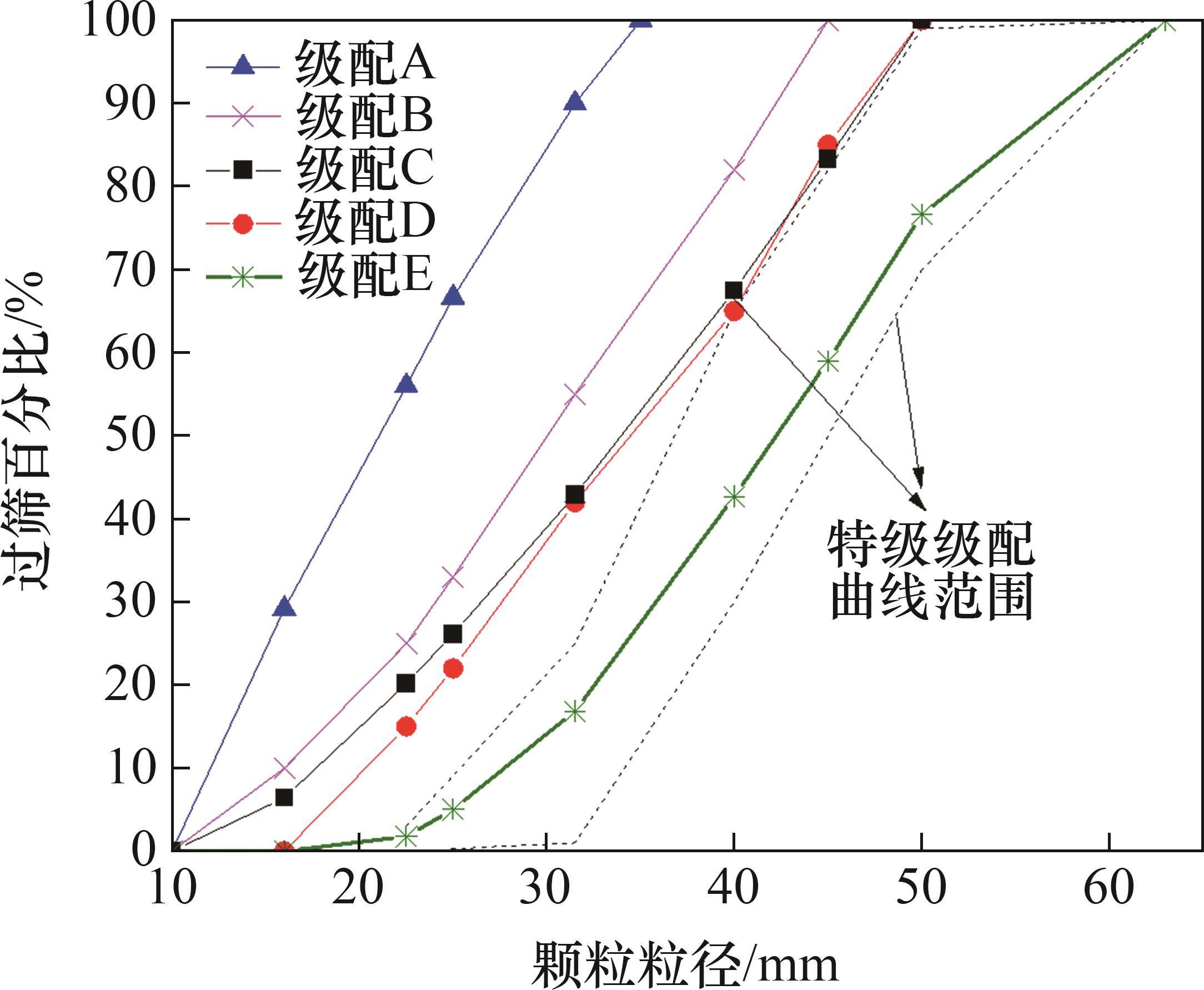
为分析不同级配道砟的力学性能差异,设计5组不同级配的试样,5组模型的过筛百分比曲线及与我国特级级配曲线的区间对比如图1所示。
在室内开展基于灌水法的孔隙率试验。为消除道砟材料的吸水性对试验结果的影响,在道砟颗粒达到饱和面干状态后进行试验,其试验具体步骤如下:1) 将道砟颗粒按照预定级配进行混合配比;2) 将道砟颗粒在纯净水中浸泡24 h,并对透明圆筒晾干;3) 将试样捞出摊平,采用毛巾吸取表面水分,使颗粒达到饱和面干状态;4) 将试样装入透明圆筒并手动振捣密实,直至道砟与圆筒顶部平齐;5) 采用量杯对试样灌水,当灌水高度为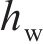
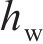
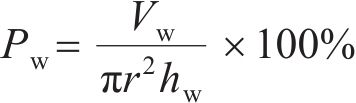
式中:r为圆筒试样的半径。分别计算并记录当灌水高度为35、105、175、245、315 mm以及灌满水时的试样孔隙率,道砟筛分配比过程如图2(a)所示,灌水后不同级配的道砟试样如图2(b)所示。

1.2 离散元模型的建立及验证
由于仅采用室内试验难以获得颗粒的细观组构特征,本文建立了相应的离散元模型,并采用室内试验获得的结果理论模型进行验证。由于采用组合球单元模拟复杂道砟颗粒外形的传统方法难以考虑由道砟颗粒棱角所导致的体积误差,参考文献[18-20],采用激光扫描法精确获取道砟颗粒的棱角特征,并通过三维点云求得道砟颗粒的体积。采用多面体单元本构对道砟颗粒间的相互作用进行分析,以准确模拟道砟颗粒的细观接触行为。道砟颗粒的三维重建过程如图3所示。

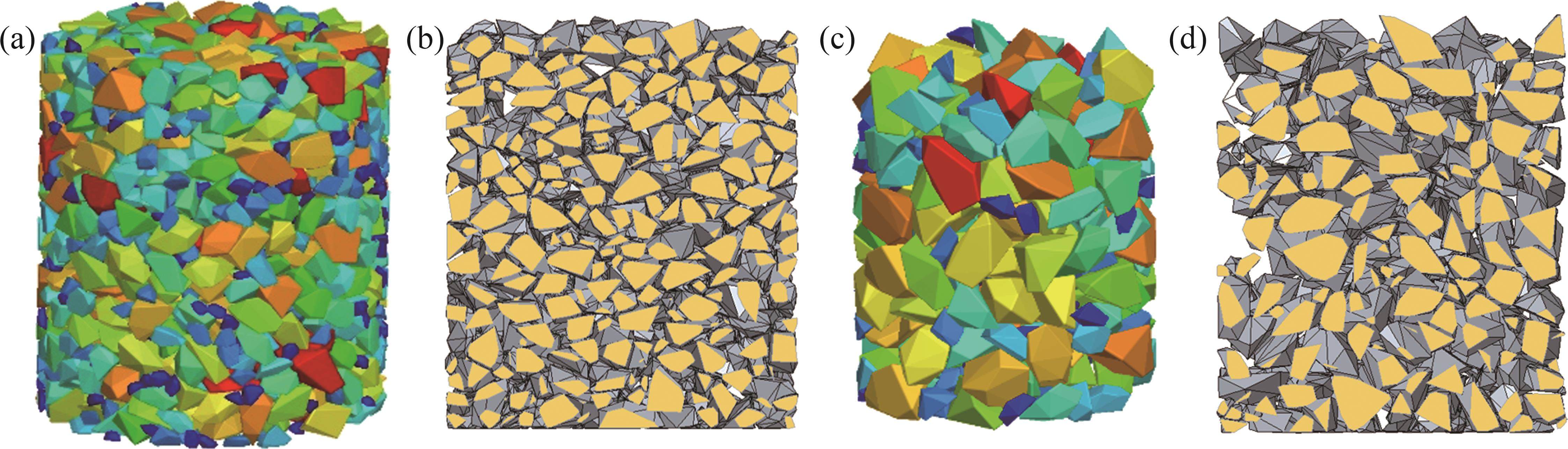
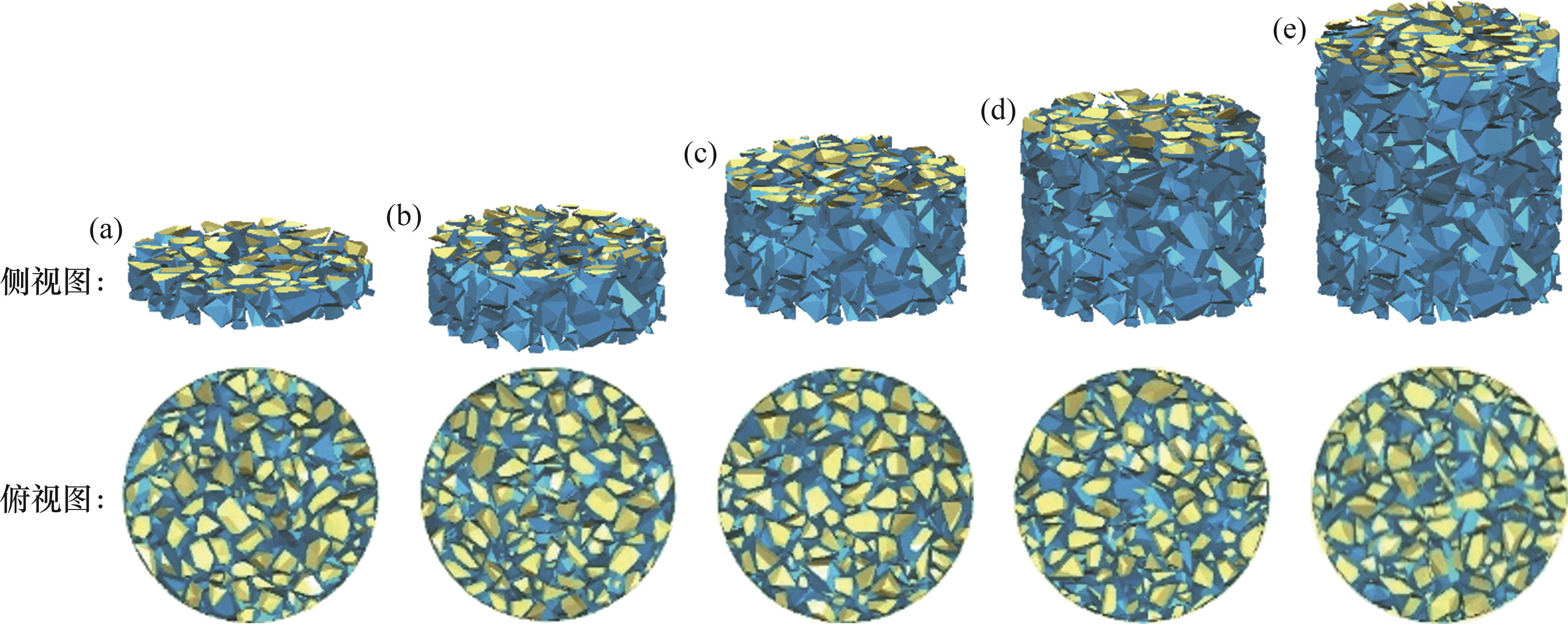
基于三维扫描获得道砟颗粒多面体单元建立直径为300 mm、高度为350 mm的圆筒试样离散元模型。模型的建立过程主要分为如下4步:1) 建立直径为300 mm、高度为700 mm的刚性无盖圆筒边界;2) 按照预定级配在圆筒内生成道砟颗;3) 在重力作用下使道砟颗粒自由下落,且堆落高度达到500 mm以上;4) 删除高度为350 mm以上的道砟颗粒,以确保数值模型与室内试验试样高度一致。试样稳定后级配A及级配D道砟的离散元模型如图4所示。
不同级配离散元模型的道砟孔隙率按下式进行计算:
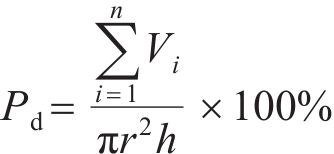
式中: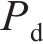
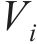
| 参数 | 值 |
|---|---|
| 道砟颗粒法向接触刚度/(N∙m-1) | 0.82×108 |
| 道砟颗粒切向接触刚度/(N∙m-1) | 0.52×108 |
| 边界法向接触刚度/(N∙m-1) | 1×108 |
| 边界切向接触刚度/(N∙m-1) | 1×108 |
| 道砟颗粒的密度/(kg∙m-3) | 2 700 |
| 道砟颗粒的摩擦因数 | 0.8 |
| 道砟与边界盒壁摩擦因数 | 0.1 |
不同道砟级配下孔隙率数值试验结果与理论分析结果对比如图5所示。
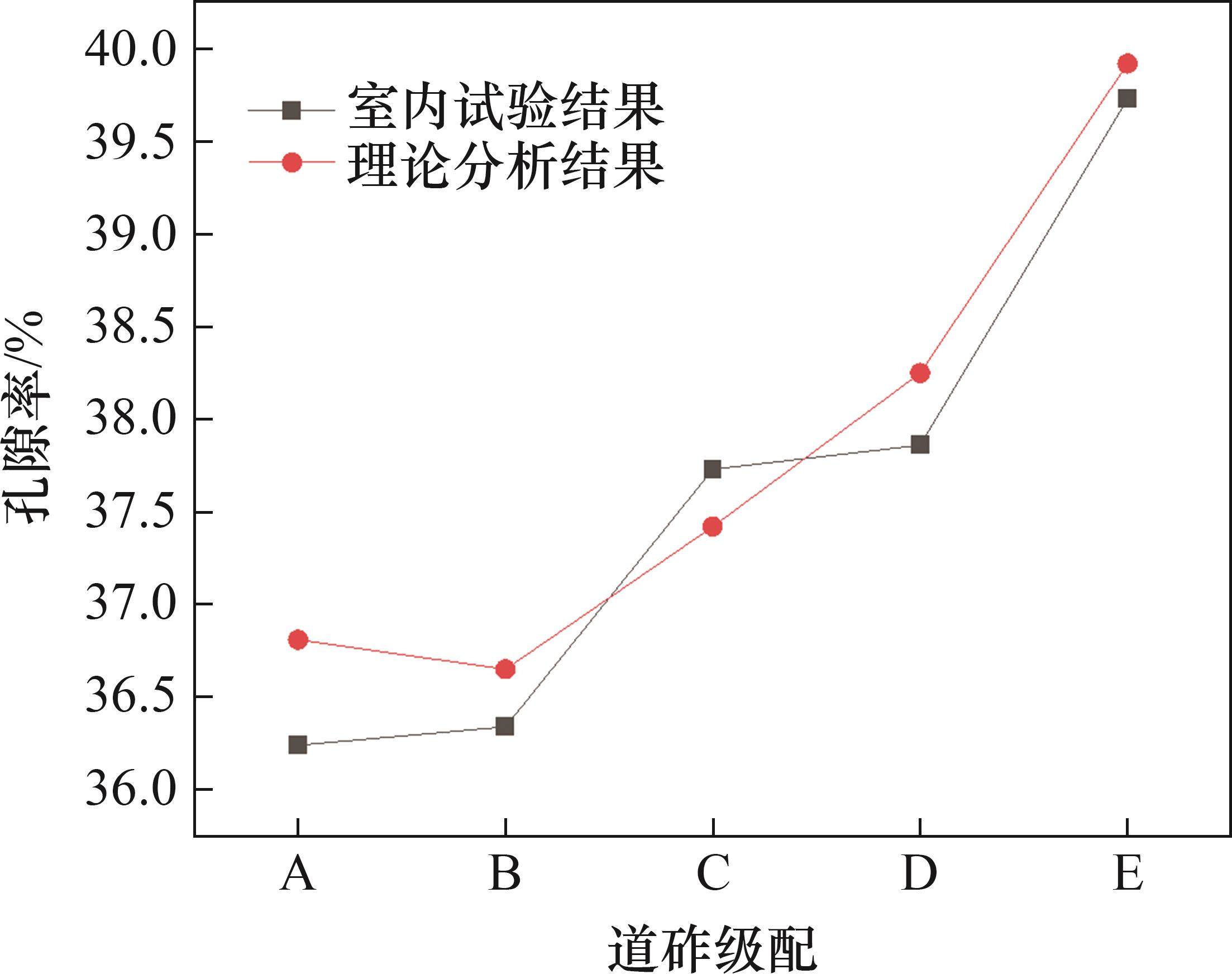
由图5可以看出:当采用表1的模型参数时,理论模型分析结果能较精确地表征室内试验结果。本文即采用验证后的理论模型开展研究工作。
2 基于图像灰度解析的道砟试样孔隙率算法
2.1 基于灰度解析的截平面图像孔隙率算法
上述离散元模型能较好地统计整体试样的孔隙率,但当试样被某个截平面切除时,既有算法难以分析截道砟颗粒的空间体积,KIM等[21]也仅通过二维图像对单个道砟颗粒的形貌进行了分析,无法解析孔隙率随试样高度的变化规律。为解决这一问题,本文研究提出一种基于道砟二维图像灰度特征对道砟试样三维层间孔隙率进行分析的方法。
以颗粒数量及细节最多的级配A试样作为标定试样,分别对高度为35、105、175、245、315 mm的试样做切平面,1~5层的试样的切平面如图6所示。
设被分析图像共有m×n个像素,将图像进行灰度处理,并将处理后的图像像素等效为共有m行n列的矩阵A。对于矩阵A中坐标为i、j的任意像素,当满足
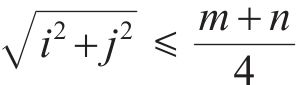
时,记录其灰度值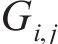
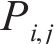
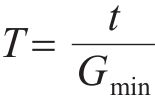
式中:t为图像判定阈值。
对B按照下式进行二值化处理:
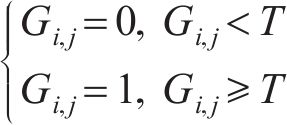
则对任意图像可得到1个仅包含0,1元素的二值化矩阵C。当选择不同T时,所得到的二值化图像图7所示,其中黑色部分为试样孔隙,白色部分为道砟。

设每组试样计算的二值化矩阵C共有z行、 y列,其中为0的元素数量为w个,定义Pp为该截空间的图像孔隙率,其计算式为
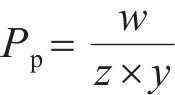
T的确定方法如下:当t在[Gmax,Gmin]之内时,有t=tmin使样本间孔隙误差Pe最小,将t=tmin代入 式(4),对应的T则为最优阈值。设被标定试样共有n个截空间图像,则Pe的计算式为
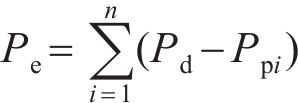
式中:Ppi为被标定试样第i个截空间的图像孔隙率。
2.2 截平面图像孔隙率算法的验证
基于上述算法得到的A级配试样图像孔隙二值化结果如图8所示。

对颗粒图像孔隙率与室内试验中灌水法测得的孔隙率进行相关性分析,所得结果如图9所示。
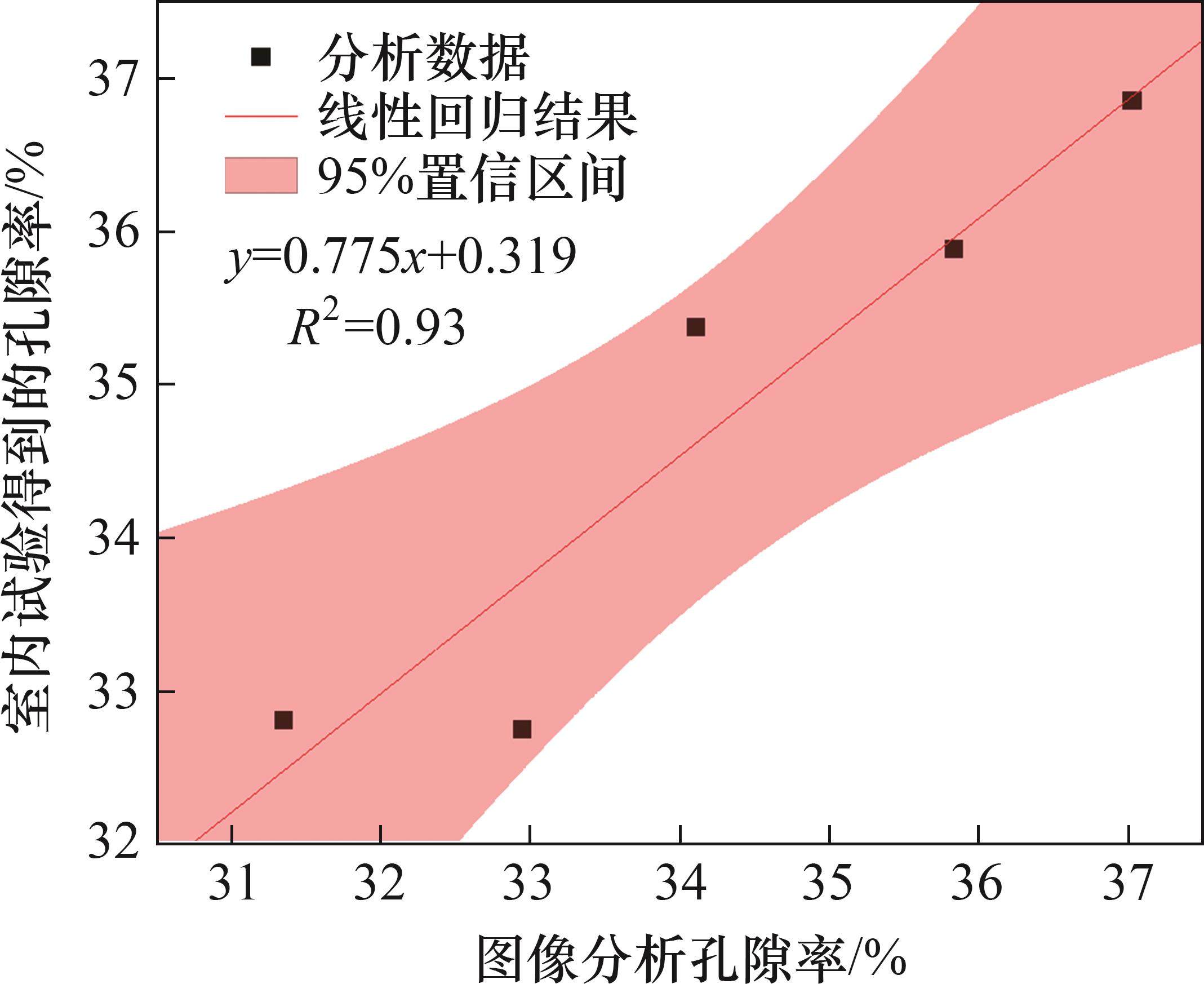
由图9可以看出:由本文所提出的基于灰度解析的图像孔隙率算法得到的孔隙率与室内试验所得孔隙率相关系数达0.93,说明该方法具有较高的准确度,可用于解决传统离散元分析难以获取道砟试样孔隙率随高度变化的难题。
3 级配对道砟几何及力学特性的影响
3.1 级配对道砟孔隙率的影响
为分析颗粒平均粒径对道砟试样孔隙率的影响,本文采用式(6)对5组道砟级配的5层孔隙率分别进行计算,并取其平均值作为该组级配的平均孔隙率。所得到的道砟平均孔隙率与道砟平均粒径的分析结果如图10所示。
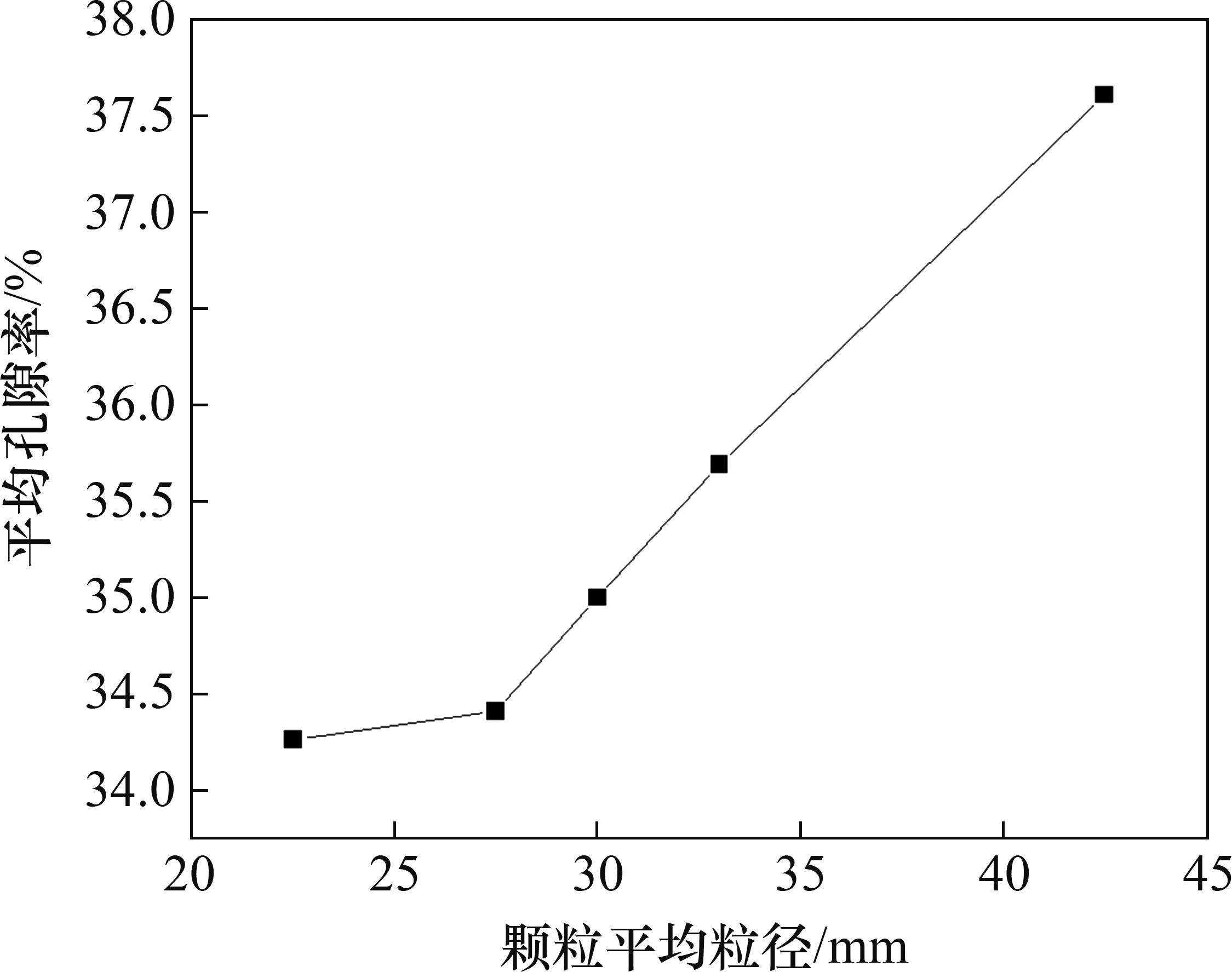
由图10可以看出:当道砟级配的平均粒径为27.5~42.5 mm时,试样平均孔隙率与颗粒平均粒径基本呈正相关关系;但当试样的平均粒径小于27.5 mm时,颗粒的平均孔隙率减小幅度会降低。
为进一步分析不同试样的孔隙率细观分布规律,研究不同级配层间孔隙率随高度的变化规律,如图11所示。
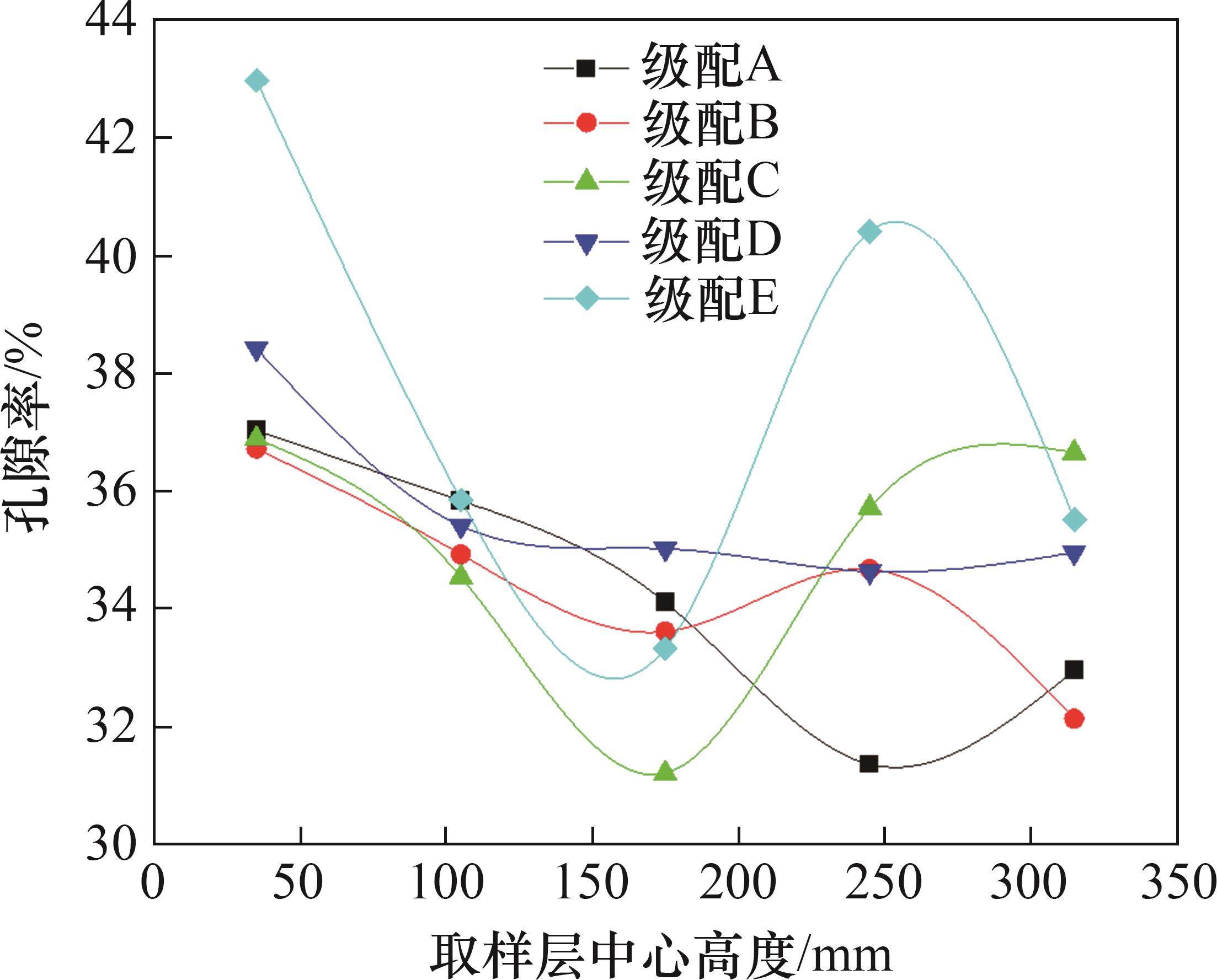
由图11可以看出:最底层的道砟孔隙率普遍较高,而最顶层的道砟孔隙率较低,这主要是试样上部受压所致,与工程实际中道床上部受轨枕荷载的情况一致。此外,不同级配试样的孔隙率均匀性差异较大。为分析层间级配孔隙率的均匀性,定义级配孔隙不均匀系数
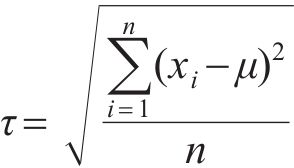
设将道砟试样沿高度方向截为n层,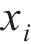
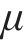
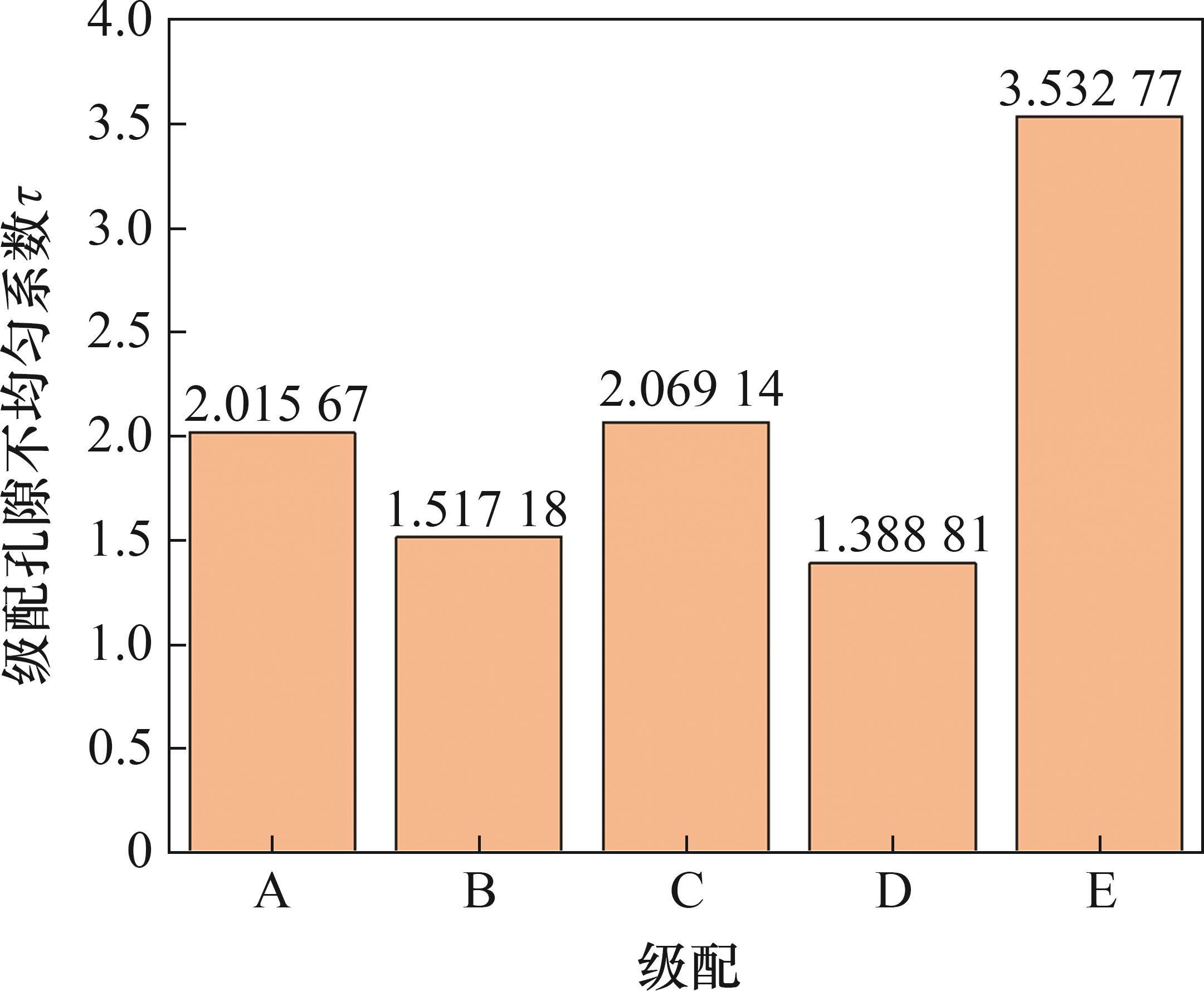
由图12可以看出:B、D组级配的层间孔隙均匀性较好,而颗粒平均粒径最大的E组级配具有较大的孔隙不均匀系数。
3.2 级配对道砟细观力学性能的影响
为研究不同级配试样的力学性能差异,通过在道砟试样离散元模型顶部加设刚性圆板,并以 2 kN/s的速率对其进行加载,分析5组不同级配的试样在荷载由20 kN增大至40 kN时的压缩变形量,所得结果如表2所示。试样变形量与试样平均粒径的关系如图13所示,试样变形量与级配孔隙率级配孔隙不均匀系数的相关性分析结果如图14所示。
| 级配 | 级配A | 级配B | 级配C | 级配D | 级配E |
|---|---|---|---|---|---|
试样变 形量/mm | 0.87 | 0.65 | 0.82 | 0.52 | 1.157 |
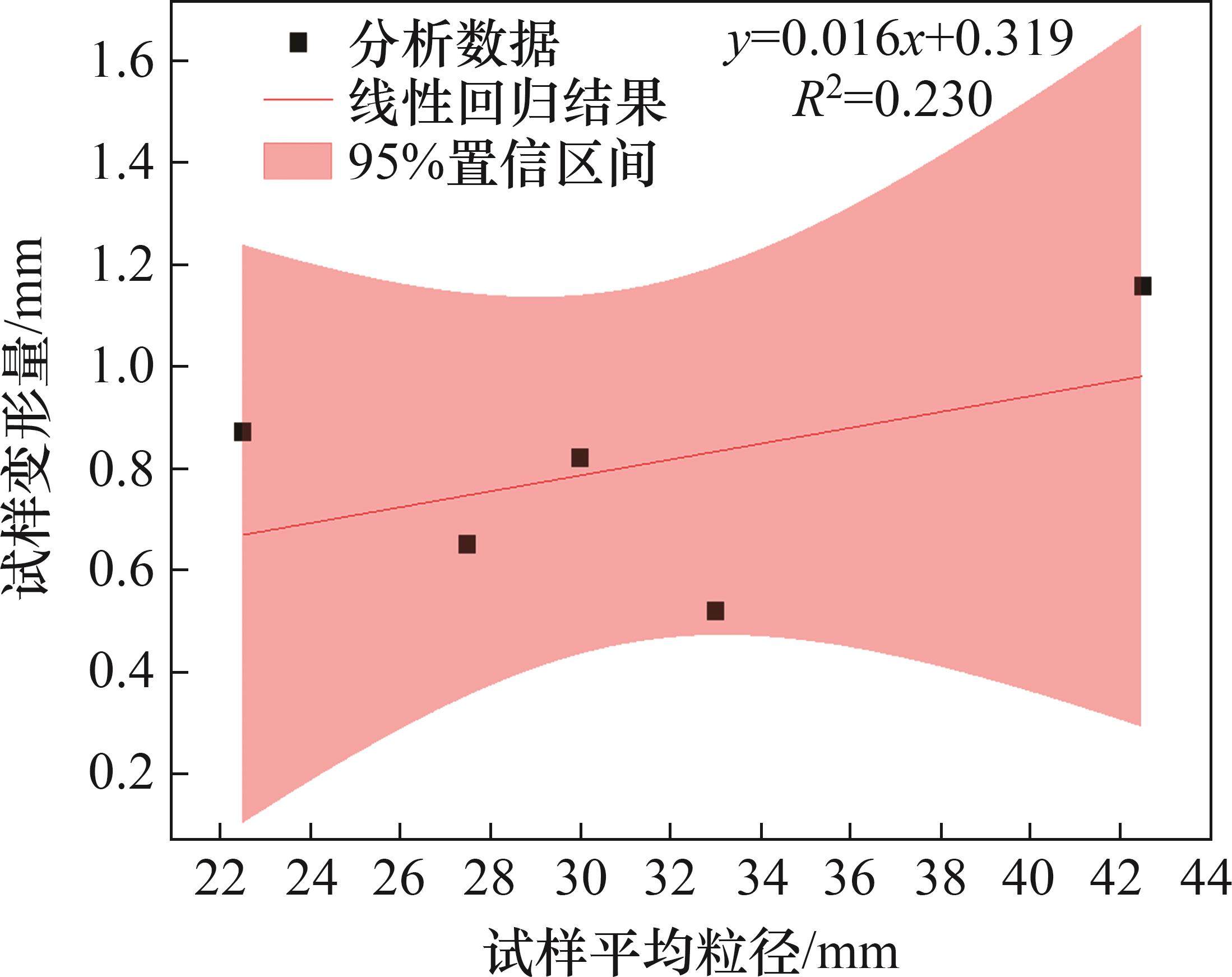
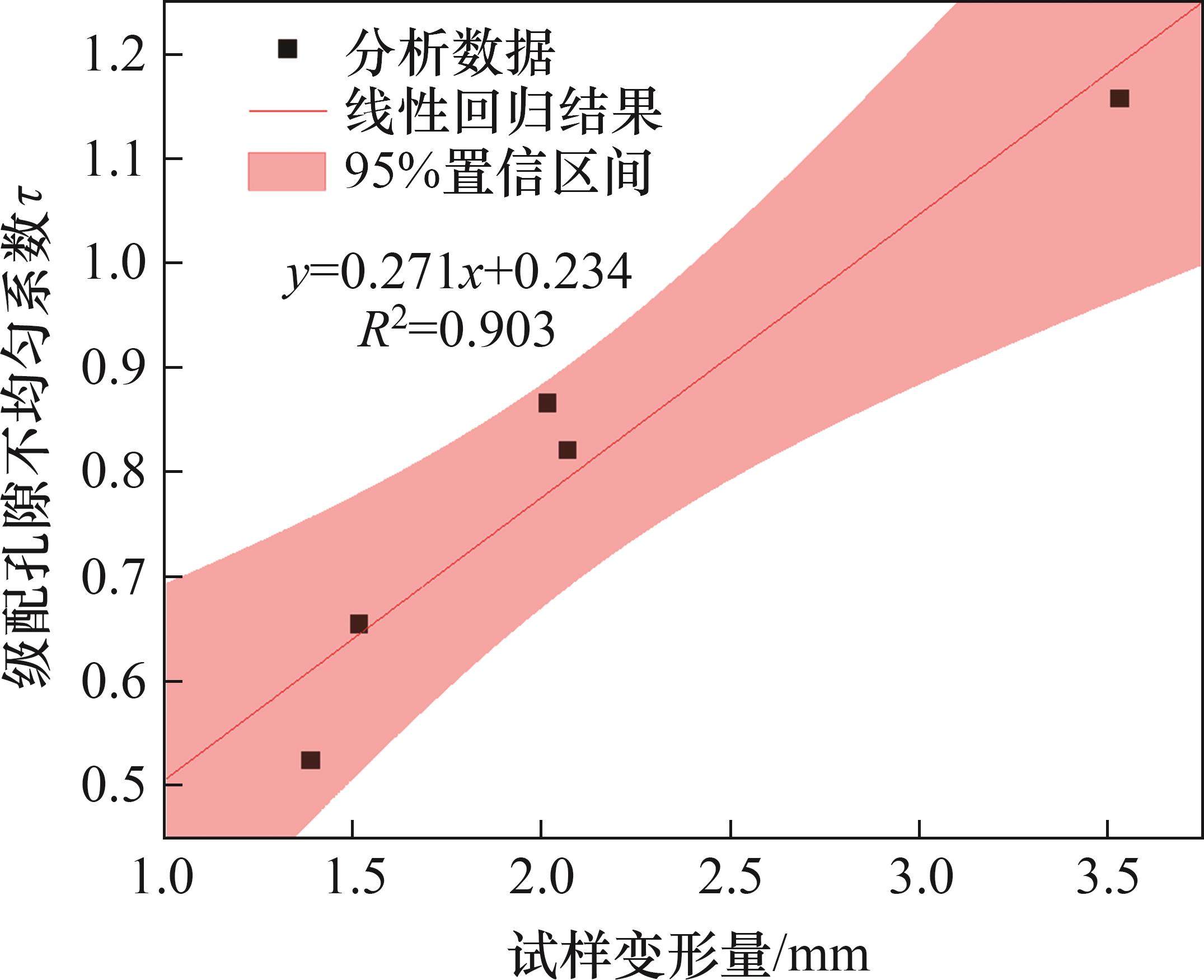
由图13和图14可以看出:道砟试样的变形量与道砟颗粒的平均粒径的R2仅为0.230,说明它们之间并无显著的相关关系。而级配孔隙不均匀系数与压缩变形量的R2为0.903,两者具有强相关性。这说明提高道砟颗粒的空间分布均匀性可提升道砟集料的抗变形能力。
为进一步分析道砟的细观接触力学行为,统计每个道砟颗粒与其他道砟颗粒的接触情况,并分析不同级配试件在40 kN荷载作用下,每个道砟颗粒所受到的其他道砟颗粒的接触力合力。所得到的接触力箱线图如图15所示。
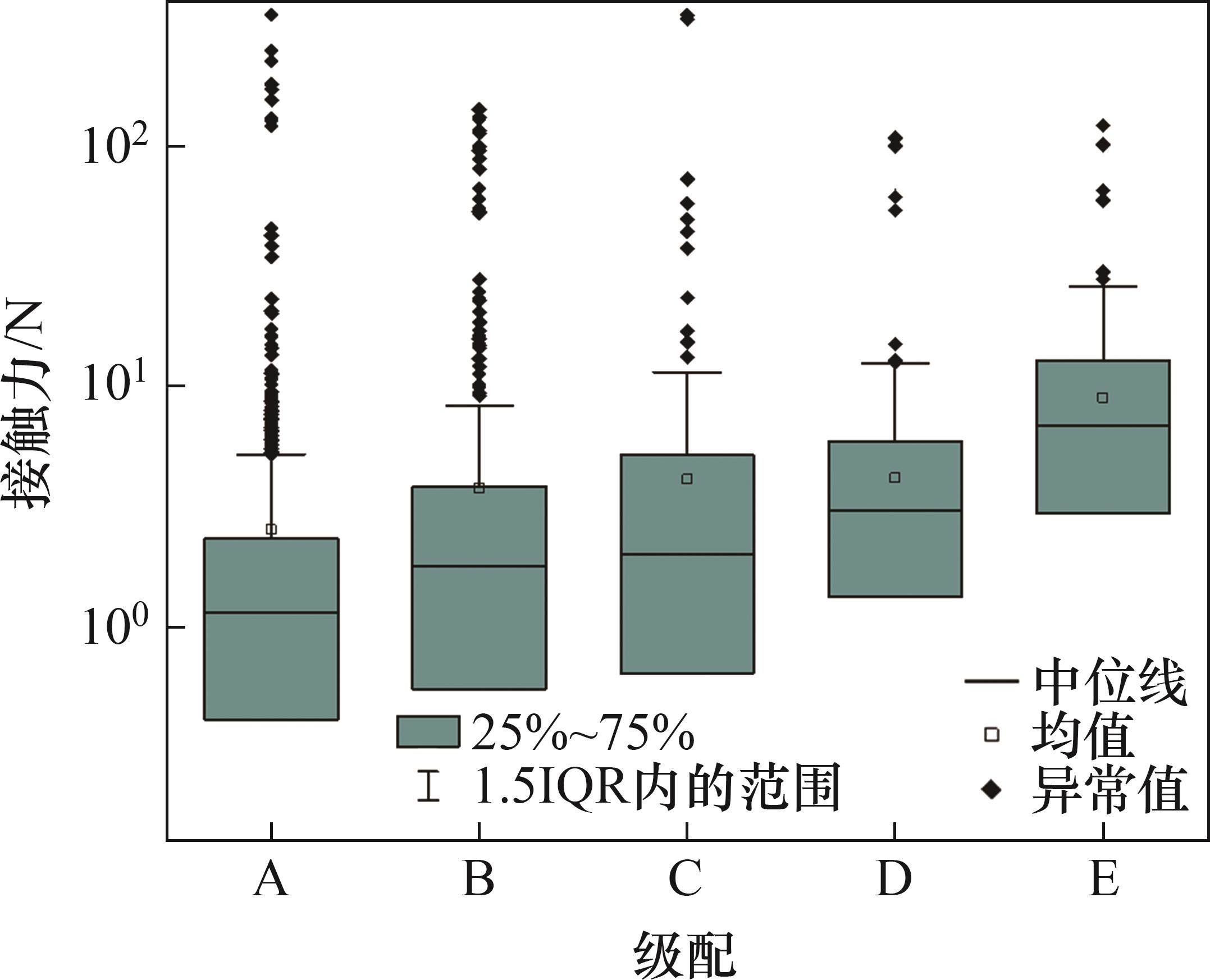
由图15可以看出:道砟颗粒接触力均值随颗粒平均粒径增大而增大,但平均粒径最小的A级配道砟颗粒出现了接触力分布均匀性较差的情况。为分析产生这一现象的原因,选取A、D组级配的道砟试样,统计试样中所有道砟颗粒的接触点、接触力、空间坐标,并采用MATLAB自编程序进行应力云图的后处理,分析接触力在试样高度及试样宽度方向的空间分布,所得结果如图16所示。图16中,取试样中点宽度为0 m,应力云图中白色区域代表颗粒间接触力接近于0,说明颗粒间的咬合摩擦力基本不产生承力作用,局部道砟颗粒出现了剪切破坏。A级配道砟出现了更多接触力接近0的白色区域,且存在较大应力集中的红色区域,而D级配的试样蓝色区域分布较广泛,说明道砟颗粒内部应力分布较均匀,且应力多集中于试样中心。结合表2分析结果可知,级配D的道砟试样具有更小的压缩变形量。
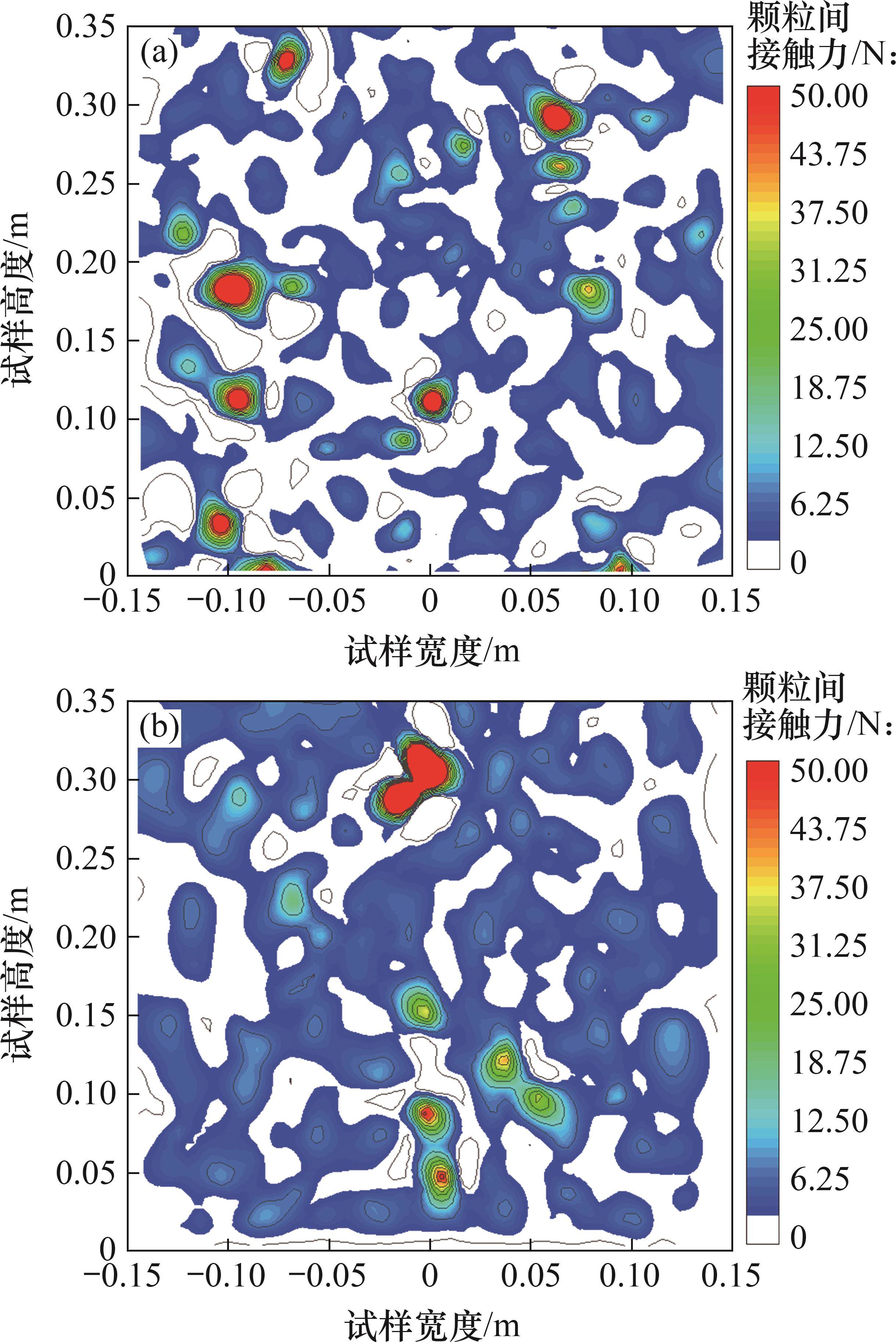
综上可知,道砟集料的抗变形能力与对应级配的平均粒径相关性不显著,而与道砟集料内部的接触力分布均匀性有强相关关系,故应在道砟级配设计时,考虑道砟集料内部应力分布均匀性的影响。
4 结论
1) 提出了基于离散元法的道砟试验样孔隙率分析方法,并通过室内试验验证了其准确性。该方法可作为不同级配碎石集料宏观孔隙率的分析手段。
2) 提出的基于灰度解析与离散元法融合的分析方法能实现基于道砟集料平面图像的层间孔隙率精确反演,可为道砟集料随机孔隙空间几何分布特征分析、道砟几何与力学性能映射关系的研究提供新的思路。
3) 道砟集料的平均粒径与试样的抗变形能力无显著的相关关系。本文提出了能表征道砟颗粒孔隙空间分布均匀性的级配孔隙不均匀系数
4) 道砟集料的抗变形能力与道砟集料内部的接触力分布均匀性有强相关关系。在对不同线路条件下设计道砟的级配时,建议考虑道砟集料内部应力分布均匀性的影响。
徐旸, 赵一馨, 余文颖, 等. 基于图像识别与离散元融合的铁路道砟孔隙空间分布解析[J]. 中南大学学报(自然科学版), 2024, 55(12): 4723-4732.
XU Yang, ZHAO Yixin, YU Wenying, et al. Analysis of void spatial distribution of railway ballast based on integration of image recognition and discrete element method[J]. Journal of Central South University(Science and Technology), 2024, 55(12): 4723-4732.

