CRTS Ⅰ型板式无砟轨道是由轨道板、CA砂浆层、底座板等部件组成的多层结构,理想状态下各结构层之间完全密贴,协调受力。然而由于CA砂浆采用袋装法施工造成其与轨道板、底座板之间的连接较弱,在环境温度变化、列车高频荷载、施工质量等因素的影响下[1-3],轨道板板底与CA砂浆之间结合不密实,易使两者之间出现缝隙,并随服役时间的增长而逐步扩大,进而导致CA砂浆脱空病害的产生。轨道系统一旦出现脱空病害,脱空区域与周围交界将成为不利受力区域,在高频列车拍打与温度荷载共同作用下[4],CA砂浆层性能逐渐劣化,导致脱空现象日益加剧。针对CRTS Ⅰ型板式轨道脱空的问题,很多学者都进行了深入研究,主要集中在脱空对轨道结构服役性能影响及脱空检测技术方面。徐浩等[5]研究了CA砂浆脱空对其疲劳性能的影响,提出脱空长度超过1.225 m会造成CA砂浆不再满足60年使用寿命。REN等[6]研究了CA砂浆脱黏的产生和发展对CRTS Ⅰ型板式无砟轨道结构损伤分布的影响,分别提出造成客运、货运线路板面破坏的砂浆脱空临界高度。张重王等[7]研究发现温度梯度荷载与板下脱空同时存在时,脱空长度超过0.8 m,其对车辆及轨道结构动力响应影响较大。为快速定位和识别无砟轨道中的砂浆脱空,HU等[8]提出一种基于贝叶斯模型识别CA砂浆脱空的方法。陈甜甜等[9]采用CNN方法识别CA砂浆脱空,脱空缺陷识别率达到98.75%。由于CA砂浆脱空病害的发展受多种复杂因素的影响,其脱空位置在空间上往往是随机分布的。既有研究中不同脱空位置对于轨道结构服役性能的影响尚不明确,运营中难以准确掌握重点检修部位。为明确脱空位置对轨道结构动态服役性能的影响,需确定合适的评价轨道结构动力状态的指标和方法。近年来国内外学者广泛采用动力学仿真手段,对不同轨道结构的动力特征进行研究,并分别从时、频域角度对轨道结构动力状态进行评价。樊卿[10]提取钢轨、轨枕、底座板等结构的时、频域响应,研究预制轨枕板式无砟轨道的动力性能,时域响应包括位移及加速度时程,频域响应包括垂向Z振级和插入损失,研究结果为轨道结构的参数优化提供了一定依据。YE等[11]分别从钢轨、轨道板的垂向位移峰值、加速度峰值和Z振级等方面,对一种新型无砟轨道结构在普通段和减振段的动力性能进行评价。ZENG等[12]采用时域、频域和1/3倍频程等分析方法,研究了4种无砟轨道的减振效果。目前主要采用的轨道结构动力状态的时、频域评价指标众多,例如加速度时程、位移时程、1/3倍频程、Z振级、功率谱密度等,造成了时、频域评价指标选取不一且不全面的现象。因此,有必要提出一种适用性更强的、能够同时考虑时、频域响应的轨道动力状态综合评价方法。为明确CA砂浆脱空位置对单元板式轨道结构动力状态的影响,采用数值模拟方法获取不同脱空位置下轨道结构的动力响应,并采用熵权法进行指标赋权,实现对轨道结构动力状态的综合评价。研究结果提供准确判定CA砂浆脱空最不利位置的方法,可为其他条件下的轨道结构服役状态的判定提供借鉴,并为轨道结构的科学养护维修提供参考依据。
1 基于熵权法的轨道动力状态评价研究
1.1 评价指标选取
轨道结构动力状态综合评价方法是由目标层、子结构层和指标层共同构成,结构如图1所示。结构的第1层为目标层,为融合时、频域的轨道结构动力状态综合评价方法。第2层为子结构层,研究的主要对象为高速铁路路基上无砟轨道系统,并将该轨道系统拆分成钢轨子结构、轨道板子结构、底座板子结构及路基子结构。第3层为指标层,指标层分为时域和频域2类响应,能够综合评价轨道结构动力响应特征。其中时域指标为子结构层各元素的加速度和位移的时程响应结果,能够有效反映各子结构层的响应随时间的幅值及趋势变化;频域指标为子结构层各元素的加速度和位移功率谱密度(PSD)结果,能够有效反映各子结构层的振动能量分布情况。
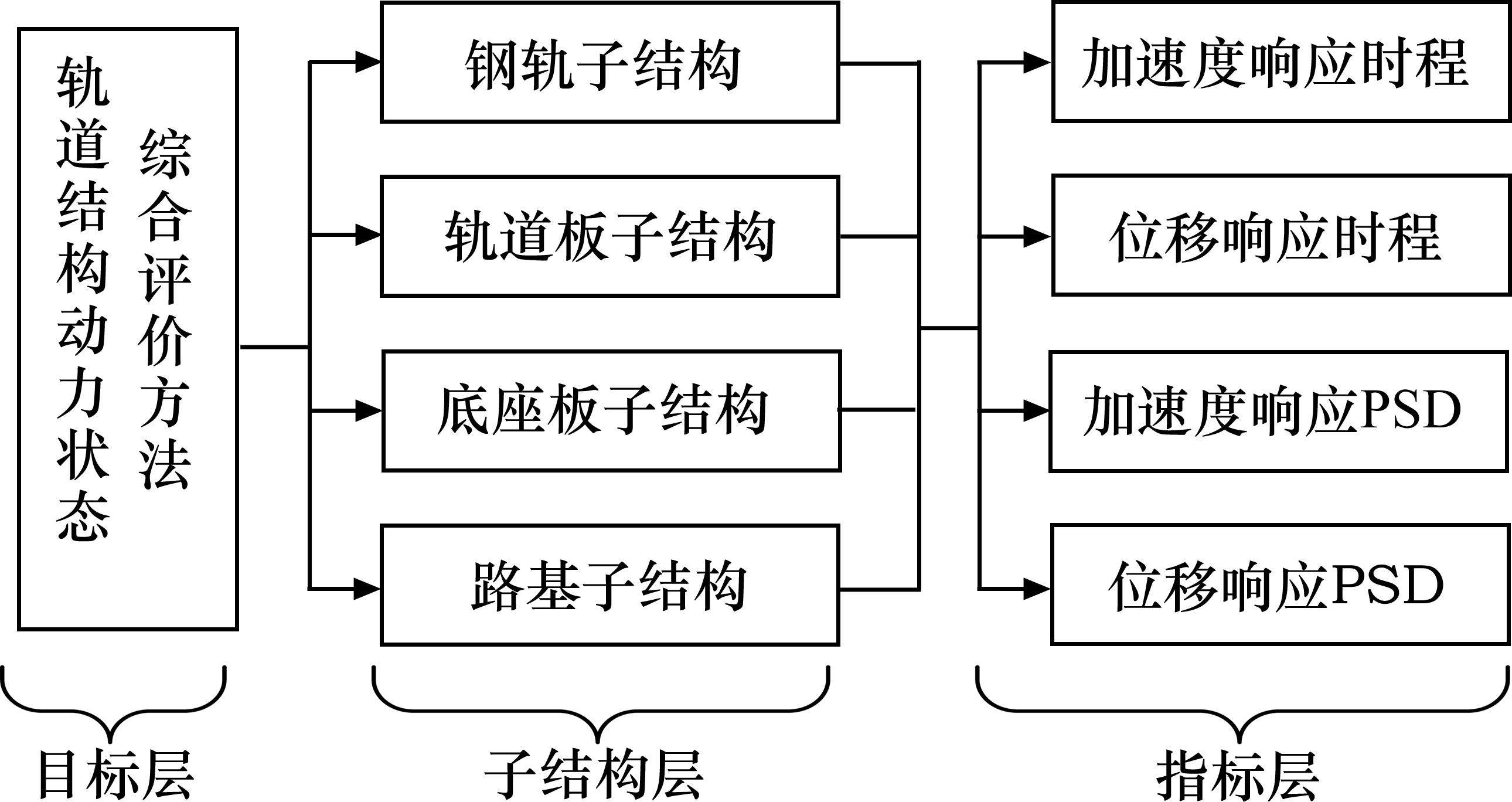
由于结构加速度、位移响应的时程和PSD结果间量纲不一致,且将其简单的响应结果叠加缺乏实际意义。为能够将时、频域的指标整合,本节采用无量纲化手段来处理上述选取的指标。选取的无量纲指标有波形因子、脉冲因子、峭度因子、偏度因子和裕度因子[13-14],上述指标的定义及数学表达式如下。
1) 波形因子kf
波形因子是表示波形信号中的一个无量纲量,是信号的均方根值和平均值之比,广义上来说波形因子可以量化波形某一方面的特征,可表示为:
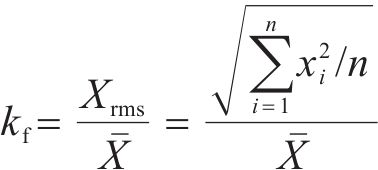
式中: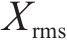
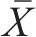
2) 脉冲因子If
脉冲因子是信号峰峰值与平均值的绝对值之比,可表示为:
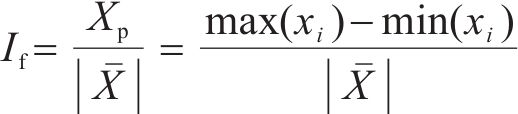
式中:Xp表示峰峰值。当信号出现异常时,峰峰值会显著变大,脉冲因子也会随之增大,所以能够通过脉冲因子变化来辅助判断信号异常情况。
3) 峭度因子Kp
峭度是指实值随机变量概率分布中“尾度[15]”的量度,描述总体中所有取值概率分布的形状。峭度因子可以用随机变量的四阶中心距表示,具体如下:
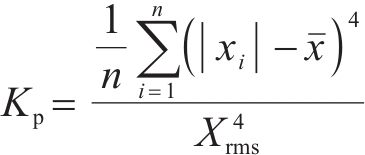
根据式(3),可以得知正态分布的峭度因子为3,所以当随机变量的峭度小于3时则分布较为平缓,也就是说随机分布内的极端值较少;若大于3时则分布较为陡峭,则随机分布内的极端值较多,并且当峭度因子的绝对值越大于3则表明其分布与正态分布的差异越明显。
4) 偏度因子Sf
偏度主要是衡量实数随机变量概率分布的不对称性。偏度因子是通过样本的三阶标准矩定义的,具体如下:
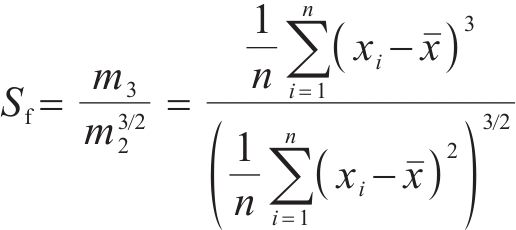
式中:m3为三阶样本中心距;m2为二阶样本中心距,即样本方差。由式(4)可知,偏度因子可以为正也可以为负,当偏度因子为负时,则表示概率密度函数左侧的部分比右侧长,并且大部分的数值位于平均值右侧;当偏度因子为正时,则表示概率密度函数右侧的部分比左侧长,并且绝大多数的数值位于平均值的左侧。但需要注意的是,当偏度因子为0,则表明变量相对均匀地分布在平均值两侧,但不一定为对称分布。
5) 裕度因子Mf
裕度因子为信号的峰峰值和方根幅值的比值,可表示为:
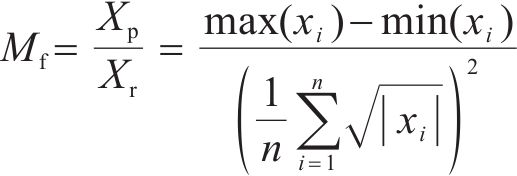
式中:Xp是峰峰值;Xr为方根幅值。
1.2 基于熵权法的指标赋权求解
在综合评价体系中,需要确定各评价指标相对应的权重才能够实现综合评价[16],权重直接影响到评价体系的可靠性和准确性。本文采用熵权法(Entropy Weight Method, EWM)进行指标赋权。
熵权法作为一种重要的信息权重模型,目前已经得到了广泛的研究和应用[17]。熵权法与其他主观权重模型相比,其最大的优势是能够避免人为因素对指标权重的干扰,从而增强综合评价结果的客观性。在赋权过程中,若某被评价对象中的某一指标值之间的差距较大,则认为该评价指标携带了较大信息量,对应的熵值则较小,即该指标权值较大。若被评价对象某一指标的值全部相等,即该指标没有携带任何有效信息,熵值达到最大,该情况下考虑将该值从评价指标中剔除[18]。因此在具体应用场景中,可根据各评价指标值之间的差异程度,进行初步筛选,然后计算出每一指标的熵权值,进而得到较为客观的各指标权重信息。
基于本文建立的轨道结构动力状态综合评价体系,将轨道系统拆分为钢轨子结构、轨道板子结构、底座板子结构和路基子结构4个部分,每个子结构包含20个评价指标,单个子结构构建成了评价指标矩阵如下所示:
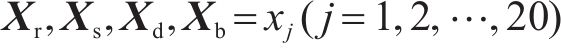
式中:下标r、s、d、b分别代表钢轨、轨道板、底座板和路基子结构,可参考表1。
| 波形因子 | 脉冲因子 | 峭度因子 | 偏度因子 | 裕度因子 | |
|---|---|---|---|---|---|
| 位移时域结果 | x1 | x2 | x3 | x4 | x5 |
| 加速度时域结果 | x6 | x7 | x8 | x9 | x10 |
| 位移功率谱密度 | x11 | x12 | x13 | x14 | x15 |
| 加速度功率谱密度 | x16 | x17 | x18 | x19 | x20 |
因此,由单个结构评价矩阵组成的轨道结构动力状态综合评价矩阵共含有80个行指标,选取不同评价工况下的多个位置作为列指标,构成完整指标矩阵。在此基础上,可进行熵权法的指标赋权计算。
1) 数据标准化
在得到指标矩阵后,需对原始指标矩阵中的元素进行标准化处理,从而得到标准化指标矩阵M,需要注意的是,在标准化处理时需区分效益型指标和成本型指标。其中,效益型指标的值越大越好,即正向型指标,可采用公式(7)进行计算;成本型指标的值越小越好,即负向型指标,可采用公式(8)进行计算。
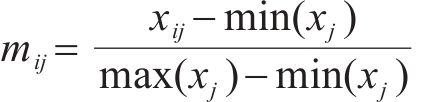
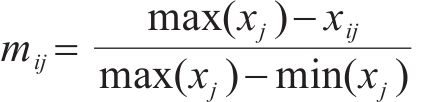
式中: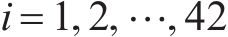
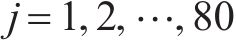
2) 比重计算
计算第j个指标中第i个样本的数值比重pij,即计算样本i在指标中所有样本中所占的比重,具体数学形式如下:
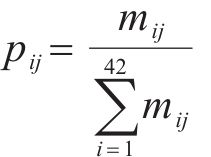
最终构成概率矩阵P,同时验证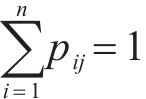
3) 各指标信息熵
指标j的信息熵Ej可通过式(10)得到:
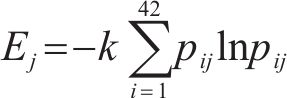
式中:pij可以通过式(11)得到;考虑到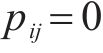
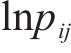
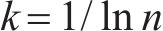
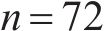
4) 通过信息熵计算权重
指标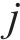
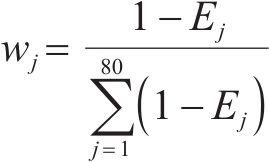
5) 综合评分
第i个评价对象的综合评价分数Zi可通过下式计算得到:
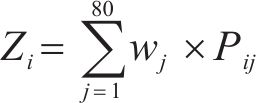
2 算例分析
2.1 数据收集与处理
考虑到砂浆脱空病害下现场检测数据的获取难度较高,且不能系统性提供不同脱空位置的动力响应数据,因此采用数值模拟方式设置多种砂浆脱空情况,以提供充分的数据进行后续研究。基于车辆-轨道耦合动力学理论,建立可考虑不同脱空位置的耦合动力学模型,如图2所示。模型主要由车辆、钢轨、扣件、轨道板、CA砂浆层、底座板、凸形挡台和路基组成。在模型中,钢轨选择CHN60钢轨,使用实体单元模拟。扣件系统采用三相弹簧-阻尼单元模拟,刚度为50 kN/mm[19],间距为0.629 m。轨道板、CA砂浆层、底座板和路基均采用实体单元模拟。模型长度约为120 m(23个轨道板)。基于CRH3型车建立车辆模型,轴重17 t,通过轮轨相互作用与轨道结构进行耦合。
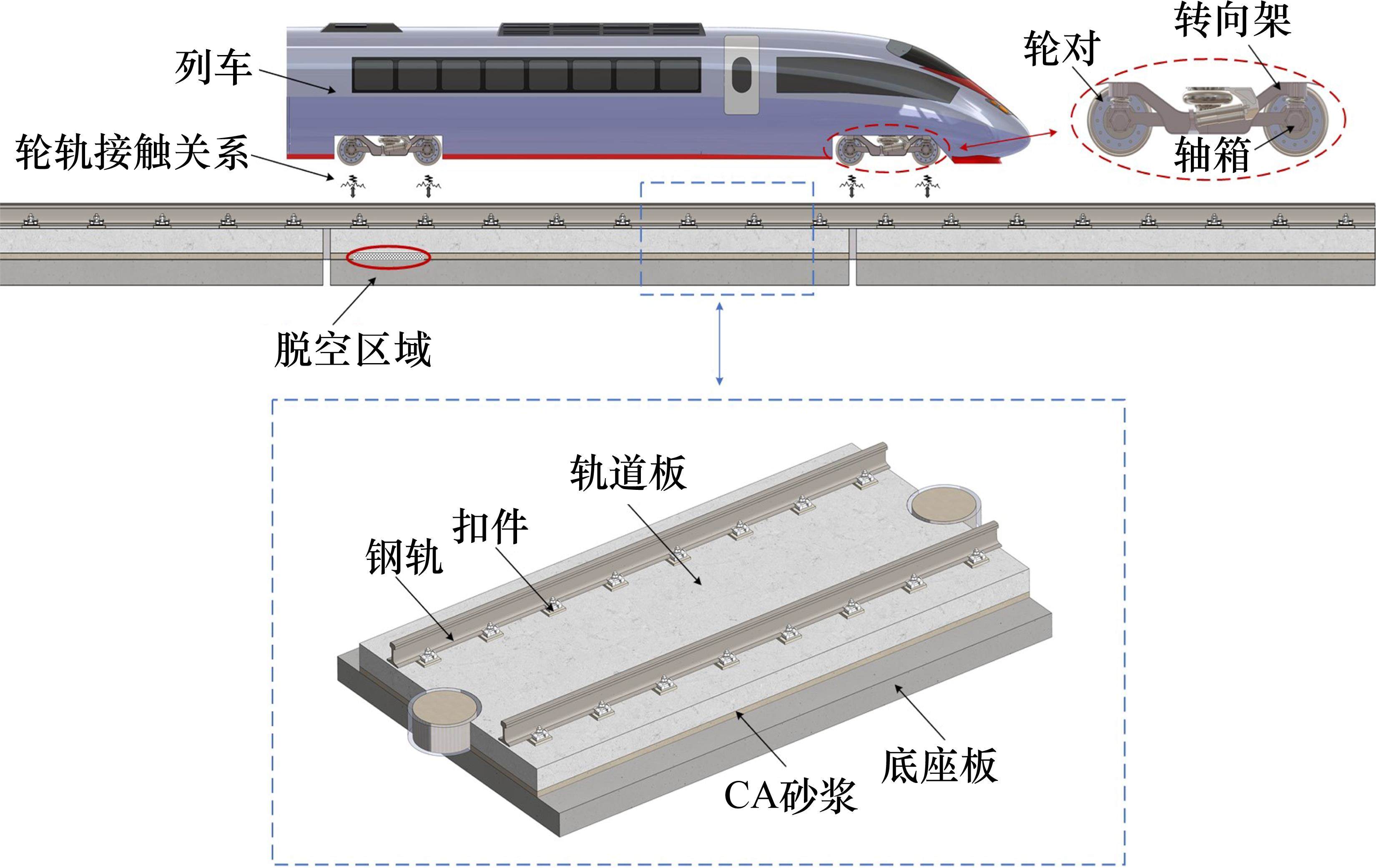
利用上述模型,计算行车速度为300 km/h,轨道结构正常条件下的轮轨垂向力、钢轨垂向位移、钢轨垂向加速度、轨道板垂向加速度等动力响应指标。由表2可以看出,计算结果与既有文献[1, 20-22]和遂渝线实测结果基本一致,验证了模型的准确性与可靠性,该模型计算结果可为后续研究提供数据支撑。
| 模型计算结果 | 文献/实测结果 | |
|---|---|---|
| 轮轨垂向力/kN | 100.3 | 98.3 |
| 钢轨垂向位移/mm | 1.40 | 1.38 |
| 钢轨垂向加速度/g | 197.6 | 222.1 |
| 轨道板垂向加速度/g | 20.1 | 23.3 |
2.2 脱空工况的设置
设定8种脱空工况,如图3所示。其中工况1到工况4为单元板横向板边脱空,工况5到工况8为横向板中脱空,工况1、5靠近单元板纵向板端,工况4、8为单元板纵向板中。参考既有研究[23, 5],由于CA砂浆脱空时,在列车荷载作用下轨道板与CA砂浆层不再接触,设定脱空高度为0.05 m,即脱空区域的CA砂浆层沿厚度方向完全损伤。纵向尺寸取为0.9 m,约为1.5个扣件间距;横向尺寸取为0.8 m,为轨道板宽度的1/3。另外设置工况9为无脱空情况。
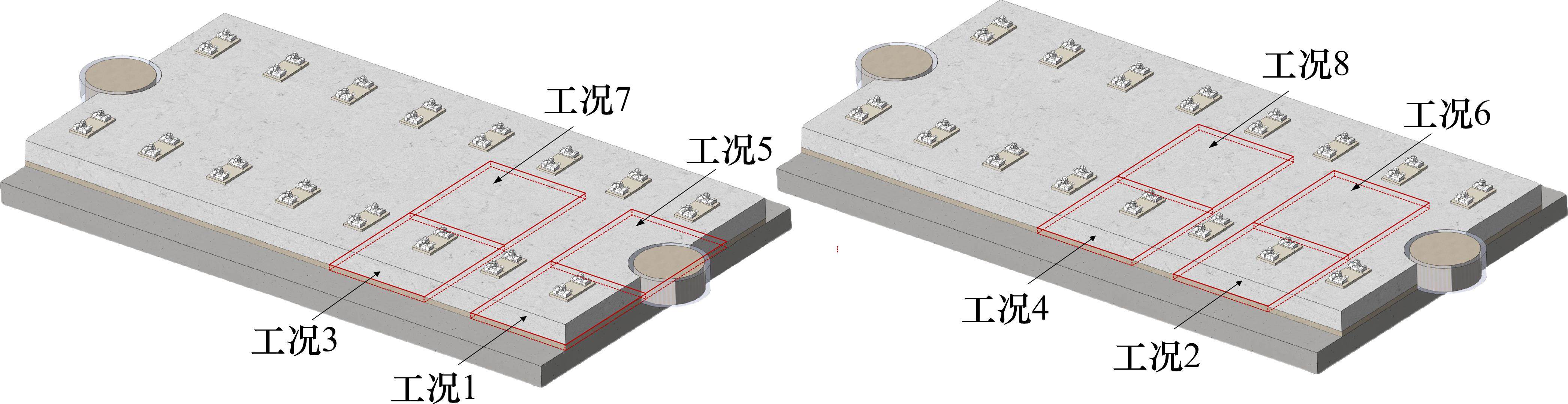
2.3 结果分析
首先提取无脱空状况(工况9)与8种脱空工况下钢轨、轨道板的垂向加速度与对应的功率谱密度结果,如图4所示。
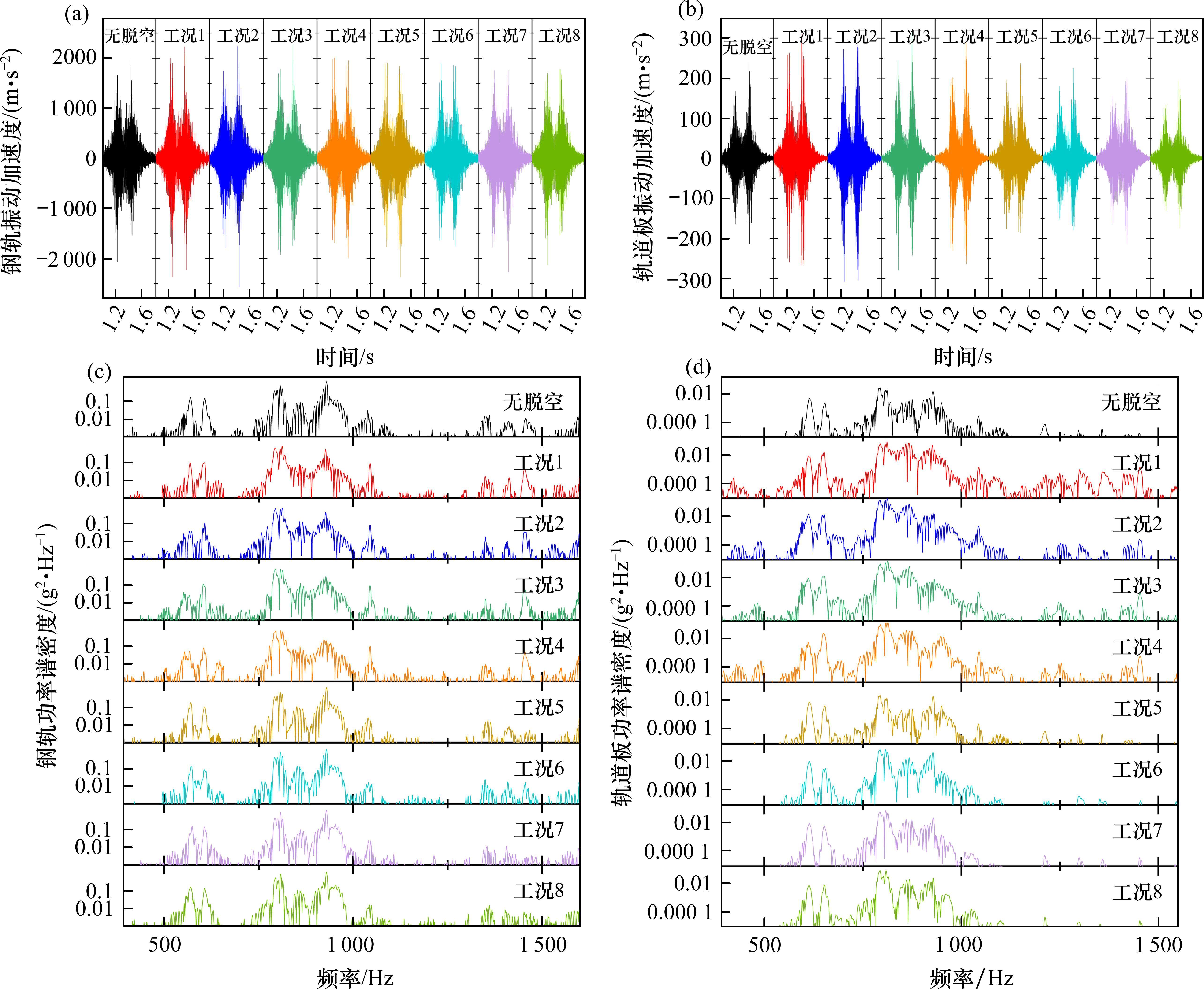
由图4(a)可知,CA砂浆层脱空导致轨道结构垂向加速度出现一定程度的增加,轨道板横向板边位置脱空(工况1、2、3、4)下钢轨垂向加速度比无脱空情况下高出50~250 m/s2,轨道板横向板中脱空(工况5、6、7、8)下钢轨垂向加速度比无脱空情况下高出20~150 m/s2。且板边位置脱空的影响整体大于轨道板中部脱空的影响,但轨道板横向板边不同位置脱空产生的钢轨垂向加速度峰值相差不大,轨道板横向板中不同位置脱空产生的影响也相差不大。然而与CA砂浆脱空对钢轨垂向加速度响应影响相比,CA砂浆脱空对轨道板垂向加速度影响更明显,如图4(b)所示,CA砂浆脱空下轨道板垂向加速度比无脱空情况下轨道板垂向加速度高出2~100 m/s2。振动加速度传递至底座板和路基结构时,无脱空、板边脱空、板中脱空产生的加速度无明显区别。
由图4(c)可知,无脱空情况下钢轨加速度存在550~600 Hz、850~1 100 Hz这2个显著的共振峰,且脱空会导致钢轨加速度共振峰的前移。如图4(d)所示,无脱空情况下轨道板加速度存在550~700 Hz、850~1 000 Hz这2个显著的共振峰,同样脱空也会导致轨道板加速度共振峰的前移。但脱空前后钢轨、轨道板功率谱密度的分布变化,较难通过峰值、频率带等参数的变化准确描述。
因此,通过时、频域响应手段分析难以准确描述不同CA砂浆脱空位置对轨道结构动力状态的影响规律,难以准确评估脱空的最不利位置。本文根据1.1节所提出的波形因子、脉冲因子、峭度因子、偏度因子和裕度因子5种评价指标,分别对钢轨子结构、轨道板子结构、底座板子结构、路基子结构的时频域响应进行评估。表3为钢轨子结构所求得的结果,轨道板、底座板、路基子结构可求得对应的评价指标结果。从评价指标的计算结果可知,不同指标之间数值大小有较为明显的差别,说明不同指标携带的信息量不同,本文选取的评价指标之间具有较强的独立性。
| 波形因子 | 脉冲因子 | 峭度因子 | 偏度因子 | 裕度因子 | |
|---|---|---|---|---|---|
| 位移时程 | 3.374/3.370 | 15.370/15.321 | 13.467/13.469 | -3.436/-3.436 | 74.984/73.888 |
| 加速度时程 | 2.294/2.206 | 37.445/34.109 | 19.535/15.571 | 0.029/-0.024 | 75.572/70.324 |
| 位移功率谱密度 | 1.006/1.006 | 0.759/0.760 | 5.094/5.002 | 1.222/1.191 | 0.762/0.762 |
| 加速度功率谱密度 | 1.041/1.043 | 1.694/1.654 | 2.741/2.854 | 0.307/0.314 | 1.736/1.696 |
接下来采用熵权法对评价指标进行赋权,首先需要对数据进行标准化处理和归一化处理,钢轨子结构指标归一化具体结果见表4。
| 波形因子 | 脉冲因子 | 峭度因子 | 偏度因子 | 裕度因子 | |
|---|---|---|---|---|---|
| 位移时程 | 0.492/0.458 | 0.110/0.076 | 0.000/0.003 | 0.963/0.962 | 0.570/0.523 |
| 加速度时程 | 0.498/0.232 | 0.643/0.447 | 0.516/0.245 | 0.304/0.243 | 0.463/0.341 |
| 位移功率谱密度 | 0.427/0.437 | 0.570/0.574 | 0.412/0.349 | 0.313/0.249 | 0.570/0.575 |
| 加速度功率谱密度 | 0.015/0.028 | 0.042/0.035 | 0.126/0.203 | 0.483/0.498 | 0.039/0.033 |
指标归一化后,下一步需要求得各指标的信息熵,信息熵求解结果见表5。根据信息熵可以通过计算求得各指标的熵权值,所得结果如表6所示。
| 波形因子 | 脉冲因子 | 峭度因子 | 偏度因子 | 裕度因子 | |
|---|---|---|---|---|---|
| 钢轨加速度信息熵 | 0.945/0.765 | 0.969/0.787 | 0.946/0.897 | 0.958/0.965 | 0.960/0.782 |
| 轨道板加速度信息熵 | 0.952/0.911 | 0.951/0.954 | 0.928/0.960 | 0.959/0.980 | 0.944/0.954 |
| 底座板加速度信息熵 | 0.958/0.963 | 0.946/0.941 | 0.936/0.961 | 0.942/0.962 | 0.957/0.943 |
| 路基加速度信息熵 | 0.959/0.950 | 0.954/0.966 | 0.954/0.961 | 0.947/0.976 | 0.956/0.967 |
| 钢轨位移信息熵 | 0.985/0.978 | 0.951/0.974 | 0.911/0.950 | 0.987/0.957 | 0.981/0.974 |
| 轨道板位移信息熵 | 0.934/0.708 | 0.721/0.722 | 0.765/0.943 | 0.715/0.950 | 0.977/0.718 |
| 底座板位移信息熵 | 0.947/0.988 | 0.973/0.940 | 0.967/0.967 | 0.976/0.979 | 0.975/0.934 |
| 路基位移信息熵 | 0.991/0.970 | 0.963/0.973 | 0.926/0.961 | 0.974/0.958 | 0.984/0.973 |
| 波形因子 | 脉冲因子 | 峭度因子 | 偏度因子 | 裕度因子 | |
|---|---|---|---|---|---|
| 钢轨加速度熵权值 | 0.010/0.044 | 0.006/0.040 | 0.010/0.019 | 0.008/0.007 | 0.008/0.041 |
| 轨道板加速度熵权值 | 0.009/0.017 | 0.009/0.009 | 0.014/0.007 | 0.008/0.004 | 0.010/0.009 |
| 底座板加速度熵权值 | 0.008/0.007 | 0.010/0.011 | 0.012/0.007 | 0.011/0.007 | 0.008/0.011 |
| 路基加速度熵权值 | 0.008/0.009 | 0.009/0.006 | 0.009/0.007 | 0.010/0.004 | 0.008/0.006 |
| 钢轨位移熵权值 | 0.003/0.004 | 0.009/0.005 | 0.017/0.009 | 0.003/0.008 | 0.004/0.005 |
| 轨道板位移熵权值 | 0.012/0.055 | 0.052/0.052 | 0.044/0.011 | 0.054/0.009 | 0.004/0.053 |
| 底座板位移熵权值 | 0.010/0.002 | 0.005/0.011 | 0.006/0.006 | 0.005/0.004 | 0.005/0.012 |
| 路基位移熵权值 | 0.002/0.006 | 0.007/0.005 | 0.014/0.007 | 0.005/0.008 | 0.003/0.005 |
值得说明的是,每个工况中共取样8个点,对应8个脱空位置,以综合评价轨道结构动力状态。通过熵权法得到各指标熵权值后,以归一化后的轨道结构特征因子为样本值,分别对钢轨、轨道板、底座板、路基的动力状态进行综合评价。对各样本值对应熵权值进行加权,计算出每个工况中每个点的分数,再对各工况下的8个点的分数求和,即代表该工况下轨道结构动力状态的分数。计算公式如下:
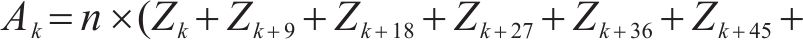
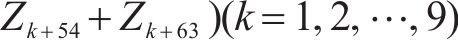
式中:Zk为第k个点的分数;Ak为第k个工况的分数;n为样本数量。最终计算结果如图5所示。
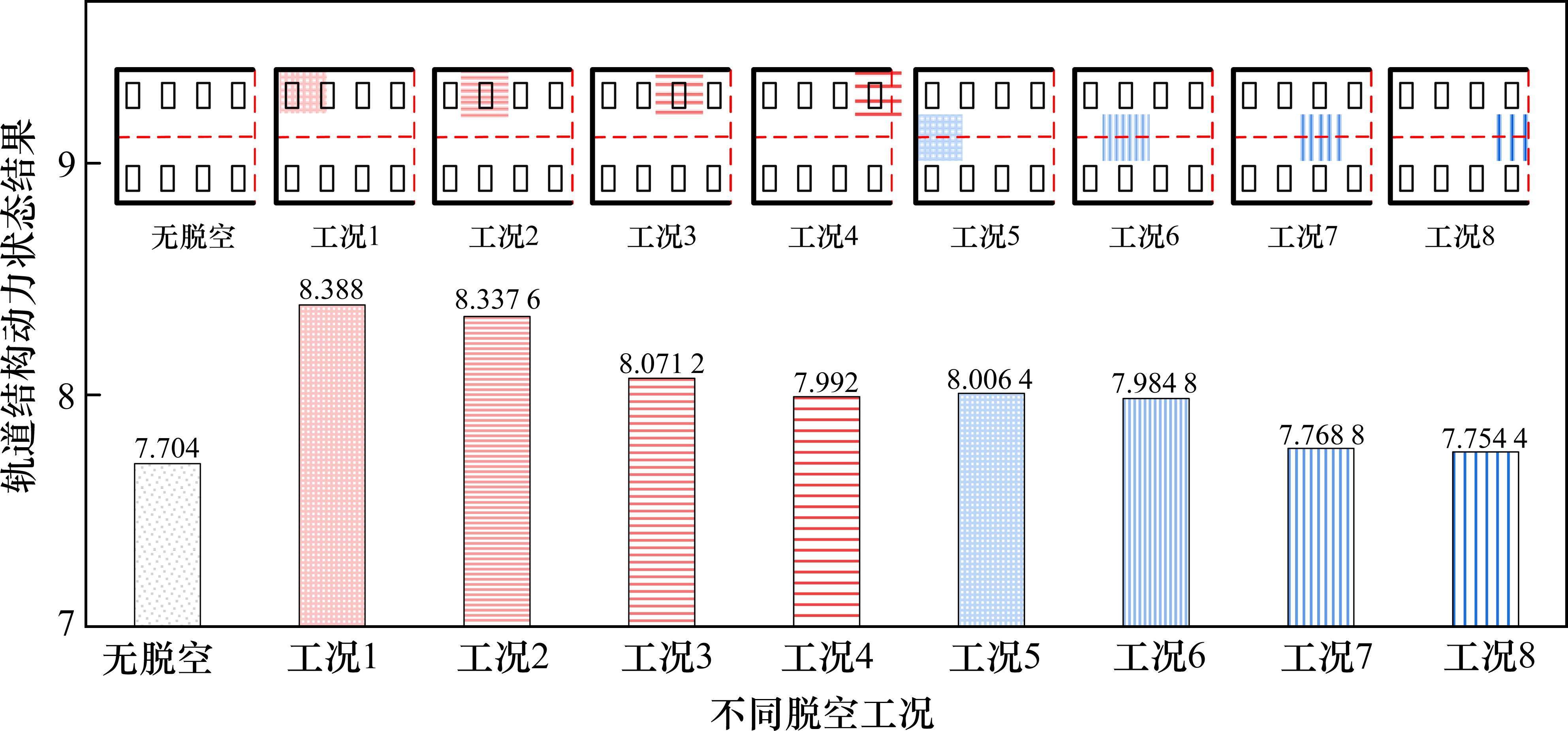
根据上述计算结果可知,相较于无脱空下轨道动力状态指标分数,脱空工况1~8的分数均大于无脱空工况9,这也说明脱空的出现会对轨道结构动力状态产生影响,导致结构动力状态响应指标的增大。由工况1、2、3、4以及工况5、6、7、8对比可知,沿线路纵向的不同位置处脱空,板端位置的脱空对轨道结构的影响大于板中位置的脱空。由工况1和5、工况2和6、工况3和7、工况4和8对比可知,沿线路横向的不同位置处脱空,板边位置的脱空对轨道结构的影响远大于板中位置的脱空。此外,对比脱空工况1~8可知,处于板端角位置脱空(工况1)是影响轨道结构动力状态最不利的位置。
3 结论和展望
1) 建立融合轨道结构时、频特征的动力状态综合评价方法,选取4个子结构的加速度、位移响应的时程和功率谱密度为评价指标,并采用熵权法进行指标赋权,实现了对轨道结构动力状态的综合评价。
2) 采用常规时、频域手段难以通过峰值、频率带等参数变化准确判断不同CA砂浆脱空位置对轨道结构动力状态的影响。
3) 采用熵权法建立的轨道动力状态评价结果表明,对比线路纵向不同位置的脱空影响,板端位置的砂浆脱空对轨道结构影响更大;对于线路横向不同位置的脱空,板边位置的砂浆脱空影响更大;CA砂浆脱空的最不利位置为板端角处。
值得说明的是,本文提出的基于熵权法的轨道动力状态评价方法可推广到其他条件下的轨道状态评价,如不同速度、不同轨道类型等,可用来确定最不利状态或最不利位置。同时,针对目前采用单一指标最值进行评价时可能出现“最值超限、其他值均保持较低水平”或“单一位置处超限、其他位置保持较低水平”,导致单一指标的评价不准确的现象,本文提出的多种因素共同影响的整体评价方法可一定程度上弥补这个缺陷。此外,未来还可根据动态检测数据设定一系列评价阈值,该阈值可以用于轨道结构服役状态判定,为养护维修提供参考依据。
张芷寒,高亮,郭志鹏等.基于熵权法的CA砂浆脱空位置对单元式无砟轨道动力状态影响评价研究[J].铁道科学与工程学报,2025,22(01):125-135.
ZHANG Zhihan,GAO Liang,GUO Zhipeng,et al.Evaluation of impact of CA mortar void position on dynamic state of unit ballastless track based on entropy weight method[J].Journal of Railway Science and Engineering,2025,22(01):125-135.

