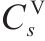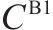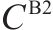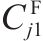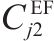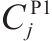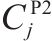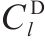铁路作为国家关键基础设施,是国民经济的大动脉。近年来,随着我国铁路网络的逐步完善,新兴铁路工程建设项目开始向末端山区地带转移,复杂地形地貌致使工程桥隧比上升,弃渣产量大幅提升,巨量弃渣的回收利用问题不容小觑[1]。此外,山区铁路工程中的道路运输需求与能力等受季节影响,探索季节变化对山区道路运输能力和运价率波动的作用机理对降低铁路工程建设物流成本至关重要。综上所述,铁路工程建设中弃渣回收利用物流网络具有规模大、季节波动明显、产出不确定、社会影响强等特点[2],需要从多角度对多项复杂资源整合规划,以实现该物流网络的多目标优化[3]。近年来,学术界对铁路工程建设项目中的网络优化问题展开了广泛深入的研究。XIE等[4]运用问卷调查和最小二乘结构方程模型,探讨了政府干预对绿色供应链管理及生态现代化的影响。张得志等[5]则从可持续性的角度出发,针对铁路工程建设中的供应链集成优化问题进行了研究,提出了一个两阶段决策框架,用以决策供应商选择、物流设施选址、路径规划和库存管理等关键问题。铁路工程建设因其规模大、标准高、周期长等特点,在各类工程建设项目中占据了极其重要的位置。中国对铁路建设项目的重视,进一步推动了国内学者对铁路建设相关科研问题的探讨。孙永福等[6]根据我国国情和铁路发展阶段,构建了一个涵盖经济效益、社会效益和环境效益3个维度的铁路建设项目综合评价指标体系。在铁路工程建设中,土石方调配和弃渣利用策略是2个紧密相连的关键科学问题。鲍学英等[7]从资源化利用弃渣和废弃混凝土的角度,研究了山区铁路工程与材料资源协调发展的关系及其面临的障碍因素。此外,季节变化对物流网络各运营环节均会产生显著影响,众多学者对此进行了深入分析。KANTARI等[8]分析了运输服务需求的季节性波动,并指出这种波动可能导致运输服务供应不足。WOLFF等[9]采用时间聚合法对季节周期进行建模,有效描述了可再生燃料物流网络中生产、运输和存储环节的季节性波动。在网络优化模型的构建和求解方面,RAZMI等[10]开发了一个多产品多周期的供应链动态混合整数规划模型,对网络中价格和质量的季节性变化进行了精确刻画。RABBANI等[11]结合非支配排序遗传算法和蒙特卡洛模拟,有效处理了废物管理网络模型中的随机组合优化问题。综上所述,目前国内外研究中对于铁路工程建设和弃渣处理的研究较为全面,也有学者针对季节对物流网络的影响机理进行研究,但缺少对季节影响下铁路工程建设中弃渣回收利用物流网络优化的研究。因此,为有效提高山区环境中铁路工程建设项目弃渣回收利用物流网络的经济效益和社会环境效益,本文结合实际山区铁路工程建设特征,考虑运输能力与运价随季节波动和弃渣的产出不确定性,针对“隧道工区-弃渣加工厂-站场工区”的多周期多产品弃渣回收物流网络,构建了多目标优化模型。模型决策了弃渣加工厂的选址与投资建设规模、采购与弃渣回收利用比例、弃渣运输路线规划与流量分配等,并采用Epsilon-约束法对模型进行转化和求解。随后以长赣铁路为案例,对案例求解结果的多目标优化和季节影响进行分析,并对采购价格和运输价格进行敏感性分析,得到了相应的管理启示。
1 问题描述与基本假设
在铁路工程建设的弃渣回收利用物流网络中,弃渣产出于隧道工区;产出的弃渣被运往弃渣加工厂进行分类筛选与加工处理,转化为废弃石料、1级机制砂和2级机制砂;废弃石料被运往废弃中心进行废弃处置,1级机制砂和2级机制砂被运往站场工区进行工程建设利用。其中,站场工区的机制砂需求可以从外部市场按照市场价进行采购。且由于铁路工程建设的工期较长,网络优化决策应以周期为单位进行决策。综上所述,该物流网络包含3级节点:弃渣产出隧道工区、弃渣加工厂和弃渣需求站场工区,如图1所示。网络优化模型需要对弃渣加工厂的选址与投资建设规模、采购与弃渣回收利用比例、弃渣和机制砂的运输路线规划与流量分配、机制砂的库存管理进行决策。依据铁路工程建设工期,该物流网络以季节和年为单位划分为多个周期。
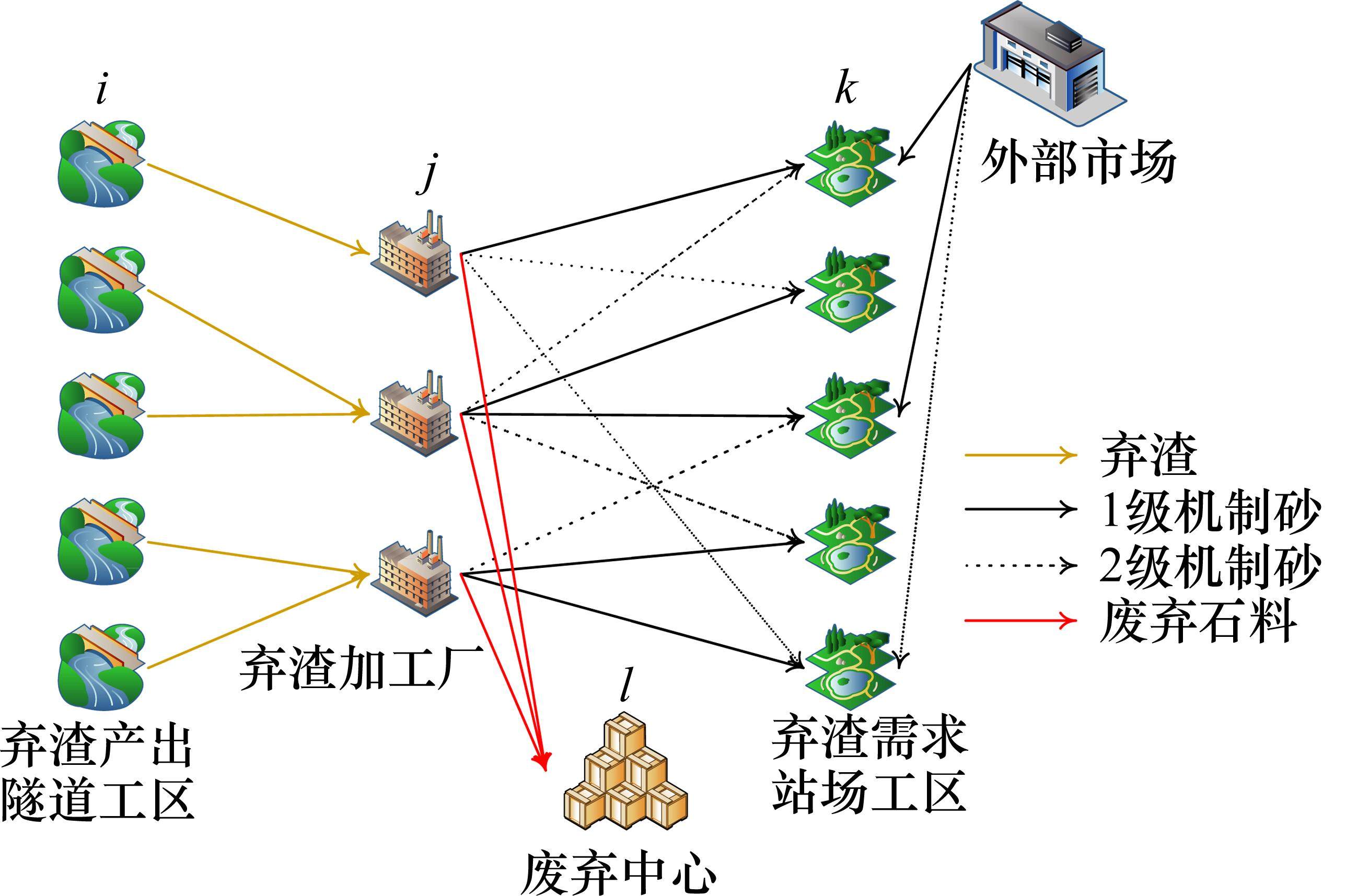
本文研究假设如下:1) 弃渣产出隧道工区、弃渣需求站场工区的位置,备选加工厂的位置、建设成本、储存能力等相关信息均已知;2) 物流网络考虑多周期,其中以季节周期为子周期,4个季节周期构成一个年周期;3) 不考虑弃渣在运输和存储过程中的损耗;4) 弃渣产出隧道工区可供应的弃渣的量是不确定的,且服从正态分布;5) 弃渣按照弃置率初步筛选分为废弃石料和砂石原料,废弃石料需要运输到废弃中心弃置,砂石原料可以加工成1级机制砂和2级机制砂;6) 弃渣需求站场工区每周期的砂石料需求量已知,且必须满足,砂石料可以从外部市场购买,采购价格已知;7) 单位运价率和道路能力随季节产生变化;8) 加工厂的富余弃渣将作为库存保留至下周期,并产生相应库存成本;9) 加工厂开设和规模一经确定,后续不再关闭、扩建等。
2 优化模型
依据山区铁路工程建设特征,建立了一个季节性运输波动的多目标优化模型,该模型综合考虑了季节变化对运输的影响以及弃渣产出不确定性,以经济效益和社会环境效益为目标,对物流网络多项决策进行优化。本章将从模型的季节变化对运输环节的影响、弃渣不确定性描述、经济效益分析、社会环境效益分析等方面展开阐述,并详细介绍模型的求解步骤。
2.1 符号说明
模型的符号说明如表1所示。其中,符号上标用于区别符号意义,符号下标为集合索引。
| 符号 | 含义 | 符号 | 含义 |
|---|---|---|---|
| 集合 | |||
 | 弃渣供应点的集合,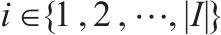 | 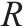 | 弃渣加工厂建设规模的集合,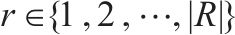 |
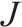 | 弃渣加工厂的集合,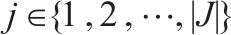 | 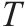 | 年周期的集合,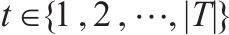 |
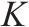 | 弃渣需求点的集合,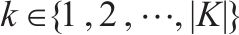 | 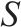 | 季节的集合,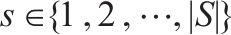 |
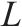 | 废弃中心的集合,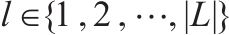 | ||
| 参数 | |||
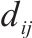 | 设施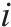 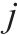 | 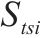 | 弃渣供应点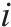 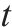 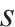 |
 | 加工厂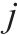 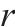 | 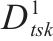 | 弃渣需求点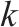 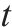 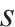 |
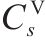 | 货物在季节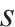 | 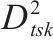 | 弃渣需求点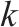 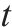 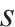 |
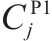 | 加工厂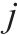 | 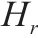 | 加工厂规模为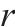 |
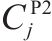 | 加工厂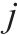 | 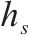 | 季节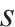 |
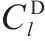 | 废弃中心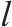 | 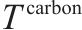 | 物流活动产生碳排放的碳税率 |
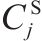 | 加工厂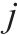 | 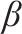 | 折标准煤系数 |
 | 加工厂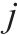 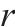 | 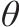 | 平均工资 |
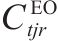 | 加工厂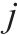 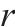 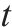 | 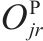 | 加工厂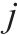 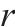 |
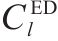 | 废弃中心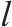 | 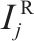 | 加工厂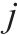 |
 | 季节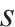 | 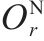 | 加工厂建设规模为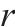 |
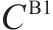 | 从外部市场采购1级机制砂的单位购买价格/(元∙t-1) | 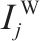 | 加工厂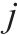 |
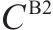 | 从外部市场采购2级机制砂的单位购买价格/(元∙t-1) | 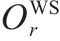 | 加工厂建设规模为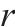 |
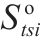 | 弃渣供应点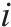 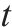 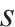 | 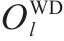 | 处置中心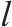 |
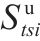 | 弃渣供应点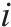 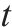 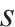 | 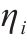 | 弃渣供应点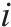 |
| 变量 | |||
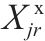 | 加工厂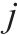 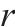 | 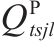 |
废弃石料的量/t |
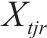 | 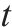 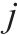 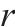 | 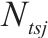 | 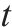 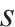 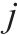 |
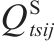 | 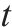 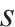 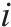 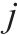 | 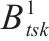 |
1级机制砂的量/t |
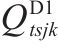 |
运输的1级机制砂的量/t | 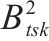 |
2级机制砂的量/t |
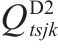 |
运输的2级机制砂的量/t | 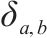 | 当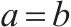 |
2.2 季节变化对运输环节影响分析
在山区环境中,季节变化会对公路运输状况产生影响,这对山区铁路工程建设物资保障带来了较大的困难。这种影响主要体现在2个方面,分别是季节性冻土和山区游客客流量的季节性波动。
在我国广东、广西、云南、福建以南的多山地带,受海拔、气候及地理位置的共同作用,季节性道路冻害现象尤为突出,表现为土壤冻胀和路面翻浆等[12]。路面受损和冻害问题会对公路运输车辆的正常通行造成影响,道路运输能力将显著下降,通行车辆的数量和规模都将受到限制。其次,由于运输环境恶劣,运输市场会进行相应的运价波动,运价率在冬季会显著上升。
山区环境中,旅游业的季节性波动同样会对山区交通状况产生影响。由于山区地理环境和气候环境的特征,夏季山区的阴凉气候会吸引大量游客前往山区游玩,旅客流量随季节变化而产生周期性波动,山区客流年内波动呈现明显的“三峰三谷”模式,春末、夏季和初冬为旅客流量高峰期。在旅游旺季,旅客数量的剧增对地区运输容量构成重大挑战,进而影响公路货物运输能力[13]。
2.3 弃渣不确定性描述
在铁路工程项目中,隧道施工的弃渣产出量受到地质条件、工程设备性能及操作技术等因素影响,其产出量存在不确定性。一般情况下,学者们会使用概率分布、蒙特卡洛模拟等方法来描述弃渣产出量的不确定性,本文采用正态分布模型对弃渣的产出进行量化分析[14],式(1)为弃渣产出量的概率密度函数。通过对隧道工区的历史数据和地质条件进行统计,可以估算出弃渣供应的期望值和方差。
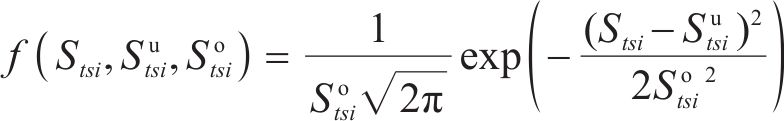
2.4 经济效益分析
根据问题描述部分对该物流网络的描述,物流网络总成本主要包含6项:固定建设成本、运输成本、加工处置成本、库存成本、采购成本和碳排放成本,分别如式(2)~式(7)。其中,固定建设成本考虑了加工厂的建设;运输成本为弃渣、机制砂和废弃石料在弃渣产出隧道工区、弃渣加工厂、弃渣需求站场工区和废弃中心之间的运输成本;加工处置成本包含了机制砂的加工成本和废弃石料的处置成本;库存成本以周期为单位,对每季度(周期)末的弃渣库存进行库存成本计算;采购成本包含了2种机制砂在外部市场按照市场价采购的成本。碳排放成本以碳税形式进行刻画[15],利用联合国政府间气候变化专门委员会(IPCC)所提出的碳排放因子法对相关物流活动的碳排放量进行量化,再参考程永伟等[16]对供应链中最优碳税模式的研究对碳排放成本进行计算。


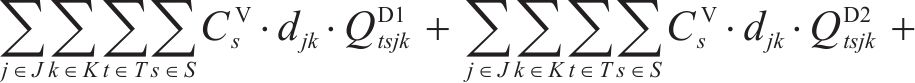

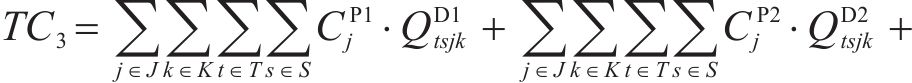


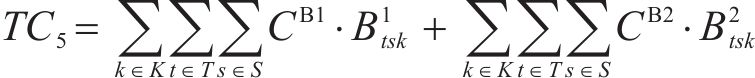
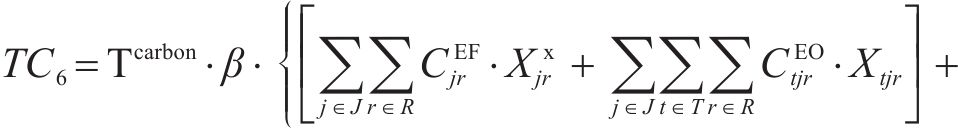
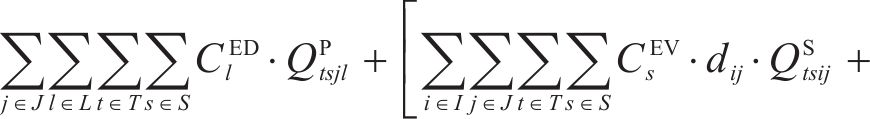
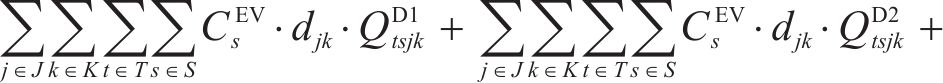
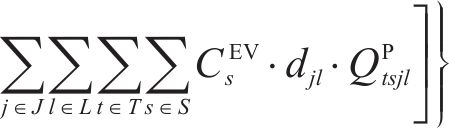
2.5 社会环境效益分析
铁路工程建设及其弃渣回收利用物流网络会对周边环境带来影响[17],模型将其刻画为可量化的社会环境效益[18]。其中,弃渣回收利用物流网络中的加工厂可以为周围城镇带来就业机会,产生的就业机会效益如式(8)。砂石原料的加工过程会对加工厂周围的居民造成声污染,噪声影响计算如式(9)。砂石料加工和处置时产生的污水排放对周边水质环境产生的负面影响计算如式(10)。

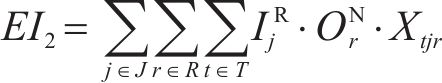
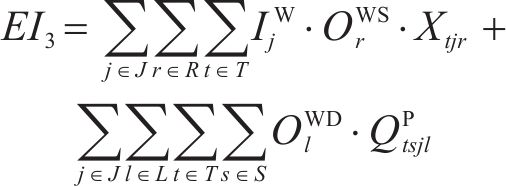
2.6 目标函数与约束条件

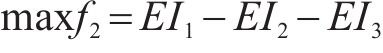
只有开设了加工厂才有弃渣的接收和加工。废弃石料的处置等物流活动函数表达如式(13)~(16)。
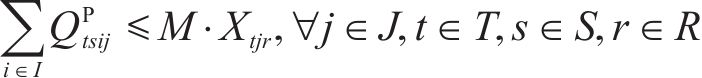
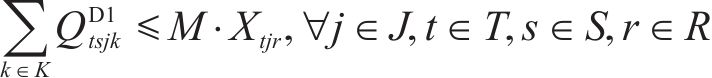
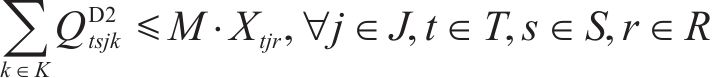
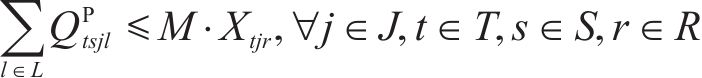
每个加工厂能且仅能有一种建设规模,如式(17)。
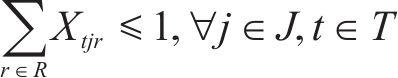
加工厂一经开设,不允许关闭、扩建,如式(18)。
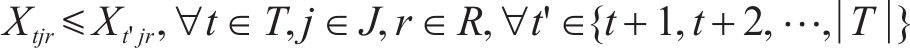
弃渣供应点可供应的弃渣量不超过该点的弃渣产出量,如式(19)。其中,弃渣供应点的弃渣供应量通过式(1)计算得出。
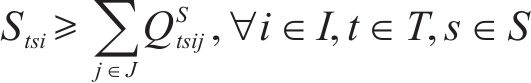
供应的弃渣将按照一定的比例筛选出废弃石料,如式(20)。
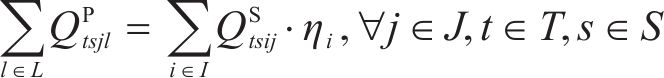
加工厂的流量平衡约束如式(21)~(22)。式(21)表示第1个周期中,所有弃渣将通过筛选和加工变为废弃石料、机制砂和富余弃渣库存;式(22)表示此后的周期中,上期末的弃渣库存将和本期的弃渣来源共同投入新一轮的弃渣筛选与加工流程,转化为新一期的废弃石料、机制砂和富余弃渣库存。
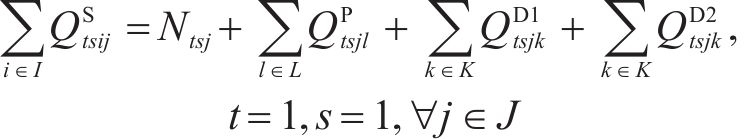
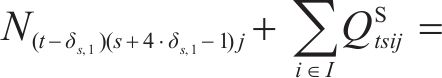

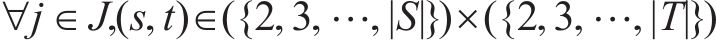
弃渣需求点的机制砂可以通过弃渣回收利用和采购2种方式满足,如式(23)~(24)。

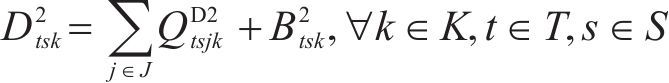
加工厂的容量约束如式(25)。

道路通行能力约束如式(26)~(27)。由于弃渣运输介于弃渣产出隧道工区与弃渣加工厂之间;1级机制砂与2级机制砂运输介于弃渣加工厂与弃渣需求站场工区之间,因此式(26)表示单独考虑弃渣的通行能力,式(27)表示合并1级机制砂与2级机制砂的通行能力。
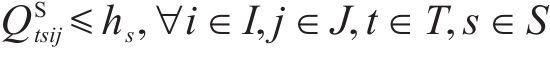
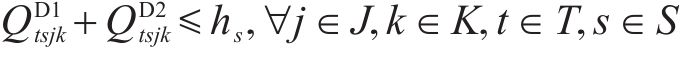
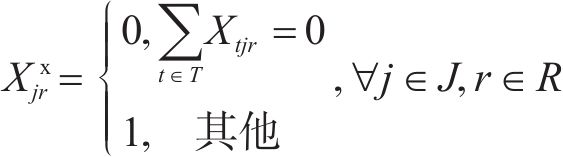
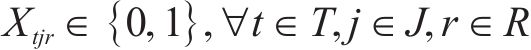
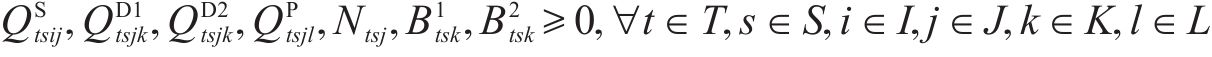
2.7 模型求解
模型中包含最小化网络总成本和最大化网络社会环境效益2个优化目标,对社会环境效益的优化无法避免付出更多的资金成本,因此,为了处理相互矛盾的2个优化目标,引入Epsilon-约束法求解模型。Epsilon-约束法是一种经典的用于处理多个矛盾目标的多目标优化方法,它利用容忍度将部分目标转化为松弛约束,将多目标问题转化为带有约束条件的单目标问题,通过定义不同的阈值来控制解的质量。模型具体求解步骤如下所示:
1) 将最小化网络总成本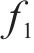
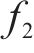
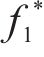
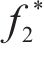
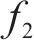
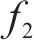
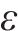
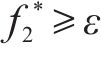
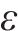
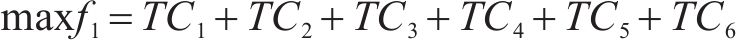
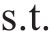
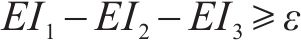
(13)~(30)
3 案例分析与结果讨论
以新建长沙至赣州高速铁路(简称“长赣铁路”)工程项目中的弃渣回收利用物流网络为研究实例进行求解分析。实验使用CPU主频为2.5 GHz、内存为16.0 GB的计算机,在将模型转化为单目标模型后,使用MATLAB 2021a进行编码,通过YALMIP工具箱调用IBMILOG CPLEX12.6求解器实现,求解器运行时间设置为1 h。
3.1 案例描述
新建长沙至赣州高速铁路(简称“长赣铁路”)是渝长厦铁路通道的关键区段,位于湖南省东部和江西省西南部,铁路正线全长429.48 km,其中湖南段正线长132.13 km,江西段正线长308.38 km,线路起源于长沙市长沙西站,终至赣州市赣州西站,途经萍乡市、株洲市、吉安市。线路经过区域地貌以丘陵区、中低山区为主,间夹河流阶地,全线桥隧比86.1%。长赣铁路正线共规划沿线隧道130座双线隧道和11座单线隧道,全线隧道弃渣约2 750.3万方,弃渣产出巨量。为满足铁路工程项目中对混凝土等建材原料的需求,全线共设41处混凝土加工厂,主要分布在长沙市、吉安市、萍乡市和赣州市。铁路全线共设车站12座,车站新建项目对混凝土等机制砂需求量大。综上所述,该铁路工程项目位于山区,隧道工程多,弃渣产出量大,符合本文所提出模型的基本特征。
依据长赣铁路工程项目建设情况确定了16个弃渣供应点隧道工区、4个备选弃渣加工厂和11个弃渣需求点站场工区,依据铁路工程项目工期,确定模型周期为5年。此外,基于项目建设环境评估报告、可行性研究报告等文件中的项目设计、生态环境影响评估、地形和气候条件描述、弃渣产出与利用方向研究[19-20]以及节点设施的实际需求数据,设定案例参数取值如表2所示。
3.2 求解结果分析
针对长赣铁路工程项目的弃渣回收利用多目标集成优化模型,采用Epsilon-约束法对该模型进行转化,求解后得到Pareto前沿下的成本结果如表3所示,本案例规模下的最优解在1 h内可求出,其中方案10为不考虑社会环境效益时最小化总成本的最优解。
| 方案序号 | 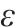 | 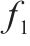 | 固定建设成本 | 运输成本 | 处置加工成本 | 库存成本 | 采购成本 | 碳排放成本 |
|---|---|---|---|---|---|---|---|---|
| 1 | 30 | 6 592 025 496 | 800 000 | 10 136 044.7 | 4 399 606.6 | 1 932.292 2 | 6 572 810 645 | 3 877 267.6 |
| 2 | 28 | 5 871 665 181 | 800 000 | 155 916 354 | 40 049 464 | 923.397 86 | 5 616 835 802 | 58 062 637 |
| 3 | 25 | 5 039 680 954 | 800 000 | 384 857 228 | 85 299 387 | 9 196 800 | 4 410 129 528 | 149 398 011 |
| 4 | 22 | 4 433 600 625 | 800 000 | 715 725 598 | 131 222 797 | 30 467 856 | 3 281 417 830 | 273 966 544 |
| 5 | 20 | 4 327 517 053 | 760 000 | 940 711 206 | 152 864 127 | 44 891 400 | 2 826 928 500 | 361 361 820 |
| 6 | 18 | 4 142 220 284 | 950 000 | 1 042 535 812 | 170 589 642 | 44 756 637 | 2 481 287 447 | 402 100 746 |
| 7 | 15 | 3 862 570 002 | 950 000 | 1 193 973 397 | 197 157 063 | 45 645 458 | 1 963 191 138 | 461 652 945 |
| 8 | 12 | 3 862 526 645 | 910 000 | 1 193 973 397 | 197 157 063 | 45 645 458 | 1 963 191 138 | 461 649 588 |
| 9 | 10 | 3 862 456 145 | 850 000 | 1 193 973 397 | 197 157 063 | 45 645 458 | 1 963 191 138 | 461 639 088 |
| 10 | — | 3 260 271 186 | 850 000 | 1 063 712 881 | 218 029 883 | 55 095 960 | 1 559 976 500 | 362 605 963 |
表3显示,随着对社会环境效益的松弛,物流网络总成本呈现先急后缓的下降趋势,并在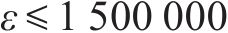
图2展示了Pareto前沿所对应的解集中选址产生变化的5个方案,由图2(a)至图2(e)社会环境效益逐步松弛。由图可知,随着对社会环境效益的松弛程度不断提高,加工厂开设情况从小规模逐步变化为大规模,加工压力不断上升;对社会环境效益的重视程度提高则会使弃渣加工被集中至加工压力点,即吉安市加工厂。因此,当社会环境效益目标值小于10万元,即决策者对经济效益的重视程度远高于社会环境效益时,应该选择方案9加工厂选址方案;随着对经济效益重视程度的松弛,决策者可以选择方案8以及后续方案。
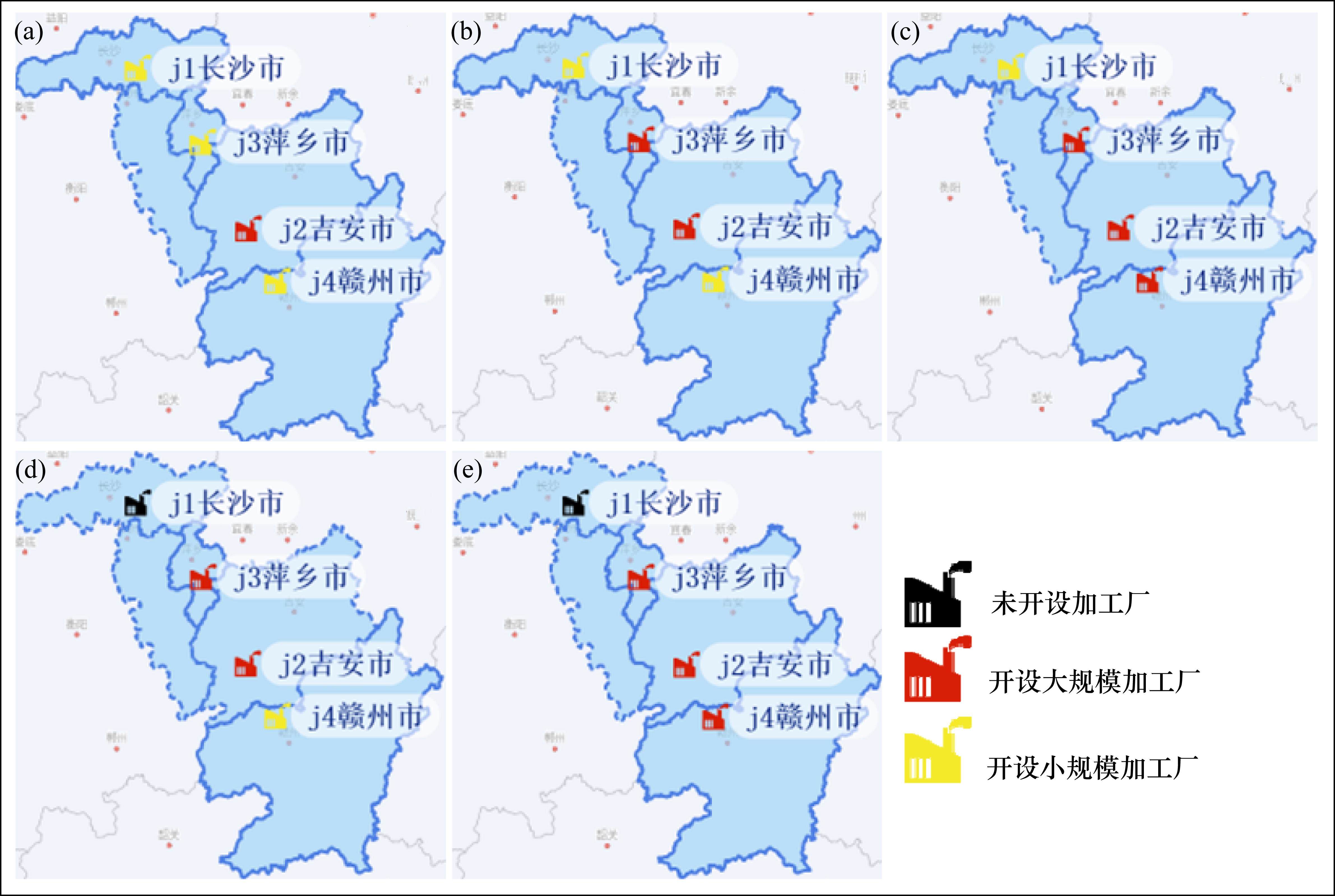
由于2个目标之间存在冲突,无法同时达到最优,决策者需根据实际情况在经济效益和社会环境效益间权衡,确定合适的网络优化方案。综合长赣铁路工程项目实施方案的环境测评和投资预算,选取方案5,即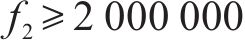
为分析季节对流量分配的影响,选取方案5第2年四季周期的流量分配情况进行展示。由图3可知,不同季节的机制砂网络流量分配情况区别明显。其中,机制砂的主要运输活动集中在春、秋2季;且在运输能力覆盖范围上,以萍乡市和吉安市的加工厂占主导地位。
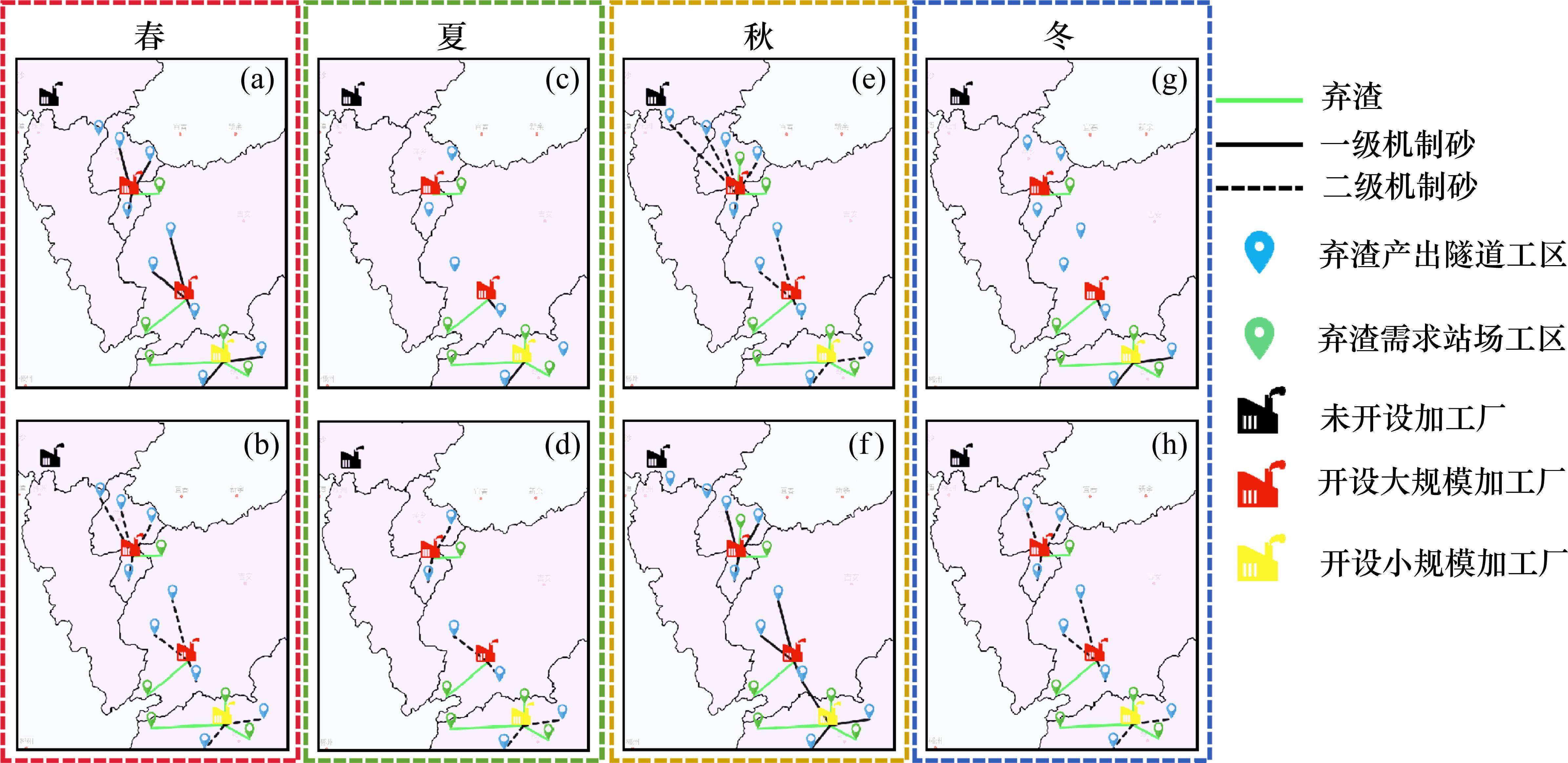
表4展示了方案5的成本构成情况,由表4可见不同成本的总成本占比差距较大,其中采购成本是最大的成本来源,占总成本65.324 5%;其次运输和采购成本分别占总成本21.738 9%和8.350 3%。因此网络规划中采购、运输和碳排放的决策对总成本控制至关重要。下文将对采购价格和运价率进行进一步敏感性分析。
| 成本类型 | 成本金额/元 | 占总成本比例/% |
|---|---|---|
| 固定建设成本 | 760 000 | 0.175 6 |
| 运输成本 | 940 711 206 | 21.738 9 |
| 加工处置成本 | 152 864 127.4 | 3.532 4 |
| 库存成本 | 44 891 400 | 1.037 3 |
| 采购成本 | 2 826 928 500 | 65.324 5 |
| 碳排放成本 | 361 361 819.8 | 8.350 3 |
| 总成本 | 4 327 517 053.145 7 | 100 |
3.3 采购价格敏感性分析
在上述求解过程中,机制砂采购价格设定为当前市场价,但实际采购中采购价格会随市场的波动情况而变化。基于此,本节构建了10种情景对机制砂采购价格进行敏感性分析。
图4(a)显示:1) 采购价格与总成本、采购成本之间基本呈线性关系;2) 购价格与运输、加工成本之间存在临界点,即采购价格下跌30%:临界点之前,运输、加工成本对采购价格的变化反应敏感;临界点之后,运输、加工成本的影响相对平缓。
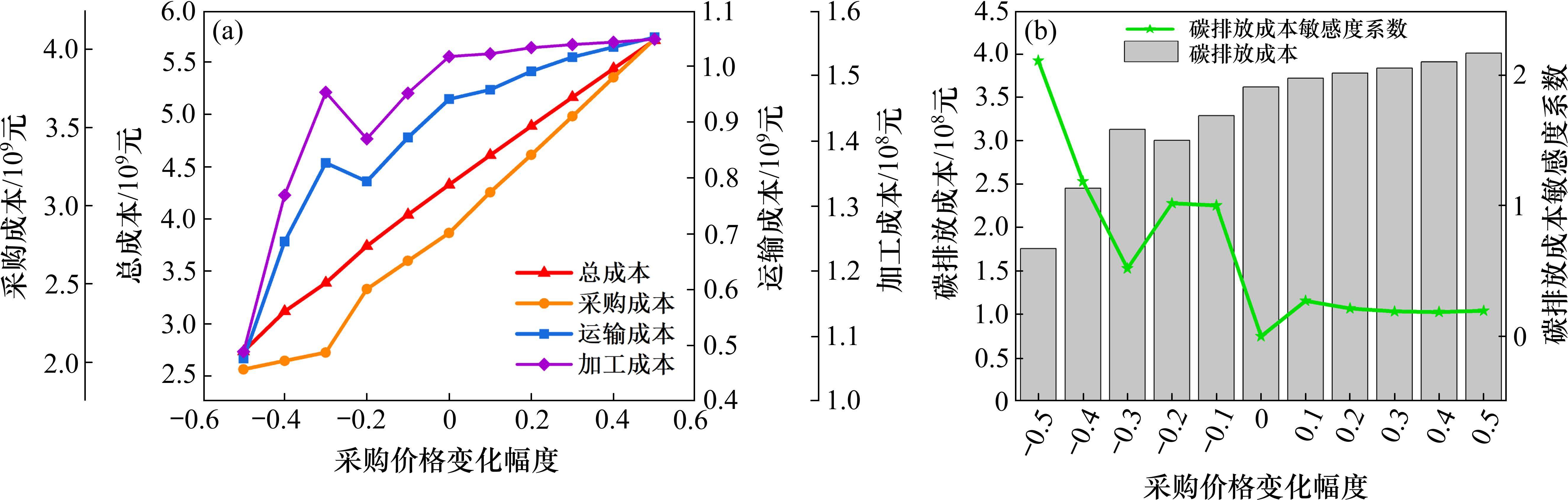
一般地,采购价格对总成本的影响主要作用于采购成本;而在该弃渣回收利用物流网络中,机制砂的采购和弃渣的回收利用共同受需求量约束,因此采购价格对弃渣的回收利用决策有间接作用,采购价格的变化也会影响运输、加工成本。以采购价格下跌30%为临界点,临界点之前,决策者将以机制砂采购为主;临界点之后,决策者则以弃渣的回收利用为主。
图4(b)显示:基准价格以下,碳排放成本的敏感度系数较高,即碳排放成本受采购价格的影响较大;而当采购价格超过基准价格时,碳排放成本受采购价格影响较小。因此为稳定物流网络碳排放量,政府可以政策颁布介入采购市场的物资定价在基准价格之上。
3.4 运价率敏感性分析
在实际生产中,运价率受多种因素影响,属于不确定因素。本模型的运价率随季节变化而波动。基于此,本节构建了10种情景对运价率进行敏感性分析。
图5显示:随运价率上涨,1) 网络总成本和运输成本均呈现稳定增长趋势;2) 库存、采购成本整体呈现波动上升态势;3) 碳排放、加工成本整体呈现下降趋势,其中碳排放成本波动稳步下降,而加工成本在运价上涨20%前下降幅度较小,之后呈现急剧下跌现象。
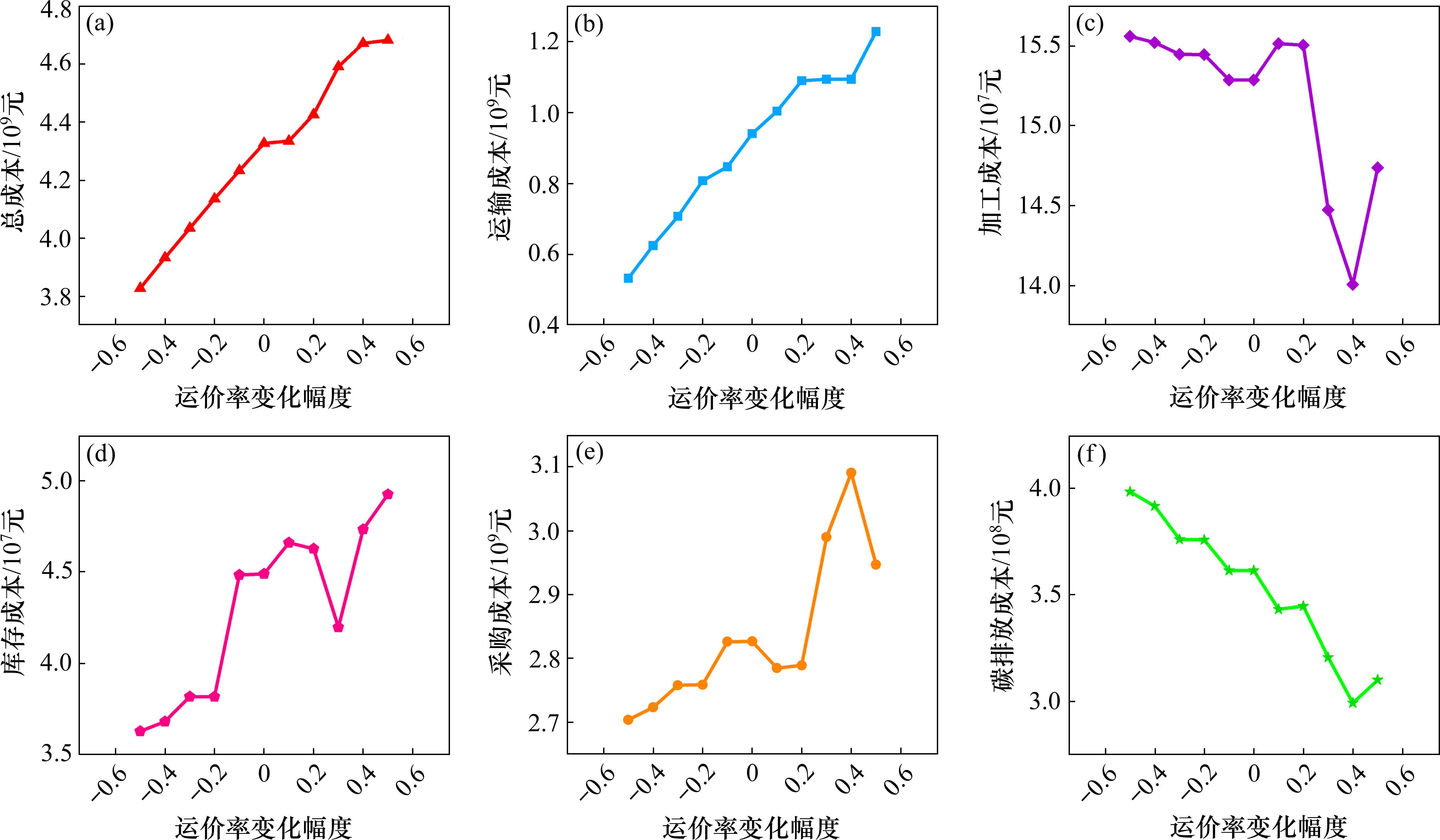
随着运价率的上涨,运输成本的增长是毋庸置疑的。其中,多项成本的变化都存在一个临界点,即运价率上涨20%。临界点之前,决策者将以弃渣的回收利用为主;临界点之后,决策者则以采购为主。除此之外,碳排放成本会随着运价率上涨而逐渐下降,因此为降低物流网络碳排放量,政府可以通过政策颁布介入运价市场,控制运价合理上涨。
图6为各成本在不同季节中随运价率变化热力图,如图显示:1) 夏季的网络总成本显著高于其他季节,且各成本在不同季节波动差异明显;2) 运输成本在秋季受运价率影响最明显;3) 当且仅当运价率在基准水平以上,秋季才开始产生库存成本;4) 碳排放成本在春、夏和冬季随运价率上升而下降,在秋季随运价率上升而上涨。
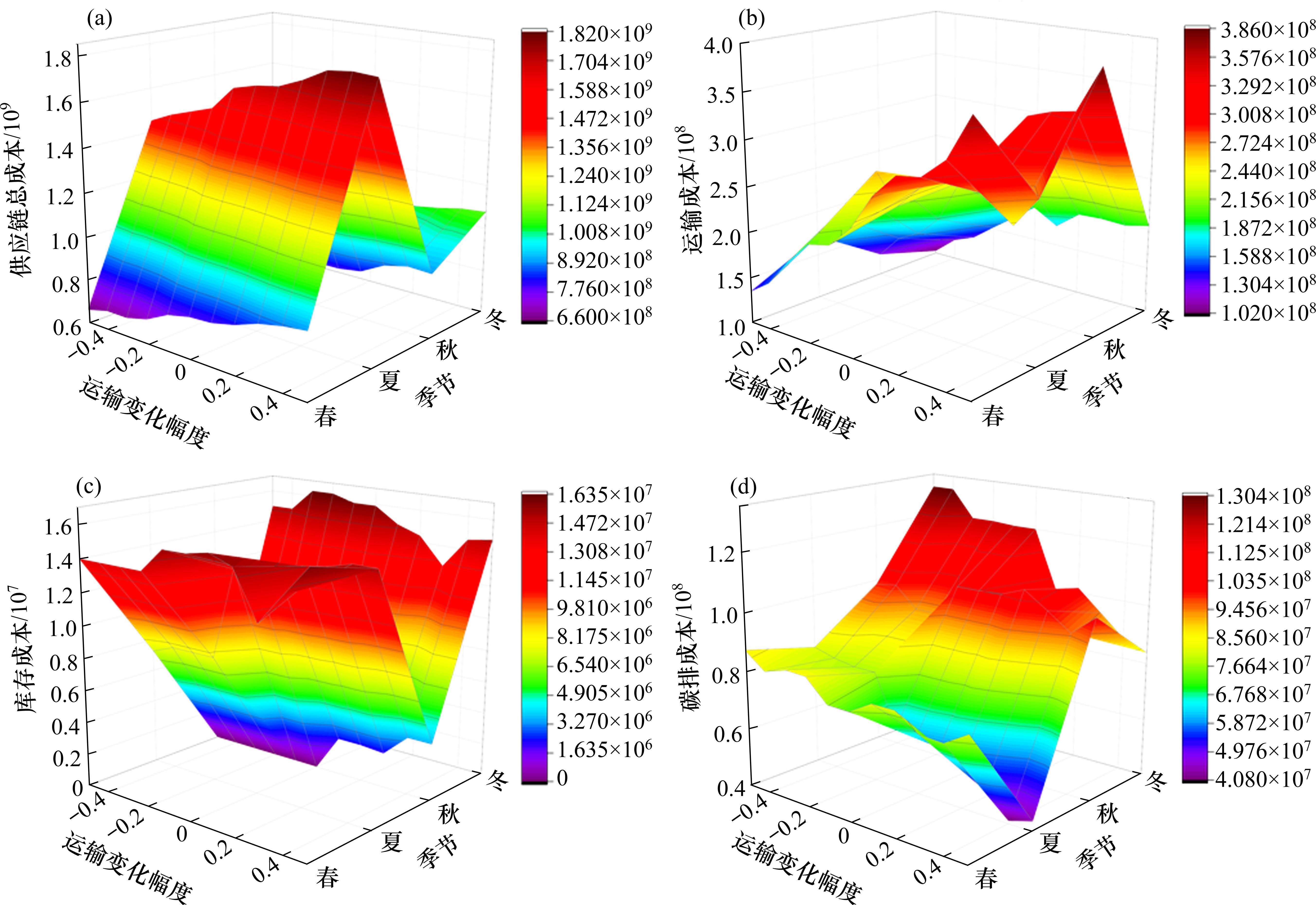
综上所述,季节波动对物流网络中不同环节的影响存在较大差别。其中,决策者应尽可能在秋季安排弃渣的回收利用,且当运价率高于基准水平时,可以通过库存将其他季节的加工压力分担至秋季。为控制物流网络碳排放量,政府可以一定程度地介入运价市场,但需要区别季节策略进行调节:主要调节秋季的运价市场上涨,避免决策者将所有运输活动转移至秋季导致秋季碳排放量的突然增加。
4 结论
1) 针对山区铁路工程建设弃渣回收利用物流网络优化问题,考虑运输能力与运价的季节性波动,以及弃渣的产出不确定性等因素,研究季节性运输波动下山区铁路工程建设弃渣回收物流网络优化,构建了多周期多产品弃渣回收物流网络多目标优化模型,优化确定物流网络中弃渣加工厂的选址及其建设规模、机制砂外购与弃渣回收利用比例、运输路线与流量分配等,并采用Epsilon-约束法对模型进行转化,调用CPLEX求解器进行求解。最后以长赣铁路工程项目为例进行案例研究,对求解结果的多目标平衡和季节影响进行详细分析,并对采购价格和运价率进行敏感性分析,进一步得到管理启示。
2) 通过研究,得到了以下管理启示。① 加工厂选址与投资规模决策方面,对社会环境效益越松弛,弃渣加工压力越大,加工厂开设规模越大。② 采购和弃渣回收利用决策方面,当采购价格低于基准30%运价率高于基准20%时以采购为主,当采购价格高于基准30%运价率低于基准20%时以弃渣的回收利用为主;决策者应将弃渣的回收利用主要安排在秋季,且当运价率高于基准水平时,可以通过将其他季节的弃渣回收利用加工作业转移到秋季来降低工程建设的物流总成本。③ 可持续决策方面,政府可以通过政策颁布介入机制砂的采购和运输市场,控制采购价和运价率的合理上升来降低物流网络的碳排放量;其中,主要调控运价率的秋季上涨,避免决策者将所有弃渣回收利用加工作业都集中在秋季,使秋季碳排放量的显著增高。
3) 本文的局限性主要在于:仅考虑了一种运输方式、对不确定性的描述和求解不够具体、对社会环境影响的刻画还不够全面。因此未来的研究方向主要集中在更合理的多式联运体系设计、更具体的不确定性因素刻画和更全面的环境影响描述。
张得志,罗湘钰,李翔等.季节性运输波动下山区铁路工程弃渣回收物流网络优化[J].铁道科学与工程学报,2025,22(01):89-101.
ZHANG Dezhi,LUO Xiangyu,LI Xiang,et al.Optimization of logistics network for railway construction waste slag recycling in mountainous areas under seasonal transportation fluctuations[J].Journal of Railway Science and Engineering,2025,22(01):89-101.