重载铁路通常采用固定车底运输方式,空车调配以“列”为单位进行,空车与重车不混编。其运输装卸作业地点分为装车端与卸车端2个部分,重车在卸车端完成卸车作业,卸后产生的空车经由重载线路回送至装车端装车点进行装车,以保证线路上重空车流的均衡性,形成了“重去空回”的运输组织模式。重载铁路“重去空回”运输组织问题与重空车协同匹配组织问题类似,其目标是:在一定的运量需求和车辆资源限制下,使空列/车的送达时间和送达量与货物的装车需求时间和需求量相匹配,保障重列/车按需完成运输。目前已有学者进行了相关研究:付建军[1]考虑重空列相伴相生的关系,但对于重空列接续循环的具体过程有待细化。马博文等[2]使用分阶段优化方法加快了求解效率。王龙[3]实现了对未来任意时点车流状态的推算。林柏梁等[4]构造了空重车流改编作业成本综合优化的模型化框架。WANG等[5]研究了重载列车在组合站的作业优化问题,并设计迭代搜索算法求解。ZHANG等[6-7]建立了重载铁路卸车端空车的反馈示意模型,对重载铁路回空列调整问题开展研究。GORMAN等[8-9]分别研究了美国与印度铁路公司的空车分配优化问题。FU等[10]从绿色运输的角度建立了重载铁路空重车流组织方案。上述文献对重空列/车协同组织问题的研究主要侧重于重空列/车供需量在时空层面的配合,但未充分考虑货车/列车车辆的供需类型匹配情况。煤运重载铁路多运营3种货车:C80、C70及C64,由于各型车辆编组的列车长度不同,且车站解编到发线长存在差异,列车车辆类型因此受到限制[11]。在实际运输组织中,虽然性能优异的C80货车已逐渐成为主流,但由于各铁路装车单位存在对C70、C64型货车的最低装车需求,仍有大量C70、C64处于运用状态[12]。因此,配送列车至装车站、组合分解站时需考虑其组成车型,各车型不能混编。基于货车车辆类型差异带来的运输组织复杂性,需将其纳入重空列协同运输中统一考虑。徐禾颖等[13]虽将车辆类型考虑在重空列运输组织中,但未进一步考虑重空列随时间推移的联动性。刘海涛等[14]建立了多品类多车种的重空车流径路联合优化模型,但其仅得出了静态流的分配方案。吴艺迪等[15]仅关注以港口站为中心的重载列车分解方案与作业计划,没有给出整体运输组织方案。另外,重载线路上的“重去空回”模式导致空车走行率偏高,车辆利用效率较低,线路资源得不到充分利用。利用回空车开展返程运输可有效提高重载铁路返程方向的铁路分担率,减少返程运力浪费;而从车辆资源全程运输的角度,需进一步考虑返程列车卸空利用,以及空走费用等问题。近年来,已有学者对利用重载铁路返程车辆运输进行研究,但多从定性的角度进行宏观分析;童瑞咏等[16]虽从定量角度研究返程方向的运输组织问题,但没有考虑车辆资源的进一步周转和利用。循环车底货物列车运输组织问题在集装箱运输领域较为常见,李思雨等[17]研究了集装箱固定车底循环班列组织。罗君培等[18]计算了反映班列质量的综合货物运输效益。韩涛等[19]将集装箱班列停站方案与运行图协同优化。STEADIESEIFI等[20]将固定费用容量多商品网络流问题扩展,解决了相应多式联运问题。上述关于固定车底循环使用产生的车底周转等问题在重载列车运输组织中仍需加以考虑。当前对重载铁路重空列车循环运输组织的文献相对较少,且多于列车实际走行径路或装卸某一端的调配优化问题着手。文献[1]是重载铁路重空列循环运输组织问题的代表作。本研究在文献[1]的基础上,对研究边界和模型构造方法均作调整:进一步考虑车辆类型影响和返程需求运输,针对列车在装卸车端、组合分解站的接续和车辆类型一致性等要求对模型进行改进,对承担返程需求的车底再次分配过程进行数学表达,建立了重载铁路重空列协同优化模型,并选取SH集团重载铁路上的部分线路与车站作为案例进行研究。
1 问题描述
重载铁路将重空列车作为整体进行组织,其普遍开行5 000 t列车(单元小列)和10 000 t列车(万吨大列),重空列伴随装卸车作业过程相互转化,在重载铁路上依据运输需求循环开行。该运输过程存在去程、返程运输,去程运输指煤运装车站至煤运卸车站(一般集中在港口、电厂或者煤炭中心等)的运输过程,返程运输指回送空车至煤运装车站或从港口运送部分非煤货物至非煤卸车站过程。
为精细刻画上述运输过程,本文建立如图1所示的离散型时间-空间-状态网络
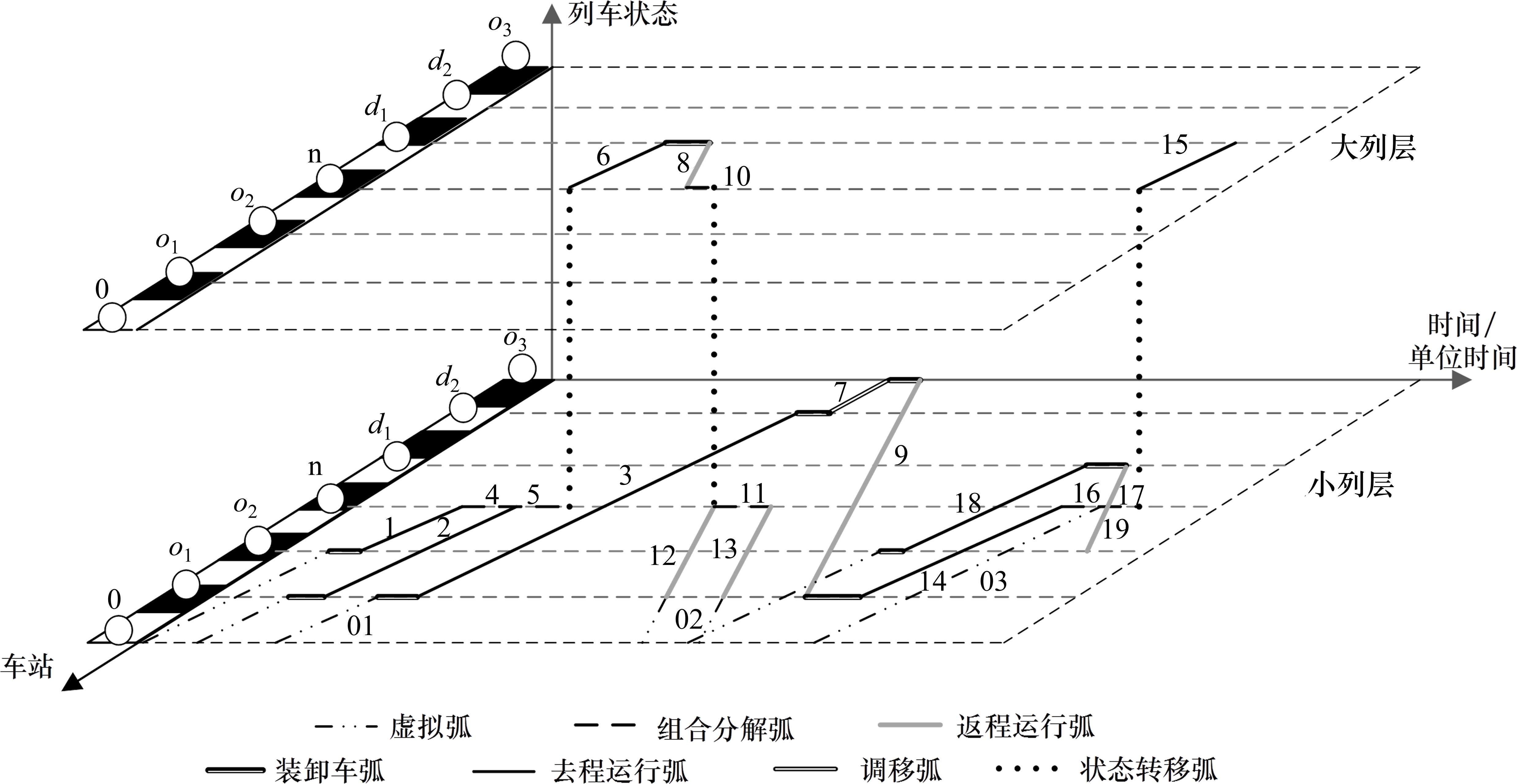
去程重列的运送过程描述如下:依据煤炭需求,空列送达装车站o1、o2并完成装车后,有以下可能的配送路径:1) 以重列形式送至卸车站d1、d2,如弧段3;2) 先通过弧1、2送达组合站n,经由弧段4、5组合成大列后送达卸车站d1。
在卸车站d卸货后,返程空列将有以下可能的配送路径:1) 以大列或小列直接配送至某一装车站,如弧段19;2) 大列空列先通过弧段8送至分解站,经由弧段10、11分解后,再根据空列需求情况,经由弧段12、13分别送达相应的装车站;3) 部分车列卸后可能需调移至非煤货物装车站,用以返程运输,如:重列到达站d2后卸车形成的空列经由调移弧7调移至非煤货物装车站o3完成装车后经弧9送至返程到达站。非煤需求被卸空后,重列再次转化为空列,根据空列需求情况再次配送至某一装车站。
重空列车如此循环往复,形成了列车随时空流转的运输过程。在此过程中,连接虚拟车辆段的01等虚拟弧在时间起点将车列送至装车站,02等将车列送至卸车站,03等在原车列不足以满足车列的接续运输需要时提供虚拟车列。
图1时空网络中的弧段集合如下:
去、返程弧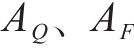
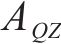
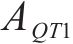
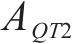
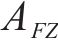
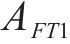
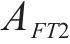
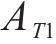
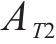
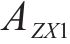
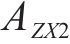
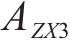
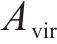
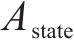
在重空列运输组织过程中,重列依据其承运的货物需求确定发到站;而空列的产生地和产生时间与重列到达密切相关,空列发往的目的地与各装车站对空列需求的车辆类型、时间和数量要求密切相关,需要综合考虑接续时间成本和运输距离成本,形成更经济的空列配送方案。空列调配方案的好坏,进一步影响需求的装车和运输过程。因此,重空列车在运输组织过程中的相互依存性、不确定性、类型一致性等特性加大了该问题量化求解的复杂度。
该问题在建模过程中的难点为:车列的身份在运输过程中不断变化,如重空、大小列等,导致满足流平衡的数学表达较复杂,尤其在煤炭装、卸车点需用车列身份信息关联重空列开行决策变量,在组合和分解站需在列车类型、编组辆数等约束下,保证相应站点进出的单位车列总量相等。在重点考虑上述问题基础上,以多商品流和运输问题为基础,完成建模和实验分析。
2 模型建立
2.1 模型假设
1) 假设大小列的组合作业只能在组合站进行。
2) 假设去程方向卸车站没有货车与列车类型要求。
3) 假设运输煤炭所用的车辆类型均为敞车,型号分为C80、C70和C64。
2.2 符号说明
本文所用到的所有参变量与集合符号如表1所示。
| 类型 | 符号 | 含义 |
|---|---|---|
| 集合 | E | 区段集合,索引为e |
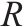 | 车站集合 | |
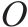 | 去程方向装车站集合,索引为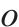 | |
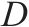 | 返程方向卸车站集合,索引为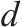 | |
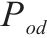 | 集合O中车站与D中车站构成的o-d对 | |
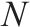 | 组合分解站集合,索引为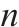 | |
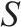 | 列车类型集合,索引为s,取1或者2分别代表小列和大列 | |
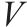 | 货车类型集合,索引为v,取64,70,80分别代表C64,C70,C80型货车 | |
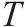 | 时间单元集合,每个值代表15 min,索引为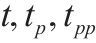 | |
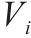 | 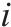 | |
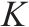 | 车底周转轮次集合,索引为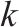 | |
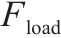 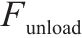 | 去、返程运输需求集合。去、返程需求索引为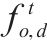 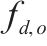 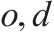 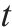 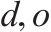 | |
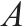 | 列车弧集合,分别表示列车发到站,发到时间,列车类型与循环次数,用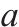 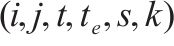 | |
| 参数 | 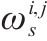 | 去程费用参数,表示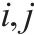 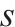 |
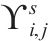 | 返程费用参数,表示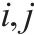 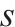 | |
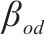 | 去程o→d间单位运输需求惩罚费用 | |
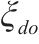 | 返程d→o间单位运输需求奖励费用 | |
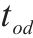 | 去程需求预计运达期限,此参数表示载运o,d需求的重列车进入组合站的预计运达期限上限 | |
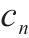 | 组合站n的组合分解能力 | |
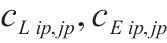 | 去、返程区段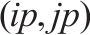 | |
| 变量 | 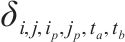 | 运输服务弧的路径索引变量:当物理区段(ip,jp)被列车服务(i,j)经过时取1,否则取0。ta为列车服务(i,j)由i站到达(ip,jp)区段起点所消耗的时间,tb为列车经过(ip,jp)区段消耗的时间 |
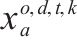 | 去程需求与列车服务弧的关联变量:若变量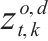 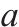 | |
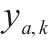 | 去程车底周转次数指引变量:若执行列车弧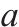 | |
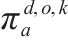 | 返程需求与列车服务弧的关联变量:若变量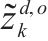 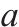 | |
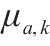 | 返程车底周转次数指引变量:若执行列车弧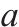 | |
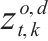 | 去程需求载运变量,表示由od间去程需求在k次循环的t时段被装运的需求量,可取值为0、1、2 | |
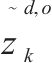 | 返程需求载运变量,表示由d到o的返程需求在k次循环中被装运的需求量,可取值为0、1、2 |
2.3 模型建立
模型构造方法方面,基于文献[1]的建模思路,在运输各阶段将车辆类型纳入考虑,确保列流转化各个环节车辆类型一致。本文进一步细化了流平衡约束,在变量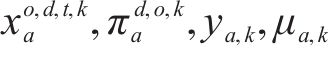
以服务网络上运输费用最小构建目标函数

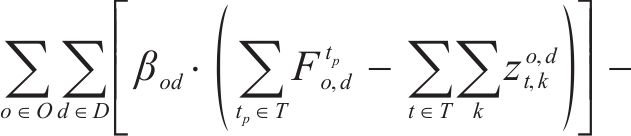
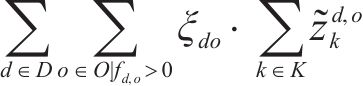
约束条件如下:
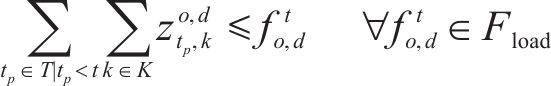
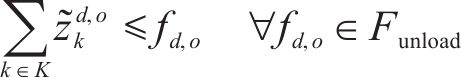
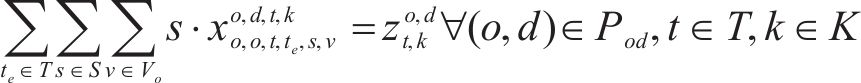
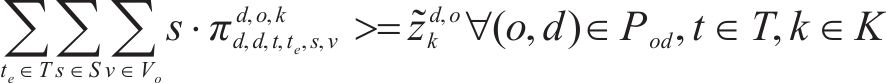
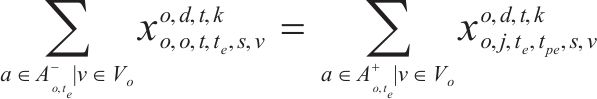
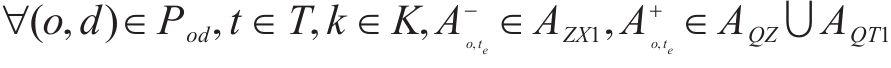
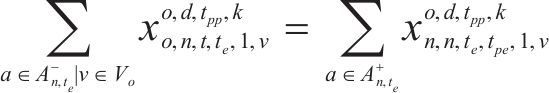
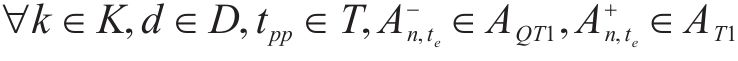
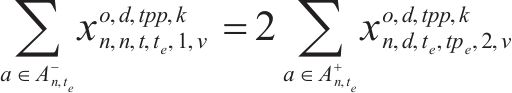
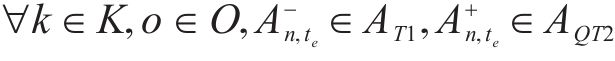
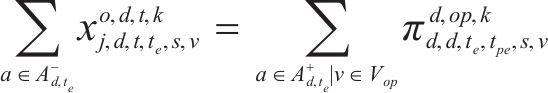
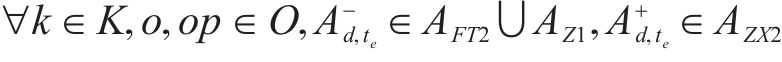
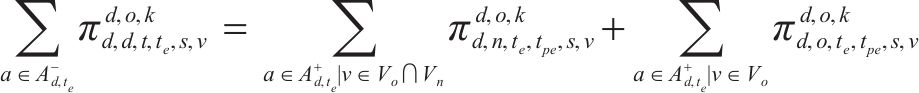
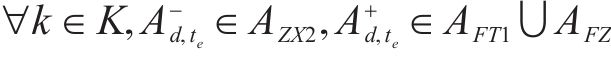
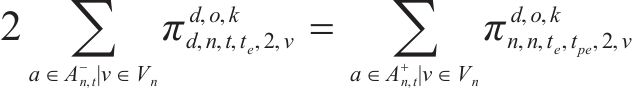
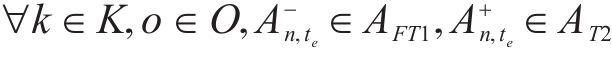
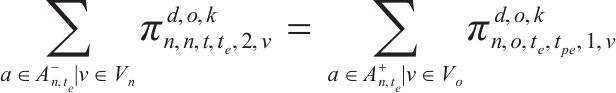
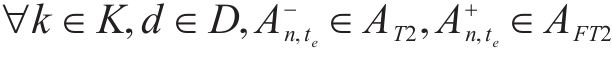
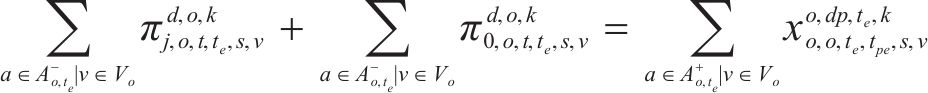
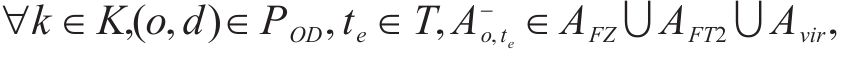

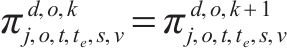
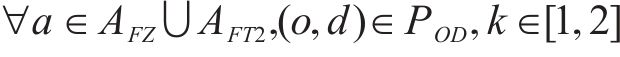
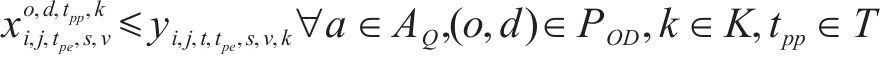
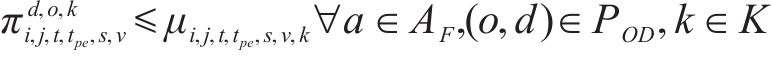
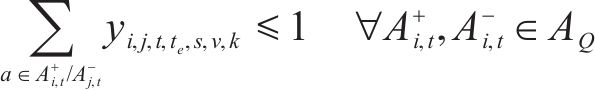
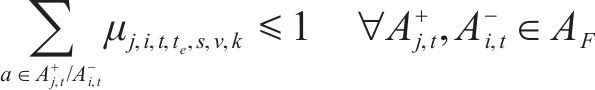
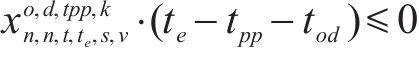
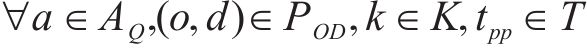
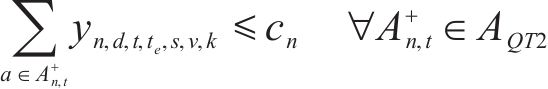
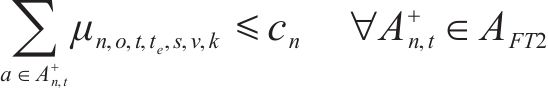
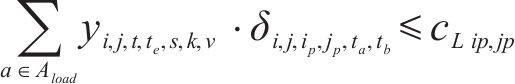

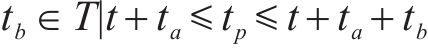
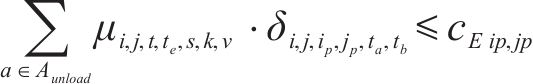

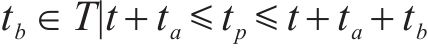
式(2)~(3)为需求分配约束,规定去、返程方向的需求量应在对应时段内选择分配,且其中只有部分需求能被成功运输。每单位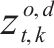
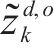
3 模型求解方法
本文构建的整数规划模型属于NP-hard问题,对于该类问题,启发式算法通常只求得可行解,并给出与实际最优解之间gap的估计值,求解质量未知。本模型本质是基于点-弧的车流分配模型,相对于弧-路模型,点-弧模型求解难度较低,求解规模较小,适合精确求解算法求解。由于运输量很大时,若对约束(2)、(3)采用等式约束,强制所有需求均运出,求解器很难在有限的时间范围内找到可行解。在模型中将对应约束(2)、(3)设置为不等式,将较大的数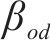

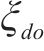
鉴于案例涵盖了众多站点,时间跨度广泛,并且需详尽展示列车种类及其所搭载车辆类型,这导致决策变量的维度显著上升。为了降低模型的复杂性,提升计算效率,有必要对整数规划模型实施预处理,以精简其行列数量。本模型区分了装卸、组合分解、虚拟站等多种车站类型,而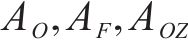
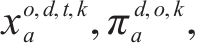

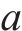
以装车弧为例,预处理前后变量个数变化如表2,其中符号
| 变量名称 | 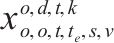 | 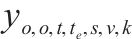 |
|---|---|---|
| 预处理前 | 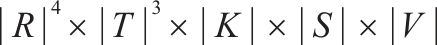 | 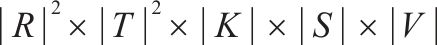 |
| 预处理后 |  | 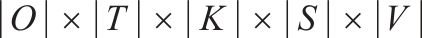 |
综合考虑模型规模与求解难度后,本文选择使用GUROBI求解器对案例进行求解。
4 案例分析
为验证模型的正确性和有效性,分别利用单通道和局部网络案例进行实验分析。
4.1 单通道案例
本案例为单通道双线线路,线路长度120 km,包含7个车站(3装车站,2组合分解站,2卸车站),如图2所示。本文假定该线路上的万吨列车可由C70、C80及C64分别组合而成。在对时间离散化处理过程中,以15 min为一个单位,将持续10 h的运输时段划分为40个时间单元。

案例1、2、4站与6、7站分别为煤炭需求的装、卸车站。站6与站1、2是非煤需求的装卸车站。煤需求的运量要求和最晚运出时间如表3所示,非煤需求无最晚运出时间限制。
| o | d | t/15 min | f/5 kt | o | d | t/15 min | f/5 kt |
|---|---|---|---|---|---|---|---|
| 1 | 6 | 10 | 2 | 4 | 6 | 30 | 2 |
| 1 | 6 | 40 | 4 | 4 | 7 | 25 | 5 |
| 1 | 7 | 20 | 2 | 6 | 5 | 3 | |
| 2 | 6 | 30 | 5 | 6 | 2 | 4 | |
| 2 | 7 | 15 | 3 |
使用Intel(R) Core(TM) i5-7200U CPU@2.50 GHz 2.70 GHz,8.00 GB RAM的PC上采用Python调用Gurobi 9.1.0进行实验,求解时间62 s,gap=0,优化方案目标值为682 000元。列车运行安排如图3所示。
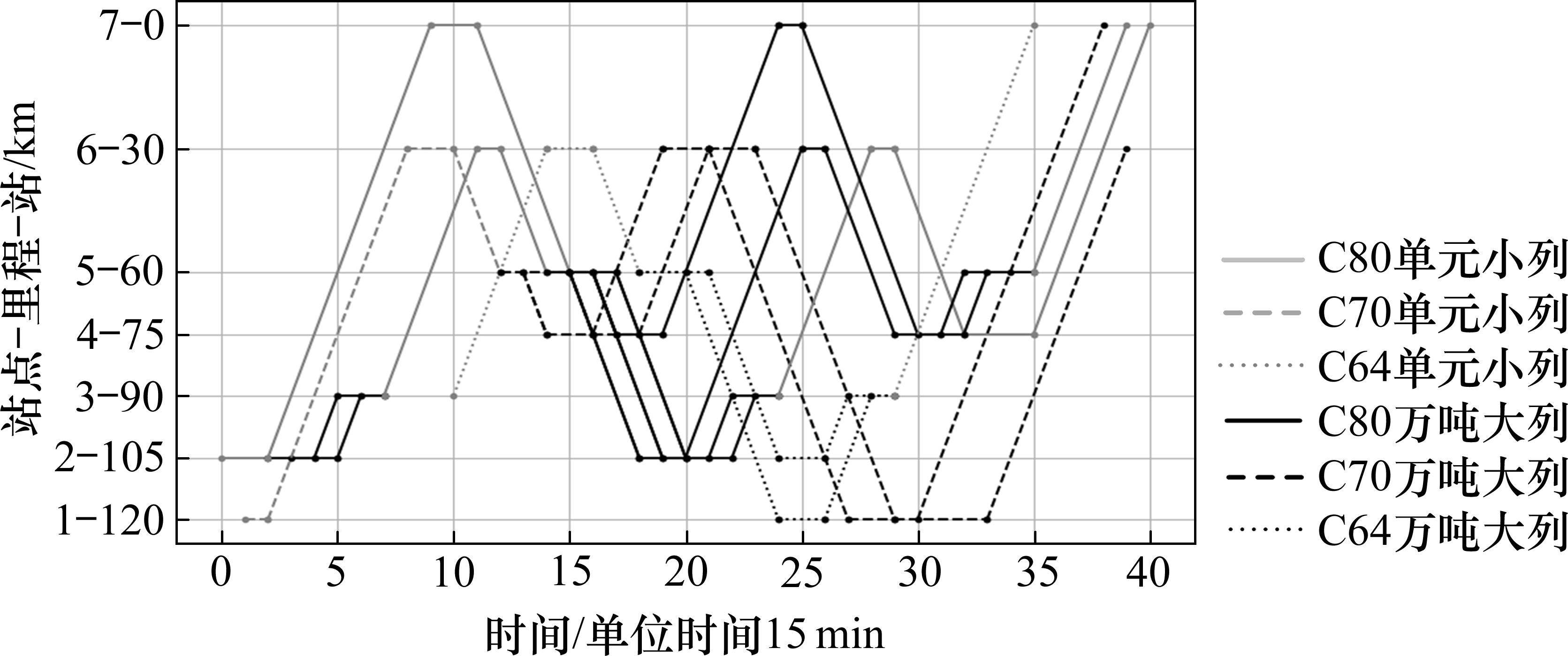
根据图3可知,去程方向共编发15列小列,8列大列;返程方向共编发20列小列,5列大列。分别有6列去程小列在组合站3,2列小列在组合站5完成组合作业,产生组合作业成本8 000元。有8列大列在分解站5完成分解作业,产生分解作业成本6 000元。完成这些运输任务共需要单元列车车底8列,各车底均参与了空重列的接续,产生56单位接续时间。接续作业成本(包括双方向重空列的转换接续)64 000元,运输成本604 000元,共计682 000元。
3类货车车底承担运输服务情况如表4所示,结果表明:由于C80货车载重大,相同重量下,由其组成的列车占用到发线、装卸线长度更短,组合分解方案更加灵活,因此各车站都倾向于运用C80组成的车列,车底运用数量达到了5列单元小列,其服务车次的数量也高于其余2种车型。
| 车型 | 车底数 | 服务车站编号 | 承担周转次数 | 服务车次数量/列 |
|---|---|---|---|---|
| C70 | 2 | 1→6→5→4→6→1→7,1→6→5→4→6→1→6→2 | 2,3 | 上行5,下行5 |
| C80 | 5 | 2→7→5→2→3→6→4→7,2→7→5→2→3→6→5→2; 2→3→6→5→4,4→7→4→5→7→2→6→4,4→5→7→2→6→4 | 2,3,1,3,2 | 上行15,下行11 |
| C64 | 2 | 3→6→5→1→3→7,3→6→5→2→3→7 | 2,2 | 上行4,下行3 |
4.2 运输网络案例
4.2.1 案例说明
为验证成网条件下各车站之间的货物运输协调、空车分配安排以及返程运输利用,以SH铁路网为例构造案例,案例设计时选取装车量较大的装车站,并将区域中相近车站合并,拓扑结构图如图4所示。
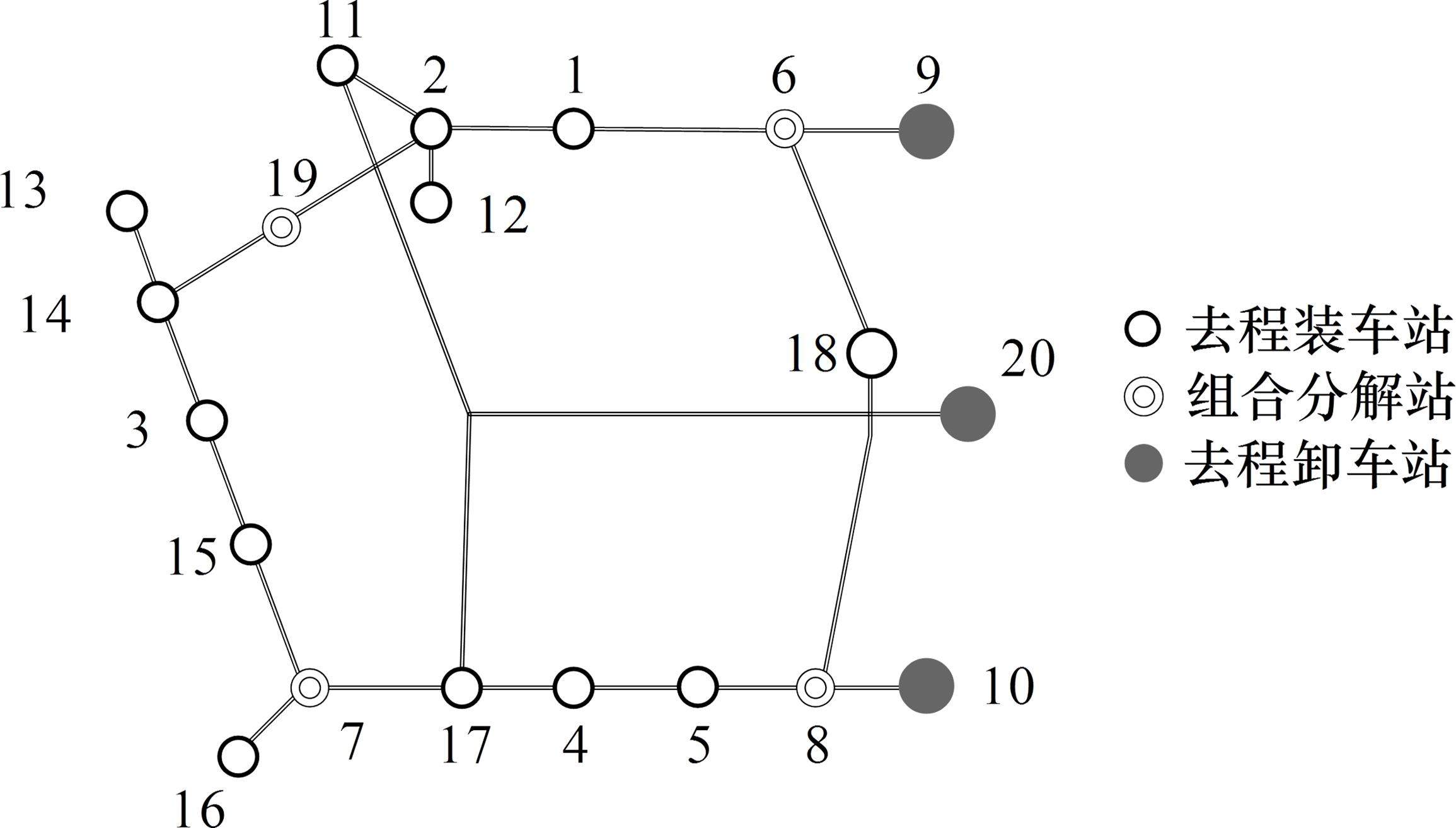
案例共20个车站,其中去程13个装车站,4个组合分解站,3个卸车站,去程方向装车站编号为1~5,11~18,组合分解站编号为6、7、19,卸车站编号为9、10、20。求解规划时段15 h,设定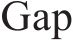
将本模型中考虑车辆类型以及返程运输需求的相关约束去除后,其求解结果同文献[1],但效率更高。将文献[1]其求解结果作为比对依据,按照这种思路,本研究设计开展了下列实验。
4.2.2 考虑车辆类型对实验结果的影响
为分析车辆类型对实验的影响,在无返程需求下设计了2类场景:一类场景煤炭需求量较小,即运力充足情形下的实验;另外一类场景中需求量相对较大,即运力紧张情形下的实验。针对2类场景,设计实验1、2和实验3、4。实验2和实验4均考虑各车站可处理的车辆类型影响,与不考虑车辆类型下的实验1和3进行对比,具体结果如表5所示。
| 编号 | 条件 | 车辆 类型 | 成本/元 | 成本增加比/% | 接续费用/元 |
|---|---|---|---|---|---|
| 1 | 运力充足 | 不考虑 | 1 852 500 | 0.0 | 114 000 |
| 2 | 考虑 | 1 982 200 | 7.0 | 126 000 | |
| 3 | 运力紧张 | 不考虑 | 11 700 000 | 0.0 | 752 000 |
| 4 | 考虑 | 12 671 300 | 8.3 | 818 000 |
由表5可知,相同需求数据和线路条件下,若不考虑车辆类型,运输方案总成本及接续费用均降低,但组合列车需遵守货车车辆一致性,且车站能够处理的货车类型有一定要求,由各车站线路长度以及所用案例集团的实际规定确定,如表6所示。
| 车站 | 车辆类型 | 站线长度/m | 车站 | 车辆类型 | 站线长度/m |
|---|---|---|---|---|---|
| 1 | C70,C64 | >1 700 | 12 | C80,C64 | >1 700 |
| 2 | C80,C70 | <1 700 | 13 | C80,C70 | <1 700 |
| 3 | C80,C70 | <1 700 | 14 | C80,C70 | <1 700 |
| 4 | C80,C70 | <1 700 | 15 | C80 | <1 700 |
| 5 | C80 | <1 700 | 16 | C70,C64 | >1 700 |
| 6 | C80,C70,C64 | >1 700 | 17 | C80,C64 | >1 700 |
| 7 | C80,C70 | <1 700 | 18 | C80 | <1 700 |
| 8 | C80,C70,C64 | >1 700 | 19 | C80,C70 | <1 700 |
| 11 | C70,C64 | >1 700 |
在实验4的基础上,进一步整理各OD使用的车辆类型,如图5所示。
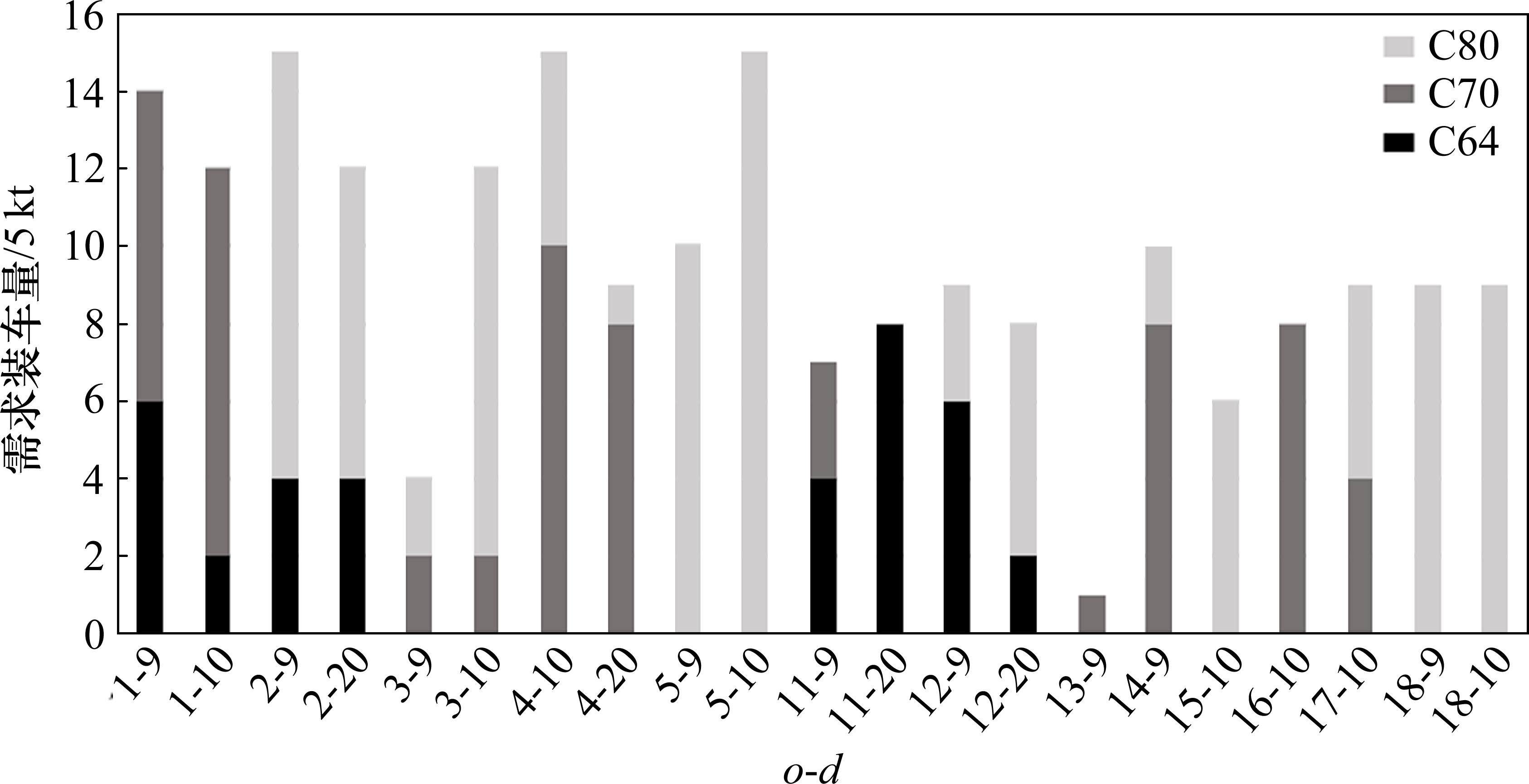
由图5可知,承运各OD对需求的车辆类型仍以C80、C70为主,C64型货车组成的列车对车站设备要求较高,并且投入使用的C64型列车数量相对较少:在站16、17,虽可编发由C64货车组成的列车,但由于到达距离最近的组合站7的C64单元列车较少,难以满足组合列车车辆类型一致性,造成车辆等待时间较长。在运力紧张的情况下,16、17选择编发由C80、C70编组成的列车,以组成更多的万吨大列,减少对通过能力的占用。
4.2.3 纳入返程需求后模型实验结果
考虑返程需求后,分别在运力充足和运力紧张场景下进行3次、2次实验,命名为实验1~5。
1) 运力充足条件
在保障运力充足的前提下,首先固定去程需求量实验。首次实验中,设定返程需求为0,随后2次实验中,逐步增加返程需求量,以探究返程需求变化对整体运输系统的影响。图6展示了第2次实验所得的时空网络图,它描绘了重空列车的循环接续关系。在此图中,纵轴上各车站的位置为相对示意,而它们之间的连接线仅代表列车的运行连接情况,线的斜率并不代表列车的实际运行速度。
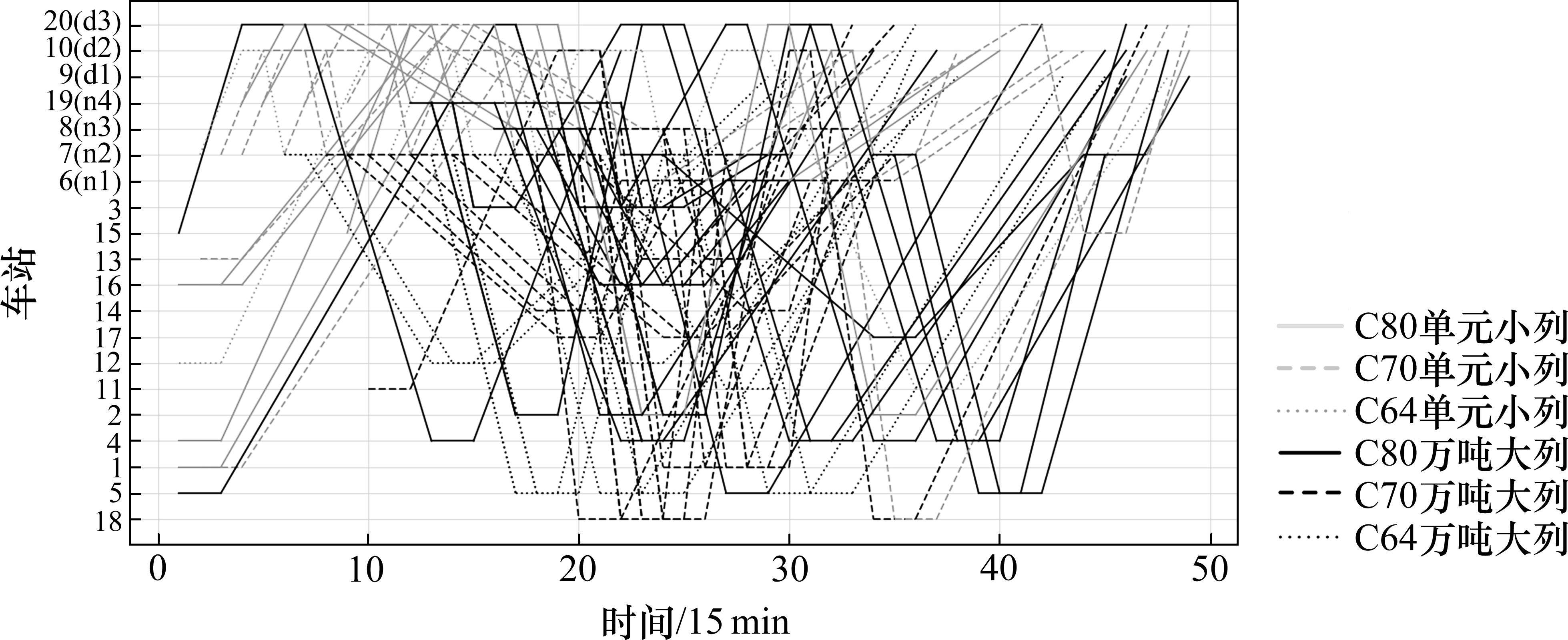
结果表明,去程需求均满足时,开展返程运输可降低空车走行率,部分返程运输需求无法由煤炭到卸后的空车车底接续,需引入新的车底或调运其他站的列车进行运输,增加一定的运输成本。如实验3中,煤运方向1至9站的运输量为15 000 t,而其返程方向运输量为45 000 t。因此,要额外增开新列车以满足运输需求:如在t=32时,组合站6新引入了一列小列C64车底,产生车底运用成本2 000元。通过调用其他车站到达9站的车底和新加开列车,9站在t=35时就完成了全部45 000 t发往1站的运输任务。
因此,总运输成本随返程运输需求量的增大而增大,实验2和实验3运输成本分别增加1.03%和1.06%,车底数相对实验1分别增加了2列、5列,但车底平均承担的运输量也分别增加了1.16%和1.18%。
2) 运力紧张条件
为验证运力紧张时返程运输对去程运输的影响,在实验1的基础上,加大去程运量需求,形成对照实验4;进一步地,加入返程需求,且考虑增运返程运输的运输成本减免,形成实验5。其中去程方向运输需求满足情况如图7所示。
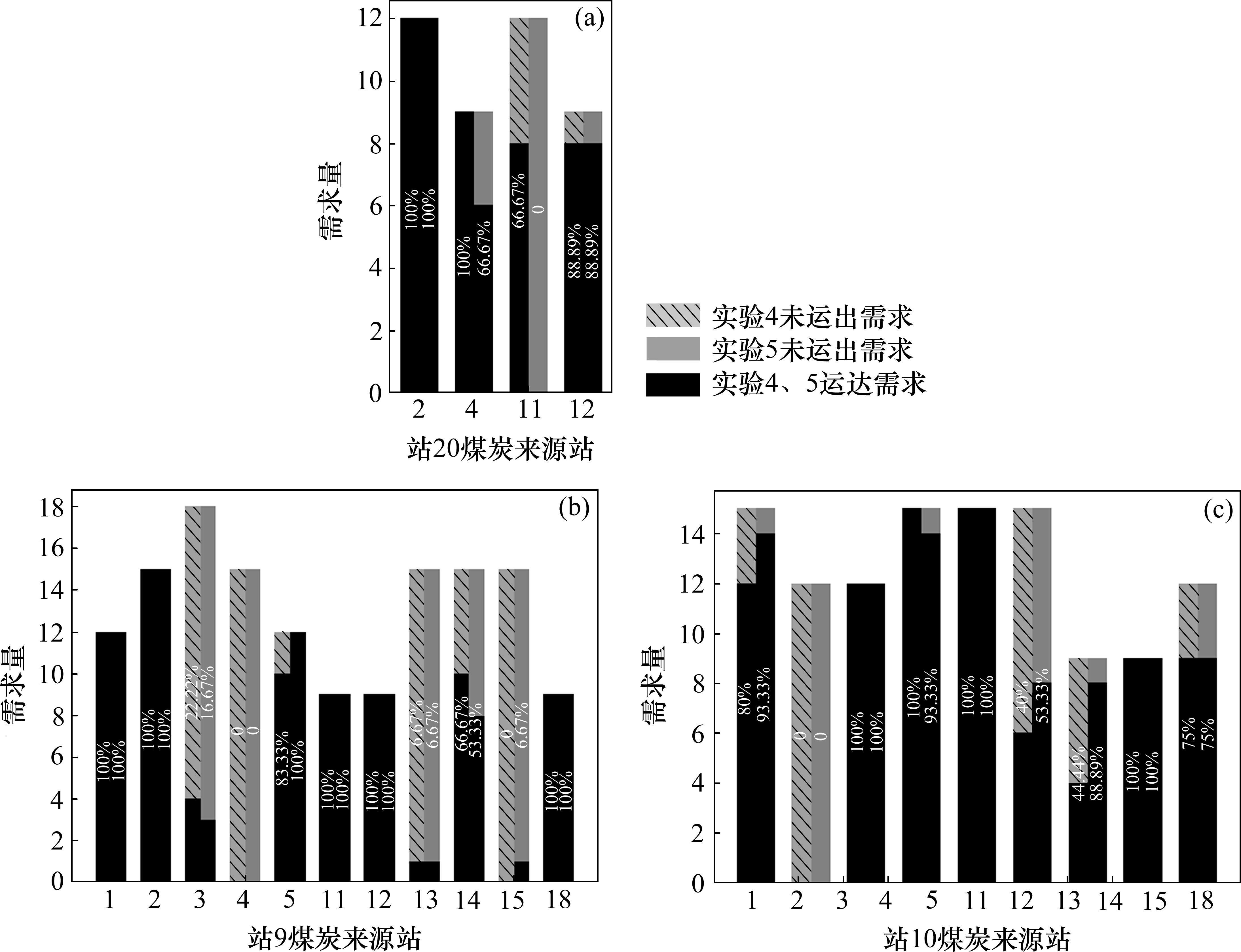
图7中柱状图上百分比为实验4、5成功运出的需求占总需求的比例,从中看出,实验5相比实验4去程需求满足情况发生变化。在实验5中,站4、11至站20共10个煤炭需求未得到运输,而站5至站9、站16至站10完成的返程需求运量分别由10单位上升至12单位、4单位上升至8单位。此方案增运的返程需求量获得的奖励为60 000元,未送达的10单位去程煤炭需求产生的惩罚为56 000元。相比实验4,增运返程需求也会增加装卸车成本及延误成本,造成改编与装卸次数增加,但与空列因减少空跑产生的收益相权衡,运输总成本相对原成本减少了1.71%。因此,在当前的需求结构下,承担一定量返程运输需求的运输方案更有竞争力。
4.2.4 综合对比分析
上述2节将车辆类型和返程运输需求纳入范畴。结果表明,考虑返程运输需求,可提高车底平均承担的运输量,为重载铁路系统统筹去、返程运输,扩展运输货物品类提供了参考;将货车类型纳入车辆周转的考虑范畴内,更贴近于运输组织实际,增强了运输组织方案的可实施性。
5 结论
1) 以重载铁路为问题背景,搭建了以近似列车发车间隔(15 min)为单位时间的离散型时空网络,在此基础上,考虑车列的编组类型和车辆类型在不同站点接续的一致性要求,构建了统筹去程煤炭运输、返程非煤运输与空列分配的优化模型。
2) 为验证模型的正确性,在含有7个站点的单通道线路进行了实验,得到了一定时间范围内重列和空列的协同运输组织方案,以及单元车列的周转方案。
3) 在连接20个站点的运输网络上设计对照实验,分析了考虑车辆类型和返程运输对于运输组织方案和运输成本的影响,在2种运量条件下,考虑车辆类型差异因素分别带来7%与8.3%的运输成本上涨,但增加了方案的可实施性;在此基础上加入返程需求因素后,总成本组仅增加1.03%和1.06%的情况下,车底平均承担的运输量分别提高了1.16%和1.18%,结果表明,增大去返程运量需求并进一步考虑增运返程运输的奖励后,总成本能得到一定下降,承担一定返程运输需求的运输方案更具竞争力。
4) 在重载铁路运输组织中,机车运用组织是至关重要的一环,在本阶段考虑车列类型和车辆构成类型基础上,进一步可将重空列适配的机车类型及交路限制条件等考虑在重空列协同优化组织研究中。
王志美,于凌志.考虑车辆资源的重载铁路重空列协同运输组织[J].铁道科学与工程学报,2024,21(12):4971-4982.
WANG Zhimei,YU Lingzhi.Heavy-haul railway cooperative transportation organization considering the utilization of vehicle resources[J].Journal of Railway Science and Engineering,2024,21(12):4971-4982.

