城市轨道交通因其具有容量大、快速便捷、安全性高等优势,得到了快速发展。随着城市轨道交通系统运营规模的不断扩大,其运营能耗也显著增加。通过对城轨系统的运营能耗进行分析,可知牵引能耗是城轨系统总电耗中占比最大的一部分,约为50%[1]。因此,降低城市轨道交通系统运行能耗的关键是降低列车的牵引能耗。目前,列车自动运行(Automatic Train Operation, ATO)系统已经在城市轨道交通系统得到了广泛应用,ATO通过对目标速度曲线进行追踪实现对列车的自动控制,列车的实际牵引能耗取决于ATO的控制性能。因此,通过优化ATO系统的算法,提供更为节能的运行控制策略,是降低牵引能耗的关键途径。1986年,ICHIKAWA等[2]对列车的最优控制问题进行了研究,构设了简单的列车运行数学模型,并利用极大值原理进行求解。此后列车控制优化问题得到了越来越广泛的关注,宿帅等[3]提出了一种基于极大值原理的能量分配方法对ATO最优速度曲线进行求解。ALBRECHT等[4]对给定最大运行时分下的列车长大坡节能控制问题进行了研究。曲健伟等[5]也利用最大值原理对地铁列车节能驾驶问题进行了简化求解。高豪等[6]利用动态规划算法对列车节能操纵的多目标优化问题进行了求解。此外,启发式算法也被大量应用于列车运行控制优化领域。李波等[7]基于遗传算法对列车的节能操纵曲线进行了求解,徐凯等[8]提出了一种协同进化的多目标混沌粒子群算法来解决ATO推荐速度曲线优化问题,LI等[9]基于改进的萤火虫算法对列车轨迹进行了多目标优化,李蔚等[10]采用模拟退火、模式搜索以及粒子群算法对2种不同速度控制模式下的列车速度曲线进行了优化,这些算法都基于一定的模型对ATO目标速度曲线进行了离线求解,在优化性能上也具有各自的特征和差异。但实际的列车运行环境是复杂多变的,一旦列车的运行场景和参数发生变化则需要进行重新建模,也使得工作量大大增加[11]。近年来,强化学习由于其对模型依赖程度较低,且具备强大的环境感知、动作探索以及经验学习能力得到了越来越多的研究和应用,不少学者尝试了将强化学习用于列车控制系统,以提高列车运行的智能化水平。冷勇林等[12]提出了基于专家规则和强化学习算法的智能列车节能控制算法,通过强化学习算法对控制器进行训练得到了最优速度曲线。张淼等[13]设计了一种基于策略梯度强化学习的列车智能控制算法,优化ATO系统的驾驶控制策略,在满足运行时分要求和保证乘客乘车舒适的前提下有效地减少列车牵引能耗。宿帅等[14]提出了一种通过对能耗进行分配的列车节能驾驶控制方法,并利用DQN算法进行求解。LIU等[15]利用深度Q网络算法对重载列车在长陡下坡路段的最优控制问题进行了求解。NING等[16]将大量的速度曲线作为经验,并通过深度确定性策略梯度DDPG(Deep Deterministic Policy Gradient)算法进行训练得到优化的列车速度曲线。ZHU等[17]提出一种基于软演员-评论家的方法来求解列车的最优驾驶策略,其在节能性和样本复杂度方面都具有优势。周敏等[18]对于临时限速下的高速列车曲线优化问题进行了研究,并利用带有优先经验回放的双深度Q网络进行求解。武晓春等[19]提出一种基于DDPG的列车节能操纵算法,能够实现连续控制下的列车节能驾驶操纵。以上的研究为解决复杂多变环境下的列车自动运行控制提供了更为智能化的参考方案,而对于运行场景变化下如何在线对控制策略进行动态调整的问题依然值得研究。本文基于上述的研究基础,针对列车节能运行优化问题,提出一种基于深度强化学习DDDQN的列车运行控制方法以提升ATO系统的控制性能,主要完成了以下的工作:1) 根据列车站间运行特性和约束建立列车强化学习仿真环境;2) 利用DDDQN算法进行求解,并设计了一种调整机制,减少智能体盲目探索的次数,提高了算法的学习效率和收敛速度,智能体通过不断地与环境进行交互,最终学习得到保证列车站间运行安全、准时、精准停车的节能控制策略;3) 以北京地铁亦庄线的实际数据为例,通过与差分进化(Differential Evolution, DE)算法和原始DQN算法进行对比实验,验证了算法的优越性,并通过设置临时限速和临时运行计划调整下的仿真案例,验证算法具备一定的在线动态调整能力。
1 问题描述
列车节能控制优化问题就是在已知时刻表、运行时分及运行距离的前提下,最小化列车运行的牵引能耗。列车在站间的运行可以用以下动力学方程来描述:
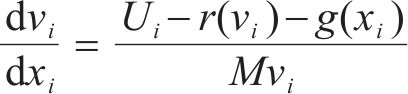
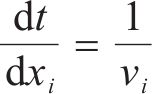
式中: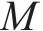
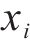
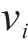
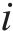
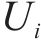
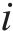
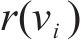
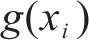
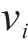
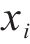
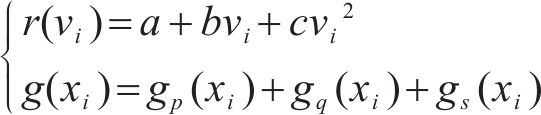
式中: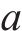
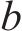
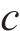
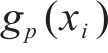
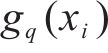
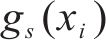
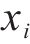
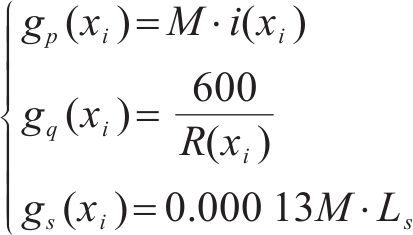
式中: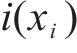
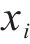
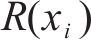
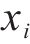
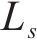
此外,列车在站间的运行是列车从静止启动到一定速度运行,最后制动停车的过程,因此列车在站间运行的初始速度和终止速度都应该为0,全程的运行速度都应该小于对应位置的线路限速,且中间运行速度一般不能为0;牵引力或制动力应该满足列车牵引制动特性的限制;为满足乘客上下车以及运行时分需求,列车的停车位置误差应在0.3 m以内,准点率应该控制在3%以内,因此应该满足以下约束条件:
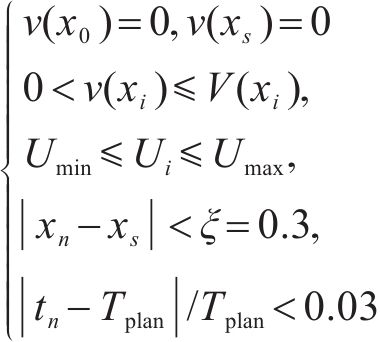
其中,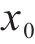
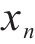
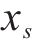
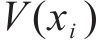
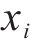
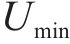
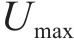
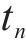
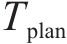
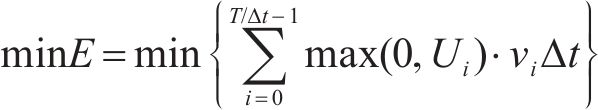
2 基于DDDQN的列车节能运行控制方法
2.1 带调整机制的列车运行控制强化学习框架设计
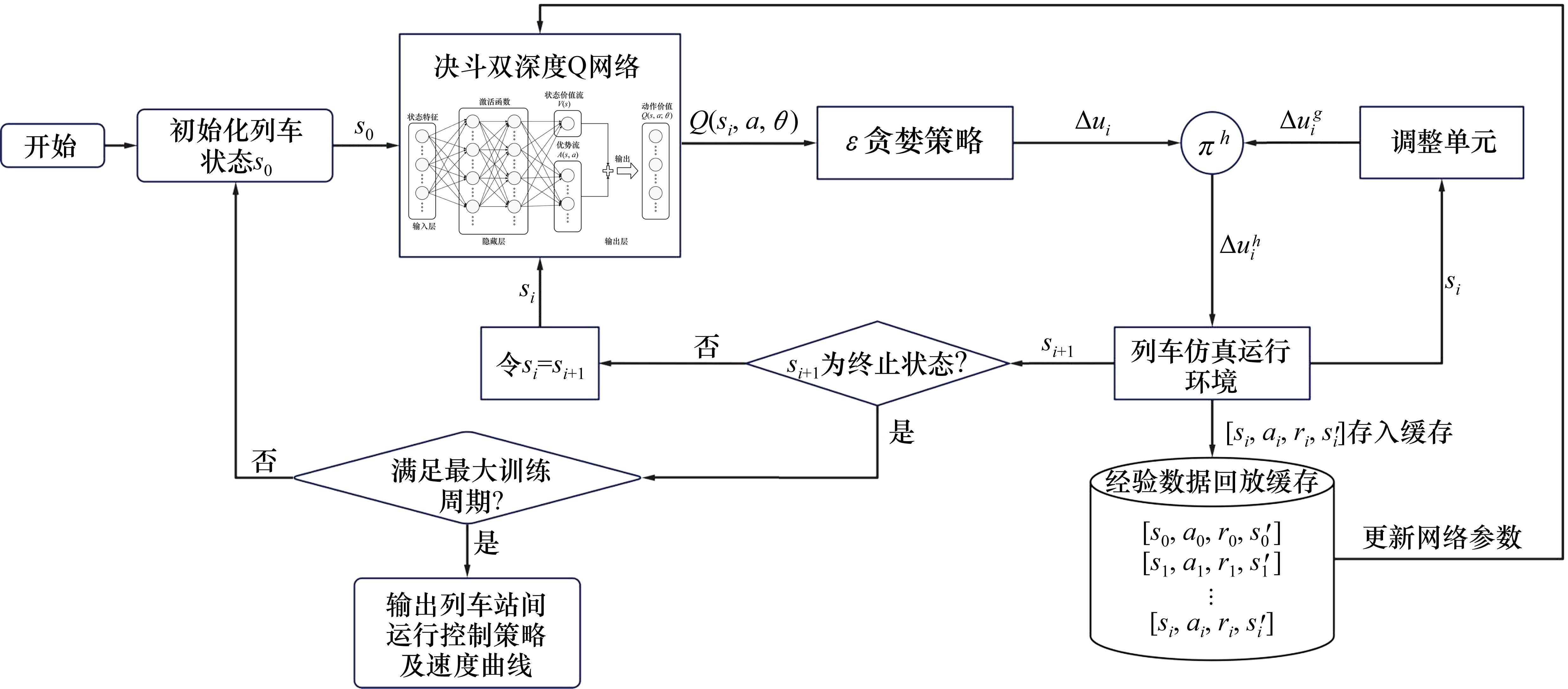
列车在站间行驶的过程中,车载控制器根据静态信息(包含线路数据、车辆信息等)和实时列车状态(包含列车当前速度、当前位置等),计算下一时刻输出的控制量大小,并作用于列车,产生下一时刻的列车状态。由此可见,列车下一时刻的状态仅由当前时刻列车的状态和当前时刻车载控制器的控制输出决定,与此前的任何历史列车状态无关,那么列车在站间由启动行驶再到制动停车的过程可以视为一个有限的马尔科夫决策过程。此外,列车当前时刻的状态也决定着车载控制器在下一时刻输出的控制量的大小和方向,使得列车在满足式(5)的约束下运行。因此,列车运行控制优化这一复杂多约束的问题可以通过强化学习方法进行求解,本文提出一种带调整机制的列车运行控制强化学习方法对列车站间驾驶策略进行优化,其框架结构如图1所示。
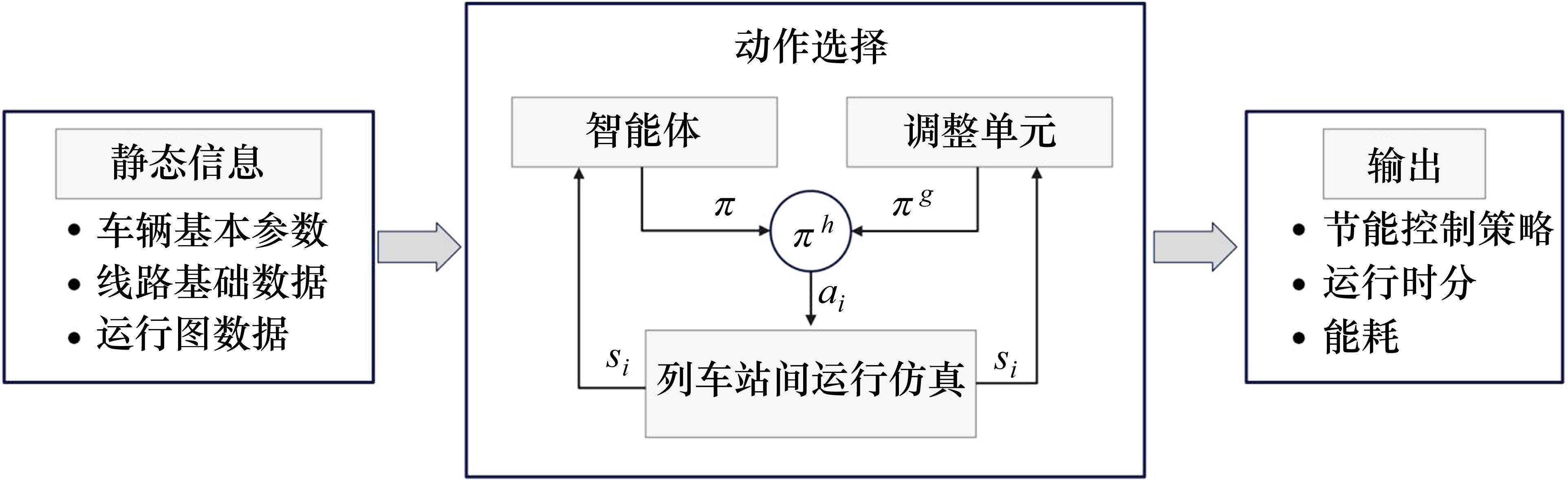
列车当前状态下的动作选择不仅取决于智能体根据策略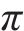
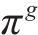
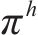
2.2 调整机制的建立
建立调整单元是为了使列车能够在保证安全的情况下尽可能按照时刻表的要求到达目的地,调整单元会根据列车当前运行状态给出一个允许速度范围,并判断列车当前速度是否处于该范围内,若不处于该范围内需要对车载控制器的输出量进行干预,确保列车最终能够安全、舒适、准时、节能地运行至终点。调整单元相当于一个经验驾驶员,以一定概率对智能体的输出进行干预,智能体将不断地学习这样的经验,以提高算法的收敛效率。
确定允许速度范围需要对列车当前状态下剩余行程的最短运行时分进行计算,如图2为一般情况下剩余行程最短运行时分的计算示意图,根据线路限速情况,将站间划分为如图2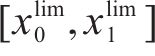
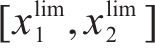
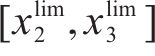
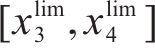
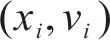
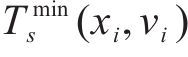
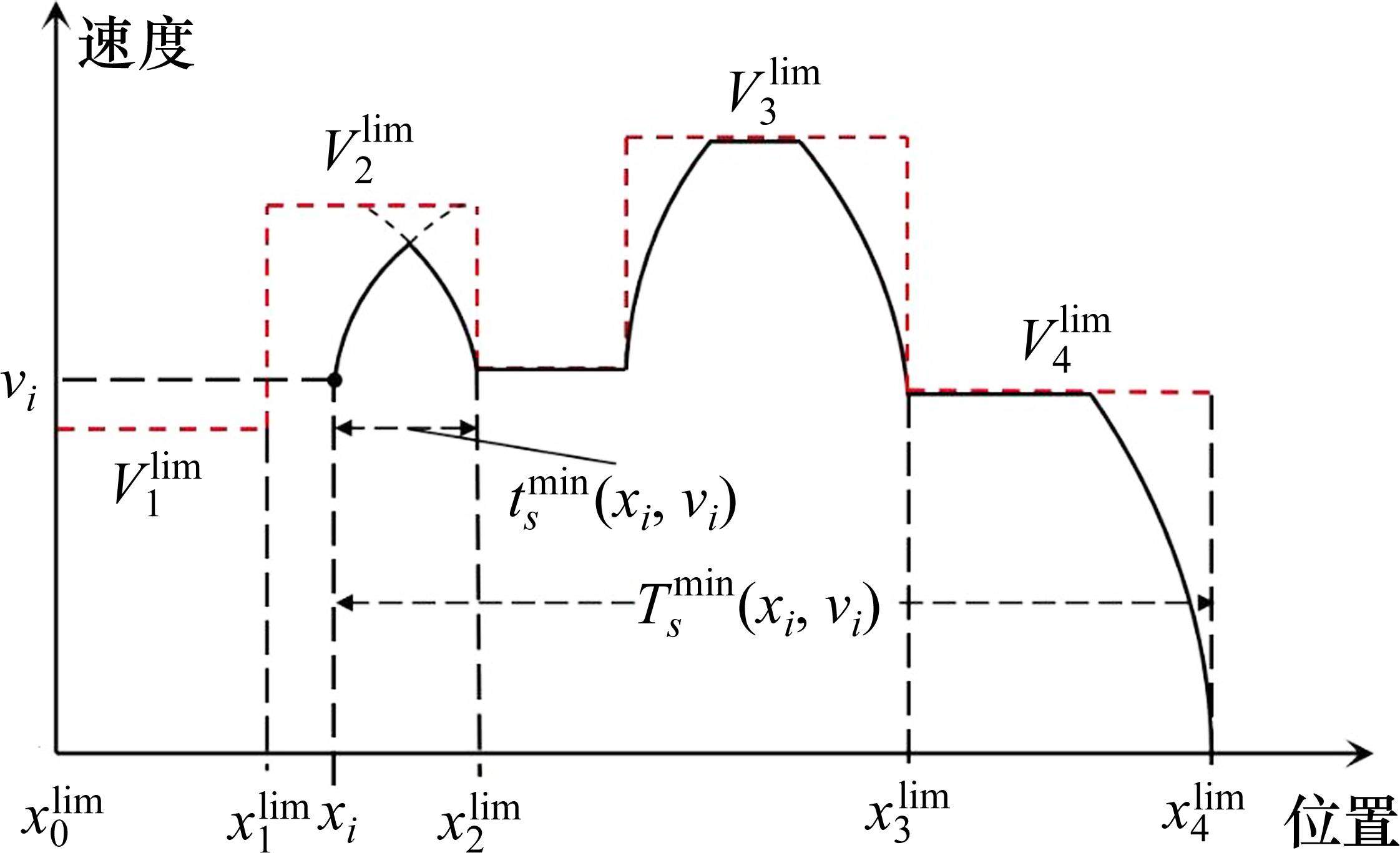
其中,在限速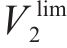
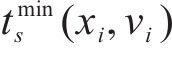
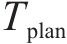
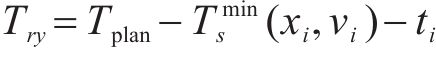
其中,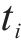
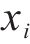
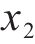
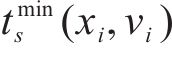
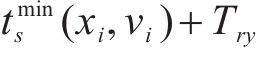
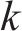
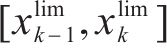
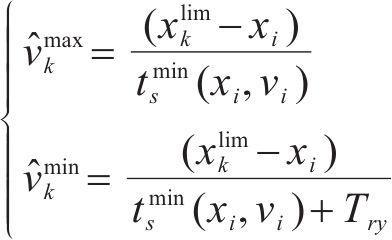
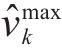
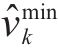
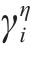
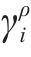
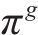
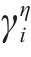
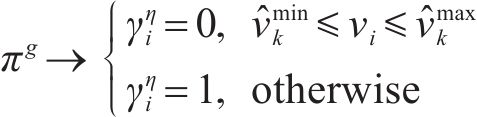
若列车当前速度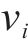
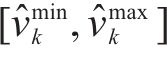
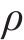
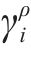
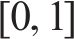
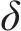
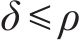
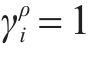
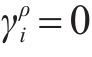
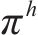
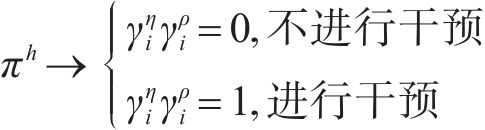
当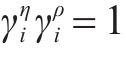
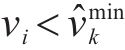
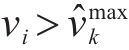
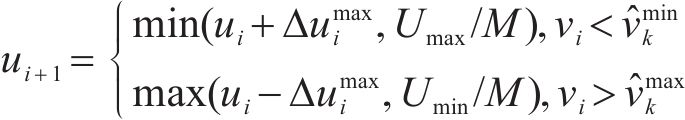
式中: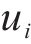
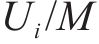
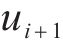
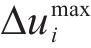
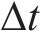
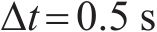
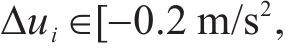
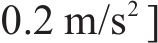
当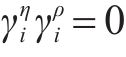
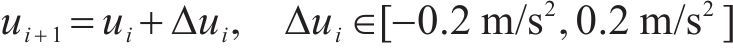
2.3 强化学习基本要素定义
转化为马尔可夫决策过程的列车运行控制优化问题,可以通过深度强化学习进行求解。列车的车载控制器相当于是智能体,根据当前环境中列车的状态选择并执行动作,然后该动作会对环境产生影响并产生新的状态、奖励值以及状态值函数,并反馈给智能体,智能体根据新的状态继续与环境进行交互。通过不断地与环境进行交互,智能体将会学习到一个最优的控制策略以达到列车站间运行节能、准时、舒适的目标。除了智能体和环境以外,还需要设置强化学习系统的另外3个元素:状态,动作,奖励。接下来针对列车运行控制优化问题对这3个元素的设置进行详细介绍。
1) 状态
在本文中,列车的当前位置、当前速度、当前行驶时间这3个重要的元素组成了状态。若智能体经过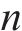
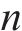
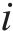
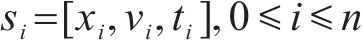
式中: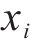
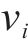
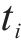
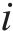
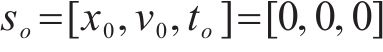
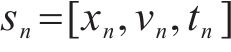
2) 动作
车载控制器作为智能体,根据列车当前状态做出动作选择并输出对应的控制指令,指导列车在站间行驶,以列车单位质量所受控制力的变化量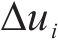
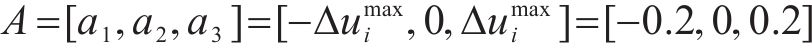
3) 奖励
强化学习将优化目标转化为奖励信号。在每一步的动作中,智能体都会收到来自环境的一个奖励,而智能体的目标则是最大化奖励的总和。根据列车运行控制的优化目标和约束条件,奖励函数应该包含对安全性、准时性,节能性以及停车位置的精准度的评价。因此,奖励函数可以被定义为安全奖励函数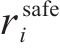
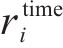
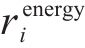
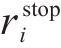
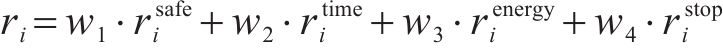
其中,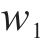
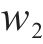
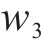
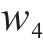
① 安全奖励函数
为了保证列车在站间行驶的安全,需要对列车速度进行约束保证其不会超过线路限速,一旦列车当前速度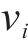
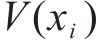
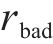
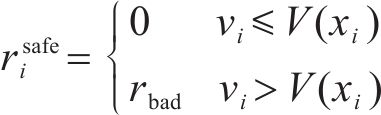
② 准时奖励函数
为了保证列车尽可能按照计划运行时分的规定到达终点,定义了当前速度与剩余行程平均速度之间的差值作为奖励项对每一中间状态的准时性进行评价,此外当列车到达终点时,将会根据实际运行时间和计划运行时分之间的差值获得一个额外的准时性奖励,因此准时奖励函数可以表示为:
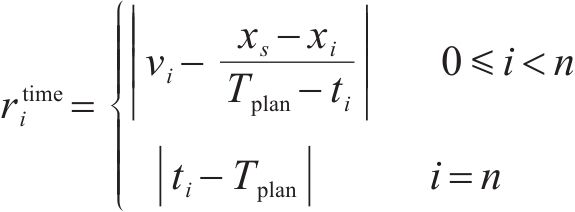
③ 节能奖励函数
列车在运行过程中的节能奖励依靠计算列车在每一步状态转换过程中单位质量消耗的牵引能耗来评价,具体可以表示为以下函数:
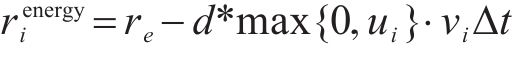
其中,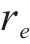
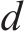
④ 停车奖励函数
为了保证乘客的正常上下车,需要控制列车的停车误差在一定范围内,因此当列车处于终止状态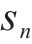
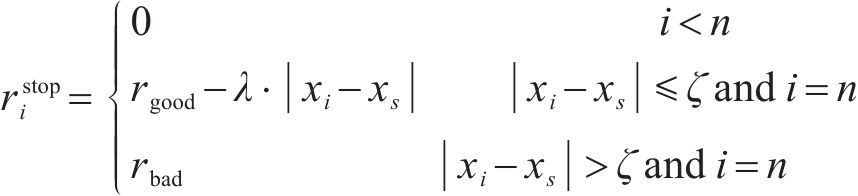
其中,
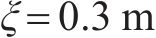
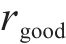
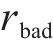
2.4 DDDQN算法设计
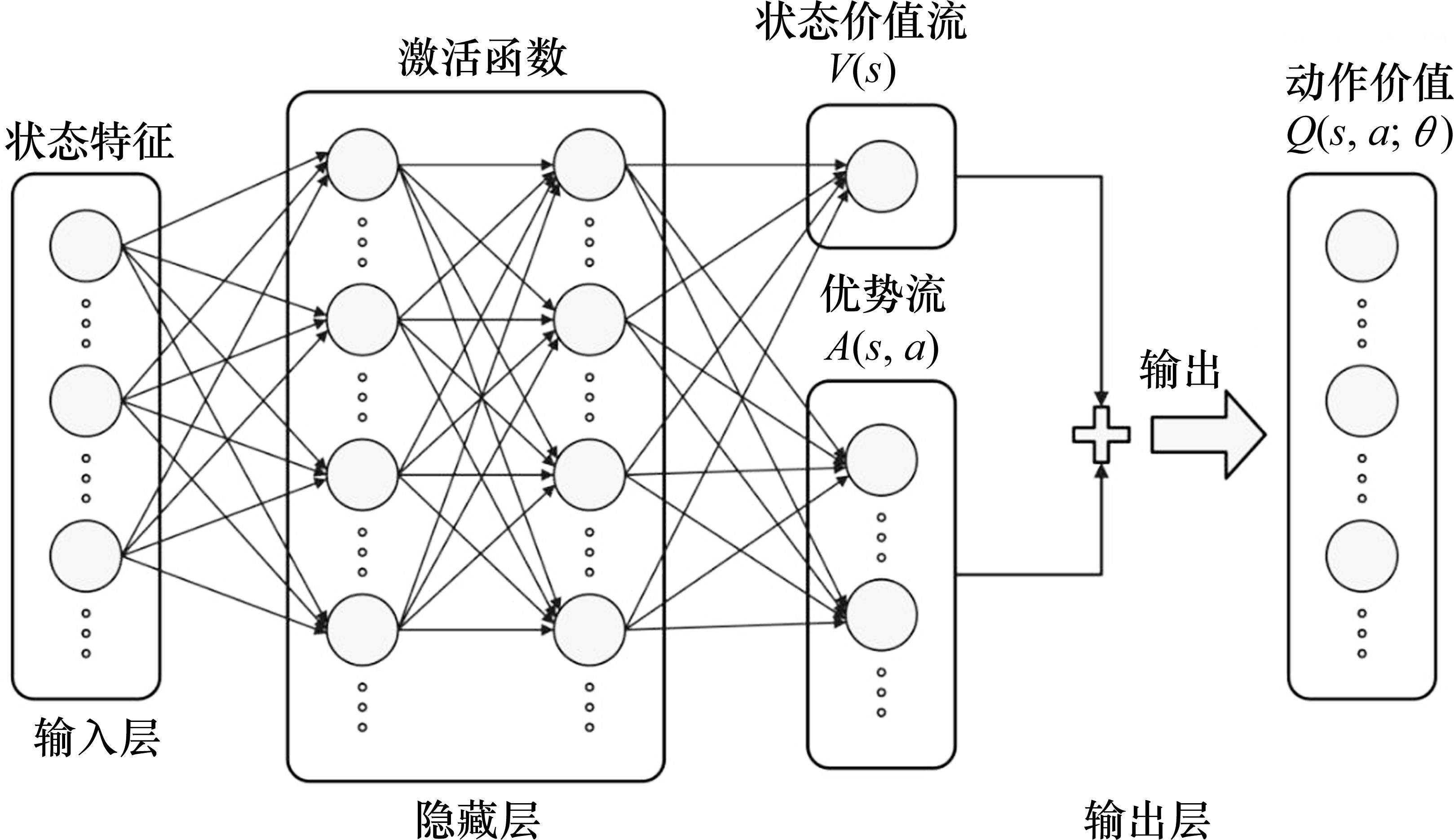
深度强化学习的核心就是智能体通过不断地与环境进行交互,优化动作选择策略使得动作价值函数不断地逼近最优值函数。本文提出的DDDQN算法,将原始DQN的单流网络结构改变为决斗网络构架(Dueling network architecture),将输出拆分成状态价值流和优势流2部分[20],如图3所示,分别对状态价值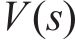
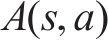
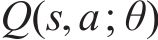
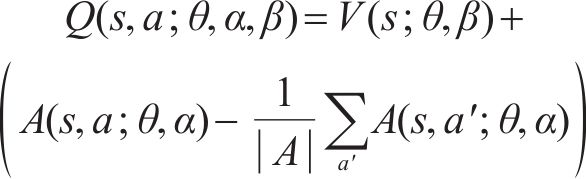
式中: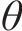
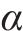
此外,DDDQN算法区别于原始DQN算法,动作选择和估值都使用Q网络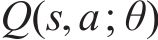
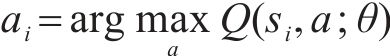
而估值则采用目标网络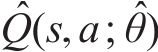
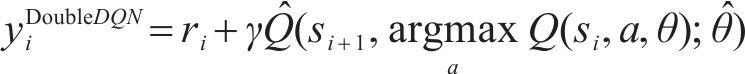
为了使智能体能够充分地对未知环境进行探索,本文采用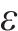
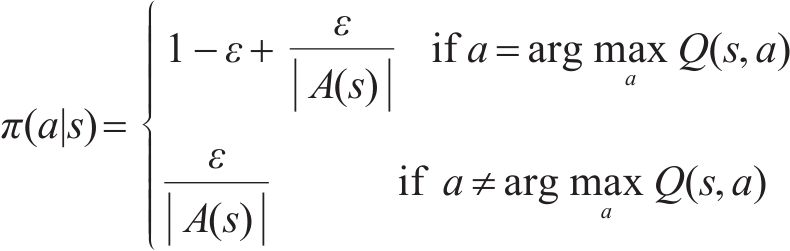
式中: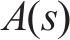
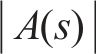
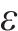
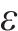
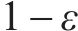
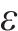
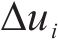
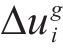
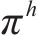
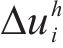
3 算例分析
为了验证算法的有效性,仿真实验选取了北京地铁亦庄线的小红门―旧宫站间的线路数据进行算例分析。所选列车车型为6编组B型的DKZ32电动车组,列车相关参数如表1所示。线路最大允许速度为80 km/h,在出站和进站的130 m范围内有55 km/h的速度限制,线路总长度为2 366 m。
| 参数名称 | 参数值 |
|---|---|
| 车型 | DKZ32 |
| 编组方式 | 3M3T |
| 列车质量M/t | 280 |
| 基本阻力方程系数a,b,c | 3.48,0.040 25,0.006 575 |
| 最大牵引加速度/(m∙s-2) | 0.8 |
| 最大制动加速度/(m∙s-2) | -0.8 |
| 最大牵引力/kN | 310 |
| 最大制动力/kN | 290 |
本算法基于Python3.7编写,利用Tensorflow 2.9.1搭建神经网络,并在配置windows1064位操作系统、内存为16G RAM、CPU为Intel i5-11300H的电脑上进行训练。算法训练相关参数如表2所示。
| 参数名称 | 参数值 |
|---|---|
学习率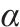 | 0.001 |
折扣因子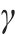 | 0.95 |
单次采样数据大小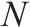 | 32 |
经验数据回放缓存容量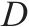 | 12 000 |
目标网络参数更新频率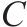 | 200 |
初始贪婪概率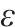 | 1 |
最终贪婪概率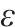 | 0.1 |
每步贪婪概率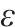 | 2.25×10-6 |
每次状态转移最大探索步数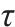 | 100 |
| 优化器 | Adam |
正向奖励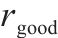 | 1 |
负向奖励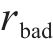 | -1 |
将提出的带调整机制的DDDQN算法计算得到的列车速度曲线与DE算法及不包含的调整机制的原始DQN算法优化的列车速度曲线进行对比。每种算法均重复进行20次实验取均值,以保证实验结果的可靠性。其中,原始DQN算法和DDDQN算法分别在设计最大训练周期数为20 000和6 000的前提下进行实验。表3给出了不同算法求解下的运行性能对比,3种算法求解的运行时分误差均在要求的3%以内,停车精度均能满足列车站间的运行需求,小于30 cm。不同算法得到的站间列车速度曲线如图5所示,DE算法采取的是先加速牵引到一定速度后巡航一段距离,再通过惰行降低牵引能耗,最后制动停车;原始的DQN算法和带有调整机制的DDDQN算法均是先牵引加速到一定速度后直接转为长惰行,减少了巡航阶段的牵引能耗。通过DDDQN算法求解下的牵引能耗相比于DE算法和原始DQN算法分别减少了6.7%和5.5%。
| 算法 | 停车位置/m | 停车误差/m | 实际运行时间/s | 运行时分误差/% | 牵引能耗/(kW∙h) |
|---|---|---|---|---|---|
| DE | 2 365.81 | 0.19 | 159.16 | 0.5 | 14.46 |
| DQN | 2 365.71 | 0.29 | 155.97 | 2.5 | 14.23 |
| DDDQN | 2 366.17 | 0.17 | 158.60 | 0.8 | 13.49 |
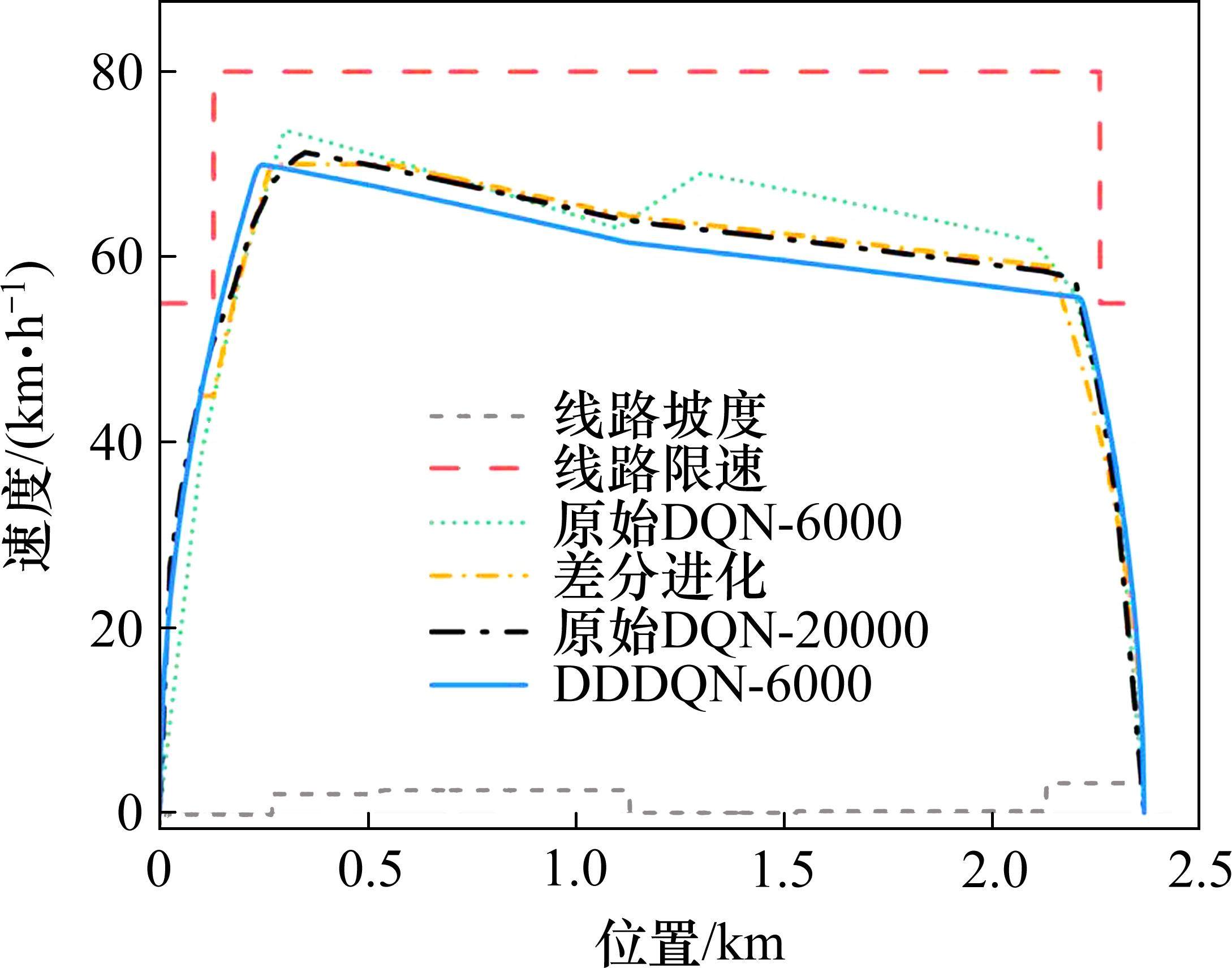
图5给出了同样设置最大训练周期数为6 000时,原始DQN计算得到的运行曲线,此时列车先加速到一定速度,然后转为惰行,在运行中段还进行了一段距离的加速操作,再转为惰行直至制动停车。通过图6对比设置最大训练周期为6 000时的原始DQN算法和DDDQN算法的能耗收敛情况,可知此时原始的DQN算法此时并未完全收敛,而DDDQN算法由于加入了调整机制,其在动作的选择和控制量的调整方面更具优势,减少了盲目试错的次数,收敛效果较好,也证明了调整机制的加入能够有效提升算法的收敛速度。
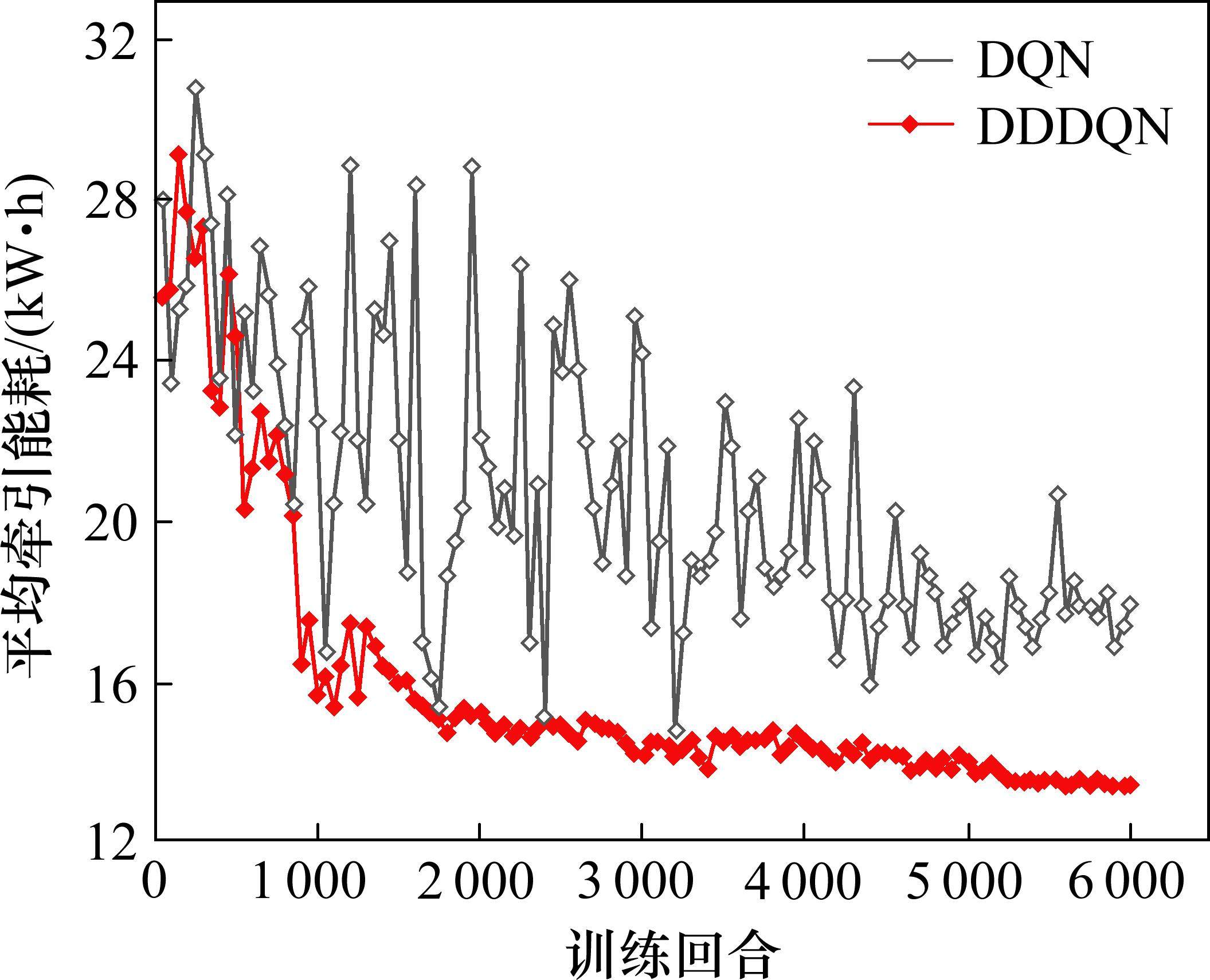
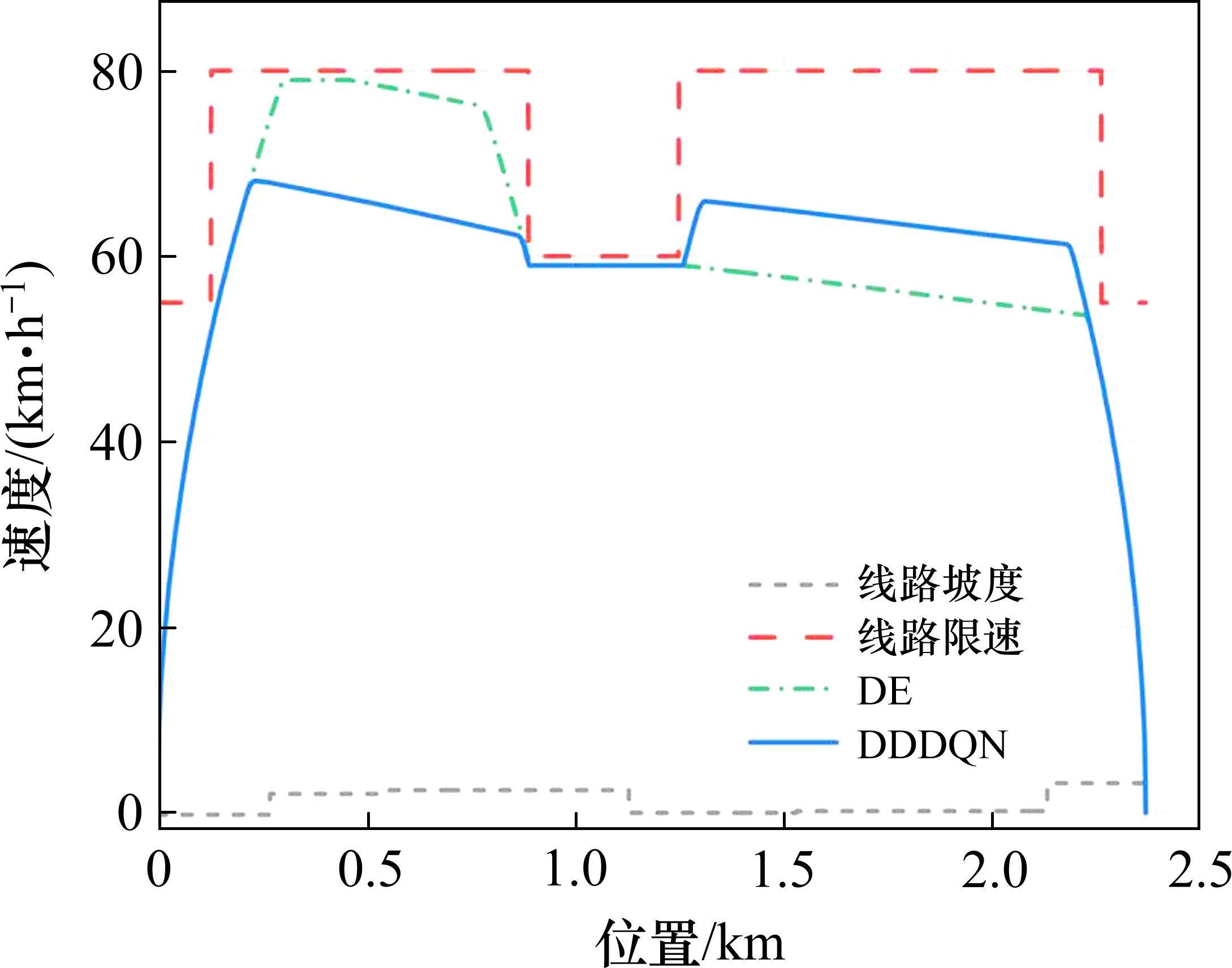
为了进一步验证算法的有效性,在原站间的890 m处添加了一段长370 m、限速60 km/h的临时限速区段,并分别利用DE算法和DDDQN算法进行求解,2种算法的性能对比如表4所示。DDDQN算法相比于DE算法降低了13.9%的牵引能耗,其在临时限速的情况下仍然能够保证列车准点到达,且具有较好的节能效益。2种算法得到的站间列车运行曲线如图7所示,可以看出DDDQN求解下列车在行驶过限速区段后并不会立即进行惰行操作,而是先加速一段距离再惰行,来保证列车能够准时到站。
| 算法 | 停车位置/m | 停车误差/m | 实际运行时间/s | 运行时分误差/% | 牵引能耗/(kW∙h) |
|---|---|---|---|---|---|
| DE | 2 366.21 | 0.21 | 159.47 | 0.3 | 18.77 |
| DDDQN | 2 365.85 | 0.15 | 157.98 | 1.3 | 16.16 |
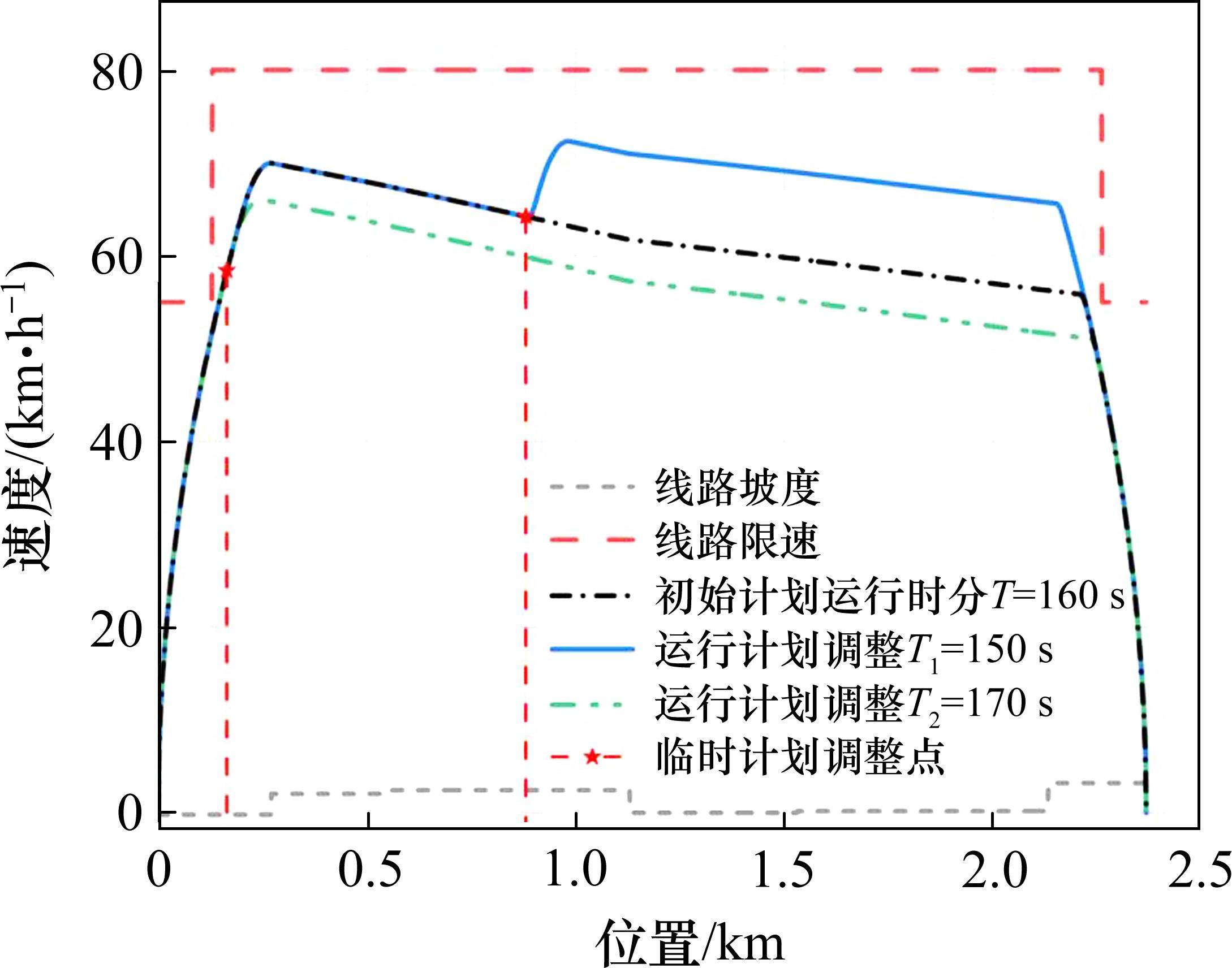
为了验证算法在突发运行计划调整情况下的应对能力,设计了2种运行时间调整案例下的仿真案例。2种案例的列车初始计划运行时分均为160 s,案例1设置列车在正常运行至60 s时接收到运行时分调整命令,需要提前10 s到站,即总站间运行时分变为T1=150 s;案例2设置列车在正常运行至20 s时接收到运行计划调整命令,需要延迟10 s进站,即总站间运行时分变为T2=170 s。图8展示了2种案例下列车站间运行曲线的调整情况,表5给出了调整后的运行性能分析。
| 案例 | 停车位置/m | 停车误差/m | 实际运行时间/s | 运行时分误差/% | 牵引能耗/(kW∙h) |
|---|---|---|---|---|---|
| 提前10 s进站(T1=150 s) | 2 365.84 | 0.16 | 149.54 | 0.3 | 16.83 |
| 推迟10 s进站(T2=170 s) | 2 366.13 | 0.13 | 170.97 | 0.6 | 11.98 |
不难看出,在接到提前进站指令时,该算法能够及时地调整运行策略,适当进行加速操作,保证列车能够按调整时分到站;在接到推迟进站指令时,能够适当降低列车平均运行速度,保证列车不会提前进站。因此,该算法可以在相应的调整点对列车的运行控制策略进行实时调整以应对不同的临时计划调整需求,确保列车能够准时到站。
4 结论
1) 针对城轨列车运行控制问题,在保证列车运行安全、舒适、准时的前提下,提出一种基于DDDQN算法的列车节能驾驶控制方法,并通过引入输出调整机制加快算法的收敛速度。
2) 以北京地铁亦庄线的实际线路数据进行仿真实验,结果显示该算法能够在满足运行时分误差要求和停车精度要求的前提下计算得到节能的列车站间控制策略,且相比于基于DE的控制策略优化算法和原始DQN算法分别能够节省6.7%和5.5%的牵引能耗。
3) 在加入临时限速区段和临时运行时分调整的情况下,该算法能够动态地对列车的控制策略进行调整,以保证列车能够准时到达终点。
该方法通过生成列车站间节能控制策略能够一定程度地降低城轨列车站间运行的牵引能耗,提升列车在线路临时限速和临时运行时分调整情况下的应对能力。后续将加入牵引故障等更多突发情况下以及多列车协同下的节能运行优化研究,以提高其对突发情况的应对能力,进一步降低系统的牵引能耗。
李茜,李蔚,曹悦等.基于DDDQN的城轨列车节能运行控制方法研究[J].铁道科学与工程学报,2024,21(12):4960-4970.
LI Qian,LI Wei,CAO Yue,et al.Research on energy-saving operation control method of urban rail train based on DDDQN[J].Journal of Railway Science and Engineering,2024,21(12):4960-4970.

