近年来,我国高速铁路迅猛发展,已成为旅客运输交通方式中不可或缺的重要组成部分。随着铁路基础设施网络的不断扩展,铁路运输组织的复杂性也显著增加,一旦发生突发事件导致列车通行中断,列车晚点将会在线路中迅速传播,造成大面积列车晚点,对铁路运营产生巨大影响,由此而带来的经济损失难以估量。因此,及时处理突发事件,使列车运行恢复正常,同时合理安排换乘,避免或减少旅客的损失,保障旅客的安全和权益,是至关重要的。面对铁路运营中的突发事件,田志强等[1]针对突发事件的应急救援设备调度,以应急救援工作的时效性为主,优先以最小化应急救援结束时刻和最小化调度费用为目标,建立了双层优化模型并设计了相应的两阶段启发式算法,最终验证了算法的有效性和实用性。刘睿等[2]利用齐次马尔可夫链描述高速铁路列车连带晚点的横向传播过程,基于状态转移矩阵分析不同情况下列车晚点传播规律,为列车运行图的优化调整提供了有效的分析和支持。在多种行车干扰事件的场景下,徐培娟等[3]基于替代图理论,考虑列车进路约束,对列车运行图进行快速求解。在受到严重干扰或区间完全中断的条件下,ZHU等[4]通过增加取消列车数量以达到快速处理中断造成的列车延误的目的。VEELENTURF等[5]通过改变列车停站方案来满足中断条件下旅客变化的出行需求。SHAKIBAYIFAR等[6]在列车日常运营中断情况下,通过调整通过顺序来疏解列车之间的冲突,针对伊朗铁路网提出了列车运行图调整模型并利用两阶段启发式算法求解。孟令云等[7]为解决列车运行调整问题,建立了带补偿随机期望值模型,进一步给出了不完全连续的多阶段决策模型并利用分支定界法求解。杨涵[8]在列车中断条件下,考虑中断过后列车速度曲线的改变导致的列车跟踪控制问题,对列车运行图进行优化。邓念等[9]以最小化取消列车数量和列车总延误为目标,考虑车站和区间的容量限制,对列车运行图进行调整,最终结果显示,通过少量增加列车总延误可以提高列车整体的正点率。此外,也有学者针对其他特殊条件突发事件下的列车运行调整进行研究,孟学雷等[10]以新冠疫情为背景,对突发传染性疫情条件下的列车运行调整进行研究,结果证明该研究可以为突发疫情条件下的列车调度工作提供决策支持。温鹏程等[11]考虑旅客的换乘接续,针对末班车阶段,对列车的运行调整进行研究,其结果对客运服务水平的提高具有借鉴意义。在城市轨道交通方面,王卓等[12]考虑列车故障救援,采用滚动优化算法求解故障发生后的列车运行图,为故障场景下列车救援方式的选择和如何对运行图进行调整提供了决策依据。由于列车运行调整问题是一个典型的NP-hard问题,没有已知的多项式时间算法能够精确求解,且随着问题规模的增大,求解难度急剧增加,因此国内外学者采取了一系列优化方法对其进行求解,比如使用拉格朗日算法求解[13],将问题简化以后,建立整数规划模型使用商用求解器求解[14],或者使用遗传算法[15-16]、模拟退火算法[17]、粒子群算法[18]等启发式算法求解,抑或采用人工智能求解列车运行图[19-20]。现有研究大多利用单一传统算法或者单一的人工智能算法对列车运行调整问题进行求解,往往难以兼顾全局优化与局部精度,导致解决方案的效率和效果受限。本文创新性地将深度学习嵌入遗传算法,结合二者优势,利用遗传算法的全局搜索能力和深度学习的局部搜索精度,并且运用多种调度手段,在中断条件下寻找更优的列车运行方案,以达到更好的优化效果。
1 模型构建
1.1 问题描述
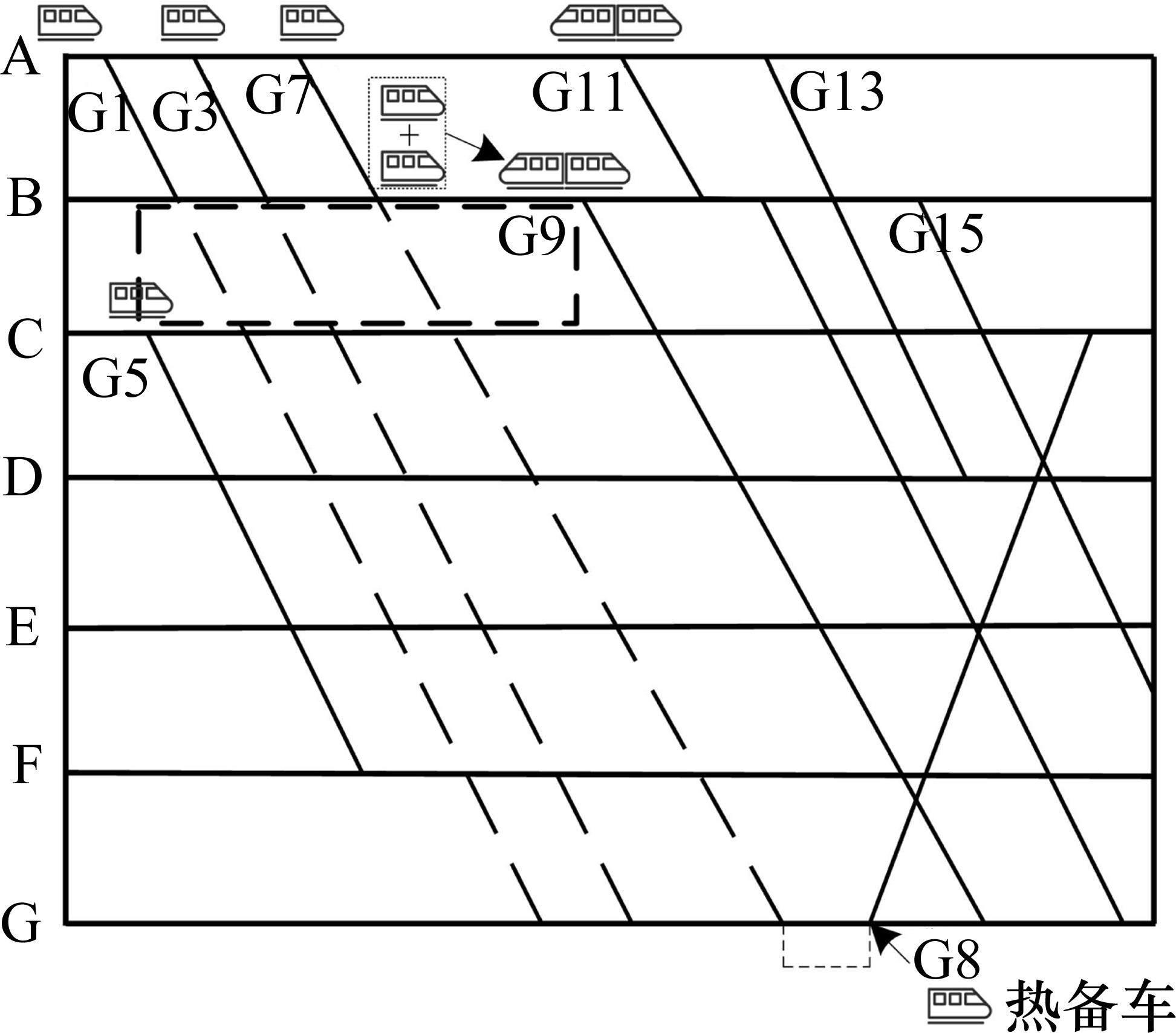
为更好地描述本文所研究的列车运行调整问题,特给出示例运行图如图1所示。图中共包含7个车站6个区间和6列列车。假定在某一时刻,区间B-C因突发事件(虚线框内的区域)发生了列车的单向通行中断,那么,整条线路会因此受到影响,列车G1、G3、G7会被迫中断运行、G11及以后的列车会出现不同程度的晚点,进而出现旅客滞留等一系列连锁反应,若不及时采取应急措施,由中断造成的延误会沿线路继续传播,造成大面积列车晚点、大量旅客滞留的严重后果。为此本文采取多种调度手段应对该突发事件,图中短编组列车G1和G3在车站B重联,中断结束后从B站出发;G8和G7原本共用同一车底,列车G7取消以后,启用热备车至G站,担当列车G8。本文采用启用热备车、短编组列车重联、列车取消等多种调度手段应对中断造成的列车晚点和旅客滞留问题,考虑动车组运用计划对列车运行调整进行研究,提出了列车运行图与动车组运用的一体化调整优化模型。
1.2 模型假设
关于该模型,做出如下假设:1) 为最小化列车运营成本,若某动车组交路计划未受影响,则按原计划执行,不会被重排;2) 中断发生前,所有列车均按图行车;3) 只有受影响的列车和热备车可以执行受影响列车的后续交路;4) 不同动车段的热备车均可以服务线路中的所有车站;5) 规定受影响旅客需求只能由受影响列车和热备车服务,不能被未受影响的列车服务;6) 本文中客流需求包含旅客人数、始发站、终到站3种属性。
1.3 符号定义
模型相关集合如下。

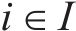
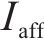
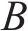
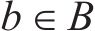
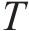

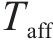
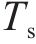
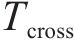



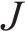
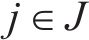
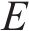
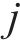
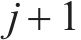
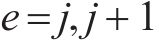
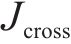
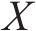

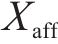
模型相关参数和决策变量见表1。
| 符号类型 | 符号 | 含义 |
|---|---|---|
| 参数 | 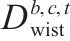 | 热备车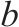   |
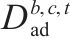 | 热备车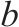   | |
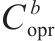 | 热备车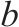 | |
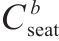 | 热备车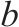 | |
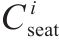 | 动车组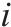 | |
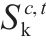 | 交路  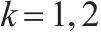 | |
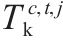 | 交路  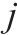 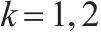 | |
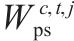 | 交路  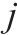 | |
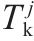 | 列车在车站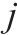 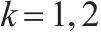 | |
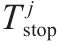 | 列车在车站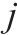 | |
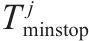 | 列车在车站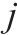 | |
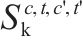 | 交路  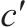 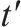 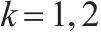 | |
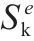 | 区间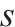 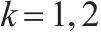 | |
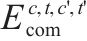 | 交路  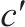 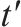 | |
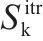 | 中断区间的起始、终点车站,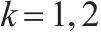 | |
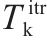 | 中断开始、结束的时刻,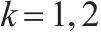 | |
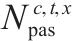 | 交路  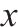 | |
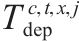 | 交路  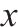 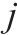 | |
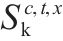 | 交路  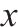  | |
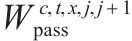 | 交路  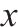 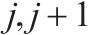 | |
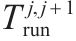 | 列车在区间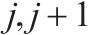 | |
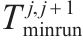 | 列车在区间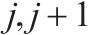 | |
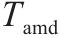 | 可接受的最大晚点时长 | |
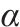 | 可接受的最大超员系数 | |
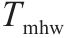 | 最小列车追踪间隔 | |
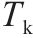 | 短编组列车重联、解编作业时间,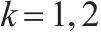 | |
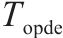 | 动车组列车解编作业时间 | |
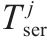 | 动车组在车站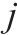 | |
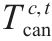 | 列车取消的惩罚时间 | |
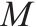 | 一个足够大的实数 | |
| 决策变量 | 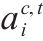 | 0-1变量,动车组   |
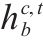 | 0-1变量,热备车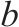   | |
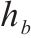 | 0-1变量,热备车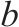 | |
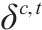 | 0-1变量,交路  | |
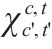 | 0-1变量,交路  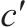 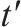 | |
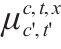 | 0-1变量,交路  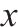 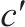 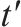 | |
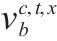 | 0-1变量,交路  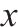 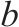 | |
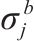 | 热备车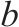 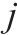 | |
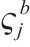 | 热备车 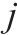 | |
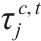 | 交路  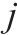 | |
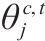 | 交路  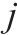 | |
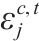 | 0-1变量,交路  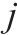 | |
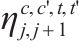 | 0-1变量,在区间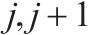   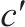 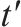 | |
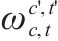 | 0-1变量,交路  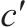 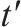 |
1.4 目标函数
为保障旅客出行需求,提升服务质量,本文将主要的优化目标定为尽量缩短旅客总晚点时长,同时要考虑热备车的使用以及动车组运用计划,因此在考虑旅客总晚点时长这一目标函数的同时,增加了热备车额外运营成本这一目标函数。
1) 旅客总晚点时长
旅客总晚点时长主要来自3部分:① 客流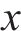
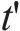
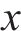
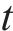
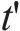
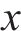
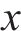
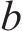
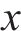
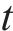
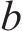
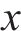
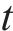
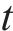
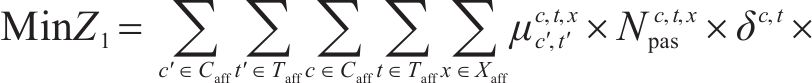

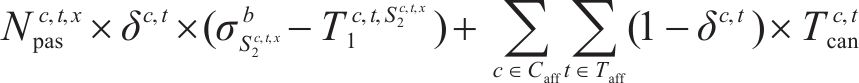
2) 热备车额外运营成本
热备车额外运营成本包括热备车承担交路中受影响列车的后续列车任务所需的运营成本以及热备车完成列车任务以后返回其配属站所需的运营成本,由3个部分相乘得到:① 热备车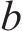
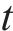
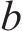
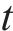
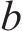
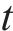
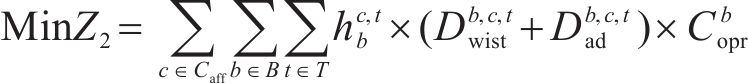
本文利用深度学习驱动的智能遗传优化算法对该模型进行求解,由于遗传算法只能对单目标模型进行求解,故需要对该模型的2个目标函数进行处理,合并为单目标函数。目前常用处理手段有理想点法、加权相加法和主要目标函数法。由于加权相加法能够通过赋予不同的权重系数来解决不同目标函数量纲不统一的问题,因此本文选择使用加权相加法。由于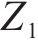
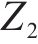
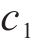
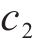
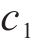
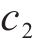
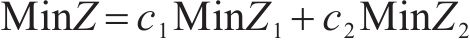
1.5 约束条件
1) 运行图基本约束
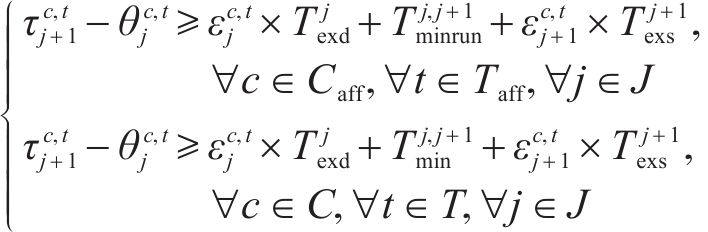
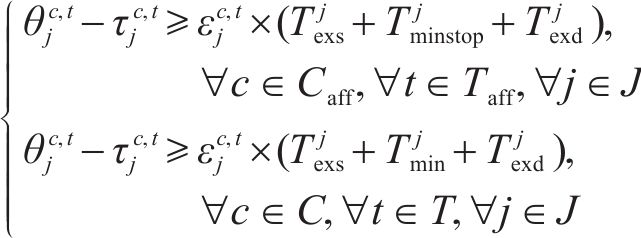
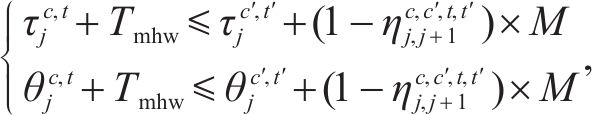
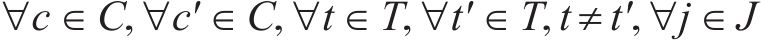
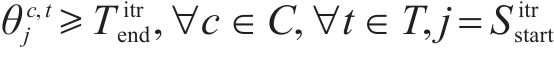
约束(4)规定受影响列车在区间的实际运行时分应该大于等于最小的列车区间运行时分,未受影响的列车应大于等于图定区间运行时分。同理约束(5)规定受影响列车在车站的实际停站时分应该大于等于最小的列车停站时分,未受影响的列车应大于等于图定停车时分。为保证列车安全运行,约束(6)相邻2列车之间必须满足到达和发车间隔时间约束。约束(7)规定在中断区间,列车的实际出发时刻应在中断结束时刻之后。
2) 取消列车约束
若某列车被取消,那么该列车必须满足以下约束:
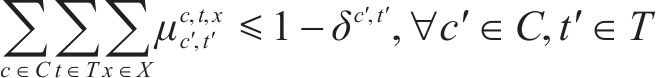
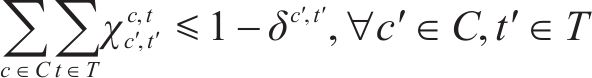
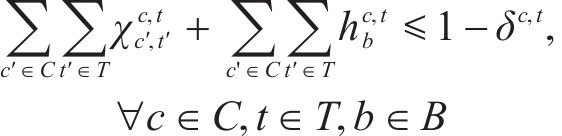
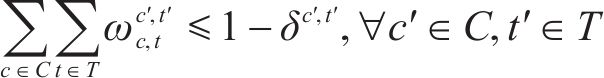
取消的列车不能服务旅客、不能承担其他受阻列车任务、不能被其他列车承担,也不能重联和解编。
3) 重联列车约束
重联的短编组列车需满足以下约束:
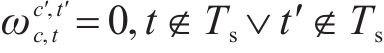
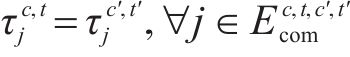
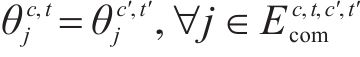
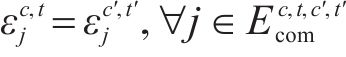
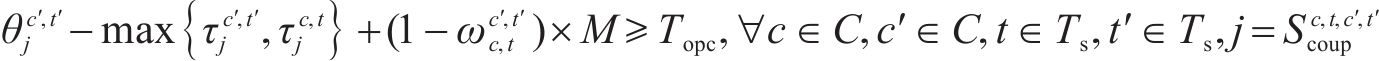
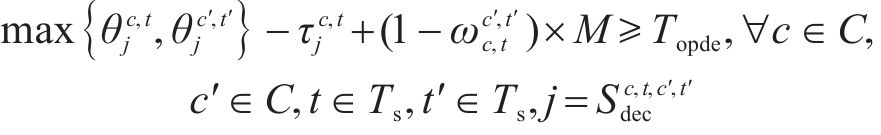
约束(12)表明只有2列车均为短编组列车才能重联,约束(13)~(15)表明2列短编组列车重联以后,在解编前,该2列车在沿途各站的到达出发时刻、停站计划均相同,约束(16)和约束(17)表明在列车重联和解编的车站,2列短编组列车的出发到达时刻必须满足重联、解编作业时间约束。
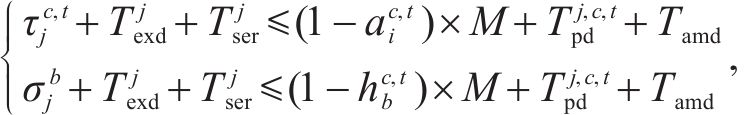
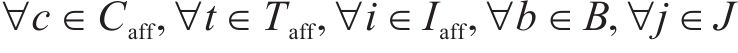
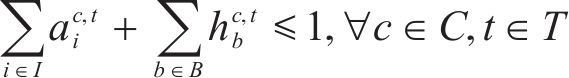
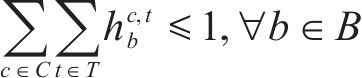
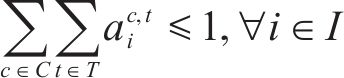
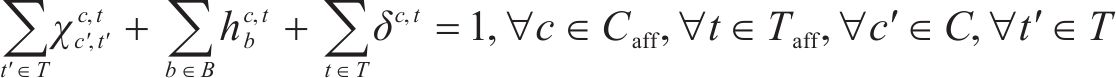
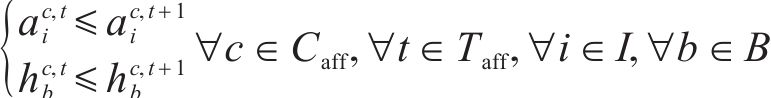
4) 动车组交路约束
约束(18)规定了动车组交路中有前后接续关系的2列车之间的到发时刻必须满足最大可接受晚点时长的要求。约束(19)限制了每个列车任务最多只能被承担一次,约束(20)规定了一台热备车最多只能承担一个列车任务,约束(21)规定了一列动车组最多只能承担一个列车任务,约束(22)规定了受影响列车任务最终的状态,被其他受影响列车承担、被热备车承担,或者被取消,约束(23)规定了动车组或热备车承担了某列车任务以后,必须承担其所在交路的所有后续列车任务。
5) 旅客需求约束
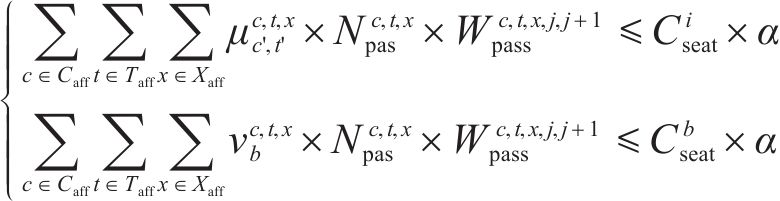
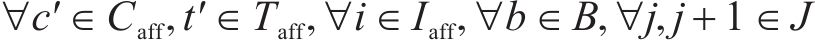
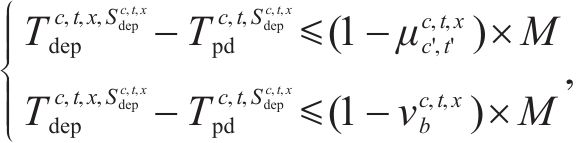
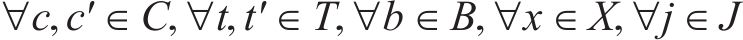
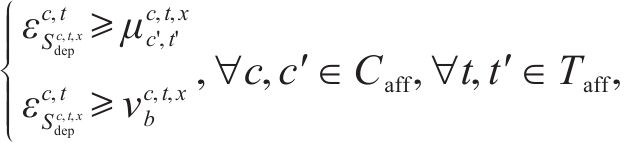
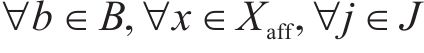
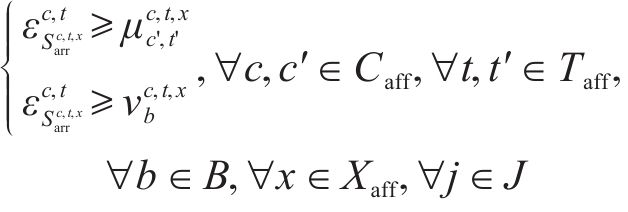
约束(24)规定了每列车上的旅客人数不能超过列车定员乘超员系数,约束(25)规定了列车的实际出发时刻不能早于其服务客流的图定出发时刻,约束(26)和约束(27)规定了列车一旦服务某一旅客需求,那么该列车必须在该旅客需求的终到站办理停站作业。
2 深度学习驱动的智能遗传优化算法
2.1 深度学习模型数据准备及训练
遗传算法虽然以其出色的全局搜索能力和并行处理优势在解决复杂优化问题时表现尚佳,但其局部搜索能力不足,容易导致搜索效率低下和早熟收敛,同时在维持种群多样性方面也面临挑战,这些局限性限制了其在复杂优化问题中的应用效果。而深度学习驱动的智能遗传优化算法恰好能够弥补这些缺点,在处理高维和复杂问题时,通过学习数据的内在规律,减少无效搜索,提高局部搜索效率,避免早熟收敛;并智能地平衡种群多样性,从而在进化后期更有效地逼近全局最优解。
常见的深度学习模型中,MLP在回归分析以及各种数据预测方面较有优势,故本文选择MLP模型来进行对遗传变异基因位点的学习与预测。
2.1.1 获得深度学习模型的训练数据
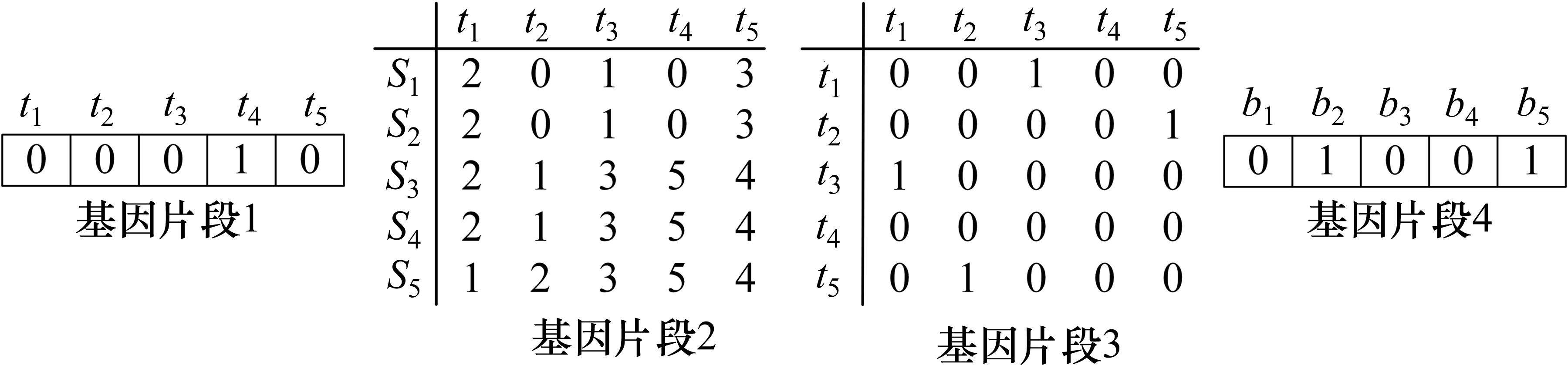
根据模型特点,设计如下求解步骤。第1步:初始化种群。种群内个体数设为N,每个个体由4个基因片段组成,各基因片段的含义如下:1) 列车取消基因片段,列代表列车,由0-1变量组成,1代表列车取消;2) 列车区间顺序基因片段,行代表区间,列代表列车,由非负整数组成,数字代表该列车在该区间的顺序,0代表该列车不经过该区间;3) 列车重联基因片段,行和列均代表列车,由0-1变量组成,1表示行和列代表的列车重联;4) 热备车启用基因片段,列代表热备车,由0-1变量组成,1代表该列对应的热备车被启用。基因片段的小规模示例如图2所示,图2所示的基因片段有5列列车、5列热备车和5个区间。中断开始时刻设为9:00,持续时间60 min。根据京沪高铁6:00—24:00的列车运行计划,设置模型各参数,设置种群内个体的每个基因片段的初始值。第2步:根据适应度函数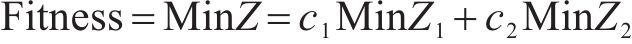
2.1.2 训练模型
第1步:将2.1.1中得到的200代的适应度和每个基因片段的特征值进行标准化处理,使其适合神经网络的输入,然后各取100代分为训练集和测试集。第2步:为每个基因片段构建MLP模型,以基因片段2为例,假设基因片段2有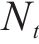
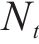
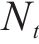
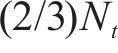
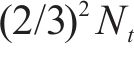
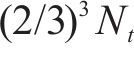
2.2 深度学习驱动的智能遗传优化算法流程
遗传算法是一种模拟自然选择和遗传学原理的搜索算法,用于解决优化和搜索问题。主要包含以下步骤:初始化、适应度评估、选择、交叉变异、生成新种群、终止条件检查、输出最优解。嵌入深度学习以后,流程图如图3所示。
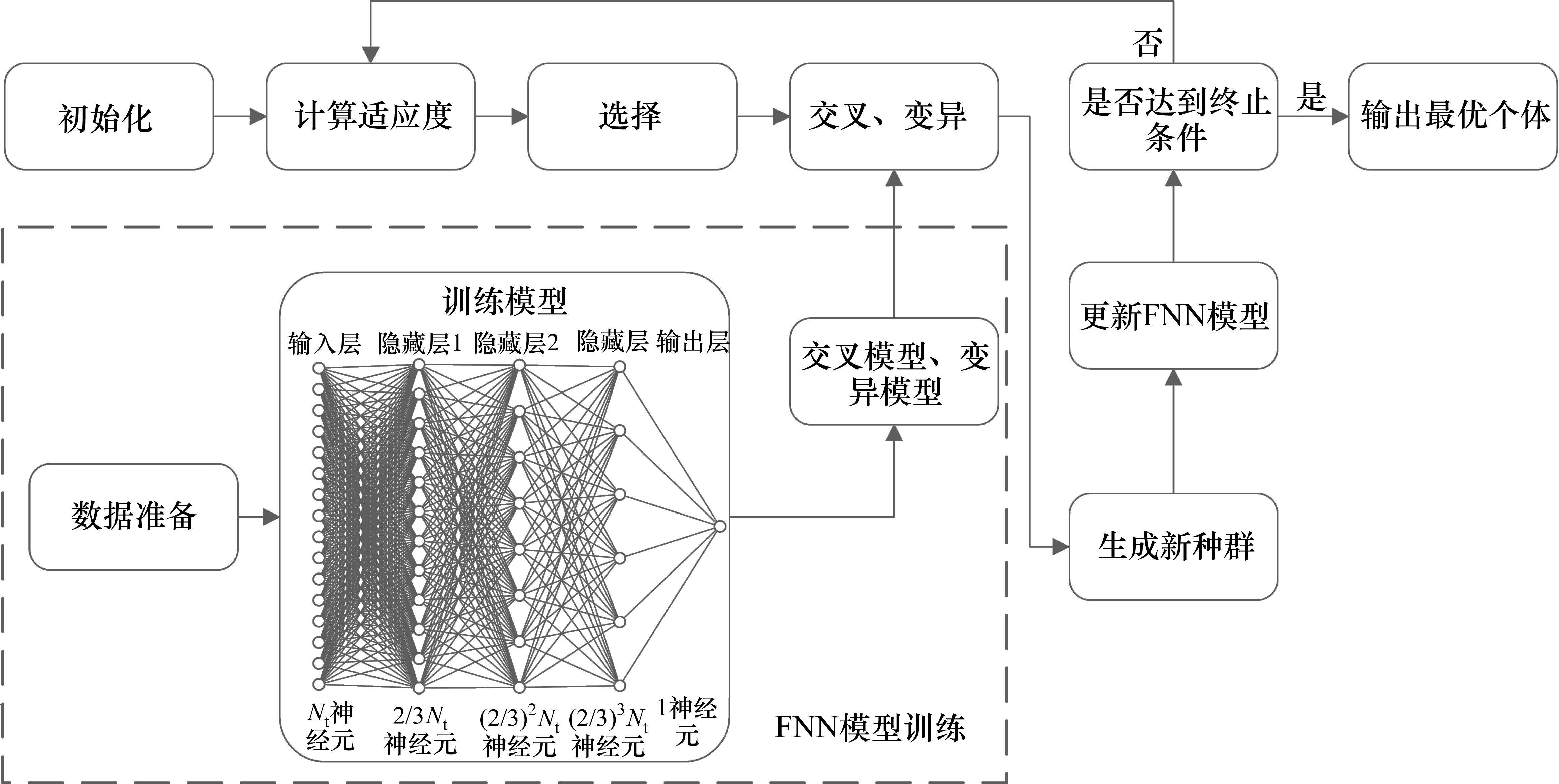
算法流程如下。第1步:初始化种群。第2步:适应度计算。第3步:选择,选择适应度高的个体进入下一代。第4步:交叉变异,将传统遗传算法中的随机选取交叉/变异的位点的方法,替换为利用训练好的MLP模型,在计算后选择权重最大的神经元对应的基因位点作为交叉/变异的位点的方法,设置交叉率为30%,变异率为10%。第5步:生成新一代种群,1) 交叉变异之后,首先由4个基因片段确定
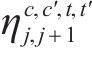
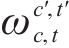
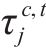
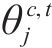
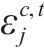
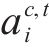
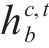
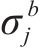
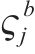
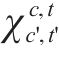
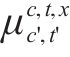
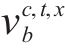
3 算例分析
3.1 基础数据
以我国京沪高速铁路全线某日6:00—24:00列车运行图为实例,对本文提出的模型和算法进行验证。京沪高铁始于北京南站,终到上海虹桥站,全长1 318 km,沿途共计23个车站,22个区间,设有北京、天津、济南、徐州东、南京、虹桥6个动车(段)所,日开行列车数550列,下行列车按发车顺序编号为G1,G3,G5,……,上行列车按发车顺序编号为G2,G4,G6,……,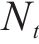
| 参数 | 值 |
|---|---|
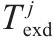 | 2 |
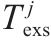 | 3 |
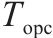 | 15 |
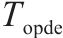 | 10 |
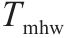 | 4 |
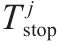 | 3 |
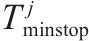 | 2 |
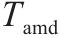 | 20 |
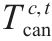 | 720 |
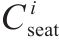 | 1 200 |
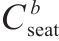 | 1 200 |
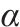 | 1.2 |
 | 330 |
京沪高铁各区间距离和运行时分见表3。
| 区间 | 距离/km | 运行时分/min | 最小运行时分(通通/min) | 区间 | 距离/km | 运行时分/min | 最小运行时分(通通/min) |
|---|---|---|---|---|---|---|---|
| 北京南—廊坊 | 59.5 | 18 | 16 | 宿州东—蚌埠南 | 88.0 | 20 | 18 |
| 廊坊—天津南 | 62.6 | 14 | 13 | 蚌埠南—定远 | 54.3 | 12 | 11 |
| 天津南—沧州西 | 87.9 | 20 | 18 | 定远—滁州 | 62.0 | 14 | 13 |
| 沧州西—德州东 | 103.8 | 23 | 21 | 滁州—南京南 | 59.0 | 14 | 13 |
| 德州东—济南西 | 92.2 | 21 | 19 | 南京南—镇江南 | 65.4 | 15 | 14 |
| 济南西—泰安 | 58.7 | 14 | 13 | 镇江南—丹阳北 | 28.6 | 7 | 6 |
| 泰安—曲阜东 | 70.4 | 15 | 14 | 丹阳北—常州北 | 32.4 | 8 | 7 |
| 曲阜东—滕州东 | 56 | 12 | 11 | 常州北—无锡东 | 57.4 | 13 | 12 |
| 滕州东—枣庄 | 36.1 | 8 | 7 | 无锡东—苏州北 | 26.8 | 6 | 5 |
| 枣庄—徐州东 | 64.4 | 14 | 13 | 苏州北—昆山南 | 31.4 | 7 | 6 |
| 徐州东—宿州东 | 67.2 | 15 | 14 | 昆山南—上海虹桥 | 44 | 13 | 12 |
3.2 算法的有效性验证
本文给出中断时长不断增加的6组算例,对算法的有效性进行验证。在区间枣庄—徐州东的下行方向设置了不同持续时长的单向区间通行中断,中断开始时刻统一设置为9:00,并采用以下3种方式进行调整,随后针对结果进行对比分析:1) 不进行优化,将原运行图向后平移;2) 使用经典遗传算法进行优化;3) 深度学习驱动的遗传算法进行优化。
3种方式的结果数据如表4所示。
| 实验 | 中断时长/min | 仅平移运行图 | 经典遗传算法 | 深度学习驱动的遗传算法 | ||||
|---|---|---|---|---|---|---|---|---|
| 目标值 | 目标值 | 收敛代数 | 用时/s | 目标值 | 收敛代数 | 用时/s | ||
| 1 | 30 | 3 729 686 | 3 051 179 | 40 | 975 | 2 831 510 | 30 | 752 |
| 2 | 60 | 8 261 849 | 7 260 481 | 46 | 1 373 | 6 281 009 | 38 | 1 044 |
| 3 | 90 | 11 780 064 | 10 448 175 | 51 | 1 896 | 8 926 184 | 40 | 1 587 |
| 4 | 120 | 15 134 906 | 13 765 080 | 67 | 2 210 | 12 151 079 | 52 | 1 971 |
| 5 | 150 | 20 293 160 | 18 201 298 | 82 | 3 052 | 15 751 157 | 59 | 2 667 |
| 6 | 180 | 22 481 512 | 19 635 784 | 92 | 3 874 | 17 051 349 | 70 | 3 154 |
从求解结果可以看出,与仅平移运行图相比,经典遗传算法和深度学习驱动的遗传算法均有比较好的优化效果,以120 min的中断时长为例,对目标值的优化效果分别提升了9.1%和19.7%,深度学习驱动的遗传算法具有更好的优化效果;在收敛速度方面,二者的收敛代数分别为67代和52代,深度学习驱动的遗传算法也有明显的优势;在求解速度方面,经典遗传算法用时2 210 s,深度学习驱动的遗传算法用时1 971 s,求解耗时降低了10.8%。在面对导致较长时间中断的突发事件时,列车恢复正常运营前的准备工作,包括对突发事件类型的快速判断、启动应急预案、热备车的紧急启用与调度、扣停列车以及旅客疏散等,需要消耗一定的时间。因此在中断时间较长的情况下,当前算法的求解效率仍然能够满足部分工程应用中的决策需求。在较短的中断时长下,求解时间在20 min以内,同样能满足现场工程应用的决策需求。此外,在铁路现场调度指挥工作中,可以使用本文提出的深度学习驱动的智能遗传优化算法进行预求解,即在当日运行图铺画的同时提前将各中断时长的调整方案计算出来,作为突发事件的应急预案辅助使用,为调度人员提供备选调整方案。在其他几组实验中,深度学习驱动的遗传算法的目标值、收敛代数和求解速度均有一定程度的提升。
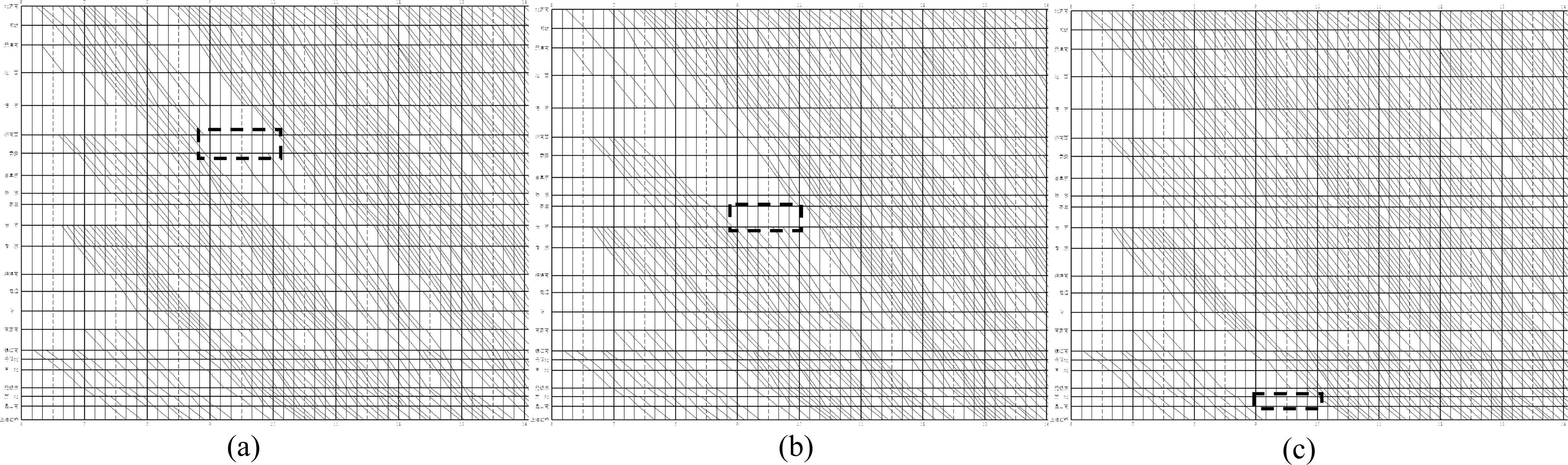
3.3 不同区间中断条件下的调整及分析
分别在济南西—泰安、徐州东—宿州东、苏州北—昆山南等3个区间的下行方向设置了单向通行中断,中断开始时刻为9:00,时长为60 min,如图3中虚线方框所示。随后利用深度学习驱动的遗传算法分别对其进行优化调整,选取调整之后的6:00—14:00的列车运行图,如图3所示。
3组实验的结果如表5所示。
| 实验 | 中断时长/min | 取消列 车数/列 | 目标函 数值 | 收敛代数 | 用时/s |
|---|---|---|---|---|---|
| 1 | 60 | 7 | 6 681 299 | 35 | 1 125 |
| 2 | 60 | 9 | 7 651 298 | 37 | 1 373 |
| 3 | 60 | 4 | 4 128 157 | 34 | 1 002 |
由表5可以看出,由于苏州北—昆山南区间靠近下行方向终点站上海虹桥站,且该区间距离较短,故该区间中断对整个运行图的影响相对较小,取消列车数和目标函数值也是相对较低的,分别为4列和4 128 157分。实验1和实验2的中断区间都临近换乘站,故区间中断后受影响的列车数量较实验3多,因此,取消的列车数量和目标函数值也高于实验3,和实验1相比,实验2的中断区间更靠近线路中段,计划在9:00—10:00时段内通过中断区间的列车数量更多,因此实验2的取消列车数量和目标函数值都要略高于实验1。
3.4 不同调度手段对比分析
在区间枣庄—徐州东的下行方向设置了时长为120 min的单向通行中断,中断开始时刻为10:00,采用深度学习驱动的智能遗传优化算法,对下列3种调度手段采用不同组合方式进行优化:①短编组列车重联,②启用热备车,③取消列车。随后对实验结果进行对比分析,结果如表6所示。
| 实验 | 调度手段 | 重联列车对数/对 | 启用热备车数量/列 | 取消列车数/列 | 目标函数值 | 旅客晚点 时长/min | 额外运营 成本/元 | 收敛 代数 | 用时/s |
|---|---|---|---|---|---|---|---|---|---|
| 1 | — | — | — | — | 15 869 801 | 15 869 801 | 0 | 40 | 1 689 |
| 2 |  | 8 | — | — | 14 952 846 | 14 952 846 | 0 | 48 | 1 786 |
| 3 |  | — | 11 | — | 14 102 369 | 11 250 466 | 3 658 967 | 43 | 1 731 |
| 4 |  | — | — | 13 | 14 286 023 | 14 286 023 | 0 | 46 | 1 752 |
| 5 |   | 7 | 9 | — | 13 480 231 | 10 964 434 | 3 045 421 | 49 | 1 889 |
| 6 |   | 7 | — | 11 | 13 642 589 | 13 642 589 | 0 | 53 | 1 922 |
| 7 |   | — | 9 | 11 | 12 953 654 | 10 754 254 | 2 845 247 | 54 | 1 956 |
| 8 |    | 6 | 10 | 14 | 11 405 632 | 9 045 173 | 2 945 742 | 56 | 2 058 |
与不启用调度手段比较,使用各种调度手段在目标函数值优化方面均有不同程度的提升,提升最大的是启用3种调度手段的实验8,目标函数值降低了28.13%,但在求解用时方面比不启用调度手段的实验1增加了21.85%,原因是启用调度手段使列车运行调整过程更为复杂,求解相对较慢。在该实验中,重连列车有6对,G11和G13,G83和G85,G177和G179,G87和G91,G193和G201,G155和G161,启用热备车10列,其中徐州东动车所4列,济南动车所2列,北京、天津、南京南、虹桥动车所各1列。
在函数值优化方面,优化效果依次大致为:3种>2种>1种>不启用,可见调度手段的引入提升了列车运行调整的优化效果;但在求解速度方面,3种<2种<1种<不启用。此外,可以看出,启用热备车时,旅客晚点时长会显著降低,但因启用热备车而导致的额外运营成本会增高。所以,铁路运营部门可以参考本文给出的①单独使用各种调度手段以及几种手段组合使用时的优化效果和求解用时②晚点时长和额外运营成本之间的关系,根据现场需求选择合适的调整方案。
4 结论
1) 展开区间单向通行中断条件下的高速铁路列车运行调整问题,给出了考虑动车运用的列车运行图优化建模思路,在此基础上提出了列车运行图与动车组运用的一体化调整优化模型。
2) 根据模型及问题的特点,选择遗传算法并结合深度学习,设计了深度学习驱动的智能遗传优化算法,在求解速度和求解质量上均优于经典遗传算法,以120 min的中断时长为例,本文提出的算法比单纯的遗传算法对目标值的优化效果提升11.7%,求解耗时降低了10.8%。讨论了单向通行中断发生在不同区间对整条线路列车运行的不同影响,最后讨论了不同调度手段组合的优化效果对比以及铁路运营部门可以根据各种调度手段组合的优化效果和求解用时选择最佳方案。
3) 通过对实际高铁线路算例的实验分析,深度学习驱动的智能遗传优化算法与经典遗传算法相比,可以有效地提高解的质量和求解的速度,从而更好地为突发状况下的运行图调整提供指导意见。针对该算法,在后续研究中将继续进行研究,如合理调整深度学习模型的学习率、迭代次数、epoch数量等超参数,致力于提高其求解速度,争取能在所有长度的中断时间条件下,在工程应用方面,对列车运行调整提供快速且较优的调整方案。此外,当前算法只能解决固定时长的列车通行中断,计划在未来开展不确定时长的通行中断条件下的列车运行调整,同时,计划结合帕累托前沿讨论运行图效率的提升和列车运营成本之间的关系来代替对2个目标函数进行加权,为铁路旅客运输工作提供进一步的技术和理论支持。
赵文强,周磊山,白紫熙等.中断条件下高铁列车运行调整优化模型与算法研究[J].铁道科学与工程学报,2025,22(03):979-990.
ZHAO Wenqiang,ZHOU Leishan,BAI Zixi,et al.Optimization model and algorithm for high-speed railway train operation adjustment under disruptions conditions[J].Journal of Railway Science and Engineering,2025,22(03):979-990.

