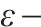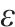受天气变化、运输特点等因素的影响,高速铁路列车延误不可避免,延误会打乱旅客的原定行程,造成旅客满意度波动。面对竞争日益激烈的旅客运输市场,如何以旅客为中心提出有效的列车延误处置方案是铁路部门发掘市场竞争力的关键之一。列车运行调整是铁路部门生成延误处置方案的主要手段,在现实场景中,通常由列车调度员负责列车运行调整工作。随着列车开行密度的增加与运输组织复杂度的提升,这种人工的列车运行调整方式往往不能及时得到有效的延误处置方案。为了辅助人工决策,许多研究改进了原有的调度辅助决策工具[1-2]。针对辅助决策工具的改进提高了调度员应对小型延误时的工作效率,但这类工具在处理大型延误时效果并不理想。当线路出现如区间中断等大型延误情况时,旅客的出行将受到极大影响,为降低延误对旅客出行的干扰,ZHU等[3]以最小化旅客广义旅行时间、停站等待时间和中转次数为目标建立了列车运行调整模型,通过模型的优化使得中断条件下更多旅客可以完成计划出行;HONG等[4]在运行调整过程中考虑了乘客的重新分配,降低了区间中断对旅客行程的影响;ZHAN等[5]在运行调整模型中同时调整了列车路径与乘客路径,进一步照顾了乘客的出行需求。随着铁路网络化水平的提升,延误产生的影响会随旅客换乘和列车跨线运行在铁路网络中传播,许多研究考虑了旅客的换乘接续过程,提高了运行调整过程中旅客的换乘成功率[6-7]。与单一线路不同,路网环境下列车数量多,运行情况复杂,导致列车运行调整问题的规模更大,求解难度更高。为解决这一问题,ZHANG等[8-10]根据列车运行调整问题的特征开发了一系列精确算法,有效提升了路网范围内列车运行调整问题的求解效率。为进一步提升求解速度,启发式算法也被广泛应用于列车运行调整优化过程中,在一定条件下,启发式算法也能在短时间内获得高质量的解[11-13]。延误的出现不仅会导致计划列车时刻表不再可行,还会影响动车组运用、到发线运用、乘务调度等方案的实施,为解决这一难题,许多研究采用协同优化的方式提升列车运行调整的全局适用性。列车运行调整与到发线运用协同优化的研究最为广泛[14-16],也有部分研究考虑了到发线运用之外的其他问题,如HOOGERVORST等[17-18]通过将列车运行调整与机车调度协同优化的方法减少了列车延误的传播。在旅客出行选择多样化的背景下,服务质量逐渐成为旅客选择出行方式的重要依据,作为衡量服务质量的重要指标,旅客满意度变化被逐渐纳入列车运行调整优化过程中。旅客满意度变化作为优化目标,通常有2种表述形式,第1种使用旅客到达终点站的延误时间表示旅客满意度[19-20];第2种则使用列车实际运行图与计划运行图的偏离程度表示旅客满意度[21-22]。本质上以上2种表述形式都将旅客满意度变化归因于列车延误,认为延误时间与旅客满意度成反比。虽然延误时间与旅客满意度之间确实存在这种线性关系,但MONSUUR等[23]研究表明,列车延误情况下的旅客满意度变化还会受旅客出行里程、乘车舒适度、服务频率、服务类型和旅客主观特性等因素影响,仅考虑延误时间并不能准确反映旅客满意度变化。为此,本文探讨列车延误背景下其他因素对旅客满意度的影响,完善旅客满意度的优化目标,提升列车运行调整优化结果的准确性。在当前社会背景下,以旅客为导向的运输服务逐渐成为市场主流,运输服务对于旅客满意度的影响受到越来越多的重视。绝大多数有关旅客满意度的研究均指出了运输企业的服务水平,服务特性及服务决策对旅客满意度的影响,相关研究为运输企业的战略决策提供了十分有意义的参考,但针对突发事件下旅客满意度实时优化的有关研究较少,且对旅客满意度的阐释模糊,难以有效体现旅客满意度对实时优化的影响。本文旨在探究突发故障情况下旅客满意度与列车运行调整优化的关系,分析不同延误处置策略对旅客满意度变化的影响,提升列车运行调整决策的人性化水平。
1 问题描述
在列车运行调整过程中,旅客期望的目标与铁路部门期望的目标并不完全一致,一个好的运行调整方案是2种目标动态博弈的结果。本文模型中分别考虑了旅客满意度和运行调整2个目标,为提升服务水平,选择旅客满意度作为首要优化目标。在列车延误情况下,旅客满意度变化不仅取决于延误时间大小,还与旅客出行里程长短,列车车厢内的旅客密集程度等因素有关,本文将旅客满意度影响因素归为列车运行特征、旅客出行特征和延误时间3类,将上述3类影响因素以参数形式导入旅客满意度的优化目标中,通过改变参数取值研究其对列车运行调整优化结果的影响。为了维持服务水平与运行调整的平衡,本文将运行调整目标转化为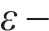
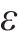
1.1 列车运行调整
图1以4个车站间运行的3趟列车为例展示了列车运行调整的流程,列车运行线被分为实线和虚线2类,其中实线表示计划的列车运行线,虚线表示调整后的列车运行线。图1(a)为计划列车运行图,图1(b)为调整列车运行图,由图1可知,当列车1在车站1延误30 min出发时,为了降低延误造成的影响,列车1在遭遇延误后压缩了区间运行时间与停站时间,与此同时,列车1在车站1被列车2和列车3越行,由于列车1的速度快于列车2,列车1在车站2早于列车2发车,列车3被迫延长停站时间供列车1越行。
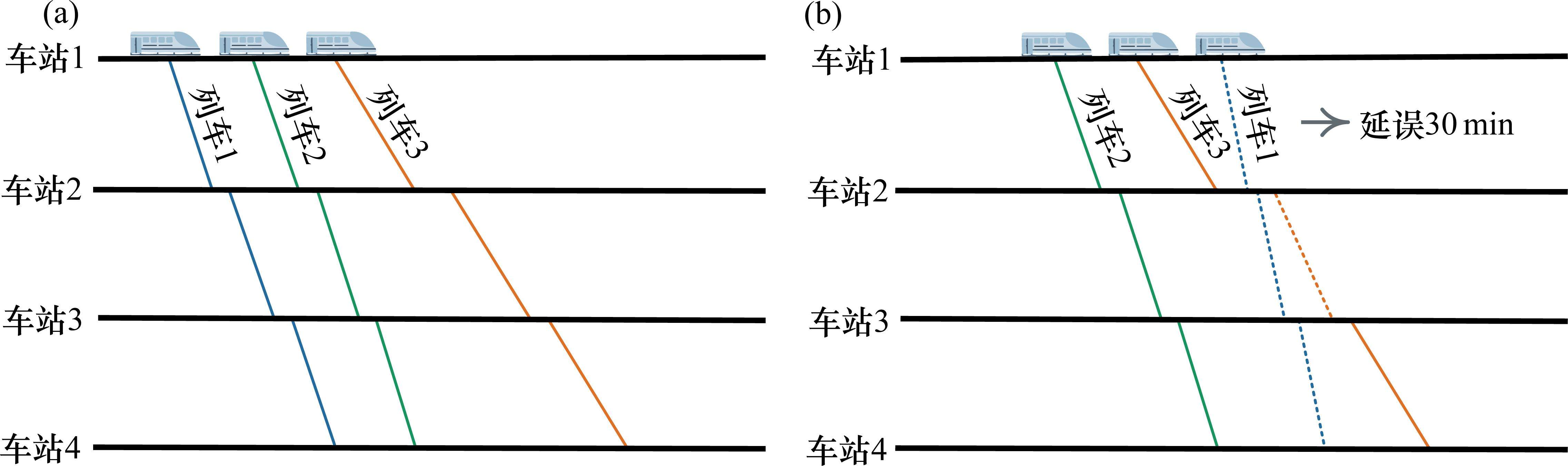
上述示例展示了2种列车运行调整方式,①当列车遭遇延误时,为减小列车时刻表偏差,列车将会加速运行并缩短停站时间等车站内作业时间;②为了减少延误在列车间的传播,未受延误影响的列车可在车站内越行已经延误的列车。本文在模型中仅考虑①、② 2种列车运行调整方式。由上述示例可知,当线路上出现列车延误情况时,列车的最长延误时间并不一定等于初始延误时间。在现实场景中,一条线路上可能运行上百趟列车,多次越行可能会导致低速列车的延误时间大于初始延误时间。为避免低速列车累积大量延误,本文为列车延误时间设置了阈值D,并为延误时间超出阈值D的列车设置了旅客满意度的惩罚值,当列车累积的延误时间大于D时,旅客满意度下降幅度将会增大,通过这种方式避免了低速列车多次让行高速列车导致延误大量累积的情况。
1.2 旅客满意度影响因素
许多旅客满意度的有关研究都揭示了列车延误背景下心情、性格和年龄等主观因素对旅客满意度的影响。在一趟列车中,旅客的主观因素是不可测的,且旅客的心情等部分主观因素还会随机变化,这些原因导致主观因素无法指导列车运行调整优化,因此本文不考虑旅客的主观因素,只考虑列车运行特征、旅客出行特征和延误时间3类客观因素对旅客满意度变化的影响,客观因素对旅客满意度的具体影响情况参考文献[23]的研究成果。
1.2.1 列车运行特征
1) 旅客密集程度: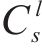

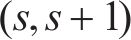
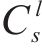
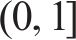
2) 列车服务类型: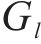

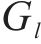
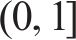
1.2.2 旅客出行特征
1) 旅客出行里程: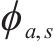
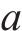
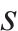
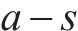
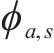
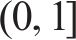
2) 旅客乘车坐席: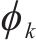

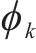
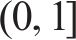
1.2.3 延误时间
延误时间是影响旅客满意度变化的主要因素,当列车发生延误时,旅客往往更关心自身到达目的地车站时列车的延误情况,本文用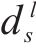

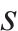
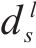
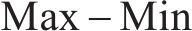
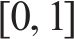
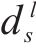
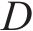
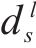
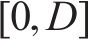
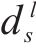
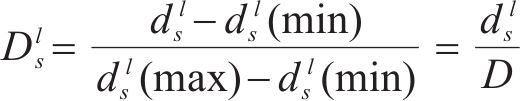
式中: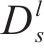
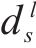
2 模型构建
2.1 变量及参数定义
为构建考虑旅客满意度的列车运行调整优化模型,引入2组整数变量和0-1变量,模型涉及的各种参数及其含义如表1所示,变量及其含义如表2所示。
| 参数 | 说明 |
|---|---|
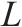 | 列车集合, 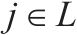 |
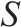 | 车站集合 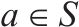 |
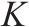 | 列车座席集合, |
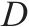 | 到达延误时间的阈值 |
 | 一个极大的整数,取值为1 440 |
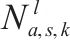 | 乘坐列车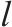 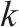 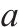 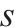 |
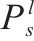 | 未发生延误时列车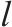 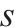 |
 | 列车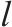 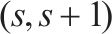 |
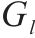 | 列车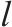 |
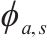 | 从车站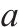 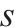 |
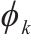 | 乘车座席为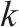 |
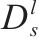 | 列车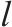 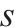 |
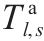 | 列车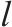 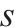 |
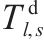 | 列车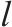 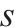 |
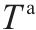 | 相邻列车在车站的最小到达间隔 |
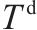 | 相邻列车在车站的最小出发间隔 |
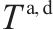 | 相邻列车在车站的最小发到间隔 |
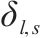 | 列车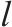 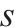 |
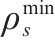 | 车站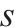 |
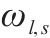 | 乘坐列车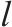 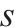 |
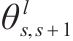 | 列车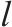 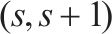 |
| 变量 | 说明 |
|---|---|
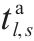 | 列车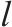 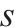 |
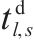 | 列车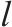 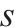 |
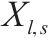 | 0-1变量,若列车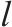 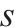 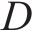 |
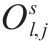 | 0-1变量,若列车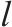 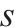 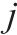 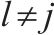 |
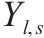 | 0-1变量,若乘坐列车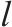 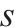 |
2.2 约束条件
2.2.1 列车运行约束
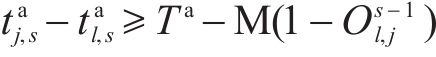
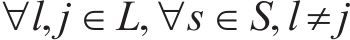
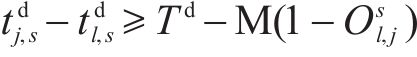
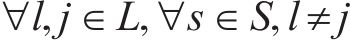
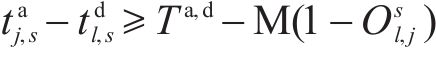
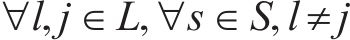
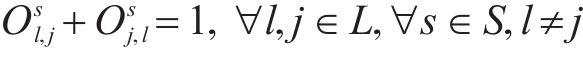
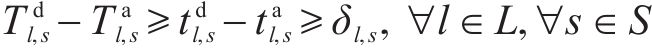

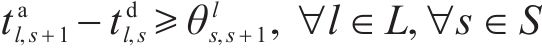
式(2)和式(3)确保相邻列车在同一车站满足最小到达和出发间隔。式(4)确保在同一车站上一趟列车的出发时间与下一趟列车的到达时间满足最小发到间隔。式(5)为列车顺序约束,确定了不同列车在车站的到达和出发顺序,避免列车在区间内越行。式(6)确保当列车在车站计划停站时,列车的停站时间不小于最小停站时间,且不大于计划停站时间。式(7)确保当列车在车站计划通过时,列车在该站的到达时间等于通过时间。式(8)确保列车在区间内的运行时间不小于该区间的最短运行时间。
2.2.2 换乘接续约束
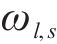
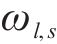
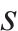
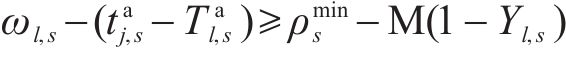
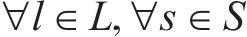
式(9)确保旅客的换乘时间不小于车站的最短换乘时间,由于式(9)为大
2.2.3 运行调整约束
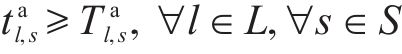
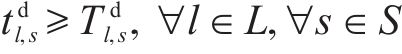
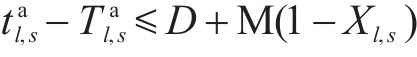
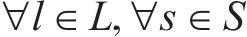
式(10)和式(11)确保调整后的列车到达和出发时间不小于计划的列车到达和出发时间,在现实场景中,如果列车在车站提前出发,会导致计划在该站上车的旅客无法正常乘车。式(12)确保列车在车站的到达延误时间不超过阈值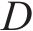
2.3 目标函数
2.3.1 旅客满意度目标
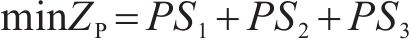
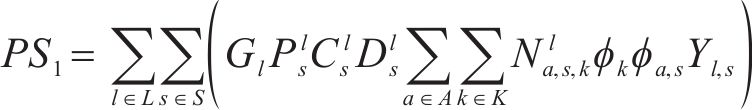
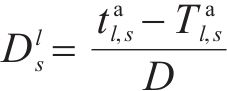
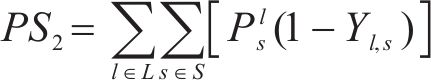
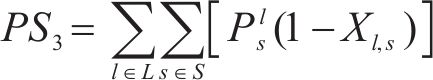
式(13)为最小化旅客满意度变化的目标函数,用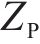
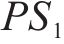
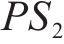
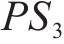
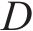
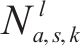


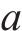
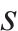
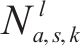
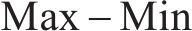
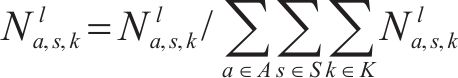
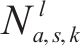
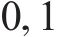
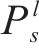

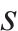

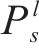
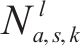



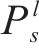
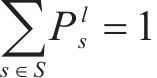
式(14)表示遭遇延误后的旅客满意度变化幅度,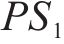
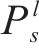
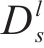
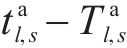
2.3.2 运行调整目标
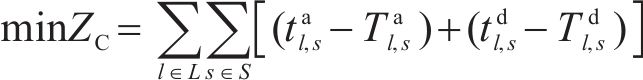
式(18)为最小化调整运行图与计划运行图偏差的目标函数,用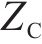
3 算法设计
3.1 多目标处理
常用的多目标优化求解方法有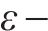
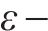
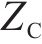
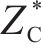
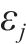
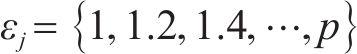
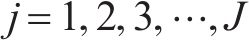
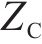
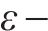
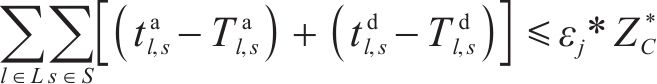
将其添加到以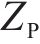
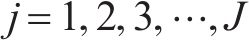
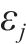
3.2 分支定切算法
本文在模型中考虑了列车越行策略,通过列车越行的方式降低延误对列车正常运行秩序的影响,为描述列车在车站越行的实际情况,引入大量0-1变量判断相邻列车在车站的到发顺序,加大了模型求解难度,直接使用商用求解器难以在有限的时间内得到可行解。为进一步提升求解效率,在考虑模型特点的基础上设计了一种分支定切算法,通过动态添加有效割的方式加快求解速度。在执行算法前,首先对模型进行线性松弛,松弛变量整数限制的同时松弛掉约束(4)、约束(6)、约束(7),令松弛后的模型为RM。
3.2.1 有效割设置
分支定切算法沿用了分支定界算法的框架,通过在松弛模型节点处添加有效割的方式不断改进模型,能够在仅搜索少量节点的情况下得到模型的最优解。分支定切算法在松弛模型节点处可添加多种有效割,Gomory割是一种通用的割生成方法,其基本思想为先求解线性松弛模型得到最优解,选择最优解中的非整数基并利用相应的约束构造割平面。Gomory割通用性强且构造简便,与另一种通用的构造割方法C-G割相比,Gomory割避免了因变量取值范围不同而需变换取整方式的困扰,因此选择Gomory割作为在松弛模型节点处添加的基本有效割。为进一步加快求解效率,另外设置了2种有效割,有效割的设置及添加方式如下所示。
1) 停站和通过有效割:约束(6)和约束(7)为停站和通过约束,用以保证列车在车站的计划停站或计划通过不受影响。在实际求解过程中,并非所有的计划停站或计划通过都因延误影响而改变,因此松弛模型中的约束(6)和约束(7),令约束(6)和约束(7)为停站和通过有效割,如果松弛模型节点的可行解违反了列车的停站或通过约束,则在松弛模型节点动态添加停站有效割或通过有效割,停站有效割与通过有效割如式(20)和式(21)所示:
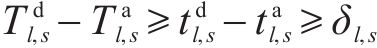
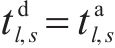
在松弛模型节点处添加少量停站和通过有效割可以切割掉不符合停站和通过约束的非整数解,由于在模型中添加了Gomory割,当模型取得整数解时,之前添加的Gomory割可能导致极个别计划停站或计划通过约束被违背,为此,当模型取得整数可行解时,如果可行解改变了列车的计划停站或计划通过,则在取得整数可行解的节点继续添加停站有效割或通过有效割,切割掉不符合停站和通过约束的整数解。
2) 发到间隔有效割:约束(4)为发到间隔约束,用以保证在同一车站前一趟列车的出发时间与下一趟列车的到达时间满足最小到发间隔。发到间隔约束与列车顺序变量耦合,但在实际求解过程中,列车顺序由约束(2)和约束(3)判定,大量的发到间隔约束判定会严重影响模型的求解速度,因此松弛模型中的约束(4),令约束(4)为到发间隔有效割,如果整数可行解节点的解违反了发到间隔约束,则在整数可行解节点动态添加发到间隔有效割,发到间隔有效割如式(22)所示:
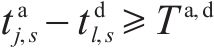
3.2.2 算法流程
分支定切算法流程如下。
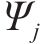
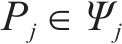
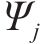
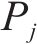
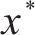
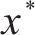
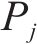
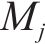
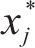
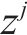
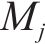
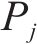
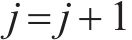
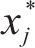
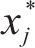
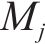
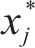
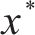
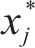
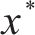
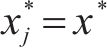
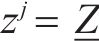
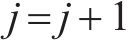
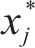
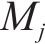
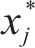
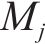
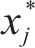
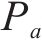
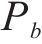
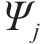
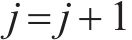
4 案例分析
为验证模型的合理性和算法的有效性,选择京沪高铁北京南―徐州东下行区段为背景线路,设置多组算例求解模型。选择14:00―17:00在北京南―徐州东下行区段运行的15趟列车为研究对象,按始发站的发车顺序排序依次为:G2557,G143,G145,G147,G2595,G2561,G2577,G149,G189,G151,G193,G195,G1567,G153,G157。
4.1 参数设置
4.1.1 旅客满意度相关参数
旅客满意度相关参数取值如下:到达延误时间阈值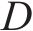
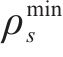
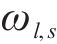
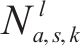

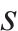
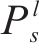
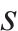

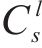
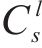
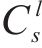
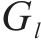
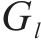
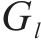
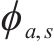
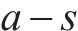
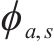
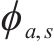
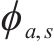
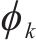

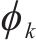
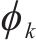
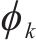
4.1.2 列车区间运行参数
京沪高铁北京南―徐州东下行区段各区间列车最小运行时间如表3所示。线路上追踪列车间隔时间均为4 min;计划停站列车在车站的最短停站时间为2 min,最长停站时间为各列车的图定停站时间。
| 区间 | 最小运行时间/min |
|---|---|
| 北京南—廊坊 | 16 |
| 廊坊—天津南 | 11 |
| 天津南—沧州东 | 16 |
| 沧州东—德州东 | 18 |
| 德州东—济南西 | 20 |
| 济南西—泰安 | 14 |
| 泰安—曲阜东 | 13 |
| 曲阜东—滕州东 | 10 |
| 滕州东—枣庄 | 7 |
| 枣庄—徐州东 | 12 |
4.2 结果分析
线路晚点场景设定为:德州东—济南西区间15:30—16:00发生故障导致区间中断,计划于15:30—16:00通过该区间的G2557、G143、G145、G147、G2595、G2561次列车延误至16:00后才能通过该区间。本文构建的模型在Intel(R) Core(TM) i7-8750H CPU@2.20 GHz,内存16 GB的设备上,采用Python调用求解器Gurobi v11.0.1求解,将本文设计的分支定切算法与Gurobi的计算结果进行对比,求解结果如下。
4.2.1 旅客满意度结果分析
利用设计的分支定切算法求解模型,首先求解以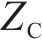
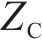
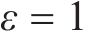
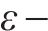
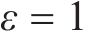
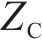
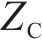
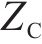
图2和图3分别为线路计划列车运行图及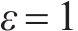
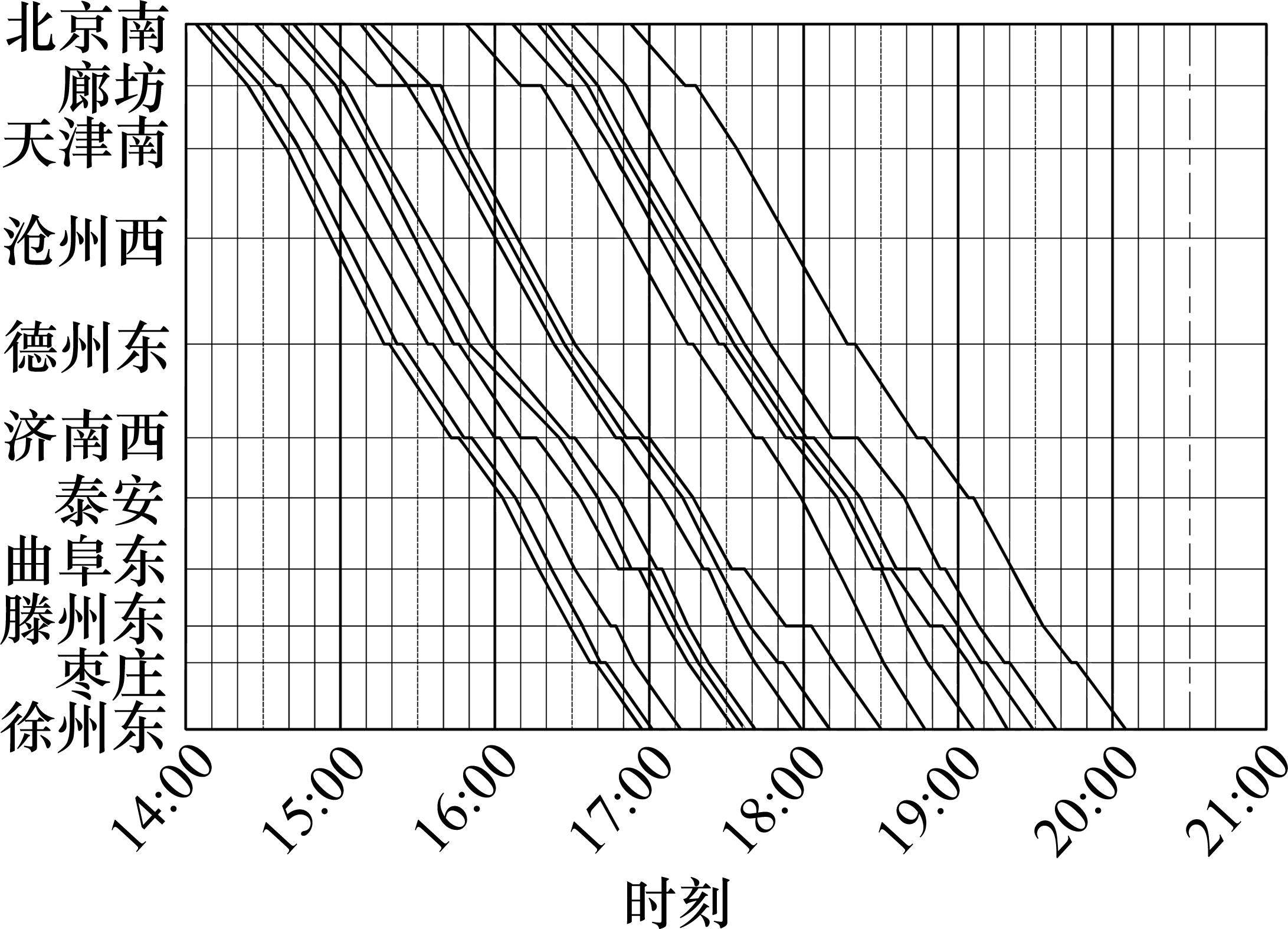
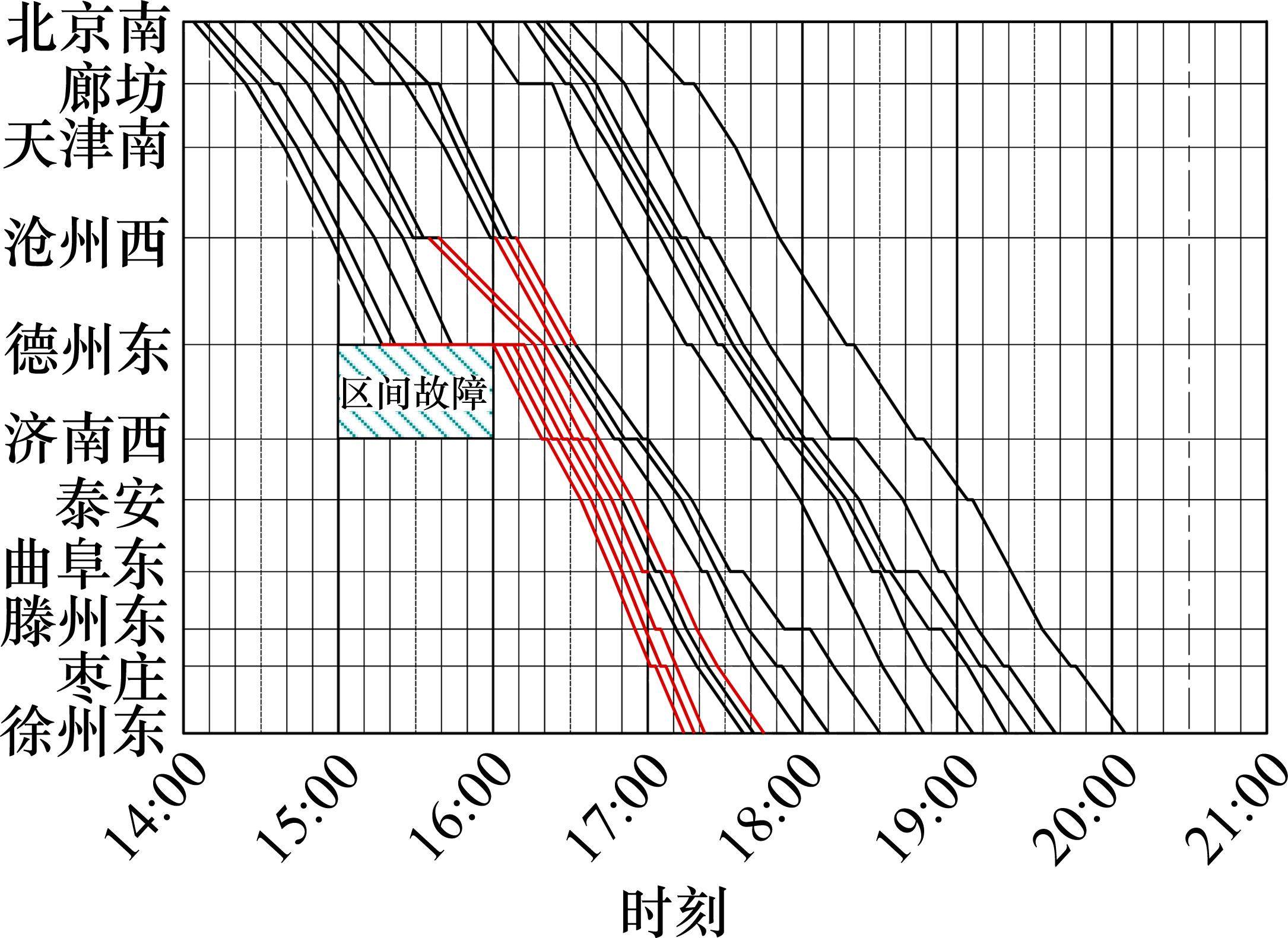
为验证所提算法的有效性,在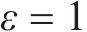
| 对比指标 | Gurobi求解 | 分支定切求解 |
|---|---|---|
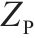 | 1.200 | 1.232↑ |
| 求解时间/s | 1.12 | 1.39↑ |
| 搜索节点数 | 449 | 1 375↑ |
| Gap/% | 12.5 | 3.41↓ |
| 约束数量 | 9 187 | 7 162↓ |
为进一步验证所提算法的高效性,在原有算例基础上将列车规模扩充至100列,在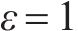
| Gurobi求解 | 分支定切求解 | ||||||
|---|---|---|---|---|---|---|---|
| Gap/% | 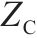 | 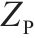 | 求解时间/s | Gap/% | 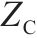 | 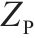 | 求解时间/s |
| 20 | 1 300 | 1.037 8 | 154 | 20 | 1 303 | 1.038 9 | 33 |
| 10 | 1 319 | 1.027 9 | 172 | 10 | 1 319 | 1.028 0 | 45 |
| 1 | — | — | — | 1 | 1 340 | 0.980 59 | 53 |
4.2.2 参数对比分析
为测试旅客满意度影响因素中各参数变化对结果的影响,在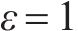
| 参数取值 | 满意度变 化幅度 | 线路总延误 时间/min |
|---|---|---|
(初始参数取值)
| 1.232 | 1 340 |
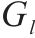  | 1.386↑ | 1 340 |
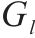  | 1.103↓ | 1 358↑ |
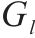  | 1.079↓ | 1 353↑ |
| 参数取值 | 满意度变化幅度 | 线路总延误 时间/min |
|---|---|---|
(初始参数取值) 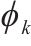 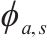 | 1.232 | 1 340 |
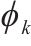 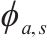 | 1.069↓ | 1 340 |
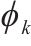 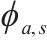 | 1.306↑ | 1 479↑ |
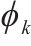 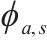 | 0.972↓ | 1 368↑ |
由表6可知,当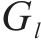
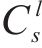
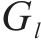
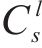
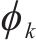
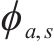
旅客满意度参数的取值间距代表了列车服务特征和服务类型的差异,由表6和表7的计算结果可知,旅客满意度参数取值间距越大,列车运行调整过程中旅客满意度变化越小。这一结果表明,一趟列车中服务特征(如座席)和服务类型(如直达、通勤)越单一,遭遇突发事件时旅客满意度的变化越大。例如当一趟列车为通勤列车时,绝大部分旅客为短途出行,当列车在途中遭遇突发事件而晚点时,即使运行调整后仍会导致大量旅客到达目的地时晚点,在这种情况下,绝大多数旅客的满意度都会降低。由这一结论分析可得,提升列车的服务特征和服务类型的差异化程度,可降低遭遇延误时列车整体旅客满意度的变化,提高以旅客为导向的列车运行调整决策的鲁棒性。
4.2.3 双目标分析
为探究旅客满意度目标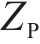
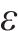
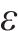
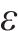
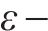
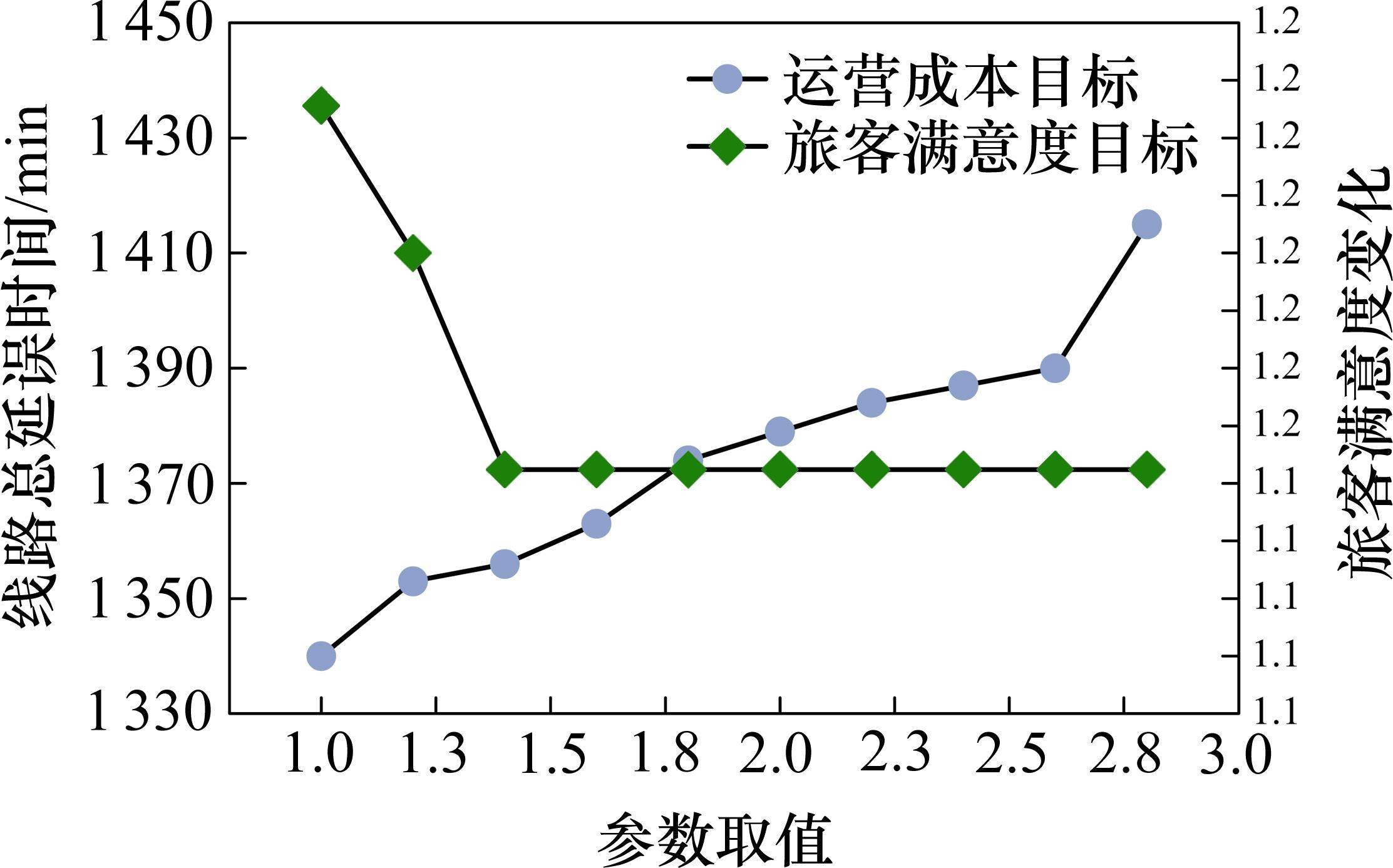
5 结论
1) 探讨了列车延误情况下旅客满意度的影响因素,并将其考虑在旅客满意度的优化目标中,提升了旅客满意度表述的准确性。
2) 提出一种混合整数线性规划模型,用于解决复杂情况下的列车运行调整问题,模型中考虑了列车运行特征、旅客出行特征和延误时间3种旅客满意度影响因素,并在实例中进行验证,研究了上述因素对优化结果的影响。
3) 充分挖掘了列车运行调整问题的特点,设计了一种分支定切算法用于模型的精确求解,在实际案例中证明了算法的有效性。
4) 将列车运行调整描述为旅客服务与运行调整的动态平衡,以旅客服务为导向,在求解过程中均衡了服务水平与运行调整决策,可为铁路部门提供更丰富的运行调整备选方案。
董傲冉,刘斌,田志强等.考虑旅客满意度的高速列车运行调整优化研究[J].铁道科学与工程学报,2025,22(03):1004-1015.
DONG Aoran,LIU Bin,TIAN Zhiqiang,et al.Optimization of high-speed train timetable rescheduling considering passenger satisfaction[J].Journal of Railway Science and Engineering,2025,22(03):1004-1015.