高速铁路因其安全可靠、节能舒适、便捷高效等优点已在世界范围内得到快速发展,并成为现代交通运输体系中的重要组成部分。随着运输需求的不断增加,如何保证在既有线路下实现高速列车高密度且安全可靠运行[1-2]已成为当前研究热点。多列车协同控制是目前提高线路利用率的主要方法之一,即基于列车之间的局部信息交换,为运行在同一轨道上的多列高速列车设计分布式控制策略,以实时调整每列车的速度与位移,在保证安全距离下,实现多列高速列车协同运行,缩小列车之间的追踪间隔,提高线路利用率[3-4]。然而,高速列车运行控制呈现时变不确定性且易受外部环境干扰影响,同时,高速列车因牵引制动输出设备的物理约束而存在控制输入饱和特性。因此,计及高速列车参数时变非线性、外部干扰及输入饱和特性,研究高速列车分布式协同控制策略,保证多列高速列车安全可靠运行,以提高运输密度满足当下运输需求。高速列车建模方法和控制策略设计是研究多列车协同控制的基础。近几十年来国内外相关学者为解决列车追踪运行控制问题,提出各种建模方法和控制策略。在列车建模方面,主要分为单质点模型[5]和多质点模型[6-7]。单质点模型将整列车视为一个质点建模,忽略列车长度,模型结构简单,易于控制策略的设计。多质点模型将列车的每节车厢视为一个质点,构成列车多质点模型,相较于单质点模型,建模精度更高,更符合列车实际运行情况,但控制策略设计较为复杂。由于高速线路里程长、线路较为平缓,因此,本文基于单质点模型研究多列车协同控制问题,并利用多智能框架,将每列车视为一个智能体,同一轨道线路上多列车模型可构成多智能体模型,即列车之间可传递速度、位移等状态信息。在列车控制方面,相关学者针对单列车追踪目标速度距离曲线,提出各种控制方法,如PID控制、智能控制、自适应控制、自抗扰控制、滑模控制、迭代学习控制等。GUO等[8]基于PID控制及其改进结构设计了列车的PID控制器,其结构简单且易于实现,但存在参数整定困难、易超调、控制切换频繁等问题。对于智能控制方法,如神经网络、模糊控制、专家系统等,GE等[9]利用神经网络的近似能力及GUO等[10]利用模糊逻辑系统逼近列车运行时变不确定阻力,设计了列车速度控制器。YUAN等[11-12]基于自适应辨识的自适应控制方法,提出列车的自适应控制策略。XUE等[13-14]基于自抗扰控制的思想,解决了外部干扰下列车的追踪运行控制问题。滑模控制因具有较好的鲁棒性及对时变参数不敏感性而广泛应用于各种受扰系统的控制研究当中,因此,为进一步提高列车控制精度,基于滑模控制策略,张友鹏等[15]提出super-twisting滑模控制、李中奇等[16]提出终端滑模控制、KONG等[17-18]提出非奇异终端滑模控制方案,实现了外部干扰及时变参数下列车的抗扰控制。由于列车运行线路较为固定,呈现出周期性运行特性,利用迭代学习的思想,HUANG等[19-21]研究了复杂运行环境下列车的迭代学习控制,当迭代次数达到一定程度时,迭代学习控制表现出了良好的追踪精度。同时,针对各种控制方法的优缺点,提出了各种复合控制策略,如WANG等[22]提出PID滑模控制、李中奇等[23]提出自适应滑模控制、LI等[24]提出滑模自抗扰控制等,这些方法对列车正常运行均有良好的控制效果。在控制策略设计中,系统收敛速度的快慢是衡量控制方案的有效标准之一,以上控制方法中多以渐近收敛方式实现系统的稳定控制,即当时间趋于无穷时,系统误差收敛至0或一定区域内,相较于渐近收敛,有限时间收敛可在一定时间内实现系统的稳定,如非奇异终端滑模控制。因此,本文利用有限时间控制思想,为多列车设计分布式控制器。相较于单列车追踪控制,多列车协同控制可进一步缩短列车之间的追踪间隔,实现列车编队协同运行。针对多列车协同运行控制,李钰[25]采用事件触发控制策略研究了在DoS攻击下高速列车的一致性控制;BAI等[26]基于普通一致性实现多列车分布式巡航控制;魏文军等[27]利用一致性及齐次理论实现了多列车分布式有限时间巡航控制。以上研究将基本阻力设为已知,未考虑外部干扰的影响。BAI等[28]提出了分布式故障检测方法,研究高速列车在多源干扰情况下的协同控制,但在面临复杂环境干扰的时候还存在局限性。GUO等[29]设计了非奇异终端滑模控制器实现多列车协同运行,但系统仍以渐进收敛的方式收敛。LI等[30]研究了多列高速列车的分布式巡航控制,基于一致性理论设计了多列车分布式控制器;HUANG等[31]基于多智能体方法,提出高速列车分布式迭代学习控制方案;YANG等[32]基于人工势场及自适应控制提出多列车自适应控制方案;REZAE等[33]在基于环境干扰未知的情况下设计了一种分布式输出反馈控制方案。以上研究考虑了列车运行的时变阻力及外部干扰,但未考虑列车输入饱和的影响。在列车运行控制中,由于列车牵引制动设备的输出约束,将导致列车控制输入存在饱和上限。本文采用动态辅助系统[34]实现对列车抗饱和控制的研究,以补偿输入饱和对系统的影响。基于以上研究分析,本文考虑列车运行时存在时变非线性动态、复杂环境外部干扰及输入饱和特性,利用非奇异终端滑模控制、有限时间干扰观测器及动态辅助系统,设计多列车分布式协同控制器,并针对传统非奇异终端滑模控制易出现抖振现象,利用反正切函数设计一种抖振较少的滑模面,削弱了传统滑模控制的抖振现象,实现复杂环境下多列高速列车的有限时间分布式协同控制。
1 系统模型及预备知识
1.1 系统模型
高速列车在轨道线路上运行时受到牵引制动设备提供的牵引/制动力,还有根据产生原因的不同分为时变的非线性阻力(机械阻力、气动阻力)、轨道线路条件引起的附加阻力(坡道、曲线、隧道)及外部环境干扰(如阵风)。高速列车追踪运行示意图如图1所示,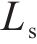
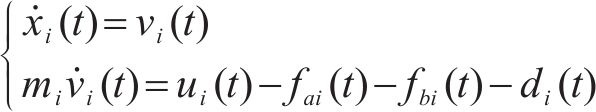
其中,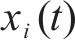
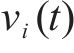
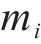
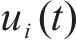
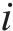
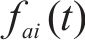
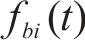
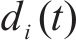

由于列车运行时所受到的基本阻力呈现时变非线性,其与列车结构参数及运行速度相关,基本阻力可用Davis方程描述为:
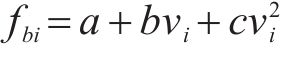
其中,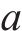
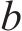
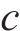
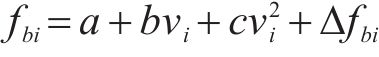
其中,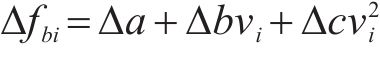
高速铁路线路相较于普速铁路,坡度和曲率较小,但线路中仍然存在一定的坡度、曲线及隧道,当列车运行在不同位置时会出现相应的附加阻力,如坡道附加阻力、曲线附加阻力、隧道附加阻力,列车所受到的附加阻力描述为:
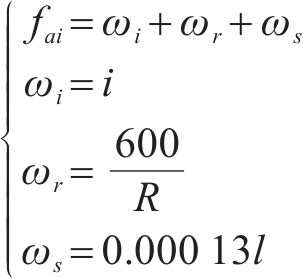
其中,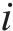
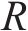

列车运行时通过牵引制动设备提供的牵引/制动力实时控制列车追踪目标速度距离曲线运行,但由于设备的物理输出约束,导致输出存在饱和约束,列车饱和约束特性描述为:
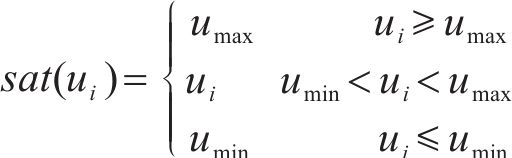
为便于后文分析设计,本文将基本阻力时变部分、附加阻力及外部干扰统一考虑为列车运行时所受到的集总干扰,则在集总干扰及输入饱和下列车动力学模型描述为:
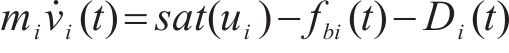
假设1:列车系统的集总干扰有界且1阶可微,即:
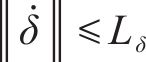
其中,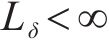
备注1:对于集总干扰,由于列车的速度、基本阻力时变参数、外部干扰、附加阻力均有界,则集总干扰亦有界,而且系统所受到的集总干扰不会无限快地变化,因此,假设1是合理的。
1.2 图论知识
多列高速列车运行在同一轨道线路时,基于车车通信技术,列车之间可传递速度、位移等状态信息。因此,将多列车系统中的每列车视为一个智能体,基于智能体框架,构建高速列车分布式多智能体模型[35]。列车之间的通信关系可用图论描述。图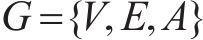
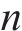
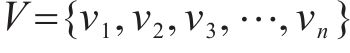
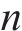
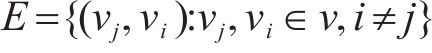
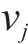
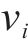
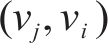
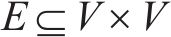
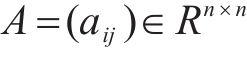

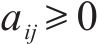
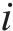
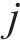
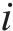
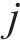
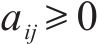
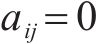

考虑到列车通信资源受限问题,采用前导-跟随单向通信模式,即第1列车追踪速度距离曲线,后续列车可以收到前一列车的状态信息,则列车之间的通信拓扑描述为:

1.3 相关数学引理
引理1[36]:对于如下系统
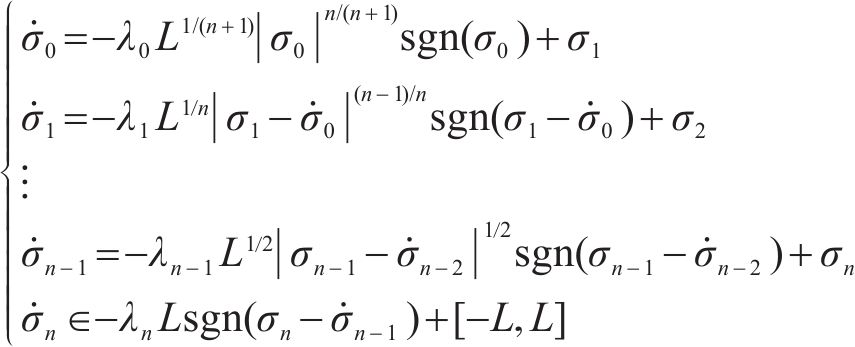
其中,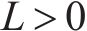
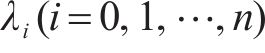
引理2[37]:对于任意变量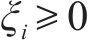
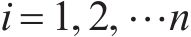
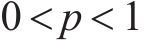
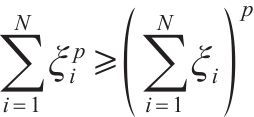
引理3[38]:对于非线性系统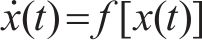
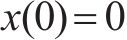
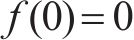
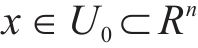
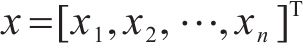
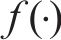
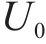
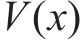
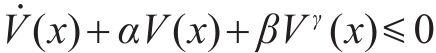
其中,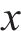
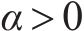
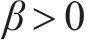
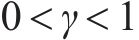
引理4[38]:对于非线性系统,假设存在一个连续的正定函数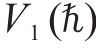
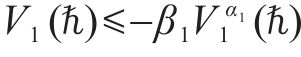
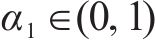
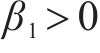
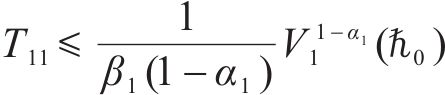
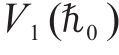
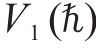
2 控制器设计及稳定性分析
针对列车协同运行控制问题,基于有限时间干扰观测器、非奇异终端滑模及动态辅助系统设计列车控制器,具体控制方案如图2所示。
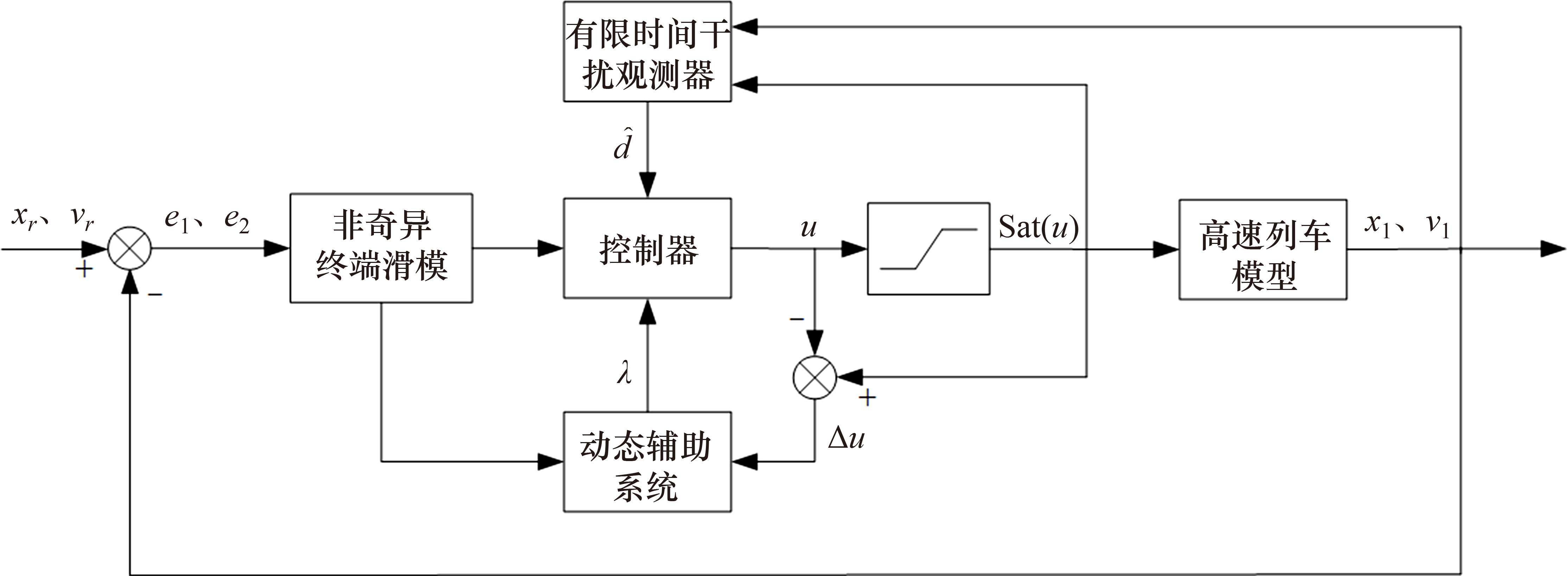
2.1 控制器设计
多列车协同运行时,第1列车追踪目标速度曲线,后续列车接收来自前一列车的状态信息,以前导跟随模式追踪运行。为便于书写,后续将省略时变参数的变量t。对于第1列车,列车位移速度追踪误差描述为:
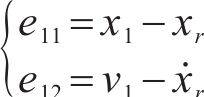
其中,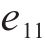
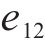
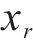
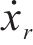
后续跟随列车与其前一列车之间的位移、速度误差描述为:
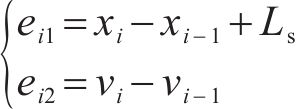
其中,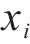
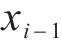
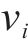
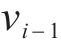
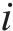
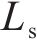
根据式(6),为解决集总干扰对列车运行控制的影响,设计有限时间干扰观测器:
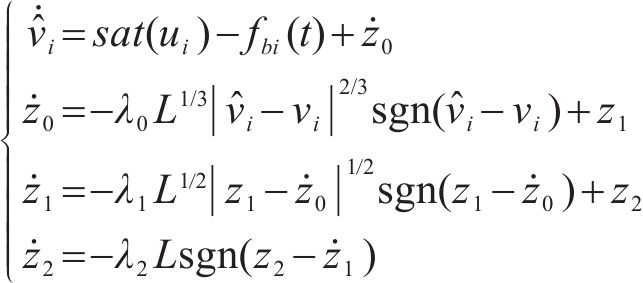
其中,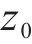
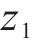
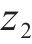
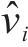
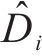
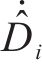
对于误差系统(14),设计新型滑模面如下:
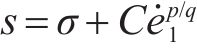
其中,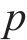
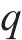
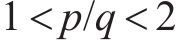
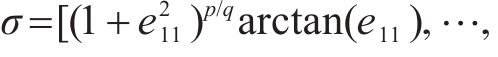
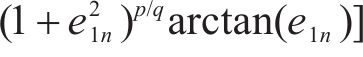
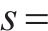
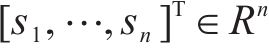
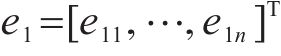
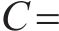
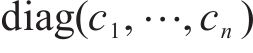
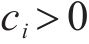
对式(16)滑模面求导,得:
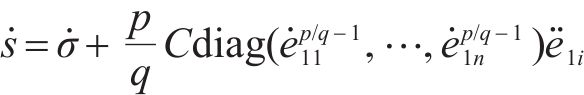
针对输入饱和特性,引入动态辅助系统解决输入饱和对列车控制系统的影响,动态辅助系统设计为:
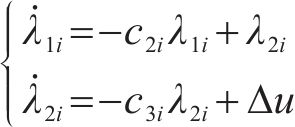
可得含有输入饱和的误差系统为:
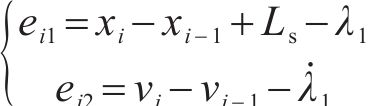
将式(19)代入式(17)中,可推出含有输入饱和系统的等效控制律为:
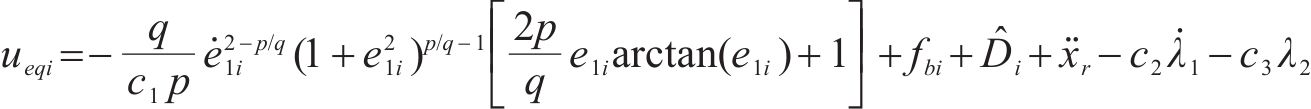
为了实现较快的趋近运动,设计趋近控制律为:
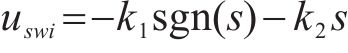
其中,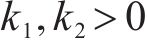
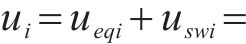
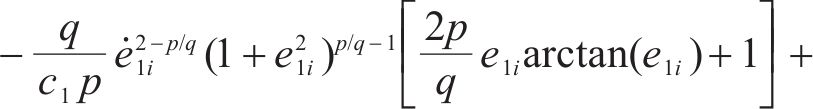
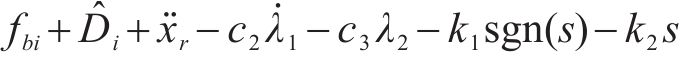
2.2 稳定性证明
针对所设计的干扰观测器,定义观测误差为: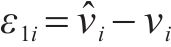
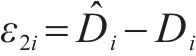
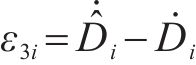
可得误差状态方程:
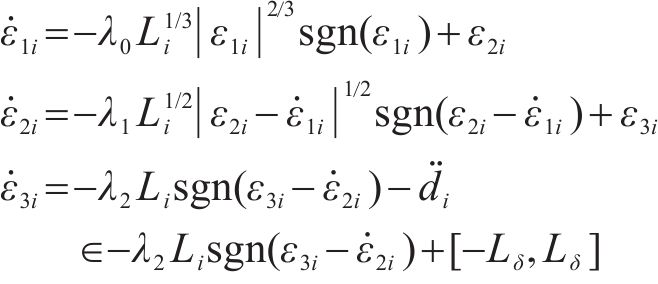
由引理1可知,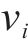
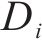
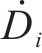
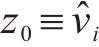
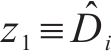
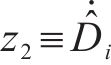
为证明所设计控制器的稳定性,构造Lyapunov函数:
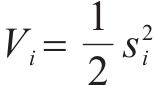
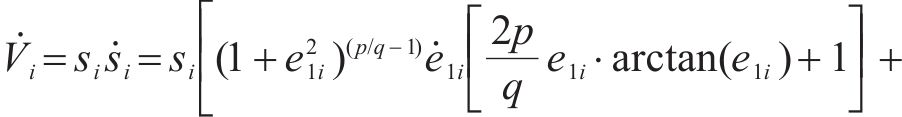
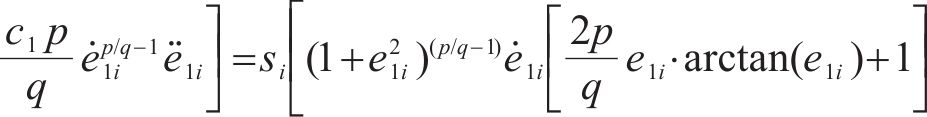
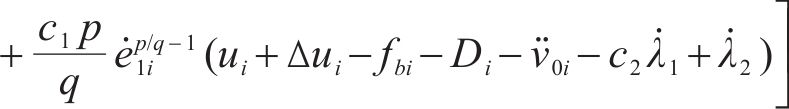
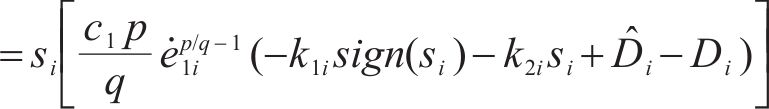
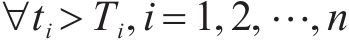
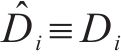
令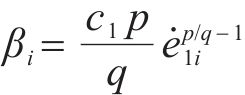
则有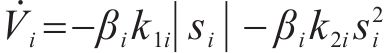
对于整个列车系统:
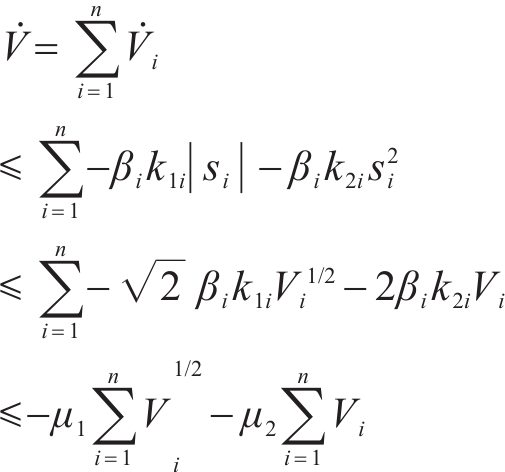
由引理2可得:
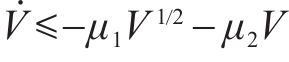
其中,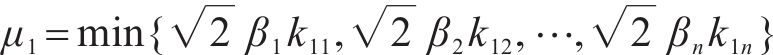
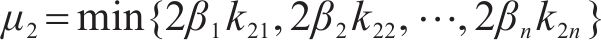
根据引理3可知,该系统可在有限时间内收敛,即系统到达滑模面。
当系统到达滑模面后,即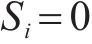
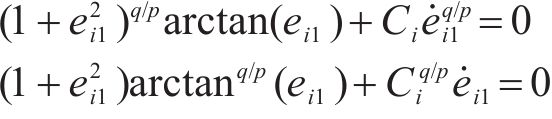
令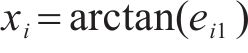
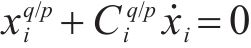
令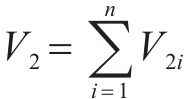
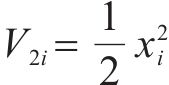
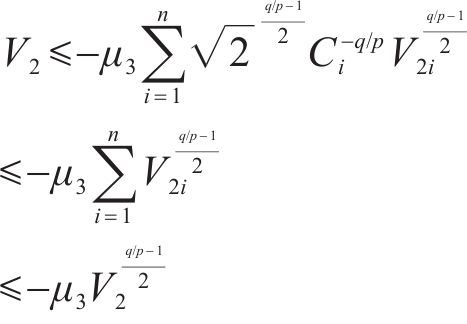
其中,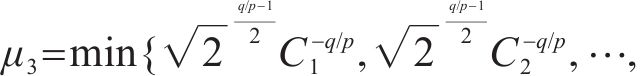
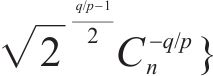
根据引理4可知,该系统到达滑模面后,可沿滑模面在有限时间内收敛至0。
3 仿真实验与结果分析
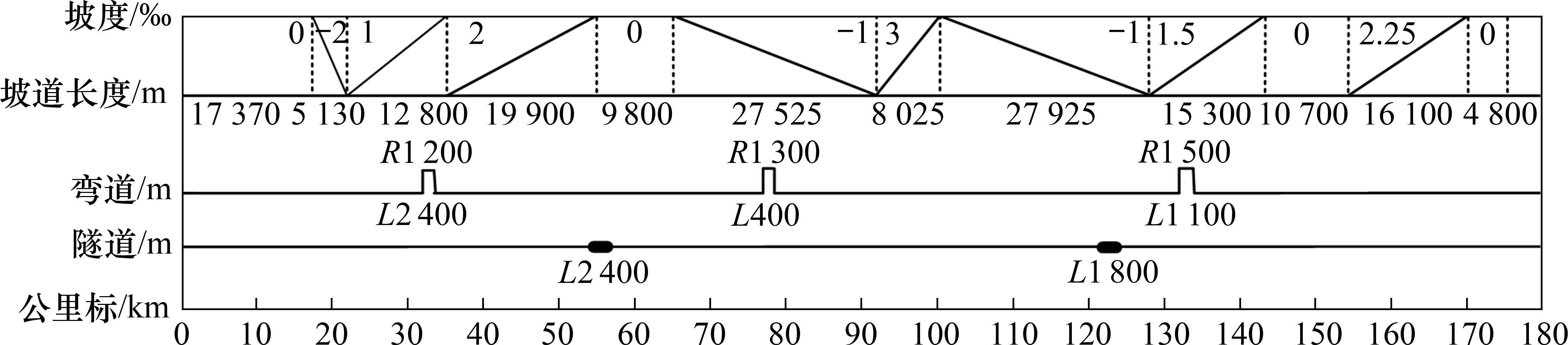
为验证所设计控制器的有效性,以4列CRH380B型高速列车为例进行仿真验证,列车参数具体如表1所示。考虑列车运行的实际线路情况,具体线路参数如图3所示。为研究列车运行时所受外部干扰的影响,对列车施加干扰信号进行模拟。在列车运行时,考虑第1列车追踪期望的速度距离目标曲线,其余3列车均与前车保持安全运行间隔,实现多列车协同追踪运行。同时,以自适应终端滑模[29](Adaptive Terminal Sliding Mode, ATSM)、有限时间干扰观测器终端滑模(Terminal Sliding Mode Finite-Time Disturbance Observer, TSM-FTDO)、有限时间干扰观测器线性滑模(Linear Sliding Mode Finite-Time Disturbance Observer, LSM-FTDO)3种控制方法为对比,验证控制器(Arctan Terminal Sliding Mode Finite-Time Disturbance Observer, ARCTSM-FTDO)的优越性。
| 列车参数 | 参数值 |
|---|---|
| m1, m2, m3, m4/kg | 3.8×105 |
| a/N | 0.66×mi |
| b/(N∙s∙m-1) | 0.002 45×mi |
| c/(N∙s2∙m-2) | 0.000 132×mi |
| L/m | 5 000 |
3.1 第1列车控制器仿真验证
4种方法控制器参数设置:ARCTSM-FTDO参数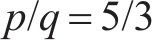
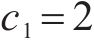
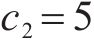
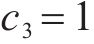
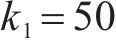
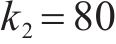
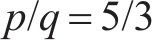
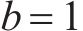
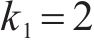
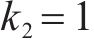
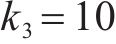
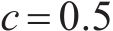
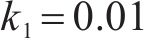
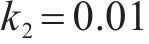
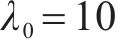
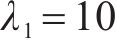
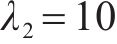
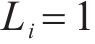
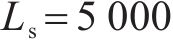
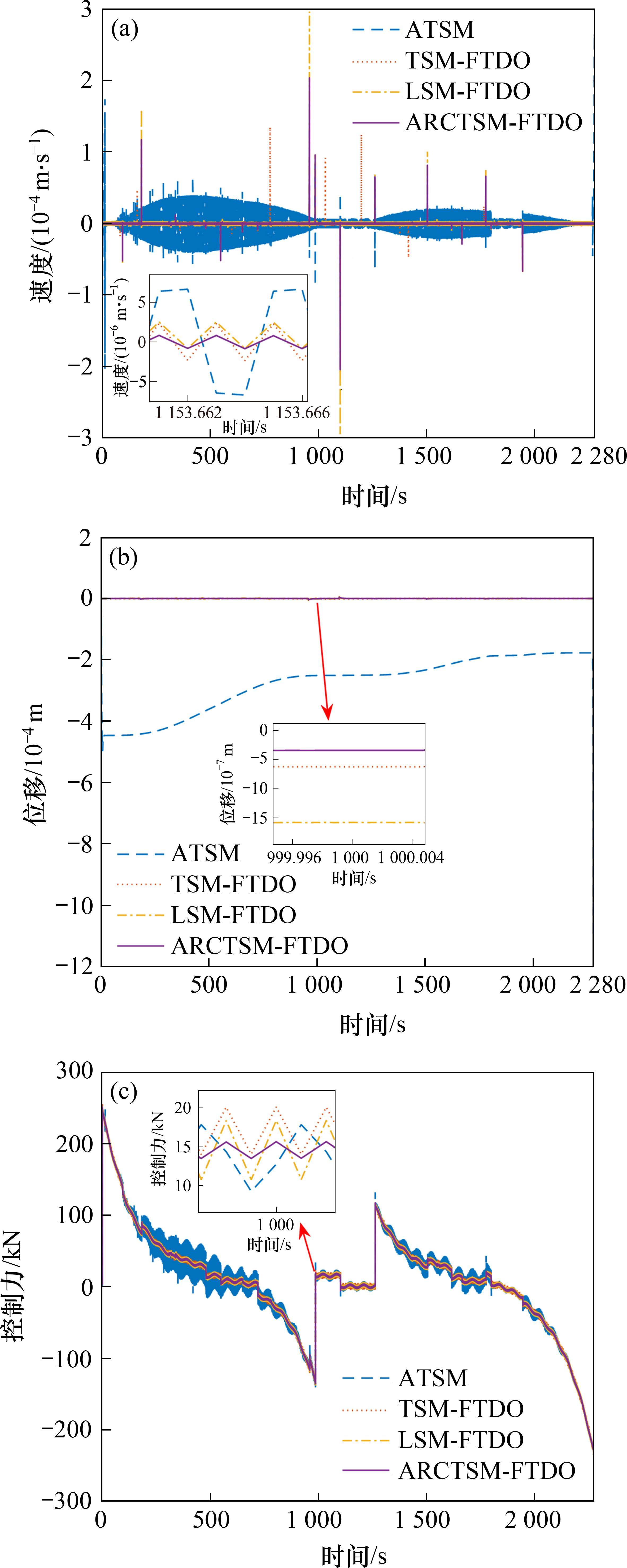
由图4(a)、图4(b)可知,4种方法均可实现第1列车对目标速度距离曲线的追踪,其中,速度误差均在[-3×10-4,3×10-4] m/s之内,而位移误差在[-5×10-4,2×10-4]之内。但由图4(a)速度追踪误差可以看出,相较于其他3种控制方法,ARCTSM-FTDO的速度误差波动变化更加平滑,但在速度突变点处,相较于TSM-FTDO、ATSM,其速度误差值较大,但整体速度误差更小。在图4(b)位移误差图中,ATSM控制下列车位移误差范围波动最大,其余3种方法波动范围较小,且从局部放大图中可以看出本文方法控制下位移误差最小,且位移误差波动变化平滑。
图4(c)为列车控制力输入图,ARCTSM-FTDO控制下,列车控制输入变化波动最小,控制输入更为平滑,更符合实际应用需求。综合以上分析可知,尽管所设计的ARCTSM-FTDO控制器下列车速度误差波动变化范围在突变点处仅次于LSM-FTDO,但位移追踪误差和控制力输入更为平滑,波动更小。
3.2 多列高速列车协同控制
在3.1节中,以第1列车为例验证了ARCTSM-FTDO的有效性和优越性。本节以4列车为例,仿真多列车协同追踪运行情况。同时考虑CRH380B型列车的牵引制动特性,即控制输入饱和情况。4列车均为同类车型,控制器中仿真参数与3.1节中一致,并在580 s和1 700 s处给列车2加入持续2 s的矩形波信号模拟外部干扰,在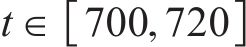
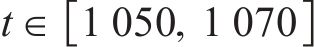
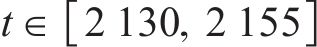
 | xi(t0)/m | vi(t0)/(m∙s-1) |
|---|---|---|
| 1 | 15 000 | 0 |
| 2 | 10 000 | 0 |
| 3 | 5 000 | 0 |
| 4 | 5 000 | 0 |
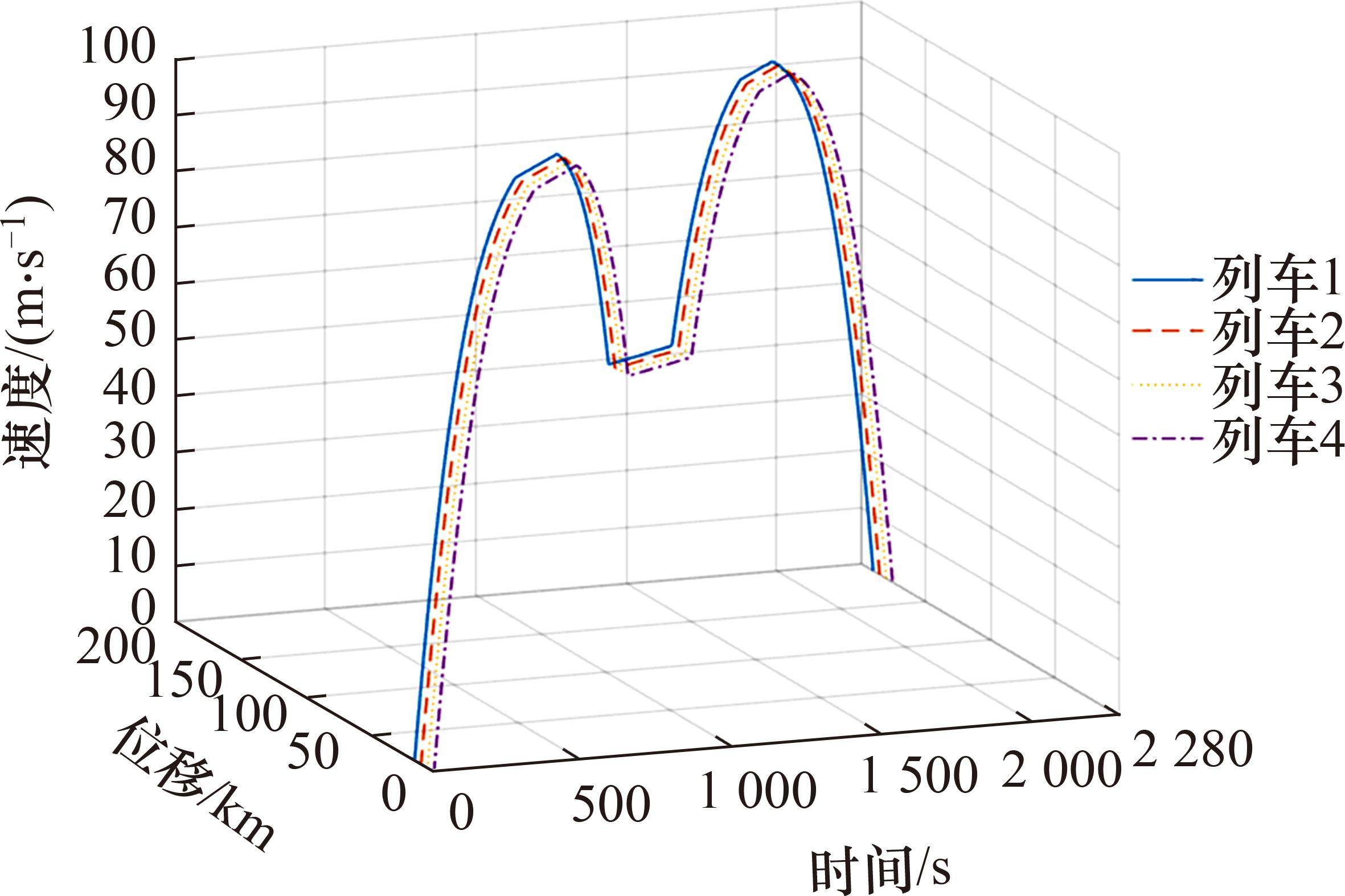
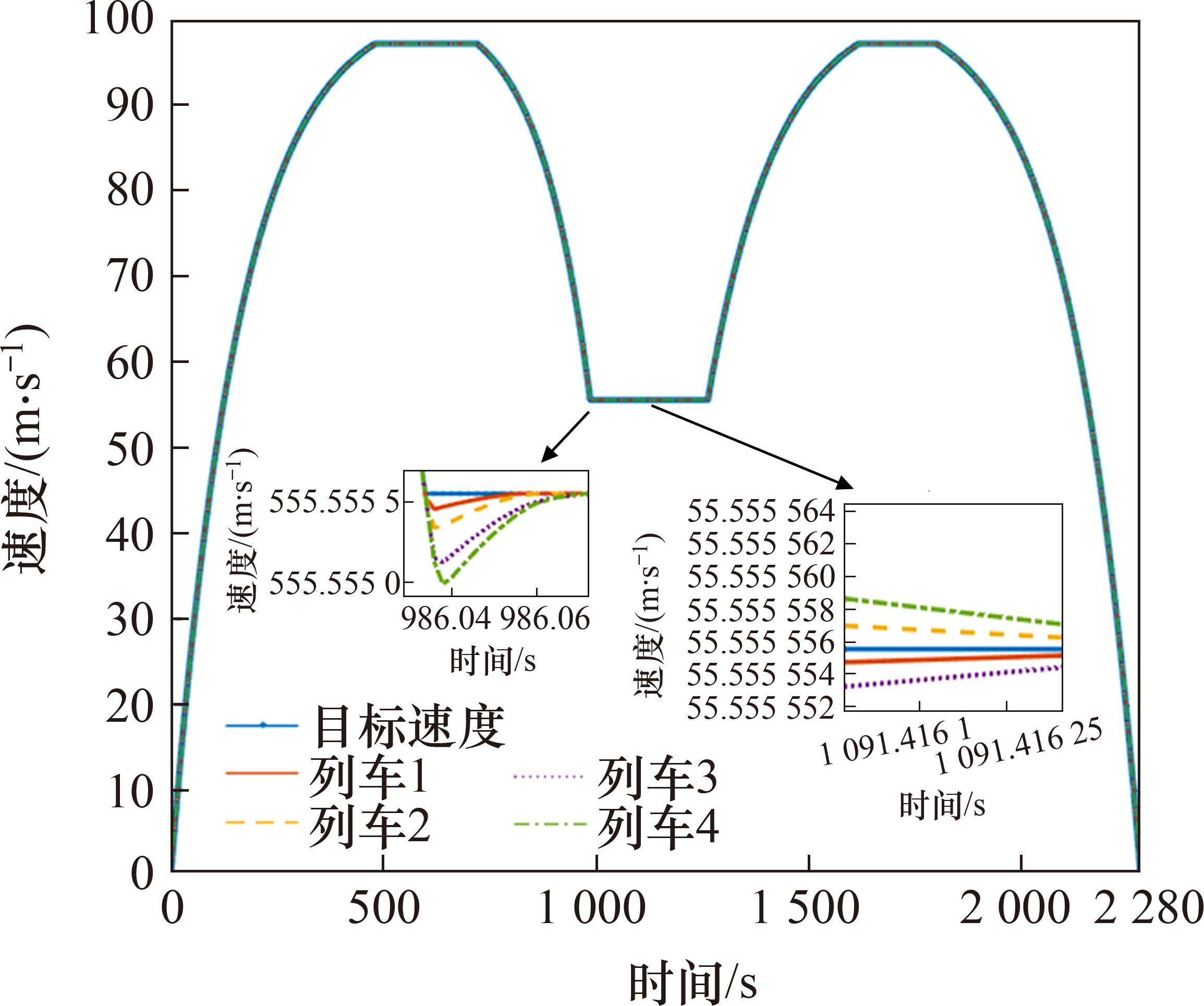
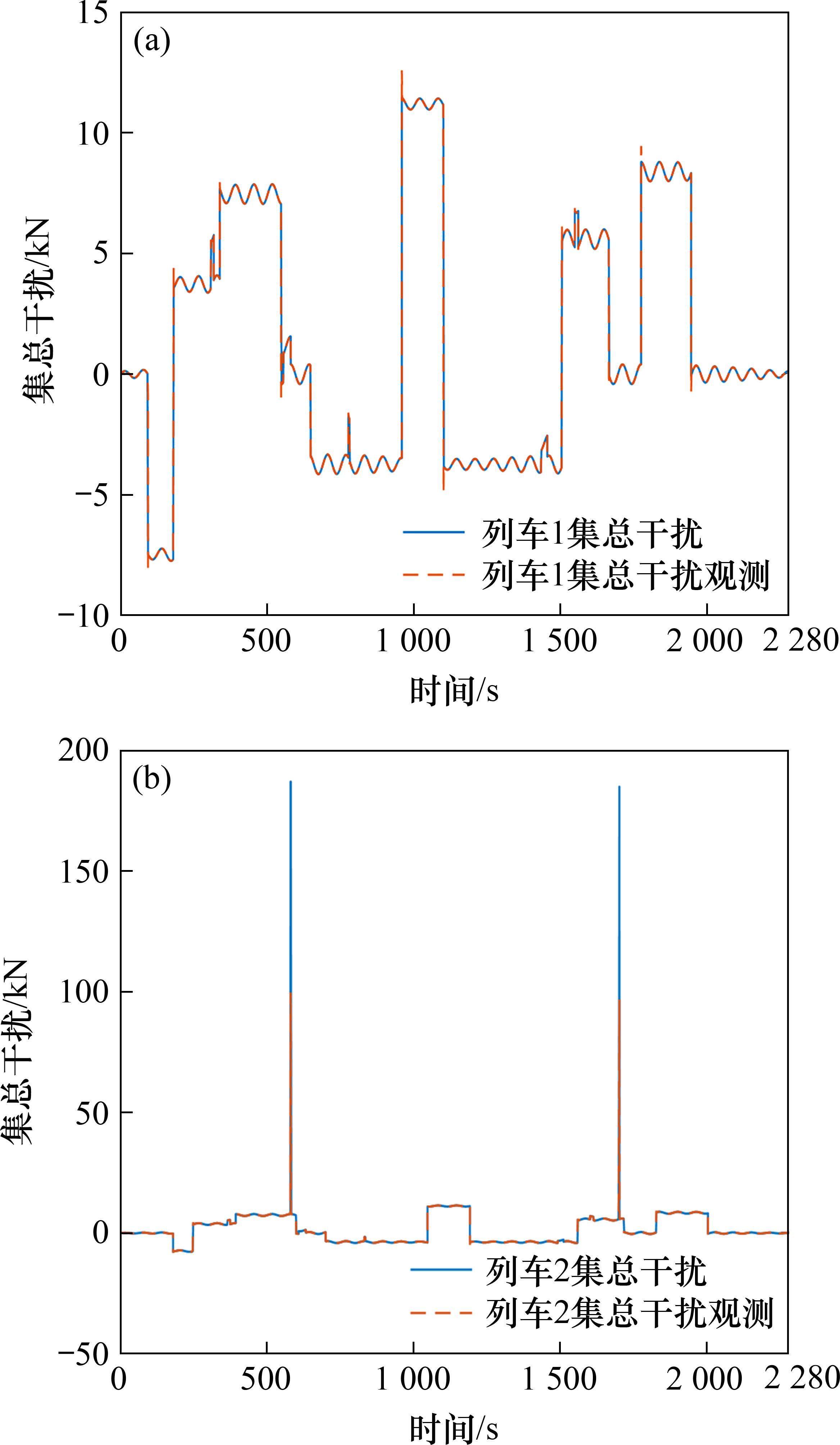
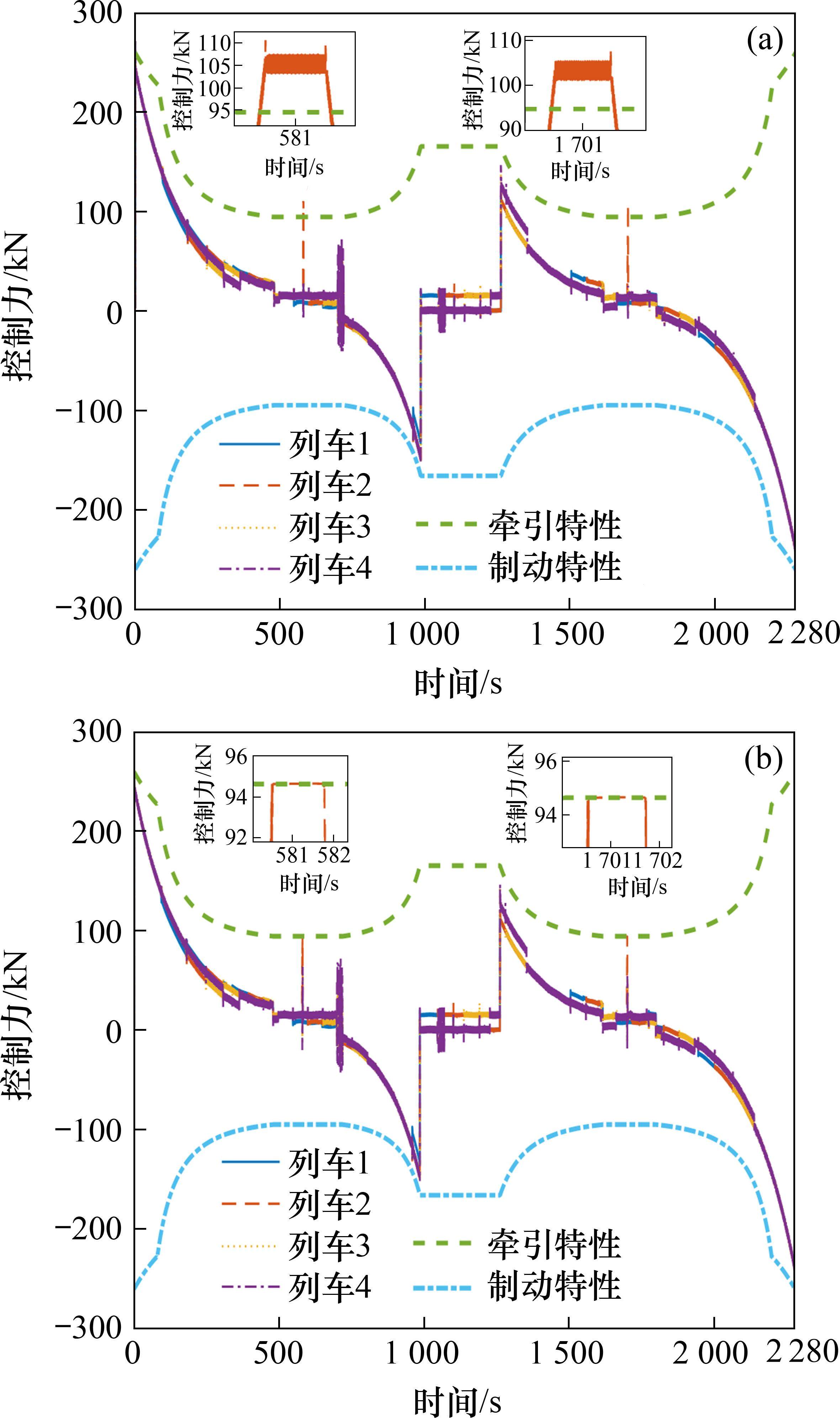
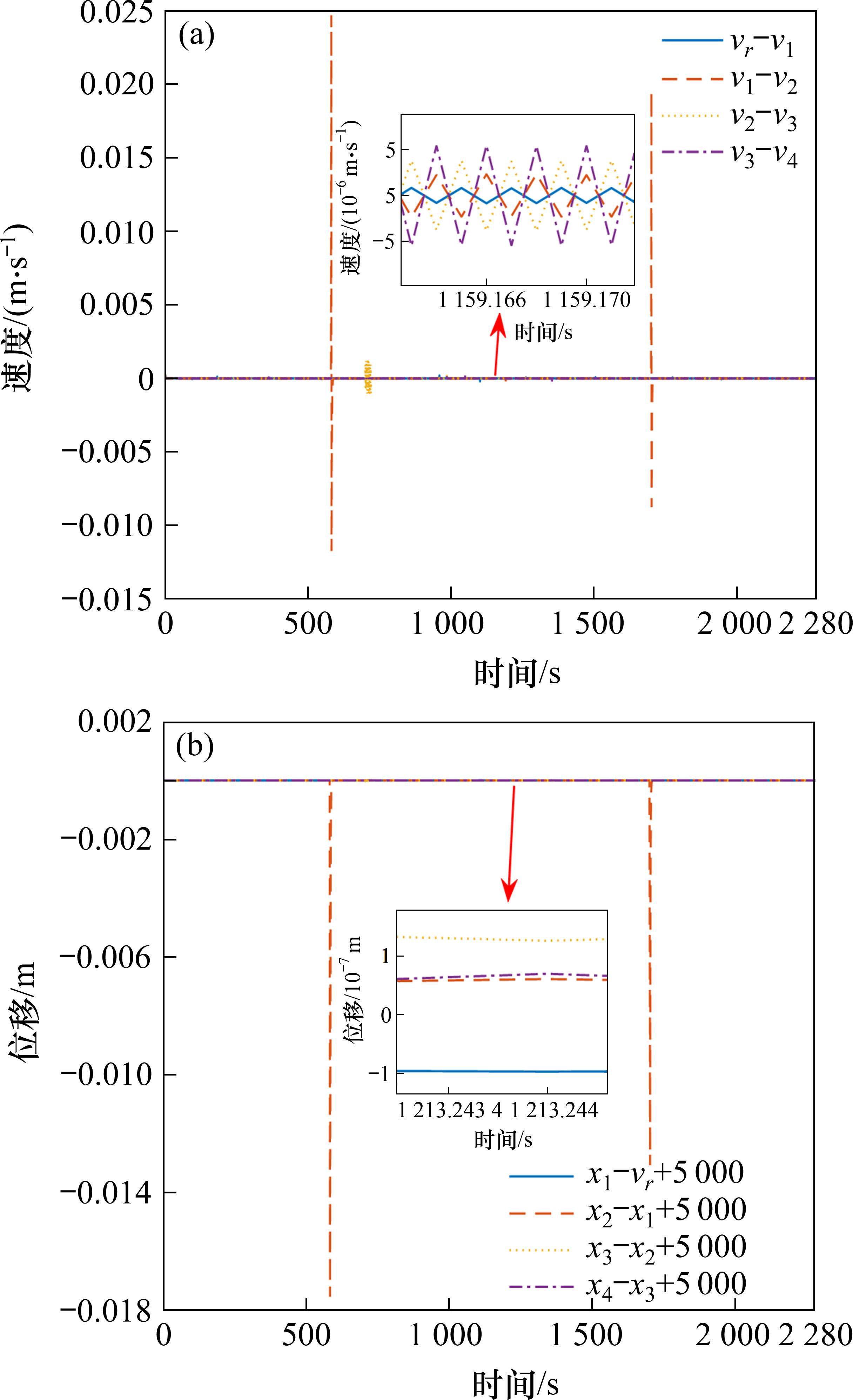
图5为4列车追踪运行的实时速度位移曲线,反映了4列车在追踪运行中的位移速度变化;图6为4列车追踪运行的速度追踪图。由图5、图6可知,在ARCTSM-FTDO控制方法下可实现4列高速列车保持设定的安全追踪间隔协同运行。
图7为列车的集总干扰观测图。由图7可看出,列车在受到外界强烈干扰的情况下跟踪观测效果略有不佳,但在列车整体的运行过程中对集总干扰都有很好的跟踪观测效果,因此可以实现对集总干扰的良好补偿。
图8(a)为不考虑输入饱和下列车控制输入图,而图8(b)为计及输入饱和下列车控制输入图。由图8(a)可知,不考虑输入饱和时,当列车2分别在不同时段遇到强烈外部干扰情况下,控制输入均超出牵引制动约束范围,而在实际情况中,列车的牵引制动设备输出物理受限,这将导致列车的牵引制动设备受损,为此,考虑输入饱和约束,并设计动态辅助系统以减小输入饱和的影响。
计及输入饱和下,4列车控制力输入图如图8(b)所示。由图8(b)可知,当列车2受到强烈外部干扰时,控制输入均在牵引制动特性约束范围之内,所设计动态辅助系统有效解决了输入饱和对列车追踪运行的影响。
图9为饱和约束下的4列车追踪运行状态,分别为4列车各自与前车的相对位移误差与速度误差。从图9(a)、图9(b)可知,计及输入饱和下,列车速度误差变化波动范围在[-0.01, 0.02] m/s之内,位移误差变化波动范围在[-0.014, 0.001] m之内。由于列车2、3、4在不同时间段加入了外部干扰,因此,导致列车2、3、4在不同时间段速度误差和位移误差会出现较大波动,但均在列车追踪运行可接受的追踪精度范围之内。基于以上分析可知,计及输入饱和下利用所设计的ARCTSM-FTDO控制器及动态辅助系统可实现多列车的协同追踪运行。
4 结论
1) 将运行中的列车视为多智能体构建了多列车多智能体系统模型,并利用图论知识描述列车间通信拓扑关系,列车间以前导-跟随模式进行通信,只有前车向后车传递速度,位移等状态信息,从而节省了通信资源。
2) 基于多智能体列车系统模型,利用反正切函数设计了一种新的终端滑模面,并利用有限时间干扰观测器观测列车的集总干扰,通过与ATSM、TSM-FTDO、LSM-FTDO这3种控制方法对比,ARCTSM-FTDO控制可使控制误差在有限时间内收敛,控制精度更高,且抖振较小,波动更为平缓。
3) 用动态辅助系统解决输入饱和的影响,当列车在遇到外部强烈干扰时,控制输入在动态辅助系统作用下对控制器的输出进行约束,使得控制力均可被约束到牵引制动特性约束范围之内且列车速度、位移基本不受影响,从而防止列车牵引电机过载,保护牵引电机正常工作和列车运行安全。
综上所述,ARCTSM-FTDO控制方法可更安全、稳定地实现多列车协同追踪运行。
张友鹏,王小天,杨军霞等.基于有限时间干扰观测器的高速列车非奇异终端滑模协同控制[J].铁道科学与工程学报,2025,22(03):967-978.
ZHANG Youpeng,WANG Xiaotian,YANG Junxia,et al.Non-singular terminals sliding mode cooperative control of high-speed train based on finite-time disturbance observer[J].Journal of Railway Science and Engineering,2025,22(03):967-978.

