高速动车组作为现代化的交通工具,已经成为我国交通运输的主要载体之一,与高速动车组相关的各项技术也在蓬勃发展,智能驾驶就是其中的关键一项。由于高速动车组系统具有多变量、非线性等特性,且运行过程中会受到外界环境干扰,控制难度较高,因此设计使高速动车组既能安全平稳运行,又能准确实时跟踪目标曲线的自动驾驶系统仍然是目前面临的重大困难和挑战。针对此类难题,需要从建模方法和控制策略2个方面展开研究。目前有关高速动车组的建模方式主要有单质点建模和多质点建模2种。传统的单质点模型是将列车看作一个质点,受力简单,模型易分析,但无法考虑列车的车间耦合力,只适用于列车的控制算法研究。目前被许多学者普遍接受的列车模型是由KHMELNITSKY[1]所创立的单质点模型,后续学者在该单质点模型的基础上进行改进并进行研究。朱晓敏等[2]从城轨列车运行需要实时仿真计算的角度出发,对传统单质点模型进行研究,建立了单质点改进模型,有效地提高了列车模型的计算精度和计算效率。连文博等[3]针对列车复杂运行环境,建立了含有扰动项的列车单质点模型,但没有考虑运行时所受附加阻力对列车的影响,因此不能完全反映列车运行情况。单质点建模方法[4-7]是对高速列车整体的基本描述,可以直观了解其运行状态。但上述研究均忽略了高速列车车钩作用力以及各节车辆的牵引力和制动力分配情况,因此不能很好地反映高速列车的运行状态,尤其在列车工况转换和路况变化时,车钩力对列车的作用更加凸显和重要,所以有必要考虑车钩对列车运行的影响。LI等[8]利用列车车辆间位移偏差函数作为车钩力,建立了列车多质点模型,但在设计控制器时默认空气阻力只作用于车头,因此不够合理。王龙生等[9]通过引入列车运行状态整数变量,建立了列车混合整数列车模型,对列车基本阻力进行分段线性化,虽然简化了计算过程,但是降低了模型的精确度。因此,考虑高速动车组车钩特点和车辆之间的相互作用,建立一种多质点动力学模型,能够更准确地反映动车组各节车辆的受力情况和运行状态,才能更好地分析和优化高速动车组的行驶稳定性、安全性和舒适性等方面的问题。同时,为实现列车的速度跟踪控制,许多学者提出了相应的解决方法。目前控制领域主要的控制方法有PID控制、模糊控制、滑模控制、预测控制等几大类[10-15]。许多学者根据上述方法对列车进行优化控制。PU等[16]将PID控制用于列车控制器设计,提高了列车的运行性能。SHEN等[17]将模糊控制用于列车优化控制中,成功实现了对列车停车和巡航的有效控制。LIN等[18]利用滑模控制解决了列车速度跟踪控制和位置区间控制问题,极大提升了列车的跟踪效率和避碰性能。ZHAO等[19]将预测控制用于解决高速列车的停车控制问题,以实现列车的精准自动停车。近年来,许多学者开始将上述控制方法和其他方法进行结合创新,用于对列车控制的研究。王玺等[20]提出了模型预测-BFGS控制方法,该方法旨在解决预测控制算法中的细节和内部工作原理,对算法进行定制或扩展,达到对控制器性能的进一步优化,然而未考虑列车真实路况以及受到的干扰对列车的影响。候涛等[21]将模糊控制和预测控制结合,设计出模糊预测控制器,解决了列车经过特殊路段时速度变化过大的问题,但是列车在运行时所受的空气阻力全部集中在车头上,因此不能真实反映列车运行状态。赵凯辉等[22]将高速列车与多智能体系统相结合,并利用干扰观测器对未知干扰进行观测补偿,设计出分布式速度协同跟踪控制器,提高了列车的跟踪精度,因引入滑模切换项,无法消除滑模抖振弊端。可以看出,目前高速列车控制方法虽然有效地提高了列车的控制性能,但是仍然存在一定的不足。综上所述,针对目前高速动车组应对复杂线路和外界扰动效果不佳以及传统单质点无法准确描述高速动车组运行过程等问题,本文在考虑车钩力的基础上,建立高速动车组多质点模型,并提出一种基于终端滑模观测器的固定时间控制器。该控制器可以实现系统的固定时间稳定,同时避免了滑模抖振问题,因此对于给定目标速度具有很好的跟踪效果。在处理复杂线路变化、未知扰动以及控制器故障时具有很强的鲁棒性,同时控制器输出更加平滑,车钩力震荡更小,能有效提升控制器和车钩的使用寿命,有利于提高高速动车组运行的安全性和平稳性。
1 高速动车组数学模型
传统单质点模型无法反映动车组车辆间内部作用力,因此本文将高速动车组每节车辆各自看做一个质点,并将车辆间的耦合关系简化为“弹簧-阻尼器”系统,建立了反映高速动车组运行状态的多质点模型。
1.1 牵引力与制动力
我国CRH3型号高速动车组结构如图1所示,其中第2、4、5、7为无动力拖车,只输出制动力,第1、3、6、8车辆为动力车辆,可输出牵引力和制动力。可以看到,动车组动力匹配方式呈镜像对称分布。

在高速动车组启动时,动力车辆需要提供最大的牵引力以克服启动阻力,加速列车的运行,而随着车速的增加,动力车辆所能提供的牵引力会受到一定限制并逐渐减小,以保持列车的稳定性和安全性。
1.2 列车阻力
1.2.1 基本阻力
高速动车组在运行过程中会受到来自于车轮与钢轨滚动产生的基本阻力,其可以表示为
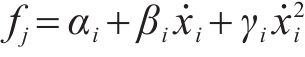
式中: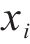
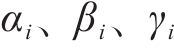
1.2.2 附加阻力
当高速动车组在线路运行时,经过坡道、隧道时会产生额外的附加阻力,其主要包括以下3种。
1) 坡道附加阻力。高速动车组在经过上下坡道时,由于车辆本身的重力,会产生坡道附加阻力,其公式如下:
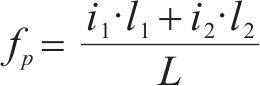
式中: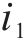
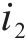
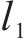
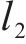
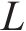
2) 曲线附加阻力。高速动车组在经过弯道时,轮轨弯曲,其产生的阻力为曲线附加阻力,可表示为
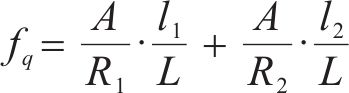
式中: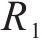
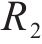
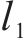
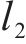
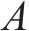
3) 隧道附加阻力。高速动车组在穿越隧道时,空气紊流在其表面会产生阻力,称为隧道附加空气阻力,其可表示为
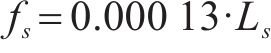
式中: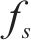
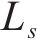
所以高速动车组在线路运行时受到的总阻力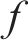
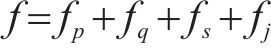
1.3 列车耦合力
在对高速动车组进行多质点建模时,可以将动车组的每节车辆看作单独的质点,目的是在分析每节车辆之间的相互作用力,即车间耦合力时,不用考虑车辆长度,从而更好地理解这一作用力。在分析车间耦合关系时,将每节车辆之间的耦合关系简化为“弹簧-阻尼器”系统来描述车辆之间的相互作用,从而更准确地模拟整个高速动车组系统的动力学行为。“弹簧-阻尼器”系统结构如图2所示。
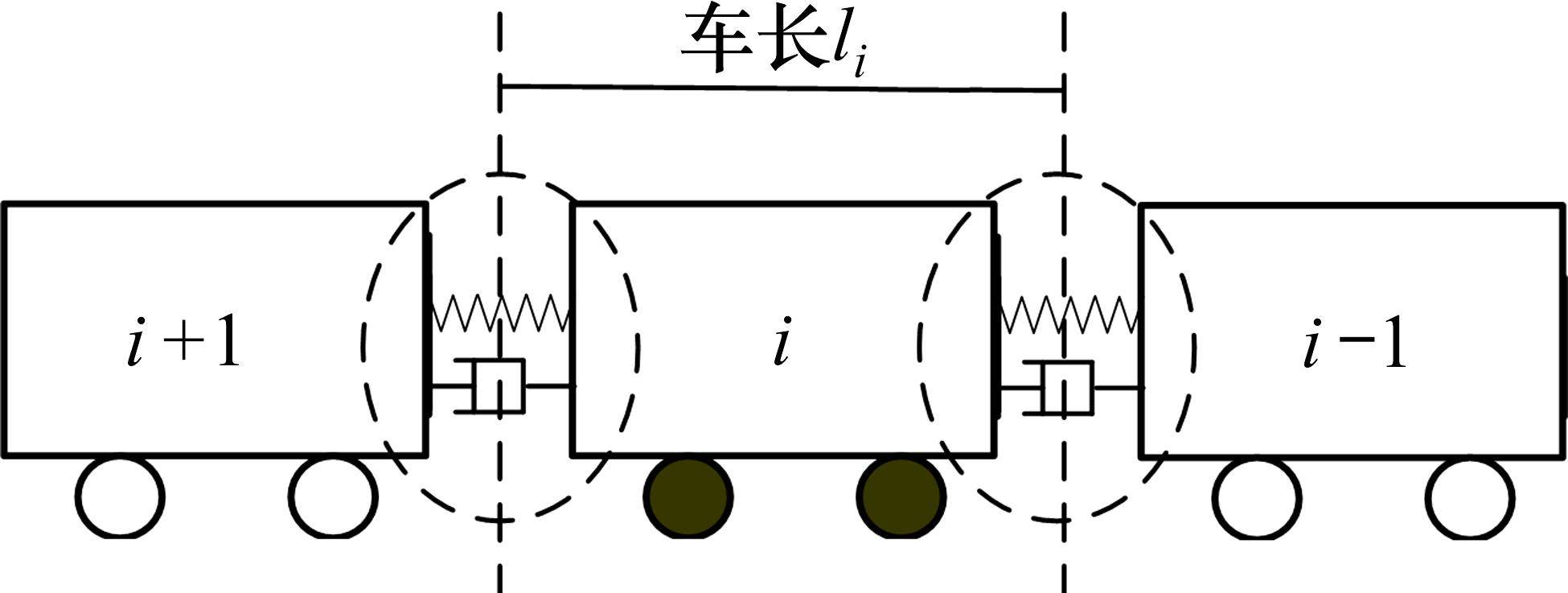
由图2可知,第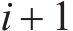
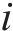
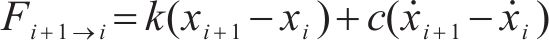
式中: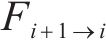
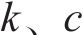
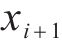
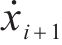
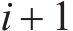
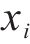
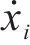
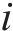
1.4 高速动车组建模
综上所述,高速动车组多质点动力学方程为
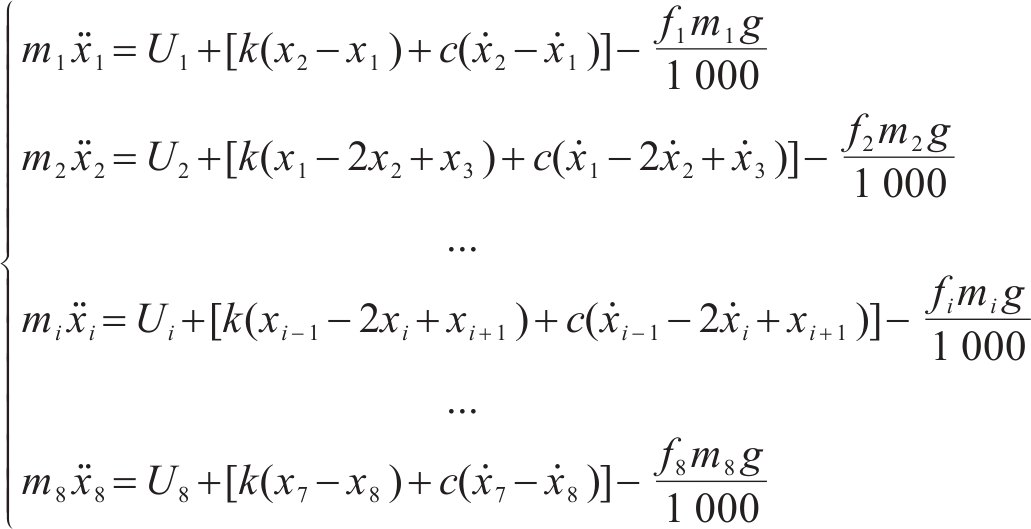
考虑到动车组在运行过程中会受到外部不确定性扰动,结合式(7)的动力学方程,列车多质点模型可写为如下形式
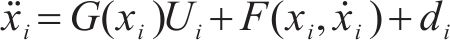
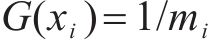
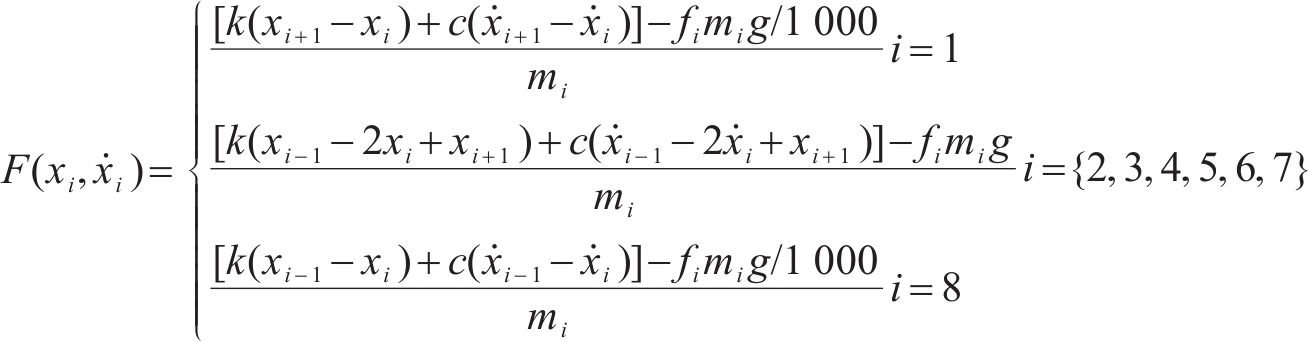
式中: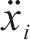
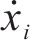
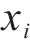
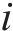
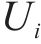
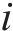
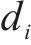
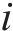
定义1:
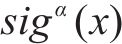
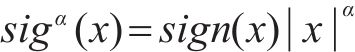
式中: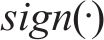
引理1[23]:假设存在一个径向无界的函数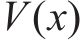
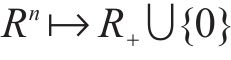
1) 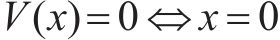
2) 若对任意的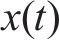
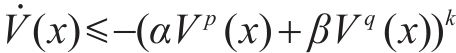
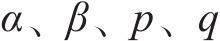
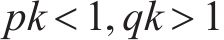
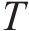
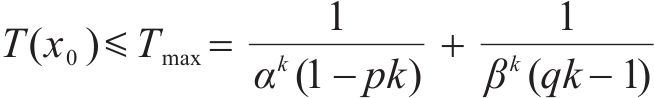
为了保证系统收敛性,给出如下假设。
假设1:高速动车组第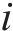
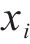
假设2:高速动车组第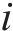
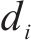
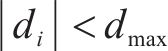
2 控制算法设计
高速动车组控制方案如图3所示。图3中,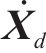
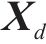
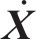
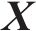

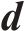
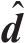
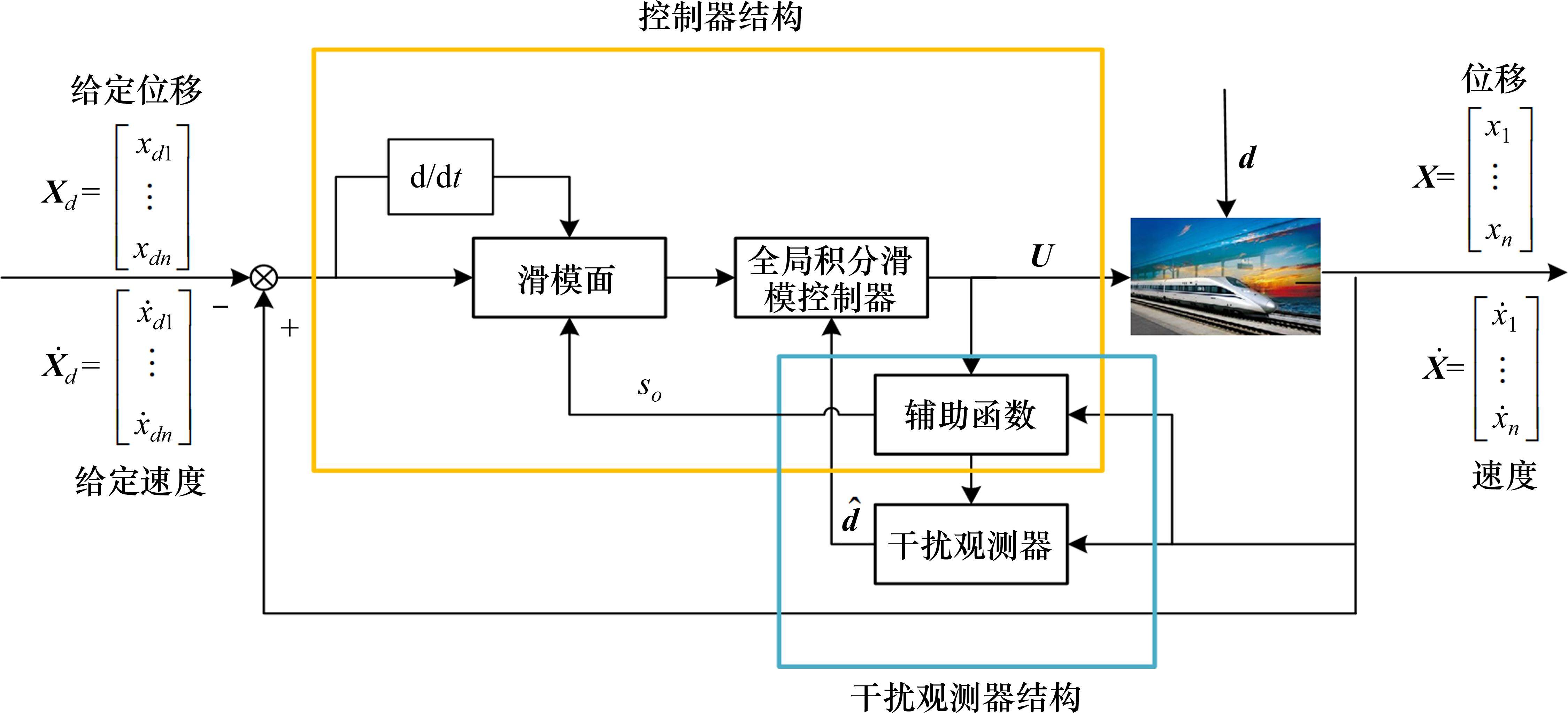
控制器的设计可以分为2步:第1步设计终端滑模干扰观测器,通过干扰观测器观测外界干扰,得到抵消外界干扰的补偿输入;第2步设计固定时间全局积分滑模控制器,用来实现列车在期望速度下的全局鲁棒控制。
2.1 固定时间干扰观测器设计
滑模控制理论在应对模型参数变化和外部干扰体现出较强的鲁棒性,被广泛应用于观测器的设计。文献[24]将滑模引入观测器,提出一种观测误差有限时间收敛的终端滑模观测器,本文将该观测器进行改进,构造固定时间观测器,其收敛时间存在确定上界,且与系统的初始状态无关。
针对非线性系统:
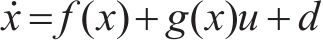
式中: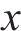
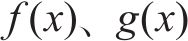
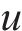
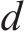
为了使观测器观测误差固定时间收敛,设计如下观测器:
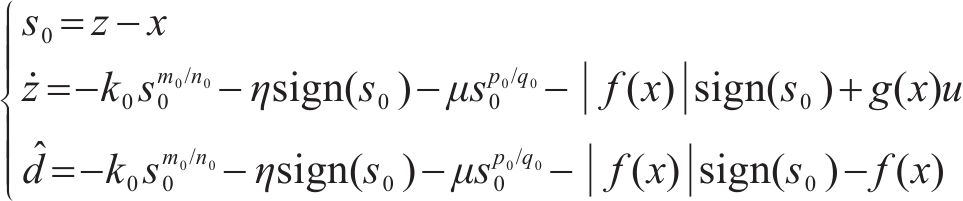
式中: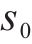
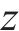
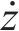
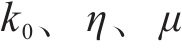
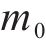
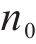
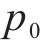
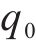
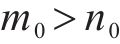
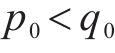
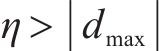
由式(14)可得:
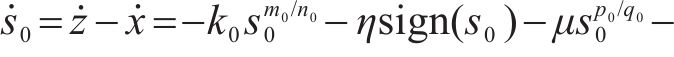
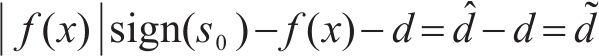
式中: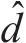
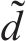
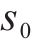
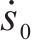
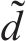
选取Lyapunov函数为
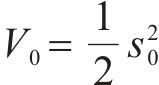
对其求导得:
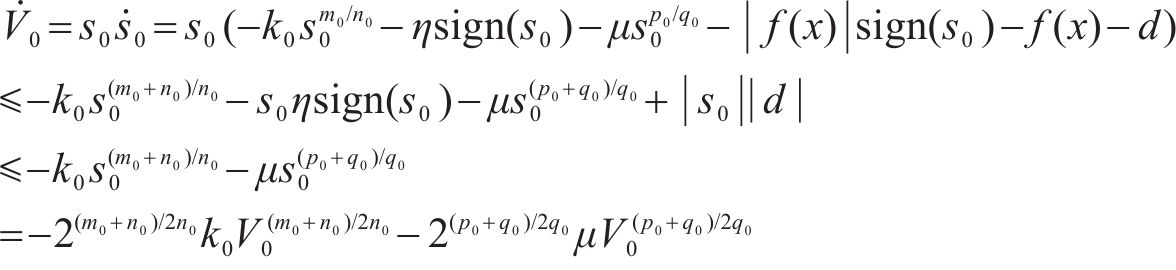
由式(17)可得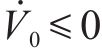
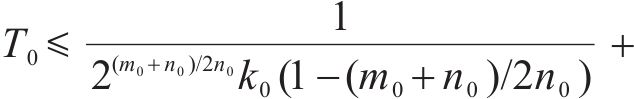
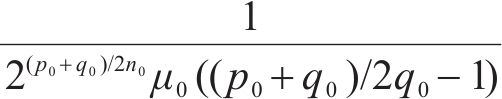
因此,只要设置合理的观测器参数,观测误差将会在固定时间内收敛。利用该观测器对干扰进行观测,在本文中,以第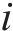
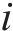
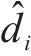
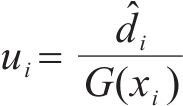
2.2 全局积分滑模面
动车组的给定位置为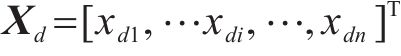
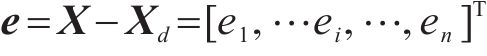
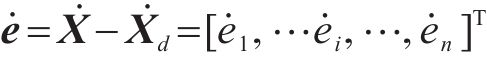
传统滑模控制中一般定义滑模面为:
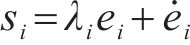
式中: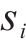
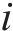
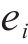
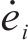
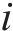
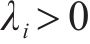
为提高系统误差收敛速度,设计全局积分滑模面为
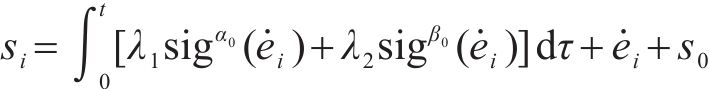
式中: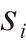
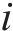
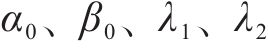
当系统状态到达滑模面上,此时若滑模观测器对干扰的观测误差已经收敛,此时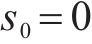
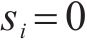
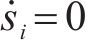
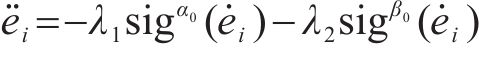
选取Lyapunov函数为
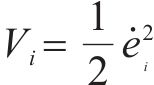
对上式求导得
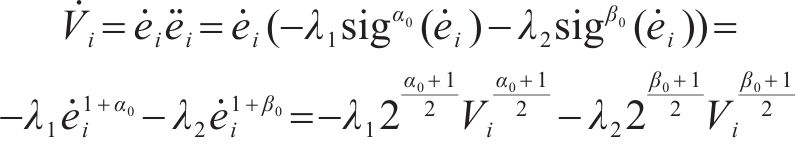
由引理1可知,滑模面速度误差是固定时间收敛的,且收敛时间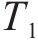
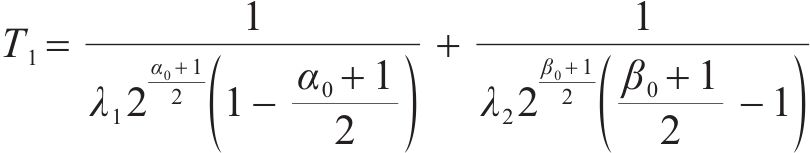
由于滑模控制存在抖振问题,严重影响系统控制精度,因此有必要对滑模趋近律进行改进。传统指数趋近律为
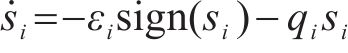
式中: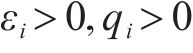
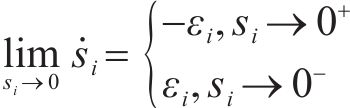
所以当系统到达滑模面时,并没有稳定于平衡点,而是在平衡点处产生幅值为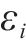
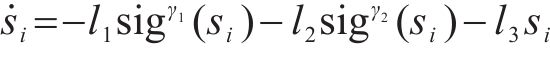
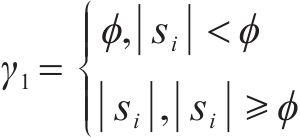
式中: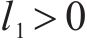
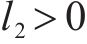
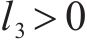
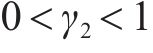
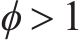
由上式可知,当系统状态为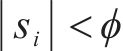
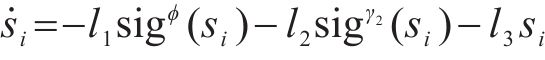
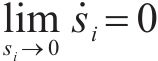
所以系统可以平滑地进入滑模段,避免抖振。当系统状态为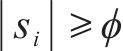
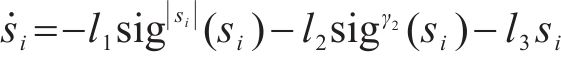
2.3 固定时间全局积分滑模控制器
为使系统在固定时间稳定,同时具有全局快速收敛性质,提高系统鲁棒性,选用式(21)全局积分滑模面和式(28)改进的变幂次趋近律设计固定时间滑模控制器。
对式(21)求导可得:
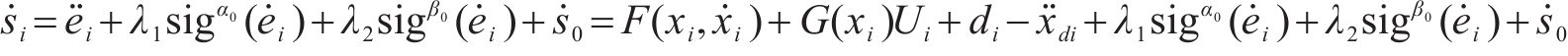
设计全局积分滑模控制器为
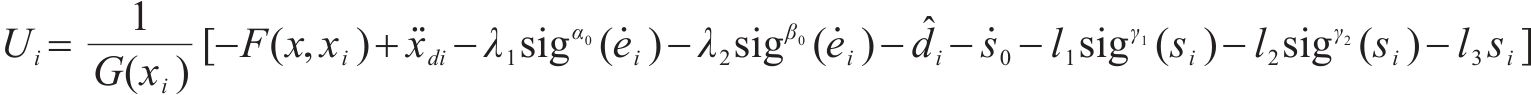
选取Lyapunov函数为
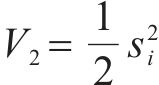
对其求导,得
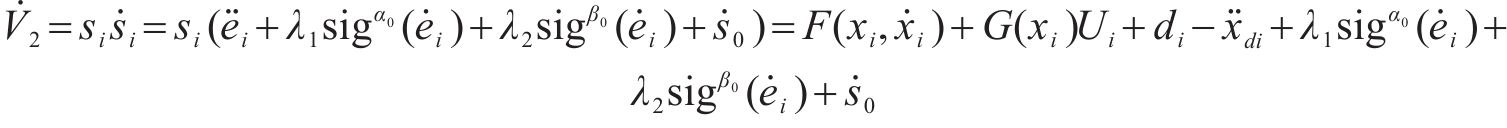
将式(32)代入,得
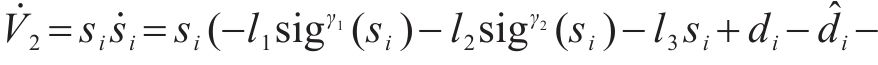
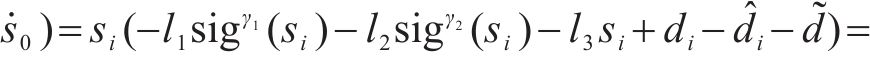
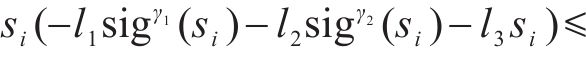
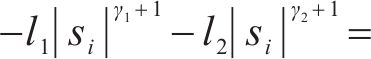
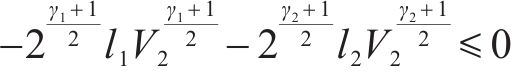
由引理1可得系统从初始状态收敛到滑模面的时间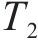
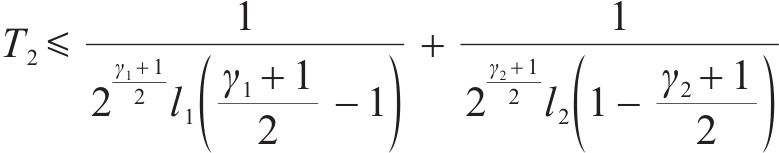
由式(29)、式(36)可知,增大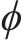
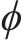
当系统从初始状态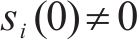
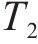
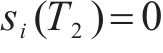
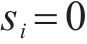
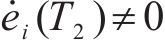
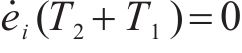
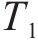
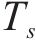
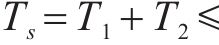
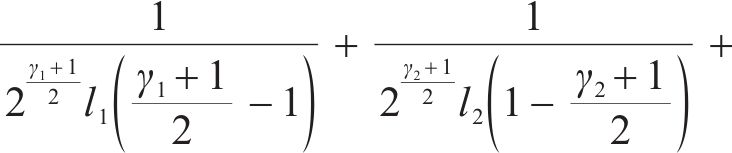
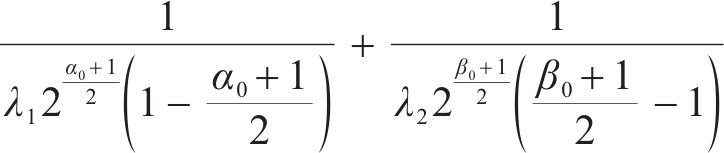
当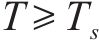
3 仿真实验结果与分析
为验证本文所提控制方法的合理性和有效性,以CRH3型高速动车组为研究对象。
其单位基本阻力为
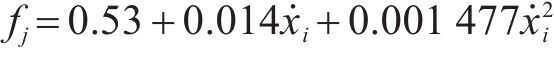
其中,动车车辆车长为25 m,拖车车长为26.5 m,每节车辆质量51+(0~9) t。
本文方法控制器参数为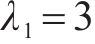
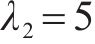
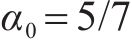
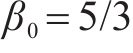
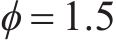
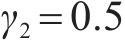
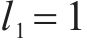
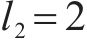
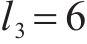
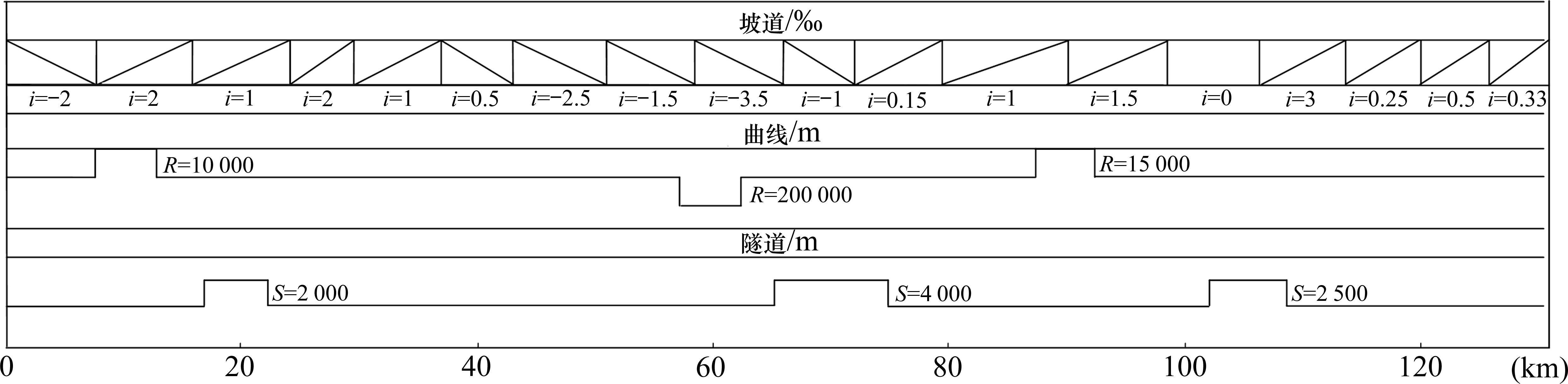
列车的期望速度曲线如图5(a)所示,整个过程包括2个加速阶段、2个减速阶段、3个巡航阶段,列车最高速度为90 m/s,运行时间为2 500 s,同时考虑高速动车组在运行过程中经过坡道、弯道、隧道等线路,其运行环境条件具体见图4。
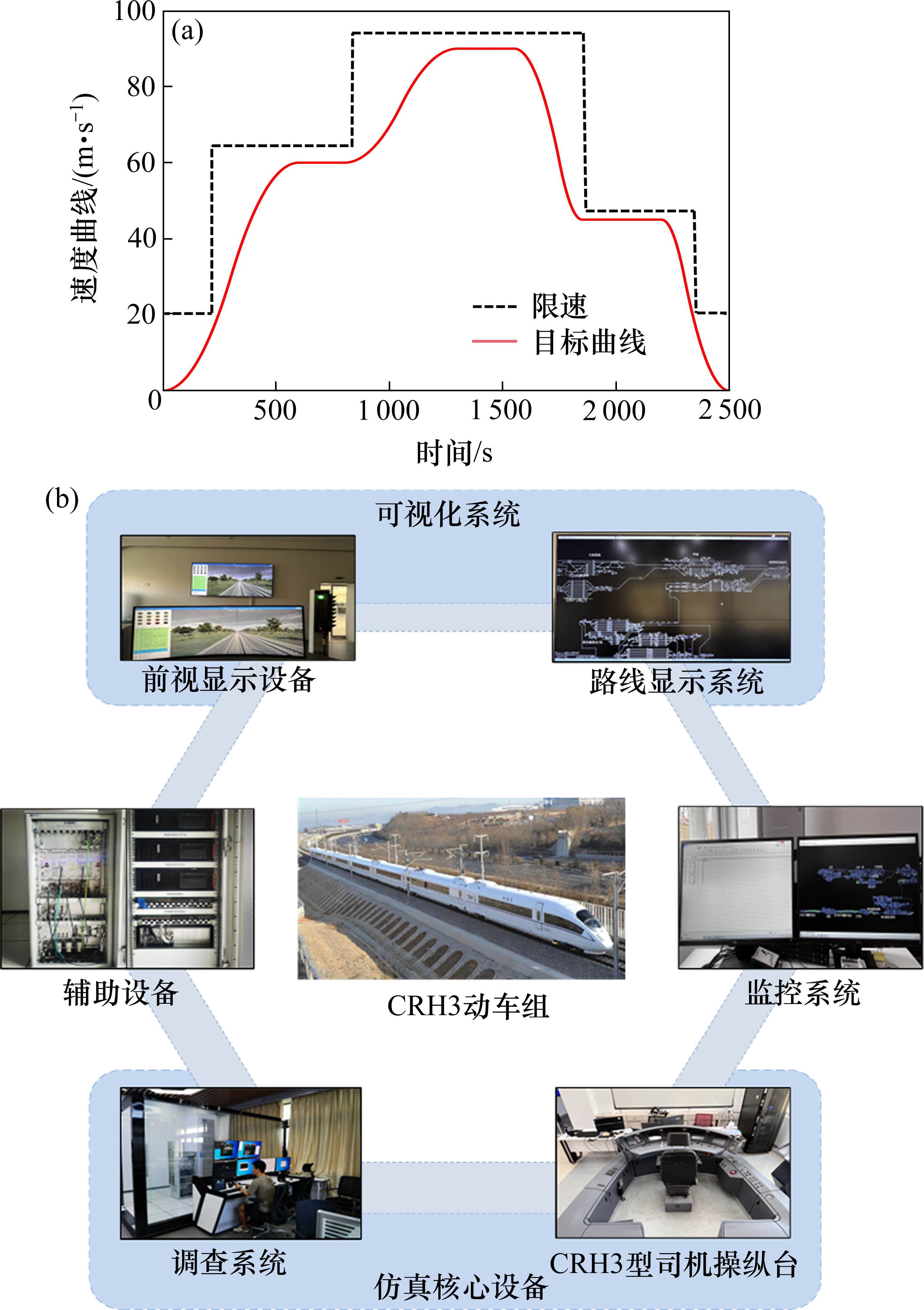
以实验室配备的CRH3型动车组半实物仿真平台,如图5(b)所示,进行仿真研究验证所提出的控制器和多质点模型的有效性,另外将本文方法同传统滑模控制方法的仿真结果作比较,并附加外界干扰、内部模型摄动,代替运行过程中不确定的干扰,同时考虑某节动车车辆故障情况,分别在不同时间施加在不同车辆单元上,以此反映运行时的复杂与多变。
3.1 固定时间控制器仿真与分析
对高速动车组的控制是对实际速度的控制,保证实际速度准确跟踪期望速度。当设定了目标信息,动车组各个车辆之间将通过“弹簧-阻尼器”系统进行信息交换,实现对高速动车组的整体控制。高速动车组车辆的速度跟踪情况如图6所示(前4节车辆)。从图6中可以看出采用本文控制器,车辆都准确跟踪上预定的速度,即高速动车组实现了整体的一致性跟踪控制。
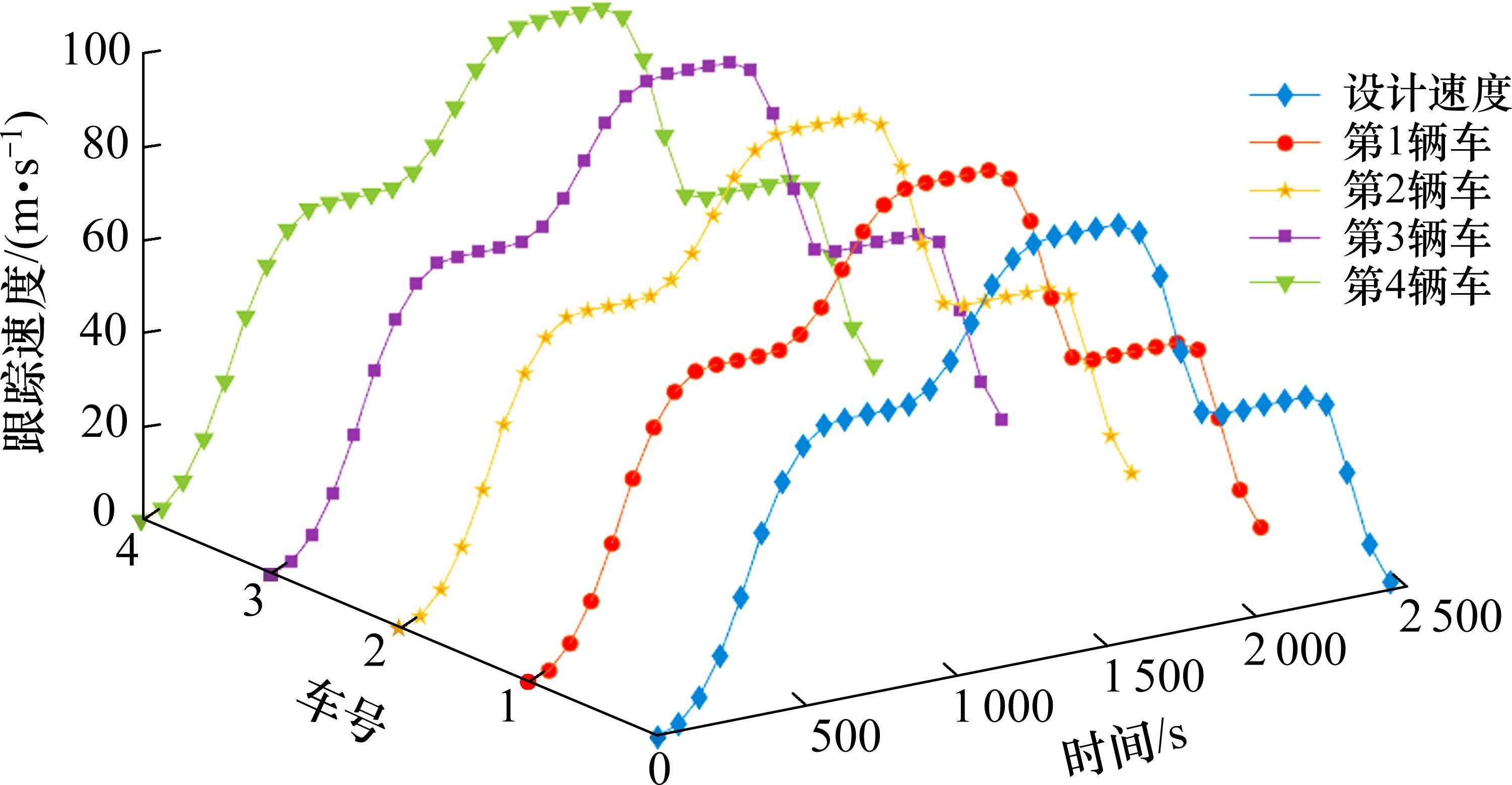
图7是固定时间控制器8节车辆的速度跟踪误差图,由图7可知,第2、4、5、7拖车在状态切换和地形变化时会产生相对较大的误差,这是因为拖车在非制动时无法提供牵引力,因此对条件变化敏感,但整个过程中误差不超过0.000 15 m/s,而1、3、6、8动车在经过工况转换点和路况切换时,由于自身能输出牵引力,误差很小基本没有波动。
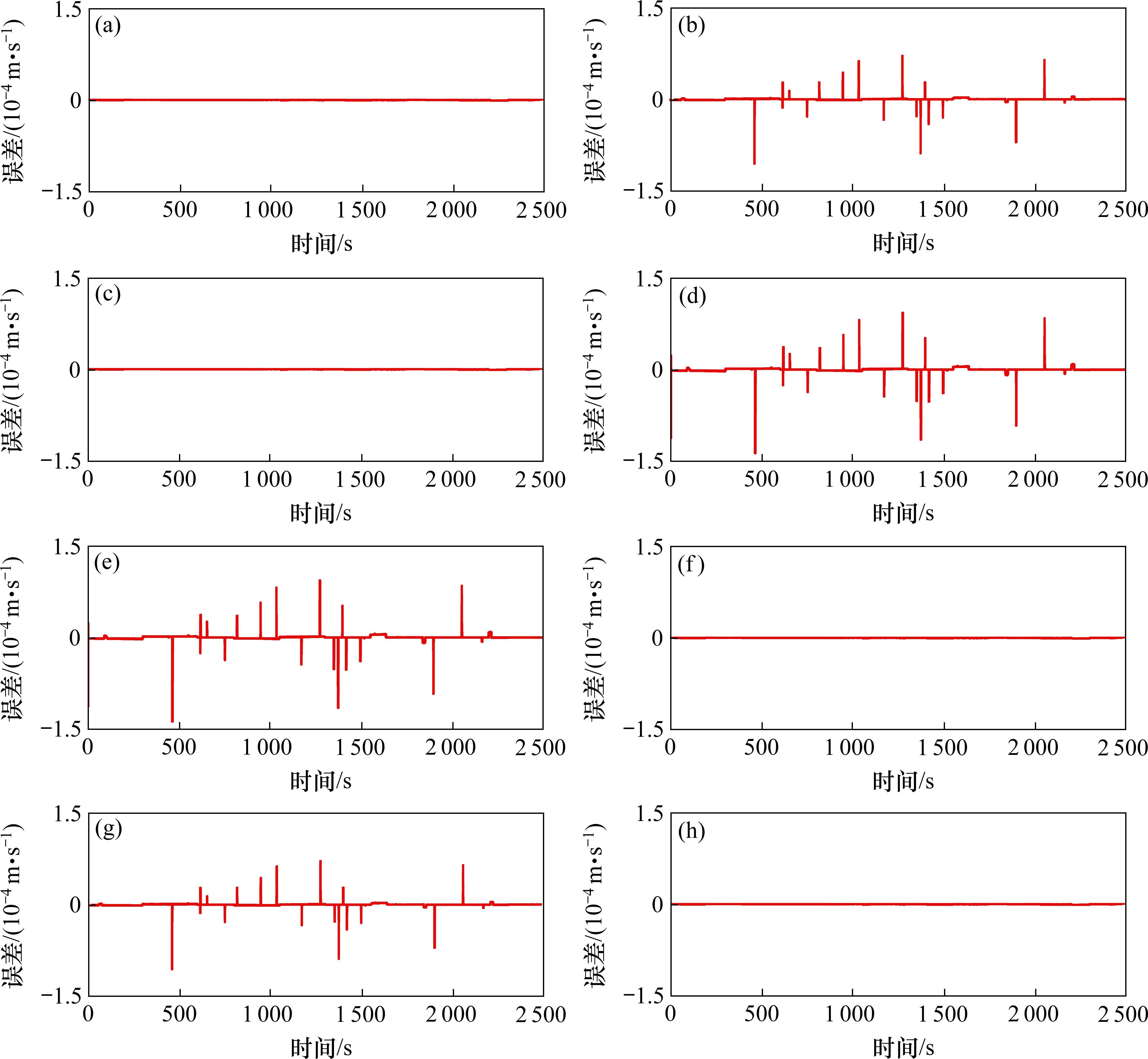
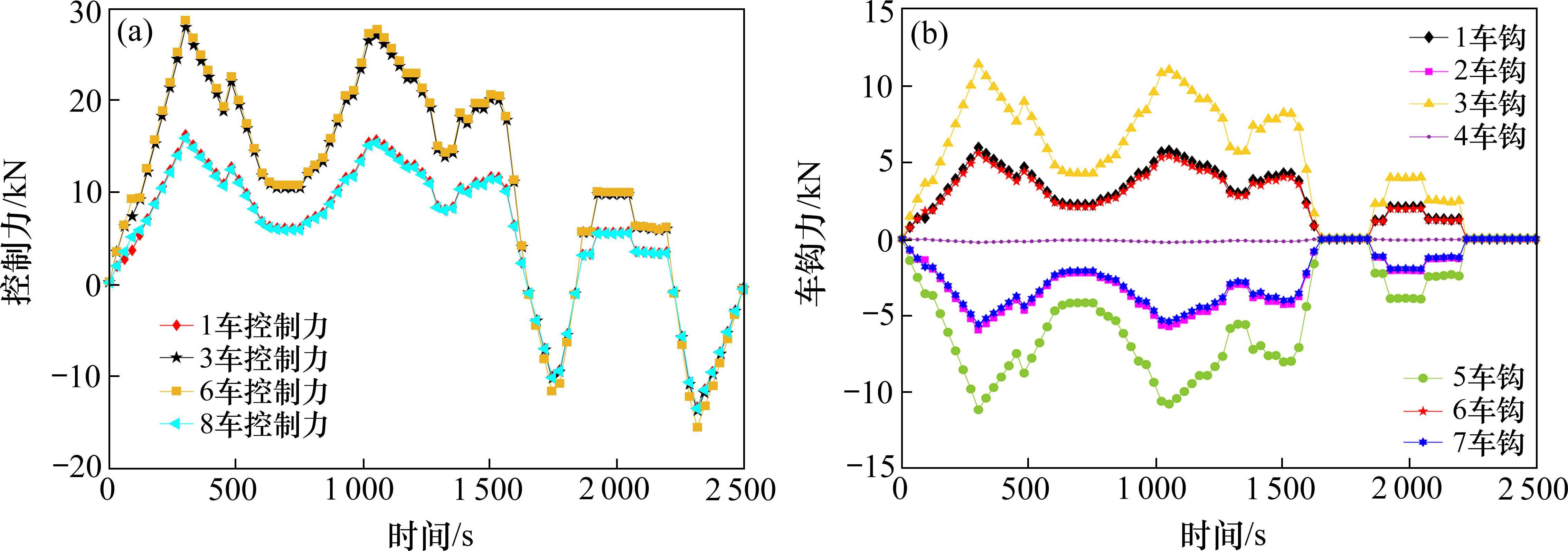
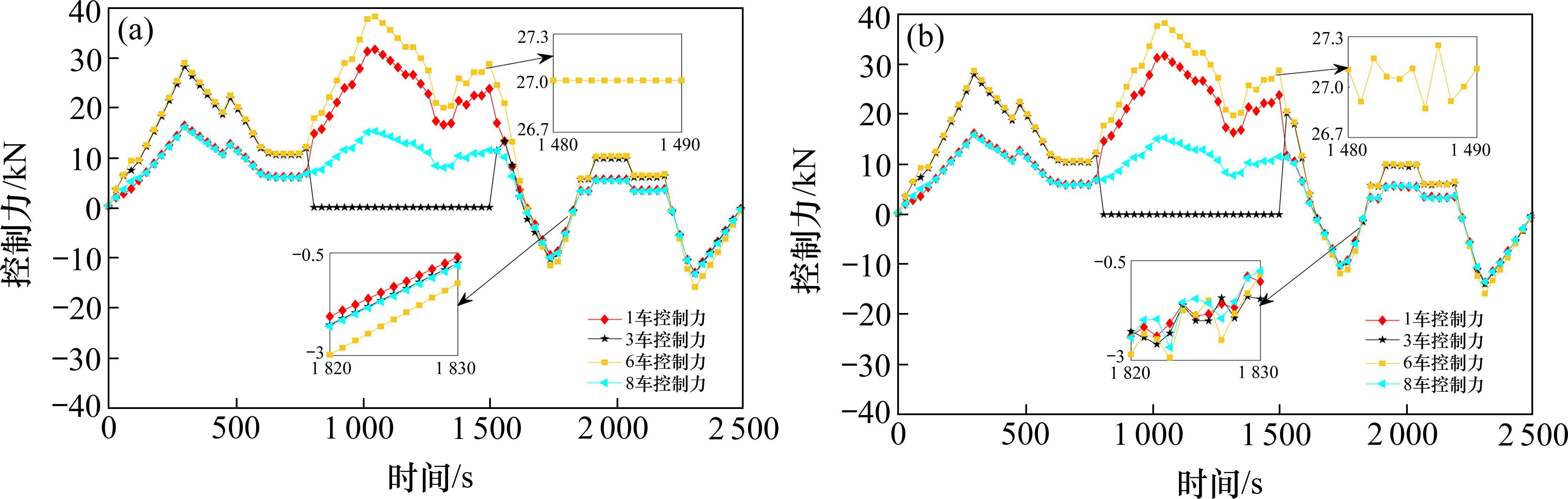
图8为高速动车组整个运行过程的动车车辆控制力和车钩力变化图。从图8(a)中可以看到,在整个运行过程中,动车车辆一直输出所需控制力,由于动车车辆其质量和状态的差异,会产生不同的控制力输出,以适应高速动车组的运行需求和保持整个动车系统的稳定性。动车车辆在经过坡道、隧道和弯道等复杂路况时,具备了较好的适应性和响应能力,其误差波动很小,当运行工况发生变化时,控制力大小也随之变化。从图8(b)中可以看出,拖车在非制动时,无法提供牵引力,所以需要依靠相邻的车辆通过“弹簧-阻尼器”系统对拖车传递运行等状态的力。当高速动车组处于制动状态时,拖车和动车均能够提供制动力满足列车制动的需求,所以此时车钩力很小,分布在零点附近。由此可以看出本文控制器可以保证某一车辆出现动力不足时,通过“弹簧-阻尼器”系统对其他车辆动力进行补充,从而保证每个车辆都能够准确地跟踪期望速度,确保整个列车系统在达到目标速度时保持稳定和一致,完成对期望曲线的精确跟踪。
3.2 控制器抗干扰对比仿真与分析
为了说明本文控制器的抗干扰性和鲁棒性,与传统滑模方法进行对比试验,为反映动车组的扰动情况,考虑外部时变函数干扰、内部模型参数摄动以及运行过程中某节动车车辆故障3种情况,分别在不同时间段加入到车辆单元上。
高速动车组在0~800 s时加上时变干扰为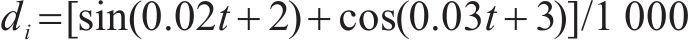
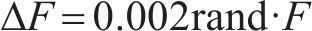
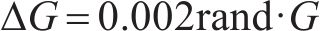
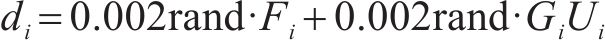
| 不同方法 | 动车负最大 误差/(m∙s-1) | 动车正最大 误差/(m∙s-1) | 拖车负最大 误差/(m∙s-1) | 拖车正最大 误差/(m∙s-1) | 标准差 |
|---|---|---|---|---|---|
| 本文方法 | 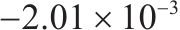 |  | 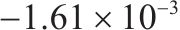 |  |  |
| 传统滑模方法 | 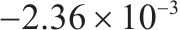 |  | 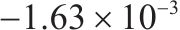 |  |  |
图9和图10分别为本文方法和传统滑模方法的高速动车组车辆速度误差,通过图10可知本文方法在控制精度方面明显强于传统滑模方法,可以看到传统滑模方法误差抖振很大,而本文方法几乎没有抖振,这是因为本文针对滑模抖振问题引入变幂次趋近律消除抖振,并运用固定时间滑模干扰观测器消除外界干扰影响,使得各节车辆速度误差变化幅度很小,只有在运行状态切换与地形变化时会对拖车车辆的速度产生相对较大的误差。由误差统计表可知,传统滑模算法动车最大正负速度误差范围为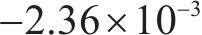

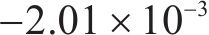

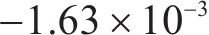

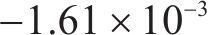
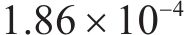
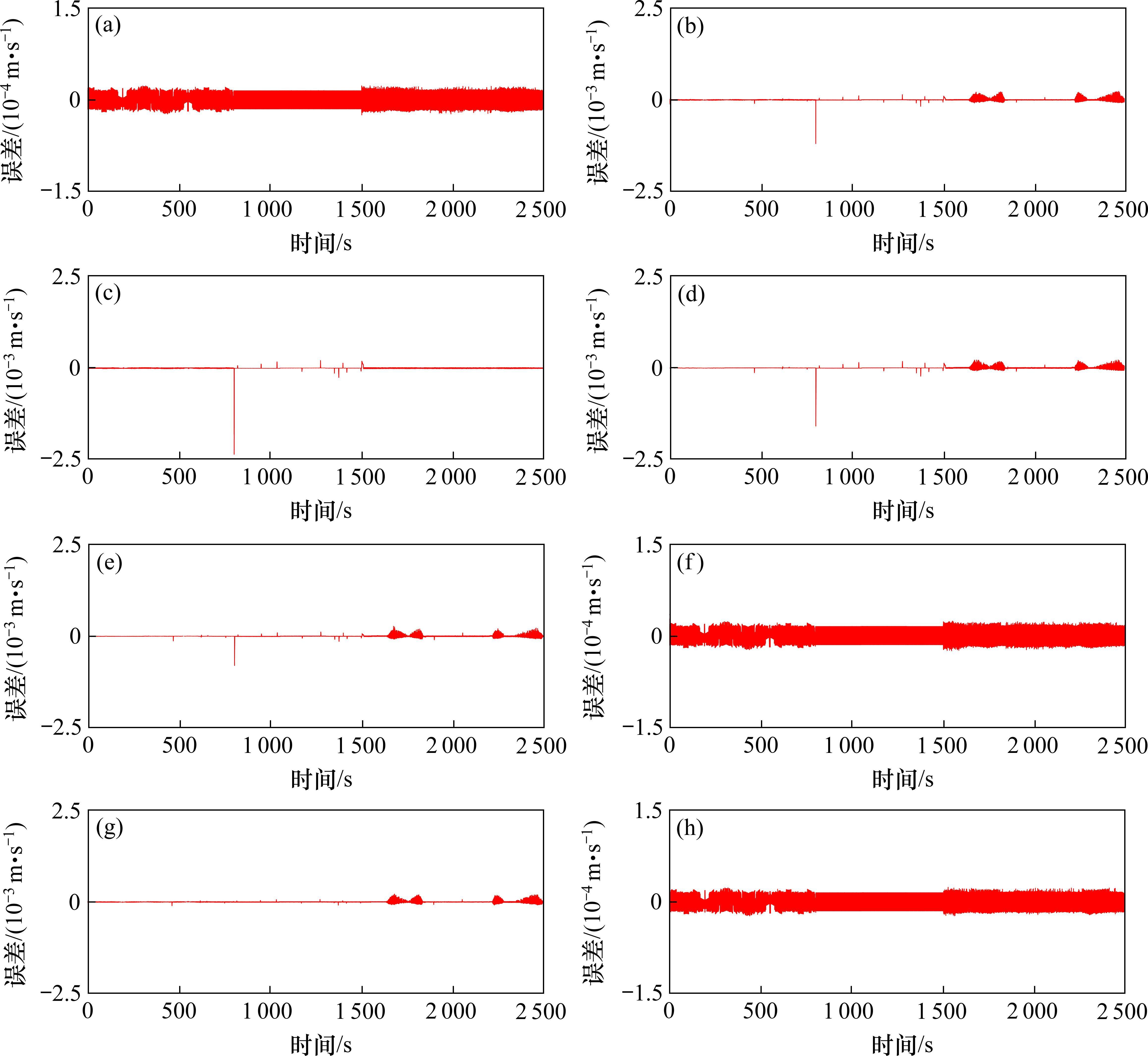
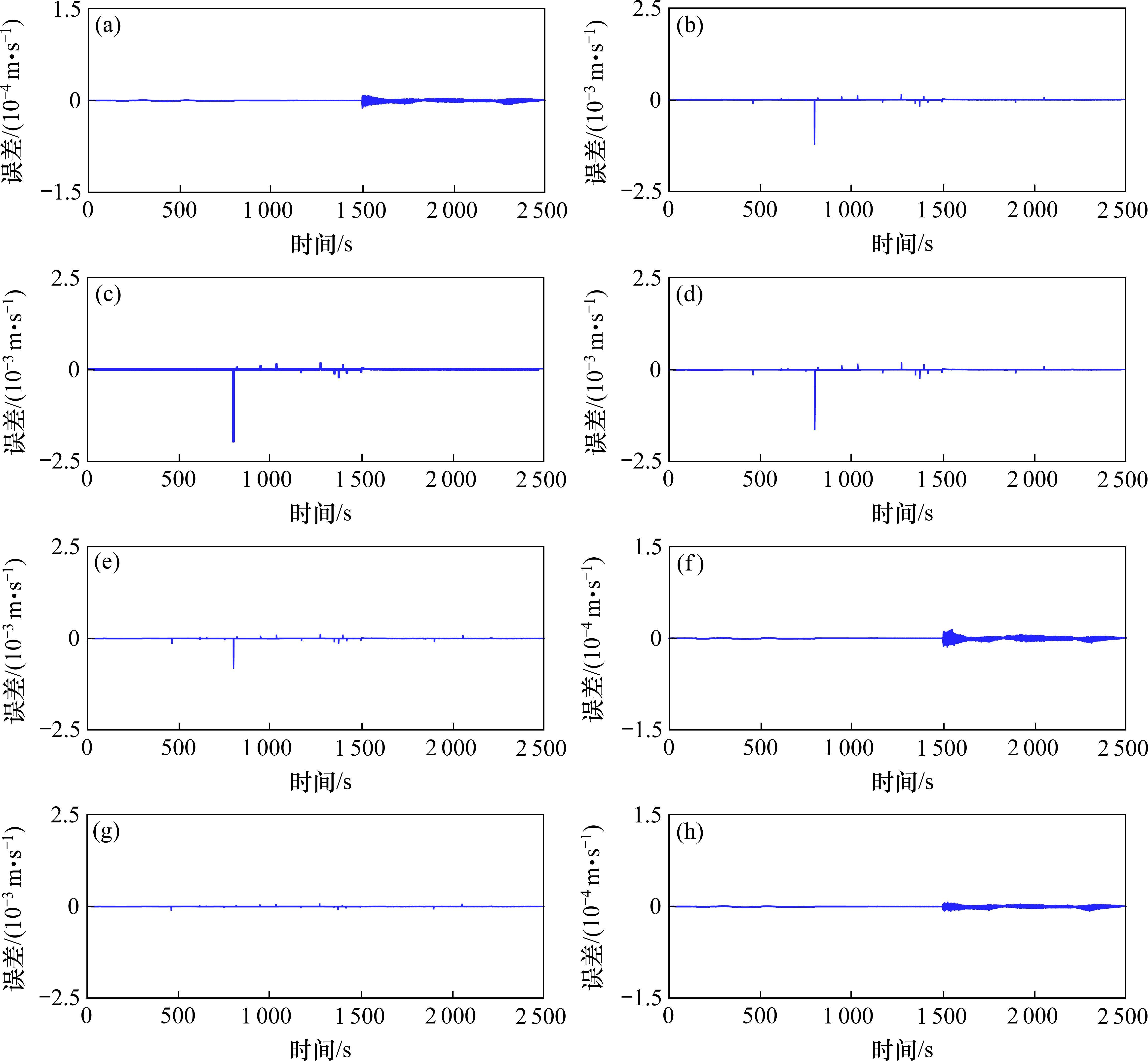
图11为本文方法和传统滑模方法的控制力对比图,从2幅图均可以看到在第800 s时,由于第3辆动力车辆故障,其控制力降为0,这也正好解释了第3节车辆速度误差增大,由于第3车控制器失效,为保证动车组正常运行所需控制力,第1节动车车辆和第6节动车车辆控制力增大,用以补充不足的控制力部分,保证动车组正常平稳运行直至第3节车辆恢复动力。对比2幅图可知传统滑模方法在整个过程中抖振剧烈,尤其在制动阶段,抖振很大,而本文方法的控制力输出十分平滑,基本没有抖振,有利于控制器的输出和动车组运行的平稳性。
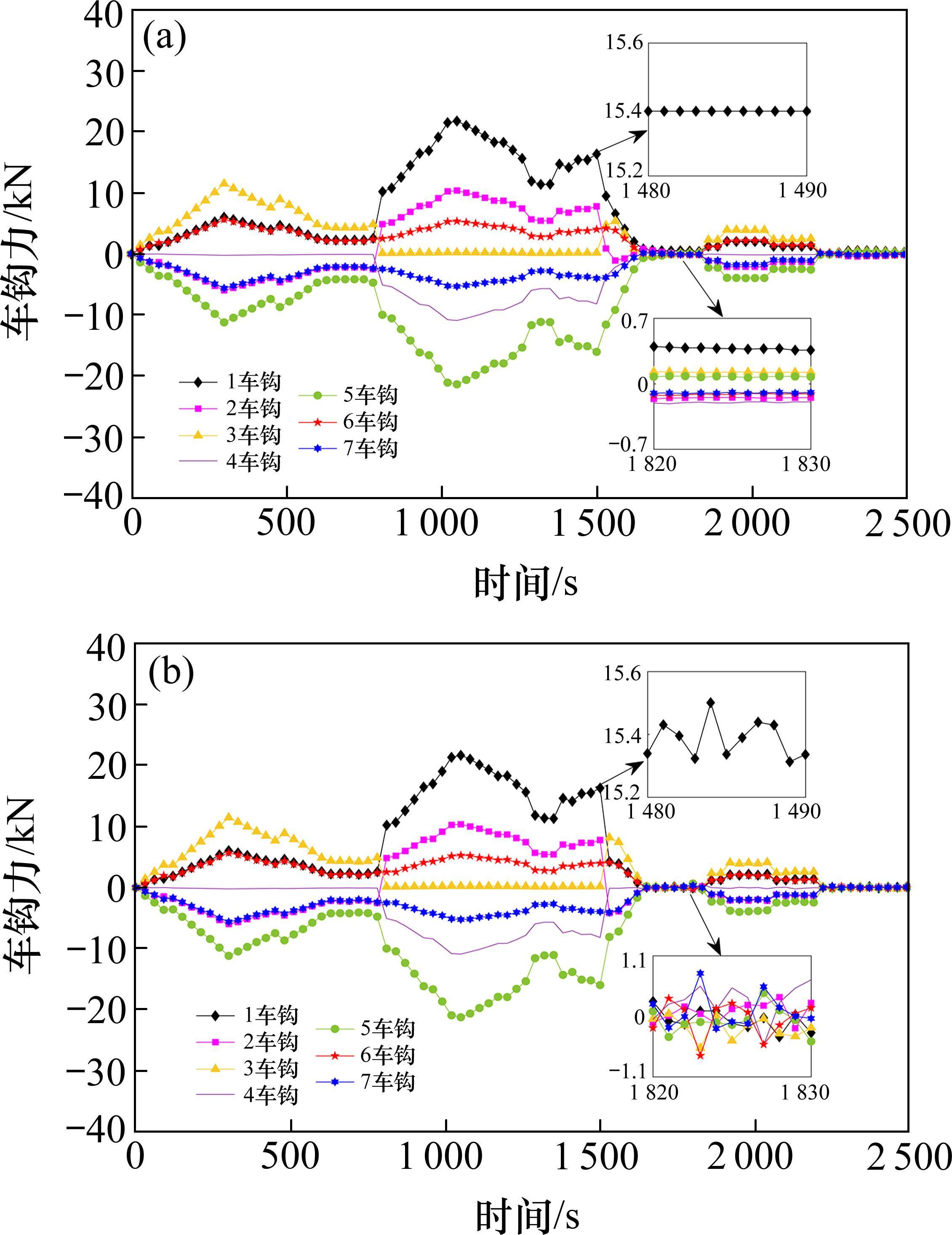
仿真得到的2种方法下高速动车组各车钩力的变化曲线如图12所示,从图12中可以明显地观察到,在第800 s时,第3动车车辆发生故障,此时动车组车钩力也随之变化,从而实现对动车组各节车辆动力的调整和补充,当第3辆动车故障解除时,由于车辆能够输出控制力,此时维持车辆状态的车钩力逐渐减小。对比2种方法的结果可以看出本文控制方法下的高速动车组车钩力的变化更为平稳,同时车钩力震荡幅度更小,有利于减小车钩磨损,延长车钩寿命,对提高动车组运行平稳性起到至关重要的作用。
4 结论
1) 针对高速列车环境干扰、模型摄动以及控制器故障问题,利用全局积分滑模的鲁棒性以及改进的变幂次趋近律的抑抖特性,并结合固定时间终端滑模干扰观测器设计了基于干扰补偿的固定时间全局积分滑模控制器,实现了高速列车的精准平稳控制。
2) 对动车组受到的环境干扰采用终端滑模观测器在线估计,极大提高了系统的抗干扰能力。Lyapunov稳定性分析保证了系统的稳定和全局固定时间收敛。仿真结果表明,在模型摄动、外界扰动和控制器故障情况下,基于干扰补偿的高速动车组固定时间控制方法实现了对目标速度的高精度跟踪,同时动车组车钩力的震荡更小,控制力的输出更为平滑,实现了高速动车组安全、精准和平稳运行。
李中奇,陈磊,周靓.基于干扰补偿的高速动车组固定时间控制方法[J].铁道科学与工程学报,2024,21(11):4417-4430.
LI Zhongqi,CHEN Lei,ZHOU Liang.Fixed-time control method of high-speed EMU based on interference compensation[J].Journal of Railway Science and Engineering,2024,21(11):4417-4430.

