高速列车装备的自动列车控制系统(ATO)能够实现列车的自动控制、监测和操作。ATO系统通过考虑多种约束条件(包括坡度、速度限制、列车参数等)来制定最优驾驶策略,以确保列车高效且准时地到达目的地[1]。鉴于高速列车以200 km/h以上的高速度运行时,所遭遇的基本阻力和牵引效率会呈现非线性变化。因此,优化驾驶策略显得尤为重要,它不仅能够有效减少碳排放,还能提升整体运营的质量[2]。目前,用于优化ATO控制策略的算法主要包括庞特亚金极大值原理(PMP)算法[3]、动态规划算法[4]、启发式算法[5]等。此外,深度强化学习(DRL)作为一种通过神经网络逼近策略函数的算法,展现出强大的鲁棒性,能够有效地适应来自嘈杂输入的不确定性。尽管如此,长距离行驶下产生的高维状态搜索空间以及稀疏奖励问题,加之奖励函数设计的动态性,直接应用DRL并不能总是得到满意的效果。张淼等[6]通过专家系统满足乘客舒适度同时利用神经网络作为列车驾驶控制器,以适应变化的运营场景。ZHAO等[7]解决了RL中的软约束,提出了一种SRL方法。俞胜平等[8]基于策略梯度的深度强化学习的高铁列车动态调度优化模型及算法,最小化延误总和。刘伯鸿等[9]提出了一种基于专家经验动作划分和状态信息熵的方法,将软演员-评论家改进为动作状态经验优先软演员-评论家,并应用于列车自动驾驶速度控制问题。武晓春等[10]利用深度确定性策略梯度算法优化列车的节能控制策略,基于状态和动作空间构建模型并利用加权奖励函数进行学习。ZHANG等[11]引入了一种名为分配闲置时间和规划速度区间(ASTPSI)算法,通过限制探索边界来减少智能体在稀疏奖励下的探索盲目性。赵子枞[12]提出了一种名为Shield保护机制的DRL方法。吴卫等[13]通过将线路划分为多个轨道区段,在最小化总晚点时间的目标下,利用深度神经网络近似值函数,并结合整数规划模型,有效降低列车晚点时间和求解时间。ZHANG等[14]将操作视为事件驱动,降低了计算成本。NING等[15]提出了一种分配运行时间和选择运行模式算法,限制了智能体的动作空间。然而,其约束依赖于超参数,有可能遗漏全局最优解且缺乏可解释性。上述研究都在不同程度上减少了状态搜索空间,缓解了智能体的学习难度。然而在高速列车运行中,存在着因计划时间调整、限速等约束条件发生变化情况,这将导致所采用的静态奖励函数设计在能效方面表现出弱鲁棒性。在面对新任务时,将进行大量实验来确定其奖励函数。LI等[16]使用数学规划求解器GUROBI来模拟竞争目标的权衡,作为一个双线性规划问题来确定奖励权重。ZHANG等[14]提出一种动态激励系统,该系统根据代理人的相对位置来调整其安全和绩效偏好。LI等[17]提出一种时间限制的权重选择算法,通过在给定时间限制内搜索权重组合来最小化多个目标函数。然而,这种算法依赖于许多离线数据和指标来进行权重选择,在搜索初期,需要一个初始权重向量,这将导致较高的计算成本。NING等[15]将ARTSOM计算出的能耗值作为代理的初步节能目标,但面对不同调度任务时,权重需要人为调整。综上,本文提出一种分层次优化的深度强化学习算法HODRL(Hierarchical Optimization of Deep Reinforcement Learning),首先通过合理的约束,滤除无效状态搜索空间,智能体只需搜索出最优的牵引-惰行组合和惰行-制动点。此外,通过设计恰当的自适应奖励函数,以确保智能体获得正确的反馈信号,用以平衡智能体能效和准时2个目标。通过仿真实验表明,HODRL算法在提升能效和准时性方面的有效性。与其他基线算法相比,在学习效率和鲁棒性方面也取得了显著的优势。
1 列车动力学模型
在进行列车牵引力/制动力计算时,可将其视为单一质点模型。然而,在计算列车阻力时,应考虑采用多质点模型,以更准确地描述列车的受力情况。再生制动是一种将制动过程中产生的动能转换并储存的技术。然而,再生制动会增加制动时间和随后的滑行时间。因此,为了避免不必要的牵引,在优化过程中应隐含考虑这一因素,而不是直接包含再生制动的具体操作[15]。列车控制可以分为列车的牵引/制动2部分。在实际驾驶中,不允许同时对列车施加牵引和制动操作,列车运动可以表示为:
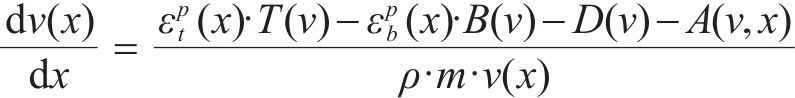
其中,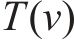
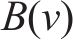
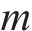
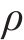
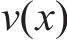
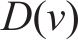
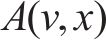
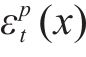
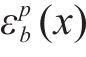
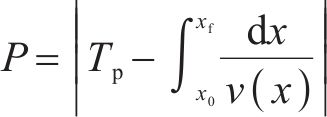
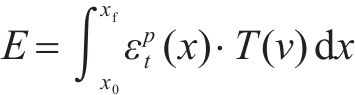
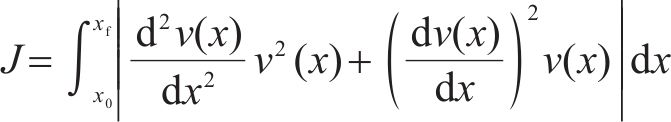
其中,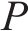
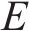
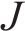
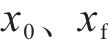
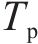
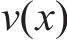
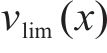
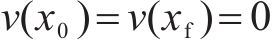
基于上述(1)~(5)式建立的模型,高速列车驾驶策略优化问题旨在求解得到最小化运行时间误差和列车波动程度的基础上,最小化牵引能耗指标如下:
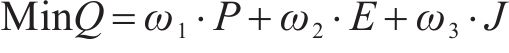
2 高速列车分层优化深度强化学习
2.1 HODRL算法框架和思想
图1是本文所提出的高速列车智能驾驶算法总体框架图,图中清晰地展示了所提算法的特点。本研究针对高速列车运行环境中庞大高维状态空间有效约束问题以及智能体在不同任务下行为评价动态性问题,实施了分层优化策略。在分层优化框架内,引入了高速列车动力学特性,并通过列车状态空间约束,有效地剔除大部分不可行状态空间,从而减少不必要的探索,使得智能体能够迅速学习目标行为。此外,自适应奖励重塑根据列车状态空间约束提供的约束数据进行奖励函数的调整,实现了在不改变奖励函数权衡关系的情况下快速完成训练,有效解决了固定奖励函数的不足。相较于传统方法,本研究的分层优化策略显著提高了智能体的收敛速度和对不同任务安排的适应性。与传统方法相比可以有效实现智能体的快速收敛和适应不同任务安排,并在策略输出层输出最优驾驶策略,具体而言,本研究的贡献包括:
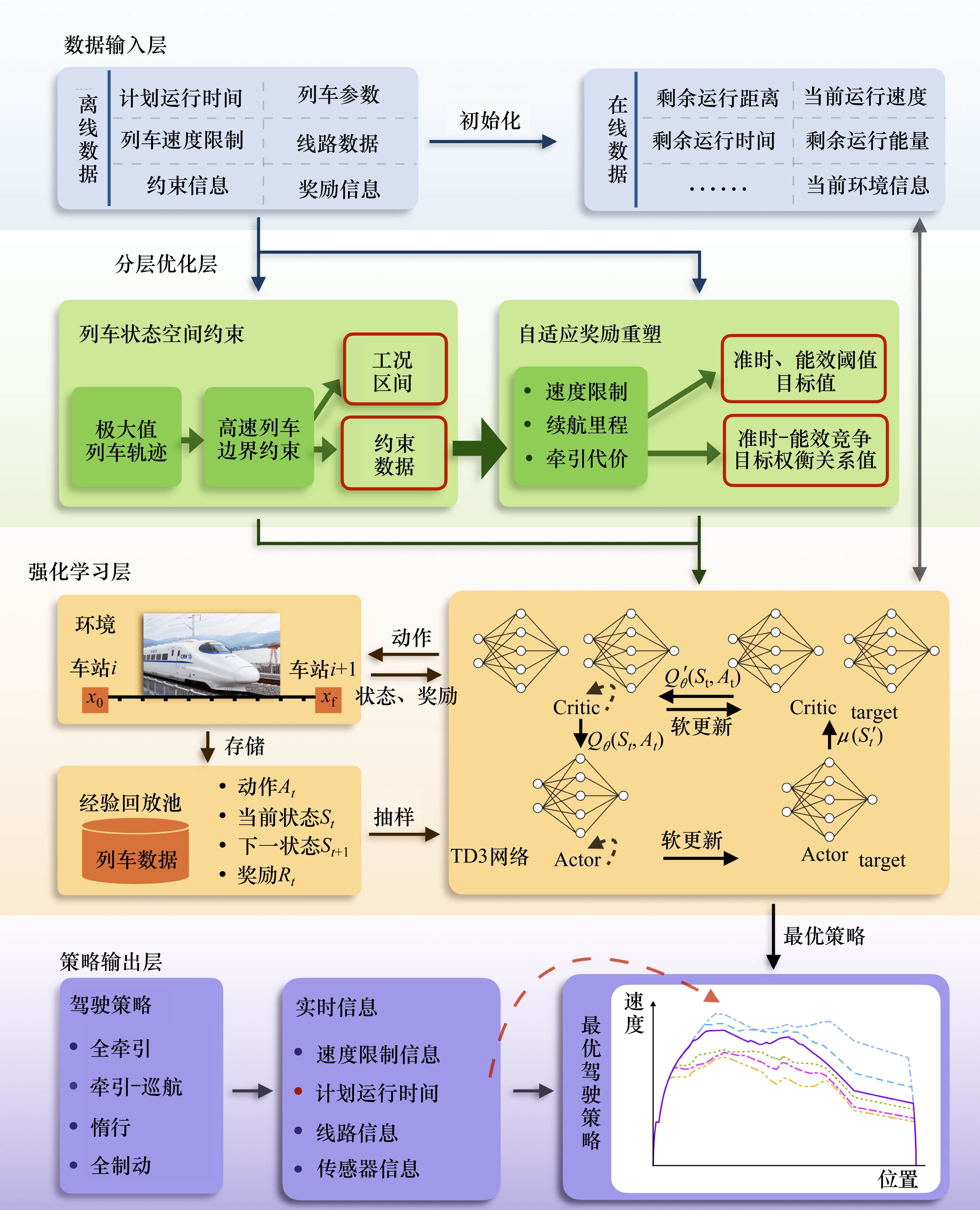
1) 列车状态空间约束。通过庞特亚金极大值原理,初步找到在理想平直轨道下的最优解,并以此生成智能体状态搜索空间中的约束边界和工况区间,有效滤除大量不可行状态搜索空间区域和无效操作序列,降低智能体探索的盲目性,并有效缓解初期智能体因稀疏奖励而导致的梯度消失问题。
2) 自适应奖励重塑。鉴于高速列车在高速运行环境下受到巨大且非线性增长的基本阻力和随之降低的牵引效率,固定奖励函数不能有效适应动态能效问题。通过列车状态空间约束所生成的信息并结合高速列车动力学特性,对奖励函数进行重塑,有效平衡了智能体准时和能效2个目标。
3) 深度强化学习。在马尔科夫决策过程中,将列车视为与环境互动的智能体,其中数据输入层将离线和在线数据存储为智能体的状态信息。将处理后的极大值列车轨迹数据用于初始化经验回放池,加速智能体学习。并通过TD3算法生成连续的动作以实现准确的列车运行。
2.2 列车状态空间约束
列车运行过程可分为4个工况:全牵引工况TR、巡航工况CR、惰行工况CO和全制动工况BR。这些工况的转换遵循特定规则:TR和BR不能相互转换,CR-CO是它们之间的中介。在此框架下,提出一个遵循由PMP导出的约束数据和工况区间。
为了确定在工况组合TR-CR-CO-BR下的最优列车轨迹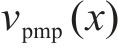
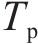
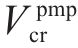
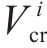
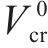
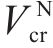
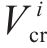
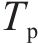
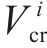
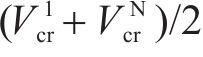
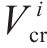
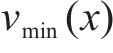
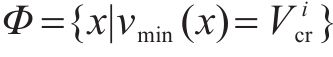
设定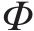
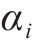
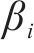
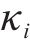
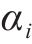
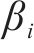
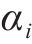
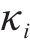
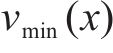
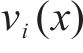
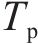
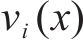
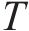
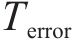

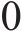
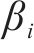
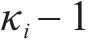

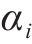
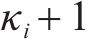
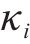
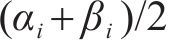
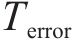
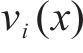
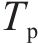
鉴于轨迹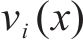
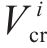
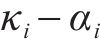
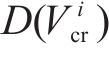
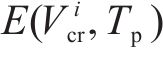
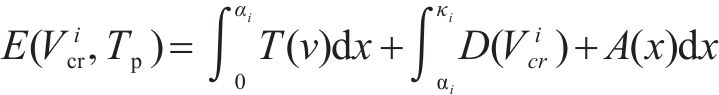
其中,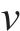
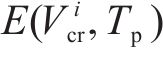
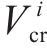
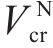
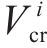
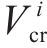
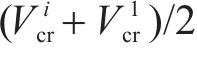
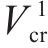
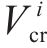
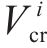
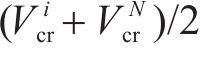
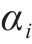
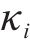
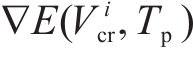
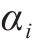
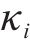
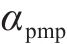
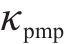
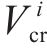
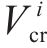
对应的状态搜索空间约束上下边界,如下:
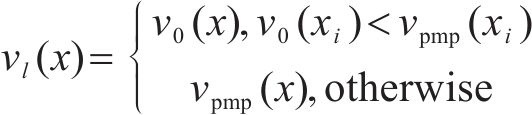
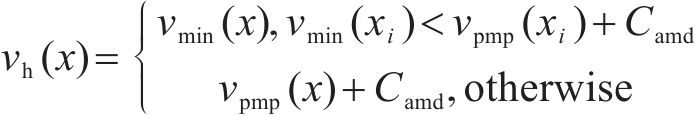
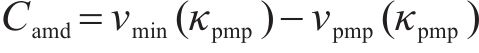
其中,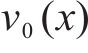
在列车的节能操作中,有以下经过论证的结论[20]:驾驶期间应避免不必要的制动。在制动前采取惰行操作以降低制动前的运行速度,有利于减少列车动能的损失。列车在起步阶段应采取全牵引操作,不可能通过优化驾驶策略来提升这部分的能效。
根据上述定义,列车运行的工况区间可分为:全牵引区间、牵引-惰行组合区间、惰行区间以及全制动区间。具体而言,当列车速度曲线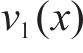
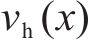
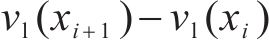
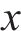
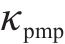
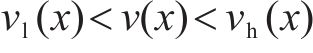
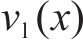
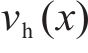
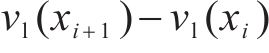
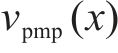
2.3 自适应奖励重塑
深度强化学习智能体的策略受到奖励信号的引导,如果奖励信号设置不合理,可能会导致智能体倾向于或忽略某一目标,从而打破目标之间的平衡。例如能效和准时目标之间存在竞争关系,对一个目标的优化可能以另一个目标的劣化为代价。此外,正奖励的阈值设置也影响训练效果。阈值过高会使智能体难以达成目标,造成梯度消失问题。阈值过低会使智能体轻易达成目标,但无法学习到更复杂的策略。
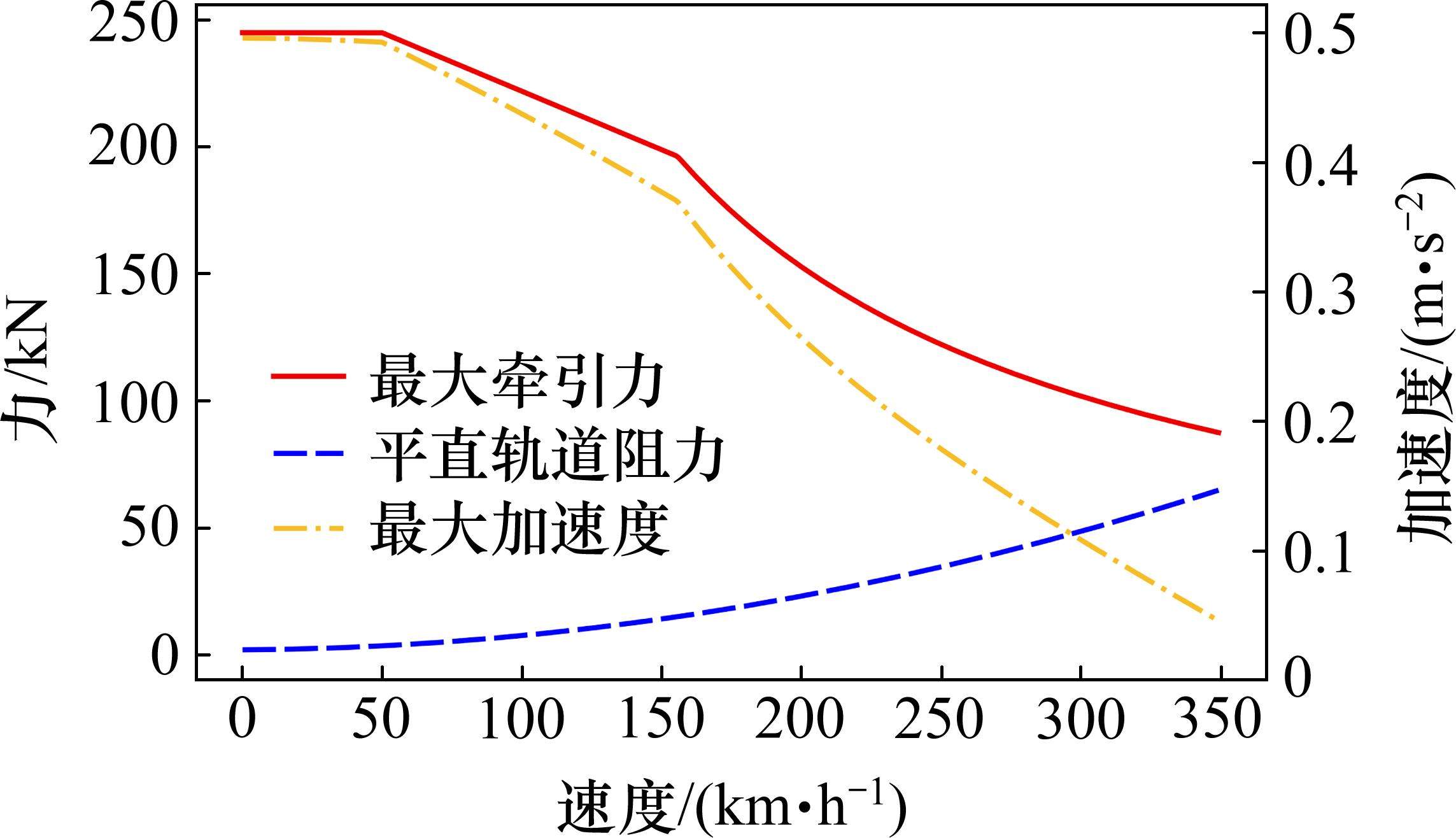
文献[14]主要通过大量的实验来人工调整,只能适应当前固定的约束。在约束更新时,需要频繁调整且难以在实际应用中得到有效应用。本文将根据列车状态空间约束计算出的极大值列车轨迹作为目标,结合速度限制、巡航里程、牵引代价来进行奖励重塑。对于能效正奖励的阈值目标选择极大值列车轨迹的能耗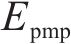
与此同时,从CO工况到TR工况的能量转换随着速度的增加而减少,更容易通过加速来提高能效。针对牵引代价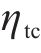
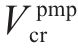
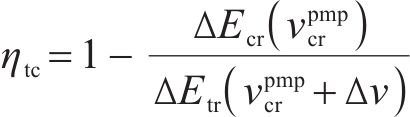
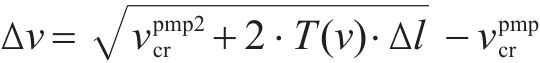
其中,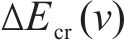
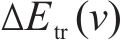
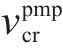
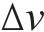
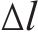
在列车运行过程中,牵引系统是能量主要的消耗来源,牵引又分为起步阶段的全牵引和运行阶段的部分牵引。起步阶段的全牵引是为了满足计划运行时间安排,这部分能量是无法节约的。而节能主要通过减少运行阶段的部分牵引。行驶过程中,牵引部分能量越多同时下坡占比越大,意味着智能体越容易去提升能效。针对巡航里程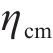
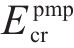
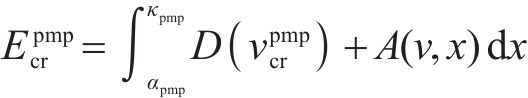
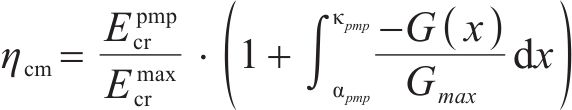
其中,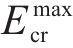
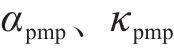
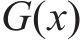
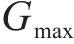
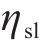
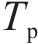
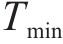
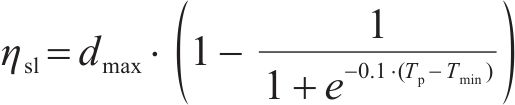
其中,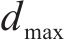
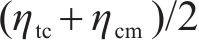
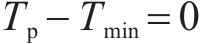
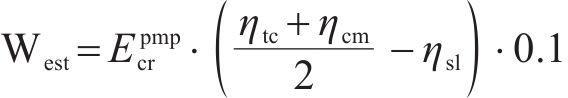
其中,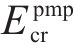

2.4 深度强化学习的马尔可夫决策过程建模
在深度强化学习中,智能体通过与环境的交互来学习如何在各种情境中做出最优决策。为了系统地描述这种交互过程,常使用马尔可夫决策过程(MDP)这一数学框架。MDP为强化学习中的决策问题提供了一个结构化的模型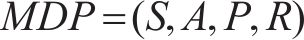
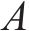
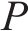

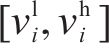
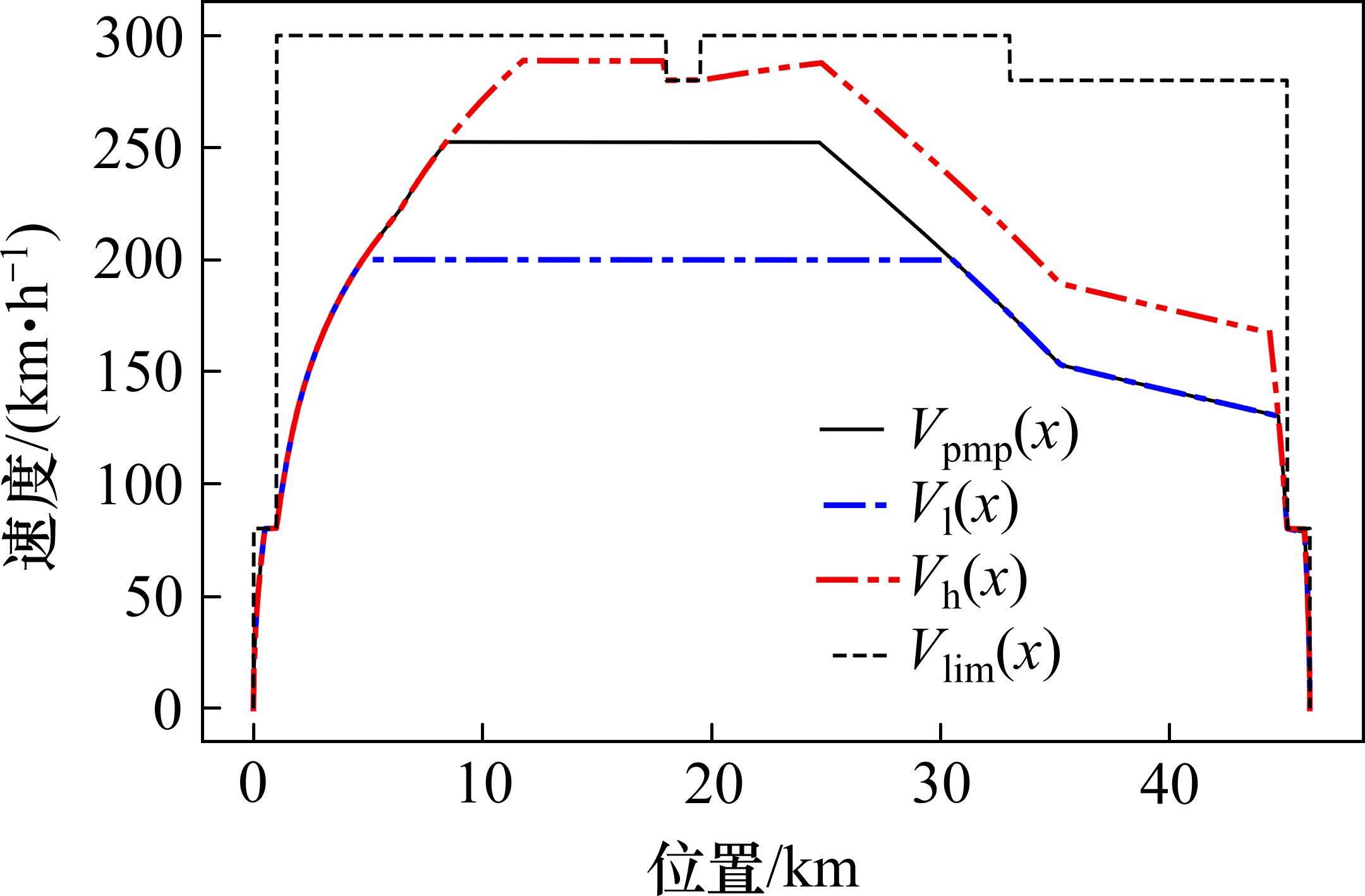
1) 状态空间定义。智能体的状态即为列车在位置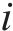
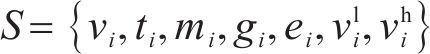
其中,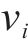
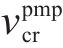
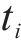
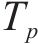
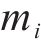
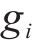
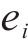
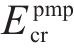
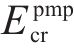
2) 动作空间定义。智能体的动作则为列车输出的功率的百分比,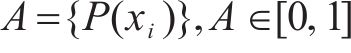
3) 奖励函数定义。在智能体与环境的交互过程中,它是以奖励信号而不是深度学习中的标签作为引导的,产生数据样本身是没有标签来判断其好坏,因此强化学习的性能的评价指标是通过奖励函数来定义。在列车驾驶策略中,需要考虑的主要因素是列车的准时、能效和乘客舒适度,将上述3点作为评价智能体驾驶质量的指标。由于列车运行中的状态不能完全反映出最优驾驶策略的差异,能效奖励和准时奖励只会在目的地给出,作为结算奖励。而列车急动度则保证乘客的舒适作为日常奖励,如下:
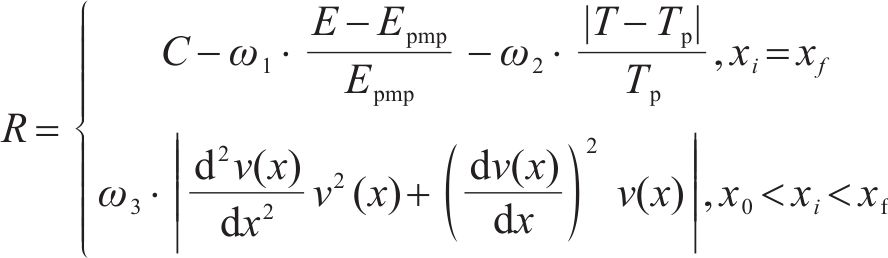
其中,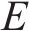
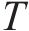

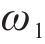
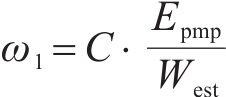
其中,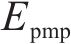
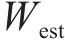
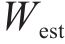
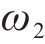
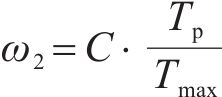
其中,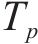
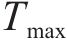
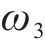
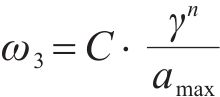
其中,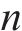
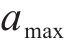
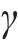

3 仿真实验及分析
3.1 仿真参数设置
1) 线路及列车相关参数。仿真实验选用京沪高铁的某一区间段线路数据。该区段上,站间限速为310 km/h和280 km/h,站内股道限速为80 km/h,线路区间长约46 km,见表1;选用CRH380A型列车,牵引特性根据在平直轨道上进行实验计算得出[21]。列车最短运行时间750 s。列车运行模拟环境使用OpenAI Gym框架,所提出的算法在Python 3.8.16中实现,并使用深度学习框架PyTorch。
| 限速/(km∙h-1) | 长度/km | 坡度/‰ | 长度/km |
|---|---|---|---|
| 80 | 1.0 | 0 | 1.52 |
| 310 | 21.0 | 3 | 4.68 |
| 280 | 1.5 | -8 | 6.11 |
| 310 | 13.0 | 3 | 6.78 |
| 280 | 8.61 | 10 | 16.01 |
| 80 | 1.0 | 0 | 11.01 |
2) 算法参数设置。HODRL算法中学习率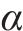

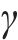
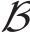
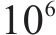
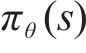
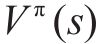
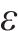
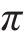
3.2 实验结果及分析
本文将3种不同的强化学算法和HODRL分别独立运行约28 000回合,并分别从收敛性、准时率、能效比、舒适度等多个指标出发,对实验结果进行比较分析。同时通过分别独立运行分层优化层中的列车状态空间约束和自适应奖励重塑,用以对比DRL智能体训练最优驾驶策略的效果。
3.2.1 基线算法与HODRL算法性能对比
HODRL通过与当前DRL中主流的3种算法进行对比,分别为DDPG[10]、TD3[11]、PPO[12]算法。这些算法都是基于在线或离线策略的连续动作空间强化学习算法,具有一定的代表性并广泛应用。它们使用相同的网络结构、超参数和训练环境,用以保证可比性。并以PMP算法的能耗值作为强化学习的基线值。
图4展示了其训练过程中的奖励曲线,从图中可以看出,HODRL算法在收敛速度、稳定性,以及智能体的策略质量方面,均明显优于其他基线算法。在约4 000个回合后,该算法即可达到较高奖励值,并在之后的训练中保持较小波动。相比之下,其他3种基线算法表现出较大的差异和不稳定性。其中,PPO算法在训练结束时仍未达到收敛状态。DDPG和TD3算法虽然最终收敛,但其收敛速度很慢且奖励值波动频繁。这些基线算法在初期训练阶段受到边界值的影响,因为边界值往往是无效的。相比之下,HODRL算法采用了分层优化的方法,有效地缩减了状态搜索空间,降低了惩罚奖励,加快了在搜索空间范围内寻找可行驾驶策略的速度。这也说明了在回合步数较长情况下,状态搜索空间过大将导致梯度消失这一问题。
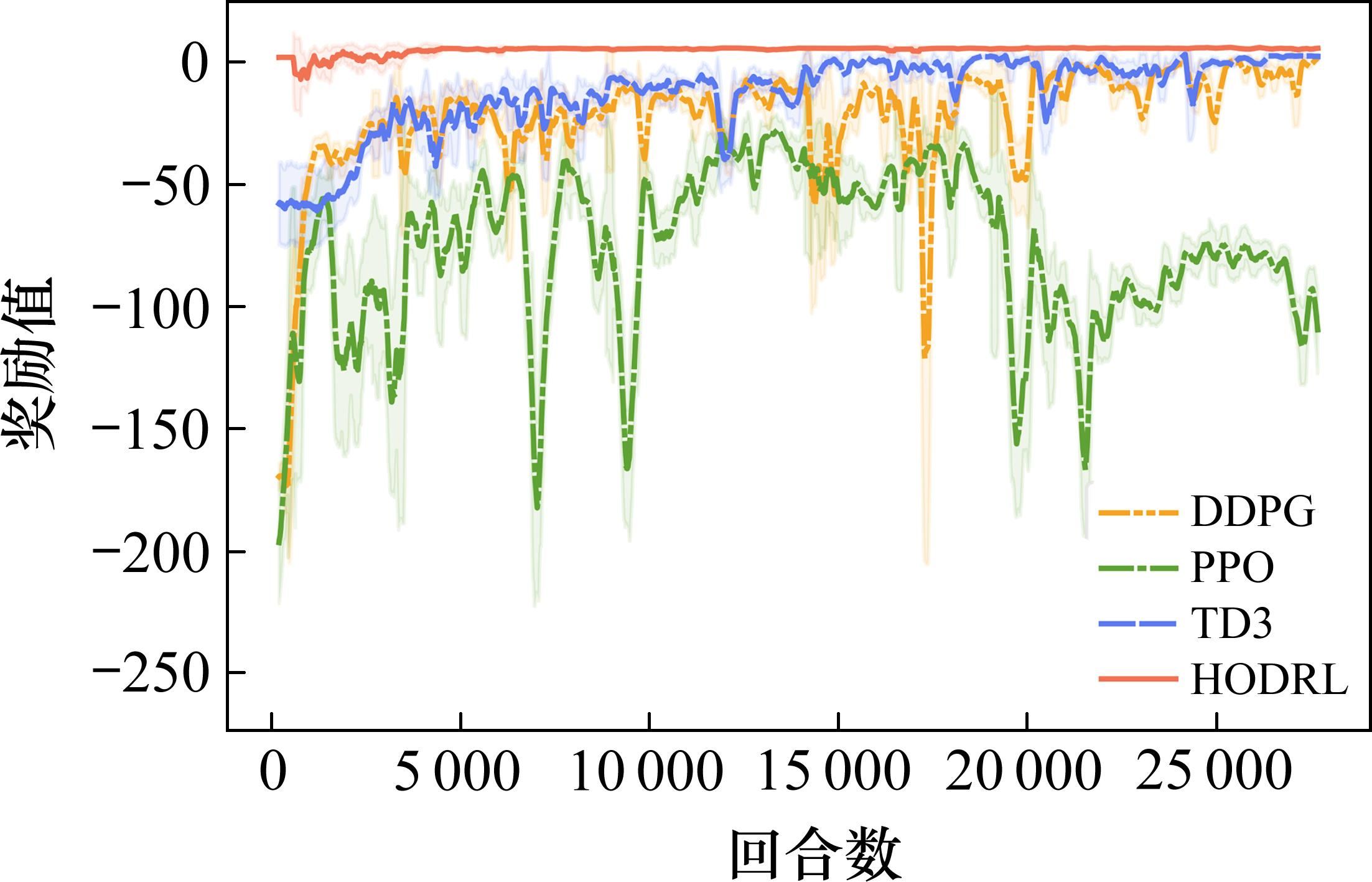
表2列出了HODRL和各种基线算法在计划运行时间950 s下的性能指标,包括列车运行时间误差、能耗、舒适度和奖励方差,数据源于各自的最优策略。其中舒适度指标反映了列车在行驶过程中驾驶曲线的波动程度,应当控制在一个尽可能低的水平,以此确保乘客体验和安全。从表中可看出,HODRL算法在列车运行的3项关键指标均取得了最佳的效果并具有最小奖励方差,证明了该算法的有效性。其中HODRL中的分层优化层时间复杂度为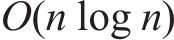
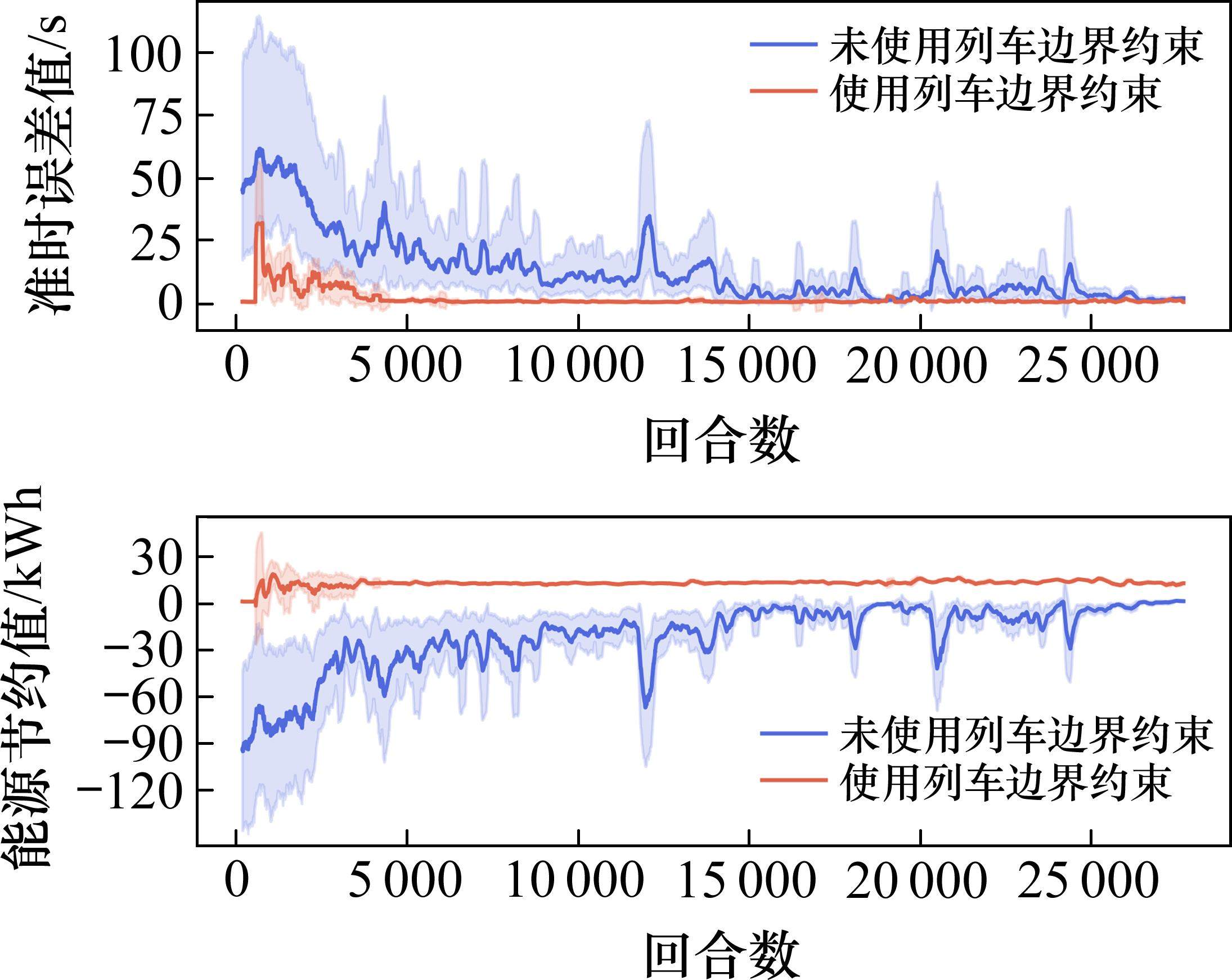
| 算法 | 准时误差/s | 能耗/kWh | 能效提升/% | 舒适度/m/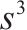 | 奖励方差/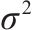 |
|---|---|---|---|---|---|
| HODRL | 0.058 | 576.27 | 1.84 | 1.24 | 3.24 |
| TD3 | 0.419 | 583.23 | 0.65 | 3.09 | 18.44 |
| PPO | 6.325 | 611.09 | -4.09 | 7.14 | 35.86 |
| DDPG | 1.214 | 586.17 | 0.153 | 5.42 | 27.52 |
| PMP | 0.057 | 587.07 | — | 1.69 | — |
图5展示了HODRL算法在不同计划运行时间下的最优驾驶策略。对比图中的驾驶轨迹,可得以下驾驶策略:在列车起步阶段,智能体选择全功率牵引以快速增加列车的动能;在运行阶段,根据坡度变化和计划运行时间调整牵引和惰行的组合以利用坡度的势能变化;在下坡段,倾向于惰行或低功率牵引以节省能量;在上坡段,选择适当的牵引力度以避免坡度势能损失,并保持适当的速度;在结束阶段,选择惰行操作以利用之前积累的动能,满足计划运行时间要求。
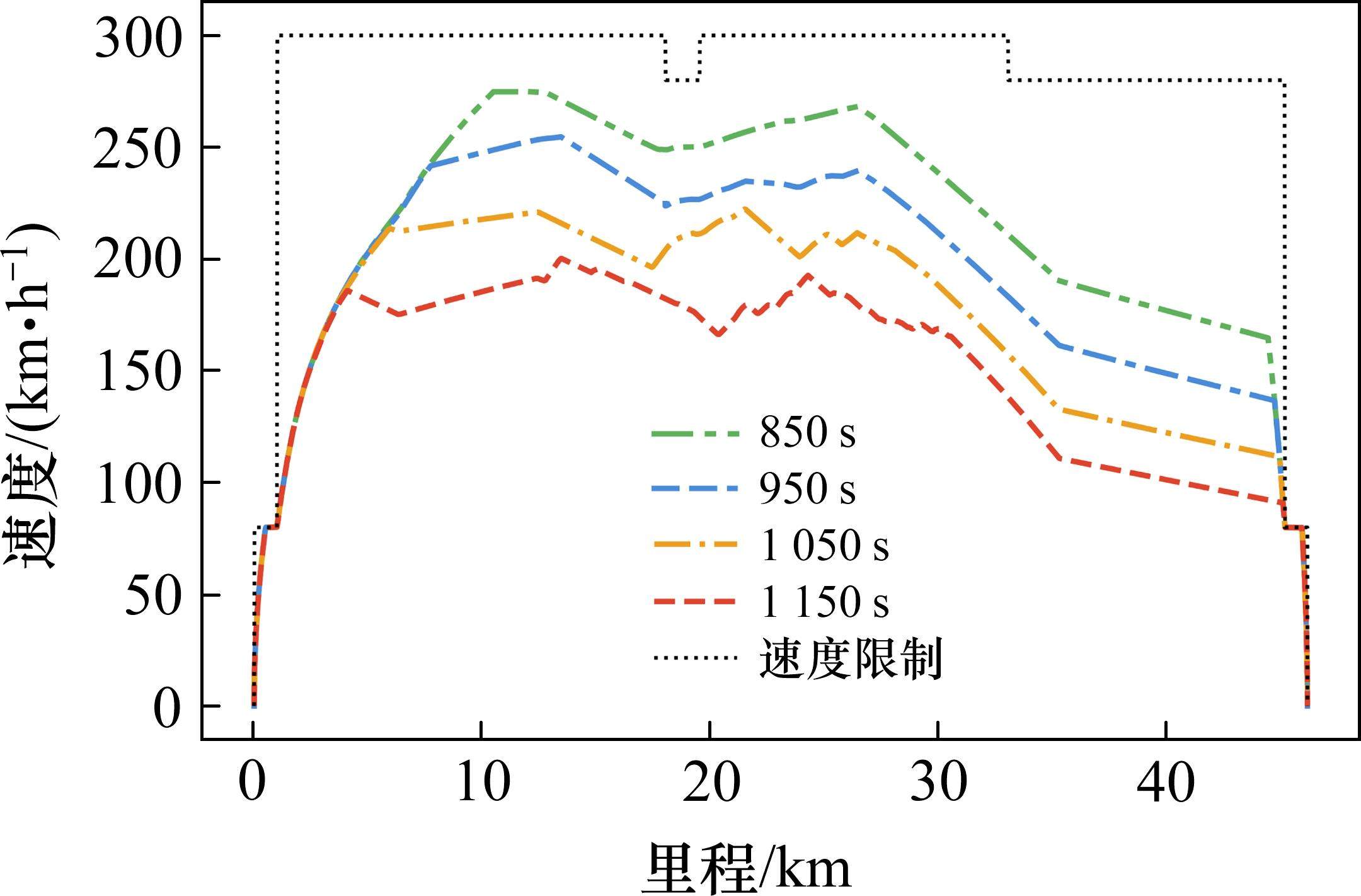
表3对比了使用分层优化前后,强化学习层中的智能体在4个不同的计划运行时间下的实际表现,其中HODRL算法中强化学习层的算法为TD3。从表3可看出,HODRL算法显著地降低了列车能耗,且都低于其阈值能耗目标,并且收敛速度比未使用分层次优化方法的TD3算法加快,达到了约一个数量级。同时智能体的实际运行时间与计划运行时间之间的误差都在±0.1%的允许范围内。
| 计划运行时间/s | 阈值能耗/kWh | HODRL | TD3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
准时误 差/s | 能耗/ kWh | 能效提升/% | 收敛回 合/ | 准时误 差/s | 能耗/ kWh | 能效提升/% | 收敛回 合/ | ||
| 850 | 701.00 | 0.045 | 683.72 | 2.47 | 3.7 | 0.445 | 690.45 | 1.50 | 24.6 |
| 950 | 587.07 | 0.058 | 576.27 | 1.84 | 4.3 | 0.419 | 583.23 | 0.65 | 26.9 |
| 1 050 | 525.25 | 0.103 | 506.67 | 3.54 | 3.6 | 0.794 | 512.31 | 2.46 | 24.2 |
| 1 150 | 480.08 | 0.062 | 456.33 | 4.95 | 3.8 | 0.208 | 465.59 | 3.02 | 25.1 |
3.2.2 列车状态空间约束有效性对比
通过状态空间约束,在计划运行时间为850,950,1 050和1 150 s计划运行时间下分别过滤了83.65%、80.71%、79.13%、75.24%的状态空间,有效缓解了智能体前期探索的盲目性,提升了学习效率。
图5对比了在计划运行时间950 s下,HODRL算法的最优能效轨迹和能效阈值轨迹,以及列车相应的运行工况区间。图中空白区域代表被剔除的状态空间,大量无效状态空间被过滤掉。空间内的不同颜色区域反映出不同的工况区间,也就是智能体可以选择的动作范围。其中最上面的虚线表示能效阈值轨迹,该轨迹是在不考虑坡度的理想情况下的局部最优解,平均准时误差小于0.1%,满足计划运行时间。从图中可以看出,最优能效轨迹位于能效阈值轨迹的附近,验证了列车状态空间约束的有效性。
图6对应计划运行时间下的能效阈值轨迹和最优能效轨迹的能效曲线。在初始牵引阶段,最优能效轨迹和能效阈值轨迹都采用全功率牵引,以最快速度提升自身动能,轨迹重合。随后最优能效轨迹在短暂牵引后转为惰行操作,利用长度6.11 km下坡段,通过坡度势能增加列车的动能。在利用完下坡段的势能后,需要再次进行牵引,以防止列车动能过大的损失。虽然最优能效轨迹在初始阶段为加速消耗了更多能量,但在后续过程中通过利用坡度势能节约下来的能量则更多。
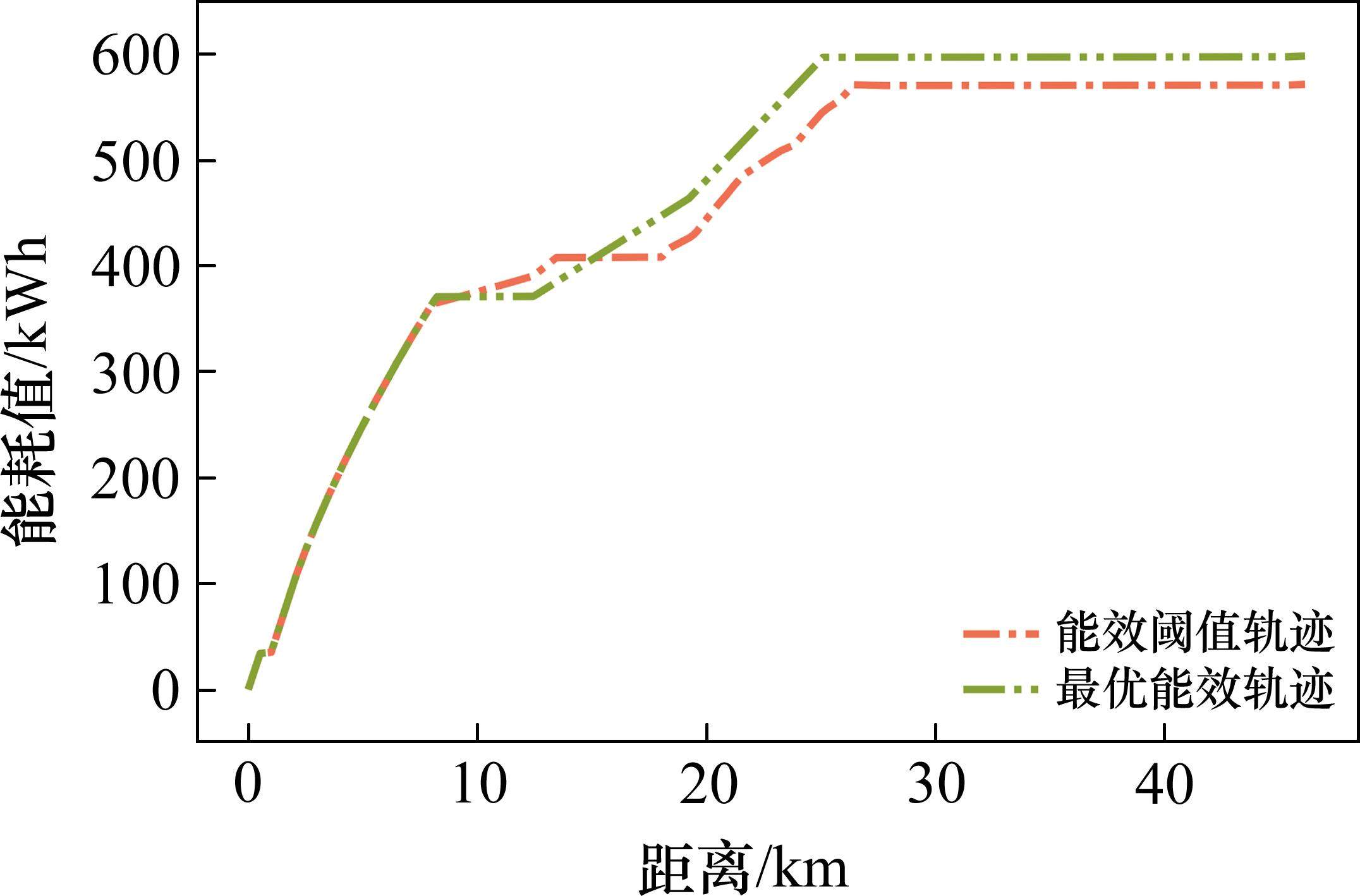
图7展示了使用列车状态空间约束前后的能效和准时目标效果曲线。可以明显看出,智能体能够快速学习到能效和准时的技巧,并产生更稳定且可行的驾驶策略。HODRL算法仅消耗TD3约16.67%的计算资源,就能让智能体获得更高质量的策略,并产生更有价值的动作。同时,HODRL只需要约4 000回合的迭代,奖励曲线就趋于稳定,而TD3则需要约24 000回合。
3.2.3 自适应奖励重塑有效性对比
通过自适应奖励重塑,可以有效平衡智能体对于能效目标和准时目标之间的权衡。即通过能效目标和准时目标中分别能够获得的最大奖励是相似的,因此预计节能和实际节能应尽可能地接近智能体实际表现。
表4为自适应奖励重塑对能效效率提升效果的对比,每个智能体经过5 000轮训练。预计能效越大任务越简单。从表中预计能效还可观察到,在不同调度运行时间下,能效的复杂度有所不同。例如,在计划运行时间为950 s,实际节能量只有计划运行时间为1 150 s下实际节能量的45.47%,说明需要给予更大的节能奖励信号,才能让智能体在能效目标和准时目标之间保持平衡。
| 计划运行时间/s | 预计节能/kWh | 实际节能/kWh | 误差/kWh | 阈值能耗/kWh | 预计能效/% |
|---|---|---|---|---|---|
| 850 | 21.64 | 18.92 | 2.72 | 701.00 | 3.09 |
| 950 | 12.50 | 11.15 | 1.35 | 587.07 | 2.13 |
| 1 050 | 16.73 | 18.19 | 1.46 | 525.25 | 3.19 |
| 1 150 | 23.16 | 24.30 | 1.14 | 480.08 | 4.82 |
图8展示了在计划运行时间范围从800~1 300 s,以每50 s间隔为单位,进行了自适应奖励重塑估计的预计节能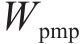
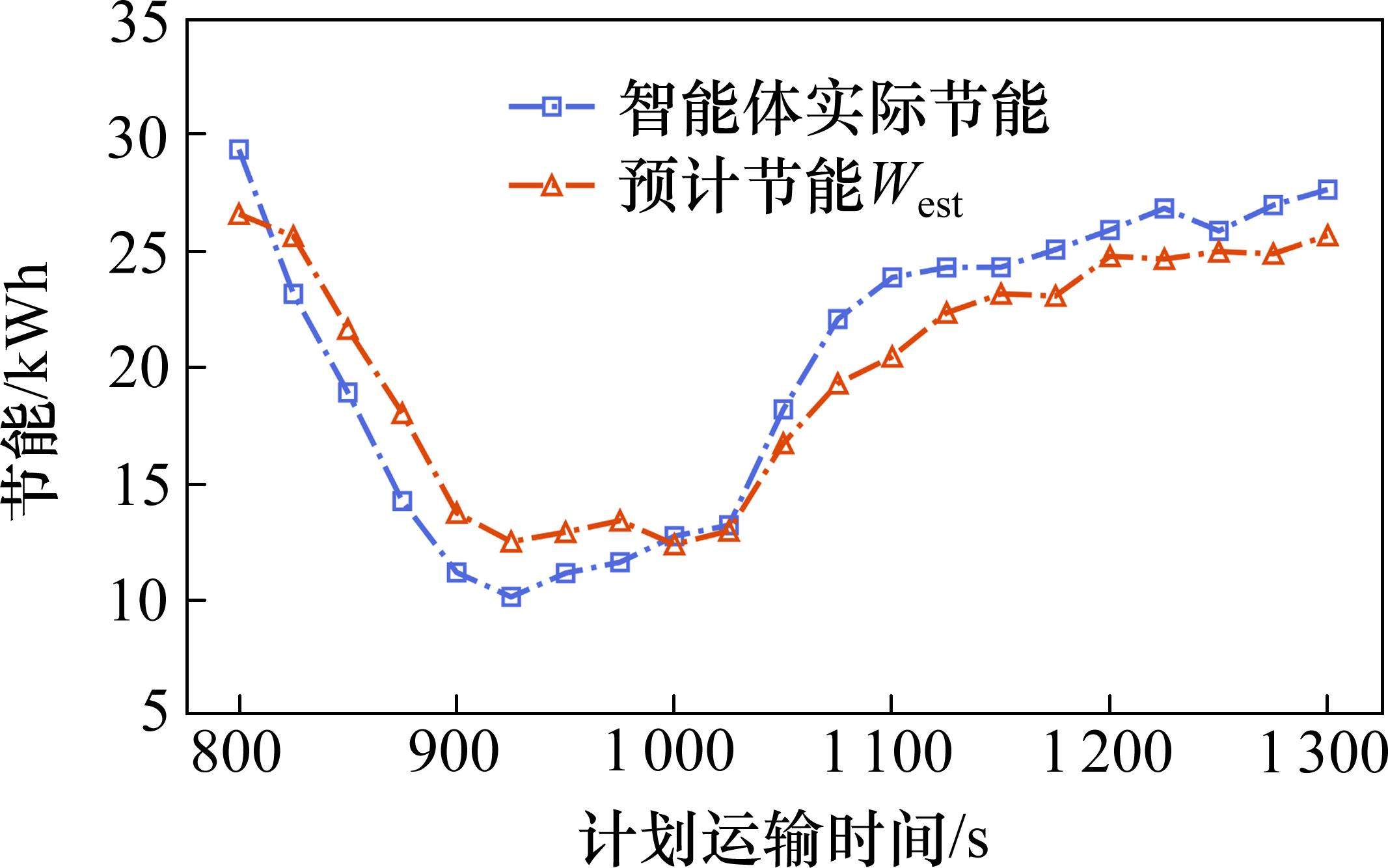
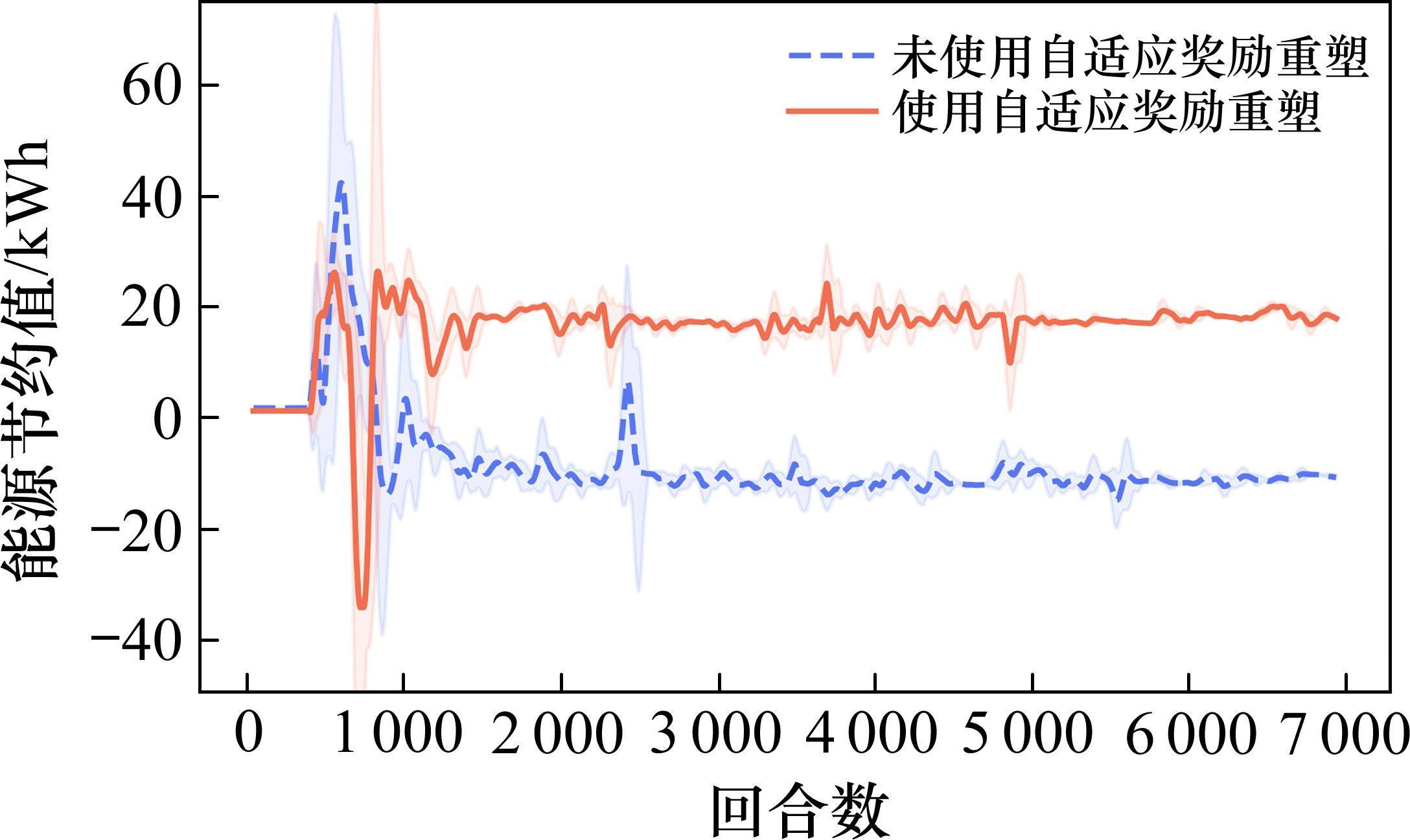
图9展示了在计划运行时间为950 s时,是否使用自适应奖励重塑对智能体的能效目标影响。在不使用自适应奖励重塑时,能效权重的选择是基于计划运行时间为1 150 s计算出的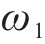
4 结论
1) 提出的算法通过列车状态空间约束,有效过滤了大量不可行的状态搜索空间,加速智能体学习状态与动作之间的映射关系,降低了探索的盲目性,同时结合先验知识避免了大量固定的动作序列,智能体只需要寻找牵引-惰行组合以及惰行-制动点,进一步减缓智能体学习难度。
2) 所提算法还采用了自适应奖励重塑,将当前计划运行时间下极大值列车轨迹的轨迹能耗作为智能体的正奖励阈值目标,并结合高速环境下的列车动力学寻找运行时间和能效的平衡点。该算法解决了在列车动态能效中难以确定阈值目标以及竞争目标之间的权衡问题。算法的奖励函数具有自适应能力,能够适应不同的调度任务和实际环境,而不需要人工频繁调整。
基于本文研究成果,未来工作将进一步完善列车实际运行环境下的约束条件,将结合列车再生制动技术和多智能体强化学习算法重点研究多智能体强化学习在多列车协同节能驾驶策略中的应用。
徐凯,张皓桐,张淼等.基于深度强化学习的高速列车驾驶策略优化[J].铁道科学与工程学报,2025,22(01):25-37.
XU Kai,ZHANG Haotong,ZHANG Miao,et al.Deep reinforcement learning for operation strategies optimization in high-speed trains[J].Journal of Railway Science and Engineering,2025,22(01):25-37.