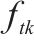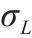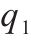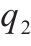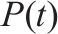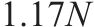重载铁路运输具有运能大、效率高、成本低等优势,在大宗战略物资运输方面发挥了关键作用,是我国铁路运输事业发展的主要方向之一[1-2]。预应力混凝土简支T梁因自重轻、刚度大、整体性好等特点,被广泛应用于重载铁路。然而,重载铁路PC简支T梁在服役期内长期承受重载列车荷载作用,导致开裂病害频发,典型情况包括跨中正截面开裂和梁端腹板斜截面开裂,严重影响了桥梁结构的耐久性能[3]。因此,需对重载铁路PC简支T梁服役期内的开裂病害加以评估与控制。为评估PC梁的抗裂性能,众多学者开展了研究工作。李进洲等[4]考虑预应力损失和混凝土抗拉强度的疲劳折减建立了PC梁的正截面疲劳抗裂验算公式,并分析了不同轴重下实桥的开裂寿命。HU等[5]通过缩尺试验和有限元分析研究了PC梁正截面的开裂规律,结果表明优化预应力筋布置能够有效提高开裂弯矩。李承君等[6]对重载铁路线上3种梁型的静力开裂性能进行了检算,结果显示部分梁型的在运营荷载下斜截面内力已超出规范限值。葛凯等[7]分析了PC梁典型斜截面在运营荷载下的主压应力和主拉应力时程,基于分析结果判断腹板斜裂缝的主要成因为混凝土疲劳损伤累积。刘永前等[8]通过运营性能测试得出,列车荷载提升对重载铁路PC梁腹板斜裂缝的影响强于混凝土强度等级变化和预应力损失。以上PC梁抗裂性能研究均在确定性条件下开展。但通常情况下结构的材料特性、几何尺寸以及列车荷载均具有明显的随机性和时变性,确定性研究无法反映客观的结构损伤状态[9]。因此,有关学者基于可靠度理论开展了PC梁抗裂性能研究。杜斌[10]基于广义抗力退化模型,应用FORM法分析了PC梁的正截面抗裂可靠度。陈强[11]以腹板内主拉应力达到容许应力限值为极限状态,通过Monte-Carlo模拟方法分析了预应力箱梁桥腹板开裂概率。YANG等[12]应用不确定性分析方法结合预应力长期损失与腐蚀扩展模型分析了腐蚀PC箱梁的腹板正截面开裂概率。既有研究主要基于时点可靠度方法分析静力条件下PC梁的正截面抗裂可靠度,鲜有基于时变可靠度方法的考虑列车荷载疲劳效应的重载铁路PC梁正截面和斜截面抗裂可靠度研究。本文考虑疲劳预应力损失,开展重载铁路PC简支T梁在列车荷载长期作用下的正截面和斜截面抗裂时变可靠度分析。建立T梁正截面和斜截面抗裂时变极限状态函数;开展列车荷载的作用效应分析,建立与荷载历程相关的疲劳预应力损失模型;应用PHI2方法开展多工况下实桥正截面和斜截面的抗裂可靠度评估;开展抗裂时变可靠度指标对前期预应力损失和二期恒载的敏感性分析。本研究可为重载铁路PC简支T梁的设计与养护维修提供参考。
1 抗裂时变极限状态函数建立
重载铁路PC简支T梁设计标准为全预应力混凝土构件[13],属于严格要求不出现裂缝的构件。本文基于预应力混凝土梁正截面和斜截面开裂极限状态分析,考虑列车荷载疲劳效应建立了重载铁路PC简支T梁正截面与斜截面抗裂时变极限状态函数。
1.1 正截面抗裂时变极限状态函数
重载铁路PC简支T梁在均布恒载及列车荷载作用下的梁内最大弯矩响应出现在跨中截面,因此,本文选取跨中截面受拉边缘作为正截面抗裂时变可靠度分析的最不利位置。而当跨中截面受拉边缘混凝土所受荷载应力超出其抗拉强度与有效预应力之和,认为此时达到开裂极限状态,则正截面抗裂时变极限状态函数可定义为:
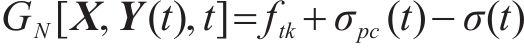
式中: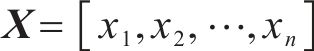
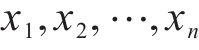
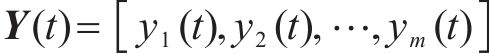
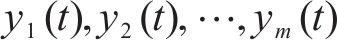
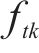
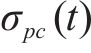
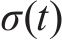
参照《混凝土结构设计规范》(GB 50010—2010)[14],混凝土预压应力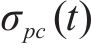
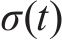
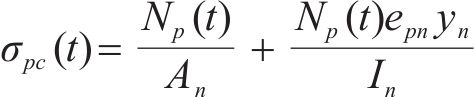
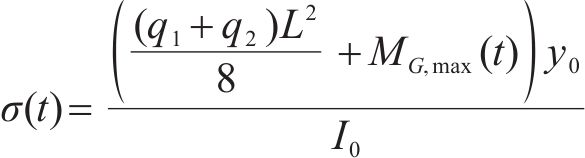
式中: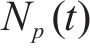
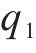
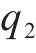
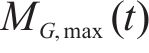
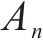
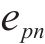
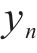
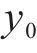
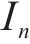
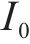
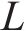
1.2 斜截面抗裂时变极限状态函数
分析认为,当T梁腹板上某计算点的主拉应力大于混凝土抗拉强度时,达到斜截面开裂极限状态。文献[3]中对朔黄重载铁路的病害调研结果显示,32 m预应力混凝土简支T梁的斜裂缝主要出现在支座至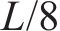
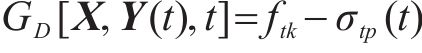
式中: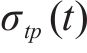
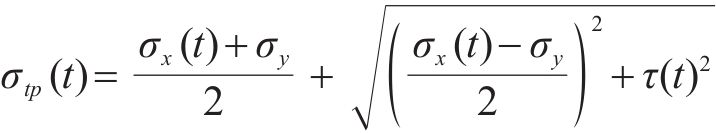
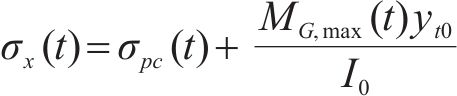
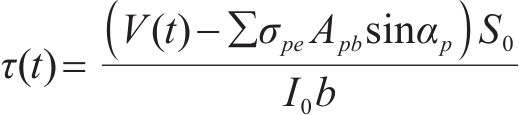
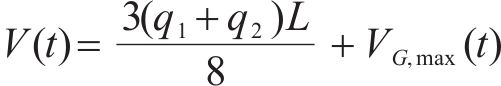
式中: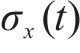
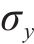
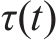
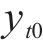
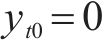
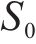
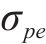
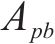
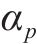
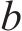
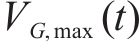
1.3 列车荷载作用效应
单节列车对简支梁桥的竖向荷载作用可简化为组合集中荷载形式,如图1所示。
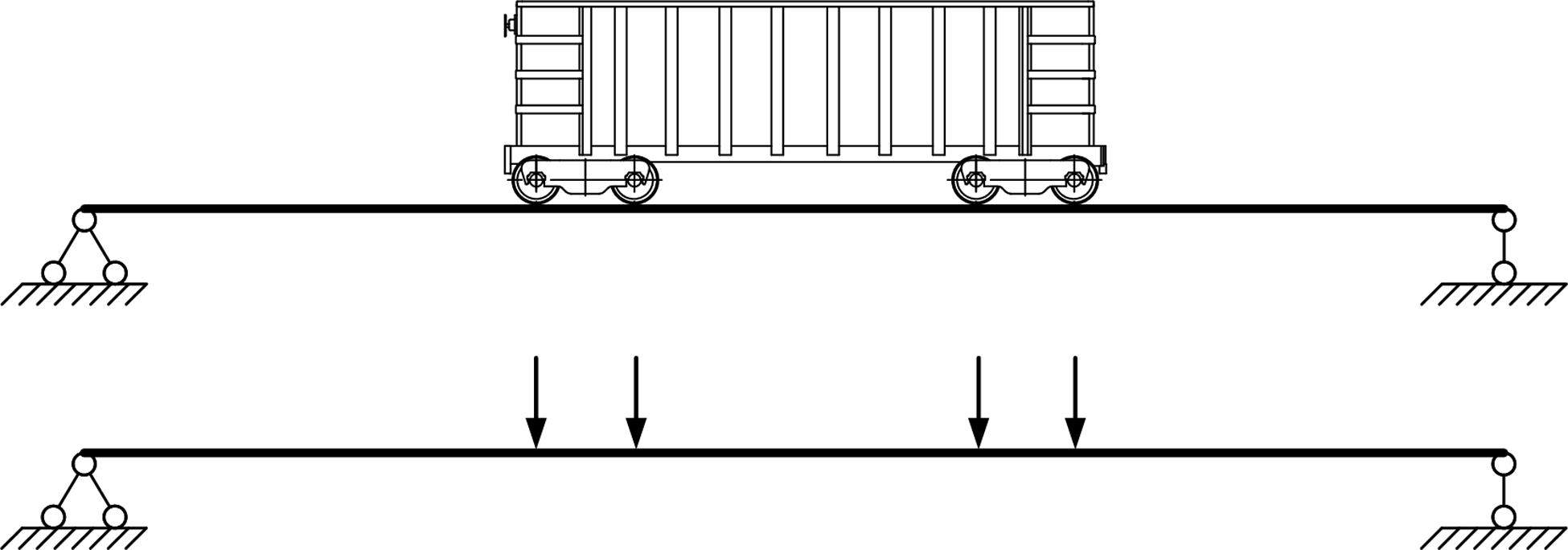
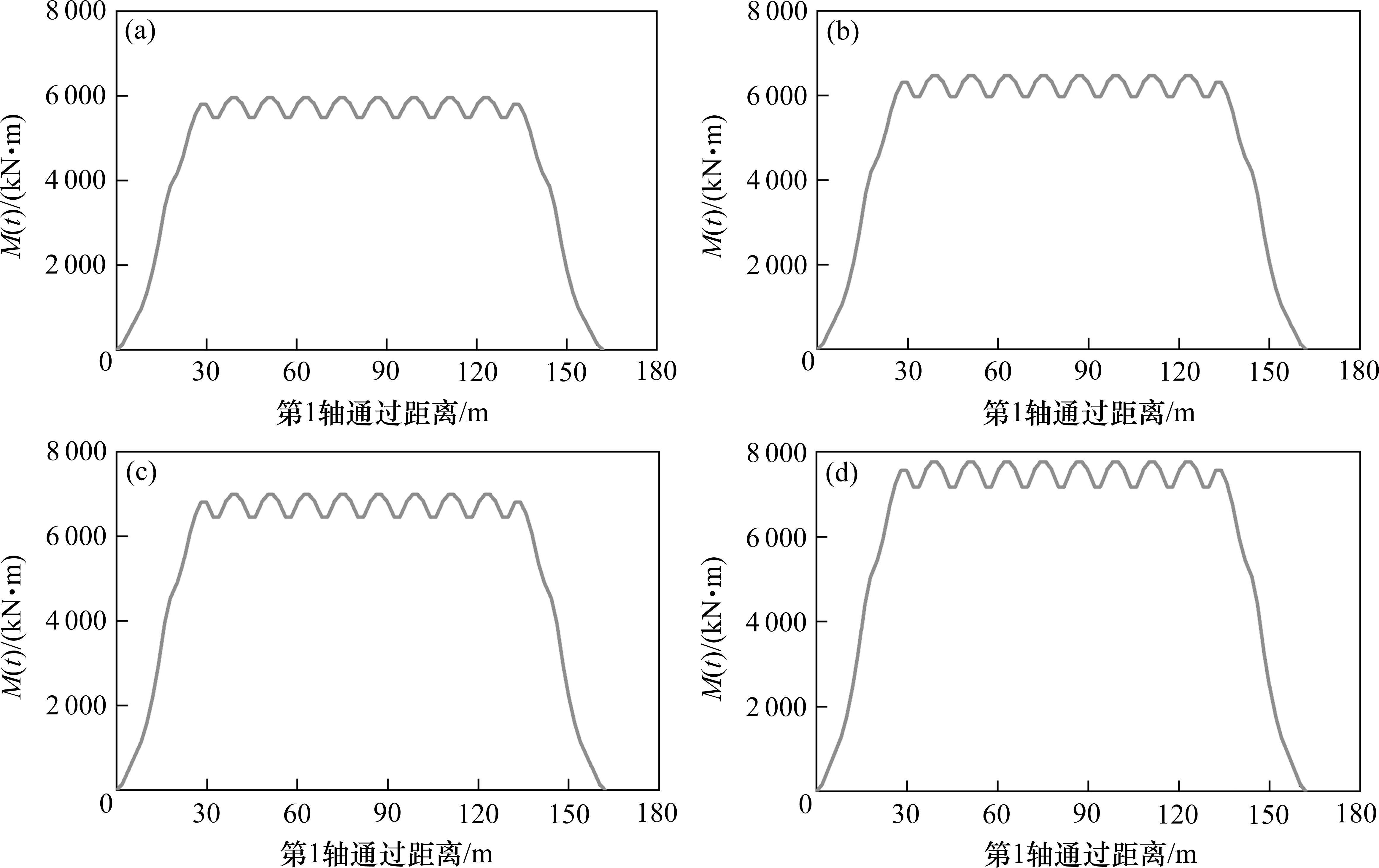
重载铁路PC简支T梁跨度一般为24~32 m,重载列车单节长度一般为12~14.5 m,根据移动集中荷载法原理可近似得到z节列车的编组过桥时在计算截面产生的弯矩和剪力响应示意图(此处只做定性分析,具体弯矩和剪力响应图见3.2节)如图2所示。
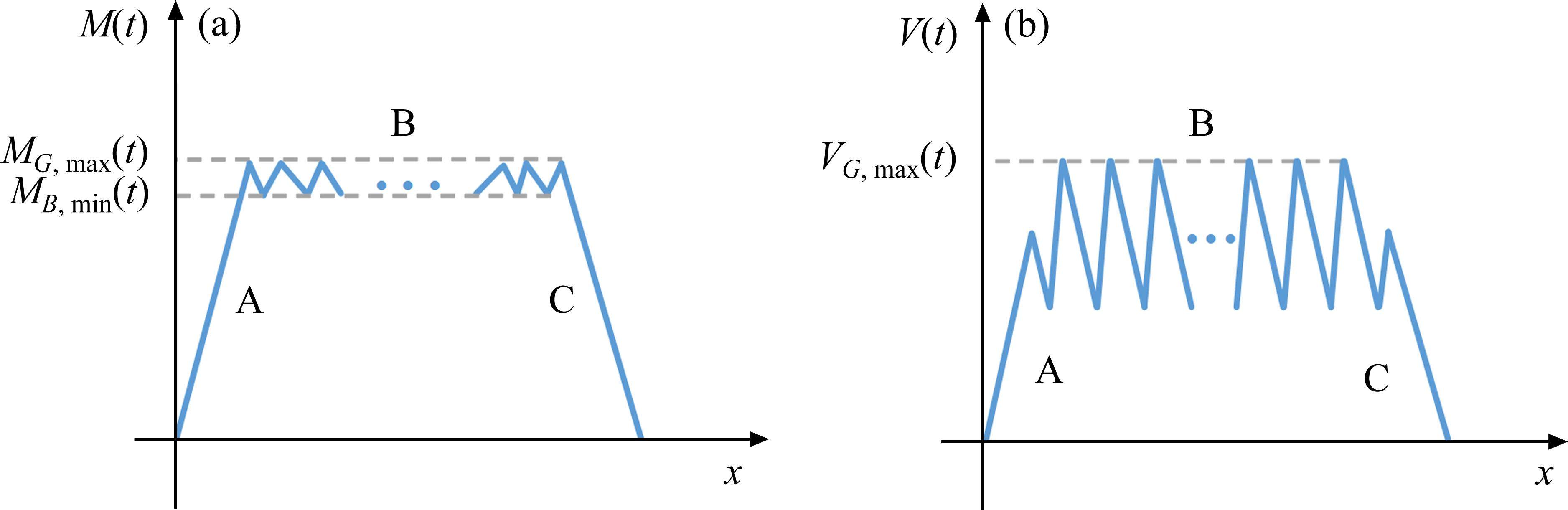
弯矩与剪力响应均可分为A、B、C共3个阶段,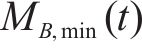
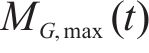
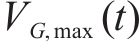
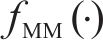
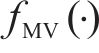
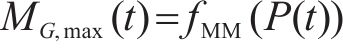
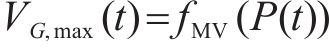
式中: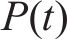
将式(2)、式(3)和式(9)代入式(1)可得到正截面抗裂时变极限状态函数为:
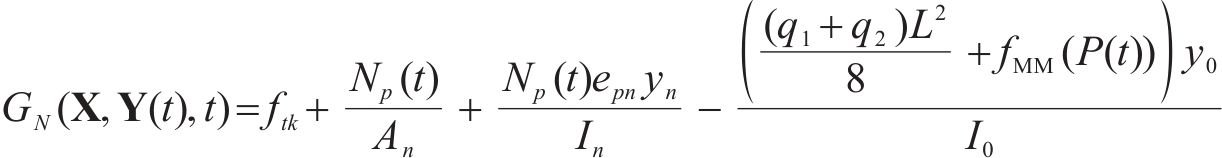
同样,将式(5)和式(10)代入式(4)可得到斜截面抗裂时变极限状态函数为:
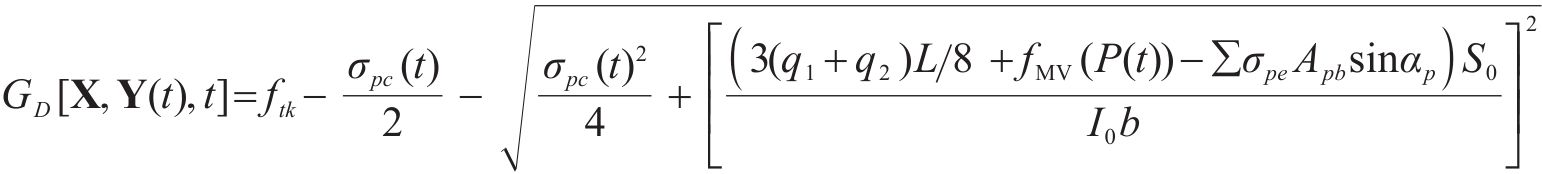
同时,列车荷载疲劳效应主要来自于弯矩时程中的循环部分,其中包括B阶段的波动循环和由A阶段和C阶段组合构成的1次峰值循环。实际工程中,由于轨道不平顺等随机激励作用导致波动循环部分呈现微小而复杂多变的特点,给疲劳分析带来困难[15]。因此本文为简化疲劳分析,基于移动集中荷载法所得到的列车荷载作用在计算截面产生的弯矩响应时程,将波动循环近似为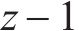
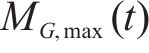
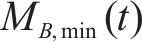
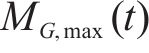
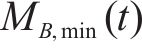
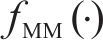
1.4 疲劳预应力损失
疲劳荷载作用下,疲劳损伤累积在混凝土中产生的不可恢复的动力徐变是导致有效预应力降低的主要原因[4]。动力徐变可由静态平均应力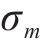
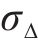
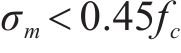
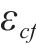
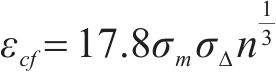
式中: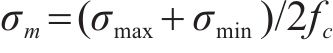
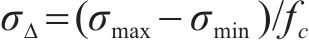
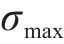
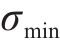
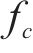
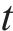
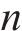
预应力混凝土梁预应力筋重心处混凝土的动力徐变一般为压应变,这将导致有效预应力的降低。参照《混凝土结构设计规范》(GB 50010—2010)[14]中混凝土收缩徐变导致的预应力损失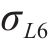
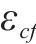
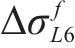
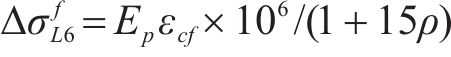
式中: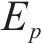
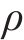
考虑前期预应力损失与疲劳预应力损失的预加力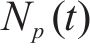
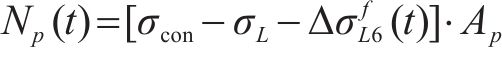
式中: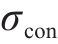
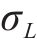
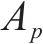
2 PHI2时变可靠度分析方法
结构在
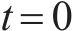
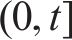
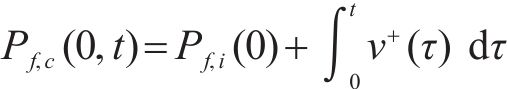
式中: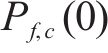
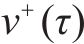

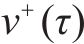
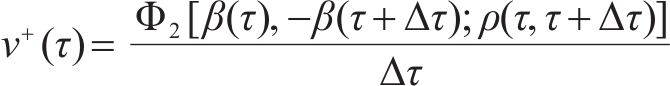
式中: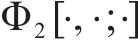
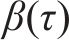
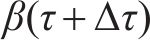

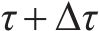
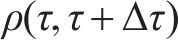

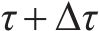
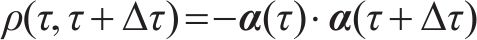
式中: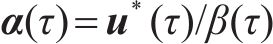
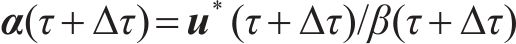

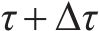
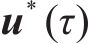
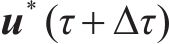

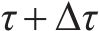
计算得到失效概率后,可根据式(19)计算相应可靠度指标:
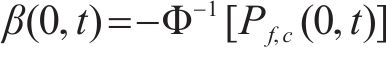
式中: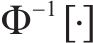
3 工程应用
本节以在重载铁路桥梁中占比最高的32 m重载铁路PC简支T梁为研究对象,开展正截面与斜截面抗裂时变可靠度研究。
3.1 工程概况
32 m重载铁路PC简支T梁高2.5 m,宽1.92 m,布置18束24Φ5钢丝束,2束18Φ5钢丝束,高强度钢丝极限抗拉强度为1 600 MPa,张拉控制应力为1 248 MPa。梁体混凝土标号为500号,按照C48混凝土抗拉强度标准值取2.68 MPa。普通钢筋为直径8 mm和10 mm的T20MnSi螺纹钢筋,材料参数可参考新标准HRB335级钢筋,T梁设计使用年限为100年,查阅资料得到一期恒载集度设计值为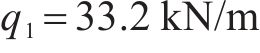
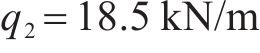
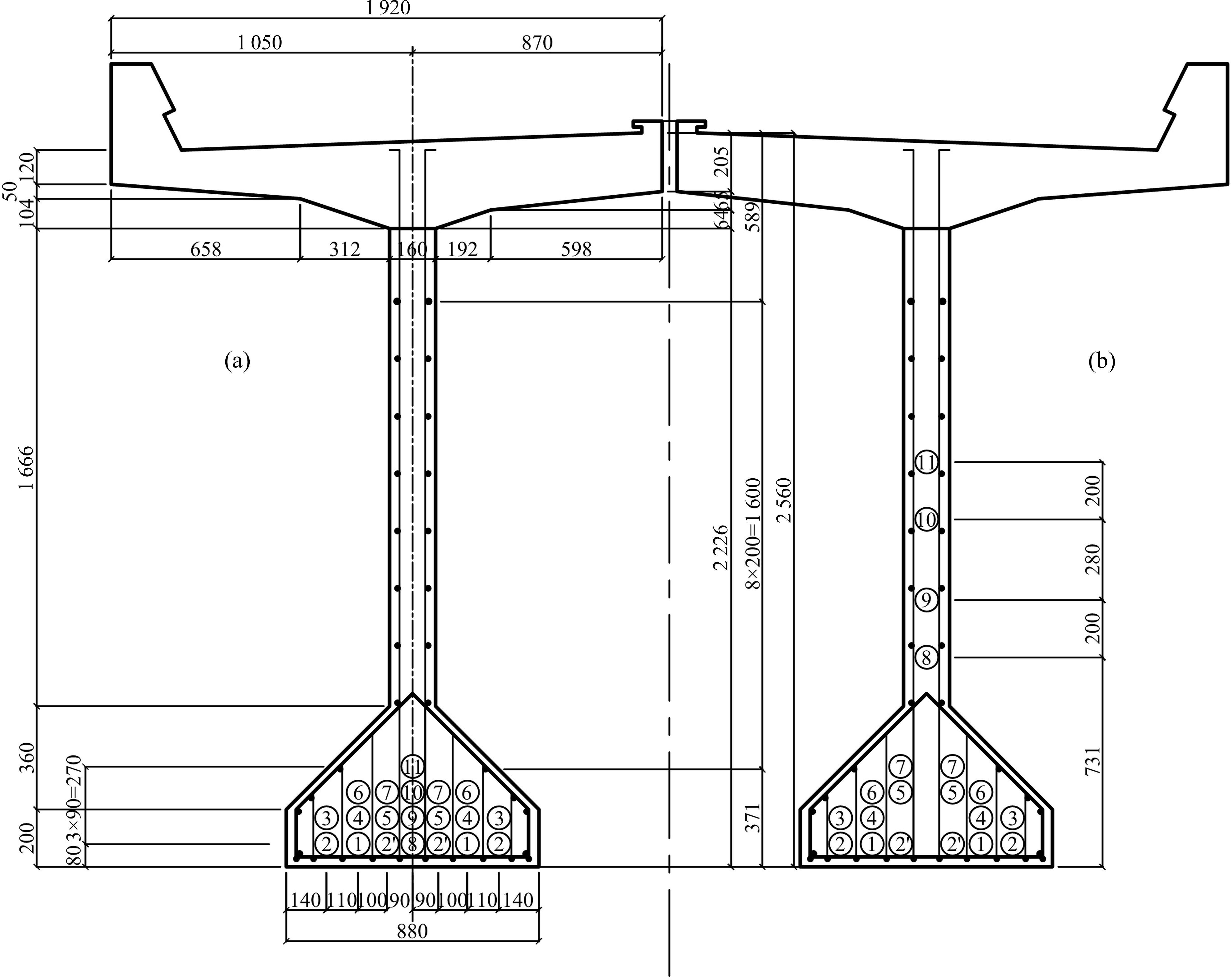
3.2 列车荷载及开行工况
本文选取重载铁路线上通行频率较高的列车编组进行计算,由216节C80重载货车组成,单节计算长度为12 m,平均轴重为N=25 t,荷载图示如图4。

C80列车单节载重80 t,单列列车满载运载量为1.73万t,参考某重载铁路最大年运量3.68亿t,换算得到日通行频率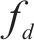
| 项目 | 工况A | 工况B | 工况C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 列车轴重/t | 23 | 25 | 27 | 30 | 25 | 23 | 25 | 27 | 30 | |||
| 日通行频率 | 59 | 40 | 59 | 80 | 100 | 64 | 59 | 55 | 49 | |||
考虑动载效应引入冲击系数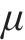
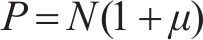
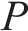
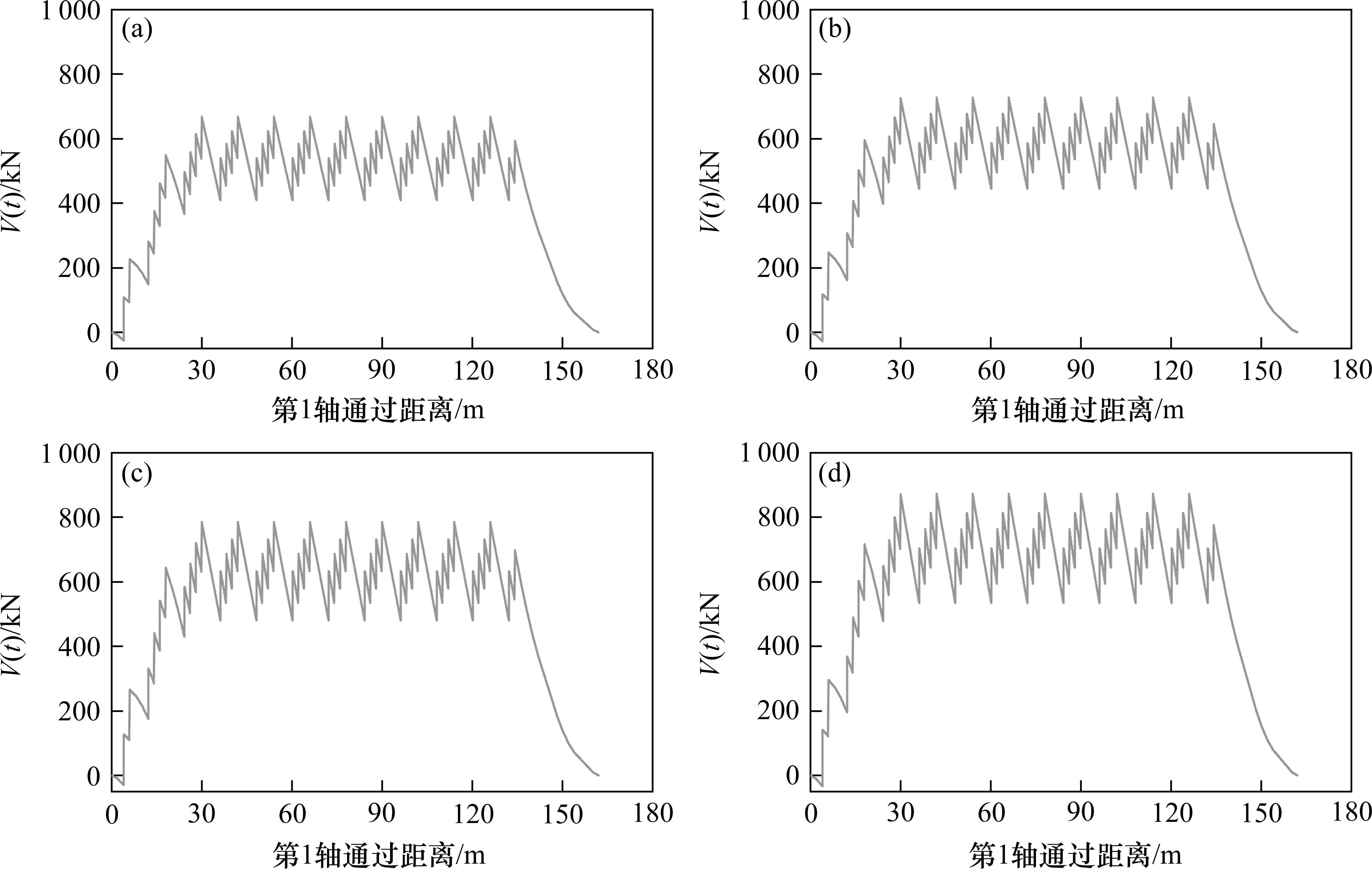
按照1.3节列车荷载疲劳效应分析结合计算工况,式(13)可以写成如下形式:
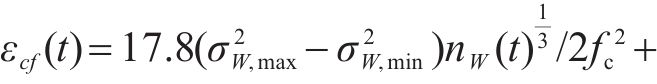
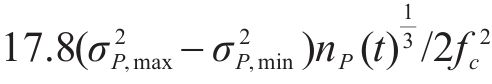
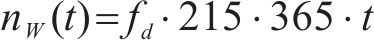
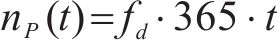
式中: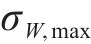
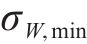
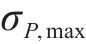
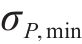
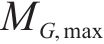
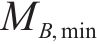
将式(14)与式(20)代入式(15)可得各工况下服役期内的预加力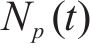
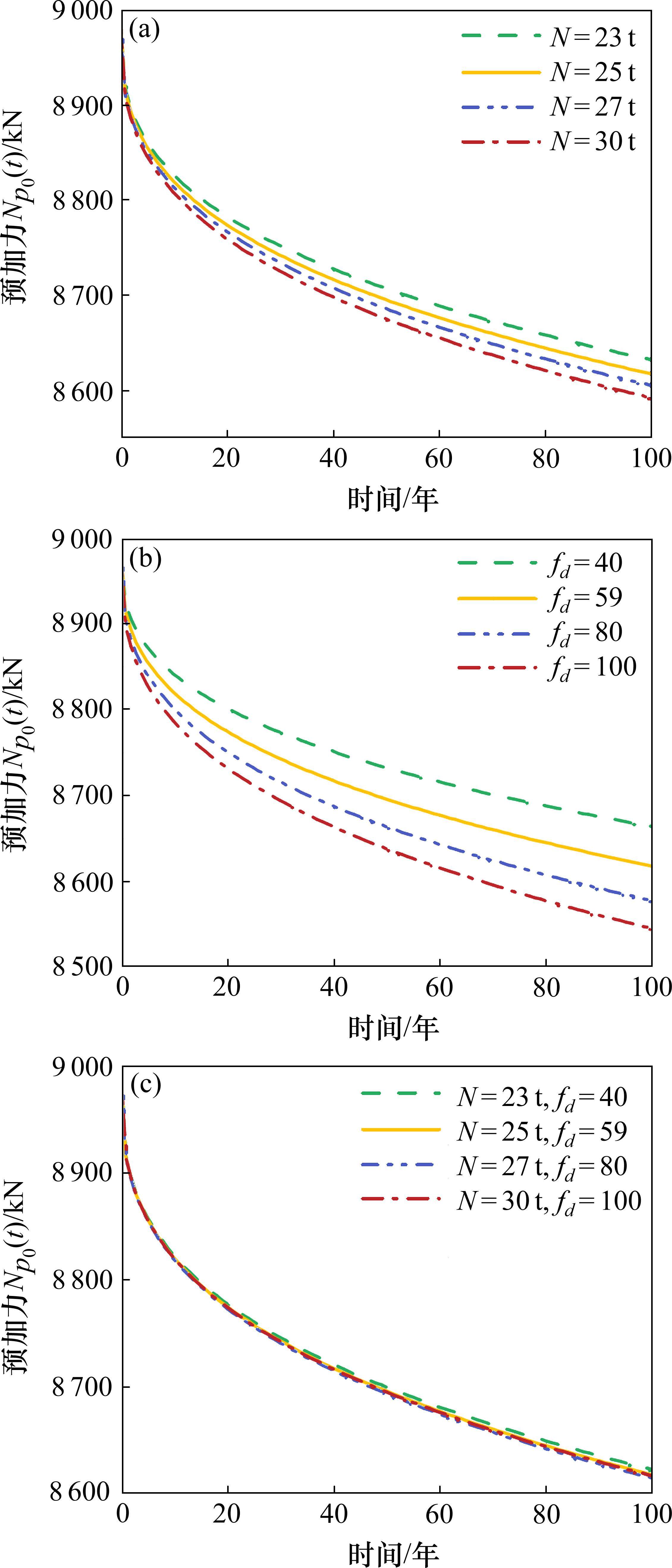
3.3 主要随机参数分布特征
本文主要依据2个基本原则选取随机变量及随机过程:对桥梁结构正截面和斜截面开裂影响较为显著;具有强随机性及随机过程不可忽略的时变特性。由此,本文将前期预应力损失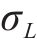
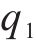
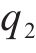
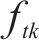
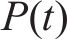
针对所选取的随机变量概率分布信息,相关研究进行了统计分析,具体分布特征见表2。同时,高天骁等[20]认为列车轴重N服从其均值为1.017 9N,标准差为0.065 7N的正态分布,冲击系数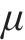
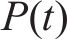
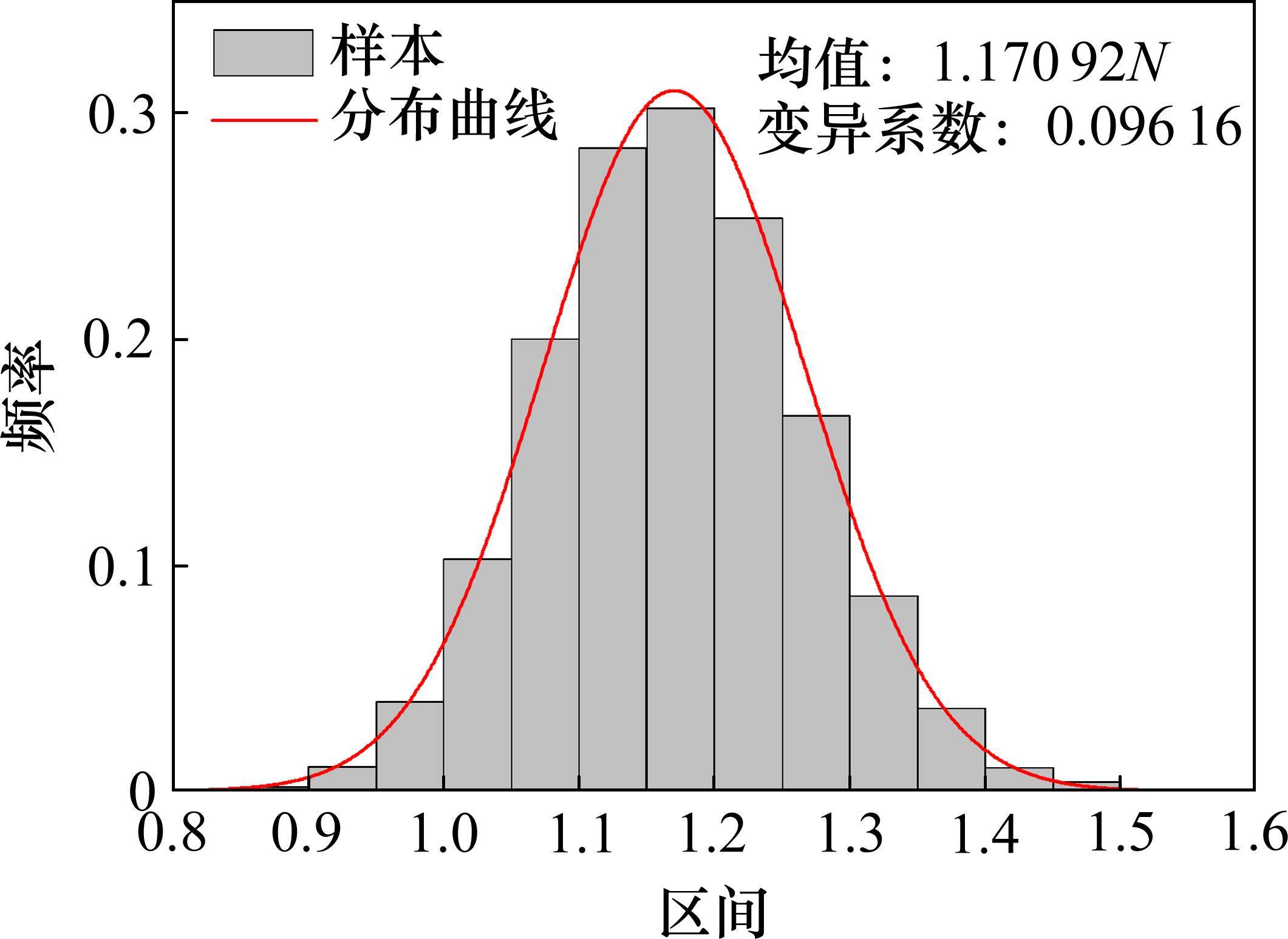
其自相关函数定义为较为稳定的指数型函数[22]:
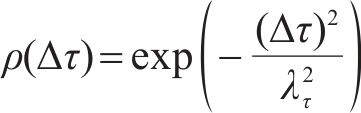
式中: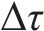
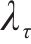
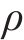
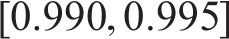
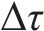
列车荷载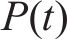
3.4 不同工况下时变可靠度对比分析
基于上述理论推导与信息收集,应用PHI2方法对不同工况下32 m重载铁路预应力混凝土简支T梁的正截面和斜截面抗裂时变可靠度进行分析。
100年服役期内,不同列车轴重、日通行频率及组合工况下T梁的正截面抗裂和斜截面抗裂时变可靠度随时间的变化情况分别如图9、图10和图11所示。
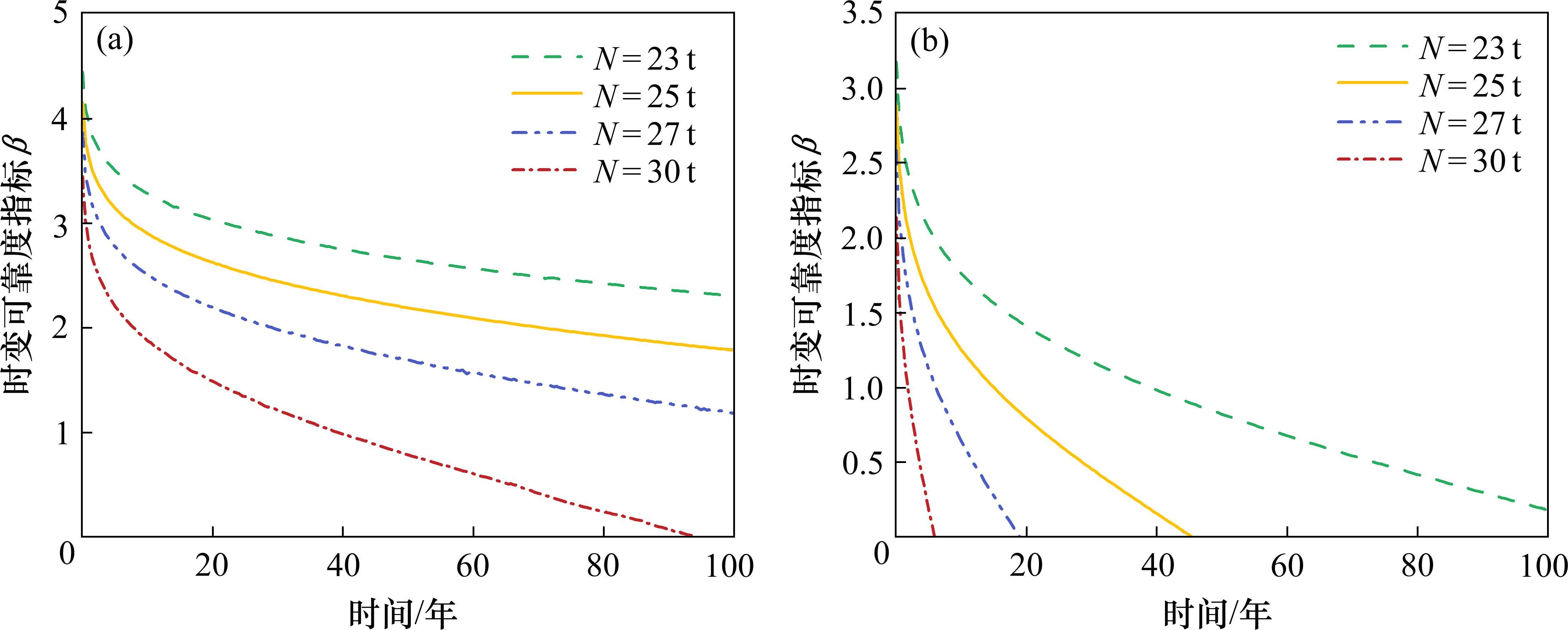
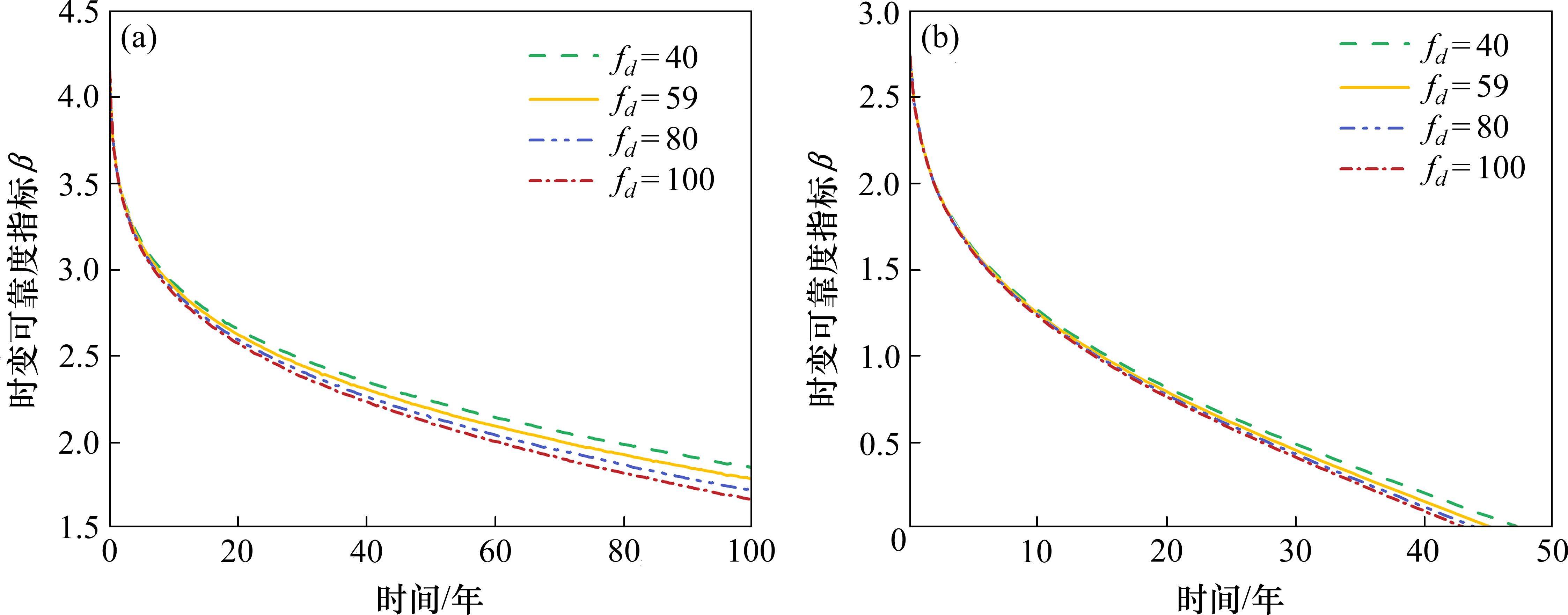
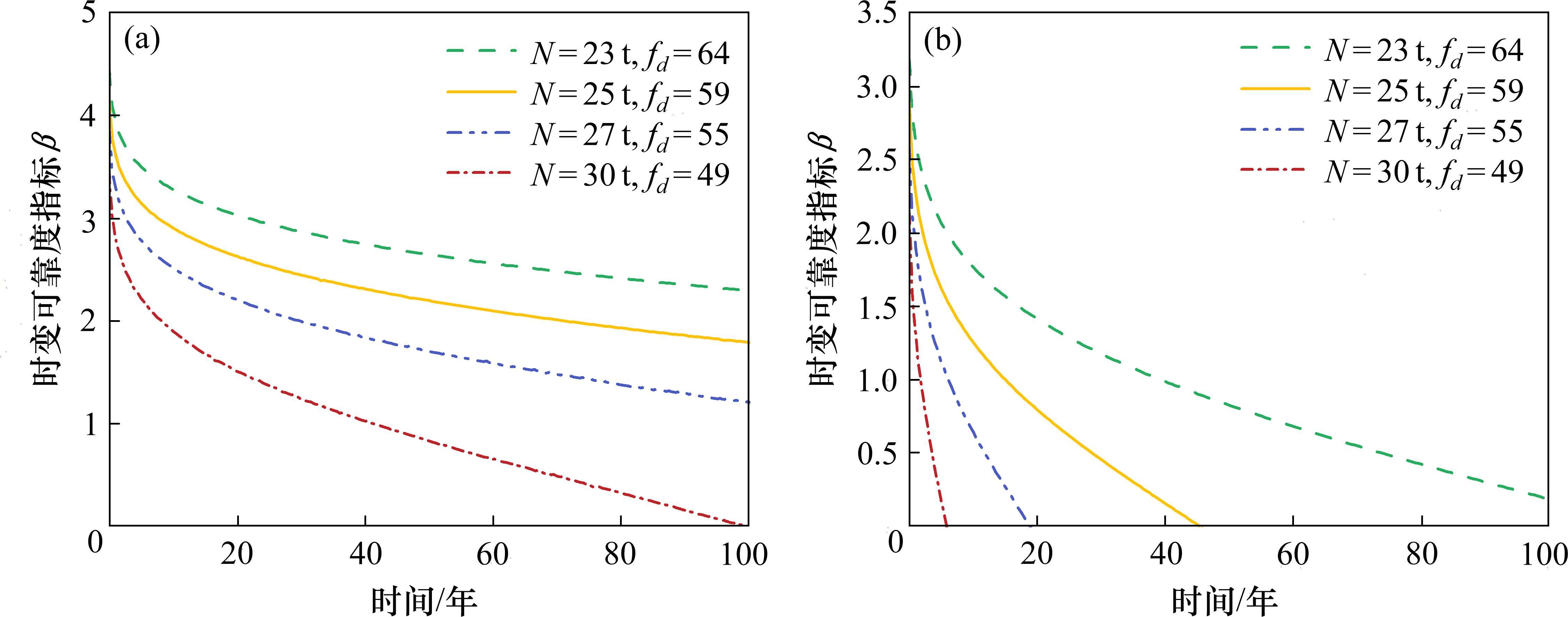
考虑开裂病害的损伤程度,参考《结构可靠性总原则》(ISO 2394:1998)中的规定,选取开裂失效的目标可靠度指标为1.5。由图9、图10和图11的可靠度指标计算结果可以看出:
1) 各工况下的正截面和斜截面抗裂时变可靠度指标随时间增加均呈现下降趋势。工况A中设计服役期内正截面和斜截面抗裂时变可靠度指标均表现出不同轴重工况下差异较大的特点。其中在23 t和25 t轴重条件下正截面抗裂时变可靠度指标满足设计要求,27 t和30 t轴重条件下分别在服役67年和19年时可靠度指标降低至目标可靠度指标以下;斜截面抗裂时变可靠度指标相较于正截面总体水平较低且下降趋势较快,30 t轴重工况下在短期内迅速破坏,23 t、25 t和27 t按设计要求规定正常使用寿命分别为17年、6年和2年。
2) 工况B中设计服役期内正截面和斜截面抗裂时变可靠度指标均表现出在不同日通行频率工况下差异很小的特点。对比工况A和工况B发现,抗裂性能表现为轴重增大导致的可靠度指标下降程度要远大于日通行频率增长,表明列车荷载轴重增大带来的开裂危害要远大于日通行频率增长。
3) 工况C中设计服役期内正截面和斜截面抗裂时变可靠度指标均表现出大轴重低日通行频率组合具有较低可靠度指标水平的特点,这表明大轴重低日通行频率组合下开裂病害出现的可能性更大,应尽量避免此种组合。对比工况A和工况C发现,2种工况中各组合条件下的正截面和斜截面抗裂可靠度指标仅有细微差距,表明组合工况下的可靠度指标变化由轴重主导。
3.5 参数敏感性分析
为研究不同荷载条件下的正截面和斜截面抗裂时变可靠度变化规律,本文选取前期预应力损失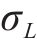
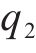
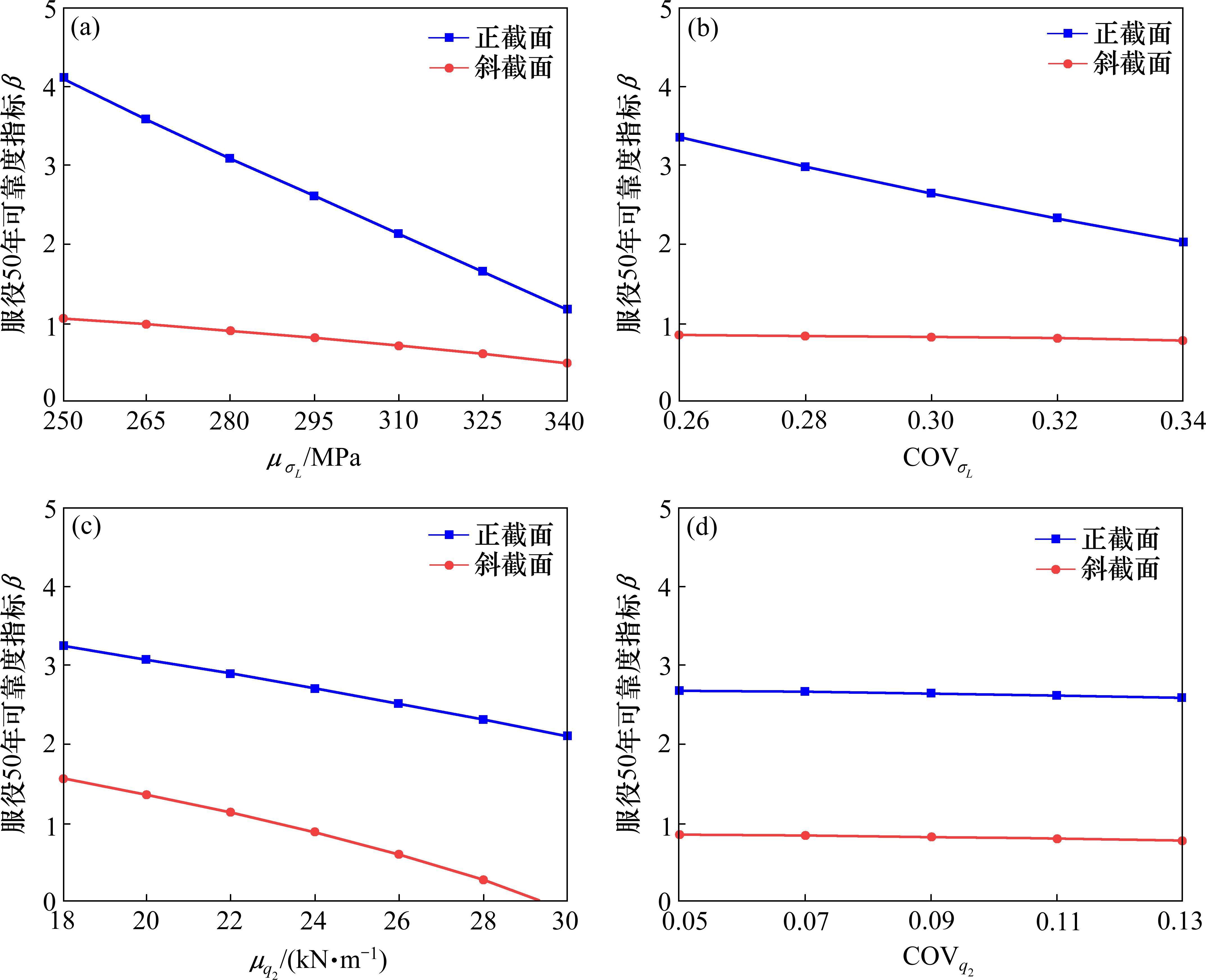
参数敏感性分析结果表明:
1) 随着随机变量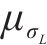
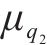


2) 随机参数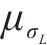

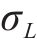
3) 随机参数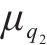
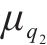

4) 在本文敏感性分析的取值范围内,随机变量的均值对可靠度指标的影响程度大于变异系数。
考虑
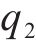
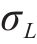
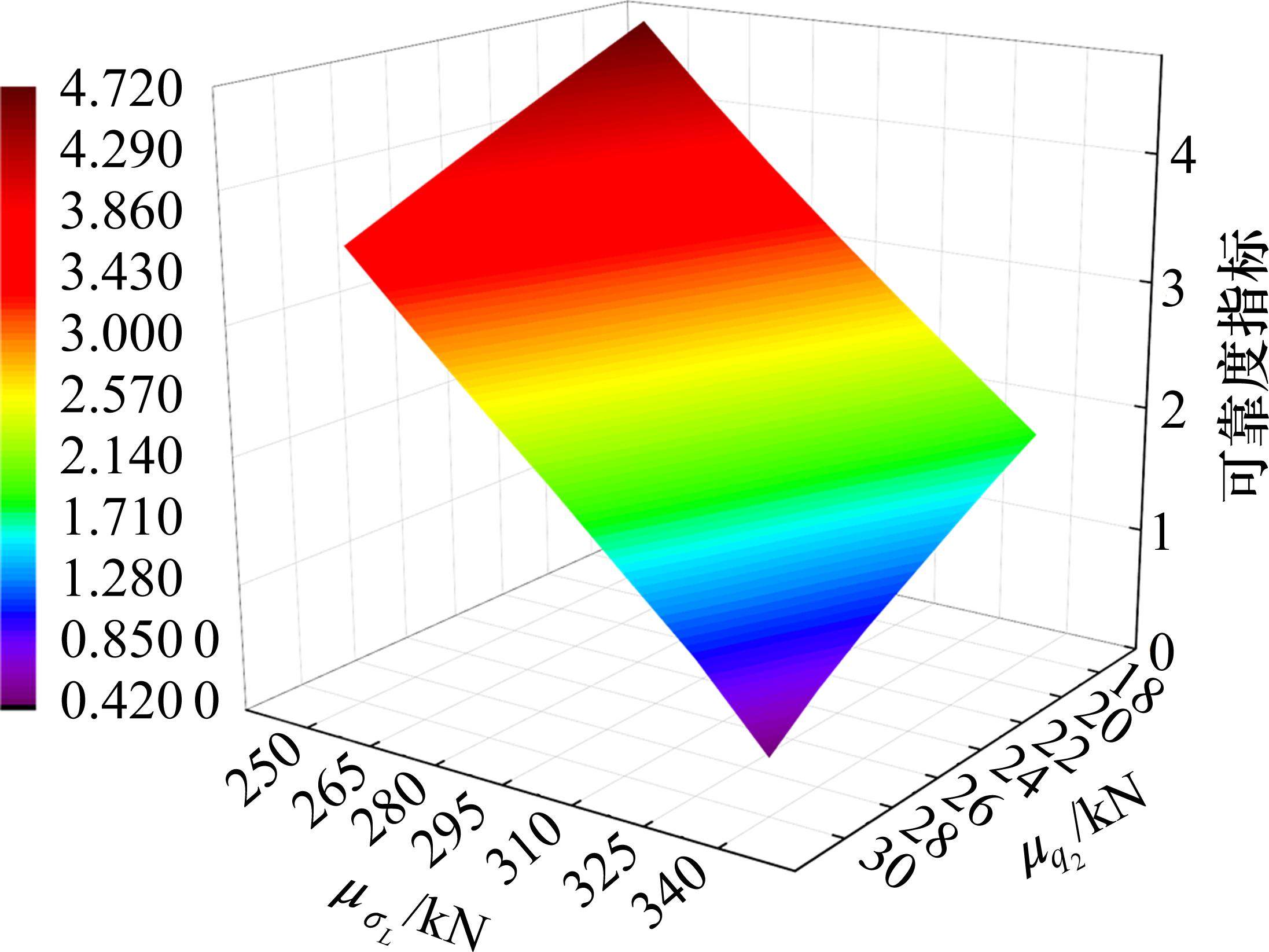
由图13可知,可靠度指标随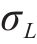
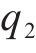
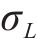
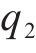
4 结论
1) 27 t和30 t轴重条件下正截面抗裂可靠度指标分别在服役67年和19年后降低至目标可靠度指标以下;斜截面抗裂可靠度指标在30 t轴重工况下短期内迅速破坏,在23,25和27 t轴重工况下分别在服役17年、6年和2年后下降至目标可靠度以下,表明在大轴重荷载工况下斜截面抗裂性能处于更为不利的状态,因此,桥梁设计中应针对此设计缺陷进行改进优化,运营中开行大轴重列车时应加强对腹板斜裂缝病害的专项巡查,并及时对已出现的斜裂缝进行环氧树脂或碳纤维布封闭加固。
2) 轴重增大导致的抗裂可靠度指标下降程度要远超日通行频率增长导致的抗裂可靠度指标下降。
3) 牵引质量相同情况下,小轴重高日通行频率组合对应正截面和斜截面抗裂可靠度指标水平均最高,表明此组合形式对桥梁造成的开裂损伤最小。
4) 前期预应力损失对正截面抗裂可靠度指标的影响要明显大于斜截面,这表明前期预应力损失变化对正截面抗裂可靠度的影响强于斜截面;二期恒载均值变化对正截面和斜截面抗裂可靠度的影响基本相同且均较为显著,二期恒载变异系数变化对正截面和斜截面抗裂可靠度的影响基本相同且均较为微弱。
宋泽伟,卢朝辉,张升旺等.基于PHI2方法的重载铁路PC简支T梁抗裂时变可靠度研究[J].铁道科学与工程学报,2025,22(02):770-782.
SONG Zewei,LU Zhaohui,ZHANG Shengwang,et al.Time-dependent reliability analysis of crack resistance in PC simply supported T-beams of heavy-haul railways based on PHI2 method[J].Journal of Railway Science and Engineering,2025,22(02):770-782.