我国沿海地区软土分布广泛且土地资源紧张,在运营高铁线路邻近区域新建道路下穿高速铁路桥梁的现象日益普遍。软土地区新建道路容易在地表形成带状堆载,改变工程区域内土体的受力状态,导致土体应力重分布和土体压缩变形,进而引起邻近高铁桥梁桥墩产生侧向位移和竖向沉降,对运营高速列车的安全性产生威胁。为确保软土地区高速铁路桥梁在道路施工和工后土体固结过程中正常运营,铁路管理部门严格限制下穿施工及运营后的高铁桥墩位移变化,由于软土土层的力学参数离散性较大,相关工程数值计算结果和实际监测值可能存在一定偏差,新建道路下穿高铁的施工及运营过程中软土的固结会导致桥墩位移随时间发生变化,因此软土地区桥墩位移的预测及其评估成为了难点。许多学者通过试验研究、数值模拟、试验与模拟相结合等多种研究方法对软土地区新建工程邻近运营高铁桥梁的实际工程问题进行了大量研究。JEONG等[1]通过一系列离心机模型试验,对邻近堆载作用下群桩的位移响应和内力响应进行研究。FELLENIUS等[2-3]通过对世界多国深厚软土地区的桩基进行长期监测,获得了软土地基中桩基结构长期沉降和内力变化的数据。SHAN等[4]通过现场和室内试验研究旋喷桩对邻近高铁桥梁变形的影响,得到了旋喷桩与高铁桥梁的临界距离。禚一等[5]采用ABAQUS建立三维实体模型研究道路下穿高铁的基坑施工对临近高铁的影响,发现基坑开挖会引起高铁路基和框构桥的隆起变形。梁喜燕等[6-7]通过建立有限元模型,拟合响应面函数对邻近高铁并行和堆载工程引起高铁轨道形位的变化进行预测,得到了考虑土层参数离散性时既有高铁轨道位移计算结果的概率分位值。胡莉[8]依托某新建道路下穿运营高铁桥梁工程,研究了下穿道路施工工序对高铁桥墩及轨道位移的时变影响,提出了减少轨道形位变化的措施。魏丽敏等[9]通过对比分析现场试验和数值分析结果,研究得到了软土地区无支护基坑开挖对邻近高铁桥梁桩基变形与内力的影响规律。KELESOGLU等[10]基于离心机试验和Simple方法,研究了群桩基础在邻近堆载作用下受到水平荷载的分布规律。现有的研究[11-13]针对软土地区新建工程引起邻近运营高铁桥梁响应得出很多理论基础和经验数据,但大部分有关研究侧重于研究软土地区高铁邻近工程施工过程对高铁桥梁的影响,施工完成后土体固结对高铁桥梁后续影响的研究相对较少,且研究的响应结果缺乏对土层力学参数离散性及软土固结时变性的考虑,部分研究[14-15]的参数选取存在一定局限性。最新研究中,李思佳[16]用时变响应面函数来评估软土随时间固结作用下新建并行道路对既有桥墩位移的影响,但其表达式形式复杂,亟需对时变响应面的拟合方法进行改进。为研究软土地区新建下穿道路对既有高铁桥墩位移的时变影响,本文依托软土地区某国道下穿京沪高铁立交工程,建立土体-桥梁-轨道的一体化三维时变有限元模型。采用修正Morris法进行敏感性分析,根据得到的高敏感参数,通过BBD试验设计法分2个阶段拟合地基固结过程中高铁桥墩竖向位移的时变响应面函数,基于最简时变响应面函数对高铁桥梁的竖向位移进行可靠概率分析,由此来评估软土地区新建下穿道路对运营高速铁路桥墩位移的影响程度。
1 相关理论及计算方法
1.1 参数敏感性分析
本文选用修正Morris法进行敏感性分析。Morris筛选法属于单一变量法[17],假定模型目标函数存在n个影响参数,选取其中任意参数X,保持其余参数不变,在参数X的取值区间按照一定规律改变X的大小,用敏感性系数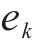
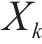
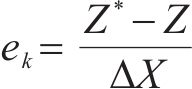
式中:


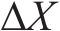
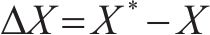
修正Morris法在Morris法基础上进行改进,让参数以固定百分比作为步长进行多次扰动,将Morris系数的平均值作为判别因子,如式(2)所示:
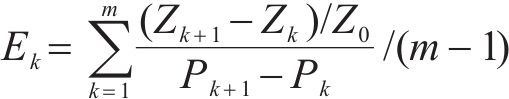
式中: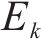
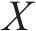
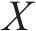
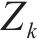
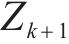
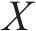
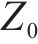
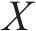
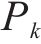
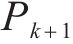
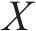
按照敏感性系数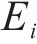
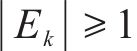
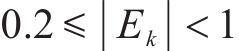
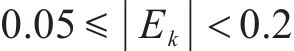
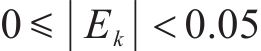
1.2 响应面拟合及检验
马小兵等[18]基于带交叉项的二次响应面函数,增加与时间相关的函数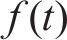
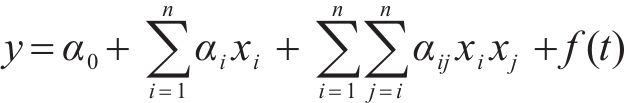
对于某些特殊工程,结构响应随时间不断变化,将响应面函数的各系数表示为时间t的函数,函数形式变为式(4):
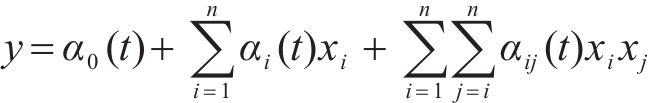
在此基础上,李思佳[16]对时变响应面函数的具体形式进行探索,但根据现有研究拟合的时变响应面函数项数多、形式复杂,基于该函数进行结构响应预测和结构可靠度计算的过程十分繁琐。
本文基于式(3)和式(4),在保证拟合精度前提下,对时变响应面法进行改进。求解时变响应面函数的过程分为2个阶段。
第1阶段,求解不同时刻下的响应面函数。
t时刻响应面函数如式(5)所示:
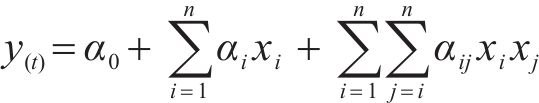
主要步骤如下。
1) 基于式(5)求解不同时刻下带交叉项的二次响应面函数,并检验各响应面函数的拟合精度。
2) 在步骤1拟合的二次响应面函数中,找出系数较小的交叉项和二次项,在式(6)中去掉这些项,重新拟合响应面函数并检验其拟合精度。
3) 在式(5)中去掉所有交叉项,对其进行响应面拟合和精度检验。
4) 在式(5)中去掉所有交叉项和二次项,对其进行响应面拟合和精度检验。
5) 对比步骤1~4拟合的各种响应面函数,在保证拟合精度前提下,选择项数最少的响应面表达式。
第2阶段,求解响应面函数各系数关于时间t的表达式。
系数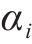
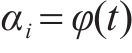
主要步骤如下。
1) 根据第1阶段的最简响应面函数,基于式(6)构建各系数关于时间t的一元函数表达式,检验各表达式的拟合精度。
2) 对比步骤1拟合的各种函数表达式,在保证拟合精度前提下,选择项数最少的函数表达式。
1.3 可靠概率分析
本文采用的蒙特卡罗方法来计算桥墩位移的可靠概率[19],在分析结构可靠度的过程中,采用编程软件MATLAB在n维随机变量空间进行大规模随机抽样,从而获得充足的样本组合。为获得较小的计算误差和较高的计算精度,本文通过MTALAB软件进行107组随机试验,得到累计失效次数并计算失效频率。计算结构可靠概率的具体过程为:构建结构功能函数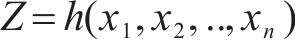
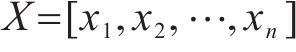
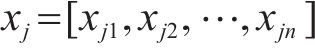
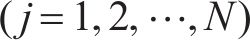
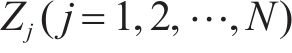
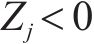
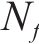

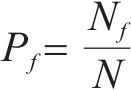
2 高铁桥墩位移变化的敏感性分析
2.1 工程实例
某国道下穿京沪高铁立交工程位于江苏省南部的软土地区,属太湖流域片区,软弱土层分布广泛。运营高铁桥梁为3跨32 m简支梁,高铁桥墩为圆端型桥墩,墩高为10.5 m;桩基础为钻孔灌注桩,桩长均为48 m。新建道路高2 m,宽11 m,道路中心线大致与运营高铁桥梁正交且从桥跨中心处下穿,路基按照1∶1放坡,道路外缘线距运营高铁中墩的水平距离为6.2 m。运营高铁桥梁与新建道路的相对位置关系如图1所示。该工程所在区域的软土分布广泛,埋深较深,地层从上到下依次为淤泥质粉质黏土(4 m)、粉质黏土(36 m)、粉土(24 m)、粉砂(36 m)。
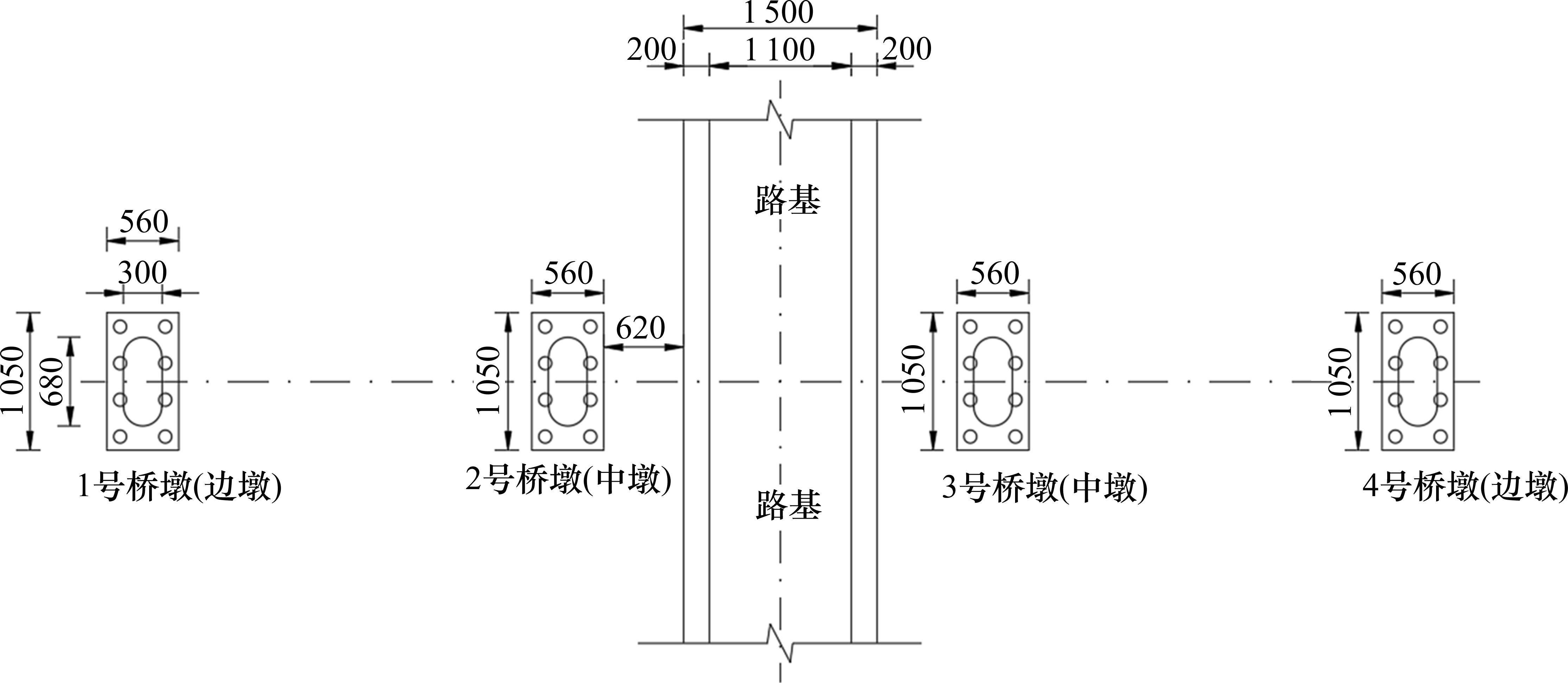
2.2 时变有限元模型建立
采用有限元软件Abaqus建立土体-梁-轨道的一体化三维有限元模型,见图2。模型土体尺寸为160 m×120 m×100 m。考虑软土固结效应,土层中软土层采用修正剑桥模型,粉砂层采用摩尔库伦模型。模型采用混合单元划分法,共划分节点59 926个,单元45 817个。土体采用C3D8P线性六面体孔隙流体/应力单元,下部结构以及路基均采用C3D8I线性六面体减缩积分单元,箱梁和轨道采用B32梁单元。
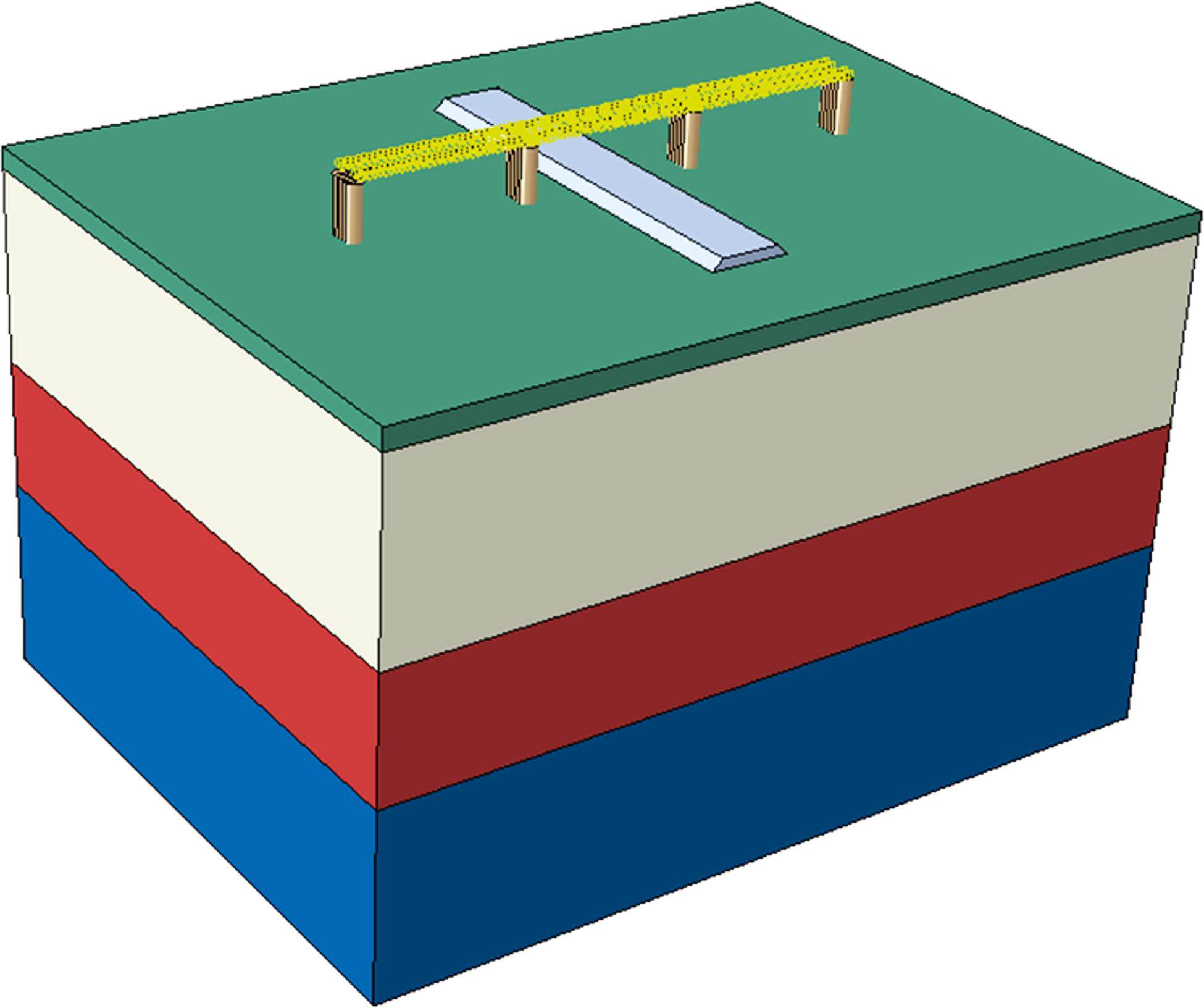
桥墩和箱梁采用耦合接触,箱梁与钢轨设置弹簧接触;土体与桩基设置面面接触,切向设置小滑动和“罚摩擦”,垂直于接触面上设置“硬接触”。土体模型X、Y方向的边界面设置法向位移约束,土体底面设置固定约束。土体顶面设置为排水面,其他面均设置为不透水面。假定整个分析过程,地下水位与土体顶面始终保持齐平。
2.3 桥墩位移的参数敏感性分析
选用淤泥质粉质黏土、粉质黏土层以及粉土的正常固结曲线斜率
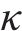
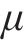
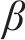
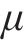
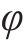
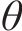
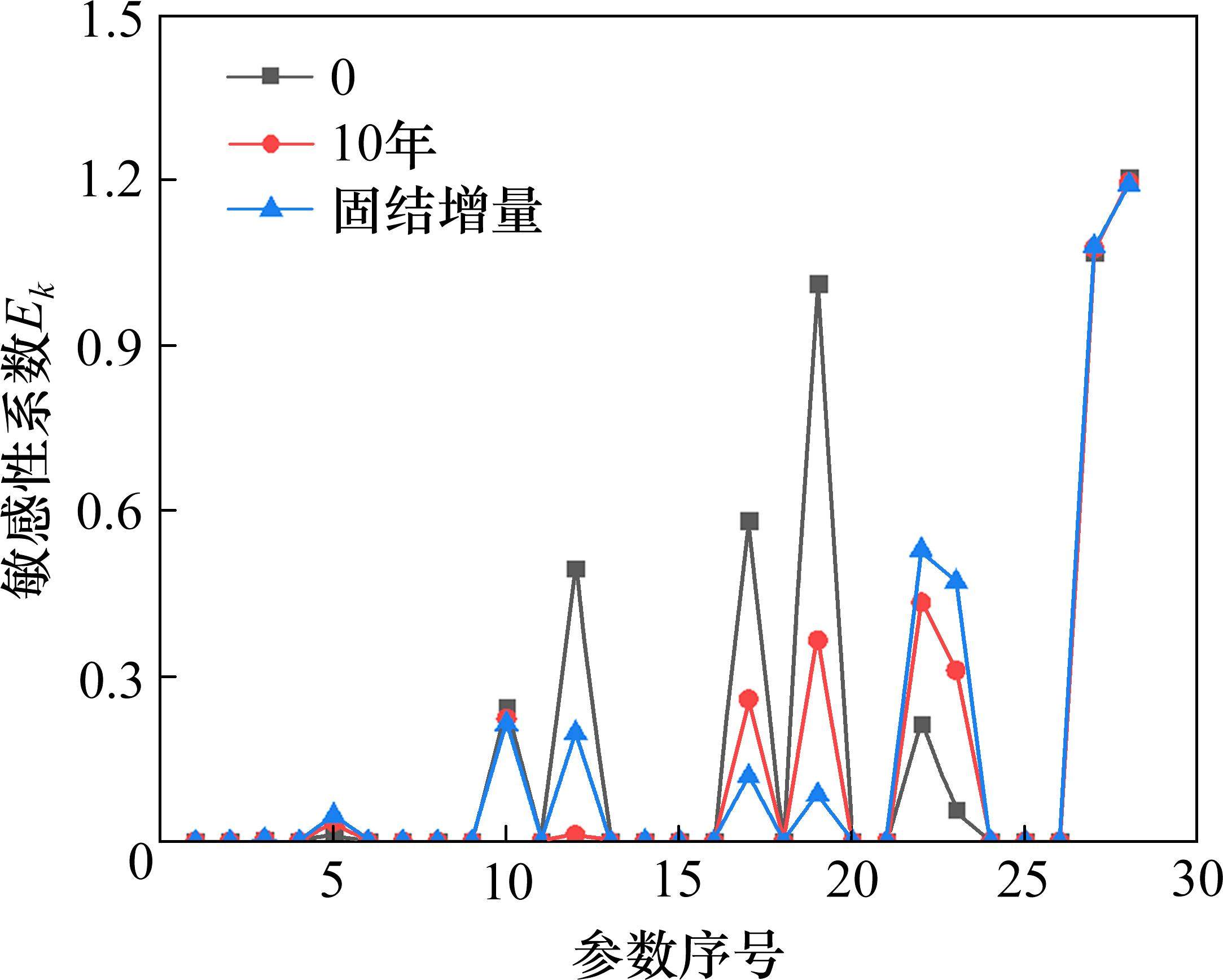
按照修正Morris法计算得到各参数的敏感性系数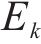
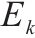
| 序号 | 参数来源 | 参数名称 | 序号 | 参数来源 | 参数名称 |
|---|---|---|---|---|---|
| 1 | 淤泥质粉质黏土 | 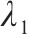 | 8 | 粉质黏土 | 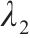 |
| 2 | 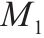 | 9 | 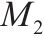 | ||
| 3 |  | 10 | 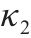 | ||
| 4 | 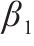 | 11 | 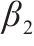 | ||
| 5 | 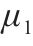 | 12 | 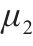 | ||
| 6 | 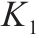 | 13 | 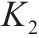 | ||
| 7 | 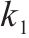 | 14 | 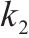 | ||
| 15 | 粉土 | 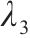 | 22 | 粉砂 | E |
| 16 | 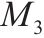 | 23 | 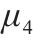 | ||
| 17 | 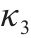 | 24 | φ | ||
| 18 | 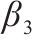 | 25 | c | ||
| 19 |  | 26 | 路基 | θ | |
| 20 | 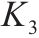 | 27 | b | ||
| 21 | 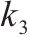 | 28 | h |
由图3可知,地基固结前,桥梁中墩竖向位移的高敏感参数为h、b、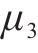
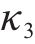
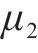
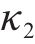
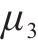
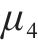
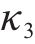
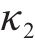
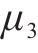
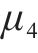
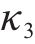
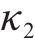
结合上述3种敏感性系数,当扰动百分比为-9%~9%时,桥梁中墩竖向位移的高敏感参数为路基高度h、路基宽度b,敏感参数为粉砂层弹性模量E、粉砂层泊松比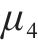
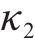
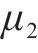
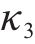
根据上述分析知,路基高度、宽度对桥梁中墩竖向位移的影响显著,土层参数中软土层的回弹曲线斜率、泊松比对桥梁中墩竖向位移的影响较大,与文献[8]和[16]研究土层参数对高铁桥墩位移的敏感性结果相似。
3 响应面拟合
3.1 试验设计及试验组合
基于参数敏感性分析结果,路基高度h、路基宽度b、粉砂层弹性模量E、粉砂层泊松比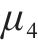
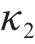
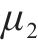
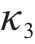
采用BBD设计方法对7个模型参数进行三水平值试验组合,三水平依次对应各因素的最小值(-1水平)、平均值(0水平)和最大值(1水平),各参数的取值情况如表2所示。
| 参数符号 | 参数含义 | -1 | 0 | 1 |
|---|---|---|---|---|
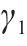 | 路基高度h | 1.6 | 2 | 2.4 |
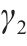 | 路基宽度b | 10 | 11 | 12 |
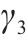 | 粉砂层弹性模量E | 100 | 115 | 130 |
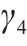 | 粉砂层泊松比μ4 | 0.27 | 0.3 | 0.33 |
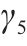 | 粉质黏土层回弹曲线斜率κ2 | 0.004 4 | 0.005 | 0.005 6 |
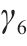 | 粉质黏土层泊松比μ2 | 0.28 | 0.32 | 0.36 |
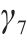 | 粉土层回弹曲线斜率κ3 | 0.001 7 | 0.002 | 0.0023 |
基于BBD设计方法对7个模型参数进行试验组合,共进行62次试验,其中包含6个中心点试验(0,0,…,0),56个因子点,每组试验模型选取地基固结14个时刻对应的高铁桥墩竖向位移为模型响应值,通过有限元模型计算得到62组试验结果。
3.2 响应面函数拟合及简化
采用MTALAB软件对桥梁中墩竖向位移进行时变响应面函数第1阶段的拟合。基于式(5)得到土体固结各时刻中墩最大竖向位移的一般式响应面函数,其形式如式(8):
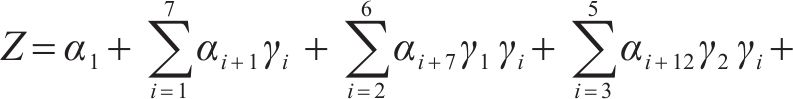
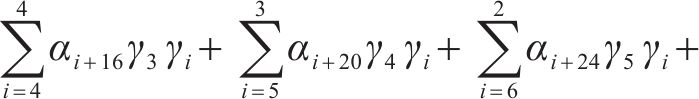
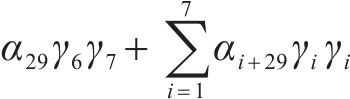
通过式(8)拟合各时刻中墩最大竖向位移与所选7个参数的函数关系,得到中墩最大竖向位移的一般式响应面函数各系数,采用相关判定系数评价响应面函数的拟合精度。经检验各时刻下一般式响应面函数表达式F值均较大,最小F值为53 271,对应P值均小于0.000 1,复合相关系数R2均大于99.99%,拟合精度良好。
在式(8)的响应面函数中,由于二次项引起的函数项数多,且随着研究参数的增多响应面函数的形式会越来越复杂,使结构响应预测和可靠度计算的效率大幅降低,需在保证响应面函数具有显著性以及良好的拟合精度的前提下,对一般式响应面函数进行合理简化。通过略去不显著项,提出以下3种简化形式,见式(9)~式(11)。
1) 形式1:剔除式(8)系数较小的函数子项,包括部分二次子项和交叉子项,如式(9)所示:
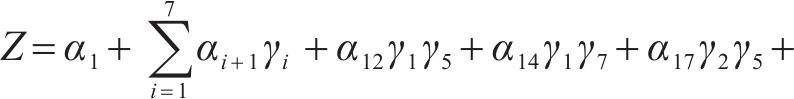
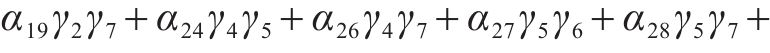
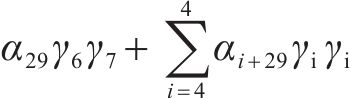
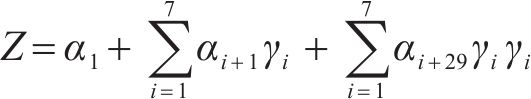
3) 形式3:剔除式(8)所有二次子项和交叉子项,如式(11)所示:
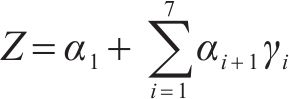
基于简化后的响应面函数形式重新进行响应面拟合,得到3种简化形式的响应面函数,统计各简化形式在各时刻下对应的判定系数,具体如表3所示。
地基固结 时间/年 | F | 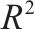 | P | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 形式1 | 形式2 | 形式3 | 形式1 | 形式2 | 形式3 | 形式1 | 形式2 | 形式3 | |
| 0.00 | 595 | 728 | 1 396 | 99.66 | 99.54 | 99.45 | <0.000 1 | <0.000 1 | <0.000 1 |
| 0.05 | 577 | 803 | 1 529 | 99.65 | 99.58 | 99.50 | |||
| 0.10 | 659 | 936 | 1 849 | 99.69 | 99.64 | 99.58 | |||
| 0.23 | 763 | 1 101 | 2 257 | 99.73 | 99.70 | 99.66 | |||
| 0.35 | 802 | 1 149 | 2 357 | 99.74 | 99.71 | 99.67 | |||
| 0.50 | 828 | 1 179 | 2 421 | 99.75 | 99.72 | 99.68 | |||
| 0.75 | 833 | 1 189 | 2 446 | 99.75 | 99.72 | 99.69 | |||
| 1.00 | 806 | 1 170 | 2 391 | 99.75 | 99.71 | 99.68 | |||
| 1.75 | 750 | 1 119 | 2 250 | 99.73 | 99.70 | 99.66 | |||
| 2.50 | 684 | 1 057 | 2 077 | 99.70 | 99.68 | 99.63 | |||
| 4.00 | 612 | 989 | 1 885 | 99.67 | 99.66 | 99.59 | |||
| 6.00 | 586 | 964 | 1 815 | 99.65 | 99.65 | 99.58 | |||
| 8.00 | 578 | 956 | 1 792 | 99.65 | 99.65 | 99.57 | |||
| 10.00 | 574 | 954 | 1 783 | 99.64 | 99.99 | 99.57 | |||
由表3可知,由于响应面函数子项式减少,形式1函数的F值相对于一般式的值明显减小,但对应的P值小于0.000 1,具有显著性;复合相关系数R2的最小值为99.64%,相较于一般式稍有减小但仍大于95%,具有良好的拟合精度。形式2、形式3具有相似结论。响应面3种简化形式拟合的函数表达式均具有函数显著性、良好拟合精度以及较小回归误差。
地基固结任意时刻下,形式1、形式2和形式3函数表达式的项数分别为21项、15项和8项。在保证拟合精度和函数显著性的前提下,选择式(11)确定的函数表达式作为第1阶段响应面拟合的函数形式。
为获得任意时刻的中墩竖向位移进行时变响应面函数第2阶段的拟合,初步拟定了一种包含幂函数项和对数函数项的一元组合函数,拟合各系数关于时间t的一般表达式如式(12)所示。
形式Ⅰ:

基于式(12),通过MTALAB对响应面函数各系数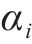
| 系数 | α1 | α2 | α3 | α4 | α5 | α6 | α7 | α8 |
|---|---|---|---|---|---|---|---|---|
| c1 | 1.075 | -0.389 | -0.060 5 | -0.001 1 | -0.331 | -60.63 | 0.286 | -29.77 |
| c2 | 0.271 | -0.038 4 | -0.006 1 | -0.001 2 | -0.400 1 | -3.862 | 0.189 | 2.389 |
| c3 | -2.210 | 0.478 | 0.074 9 | 0.007 4 | 2.404 | 60.90 | -1.22 | 7.13 |
| c4 | 2.542 | -0.897 | -0.146 | -0.003 5 | -1.647 | -55.85 | 1.355 | -126.2 |
| c5 | 0.455 | -0.141 | -0.021 4 | -6.25×10-5 | 0.018 2 | -35.06 | -0.183 | -14.60 |
| c6 | -4.55×10-6 | 1.41×10-6 | 2.14×10-7 | 6.23×10-10 | -1.83×10-7 | 3.5×10-4 | 1.83×10-6 | 1.46×10-4 |
| F | 52 | 21 112 | 26 575 | 571 | 463 | 600 | 80 | 2 591 |
| P | <0.000 1 | <0.000 1 | <0.000 1 | <0.000 1 | <0.000 1 | <0.000 1 | <0.000 1 | <0.000 1 |
| R2/% | 97.00 | 99.99 | 99.99 | 99.72 | 99.66 | 99.73 | 98.03 | 99.94 |
由表4可知,各系数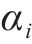
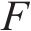
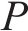
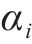
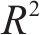
由于表4中各系数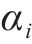
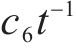
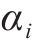
形式Ⅱ:
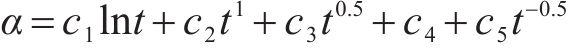
基于式(13)采用MTALAB对响应面系数关于时间t的表达式进行拟合,得到形式Ⅱ表达式判定系数如表5所示。
| 系数 | α1 | α2 | α3 | α4 | α5 | α6 | α7 | α8 |
|---|---|---|---|---|---|---|---|---|
| F | 9 | 524 | 593 | 801 | 649 | 69 | 93 | 564 |
| P | <0.005 | <0.000 1 | <0.000 1 | <0.000 1 | <0.000 1 | <0.000 1 | <0.000 1 | <0.000 1 |
| R2/% | 79.08 | 99.57 | 99.62 | 99.72 | 99.65 | 96.85 | 97.64 | 99.60 |
由表5可知,形式Ⅱ表达式的F值相较于形式Ⅰ均明显减小,部分系数的复合相关系数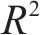
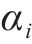
基于函数拟合显著性、精确性和简便性的原则,第1阶段选取式(11)确定的形式3,第2阶段选取式(12)确定的形式Ⅰ。桥梁中墩竖向位移的时变响应面函数的表达式如式(14)和式(15)所示:
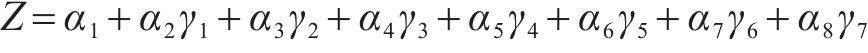
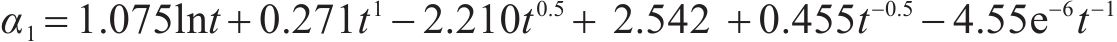
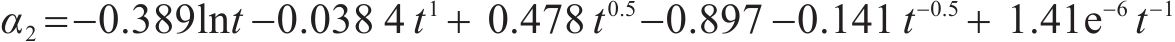
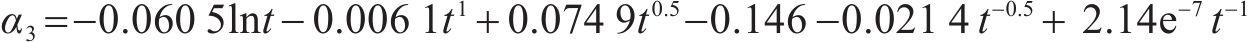

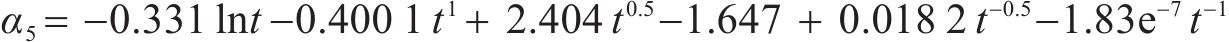
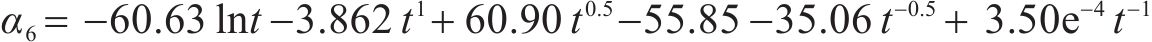
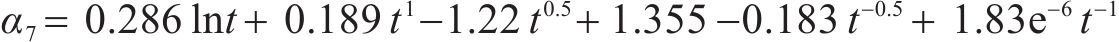
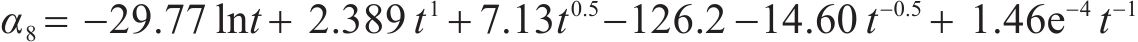
在时变响应面函数具体形式的探讨过程中,第1阶段的一般式及形式1~形式3均满足函数拟合显著性和精确性要求,第2阶段仅形式Ⅰ满足要求。第1阶段分别采用式(8)~式(11)确定的一般式及形式1~形式3,第2阶段采用式(12)确定的形式Ⅰ,一共得到4种拟合精度较高的时变响应面函数。
将第1阶段采用一般式、第2阶段采用形式Ⅰ的时变响应面函数作为一般形式,统计其余3种时变响应面函数的减少项数并计算其简化率。得到当时变响应面采用简化1~简化3形式时,对应表达式减少项数为90项、126项、168项,对应的简化率依次为41.7%、58.3%、77.8%,简化3形式实现了响应面函数的显著简化,且在响应面拟合参数越多的情况下该形式简化率越高,证明本文时变响应面函数的简化拟合方法高效可行。
3.3 响应面模型精度评估
为检验时变响应面函数的预测精度,采用MTALAB软件随机生成24组试验参数组合,基于24组随机参数试验,通过响应面函数和ABAQUS软件,分别得到桥梁中墩竖向位移的响应面预测值和有限元计算值。
对地基固结中各随机组合桥梁中墩竖向位移的预测值和计算值进行分析,限于篇幅,此处给出响应面预测值与有限元计算值差值最大的组合7的对比图形,如图4所示。
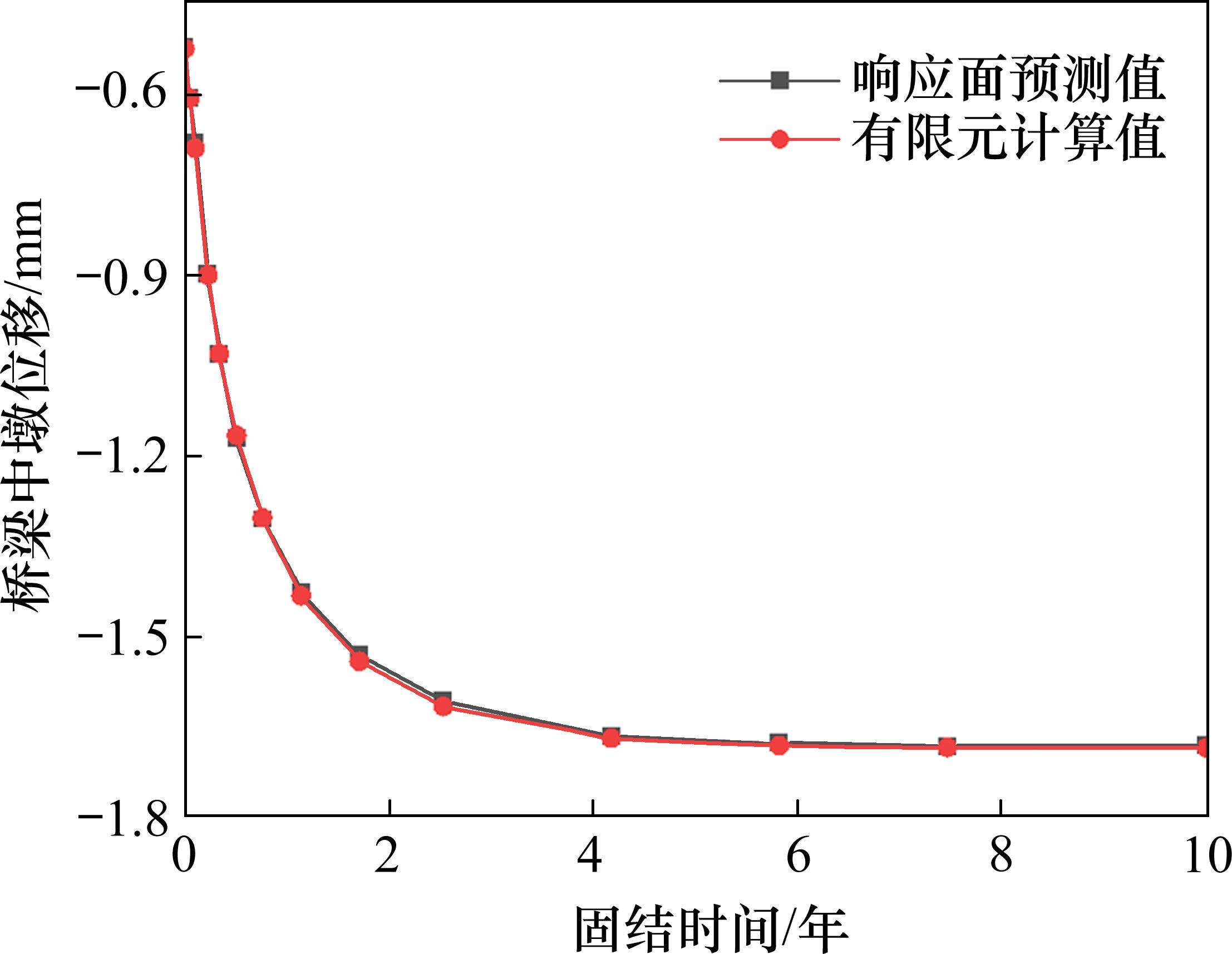
由图4可知,各随机组合中墩竖向位移的响应面预测值与有限元计算值的最大绝对差值为0.01 mm,远小于0.1 mm;预测值与计算值的最大相对差值为1.34%,对应预测值的准确率为98.66%,大于95%;各组合的响应面预测曲线和有限元计算曲线,在地基固结各时刻几乎完全吻合,说明时变响应面函数对有限元模拟的计算结果具有良好的预测精度。将有限元计算结果拟合的时变响应面函数作为后续可靠概率计算的结构功能函数,能保证精度的同时提高计算效率,减少了大量复杂的有限元计算。
4 可靠度计算
按照《公路与市政工程下穿高速铁路技术规程》(TB 10182—2017)[20],在不限速情况下,运营高铁桥梁墩台的位移限值应满足表6的相关要求。本文依托背景的高铁轨道采用无砟轨道,高铁桥墩竖向位移的限值为2 mm。
| 轨道类型 | 横向水平 位移 | 纵向水平 位移 | 竖向 位移 |
|---|---|---|---|
| 有砟轨道 | 3 | 3 | 3 |
| 无砟轨道 | 2 | 2 | 2 |
采用蒙特卡罗抽样法,进行107次随机抽样,计算地基固结各时刻高铁桥梁中墩的竖向位移分别小于1,1.2,1.4,1.6,1.8和2 mm的可靠概率,计算结果如表7所示。
地基固结 时间t/年 | 中墩竖向位移的可靠概率/% | |||||
|---|---|---|---|---|---|---|
| 1.0 mm | 1.2 mm | 1.4 mm | 1.6 mm | 1.8 mm | 2.0 mm | |
| 0.00 | 99.99 | 99.99 | 99.99 | 99.99 | 99.99 | 99.99 |
| 0.10 | 99.99 | 99.99 | 99.99 | 99.99 | 99.99 | 99.99 |
| 0.25 | 99.91 | 99.99 | 99.99 | 99.99 | 99.99 | 99.99 |
| 0.50 | 49.93 | 99.36 | 99.99 | 99.99 | 99.99 | 99.99 |
| 0.75 | 9.83 | 83.07 | 99.93 | 99.99 | 99.99 | 99.99 |
| 1.00 | 2.28 | 54.42 | 98.69 | 99.99 | 99.99 | 99.99 |
| 2.00 | 0.09 | 10.65 | 73.64 | 99.40 | 99.99 | 99.99 |
| 3.00 | 0.03 | 4.78 | 55.11 | 97.28 | 99.99 | 99.99 |
| 4.00 | 0.02 | 3.37 | 47.10 | 95.40 | 99.97 | 99.99 |
| 5.00 | 0.01 | 2.92 | 43.87 | 94.34 | 99.96 | 99.99 |
| 6.00 | 0.01 | 2.87 | 43.55 | 94.25 | 99.95 | 99.99 |
| 7.00 | 0.01 | 2.87 | 43.32 | 94.12 | 99.95 | 99.99 |
| 8.00 | 0.01 | 2.83 | 42.97 | 93.97 | 99.95 | 99.99 |
| 9.00 | 0.01 | 2.80 | 42.79 | 93.93 | 99.95 | 99.99 |
| 10.00 | 0.01 | 2.80 | 42.69 | 93.87 | 99.95 | 99.99 |
由表7可知,在误差少于20%的置信度为95%的保证度下,地基固结前(t=0),最不利中墩竖向位移小于1 mm的可靠概率为99.99%,说明此时桥梁中墩竖向位移小于1 mm的可靠概率较大;地基固结稳定时(t=10),最不利中墩竖向位移小于1 mm的可靠概率为0.01%,小于1.8 mm的可靠概率为99.95%,说明此时桥梁中墩的竖向位移处于1~1.8 mm的概率较大;各时刻最不利中墩竖向位移小于规范限值2 mm的可靠概率为99.99%,说明在新建道路引起的地基固结过程中,运营高速铁路桥梁处于安全状态的概率很高。
5 结论
1) 采用修正Morris法进行参数敏感性分析。结果表明,当扰动百分比为-9%~9%时,路基高度、宽度及主要持力土层的回弹曲线斜率、泊松比等参数对于桥墩竖向位移为高敏感参数。
2) 提出时变响应面函数的简化拟合方法,分阶段拟合得到4种精度较高的时变响应面函数;本文采用的简化形式简化率接近80%;根据预测精度分析,响应面函数的预测值与有限元计算值的最大相对误差为1.34%。
3) 根据桥墩附加位移的可靠概率分析,地基固结稳定时,最不利中墩竖向位移小于1 mm的可靠概率为0.01%,小于1.8 mm的可靠概率为99.95%,说明此时桥梁中墩的竖向位移处于1~1.8 mm的概率较大;地基固结各时刻最不利中墩竖向位移小于规范限值2 mm的可靠概率为99.99%,说明在新建道路引起的地基固结过程中,运营高速铁路桥梁处于安全状态的概率很高。
4) 研究时变响应面函数的具体拟合形式并对其进行合理简化,得到的时变响应面函数能较准确计算软土固结的任意时刻下高铁桥墩位移的变化,可为软土地区类似新建工程致既有桥墩位移的计算提供参考。本文提出的时变响应面函数在拟合参数较多的响应面计算中具有显著优势,提高了可靠度计算的效率,但响应面函数预测值仍与有限元计算值存在一定偏差,后续研究可采用精度更高的改进响应面法,以减少拟合误差。
唐冕,卿岑,宋旭明等.新建下穿道路致高铁桥墩位移的时变响应面研究[J].铁道科学与工程学报,2024,21(12):4861-4871.
TANG Mian,QING Cen,SONG Xuming,et al.Study on the time-varying response surface of high-speed railway pier displacement caused by new underpass road[J].Journal of Railway Science and Engineering,2024,21(12):4861-4871.

