由于城市土地资源的稀缺,新建地铁盾构隧道穿越市区内既有高速铁路不可避免。盾构下穿施工开挖会对地层结构造成一定的破坏,引起既有桥梁的整体结构产生不均匀沉降,严重威胁高铁运营安全。为保障高速列车在下穿盾构隧道路段的安全平稳运行,一般需要对该路段轨道路基的不均匀沉降进行严格控制。因此确定高速列车的行车安全指标与下穿盾构隧道施工参数的关系显得尤为重要。在以往的高速列车行车安全指标与盾构隧道施工参数的相关研究中,计算模型难以完全考虑土层不均匀性和不确定性等因素,从而导致分析结果的准确性和可靠性存在较大差异。为更准确地研究地层土壤变异性对环境振动的影响,通过概率方法考虑不同地层性质的随机场模型被提出。田宁等[1]利用三维随机场理论研究地表堆载条件下,盾构隧道衬砌的应力分布以及变形特征。康玉梅等[2]利用三维随机场分析岩土体参数的空间变异性对地下洞室的变形影响。程红战等[3]将随机场理论和数值分析相结合,研究土层弹性模量的变异系数和相关距离对地表变形的影响。李健斌等[4]将随机场理论应用于双线盾构隧道的地层变形分析。AYAD等[5]基于Karhunen-Loève Expansion(KLE)方法对具有空间变异性的不确定土壤随机场进行离散化模拟,研究地震作用下土壤剪切模量变异系数对土壤开裂概率的影响。LI等[6]在随机振动领域提出的概率密度演化理论为列车-轨道-盾构隧道-路基土耦合系统随机振动分析提供了全新的研究途径。唐钱龙等[7]探讨地铁盾构隧道周围土体的随机场特性对地面既有铁路交通安全的影响,研究表明考虑土层参数随机性的高速列车行车安全指标满足正态分布,且能够提供概率密度保证率。TANG等[8]基于概率密度演化方法和随机场理论,建立地铁列车轨道盾构隧道路基土的耦合模型,研究地铁列车在盾构隧道中引起的环境振动,分析不同地铁列车速度下的地表振动位移结果,给出了地表振动位移的上下限和概率密度信息。仉文岗等[9]系统介绍了隧道施工与运行期间可靠度分析方法的应用,并得出现有隧道施工研究中,隧道掌子面的可靠度研究较多,但隧道开挖对地表沉降以及邻近建筑物的影响可靠度分析较少。陈福勇等[10]基于随机场理论提出大尺度地铁隧道三维随机场生成方法,并将该方法与数值计算和可靠度理论相结合,分析了李家坪地铁车站隧道在开挖过程中的失效概率。以上研究表明,随机场理论被大量应用于盾构隧道的风险评价,相关研究除关注随机场理论的计算方法优化方面,也关注随机场在土层环境振动方面的影响。然而,关于概率密度演化理论应用于盾构施工变形条件下既有铁路行车安全性评估的研究仍然较少,并且将随机场理论与可靠度理论结合应用于评估盾构隧道施工过程中的工程失效概率的研究也相对有限。针对以上问题,建立三维列车-轨道-地基土-隧道耦合系统模型,利用随机可靠度评价方法对列车行车安全可靠度进行评估。分析不同工程设计因素、不同盾构掘进因素和不同行车条件下列车车体的竖向加速度、脱轨系数和轮重减载率的失效概率和可靠度指标。结合现有规范对不同车速等级下的影响因素提出限值要求。
1 列车-轨道-地基土-盾构隧道动力学模型
1.1 列车-轨道-地基土-隧道耦合系统模型
列车子系统基于多体系统动力学方法[11-12]建立,将列车每节车厢建模为7个刚体,包括1个车体、2个转向架、4个轮对以及上下悬架。将轨道结构模拟为弹簧-阻尼器单元,仅考虑其对钢轨的支撑作用,采用有限元法建立轨道-盾构隧道-地基土结构整体计算模型。在此模型中,钢轨采用空间梁单元模拟;拱肋和主梁采用空间梁单元模拟;吊杆采用杆单元模拟。所有材料均假设为线弹性,盾构隧道-地基土除钢轨以外的二期恒载均作为自重施加在盾构隧道-地基土模型上。采用有限元直接刚度法,建立轨道-盾构隧道-地基土子系统动力方程。
将列车子系统和轨道-盾构隧道-地基土子系统通过轮轨接触关系组成整体耦合时变系统,可建立列车-轨道-盾构隧道-地基土耦合时变系统动力方程[13-17]。
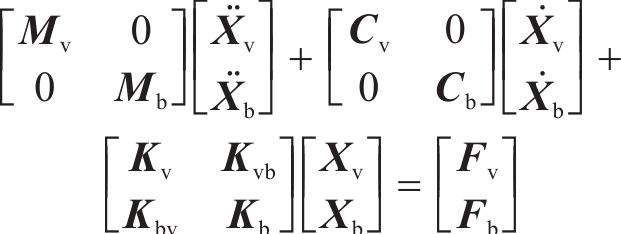
式中:
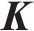

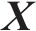
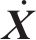
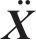
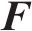
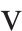
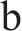
1.2 模型验证
根据本车轨耦合模型建立方法,选取某段高铁的地层、材料、车辆参数进行动力计算。提取本模型计算结果中道床加速度时域曲线并进行频谱分析,如图1(a)所示,文献[18]实测值见图1(b)所示。
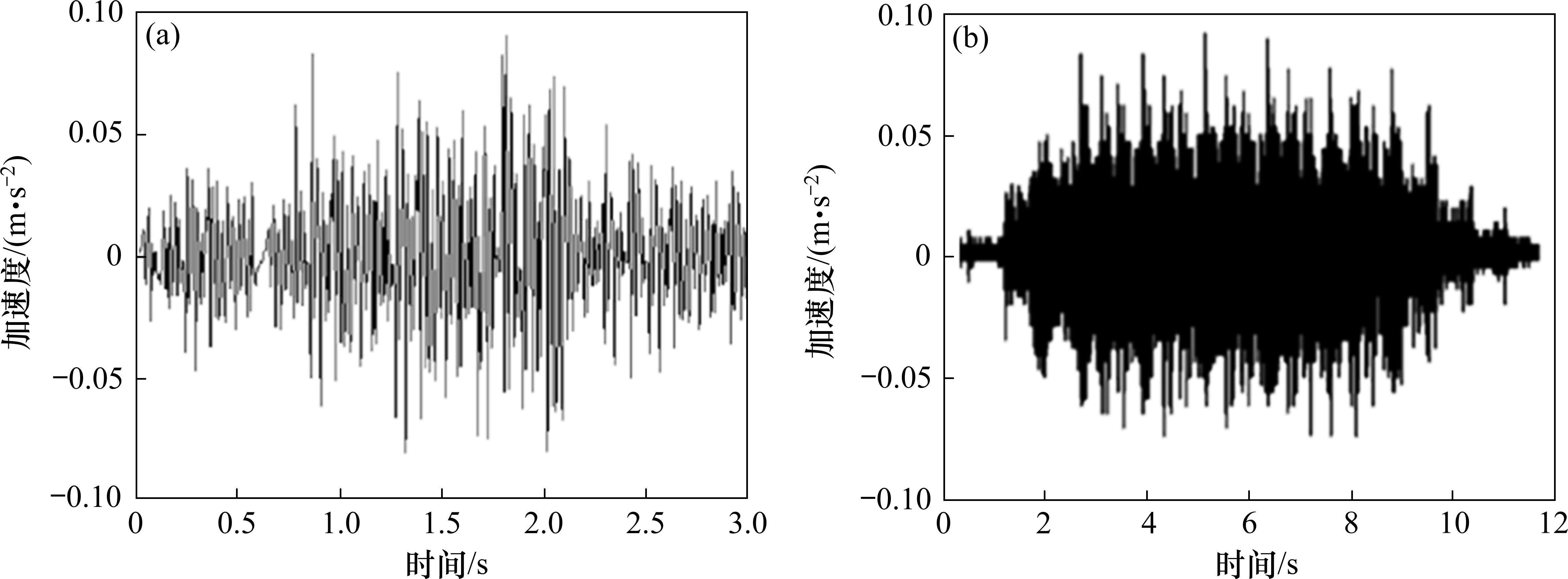
从图1中可以看出,采用本文中的列车-轨道-地基土-隧道耦合模型计算得到的道床加速度时域曲线与文献中的实测值相似,模型计算得到的道床加速度峰值为0.093 m/s2,文献[18]中道床加速度峰值为0.090 m/s2。2个模型的计算结果吻合较好,可以验证本文中列车-轨道-地基土-隧道耦合模型建模方法的合理性与计算的准确性。
2 随机可靠度评估方法
随机可靠性评估方法是一种综合应用随机变量的影响进行可靠性分析的方法。从基本方法看,随机可靠度与常规可靠度在表达方式上没有区别,但将随机场理论应用于工程可靠度计算时,还需通过相关函数和方差折减函数来充分考虑统计参数均值和方差的自相关性,使得用于计算失效概率的方差更趋于合理,能得到更符合工程实际的失效概率值和可靠度指标。在土层参数为常数时得到的车辆动力学指标通常是确定值,但在实际运行环境中,车辆动力学指标结构(车体竖向加速度、脱轨系数和轮重减载率)等往往具有随机性。仅采用均值作为车辆动力学指标限值存在显著不足,因此根据随机可靠度方法确定动力学指标失效的概率和可靠度指标。
2.1 可靠度基本理论
在进行结构可靠性分析中,结构的功能函数可用下式来表示:
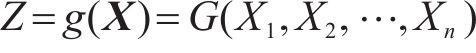
式中:X为随机矢量,X=(X1,X2,…,Xn)T,表示影响工程结构某一功能的n个随机变量。考虑结构功能仅与“结构抗力R”和“作用效应S”2个基本变量有关的情况时,结构的功能函数为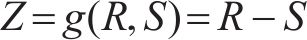
通常可用等式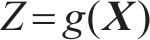
工程中常用可靠指标b代替Pf作为衡量结构失效概率的指标。假设R和S分别服从正态分布(非正态情况处理方式见文献[19]),则功能函数Z也服从正态分布其平均值和标准差分别为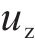
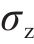
2.2 列车安全运行的功能函数和失效概率
设盾构下穿施工诱发的地层沉降对高速列车运行可靠性的所有随机变量评价总集合为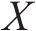
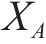
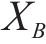
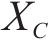
取盾构下穿施工时满足高速列车运行安全的“总系统”可靠度为Pr,它又由竖向加速度、脱轨系数和轮重减载率3项评价指标的“子系统”可靠度构成,且轨道在发生沉降时这3个“子系统”的可靠度均应保证列车运行的安全,并视其为相互独立事件,故有:
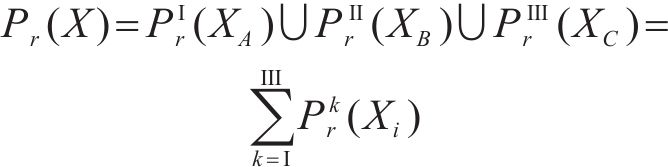
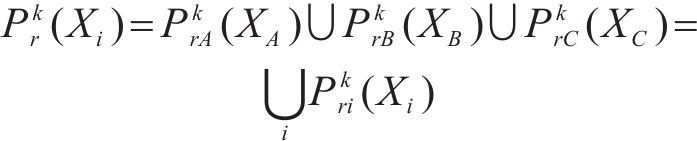
式中: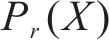
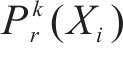
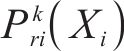
可靠度指标与失效概率密切相关,通常用可靠度指标来衡量结构的可靠性。可靠度指标越大,结构越不容易失效。在工程实际研究与应用中,通常会设定一个目标可靠度指标,以确保失效概率低于某个可接受的阈值,这样可以保证工程结构的安全性和可靠性。参考相关规范标准[20],设高速列车安全运行可靠度评价指标的阈值为[β],其安全等级显然不能低于一级标准。结合考虑高速列车运行的安全性、平稳性、舒适性等方面要求,设定[β]>4.0,所对应的失效概率则是Pf<0.317×10-5,对应的功能等级为“好”以上。
2.3 计算流程与工况设置
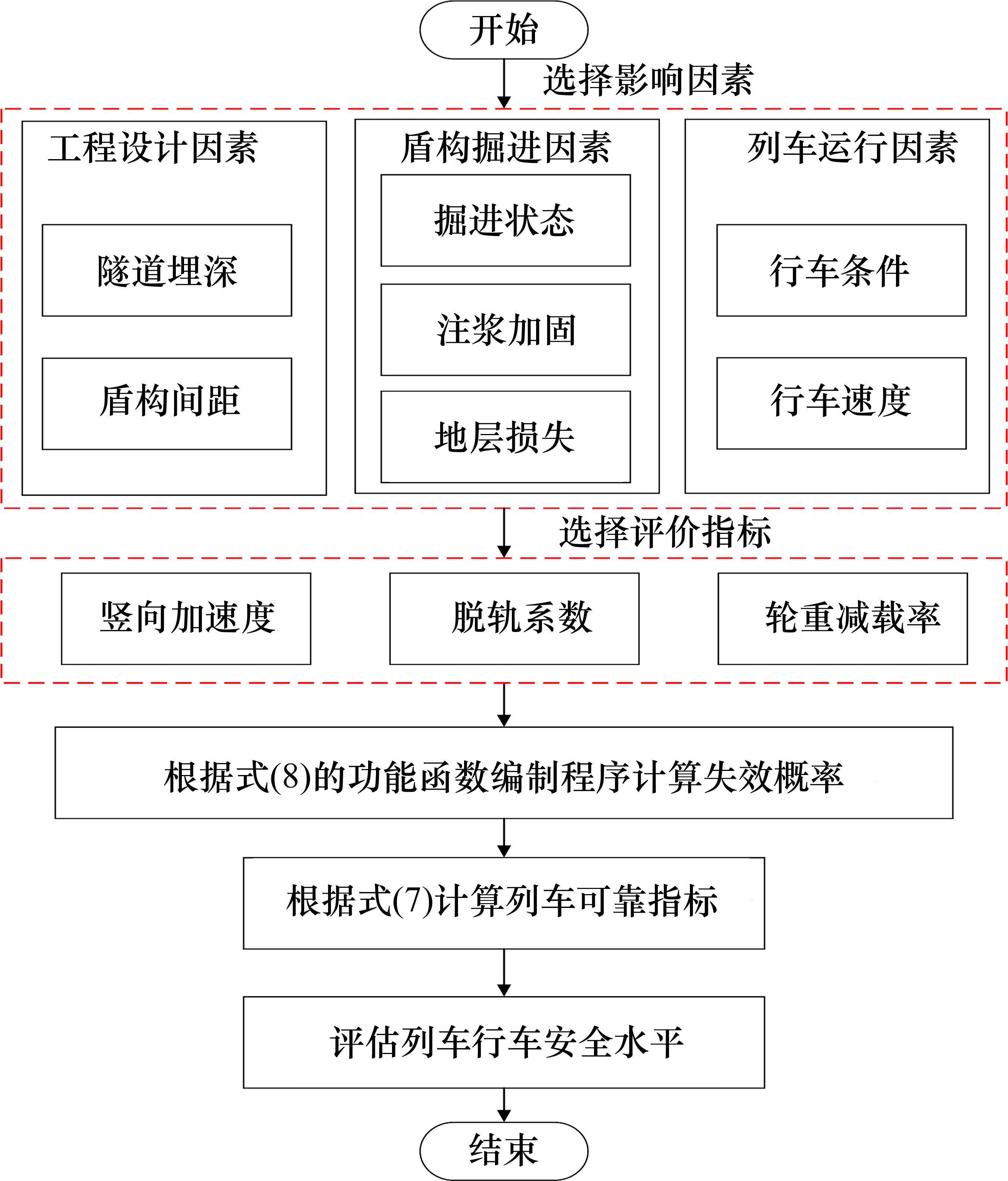
不同影响因素下列车失效概率和可靠度指标的计算流程如图2所示。在随机场理论以及车辆-轨道动力学耦合计算的基础上,分析不同工程设计因素、不同盾构掘进因素和不同列车运行因素与列车行车安全的关系。计算工况如下:工程设计因素考虑不同隧道埋深(10、15、20、25和30 m)和不同盾构间距(8、10、12、15、20和25 m)的影响;盾构掘进因素考虑不同掘进状态(① 先行盾构到达高铁路基线路中心下方时。② 后行盾构到达高铁路基线路中心下方时。③后行盾构出整个路基段时)、不同注浆范围(0、1.5、3和4.5 m)和不同地层损失率(0.2%、0.4%、0.6%、0.8%、1.0%和1.2%)的影响;列车运行因素考虑单车运行和双车交会2种情况的影响。列车运行速度为200、250、300和350 km/h,列车型号为CRH380B。
3 不同因素下列车运行安全可靠度评价
根据不同工况条件下高速列车车体竖向加速度、脱轨系数和轮重减载率指标的均值和标准差计算值,基于可靠度评价方法,研究不同工程设计因素、不同盾构掘进因素和不同行车条件对列车行车安全可靠度指标的影响。
3.1 不同工程设计因素
1) 隧道埋深
不同隧道埋深下列车运行安全可靠度指标如图3所示。从图3中可以发现,当列车速度取定值时,车体竖向加速度、脱轨系数和轮重减载率的可靠度指标均随隧道埋深的增大而增大。而当隧道埋深取定值时,车体竖向加速度、脱轨系数和轮重减载率可靠度指标均随车速的增大而减小。
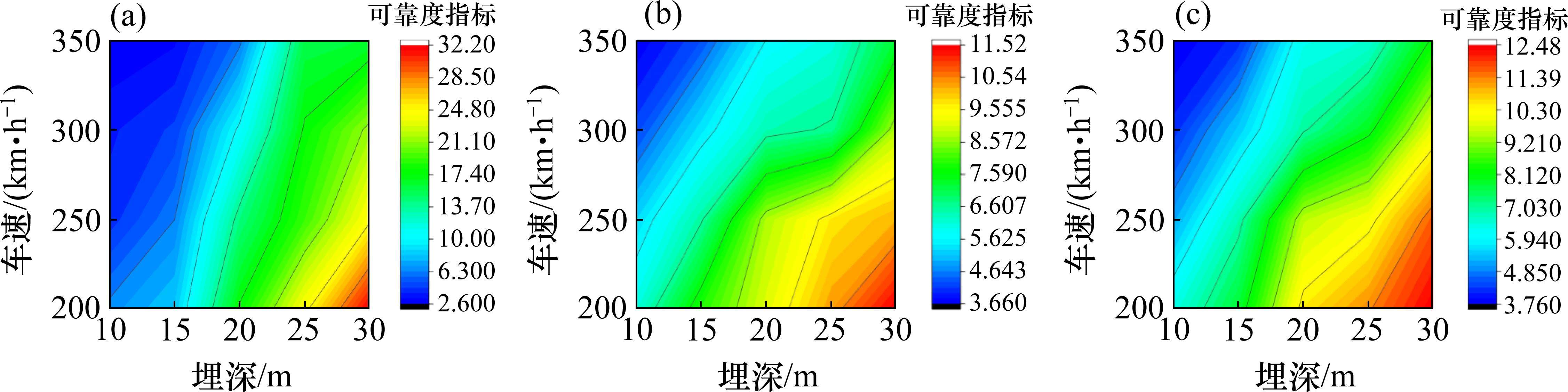
对于车体竖向加速度而言,当隧道埋深为10 m和15 m,列车速度大于300 km/h时,可靠度指标小于4;当隧道埋深大于20 m时,不同车速下的可靠度指标均大于4。对于脱轨系数而言,当隧道埋深为10 m和15 m时,不同车速下的可靠度指标均小于4;当隧道埋深为20 m,列车速度大于250 km/h时,对应可靠度指标均小于4;当隧道埋深大于25 m时,不同列车速度下的可靠度指标均大于4。对于轮重减载率而言,当隧道埋深为10 m和15 m时,不同车速下的可靠度指标均小于4;当隧道埋深为20 m,列车速度大于350 km/h时,可靠度指标小于4;当隧道埋深大于25 m时,不同列车速度下的可靠度指标均大于4。
表1给出了不同隧道埋深下,同时考虑竖向加速度、脱轨系数和轮重减载率的列车运行安全可靠度指标和失效概率。从表1可以发现,当隧道埋深取值确定时,随着列车速度增加,考虑设计因素影响下的失效概率逐渐增大,可靠度指标逐渐降低。而对于同一列车行驶速度下,随着隧道埋深逐渐增加,考虑设计因素影响下的失效概率逐渐降低,可靠度指标逐渐增大。综合以上趋势,若要求200~350 km/h车速范围内,列车的功能水平均处于等级“好”(可靠度指标大于4,失效概率少于0.003 17%)以上,隧道埋深条件应不小于15 m,即2~2.5倍洞径以上。
| 车速/(km∙h-1) | 8 m | 10 m | 15 m | 20 m | 25 m | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| β | Pf /% | β | Pf /% | β | Pf /% | β | Pf /% | β | Pf /% | |
| 200 | 6.03 | 7.97×10-8 | 7.75 | 4.44×10-13 | 9.13 | 2.13×10-18 | 10.37 | 8.45×10-24 | 11.52 | 5.43×10-29 |
| 250 | 4.09 | 2.16×10-3 | 6.26 | 1.95×10-8 | 8.78 | 8.65×10-16 | 9.75 | 4.43×10-21 | 10.21 | 8.45×10-23 |
| 300 | 3.42 | 3.11×10-2 | 4.57 | 2.45×10-4 | 6.42 | 6.98×10-9 | 6.68 | 1.19×10-9 | 8.84 | 4.83×10-17 |
| 350 | 2.58 | 0.49 | 3.08 | 1.04×10-1 | 5.60 | 1.06×10-6 | 6.02 | 8.60×10-8 | 7.32 | 1.25×10-11 |
2) 盾构间距
图4给出了不同盾构间距下列车运行安全可靠度指标。从图4中可以发现,当车速取定值时,车体竖向加速度、脱轨系数和轮重减载率的可靠度指标均随盾构间距的增大而增大。而在相同的盾构间距下,随着列车速度增加,车体竖向加速度、脱轨系数和轮重减载率的可靠度指标均逐渐降低。
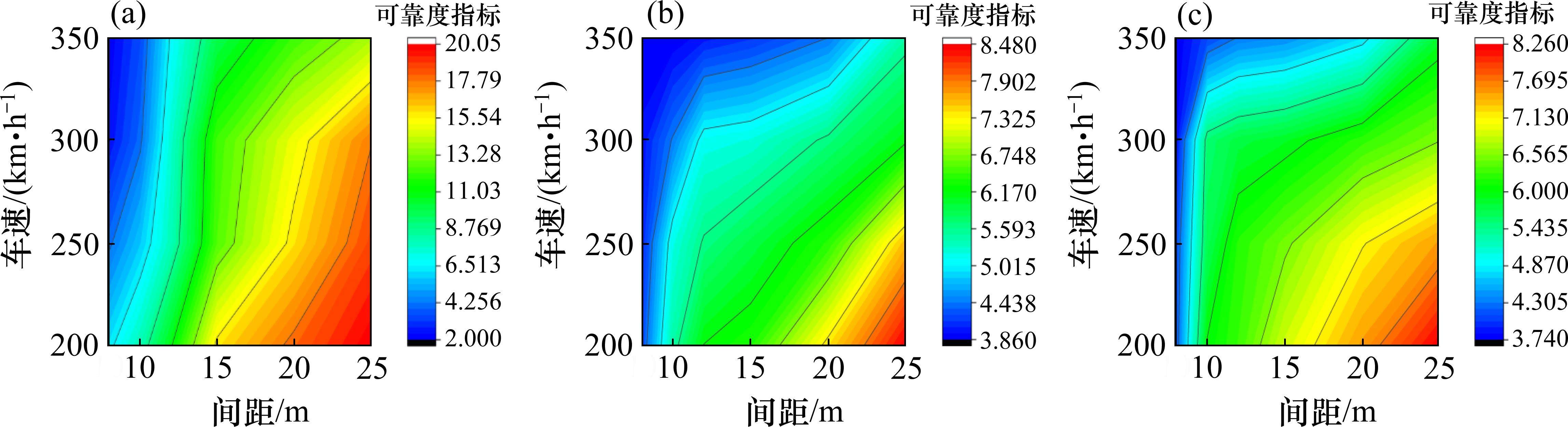
对于车体竖向加速度而言,当盾构间距为8 m和10 m,列车速度大于300 km/h时,可靠度指标小于4;当盾构间距为12 m,列车速度大于350 km/h时,可靠度指标小于4;当盾构间距为15~25 m,不同车速下的可靠度指标均大于4。对于脱轨系数而言,当盾构间距为8~12 m,不同车速下的可靠度指标均小于4,;当盾构间距为15~25 m,不同车速下的可靠度指标均大于4。对于轮重减载率而言,当盾构间距为8~10 m,不同车速下的可靠度指标均小于4;当盾构间距为12 m,列车速度大于250 km/h时,可靠度指标小于4,;当盾构间距为15~25 m,不同车速下的可靠度指标均大于4。
表2中给出了不同盾构间距下,同时考虑竖向加速度、脱轨系数和轮重减载率的列车运行安全可靠度指标和失效概率。从表2中可以看出,随着列车速度增加,考虑整个设计因素影响下的失效概率逐渐增大,可靠度指标逐渐降低。而在同一列车行驶速度下,随着盾构间距的增大,考虑整个设计因素影响下的失效概率逐渐减小,可靠度指标逐渐增大。综合以上趋势,若要求在200~350 km/h车速范围内,列车的功能水平处于等级“好”(可靠度指标大于4,失效概率小于0.003 17%)以上,盾构间距应大于15 m。
| 车速/(km∙h-1) | 8 m | 10 m | 12 m | 15 m | 20 m | 25 m | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Β | Pf /% | β | Pf /% | β | Pf /% | β | Pf /% | β | Pf /% | β | Pf /% | |
| 200 | 4.15 | 1.63×10-3 | 5.46 | 2.33×10-6 | 6.12 | 4.79×10-8 | 6.34 | 1.15×10-8 | 7.38 | 8.17×10-12 | 8.43 | 1.11×10-14 |
| 250 | 3.87 | 5.34×10-3 | 5.16 | 1.22×10-5 | 5.62 | 9.28×10-7 | 5.90 | 1.78×10-7 | 6.39 | 8.48×10-9 | 7.46 | 4.30×10-12 |
| 300 | 2.46 | 6.85×10-1 | 4.06 | 2.45×10-3 | 5.13 | 1.41×10-5 | 5.21 | 9.39×10-6 | 5.65 | 7.98×10-7 | 6.13 | 4.29×10-8 |
| 350 | 2.12 | 1.71×100 | 3.39 | 3.46×10-2 | 3.96 | 3.82×10-3 | 4.07 | 2.33×10-3 | 4.40 | 5.44×10-4 | 5.47 | 2.19×10-6 |
3.2 不同盾构掘进因素
1) 掘进状态
图5给出了不同掘进状态下列车运行安全可靠度指标。从图5中可以发现,当车速取定值,掘进状态由①过渡到③时,车体竖向加速度、脱轨系数和轮重减载率的可靠度指标均逐渐减小。对于相同的掘进状态下,随着列车速度增加,车体竖向加速度、脱轨系数和轮重减载率的可靠度指标均逐渐降低。
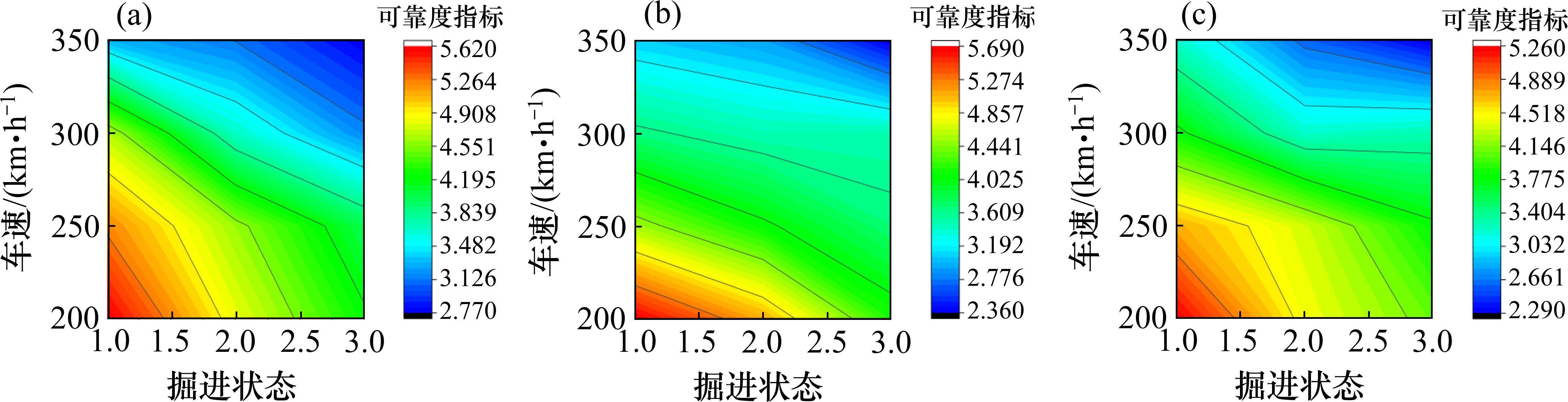
对于车体竖向加速度而言,3种掘进状态下,不同车速下的可靠度指标均大于4。对于脱轨系数而言,在掘进状态①情况下,不同车速下的可靠度指标均大于4;在掘进状态②情况下,当列车速度大于300 km/h时可靠度指标均小于4;在掘进状态③情况下,当列车速度大于250 km/h时可靠度指标均小于4。对于轮重减载率而言,在掘进状态①情况下,不同车速下的可靠度指标均大于4;在掘进状态②情况下,当列车速度大于300 km/h时可靠度指标均小于4;在掘进状态③情况下,当列车速度大于250 km/h时可靠度指标均小于4。
表3给出了不同掘进状态下,同时考虑竖向加速度、脱轨系数和轮重减载率的列车运行安全可靠度指标和失效概率。从表3可以看出,随着列车速度增加,考虑整个设计因素影响下失效概率逐渐增大,可靠度指标逐渐降低。而对于同一列车行驶速度下,掘进状态由①过渡到③时,考虑整个设计因素影响下的失效概率逐渐增大,可靠度指标逐渐减小。综合以上趋势,若要求200~350 km/h车速范围内,列车功能均处于等级“好”(可靠度指标大于4,失效概率少于0.003 17%)以上,应当对掘进状态②和掘进状态③采取相应的地层加固措施。
车速/ (km∙h-1) | ① | ② | ③ | |||
|---|---|---|---|---|---|---|
| β | Pf /% | β | Pf /% | β | Pf /% | |
| 200 | 11.31 | 5.64×10-26 | 6.27 | 1.81×10-8 | 5.22 | 8.80×10-6 |
| 250 | 9.90 | 1.98×10-19 | 3.95 | 3.87×10-3 | 3.12 | 9.10×10-2 |
| 300 | 8.44 | 3.66×10-13 | 3.11 | 9.26×10-2 | 2.25 | 1.24 |
| 350 | 6.26 | 1.93×10-8 | 2.45 | 7.18×10-1 | 1.92 | 2.74 |
2) 注浆范围
图6给出了不同注浆范围下列车运行安全可靠度指标。从图6可以发现,当列车速度取定值时,车体竖向加速度、脱轨系数和轮重减载率的可靠度指标均随注浆范围的增大而增大。而当注浆范围取定值时,车体竖向加速度、脱轨系数和轮重减载率的可靠度指标均随车速的增大而减小。
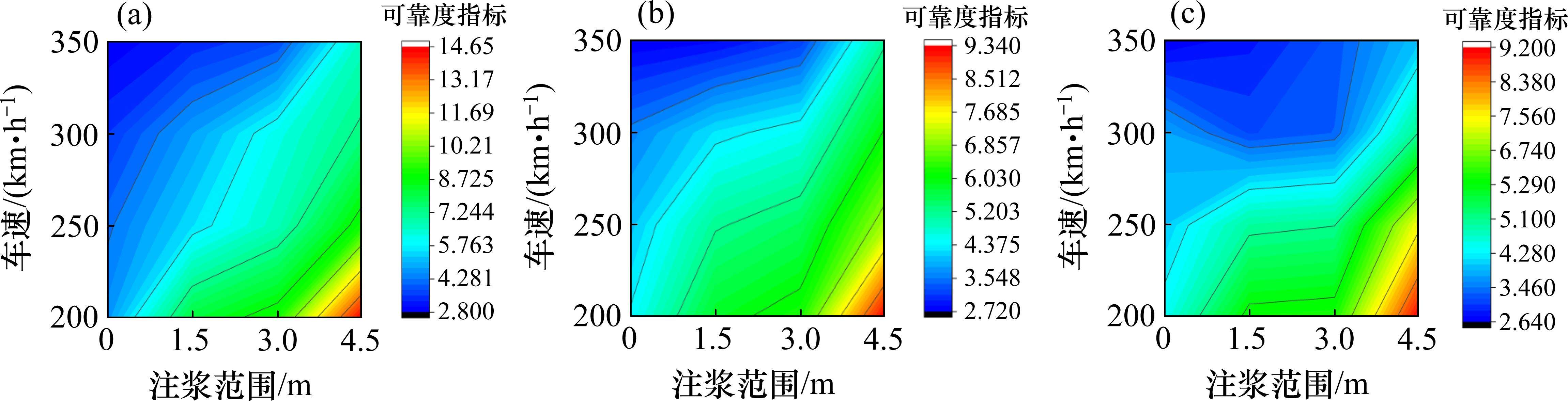
对于车体竖向加速度而言,当注浆范围为0 m时,不同车速下的可靠度指标均小于4,且车速达到350 km/h时,可靠度指标已小于1,对应的功能水平等级为“危险”。当注浆范围分别为1.5 m和3 m,车速分别小于250 km/h和300 km/h时,可靠度指标均大于4;当注浆范围为4.5 m时,可靠度指标均大于4。对于脱轨系数而言,当注浆范围为0 m和1.5 m时,不同列车速度下的可靠度指标均小于4;当注浆范围为3 m,列车速度小于300 km/h时可靠度指标均大于4;当注浆范围为4.5 m时,不同列车速度下的可靠度指标均大于4。对于轮重减载率而言,当注浆范围为0 m和1.5 m时,不同列车速度下的可靠度指标均小于4;当注浆范围为3 m,列车速度小于250 km/h时的可靠度均大于4;当注浆范围为4.5 m时,不同列车速度下的可靠度指标均大于4。
表4中给出了不同注浆范围下,同时考虑竖向加速度、脱轨系数和轮重减载率的列车运行安全可靠度指标和失效概率。从表4可以发现,当注浆范围取值确定时,随着列车速度增加,考虑整个设计因素影响下的失效概率逐渐增大,同时其可靠度指标逐渐降低。而对于同一列车行驶速度下,随着注浆范围逐渐增加,考虑整个设计因素影响下的失效概率逐渐降低,同时其可靠度逐渐增大。综合以上趋势,若要求200~350 km/h车速范围内,列车的功能水平均处于“好”等级(可靠度指标大于4,失效概率少于0.003 17%)以上,注浆范围应大于4.5 m。
车速/ (km∙h-1) | 0 m(未注浆) | 1.5 m | 3 m | 4.5 m | ||||
|---|---|---|---|---|---|---|---|---|
| β | Pf /% | β | Pf /% | β | Pf /% | β | Pf /% | |
| 200 | 4.23 | 1.16×10-3 | 5.82 | 2.92×10-7 | 6.09 | 5.68×10-8 | 9.18 | 0 |
| 250 | 3.80 | 7.30×10-3 | 4.90 | 4.68×10-5 | 5.07 | 1.97×10-5 | 7.08 | 7.31×10-11 |
| 300 | 3.33 | 4.37×10-2 | 3.17 | 7.73×10-2 | 3.33 | 4.36×10-2 | 5.14 | 1.36×10-5 |
| 350 | 2.34 | 0.95 | 2.59 | 0.49 | 2.97 | 1.46×10-1 | 4.00 | 3.14×10-3 |
3) 不同地层损失率
图7给出了不同地层损失率下列车运行安全可靠度指标。从图7可以发现,当列车速度取定值时,车体竖向加速度、脱轨系数和轮重减载率的可靠度指标均随不同地层损失率的增大而减小。而当不同地层损失率取定值时,车体竖向加速度、脱轨系数和轮重减载率的可靠度指标均随车速的增大而减小。
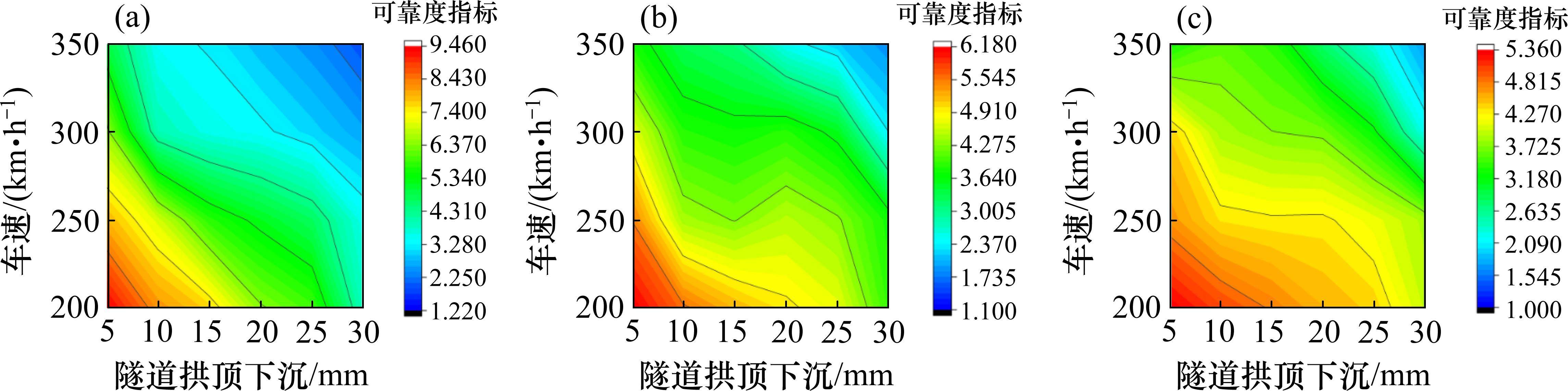
对于车体竖向加速度而言,当列车速度取定值时,车体竖向加速度的失效概率随地层损失率的增大而增大,可靠度指标随地层损失率的增大而减小;而当地层损失率取定值时,失效概率随车速的增大而增大,可靠度指标随车速的增大而减小。当地层损失率少于0.4%时,列车速度小于250 km/h时,车体竖向加速度对应的可靠度指标均大于4,失效概率少于0.003 17%,对应功能水平均处于“好”等级以上;当地层损失率超过1.0%后,无论列车速度多大,车体竖向加速度对应的可靠度指标均小于4,失效概率均大于0.003 17%,对应功能水平均处于“好”等级以下。
表5给出了不同地层损失率下,同时考虑竖向加速度、脱轨系数和轮重减载率的列车运行安全可靠度指标和失效概率。从表中可以发现,当地层损失率取值确定时,随着列车速度增加,3项评价指标因素共同影响下的失效概率逐步增大,同时其可靠度指标逐步降低;而对于同一列车行驶速度下,随着地层损失率逐步增加,整体失效概率逐步降低,同时其可靠度逐步增大。由此表明,若要求200~350 km/h车速范围内,可靠度指标大于4,失效概率少于0.003 17%以上,列车的功能水平均处于“好”等级,地层损失率应控制在0.2%以内,说明盾构施工过程中控制地层损失率尤为关键。
| 车速/(km∙h-1) | 0.2% | 0.4% | 0.6% | 0.8% | 1.0% | 1.2% | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| β | Pf | β | Pf | β | Pf | β | Pf | β | Pf | β | Pf | |
| 200 | 5.35 | 4.45×10-6 | 5.02 | 2.52×10-5 | 4.38 | 5.80×10-4 | 4.53 | 3.02×10-4 | 4.38 | 6.01×10-4 | 3.65 | 1.31×10-2 |
| 250 | 4.69 | 1.35×10-4 | 4.24 | 1.14×10-3 | 4.12 | 1.88×10-3 | 4.24 | 1.14×10-3 | 4.04 | 2.70×10-3 | 3.39 | 3.54×10-2 |
| 300 | 4.40 | 5.52×10-4 | 3.63 | 1.43×10-2 | 3.37 | 3.81×10-2 | 3.27 | 5.45×10-2 | 2.87 | 2.10×10-1 | 1.93 | 2.70 |
| 350 | 3.26 | 5.57×10-2 | 3.10 | 9.73×10-2 | 2.90 | 1.84×10-1 | 2.32 | 1.01 | 1.83 | 3.35×100 | 1.29 | 9.89 |
3.3 不同行车条件下因素
分别以单车和双车交会的竖向加速度、脱轨系数和轮重减载率作为控制变量,根据本文的分析方法,可得到不同车速下列车行车安全的综合失效概率和可靠度指标,如表6和表7,以及随列车速度的变化折线图,见图8和图9。
车速/ (km∙h-1) | 竖向加速度 | 脱轨系数 | 轮重减载率 | |||
|---|---|---|---|---|---|---|
| β | Pf /% | β | Pf /% | β | Pf /% | |
| 200 | 4.71 | 1.24×10-4 | 4.87 | 5.58×10-5 | 4.77 | 9.21×10-5 |
| 250 | 4.57 | 2.44×10-4 | 4.32 | 7.80×10-4 | 4.67 | 1.51×10-4 |
| 300 | 3.91 | 4.61×10-3 | 3.44 | 2.91×10-2 | 3.39 | 3.49×10-2 |
| 350 | 3.48 | 2.51×10-2 | 3.23 | 6.19×10-2 | 3.02 | 1.26×10-1 |
车速/ (km∙h-1) | 竖向加速度 | 脱轨系数 | 轮重减载率 | |||
|---|---|---|---|---|---|---|
| β | Pf /% | β | Pf /% | β | Pf /% | |
| 200 | 4.69 | 1.37×10-4 | 4.85 | 6.17×10-5 | 4.75 | 1.02×10-4 |
| 250 | 4.55 | 2.68×10-4 | 4.28 | 9.34×10-4 | 4.65 | 1.66×10-4 |
| 300 | 3.86 | 5.67×10-3 | 3.37 | 3.76×10-2 | 3.35 | 4.04×10-2 |
| 350 | 3.41 | 3.25×10-2 | 3.13 | 8.74×10-2 | 2.96 | 1.54×10-1 |
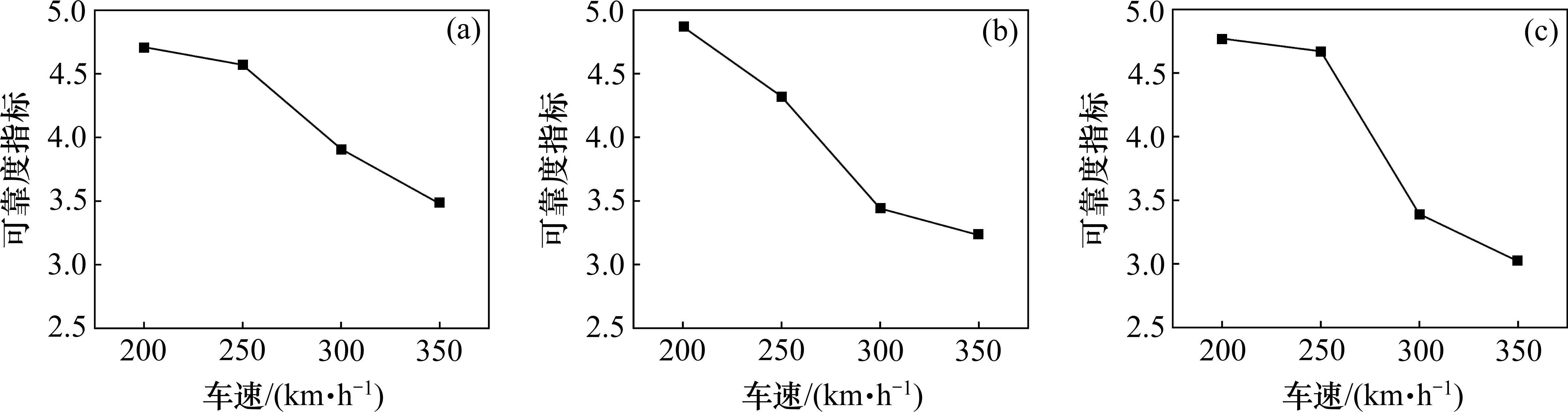
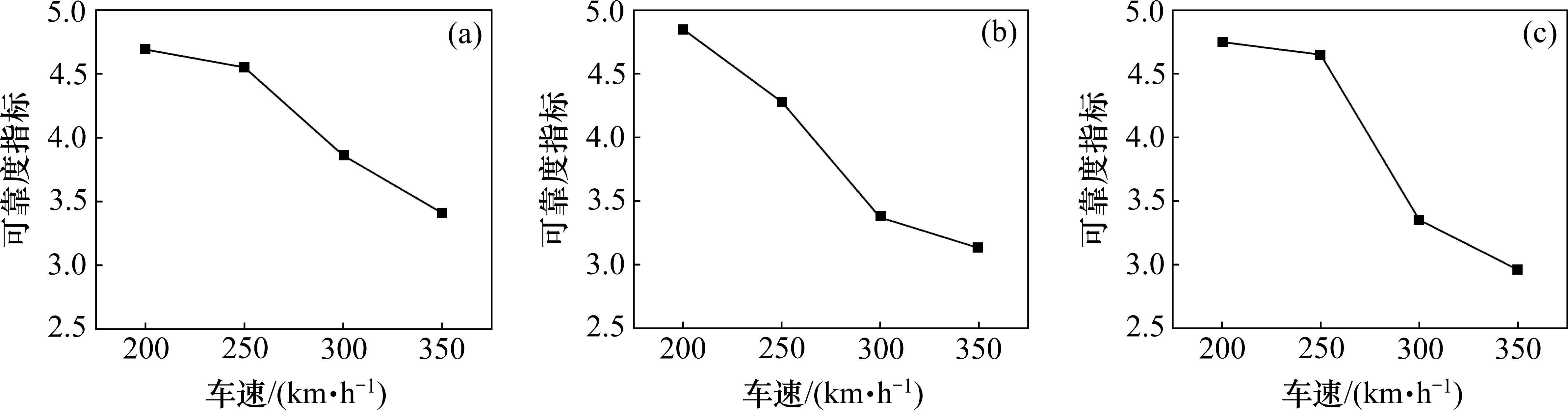
同时根据图8和图9的数据结果,不同车速双车交会运行工况下的失效概率与单车运行工况下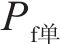
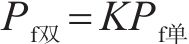
式中:K可称为增大系数,K与车速v基本呈式(9)的线性关系,如图10所示。
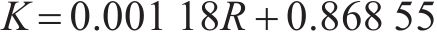
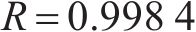
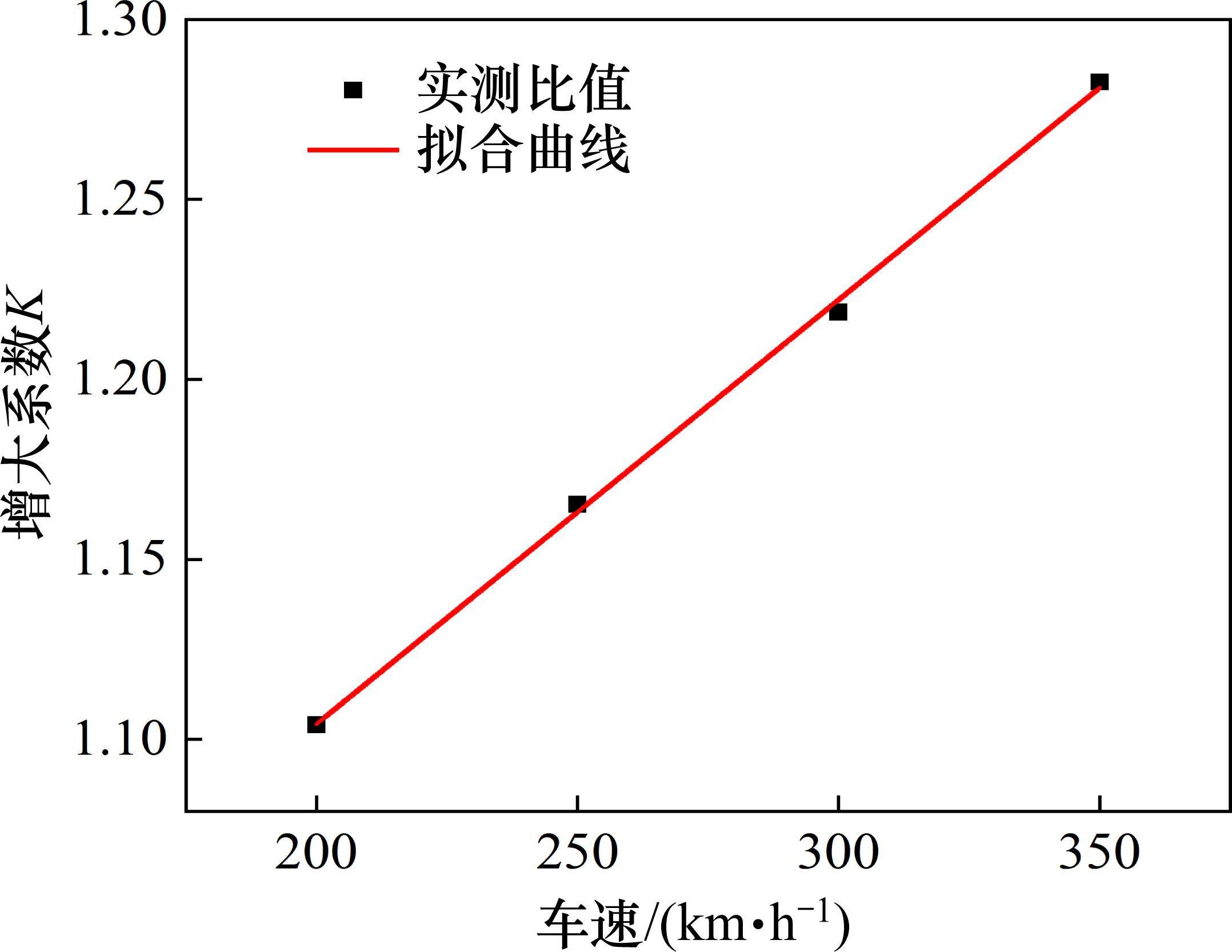
4 盾构下穿高铁路基时行车安全可靠度指标
1) 考虑所有因素下子系统和总评价系统可靠度
根据可靠度分析结果给出考虑所有因素下子系统和总评价系统的可靠度和失效概率,如表8所示。从表8中可以看出,考虑因素越多,列车行车安全可靠度越低。总评价系统的可靠度指标比各子系统更小。
车速/ (km∙h-1) | 评价子系统Ⅰ (竖向加速度系统) | 评价子系统Ⅱ (脱轨系数系统) | 评价子系统Ⅲ (轮重减载率系统) | 总评价系统 | ||||
|---|---|---|---|---|---|---|---|---|
| β | Pf /% | β | Pf /% | β | Pf /% | β | Pf /% | |
| 200 | 3.81 | 7.08×10-3 | 3.78 | 7.77×10-3 | 3.81 | 7.07×10-3 | 3.52 | 2.19×10-2 |
| 250 | 3.42 | 3.17×10-2 | 3.46 | 2.69×10-2 | 3.58 | 1.71×10-2 | 3.17 | 7.57×10-2 |
| 300 | 2.25 | 1.24 | 2.30 | 1.08 | 2.16 | 1.53 | 1.77 | 3.80 |
| 350 | 1.59 | 5.58 | 1.66 | 4.87 | 1.54 | 6.15 | 1.01 | 15.70 |
2) 行车安全可靠度指标
表9给出不同车速等级下各因素的安全限值。从表9中可以看出,车速等级越高,隧道埋深、盾构间距和注浆范围的安全限值越小,地层损失率的限值越大。
| 可靠度及限值 | I级 | II级 | III级 | IV级 |
|---|---|---|---|---|
| >300 km/h | 250~300 km/h | 200~250 km/h | <200 km/h | |
| 可靠度指标β | >5.2 | 4.7~5.2 | 4.2~4.7 | 3.7~4.2 |
| 失效概率Pf /% | 9.96×10-6 | 1.30×10-4 | 1.33×10-3 | 6.87×10-2 |
| 隧道埋深/m | >25 | 20~25 | 15~20 | >12 |
| 盾构间距/m | >15 | 12~15 | 8~15 | >8 |
| 地层损失率/% | <0.4 | <0.6 | <0.8 | <1.0 |
5 结论
1) 工程设计、盾构掘进和行车条件3种影响因素对竖向加速度、脱轨系数、轮重减载率3个评价子系统以及总评价系统的可靠度指标和失效概率均随行车速度的增大而减小,而失效概率均与车速呈负相关的关系。
2) 列车交会时的可靠度指标比单车行驶时更小,列车在沉降区交会时发生脱轨事故的概率高于单车运行。车速200、250、300和350 km/h下,不同车速双车交会运行工况下的失效概率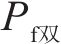
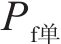
3) 当行车速度大于250 km/h时,3种影响因素影响下3个评价子系统以及总评价系统的可靠度指标均小于4,失效概率大于0.003 17%。因此,如要保证在盾构穿越过程中高速列车的行车安全,除了选择合理的盾构掘进参数外,还需采取限制行车速度的措施。
唐钱龙,邹洋,刘妙等.盾构下穿时高铁行车安全随机可靠度评估方法[J].铁道科学与工程学报,2025,22(02):496-508.
TANG Qianlong,ZOU Yang,LIU Miao,et al.The stochastic reliability evaluation method for driving safety of high-speed railway during shield tunneling[J].Journal of Railway Science and Engineering,2025,22(02):496-508.

