市场中常见的铁路货运风险保障产品有铁路运输企业提供的铁路保价运输、铁路运输企业出资设立的自保公司提供的铁路国内货运保险(下文简称“铁路货运保险”)、其他商业保险企业提供的铁路国内货运保险(下文简称“商业货运保险”),三者均在保护客户权益、分散货运风险等方面发挥了重要作用。随着向现代物流企业转型发展,铁路运输企业为满足客户对货运风险保障产品的多样化和市场化需求,提出了保价保险协同发展、费率优化等新时期发展方向[1]。但铁路货物保价费率自1991年制定以来鲜有调整,铁路运输企业在保价保险协同发展时如何市场化调整各货运风险保障产品费率,是亟待解决的问题。在货运风险保障产品费率优化方面,何晓蕾[2]分析了铁路保价运输现状及在市场化运营方面存在的问题,提出阶段性调整费率水平等对策建议;FENG等[3]以服务水平和费率为指标计算广义费用,采用logit模型求解市场份额,在竞争与合作2种情景下构建了铁路保价运输与商业货运保险的收益函数,得到最优费率组合;WANG等[4]在加法、乘法2种费率计算方式下,分别采用主从博弈求出货运风险保障产品的优化后费率及客户的选择偏好,针对不同的市场情况提出费率计算方式选择建议。现有研究多集中于根据现场工作经验定性提出优化方案,部分学者考虑铁路货运风险保障产品之间、铁路货运风险保障产品与客户之间的关系,定量计算费率优化后取值,目前未有学者探讨铁路保价运输与铁路货运保险协同发展下的费率市场化调整策略。在市场化运营决策和协同定价问题中,博弈论作为研究多主体间交互性决策行为的数学分析工具,得到了广泛应用。谭春桥等[5]构建了关于共享单车企业租赁定价与投放数量联合决策的二维Bertrand博弈模型,研究差异定价与协同定价2种情形下的企业最优策略组合;王海洋等[6]基于主从博弈将综合能源销售商作为领导者,新能源冷热电联供运营商和负荷聚合商作为跟随者,求解多主体分布式协同优化运行策略。江彬倩等[7]建立自由销售模式下代码共享协议选择和代码共享机票定价的两阶段博弈模型,并提出其简便求解方法,证明了代码共享协议提升平均机票价格。因此,本文在铁路运输企业推行保价保险协同发展的背景下,从博弈视角刻画了市场主体间关系,结合费率影响因素、精算技术构建多主体博弈定价模型,协同优化铁路运输企业货运风险保障产品费率,并探究商业保险公司与客户在铁路运输企业优化费率后的决策与行动,为铁路运输企业开展合理决策提供理论支撑。
1 问题描述
铁路保价运输是一种限制承运人赔偿责任的运输条款,铁路货运保险和商业货运保险是一种基于大数法则分散运输风险的保险协议,三者均为运输风险管理工具,具有替代性,铁路保价运输和铁路货运保险、商业货运保险之间在制定目的、责任期限、保障范围等方面又存在差异,具有互补性。已有学者从定性和定量2个方面证明了铁路运输企业推行保价保险协同发展并新推出保价保险一体化的货运风险保障产品(下文简称“保价保险一体化产品”)是可行的[8-9]。因此,假设铁路运输企业在推行保价保险协同发展的基础上,拟向市场中新推出保价保险一体化产品,为合理市场化调整货运风险保障产品费率,使产品既能保持一定的市场份额,又能保障铁路运输企业在风险保障方面的利润水平,需要解决3方面问题:1) 确定铁路保价运输、铁路货运保险推出保价保险一体化产品的合作方案;2) 优化铁路运输企业提供的货运风险保障产品费率;3) 确定商业保险公司之后的决策与行动及对市场的影响。
2 模型建立
2.1 市场主体间的博弈关系
市场中有铁路运输企业、商业保险企业、客户3类主体,根据市场情境,从博弈视角分析三者间的关系,如图1所示。
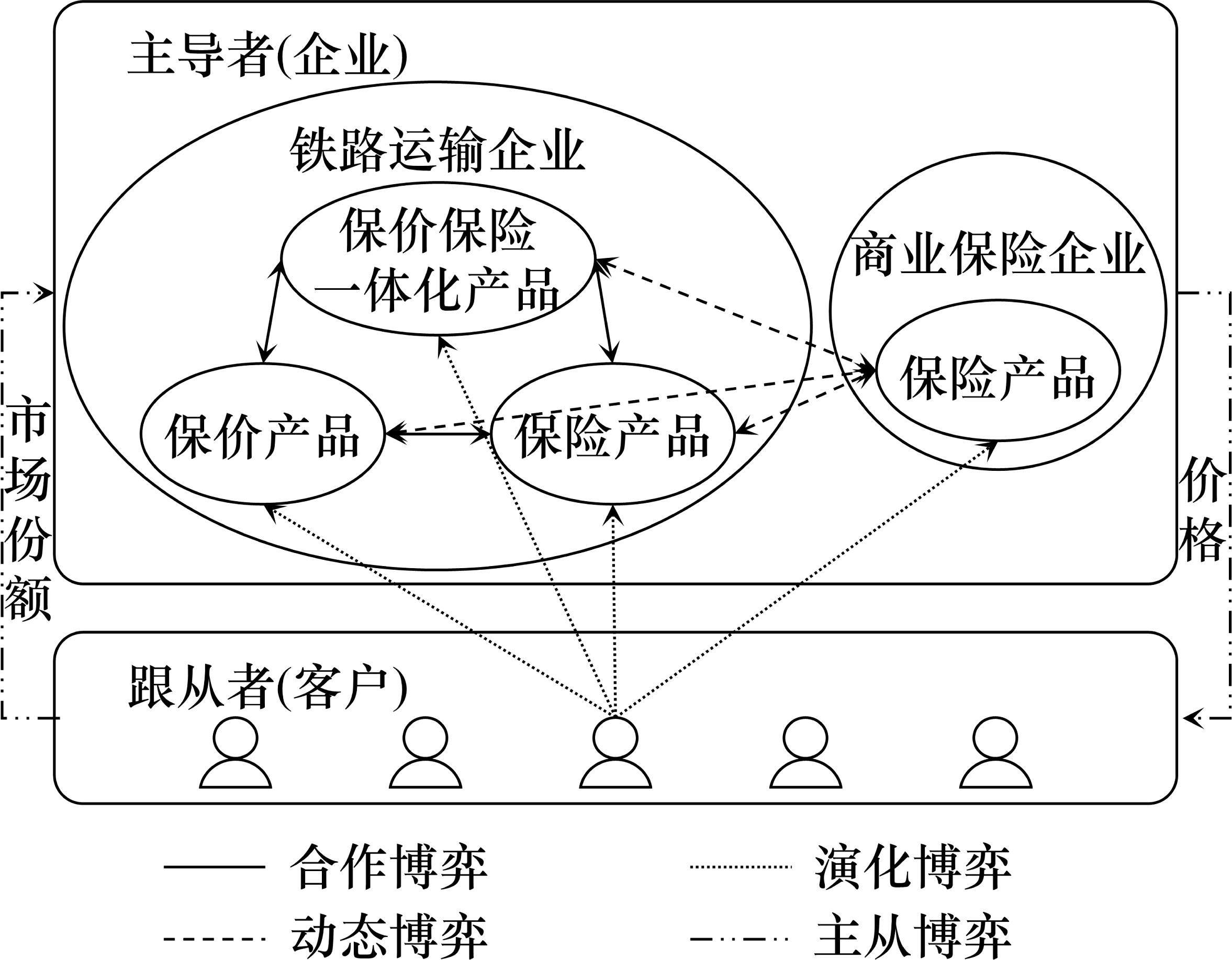
铁路保价运输、铁路货运保险、保价保险一体化产品由同一市场主体铁路运输企业提供,三者之间为合作博弈关系。众多商业保险企业均提供商业货运保险,如中国平安、太平洋保险、中国人民保险等,由于不同商业保险企业提供的保险之间替代性强,本文不考虑各商业保险公司之间的竞争关系,假设市场中有一种商业货运保险。商业货运保险可参照已公开的铁路运输企业货运风险保障产品制定费率,自身费率不公开,为客户向商业保险企业询价,因此认为商业货运保险与铁路运输企业提供的3种货运风险保障产品之间为非合作博弈中的完全且完美信息动态博弈关系。有限理性的客户无法捕捉到全部市场信息[10],随机选取一种策略与上一轮的策略进行对比,购买效用更高的一方,逐步实现效用最大化,客户与货运风险保障产品之间为演化博弈关系。铁路运输企业和商业保险企业为主导者,客户为跟从者,企业根据市场份额调整产品费率,客户根据产品费率修改购买策略,经不断的循环互动后,3类市场主体均使自身效益达到最大,该过程为主从博弈。
2.2 基本假设
假设1:货运风险保障产品依托于铁路货物运输产品。对于有货物运输需求的客户来说,有无风险保障、商业货运保险、铁路货运保险、保价保险一体化产品、铁路保价运输5种货运风险保障方式可以选择。5种货运风险保障方式的市场份额之和为1。
假设2:保价与保险可视作有较强替代性的横向差异化产品[11],因此借鉴Salop模型建立长度为1的线性环形市场[12],将各货运风险保障方式与客户分布其中。线性环形市场如图2所示。
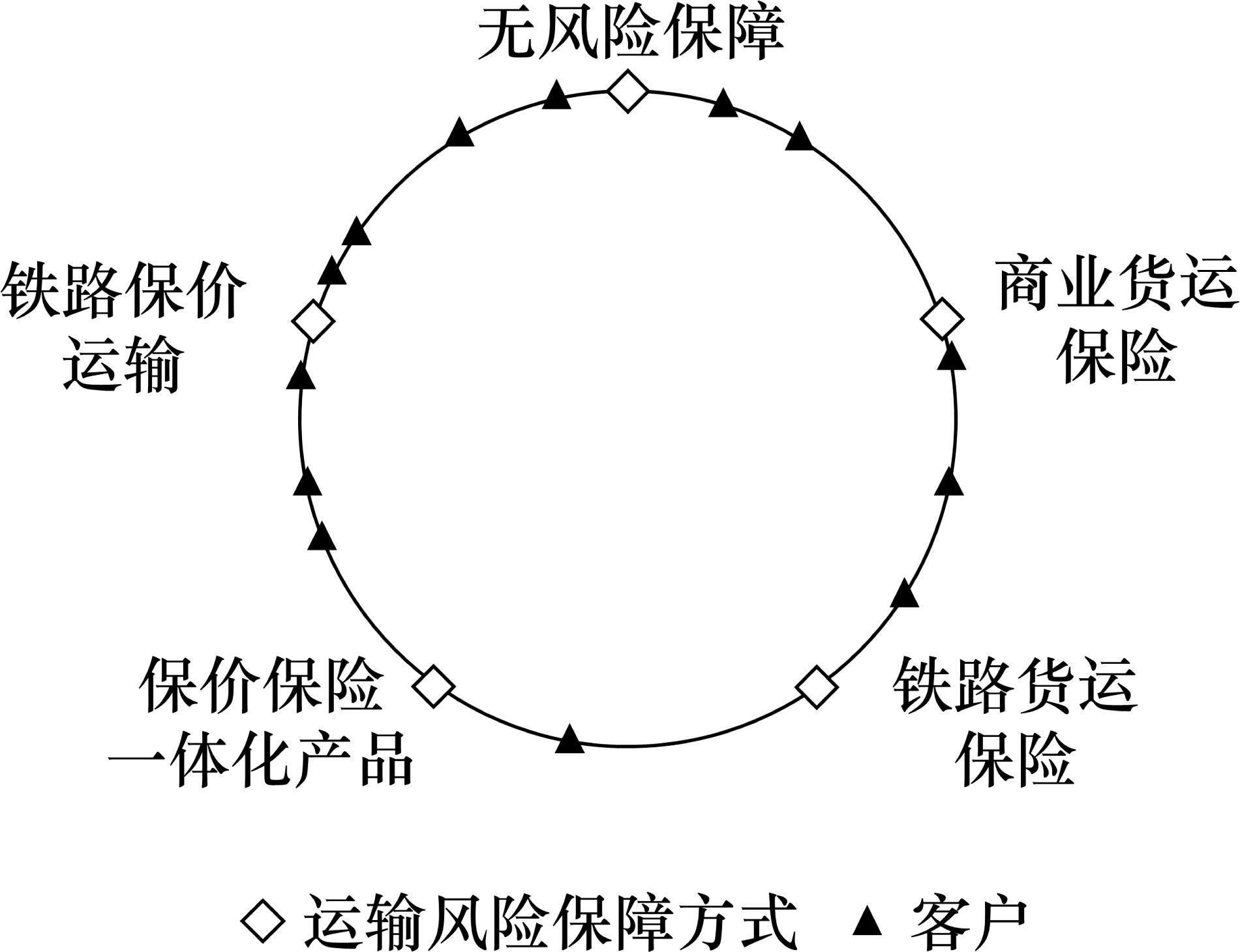
假设3:货运风险保障方式在市场中的排列顺序按照所属企业相同则位置相邻、性质相似则位置相邻2种原则确定,为无风险保障、商业货运保险、铁路货运保险、保价保险一体化产品、铁路保价运输,依次记作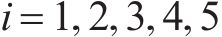
假设4:客户所在位置代表了他们对于各货运风险保障方式的偏好,客户对货运风险保障方式的需求为1。
假设5:各货运风险保障方式的效用均大于0,并可以独立满足市场需求。
假设6:客户独立选择购买策略,各货运风险保障产品在成本价和市场限定最高价之间自由定价。
假设1保证了市场完全覆盖,假设2~假设4构建了市场结构,假设5确保了市场充分竞争,假设6给出了各主体的策略空间。
2.3 多主体博弈定价模型的构建
考虑市场主体间的博弈关系,构建多主体博弈定价模型如图3所示,为2个阶段的双层模型。
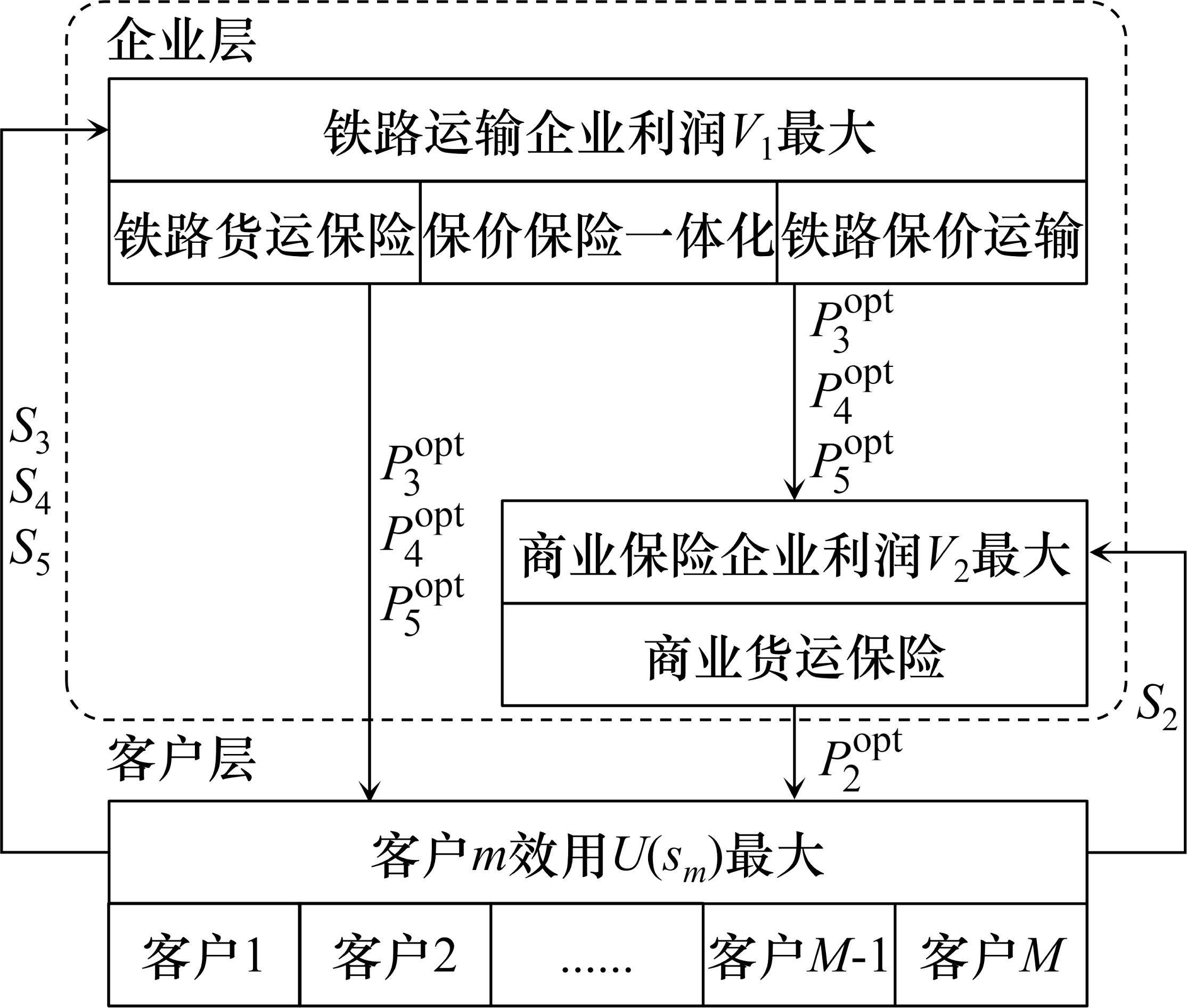
主要计算步骤:1) 第1阶段:上层模型中铁路运输企业通过合作博弈确定保价保险一体化产品的推出方案,以实现自身利润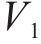
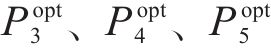
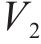
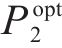
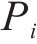
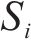
2.3.1 下层客户购买策略模型
记市场中有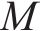
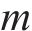
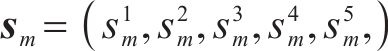
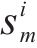
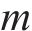
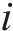
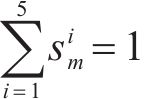
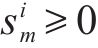
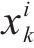
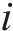
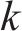
| 序号 | 影响因素 | 含义 | 量化指标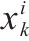 | 类型 |
|---|---|---|---|---|
| 1 | 经济性 | 费率水平高低 | 费率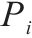 | 成本型 |
| 2 | 安全性 | 在货物运输过程中提供安全保障措施的水平 | 货运安全 保障 | 效益型 |
| 3 | 补偿性 | 发生货物损失时,赔偿损失的水平 | 赔偿责任 范围 | 效益型 |
| 4 | 便捷性 | 受理、理赔的手续和流程是否简洁 | 客户打分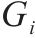 | 效益型 |
| 参数符号 | 参数含义 | 取值 | 数据来源 |
|---|---|---|---|
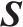 | 原货运风险保障方式市场份额 | 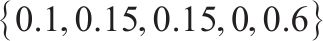 | 市场调研 |
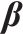 | 客户决策影响因素权重 | 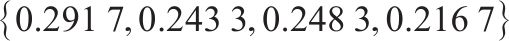 | 专家打分、模糊层次分析法 |
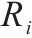 | 每危险单位的纯保费 | 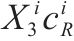 | 公式估算 |
 | 每危险单位的固定成本 | 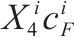 | |
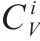 | 可变成本因子 | 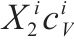 | |
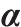 | 货运安全保障 | 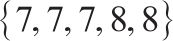 | 文献查阅 |
 | 赔偿责任范围 | 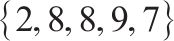 | |
 | 客户对便捷性评分 | 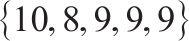 | |
 | 客户总数 | 20 | 模型假设 |
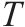 | 铁路货物运输固定效用 | 3 | |
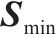 | 企业可接受的最低产品市场份额 | 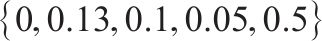 | |
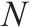 | 蜜源数量 | 50 | |
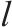 | 侦查蜂选择控制参数 | 50 | |
 | 最大迭代循环 | 300 |
分别将效益型、成本型指标无量纲化,记作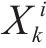
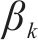
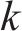
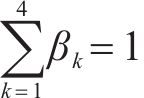
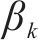
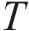
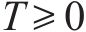
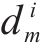
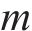
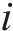
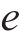
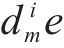
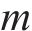
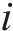
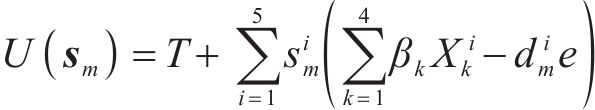
在新一轮决策中,客户的期望效用
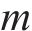
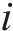
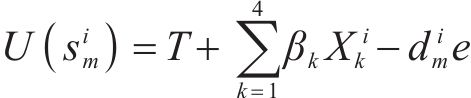

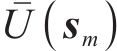
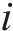
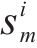
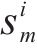
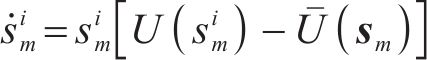
为便于使用迭代算法求解演化博弈均衡,将连续型复制动态方程将转换为离散型[14]。客户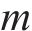
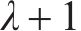
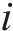
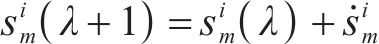
此时货运风险保障方式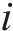
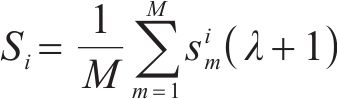
客户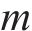
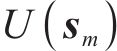
2.3.2 上层企业产品定价模型
货运风险保障产品收入主要用于赔偿货物损失、支付成本和获得利润。根据非寿险精算理论,采用纯保费法表示货运风险保障产品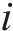
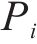
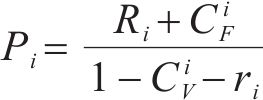
其中,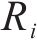
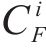

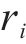
1) 第1阶段:铁路运输企业提供的3种货运风险保障产品定价
铁路保价运输的优势在于预防损失发生,可监控货物运输过程。铁路货运保险的优势在于转嫁风险、分担损失的能力强。假设两者根据自身优势合作推出保价保险一体化产品,并优化各货运风险保障产品费率,其合作博弈关系如图4所示。记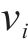
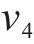
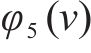
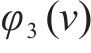
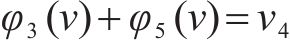
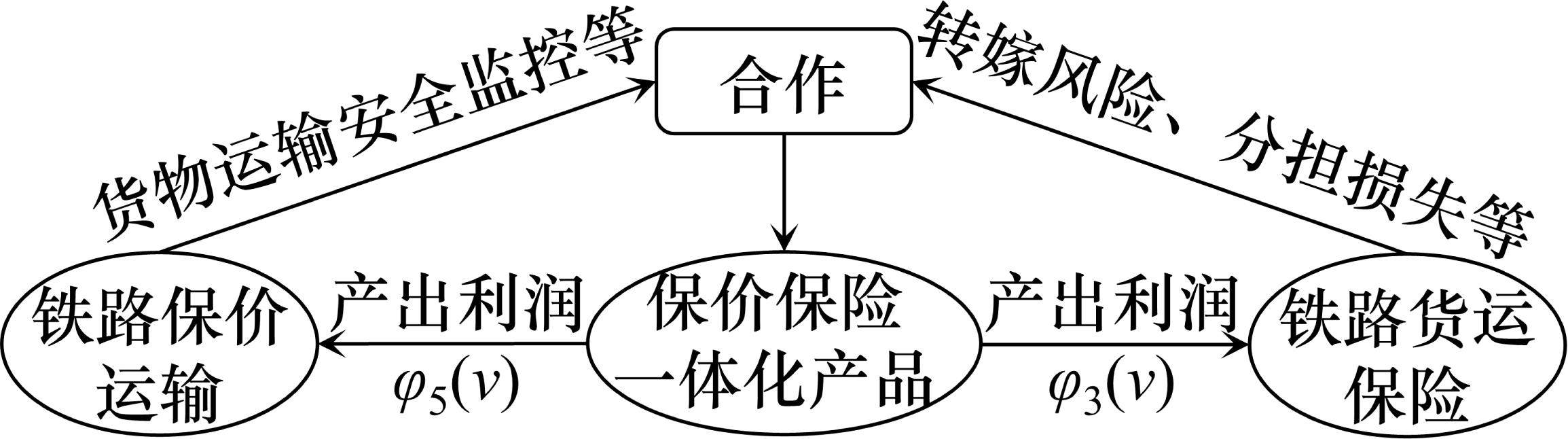
合作博弈包含参与者集
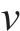
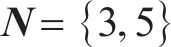
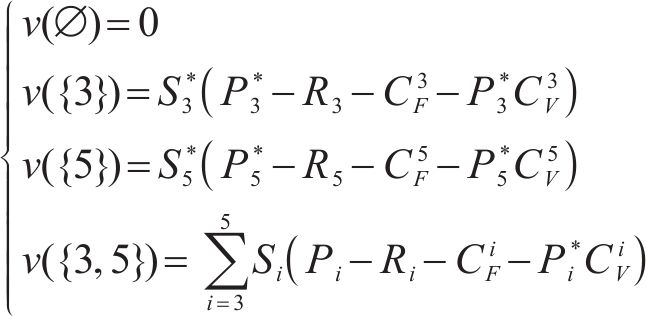
其中,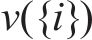
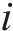
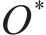
Shapley值是根据参与者的“平均”边际贡献来公平分配利润的方法[15],以该方法分配保价保险一体化产品利润,计算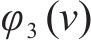
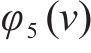
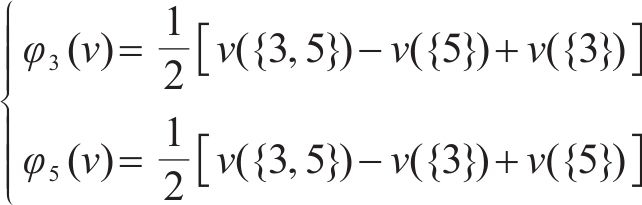
为保证推出保价保险一体化产品可行,需满足以下条件:1) 铁路运输企业利润满足超可加性,即推出保价保险一体化产品时的铁路运输企业利润大于铁路保价运输与铁路货运保险单干时的利润之和;2) 铁路保价运输和铁路货运保险利润满足个体合理性,即推出保价保险一体化产品时铁路保价运输与铁路货运保险的利润比单干多。综上所述,在铁路保价运输与铁路货运保险合作的基础上,考虑铁路运输企业可接受的最低产品市场份额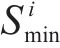

2) 第2阶段:商业保险企业提供的1种货运风险保障产品定价
在已知第1阶段铁路运输企业3种货运风险保障产品费率的基础上,商业货运保险以利润最大化为目标确定最优费率,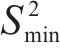
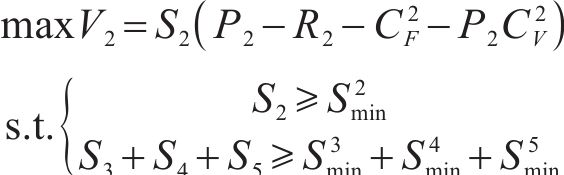
3 模型求解
由于本文构建的多主体博弈定价模型为双层规划模型且规模较大,因此为保证运算的速度和效率,采用启发式算法寻找帕累托最优解[16]。通过迭代算法求解下层客户的最优购买策略,通过混合人工蜂群算法求解上层企业的最优产品定价,具体流程为:首先,根据原货运风险保障方式的市场份额构建线性环形市场,生成货运风险保障方式、客户位置。之后,在已知现行商业货运保险费率的基础上,调用客户层的迭代算法得到各货运风险保障方式费率组合对应的适应度,采用企业层的混合人工蜂群算法寻找符合约束条件的铁路运输企业货运风险保障产品最优费率组合。最后,在已知铁路运输企业货运风险保障产品最优费率组合的基础上,再次使用企业层的混合人工蜂群算法与客户层的迭代算法,得出商业货运保险最优费率。
3.1 客户层的迭代算法
设
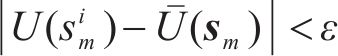
客户层的迭代算法计算流程如下。
1) 输入:货运风险保障方式的费率组合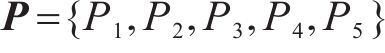
3.2 企业层的混合人工蜂群算法
人工蜂群算法(ABC)是一种模拟蜜蜂蜂群智能搜索行为的全局寻优算法,具有控制参数少、易于实现、计算简洁等优点,在求解双层模型时被广泛应用。为解决ABC算法存在的以牺牲算法开采能力为代价来提高开发探索能力的问题,本文借鉴CHAMCHUEN等[17]对ABC算法的改进,在ABC算法中加入具有较强全局搜索能力的粒子群算法(PSO),构成混合人工蜂群算法,用于求解上层企业的最优产品定价。
在混合人工蜂群算法中,蜜源代表优化问题的可行解,花蜜量代表可行解的适应度。人工蜂群由采蜜蜂、观察蜂、侦查蜂3个部分组成。采蜜蜂和观察蜂负责执行开采过程,采蜜蜂寻找蜜源,观察蜂确认是否跟随,提高收敛速度。侦查蜂负责执行探索过程,若蜜源位置长时间未更新,采蜜蜂转成侦查蜂寻找新蜜源,阻止陷入局部最优。计算流程如下。
1) 根据式(11)随机产生
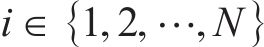
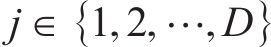
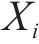
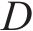
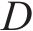
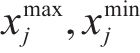
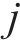
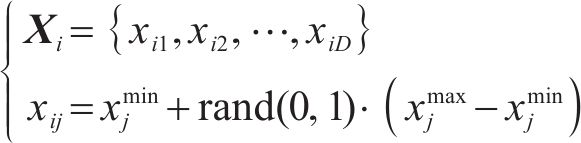
2) 采蜜蜂根据式(12)在原蜜源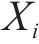
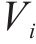
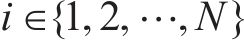
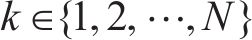
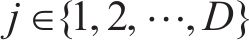
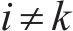
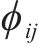
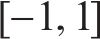
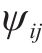
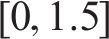
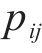
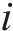
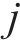
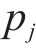
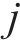
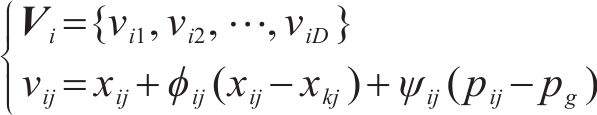
3) 采蜜蜂与观察蜂共享信息,观察蜂采用轮盘赌选择法,根据式(13)以与花蜜量有关的概率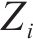
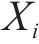
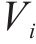
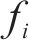
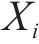
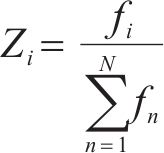
4) 若蜜源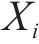

5) 若满足迭代终止条件,则输出最优解,否则转步骤2。
4 算例分析
假设数量为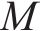
模糊层次分析法是一种结合层次分析法和模糊综合评价法优点的系统分析方法[19]。以客户效用为目标层、经济安全补偿便捷4种影响因素为准则层、5种货运风险保障方式为方案层建立层次结构模型,根据10位专家意见构造模糊判断矩阵并检验其一致性,计算得出客户决策影响因素权重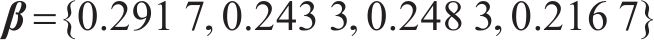
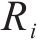
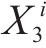
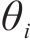
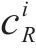
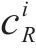
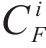
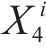
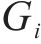
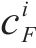
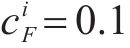

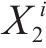
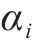
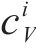
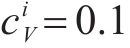
| 等级 | 主要货物品类 | 现行的铁路货物 保价费率/‰ |
|---|---|---|
| 1 | 煤、焦炭、金属矿石 | 1 |
| 2 | 钢材、粮食、化学化肥 | 2 |
| 3 | 石油、棉花、化工品 | 3 |
| 4 | 水泥、半导体材料、汽油 | 4 |
| 5 | 爆炸品、鲜冻肉、水产加工品 | 6 |
| 6 | 鲜瓜果、活鱼、花卉 | 10 |
| 7 | 玻璃 | 15 |
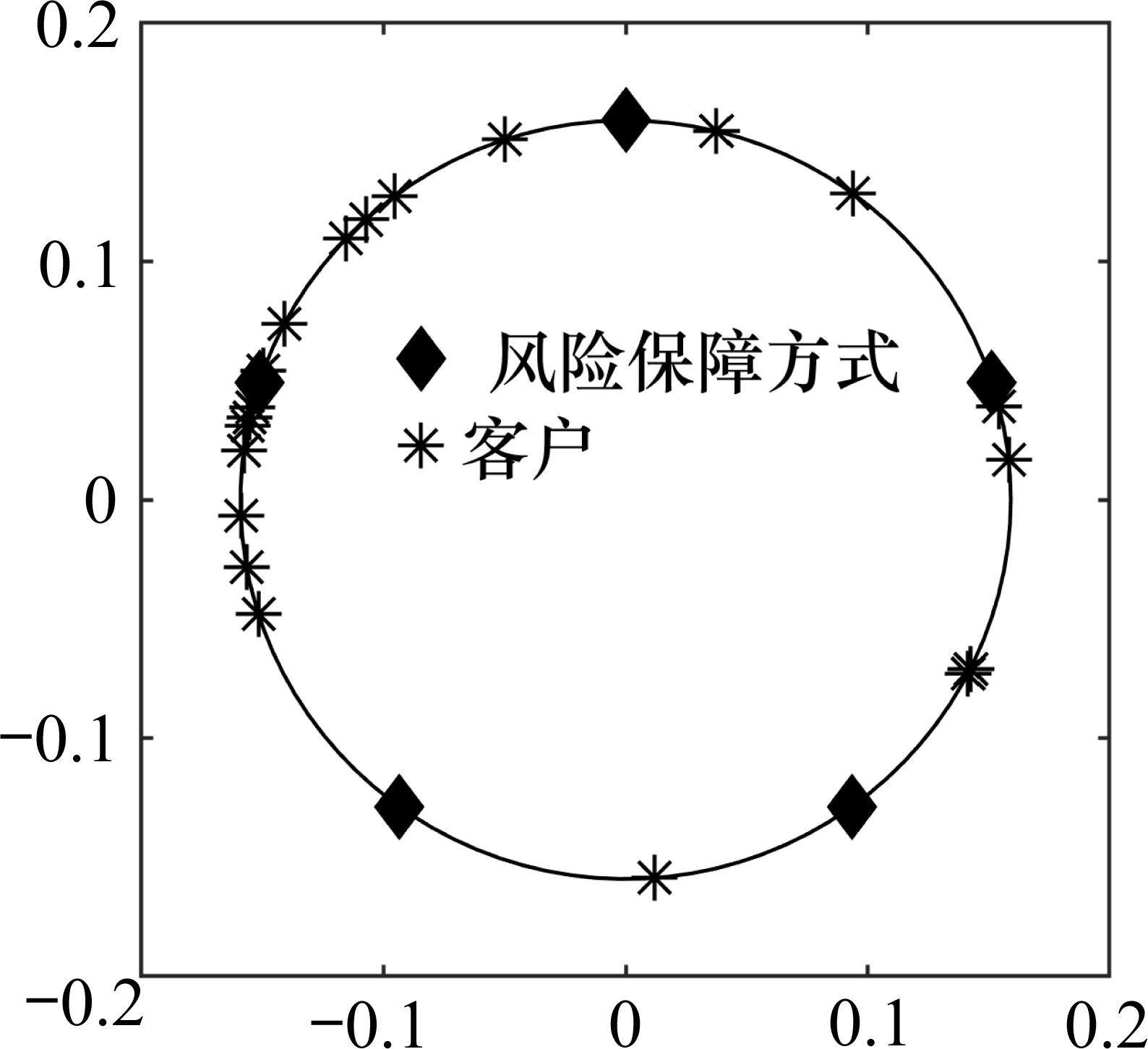
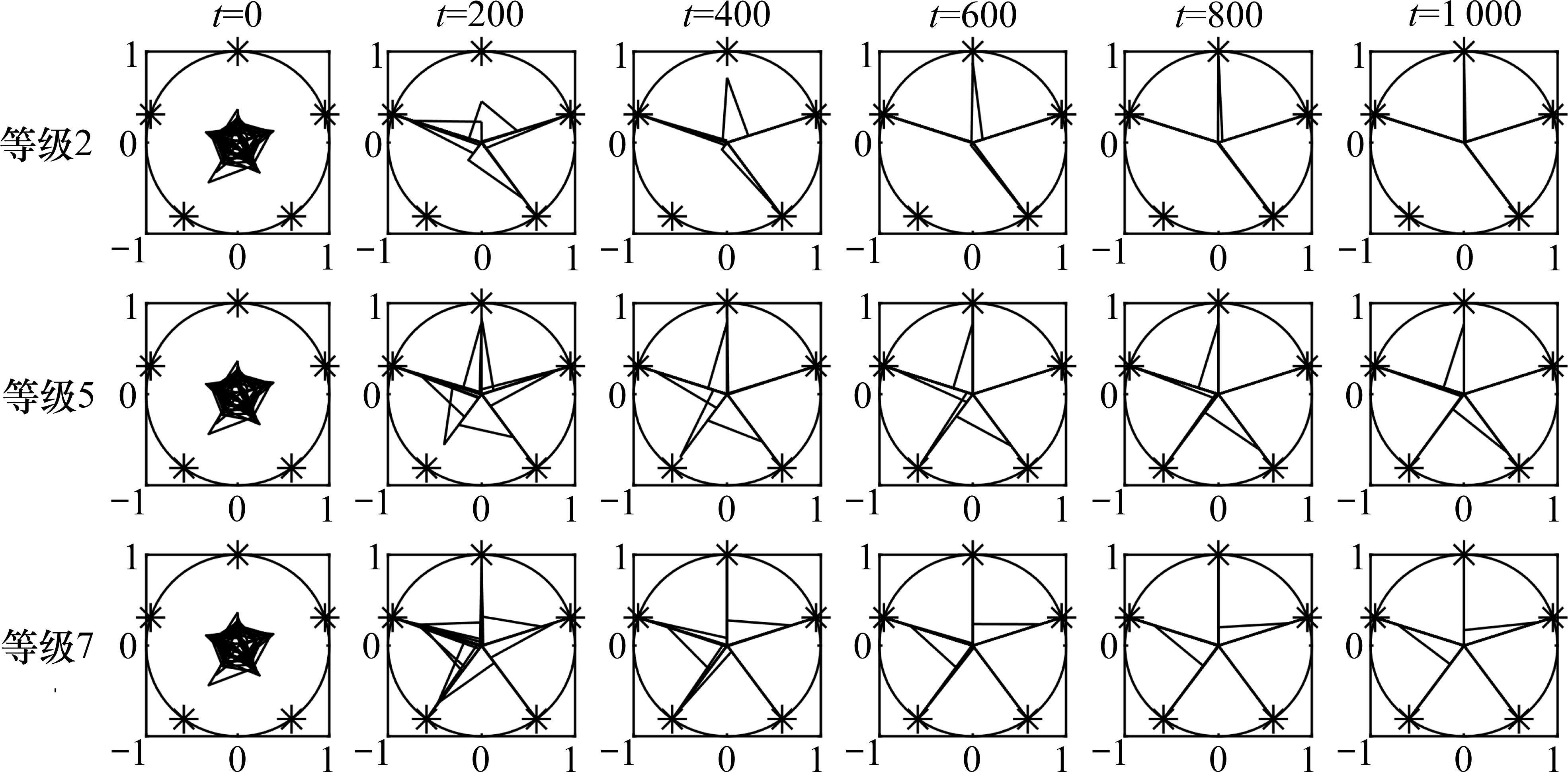
根据模型参数取值生成周长为1的线性环形市场,确定货运风险保障方式与客户位置如图5所示。
在不同单位距离转换成本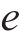
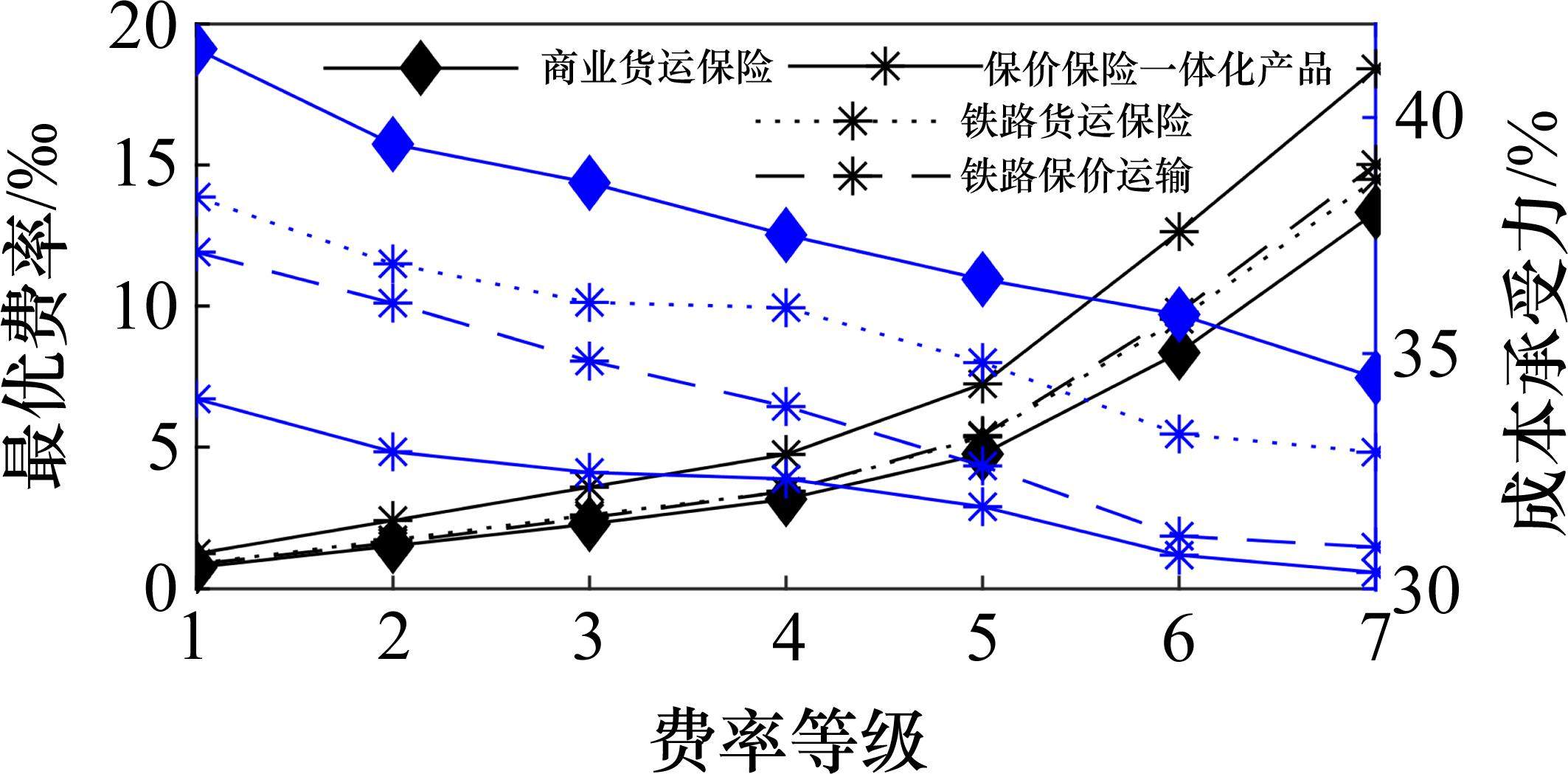
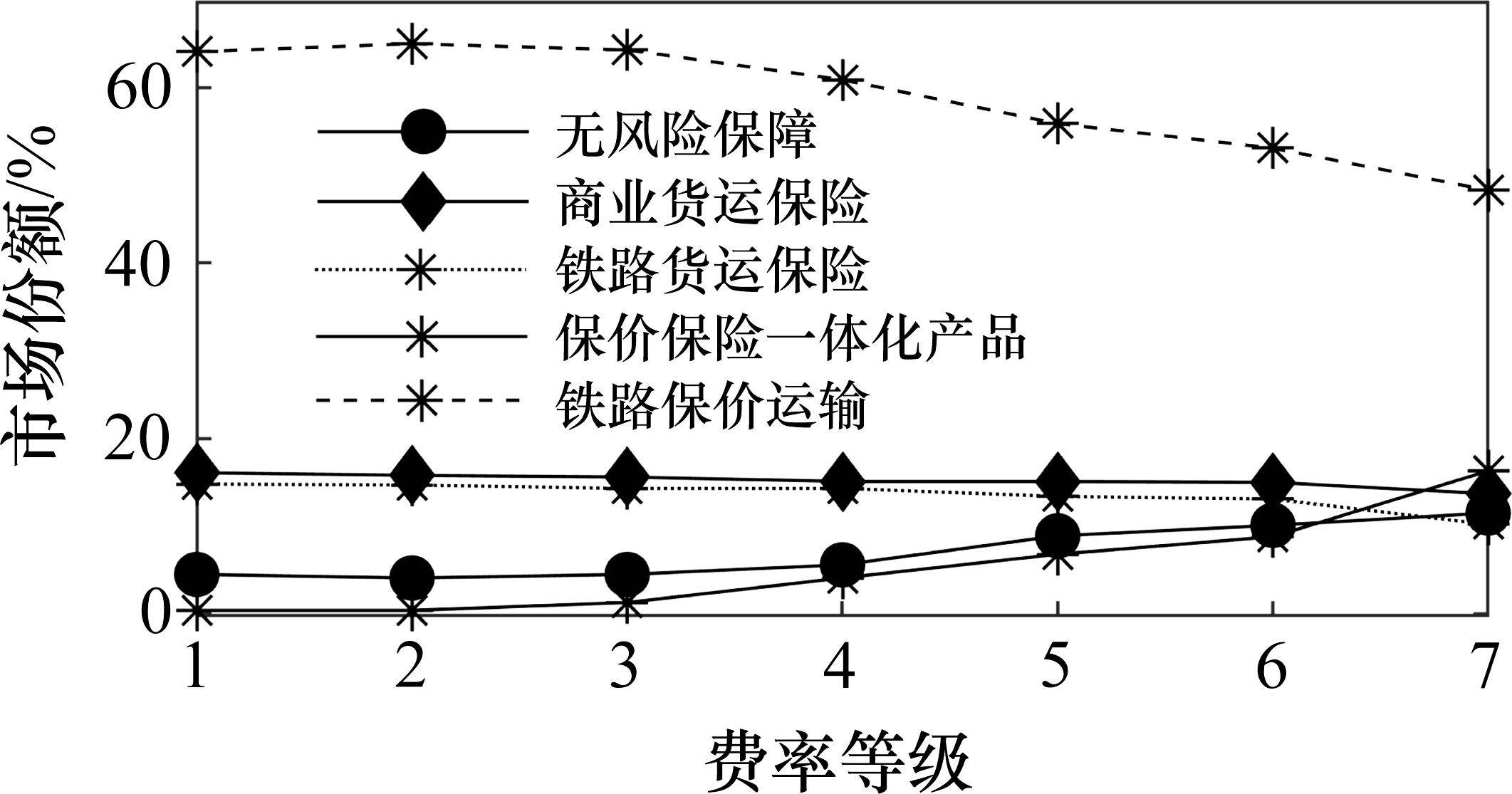
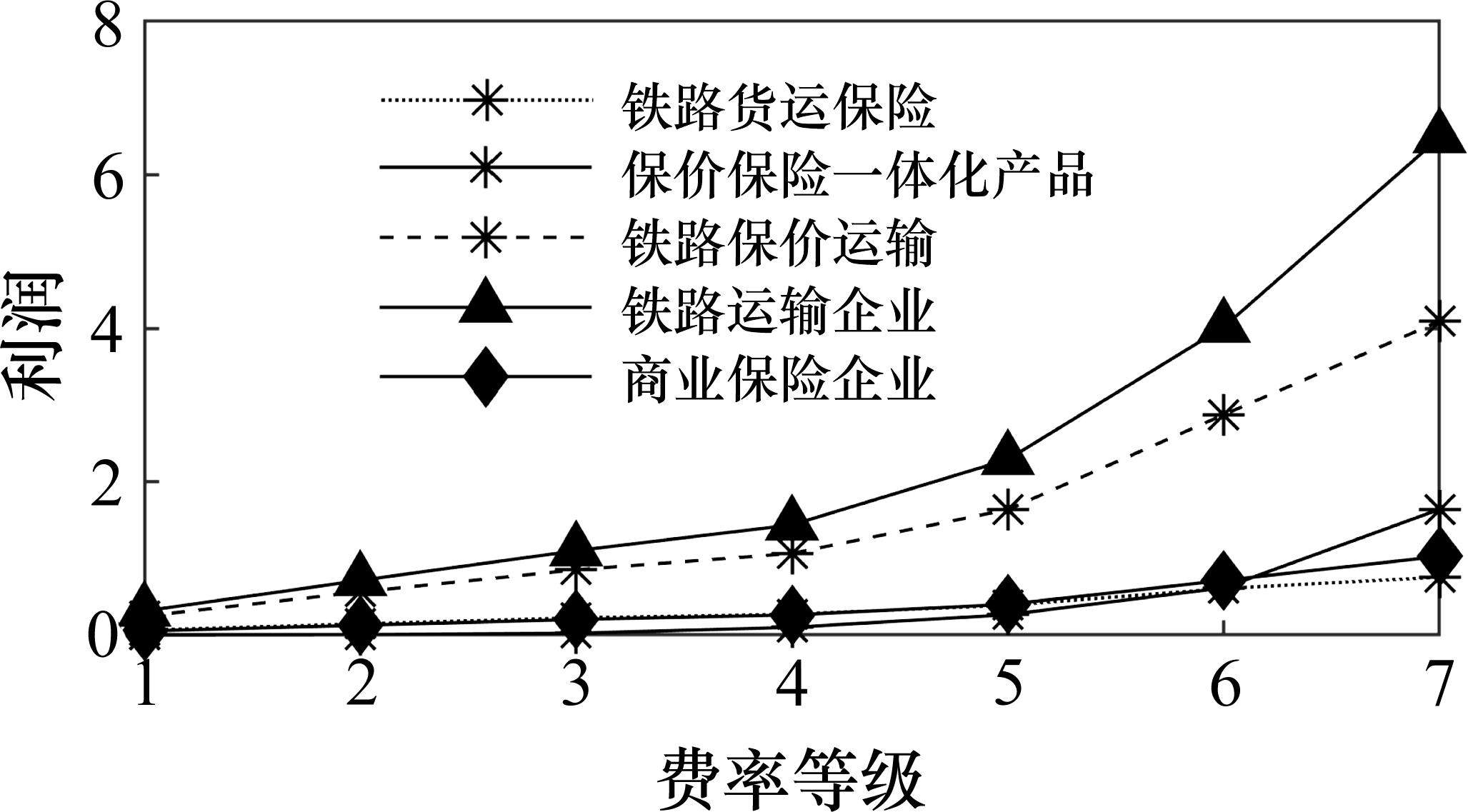
根据货运风险保障方式最优费率组合与对应市场份额,按公式(8)~公式(10)计算各企业及其提供的货运风险保障产品最大利润如图8所示。从图中可以看出:1) 费率调整后,等级1至等级5的铁路运输企业利润增长幅度在5%以内,而等级6和等级7的增长幅度分别为11.3%和16.8%。这说明对于更易发生损失的货物品类,铁路运输企业推行保价保险协同发展、市场化调整费率的优势更加明显。2) 随着费率等级的提高,保价保险一体化产品利润占铁路运输企业货运风险保障产品总利润的比重分别为0.64%、0.68%、2.20%、7.04%、11.59%、15.05%、25.28%。说明针对易损货物品类推出保价保险一体化产品是可行的,收益情况良好。3) 在各个费率等级中,商业保险企业利润均低于原利润,下降幅度在3.4%~15.9%之间。这表明铁路运输企业市场化调整其提供的货运风险保障产品费率并推出保价保险一体化产品,会给商业货运保险带来一定压力,商业保险企业将采用降价策略,牺牲部分利润以达成期望市场份额。
设
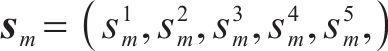
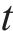
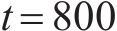
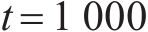
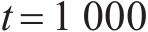
5 结论
1) 铁路保价运输与铁路货运保险按“平均”边际贡献分配利润,共同推出保价保险一体化产品是可行的,收益情况良好。按货物品类划分费率等级,各等级的保价保险一体化产品费率取值在铁路货运保险和铁路保价运输费率之和的62.4%~71.8%,利润占铁路运输企业货运风险保障产品总利润的0.64%~25.28%。
2) 货运风险保障产品市场化发展后,铁路保价运输与铁路货运保险优化后的费率均会低于原数值,货物越易损,费率下降幅度越小。铁路保价运输、铁路货运保险分别对损失概率较高、较低的货物品类拥有更强的定价能力。
3) 铁路运输企业市场化调整货运风险保障产品费率、推出保价保险一体化产品,有利于增强其竞争力,且对于损失概率越高的货物,优势越显著,商业保险企业将采用降价、保障市场份额的应对策略。
4) 货物越易损、运输难度越大,客户的选择策略越多样,部分客户更倾向于支付高费用获取全面的风险保障,或是存在侥幸心理不购买货运风险保障产品以降低支出。
冯芬玲,战映辰,刘承光等.多主体博弈下铁路保价运输与货运保险协同定价策略[J].铁道科学与工程学报,2024,21(11):4467-4477.
FENG Fenling,ZHAN Yingchen,LIU Chengguang,et al.Collaborative pricing strategy of railway value-insured transportation and freight transport insurance in multi-agent game[J].Journal of Railway Science and Engineering,2024,21(11):4467-4477.