城际铁路在促进城市群内经济增长的同时极大地方便了城市群内居民的出行。随着城市居民对出行服务水平要求的提高,城际铁路列车运行组织需更加关注出行服务的提升。相比非周期列车运行图,周期列车运行图便于旅客熟悉列车到发时刻规律,有利于旅客合理安排出行[1]。城际铁路列车具有旅行时间短、列车速差小等运行特点,有利于安排列车周期性运行,更好地为旅客提供便捷的出行服务[2]。为了提高周期运行图服务质量,国内外学者以降低旅客在车时长、换乘时长和候车时长为目标对周期列车运行图编制进行了广泛研究[3-6]。在降低在车时长方面,高如虎等[7]结合我国列车运行组织特点对PESP模型进行改造,以最小化列车总旅行时间为目标建立基于定序的周期运行图优化模型,提高了列车运行效率并减少了列车停站时间;ZHOU等[8-9]致力于多周期列车调度问题,在构建加权有向图的基础上,建立了多路径搜索模型,减少了列车总旅行时间。在降低旅客换乘时长方面,郭根材等[10-11]综合考虑了列车接续的各类影响因素建立了周期列车运行图的接续约束生成模型,降低了旅客换乘时间;李天琦等[12]以最小化换乘服务频率欠缺值为优化目标,为列车直达服务频率不足的OD客流增加了快速换乘服务。既有周期列车运行图研究充分考虑了旅客在车时长和换乘时长,但在旅客候车时长,即考虑列车服务频率和服务均衡性方面,仅考虑了同类型或同线路列车的发车均衡或频率约束,未考虑OD服务均衡和OD服务频率,如谢美全等[13]在铺划某线路的周期列车运行图中考虑了同类列车的频率约束;汪波等[14-16]引入同线路列车在始发车站的发车均衡约束,使随机到达的旅客等待时间较短;YAO等[17]认为同线路列车的发车时间均匀分布意味着严格遵守时间间隔,因此采用灵活的列车运行规律[18-19],允许同线路列车在车站的发车时刻有一定偏差。然而,尽管一天内城际铁路的OD客流分布并不均衡,但在同一时段本文认为其均衡分布。因此忽视OD服务均衡会导致各OD旅客期望出行时间和实际出行时间偏差的差距较大,产生服务不公平性等问题。固定列车停站会限制最佳列车服务方案的生成,从而影响OD列车服务均衡性[20]。为了减少旅客期望出行时间和实际出行时间偏差、提高OD旅客服务公平性,本文结合列车停站选择,考虑OD最小服务列车数量约束,以降低列车总旅行时间和提升所有OD列车服务均衡性为目标对城际铁路周期列车运行图进行优化。并且设计了一种基于有向图弧权优化的启发式算法对模型进行求解,为了体现不同列车对相同有向弧使用成本的差异性,提出了考虑列车差异的弧权体系,通过弧权迭代优化引导列车进行路径搜索以获得出行服务均衡的周期列车运行图。
1 周期时空网络构造
本节首先基于给定线路、周期等构造描述列车运行的时空网络,为后续模型与算法设计奠定基础。将列车运行周期离散为若干个时刻,针对每个离散时刻分别为各车站构造到达节点、通过节点和出发节点,如图1(a)所示。记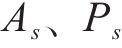
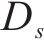
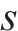
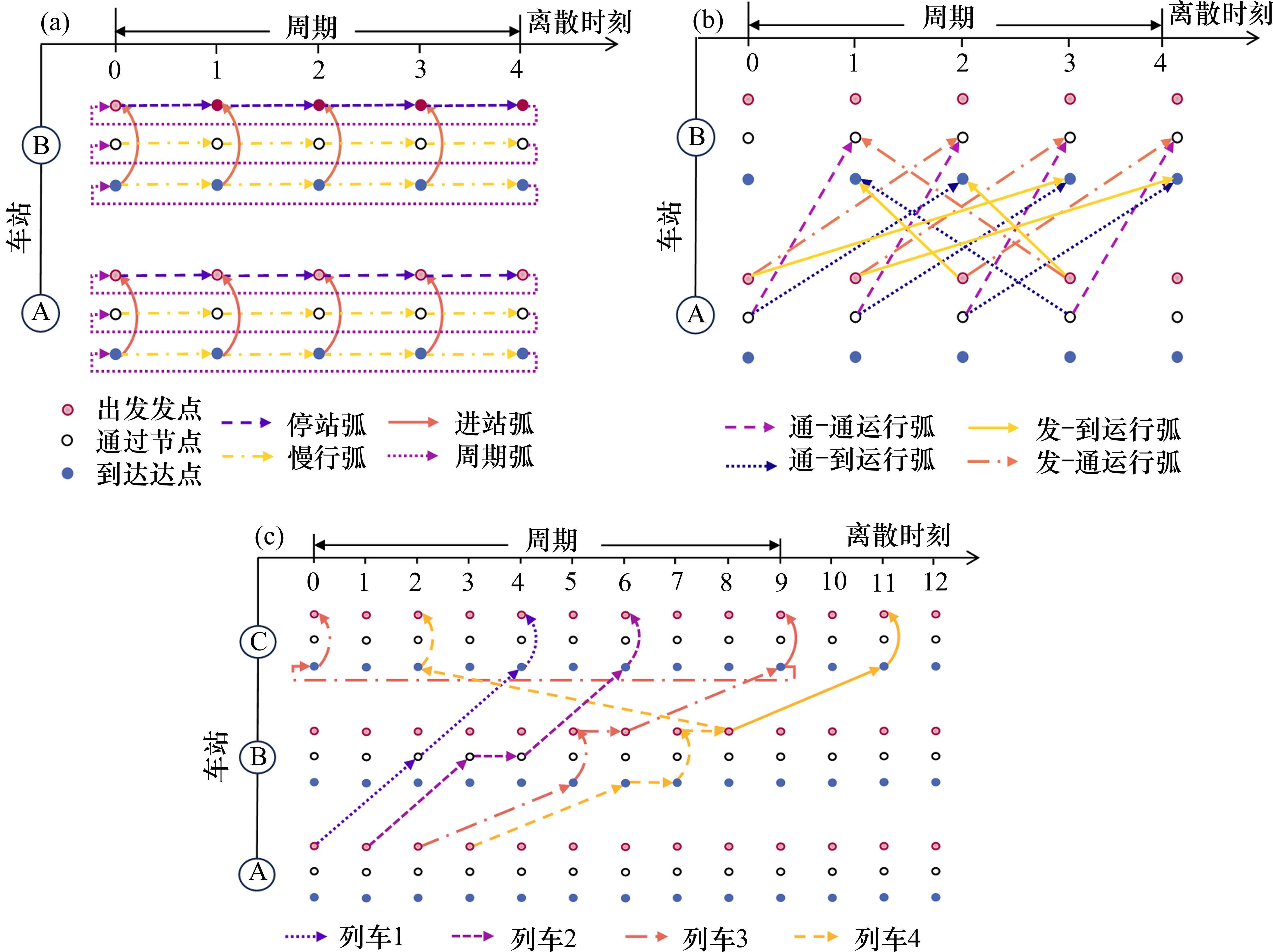
基于上述3类节点,在周期时空网络中添加以下5类有向弧:1) 慢行弧。其构造于车站相邻通过节点或相邻到达节点之间。当列车在区间的运行时分需要超过最小值时,列车使用慢行弧来延长区间运行时分;2) 进站弧。在车站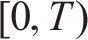


列车1至列车4在周期时空网络中的路径如图1(c)所示,其中列车3和列车4跨周期运行,图中实线弧表示列车3和列车4在相应非周期时空网络图中的运行路径。
以上时空网络为面向所有列车运行的总网络,但每列列车的经由车站是确定的,其只能使用经由车站的节点,为了便于算法设计并降低列车路径搜索规模,本文为每列列车构建运行子网络,列车路径搜索时只需在其子网络中搜索即可。对于列车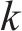
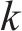
2 考虑停站协同的周期运行图优化模型
考虑由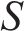
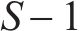
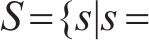

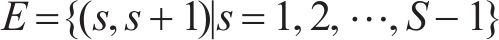
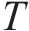
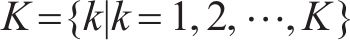
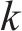
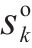
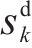
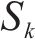
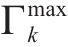
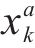
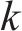
| 符号 | 定义 | 符号 | 定义 |
|---|---|---|---|
| S | 车站集,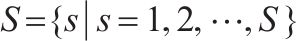 |  | 节点 |
| K | 优化列车集,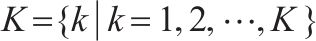 | 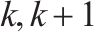 | 相邻2列列车 |
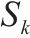 | 列车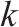 | 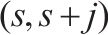 | O、D分别为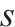 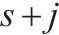 |
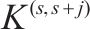 | 服务OD对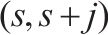 | 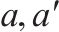 | 周期时空网络中的任意弧 |
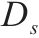 | 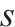 | 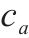 | 弧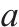 |
| A | 时空网络中的有向弧集 | 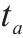 | 弧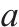 |
| ys | 从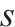 | 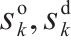 | 列车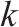 |
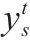 | 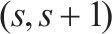 | 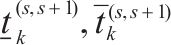 | 列车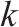 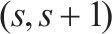 |
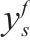 | 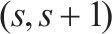 | 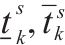 | 列车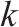 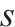 |
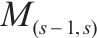 | 区间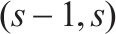 | 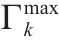 | 列车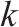 |
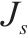 | 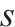 | 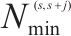 | OD对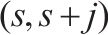 |
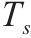 | 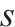 | 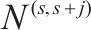 | OD对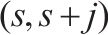 |
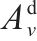 | 节点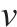 | 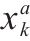 | 0-1决策变量,列车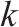 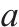 |
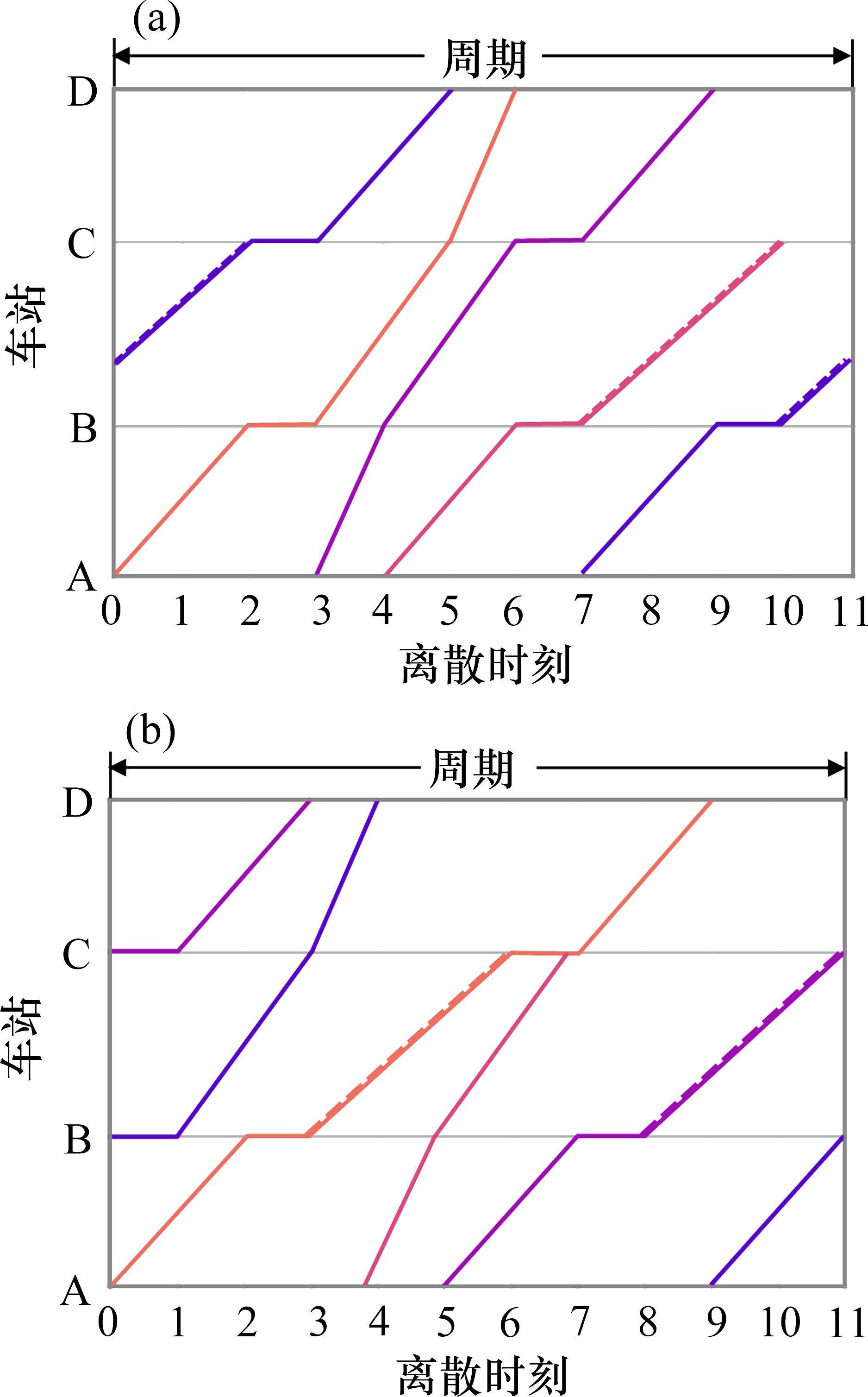
为了体现列车停站对OD服务均衡的影响,图2展示了固定停站和考虑停站的运行图优化结果,在各列车运行线路不变、仅对列车停站方式进行调整的情况下,优化后列车停站总数和总旅行时长未发生改变,但OD服务列车出发时间间隔方差总和从17.42降至9.39,均衡性提高了46%。以OD对(B,C)为例,其考虑停站前后服务列车的运行线如图2中锯齿线所示,明显考虑停站后其服务列车在B站的出发时间更为均衡。
2.1 目标函数
模型以提高旅客出行服务质量为目标,一方面应尽可能减少列车旅行时长,另一方面应使周期内列车均衡服务各OD出行旅客。列车总旅行时长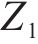
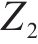
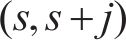
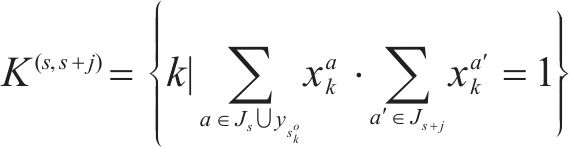
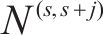
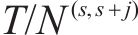
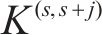
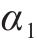
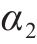

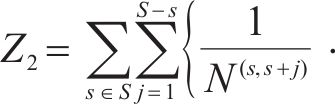
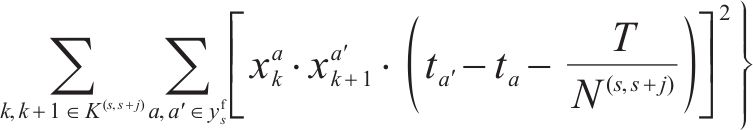
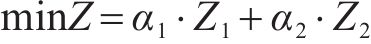
2.2 约束条件
模型除了考虑一般的列车区间运行时长约束、停站时长约束、安全间隔约束外,还进一步考虑了OD最小服务列车数量约束和列车最大旅行时长约束。
1) OD最小服务列车数量约束
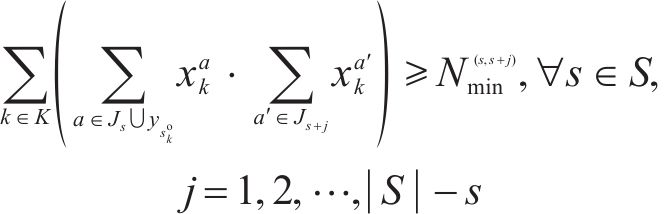
OD对的服务列车数为经过O、D站进站弧的列车总数,其服务列车数越多,OD旅客期望出行时间和实际出行时间的偏差就越小,式(4)保证了OD服务列车数不小于设定的最小值。此外,不同OD的最小服务列车数需根据OD实际客流设定,避免OD出行客流量和列车服务频率不匹配,导致资源浪费问题。
2) 最大慢行时分约束
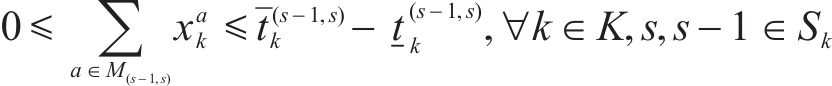
列车在区间的运行时间为列车经过该区间的运行弧和慢行弧时间费用之和。不同种类运行弧的时长即为相应进出区间方式的最小运行时分,无论选择哪条区间运行弧,均满足相应的区间最小运行时分要求。此外,考虑到实际编图过程中允许列车在区间慢行,式(5)保证了慢行时分不超过允许的最大值。
3) 列车停站时长约束
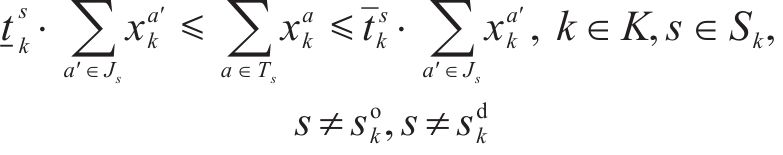
列车的停站时间为列车经过该车站的停站弧时间费用之和。式(6)保证了列车
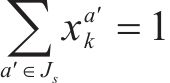
4) 列车间出发安全时间间隔约束
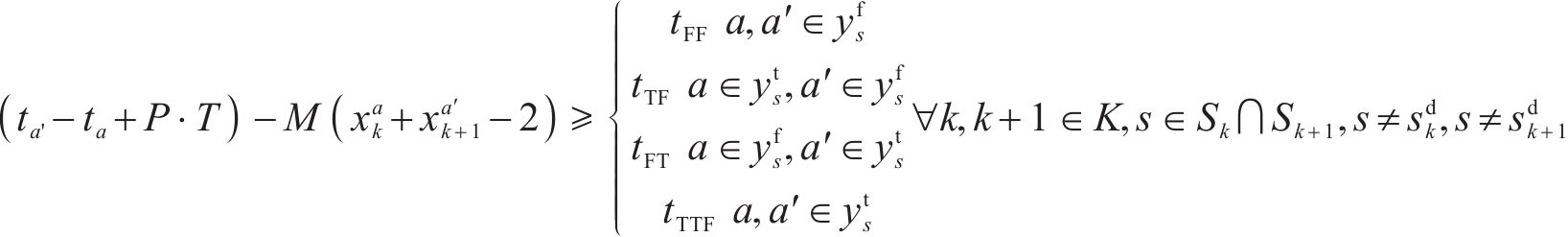
当2列列车从同一车站
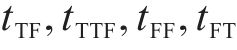
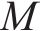
5) 列车间到达安全时间间隔约束
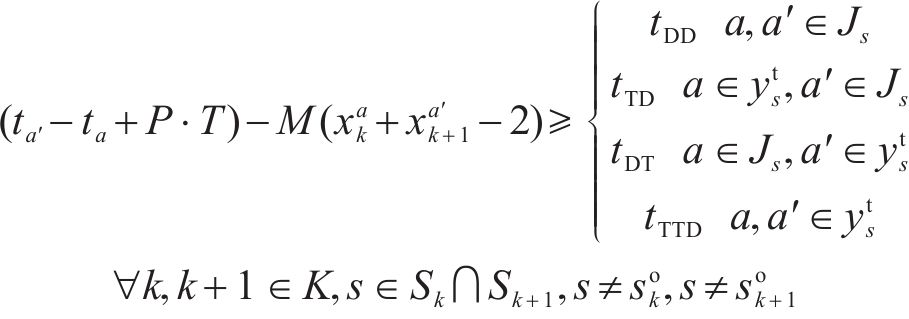
当2列列车从同一区间相继到达同一车站
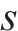
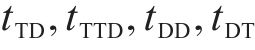
6) 列车最大旅行时长约束
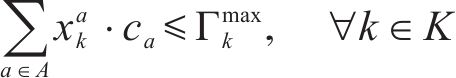
列车旅行时间为列车经过有向弧的时间费用之和。式(9)保证了列车旅行时长不超过其允许的最大值,避免因列车旅行时长增加而导致列车服务质量降低。
7) 流量平衡约束
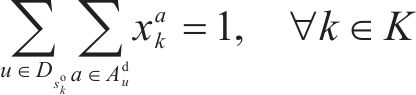
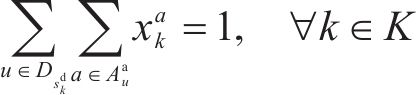
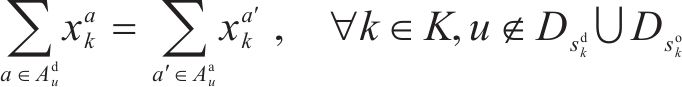
流量平衡约束保证了一条路径在时空网络中的可行性。式(10)和式(11)分别满足了列车在起始站的必出和终点站的必回要求,式(12)保证了中间节点的入弧数等于出弧数。
3 算法设计
本文提出一种基于冲突消解的启发式搜索算法对模型进行求解。算法主要通过对周期时空网络中的有向弧设置多类惩罚权值来引导列车搜索满足相关条件的路径,其实现关键在于时空网络中的弧权体系设计和弧惩罚权迭代优化。
3.1 考虑列车差异的弧权体系设计
时空网络中各有向弧的权值体现了列车使用该弧的成本,其大小直接影响列车的路径搜索。为了引导列车选择特定路径,除了为每条有向弧设置时间权外,还添加均衡惩罚权、安全间隔惩罚权、停站惩罚权3类权,且允许针对不同列车为此3类权设置不同权值。
1) 均衡惩罚权。针对以车站出发节点为起点的运行弧设置均衡惩罚权,以此引导相关OD的服务列车尽可能等间隔均匀发车。以图3(a)中的列车2为例,其服务OD仅有(s1,s3),同时服务该OD的列车1和列车3的出发时刻分别为0和5,周期T=7,则列车2在该OD的均衡发车时刻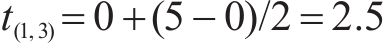
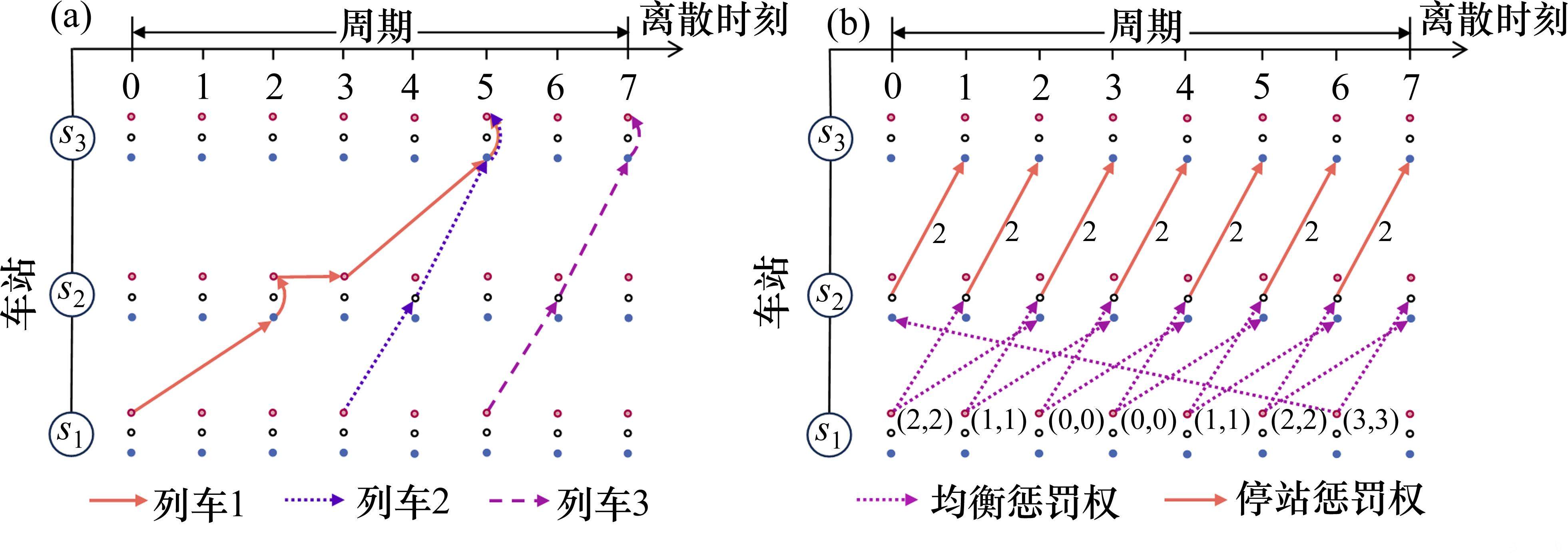
2) 安全间隔惩罚权。当一列列车占用某条路径后,为防止其他列车继续使用该路径占用弧,需要在其他列车子网络中为这些占用弧添加安全间隔惩罚权。对于列车
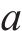
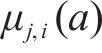

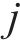
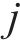
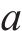
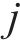
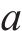
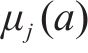
3) 停站惩罚权。若当前车站因列车停站数较少,而未满足相关OD的最小服务列车数要求时,针对起点为该站通过节点的运行弧设置较大的停站惩罚权;否则,其承担的停站惩罚权可设为0。假设各列车当前路径如图3(a)所示,OD对(s1,s2),(s1,s3)和(s2,s3)的最小服务列车数分别为2、3、2,(s1,s2)和(s2,s3)的服务列车数不满足最小OD服务列车数要求,需要通过停站惩罚权来引导列车在s2站停车。列车2子网络中有向弧的停站惩罚权如图3(b)所示。
3.2 基于弧惩罚权迭代优化的算法设计
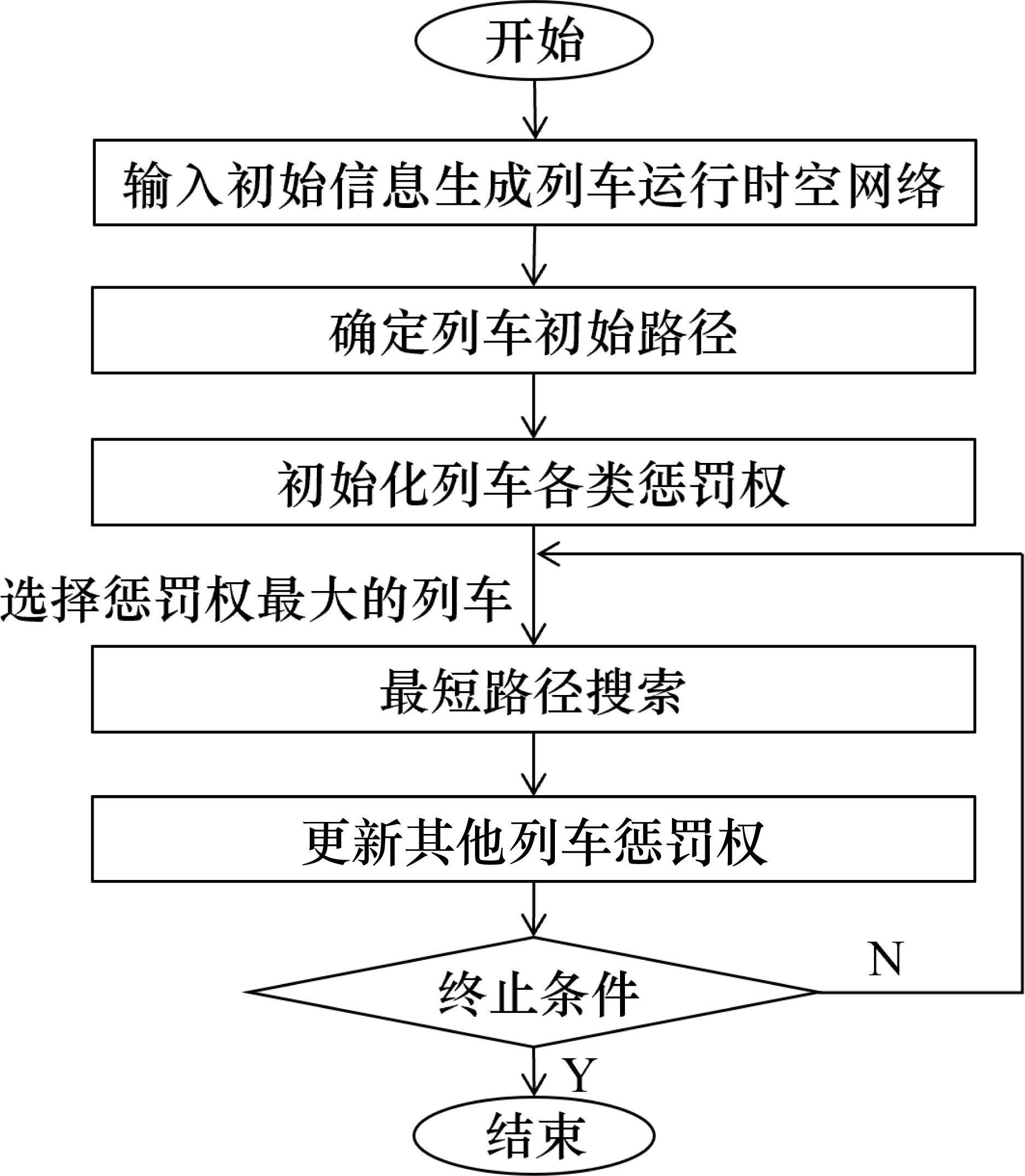
算法首先初始化所有列车的路径,根据各列车初始路径分别为其他列车子网络初始化各有向弧的惩罚权,进而针对惩罚权最大,即冲突最严重、均衡性最差或不满足停站要求的列车重新搜索路径,并由此更新其他列车子网络中的弧惩罚权,直至满足算法终止条件而停止。其中终止条件为所有列车无安全间隔冲突且所有OD的服务列车数达到最小值要求。算法实现框架如图4所示。
3.2.1 各列车子网络的弧惩罚权初始化
在周期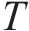
1) 均衡惩罚权。记列车
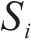
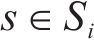
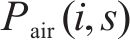
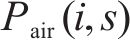


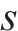
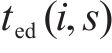
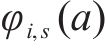
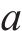
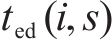
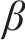


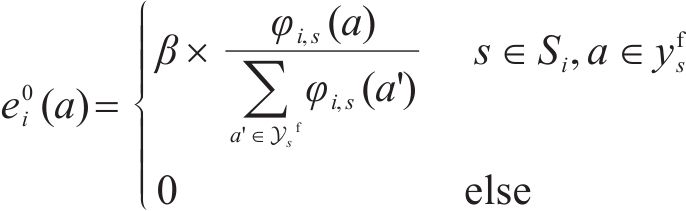
2) 安全间隔惩罚权。记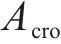
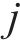
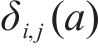

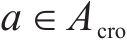
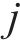

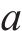
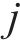

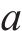
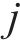
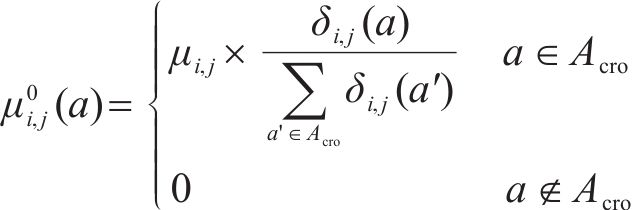
其中,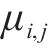

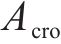
针对列车
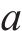


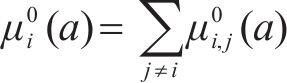
3) 停站惩罚权。记除首末站外的其他车站集为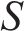

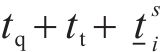
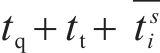
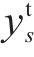
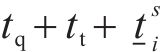
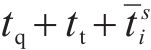
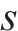

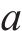
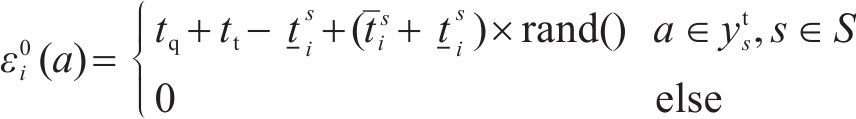
3.2.2 各列车子网络弧惩罚权迭代更新
当列车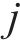


1) 均衡惩罚权。列车
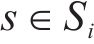
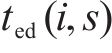
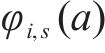
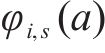
2) 安全间隔惩罚权。对于列车
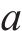
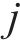
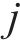
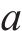
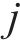
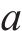
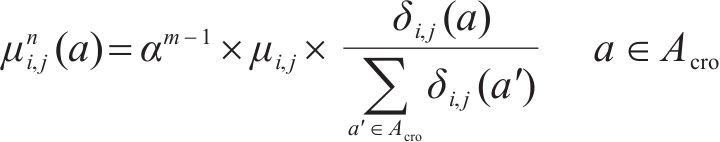
其中,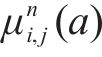
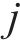

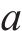
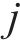
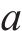
3) 停站惩罚权。在更新列车

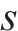
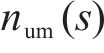
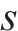
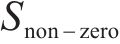
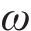

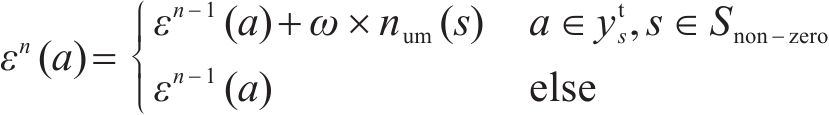
4 算例分析
周期运行图编制的关键在于高峰单元运行图,高峰单元运行图编制完成后根据其他周期的客流情况删除或停开部分运行线便可形成平峰周期运行图。本文以京津城际铁路为例编制单元高峰周期运行图。
4.1 基础数据
京津城际铁路全线长166 km,设7个车站,分别为北京南站、亦庄站(暂不办理客运业务)、武清站、天津站、军粮城北站、塘沽站和滨海站。选取京津城际铁路现行运行图中在11:10至14:40出发的20列列车作为本案例高峰时段开行列车,各列车运行区段如图5所示。各OD最小服务列车数取现行运行图中的实际服务列车数。车站到-到、通-到、到-通和通-通安全时间间隔值分别为2,3,2和2 min,发-发、通-发、发-通和通-通安全时间间隔值分别为2,1,3和2 min。列车在各车站和区间的参数如表2所示。算例中运行图的周期为1 h。
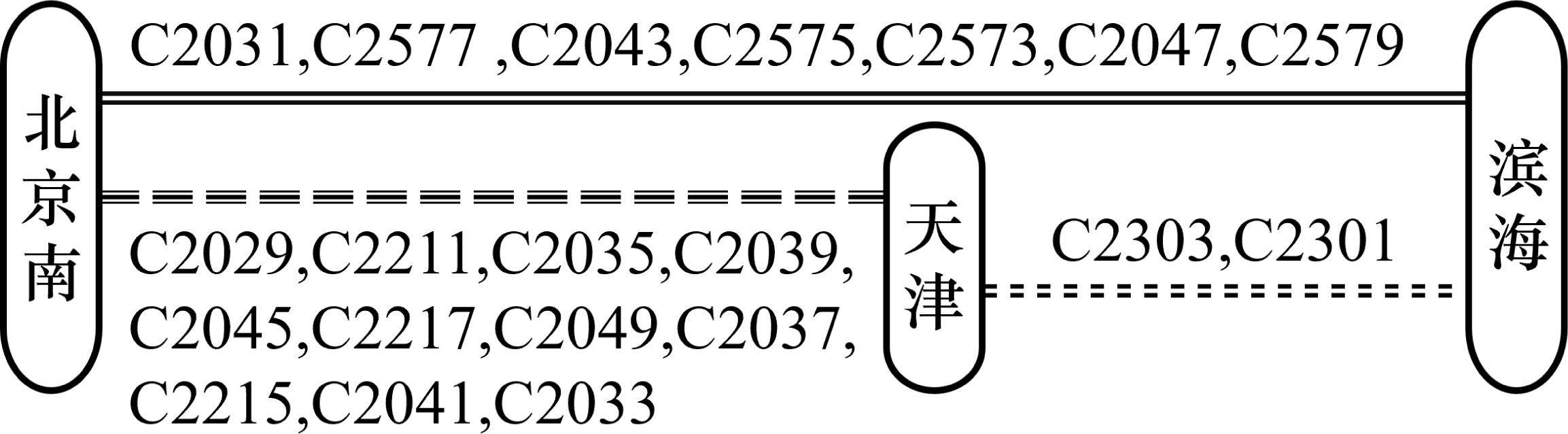
| 车站 | 里程/km | 最小停站 时分/min | 最大停站 时分/min | 启停附加 时分/min | 最小纯运行 时分/min | 最大纯运行 时分/min |
|---|---|---|---|---|---|---|
| 北京南 | 0 | 2 | 6 | 2 | 17 | 20 |
| 武清 | 84 | 2 | 6 | 2 | ||
| 天津 | 120 | 3 | 6 | 2 | 8 | 11 |
| 军粮城北 | 140 | 2 | 6 | 2 | 6 | 9 |
| 塘沽 | 160 | 2 | 6 | 2 | 5 | 8 |
| 滨海 | 166 | 2 | 6 | 2 | 4 | 7 |
4.2 结果分析
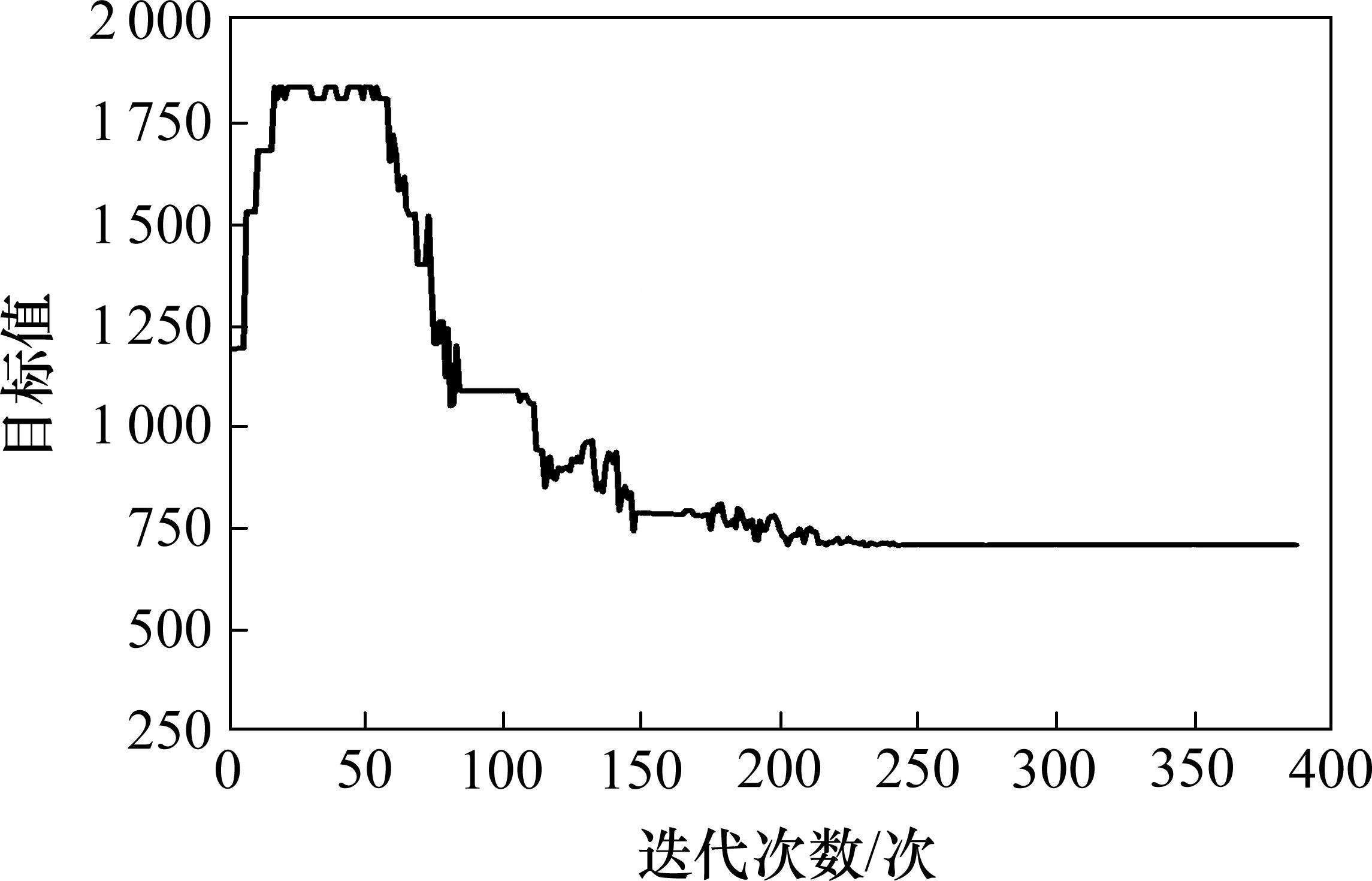
算法求解的迭代过程如图6所示。初始路径中列车在经由车站均不停车,因此,在算法迭代前期,较多列车选择停站导致运行时间增加,且列车停站方式频繁发生改变使OD服务均衡的优化微乎其微,故在迭代前期优化结果出现急剧上升趋势;在算法迭代中期,各OD最小服务列车数几乎得到满足,列车停站方式改变频次变少,OD服务均衡得到一定优化,但列车运行时间的增加和OD服务均衡的优化相互抵消,使得优化结果大致未变;在算法迭代后期,停站方式几乎不发生改变,列车运行时间变化很小,而OD服务均衡得到改善,使得优化结果逐渐变小直至运算第105 s、迭代结果150次未发生变化时得到较优解,优化后目标值为711.0。生成的高峰单元周期运行图如图7(b)所示,初始运行图如图7(a)所示。
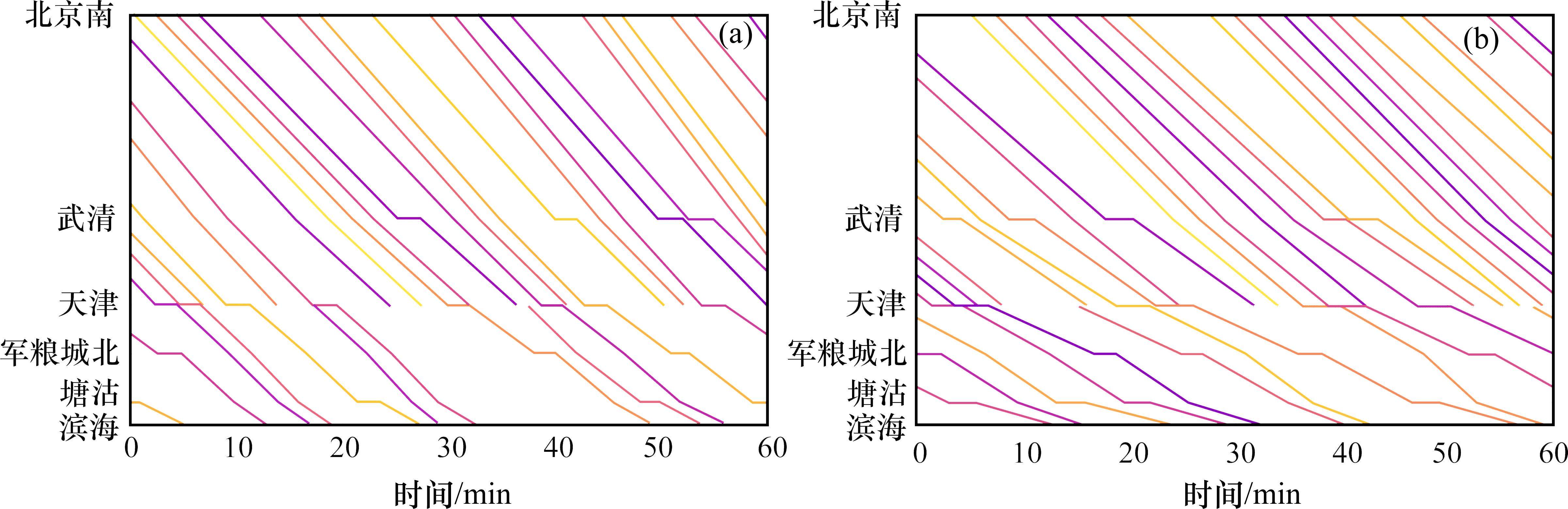
初始运行图和优化运行图的相关指标见表3中的方案1和方案5,2张运行图均铺画20列车,优化运行图增加了2次停站,但列车未因躲避冲突而过多延长停站或区间运行时间,故列车旅行时长得到一定优化,详见图8(a),此外,优化运行图的均衡性提高了57%。初始运行图和优化运行图中OD服务列车出发时间间隔方差见图8(b)中的方案1和方案5,因以北京站为起点的OD较多,各OD的均衡发车时刻不尽相同且相互嵌套,故以北京为起点的OD服务均衡相对较差,其他OD的列车服务时间间隔较为均衡。
| 方案1 | 方案2 | 方案3 | 方案4 | 方案5 | |
|---|---|---|---|---|---|
| 列车运行图 | 初始运行图 | 单目标优化时间 | 单目标优化均衡 | 固定停站优化 | 考虑停站优化 |
| 铺画列车总数 | 20 | 20 | 20 | 20 | 20 |
| 总目标值 | 1 154.5 | 1 078.0 | 738.0 | 788.5 | 711.0 |
| 总均衡性 | 715.0 | 682.5 | 290.0 | 380.0 | 304.0 |
| 总旅行时间/min | 439.5 | 395.5 | 448.0 | 408.5 | 407.0 |
| 平均旅行速度/(km∙h-1) | 175.70 | 195.25 | 172.37 | 193.78 | 189.50 |
| 总停站数 | 59 | 59 | 65 | 59 | 61 |
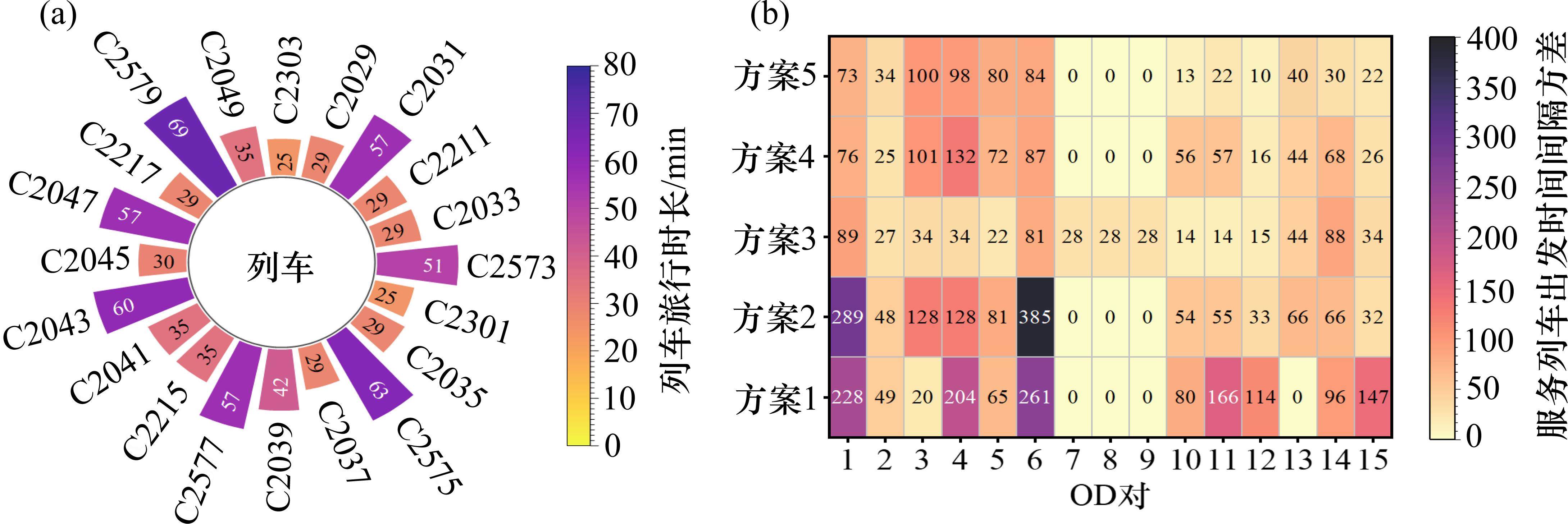
为了进一步验证所提方法的优化性能,仍以京津城际为背景分别进行单目标优化时间、单目标优化OD服务均衡和固定列车停站优化,得到方案2、3、4。此外,方案1为初始运行图,方案5为考虑停站的运行图优化,5个方案的结果对比见表3。各运行图均铺画20列列车,方案2中列车不考虑OD服务均衡,单一追求旅行时长最短,故列车总旅行时间最少,但OD服务均衡最差;方案3中,列车追求OD服务均衡最优,使得停站次数增多,列车旅行时间变长;方案4中列车旅行时间和OD服务均衡均得到优化,但固定停站使得OD服务均衡的优化受到一定限制;方案5中列车旅行时间和OD服务均衡得到了最大程度的优化。利用所提方法优化后的方案2至方案5的目标函数值均低于初始运行图,且方案5的目标函数值最小,说明所提方法能够有效提高列车旅行时间和OD服务均衡的整体效益,且考虑停站进行优化可以更大程度发挥作用。
为了更详细地证实所提方法对OD服务均衡的优化,图8(b)对上述5种方案中的OD服务列车出发时间间隔方差进行了对比。可以看出,考虑了均衡优化的方案3至方案5的OD服务较未考虑均衡优化的方案1和方案2更为均衡。方案5中各OD服务均衡基本优于方案4,进一步说明了固定停站不利于OD服务均衡的优化;方案3为了提高OD服务均衡而使列车停站增多,导致其大多OD服务均衡优于方案5,证明了所提方法对OD服务均衡优化的有效性,但因OD对7、8、9的最小服务列车数为1,其他方案相应的服务列车出发时间间隔方差为0,而方案3的服务列车数大于1,故其服务列车出发时间间隔方差大于其他方案。
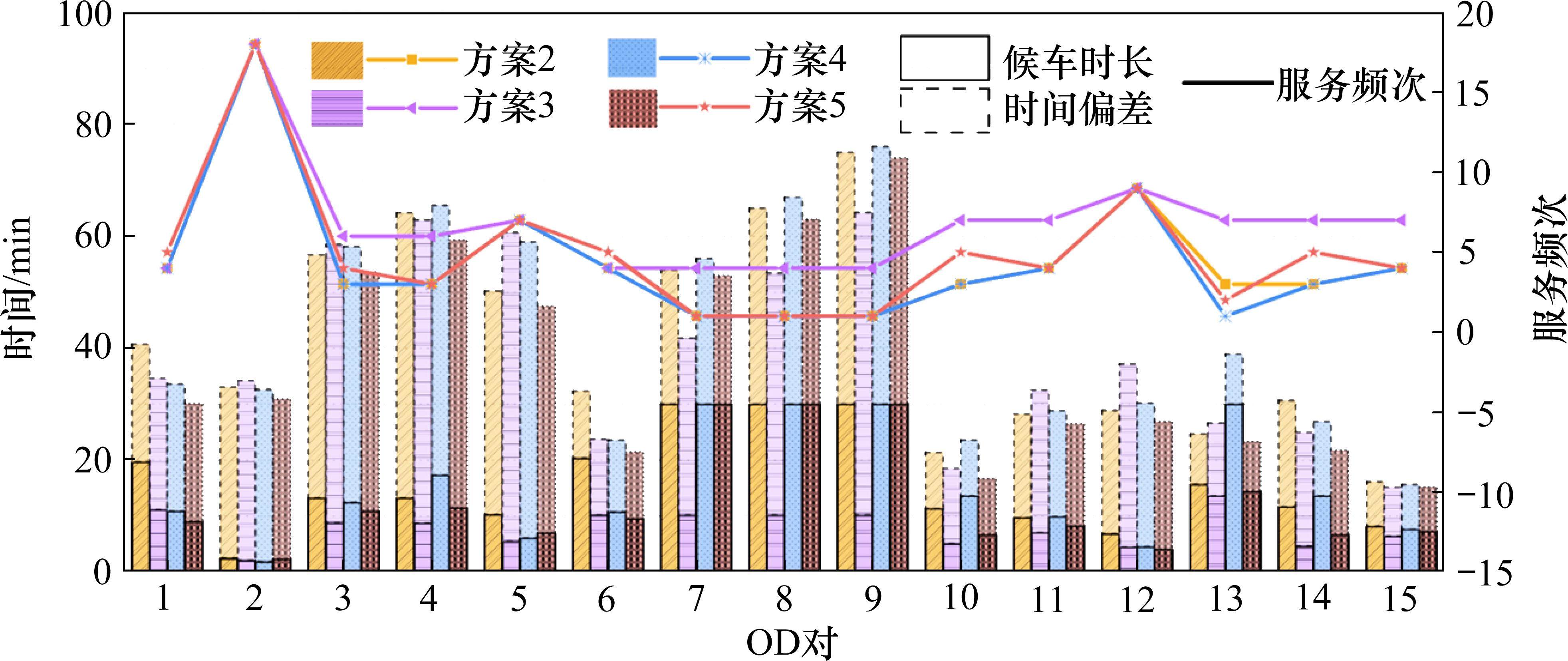
方案2至方案5中各OD列车服务频次详见图9。假设周期T内各OD客流均为800且均匀分布,计算得到不同方案中各OD旅客平均期望出行时间与实际出行时间偏差和服务列车平均运行时间如图9所示。在方案2、4、5中,各OD列车服务频率相似,方案5因OD服务均衡较优,其OD旅客平均期望出行时间和实际出行时间偏差较小,旅客随机到达车站,不需要等待过长时间便会有相应OD服务列车到站,提高了旅客出行便利性和候车体验。方案3中OD服务列车数较多,其大多OD旅客期望出行时间和实际出行时间偏差小于方案5,但因其未优化列车旅行时长,导致OD服务列车平均运行时间较长,故方案5中OD旅客整体出行效率最高。
5 结论
1) 为描述列车在时间-空间的运行状态,基于铁路线路构建了周期时间-空间网络图,以时空弧为变量建立0-1整数非线性模型;同时,设计了一种基于有向图弧权优化的启发式算法对模型进行求解。
2) 针对京津城际铁路算例,所提方法能够实现周期列车运行图优化,并且在短时间内获得较为满意的可行周期运行图。与初始运行图、单目标优化时间、单目标优化均衡和固定停站优化运行图相比,考虑列车停站的优化运行图能够显著提高列车旅行时间和OD服务均衡性的整体效益,体现了所提方法的有效性。
3) 本文考虑停站的周期运行图优化模型只适用于周期内OD客流均衡分布的线路,对于同时段客流需求变化较大的线路并不适用。此外,由于高峰小时的OD客流量无法获取,本文选取初始运行图中OD实际服务列车数作为最小OD服务列车数。为此,考虑更复杂的旅客需求因素是下一步研究方向。
周文梁,闫璐云.考虑均衡服务和停站协同的城际铁路周期运行图优化[J].铁道科学与工程学报,2025,22(02):557-568.
ZHOU Wenliang,YAN Luyun.The optimization of intercity periodic train diagram considering balanced service and stop cooperation[J].Journal of Railway Science and Engineering,2025,22(02):557-568.

