基于多尺度动态时空神经网络的OD客流预测

智慧交通与物流

基于多尺度动态时空神经网络的OD客流预测

林立，

孟学雷，

高如虎，

韩正，

付艳欣

铁道科学与工程学报

第21卷, 第12期

pp.4924-4935

纸质出版 2024-12-28

DOI：10.19713/j.cnki.43-1423/u.T20240474

中图分类号：U293.13

800

精确的OD(origin-destination)客流预测可为铁路运行管理、决策优化等提供良好保障。为准确捕捉高速铁路站点间的动态时空关联，解决全局流量特征和局部拓扑特征难以共同学习的问题，提出一种考虑站间协同作用的多尺度动态时空神经网络(multi-scale synergistic station-based dynamic spatio-temporal neural network, MSSDSTNN)OD客流预测模型。模型多分支并行结构的设计，可以有效地捕获与客流量相关的复杂时空特征；通过融合全局与局部注意力机制，达到识别站点间动态时空关联及线网拓扑结构的目的；同时采用自适应噪声完全集成经验模式分解方法对站点的原始客流数据进行分析，并引入简化粒子群算法实现对长短期记忆神经网络关键参数的动态寻优。选取成绵乐城际与成渝高铁的客流数据，在不同时间粒度下，运用12种既有模型进行比较研究，以评估它们与MSSDSTNN模型的性能差异。结果表明：MSSDSTNN模型比其他模型具有更高的预测精度和拟合效果，尤其在较短的时间粒度下，MSSDSTNN模型展现出显著的优越性。在15 min时间粒度下，MSSDSTNN模型的平均绝对误差、均方根误差、平均绝对百分比误差相较于对比方法中性能排名第2的预测模型分别下降了7.55%、12.12%和26.15%；在拟合优度方面，MSSDSTNN模型的决定系数相较于第2名上升了0.41%。可视化结果展现了模型对时空关联动态变化的学习效果，消融实验证明了各分支的必要性，所提方法可为运营部门的决策提供有价值的参考。

高速铁路OD客流预测动态时空神经网络时空特征注意力机制

当前，我国铁路客运服务网络规模巨大，其中高速铁路网络规模稳居世界前列。随着高速铁路网络的扩张，路网的拓扑结构呈现出不同形态，跨线运营和区域间协同成为常态；且高速铁路客流受季节、节假日、天气、突发事件等多种因素影响，其动态特征明显，因此对运力调度和资源配置都提出了更高的要求。现阶段需求与运力不匹配、高峰时段客流过饱和、跨线客流出行效率低、大客流管理困难等问题日益凸显^[1-2]。客流预测是运输组织方案制定及调度决策的重要依据，也是线网规划设计的关键环节^[3]。准确、可靠的客流预测可提供全面、动态的客流信息，对于缓解高峰时段的客运压力，实现运输需求与运力的良好匹配，提升旅客出行体验和企业运营效率具有重要意义。客流预测的既有研究多聚焦于进出站客流^[4-5]，研究方法包括最小二乘支持向量机^[6]、多层感知机^[7]等传统机器学习方法，以及动态时空神经网络^[8]、长短期记忆网络^[9]、DEASeq2Seq^[10]等深度学习方法。上述研究在客流预测模型的构建与算法的设计等方面都具有较高的参考价值，但仅对进出站客流量展开预测，往往难以全面反映乘客需求的空间分布及各站点间的输送需求，对于列车调度、运力资源配置、票价策略制定等关键运营决策问题的数据支撑力度不足。而对于乘客出行径路起讫站间的OD(origin-destination)需求预测，能够弥补上述不足，为运营决策提供更为全面和精准的参考数据。OD需求预测的主流方法包括经典数学模型、传统机器学习、深度学习方法3种^[11-14]。经典数学预测模型计算复杂度高，泛化能力和动态变化适应性差，且存在参数敏感、预测精度低等问题，因此，越来越多的相关研究开始融入机器学习和深度学习技术^[15]。尽管传统机器学习方法较之经典数学模型在预测精度方面有了较大改善，但在处理大数据量、高时变性的客流需求时，仍然存在一定的局限，而深度学习作为机器学习领域的前沿技术，其数据学习能力更显卓越^[16]。王欣等^[17]结合迁移学习和改进的Boost算法对特殊情况下客流OD展开预测，可有效减少小样本带来的误差率高的情况。赵利强等^[18]设计了一种融合PCA-Kmeans算法的短期OD预测方法，实现了线网范围内的城轨短期客流预测，且预测误差百分比较低。LIU等^[19]通过融合多种数据源并运用循环神经网络对OD需求进行预测，其预测准确度明显优于经典数学模型和传统机器学习方法。林友芳等^[20]利用基于时空LSTM的预测方法，证明了深度学习技术在捕捉OD数据非线性特征方面的显著优势。李浩然等^[21]提出了一种结合时空分解和动态模式分解技术的短期OD预测模型，将原始数据拆分成若干分量以提炼数据特性，实现了OD客流的高效、准确预测。申慧涛等^[22]融合条件生成对抗网络和基于Wasserstein的生成对抗网络技术，通过深入探究客流数据的时空分布特性，有效提升了模型的稳定性和预测结果的准确性。总结来看，经典数学建模方法无法充分考虑预测场景中的复杂动态因素和非线性关联，对客流时空特征的捕捉能力有限；传统机器学习方法在处理海量、高维度数据时效率不高，对复杂场景下客流预测缺乏适应性和灵活性；深度学习方法虽能较好地刻画客流数据的时空特征，但既有研究尚未关注站点间的协同作用或深入分析时空关联的动态性，因此未能有效兼顾客流全局特征与线网局部拓扑特征的共同学习。鉴于此，本文设计了一种考虑站间协同效应的多尺度动态时空神经网络(MSSDSTNN)模型。在传统单一预测模型的基础上融合了空间、时间双视角，从而更好地描述站点间客流数据中的复杂时空特征，可以更好地应对路网拓扑结构发生改变以及客流动态变化的复杂场景，实现OD客流的精准预测。本文模型可以更好地为列车运行调整、票价策略制定提供决策依据，同时有助于提升运营服务质量，实现高效、智能、便捷的铁路运输服务。

1 问题描述

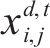
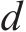
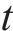
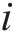
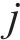
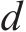
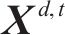
OD客流即出发站到目的站之间的客流需求，一般以客流矩阵形式表示。本文定义为在第天第时段内由站去往站的客流，将一个路网中第天所有OD对的客流通过矩阵表示为：

(1)

其中：为车站数量。

站间协同效应是指站点间的动态时空关联性及其对全局OD流量特征和局部客流特征变化的影响，这种效应体现了站点间OD客流的相互依赖性和随时间变化的动态特性。通过考虑站间协同效应，能够提高客流预测精度和可靠性，增强模型面对复杂客流情况时的适应性。

在时间维度上，任一时段的客流需求均会受到上一时段客流的影响，OD客流展现出显著的周期性以及短期自相关性^[23-25]。因此，本文利用历史OD客流及实时的进、出站客流相关数据，预测未来一定时间内的OD需求，如式(2)所示。

(2)

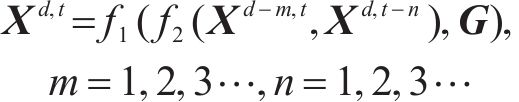
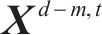
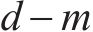
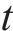
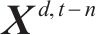
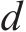
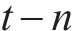
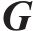
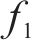
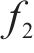
其中：为临近的第天同一时段(第时间段)内的OD矩阵；为同一天(第天)临近的第时间段内的OD矩阵；为描述站间拓扑结构的矩阵；和为映射函数。

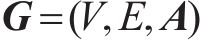
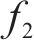
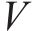
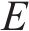
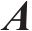
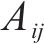
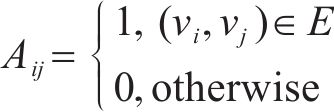
在空间层面，特定OD对的客流亦会受其他不同OD对的影响，基于图论构建无向图，通过映射关系将站间动态时空关联和静态拓扑结构作为输入参数。其中，为车站站点；为线路；为考虑连通性基础上构建的邻接矩阵，当两站间存在连通边时，对应矩阵的项为1。可记作：

(3)

2 模型构建

本文模型可应用于跨线运营场景下或线路互联互通后路网拓扑结构发生改变时以及大数据量、复杂客流条件下的预测。为充分挖掘客流数据所包含的复杂时空特性，本文构建了3个并行的计算分支，多分支结构的设计是为了更好地匹配从日常运营到特殊情况下的多变需求，协同作用机制旨在捕捉站点间复杂的影响关系，这对于线路调整和资源优化至关重要，模型整体结构如图1所示。分支1通过集成双层多头注意力机制，旨在动态捕捉站点间的全局语义相似性，从而深入理解各站点间的关联和相互影响；分支2采用空间多视角动态图卷积网络，用于有效地学习线网结构特征及多元空间相关性；分支3融合了CEEMDAN-SPSO-LSTM与多头注意力机制，目的是掌握时间序列特性，利用注意力机制来识别不同时间段之间的关联性，例如季节、节假日、天气等信息，由分支3也即时间注意力分支模块进行处理。分支1和分支2的设计可以体现站点间的动态时空关联性以及全局OD流量特征和局部客流特征变化，这种多分支结构的设计使得模型能够从多个维度掌握和预测客流的动态变化，提高了预测的准确度和可靠性。

图1

预测模型结构

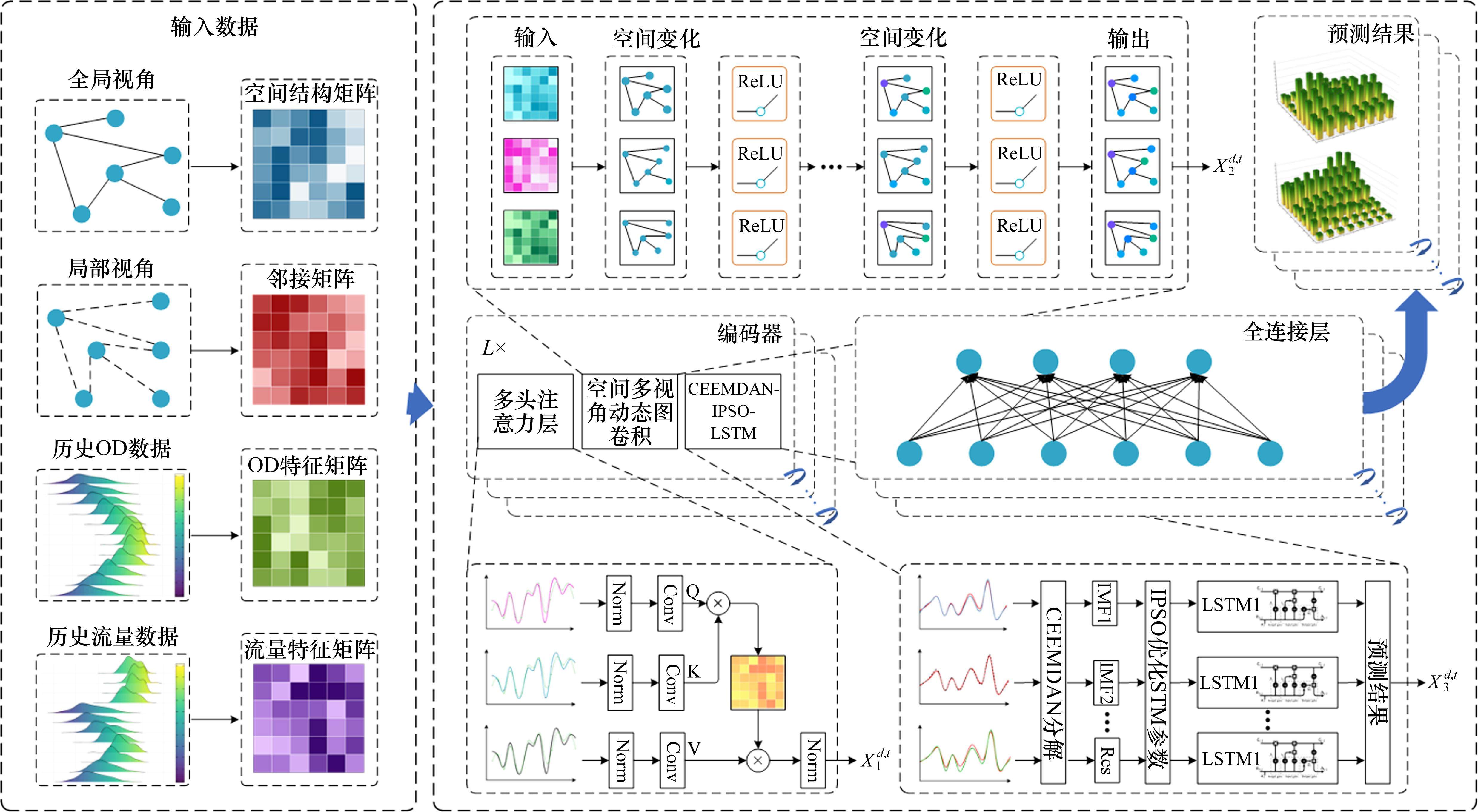
2.1　全局注意力分支

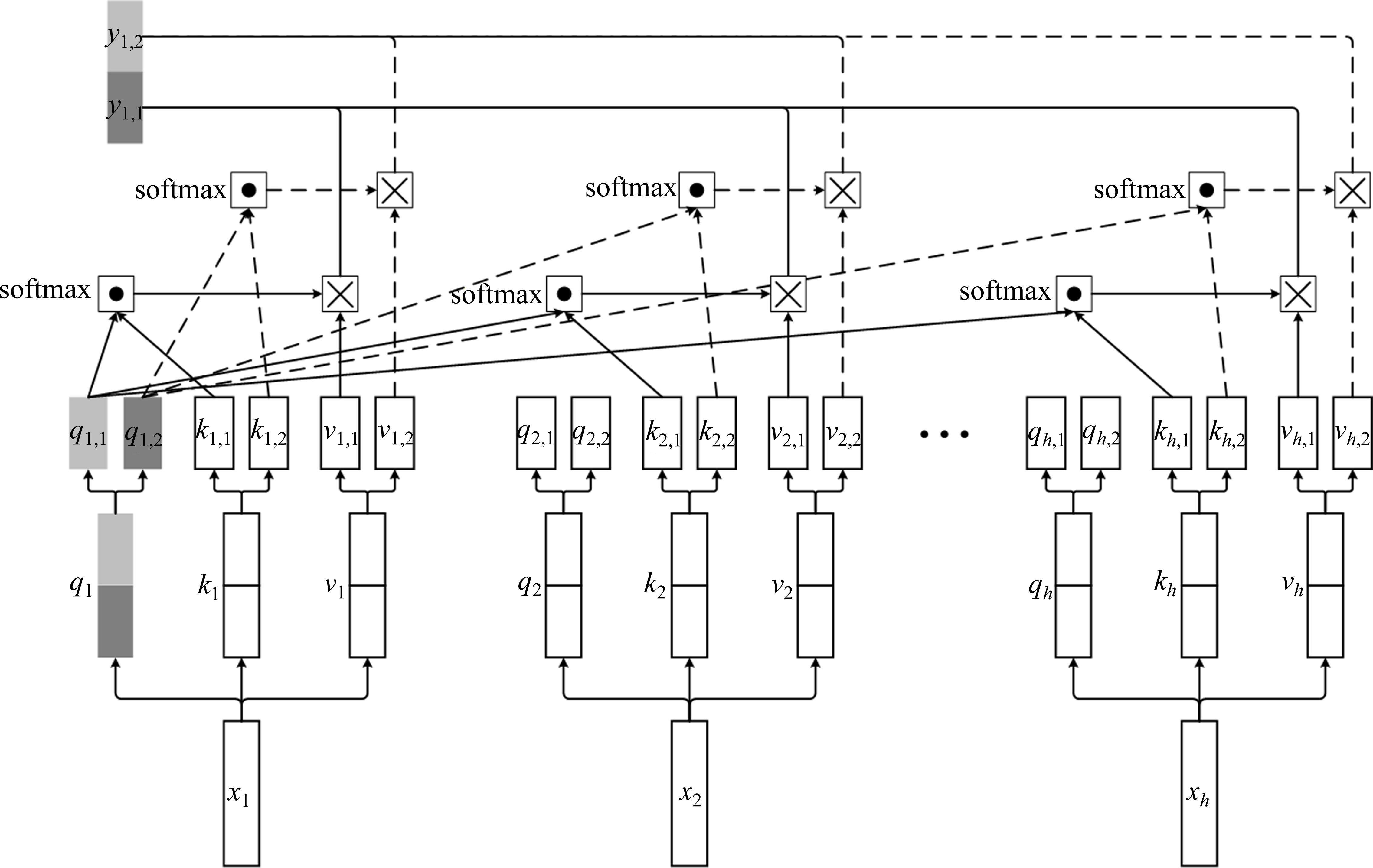
注意力机制通过模拟人类的认知方式，利用差异化的权重分配来体现对不同信息元素的专注度。该机制在处理网络数据时，能够有效识别并调整网络中各节点的相对重要性。全局注意力分支的设计使得模型能够动态地展现站点在客流分布上的关联，强化模型对站点间客流相互作用的捕捉能力，深入刻画车站之间的协同作用。

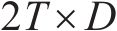
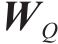
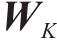
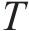
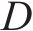
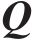
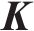
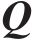
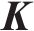
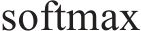
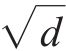
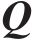
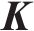
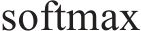
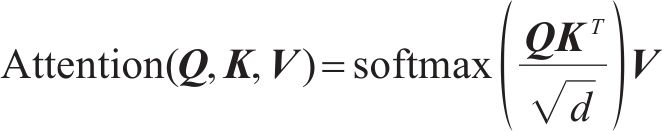
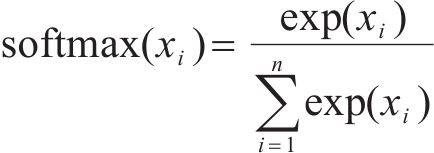
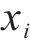
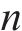
注意力机制的核心在于以不同节点的重要度为基础进行加权转换。此过程涉及输入数据与3个维度为的参数矩阵、、的乘积，其中，表示时间步，表示隐层维度。而后生成查询矩阵、键矩阵和值矩阵，每个矩阵的维度均为。采用点积方法计算和的相关性时，结果可能存在一定误差，经过函数处理后导致梯度消失。鉴于此，本文引入缩放因子，通过缩放和的点积结果进而得到维度为的注意力矩阵，该矩阵再与值矩阵相乘，从而完成注意力运算。函数和全局注意力机制可以表示为：

(4)

(5)

其中：为缩放后的点积结果；为缩放点积结果的数量。

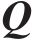
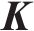
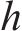
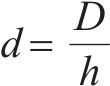
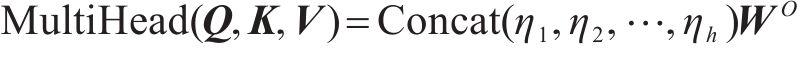
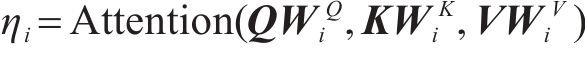
为了增强模型中注意力机制的性能，本文采用了多头注意力的策略。在此策略中，、、矩阵被等量划分，分割后每部分构成一个独立的注意力单元。若模型并行处理的注意力单元数为，则每个单元处理的维度。多头注意力机制计算公式可表示为：

(6)

(7)

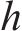
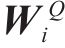
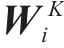
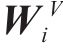
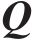
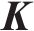
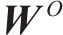
其中：表示不同的注意力模块(头)数量，，，分别表示针对、、的转换矩阵，表示输出映射矩阵；函数用于联结操作。多头自我注意力机制有效揭示了OD数据中不同站点间的协同效应，使得模型能够对序列中的元素关联性进行建模，并通过将多层自我注意力层叠加，学习不同层次的特征表达，从而有效地识别客流相关数据中的复杂模式和动态联系，上述过程可用图2表示。

图2

多头注意力运算流程

2.2　局部注意力分支

利用双视角下的动态图卷积网络，可以有效掌握线路的复杂空间关联，自适应地调整节点间的连接关系。对于某节点时间维度局部卷积多头注意力输出，其空间关系的权重矩阵计算方法如下：

(8)

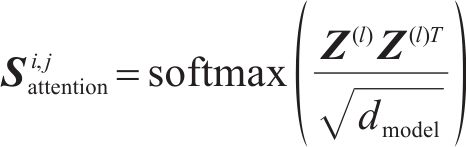
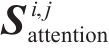
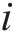
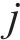
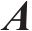
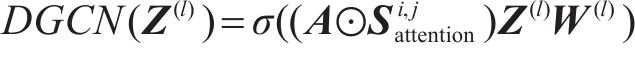
其中：表示任意节点和节点之间的关联度。采用空间注意力权重矩阵，可以对邻接矩阵进行调整，以输出动态图卷积结构。动态图卷积的计算方法可表示为：

(9)

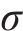
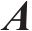
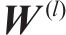
其中：为激活函数；为邻接矩阵；表示哈达玛积；表示第层的可学习权重矩阵。在路网的所有节点上执行时间局部卷积和多头自注意力操作，可以获得时间序列的中间表征，进而将其作为动态图卷积的输入。

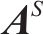
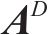
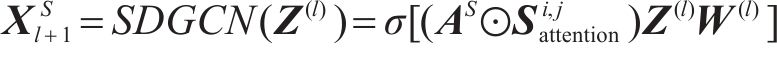
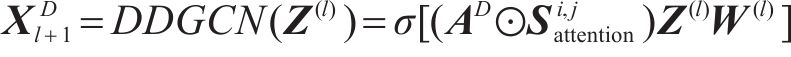
引入静态结构矩阵和动态关系矩阵，可分别捕获客流中的静态空间关联和动态时序相似性^[21]，基于此构建了包含静态卷积模块和动态关系图卷积模块的多视角局部注意力分支，可分别表示为：

(10)

(11)

2.3　时间注意力分支

1) CEEMDAN算法

通过分解时间序列为多个固有模态函数(IMFs)和一个独立的残差分量(Res)，自适应噪声完全集成经验模式分解算法(CEEMDAN)能够有效地减少数据中的噪声影响。

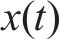
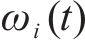
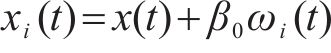
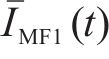
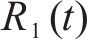
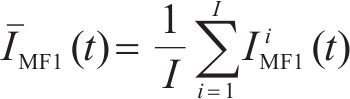
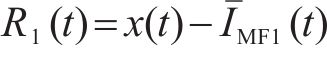
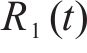
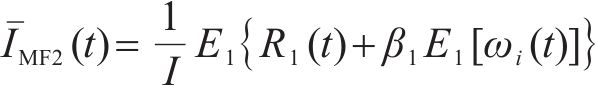
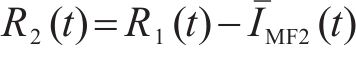
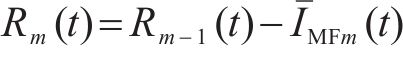
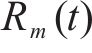
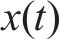
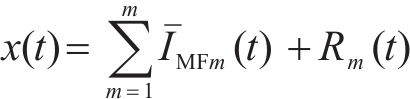
在处理原始客流时间序列数据时，模型引入自适应高斯白噪声生成新序列，通过CEEMDAN分解，可以得到1阶和1阶，其中，。随后，以为新序列继续分解，得到和剩余分量。计算至，单调时结束；反之，继续进行计算。至此，原始序列执行CEEMDAN算法后最终被分解为：。

2) 长短期记忆网络

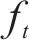
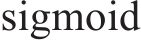
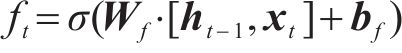
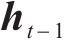
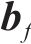
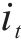
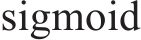
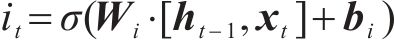
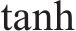
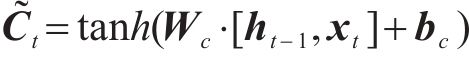
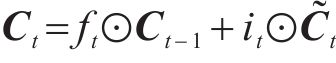
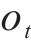
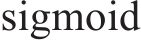
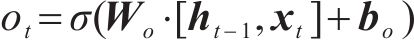
长短期记忆网络(LSTM)的运作过程分为3个核心阶段：遗忘阶段、记忆阶段和输出阶段。对于遗忘门的状态，利用激活函数可得，其中为前一时刻的输出，为当前的输入，、为权重矩阵与偏置项；输入门可用函数确定，而新的候选向量通过函数产生，公式为。这些元素共同作用于细胞状态的更新，即。最后，在输出阶段，输出门由函数控制，而当前时刻的输出则通过哈达玛积运算得出，即。

3) SPSO算法

粒子群优化算法(Particle Swarm Optimization, PSO)依赖于速度和位置2个向量，在迭代后期常导致收敛速度变缓。为了提升算法性能，常见的改进方法是去除速度向量，即采用简化粒子群优化算法(SPSO)。如式(12)所列，SPSO每次迭代仅由位置向量控制。

(12)

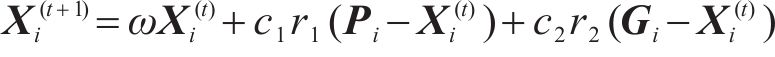
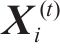
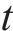
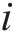
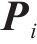
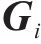
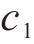
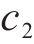
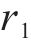
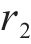
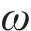
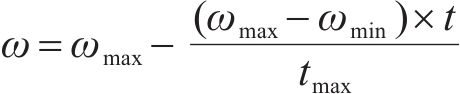
其中：为第次迭代后的第个位置向量；为个体最佳值；为群体最佳值；及为学习参数；与为[0,1]之间的随机系数；为惯性权重。本文对惯性权重加以改进，设计为自适应动态调整的模式，如式(13)所列。

(13)

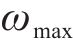
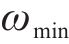
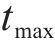
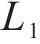
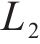
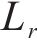
其中：、分别为最大、最小惯性权重；为最大迭代次数。将LSTM网络的4个关键超参数即第1层和第2层隐藏层单元数(、)、学习速率()、训练迭代次数()，与SPSO相结合，以动态寻求最优的LSTM超参数组合，提升模型效能。

4) 编码器设计

本文采用了特征嵌入式编码器-解码器架构，该架构通过序列映射技术处理历史客流数据，编码器层用于提取时空特征，而解码器层则基于上述特征预测未来趋势。该模型结构中，编解码器由层标准化结构组成，融合全局和局部多头注意力机制和时间注意力分支，分别负责空间关联特性和时间依赖特性的分析。

3 算例分析

3.1　数据来源与数据处理

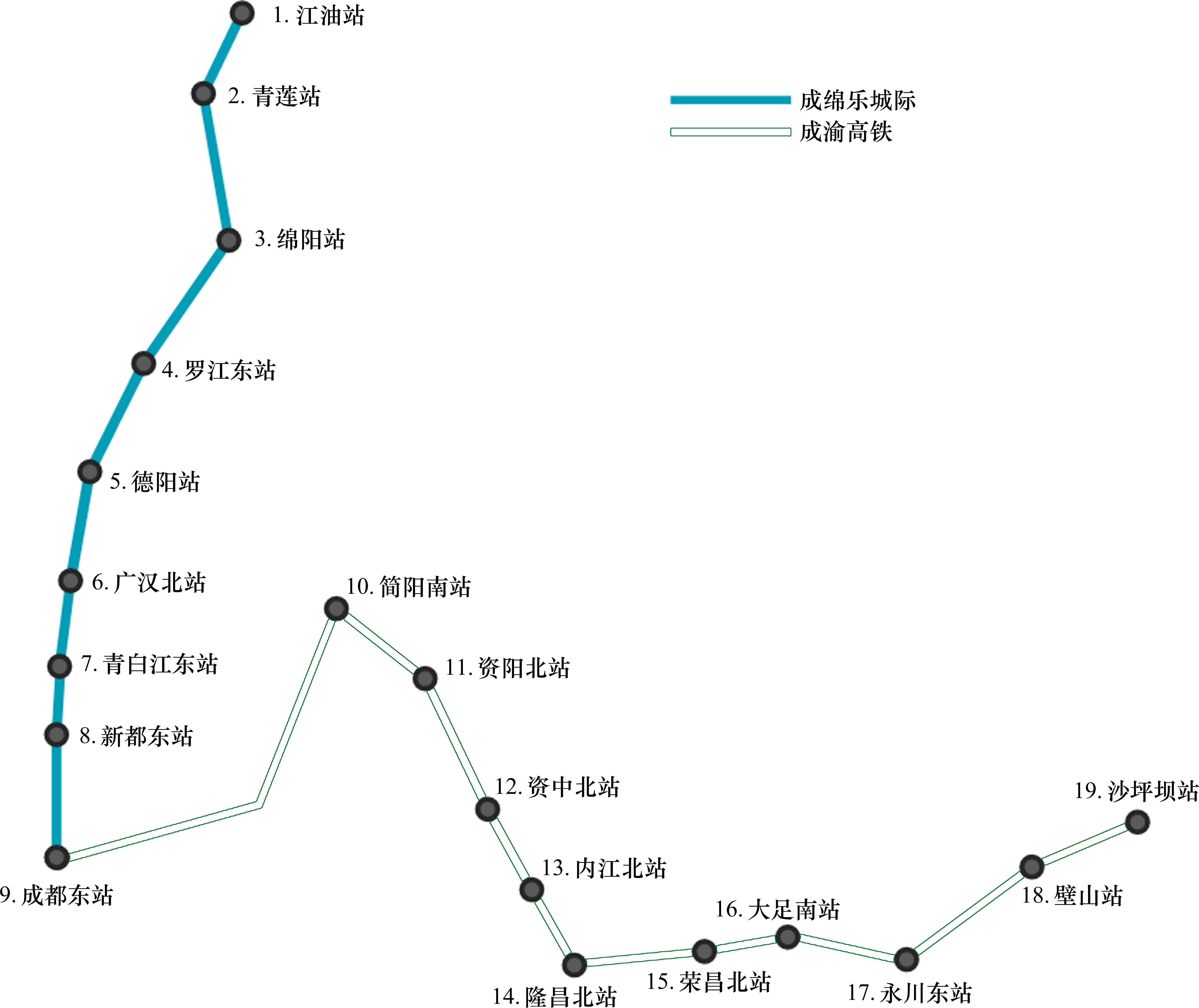
本文选取成绵乐城际和成渝高铁上的19个站点作为研究案例，如图3所示，各站点间共包含361个OD对。该数据集包含自2023年3月10日至8月7日期间，每日6:00―23:00运营时段内，15 min时间粒度下的客流信息，共计368万余条OD数据。其中3月10日―6月22日的数据设定为训练集，其余数据被用作测试集。原始数据做如下处理：1) 筛选出成绵乐城际及成渝高铁线路各站的客流数据，并从中提取站间的OD数据；2) 对数据集进行有效性检验，剔除非运营时段的进出站记录和同站进出记录；3)转换并处理OD信息和相关辅助信息，形成19×19维的OD矩阵，并记录影响客流变化的关键因素。应用min-max归一化算法，将OD数据映射到[-1,1]范围内。

图3

线路及站点示意图

3.2　对比模型与评价指标

选取历史均值法(HA)、向量自回归模型(VAR)、长短时记忆网络(LSTM)、卷积神经网络(CNN)、卷积长短期记忆网络(ConvLSTM)、卷积神经网络-长短时记忆网络(CNN-LSTM)、时间正则化矩阵分解(TRMF)、条件生成对抗网络(CGAN)、基于Wasserstein散度的生成对抗网络(CWGAN-div)、基于时空分解和动态模式分解的混合预测模型(STDMD)，以及移除了全局注意力分支的本文模型变体(MS-1)，移除了局部注意力分支的本文模型变体(MS-2)，12种不同的OD预测方法与本文设计的动态时空神经网络预测模型(MSSDSTNN)进行对比分析。

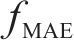
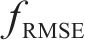
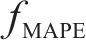
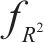
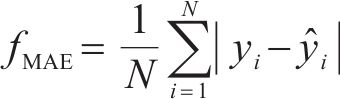
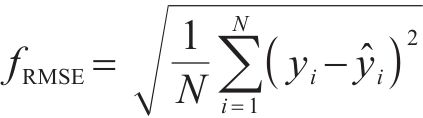
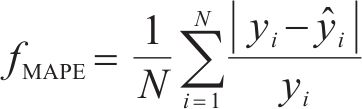
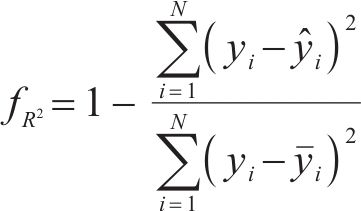
为全面评估预测模型的性能优劣，采用平均绝对误差、均方根误差、平均绝对百分比误差及决定系数这4个指标进行评价，指标计算公式为：

(14)

(15)

(16)

(17)

其中：为样本数据的数量；为真实值；为预测值。

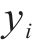
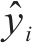
3.3　实验结果分析

本文在PyTorch框架下实现MSSDSTNN模型，所有数值实验均在配备16GB RAM、i7-10200H CPU及RTX 3060 GPU的计算机上进行。空间全局注意力的隐藏层尺寸取64，注意力机制的头部数量定为4，LSTM循环单元数为64，其余超参数通过SPSO算法优化确定。

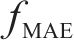
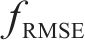
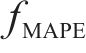
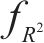
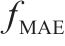
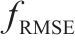
为全面评估模型在不同时间粒度下的预测性能，本文设定了15，30，45和60 min共4个时间粒度。由表1和表2的实验结果可知(加粗部分为最优结果，表格从上到下按照评价效果排序)，MSSDSTNN模型性能整体最优。由于小时间粒度的客流预测对现场生产运营工作更具指导价值，因此本文将重点分析15 min和30 min时间粒度下的计算结果。在15 min时间粒度下，MSSDSTNN模型的预测性能与排名第2的STDMD模型相比，其、、分别下降了7.55%、12.12%、26.15%，决定系数提高了0.41%。

不同模型的

和

指标对比

模型
模型	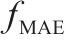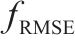15 min	30 min	45 min	60 min	15 min	30 min	45 min	60 min
MSSDSTNN	0.98	5.99	2.69	4.08	1.16	9.53	2.31	6.29
STDMD	1.06	6.18	2.05	5.09	1.32	9.87	3.56	7.56
CWGAN-div	1.15	6.36	2.97	5.51	1.39	10.05	3.99	8.65
ConvLSTM	2.21	9.85	4.89	5.83	3.43	13.56	9.32	10.56
MS-1	2.43	13.03	8.57	9.48	3.74	19.66	11.21	13.05
CGAN	3.68	13.39	10.56	10.52	5.63	19.77	12.56	19.56
CNN-LSTM	4.05	13.43	15.21	15.32	6.85	19.91	19.27	23.41
MS-2	4.29	13.75	17.86	16.46	7.17	46.27	19.06	24.21
LSTM	5.11	13.54	22.07	15.49	7.87	45.25	20.93	25.22
TRMF	5.19	15.78	28.43	17.53	8.26	55.61	42.31	37.86
VAR	7.51	15.78	30.86	18.90	12.64	59.79	43.29	58.70
CNN	6.23	17.52	35.93	21.79	10.03	67.06	45.69	42.16

展开更多

不同模型的

和

指标对比

模型
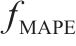
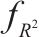
模型	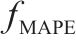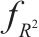15 min	30 min	45 min	60 min	15 min	30 min	45 min	60 min
MSSDSTNN	2.09	2.97	5.57	9.96	0.990	0.991	0.993	0.865
STDMD	2.83	3.09	3.56	9.98	0.986	0.986	0.994	0.842
CWGAN-div	3.09	3.15	5.83	10.15	0.983	0.986	0.993	0.830
ConvLSTM	4.36	5.89	7.98	17.88	0.983	0.981	0.990	0.829
MS-1	4.99	6.30	14.49	21.44	0.996	0.984	0.959	0.806
CGAN	5.98	8.73	16.98	26.73	0.811	0.859	0.893	0.801
CNN-LSTM	6.24	10.33	20.42	29.01	0.808	0.802	0.881	0.788
MS-2	6.70	10.74	21.20	30.73	0.917	0.909	0.882	0.758
LSTM	9.81	11.62	24.39	31.39	0.914	0.897	0.858	0.802
TRMF	9.62	11.70	24.98	32.38	0.912	0.808	0.739	0.709
VAR	11.55	11.81	22.96	32.66	0.858	0.768	0.724	0.567
CNN	10.48	13.90	25.51	36.05	0.874	0.788	0.736	0.532

展开更多

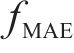
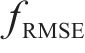
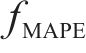
以30 min时间粒度下的预测结果为例，本文模型与STDMD模型相比，、和分别降低了3.07%、3.44%、3.88%，同时提高了0.51%。与传统的单一预测模型或组合模型相比，MSSDSTNN模型构建了3个分支，分别用于提取系统的全局特征、局部特征及时间特征，并借助全连接层来增强全局特征提取和整合能力，因此在多个评价指标上优于传统的单一或组合预测模型。

对比MSSDSTNN模型与其2个变体模型MS-1、MS-2的性能，在30 min时间粒度下，相较于完整的MSSDSTNN模型，移除第1分支的MS-1模型的指标增加了7.04，移除第2分支的MS-2模型的指标增加了7.76。分支1主要以全局视角来分析各节点的重要度，进而有效地辨识各节点在整体网络结构中的相对重要性；分支2主要反映了与周围邻近站点的关联程度，该分支不仅有效捕获了静态的空间结构信息，还进一步学习了节点之间的时序动态关系。消融实验结果证明了模型中每个分支对提升整体预测性能的重要作用，并进一步验证了MSSDSTNN模型设计的合理性和考虑站间协同的必要性。

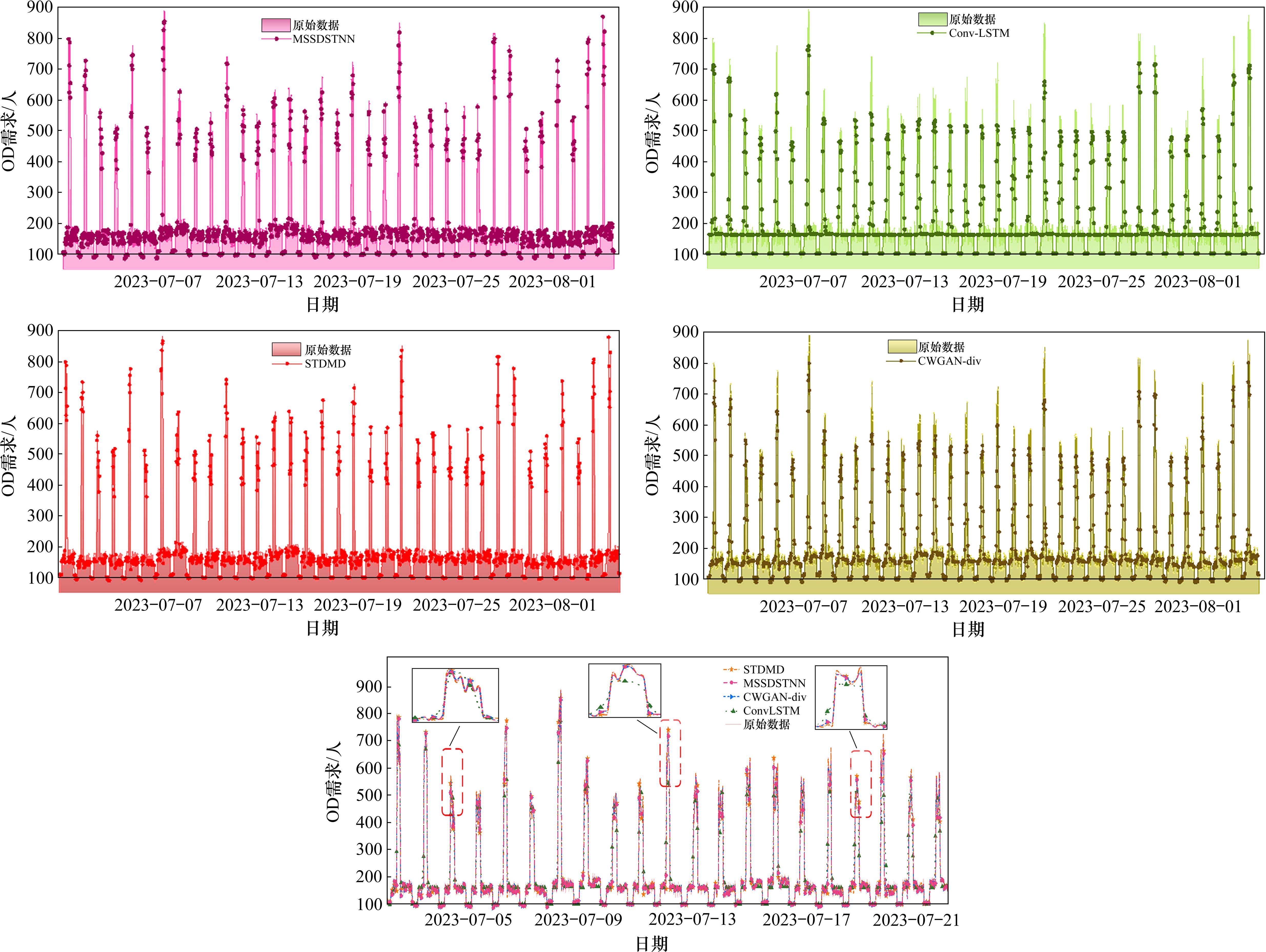
选取实验过程中性能最优的前4组模型，绘制其预测OD需求曲线如图4所示。由图4可知，本文设计的MSSDSTNN模型与原始数据真实值的偏差最小，MSSDSTNN模型可对OD客流的变化趋势进行很好的拟合，较之其他模型，该模型可以更好地用于站点间动态关联的描述，提供可靠的预测信息，指导现场的生产运营工作。

图4

多种模型预测结果对比

3.4　注意力可视化分析

本文采用注意力机制量化站点间客流相似度，实现了站点间时空关系的动态映射。选取数据集中前16天的客流分布规律进行可视化展示，生成的注意力可视化矩阵如图5所示，其中矩阵的颜色亮度表示站点间的注意力强度，横纵坐标表示站点的编号。

图 5

注意力矩阵热力图

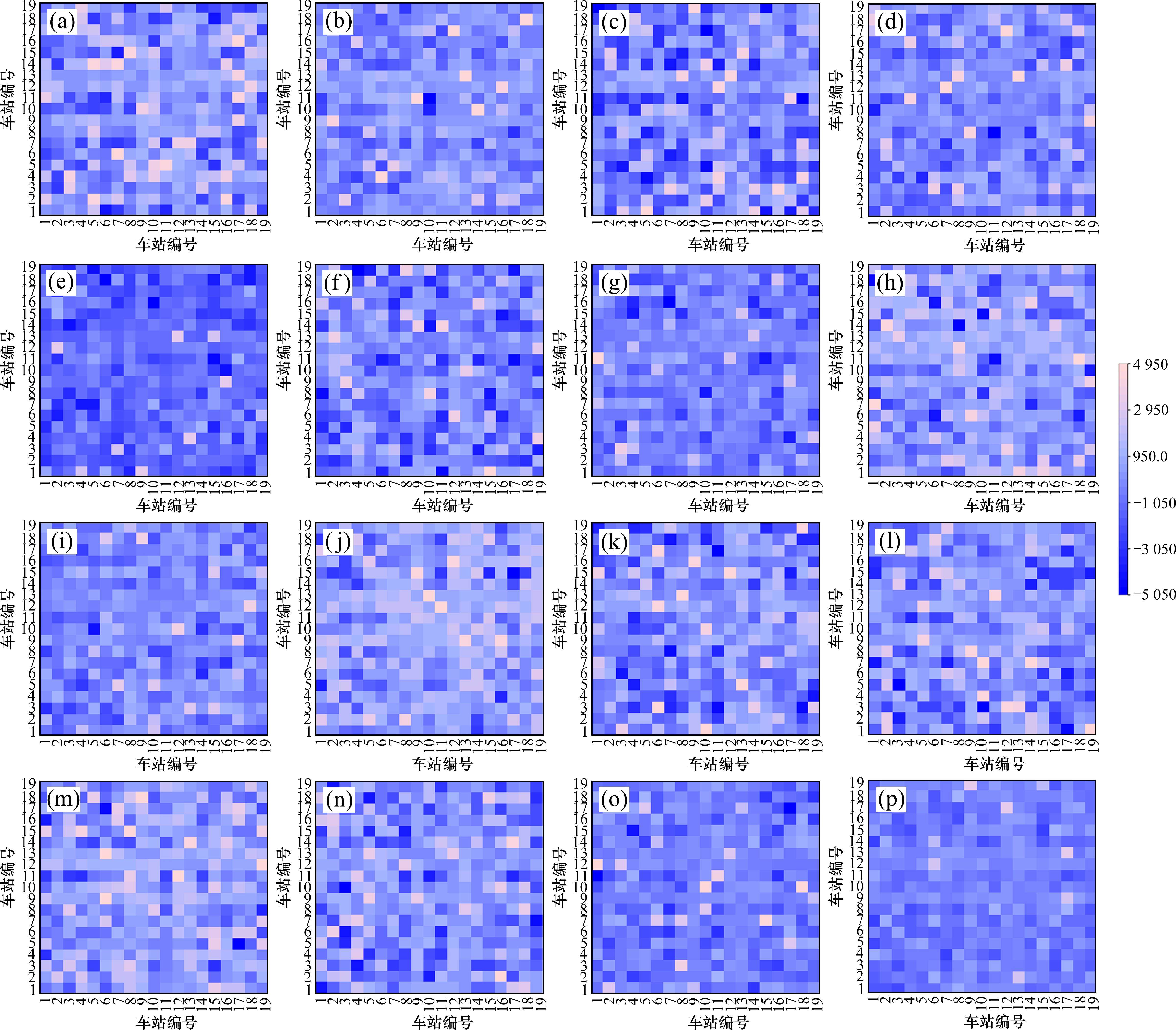
图5的可视化分析结果表明，在不同观测周期下，站点间存在普遍的动态时空关联。通过分析各周期的注意力矩阵，可以发现在所有矩阵中均存在浅色高亮线条，这些线条对于全局OD有着重要的影响。特别是第9列(成都东站)在整体的影响力最为显著，第12列和第13列(资中北站和内江北站)虽然稍逊于成都东站，但对于全局OD也有较大的影响。此外，注意力机制的动态捕捉能力在可视化分析中得以验证，例如Day10和Day13的矩阵中，出现了更多亮线条，代表站间的相关性发生了较大变化，说明模型可以有效捕捉客流数据的动态时空相关性。

4 结论及展望

1) 采用多分支并行架构的多尺度动态时空神经网络模型(MSSDSTNN)，与经典的预测模型相比，可以有效学习车站间协同规律、为预测提供更全面的信息，捕捉更细致的时空特征，从而更准确地刻画站点之间的相互关联，满足现阶段高速铁路运营发展的需求。

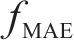
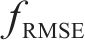
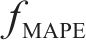
2) 以成绵乐城际和成渝高铁的OD数据进行验证，实验结果表明，MSSDSTNN展现出优于经典预测模型、深度学习模型以及既有的OD预测模型的预测精度。尤其在小时间粒度下，其、、和评价指标明显更优。

3) 分别使用15，30，45和60 min共4个时间粒度对MSSDSTNN模型的性能进行测试，计算结果充分证明了模型的稳健性，并通过消融实验进一步佐证了模型各分支设计的科学性和有效性。

4) 考虑站间协同效应的MSSDSTNN预测模型可为铁路部门运输资源的分配及决策方案的制定提供有益参考，对于提升客运服务水平和乘客满意度具有重要的现实意义。未来将进一步探索数据压缩降维、时空特征提取等技术，扩展本文的应用范围并优化模型性能。

参考文献

何必胜, 朱永俊, 陈路锋, 等.

基于时空图神经网络的高速铁路车站短期客流预测方法

[J]. 铁道学报, 2022, 44(9): 1-8.

百度学术

谷歌学术

禹倩, 张亚东, 郭进, 等.

基于深度集成神经网络的城市轨道交通短时进站客流预测

[J]. 铁道学报, 2023, 45(12): 37-46.

百度学术

谷歌学术

SHAHRIARI S, GHASRI M, SISSON S A, et al.

Ensemble of ARIMA: combining parametric and bootstrapping technique for traffic flow prediction

[J]. Transportmetrica A: Transport Science, 2020, 16(3): 1552-1573.

百度学术

谷歌学术

ZHENG Zhihao, LING Ximan, WANG Pu, et al.

Hybrid model for predicting anomalous large passenger flow in urban metros

[J]. IET Intelligent Transport Systems, 2020, 14(14): 1987-1996.

百度学术

谷歌学术

ROOS J, GAVIN G, BONNEVAY S.

A dynamic Bayesian network approach to forecast short-term urban rail passenger flows with incomplete data

[J]. Transportation Research Procedia, 2017, 26: 53-61.

百度学术

谷歌学术

谭一帆, 巫雪梅, 刘海旭, 等.

基于IGA优化LSSVM的城轨短期客流预测

[J]. 计算机仿真, 2022, 39(11): 169-172, 252.

百度学术

谷歌学术

LIN Luzhou, GAO Yuezhe, CAO Bingxin, et al.

Passenger flow scale prediction of urban rail transit stations based on multilayer perceptron (MLP)

[J]. Complexity, 2023, 2023: 1430449.

百度学术

谷歌学术

施俊庆, 李睿, 程明慧, 等.

基于动态时空神经网络模型的地铁客流预测

[J]. 交通运输系统工程与信息, 2023, 23(2): 139-147.

百度学术

谷歌学术

张开雯, 何勇.

基于EMD-SSA-LSTM模型的城市轨道交通站点客流预测

[J/OL]. 武汉理工大学学报(交通科学与工程版), 1-9[2024-01-18]. https://kns.cnki.net/kcms2/detail/42.1824.u.20230704.1748.104.html.

百度学术

谷歌学术

HUANG Hao, MAO Jiannan, LU Weike, et al.

DEASeq2Seq: an attention based sequence to sequence model for short-term metro passenger flow prediction within decomposition-ensemble strategy

[J]. Transportation Research Part C: Emerging Technologies, 2023, 146: 103965.

百度学术

谷歌学术

NOURSALEHI P, KOUTSOPOULOS H N, ZHAO Jinhua.

Dynamic origin-destination prediction in urban rail systems: a multi-resolution spatio-temporal deep learning approach

[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(6): 5106-5115.

百度学术

谷歌学术

ZHANG Jinlei, CHE Hongshu, CHEN Feng, et al.

Short-term origin-destination demand prediction in urban rail transit systems: a channel-wise attentive split-convolutional neural network method

[J]. Transportation Research Part C: Emerging Technologies, 2021, 124: 102928.

百度学术

谷歌学术

CHENG Zhanhong, TRÉPANIER M, SUN Lijun.

Real-time forecasting of metro origin-destination matrices with high-order weighted dynamic mode decomposition

[J]. ArXiv e-Prints, 2021: arXiv: 2101.00466.

百度学术

谷歌学术

HE Yuxin, ZHAO Yang, TSUI K L.

Short-term forecasting of origin-destination matrix in transit system via a deep learning approach

[J]. Transportmetrica A: Transport Science, 2023, 19(2):2033348.

百度学术

谷歌学术

王金水, 欧雪雯, 陈俊岩, 等.

基于组合模型的城市轨道站点短时客流分类预测

[J]. 铁道科学与工程学报, 2023, 20(6): 2004-2012.

百度学术

谷歌学术

HAYDARI A, YILMAZ Y.

Deep reinforcement learning for intelligent transportation systems: a survey

[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(1): 11-32.

百度学术

谷歌学术

王欣, 王志飞, 王煜.

基于迁移学习的轨道交通特殊OD客流预测研究

[J]. 铁道运输与经济, 2024, 46(3): 182-188.

百度学术

谷歌学术

赵利强, 张涛, 唐水雄, 等.

基于PCA-Kmeans算法的城市轨道交通短期OD客流预测

[J]. 工业技术创新, 2023, 10(4): 60-68.

百度学术

谷歌学术

LIU Yang, LIU Zhiyuan, JIA Ruo.

DeepPF: a deep learning based architecture for metro passenger flow prediction

[J]. Transportation Research Part C: Emerging Technologies, 2019, 101: 18-34.

百度学术

谷歌学术

林友芳, 尹康, 党毅, 等.

基于时空LSTM的OD客运需求预测

[J]. 北京交通大学学报, 2019, 43(1): 114-121.

百度学术

谷歌学术

李浩然, 许心越, 李建民, 等.

考虑稀疏特性的城市轨道交通短时OD时空预测方法

[J]. 铁道科学与工程学报, 2023, 20(10): 3685-3695.

百度学术

谷歌学术

申慧涛, 郑亮, 李树凯, 等.

基于生成对抗网络的地铁OD需求短时预测

[J]. 铁道科学与工程学报, 2022, 19(6): 1530-1539.

百度学术

谷歌学术

WANG Yunshan, ZHANG Wenbo, TANG Tianli, et al.

Bus OD matrix reconstruction based on clustering Wi-Fi probe data

[J]. Transportmetrica B: Transport Dynamics, 2022, 10(1): 864-879.

百度学术

谷歌学术

PAMUŁA T, ŻOCHOWSKA R.

Estimation and prediction of the OD matrix in uncongested urban road network based on traffic flows using deep learning

[J]. Engineering Applications of Artificial Intelligence, 2023, 117: 105550.

百度学术

谷歌学术

ZHENG Han, CHEN Junhua, HUANG Zhaocha, et al.

Short-term online forecasting for passenger origin-destination (OD) flows of urban rail transit: a graph-temporal fused deep learning method

[J]. Mathematics, 2022, 10(19): 3664.

百度学术

谷歌学术

注释

林立,孟学雷,高如虎等.基于多尺度动态时空神经网络的OD客流预测[J].铁道科学与工程学报,2024,21(12):4924-4935.

LIN Li,MENG Xuelei,GAO Ruhu,et al.OD passenger flow prediction based on multi-scale dynamic spatio-temporal neural network[J].Journal of Railway Science and Engineering,2024,21(12):4924-4935.

论文推荐

1 问题描述

2 模型构建

2.1　全局注意力分支

2.2　局部注意力分支

2.3　时间注意力分支

3 算例分析

3.1　数据来源与数据处理

3.2　对比模型与评价指标

3.3　实验结果分析

3.4　注意力可视化分析

4 结论及展望

参考文献

基于多尺度动态时空神经网络的OD客流预测

1 问题描述

2 模型构建

2.1 全局注意力分支

2.2 局部注意力分支

2.3 时间注意力分支

3 算例分析

3.1 数据来源与数据处理

3.2 对比模型与评价指标

3.3 实验结果分析

3.4 注意力可视化分析

4 结论及展望

2.1　全局注意力分支

2.2　局部注意力分支

2.3　时间注意力分支

3.1　数据来源与数据处理

3.2　对比模型与评价指标

3.3　实验结果分析

3.4　注意力可视化分析