近年来,快速的城市化进程为当代城市交通管理带来了巨大的挑战。作为当代智慧城市的关键组成部分,智能交通系统已经被研发用于分析、管理和优化交通状况。交通流预测作为智能交通系统不可或缺的要素,在优化交通资源调度方面发挥着至关重要的作用。地铁交通作为公共交通系统中不可或缺的重要组成部分,在实际交通运输系统中扮演着极其重要的角色。精准的地铁客流预测不仅对路线规划和交通资源调度具有重要价值,而且对整个智能交通系统在城市层面的控制也至关重要,因此受到了广泛研究[1-2]。交通数据是一种时间序列数据。早期交通流量预测采用时间序列模型预测,仅捕获时间相关性,忽略了交通数据的空间相关性。例如,传统统计方法包括自回归综合移动平均(ARIMA)、向量自回归(VAR)。此类方法只能捕获线性时间相关性,而交通数据的演变是复杂和非线性的。传统机器学习方法可以捕获非线性相关性,代表方法有支持向量回归(SVR)和k近邻(KNN)。然而,此类方法需要手动提取交通数据的高阶特征,而提取这些特征需要耗费巨大的人力。为了避免这个问题,最近越来越多的研究基于深度学习的方法来解决交通预测问题。例如,长短期记忆(LSTM)和门控循环单元(GRU)。相较之前的方法,它们在性能上取得了更好的成绩,但仍未考虑交通数据中的空间相关性。MA等[3]使用卷积神经网络对空间相关性进行建模,但面向的是欧式空间结构,而道路交通网络是非欧式空间结构,因此并不适用于道路交通网络的交通流量预测任务。当前,一些研究者采用图神经网络来处理由道路网络生成的图结构。例如,LI等[4]在基于路网的交通预测任务中使用扩散卷积[5]代替了GRU中的线性运算,以捕捉每个时间片的空间相关性。YU等[6]将GCN与因果卷积[7]结合,用于流量预测。WU等[8-10]通过反向传播学习的自适应矩阵捕捉了道路网络中的全局空间依赖性。LIU等[11]通过构建1个物理图和2个基于领域知识的虚拟图进行图卷积。YE等[12]设计了3个空间矩阵,用于提取目标站的空间相关性,并将其划分为近邻居、中邻居和远邻居。王金水等[13]利用超图对客流的时空数据进行表征,用于短时进站客流预测。然而,这些方法未能有效捕捉道路网络中的动态时空相关性和潜在的空间相关性。PARK等[14]使用了常规Transformer[15]结构,通过堆叠空间和时间注意力来进行流量预测。与此不同,ZHENG等[16]同时应用了空间和时间注意力进行流量预测,并引入了编码器和解码器之间的转换注意力以减少预测时间。YE等[17]在时间和空间维度上使用注意力机制,并使用多个图来捕捉空间相关性进行流量预测。他们未考虑交通数据的局部时空相关性,且其对空间相关性的考虑不够全面,未能有效捕捉交通数据中潜在的空间相关性。现有交通流预测相关模型主要基于路网图结构和时空相关性保持不变的假设构建,这使得它们未能提取交通系统中隐藏的空间特征和动态时空特征。同时很少有模型能够有效处理交通流量数据中的局部和全局时空相关性。为了解决上述问题,提出了一种自适应扩散图卷积注意力网络,用于预测地铁交通网络中各站点的交通流量。首先,基于对地铁交通数据的分析,通过构建多图和自适应矩阵,并结合多头注意力机制,模型能够更全面地提取地铁系统中真实的空间信息特征,从而使得模型的预测结果更贴近实际交通系统的运行情况。其次,ADGCA模型使用因果卷积、自适应扩散图卷积以及多头注意力机制来提取局部和全局的动态时空相关性,从而有效提高模型的预测精确度。这意味着该模型在实际应用中具有更高的可信度和实用性,能够为城市地铁交通管理部门提供更准确的数据支持,帮助其更好地规划交通运输系统和优化运营策略。所提出的模型在2个真实的地铁交通数据集的客流量预测中,准确度优于以前的模型。
1 问题描述与准备工作
1.1 问题描述
定义1(交通网络):交通网络是一个有向图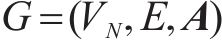
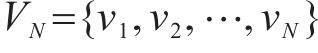
定义2(交通流张量):节点i在时刻t的客流量数据表示为X
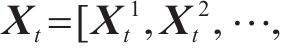
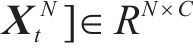
定义3(时间属性):每个时间间隔t都附加了几个时间属性,例如一天中的时间、一周中的某一天和该天是否为休息日。假设有M个可用的时间属性。时间间隔t的第m个属性记为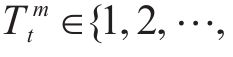
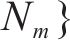
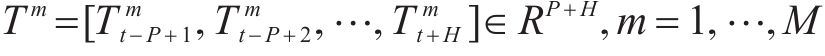
问题描述:地铁客流预测是指利用历史数据进行函数学习,从而预测未来时间段内各地铁站点的客流量情况。即从过去P时间片的历史交通流量数据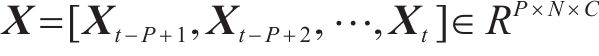
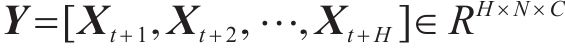
1.2 转移矩阵和自适应矩阵
仅基于地铁物理拓扑图,模型无法捕捉真实的空间相关性,根据专业领域相关知识构造多个加权图能够让模型捕捉节点之间的各种类型的关系特征,同时使用自适应矩阵可以捕捉节点之间潜在的空间相关性。这些图用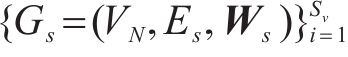
基于地铁物理拓扑图的转移矩阵:地铁交通网络本身可以看作是一个简单的加权图,相连的地铁站点表示节点之间存在边,其中所有边的权重值为1。将对角元素设置1,然后对每一行进行线性归一化,得到权重矩阵W1。此时W1即为地铁物理拓扑图转移矩阵。
基于功能相似图的转移矩阵:除了地铁物理拓扑图外,功能相似性也是空间相关性探索的关键因素。虽然有些地铁站点在现实中可能并不相连,甚至相距较远,但它们属于同一个功能区域(如办公区、商业区、休闲娱乐区、住宅区等)可能具有相同的功能,从而具有相似的交通特征。节点vi和节点vj之间的相似度定义为:
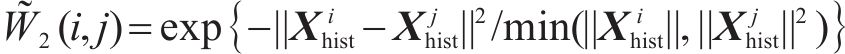
其中,X
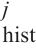
基于源-目的地关联图的转移矩阵:另一个图的构造是基于地铁交通客流量训练集提供的源-目的地(OD)信息。节点vi到节点vj基于OD相关性可以定义为:
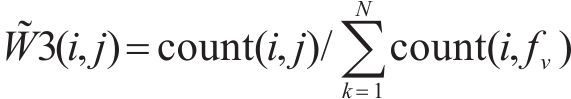
其中,count(i,j)为节点vi到节点vj的客流总数。通过选择相关率最高的前fv个站点来构造权重矩阵,将其对角元素设置1,然后对每一行进行线性归一化得到源-目的地关联图的转移矩阵W3。
自适应矩阵:自适应矩阵的构建使得模型能够捕捉到未被以上多图所捕捉的隐藏空间相关性。自适应矩阵Wa为:
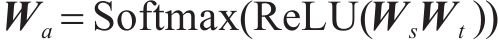
其中,Ws∈RN×q和Wt∈Rq×N为可学习的源节点嵌入、目标节点嵌入,q为嵌入维度。ReLU激活函数去除节点之间的弱连接,最后通过Softmax激活函数归一化得到自适应矩阵。
1.3 自适应扩散图卷积
图卷积是在给定结构信息的情况下提取节点特征的基本操作,KIPF等[18]将图卷积层定义为:
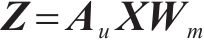
其中,Au∈RN×N表示归一化自环邻接矩阵;X∈RN×C表示输入信息;Z∈RN×D表示输出信息;Wm∈RC×D表示可学习参数矩阵。LI等[4]提出了一种扩散卷积层,该层被证明在时空建模中是有效的,用K个有限步长对图信号的扩散过程进行了建模。WU等[8]将扩散卷积层推广为式(6)的形式:
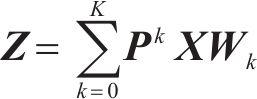
其中,Pk表示转移矩阵的幂级数;k为整数,取值为0≤k≤K。对于无向图,


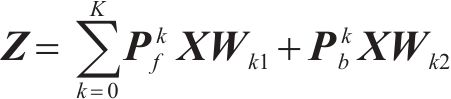
1.4 因果卷积
因果卷积在卷积操作中限制信息传递的方向,以确保当前时刻的输出仅受过去时刻输入的影响,而不受未来时刻信息的影响。该卷积结构包含输入层、隐藏层和输出层,每一层均采用相同类型的神经元。
对于时序数据X,采用大小为a的卷积核,因果卷积的函数F的表达式为:
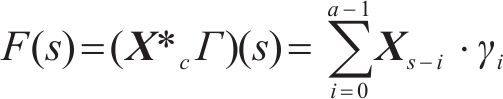
其中,F(s)为经过一层因果卷积后输出的第s个元素;*c表示因果卷积操作;Г和γi表示卷积核,γi=Г[s,i];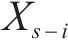
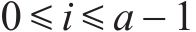
1.5 多头注意力机制
注意力机制可以看作是一个将查询和键值对集合映射到输出的函数,其中查询、键和值都是向量。采用缩放点积注意力,通过矩阵乘法对所有查询并行执行操作。自注意力计算如下:
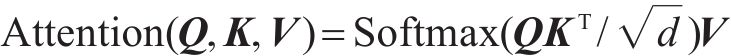
其中,Q∈RN×d、K∈RN×d、V∈RN×d是查询、键和值;d是查询、键和值的维度。为了让模型能够共同参与不同的表示子空间,引入多头注意力机制。多头自注意力允许对序列中元素之间的相关性进行建模,无论它们之间的距离如何,都会产生有效的全局感受野,从而能够很好地捕捉交通流数据中的长期依赖性。用D表示模型的特征大小。给定查询Q∈RN×D,键K∈RN×D,值V∈RN×D,多头注意力计算如下:
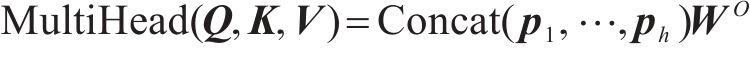

其中,h是头的数量;W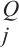
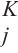
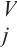
注意力机制主要关注整个输入数据中不同部分之间的相关性,使模型能够在大量的信息中更加关注与当前节点相关的关键信息。自注意力机制中,查询Q与键K之间的相关性是基于它们的缩放点积计算,然后进行相应的加权聚合。然而,这种方法并没有融合当前时间点前后的局部信息,容易忽略当前时间点的周围因素变化的影响。因果卷积能够有效地捕捉到时间序列中的局部特征和依赖关系。通过融合因果卷积和多头注意力机制可以使模型更好地捕捉当前时间点的上下文信息。自适应扩散图卷积可以捕捉地铁客流时间序列数据中隐藏的空间相关性。结合三者可以更好地提取地铁客流时间序列数据中的时空特征,从而提高模型性能。其充分考虑时间序列数据在时间维度上具有很强的依赖性特征以及可能会出现的异常波动问题,处理数据时,将输入的序列数据纳入一维因果卷积模块中,利用因果卷积提取每个时间节点周围的信息,利用自适应扩散图卷积提取地铁站点之间隐藏的空间相关性,然后利用多头注意力机制和时空嵌入引导的方法学习时间节点之间的动态时间相关性和地铁站点之间的动态空间相关性。
2 自适应扩散图卷积注意力网络
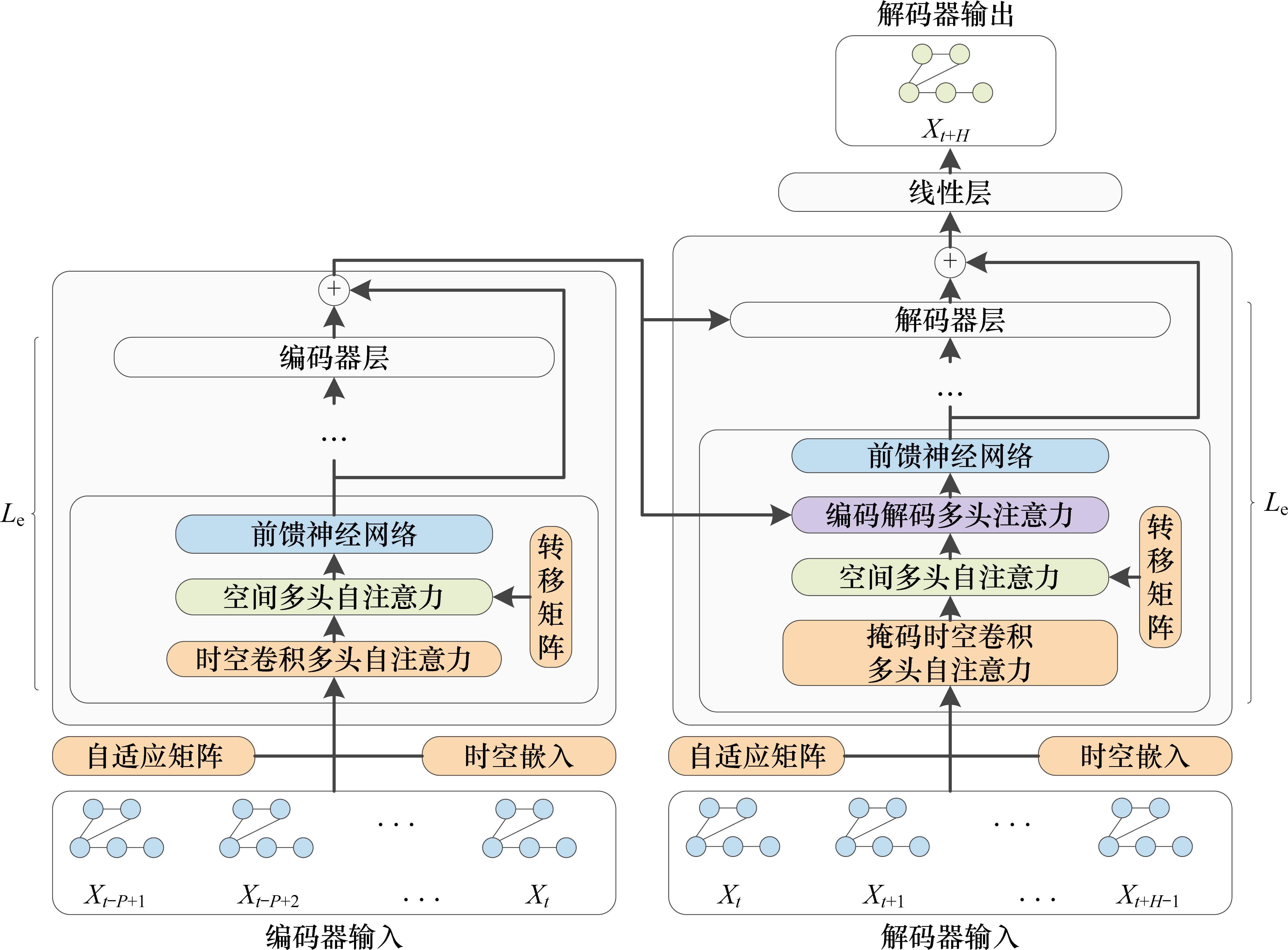
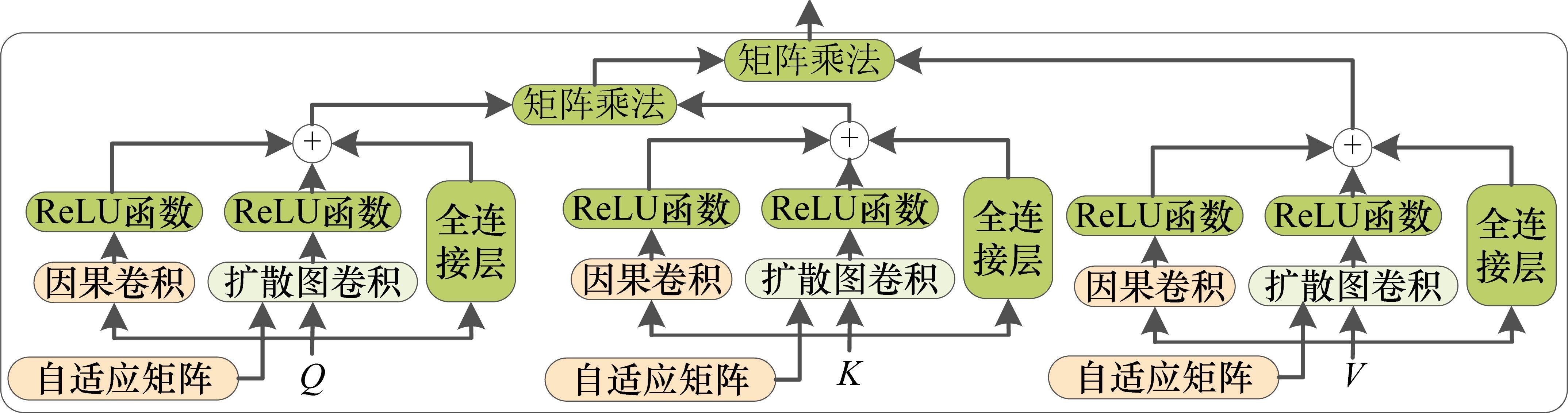
在本节中,将对提出的ADGCA模型进行详细阐述。图1展示了ADGCA框架,该框架包括编码器和解码器2个部分,它们均由多个相同的子层堆叠而成。在这些子层中,通过3种不同类型的组件学习时间和空间相关性,分别是时空卷积多头自注意力、空间多头自注意力以及编码解码多头注意力。输入的原特征信息首先经过时空嵌入组件得到具有时间位置信息的时空嵌入信息特征,进而通过时空卷积多头自注意力提取动态时空特征,通过空间多头自注意力提取不同类型的空间相关性,通过前馈神经网络提取更多的复杂关系特征。编码器和解码器均使用时空卷积多头自注意力和空间多头自注意力来对动态时空相关性进行建模。解码器进一步使用编码解码多头注意力,以使得解码器中的每个位置能够在时间上响应输入序列中的所有位置。为了确保模型在深层时能够有效训练,在模型内部采用残差连接和层归一化。
2.1 时空嵌入
时空嵌入组件包括时间嵌入、时间位置嵌入和空间嵌入,时空嵌入由三者通过连接和线性变化得到。
2.1.1 时间嵌入与时间位置嵌入
多头注意力机制对序列中数据的顺序是完全不可知的,而顺序信息在时间序列建模任务中起着非常重要的作用。因此,除了将所有时间属性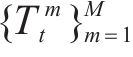
对于时间间隔t处的时间嵌入与时间位置嵌入构建方式如下。首先,将每个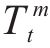
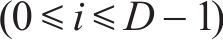
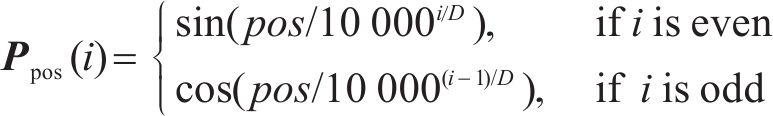
接着,将基于时间属性和时间位置计算出的D维向量连接在一起,并与可学习参数进行线性变换,以在时间间隔t生成最终具有时间位置信息的时间嵌入Ut∈RD。
2.1.2 空间嵌入
通过特征映射(Eigenmaps)[19]这种经典的图嵌入技术,将图结构信息编码到空间嵌入中。为了满足要求,邻接矩阵A对称定义为As=max(A,AT),所得的无向图假设是连通的。接下来执行特征映射算法。首先,计算归一化拉普拉斯矩阵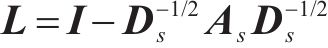
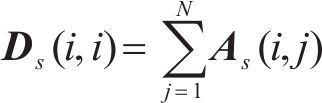
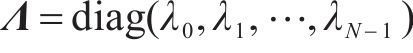
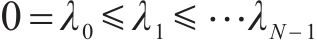
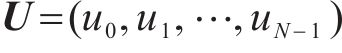
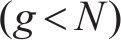
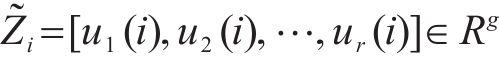

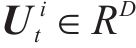
2.2 时空编码器
时空编码器通过跳跃连接将输入和Le层相同的编码器层堆叠起来。每个编码器层由时空卷积多头自注意力、空间多头自注意力以及前馈神经网络3个组件组成,同时使用了残差连接和层归一化。前馈神经网络是一个简单的全连接网络,它包括2个线性变换层和1个ReLU激活函数,能够让模型在注意力机制和卷积神经网络的基础上捕获更多的复杂关系。
2.2.1 时空卷积多头自注意力
如图2所示,时空卷积多头自注意力包括因果卷积、扩散图卷积、全连接层和多头注意力模块。利用自适应扩散图卷积提取隐藏的空间相关性,因果卷积和多头注意力则可提取局部和全局的动态时间相关性。多头自注意力是一个多头注意力的特例,它专门应用于自注意力机制。自注意力是在一个序列内部计算注意力权重,让序列中的每个元素都可以关注到序列中的所有其他元素。因此,多头自注意力就是在同一个序列上并行运行多个子自注意力机制。在时间维度的输出上应用多头自注意力时,其参数在所有时间位置上都是共享的。然而,这种共享机制忽略了交通状态在时间和地点上动态变化的现象。为解决这一问题,采用时空嵌入引导的方法,通过在多头注意力中引入相应的函数替代共享参数,将查询、键和值的学习与特定的时空条件相联系。通过这种方式,时空卷积多头自注意力能够进行自注意力操作,为每个头创建一个隐藏层的多层感知器:
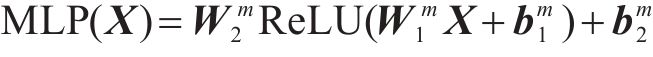
其中,W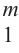
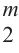
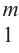
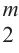

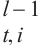
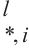
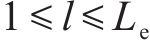
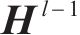
输入: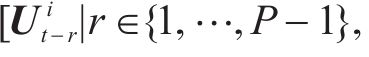
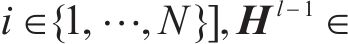
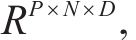
输出: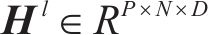
1: for i ← 1 to N do
2: for j ← 1 to h do
3: for r ← 1 to P-1 do
4: WQ,WK,WV ← MLP(U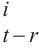
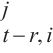
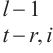
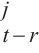
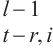
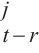
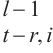
5: Q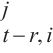
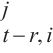
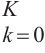
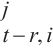
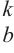
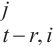
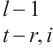
6: K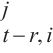
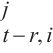
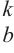
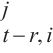
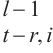
7: V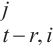
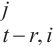
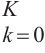
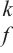
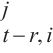
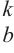
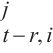
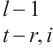
8: end
9: Q ← [Q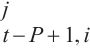
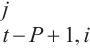
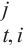
10: end
11:H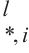
12:end
13:Hl← LayerNorm(Hl-1 + Hl);
14:end
2.2.2 空间多头自注意力
空间多头自注意力可以利用多个图的等效转移矩阵来捕捉不同类型的空间相关性。多图的构建使模型更加关注与中心节点相关的节点,与关注所有节点相比更加合理,这可以让模型更专注于与当前节点密切相关的信息特征,从而提高模型提取有效信息特征的能力。对于每个图Gs,节点vi将参与邻居聚合h次,从而得到vi向量,然后通过连接和线性变化得到最终向量。分配给相邻节点的权重是由动态多头注意力值与转移矩阵中的静态值逐元素相乘确定的,其在生成注意力参数时使用时空嵌入引导的方法。第l编码层的空间多图注意力组件接收第l-1编码层输出为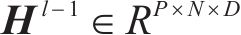

输入:Hl-1 ∈ RP×N×D, {U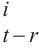
输出:Hl ∈ RP×N×D;
1: for r ← 1 to P-1 do
2: for b ← 1 to 3 do
3: km ← -ꝏ; km[Wb != 0] ← 0;
4: for j ← 1 to h do
5: for i ← 1 to N do
6: WQ, WK, WV ← MLP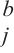
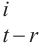
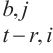
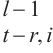
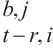
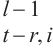
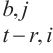
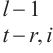
7: end
8: Q ← [Q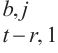
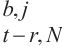
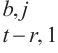
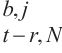
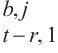
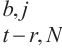
9: p
10: end
11: end
12: H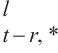
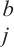
13:end
14:Hl← LayerNorm(Hl-1 + Hl);
15:end
2.3 时空解码器
时空解码器由跳跃连接的Le个相同解码器层和用于输出预测结果的线性层组成。每个解码器层由掩码时空卷积多头自注意力、空间多头自注意力、编码解码多头注意力和前馈神经网络组成。空间多头自注意力和前馈神经网络的结构与编码器中的相同,而掩码时空卷积多头自注意力使用掩码进行操作,以防止模型使用未来序列的信息。同时时空解码器也使用了残差连接和层归一化。
2.3.1 掩码时空卷积多头自注意力
掩码时空卷积多头注意力的工作机制与编码器中的时空卷积多头注意力基本相同,唯一的区别是在缩放点积注意力之后会添加一个掩码。掩码kmas为正方矩阵,对角线上方的元素取值负无穷大,对角线下方的元素取值0。其使用的注意力机制定义为:
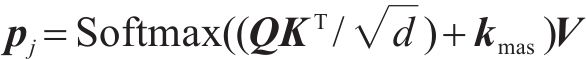
2.3.2 编码解码多头注意力
编码解码多头注意力为连接编码器输出与每个解码器层的桥梁,可以从历史地铁交通数据中自适应学习特征。该组件使用的键K和值V来源于时空编码器,而查询Q来自时空解码器,其通过使用时空编码器输出的键和值来执行时空嵌入引导的多头注意力操作。第l层的编码解码多头注意力组件接收第l-1解码层输出

输入:Hl-1 ∈ RT×N×D, {U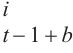
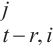
{V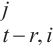
输出:Hl ∈ RT×N×D;
1: for i ← 1 to N do
2: for j ← 1 to h do
3: for b ← 1 to T do
4: WQ ← MLPj (U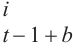
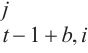
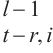
5: end
6: Q ← [Q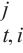
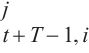
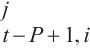
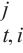
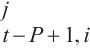
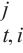
7: end
8: H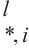
9: end
10:Hl← LayerNorm(Hl-1 + Hl);
11:end
3 实验
3.1 数据集
为了评估所提模型的性能,在2个现实世界地铁交通数据集进行了广泛的实验。分别为上海地铁数据集和杭州地铁数据集[11]。
上海地铁数据集:该数据集根据中国上海地铁系统的交易数据创建,日期范围为2016年7月1日至2016年9月30日。运行的车站数量为288个,共有985条自然边。每日的时间段为5:30—23:30,日均客流量为882万人次。客流量(包括流入和流出)按照15 min的时间间隔进行聚合,一天总共有73个间隔。为每天创建休息日指示器。该数据集分为3部分,包括训练集(7月1日—8月31日)、验证集(9月1日—9月9日)和测试集(9月10日—9月30日)。
杭州地铁数据集:该数据集根据中国杭州地铁系统的交易数据创建。日期范围为2019年1月1日至2019年1月25日。运行站点数量为80个,共有248条自然边。每日的时间段为5:30—23:30,日均客流量为235万人次。客流(包括流入和流出)时间间隔为15 min。并为每天创建休息日指示器。该数据集分为3部分,包括训练集(1月1日—1月18日)、验证集(1月19日—1月20日)和测试集(1月21日—1月25日)。
3.2 基线模型
1) 历史平均值(HA);2) 随机森林(RF);3) 向量自回归(VAR);4) 前馈神经网络(FNN);5) 全连接门控循环单元(FCGRU);6) 扩散卷积循环神经网络(DCRNN);7) 图波网络(Graph WaveNet);8) 基于注意力的时空图卷积网络(ASTGCN)[20];9) 时空图序列模型(STG2Seq)[21];10) 物理虚拟协作图网络(PVCGN);11) 自适应矩阵卷积循环网络(AGCRN);12) 长短时图卷积网络(LSGCN)[22];13) 基于注意力的时空图神经网络(ASTGNN)[23];14) 基于元图转换器的网络(MGT)。
3.3 实验设置
在实验中,使用过去1 h的历史地铁客流数据来预测接下来1 h进出站的客流情况。实验所用硬件环境为NVIDIA Tesla T4 16 GB GPU。使用PyTorch框架来实现提出的模型。因为地铁客流受通勤影响较大,模型考虑了一天中的时间和日期是否为休息日。基于2个地铁数据集构建的多图转移矩阵的数量均为3,且都采用了一个自适应矩阵。在测试阶段,采用自回归方式进行预测,即当前预测的输出将用于下一步的预测。时空编码器和时空解码器的层数Le设置为6。模型的特征维度D被设定为16。在注意力层中,头的数量为4。在应用残差连接之前,将dropout层添加到时空卷积注意力中,其中在训练杭州地铁数据集时,概率被设定为0.3,而在上海地铁数据集上则为0.2。批处理大小设置为2,损失函数选择平均绝对误差。训练阶段采用Adam优化方法,初始学习率为0.001,权重衰减为0.000 2。模型的迭代次数为100。基线模型的参数按照原文献[11, 17]进行设置。
3.4 评估指标
实验选用平均绝对误差Ema、均方根误差Erms和平均绝对百分比误差Emap这3个评估指标[11]。
3.5 交通流预测结果对比分析
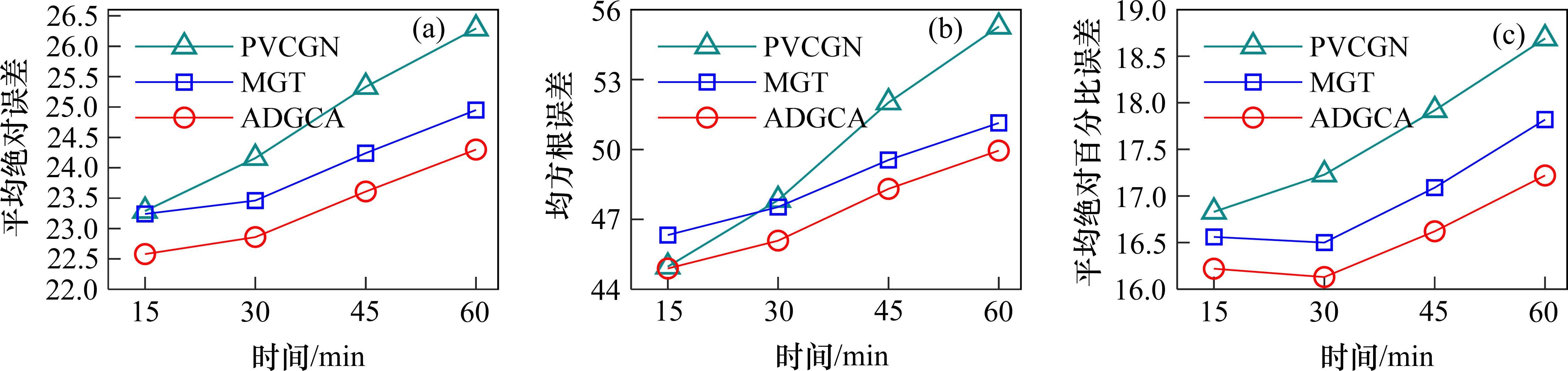
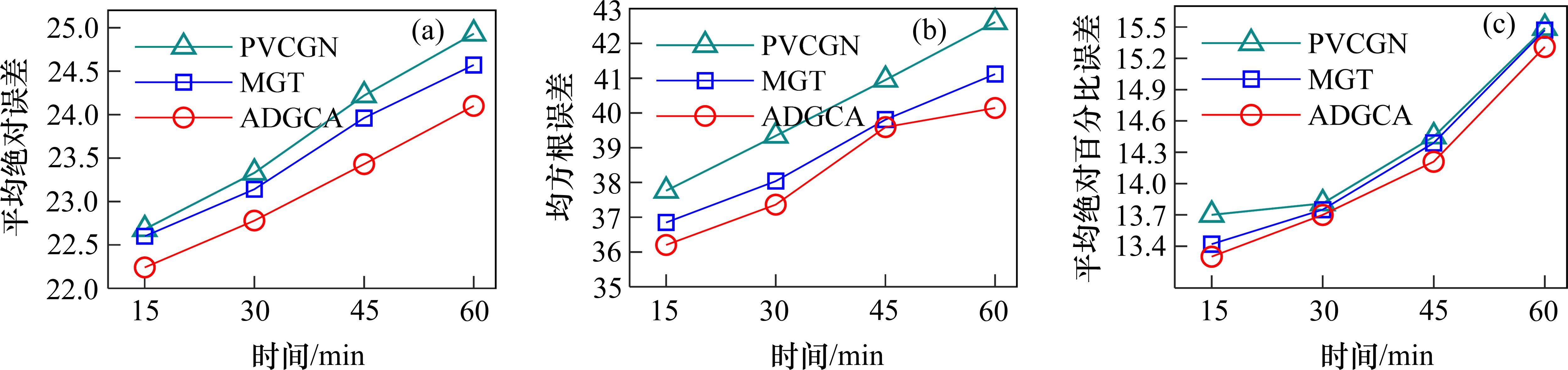
表1显示了不同方法在2个地铁数据集上的性能。表中评估指标值是15,30,45和60 min时间步长的平均值,为便于比较,基线模型的相关结果根据PVCGN和MGT给出[11, 17]。评估指标的值越小说明模型的性能越好,为了便于观察,对最小值进行加粗。从表1中可以观察到,模型ADGCA在所有情况下始终优于所有基线模型。在上海地铁数据集上,与预测准确度第2的模型相比,ADGCA模型在预测准确度指标Ema、Erms、Emap分别提高了2.26%、1.27%、2.47%,在杭州数据集上分别提高了1.07%、1.96%、0.49%。
| 模型 | 上海地铁数据集 | 杭州地铁数据集 | ||||
|---|---|---|---|---|---|---|
| Ema | Erms | Emap | Ema | Erms | Emap | |
| HA | 45.44 | 135.90 | 29.10 | 31.02 | 53.57 | 17.18 |
| RF | 46.20 | 99.80 | 45.51 | 43.00 | 76.95 | 31.05 |
| VAR | 39.94 | 67.66 | 46.63 | 41.39 | 65.38 | 34.72 |
| FNN | 32.43 | 67.76 | 23.85 | 25.57 | 43.98 | 17.23 |
| FCGRU | 27.26 | 60.22 | 18.29 | 24.95 | 41.75 | 15.69 |
| DCRNN | 28.78 | 58.69 | 21.63 | 26.13 | 44.30 | 15.47 |
| Graph WaveNet | 25.85 | 51.47 | 18.76 | 24.73 | 41.82 | 15.21 |
| ASTGCN | 42.37 | 113.37 | 27.33 | 28.03 | 47.21 | 16.21 |
| STG2Seq | 26.01 | 58.94 | 18.98 | 25.25 | 42.41 | 22.02 |
| PVCGN | 24.77 | 50.02 | 17.67 | 23.79 | 40.12 | 14.38 |
| AGCRN | 29.51 | 59.78 | 23.17 | 26.67 | 45.42 | 16.49 |
| LSGCN | 33.94 | 65.77 | 44.42 | 34.24 | 57.89 | 25.71 |
| ASTGNN | 27.37 | 56.39 | 30.05 | 26.36 | 45.51 | 16.64 |
| MGT | 23.88 | 47.92 | 16.97 | 23.39 | 38.83 | 14.20 |
| ADGCA | 23.34 | 47.31 | 16.55 | 23.14 | 38.07 | 14.13 |
根据表1实验结果可得以下观察结果。1) 相对于统计学模型(VAR)和传统机器学习模型(RF),未考虑空间相关性的深度学习模型(FNN和FCGRU)具有更好预测性能。因为其能够捕捉到交通数据中更为复杂的时间相关性。2) 与未考虑空间相关性的深度学习模型相比,基于图卷积神经网络的深度学习模型(DCRNN、Graph WaveNet、ASTGCN、STG2Seq等)具有更好的预测性能。因为结合了图神经网络的深度学习模型能够捕捉交通数据时间和空间2个维度的相关性,从而取得更好的预测效果。3) 基于自适应扩散图卷积注意力网络的模型(ADGCA)具有最佳的预测性能。因为其根据历史地铁交通数据构建多图和自适应矩阵,并结合多头注意力机制进行建模,相比于仅基于物理网络拓扑图构建的图卷积神经网络深度学习模型,能够有效地提取到交通数据中更加真实的时空相关性。
图3和图4展示了预测性能前三的模型在上海和杭州地铁数据集上的多步预测结果。从图可知,随着预测时间步长的增加,3个模型的相关预测评估指标值普遍呈现增长趋势,这表明随着时间步长的增加,预测难度也相应上升。相较于其他模型,ADGCA模型在各个步长上展现出了最为出色的性能。而且随着时间的推移,ADGCA的优势也依然存在。这说明ADGCA模型在长短期预测方面表现卓越,充分验证了其在不同预测步长上的优越性。其主要原因有:首先,ADGCA模型基于高效的多头注意力机制,其在提取长期相关性方面具有卓越的性能。其次,ADGCA模型中的时空卷积多头注意力组件能够有效地提取局部和全局的动态时空相关性。最后,ADGCA模型基于所构建的多图和自适应矩阵进行建模,能够提取到交通数据中更加真实的空间相关性。
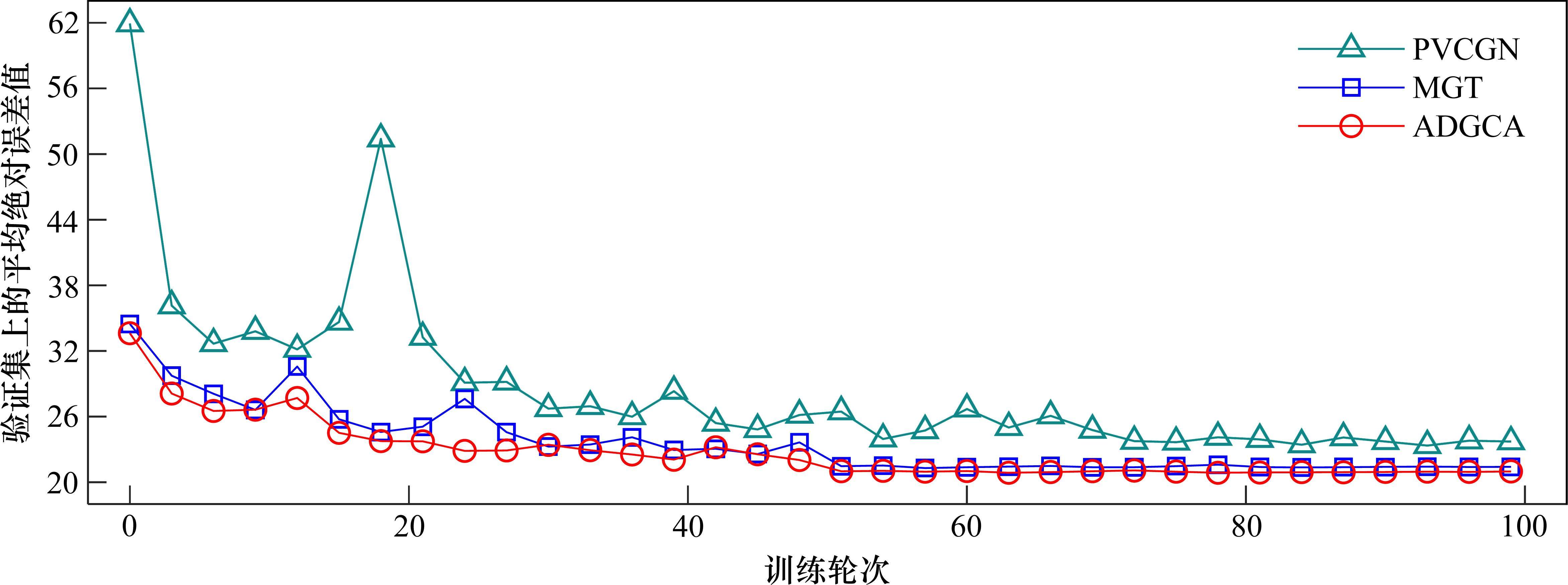
所构建的模型通过在训练集上进行多轮次的迭代训练,更新其参数,以提升模型性能。每次迭代训练完成后,在验证集上评估模型在训练过程中的泛化能力和性能。模型在验证集上的平均绝对误差值越小,说明性能越好。当模型在验证集上的性能不再提升时,可以停止训练,以避免过拟合并节省计算资源。对在训练过程中最佳性能的模型在测试集上的表现进行评估。基线模型在2个地铁数据集上的预测结果均采用在训练过程中最佳性能的模型。图5展示了杭州地铁数据集上预测性能排名前3的模型不同训练轮次的性能变化趋势。由图可知,在杭州地铁数据集上,相关基线模型的性能随着训练轮次的增加逐渐提升,并最终趋于稳定。然而,在迭代训练过程中,模型也出现了性能下降的情况。ADGCA和MGT模型在所有迭代轮次中均表现出优于PVCGN模型的性能,其中ADGCA模型相较于其他模型在绝大多数迭代轮次中表现更为出色,并且其在最佳性能方面具有最优水平。
3.6 消融实验
为了进一步验证模型中各个组件的有效性,构建了不同的变体时空预测模型与ADGCA模型进行比较。其中:1) w/o CausalCon表示移除因果卷积,使其无法提取局部时间相关性。2) w/o AaptiveDGC表示移除自适应扩散图卷积,使其无法提取潜在的空间相关性。3) w/o TSCMA表示移除时空卷积多头自注意力,使其无法提取局部时空相关性和潜在的空间相关性。4) w/o SMA表示移除空间多头自注意力组件,使其无法提取多类型的空间相关性。5) w/GCN表示使用图卷积网络取代空间多头注意力组件中的注意力机制,使其无法提取长距离的动态空间相关性。
表2为各变体模型和ADGCA模型在上海地铁数据集和杭州地铁数据集上的预测结果。其中评估指标值为多步预测的平均值,向下的箭头表示该评估指标下模型的性能相比于ADGCA模型是下降的。在上海地铁数据集中,w/GCN模型预测性能相比于ADGCA模型下降最多,Ema、Erms、Emap值上升了1.49、1.23和1.86,这说明空间多头注意力组件中的注意力机制相比于图卷积网络能够更好地提取交通数据中的空间特征;w/o CausalCon模型预测性能相比于ADGCA模型下降最少,Ema、Erms、Emap值上升了0.31、0.82和0.12,这说明因果卷积对于ADGCA模型的预测性能提升效果有限。在杭州地铁数据集中,w/o TSCMA模型预测性能相比于ADGCA模型下降最多,Ema、Erms、Emap值上升了0.89、2.09和0.34,这说明在更小的杭州地铁数据集中移除时空卷积多头自注意力对模型的预测效果影响明显;预测性能下降最少的变体模型与上海地铁数据集中的一致且具有相同结论。根据预测结果表明,w/o CausalCon、w/o AaptiveDGC和w/o TSCMA变体模型预测性能均低于完整模型,由此可见因果卷积、自适应扩散图卷积和时空卷积多头自注意力组件的有效性;空间多头注意力组件中的注意力机制在提取长距离的动态空间依赖性方面优于GCN,其预测性能低于使用注意力机制的完整模型;w/o SMA模型的预测性能低于完整模型,这表明空间多头注意力模块具有有效性。消融实验结果整体表明,所构建模型具有合理性和有效性。
| 方法 | 上海地铁数据集 | 杭州地铁数据集 | ||||
|---|---|---|---|---|---|---|
| Ema | Erms | Emap | Ema | Erms | Emap | |
| w/o CausalCon | 23.65(0.31↓) | 48.13(0.82↓) | 16.67(0.12↓) | 23.42(0.28↓) | 38.90(0.83↓) | 14.19(0.06↓) |
| w/o AaptiveDGC | 23.84(0.50↓) | 48.29(0.98↓) | 16.82(0.27↓) | 23.45(0.31↓) | 38.98(0.91↓) | 14.25(0.12↓) |
| w/o TSCMA | 24.41(1.08↓) | 48.31(1. 00↓) | 17.61(1.06↓) | 24.03(0.89↓) | 40.16(2.09↓) | 14.47(0.34↓) |
| w/o SMA | 24.56(1.22↓) | 47.94(0.63↓) | 18.48(1.93↓) | 23.43(0.29↓) | 38.31(0.24↓) | 14.35(0.22↓) |
| w/GCN | 24.83(1.49↓) | 48.54(1.23↓) | 18.41(1.86↓) | 23.72(0.58↓) | 39.06(0.99↓) | 14.59(0.46↓) |
| ADGCA | 23.34 | 47.31 | 16.55 | 23.14 | 38.07 | 14.13 |
4 结论
1) 针对交通流数据中复杂的动态时空相关性,提出一种新颖的基于自适应扩散图卷积注意力网络(ADGCA)的建模方法,用于地铁客流预测。
2) 针对现有模型难以同时捕捉交通数据之间的局部和全局动态时空相关性的问题,构建的时空卷积多头自注意力组件,通过引入因果卷积、自适应扩散图卷积和多头注意力机制,能够高效地提取交通数据中局部和全局的动态时空特征,从而提升模型性能。针对大多数现有模型仅基于地铁物理拓扑图捕捉空间相关性的问题,利用构建的多图和自适应矩阵,并结合空间多头自注意力组件和时空卷积多头自注意力组件,能够充分挖掘交通数据中更加真实的空间相关性。
3) ADGCA模型的有效性在上海和杭州2个地铁数据集上得到了验证,实验结果表明ADGCA模型的预测精确度均优于现有的基线模型。
当前研究未能充分考虑外部因素如天气状况和突发事件等对客流量的影响,这可能导致模型在某些情况下的准确性受到限制。未来的研究将综合考虑这些因素,同时考虑将模型扩展到包括天气预报和股票价格预测在内的更广泛的时间序列预测任务中。
Diffusion convolutional recurrent neural network: data-driven traffic forecasting
[EB/OL]. (Spatio-temporal graph convolutional networks: a deep learning framework for traffic forecasting
[C]//Graph wavenet for deep spatial-temporal graph modeling
[C]//Connecting the dots: multivariate time series forecasting with graph neural networks
[C]//ST-GRAT: a novel spatio-temporal graph attention networks for accurately forecasting dynamically changing road speed
[C]//Semi-supervised classification with graph convolutional networks
[EB/OL]. (STG2Seq: spatial-temporal graph to sequence model for multi-step passenger demand forecasting
[C]//LSGCN: long short-term traffic prediction with graph convolutional networks
[C]//唐郑熠,黄嘉欢,王金水等.基于自适应扩散图卷积注意力网络的地铁客流预测[J].铁道科学与工程学报,2024,21(12):4910-4923.
TANG Zhengyi,HUANG Jiahuan,WANG Jinshui,et al.Metro passenger flow prediction based on the adaptive diffusion graph convolution attention network[J].Journal of Railway Science and Engineering,2024,21(12):4910-4923.

