高速列车蓄电池组作为辅助供电系统的备用电源,在动车组架线停电或辅助电源装置出现故障时,为照明、通信及紧急换气等系统提供电源[1-2]。随着列车运行时间的增加,蓄电池性能会不断发生退化直至失效,而蓄电池当前特征量退化至失效阈值的时长或剩余可充放电循环次数被称为蓄电池剩余使用寿命(Remaining Useful Life, RUL)[3]。我国大部分高速列车选用镍镉蓄电池,对其进行RUL预测有利于保障列车行车安全和制定检修方案。关于蓄电池RUL预测的方法可分为等效模型方法和数据驱动方法[4]。等效模型方法通过模拟电池内部物理化学反应以预测电池退化趋势[5],但模型复杂度高、应用难度较大[6];数据驱动方法则从电池外部特性数据中挖掘其性能变化规律,实用性更强[7]。DAI等[8]根据维纳过程分析容量与能量的相关性,建立了具有高精度的镍镉蓄电池二元线性维纳退化模型。XUE等[9]提出了一种融合自适应无迹卡尔曼滤波和遗传算法优化的电池RUL模型,然而在初始化过程中收敛缓慢[10]。KHUMPROM等[11]采用深度神经网络预测锂电池RUL,验证其性能优于向量机和线性回归模型。LI等[12]利用经验模态分解将电池容量分层,提高了长短时记忆网络(Long Short-Term Memory, LSTM)的预测精度,但对超参数调整要求较高。门控循环单元(Gated Recurrent Unit,GRU)继承了LSTM学习序列相关性的能力[13],WEI等[14]采用蒙特卡罗丢弃法来避免GRU对RUL预测过程中的梯度消失和过拟合问题,但前期预测准确度仍有待优化。ARDESHIRI等[15]以GRU作为生成对抗网络(Generative Adversarial Networks, GAN)的生成器,深入挖掘蓄电池数据中的退化信息。尽管基于数据驱动的方法具有学习能力强、适用于非线性系统等优点,然而模型预测效果依赖训练数据集,且对于不同劣化程度的蓄电池RUL预测效果并不理想[16]。相比锂电池、铅酸电池等,镍镉蓄电池自放电率高、存在“记忆效应”。自放电是指电池在非工作状态下的容量自然损失现象;记忆效应是指镍镉蓄电池若在不完全放电时开始下一次充电,则会缩短下一次最大放电能量,且这一过程可以累积。较大的自放电率和不能完全消除的记忆效应,致使镍镉蓄电池健康特征与容量间表现出更复杂的映射关系。此外,目前没有高速列车镍镉蓄电池的开源大样本数据,且获取实际工况监测数据存在困难,周期过长,进而难以支持建立具有高精度和泛化性能的蓄电池寿命模型。因此,本文依据《TB/T 3061—2016》进行了镍镉蓄电池循环寿命实验,获得模拟失效过程的电池退化数据集,进一步挖掘所包含的关于蓄电池退化的信息。本文设计了能学习时间序列相关性的时序对抗生成网络(Time-series Generative Adversarial Network, TimeGAN)[17]对电池退化数据进行数据增强,并采用分类分数、预测分数、主成分分析(Principal Component Analysis, PCA)和t-分布随机邻域嵌入(t-distributed Stochastic Neighbor Embedding, t-SNE)对其结果进行评价。在此基础上,利用GRU对镍镉蓄电池RUL进行预测,并验证其泛化性能和预测精度。
1 基于TimeGAN-GRU的镉镍蓄电池RUL预测设计
根据《TB/T 3061—2016》规定,高速列车镍镉蓄电池容量退化至初始容量的70%可判定其失效,根据蓄电池特性分析可将容量失效阈值换算为健康状态(State of Health, SOH)失效阈值[18]。SOH反映电池当前容量能力,体现了电池健康状态长期变化的特征[19],因此本文将镍镉蓄电池循环寿命实验的SOH序列数据作为RUL预测模型的数据支撑。
1.1 基于TimeGAN的数据增强方法
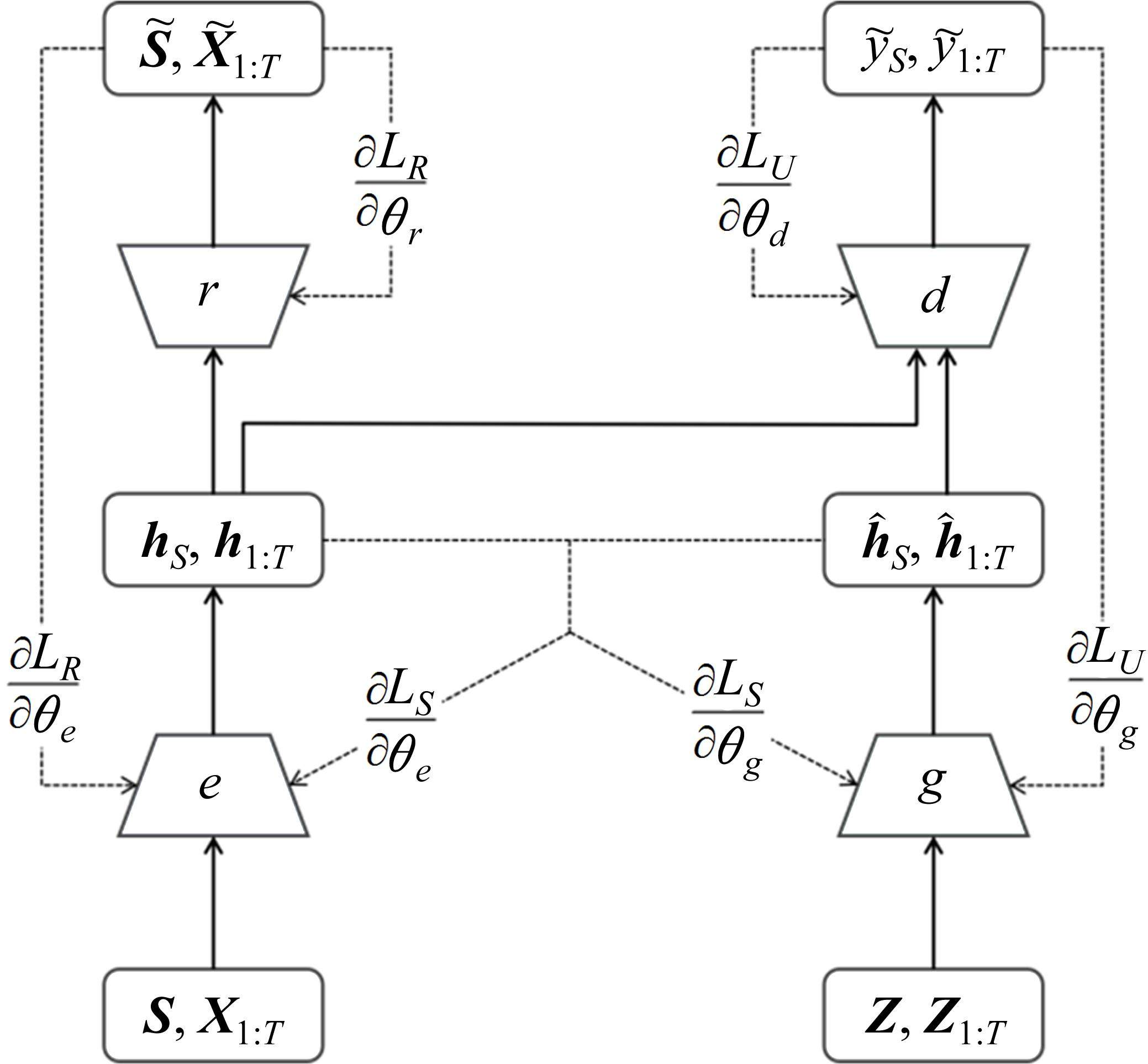
为了提高现有实验数据规模和质量以改善模型预测精确性,需要对镍镉蓄电池数据进行增强。原始GAN通过无监督学习实现少量样本数据增强,但镍镉蓄电池老化数据具有小样本特点,也具有复杂的时间序列自相关性,因此采用无监督学习结合有监督学习的TimeGAN来实现镍镉蓄电池SOH数据增强。TimeGAN无监督地捕获序列的静态分布特征,同时有监督地捕获序列的时间动态特征,通过自编码网络和对抗生成网络联合编码训练,实现有效的数据增强效果。TimeGAN具体结构如图1所示。
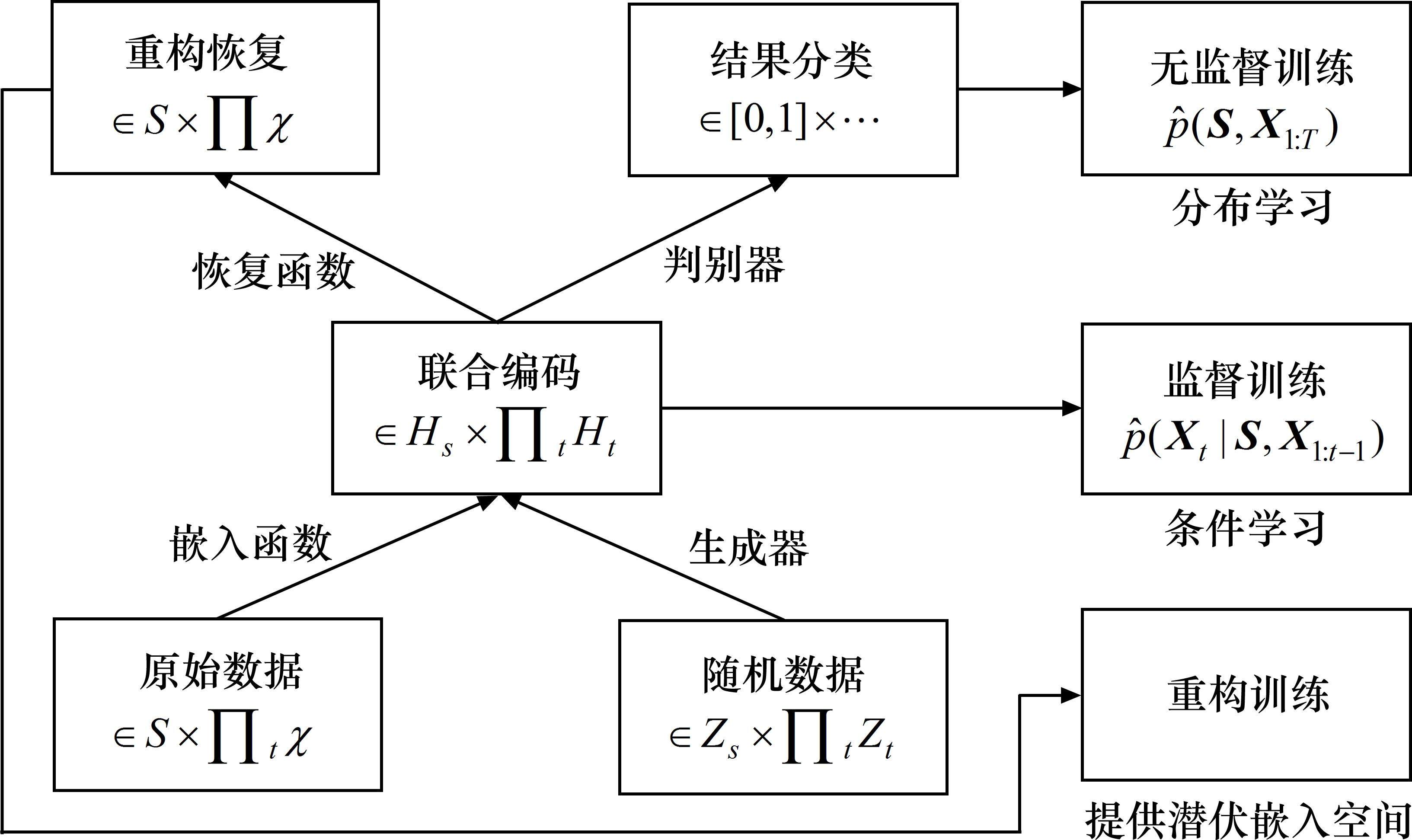
1.1.1 构建自编码网络
首先分别设计自编码网络的嵌入函数和恢复函数。
1) 嵌入函数将高维度SOH数据降维以便学习其隐含特性。设S与X分别表示真实SOH数据静态特征向量空间S和时态特征向量空间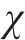
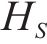
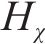
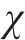
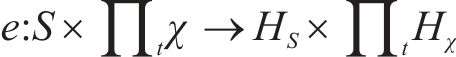
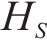
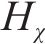
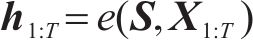
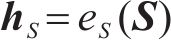
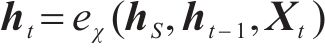
式中: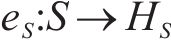
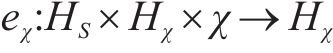
2) 恢复函数
恢复函数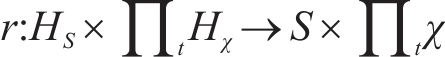
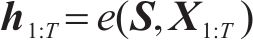
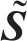
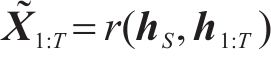
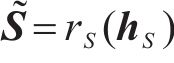
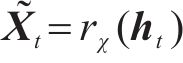
式中: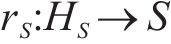
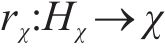
1.1.2 构建对抗生成网络
对抗生成网络能够在低维空间学习降维后SOH数据的隐含时序特性,其生成器和判别器二者相互对抗直至达到纳什均衡[20]。
1) 生成器
生成器负责模拟真实数据分布,生成虚假数据集。本文采用高斯分布作为生成器的输入进行数据生成。ZS和ZX表示随机向量空间,生成器函数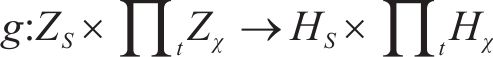
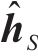
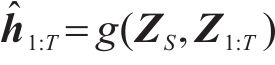
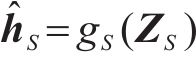
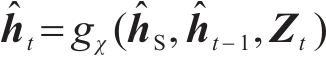
式中: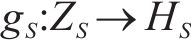
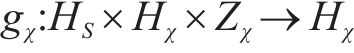
2) 判别器
判别器负责在隐含空间识别输入的模拟SOH数据与真实SOH数据被分类为真实数据的概率值。判别器函数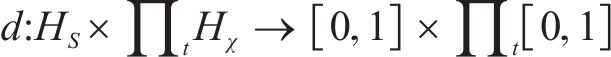
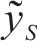
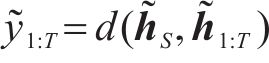
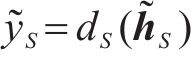
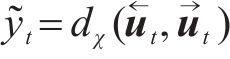
式中: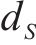
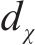


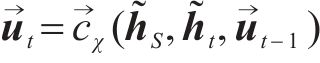
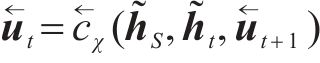
式中: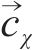
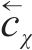
1.1.3 构建损失函数
根据自编码网络和生成对抗网络,构建TimeGAN的损失函数:重构损失、无监督损失和监督损失。
1) 重构损失函数
重构损失LR用于训练嵌入函数和恢复函数,以便构建特征空间与隐含空间之间的可逆映射,表示为:
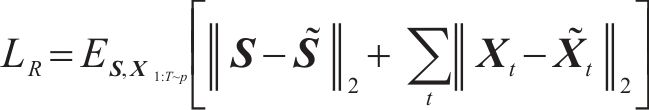
2) 无监督损失函数
TimeGAN中判别器用来最大化判别输入数据是真实数据或模拟数据,则该无监督损失LU可表示为:
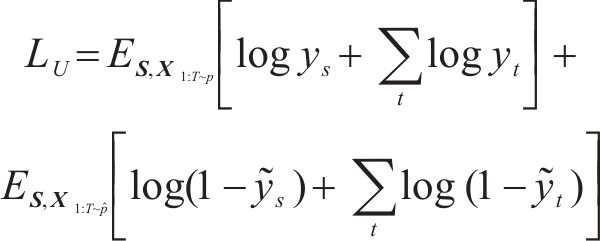
3) 监督损失函数
TimeGAN选择最大似然来监督损失LS,保障模拟数据分布逼近真实数据分布,表示为:
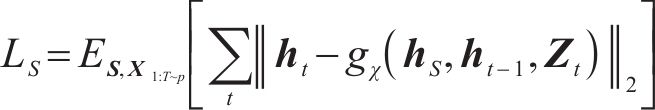
综上所述,基于TimeGAN的镍镉蓄电池SOH数据增强模型联合训练流程如图2所示。
1.2 基于GRU的序列学习算法
GRU继承了LSTM对于长时间序列间依赖关系的捕捉能力,具有结构简单、运算效率高等优点,故采用GRU学习蓄电池SOH数据的时间序列相关性。本文将模拟SOH数据和真实SOH数据混合重构,利用GRU训练重构数据集以建立蓄电池RUL预测模型。GRU由更新门和重置门构成,其结构如图3所示。
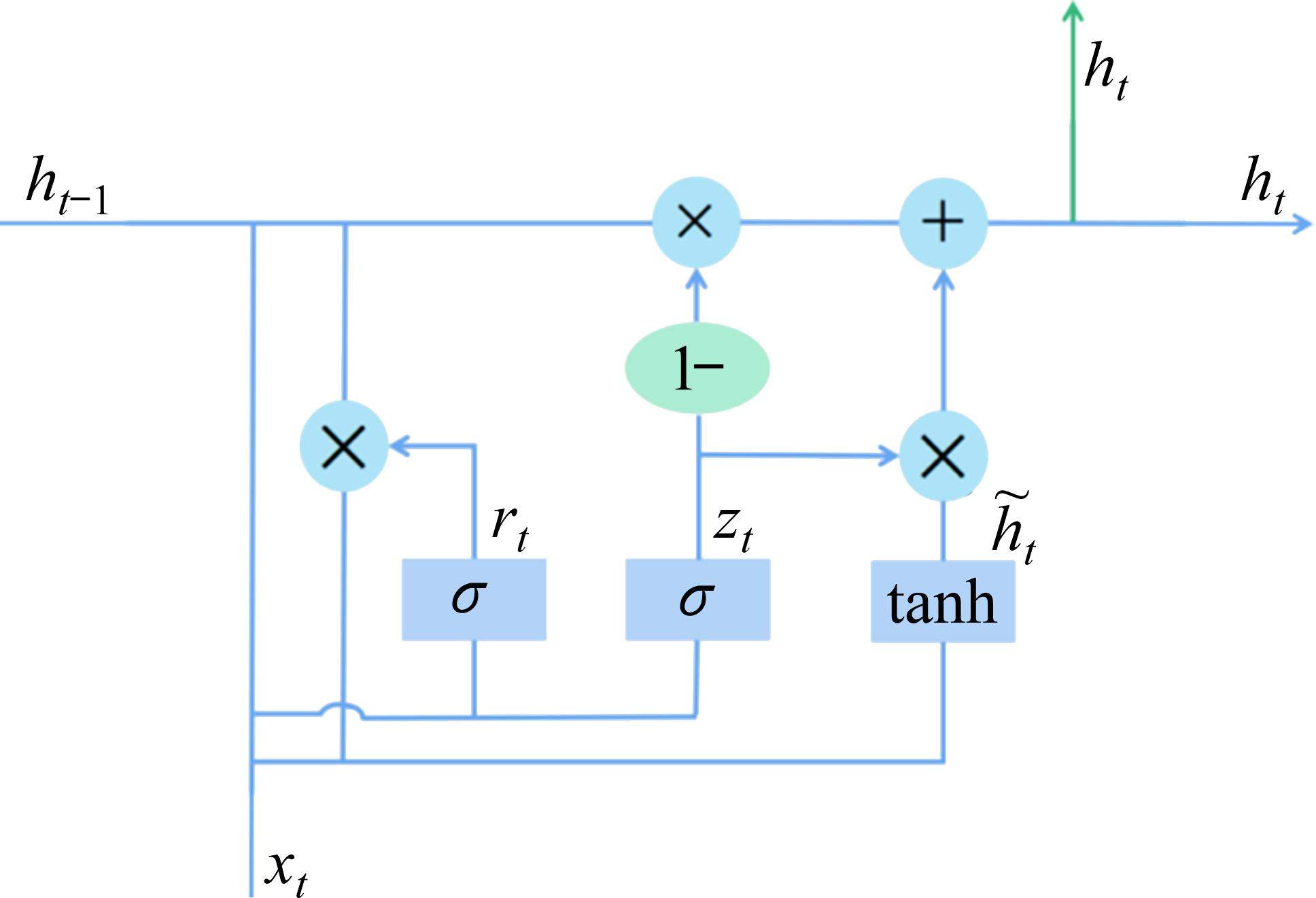
其中,更新门控制历史状态信息进入当前状态的程度,更新门的值越小表明历史状态信息进入得越少,而重置门控制历史状态信息写入当前候选隐藏状态的程度。GRU通过更新门控制前一时刻的隐藏状态和当前时刻的候选隐藏状态,不仅能够学习SOH序列数据的自相关性,同时还能够解决梯度消失问题。
1) 重置门
首先构建重置门,用于控制t时刻SOH输入xt与t-1时刻隐藏状态ht-1的写入程度,可表示如下:
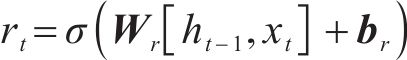
式中:rt为t时刻的重置门输出,其输出区间为[0,1],代表信息保留程度;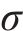
2) 更新门
其次构建更新门,用于控制当前状态信息传递程度,可表示如下:
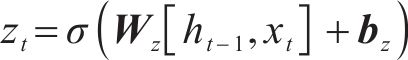
式中:zt为t时刻的更新门输出,其输出区间为[0,1],同样代表信息保留程度;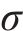
3) 输出隐藏状态
因此,t时刻的候选隐藏状态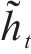
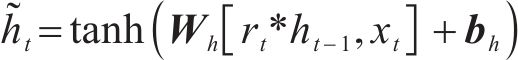
式中:rt为t时刻的重置门输出;tanh为激活函数;Wh为更新门的权重矩阵;bh为更新门的偏置矩阵;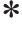
根据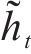
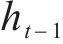
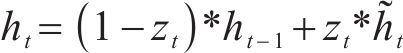
1.3 融合TimeGAN-GRU的镍镉蓄电池RUL预测
为了实现镍镉蓄电池RUL的准确预测,首先采用TimeGAN方法对小样本镍镉蓄电池SOH数据进行有效增强,并采用多方面指标验证模拟数据的有效性;其次,在增强后的数据基础上采用GRU方法学习序列分布并建立蓄电池RUL预测模型,建立完整的镍镉蓄电池RUL模型;最后,通过高速列车实际拆卸的四级修蓄电池SOH数据作为测试集,以验证模型的精确性和泛化性能。基于TimeGAN-GRU的蓄电池RUL预测整体流程如图4所示,具体步骤如下。
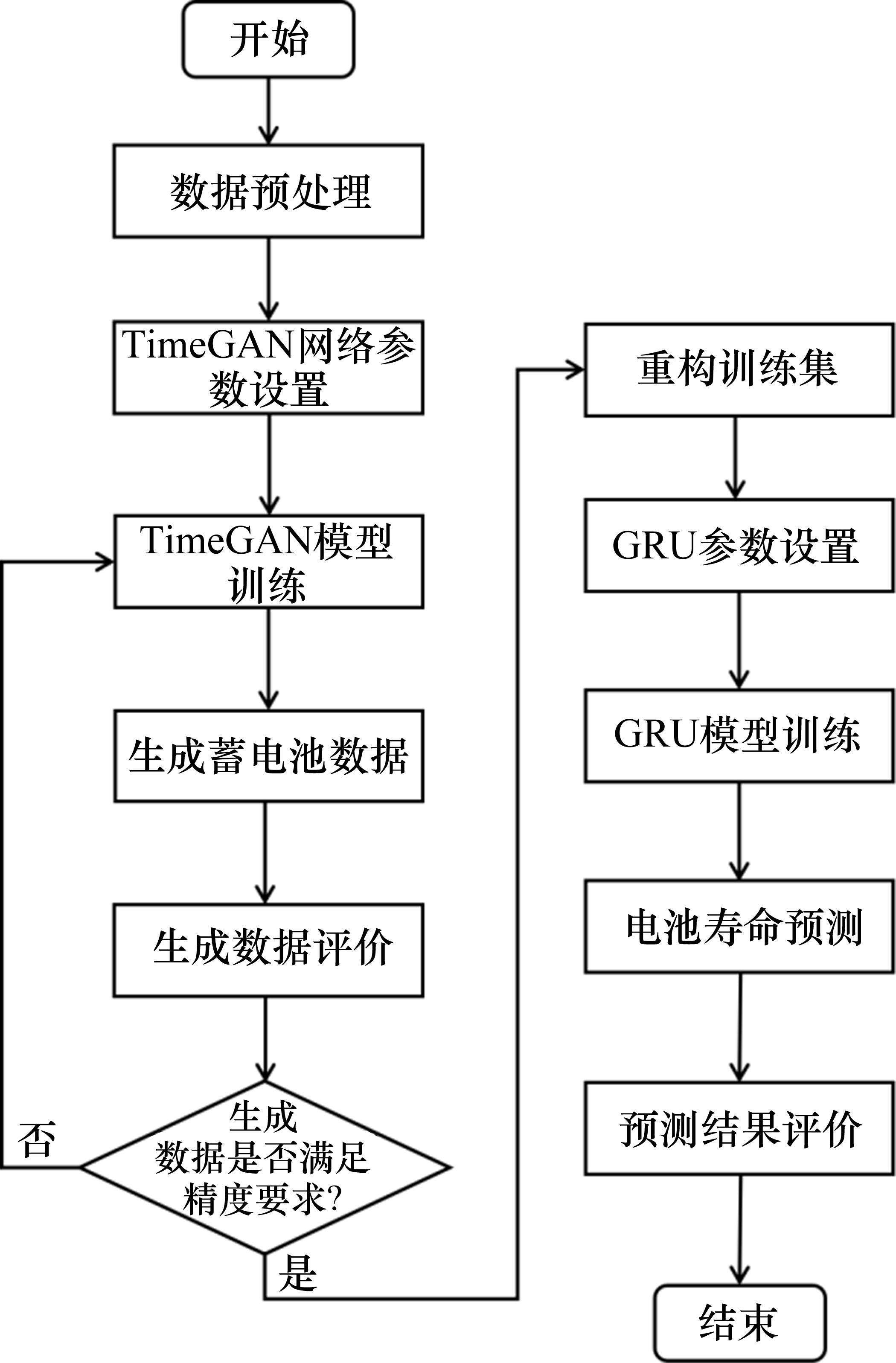
1) 数据预处理。选取全新蓄电池和四级修蓄电池SOH数据为样本进行归一化,设置随机分布向量。
2) TimeGAN网络参数设置。选择TimeGAN中嵌入网络、恢复网络、生成器网络和判别器网络,并设置神经网络的输入及输出神经元数量、隐藏层数、隐藏层神经元、迭代次数等参数。
3) TimeGAN模型训练。选取全新蓄电池真实SOH数据和随机分布向量作为TimeGAN的输入,首先训练自编码网络以优化重构过程,再优化监督损失以学习序列相关性,最后联合训练自编码网络和对抗生成网络。
4) 生成数据及评价。通过TimeGAN模型生成模拟SOH数据,并采用分类分数、预测分数、PCA和t-SNE对其进行评价。
5) 迭代判断。根据评价指标判断模拟数据是否满足精度要求,若满足要求则前往下一步骤,若不满足要求则返回步骤3。
6) 重构训练集和GRU参数设置。将真实SOH数据和模拟SOH数据混合重构,设置GRU网络的输入及输出神经元数量、隐藏层数、隐藏层神经元、迭代次数等参数。
7) GRU模型训练。将重构训练集输入GRU模型,迭代至满足精度或达到迭代次数为止。
8) RUL预测及结果评价。利用GRU模型对四级修蓄电池SOH变化趋势进行预测,直至SOH衰减到失效阈值的70%,从而得到四级修蓄电池的RUL,并采用多个指标对预测结果进行评价。
2 实验验证
2.1 获取数据集
根据《TB/T 3061—2016》规定,高速列车镍镉蓄电池容量失效阈值为初始容量的70%。根据式(18)可计算蓄电池SOH失效阈值为70%:
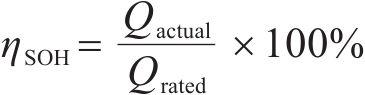
式中:Qactual表示当前蓄电池测量容量;Qrated表示该蓄电池初始容量。
依据《TB/T 3061—2016》展开循环寿命实验,选取全新镍镉蓄电池和四级修镍镉蓄电池作为研究对象,得到全新蓄电池与四级修蓄电池SOH曲线,如图5所示。
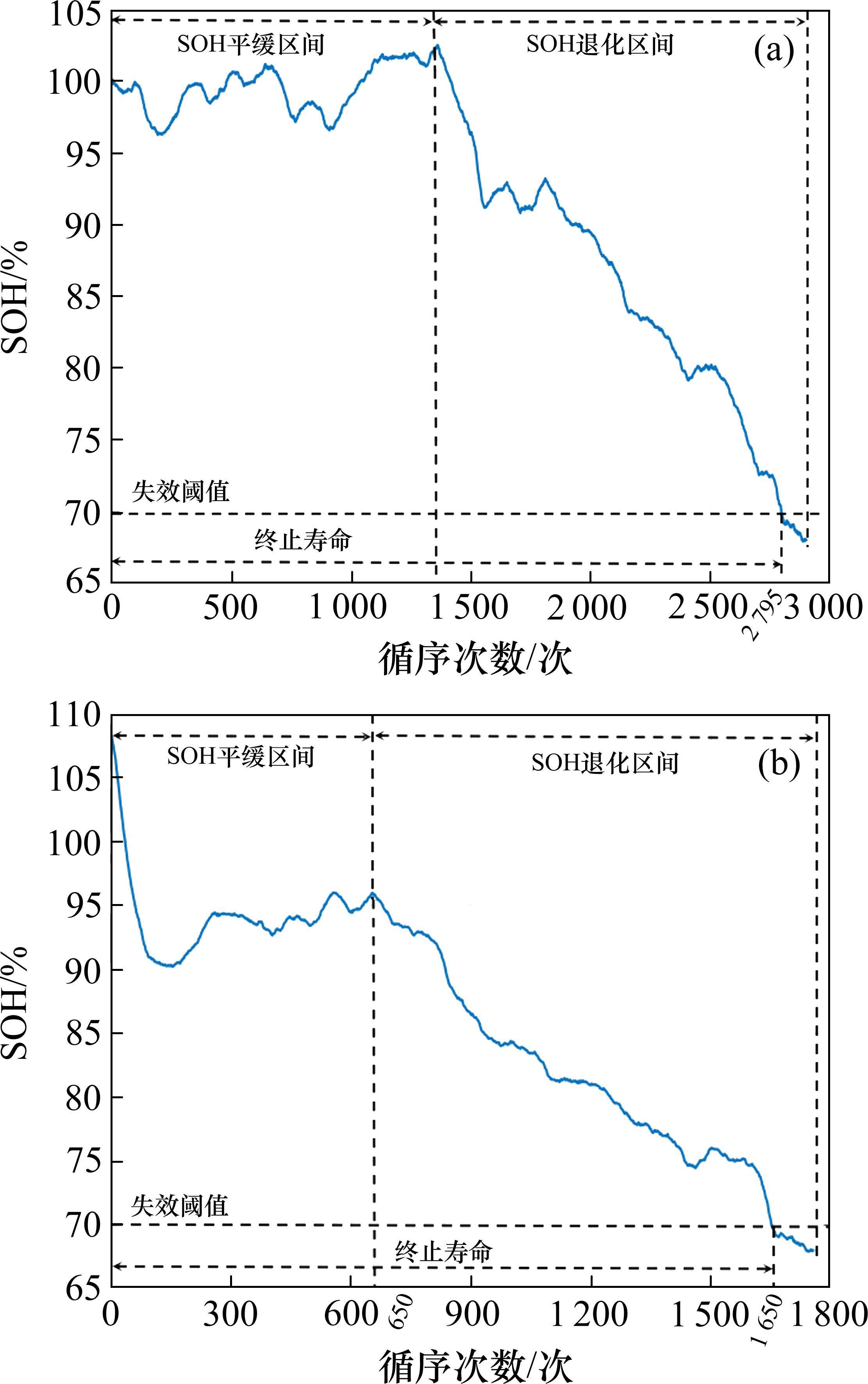
从图5可以看出,以70%为失效阈值,全新蓄电池、四级修蓄电池的终止寿命分别为2 795次、1 650次循环,两者在前期一段平缓区间内SOH基本保持不变,而在后续退化区间内SOH的衰减趋势相似。另一方面可以看出,由于镍镉蓄电池个体差异,2组数据的变化趋势不完全一致,此时若仅仅采用全新蓄电池SOH数据建立模型来预测四级修蓄电池SOH变化,结果将存在较大差异,即模型泛化性能不佳。
因此,前文选择使用全新蓄电池SOH数据训练TimeGAN-GRU镍镉蓄电池RUL预测模型,使用四级修蓄电池SOH数据评价该预测模型的设计是合理的。
2.2 TimeGAN模型数据生成结果分析
本文TimeGAN中的嵌入网络、恢复网络、生成器和判别器均由LSTM构成,其网络结构如表1所示。设置TimeGAN训练参数,包括序列长度为10,迭代次数为30 000,最小批次数为128。
| 层数 | 名称 | 嵌入网络及生成器 | 恢复网络 | 判别器网络 | |||
|---|---|---|---|---|---|---|---|
| 神经元数量 | 激活函数 | 神经元数量 | 激活函数 | 神经元数量 | 激活函数 | ||
| 0 | 输入层 | 1 | 1 | 1 | |||
| 1 | LSTM | 20 | tanh | 20 | tanh | 20 | tanh |
| 2 | LSTM | 20 | tanh | 20 | tanh | 20 | tanh |
| 3 | 全连接层 | 20 | sigmoid | 1 | sigmoid | 1 | None |
为检验模型性能,采用分类分数、预测分数、PCA和t-SNE方法对TimeGAN生成数据进行评价。
2.2.1 分类分数评价
分类分数方法对真实数据和模拟数据进行分类,标签为1表示完全判定为真实样本,标签为0表示完全判定为生成样本。本文选择GRU网络进行分类,部分标签为1的真实SOH数据和部分标签为0的模拟SOH数据构成其训练集,剩余数据则构成测试集,二者比例为4∶1。分类结果的混淆矩阵如表2。
| 真实数据(预测) | 生成数据(预测) | |
|---|---|---|
| 真实数据(实际) | 67 | 152 |
| 生成数据(实际) | 75 | 144 |
表2显示,真实样本和生成样本的样本数据非常接近,表明分类网络无法判别输入样本是真实样本或生成样本,即TimeGAN模型较好捕捉了真实SOH数据的分布规律,并生成了与之相似的数据。
进一步分析分类结果混淆矩阵,计算分类结果的分类分数,计算式如下:
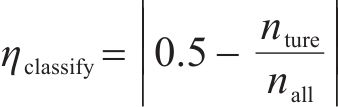
式中:
2.2.2 预测分数评价
预测分数方法同样采用GRU网络进行分析,以模拟SOH数据作为训练集,以真实SOH数据作为验证集建立SOH预测模型,其预测结果如图6所示。可以得知,SOH预测值与实际值相差较小,此时采用平均绝对误差(Mean Absolute Error,MAE)作为预测分数,计算公式如下:
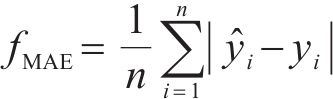
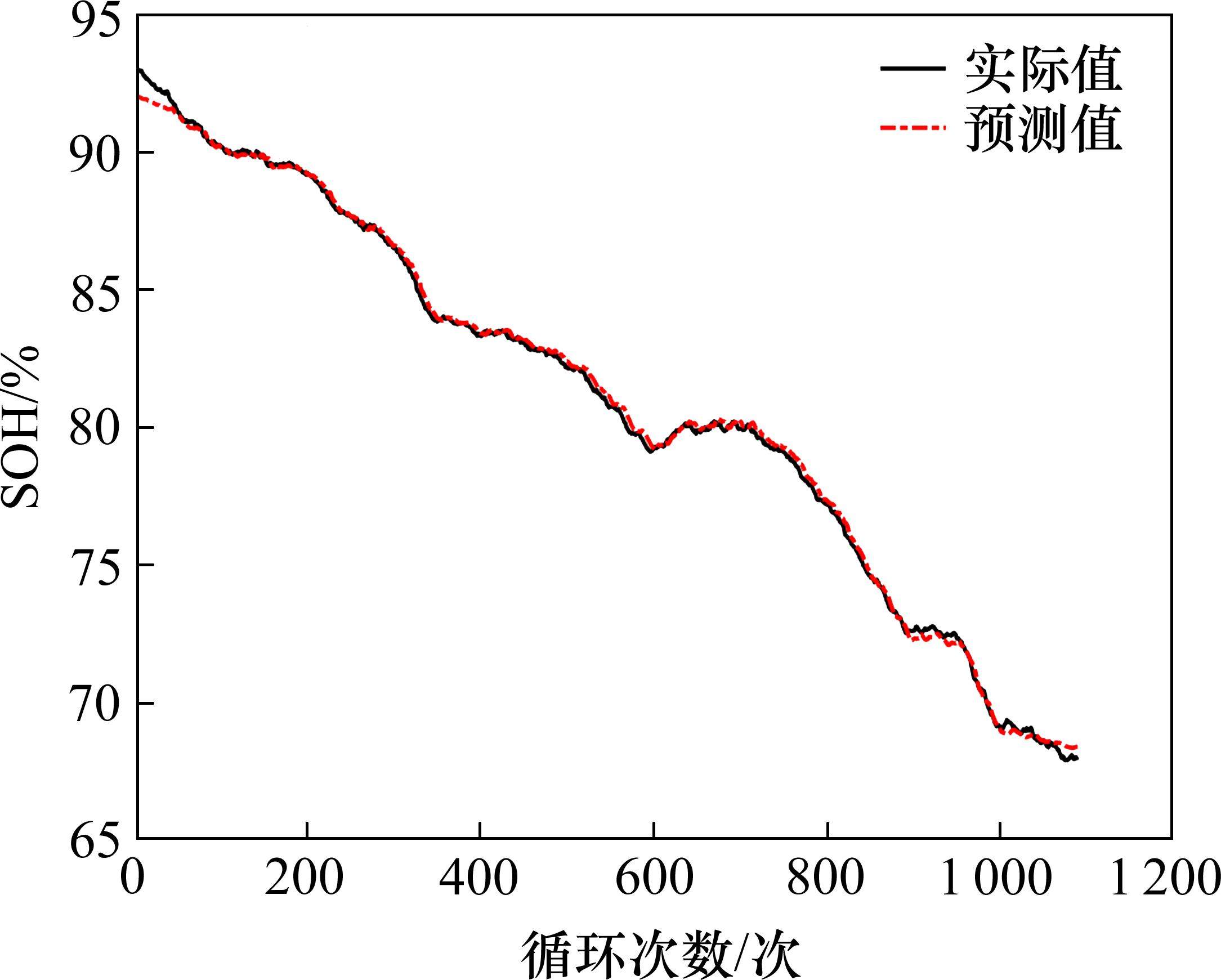
通过式(20)计算得到生成数据的预测分数为0.189 2,数值较小表明模型预测效果较好,即TimeGAN生成效果较好。
2.2.3 PCA与t-SNE评价
PCA通过正交变换将数据分解为一组互不相关的变量,用以反映数据的主要信息。t-SNE则是利用高斯分布将高维数据点之间的距离换算为概率分布,并在低维空间进行可视化。PCA和t-SNE都是数据降维分析,其中PCA着重于分析2组数据的整体分布特征,而t-SNE则更着重于分析2组数据的局部分布特征。对模拟SOH数据和真实SOH数据进行PCA和t-SNE分析,结果如图7所示。
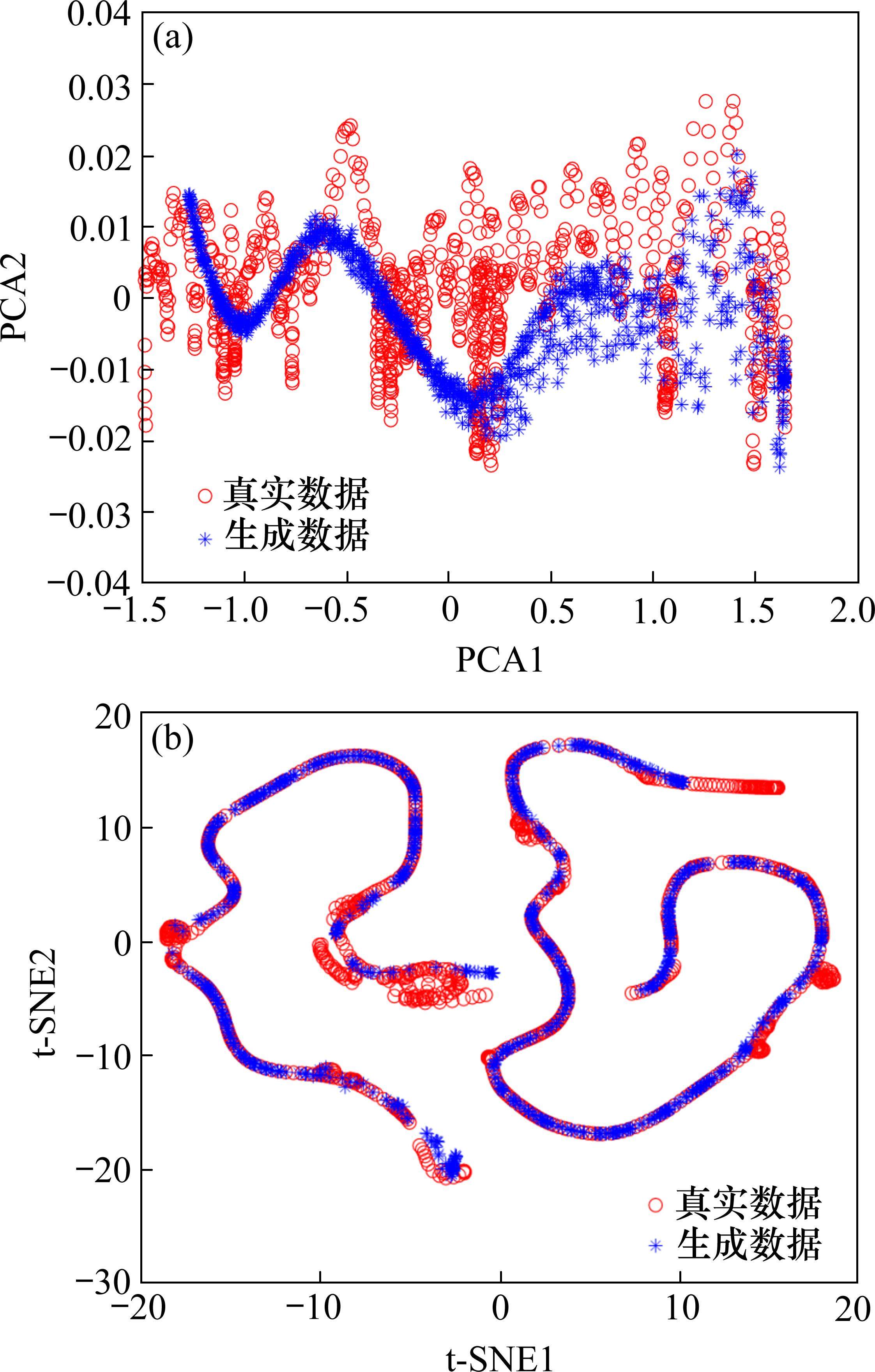
如图7(a)所示,真实数据和模拟数据PCA结果的第1主成分重合部分较多,第2主成分有所差异,但第1主成分的数量级远大于第2主成分,因此主要考虑第1主成分。由此得出:真实数据与模拟数据第1主成分分布相近,两者具有较好的相似性。如图7(b)所示,t-SNE分析结果显示真实数据与模拟数据有大量重合,两者的分布极其相似,表明拥有相似的分布规律。
综上,通过分类分数、预测分数、PCA和t-SNE分析可知,TimeGAN生成数据具有较好的效果。
2.3 融合TimeGAN-GRU模型预测结果
将真实数据与模拟数据混合重构,设置GRU网络结构,隐藏层数量为3,隐藏层神经元数量为15,学习率为0.001 5,输入长度为7,预测步长为3,迭代次数为500,最小批次数为128,如表3所示。
| 层数 | 名称 | 神经元数量 | 激活函数 |
|---|---|---|---|
| 0 | 输入层 | 7 | |
| 1 | GRU层 | 15 | tanh |
| 2 | GRU层 | 15 | tanh |
| 3 | GRU层 | 15 | tanh |
| 3 | 全连接层 | 3 | linear |
为了验证TimeGAN-GRU在蓄电池寿命预测上的优势,使用未经数据增强的全新蓄电池SOH数据训练GRU和LSTM,在不同预测起点的情况下对比TimeGAN-GRU、GRU和LSTM这3种方法预测四级修镍镉蓄电池寿命的效果。以上3种方法的四级修蓄电池寿命预测结果分别如图8~图10所示。
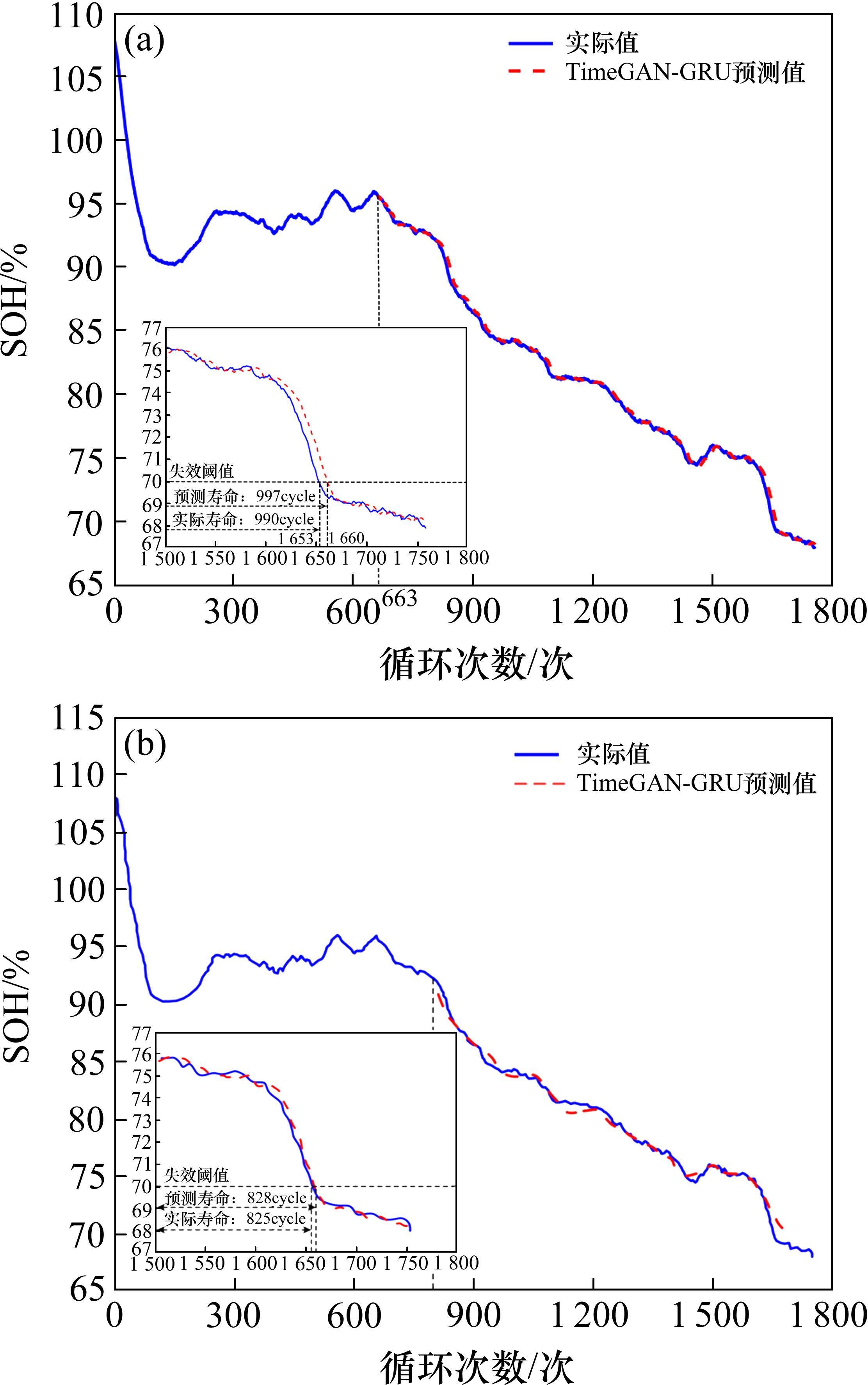
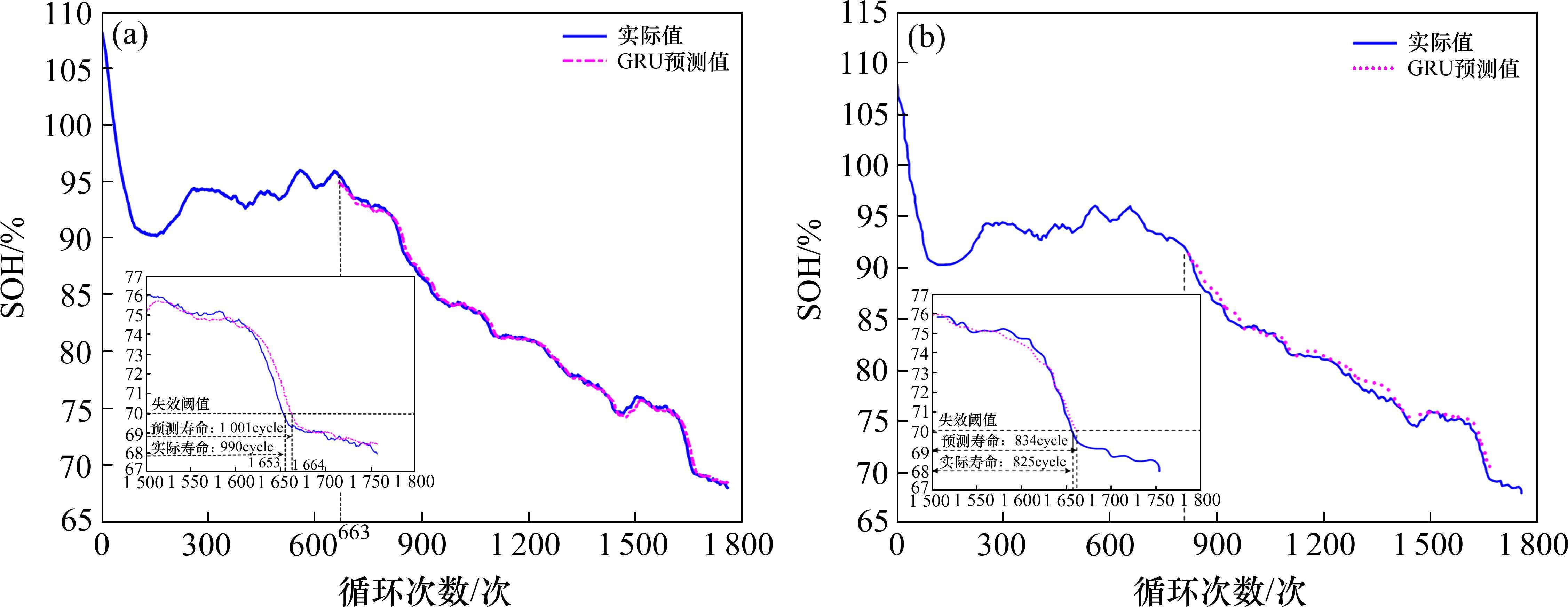
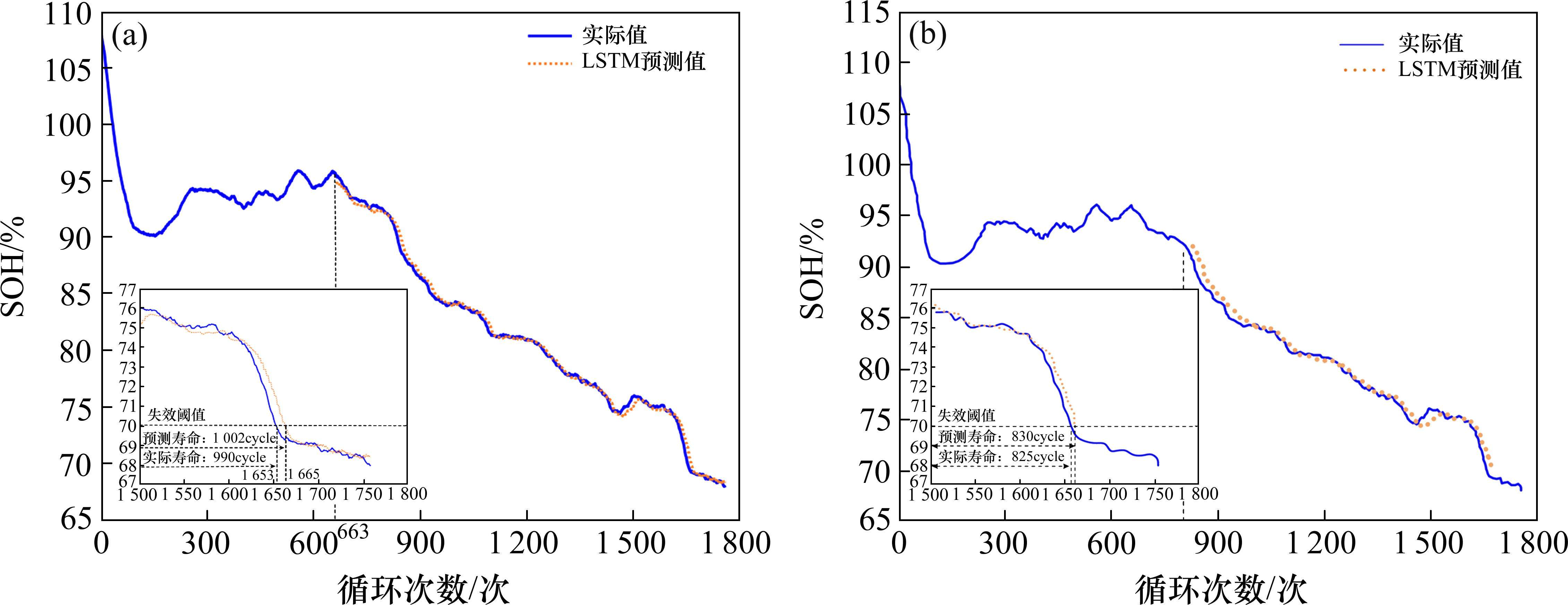
由图8~图10可知,3种方法均能预测出四级修蓄电池SOH的变化趋势,但在预测起始阶段,GRU和LSTM存在较大的预测误差,因此就整体而言,TimeGAN-GRU更能精确预测RUL。
当预测起点为第663次循环时,电池实际寿命为987次循环,TimeGAN-GRU、GRU和LSTM的预测寿命分别为997、1 001和1 002次循环,预测结果的绝对误差和相对误差如表4所示。据表4可知,3种模型的绝对误差均不超过15cycle,表明模型具有一定的预测准确度。对比GRU和LSTM,TimeGAN-GRU预测结果的相对误差降低了0.405 2个百分点和0.506 6个百分点,表明利用TimeGAN进行数据增强可以提高模型的精确性。
| 预测算法 | 实际寿 命/cycle | 预测寿 命/cycle | 绝对误 差/cycle | 相对误差/% |
|---|---|---|---|---|
| TimeGAN-GRU | 987 | 997 | 10 | 1.013 2 |
| GRU | 987 | 100 1 | 14 | 1.418 4 |
| LSTM | 987 | 100 2 | 15 | 1.519 8 |
此外,采用对异常值敏感的均方误差(Mean Square Error, MSE)指标验证预测起点663次循环后预测值与真实值偏离程度:
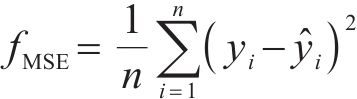
TimeGAN-GRU、GRU、LSTM模型的MSE计算结果分别为0.026 53、0.048 12、0.051 69,TimeGAN-GRU相比后两者预测模型分别减少了44.85%和48.67%,3种预测模型MSE值均趋近于0,说明在预测起点为825cycle时,模型具有一定的准确性,而TimeGAN-GRU预测模型准确度相较于后两者提升显著。
当预测起点为第825次循环时,蓄电池实际寿命为825次循环,TimeGAN-GRU、GRU和LSTM的预测寿命分别为828、834、830次循环,预测结果的绝对误差和相对误差如表5所示。据表5可知,3种模型的绝对误差均不超过10cycle,表明模型具有一定的预测准确度。对比GRU和LSTM,TimeGAN-GRU预测结果的相对误差降低了0.727 5个百分点和0.303 1个百分点,表明利用TimeGAN进行数据增强可以提高模型的精确性。
| 预测算法 | 实际寿 命/cycle | 预测寿 命/cycle | 绝对误 差/cycle | 相对误差/% |
|---|---|---|---|---|
| TimeGAN-GRU | 825 | 828 | 3 | 0.363 6 |
| GRU | 825 | 834 | 9 | 1.091 1 |
| LSTM | 825 | 830 | 5 | 0.666 7 |
同样地,采用MSE指标验证预测起点为825次循环时的预测值与真实值的偏离程度。TimeGAN-GRU、GRU、LSTM模型的MSE计算结果分别为0.010 65、0.022 71、0.014 39,以上MSE值均趋近于0,表明在预测起点为825cycle时,3种预测模型表现出很好的准确性,TimeGAN-GRU相比后两者,预测模型分别减少了53.10%、25.99%,说明其依然具有相对更佳的预测效果。
根据不同预测起点的3种方法预测结果对比分析可知:
1) 随着预测起点延后、算法学习过程增加,TimeGAN-GRU、GRU、LSTM模型的预测RUL绝对误差周期、相对误差与MSE值均有所减小,即模型预测准确度均得到了提升,表明用于训练的数据越多,3种模型预测效果越好。
2) 同一预测起点下,TimeGAN-GRU模型相对GRU和LSTM都能表现出更好的预测效果,并且随着预测起点延后,TimeGAN-GRU模型相对GRU预测效果提升程度也有所增大,表明其泛化性更优。
3) 在相同预测效果目标的情况下,TimeGAN-GRU模型相对GRU和LSTM所需的训练数据规模更小,表明其能够更好地适应小样本镍镉蓄电池RUL预测,同时具有更好的镍镉蓄电池RUL在线估计能力。
本文采用四级修镍镉蓄电池实验数据作为验证,在预测起点为663cycle/825cycle时,采用了3种模型预测蓄电池RUL,结果表明相较于未利用TimeGAN进行数据增强的GRU和LSTM模型,TimeGAN-GRU预测模型具有更高的精确度,表明TimeGAN进行数据增强可以提高蓄电池RUL预测模型的精确性和泛化性。
3 结论
1) 针对高速列车镍铬碱性蓄电池性能退化现象,实现了以全新蓄电池对实际工况蓄电池的性能预测,完善了对其剩余寿命预测算法的研究,为高速列车镍镉电池检修方案的制定提供理论支撑。
2) 针对小样本蓄电池实验数据导致模型精确性和泛化性差的问题,本文采用TimeGAN学习原始数据分布用于生成数据,将二者混合重构,提高了数据规模和质量。
3) 在TimeGAN数据增强的基础上,利用GRU建立蓄电池RUL预测模型,并通过四级修蓄电池实验数据对其进行验证,结果表明在不同预测起点情况下,相较于GRU和LSTM,基于TimeGAN-GRU的镍镉蓄电池RUL预测模型具有更高的精确性和泛化性。
4) 在相同预测效果目标的情况下,TimeGAN-GRU模型相对GRU、LSTM能够更好地适应小样本镍镉蓄电池RUL预测,具有更好的RUL在线估计能力。
于天剑,杨雨萌,刘海涛等.基于TimeGAN-GRU的镍镉蓄电池RUL预测[J].铁道科学与工程学报,2024,21(12):4899-4909.
YU Tianjian,YANG Yumeng,LIU Haitao,et al.TimeGAN-GRU method for RUL prediction of Ni-Cd battery[J].Journal of Railway Science and Engineering,2024,21(12):4899-4909.

