在我国“双碳”战略目标和国家发展改革委员会“三改”联动节能降耗改造要求下,需要提升锅炉效率、减少污染物的生成量和排放量。通过使用大数据和人工智能的方法,建立具有准确预测能力的锅炉燃烧系统预测模型有助于锅炉的控制参数优化[1]。
氮氧化物NOx是燃煤锅炉生成的一种主要污染物[2-3],相比于飞灰含碳量和灰渣含碳量,NOx在锅炉运行中的采样频率更高,与很多无法实时、高频、精确获取参数的锅炉相比,NOx生成量具有更好的实时性和更高的准确性,因此,可将NOx作为锅炉燃烧系统建模的目标变量。但锅炉燃烧系统具有延迟高和多变量耦合的特点[4-5],NOx的形成机理较复杂且受多种因素(如煤质参数、热负荷、风煤比、配风方式炉膛温度等[6-9])的影响,用简单的数学模型难以进行描述,可以通过机器学习的方法构建准确的NOx生成量与各输入变量之间的关系模型[10]。
目前已经有大量研究学者将机器学习的各类算法应用到锅炉燃烧系统建模中。唐振浩等[11]以神经网络、多层感知器(multilayer perceptron, MLP)等算法建立基模型,以回声状态网络为元模型,使用5折交叉验证对基学习器和元学习器进行验证,构建了Stacking集成学习NOx排放浓度预测模型,该模型能够对锅炉NOx排放浓度实现精准预测。许烨烽[12]基于MLP和火焰辐射图像,针对乙烯层流火焰建立了一维径向温度场的模型,该模型具有较强的预测能力及抗噪能力。张佳宁[13]为了优化NOx模型,构建了多个模型(例如MLP神经网络模型)并进行对比,使用网格搜索对模型的超参数进行优化。XU等[14]基于改进的生物地理优化的长短期记忆神经网络,使用相似性测量方法,建立了锅炉的自适应动态燃烧模型,并使用改进的非支配排序遗传算法-II对锅炉燃烧系统控制参数进行优化。
蓝茂蔚等[15]提出了一种改进的蚂蚁-粒子群算法,用于向量机模型超参数的优化,通过与蚁群算法移动规则的结合改进粒子群(particle swam optimization, PSO)算法,克服了PSO算法容易陷于局部最优解的缺点,以找到全局最优解。相比于原始的PSO算法,改进的蚂蚁-粒子群算法具有更快的收敛速度和更高的预测精度。董凌霄等[16]通过数值模拟得到数据集,以交叉验证结果为目标函数,利用贝叶斯优化方法对超参数进行优化,以支持向量机、提升树和决策树3种算法作为初选模型,最终选择支持向量机算法作为模型,建立了具有较高预测精度和较强泛化能力的水冷壁热流密度分布预测模型。
TURNER等[17]阐述了超参数优化对于模型性能的重要性,BERGSTRA等[18]指出模型超参数优化是大型模型面临的一个重要问题,除了对机器学习策略和建模算法进行改进外,对模型超参数的搜索也能够大幅提升模型性能。PSO算法是一种给定搜索方向的随机搜索方法,以全局历史最优搜索结果和各粒子最优搜索结果为方向进行搜索,但PSO算法的搜索能力受到多个超参数的制约,容易陷入局部最优解中。模型超参数优化常用的随机搜索没有明确的搜索方向,在参数空间中可能需要大量的评估次数,导致搜索效率较低。网格搜索将参数空间划分为固定的网格,若网格稀疏,则可能会错过一些最优解,若网格较密,则导致计算量大,难以用于高维空间搜索。未对模型超参数进行深入优化可能导致对模型和算法的性能评估产生影响,因此,需对建模流程的各个环节进行客观、准确的对比和评价,本文使用贝叶斯超参数优化方法对高度复杂和计算成本较高的目标函数根据观测结果建立目标函数的概率分布估计模型,用于调整超参数搜索方向,对锅炉燃烧系统的模型参数进行更好地优化[19]。
在进行数据集的划分时,大多数研究者没有充分考虑锅炉系统的时序特性,对数据集采用了随机划分的方式,使不满足数据独立同分布的时序数据模型在训练集和测试集上的评价指标很好,但实际应用时精度很低,出现了数据泄漏[20-23],此时,建模和评估流程中获得的模型评价结果难以很好地反映模型在实际中的真实性能。当对锅炉的运行数据进行采样时,对于较稳定的工况,相邻采样点之间的记录是相似的,若采取随机方式划分数据集,相似的记录大概率同时出现在训练集和测试集中,此时,测试数据泄漏到训练数据中,导致模型在测试集上的测试结果非常好,但在实际应用中,模型的预测精度大幅下降,低于测试结果得出模型NOx生成量的预测。
针对随机数据集划分导致的数据泄露问题,本研究提出采用时序数据集划分方式对数据集进行划分。将交叉验证评分作为模型超参数优化的目标函数,交叉验证的数据子集采用时序数据集划分方式,即进行时序交叉验证。为了验证基于时序数据集划分和时序交叉验证方法的有效性,本研究对比了时序模型在随机森林(random forest, RF)、支持向量回归机(support vector regression, SVR)、多层感知器(MLP)、弹性网络回归(Elastic Net, EN)这4种常用建模算法下的性能,并且划分了一个独立的进一步测试数据集,用于模拟和测试模型NOx生成量在应用时的实际精度。
1 模型算法
1.1 时序数据集划分
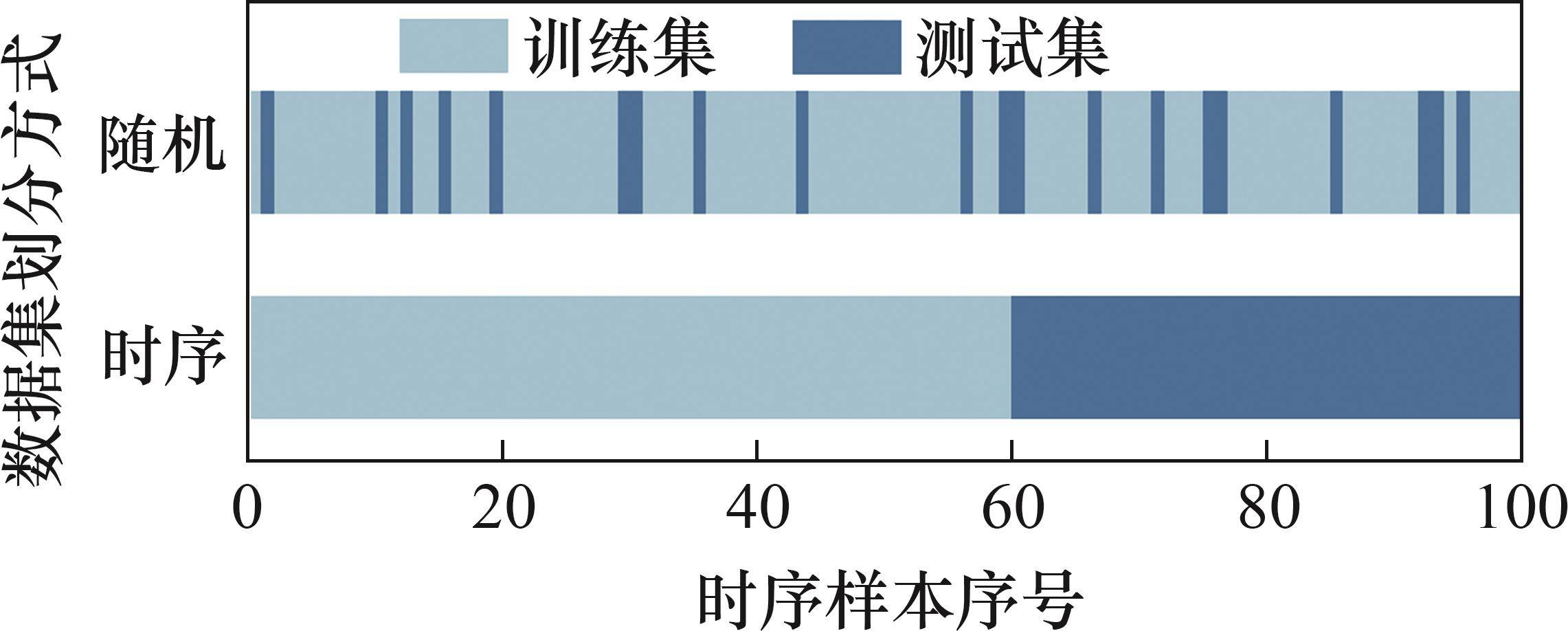
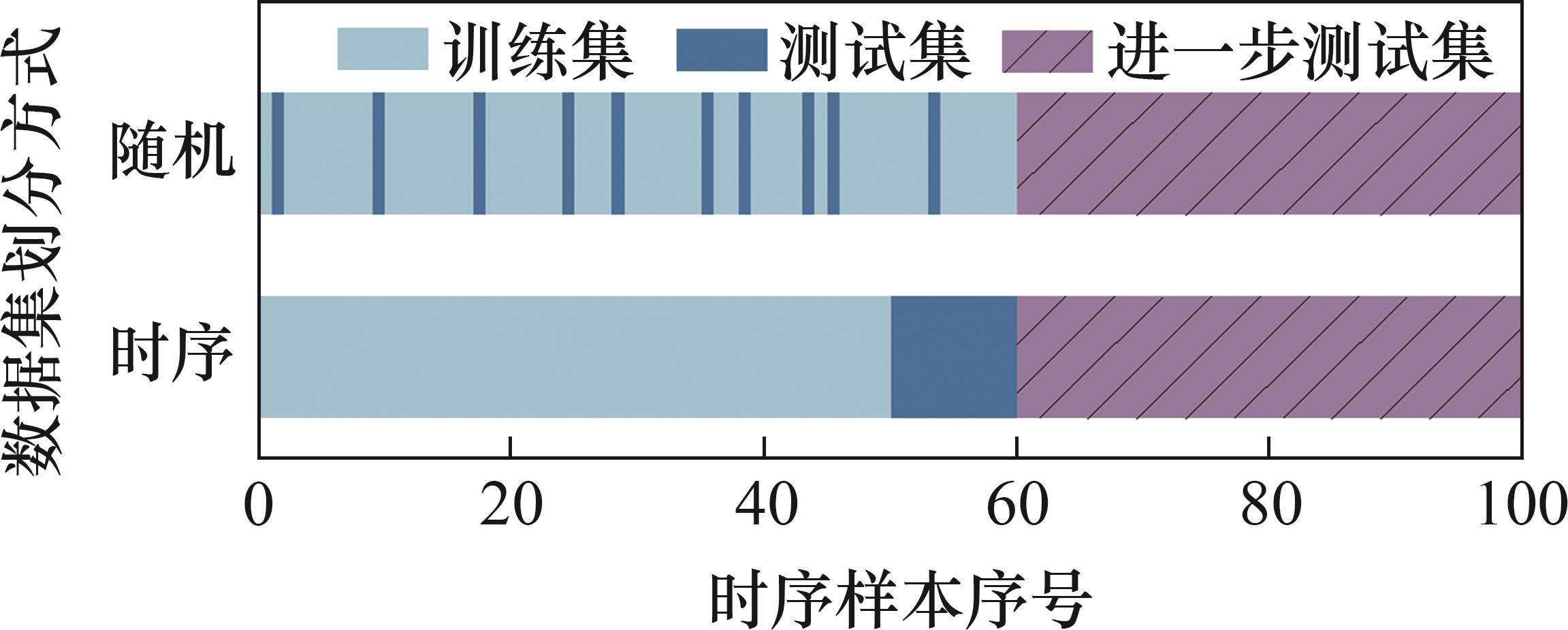
锅炉燃烧系统具有时序性和系统延迟,对于这类系统的随机数据集划分方式存在数据泄露的问题,无法准确得出模型NOx生成量的预测精度。使用时序数据集划分方式能够有效避免这一问题,按时序划分方式将数据集分为训练集和测试集,按采样时间顺序对样本进行排序,然后,按照设定比例进行数据集的划分。时序数据集划分方式与随机数据集划分方式如图1所示。
1.2 时序交叉验证
时序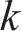
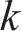
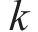
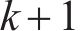
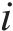
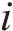
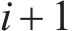
设数据集大小为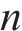
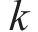

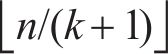
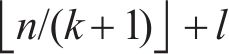
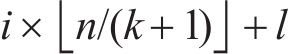
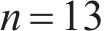

1.3 贝叶斯超参数优化
基于贝叶斯方法对超参数进行优化的流程可以总结为SMBO(sequential model-based global optimization)算法框架[18],其流程如图3所示。图3中,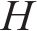
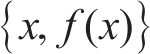
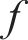
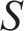
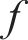
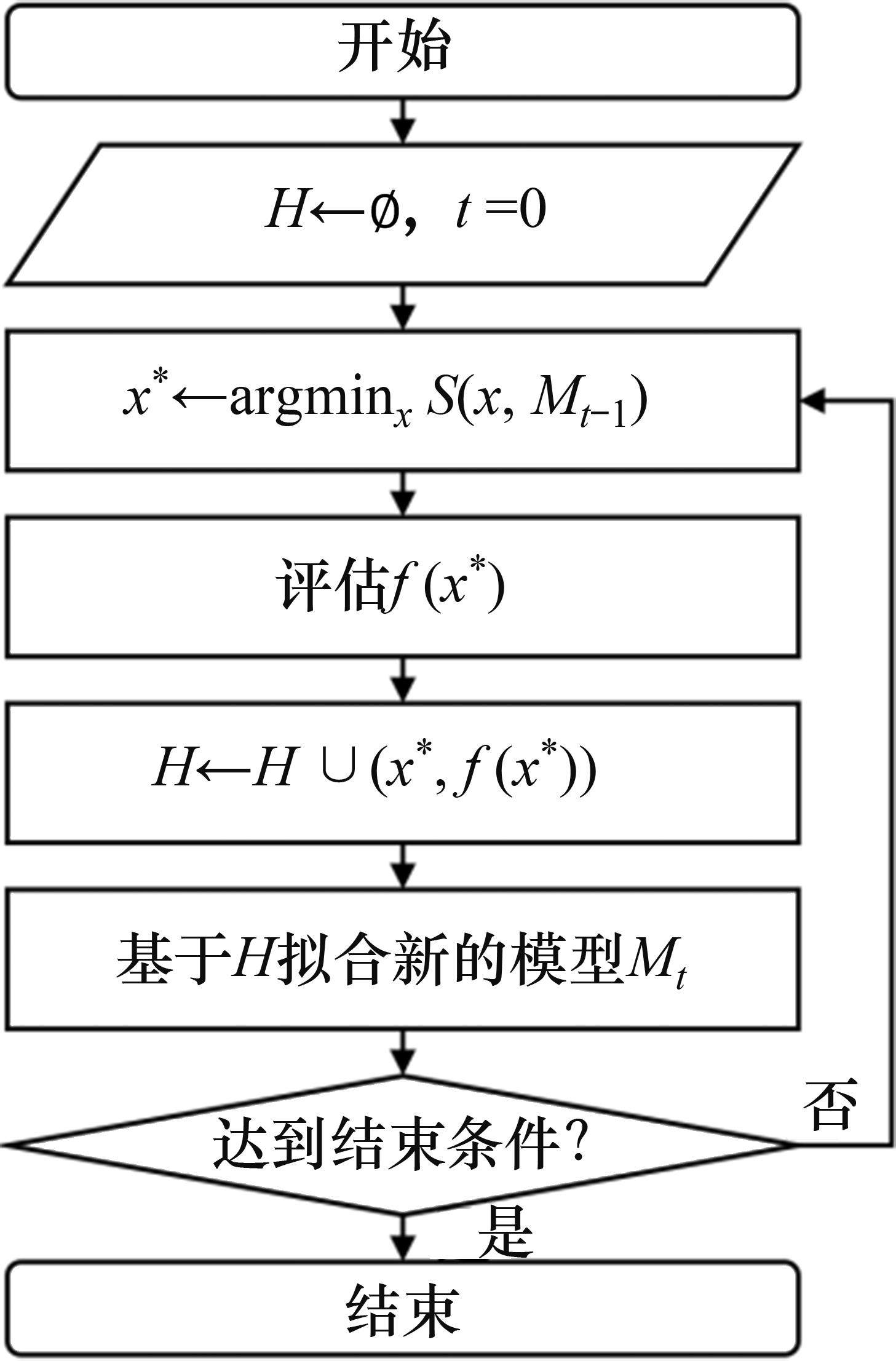
待测试的超参数组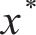
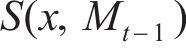
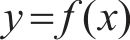
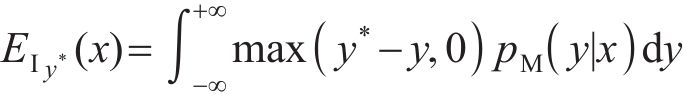
式中: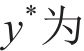
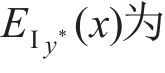
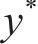
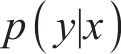
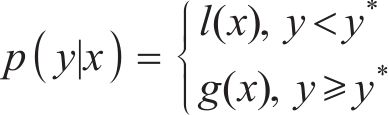
引入超参数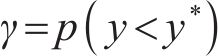
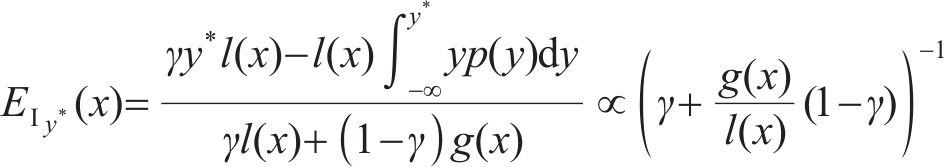
待测试的超参数组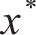
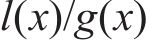
2 锅炉燃烧系统简介及参数选择
2.1 锅炉特性
本文以某电站负荷330 MW的亚临界压力、一次中间再热、自然循环燃煤汽包炉为建模对象。该锅炉采用中速磨直吹式正压制粉系统,四角切圆燃烧,三级混合式喷水系统调节过热蒸汽温度,对于再热蒸汽温度的调节采用烟道挡板作为主要调节,燃烧器摆角为辅助调节,喷水减温作为细调和蒸汽温度偏差控制。
2.2 模型的输入与输出变量
锅炉燃烧系统的相关输入主要由五部分组成:煤、一次风、二次风、给水、高压缸流出蒸汽;锅炉燃烧系统的相关输出主要有烟气、主蒸汽、再热蒸汽。根据相关控制参数和状态参数测点,选择锅炉燃烧系统NOx生成量预测模型的输入参数如表1所示。由于电厂煤质数据每日仅采样一次,明显低于本研究所用样本数据采样频率,低质量的数据会给模型引入噪声和误差,因此,在本研究中不使用煤质数据作为输入参数。对于输出变量,该电站锅炉为尾部双烟道布置,针对NOx生成量有A、B两侧2个测点,因此,以选择性催化还原法反应器SCR两侧入口烟气的NOx浓度均值为模型的输出变量,即样本标签。
| 参数 | 值 | 参数 | 值 |
|---|---|---|---|
| 目标负荷/MW | 1 | 燃尽风、周界风、辅助风门层操5)/% | 14 |
| 实际负荷/MW | 1 | 烟气氧量/% | 1 |
| BTU校正系数1) | 1 | 过热器减温水总量/(t∙h-1) | 1 |
| 总煤量/(t∙h-1) | 1 | 过热侧挡板总操2)/% | 1 |
| 各给煤机给煤量/(t∙h-1) | 5 | 再热侧挡板总操2)/% | 1 |
| 一次风机变频总操2)/% | 1 | 引风机总操2)/% | 1 |
| 一次风总流量/(t∙h-1) | 1 | 炉膛负压/Pa | 1 |
| 一次风冷风温度/℃ | 1 | 高压缸排汽压力/MPa | 1 |
| 一次风热风温度/℃ | 1 | 再热器入口蒸汽温度/℃ | 1 |
| 一次冷风量/(t∙h-1) | 1 | 再热器减温水总量/(t∙h-1) | 1 |
| 一次热风量/(t∙h-1) | 1 | 给水流量/(t∙h-1) | 1 |
| 各磨一次风量/(t∙h-1) | 5 | 给水温度/℃ | 1 |
| 冷、热一次风门开度/% | 10 | 给水压力/MPa | 1 |
| 各磨出口风粉混合温度/℃ | 5 | 高温过热器出口蒸汽压力/MPa | 1 |
| 燃烧器摆角3)/% | 3 | 高温过热器出口蒸汽温度/℃ | 1 |
| 二次风主控4)/% | 1 | 主汽流量/(t∙h-1) | 1 |
| 辅助风主控4)/% | 1 | 再热器出口蒸汽压力/MPa | 1 |
| 二次风流量/(t∙h-1) | 1 | 再热器出口蒸汽温度/℃ | 1 |
| 二次风温度/℃ | 1 |
3 模型构建
3.1 建模流程
基于时序划分方式(时序数据集划分和时序交叉验证)的锅炉燃烧系统NOx生成量预测模型建模的流程与评价如图4所示,为了对模型的预测精度及耗时进行对比评价,将基于时序划分方式获得的模型与随机划分方式(随机数据集划分和随机交叉验证方式)获得的模型对比。
为了验证和说明时序划分方式的实际应用效果,建模算法选择随机森林RF、支持向量回归机SVR、多层感知器MLP和弹性网络回归EN。
3.2 数据预处理
为了查看数据的分布情况,剔除异常数据,对比随机划分方式和时序划分方式对超参数优化及模型精度评估的影响,本研究数据预处理流程如图5所示。

3.2.1 异常数据剔除
本研究所用数据取自该电厂的SIS系统历史数据库,时间为2022-01-01至2023-04-06,采样间隔为1 min,原始数据共662 400个。根据机组运行规程,使用锅炉是否处于协调控制模式(CCS)判断机组是否处于停机状态;根据是否投入自动发电控制(AGC)模式判断辅机是否存在故障。首先使用CCS模式剔除停机数据,再根据机组投入AGC模式运行情况,剔除运行时的异常工况,机组处于不同工况下的数据记录数量如表2所示。
| 所有工况 | 投入CCS | 投入AGC |
|---|---|---|
| 662 400 | 506 375 | 497 696 |
使用AGC模式剔除运行时段的异常数据后,绘制各参数的概率分布图、折线图,经检查未发现其他明显数据异常的记录。
3.2.2 数据归一化
为了解决不同输入变量之间的量纲差距导致的变量可比性问题,本研究对输入和输出变量均使用最大值最小值归一化方法进行预处理,将每一个特征变量和输出变量的最大值和最小值映射到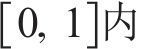
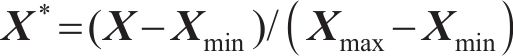
其中: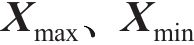
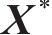
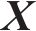
3.2.3 数据集划分
为了对模型实际部署应用时的预测精度进行模拟测试,本研究将预处理后的数据集划分为训练集、测试集和进一步测试集,划分比例分别为50%、10%和40%。
为了确保进一步测试集能够模拟实际效果并保持独立性,该数据集取自数据清洗后时序升序排列在后40%的数据记录,排列在前60%的数据记录设为待划分数据集,待进一步划分为训练集和测试集。
训练集和测试集的划分有2种划分方式:一种是时序划分方式(即时序交叉验证),对训练集和测试集采用时序数据集划分方式,训练集为待划分数据集时序靠前的5/6,测试集为待划分数据集时序靠后的1/6,分别对应总体数据集时序升序排列时前50%和前50%~60%的部分;另一种是随机划分方式(即随机交叉验证),对训练集和测试集采用随机数据集划分方式,训练集和测试集分别取自待划分数据集随机打乱后的5/6和1/6,数据集的划分方式如图6所示。
3.3 模型评价指标
在进行超参数优化前,需要将损失函数作为优化的目标,最终模型在测试集、进一步测试集上的预测精度需要通过评价指标进行表征。模型的4个性能评价指标为均方误差(EMS)、均方根误差(ERMS)、平均绝对误差(EMA)、拟合优度R方(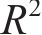
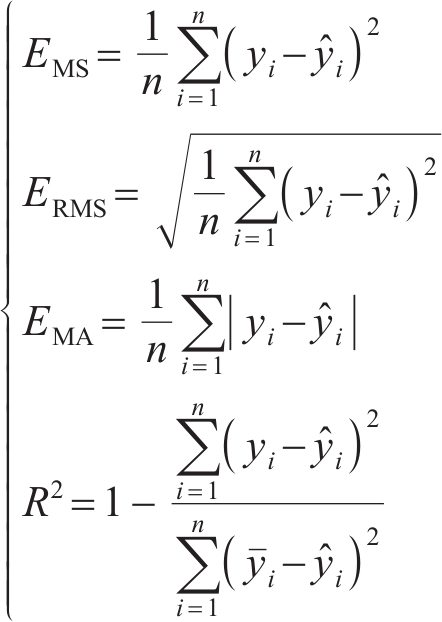
其中:n为样本数;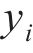
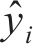
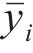
超参数优化选择目标函数时,虽然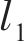
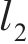
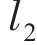
4 预测结果及分析
4.1 模型超参数优化结果
基于随机划分方式和时序划分方式,采用贝叶斯超参数优化方法对模型超参数进行优化。模型超参数优化结果如表3所示,最优超参数对应的目标函数值如表4所示。由表4可见:在训练集上,对于未正则化的模型RF、MLP、SVR,随机划分方式的EMS远小于时序划分方式的EMS;对于有正则化的建模算法EN,随机划分的EMS与时序划分的EMS在数量级上相当,但随机划分的EMS仍比时序划分的EMS小26%。这说明对未正则化的模型随机划分方式存在一定程度的过拟合。
| 建模算法 | 模型超参数 | 随机划分 | 时序划分 | 相同超参数 |
|---|---|---|---|---|
| RF | 树的数量/个 | 403 | 622 | — |
| 树最大深度/层 | 32 | 30 | — | |
| 节点划分最小样本数/个 | 29 | 2 | — | |
| 叶节点最小样本数/个 | 2 | 8 | — | |
| 所用特征最大占比 | 0.342 738 | 0.159 927 | — | |
| 是否自助重采样 | 否 | 是 | — | |
| MLP | 隐藏层大小 | (182,154,182,274) | (136,20,177) | 激活函数:ReLU 优化器:Adam 学习率:恒定 |
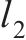 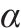 | 1.216 20×10-5 | 2.295 01×10-3 | ||
| 最大迭代数/次 | 30 620 | 26 838 | ||
| EN | 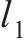 | 0.070 134 6 | 0.030 085 5 | — |
正则化强度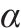 | 1.017 74×10-5 | 1.694 34×10-3 | — | |
| SVR | 正则化参数C | 3.589 57 | 1.031 89×10-2 | 核函数:径向基 |
容差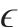 | 1.118 91×10-4 | 8.810 15×10-3 |
| 划分方式 | RF | MLP | SVR | EN |
|---|---|---|---|---|
| 随机划分 | -0.000 174 193 | -0.000 357 627 | -0.000 275 971 | -0.001 734 84 |
| 时序划分 | -0.002 390 46 | -0.001 985 04 | -0.002 045 70 | -0.002 361 90 |
4.2 模型测试结果
一般的建模和评价流程使用训练集进行拟合,用测试集进行测试,得到的测试结果作为该模型NOx生成量的预测精度。使用训练集和测试集的数据基于最优化超参数重新拟合,作为实际模型。本研究以独立的进一步测试集模拟,可得模型的实际预测精度。不同划分方式和建模算法下模型的预期精度和实际精度如表5所示。
| 算法 | 划分方式 | 评价目的 | EMA | EMS | ERMS | R2 |
|---|---|---|---|---|---|---|
| RF | 随机 | 预期精度 | 5.06 | 80.72 | 8.98 | 0.99 |
| 实际精度 | 24.37 | 1 044.81 | 32.32 | 0.78 | ||
| 时序 | 预期精度 | 34.44 | 1 850.91 | 43.02 | 0.51 | |
| 实际精度 | 24.56 | 1 052.31 | 32.44 | 0.78 | ||
| MLP | 随机 | 预期精度 | 10.58 | 212.38 | 14.57 | 0.96 |
| 实际精度 | 23.23 | 941.95 | 30.69 | 0.80 | ||
| 时序 | 预期精度 | 29.28 | 1 247.26 | 35.32 | 0.67 | |
| 实际精度 | 23.06 | 906.22 | 30.10 | 0.81 | ||
| EN | 随机 | 预期精度 | 22.42 | 889.44 | 29.82 | 0.85 |
| 实际精度 | 24.88 | 1 037.68 | 32.21 | 0.78 | ||
| 时序 | 预期精度 | 35.82 | 1 878.58 | 43.34 | 0.51 | |
| 实际精度 | 24.49 | 1 022.86 | 31.98 | 0.78 | ||
| SVR | 随机 | 预期精度 | 7.12 | 135.24 | 11.63 | 0.98 |
| 实际精度 | 27.63 | 1 331.24 | 36.49 | 0.72 | ||
| 时序 | 预期精度 | 29.49 | 1 380.25 | 37.15 | 0.64 | |
| 实际精度 | 22.52 | 860.46 | 29.33 | 0.82 |
由表5可见:对于未正则化的算法RF、MLP、SVR,使用随机划分方式得到的模型预期精度均显著高于模型的实际精度。RF算法的预期EMA为5.06,实际EMA为24.37,实际与预期EMA相对偏差为381.62%;预期ERMS为8.98,实际ERMS为32.32,实际与预期ERMS相对偏差为259.91%。MLP算法预期EMA为10.58,实际EMA为23.23,实际与预期ERMS相对偏差为119.57%;预期ERMS为14.57,实际ERMS为30.69,实际与预期ERMS相对偏差为110.64%。SVR算法预期EMA为7.12,实际EMA为27.63,实际与预期EMA相对偏差为288.06%;预期ERMS为11.63,实际ERMS为36.49,实际与预期ERMS相对偏差为213.76%。对于未正则化模型,随机划分给出的预期精度与实际精度相对偏差较大,EMA最大偏差达381.62%,ERMS最大偏差达259.91%。
数据集使用随机划分方式时出现了数据泄露的情况,导致模型过拟合,虽然在训练集和测试集的效果都很好,但在实际应用中(即进一步测试数据集上),RF、MLP、SVR模型预测精度大幅下降,显著低于测试数据集给出的预期精度。对于有正则化的模型EN则不存在这一问题,因为正则化模型在训练时,通过正则化项避免了过拟合的发生。
不同划分方式和不同算法下的预期精度ERMS和实际精度ERMS及其相对误差如图7所示。由图7可见:时序划分方式在未正则化建模算法RF、MLP、SVR的模型上,预期ERMS与实际ERMS之间的误差更小,其相对误差相比于随机划分方式分别减少了235.32%,95.86%,192.71%。使用时序划分方式时,能够有效避免随机划分方式存在的过拟合和数据泄露的情况,时序划分方式训练的模型给出的预期精度与实际精度之间的误差更小。
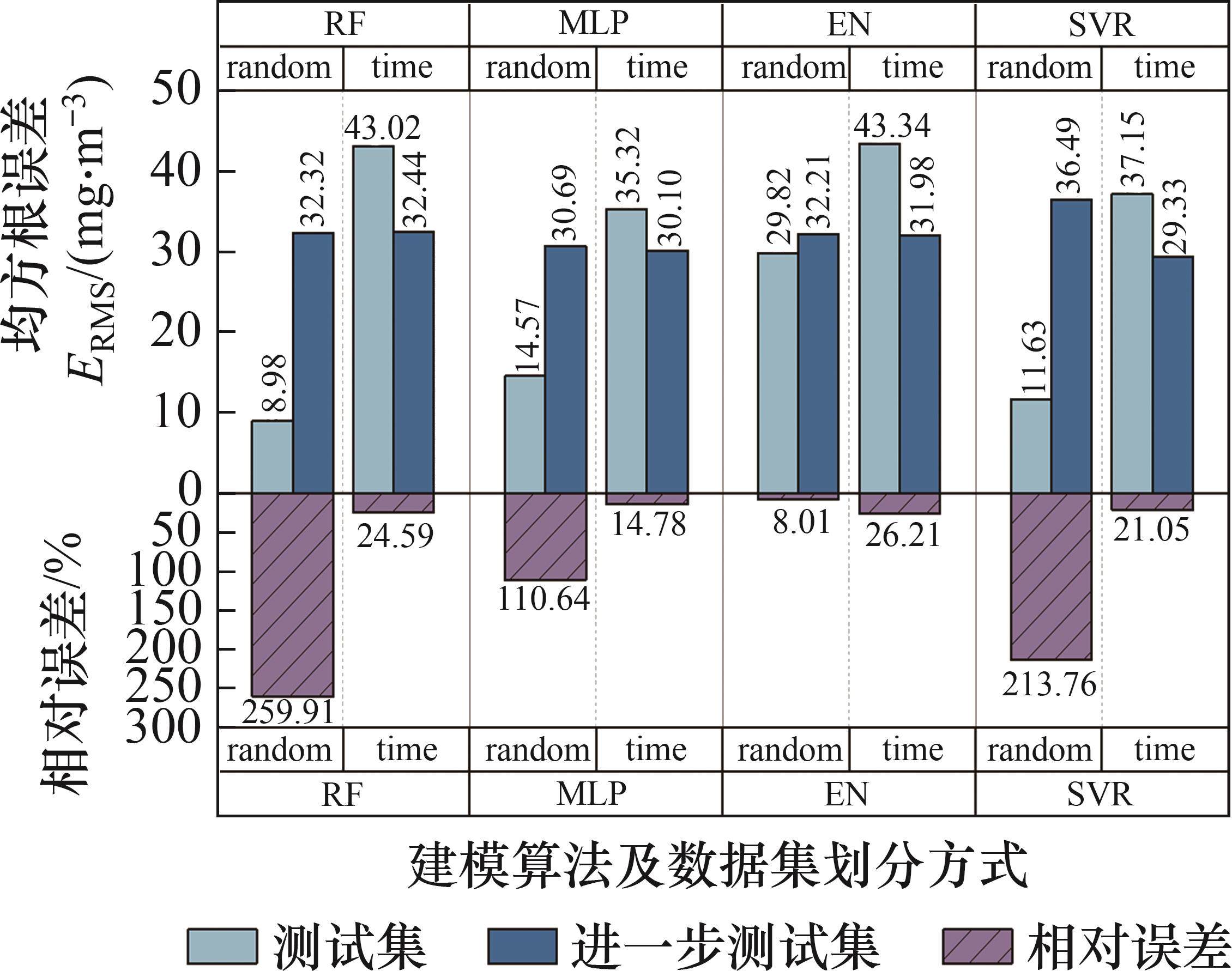
不同模型对模拟实际应用的进一步测试集进行预测得到的实际EMA和ERMS如图8所示。由图8可见:除了RF模型外,其他模型(即MLP、SVR、EN模型)时序划分方式都能提升模型的实际预测精度。对于MLP模型,时序划分方式与随机划分方式相比,模型的EMA减小了0.17(相对减少0.73%),模型的ERMS减小了0.59(相对减少1.92%);对于EN模型,时序划分方式与随机划分方式相比,模型的EMA减小了0.39(相对减少1.57%),模型的ERMS减小了0.23(相对减少0.71%);对于SVR模型,时序划分方式与随机划分方式相比,模型的EMA减小了5.11(相对减少18.49%),模型的ERMS减小了7.16(相对减少19.62%)。对于RF模型,时序划分方式与随机划分方式的预测精度基本一致,两者差距不超过0.8%。
4.3 模型训练耗时
以最优超参数为例,计量一组模型(包括基于交叉验证进行训练和测试)超参数优化的总耗时。所用设备的处理器为13th Gen Intel(R) Core(TM) i7-13700,基准频率为2.10 GHz,实际测试时频率在3.0~4.7 GHz之间波动,内存为32.0 GB。进行3次测试,在不同建模算法和不同交叉验证方式下,一组超参数的评估总耗时均值和标准差如表6所示。
| 交叉验证方式 | RF | MLP | SVR | EN |
|---|---|---|---|---|
| 随机交叉验证 | 5 511±150 | 747±96 | 1 002 865±206 | 20.48±0.20 |
| 时序交叉验证 | 1 587±43 | 238±11 | 58 236±31 | 9.95±0.19 |
总耗时的变化主要受处理器主频波动的影响,SVR模型的训练耗时受超参数容差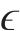
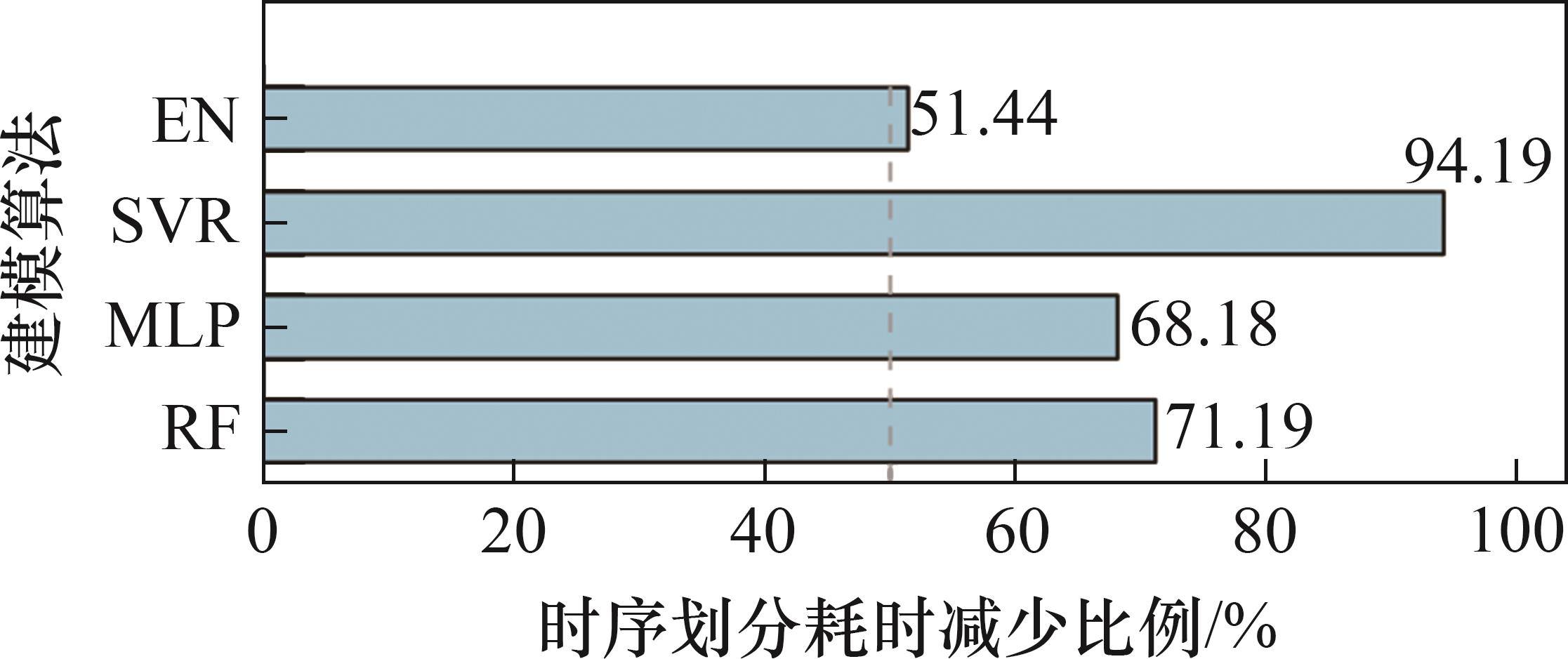
从图9可见:相比于随机交叉验证,时序交叉验证方式能够使计算时间缩短50%以上;对于EN,时序交叉验证耗时减少了51.44%;对于SVR,时序交叉验证耗时减少了94.19%。时序交叉验证能够减少超参数优化和训练耗时的原因在于随机交叉验证使用的总数据量约为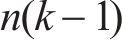
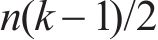
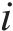
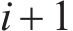
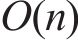
5 结论
1) 时序数据集划分方式能够避免随机数据集划分方式导致的过拟合和测试数据泄露问题,基于测试集给出的预期精度与模型实际精度之间的误差更小,相比于随机数据集划分方式,时序数据集划分方式的预期ERMS与实际ERMS之间的相对误差最大可减少235.32%。
2) 时序划分方式能提升模型实际预测精度,对SVR模型的提升效果最明显,相比于随机划分方式,时序划分方式的EMA减小了18.49%,ERMS减小了19.62%。
3) 在同样数据集大小下,相比随机交叉验证方式,时序交叉验证方式能够有效减少评估的总耗时。对复杂度高的SVR算法,耗时可减少94.19%,对线性时间复杂度的算法,计算量和耗时均可减少50%。
基于树状结构Parzen估计器优化长短期记忆神经网络的燃煤机组NOx生成浓度预测
[J/OL]. 中国电机工程学报. 2024, https://doi.org/10.13334/j.0258-8013.pcsee.232281.屈可扬, 程静, 甘云华, 等. 基于时序数据集划分和时序交叉验证优化燃煤锅炉NOx建模[J]. 中南大学学报(自然科学版), 2024, 55(12): 4665-4674.
QU Keyang, CHENG Jing, GAN Yunhua, et al. Optimization of NOx modeling for coal-fired boilers based on time series dataset division and time series cross-validation[J]. Journal of Central South University(Science and Technology), 2024, 55(12): 4665-4674.

