动态、精准的道路行程速度数据是开展城市交通规划[1-3]、堵点治理[4-5]、交通组织[6-8]、信号协同等交通改善优化的基础前提,目前道路行程速度多以浮动车数据为数据源进行集计所得,但受浮动车车辆分布不均、地形高差限制影响,次支道路等局部道路容易产生空值或零值,即存在一定比例的稀疏数据,因此需要对稀疏数据进行修复和填补[9-10]。目前道路行程速度稀疏数据修复方法多从时间序列角度出发,通过构建时间序列样本数据集,再以自回归积分移动平均算法、随机森林、深度学习等方法进行预测,如杨建喜等[11]提出多周期组件时空神经网络模型,利用多尺度卷积神经网络模型对不同时间粒度下的路网通行速度进行预测;张凯等[12]提出了双向长短期记忆网络(bidirectional long short term memory network,BiLSTM)短时车速预测模型,对噪声进行了预处理,但所测试数据为仿真数据,无法验证模型的实际适应性;少部分学者考虑了路网时空特性,如杨顶等[13]利用图卷积神经网络对道路车速进行预测,ZHAO等[14]结合图卷积网络提出了用于车速短时预测的时间序列(temporal graph convolutional network,T-GCN)模型,但都存在所需路网运行数据较多、可解释性较差等问题。相较于神经网络(artificial neural network,ANN)、支持向量机support vector machine, SVM)等个体模型,集成学习可以合并多个个体学习,具有更好的预测性能和学习效率[15],大量学者运用极限梯度提升(extreme gradient boosting,XGBoost)等集成学习算法进行稀疏数据填补,如裴莉莉等[16]利用改进XGBoost对高速公路异常收费数据进行填补预测,LARTEY等[17]构建了美国明尼苏达州94号州际公路交通量数据集,运用XGBoost算法对缺失数据进行预测,预测精度超过80%,ZHANG等[18]通过XGBoost、随机森林算法对高速公路行程速度数据进行预测,验证了XGBoost算法的预测性能,QIAN等[19]通过高速公路龙门架数据提取行程速度时间序列,利用XGBoost算法进行行程速度预测,预测准确率超过85%,同时其他领域学者也从不同角度验证了集成学习算法在异常或稀疏数据预测和填补时的有效性和适用性[20-22],但是由于大多通过人工经验设置超参数,导致预测和数据修复精度不够理想。因此近年来部分学者通过群智能算法与集成学习模型相结合,提高模型预测精度,如孙朝云等[23]利用遗传算法(Genetic Algorithm, GA)对XGBoost中Max_depth等超参数进行寻优,并对道路环境感知异常数据进行修复,模型R2提升了1.7%。YUN等[24]运用GA算法优化XGBoost超参数,提高了股票价格数据预测的精准度,但未解决原始GA算法存在收敛速度慢、易陷入局部最优等问题。WU等[25]提出了GA算法个体选择概率自适应机制,但会出现后续优秀个体选择概率较低问题,需要进一步改进GA算法,提升模型预测性能。综上,现有道路行程速度数据修复多从时间序列出发,对路网时空信息考虑欠佳,同时缺乏对道路空间距离和预测结果贡献度的耦合关系分析,且多数算法对预测结果的可解释性不足,如神经网络模型无法通过直接阐述输入特征值与目标值间的量化关系,即存在“黑箱”[26-27],不利于开展进一步深入分析和实践应用,且现有GA算法需要进一步解决寻优性较差、易陷入局部最优解等问题。基于此,本文利用机器学习高预测精度特点,在XGBoost基础上提出了利用改进GA算法进行超参数寻优的IGA-XGBoost组合算法,引入空间关联指数研究不同空间位置相连道路对数据修复结果的交互影响,利用SHAP算法进行可解释性分析,分析了空间关联指数与预测结果贡献度的耦合机理,最后通过重庆市中心城区实际案例进行验证,证明了组合算法的有效性和先进性。
1 问题及解决方法
1.1 问题的数学描述
城市路网中相连道路交通流量在空间和时间上具有相关性,杨顶等[13]发现相连道路行程车速在空间和时间上也存在类似特征,即目标修复道路与其相连接的道路在平均运行车速上存在映射关系,因此可利用相连道路在时空上的相关性对目标道路稀疏数值进行修复。
基于此,本文将路网中与目标道路相连道路行程速度为输入,以目标道路行程速度为输出,假设目标道路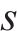
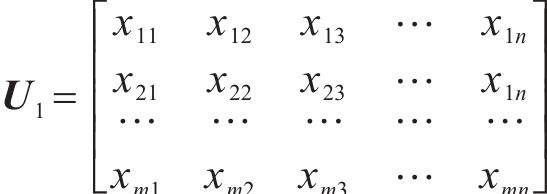
输出数据集为道路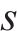
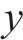
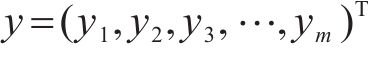
设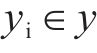
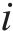
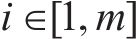
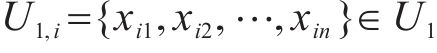
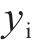
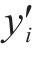
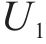
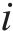
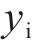
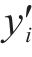
为衡量目标道路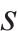
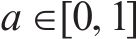
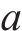
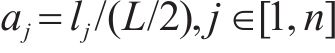
式中: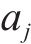
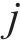
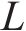
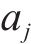
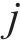
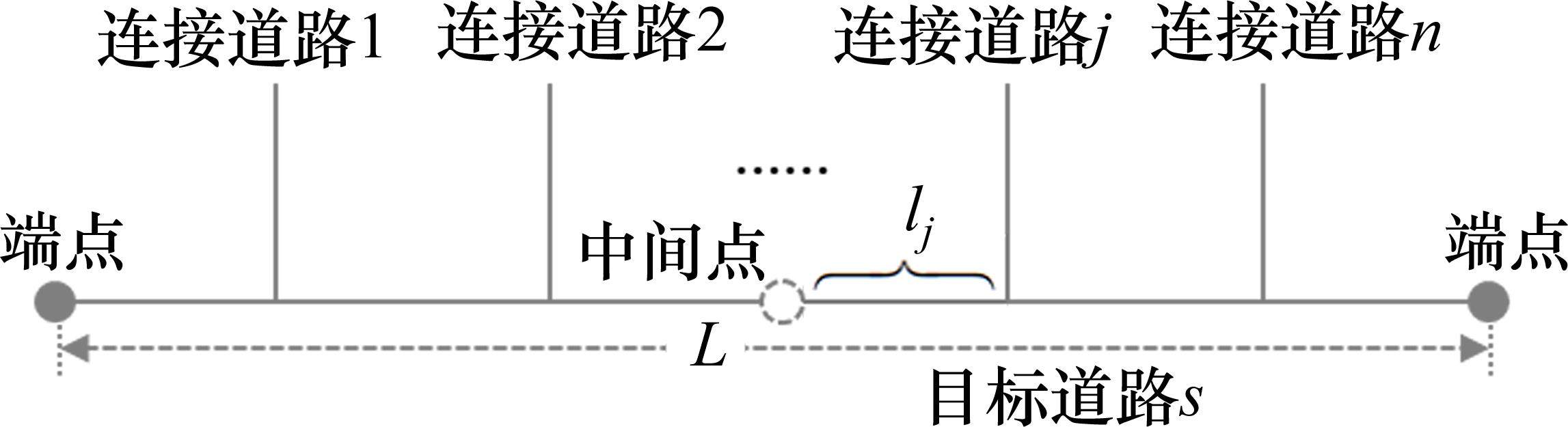
1.2 解决方法
本研究首先基于城市GIS路网精准测量出各路段空间关联数据,即RSCI值,利用改进的GA算法寻找出XGBoost超参数的最优数值,然后构建了考虑空间关联特征的XGBoost缺失数据预测模型,对缺失数据进行预测,并利用SHAP可解释性方法计算不同输入特征的特征重要度,对不同RSCI值的路段贡献度进行量化分析,同时进行RSCI、特征重要度的双因素分析,进一步验证两者间的交互关系,如图2所示。
2 建立IGA-XGBoost组合模型
XGBoost算法存在多个超参数,传统网格搜索(Grid Search,GS)算法存在收敛速度慢、运行时耗长等问题,部分学者采用GA算法优化XGBoost超参数,但GA算法存在局部收敛问题,因此本文提出了一种优化选择操作的自适应遗传算法IGA。
2.1 GA算法自适应改进
遗传算法需经历选择、交叉、变异3个过程,贺锋涛等[28]对交叉、变异操作和算子进行了改进,本文侧重对选择过程和算子进行优化。
选择操作是GA算法的重要操作,该操作核心目的是选择出优秀的个体并存储于种群中,本文在传统轮盘算法的基础上,提出了自适应机制以对个体选择概率进行优化。通过适应度函数计算出个体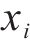
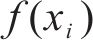
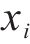
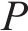
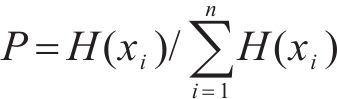
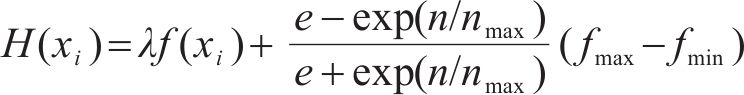
式中:
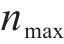
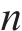
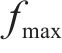
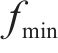
由于

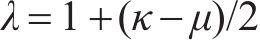
式中: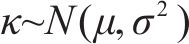
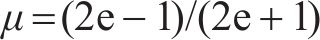
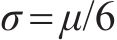
在服从正态分布情况下,
2.2 IGA优化XGBoost算法
XGBoost属于boosting家族,是梯度提升决策树(Gradient Boosting Decision Tree, GBDT)算法的改进型,通过改进损失函数与损失优化过程,提高模型预测性能。XGBoost由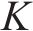
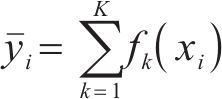
式中: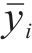
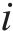
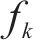
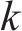
XGBoost的目标函数由模型损失函数和正则项2部分构成:
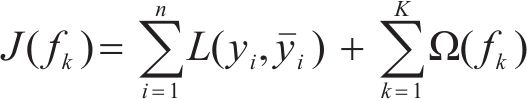
式中: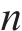
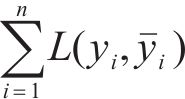
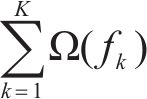
在XGBoost模型的目标函数优化过程中,XGBoost先确定第1棵基准树,并在第1棵基准树上学习第2棵,则第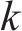
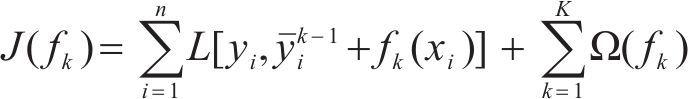
因此,目标函数优化过程为找到使得目标函数达到最小值的树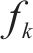
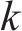
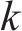
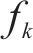
超参数寻优是XGBoost算法的重要优化方向,陈曦泽等[15]提出树的个数(n_estimators)、学习率(Learning_rate)、最大深度(Max_depth)是影响模型精度的主要超参数,本文在其基础上增加了子节点最小样本数(min_child_weight)参数,因此寻优超参数包括n_estimators、learning_rate、max_depth、min_child_weight这4个超参数。
结合公式(4)~(6)选择算子计算方法,本文IGA-XGBoost流程步骤如下。
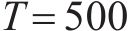
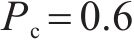
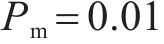
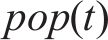
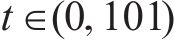
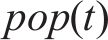
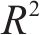
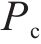
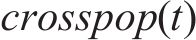
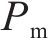
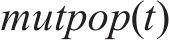
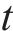
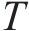
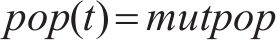
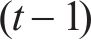
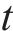
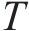
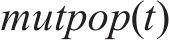
3 实验与结果分析
3.1 浮动车数据集构建
依托重庆市道路监测运行平台获取道路双向行程速度数据,目标道路为五红路,道路里程为3.0 km,其相连道路分别为紫荆路、黄龙路、兴隆路、洋河路、万丰路、渝鲁大道等共计8条道路,数据采集时间为2023年7月10日(星期一)0:00至12:00,由于浮动车采样间隔为10 s,单个浮动车数据数值波动较大,实际应用中通常最低分析间隔为5 min,故本文样本采样时间间隔为5 min,共收集到样本数据288条,其中80%数据作为模型训练集Utest,20%数据作为测试集Uval,各道路采集数据及空间关联指数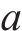
| 道路名称 | 编号 | Max | Min | 均值 | 空间关联指数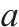 |
|---|---|---|---|---|---|
| 五红路 | y | 57.6 | 17.9 | 38.2 | — |
| 黄龙路 | R1 | 36.3 | 9.8 | 22.8 | 0.64 |
| 渝鲁大道 | R2 | 65.8 | 15.7 | 42.0 | 1.00 |
| 万丰路 | R3 | 34.0 | 12.9 | 21.1 | 0.53 |
| 兴隆路 | R4 | 27.7 | 10.4 | 17.8 | 0.40 |
| 洋河北路 | R5 | 33.0 | 15.6 | 22.7 | 0.63 |
| 洋河东路 | R6 | 39.4 | 25.0 | 33.0 | 0.07 |
| 洋河路 | R7 | 24.0 | 10.9 | 17.1 | 0.26 |
| 紫荆路 | R8 | 46.0 | 15.4 | 32.5 | 0.93 |
3.2 结果对比与分析
1) 评价指标选取
选取平均绝对误差fMAE、平均相对误差fRMSE对模型修复误差进行评价,选择决定系数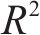
| 评价指标 | 算式 | 数值说明 |
|---|---|---|
| fMAE | 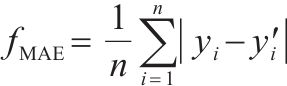 | 数值越小,误差越小 |
| fRMSE | 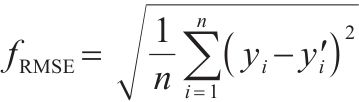 | 数值越小,误差越小 |
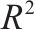 | 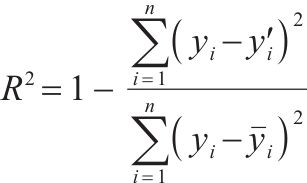 | 数值越大,精度越高 |
2) IGA-XGBoost数据预测结果分析
为避免训练集产生的随机抽样偏差,选择K折交叉验证K-Fold CV进一步划分训练集,将训练集样本平均分为K份(文中取K=10),不重复地随机抽取其中一份作为评估样本数据,另K-1份作为训练数据训练模型,每一次计算一次R2,重复上述步骤K次,得到K组R2数据,最后取所有R2算术平均值作为模型的最终R2,K-Fold CV运行过程如图3所示。
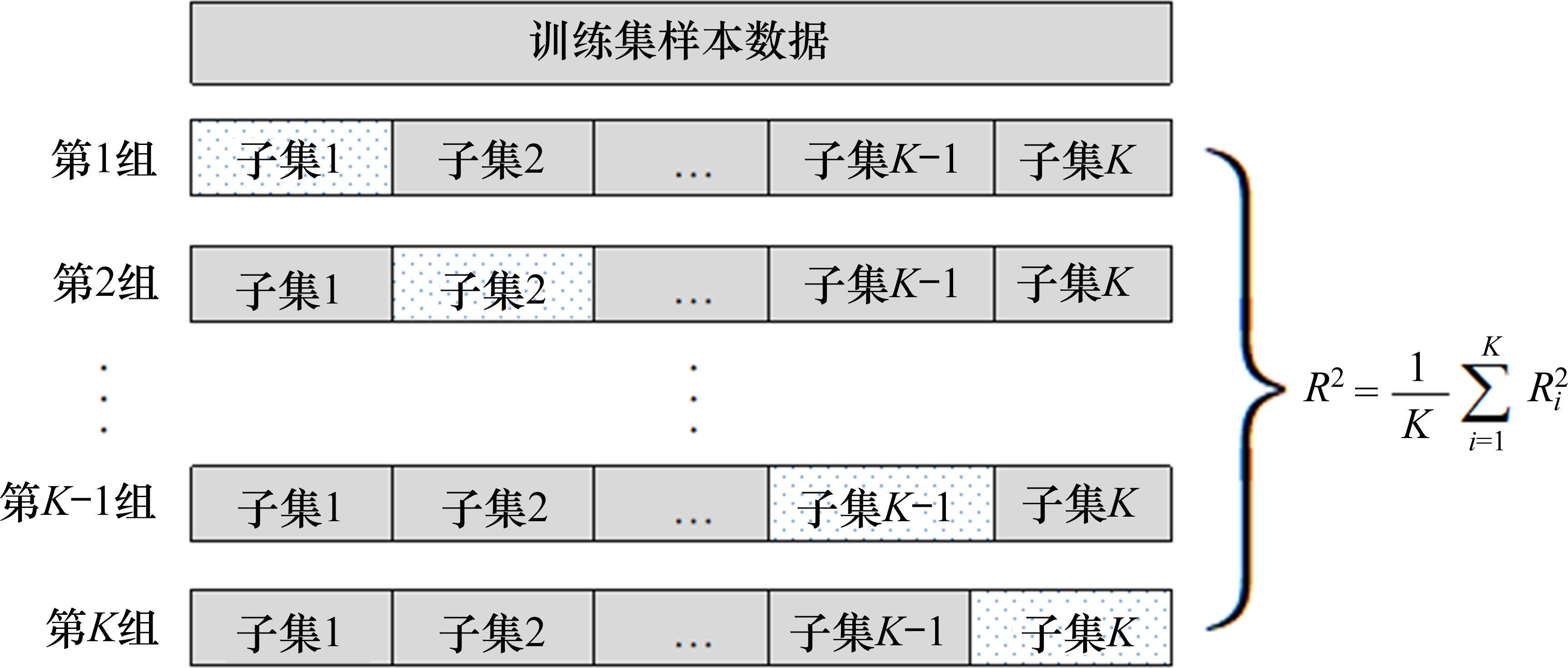
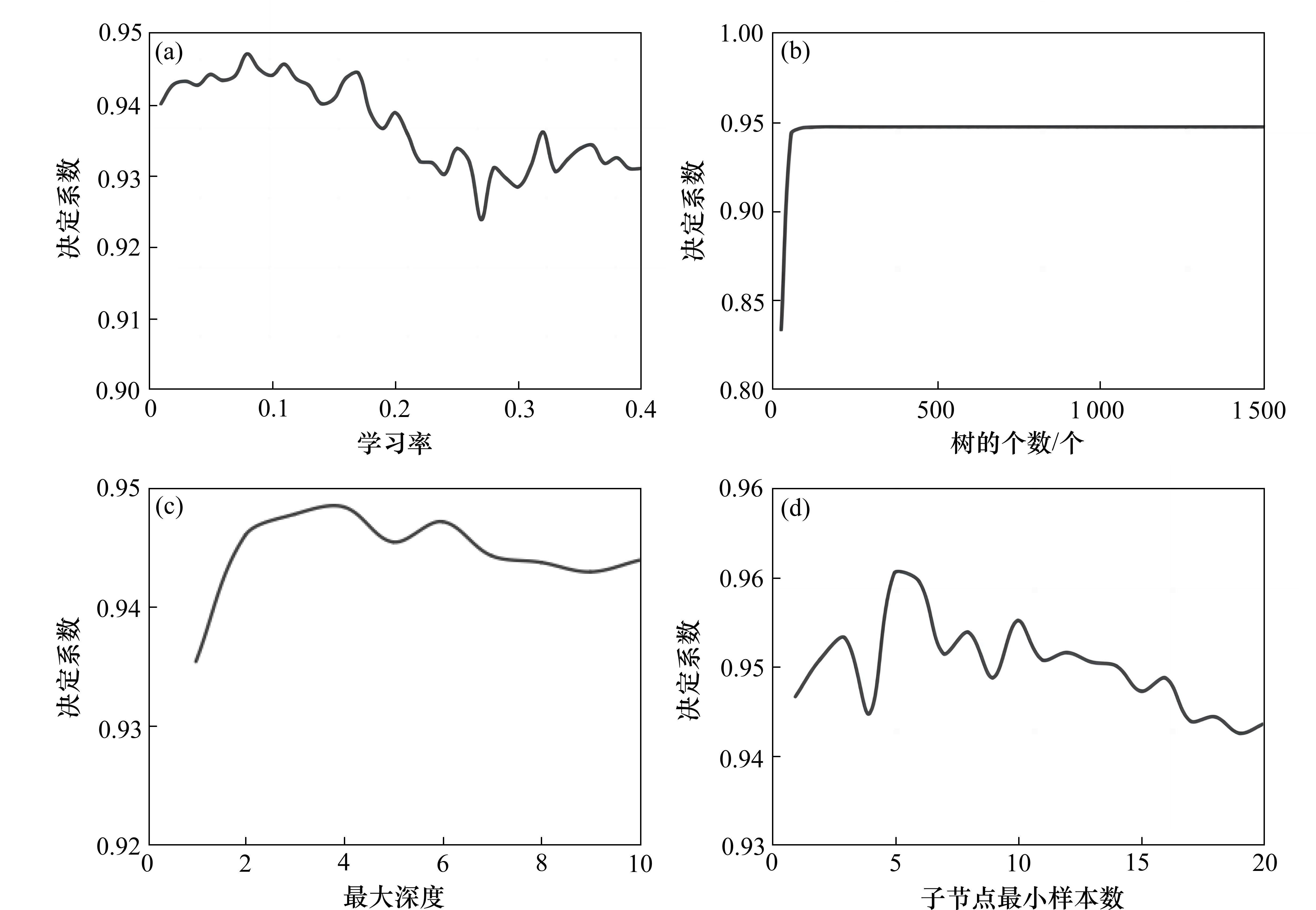
本文通过IGA算法对XGBoost模型超参数进行组合寻优,learning_rate最优范围区间为[0.06, 0.13],最优取值为0.08,n_estimators最优范围区间为[200,1 500],最优取值为240,max_depth最优范围区间为[3, 5],最优取值为4,min_child_weight最优范围区间为[5, 7],最优取值为5,详见图4。可以看出,随着learning_rate的不断增加,模型R2先增大,当learning_rate大于0.17后,R2持续下降;n_estimators在200左右R2达到最大值后,随着n_estimators增大,模型R2保持持平;随着max_depth的增加,模型R2持续增大,在max_depth=4时达到最大值,随后呈现震荡下降态势;随着min_child_weight增大,初期模型R2持续增大,在min_child_weight=5时达到最大值,随后呈持续下降态势。
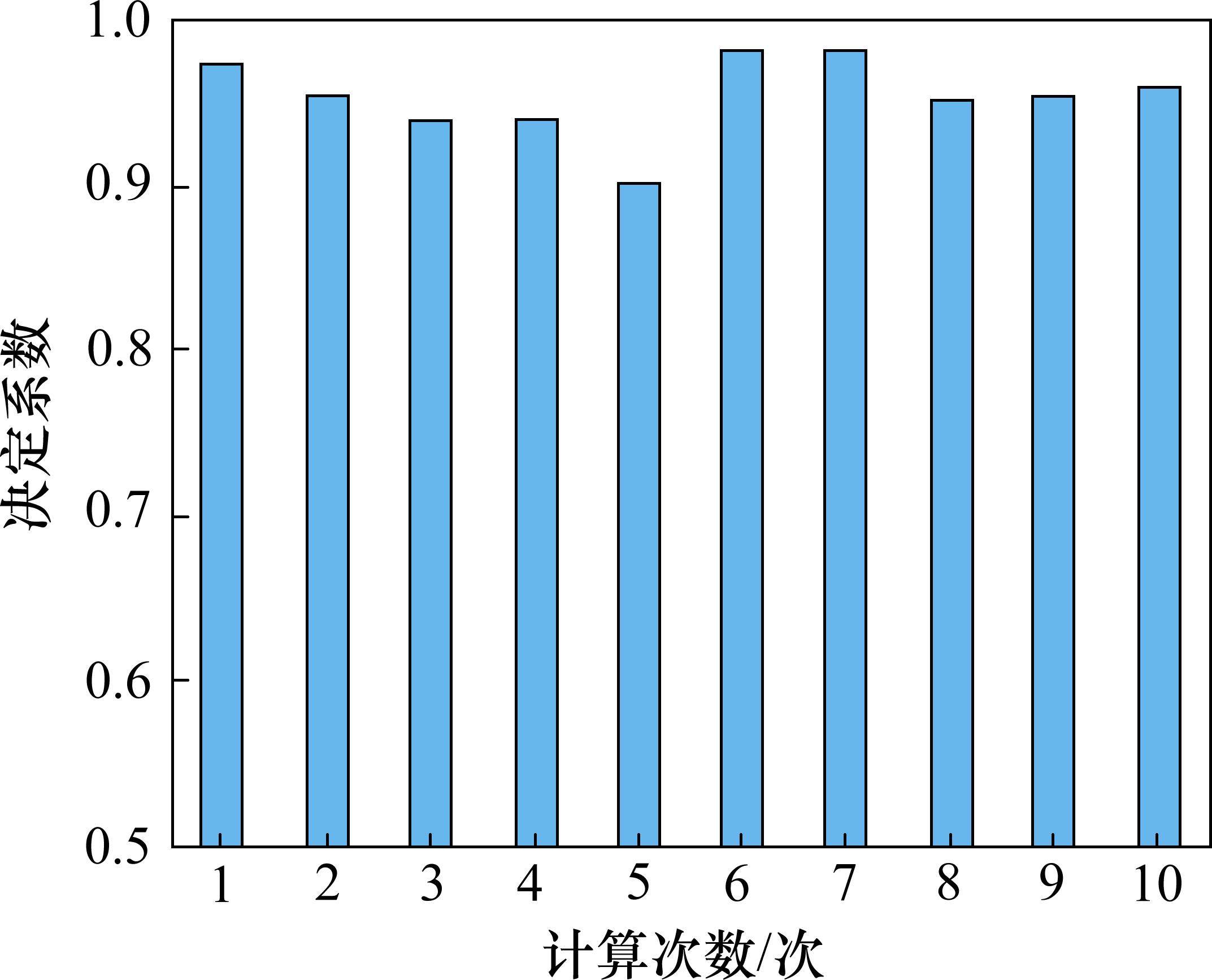
利用最优超参数作为XGBoost模型参数进行建模,其中learning_rate=0.08,n_estimators=240,max_depth=4,min_child_weight=5,其余参数均选择模型默认值,通过训练集Utest经10折交叉验证后,模型R2分别为0.974、0.955、0.942、0.942、0.903、0.983、0.981、0.954、0.956、0.961,取算术平均值后模型R2为0.955>0.75,可见预测精度较高,见图5。
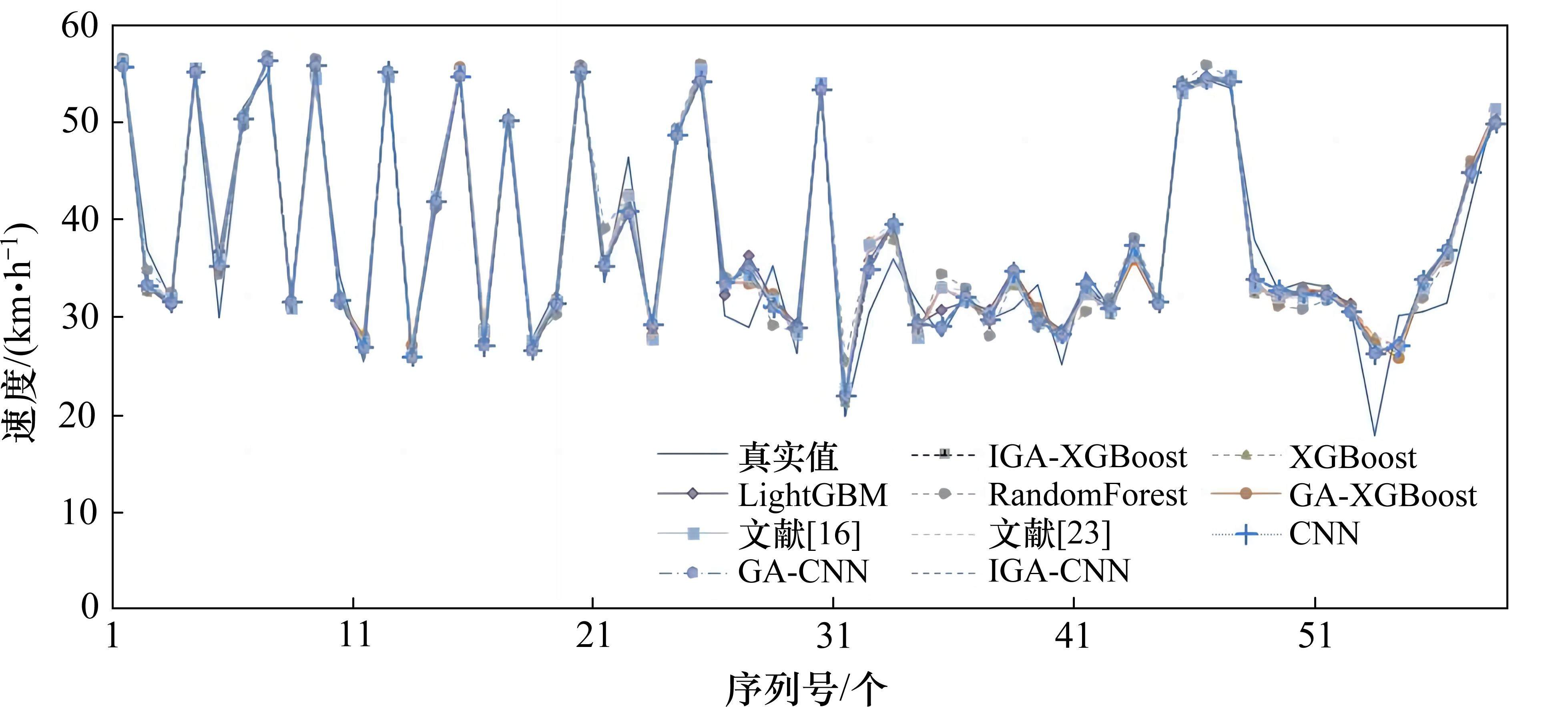
为验证IGA-XGBoost组合模型的有效性,选择XGBoost、LightGBM(Light Gradient Boosting Machine,LightGBM)、RandomForest、GA-XGBoost、卷积神经网络(Convolutional Neural Networks, CNN)、GA-CNN、IGA-CNN、裴莉莉等[16]、孙朝云等[23]算法进行预测精度对比分析,其中XGBoost、LightGBM、RandomForest模型采用网格搜索GS算法确定n_estimators、learning_rate、max_depth、min_child_weight等4个超参数,GA-XGBoost通过传统GA算法确定上述4个超参数,RandomForest通过GS算法确定n_estimators、learning_rate、max_depth等3个超参数,GA-CNN、IGA-CNN模型分别通过GA、IGA算法确定learning_rate、神经网络层数、批样本数量超参数,其余超参数为默认值。Utest用以训练各模型,Uval用以开展模型评价,经统计,本文IGA-XGBoost组合模型的平均绝对误差fMAE(Mean Absolute Error, MAE)、均方根误差fRMSE(Root Mean Square Error, RMSE)最小,分别为1.95、2.66,各对比算法R2依次为0.928、0.935、0.917、0.938、0.889、0.923、0.926、0.937、0.931,可见IGA-XGBoost组合模型预测误差明显低于其他对比算法,预测精度明显高于其他对比算法,且预测值与真实值拟合精度较高,没有发生过拟合现象,见表4和图6。与GA-XGBoost模型相比,本文IGA-XGBoost组合模型不仅在预测精度上有一定提升,且运行时间为1.532 s,较GA-XGBoost模型的1.658 s,运行时间减少7.6%,运行效率有明显提升,这是因为本文IGA算法在传统轮盘算法的基础上,通过引入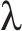
3) 基于SHAP的空间距离可解释性分析
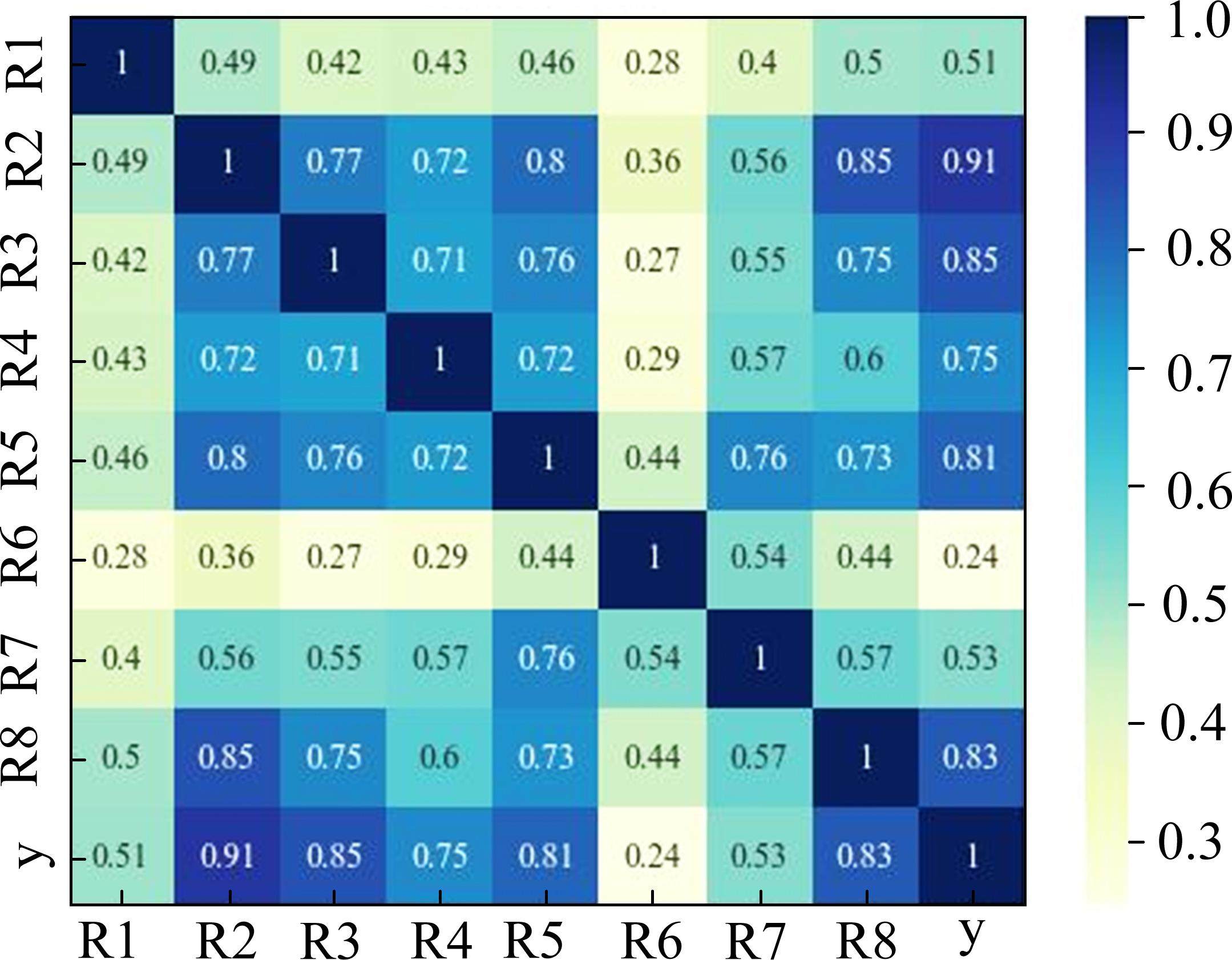
通过各输入特征和输出值皮尔逊相关系数矩阵可知,不同输入特征的相关系数存在显著差异,R2、R3、R8相关系数位列前3,分别为0.91、0.85、0.83,其空间关联指数
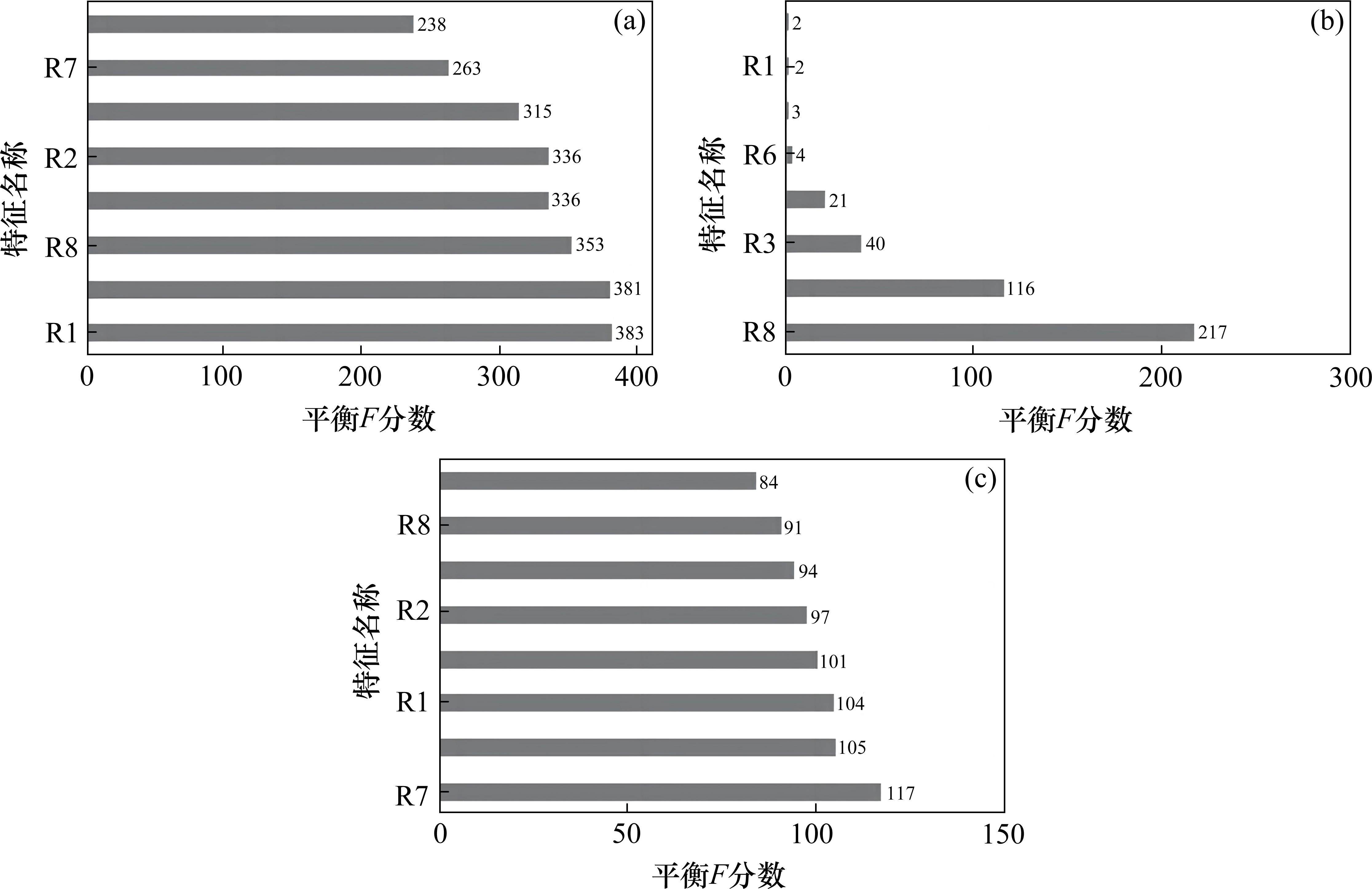
XGBoost模型提供了基于weight(单个特征在所有树中被使用的次数)、gain(单个特征在所有树中对预测结果的平均增益)、cover(单个特征在所有树中对样本的平均覆盖度)等3种特征重要性分析方法,调用Python中plot_importance函数开展3种特征重要性分析,可见基于weight的结果显示R1特征重要性最高,对预测结果有最大影响,基于gain的结果显示R8特征重要性最高,而在基于cover的结果显示R7特征重要性最高,不同计算标准下特征重要性排序出现显著差异,即特征重要性分析结果出现不一致性,使模型的可解释性较差,见图8。
为解决不同评价标准下特征分析结果一致性缺失问题,计算出所有样本不同特征值的贡献值,将基线值与各特征贡献值累加值之和作为模型预测值:
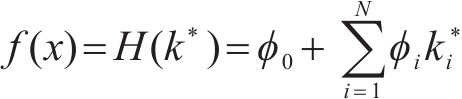
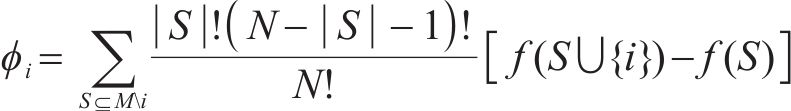
式中: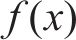
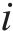

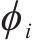
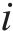
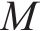
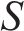
SHAP有Kernel SHAP、Deep SHAP、Tree SHAP等3种内核,本文选择Tree SHAP内核开展XGBoost模型可解释性分析。从不同特征的SHAP值分布可知,R2、R8、R5为影响预测结果的前3个最关键特征,3个特征样本SHAP绝对值的均值分别为3.8、2.7、1.7,且随着样本值R2的增大,其SHAP值也明显增大,表明R2对预测结果造成正面影响,即该特征为正向贡献,R8、R5、R3、R1均呈现上述现象,但R7、R6表现出一定负向影响,当样本值>0时,SHAP值出现负值,R4的SHAP值在0左右徘徊,对预测结果影响最小,见图9、图10。
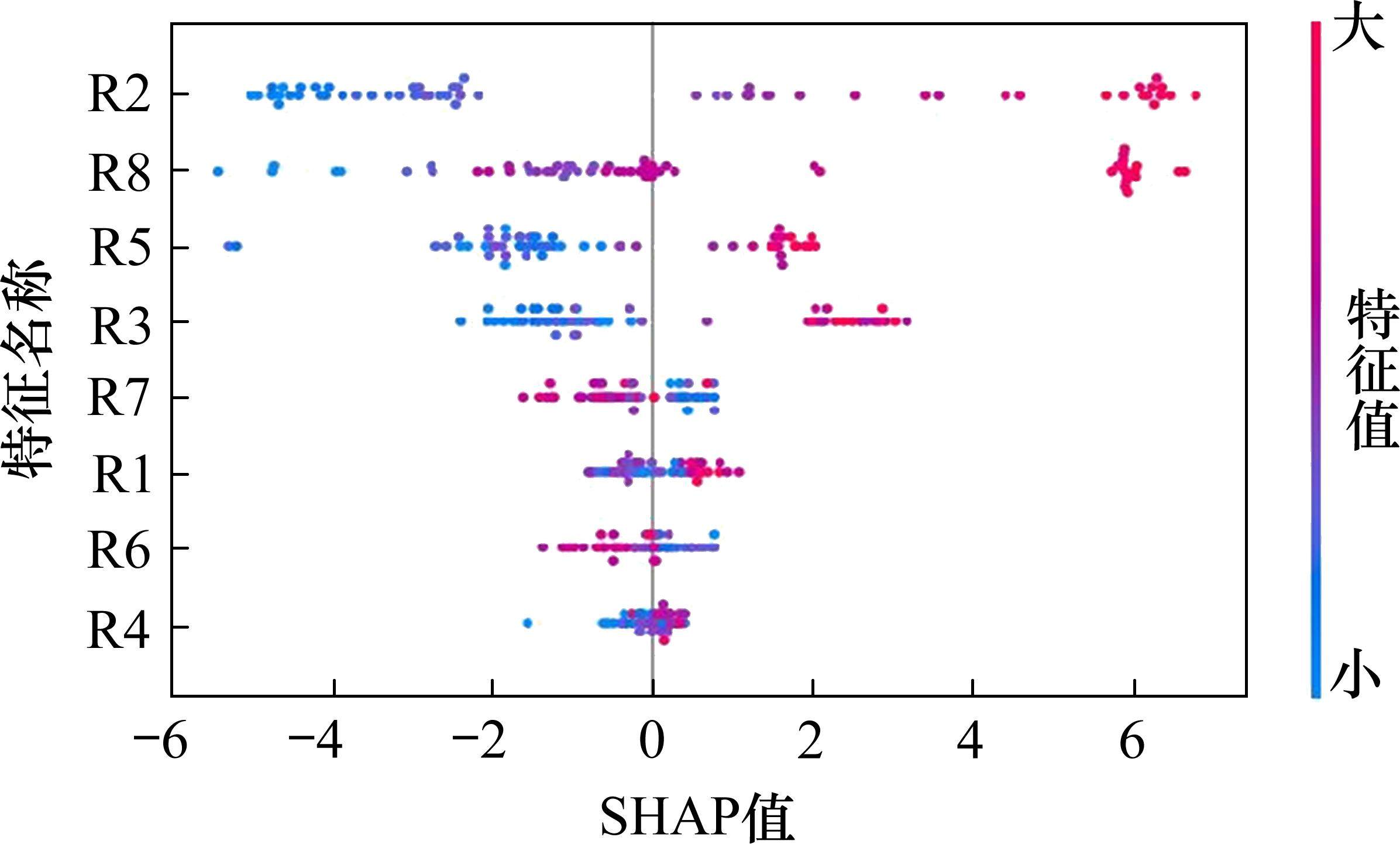
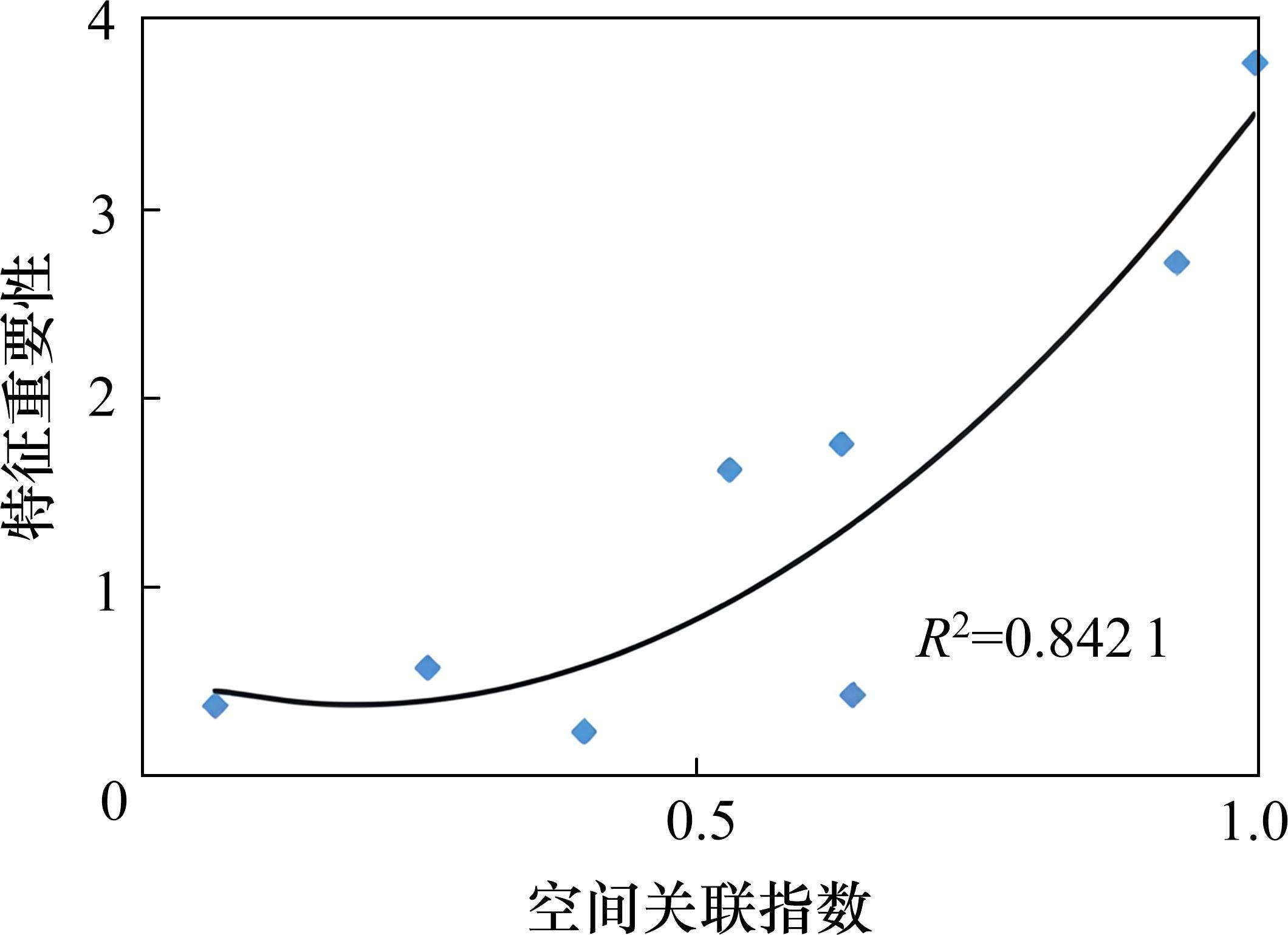
以输入的8个特征SHAP绝对值的均值作为特征重要性,开展特征重要性与各连接道路空间关联指数拟合分析,可见随着空间关联指数的增加,特征重要性随之增大,利用相关系数检验法发现,两者相关系数R为0.92,通过显著性水平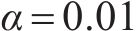
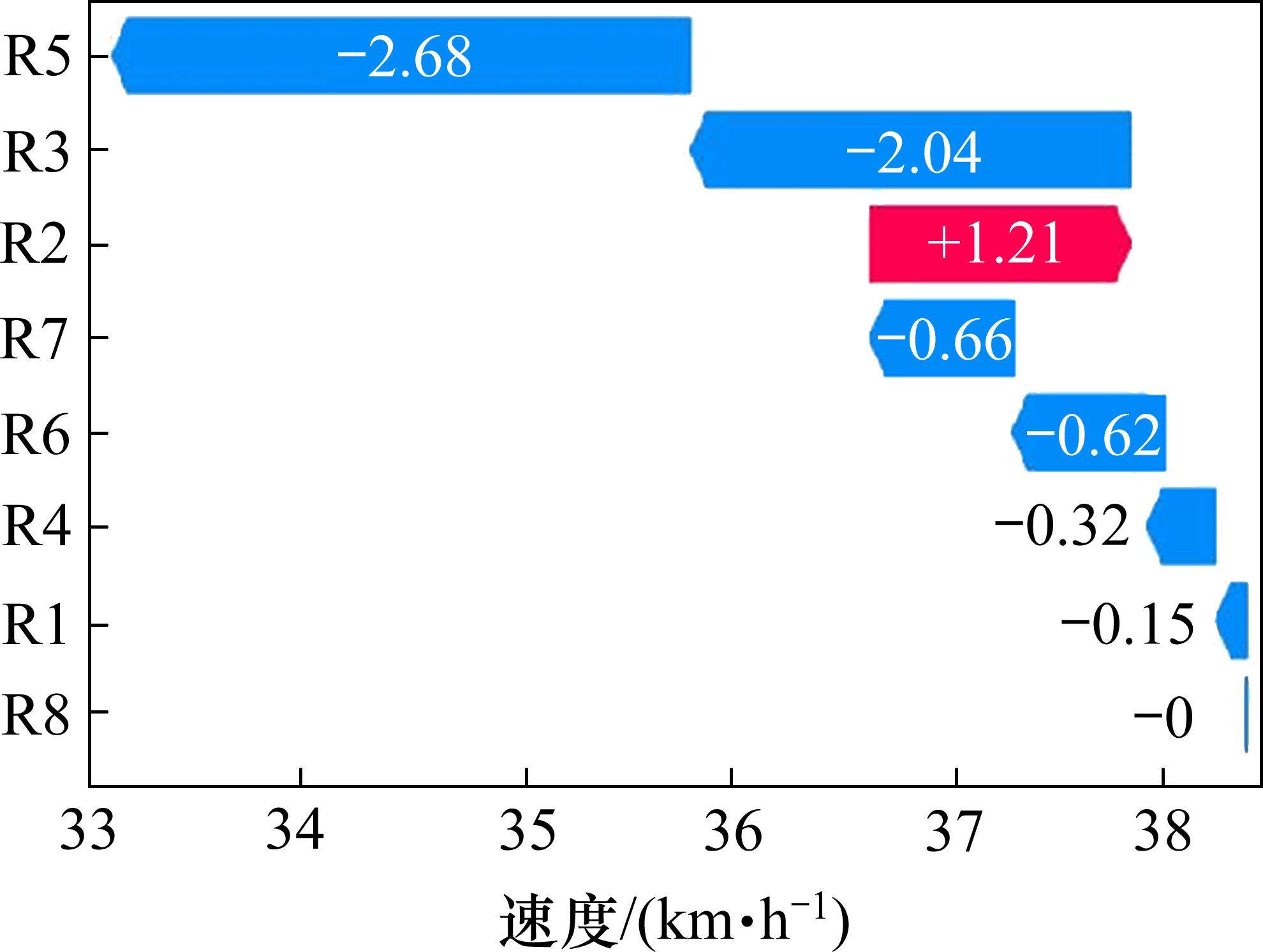
利用SHAP方法对单个样本进行预测可解释性分析,如测试集Uval中第2号测试样本预测值为33.1 km/h,真实值为36.9 km/h,预测基准值38.3(即本文中IGA-XGBoost模型的预测平均值)。单个样本预测解释图中,向左箭头为负向贡献,向右箭头为正向贡献,可见R2使预测值在预测基准值上增加1.21,R5、R3使预测值在预测基准值上减少2.68、2.04,预测基准值与所有特征SHAP值之和即为最终预测值36.9 km/h,可知SHAP方法能详细可视化出单个样本预测值的计算过程以及各特征对预测值的贡献大小,如图12所示。值得注意的是,由于上图仅展示了单个样本的特征SHAP值,单个样本中各特征重要性排序不一定完全一致,与各特征的总的重要性排序也可能存在不同。
4) 基于SHAP值的输入特征数量精度分析
本文利用与目标道路空间关联的7条道路数据修复目标道路数据,受制于数据购买成本限制、浮动车信号缺失等影响,实践中可能存在多条空间关联道路数据量不足情况,因此需要考虑在输入特征数量较少情况下对目标道路数据进行预测修复,因此选取关联道路中SHAP值排名前3、前4、前5的道路,对目标道路进行数据修复并开展精度分析。结果显示,仅使用排名前3时道路下,fMAE、fRMSE、R2分别为2.53、3.30、0.905;使用排名前5时,fMAE、fRMSE、R2分别为2.01、2.73、0.938,见表5。可见随着输入特征数量的增大,数据修复精度提高,且使用排名前3的特征数量时,模型预测精度也较高,能满足实践需求,因此实践中可利用少量SHAP值排名靠前的道路实现目标道路数据修复和分析,降低数据购买成本,提高算法应用的适应性和普遍性。
| 特征数量类型 | fMAE | fRMSE | R2 |
|---|---|---|---|
| SHAP值前3 | 2.53 | 3.3 | 0.905 |
| SHAP值前4 | 2.32 | 3.08 | 0.922 |
| SHAP值前5 | 2.01 | 2.73 | 0.938 |
4 结论
1) 构建了基于集成学习的道路行程速度稀疏数据修复算法,实现了利用连接道路运行数据对目标道路缺失数据高精度预测修复,并以重庆市中心城区实际案例为例进行验证,结果表明,组合模型对缺失数据的修复值fMAE、fRMSE分别为1.95、2.66,预测准确率R2为0.941,整体预测精度较高。
2) 提出的自适应遗传算法IGA能优化选择操作,IGA-XGBoost的R2较GA-XGBoost提高0.4%,预测精度有一定提升,运行时间为1.532 s,较GA-XGBoost的1.658 s缩短7.6%,收敛速度更快,改进算法提高了模型运行效率。
3) SHAP可解释性方法能对各输入特征重要性进行分析,并具有评价一致性特点,特征重要性与各连接道路空间关联指数呈现正相关,随着空间关联指数的增加,特征重要性随之增大,两者相关系数R为0.92,且SHAP方法可对单个样本预测结果进行溯源分析,为道路行程速度预测提供了充分量化依据。
4) 在输入特征样本数据不足时,可通过历史数据开展各输入特征SHAP值分析,选取SHAP值排名前3的道路数据,对目标道路开展数据预测修复,提升算法应用适应度。
5) 虽然本文IGA-XGBoost模型预测精度较高,能满足城市道路交通运行分析及决策需要,但是城市交通运行数据庞大,后续仍可通过数据前期预处理、特征工程以及多模型组合方式提高模型的泛化能力和鲁棒性,进一步提升城市交通大规模数据集挖掘和处理效率。
徐韬,任其亮,张磊等.考虑时空关联的道路行程速度稀疏数据修复与解释性算法[J].铁道科学与工程学报,2025,22(01):77-88.
XU Tao,REN Qiliang,ZHANG Lei,et al.Restoration and interpretive algorithm for sparse road travel speed data considering spatiotemporal correlation[J].Journal of Railway Science and Engineering,2025,22(01):77-88.


