随着我国基础设施建设的蓬勃发展,隧道已广泛应用于我国交通、水利、能源、国防等领域,其中盾构法隧道具有机械化程度高、预制构件质量可靠的特点,已成为隧道施工首选工法。盾尾间隙是指盾构机尾部壳体与管片外壁之间的间隙,盾尾间隙过小时,管片受到盾尾的挤压作用,导致管片损坏;与此相反,过大的盾尾间隙也存在漏浆的风险,因此对盾尾间隙实时检测和控制至关重要。同时盾尾各方位的盾尾间隙值反映了管片轴线与盾构机轴线的偏离程度,盾尾间隙是管片拼装选型、盾构掘进姿态调整的重要数据依据[1-2],研究盾尾间隙的精准测量方法具有重要意义。现阶段施工中多采用人工测量盾尾间隙数据,这种方式作业效率低下,高空位置处的盾尾间隙需攀爬作业进行测量,安全风险大,且人工测量误差因人而异。为了提高盾尾间隙测量的便利性,国内外学者与工程技术人员进行了大量研究,提出了不同的测量方法,主要分为接触式测量和非接触式测量。接触式测量常采用机械式测量方法,杨光等[3]、王俊杰等[4]分别开发了机械杆结合倾角仪、电阻应变片方式测量盾尾间隙,上海隧道开发了通过机械臂旋转角度测量盾尾间隙的装置[5],这些测量方法易于操作,但部分也存在易损坏且不易更换的缺点。非接触式测量方式包括超声波测量、激光测距和机器视觉检测。德国VMT公司开发了一种超声波测量盾尾间隙的设备,中铁装备公司[6]也对该技术进行了应用研究,但设备安装在盾尾内壳上,对盾尾厚度有一定要求,通用性不强。孙连等[7]通过高精度转台与激光测距仪实现盾尾间隙的机械化测量。机器视觉技术由于计算机图像处理技术的飞速发展,其精度逐步提升,通过视觉技术获取盾尾间隙方式逐渐被广泛认可。吴朝来等[8-12]采用数字图像处理技术计算盾尾间隙,先获取管片端面与盾尾的图像,再识别管片外边缘,通过像素距离计算盾尾间隙。HUANG等[13-15]通过双道线激光辅助成像,来提升图像识别方法计算盾尾间隙的精度。这些视觉检测技术需根据像素距离计算物理尺寸[16-18],传感器设备安装在盾壳表面,盾尾潮湿容易积水,容易引起设备故障。将上述盾尾间隙测量方法总结如表1所示。现有测量方法中,部分测量装置抗环境干扰性能低,对设备安装精度要求高,部分测量方法不具备通用性,部分测量方法准确性受管片构造和杂质干扰,精度难以保证;上述测量方法中测量多个位置的盾尾间隙均需配置多台传感器设备,成本高。因此,有必要研究新的盾尾间隙测量方法,以提高其在盾尾施工环境中的适用性,并确保测量结果的可靠性和精度。为实现盾尾间隙非接触式高精度测量技术,本文采用面阵结构光相机获取管片与盾尾内表面的点云数据,通过智能检测算法计算管片内表面与盾尾内表面之间的距离以精确求解盾尾间隙。与传统接触式测量系统相比,该方法无需在盾尾的内壳上安装机械设备,不易损坏;与激光测量方法相比,该方法测量的盾尾间隙方向更为准确;与现有视觉测量方法相比,该方法无需依赖盾尾伸缩油缸行程进行计算,可以独立完成盾尾间隙测量,省去现场设备标定过程,设备安装位置灵活。该测量系统可以获取三维盾尾间隙信息,通过几何空间距离求取盾尾间隙,相对于图像检测方法可以更准确地测量长度;且可以同时计算需测量位置小距离领域范围内的多处盾尾间隙,采用多点测量均值作为该位置处盾尾间隙,降低了单点测量时局部表面不平整对测量结果的影响,鲁棒性更强。研究技术路线如图1所示,本文首次采用面阵结构光系统检测三维盾尾间隙信息,测量准确度更高;创新性地设计了基于面激光点云的盾尾间隙解算算法,利用管片内表面和盾尾内表面的线间距解算盾尾间隙,取代以管片边缘点与盾尾内表面点间距解算盾尾间隙的传统计算方法,克服了边缘点不准确性对测量结果造成的误差,该算法不受相机安装位置偏差、管片及盾尾局部杂质影响;在测量系统算法中,引入粒子群优化(PSO)算法求解管片点云轴线,提升了盾尾间隙测量方向的准确度;同时,采用RANSAC算法改进最小二乘拟合法,提升了盾尾间隙解算精度。该测量系统整体精度高,鲁棒性强。
| 序号 | 测量方法 | 优点 | 缺点 |
|---|---|---|---|
| 1 | 人工测量 | 灵活方便,可测量任意位置 | 效率低,消耗人力成本,安全风险高 |
| 2 | 机械杆式测量 | 成本低,可克服潮湿、泥浆环境 | 盾尾油脂溢出时影响测量精度,装置损坏时不易更换 |
| 3 | 超声波测量 | 传感器嵌入式安装,防护等级高 | 传感器预埋在盾壳内壁中,不适用于壁厚较薄的盾构机 |
| 4 | 激光测距 | 非接触式测量,测量速度快 | 易受物体表面杂质干扰,准确性难以保证 |
| 5 | 基于图像的机器视觉测量 | 自动化,非接触式测量 | 需结合推进油缸行程数据计算盾尾间隙;管片外壁边缘倒角构造 影响管片边缘检测准确度,降低测量精度 |
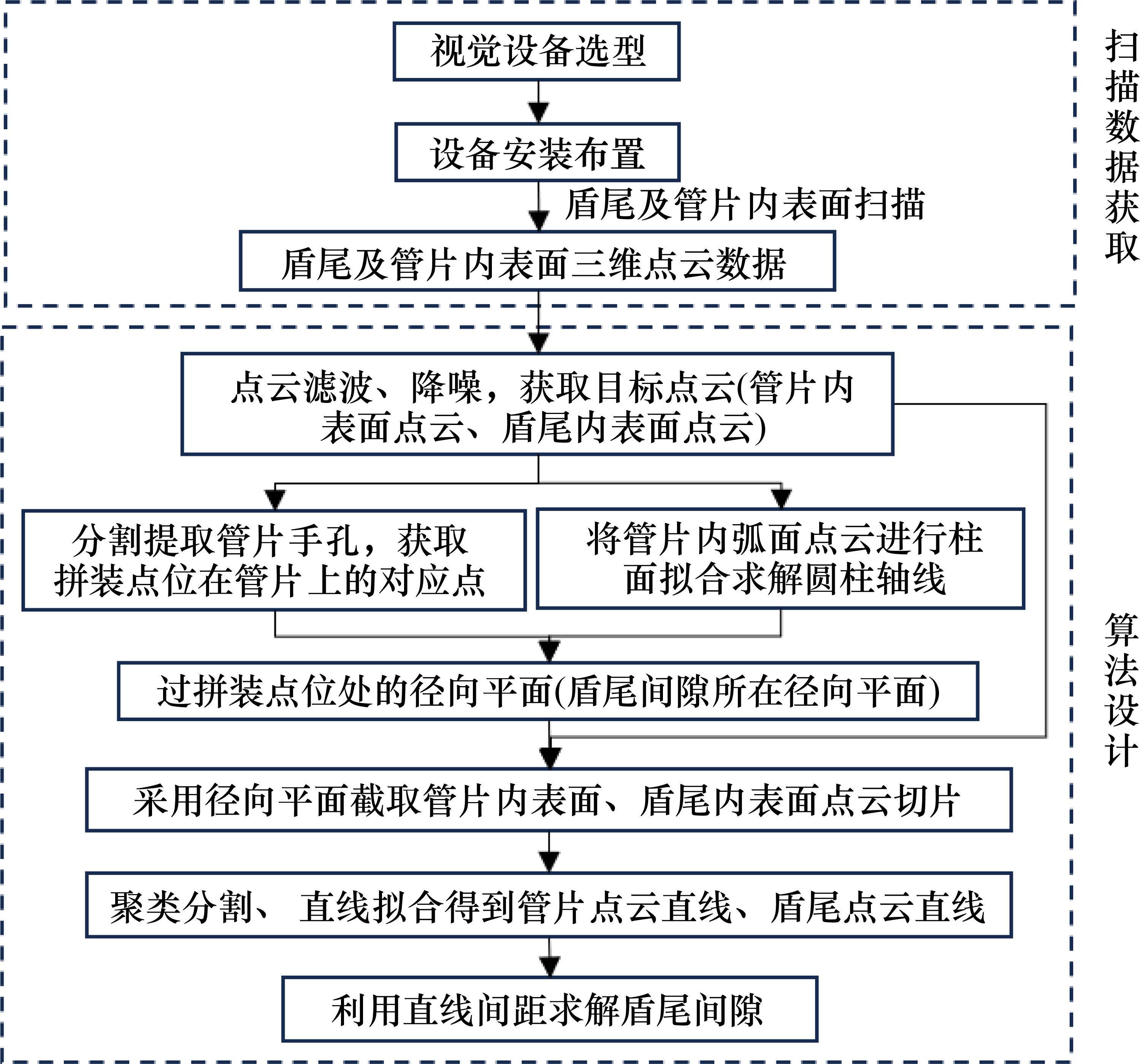
1 系统总体架构
1.1 系统概述
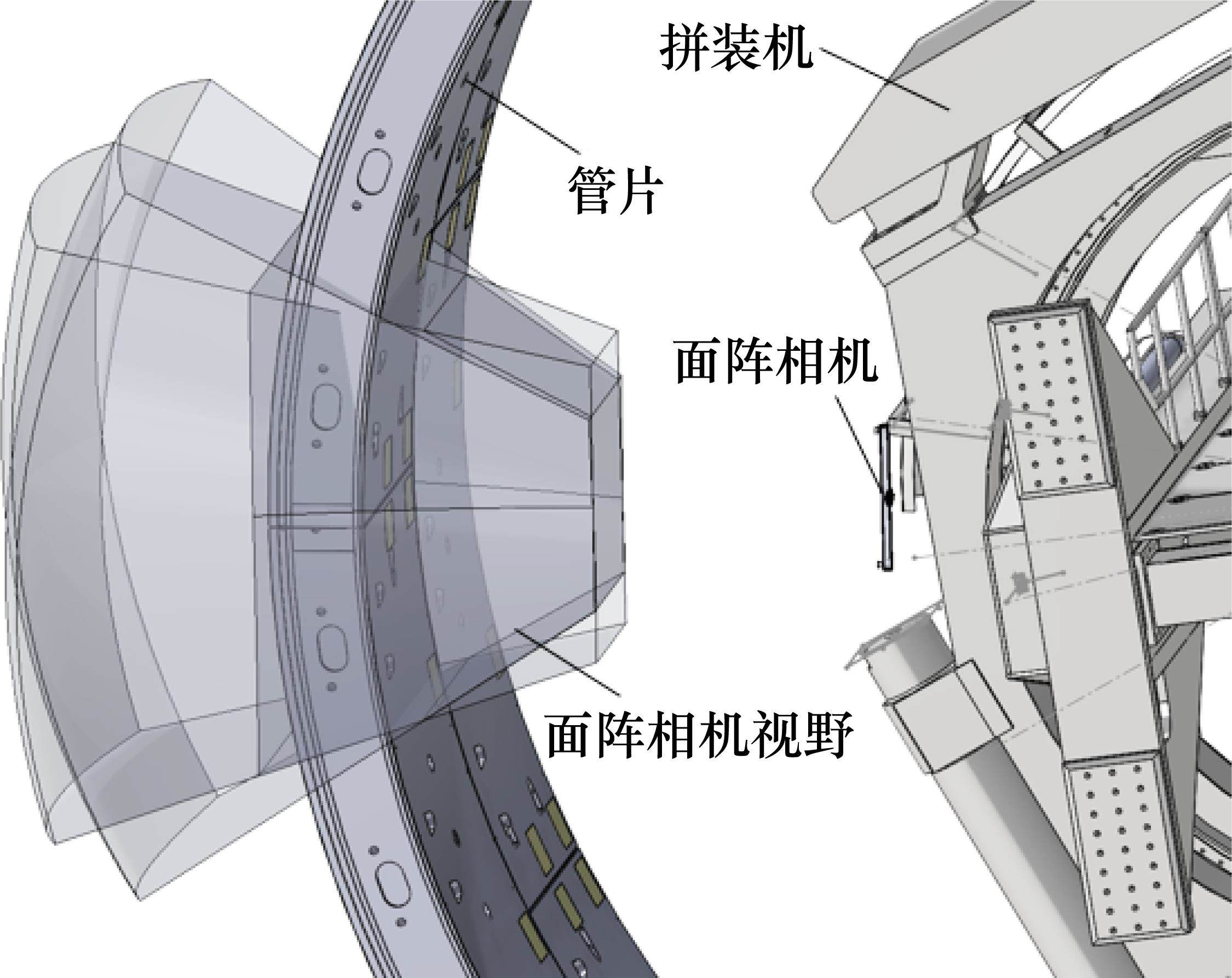
本文所述的盾尾间隙测量系统由用于获取盾尾与管片点云信息的机器视觉设备及相应的点云信息处理算法组成。总体结构如图2所示,硬件部分包括面阵相机和拼装机角度编码器。面阵相机具有分辨率高、拍摄帧率高、视野范围广等优点,可以对盾尾进行动态扫描,得到高精度的点云,适用于实时检测盾尾间隙。面阵相机安装在拼装机回转盘上,正对管片位置,如图3所示。拼装机回转盘可以绕中心转动,动态扫描时转动拼装机,面阵相机可以扫描获取不同角度处盾尾与管片内表面点云信息,通过智能检测算法进行点云数据处理,精确求解整环各角度处盾尾间隙值。不同直径盾构机中拼装机回转盘与管片内表面的距离不尽相同,可采用安装支架使相机与管片距离处于有效测距范围内。
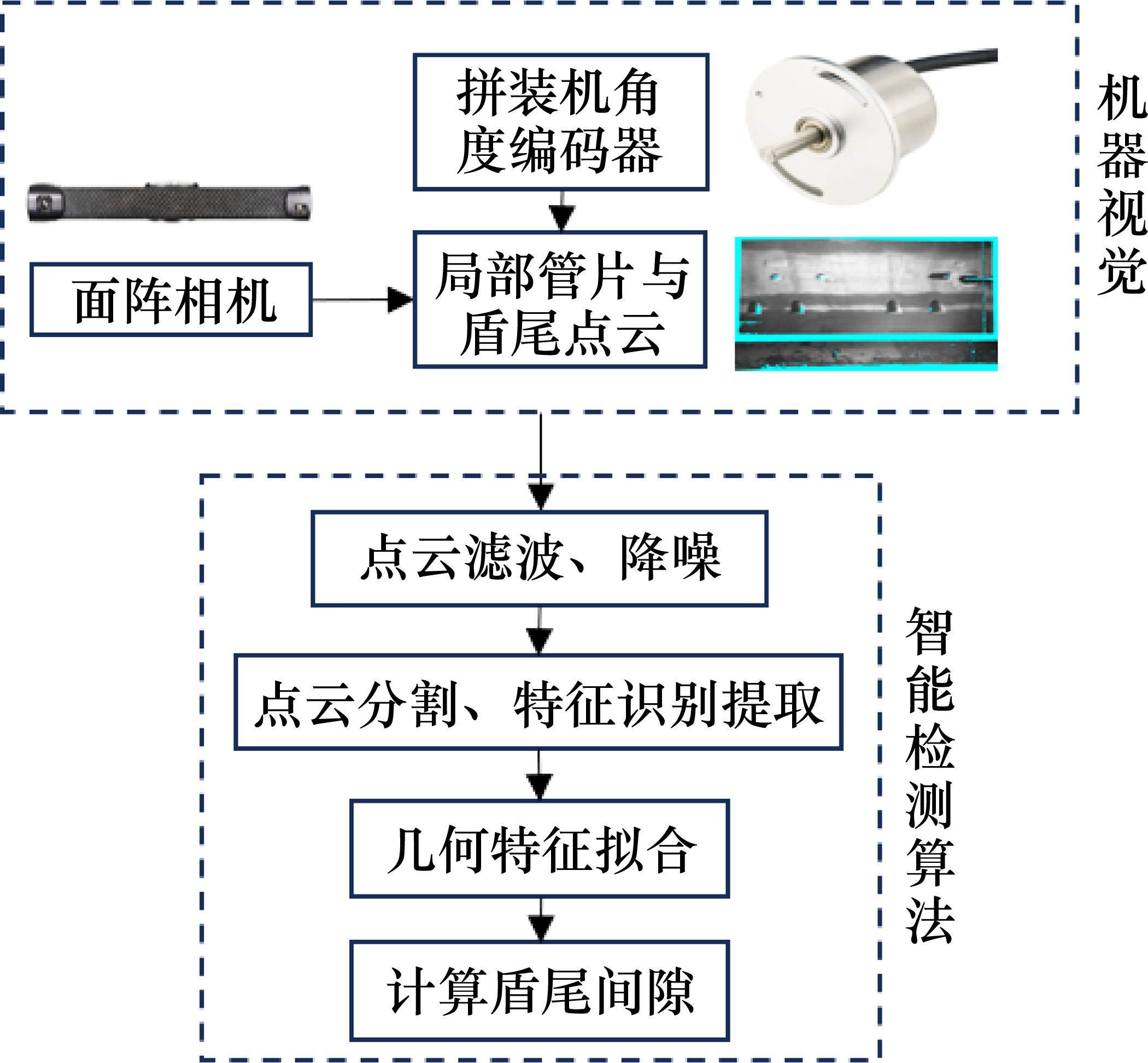
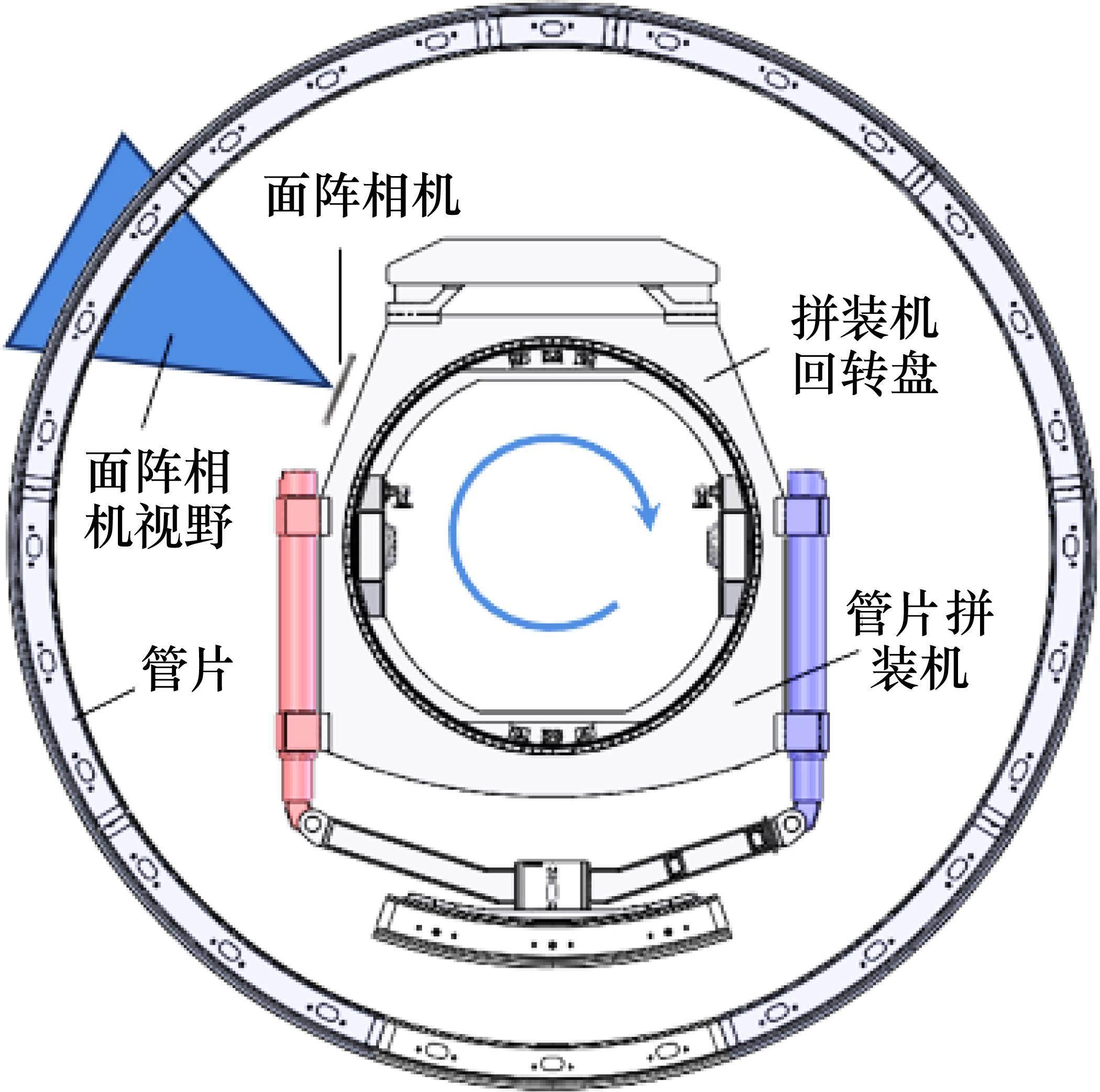
本扫描系统所获取的原始点云数据能够真实反映物体的空间坐标,具有轮廓清晰、精度高的特点,相比图像拍摄寻找管片与盾尾边缘的方法,该系统在复杂的盾尾环境中具有更强的适用性和可靠性。
1.2 机器视觉及测量原理
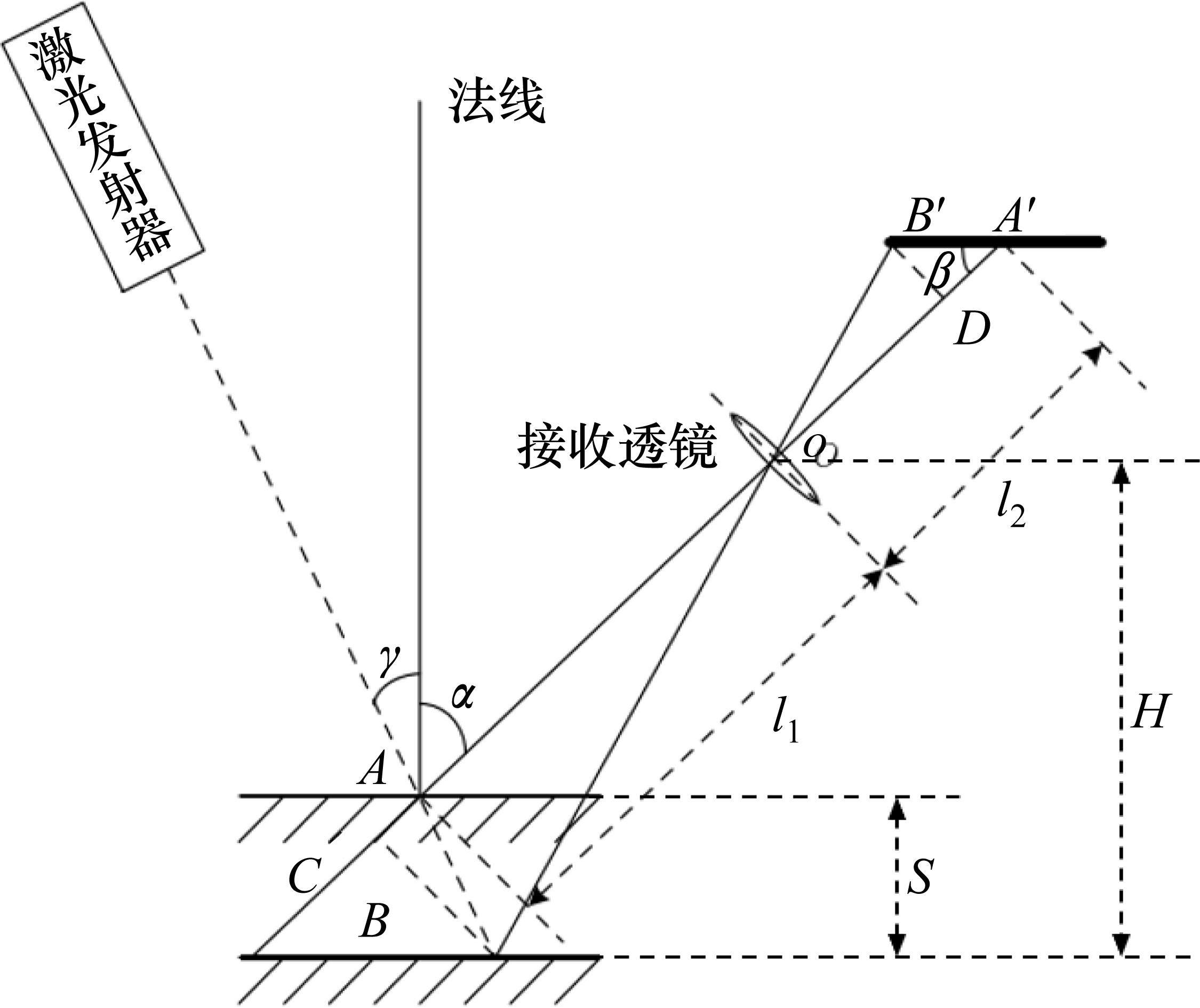
本系统机器视觉设备采用面阵相机,由激光发射器和相机组成,根据相机焦距、扫描物距范围,选择合适的入射角度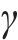
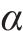
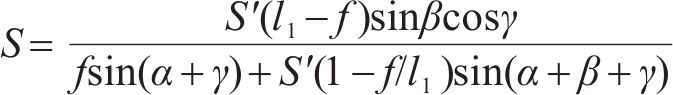
其中,f为相机焦距;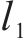
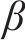
1.3 盾尾间隙计算原理
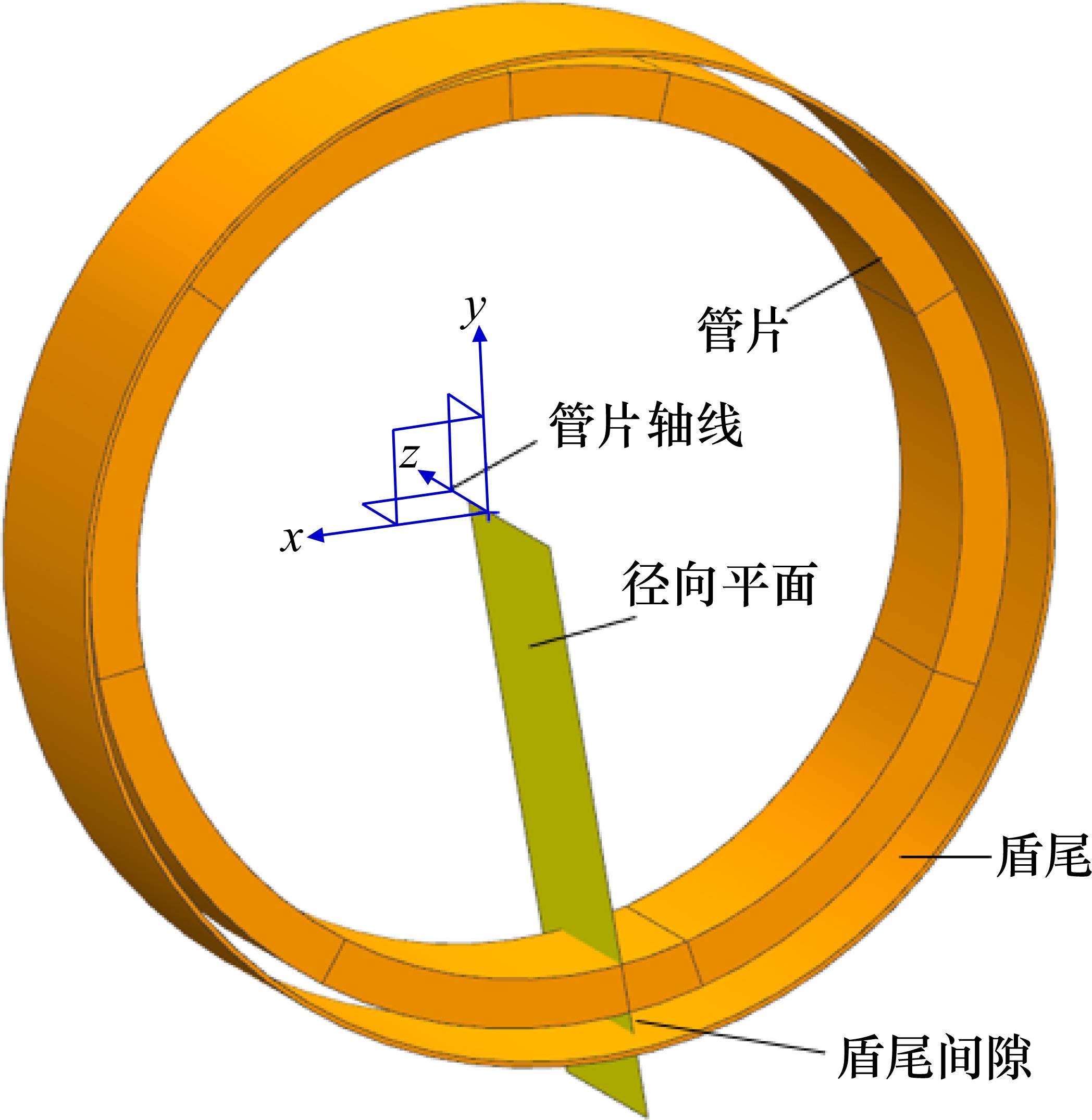
如图5所示,管片上某位置处的盾尾间隙应定义为该位置处管片外弧面距盾尾内弧面的径向距离,即径向平面与管片外弧面交线和径向平面与盾尾内弧面交线之间的距离。本文采用的面阵相机仅可获取管片内弧面与盾尾内弧面的点云数据,需先计算出检测位置处的径向平面,并求取径向平面与管片内弧面及盾尾内弧面的交线。在管片端面处,这2条交线之间的空间距离为管片厚度与盾尾间隙之和。
2 智能检测算法
盾尾间隙测量系统算法流程如图6所示,首先,求取径向平面方程,然后利用该径向平面截取管片与盾尾的点云切片。通过计算点云切片上两直线的空间距离,最终得到盾尾间隙。
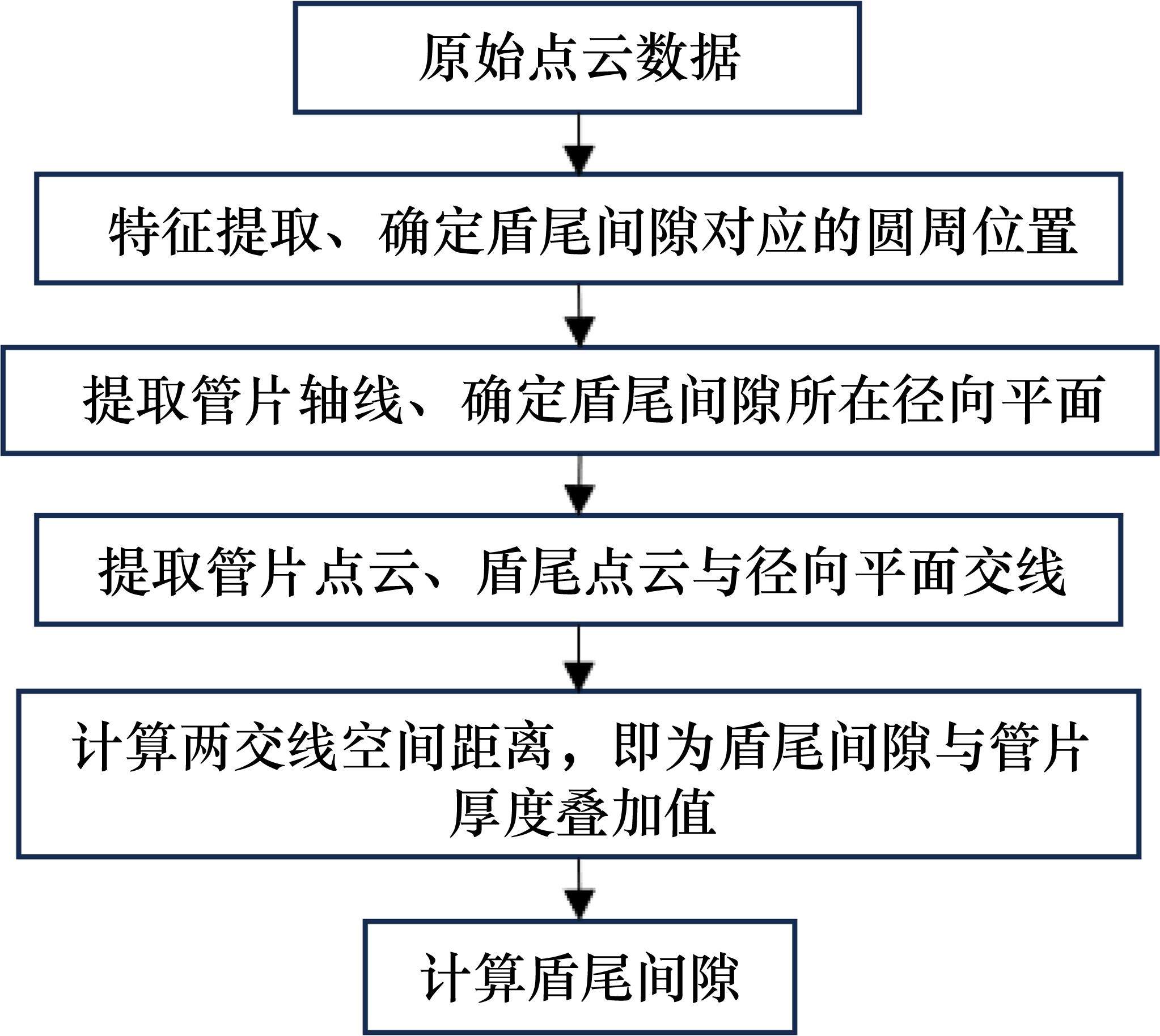
2.1 管片特征点提取算法
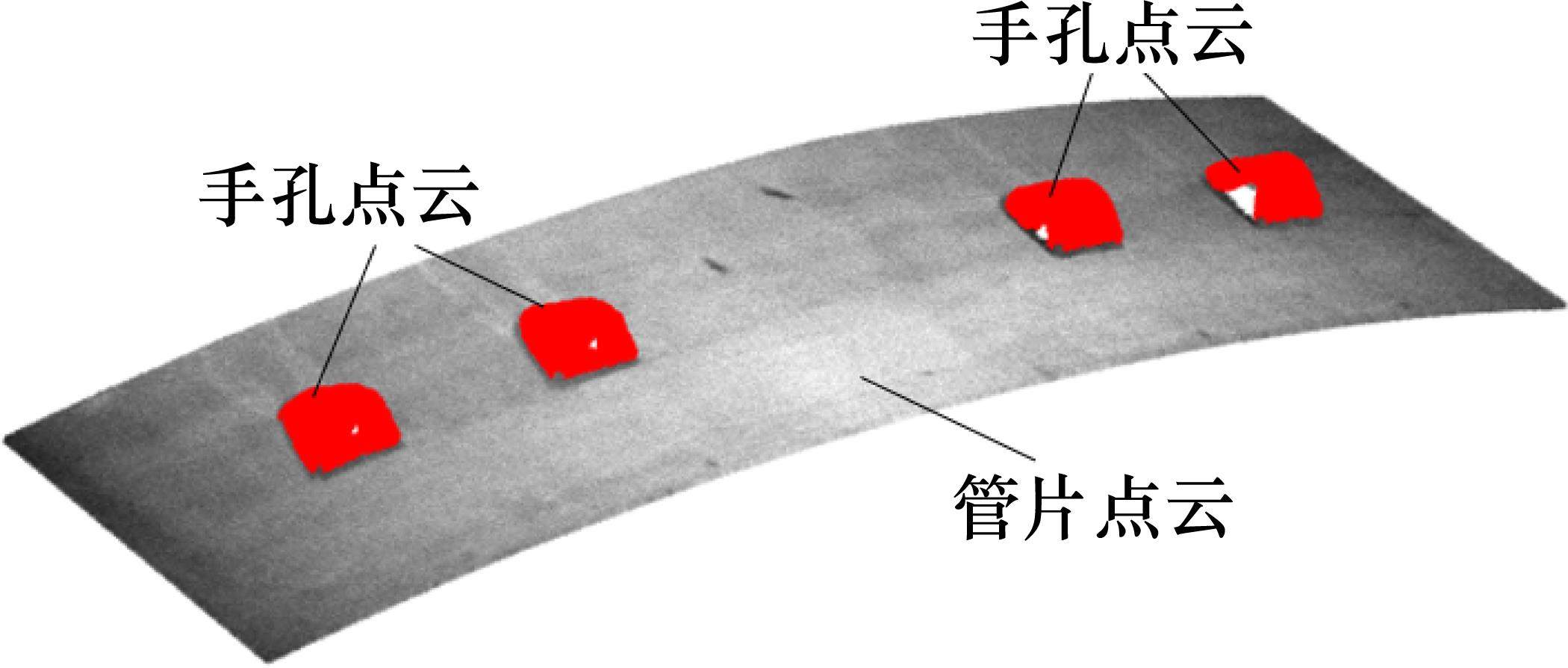
面阵相机获取的原始点云包含管片点云、盾尾点云、噪点,为了获取管片拼装点位处盾尾间隙,需要提取该检测位置处特征点坐标。基于管片几何构造特点,本文选取管片手孔特征进行特征提取。提取管片手孔后,计算各手孔中心点坐标,相邻手孔中心点连线的中点即为管片拼装点位的对应特征点。
由于设备系统误差、盾尾环境的复杂性,扫描获取的原始点云中存在多种噪点。在提取管片手孔点云前,需要先提取管片点云,并对非管片点云进行降噪处理。经过KNN算法降噪后,可以得到相对纯净的管片点云和盾尾点云。本文采用密度聚类方法将管片点云与盾尾点云进行分割,可以有效剔除所有非管片点云。
管片内弧面是一个固定半径的圆柱面,而手孔点则偏离圆柱面,采用柱面拟合的方法可以提取非管片内弧面点云。为了提升算法速度,采用RANSAC算法初步拟合管片柱面方程,其计算流程如下:1) 随机抽取管片点云中较分散的若干点,进行PCA(主成分分析)得到圆柱轴线方向向量;2) 将点云转换至与轴线方向向量垂直的平面上,拟合圆可得到圆柱半径及轴线中心坐标,确定圆柱方程;3) 计算点云中所有点偏离圆柱面的距离,计算点云中处于圆柱面上的点的百分比;4) 重复1~3过程进行多次迭代计算,选取点云中处于圆柱面上点比例最高的一组参数作为管片柱面参数解。采用上述RANSAC算法进行管片内弧面柱面拟合,同时设定合适的距离阀值,可以有效分割出管片上手孔点云,分割效果如图7所示。
2.2 管片轴线拟合算法
径向平面由拼装点位对应特征点和管片轴线确定,径向平面方向影响盾尾间隙检测精度,因此需要精准解算管片轴线。本文采用2.1节中介绍的RANSAC算法分割出管片手孔,从管片点云中剔除手孔点云得到适于拟合圆柱的内弧面点云。
在点云柱面拟合问题中,较多学者采用最小二乘法求解柱面参数,非线性最小二乘优化通常需迭代计算进行精确的拟合,较多的采用梯度下降法或内点算法进行迭代计算,部分算法需要计算海塞矩阵,收敛速度受初始值选取影响较大,且容易陷入局部最优解的情况。PSO算法[19]是一种模拟鸟类捕食行为的群体智能算法,该算法设计中保留了最优全局位置和粒子已知的最优位置2个信息,更能有效找到问题的全局最优解;PSO能够处理连续、离散等多类型优化问题,在粒子更新过程中可以并行计算,提升计算效率,且收敛速度快。本文采用PSO算法对管片内弧面点云的柱面方程进行求解,假定管片无制造误差,设定管片内半径R0已知。圆柱侧面可以表述为距离圆柱轴线L的距离为定长R0的一系列点的集合,则空间中半径已知的圆柱体包含6个参数,分别为圆柱轴线方向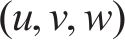
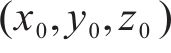
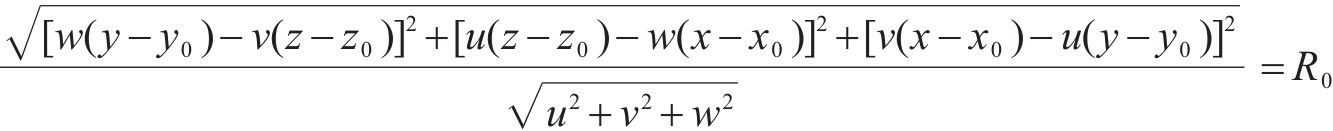
式中: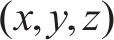
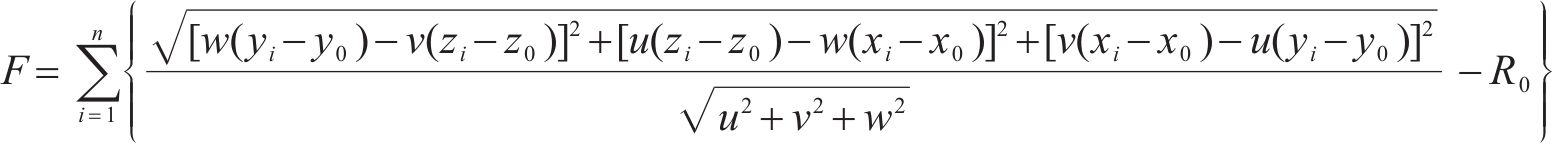
PSO算法流程可参照文献[20],设定圆柱体6个参数的边界范围和初始值后,选定粒子群规模为80,最大迭代次数为100[20],目标函数变化小于10-6时停止迭代[21]。依据相同的原始点云数据,采用传统非线性最小二乘优化中的内点法对圆柱体模型参数进行拟合,迭代停止条件设置与PSO算法相同,为便于对比,将中心坐标沿圆柱轴线方向向量移动至Y0值相同的位置,拟合结果如表2所示。
| 优化解 | PSO算法 | 非线性最小二乘-内点法 |
|---|---|---|
| X0/mm | -718.77 | -708.98 |
| Y0/mm | 0 | 0 |
| Z0/mm | -3 480.84 | -3 480.66 |
| u/rad | 0.035 6 | 0.038 1 |
| v/rad | 0.998 7 | 0.998 6 |
| w/rad | -0.035 5 | -0.034 6 |
| 目标函数值/mm2 | 1.611×105 | 6.417×107 |
2种算法拟合的中心坐标在X方向偏差9.8 mm,在Z方向偏差0.2 mm;最小二乘-内点法优化后目标函数值为6.41×107 mm2,PSO算法优化后的目标函数值为1.61×105 mm2,PSO算法优化结果更趋近于全局最优解,最小二乘-内点法优化结果可能受初始值选取影响逼近于局部最优解,PSO算法精度更高。采用PSO算法拟合的圆柱面如图8所示,管片内弧面点云与圆柱面吻合度较高,轴线位置和方向较精确。
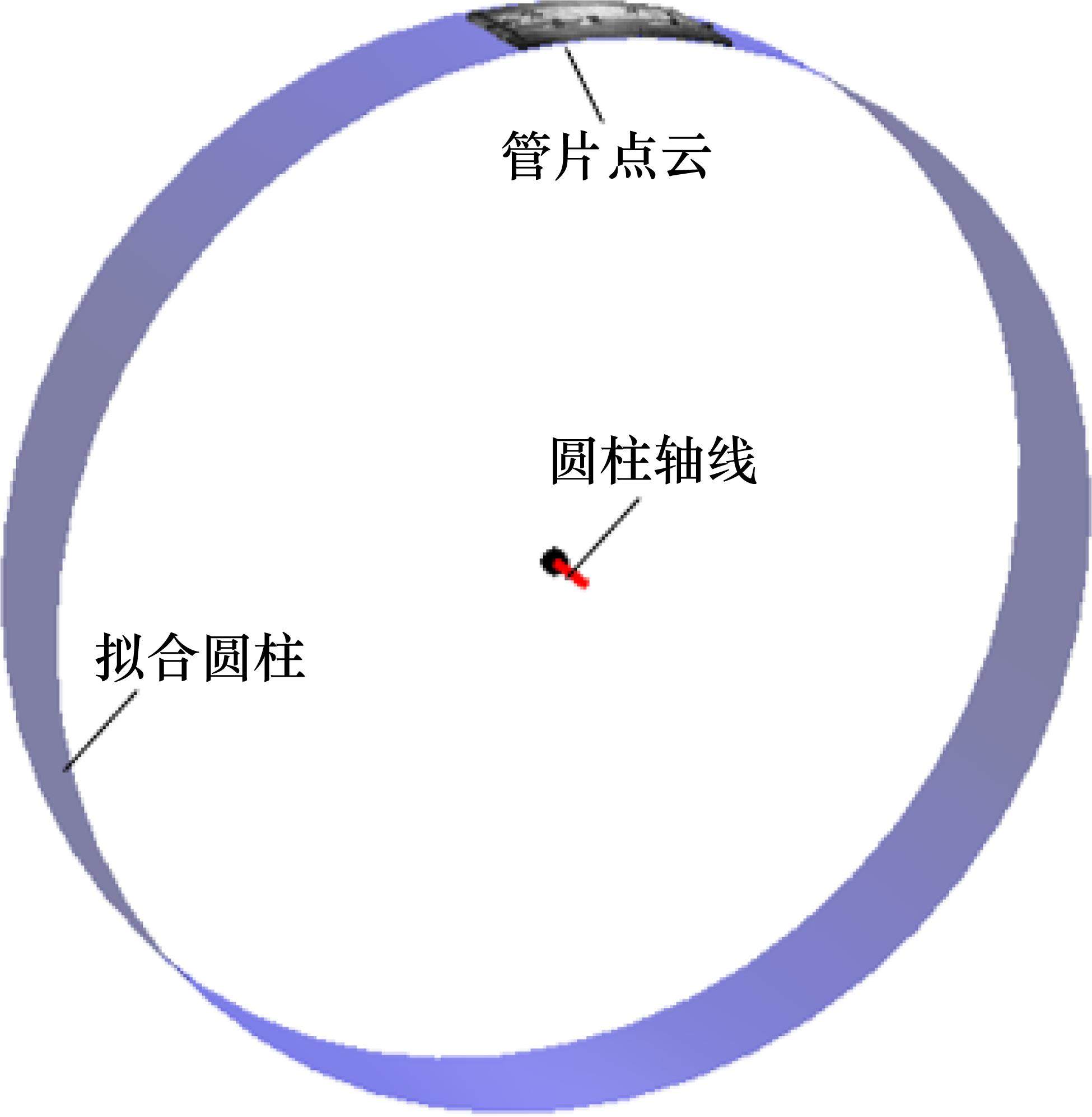
2.3 点云切片上盾尾间隙计算
根据2.1节确定的拼装点位对应特征点坐标与PSO算法拟合的圆柱轴线可确定盾尾间隙所在的径向平面。实际施工中的管片轴线与盾尾轴线并不平行,盾尾间隙应为交线B(径向平面与盾尾内弧面交线)近管片端面处端点至交线A(径向平面与管片内弧面交线)的距离扣除管片厚度之后的距离。实际获取的管片内弧面和盾尾内弧面点云由于光线传播、施工杂质等原因,存在上下起伏、难以剔除的噪点,影响交线A、交线B的拟合精度,进而影响盾尾间隙的检测精度。RANSAC算法具有较强的鲁棒性,当数据集中存在较多异常点时,最小二乘法性能显著下降,而RANSAC通过迭代随机抽样和模型验证,能够有效地忽略异常点,找到主要数据的模型参数;RANSAC在低维和高维数据中均表现良好,且内置模型验证步骤,可自动选择最优模型。为了提升径向平面与点云交线的拟合精度,克服实际扫描点云中因光照、杂质等原因产生的异常点的干扰,本文采用RANSAC算法对最小二乘法进行改进来拟合上述交线。
在进行直线拟合前,需要从管片内弧面点云和盾尾内弧面点云中提取位于径向平面上的点云,即制作点云切片。点云与径向平面存在交叉部分,将距离径向平面小于50 mm的点云进行alphaShape曲面重构,然后求解三角网格边线与径向平面交点,可以获取管片内弧面点云和盾尾内弧面点云的径向切片,如图9所示。
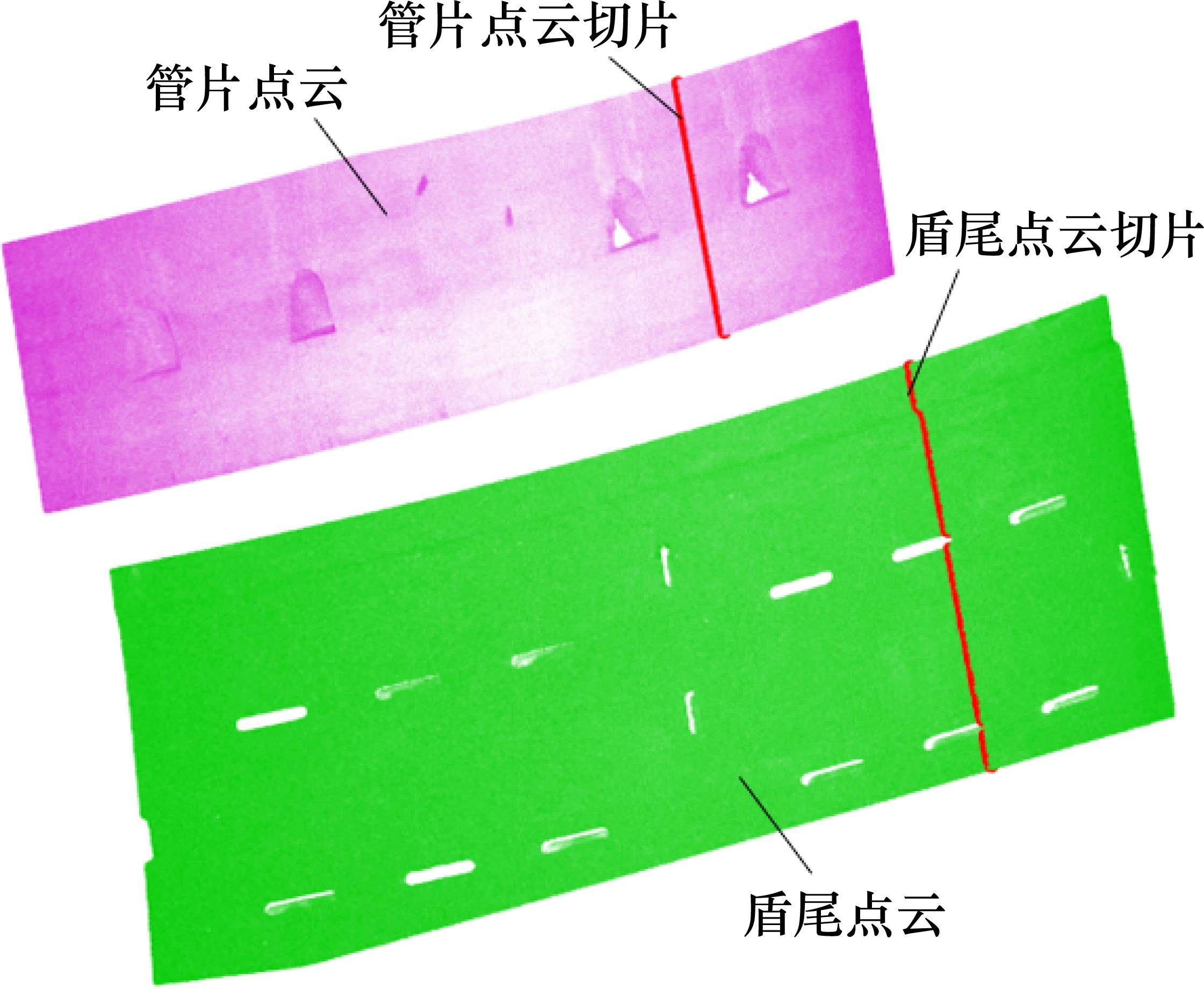
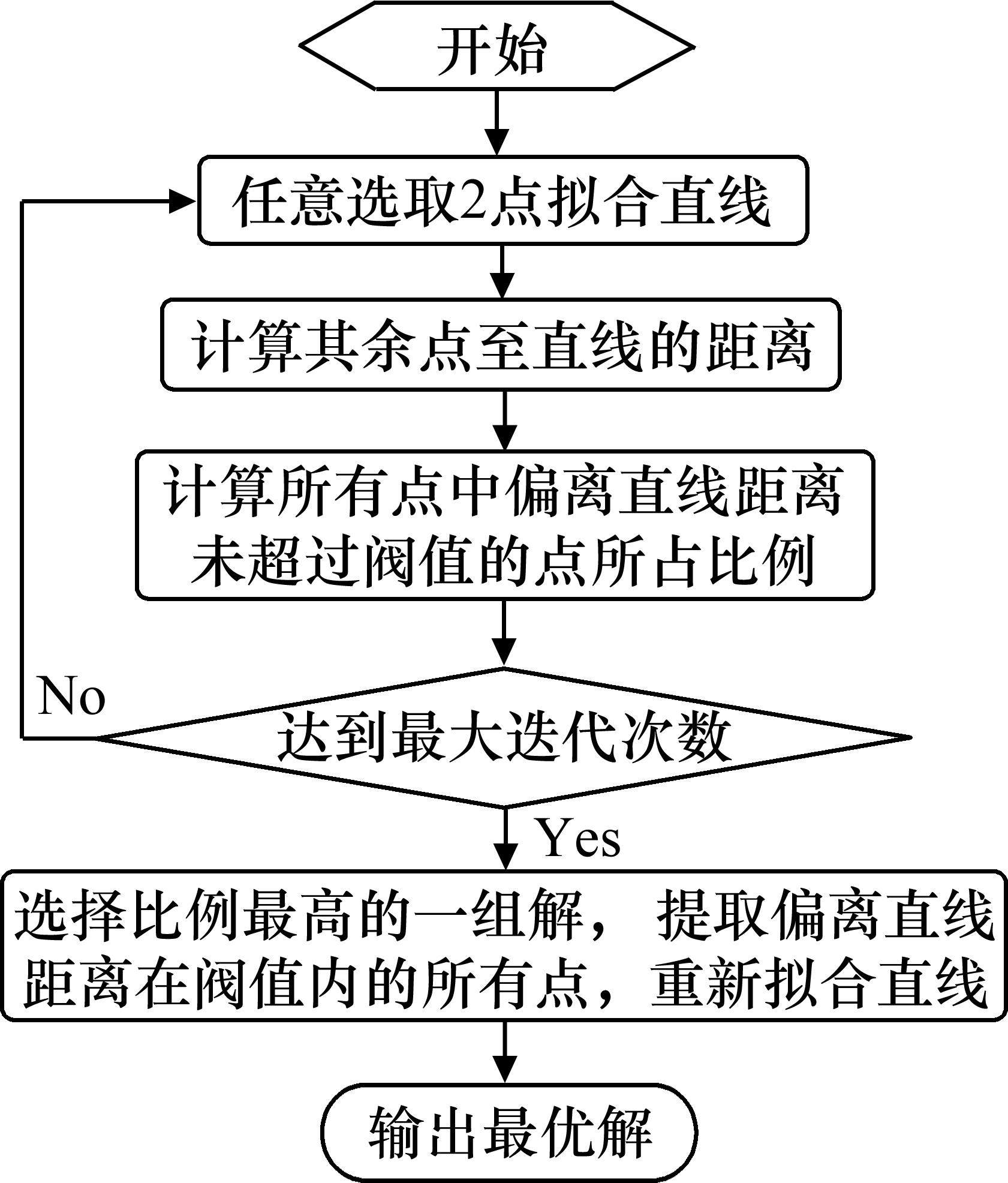
获取点云切片后采用改进后的最小二乘法对切片点云进行直线拟合,算法流程如图10所示,选择内点比例最高的一组解重新拟合直线,采用最小二乘法进行解算。直线参数方程定义为:
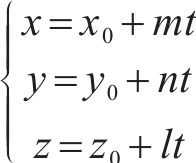
式中: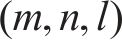
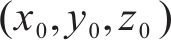
构建点云的协方差矩阵C,其矩阵元素可以表示为:
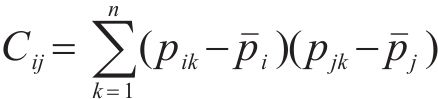
式中: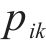
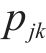
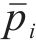
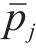
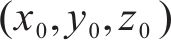
为便于对比,分别采用RANSAC算法和传统最小二乘法对径向平面与盾尾内弧面点云交线进行拟合,拟合结果如图11所示。由于盾尾内表面存在部分注浆管线或凸起钢板等原因导致盾尾内弧面点云存在部分难以剔除的噪点,传统最小二乘法拟合得到的直线受噪点影响偏离盾尾内表面较大,而采用RANSAC算法进行改进后可以避免噪点影响,拟合得到的直线更贴近盾尾内弧面,精度更高。

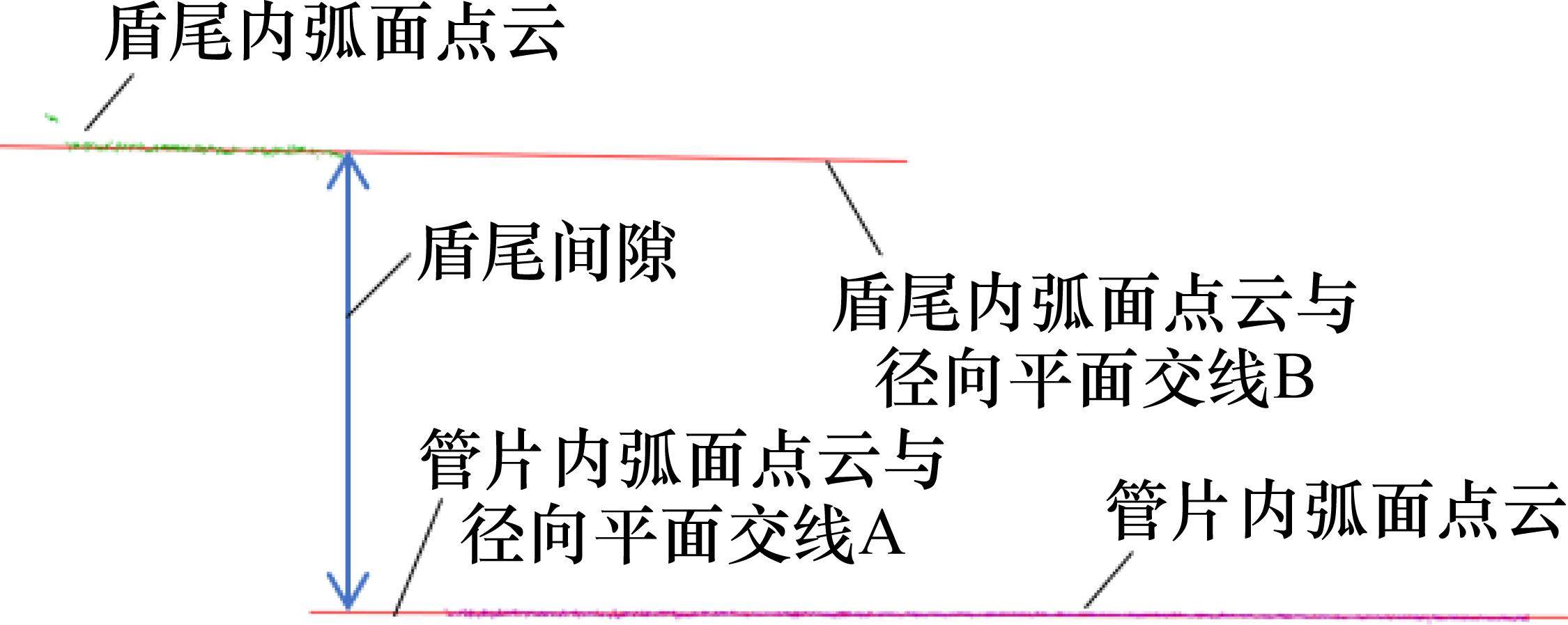
利用改进后的最小二乘法分别拟合径向平面与点云的交线A、交线B,如图12所示,提取交线B靠近管片端面侧的端点至交线A的距离,即为盾尾间隙与管片厚度的叠加值,扣除管片厚度后可以得到真实盾尾间隙值。在盾尾间隙计算中,由于实际管片和盾尾表面可能因局部破损或杂质导致径向平面截取的点云切片准确性降低,可以通过将径向平面局部偏移微小位移后重新截取点云切片来计算盾尾间隙。取多次计算的均值作为最终的盾尾间隙值,以保证测量结果的准确性。
3 试验测试与分析
3.1 测量系统布设
盾尾间隙测量系统布置方式如图13所示,面阵相机安装在拼装机的回转盘上,进行盾尾间隙测量时,可以将面阵相机回转至大致面对所需测量部位,随后进行扫描以获取该部位管片内弧面及盾尾内弧面的点云数据。通过点云处理算法计算盾尾间隙,可以实时检测该位置处盾尾间隙。
为了验证测量系统的实用性及本文盾尾间隙检测算法的准确度,在上海某盾构机内搭建试验平台开展盾尾间隙智能化检测测试,盾构机盾尾内部已拼装完一环管片,试验现场如图14所示。试验过程中对单环管片的27个拼装点位处的盾尾间隙进行了测量。

3.2 光学系统参数
本机器视觉测量系统采用Photoneo公司的 PhoXi 3D Scanner XL型号面阵相机,将面阵相机安装在拼装机回转盘外侧,正对管片及盾尾内弧面进行扫描检测,设备参数如表3所示。本次扫描物距2.7~3.4 m,满足视觉系统有效测量范围要求;视觉设备测距精度0.5 mm,满足工程中盾尾间隙测量精度要求。
| 参数 | 值 |
|---|---|
| 有效物距范围/mm | 1 680~3 780 |
| 扫描范围(物距为2.3 m时)/mm2 | 1 954×1 459 |
| 平面精度(物距为2.3 m时)/mm | 0.95 |
| 测距精度/mm | 0.5 |
| 单帧扫描点数 | 2 064×1 544 |
| 工作温度/(°C) | 0~40 |
| 拍摄参数 | 值 |
| 扫描物距/mm | 2 700~3 400 |
| 激光功率/W | 3 000 |
| 曝光/ms | 20.4 |
| 拍摄温度/(°C) | 20~25 |
3.3 算法重复精度评定试验
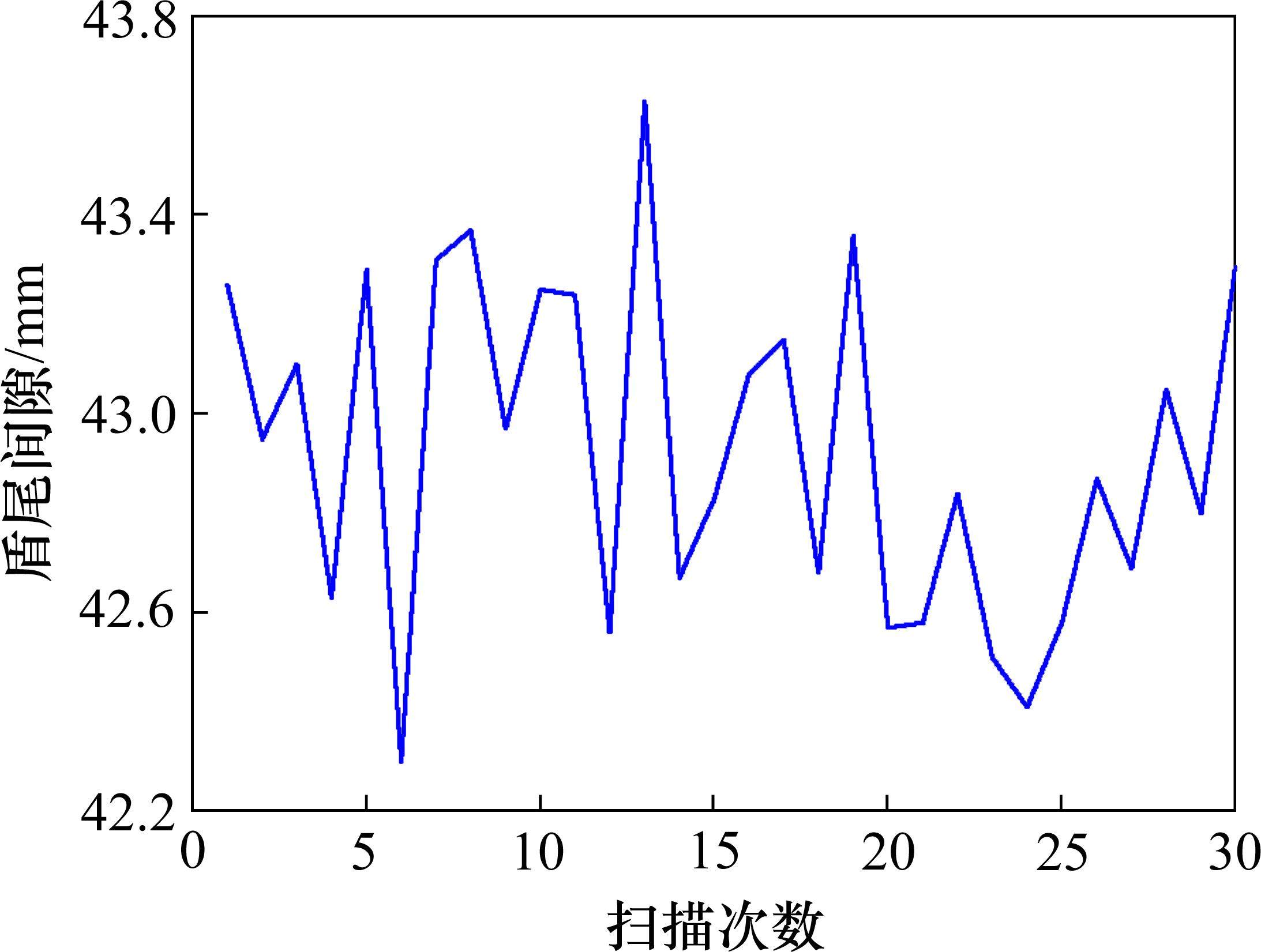
为了验证盾尾间隙检测系统的鲁棒性,对智能检测系统的重复精度进行测试。将面阵相机旋转至正对管片某拼装点位处,多次小幅度调整拼装机位置,每次扫描相同拼装点位处的管片和盾尾点云数据,如图15所示,采用本文的智能算法计算盾尾间隙。共采集30次扫描数据,所检测的盾尾间隙如图16所示,盾尾间隙在42.3~43.6 mm范围内,经过统计分析,盾尾间隙检测最大值与最小值差值为1.3 mm,标准差σ为0.33 mm,满足工程测量需求。

3.4 算法绝对精度评定试验
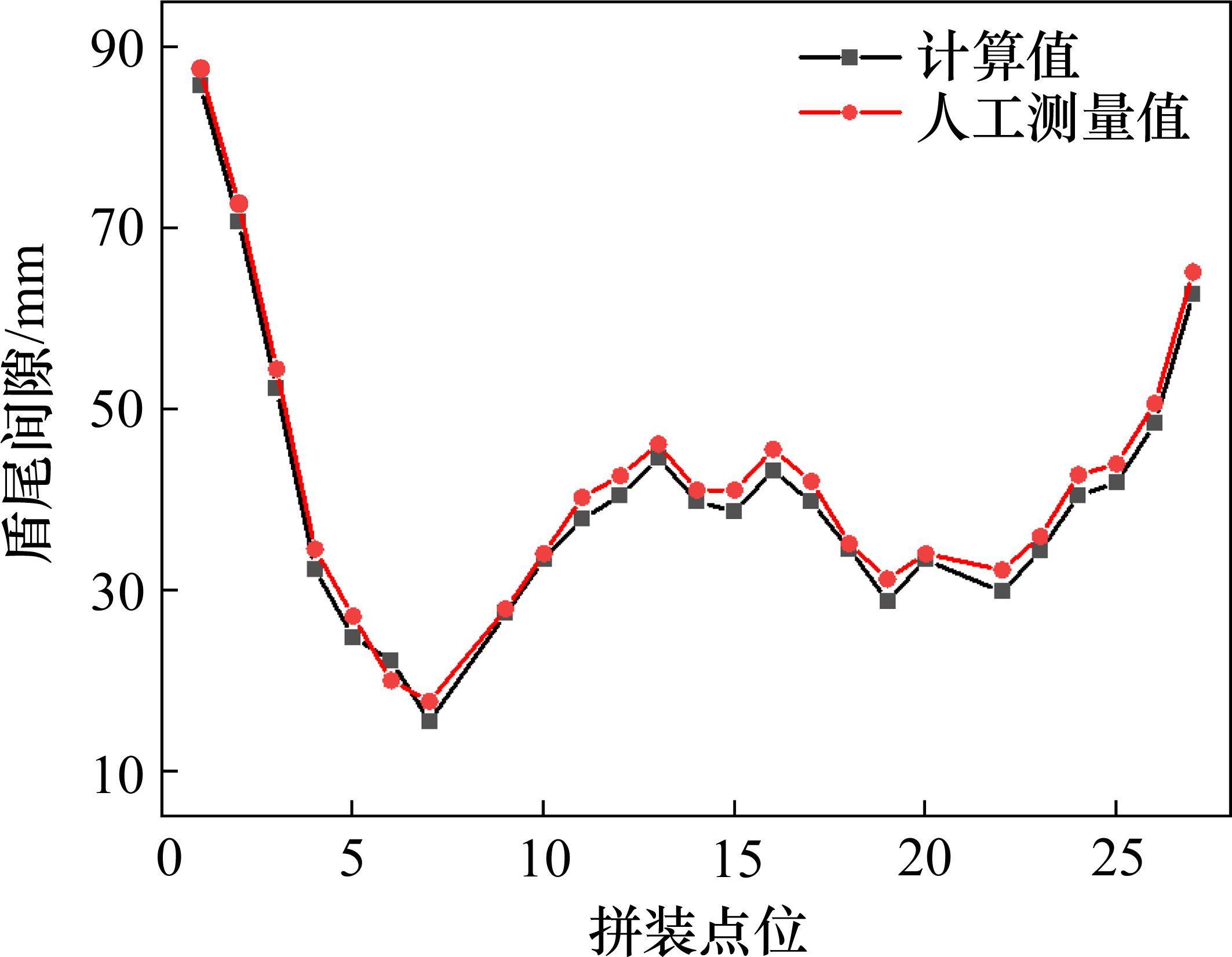
为了检验盾尾间隙检测系统的准确性,对智能检测系统的绝对精度进行测试。试验中对管片27个拼装点位的盾尾间隙进行扫描测量和人工测量,其中人工测量方式为先在管片拼装点位处做好标记,然后采用直尺测量标记位置处的盾尾间隙,如图17所示。以人工测量值为基准对本文提出的盾尾间隙检测方法进行绝对精度验证,2种方法的测量结果如图18所示。27个点位处盾尾间隙呈现出顶部点位大、底部点位小的趋势,且腰部点位盾尾间隙较小,这是由于盾尾内拼装的管片呈现横鸭蛋变形所致,隧道顶底收敛,腰部外扩。本文提出的盾尾间隙智能检测系统绝对误差小于2.4 mm,满足盾尾间隙测量需求。

3.5 测量系统抗环境光干扰试验
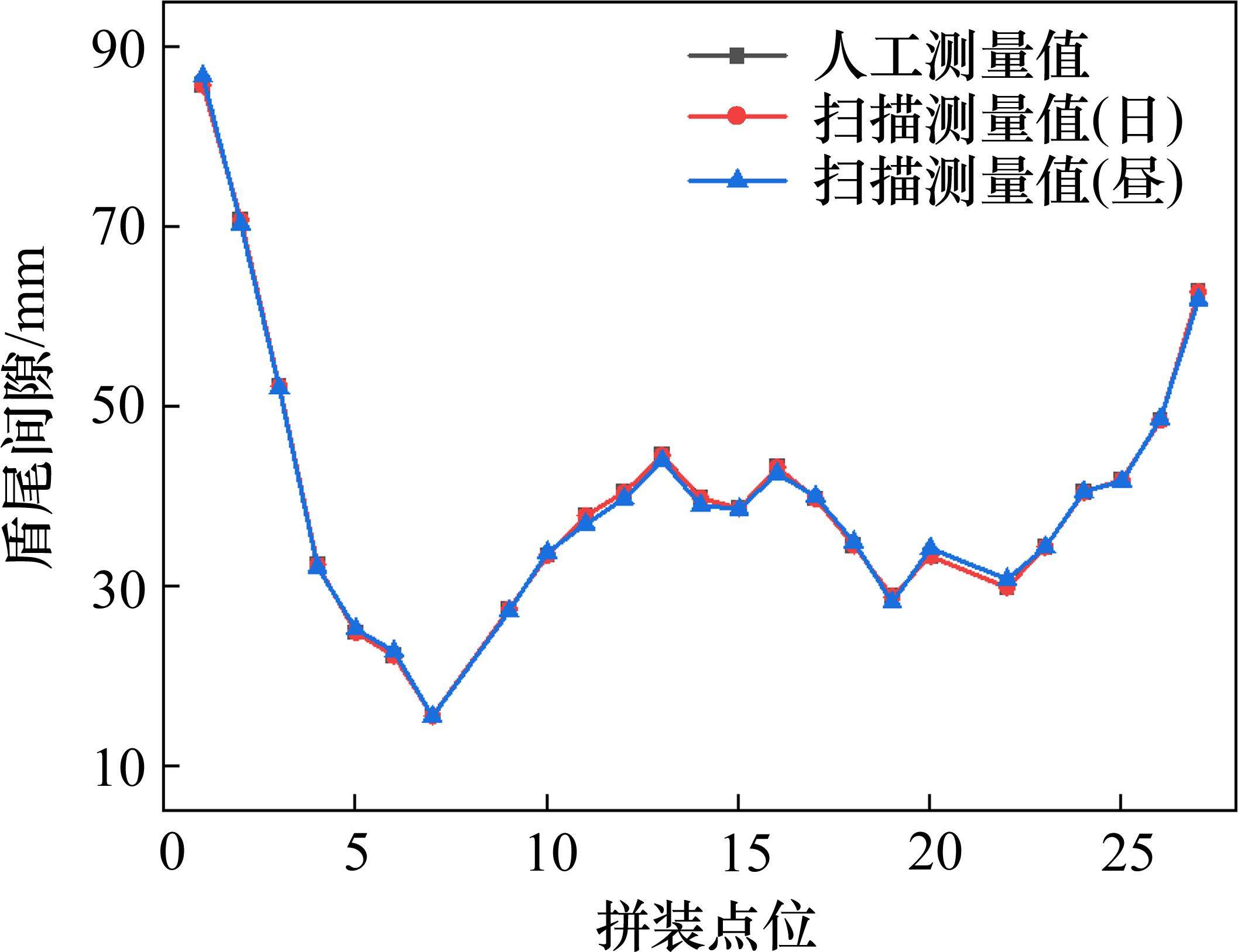
盾构隧道施工过程中,隧道内光线昏暗,且光照强度变换不定,为了检验本测量系统在实际盾构隧道施工环境中的性能,开展了不同光照强度条件下的盾尾间隙测量试验。试验中光照条件分为日(常规日光照射)、昼(无日光照射),分别在不同光照条件下扫描检测盾尾管片27个拼装点位的盾尾间隙。测量结果如图19所示,所有点位测量中无日光照射条件下测量结果与常规日照条件下测量结果最大偏差为0.9 mm,部分偏差来源于算法重复测量精度误差,与人工测量结果的绝对误差小于2.5 mm,说明本测量系统抗环境光干扰能力强,在隧道复杂施工环境中性能并未减弱。
4 结论
1) 采用粒子群优化算法进行管片点云柱面拟合,相较于非线性最小二乘拟合法,具有更高的拟合精度和避免局部最优解的能力,从而提升了管片轴线求解的精度,进而提高了盾尾间隙测量的方向准确度。
2) 在径向平面与管片或盾尾交线拟合中,利用RANSAC算法改进传统最小二乘拟合法,降低了局部噪点的影响,显著提升了交线拟合的精度,有助于整体提高盾尾间隙测量的准确性。
3) 通过现场测试,验证了本文提出的盾尾间隙智能测量系统的精度和稳定性,系统重复性测量精度优于1.3 mm,绝对测量精度优于2.4 mm,满足工程测量的需求。
4) 盾尾间隙自动化测量技术具有广阔的应用前景,可推广该技术在更多复杂工程环境中的应用,通过实际工程案例的积累,不断完善系统功能和性能;可引入深度学习技术,进一步提升系统的智能化水平,增强算法在复杂施工环境中的抗干扰能力,推动盾构施工智能测量技术的发展。
胡秋斌,毛仁利,庄欠伟等.基于机器视觉的盾尾间隙智能检测方法研究[J].铁道科学与工程学报,2025,22(03):1357-1368.
HU Qiubin,MAO Renli,ZHUANG Qianwei,et al.Intelligent detection method of shield tail clearance based on machine vision[J].Journal of Railway Science and Engineering,2025,22(03):1357-1368.

