在“公转铁”政策的推动下,我国铁路货运量实现了显著增长,截至2023年底,国家铁路货运总发送量已达39.11亿t,连续7年的稳步增长展现出铁路货运市场的巨大潜力[1]。随着铁路货运加速向现代物流转型,市场对货运产品运输时效和服务质量的要求也愈发提高。据统计,货车在站停留时间约占其总周转时间的2/3,是影响货物运输时效的关键因素[2]。而专用线作为连接铁路与厂矿企业的桥梁,是车站运输网络的重要组成部分,目前全国铁路共有超过8 000条专用线,约80%的货物在专用线进行装卸作业。优化铁路专用线取送车作业过程,对于缩短货车在站停留时间和提高货物运输效率有着重要的作用。铁路专用线按布置形式可分为树枝形、放射形和混合型3种类型,其中兼具树枝形和放射形特点的混合型布置形式在我国铁路车站中占比最大[3]。在树枝形布置形式中各专用线集中分布于单一放射枝的一侧或两侧,取送作业时无需返回车站便可在就近节点折返;在放射形布置形式中各专用线分别位于多条放射枝上,必须返回车站才能进行下一批取送作业。而在混合型专用线中,同一放射枝的作业性质与树枝形相同,在跨放射枝间作业时则与放射形相同。在铁路专用线取送车问题的早期研究中,学者们普遍采用图论方法进行探索,通过构建相应的数学模型来优化取送车顺序,以期达到提高作业效率和降低运营成本的目的[4-6]。JAEHN等[7]研究解决平面调车场取回货车问题,提出混合整数规划模型,设计了可在多项式时间内求解的精确算法。ALYASIRY等[8]设计精确算法求解取送车问题,采用片段构建网络流模型,通过实例求解验证了算法的有效性。张文晰等[9]建立了最小化直达车流总停留时间的数学模型,采用隐枚举算法,并结合作业准则和代价评估,有效求解了树枝形专用线的取送车问题。程磊等[10]设计了改进元胞蚁群算法,通过优化转移概率与信息素策略,并融入元胞自动机规则,实现对树枝形专用线取送车问题的有效求解。GUO[11]综合考虑调机牵引能力及货物作业优先级等多重因素,对树枝形专用线取送问题展开研究,并设计了启发式算法实现对问题的求解。近年来,学者们从多调机、不同车流到发方式等角度广泛研究了树枝形和放射形专用线取送车问题,并设计多种求解算法,实现了大规模取送车问题的高效求解[12-15]。随着树枝形和放射形专用线取送车问题研究的深入,学者们开始对更为复杂的混合型专用线取送车问题展开研究,分析考虑调机访问次序、车组作业顺序和牵引能力限制下的最优取送方案[16-18]。LI等[19]提出多种专用线取送车组合策略,并应用Arena软件开发了包含典型调车模式的仿真平台,在多种场景下验证了取送车策略的合理性和应用效果。在铁路专用线取送车问题的研究中,国内外学者对树枝形和放射形专用线的研究较为深入,涵盖了图论、整数规划和启发式算法等多种方法,但对于更为复杂的混合型专用线取送车问题研究相对较少。在混合型专用线中,穿越正线调车作业(以下简称侵正作业)时会影响正线行车,调机需要在图定客车车次的间隙时间窗内穿越正线,这在传统模型中难以体现。本文在模型构建中综合考虑了侵正作业时间窗约束和各批次任务的具体作业时间,从而提高运输方案的指导性及现实可操作性。同时考虑到模型的计算复杂度和问题规模,设计了基于优势基因结构的微进化算法进行求解,并结合案例验证模型和算法的有效性,有助于提高专用线取送车作业效率,缩短货车在站停留时间,为混合型专用线取送作业方案的快速决策和科学编制提供理论支撑。
1 问题描述
本文对混合型专用线布置形式车站的取送车计划编制问题进行研究。以最小化调机作业时间与货车取送影响时间为目标,综合考虑取送顺序、调机牵引能力、专用线容车数、装卸时间、侵正作业时间窗、作业及批次接续等限制条件,确定合理的专用线取送方案。
以某混合型专用线布置形式车站为例,构建取送作业网络如图1所示,车站专用线由r1~r3这3条放射枝下的i1~i4共4条专用线组成。为便于描述调机在专用线的取送作业过程,将车站及专用线拆分为车站节点、专用线节点和走行节点,各节点间由走行弧段相连接,包括站内走行弧、专用线走行弧和取送走行弧3类。由于车站共衔接r1~r3这3条放射枝,因此在网络图中按衔接方向将车站拆分为A~E共6个车站节点,各节点间由站内走行弧连接;i1~i4这4个专用线节点通过专用线走行弧与1~8的8个走行节点相连,走行节点与车站节点间由取送走行弧连接,调机在专用线的走行径路可用连续弧段表示。定义从车站出发到再次回到车站的取送作业过程为1个批次,每个批次可以完成多项作业任务
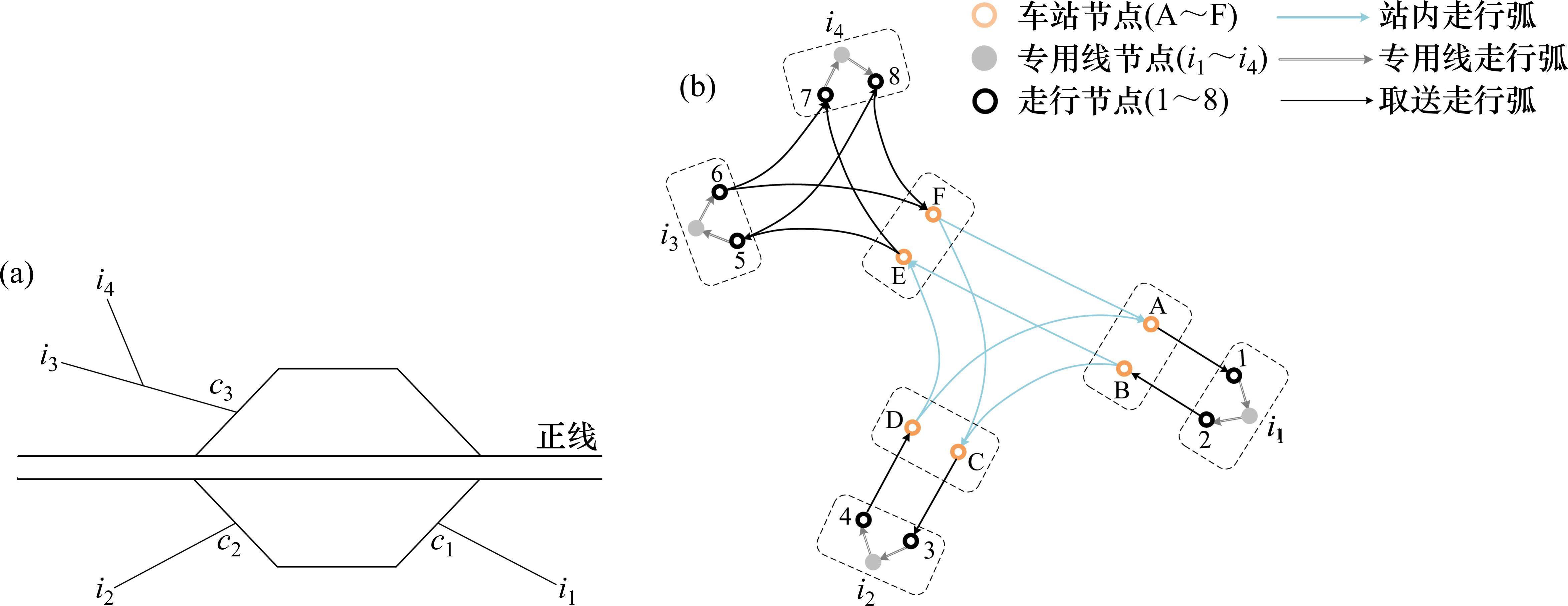
由于每个取送批次
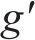
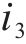
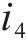
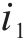
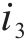
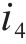
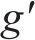
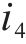
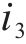
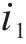
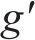
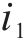
2 模型构建
2.1 模型假设
为便于建模研究,结合调车作业实际情况,本文做出如下假设:
1) 作业车组均为1次货物作业车;
2) 取送车作业由1台调机完成;
3) 各专用线间走行时间已知且不受调机牵引车数影响。
2.2 符号说明
本文模型中所涉及的集合、参数和变量符号及其定义如表1至表3所示。
| 符号 | 定义 |
|---|---|
 | 专用线节点集合, 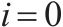 |
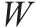 | 取送作业走行弧段集合, 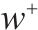 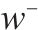 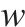 |
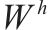 | 侵正作业走行弧段编号集合, |
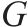 | 取送作业任务集合,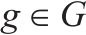 |
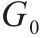 | 虚拟作业任务集合,表示调机作业过程,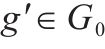 |
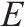 | 作业批次集合, |
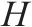 | 侵正作业时间窗集合, |
| 符号 | 定义 |
|---|---|
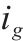 | 第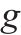 |
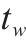 | 在弧段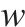 |
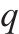 | 调机的最大货车牵引辆数限制/辆 |
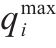 | 专用线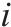 |
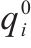 | 专用线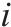 |
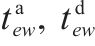 | 第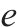 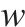 |
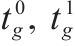 | 第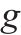 |
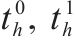 | 侵正作业时间窗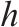 |
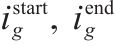 | 第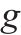 |
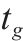 | 第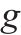 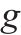 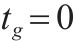 |
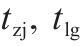 | 摘解和连挂作业时间/min |
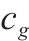 | 第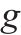 |
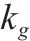 | 取送作业性质,第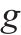 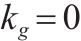 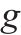 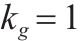 |
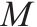 | 一个足够大的正数 |
| 符号 | 定义 |
|---|---|
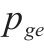 | 第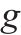 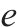 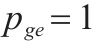 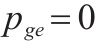 |
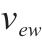 | 第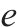 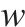 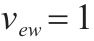 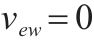 |
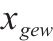 | 第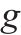 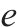 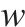 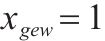 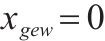 |
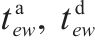 | 第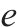 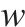 |
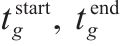 | 第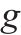 |
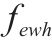 | 第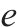 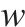 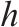 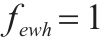 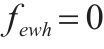 |
2.3 目标函数
本文的优化目标是在减少调机作业时间的同时加速货车周转。为此,在构建目标函数时,不仅考虑了调机作业时间最小化的目标,还考虑了减少一次货物作业平均停留时间的目标,从而更好地兼顾专用线取送车作业的效率与经济性。调机作业时间包括取送走行时间和在专用线等待货运作业的时间,一次货物作业平均停留时间受到列车到达、解体、集结、编组、出发的行车组织过程,以及车组的待送、送车、装卸车和取车的调车和货运作业过程共同影响[3]。其中行车组织过程由列车运行计划确定,而调车和货运作业方案则直接影响货车的在站停留时间。为更好地衡量取送作业策略对1次货物平均停留时间的影响关系,定义调车和货运作业过程的总时间为货车取送影响时间,确定目标函数如式(1)所示。
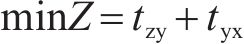
调机作业时间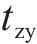
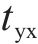
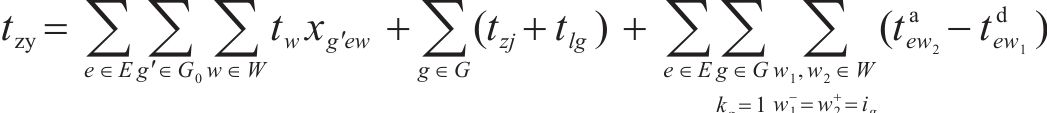
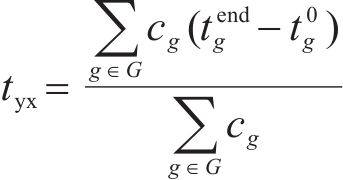
2.4 约束条件
1) 能力相关约束
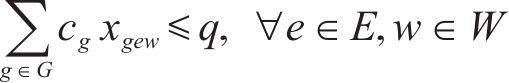
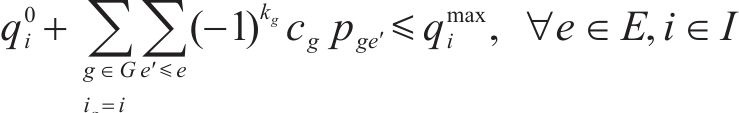
式(4)表示调机最大牵引能力约束,在每批取送作业过程中调机的牵引辆数不能超过调机的最大牵引能力;式(5)表示专用线最大容车数约束,在每批取送作业过程中各专用线的存车数不能超过专用线的最大容车能力。
2) 取送作业流平衡相关约束
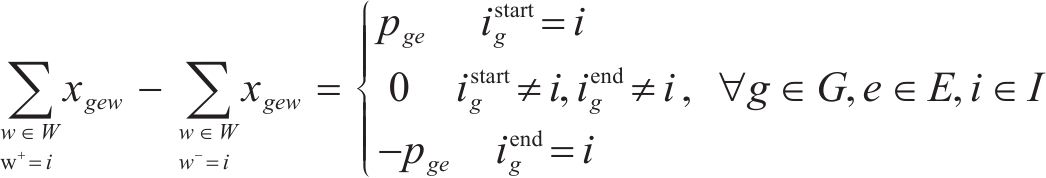
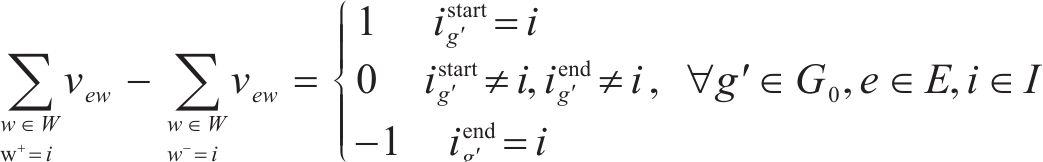
式(6)表示取送作业过程中的任务流平衡约束,用来确保服务网络中每次作业的节点流量平衡,同时确保所有运输需求得到满足;式(7)表示取送作业过程中的批次流平衡约束,用来确保每批次作业中调机的路径连续合理。
3) 取送作业时间相关约束
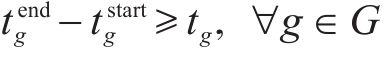
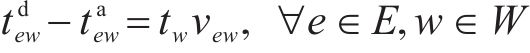
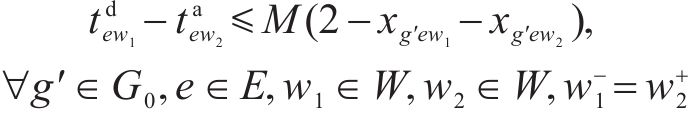
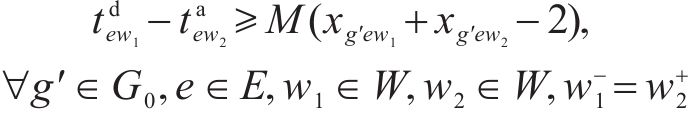
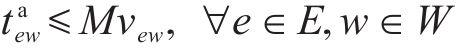
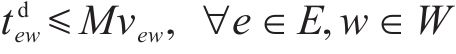
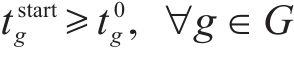
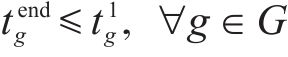
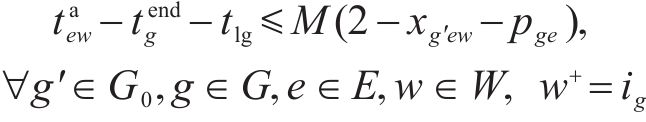
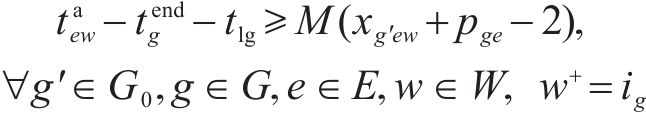
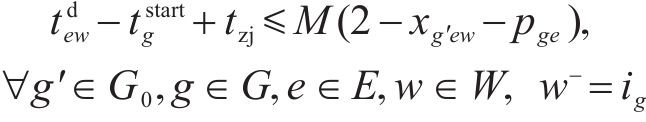
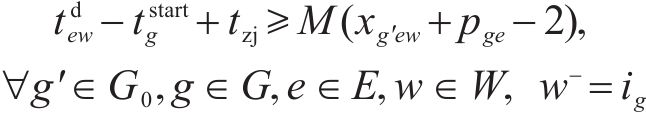
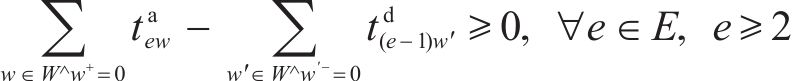
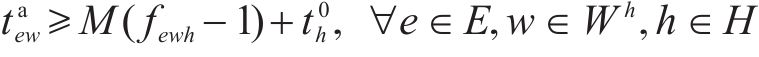
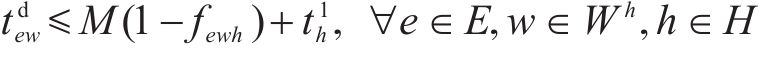
式(8)表示装卸时间约束,即车组必须保证满足作业时间要求;式(9)表示弧段上的接续时间约束;式(10)和式(11)表示走行弧段间的连续性约束,即每个弧段的开始时刻应为上一服务弧段的结束时刻;式(12)和式(13)分别表示第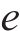
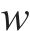
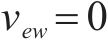
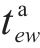
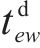
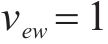
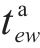
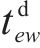
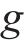
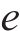
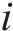
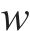
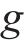
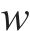
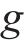
4) 取送作业性质相关约束
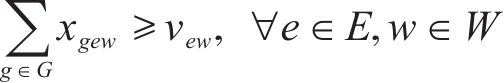
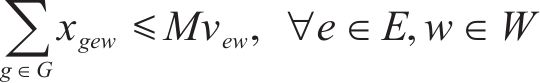
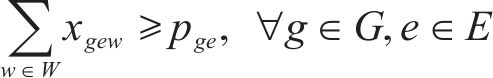
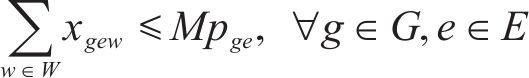
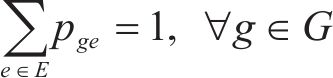
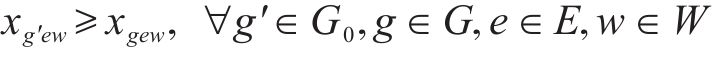
式(23)和式(24)表示批次作业弧段关系约束;式(25)~式(27)表示取送作业任务批次约束;式(28)表示保证调机走行路径与其所完成取送任务对应车组走行路径的一致性约束。
3 算法设计
专用线取送车问题属于NP-hard问题,利用商业求解器计算全局最优解的效率难以保证[20]。因此本文设计了基于优势基因结构的微进化算法(Micro-Evolution Algorithm, MEA)进行求解,本算法旨在实现对专用线取送车问题的高效求解,并在搜索过程中保留较优的可行解[21-22],微进化算法流程如图2所示。
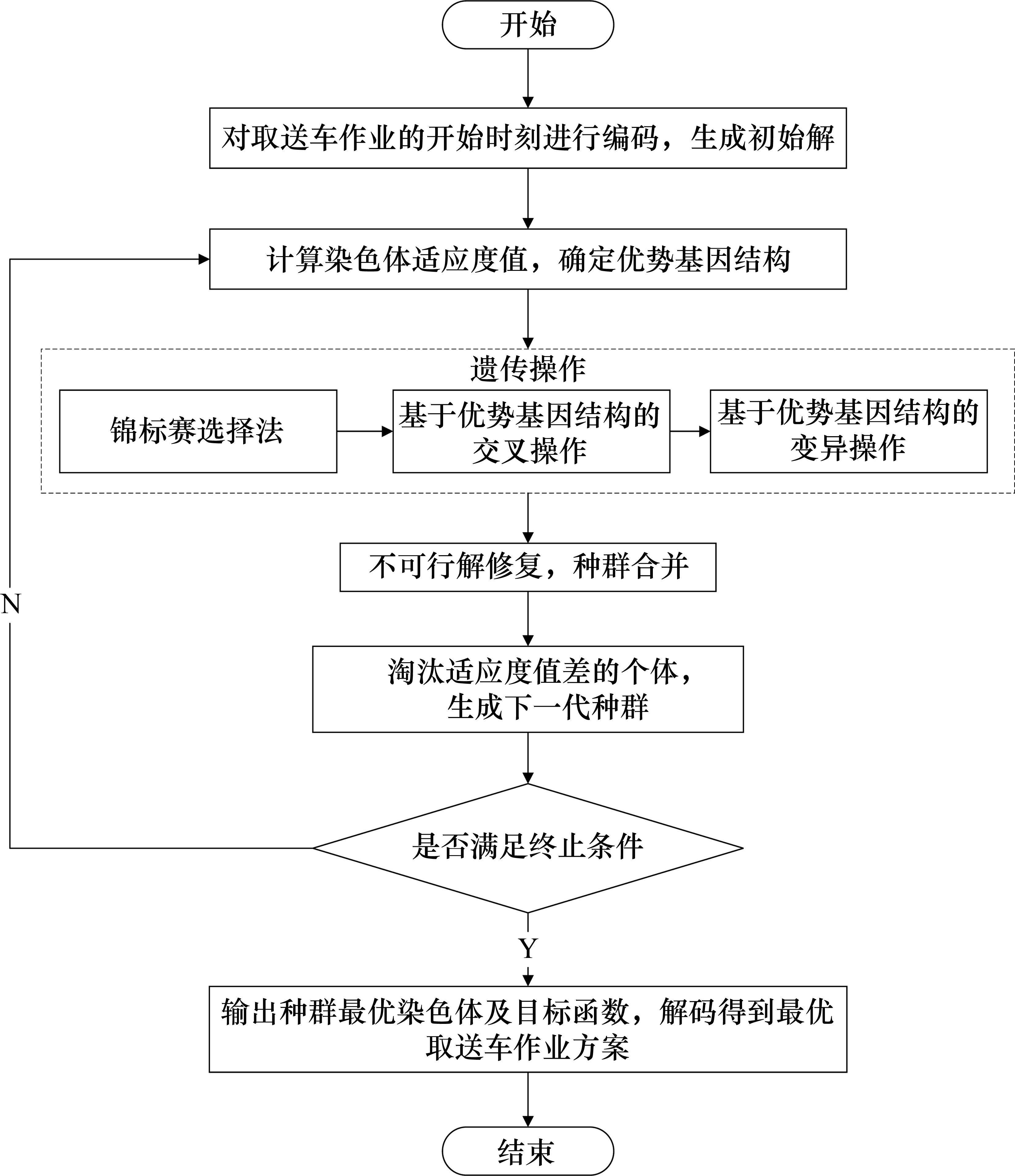
3.1 编码操作
在本文构建的模型中,决策变量包括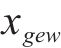
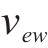
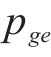
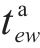
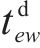
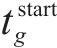
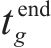
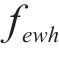
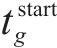
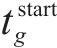
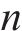
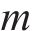
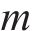
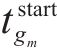
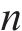
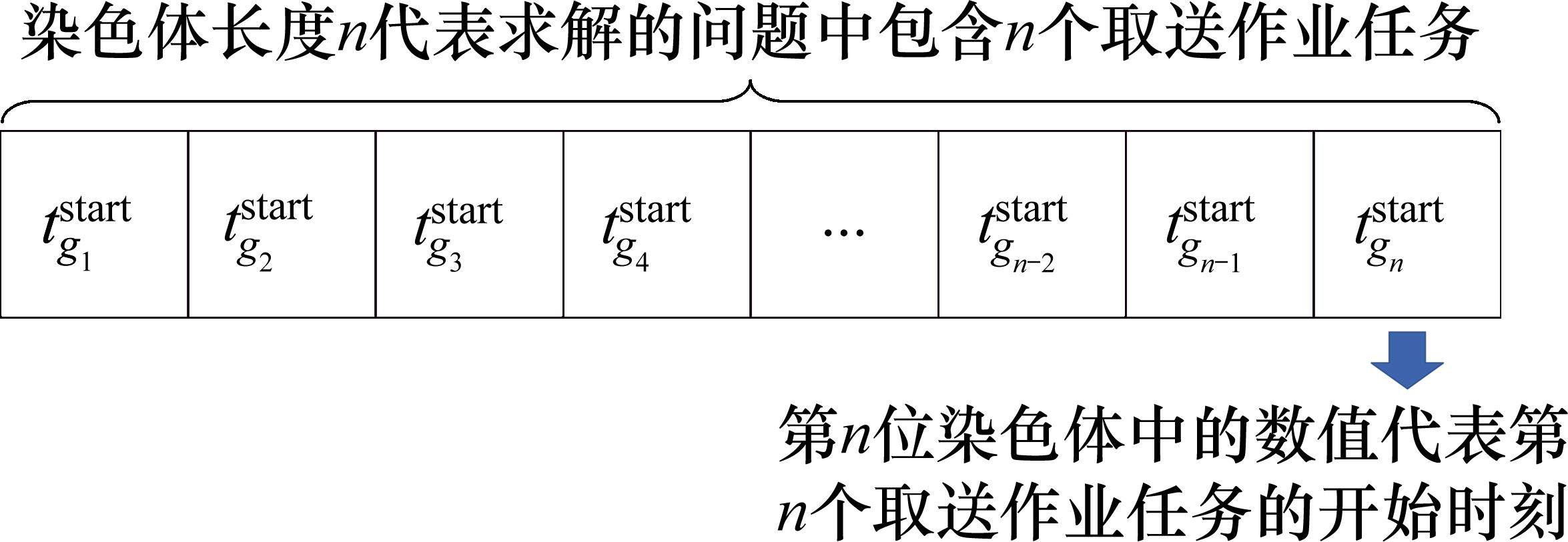
3.2 解码操作
在得到染色体对应取送作业任务的开始时刻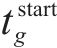
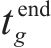
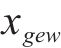
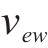
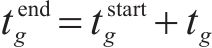
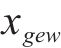
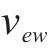
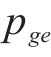
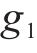
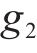
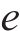
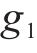
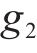
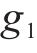
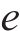
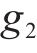
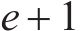
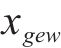
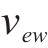
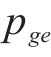
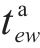
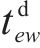
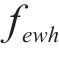
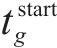
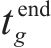
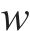
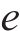
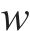
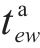
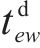
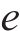
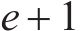
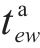
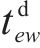
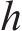
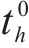
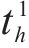
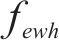
3.3 不可行染色体修复
当染色体的决策变量取值不可行时,可能出现超出能力限制和作业时间不合理2种情况。针对每种情况分别设计修复策略如下。
1) 超出能力限制修复
能力限制涵盖调机牵引辆数和专用线的容车数限制,当染色体对应的取送作业任务顺序中存在超出能力限制的不合理顺序时,其修复策略为首先筛选超出能力限制的取送作业任务,之后重新将该部分任务分配至有能力富余且分配后仍满足调机牵引辆数和专用线容车数限制的其他批次中,之后根据每项取送作业的时间要求,调整各项任务的开始作业时刻并对应修改染色体各位取值。
2) 不合理作业时间修复
染色体在完成超出能力限制修复后,继续对各项任务的不合理作业间隔时间以及各作业批次的不合理侵正作业时间进行修复。在不合理作业间隔时间的修复中,由于任意2个取送任务所在专用线间存在最短走行时间,因此对于相邻2个任务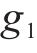
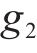
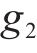
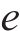
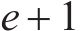
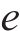
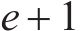
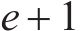
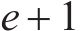
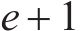
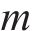
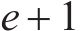
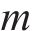
3.4 微进化操作流程
针对专用线取送车问题的特点,下面介绍微进化操作和优势基因结构设计在算法中的具体实现。
1) 微进化操作
本文中的微进化算法设计包括3个主要操作:选择、交叉和变异。选择操作采用锦标赛选择法,通过比较个体适应度来选出较优个体。交叉操作采用多点交叉,以交换2个个体的部分基因序列来产生新个体。变异操作采用多点变异,随机改变个体的某些基因位点,引入新的基因组合。
2) 优势基因结构确定
通过计算染色体的适应度值,筛选出本代的优势种群。然后,对优势种群中的染色体进行统计,分析各基因位上的取值情况,找出频率高的基因位点并构建优势基因结构。在交叉和变异过程中,有更大概率保留优势基因结构至新生成的染色体中。
4 案例分析
4.1 案例介绍
选取我国东北地区某铁路货运站作为研究对象,该车站共有分布于3条放射枝r1~r3上的19条专用线i1~i19,车站的专用线示意图如图4所示,其中各节点间的走行时间标注于弧段上(单位为min),各专用线容车数标注于专用线编号后(单位为辆)。所有专用线取送作业任务均由同一台调机负责,其最大牵引能力为45辆,摘解和连挂作业时间分别为4 min和5 min。
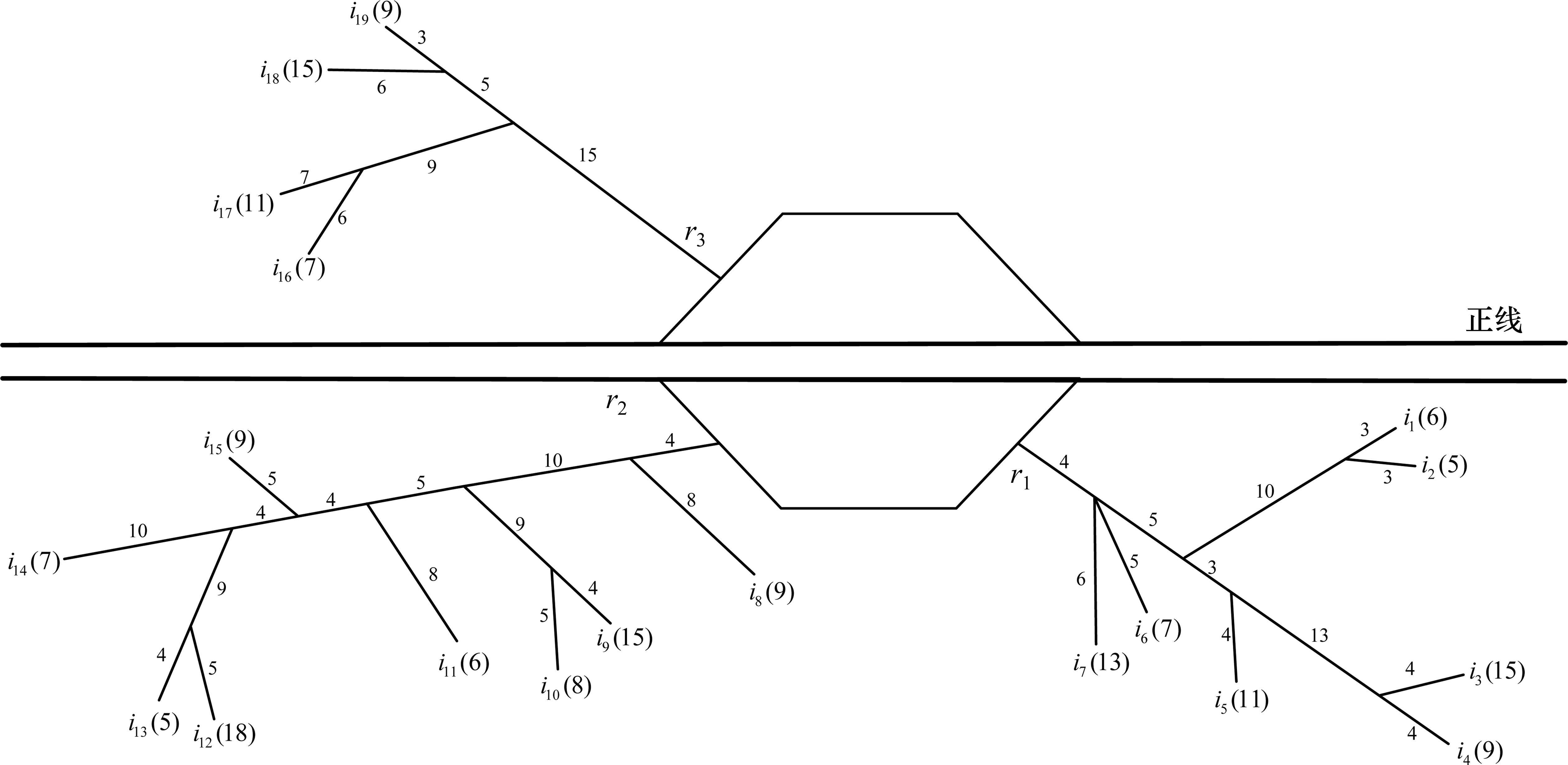
选定某日0:00—24:00专用线取送作业任务进行测试,取送作业开始时各专用线均为空线,当日侵正作业时间窗为[1:15—2:12],[4:23—5:15],[7:25—8:13],[9:40—10:24],[12:05—12:51],[13:54—14:52],[17:30—18:28],[20:41—21:26],[22:35—23:34]。以0:00为0时刻,24:00为1 440时刻,将1 d内时间离散为[0~1 440)中对应的整数进行计算。根据车站实际作业情况,部分专用线取送作业任务信息如表4所示。
| 编号 | 性质 | 车数 | 地点 | 装卸时间 | 最早送车时刻 | 编号 | 性质 | 车数 | 地点 | 装卸时间 | 最晚取车时刻 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 送车 | 2 | 1 | 40 | 13:35 | 20 | 取车 | 2 | 1 | 0 | 18:20 |
| 2 | 送车 | 2 | 2 | 65 | 2:55 | 21 | 取车 | 2 | 2 | 0 | 18:05 |
| 3 | 送车 | 12 | 3 | 145 | 3:10 | 22 | 取车 | 12 | 3 | 0 | 18:05 |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 17 | 送车 | 8 | 17 | 85 | 6:10 | 36 | 取车 | 8 | 17 | 0 | 15:15 |
| 18 | 送车 | 11 | 18 | 115 | 9:45 | 37 | 取车 | 11 | 18 | 0 | 15:15 |
| 19 | 送车 | 6 | 19 | 70 | 6:10 | 38 | 取车 | 6 | 19 | 0 | 15:15 |
4.2 结果分析
首先基于Python调用GUROBI求解器对混合型专用线取送车优化模型进行求解,设置求解器参数MIP Gap为5%,运行环境为一台Intel(R) Core(TM) i9-13900HX@2.20 GHz,16 GB RAM的个人计算机,求解程序运行1 796 s,可得到较优的可行解,此时的目标函数值为1 286 min,得到最优取送作业方案如表5所示,验证了模型的可行有效。
| 批次 | 起点 | 终点 | 性质 | 调车径路 |
|---|---|---|---|---|
| 1 | 0 | 11 | 送车 | 0-8-9-10-11 |
| 2 | 0 | 5 | 送车 | 0-2-3-4-5 |
| 3 | 0 | 0 | 取送车 | 0-16-17-19-18-11-9-10-8-0 |
| 4 | 0 | 0 | 取送车 | 0-15-12-13-14-19-16-17-18-0 |
| 5 | 0 | 0 | 取送车 | 0-6-7-1-2-3-4-5-0 |
| 6 | 14 | 0 | 取车 | 14-12-13-15-1-6-7-0 |
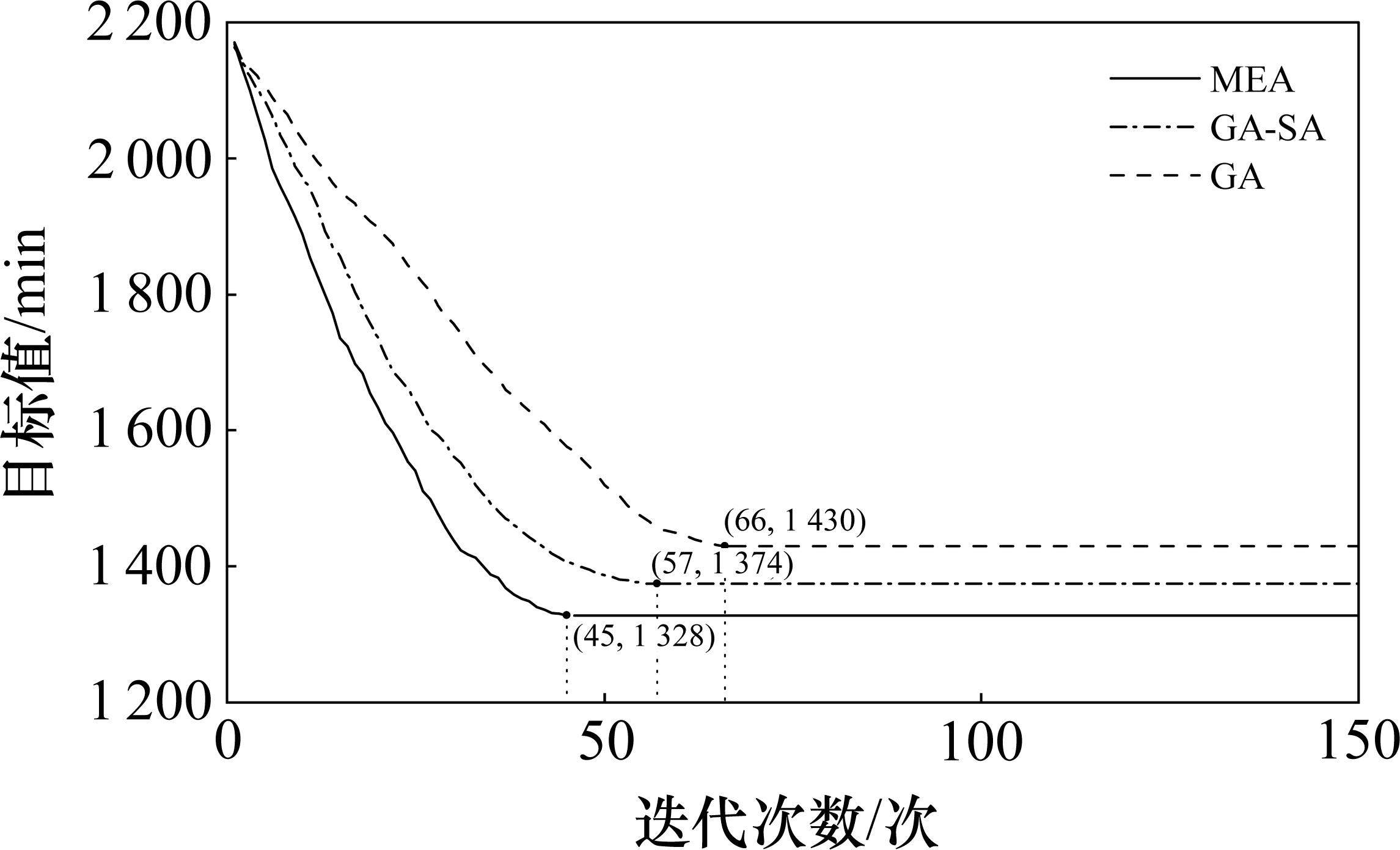
之后分别采用遗传算法(GA)、遗传模拟退火算法(GA-SA)和微进化算法(MEA)对模型进行求解,在算法参数上,设置种群规模为100,最大迭代次数为150,微进化算法中优势种群比例为15%,退火操作中初始温度为5 000 ℃,终止最低温度为0.001 ℃。为减少算法求解中的随机性,进行20组重复实验,遗传算法平均在第66代完成收敛,求得最优解所需的时间为697 s,最优结果为1 430 min;遗传模拟退火算法平均在第57代完成收敛,求得最优解所需的时间为584 s,最优结果为1 374 min;微进化算法平均在第45代完成收敛,求得最优解所需时间为406 s,最优结果为1 328 min。不同求解方法所得结果如表6所示,微进化算法、遗传模拟退火算法与遗传算法的收敛曲线如图5所示。可知微进化算法相较于GUROBI求解器的求解时间减少77.39%,相较于遗传算法的求解时间减少41.75%,相较于遗传模拟退火算法的求解时间减少30.48%,且微进化算法所得专用线取送方案质量优于其他2种算法并接近于GUROBI求解器的结果,证明微进化算法可以在保证专用线取送方案质量的同时有效提高计划编制效率。基于上述分析可知:本文所设计的微进化算法在求解混合型专用线取送车优化问题中是可行有效的。
| 求得最优解时间/s | 最优结果/min | |
|---|---|---|
| GUROBI求解器 | 1 796 | 1 286 |
| 遗传算法 | 697 | 1 430 |
| 遗传模拟退火算法 | 584 | 1 374 |
| 微进化算法 | 406 | 1 328 |
5 结论
1) 针对混合型专用线取送车优化问题,为兼顾取送作业方案的效率与经济性,以最小化调机作业时间和货车取送影响时间为目标,综合考虑调机、专用线能力和侵正作业时间窗等约束条件,构建了混合型专用线取送车优化模型。
2) 根据混合型专用线取送车问题特点,设计了基于优势基因结构的微进化算法,本算法在案例求解中相较于GUROBI求解器、遗传算法和遗传模拟退火算法分别减少了77.39%、41.75%和30.48%的求解时间,且微进化算法所得专用线取送方案质量优于其他2种算法并接近于GUROBI求解器的结果,证明了本文所构建的模型和算法的有效性。
3) 通过应用本文所设计的模型和算法,可以有效提高车站专用线取送方案的质量,从而实现货车在站停留时间的压缩,提高货物运输效率,并为车站进一步实现专用线取送作业方案的高效自动编制提供决策支持。
丛铭,宋瑞,何世伟等.混合型专用线取送作业方案编制优化研究[J].铁道科学与工程学报,2025,22(04):1519-1529.
CONG Ming,SONG Rui,HE Shiwei,et al.Optimization of placing-in and taking-out operation scheme on mixed-type sidings[J].Journal of Railway Science and Engineering,2025,22(04):1519-1529.

