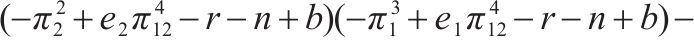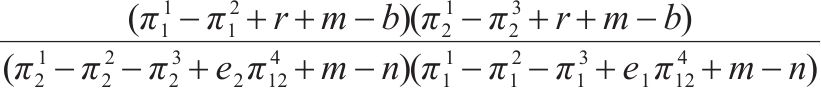随着“一带一路”倡议的实施,中欧班列在国家政策、资金等方面都有了长足的发展。为提高中欧班列与其他运输方式之间的竞争力,各开行城市给予中欧班列运营商高额补贴,促进了中欧班列的发展[1-2]。但随着中欧班列的迅速发展,会伴随诸多问题,如中欧班列运营商竞相低价揽货,恶性竞争严重,扰乱正常市场秩序,影响中欧班列的服务质量以及可持续发展[3-4]。相关研究方面,吕靖等[5]建立改进的Hotelling模型,分析新运输通道与既有运输通道的竞争博弈关系,探讨运营商最优定价及政府最优补贴策略。FENG等[6]建立中欧班列及其他运输方式的竞争博弈模型来确定中欧班列运营商的竞争策略。LI等[7]构建多重logit模型研究中欧班列与中欧航运之间的市场份额竞争。关于中欧班列竞合问题,MA等[8]建立博弈模型探讨中欧班列之间竞争及定价策略。张晶蓉等[9]将中欧班列市场竞争分为班列运营商间的内部竞争和海运的外部竞争,在考虑海运竞争的影响下,班列运营商应采取哪种竞合策略。张蒙蒙等[10]从竞合博弈角度出发并考虑政府补贴情况,比较并分析中欧班列平台公司间完全竞争、平台公司主动合作、政府牵头合作3种情况下竞合策略的选择。李玉民等[11]针对多个中欧班列运营商,运用改进Hotelling模型,综合考虑集装箱运输成本、位置、运输费率、利润分配占比等影响因素,对比分析各运营商的最优竞合策略。龚燕秋[12]运用演化博弈模型,研究中欧班列开行城市间的协同演化博弈稳定策略,并研究影响协同关系稳定性的主要因素。现有研究多是通过静态博弈研究运营商之间不同竞合策略选择下的利润及市场份额等问题,或通过演化博弈研究竞合策略的演化过程,缺乏对于不同竞合策略的基于静态博弈下各影响因素的动态演化博弈分析。且少有学者对“部分合作模式”进行研究。为了更好地为运营商竞合策略决策提供理论支持,有必要对中欧班列经营主体间的竞合策略,及各因素对竞合策略的影响机制进行综合分析。因此,本文将静态Hotelling模型与动态演化博弈模型相结合,首先利用静态博弈分析班列运营商对于3种竞合策略该如何选择以使其利润最大化;然后引入收益损失、额外收益、抗风险成本、违约金等因素,通过动态博弈分析这些因素对竞合策略演化博弈及演化路径的影响。从而为中欧班列运营商的竞合策略决策提供理论依据,并了解各影响因素对竞合策略演化过程的影响机制,从而适时调整竞合策略,为中欧班列可持续健康发展提供依据。
1 问题描述
对于中欧班列运营商竞合策略选择问题,本文运用Hotelling模型和演化博弈模型相结合的方法进行研究分析。Hotelling模型的基本思想是:在一个线性市场上的多个厂商提供同样的商品,但各厂商之间地理位置不同。由于地理位置不同,运输成本也不同。因此,消费者所关注的不仅仅是价格,而是价格与运输成本之和。演化博弈论是一种用于研究群体中策略演化的理论,是把博弈理论分析和动态演化过程分析结合起来的一种理论,旨在理解在群体中个体之间互动的情况下,策略是如何动态演化和传播的。相对于静态博弈论是将重点放在静态均衡和比较静态均衡上,演化博弈论强调的是一种动态的均衡。
本文考虑存在多个中欧班列运营商提供货运服务,运用Hotelling模型和演化博弈模型分析运营商采用竞争还是合作策略,对此展开的博弈如下。
运用Hotelling模型,以既定区域内的3个中欧班列运营商为研究对象,分析其运输服务成本、单位距离运输费用等因素对其最大利润的影响。分析了3种竞合模式:完全竞争模式、部分合作模式和合作模式。对3种竞合模式的均衡解进行仿真分析,探讨合作模式是否有效。
对运营商M1、M2之间竞争与合作的关系随时间的变化进行演化博弈分析。结合Hotelling模型得到的不同竞合策略下运营商的利润,并引入收益损失、额外收益、抗风险成本、违约金等因素建立演化博弈模型。对演化博弈模型进行求解得到模型的各均衡点,对均衡点进行分析可以得到各条件下的均衡解,即演化稳定策略。进而分析各因素对运营商竞合策略演化过程的影响机制,从而为运营商的竞合策略决策提供理论支持。
2 Hotelling模型构建
2.1 符号说明
针对Hotelling模型的竞合策略问题,定义如表1所示的参数及变量。假设有3个中欧班列运营商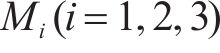
| 符号 | 含义 |
|---|---|
| Mi | 中欧班列运营商,i=1,2,3 |
| ci | 运营商Mi的运输服务成本 |
| qi | 运营商Mi的市场份额 |
| t | 单位距离运输成本,即货物从货源地到运营商所在地的单位成本 |
| M12 | 运营商联盟 |
| xi | 运营商位置 |
| ui | 发货人选择运营商Mi的效用 |
| πi | 运营商Mi的利润 |
| xm,xn,x23 | 效用无差异点 |
| ei | 利润分配占比 |
| a | 运营商M2的位置 |
| pi | 运营商Mi的定价 |
| v | 基础效用 |
| πig | g模式下利润的均衡解,g=1,2,3,4,分别代表完全竞争模式,合作-竞争模式,竞争-合作模式,合作模式 |
| πg | g模式下运营商M1、M2均衡利润之和 |
2.2 模型构建
2.2.1 完全竞争模式
在完全竞争模式下,3个班列运营商之间以定价和地理位置的差异等方式展开竞争。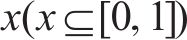
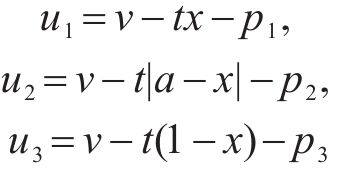
从式(1)可以看出,存在位置xm,使发货人选择运营商M1和M2效用无差异,即u1=u2;存在位置xn,使发货人选择M2和M3效用无差异,即u2=u3。由u1=u2,u2=u3解得:
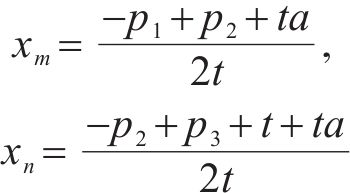
发货人根据效用最大化原则选择运营商。因此,区间[0, xm]的发货人会选择运营商M1;区间[xm,xn]的发货人会选择运营商M2;区间[xn, 1]的发货人会选择运营商M3。由于市场上的发货人均匀分布在市场区间内,则运营商Mi的市场份额qi可表示为:
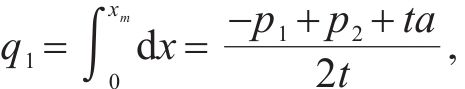
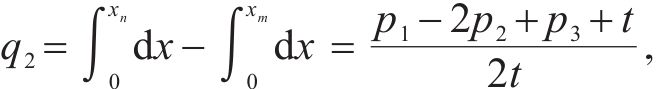
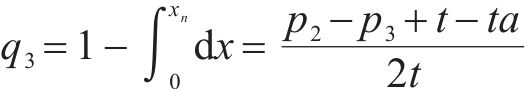
因为运营商Mi的利润函数πi为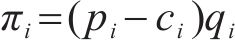
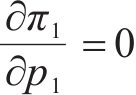
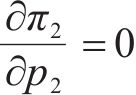
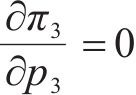
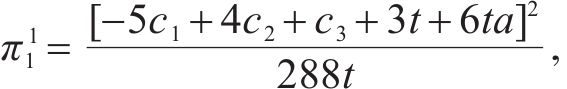
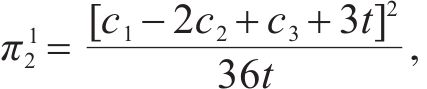
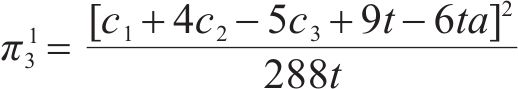
2.2.2 部分合作模式
部分合作模式分2种情况:一种情况为运营商M1、M2采取合作-竞争策略;另一种情况为运营商M1、M2采取竞争-合作策略。当运营商M1、M2采取合作-竞争策略时,运营商M1、M2达成合作协议与运营商M3竞争,但M1遵守协议选择合作,M2违反协议选择竞争。因此,M1以M1、M2共同利润最大化为目标,M2以自身利润最大化为目标,M3以自身利润最大化为目标[15],即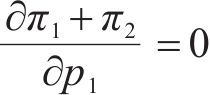
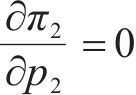
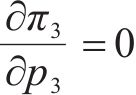
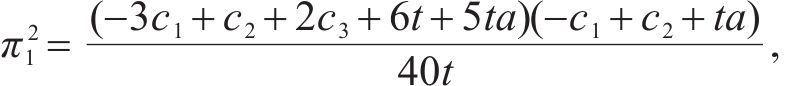
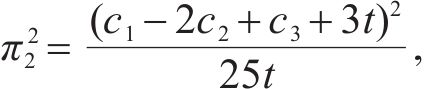
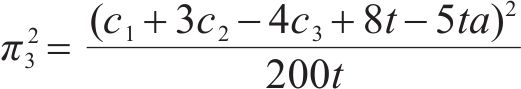
当运营商M1、M2采取竞争-合作策略时,运营商M1、M2达成合作协议与运营商M3竞争,但M1违反协议选择竞争,M2遵守协议选择合作。因此M1以自身利润最大化为目标,M2以M1、M2共同利润最大化为目标,M3以自身利润最大化为目标,即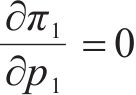
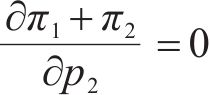
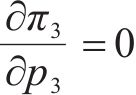
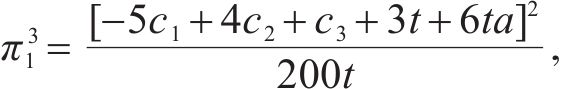
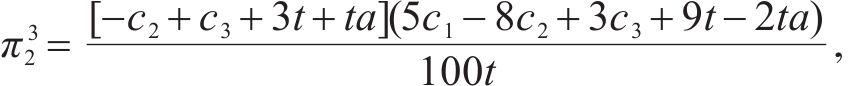
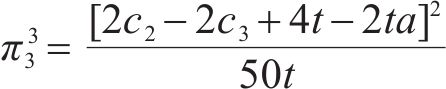
2.2.3 合作模式
合作模式下,运营商M1与M2达成合作协议,以运营商联盟M12的方式,与运营商M3进行竞争。P12为M12制定的统一定价;c12为M12的运输服务成本;q12为M12的市场份额;π12为M12的利润;M1和M2的利润分配占比分别为e1和e2,其中0<e1<1,0<e2<1,e1+e2=1,则合作模式下,x位置处发货人选择运营商M12和M3的效用u12,u3分别是:
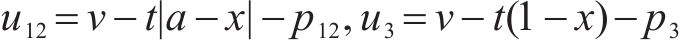
存在位置x23,使发货人选择运营商M12和M3效用无差异,即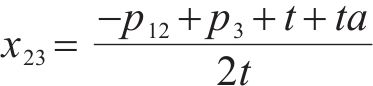
则合作模式下运营商联盟M12和运营商M3的市场份额qi分别为:
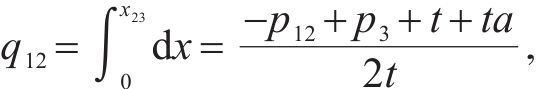
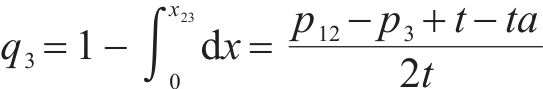
合作模式下,运营商联盟M12以共同利润最大化为目标设定运价,则各运营商对其利润函数求关于其定价的1阶偏导,即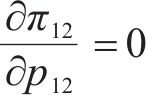
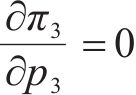
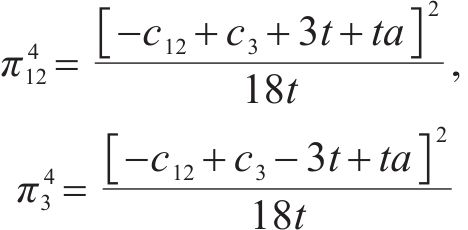
2.3 仿真分析
通过仿真分析能直观地观察各运营商选择不同竞合策略时的利润变化。参考相关文献[9],假设a∈(0.4,0.6),t∈(320,520)USD/(FEU•km),c∈(6 250,8 750)USD/FEU,且假设c1、c2、c3、c12之间最大相差500。使用python进行仿真,在各参数的假设范围内随机取50组数值,对这50组取值分别求各运营商的利润,对比各模式下运营商之间的利润,得到折线图如图1所示。其中π1为运营商M1、M2完全竞争模式下利润之和,π2为合作-竞争模式下利润之和,π3为竞争-合作模式下利润之和,π4为合作模式下利润之和,即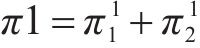
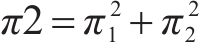
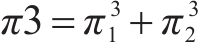
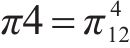
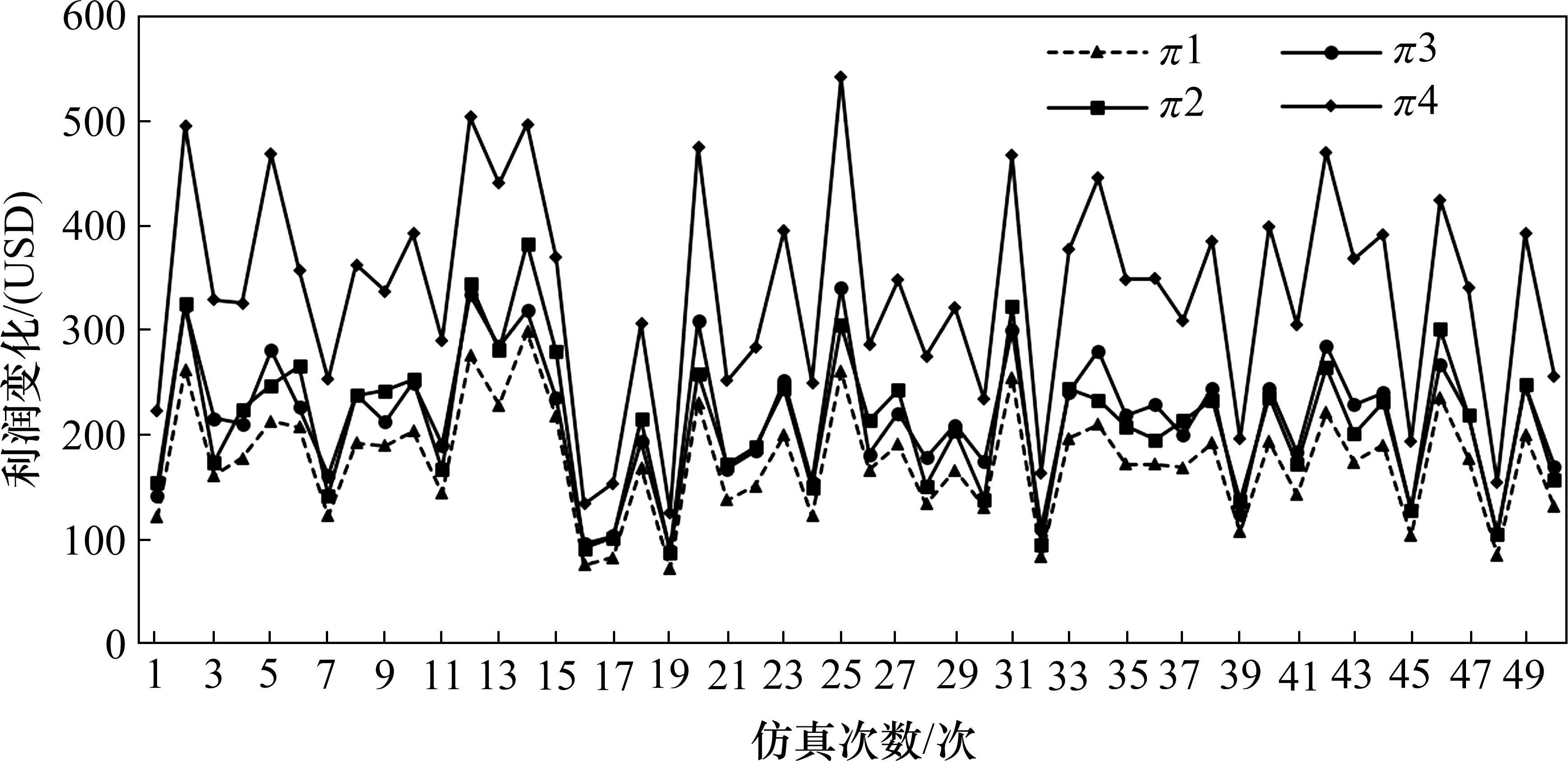
3 演化博弈模型构建
3.1 模型构建
针对竞合策略演化博弈问题,定义如表2所示的参数及变量。两运营商均可以选择竞争和合作2种策略,设运营商M1、M2选择合作的概率分别为p、q,则选择竞争的概率分别为1-p、1-q。无论两运营商选择竞争还是合作,都会存在基础收益π1、π2或π12,由前文Hotelling模型给出。各运营商的收益等于基础收益(Hotelling模型得到的利润均衡解)加减其他收益(收益损失、额外收益、抗风险成本、违约金等)。当两中欧班列运营商均选择竞争时,双方收益均为基础收益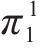
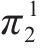
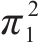
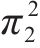
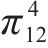
| 符号 | 含义 |
|---|---|
| Mi | 中欧班列运营商,i=1,2,3 |
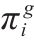 | g模式下利润的均衡解,g=1,2,3,4, 分别代表完全竞争模式,合作-竞争模式, 竞争-合作模式,合作模式 |
| ei | 利润分配占比 |
| w | 运营商收益 |
| p | 运营商M1选择合作的概率 |
| m | 收益损失 |
| r | 抗风险成本 |
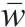 | 运营商平均期望收益 |
| q | 运营商M2选择合作的概率 |
| n | 额外收益 |
| b | 违约金 |
| (p*, q*) | 演化博弈均衡点 |
| 对策与收益 | 运营商M2 | ||
|---|---|---|---|
| 合作(q) | 竞争(1-q) | ||
| 运营商M1 | 合作(p) | 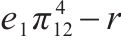 | 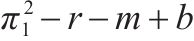 |
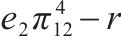 | 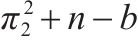 | ||
| 竞争(1-p) | 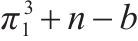 | 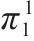 | |
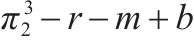 | 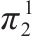 | ||
3.2 演化博弈模型求解
利用表3中的收入矩阵,分别求出2家运营商在采用不同策略时的收益以及平均期望收益[17]。如式(10)、式(11)、式(13)和式(14)所示。
计算得运营商M1选择合作的收益为w11,选择竞争的收益为w12,平均期望收益为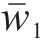
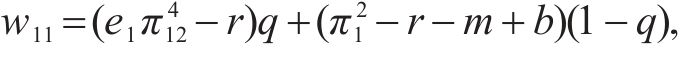
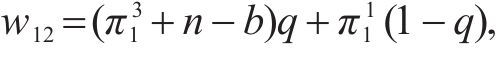
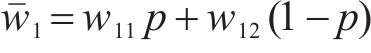
根据式(10)计算得到运营商M1的复制动态方程为:
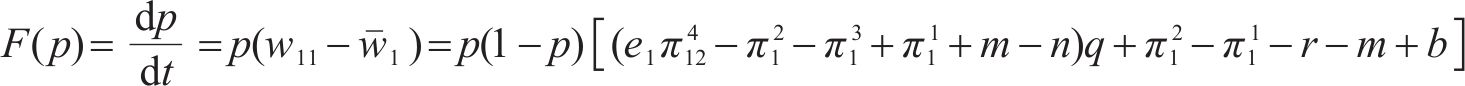
令复制动态方程F(p)=0,求得均衡解为:
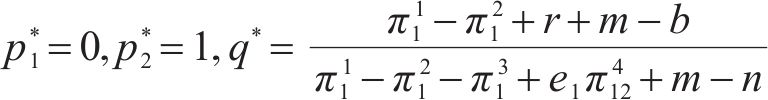
计算得运营商M2选择合作的收益为w21,选择竞争的收益为w22,平均期望收益为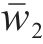
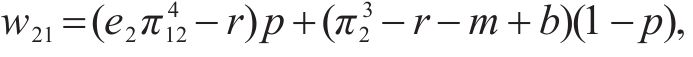
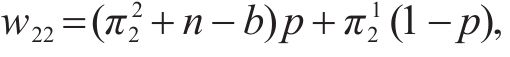
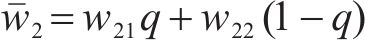
根据式(13)计算得到运营商M2复制动态方程为:
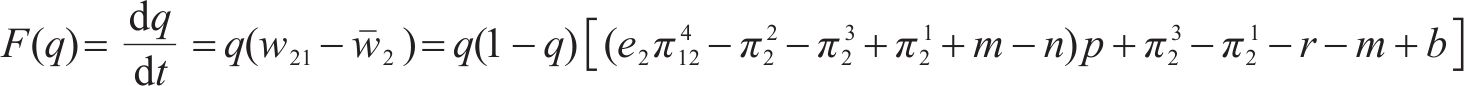
令复制动态方程F(q)=0,求得均衡解为:
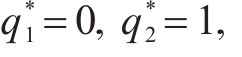
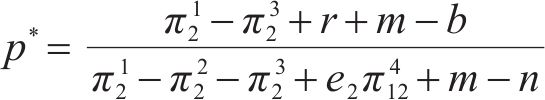
3.3 演化博弈均衡点稳定性分析
通过对博弈过程的稳定性分析,可以判断出经过几个回合的博弈后,参与者的最终战略选择。从上述得到的复制动态方程的均衡解可以看出,该博弈模型存在5个局部平衡点,分别是(0, 0),(0, 1),(1, 0),(1, 1),(p*, q*)。因为p*、q*是运营商M1和M2之间选择合作的概率,则0≤p*≤1,0≤q*≤1。结合式(12)、式(15),将它们划分为以下4种情况。
(Ⅰ)对于p*
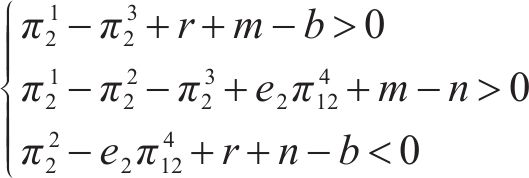
(Ⅱ)对于p*
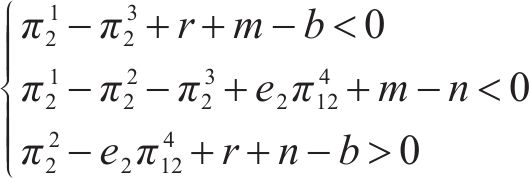
(Ⅲ)对于q*
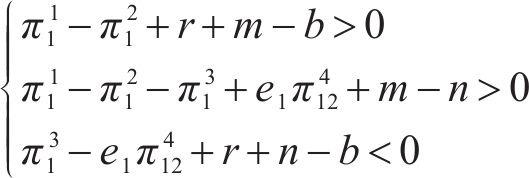
(Ⅳ)对于q*
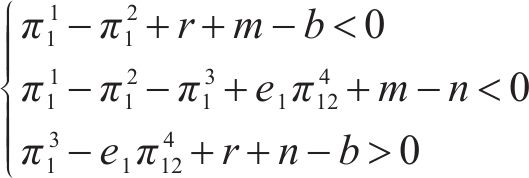
可得均衡点(p*, q*)的4种情况:分别为(Ⅰ, Ⅲ)、(Ⅰ, Ⅳ)、(Ⅱ, Ⅲ)、(Ⅱ, Ⅳ)。
根据雅可比矩阵J的行列式De(J)和迹Tr(J)对各个均衡点的稳定性进行判定[18]。
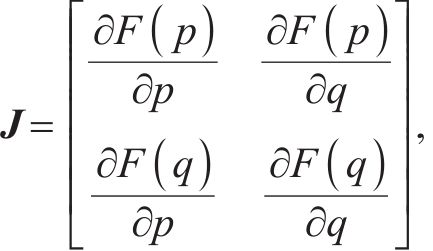
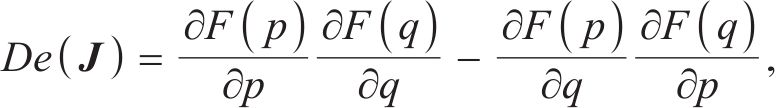
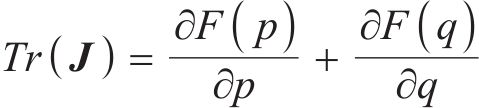
运用python的sympy库,并根据式(16)对各均衡点行列式De(J)和迹Tr(J)进行数学符号计算,计算得到行列式De(J)和迹Tr(J)的表达式如表4所示。
| 均衡点 | De(J) | Tr(J) |
|---|---|---|
| (0, 0) | 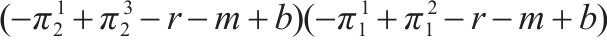 | 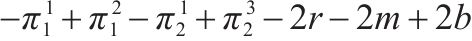 |
| (0, 1) | 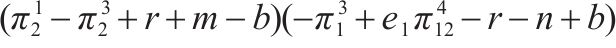 | 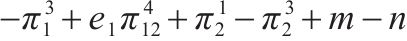 |
| (1, 0) | 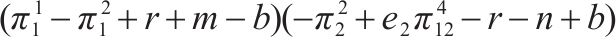 | 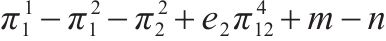 |
| (1, 1) | 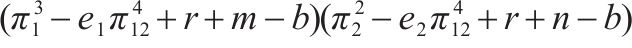 | 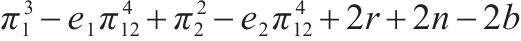 |
| (p*, q*) |
| 0 |
将均衡点(p*,q*)的4种情况(Ⅰ, Ⅲ)、(Ⅰ, Ⅳ)、(Ⅱ, Ⅲ)、(Ⅱ, Ⅳ)代入表4的表达式中,判断De(J)和Tr(J)的正负号,并通过稳定性分析方法对各均衡点进行稳定性评价[19]。稳定性分析结果如表5所示。
| 均衡点 | (Ⅰ, Ⅲ) | (Ⅰ, Ⅳ) | ||||
|---|---|---|---|---|---|---|
| De(J) | Tr(J) | 稳定性 | De(J) | Tr(J) | 稳定性 | |
| (0, 0) | + | - | ESS | - | 未知 | 鞍点 |
| (0, 1) | + | + | 不稳定 | - | 未知 | 鞍点 |
| (1, 0) | + | + | 不稳定 | - | 未知 | 鞍点 |
| (1, 1) | + | - | ESS | - | 未知 | 鞍点 |
| (p*, q*) | - | 0 | 鞍点 | + | 0 | 鞍点 |
| 均衡点 | (Ⅱ, Ⅲ) | (Ⅱ, Ⅳ) | ||||
| De(J) | Tr(J) | 稳定性 | De(J) | Tr(J) | 稳定性 | |
| (0, 0) | - | 未知 | 鞍点 | + | + | 不稳定 |
| (0, 1) | - | 未知 | 鞍点 | + | - | ESS |
| (1, 0) | - | 未知 | 鞍点 | + | - | ESS |
| (1, 1) | - | 未知 | 鞍点 | + | + | 不稳定 |
| (p*, q*) | + | 0 | 鞍点 | - | 0 | 鞍点 |
由表5可知,当满足(Ⅰ, Ⅲ)条件时,(0, 0)和(1, 1)为最终演化稳定策略;当满足(Ⅰ, Ⅳ)或(Ⅱ, Ⅲ)条件时,系统没有演化稳定均衡点。当满足(Ⅱ,Ⅳ)条件时,(0,1)和(1,0)为最终演化稳定策略。
在建立演化博弈模型后,下面对各因素对演化博弈的影响进行分析。
3.4 演化博弈影响因素分析
各因素的变化会影响系统演化结果,因此对违约金b、抗风险成本r、收益损失m和额外收益n等因素进行模型参数分析,并使用MATLAB进行仿真分析。
3.4.1 模型参数分析
由前文的Hotelling模型仿真得到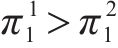
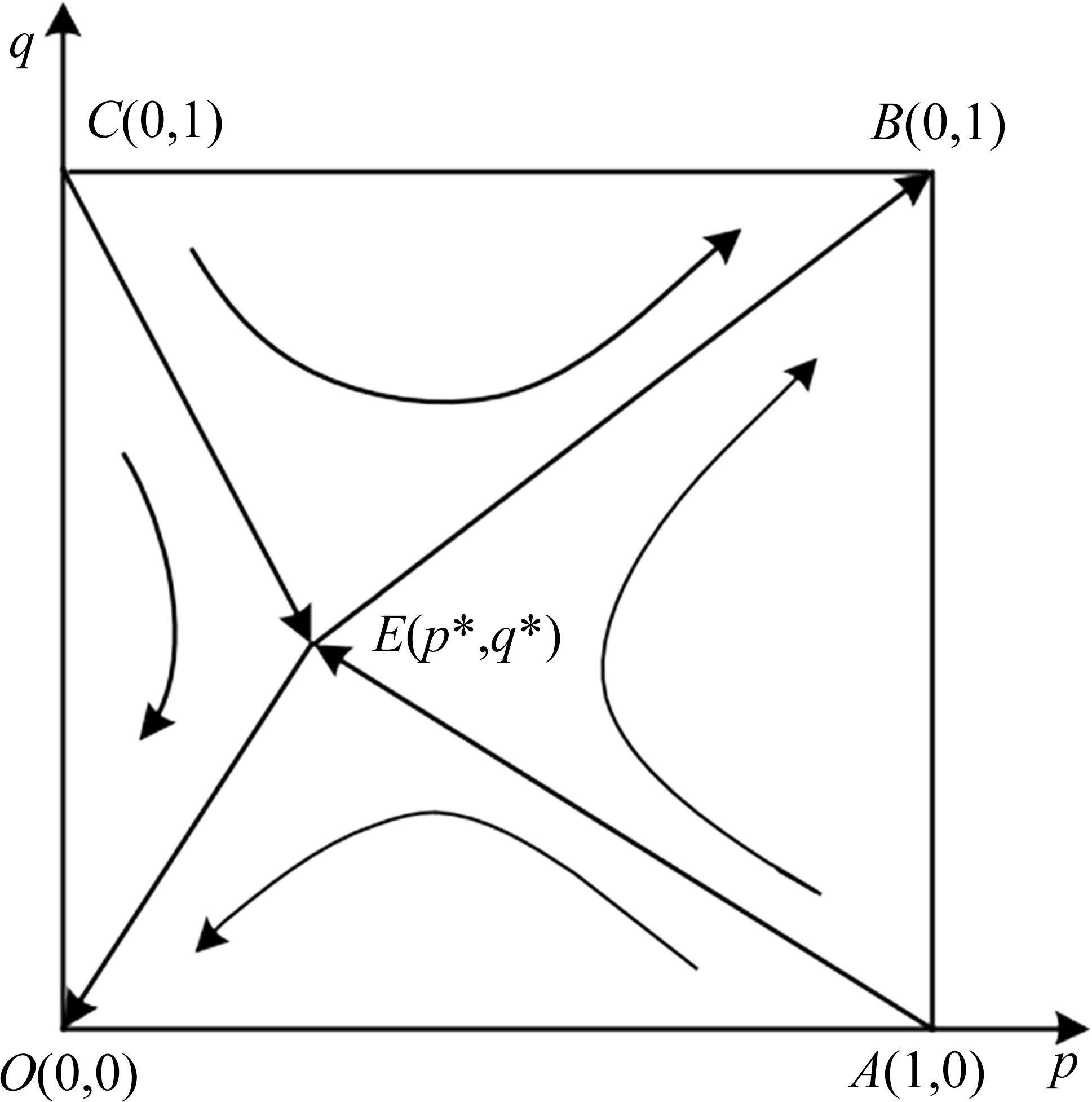
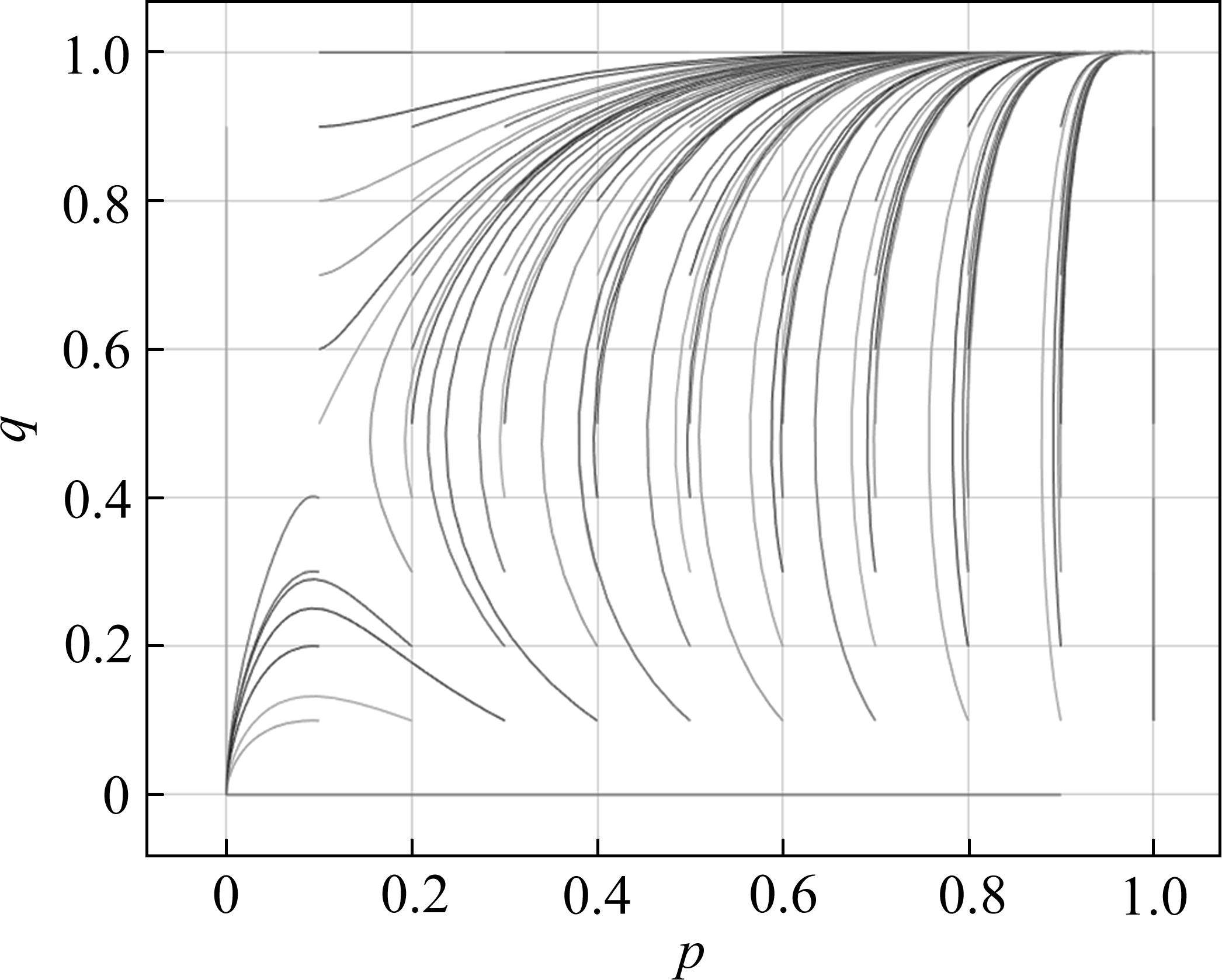
由图2可知,正方形OABC被折线AEC分成左右2块区域。如果初始点即两运营商策略选择初始概率位于AECB区域时,博弈会向B(1, 1)点演化,即两运营商最终都会选择合作;如果初始点位于AECO区域时,博弈会向O(0, 0)点演化,即两运营商最终都会选择竞争。2块区域面积的大小可以用来表示系统演化的概率,且面积大小取决于E点的坐标。若p*、q*的取值越小,则AECB的面积越大,两运营商最终都选择合作的概率就越大。
其中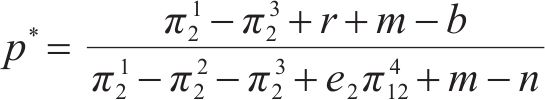
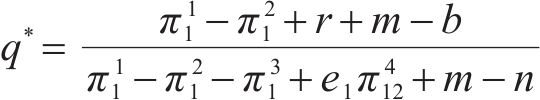
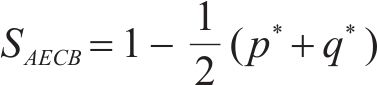
在保证其他参数不变的条件下,分别对其他参数求其对AECB面积的偏导,由此可判断各参数对博弈的影响,最终得到以下结论:
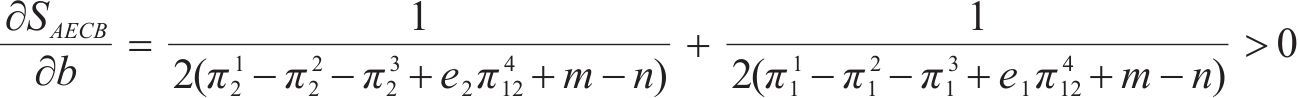
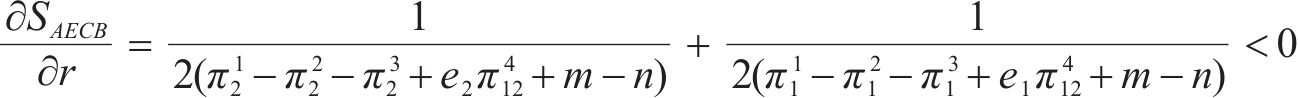
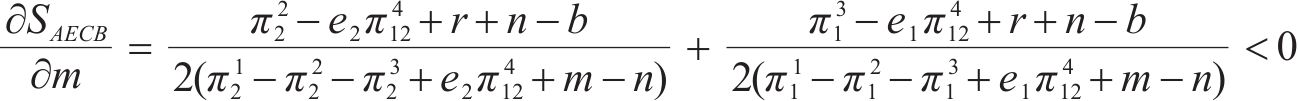
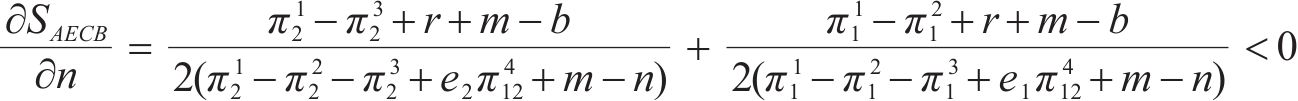
由式(18)~(21)分析可知,违约金b越大,AECB面积越大,博弈向B(1, 1)点演化的概率越大,即两运营商最终选择合作的概率越大。抗风险成本r、收益损失m和额外收益n越大,AECB面积越小,博弈向B(1, 1)点演化的概率越小,即两运营商最终选择合作的概率越小。
3.4.2 仿真分析
为更直观地说明中欧班列运营商竞合策略演化过程及状态,使用MATLAB对演化博弈进行模拟仿真。首先参考相关文献[12]对各参数进行初始化赋值,其中利润根据第2节的Hotelling模型进行计算,e1、e2按照双方竞争时的市场份额占有量进行分配,各参数初始赋值如表6所示。
| 参数 | 赋值 | 参数 | 赋值 |
|---|---|---|---|
| a | 0.42 | e1 | 0.46 |
| t | 420 | e2 | 0.54 |
| c1 | 7 300 | b | 11 |
| c2 | 7 500 | r | 12 |
| c3 | 7 400 | m | 14 |
| c12 | 7 200 | n | 22 |
此时演化仿真结果如图3所示。p、q分别代表两运营商初始的合作概率。从图3中可以看出,当初始状态在左下方时,系统最终收敛于(0, 0),即该区域内两运营商最终都会选择竞争。当初始状态在右上方时,系统最终收敛于(1, 1),即该区域内两运营商最终都会选择合作。
根据参数的设定,可得演化博弈的鞍点在(0.1, 0.4)附近,因此初始比例取(0.1, 0.4)。通过对各重要参数设置不同的取值进行仿真,可以看出各参数对系统演化的影响。
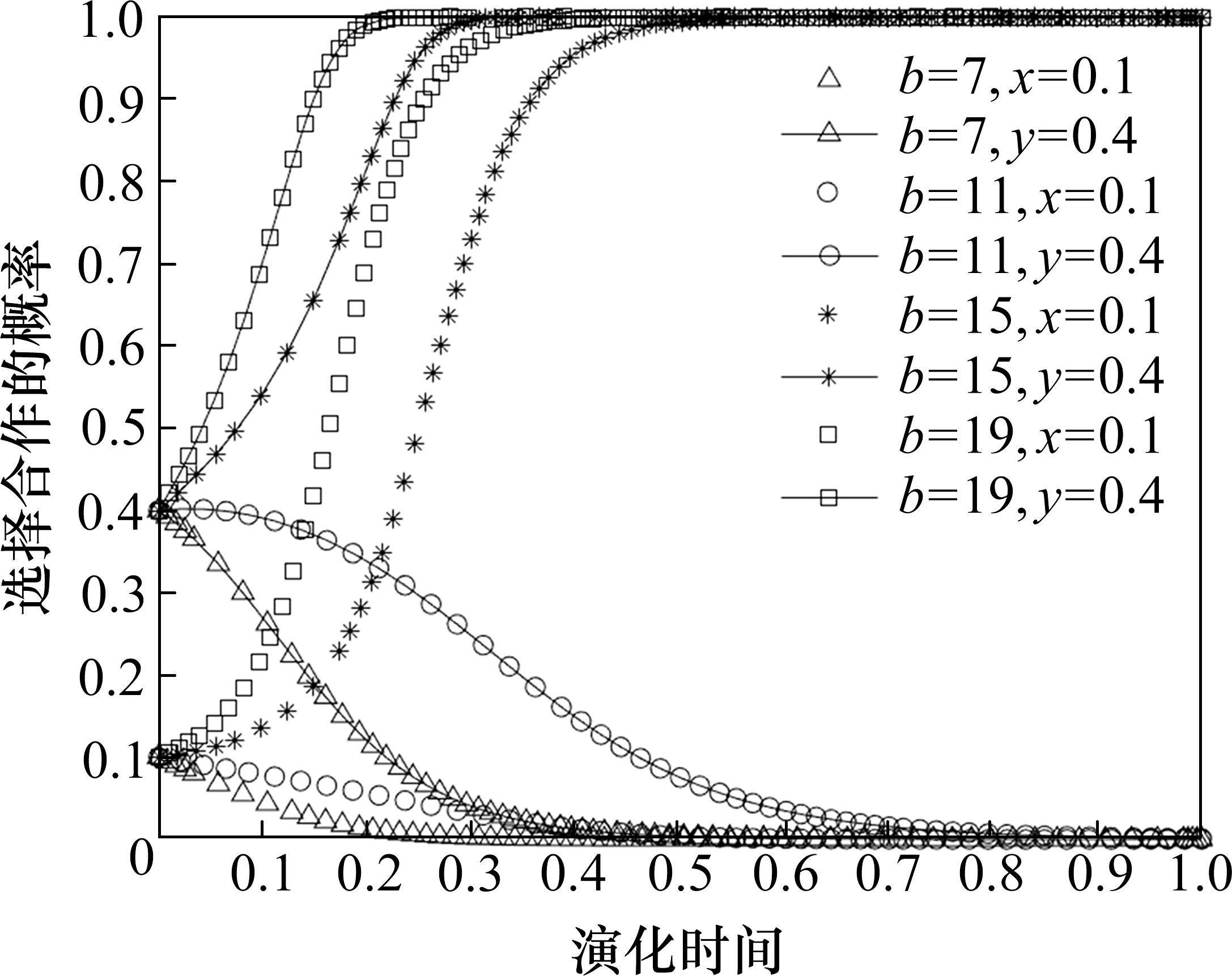
在保证其他参数不变的情况下,令b取不同的值进行仿真,观察博弈双方的演化情况,如图4所示。从图中可以看出,随着违约金b的增大,两运营商选择合作的概率会逐渐从0变为1,且变化速度也会变快,由于违约金会使选择竞争的一方产生收益损失。因此,违约金的增大会促进运营商合作。
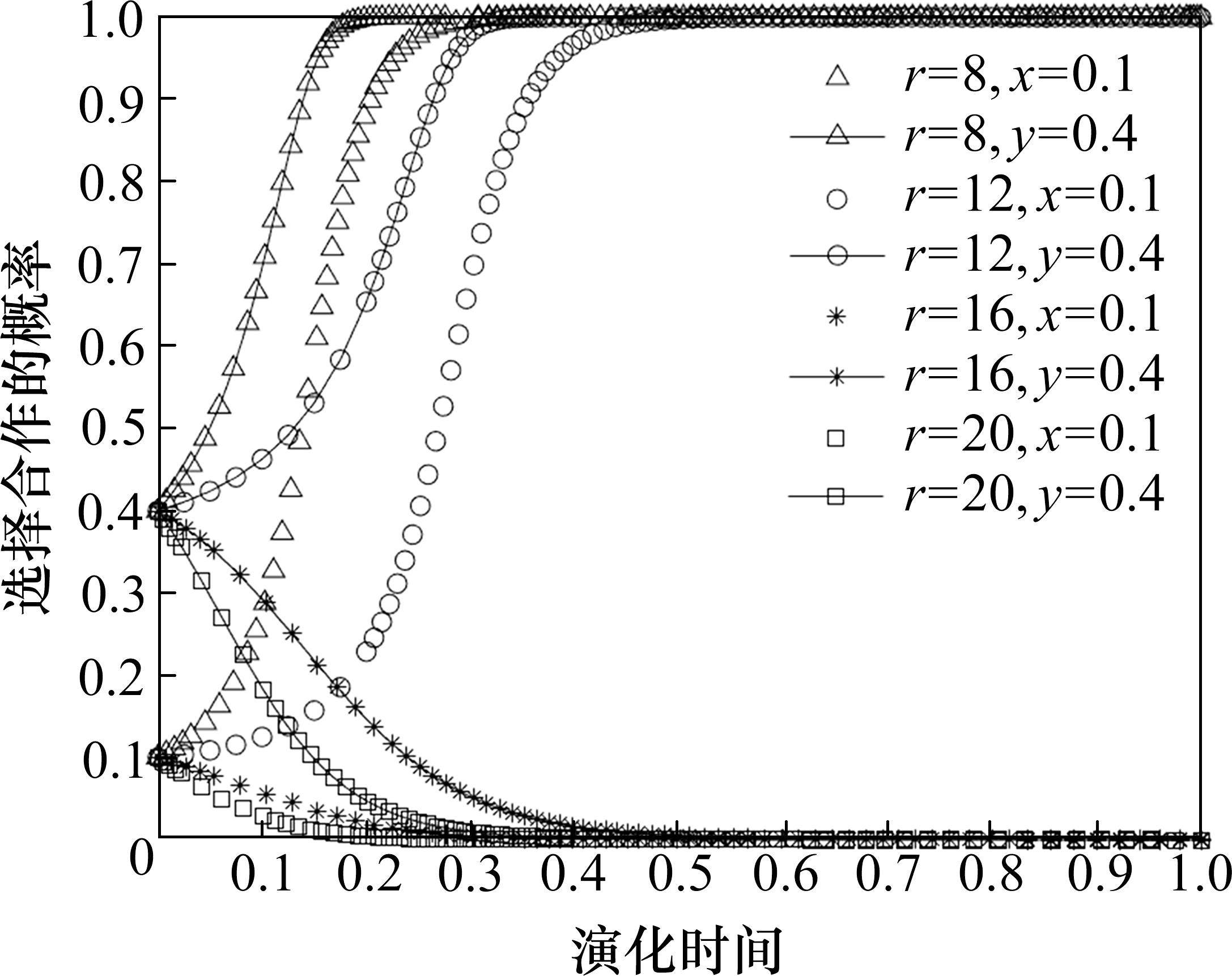
在保证其他参数不变的情况下,令r取不同的值进行仿真,观察博弈双方的演化情况,如图5所示。从图中可以看出,随着抗风险成本r的增大,两运营商选择合作的概率会逐渐从1变为0,且变化速度也会变快,由于抗风险成本会使选择合作的一方为应对采取合作策略造成的风险而产生额外的成本,因此,抗风险成本的增大会导致运营商选择竞争。
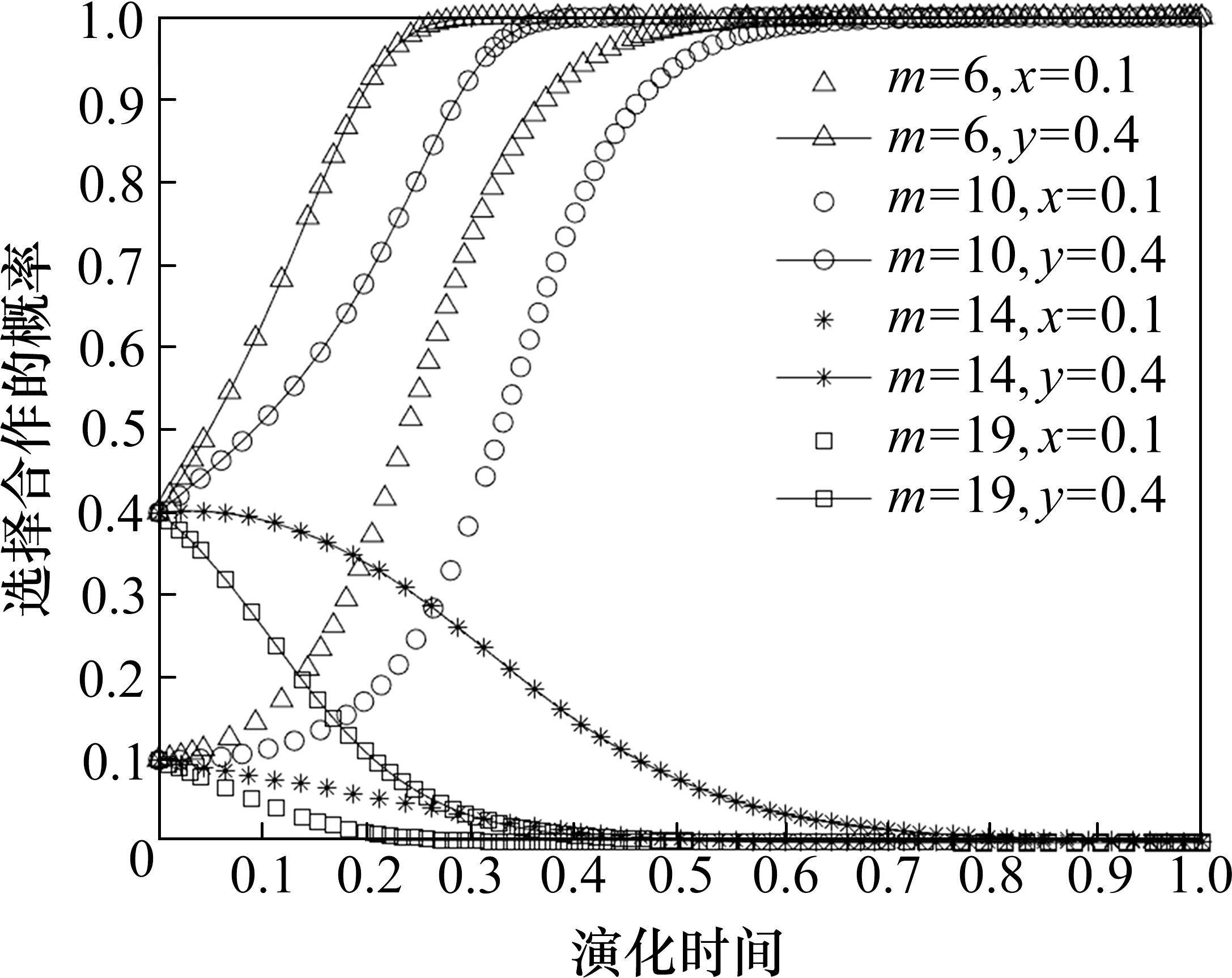
在保证其他参数不变的情况下,令m取不同的值进行仿真,观察博弈双方的演化情况,如图6所示。从图中可以看出,随着收益损失m的增大,两运营商选择合作的概率会逐渐从1变为0,且变化速度也会变快。当两运营商一方选择合作,一方选择竞争时,选择合作的一方会由于信息共享而丢失一定的货源,造成一定的收益损失。因此,收益损失的增大会导致运营商选择竞争。
在保证其他参数不变的情况下,令n取不同的值进行仿真,观察博弈双方的演化情况,如图7所示。从图中可以看出,随着额外收益n的增大,两运营商选择合作的概率会逐渐从1变为0,且变化速度也会变快。当两运营商一方选择合作,一方选择竞争时,选择竞争的一方会获得选择合作的一方提供的共享信息,产生一定的额外收益。因此,额外收益的增大会导致运营商选择竞争。
4 结论
1) 通过Hotelling模型分析,中欧班列运营商之间采取不同合作策略均会存在最优解。采取合作策略可以提高运营商定价,从而增大运营商的利润。不必降低价格来争取市场,避免恶性竞争,可促进中欧班列高质量发展。因此要促进运营商之间的合作。
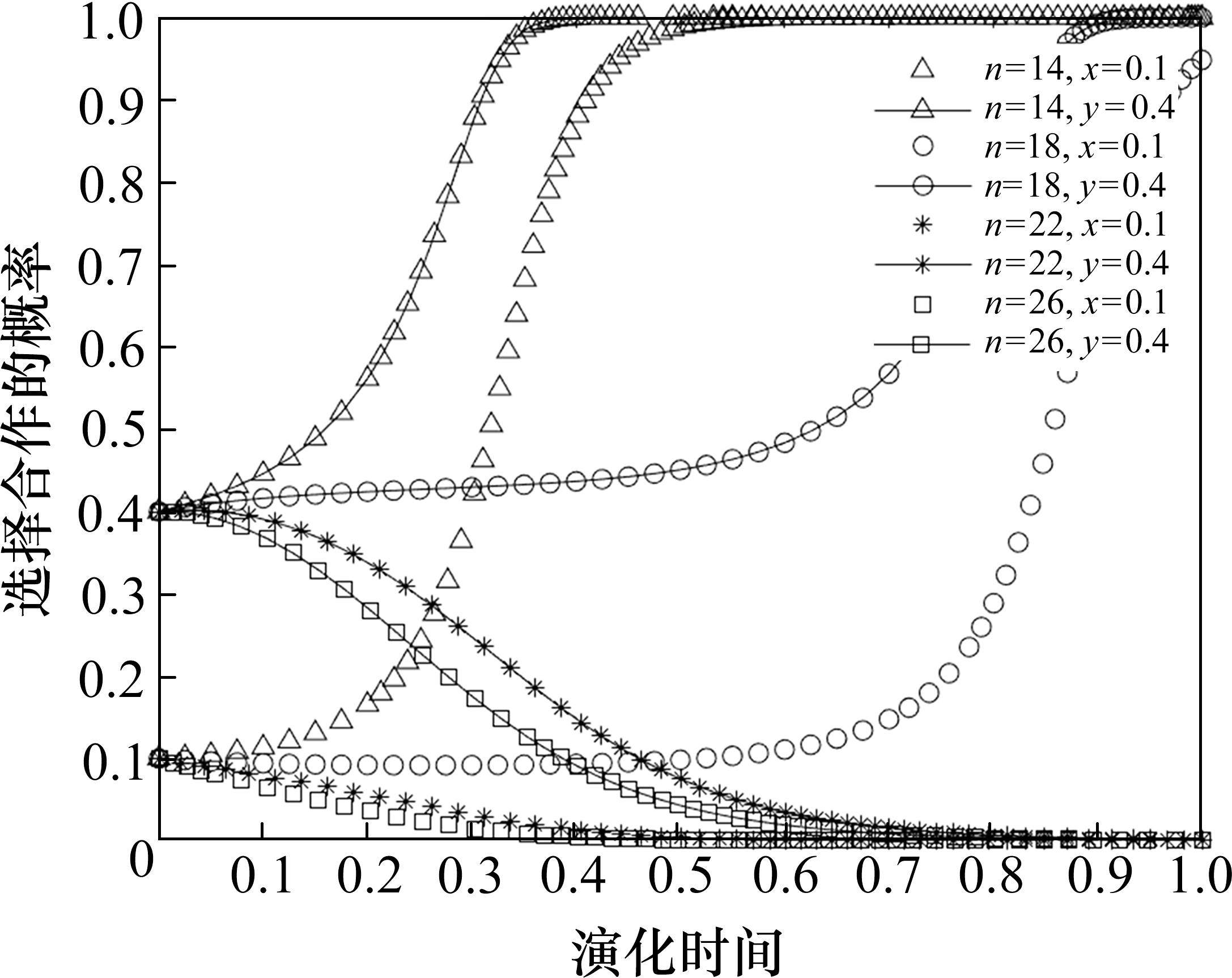
2) 通过对演化博弈均衡点的分析可以得到,演化博弈均衡点(p*, q*)存在4种情况,分别为(Ⅰ, Ⅲ)、(Ⅰ, Ⅳ)、(Ⅱ, Ⅲ)、(Ⅱ, Ⅳ)。当(p*, q*)满足(Ⅰ, Ⅳ)或(Ⅱ, Ⅲ)条件时,系统没有演化稳定均衡点;当满足(Ⅱ, Ⅳ)条件时,(0, 1)和(1, 0)为最终演化稳定策略;当满足(Ⅰ, Ⅲ)条件时,演化结果为(0, 0)和(1, 1),即两运营商均选择竞争或合作为最终演化稳定策略。由Hotelling模型仿真分析得到
3) 通过演化博弈分析,运营商竞合策略演化路径受违约金、抗风险成本、收益损失、额外收益等影响,这些影响因素会影响演化结果及演化速度。违约金的增大会促进双方达成合作,防止运营商之间利益受损,实现双方互利共赢。抗风险成本的增大会增大合作运营商的成本支出,对双方达成合作起到消极作用。运营商之间合作时,收益损失是一种潜在的风险,若一方运营商选择竞争,会对另一运营商产生利润损失,对双方达成合作起到消极作用。运营商之间合作时,额外收益增大会增加运营商的利润,增大运营商选择竞争的可能性,对双方达成合作起到消极作用。
赵鲁华,邢惠尧,武光娜等.基于Hotelling模型的中欧班列运营商竞合策略演化博弈研究[J].铁道科学与工程学报,2024,21(11):4456-4466.
ZHAO Luhua,XING Huiyao,WU Guangna,et al.Evolutionary game study of China Railway Express operators’ competition and cooperation strategy based on Hotelling model[J].Journal of Railway Science and Engineering,2024,21(11):4456-4466.