CRTS Ⅲ型板式无砟轨道由于其高稳定性、高舒适性等优点,在我国高速铁路中得到广泛应用[1-2]。路基段CRTS Ⅲ型板式无砟轨道是由路基-无砟轨道-无缝钢轨组成的相互作用体系。限位凹槽作为传力部件,集中承受不均匀沉降、温度梯度等荷载的作用,极易发生破坏,从而影响行车安全[3]。此外,由于施工和过渡区段结构尺寸调整等因素,现场底座凹槽位置常出现纵向间距偏差等问题。因此,亟需探明无砟轨道限位凹槽对轨道传力机制及变形的影响规律,为无砟轨道的优化设计和养护维修提供理论指导。
在CRTS Ⅲ型板中,自密实混凝土的限位挡台与底座的限位凹槽是重要的传力部位,限位凹槽对线路安全服役及轨道的高稳定性具有重要作用[4-6]。王璞等[7]针对路基地段CRTS Ⅲ型板式无砟轨道底座的纵向连接工况,进行了限位凹槽设置方式的研究。韦有信等[8]通过理论推导和现场试验验证等确立了简单可靠的传力杆配置计算方法。刘增杰等[9]对CRTS Ⅲ型板式无砟轨道底座凹槽四角裂缝产生机理及结构优化措施进行了研究。高速铁路运行情况表明,路基不均匀沉降和夏季高温已成为引发路基段板式无砟轨道病害的主要原因[10-12]。
目前的研究主要侧重于设计阶段的计算分析,对于运营线路中传力部位的实际工作状态尤其是在极端条件下的传力机制研究相对较少[13-14]。限位凹槽对线路安全服役及轨道的高稳定性具有重要作用,且CRTS Ⅲ型板式无砟轨道限位凹槽属于隐蔽部位,初期发生病害不易发现[15-17]。因此,开展限位凹槽传力机制研究具有重要理论和现实意义。本文考虑纵向传力杆结构,基于有限元理论建立无砟轨道-路基空间耦合模型,分析不均匀沉降、夏季高温条件下,路基段无砟轨道受力特性、层间脱空值及轨面变形规律,研究CRTS Ⅲ型板式无砟轨道限位凹槽纵向间距对轨道受力和变形的影响,以便为基础大变形路段无砟轨道结构的设计优化提供理论参考。
1 计算模型
1.1 有限元模型的建立
路基段CRTS Ⅲ型板式无砟轨道主要由钢轨、扣件、轨道板、自密实混凝土、隔离层、弹性缓冲垫层、底座、传力杆等构成,CRTS Ⅲ板式无砟轨道-路基有限元模型如图1所示。扣件类型为WJ-8型,采用Spring单元模拟其纵、横、垂3个方向的刚度特性;为准确反映结构的受力状态,采用C3D8单元进行三维实体模拟。
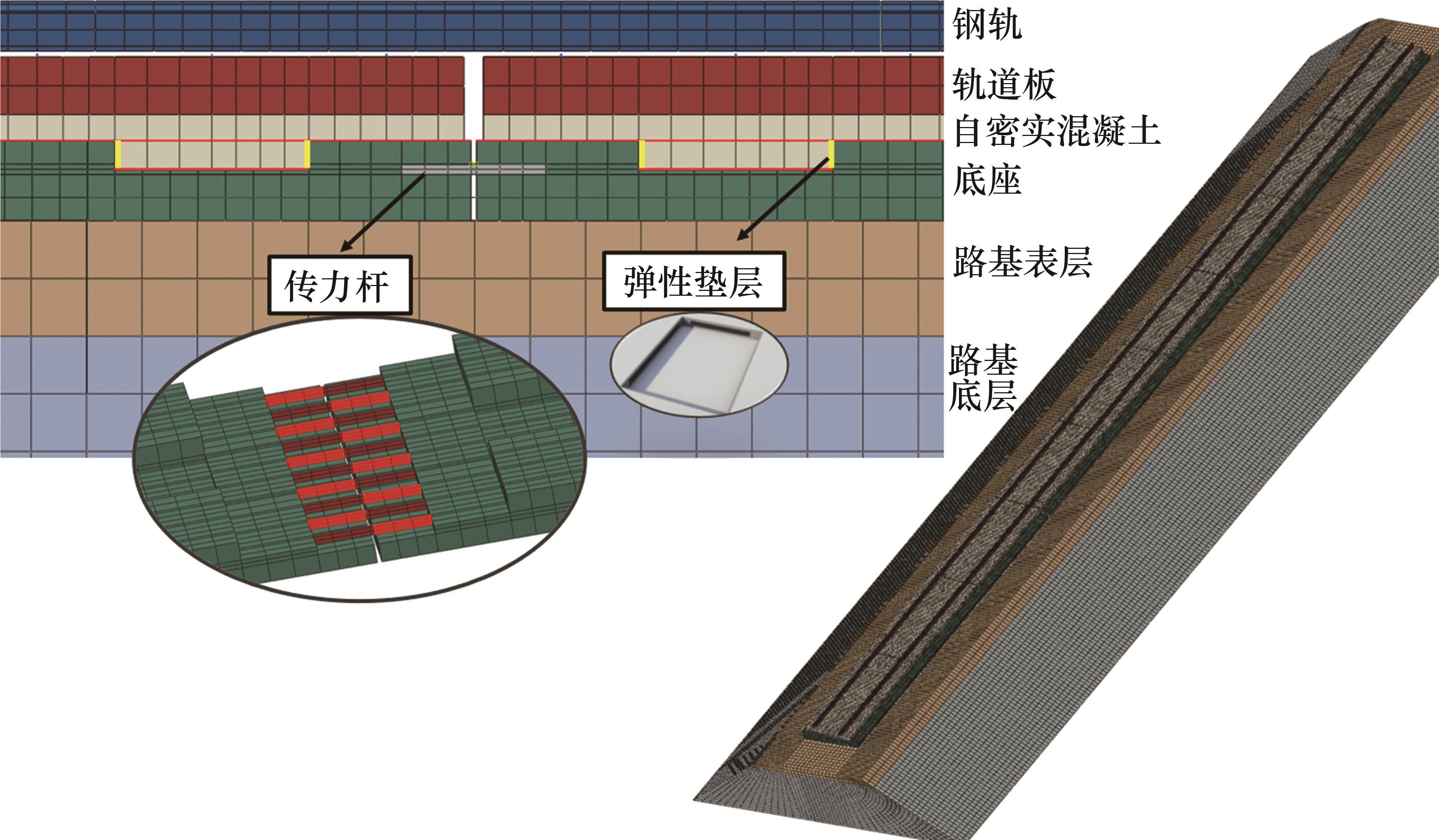
考虑扣件对轨道板温度变形的约束作用,模型采用CHN60标准钢轨,扣件间距为0.63 m。轨道板材料为C60混凝土,自密实混凝土底部预留2个长×宽×高为1.0 m×0.7 m×0.1 m的凸台,与底座凹槽榫接;路基段底座3块纵连,其总长×宽×高为16.99 m×3.1 m×0.3 m,相邻的底座之间有传力杆相互连接。轨道板下预留门型筋与自密实混凝土浇筑为一体形成复合板,板下设置土工布隔离层与底座间隔离,隔离层刚度为0.4 N/mm3。底座凹槽四周设置弹性缓冲垫层,刚度为0.12 N/mm3。路基按照实体结构建立基床,表层和底层的高度分别为0.40 m和2.30 m,边坡坡率均为1꞉1.5,底座底部与路基表层间纵横向摩擦因数取0.5。CRTS Ⅲ型板式无砟轨道与路基材料参数如表1所示。
| 部件 | 密度/(kg·m-3) | 弹性模量/MPa | 泊松比 | 比热容/(J·kg-1·℃-1) | 热膨胀系数/℃ |
|---|---|---|---|---|---|
| 轨道板 | 2 500 | 36 500 | 0.2 | 973 | 1×10-5 |
| 自密实混凝土 | 2 450 | 32 500 | 0.2 | 925 | 1.3×10-5 |
| 底座 | 2 450 | 32 500 | 0.2 | 973 | 1×10-5 |
| 基床表层 | 2 300 | 180 | 0.3 | 920 | 2×10-5 |
| 基床底层 | 2 000 | 120 | 0.3 | 920 | 2×10-5 |
1.2 传力杆与层间关系
路基段的底座为局部纵连结构,沿线路相邻底座间设置20 mm宽的伸缩缝,伸缩缝内填充嵌缝板,顶部及侧边均采用密封嵌缝胶封闭。路基填料为级配碎石地段的底座伸缩缝处可设置传力杆,传力杆长度不小于500 mm,直径不小于34 mm,材质为45号优质碳素钢,表面进行防锈处理。传力杆分固定区和滑动区两部分,滑动区涂注润滑机械用矿物脂,同时采用聚乙烯材料热合冷凝塑封处理,中间设置20 mm泡沫可压缩段。传力杆设置于底座横截面的中部,按间隔首尾交错布设,相邻传力杆对称反向布置,每个伸缩缝设10根,如图2所示。
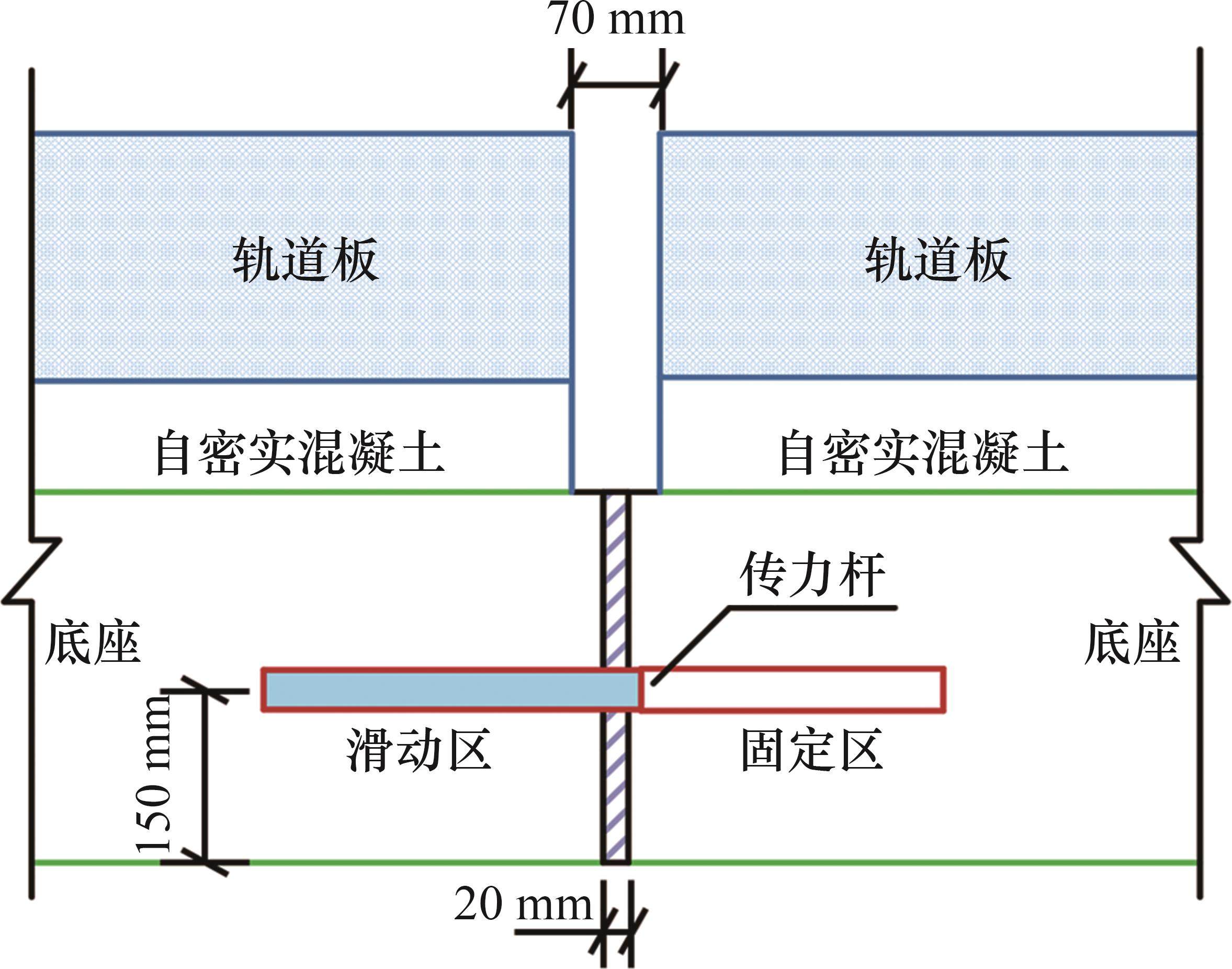
1.3 模型验证
现有设计规范规定,轨道板200 mm范围内的正温度梯度取90 ℃/m[18]。参考无砟轨道设计规范,本文采用夏季某线路CRTS Ⅲ型板式无砟轨道的实测温度作为加载依据,选取轨道板上下(竖向200 mm范围)的温度差,通过线性拟合进行加载,将板中和板端竖向变形仿真值与实测值进行对比,结果如图3所示。
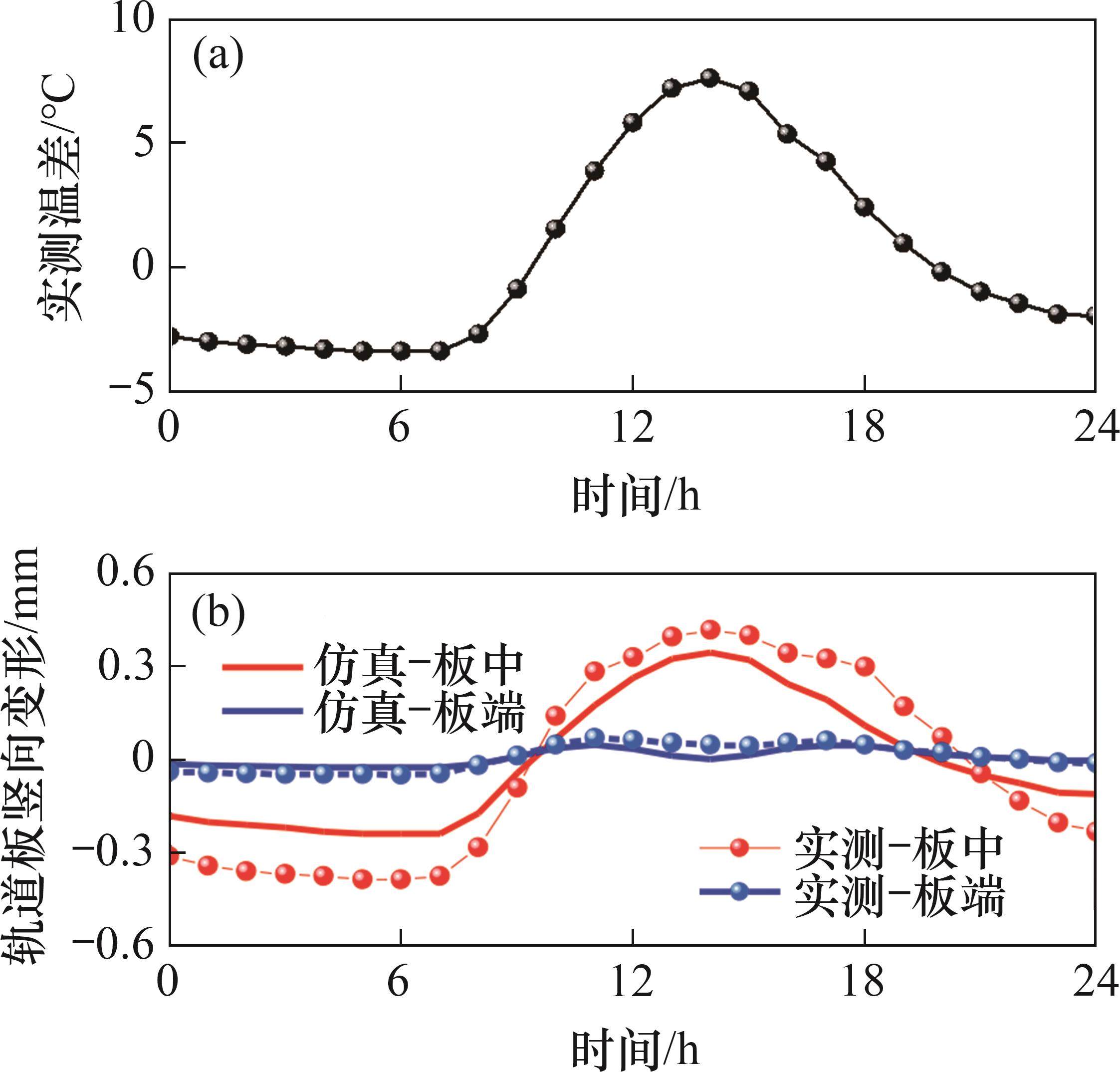
对比结果表明,本文模型轨道板中部和端部竖向变形计算结果与实测结果吻合较好,实测结果略大于仿真分析结果,这是因为本文采用线性温度梯度进行简化加载,因此,竖向变形计算值偏小。
2 无砟轨道计算工况
为揭示限位凹槽纵向位置与轨道结构传力机制的关系,建立限位凹槽不同纵向间距的路基段实体模型,分析轨道多层结构间非线性相互作用关系,研究不同凹槽纵向位置条件下,不均匀沉降和温度荷载对轨道结构受力及轨面变形的影响。
2.1 限位凹槽纵向位置计算工况
CRTS Ⅲ型板式无砟轨道中自密实混凝土凸台与底座限位凹槽相结合,以实现结构层之间的传力、限位功能。CRTS Ⅲ型板式无砟轨道的轨道板布置不变,仅改变限位凹槽位置,计算不同荷载条件下轨道结构的受力与变形情况。依据现场偏差工况与现有文献[7],将底座限位凹槽的纵向间距分别设置为3 080、2 080和1 080 mm,以研究不同凹槽纵向间距对轨道板竖向变形的影响,如图4所示。
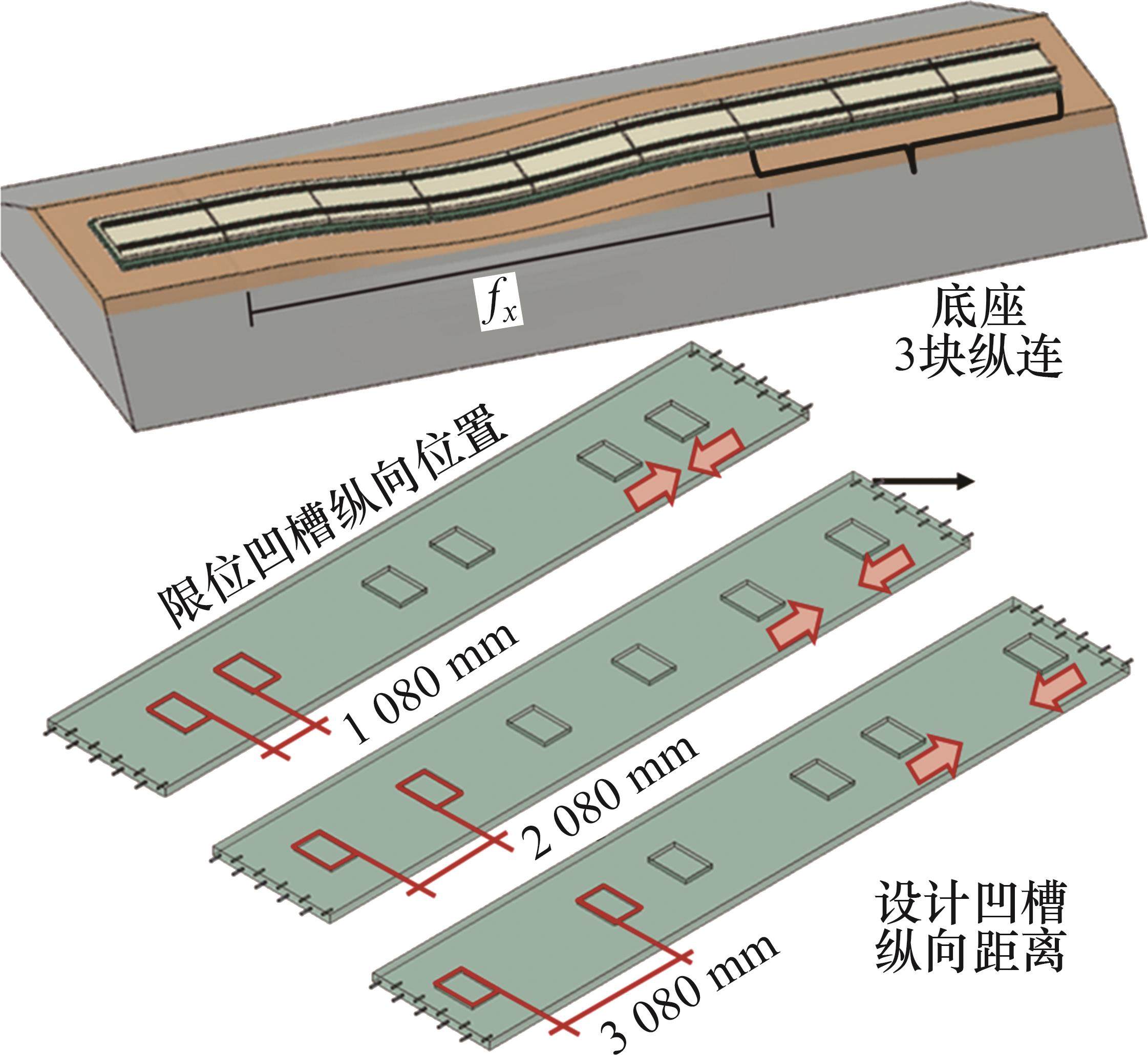
限位凹槽位置的变化导致无砟轨道在荷载作用下的应力分布发生变化,结构受力与变形需重新计算。
2.2 计算荷载
针对路基段无砟轨道主要荷载形式,考虑路基不均匀沉降和夏季高温荷载2个工况。
1) 路基不均匀沉降。路基不均沉降形式考虑为沿线路纵向的余弦型曲线,其表达式如下:
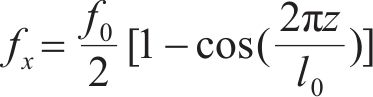
3 凹槽纵向间距对轨道传力机制影响
3.1 路基不均匀沉降
为直观反映无砟轨道多层结构随路基沉降的变形规律,选择路基段50 m范围内无砟轨道进行各层结构传力特征分析。不同限位凹槽纵向间距下轨道板和自密实混凝土的横向应力的分布如图5所示,其中,横向应力云图对应工况为限位凹槽纵向间距为2 080 mm的工况。
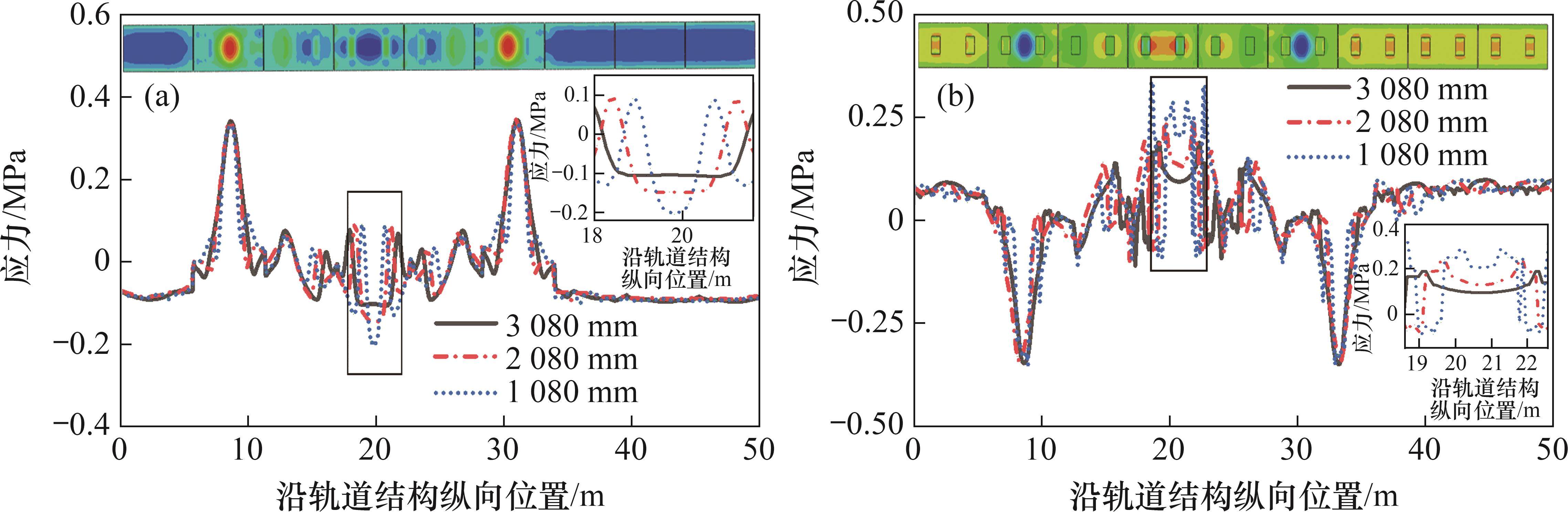
从图5可见:当路基不均匀沉降时,随着凹槽纵向间距减小,轨道板、自密实混凝土的横向应力增大,底座受力变化差异较小,轨道板横向应力差最大达到0.189 MPa,自密实混凝土横向应力差最大达到0.277 MPa。
不同限位凹槽纵向间距下轨道板、自密实混凝土纵向应力的分布如图6所示,其中,纵向应力云图对应工况为限位凹槽纵向间距为2 080 mm的工况。从图6可见:当路基不均匀沉降时,随着限位凹槽纵向间距的缩小,轨道结构纵向拉应力极值不断增加,轨道板纵向应力差最大达到0.319 MPa,自密实混凝土纵向应力差最大达到1.029 MPa。
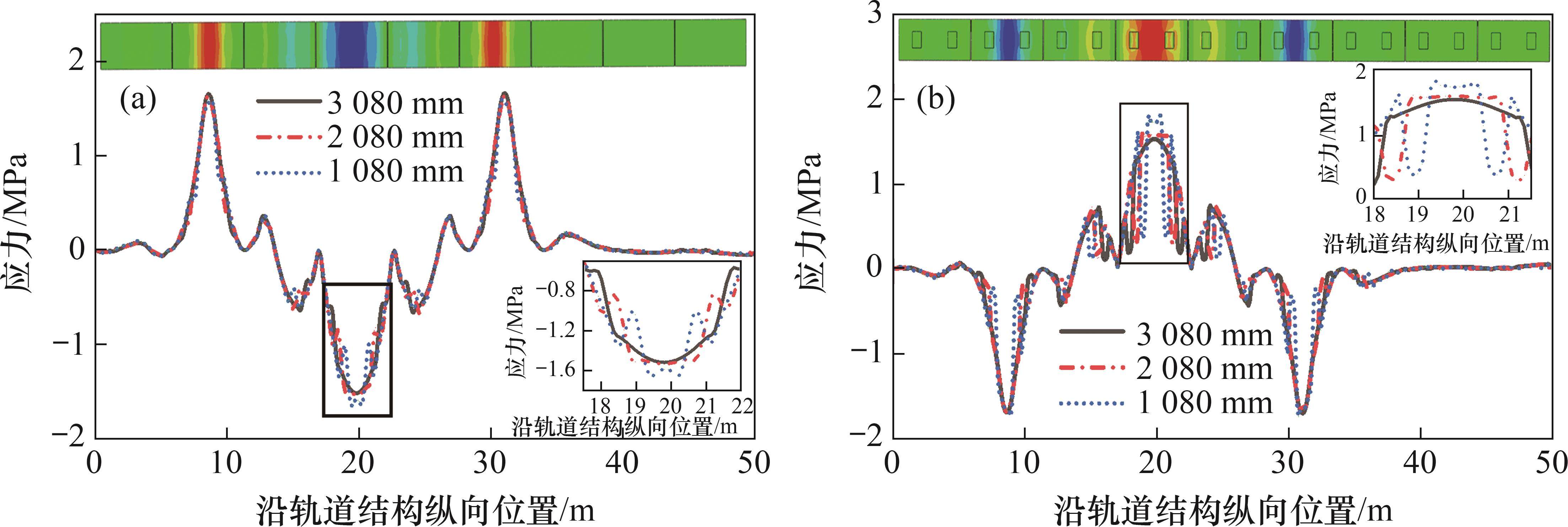
3.2 夏季高温荷载
在夏季高温环境下,轨道板内部的温度分布呈现正温度梯度趋势。为模拟更真实的边界条件,选择模型中间的无砟轨道进行各层受力分析。
不同限位凹槽纵向间距下轨道板、自密实混凝土和底座的横向应力的分布如图7所示,其中,横向应力云图对应工况取限位凹槽纵向间距为 2 080 mm的工况。
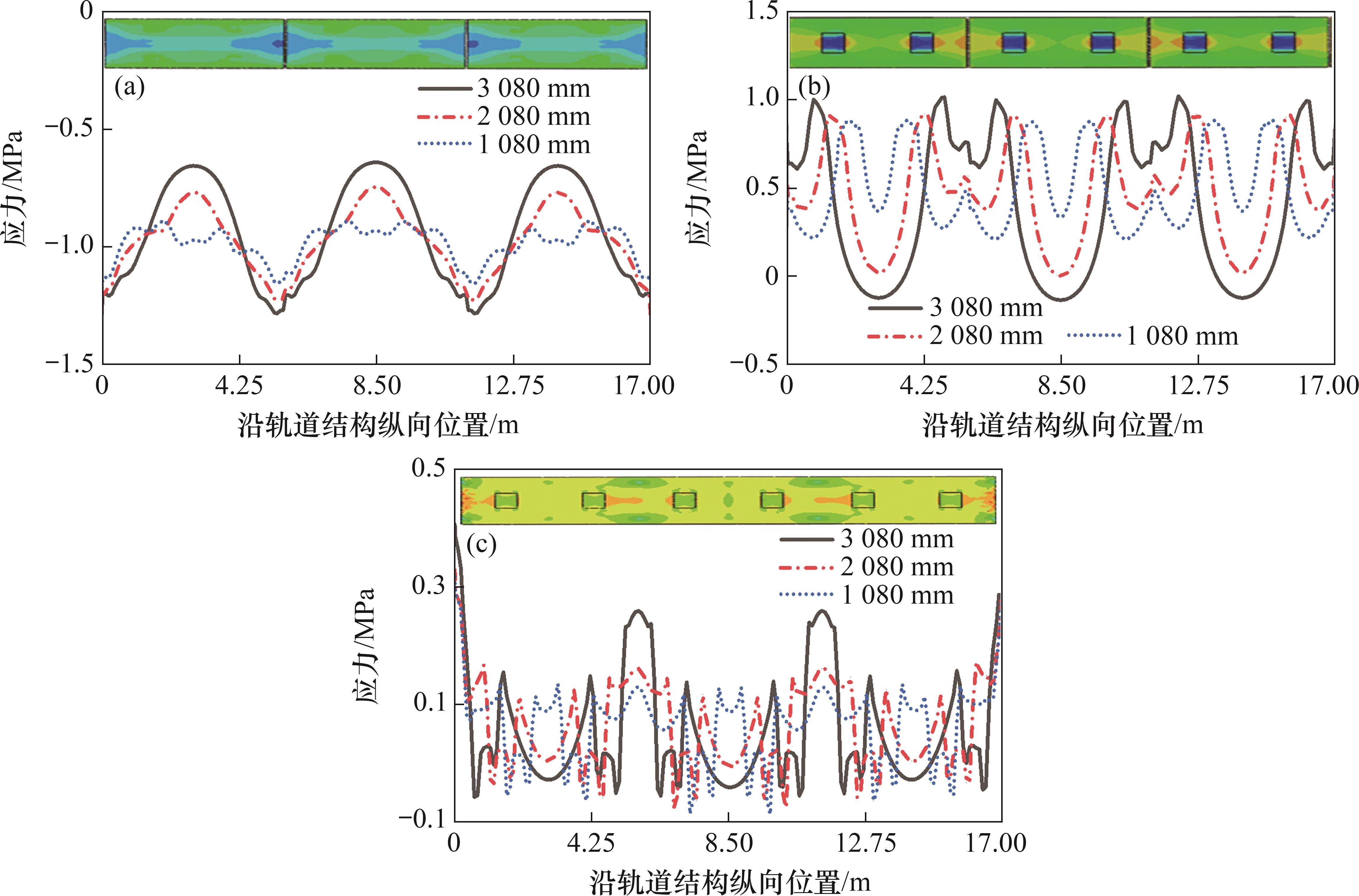
从图7可见:在高温条件下,轨道结构的横向应力分布随着限位凹槽的纵向位置变化差异显著,且随着限位凹槽纵向间距的缩小,轨道结构横向拉应力极值不断减小,轨道板横向应力差值最大达到0.463 MPa,自密实混凝土横向应力差值最大达到0.468 MPa,底座横向应力差值最大达到0.131 MPa。由于传力杆的作用,底座两端出现横向应力集中现象。此外,限位凹槽的纵向位置差异导致应力集中有所不同,在限位凹槽纵向间距为3 080 mm时,横向应力极值达到0.4 MPa。
不同限位凹槽纵向间距下轨道板、自密实混凝土和底座的纵向应力的分布如图8所示,其中,纵向应力云图对应工况取限位凹槽纵向间距为 2 080 mm的工况。
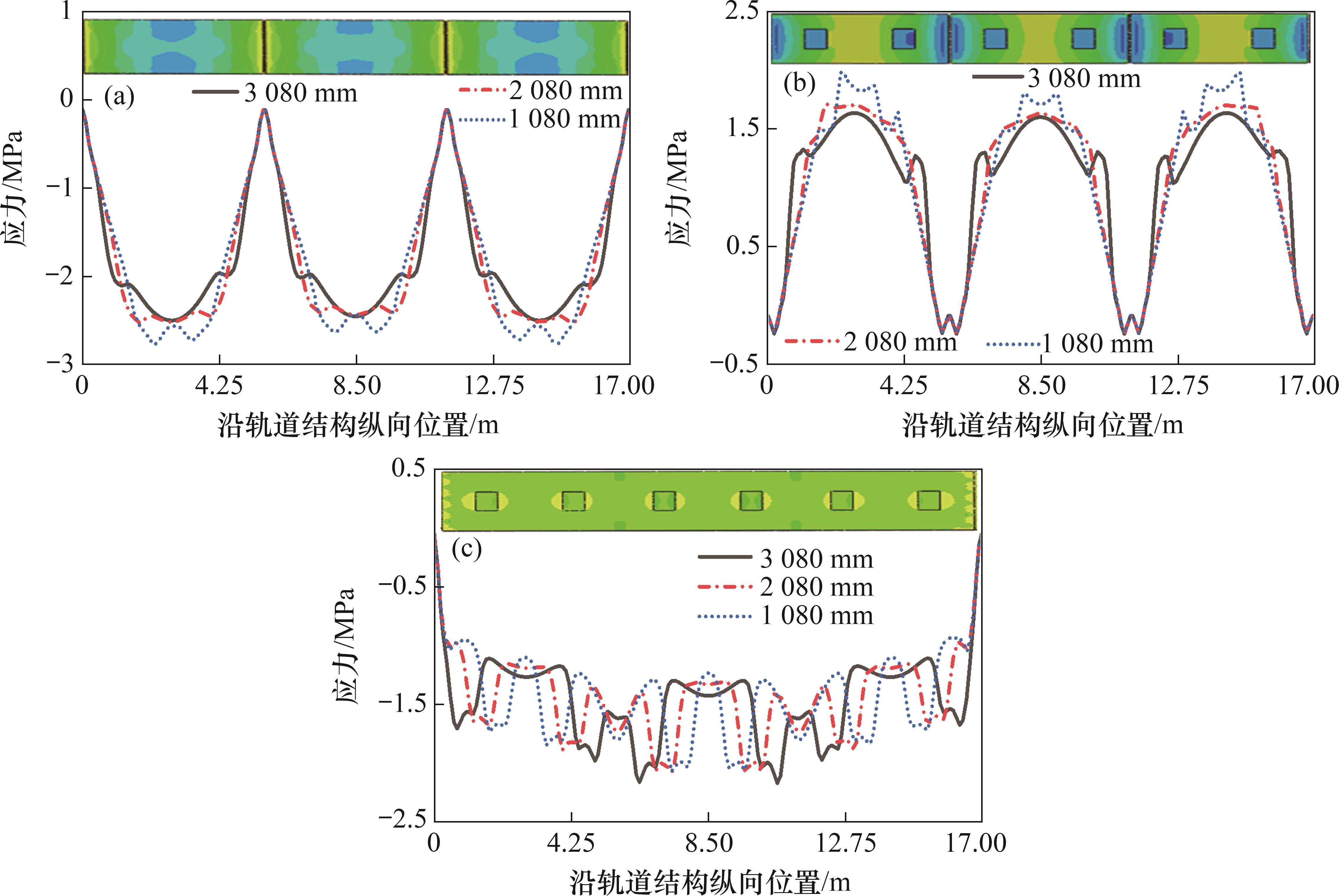
从图8可见:在高温荷载条件下,轨道结构的纵向应力分布与限位凹槽的纵向位置密切相关;随着限位凹槽纵向间距的缩小,轨道结构纵向应力极值呈增大趋势,轨道板纵向应力差值最大达到0.403 MPa,自密实混凝土纵向应力差值最大达到0.394 MPa,由于底座板端传力杆作用,板端呈现纵向应力集中现象,不同工况下底座纵向应力极值差异较小。
基于上述分析,在路基不均匀沉降和夏季高温荷载条件下,横、纵向应力最大值分别为1.114 MPa和1.791 MPa,且自密实混凝土的横、纵向应力最大,其中最不利应力水平达到自密实混凝土允许拉应力[23]的74.9%。
3.3 传力杆分析
在路基不均匀沉降和夏季高温荷载的影响下,底座板端部易出现受力集中现象,从而导致传力杆的承载力显著增加。在不同限位凹槽纵向间距条件下,传力杆结构纵向应力最值的变化情况如图9所示。由图9可知:在路基不均匀沉降条件下,随着限位凹槽纵向间距的减小,传力杆的纵向应力极值呈现增大趋势,其中,纵向拉应力增加量达到1.51 MPa;在夏季高温条件下,由于底座受到整体升温荷载作用呈现受拉状态,板端传力杆整体为受压状态。随着限位凹槽纵向间距的减小,传力杆压力最大变化量为1.17 MPa。
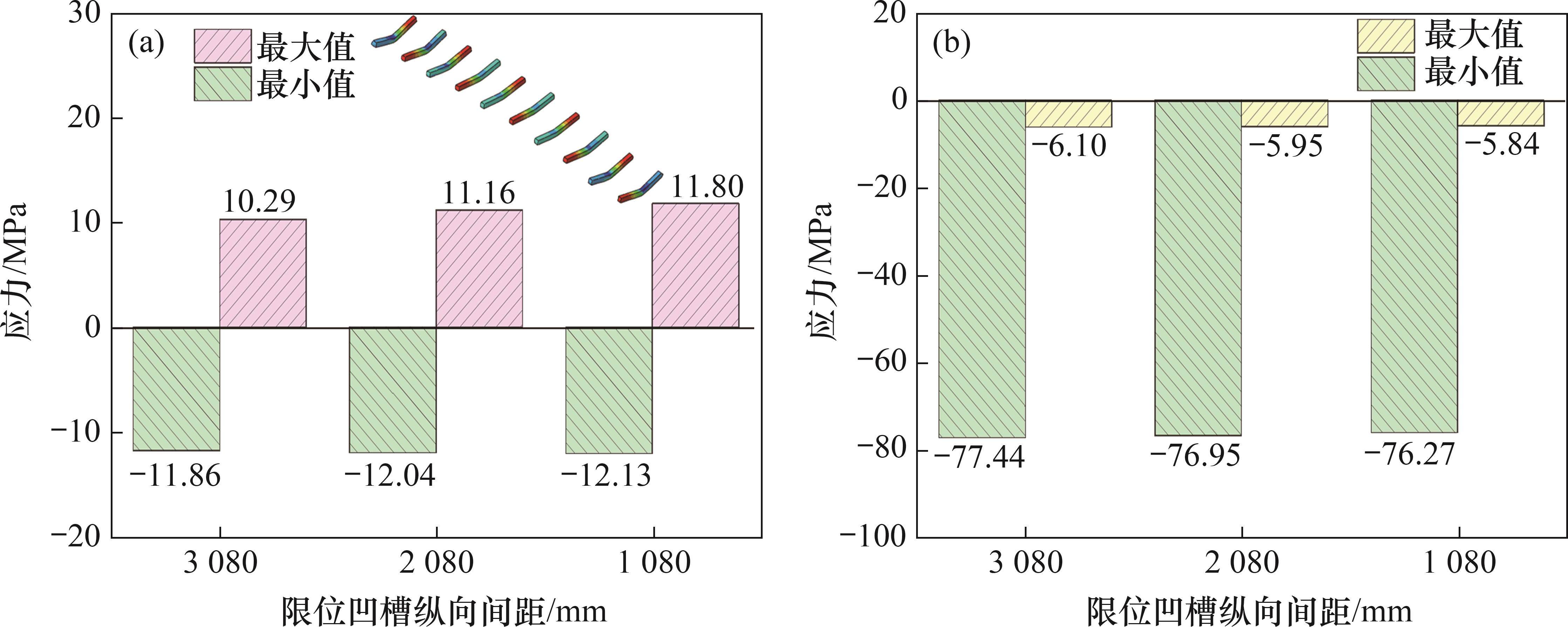
在路基不均匀沉降下,限位凹槽间距减小增强了轨道板与底座之间的约束,导致应力集中,尤其是自密实混凝土应力变化显著;在高温条件下,限位凹槽间距减小限制了轨道的变形空间,导致横向应力减小而纵向应力增大。此外,随着限位凹槽间距减小,传力杆在轨道结构中的纵向应力有所增加。
4 层间脱空与轨面平顺性分析
无砟轨道整体刚度较大,在路基不均匀沉降和夏季高温条件下,易出现层间脱空现象[24]。CRTS Ⅲ型板式无砟轨道中轨道板与自密实混凝土间预留门型钢筋,层间连结性能良好,未发生层间脱空,自密实混凝土与底座间设置隔离层,是层间脱空行为主要发生位置。
根据无砟轨道结构间的传力机制可知,不同限位凹槽纵向间距下,无砟轨道受力规律不同,自密实混凝土与底座间形成不同的脱空状态及轨面变形规律。在路基不均匀沉降下,限位凹槽纵向间距对层间脱空及钢轨垂向变形量的影响如图10所示。
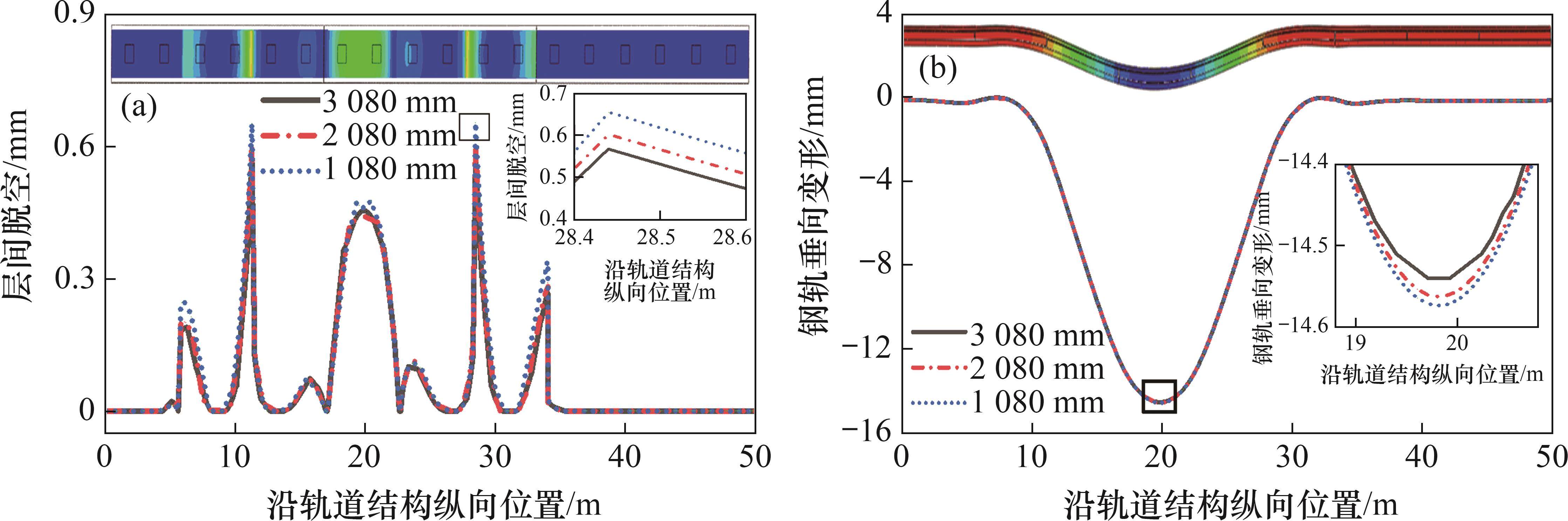
在路基不均匀沉降下,自密实混凝土与底座层间的垂向脱空量与路基沉降位置、沉降幅值密切相关。由图10(a)可知:层间脱空最值出现在底座端部接缝位置;随着限位凹槽纵向间距的减小,层间脱空极值呈现增大趋势,层间脱空值增加量达到0.276 mm。由图10(b)可知,在路基沉降幅值15 mm时,钢轨垂向变形幅值达到14.57 mm;在不同限位凹槽纵向间距条件下,钢轨垂向变形差异较小,随着限位凹槽纵向间距的减小,钢轨变形极值呈现增大趋势。
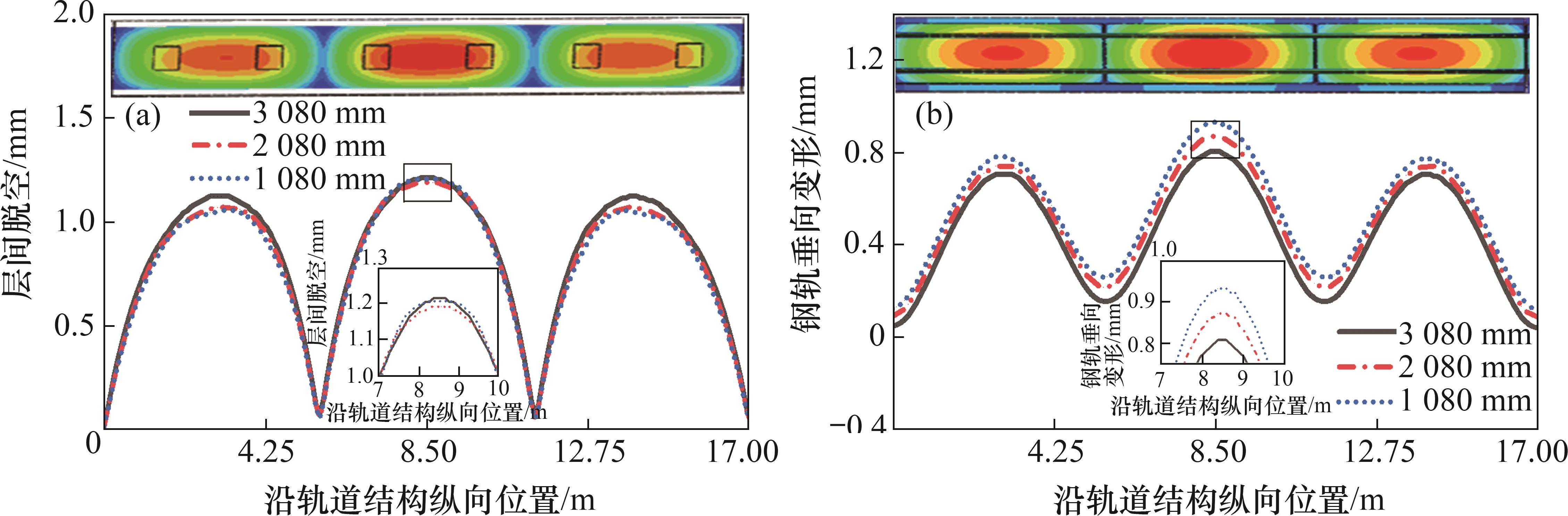
在夏季高温条件下,限位凹槽纵向间距对层间垂向脱空、钢轨垂向变形量的影响如图11所示。从图11可见:随着限位凹槽纵向间距的减小,层间脱空、钢轨变形极值呈现增大趋势,但极值差异较小。CRTS Ⅲ型板式无砟轨道中,自密实混凝土与底座之间设置隔离层,在高温荷载下,轨道板与自密实混凝土发生上拱变形,层间产生脱空,其最值出现在轨道板中部上拱幅值最大位置。
5 结论
1) 在路基不均匀沉降条件下,随着限位凹槽纵向间距减小,轨道应力不断增加。在各工况下,自密实混凝土纵向应力差值最大为1.029 MPa。
2) 在夏季高温荷载下,无砟轨道的应力分布与限位凹槽纵向位置紧密关联。随着限位凹槽纵向间距减小,横向应力逐渐减小,最大减小0.468 MPa;而纵向应力则持续增加,最大增加0.403 MPa。
3) 传力杆结构对底座受力影响较大。为准确模拟轨道的受力特征,传力杆结构不容忽视。随着限位凹槽纵向间距减小,传力杆的纵向应力极值增大,其纵向应力增量极值达到1.51 MPa。
4) 随着限位凹槽纵向间距减小,自密实混凝土与底座的层间脱空和钢轨变形量逐渐增加。在路基不均匀沉降幅值为15 mm的条件下,层间脱空的增量达到0.276 mm;在夏季高温荷载下,各工况层间脱空、钢轨变形量较小。限位凹槽纵向间距变化对轨面平顺性影响较小。
陈泽林, 蔡小培, 赵磊, 等. 限位凹槽纵向间距对CRTS Ⅲ型板式无砟轨道受力及轨面平顺性的影响分析[J]. 中南大学学报(自然科学版), 2024, 55(12): 4560-4569.
CHEN Zelin, CAI Xiaopei, ZHAO Lei, et al. Analysis of impact of longitudinal position of position-limitation recess on stress and rail regularity of CRTS Ⅲ slab track[J]. Journal of Central South University(Science and Technology), 2024, 55(12): 4560-4569.

