随着我国西部大开发的推进,完善西部地区路网的需求迫在眉睫[1]。我国西部山脉纵横,地质条件复杂,高地温、高地应力、活动断裂带的地段较多[2],铁路隧道结构施工后变形频发。轨下基础变形将引发轨道结构各层跟随性变形,导致轨道不平顺加剧、层间产生离缝甚至脱空,恶化轨道结构受力情况,加剧轨道结构材料破坏,危害行车舒适性、平稳性与安全性,进一步降低了轨道结构耐久性。目前国内外诸多学者就路基段与桥梁段无砟轨道在轨下基础不均匀沉降作用下的力学行为进行了研究。CHEN[3]、吴楠等[4]分别研究了桥墩沉降作用下纵连板式、单元板式无砟轨道系统力学行为;在此基础上,GOU等[5]关注梁体错台及梁端转角探究了其对无砟轨道结构变形的影响;FENG等[6]进一步提出了高速铁路基础变形诱发无砟轨道-桥梁系统关键构件变形累积与刚度突变的轨面解析表征模式。PAIXÃO等[7]采用Dirac函数描述道床不均匀沉降,深入讨论了不同沉降剖面,尤其是轨道倾角对轨道结构动力性能的影响。蔡小培等[8-9]集中研究了路基不均匀沉降对双块式无砟轨道结构的平顺性、结构损伤与列车动力性能的影响;向俊等[10]探究了路基冻胀变形作用对无砟轨道力学行为的影响特征;李正等[11]深入分析了不同土层变形波长和幅值组合下单元板的动力响应差异;肖源杰等[12]关注有砟铁路轨道结构,探究了列车动载作用下路基不均匀沉降对轨道结构动力响应和行车安全性影响。虽然国内外学者已就基础不均匀沉降作用下铁路轨道力学分析建立了相对完善的理论体系[13-14],但目前还未有相关研究体现隧道内无砟轨道结构体系在该作用下的空间变形规律。弹性支承块式无砟轨道具有良好的弹性性能,在我国的长大隧道段无砟铁路工程中得到广泛应用[15]。对于应用在基础变形区域内的隧道段无砟轨道结构,基础变形对其结构几何形位影响巨大,例如:门源地震导致兰新高铁大梁隧道无砟轨道结构变形剧烈,整体伤损严重,断裂带附近形成高差约40 cm错台,垂向变形最大达688 mm[16]。故本文针对基础变形区域隧道地段弹性支承块式无砟轨道,采用Abaqus有限元分析软件建立静力学空间有限元分析模型,以仰拱不均匀沉降作为基础变形输入形式,探讨在不同变形幅值和不同波长作用下,钢轨、道床板及层间离缝的变化发展规律,以期为基础变形区域隧道地段无砟轨道的优化设计与运维提供参考。
1 理论模型的建立
1.1 空间有限元模型建立
将隧道地段弹性支承块式无砟轨道(如图1(a))划分为隧道结构(如图1(b))与弹性支承块式无砟轨道结构(如图1(c))。以仰拱不均匀沉降作为基础变形输入形式,建立隧道地段弹性支承块式无砟轨道空间有限元实体模型,考虑到在线路横向上呈现为轴对称,模型取横向半结构,在对称面上施加横向对称约束。
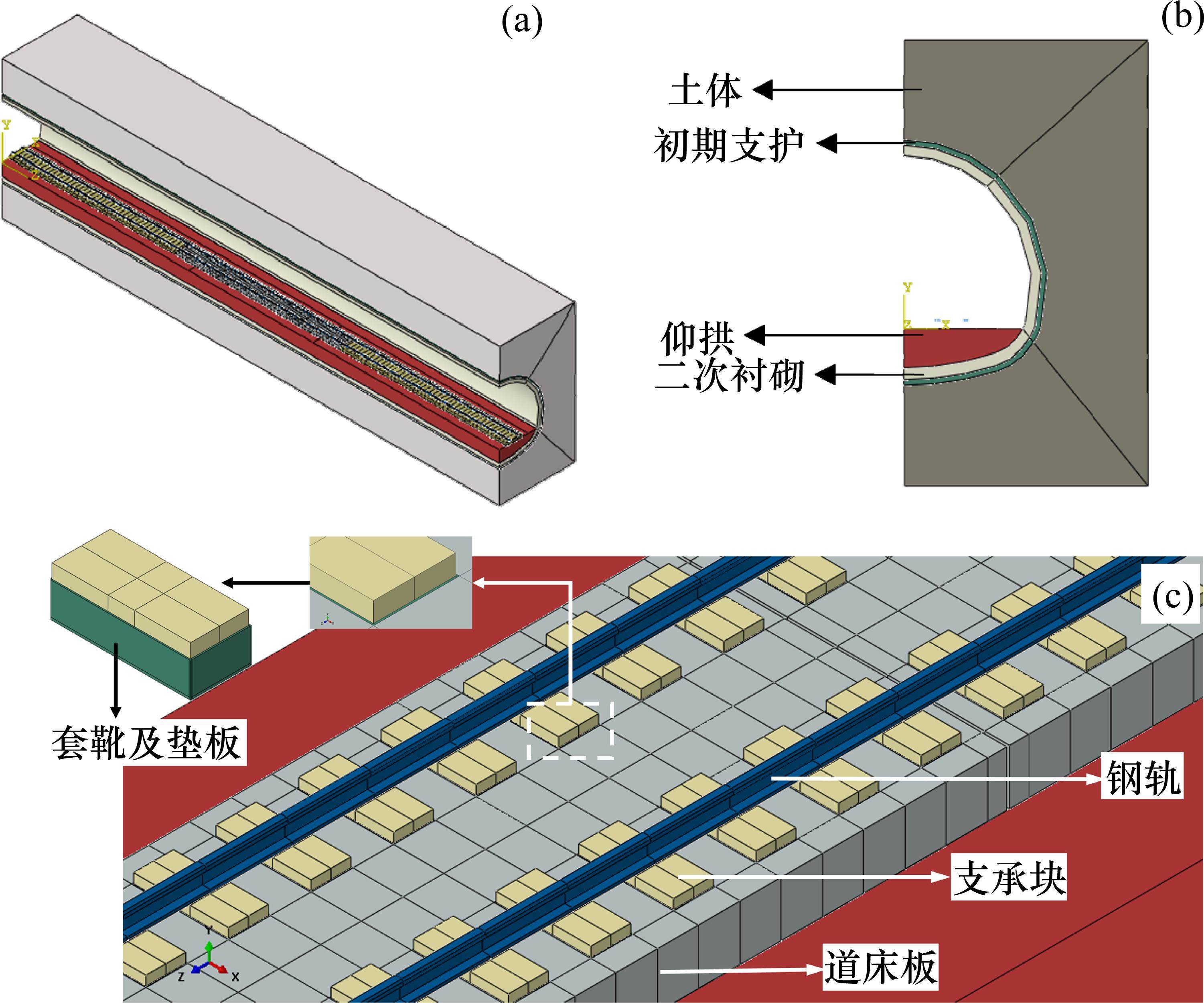
本文侧重于研究基础变形区域弹性支承块式无砟轨道结构变形及道床板与仰拱间离缝发展,因此对有限元模型采取如下简化:1) 考虑重力作用下地应力平衡,在仰拱顶面施加位移约束模拟基础变形;2) 假设钢轨、支承块、套靴、垫板、道床板、仰拱、二次衬砌、初期支护、土体的变形均处于材料弹性变形条件范围内;3) 弹性支承块式无砟轨道扣件类型为弹条Ⅶ型扣件,模拟为空间线性三向弹簧;4) 支承块-套靴-垫板-道床板间接触节点具有相同自由度,道床板-仰拱间采用接触模拟[17]。
1.2 模型参数
1.2.1 结构尺寸及材料参数
弹性支承块式无砟轨道各层结构材料参数[18]见表1,结构尺寸如下所述:1) 钢轨为60轨;2) 支承块长0.69 m,宽0.29 m,高0.23 m,埋深0.16 m;3) 道床板长6.58 m,宽2.5 m,高0.4 m;4) 套靴厚0.007 m,垫板厚0.012 m。
| 结构层 | 弹性模量/MPa | 泊松比 | 密度/(kg∙m-3) |
|---|---|---|---|
| 钢轨 | 2.10×105 | 0.30 | 7 800 |
| 支承块 | 3.45×104 | 0.20 | 2 500 |
| 道床板 | 3.25×104 | 0.20 | 2 500 |
| 套靴 | 36.50 | 0.47 | 1 400 |
| 垫板 | 36.00 | 0.40 | 1 400 |
1.2.2 基础变形参数
根据文献[19-20],可将基础变形形式考虑为余弦型下凹曲线,如图2,表达式为式(1)。
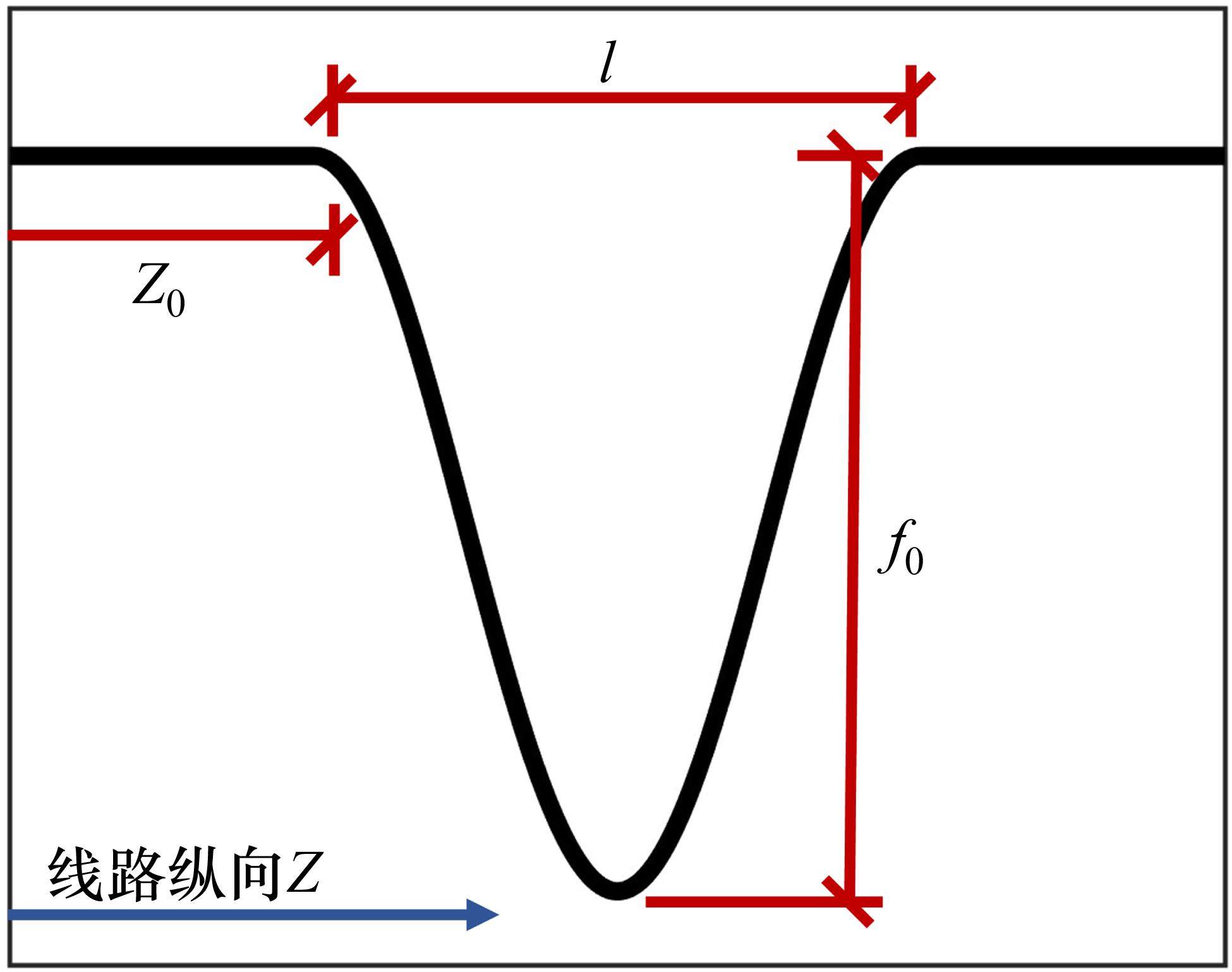
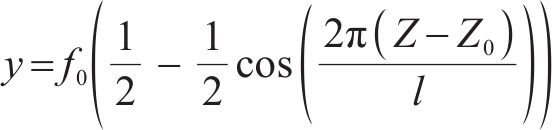
式中: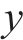

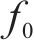

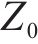
1.3 模型检验
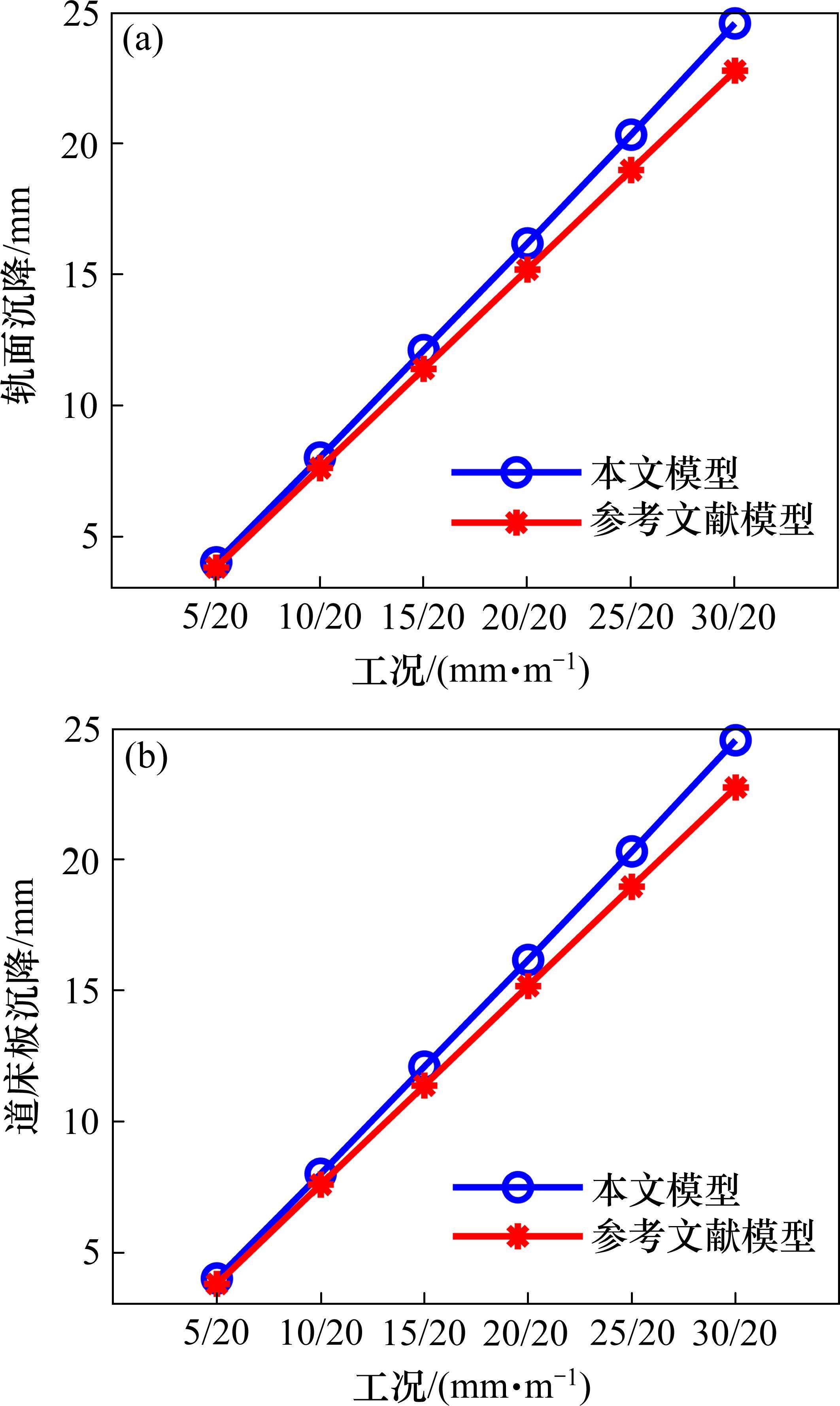
为验证建模方法与有限元求解算法选取的准确性,根据文献[8]中给出相关参数,选取沉降波长为20 m,幅值为5,10,15,20和30 mm的工况,在Abaqus中建立与文献[8]中完全相同的双块式无砟轨道结构模型进行求解。将结果与文献[8]进行对比,如图3所示,分析结果与参考文献结果趋势一致,数值差异在可接受范围内,考虑是有限元分析软件不同版本间的算法差异等原因导致,故本文采用的求解方式准确可靠。
2 基础变形作用下轨道结构变形特征分析
2.1 基础变形工况
根据文献[16]可知,门源地震后大梁隧道无砟轨道结构产生严重整体伤损,垂向变形最大达688 mm。选取20 m为沉降波长,分析沉降幅值分别为5,10,15,20,30,40,60和80 mm工况下隧道段弹性支承块式无砟轨道结构沉降变化;选取80 mm为沉降幅值,计算沉降波长分别为20,25,30,40,50,60,70,80,90和100 m工况下隧道段弹性支承块式无砟轨道结构沉降变化。
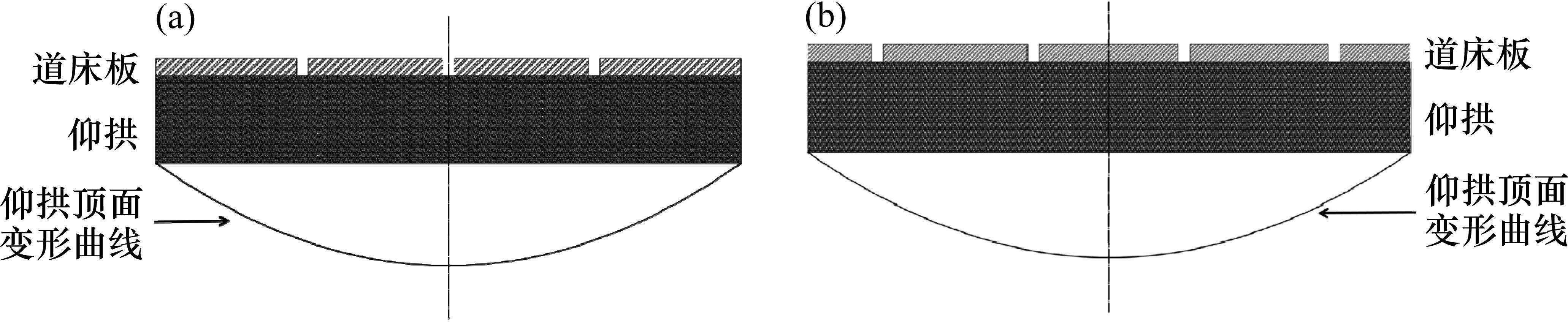
由于路基段、桥梁段无砟轨道在基础和道床板间设有支承层,但隧道段无砟轨道是将道床板直接构筑在仰拱上[21],根据道床板位置与余弦波相对位置的不同,分2类讨论,分别是沉降中心为板端(如图4(a))以及沉降中心为板中(如图4(b))。
2.2 沉降幅值对轨道结构的影响
2.2.1 沉降幅值对钢轨高低不平顺的影响
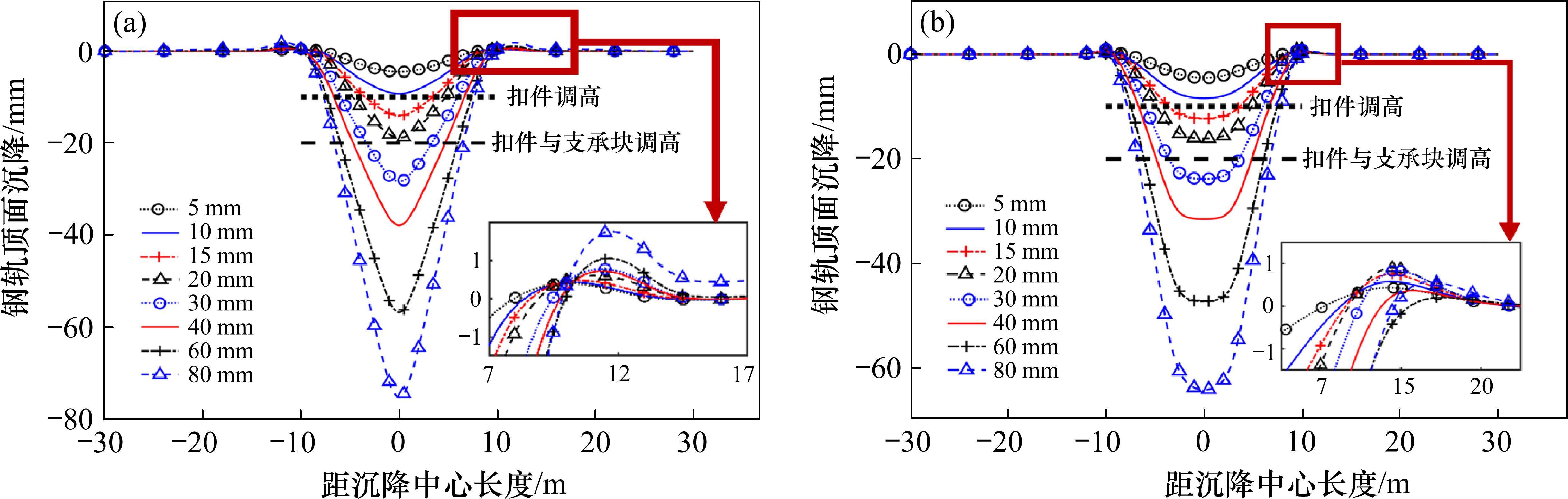
沉降波长为20 m时,不同幅值下钢轨轨面变形特征如图5所示,钢轨轨面变形峰值如表2所示。
| 幅值/mm | 波长/m | 沉降中心为板端 | 沉降中心为板中 | ||
|---|---|---|---|---|---|
最大下沉 值/mm | 最大上拱值/mm | 最大下 沉值/mm | 最大上拱值/mm | ||
| 5 | 20 | 4.467 | 0.407 | 4.533 | 0.433 |
| 10 | 20 | 9.3 | 0.43 | 8.443 | 0.581 |
| 15 | 20 | 14.081 | 0.48 | 12.287 | 0.753 |
| 20 | 20 | 18.856 | 0.609 | 16.141 | 0.898 |
| 30 | 20 | 28.375 | 0.775 | 23.85 | 0.994 |
| 40 | 20 | 37.89 | 0.737 | 31.557 | 0.491 |
| 60 | 20 | 56.8 | 1.079 | 47.27 | 0.203 |
| 80 | 20 | 75.218 | 1.784 | 64.224 | 0.61 |
由表2可知,当沉降波长相同时,沉降范围内,钢轨随基础沉降,沉降值随幅值增大而增大;沉降余弦波始末端,由于端部法向支承力,钢轨出现小幅上拱反弯,沉降沿线路纵向向外扩散,且随着沉降幅值增大,反弯点逐渐远离沉降区,扩散范围随之增大。
由图5(a)可知,当沉降中心为板端时,钢轨沉降形式与基础变形形式一致性较高;沉降区两端上拱最大值随沉降波长的增大而增大。由图5(b)可知,当沉降中心为板中时,沉降中心的沉降变化较为缓和,钢轨变形形式一致性较低。对比图5与轨面变形峰值可知,当沉降中心为板中时,钢轨变形较为缓和;相同工况下,沉降中心为板端时的钢轨沉降值大于沉降中心为板中时的钢轨沉降值,故沉降中心为板端的情况更为不利。
弹性支承块式无砟轨道可以通过扣件和支承块下垫板实现快速调高。当沉降波长为20 m时,沉降幅值小于10 mm时,通过扣件调高即可恢复轨面高低平顺;当沉降幅值在10~20 mm时,通过调整沉降中心左右支承块下垫板与调高扣件可恢复线路高低平顺;当沉降幅值超过20 mm时,仅对扣件和道床板进行调高已无法满足线路平顺性要求,需对轨下结构进行修补[22]。
2.2.2 沉降幅值对道床板的影响
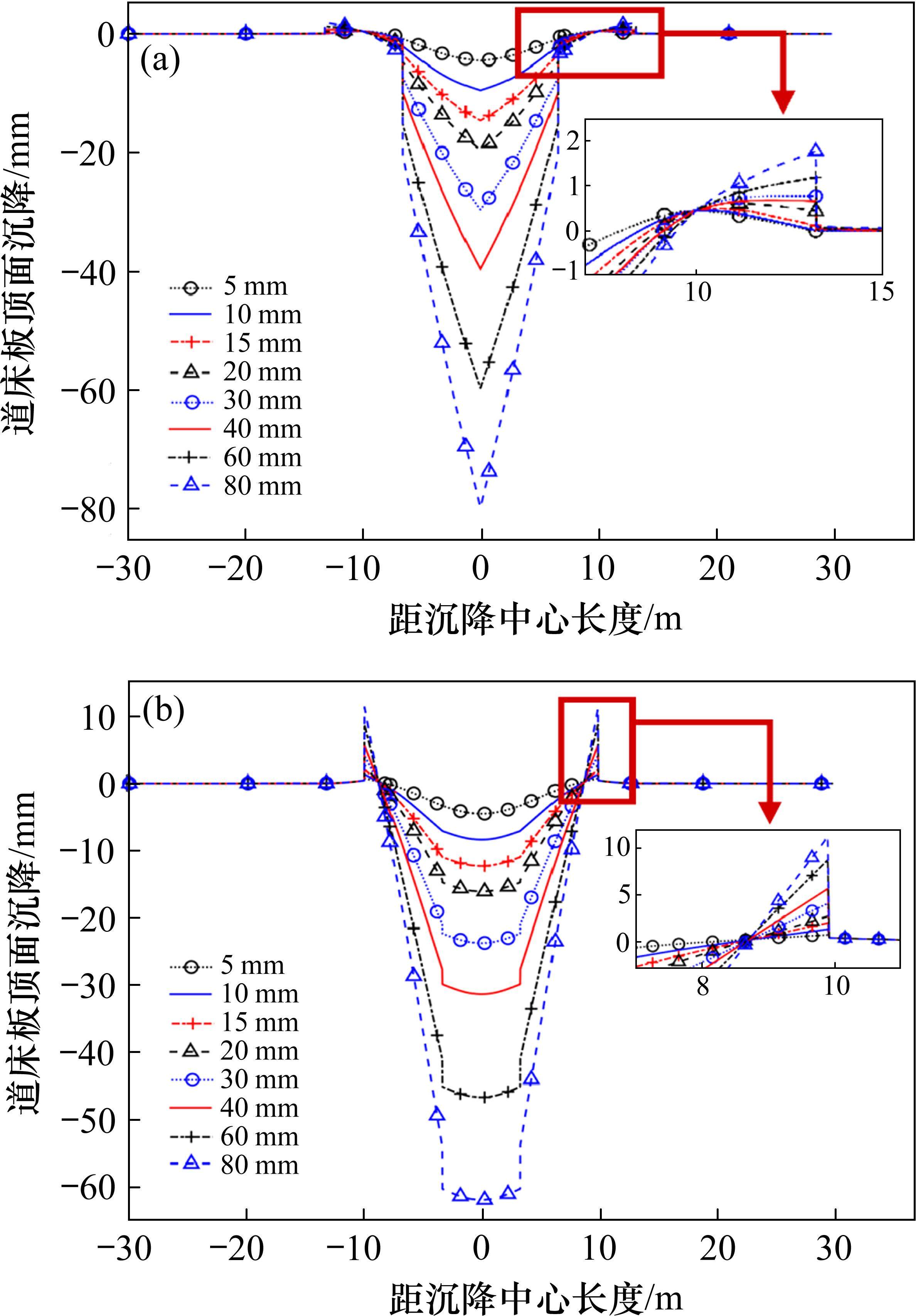
沉降波长为20 m时,不同幅值下道床板变形特征如图6所示,道床板变形峰值如表3所示。
| 幅值/mm | 波长/m | 沉降中心为板端 | 沉降中心为板中 | ||
|---|---|---|---|---|---|
| 最大下沉值/mm | 最大上拱值/mm | 最大下沉值/mm | 最大上拱值/mm | ||
| 5 | 20 | 4.567 | 0.437 | 4.531 | 0.748 |
| 10 | 20 | 9.579 | 0.449 | 8.429 | 1.349 |
| 15 | 20 | 14.593 | 0.489 | 12.258 | 2.032 |
| 20 | 20 | 19.609 | 0.597 | 16.09 | 2.718 |
| 30 | 20 | 29.643 | 0.769 | 23.75 | 4.084 |
| 40 | 20 | 39.677 | 0.696 | 31.408 | 5.66 |
| 60 | 20 | 59.746 | 1.245 | 46.701 | 8.75 |
| 80 | 20 | 79.815 | 1.839 | 61.934 | 11.372 |
由上可知,当沉降波长相同时,沉降范围内,由于存在板缝,道床板在线路纵向不连续,沉降形式与基础沉降形式一致性较低,在板端处出现突变,道床板在沉降区域两侧出现错台现象;道床板沉降值与端部上拱值随幅值增大而增大。
由图6(a)可知,当沉降中心为板端时,沉降在接近沉降中心时达到最大且出现尖角突变。由图6(b)可知,当沉降中心为板中时,沉降在沉降中心处最大且变化平缓。对比图6及道床板变形峰值可知,当沉降中心为板中时,道床板沉降较小且变化缓和,故沉降中心为板端的情况更为不利。
2.3 沉降波长对轨道结构的影响
根据上文研究可知当沉降中心为板端时,钢轨和道床板沉降情况较为恶劣,故本节针对沉降中心为板端的情况进行研究。
2.3.1 沉降波长对钢轨高低不平顺的影响
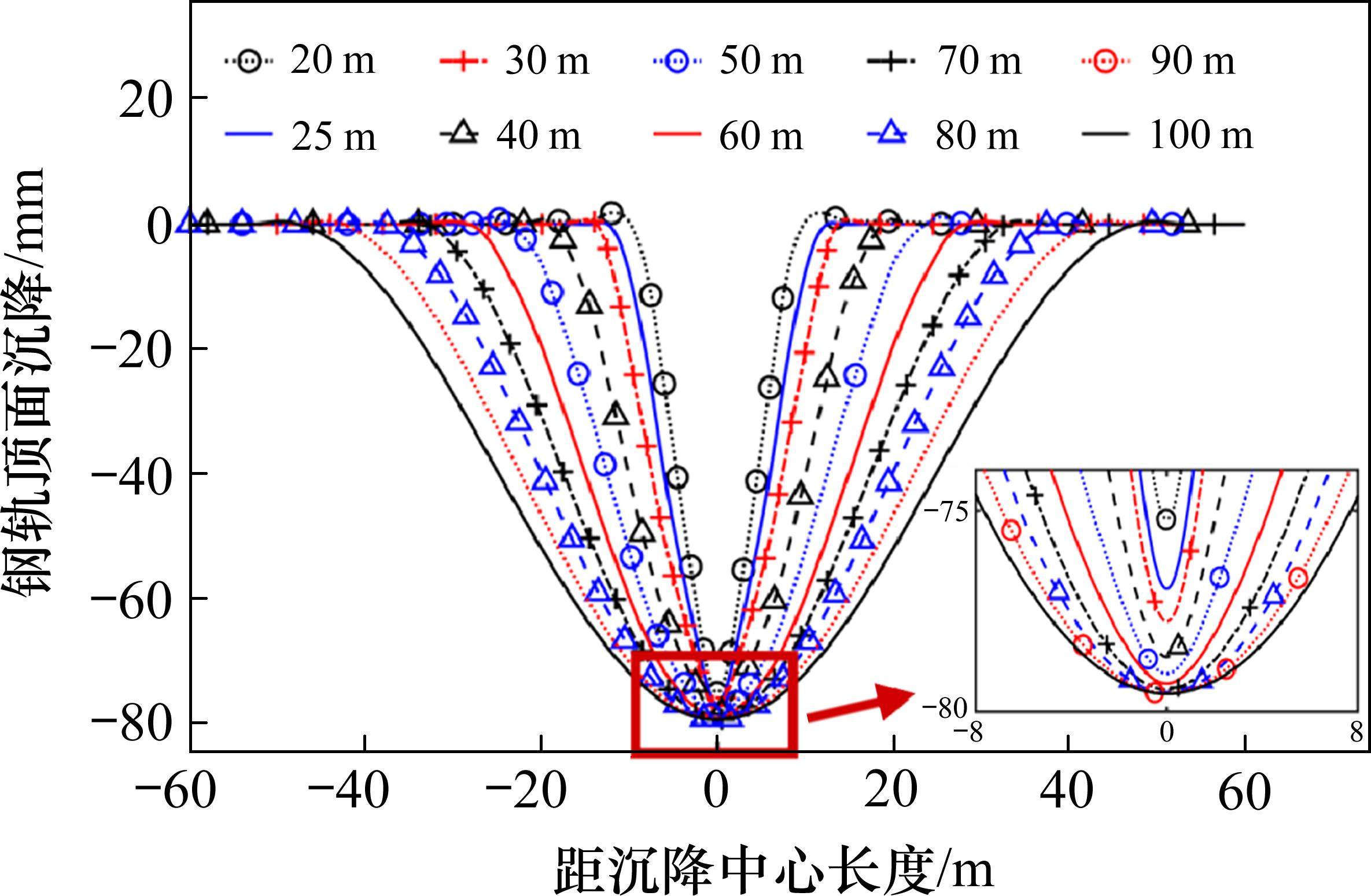
沉降幅值为80 mm时,不同波长下轨面变形特征如图7所示,轨面变形峰值如表4所示。
| 幅值/mm | 波长/m | 最大下沉值/mm | 最大上拱值/mm |
|---|---|---|---|
| 80 | 20 | 75.219 | 0.407 |
| 80 | 25 | 76.938 | 0.206 |
| 80 | 30 | 77.751 | 0.698 |
| 80 | 40 | 78.624 | 0.609 |
| 80 | 50 | 79.042 | 1.076 |
| 80 | 60 | 79.284 | 0.419 |
| 80 | 70 | 79.439 | 0.5 |
| 80 | 80 | 79.508 | 0.415 |
| 80 | 90 | 79.536 | 0.484 |
| 80 | 100 | 79.546 | 0.44 |
由上可知,当沉降幅值相同时,在基础不均匀沉降范围内,钢轨变形形式与基础变形形式一致性较高;钢轨沉降随波长增加而增加。
2.3.2 沉降波长对道床板的影响
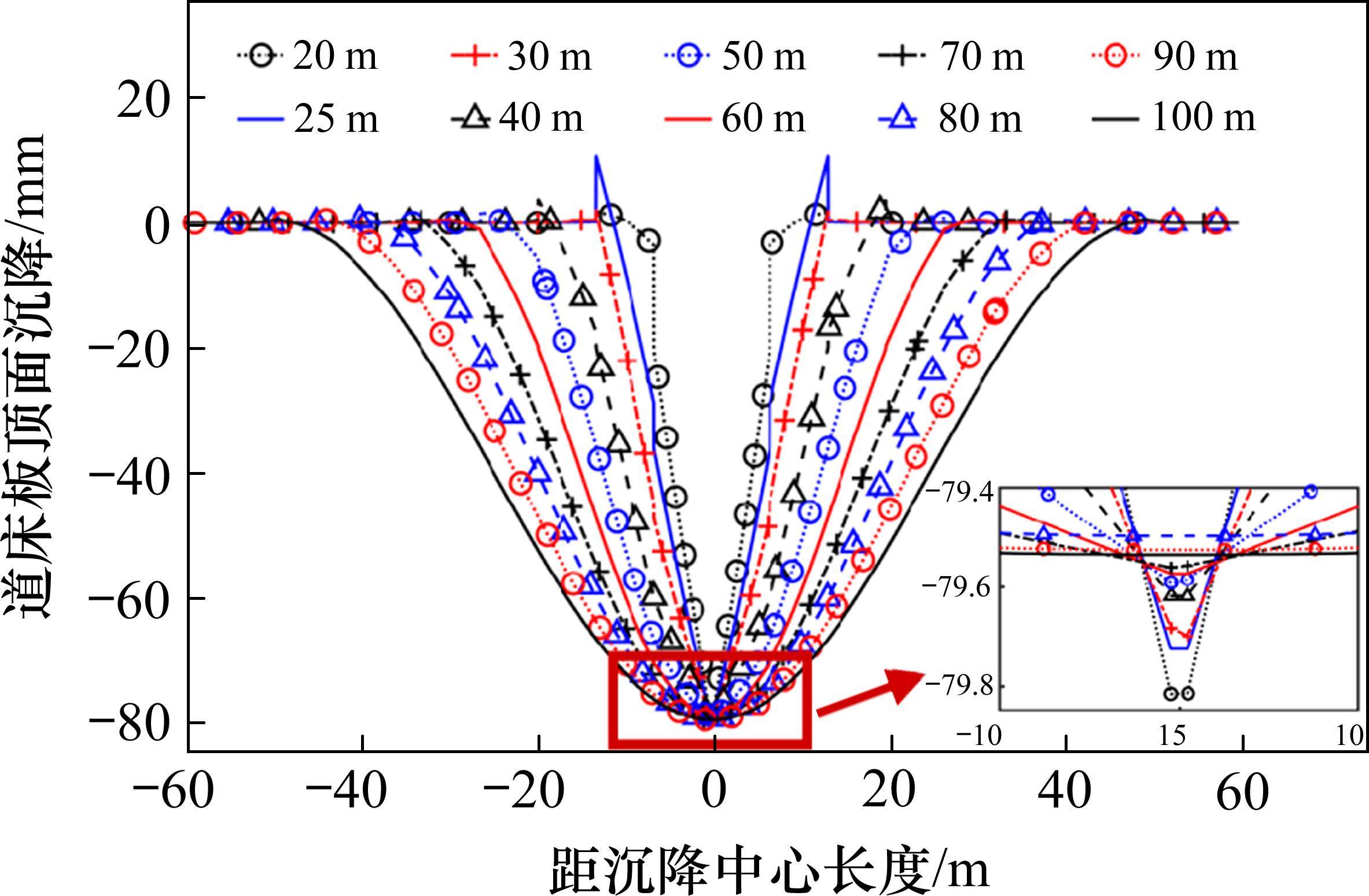
沉降幅值为80 mm时,不同波长下道床板变形特征如图8所示,道床板变形峰值如表5所示。
| 幅值/mm | 波长/m | 最大下沉值/mm | 最大上拱值/mm |
|---|---|---|---|
| 80 | 20 | 79.815 | 1.839 |
| 80 | 25 | 79.725 | 10.556 |
| 80 | 30 | 79.699 | 1.987 |
| 80 | 40 | 79.618 | 3.742 |
| 80 | 50 | 79.591 | 1.875 |
| 80 | 60 | 79.573 | 0.459 |
| 80 | 70 | 79.561 | 0.484 |
| 80 | 80 | 79.498 | 0.456 |
| 80 | 90 | 79.526 | 0.473 |
| 80 | 100 | 79.535 | 0.62 |
由上可知,当沉降幅值相同时,沉降范围内,随着沉降波长增加,道床板沉降形式与基础沉降形式一致性逐渐升高;由于道床板在线路纵向上不连续,当波长较小时,道床板沉降突变性较强。
3 基础变形作用下轨道结构层间离缝及脱空特征分析
3.1 沉降幅值对层间离缝及脱空的影响
沉降波长为20 m时,不同沉降幅值下仰拱与道床板间离缝及脱空发展特征如图9所示。
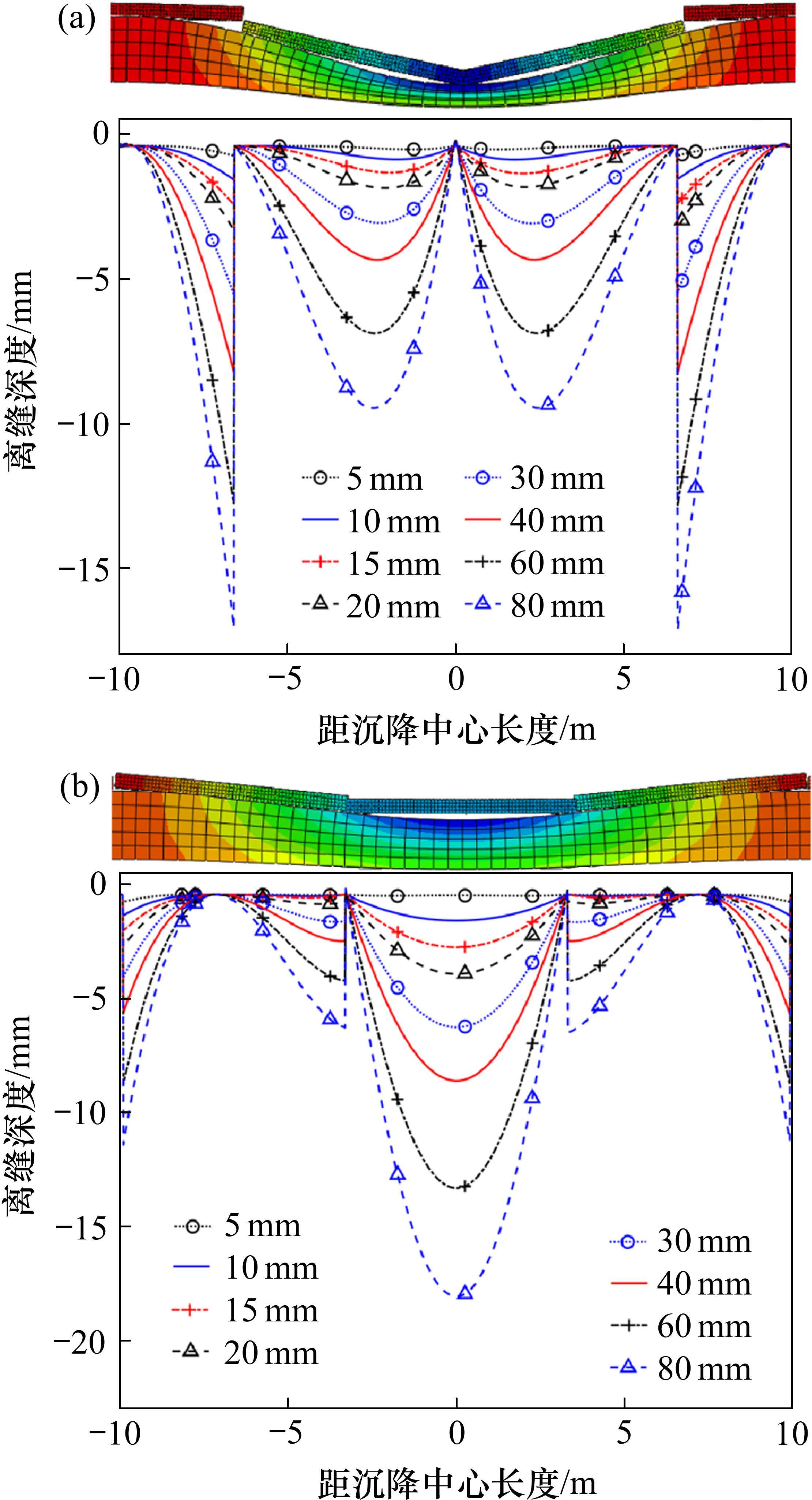
3.1.1 沉降幅值对层间离缝及脱空高度的影响
沉降波长为20 m时,不同沉降幅值下基础与道床板间离缝及脱空高度最大值如表6所示。
| 幅值/mm | 波 长/m | 沉降中心为板端时,离缝高度最大值/mm | 沉降中心为板中时,离缝高度最大值/mm |
|---|---|---|---|
| 5 | 20 | 0.772 | 0.75 |
| 10 | 20 | 1.602 | 1.571 |
| 15 | 20 | 2.469 | 2.741 |
| 20 | 20 | 3.332 | 3.909 |
| 30 | 20 | 5.549 | 6.248 |
| 40 | 20 | 8.28 | 8.59 |
| 60 | 20 | 12.83 | 13.295 |
| 80 | 20 | 17.131 | 18.061 |
由上可知,沉降范围内,道床板与基础间发生离缝,离缝及脱空高度随沉降幅值增大而增大;沉降中心表现为板中离缝;沉降两端表现为板端离缝。道床板在线路纵向上不连续,板端处出现离缝高度突变。
由图9(a)可知,当沉降中心为板端时,靠近沉降中心的道床板的板中位置出现离缝高度极值,在沉降中心两侧的板端位置出现离缝高度最大值。由图9(b)可知,当沉降中心为板中时,沉降中心处出现离缝高度最大值。对比图9与离缝及脱空高度最大值可知,当沉降波长与沉降幅值相同时,沉降中心附近,沉降中心为板中情况下离缝高度较大;在沉降始末端,沉降中心为板端情况下离缝高度较大。
进一步计算可知,当工况为幅值5 mm/波长25 m时,最大离缝高度为0.554 mm;当工况为幅值5 mm/波长30 m时,最大离缝高度为0.485 mm。故可认为,当沉降波长小于30 m时,只要发生沉降即需密切关注道床板与仰拱间离缝情况及时采取修补措施[22]。
3.1.2 沉降幅值对层间离缝及脱空范围的影响
沉降波长为20 m时,不同沉降幅值下仰拱与道床板间离缝及脱空长度如表7所示。
| 幅值/mm | 波长/ m | 沉降中心为板端时,离缝及脱空长度/m | 沉降中心为板中时,离缝及脱空长度/m |
|---|---|---|---|
| 5 | 20 | 9.203 | 2.003 |
| 10 | 20 | 15.296 | 11.245 |
| 15 | 20 | 17.599 | 14.341 |
| 20 | 20 | 17.999 | 16.445 |
| 30 | 20 | 18.396 | 17.645 |
| 40 | 20 | 18.801 | 18.045 |
| 60 | 20 | 18.902 | 18.442 |
| 80 | 20 | 19 | 18.639 |
由表7可知,在沉降范围内,道床板与基础间离缝及脱空长度随沉降幅值的增大而增大;沉降中心为板端时的离缝及脱空长度大于沉降中心为板中时的长度。
由图9与离缝及脱空长度可知,随着沉降幅值的增加,离缝及脱空的长度快速增大;当沉降幅值达到15 mm后,离缝及脱空长度增大速度逐渐放缓,道床板大范围脱空,将极大危害轨道结构受力传递。
3.2 沉降波长对层间离缝及脱空的影响
根据上文研究可知,沉降中心为板端时离缝及脱空高度略小于沉降中心为板中,但长度大于沉降中心为板中,在小幅值工况下更为突出,可认为当沉降中心为板端时层间离缝及脱空情况较为严重,故本节针对沉降中心为板端的情况进行研究。沉降幅值为80 mm时,不同波长下道床板与基础间离缝及脱空变化特征如图10所示。
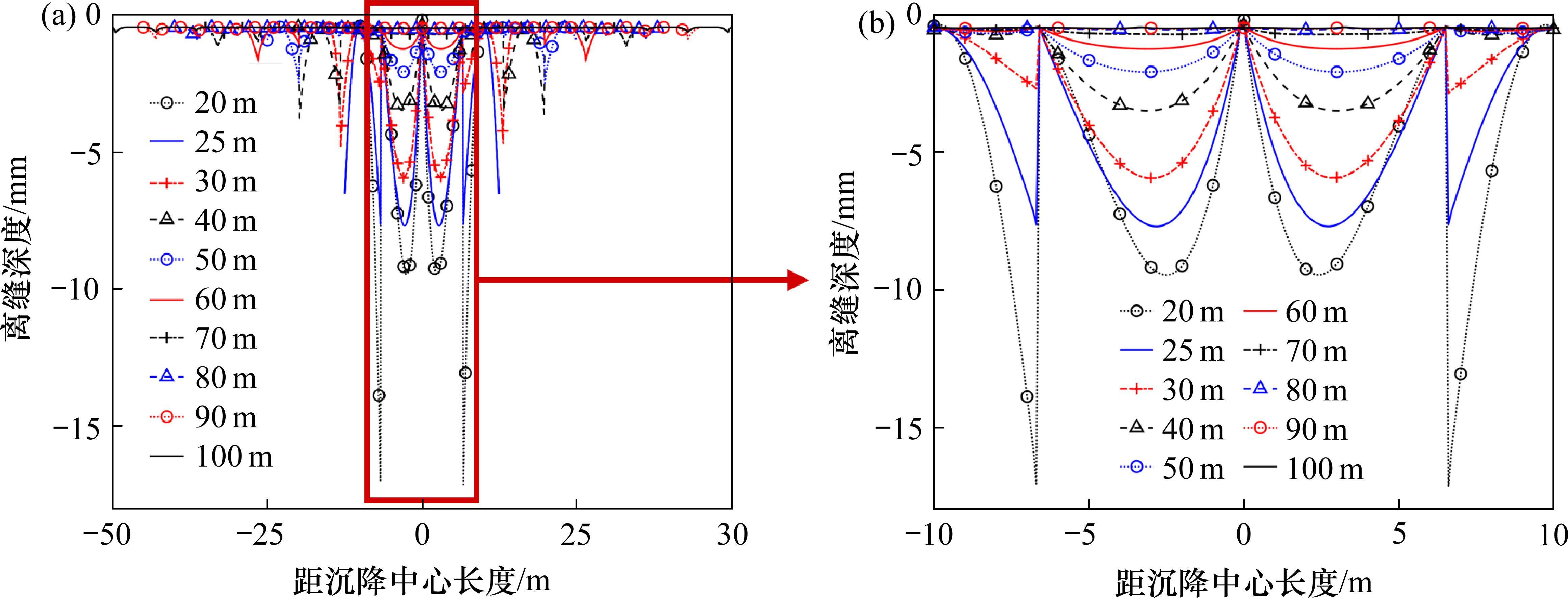
3.2.1 沉降波长对层间离缝及脱空高度的影响
沉降幅值为80 mm时,不同沉降波长下仰拱与道床板离缝及脱空高度最大值如表8所示。
幅值/ mm | 波长/ m | 板中离缝 最大值/mm | 板边离缝 最大值/mm |
|---|---|---|---|
| 80 | 20 | 9.466 | 17.131 |
| 80 | 25 | 7.691 | 7.626 |
| 80 | 30 | 5.935 | 4.836 |
| 80 | 40 | 3.489 | 0.728 |
| 80 | 50 | 2.082 | 0.681 |
| 80 | 60 | 1.24 | 0.599 |
| 80 | 70 | 0.71 | 0.549 |
| 80 | 80 | 0.549 | 0.511 |
| 80 | 90 | 0.504 | 0.492 |
| 80 | 100 | 0.49 | 0.481 |
由表8可知,当沉降幅值相同时,随着波长增加离缝值逐步减小;最靠近沉降中心的2块板表现为板中离缝,离缝最大值随着波长增加而减小;旁边2块板表现为板边离缝,离缝最大值随着波长增加而减小;当波长大于等于25 m时,板中离缝值大于板边离缝。当波长大于等于80 m时,可认为板中离缝和板边离缝小于等于0.5 mm,可认为当基础变形波长大于80 m时,不需要对离缝进行修补[22]。
3.2.2 沉降波长对层间离缝及脱空范围的影响
沉降幅值为80 mm时,不同沉降波长下仰拱与道床板离缝及脱空长度及占比如表9所示。
| 幅值/mm | 波长/m | 离缝长度/m |
|---|---|---|
| 80 | 20 | 19 |
| 80 | 25 | 23.386 |
| 80 | 30 | 27.285 |
| 80 | 40 | 33.928 |
| 80 | 50 | 33.795 |
| 80 | 60 | 33.291 |
| 80 | 70 | 30.721 |
| 80 | 80 | 26.697 |
| 80 | 90 | 14.07 |
| 80 | 100 | 6.594 |
由表9可知,在沉降范围内,道床板与基础间离缝及脱空长度随沉降波长的增大而减小。随着沉降幅值的增加,离缝及脱空的长度先增大后减小。
4 结论
1) 当基础大变形形式为余弦型不均匀沉降时,钢轨变形形式与基础变形形式一致性较高,道床板变形形式一致性较低;结构沉降随基础沉降幅值增大而增大;基础沉降波长对结构沉降最大值影响较小,在沉降中心出现沉降最大值,在沉降端部出现小幅上拱。
2) 当沉降幅值与波长相同时,考虑弹性支承块式无砟轨道结构中道床板直接浇筑在基础上的结构特殊性,沉降中心为板中的情况变形较为缓和,沉降中心为板端的情况变形较为剧烈。
3) 当沉降波长为20 m时,沉降幅值10 mm以下,可通过扣件调高恢复轨面平顺;沉降幅值在10~20 mm时可通过同时调高扣件和块下垫板恢复轨面平顺;达到30 mm时需要结合对中心板进行注浆填充调节,超过40 mm的情况需要重点关注轨道整体结构,并及时进行大修。
4) 层间离缝及脱空高度随基础沉降幅值的增加而增加,随沉降波长的增加而减小;层间离缝及脱空长度随沉降幅值的增加而增大,随沉降波长的增加先增加后减小。基础沉降波长小于40 m时,只要发生沉降不论幅值大小即需进行离缝检查修补;基础沉降波长超过80 m时,可不进行离缝修补。
曾志平,吴霁崟,王卫东等.基础变形对弹性支承块式无砟轨道变形及离缝影响研究[J].铁道科学与工程学报,2025,22(02):602-612.
ZENG Zhiping,WU Jiyin,WANG Weidong,et al.Study on the deformation and the gap of low vibration track under the influence of foundation deformation[J].Journal of Railway Science and Engineering,2025,22(02):602-612.

