随着技术的进步,我国建造的高速铁路大跨度桥梁越来越多,但大跨度桥梁受温度、荷载等因素影响大,其垂向变形与轨道设计线形间的矛盾非常突出[1-2]。聚焦该问题,很多学者围绕桥上轨道线形影响因素[3-4]、线形平顺性特征[5-6]、线形平顺性评价方法[7-8]、线形验收控制标准[9-10]、线形对车线桥系统动力性能评估分析[11-12]等方面开展了研究,这为大跨度桥梁的设计、施工提供了重要的理论与技术支持。相对而言,涉及线路平顺性调整的研究较少,而这对保障运营阶段桥上线路平顺性及行车安全性能又尤为重要。大跨度桥上线路线形具有时间动态演化和空间变形严重的显著特点,基于此衍生的桥上线路线形调整方法主要有多基准线法[13-14]和高通滤波法[15]。传统方法[16-17]是以轨道设计线形为基准,桥上轨道实测线形和该基准的偏差即为轨道不平顺。多基准线法则是在充分认知大跨度桥上轨道线形受温度影响而产生垂向变形较大的前提下,以温度变化幅度构造多条轨道设计线形(仅调整垂向基准、不调整横向基准),桥上轨道实测线形与对应温度的基准线偏差为轨道不平顺,其实质是基准线不唯一,选取合适的基准线降低了垂向不平顺偏差量。高通滤波法是根据大跨度桥上轨道线形受温度影响产生的变形主要是垂向长波成分为前提,计算轨道实测线形和轨道设计线形偏差量,然后对阈值范围内的波长采取滤波处理,得到新的轨道垂向偏差即为轨道垂向不平顺,其实质是过滤了温度影响的长波成分,降低了垂向不平顺偏差量。鉴于多基准线法与高通滤波法原理不同,为深入剖析2种方法在处理轨道不平顺数据及制定轨道精调方案的异同,应用有限元仿真模型阐释了2种方法的核心要义,结合实测数据分析了2种方法数据处理后的轨道平顺性特征,并通过精调方案对比评估了2种方法的精调效果及其适用性,以期为高速铁路大跨度桥上轨道不平顺评定及调控提供参考。
1 基于仿真模型的桥上轨道线形分离方法
1.1 有限元模型的建立与验证
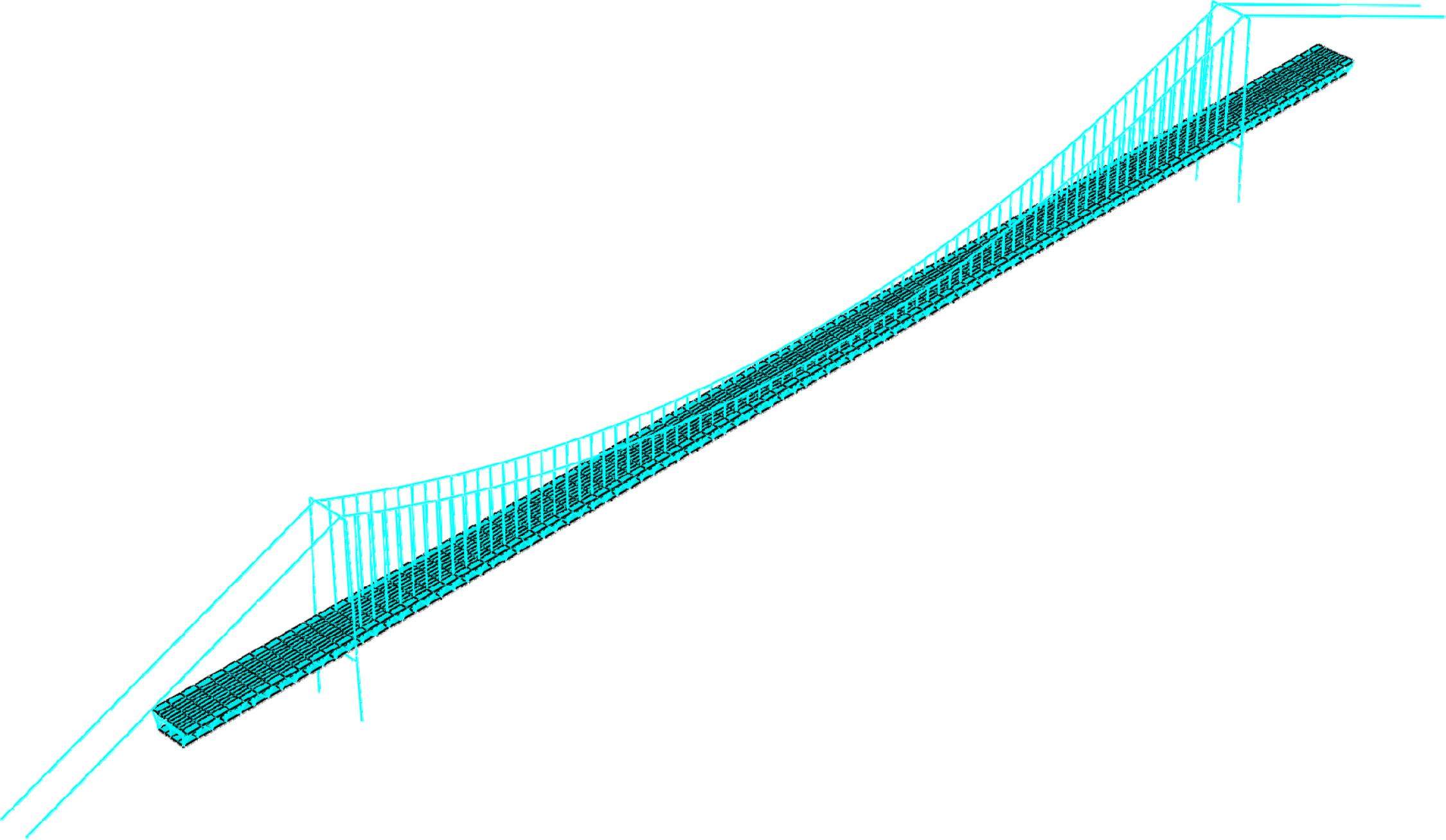
基于Abaqus有限元软件建立五峰山长江大桥(主跨1 092 m的公铁两用悬索桥)的有限元模型,如图1所示。主缆和吊索采用只受拉不受压的3D杆单元模拟,主缆线形考虑为抛物线,采用重力自平衡法[18]加载主缆和吊索预应力。主塔和桁架杆采用3D梁单元模拟,桥面采用3D板单元模拟。主塔采用混凝土材料,其余部件均为钢材,并考虑桥面二期恒载作用。主塔底部和主缆两端完全固定,边墩和辅助墩提供竖向和横向支承,边墩中部提供竖向支承。主塔约束桥梁的横向、竖向位移,桥梁纵向可自由伸缩,其余部件连接均采用共节点法。全桥三维空间模型共有15 233个节点,6 899个单元。
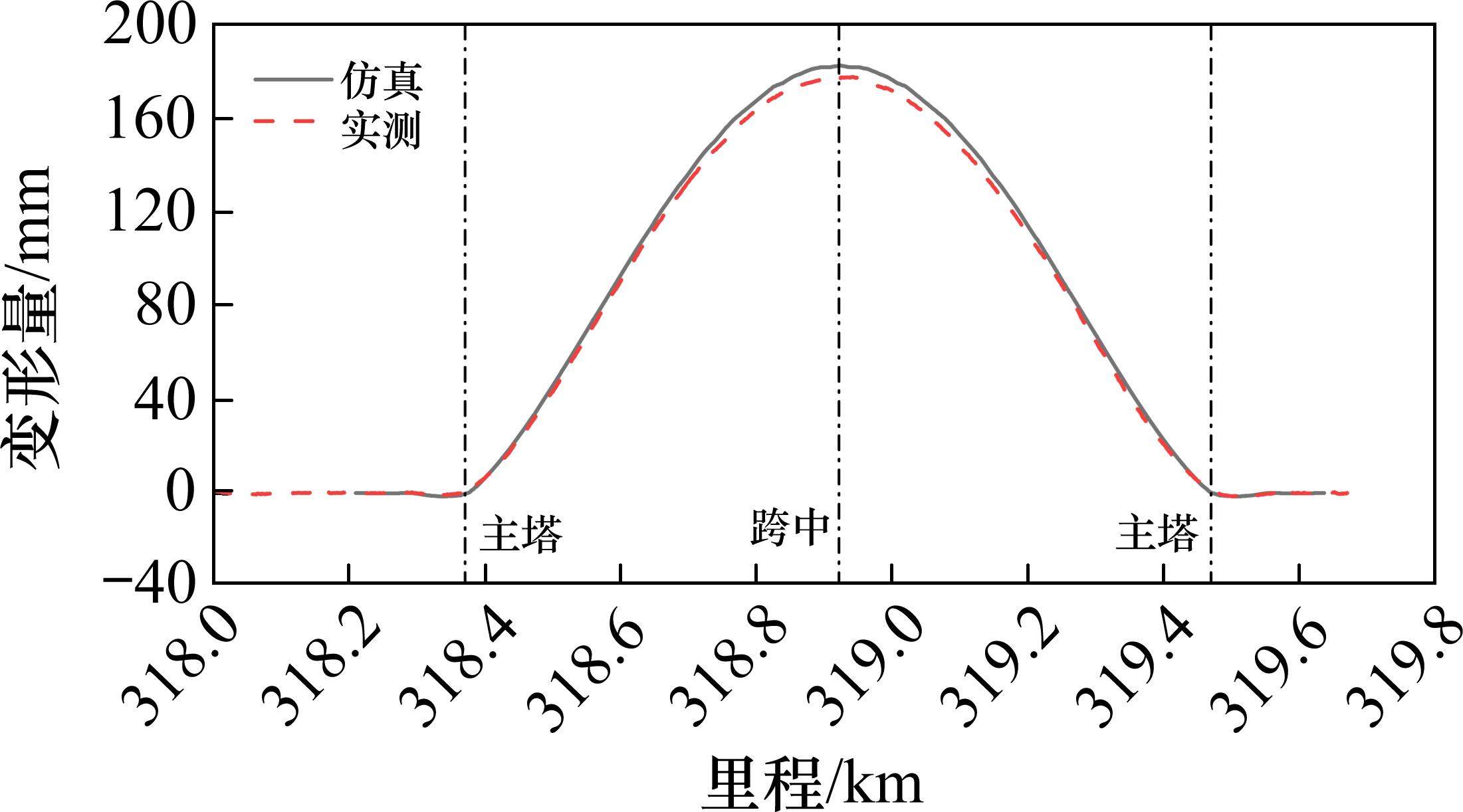
对建立的桥梁有限元模型从桥梁自振特性和温变线形2个方面进行验证。表1为桥梁自振频率结果对比,对应主桁一阶对称横弯振型,仿真模型为0.110 Hz,实测频率为0.109 Hz,两者基本一致。图2为温度下降5 ℃前后2种工况下的桥上轨道线形,对于主跨跨中桥面高程随温度变形量,仿真计算为36.5 mm/℃,实测数据约为35.5 mm/℃,设计计算为36.0 mm/℃,三者结果相当。综上,模型较为精准,用于计算桥上轨道线形合理可行。
| 振型 | 实测/Hz | 仿真/Hz |
|---|---|---|
| 主桁一阶对称横弯 | 0.109 | 0.110 |
| 主桁一阶对称竖弯 | 0.169 | 0.186 |
| 主桁一阶反对称竖弯 | 0.204 | 0.198 |
| 主桁一阶反对称横弯 | 0.274 | 0.315 |
1.2 多基准线法
多基准线法操作简单,但针对不同跨度、不同类型桥上轨道线形需要构造不同的基准线,不具备通用性。
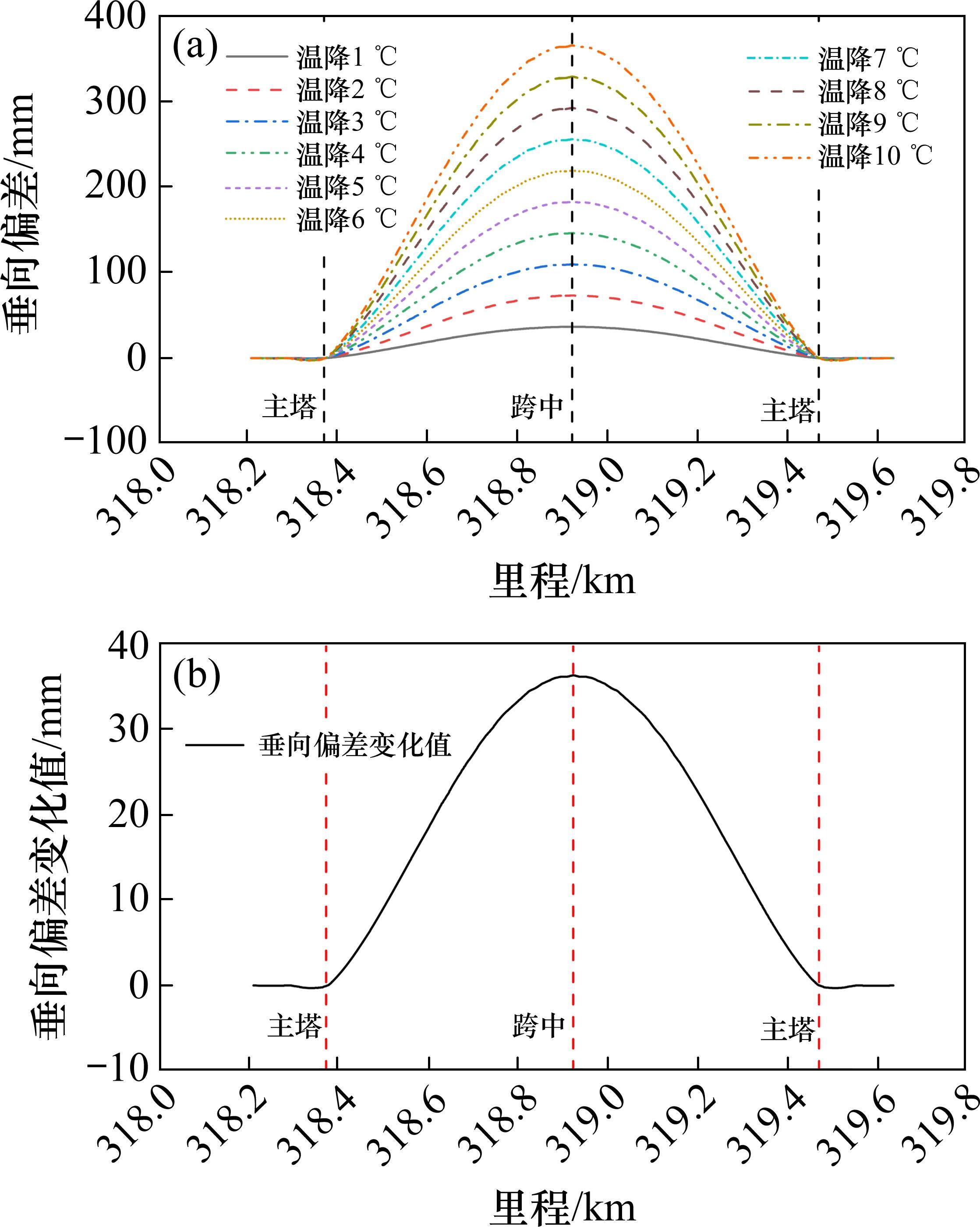
五峰山长江大桥以29 ℃条件下对应的线形为轨道设计线形。根据有限元模型仿真结果可知,桥梁随温度下降而上拱,桥上轨道线形随之发生垂向变化。由图3可知,垂向偏差随温度的变化率向主塔方向逐渐递减,跨中变化率为36.5 mm/℃,主塔变化率为0。
依据《国家铁路局关于发布铁道行业标准的公告(工程建设标准2023年第2批)》(2023第4号)[15],跨度200~1 100 m的桥梁,轨道静态高低长波不平顺采取60 m中点弦测值评价。根据桥上轨道垂向偏差计算60 m中点弦测值,如图4所示,60 m中点弦测值随温度变化幅值逐渐增大,主塔位置变化尤为显著,为0.65 mm/℃。
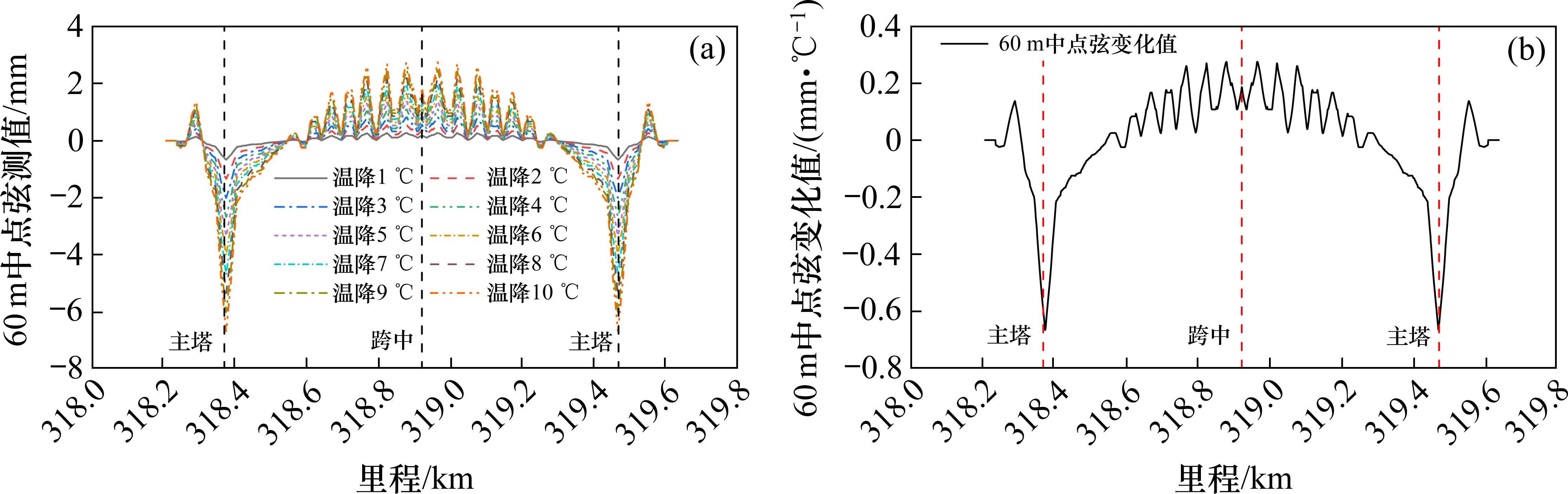
五峰山长江大桥设计速度为250 km/h,对应的60 m中点弦测值容许偏差为10 mm。由0.65 mm/℃的变化率可知,温度每变化15 ℃至少需要设置一条基准线。
基于线路随机不平顺考虑,根据我国高速铁路有砟轨道不平顺谱,反演高低随机不平顺如图5(a)所示,根据15组高低随机不平顺样本计算得到的60 m中点弦测值高低幅值如图5(b)所示,60 m中点弦测值幅值稳定在5 mm以下。考虑最不利工况,60 m中点弦测值幅值取5 mm。
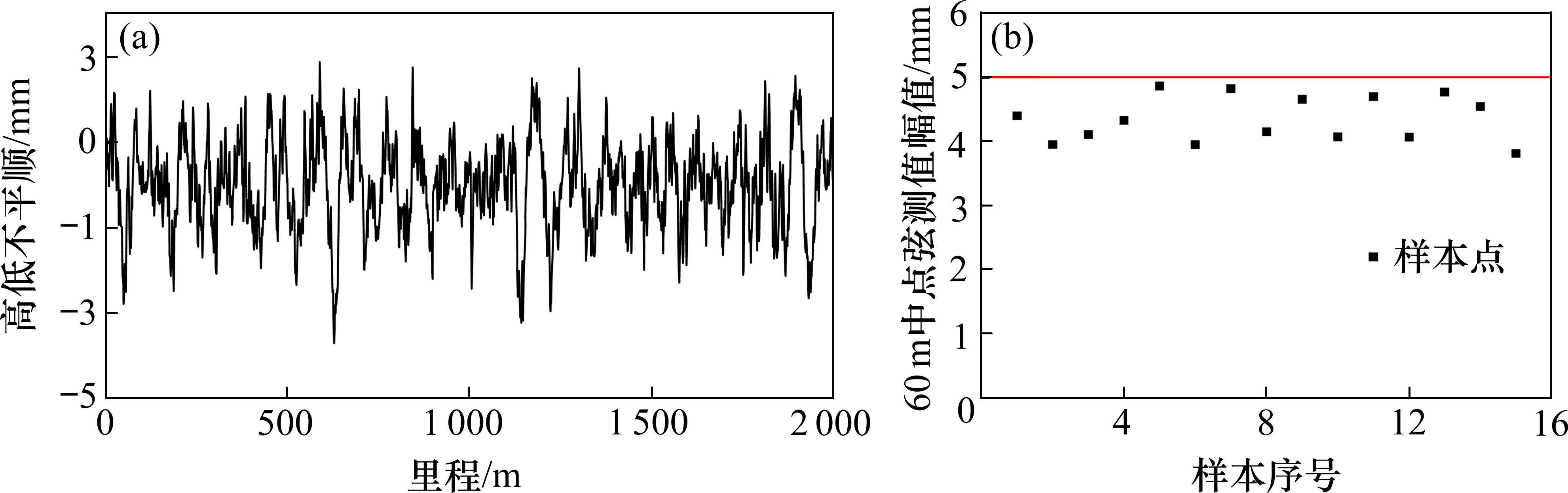
基于线形拟合偏差考虑,对仿真模型中存在温度变形的轨道高程数据进行线形拟合,线形拟合标准为高速铁路设计规范(TB 10621—2014),及针对高速铁路大跨桥轨道线形参数的研究成果[16]。根据拟合线形与待拟合目标线形之间的垂向偏差计算60 m中点弦测值如图6(a)所示,统计15组不同温度变形样本在主塔位置的60 m中点弦测值高低幅值,如图6(b)所示。由图可知,主塔位置的60 m中点弦测值幅值分布在2.7 mm以下,即为线形拟合偏差(受竖曲线、夹直线等因素影响,拟合线形与目标线形之间会存在差异)引起的60 m中点弦测值。
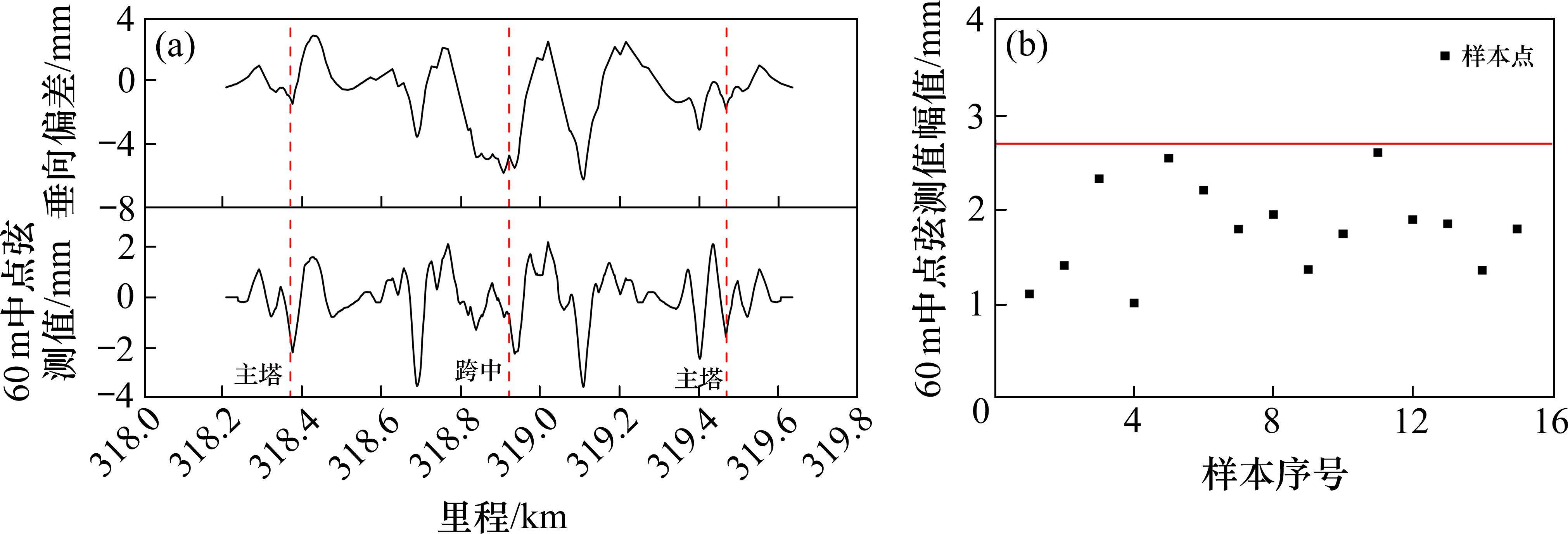
将高低随机不平顺和线形拟合偏差引起的60 m中点弦测值叠加,主塔位置60 m中点弦幅值达到了7.7 mm,再叠加温度变形影响量0.65 mm/℃后,温度变化3.54 ℃将达到10 mm临界值,因此一条基准线覆盖的温度变化范围为±3.54 ℃,即温度每变化7.1 ℃(取整为7 ℃)需要设置一条基准线。当然,为降低温度变化对高低不平顺的影响,也可对每一条实测线形进行拟合,制定基准线。需要说明的是,该做法的实质是设计线形不是事先给定的,而是依据实测线形拟合的,如何统一线形拟合原则,仍需进一步探讨。
需指出的是,各条基准线具体设计参数由大量实测数据样本推算得到,其构造过程包括以下4个步骤:1) 拟合实测数据样本,得到拟合线形参数;2) 分析变坡点位置随温度变化规律;3) 分析坡度和竖曲线半径随温度变化规律;4) 根据线形参数随温度变化的回归方程提取基准线参数。具体推算方法见文献[13]。
1.3 高通滤波法
高通滤波方法通用性强,确定滤波波长是该方法的关键,五峰山长江大桥以29 ℃条件下的轨道线形为轨道设计线形。根据2020年11月至2023年2月期间的实测数据可知,大桥桥址的环境最低温约为0 ℃、最高温约为35 ℃。由前文可知,实际温度与29 ℃差值越大,则60 m中点弦测值越大,因此选取0 ℃条件下的线形进行高通滤波波长推算。采用50~400 m高通滤波进行滤波处理,50~250 m步长为10 m,250~400 m步长为50 m,将滤波后的桥上轨道垂向变形量作为新的轨道垂向不平顺输入车线动力学模型,以29 ℃条件下的轨道设计线形为基准,计算得到250 km/h速度下的车体垂向加速度时程响应。
绝对平均值是对一组数据取绝对值后求取平均,可反映这组数据的总体幅值变化水平。pearson系数[19-20]用于度量2组数据变化趋势的相似性,达到0.8以上时认为2组数据变化一致。选取绝对平均值降幅和pearson相关系数对其进行分析,得到2个指标随高通滤波波长的变化关系如图7所示。以pearson相关系数在0.8以上,绝对平均值降幅基本稳定来确定临界高通滤波波长。由图7可知,临界高通滤波波长为210 m,表明210 m以下范围的波长成分会显著影响车体振动加速度。这与《国家铁路局关于发布铁道行业标准的公告(工程建设标准2023年第2批)》(2023第4号)[15]要求的滤波波长200 m基本一致。为保持统一,后续实例计算采用200 m滤波。
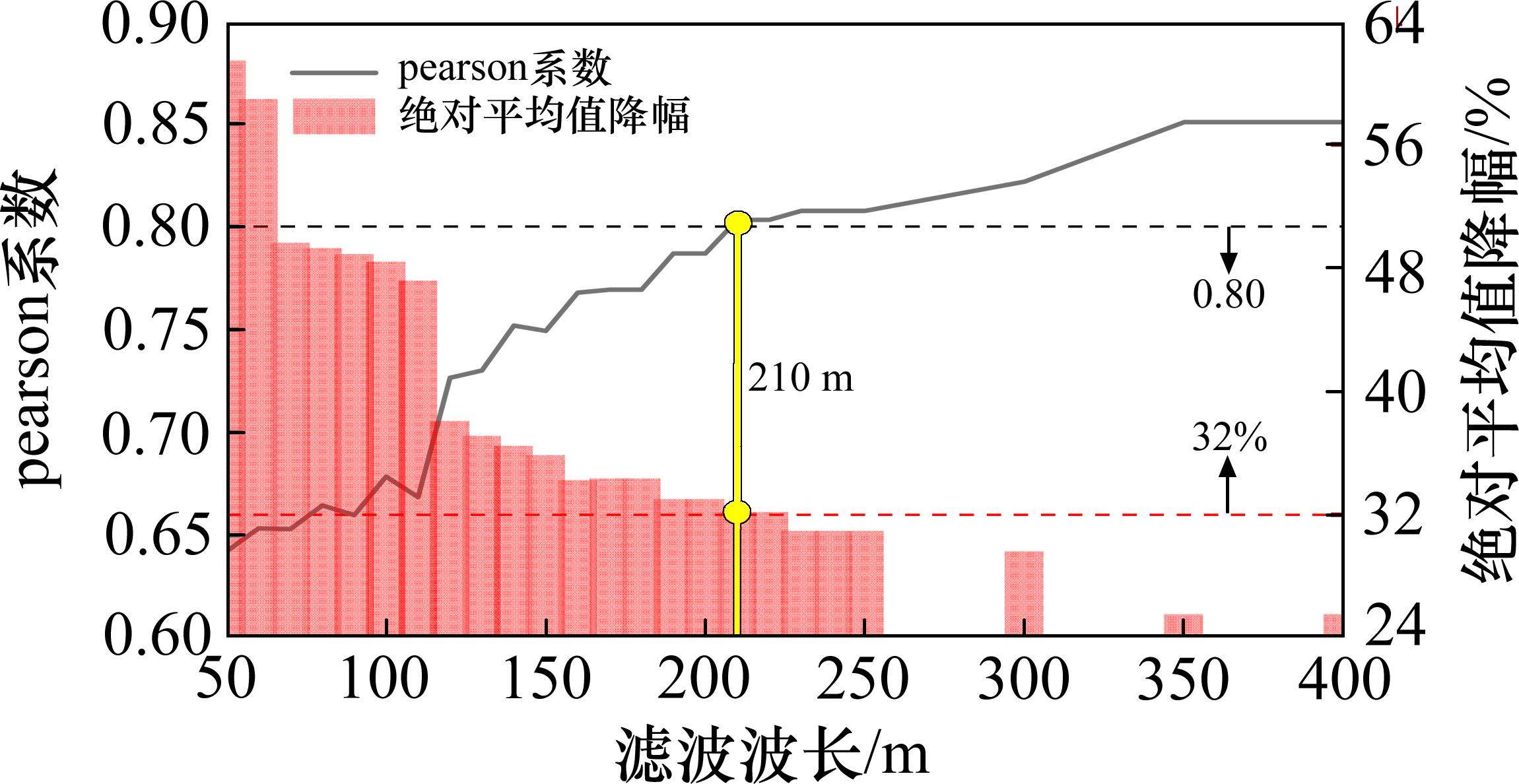
对以上推算的临界高通滤波波长进行验证,选取19 ℃(温降10 ℃)对应的桥上轨道线形进行滤波处理,如图8所示。可见,跨中位置的高低不平顺在200 m以上成分与无滤波状态下分别为364.8 mm和364.2 mm,极为相似;200 m以下成分的高低不平顺幅值整体较小,最大为4.2 mm。因此,采用200 m临界波长可以保留既有的轨道高低不平顺。
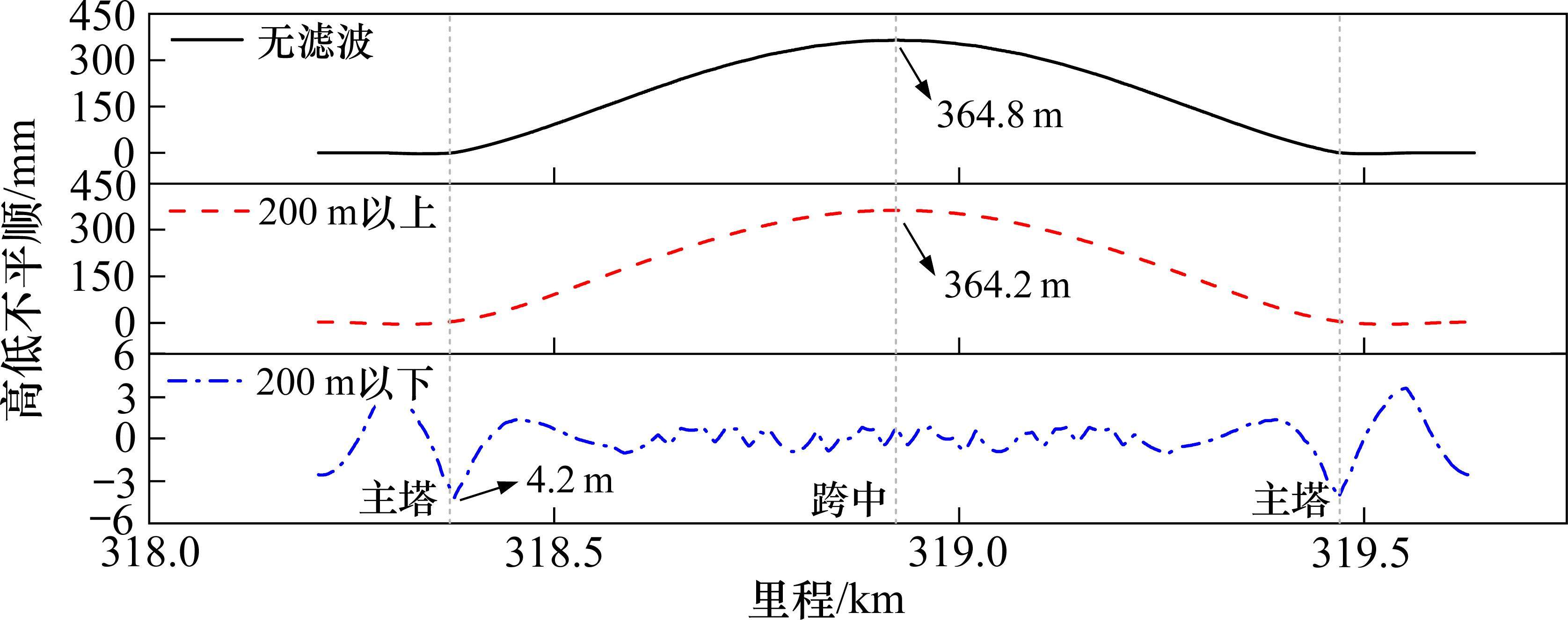
将图8中3种轨道不平顺输入车线动力学模型,得到车体垂向加速度时程响应如图9所示。可见,200 m以上波长的轨道不平顺在转角变化大的桥塔、跨中位置会引起明显车体垂向加速度变化,其原因是在温度荷载作用下线形发生了改变,产生了离心加速度。在无滤波不平顺与200 m以下不平顺条件下,车体垂向加速度之间的pearson系数达到0.72,且二者在主塔、跨中位置的差值仅为0.06 m/s2和0.03 m/s2,说明200 m以下波长的轨道不平顺对车体垂向加速度的振动幅值基本一致。桥塔和主跨跨中存在些许偏移,原因是200 m以上波长成分产生的离心加速度已进行了过滤。将200 m以上和200 m以下轨道不平顺作用下的车体垂向加速度相加,可发现与无滤波条件下车体垂向加速度完全重合。这说明车体垂向加速度是由车体振动加速度和车体离心加速度2部分构成,前者主要受临界高通滤波波长以下范围的轨道不平顺影响,后者主要受临界高通滤波波长以上范围的轨道不平顺影响。因此,高通滤波法实质是消除对车体振动加速度无影响或影响极少的轨道不平顺长波成分。
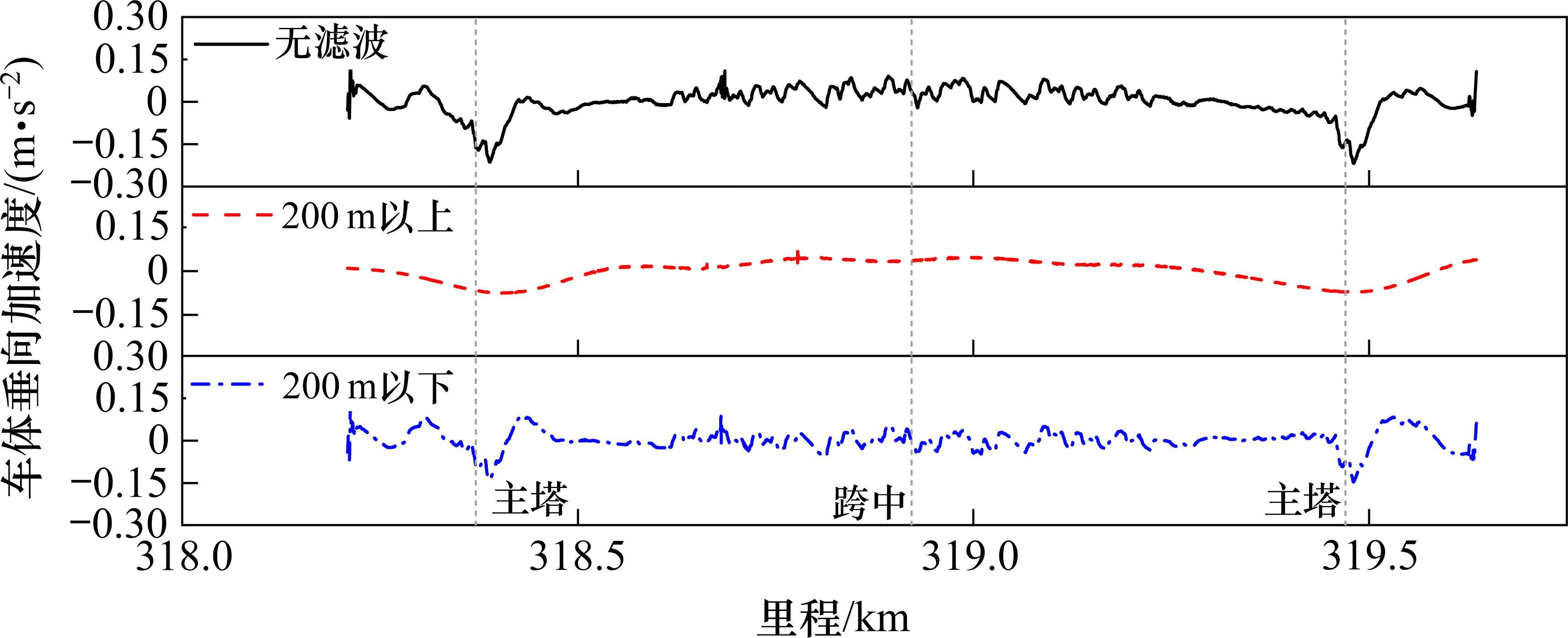
pearson系数为正值,则二者呈正相关,且绝对值越大,相关性越强。对比无滤波条件和200 m滤波条件下的车体垂向加速度pearson系数和绝对平均值降幅,分别为0.72和10.3%,这说明200 m作为临界高通滤波波长是较为合理的。
2 基于实测数据的高低平顺性特征分析
2.1 轨道不平顺时域特征对比
2.1.1 2种方法轨道垂向偏差对比
根据五峰山长江大桥桥址温度,构造得到了5个类别的基准线,对应的温度区间分别为0~7 ℃、7~14 ℃、14~21 ℃、21~28 ℃、28~35 ℃。现以实测温度11.5 ℃对应的线形数据为例,该实测线形所属的温度区间为7~14 ℃,采用该温度区间对应类别的基准线时,垂向偏差如图10所示。图中“原始偏差”表示实测线形与29 ℃时的轨道设计线形之间的垂向偏差;图中“多基准线偏差1”表示实测线形与7~14 ℃温度区间对应基准线之间的垂向偏差,图中“多基准线偏差2”表示实测线形与对应11.5 ℃基准线之间的垂向偏差。由图10可知,多基准线法有效减小了垂向偏差,其中对应温度基准线偏差降幅最大。
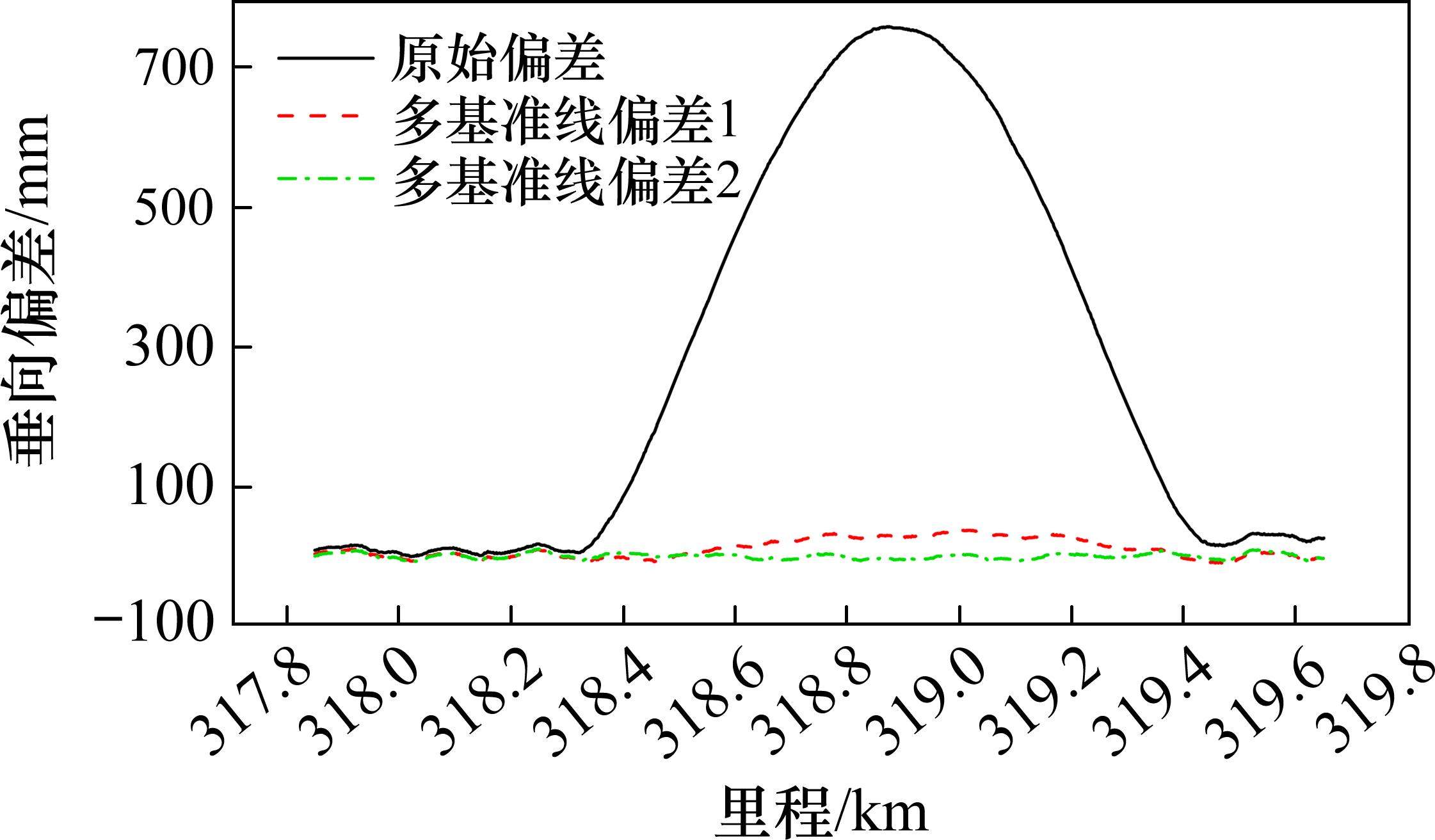
对图10中的“原始偏差”进行200 m高通滤波,将滤波后的垂向偏差与多基准线偏差进行对比,如图11所示,图中黑线为200 m滤波后的原始偏差。由图可知,多基准线和200 m滤波这2种方法均可有效减小垂向偏差。高通滤波法基本不包含温度偏差,多基准线法包含温度偏差的成分越小降幅越大,如基准线选取的温度与实测线形时温度相同,则2种方法偏差量一致。
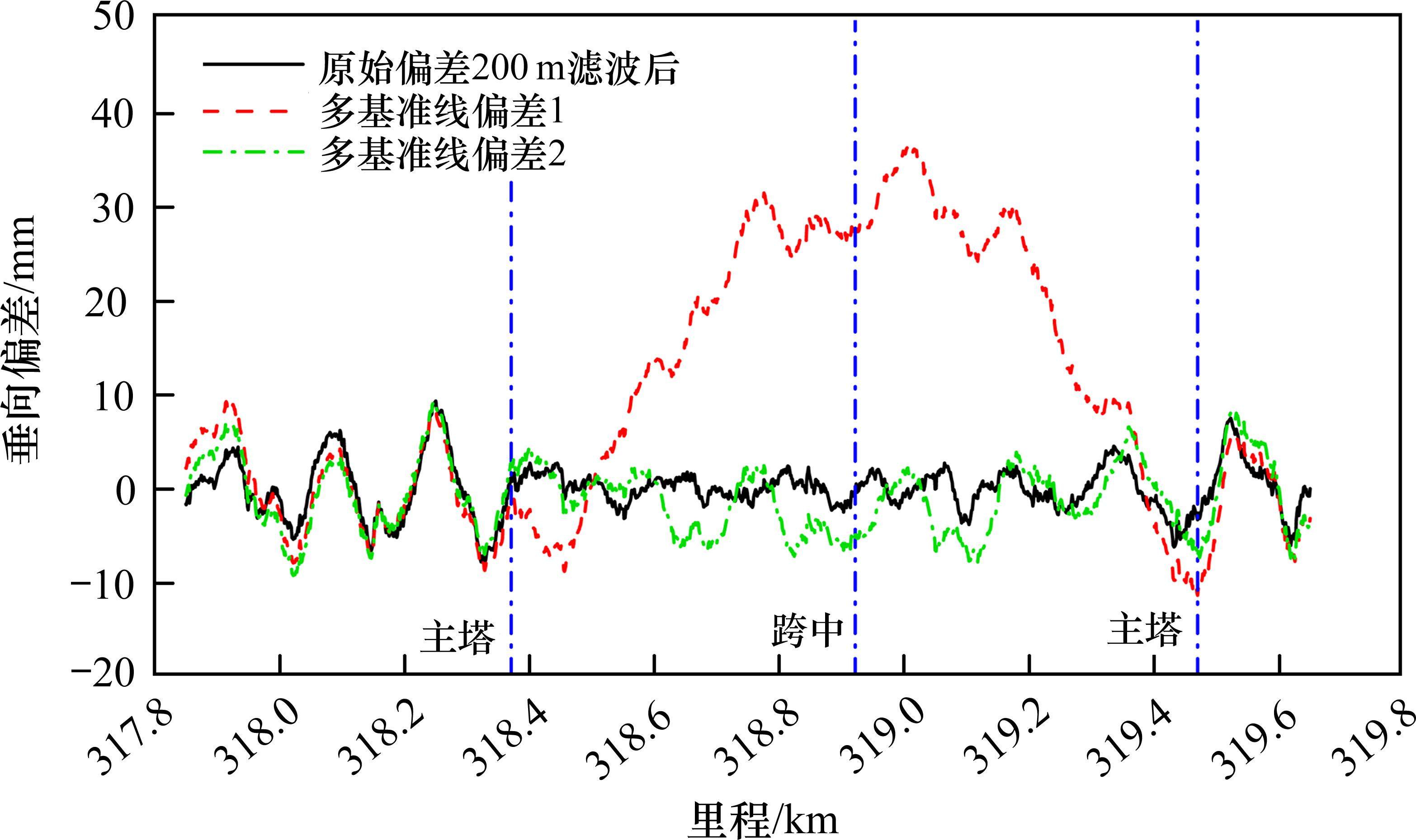
拟合线偏差的幅值相比多基准线偏差更小,且与200 m滤波后的原始偏差更为相似,较好地剔除了温度变形影响,还原了轨道高低不平顺。
2.1.2 60 m中点弦对比
按温度不同分别选取5条实测线形,对应的实测温度分别为2.5,11.5,17.0,24.0和28.8 ℃。对以设计线为基准的垂向偏差、200 m滤波后的垂向偏差、多基准线下的垂向偏差,分别进行60 m中点弦测值计算,将结果进行对比,如图12所示。图中,“200 m滤波前”表示原始偏差对应的60 m中点弦测值;“200 m滤波后”表示原始偏差经过200 m滤波后再计算的60 m中点弦测值;“多基准线1”表示采用实测线形与所属温度区间对应的基准线之间垂向偏差计算的60 m中点弦测值;“多基准线2”表示采用实测线形与对应11.5 ℃基准线之间垂向偏差计算的60 m中点弦测值。
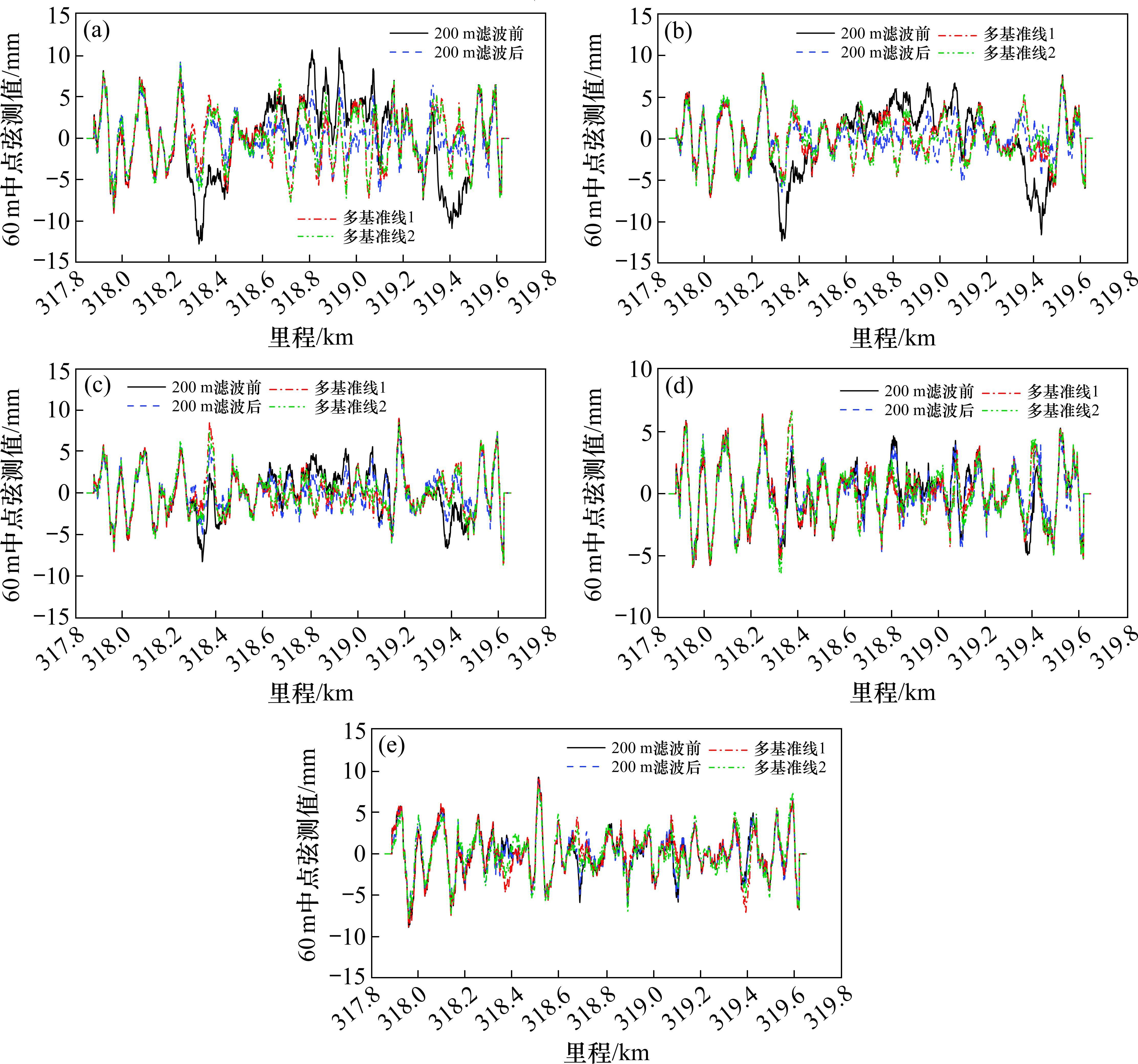
由图12可知,无滤波的原始偏差计算得到的60 m中点弦测值在跨中和前、后主塔位置存在明显的趋势项,另外3种方法计算得到的60 m中点弦测值不存在趋势项,说明多基准线和原始偏差200 m滤波这2种方法均可剔除大跨桥温度变形引起的垂向长波不平顺成分。此外,经过多基准线和高通滤波处理后的不同温度实测线形60 m中点弦测值均小于10 mm管理限值,说明不同温度条件下高速列车行车舒适性无明显差异,这与动态检测情况一致,符合列车实际运行情况。也就是说,运营过程中,可保留温度变形引起的轨道变形成分,调整影响行车品质的轨道不平顺成分。
2.2 轨道不平顺频域特征对比
轨道不平顺功率谱密度不仅能反映线路整体质量状况,也能从频域角度定性和定量刻画轨道不平顺的频率或波长特征。选取中国高速铁路有砟轨道高低不平顺谱生成一条随机不平顺样本,对无滤波原始偏差和该随机轨道不平顺计算功率谱密度如图13所示。对比无滤波原始偏差可知,温度引起轨道偏差主要为200 m以上的长波成分,温度越低对应200 m以上波段的功率谱密度幅值越大。
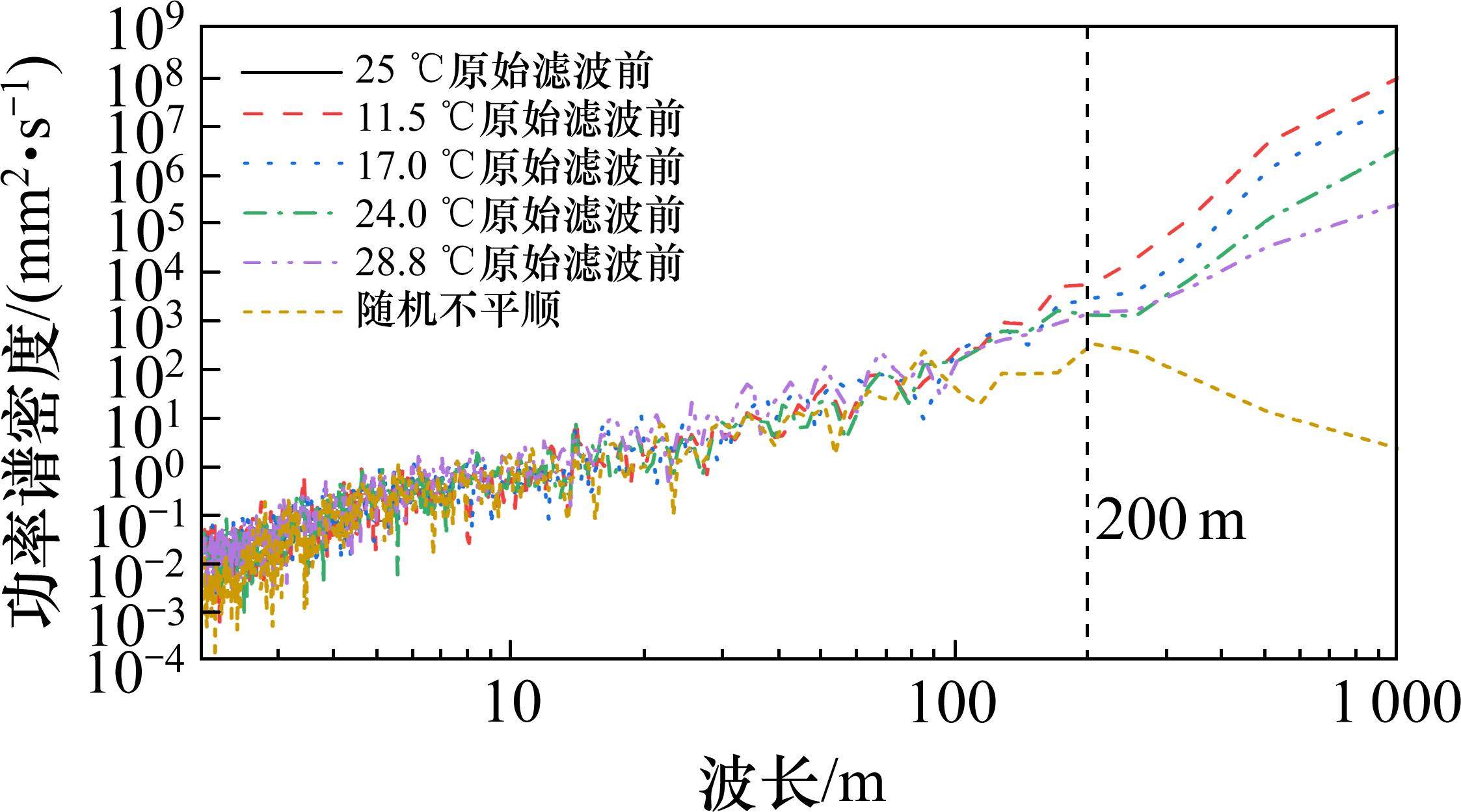
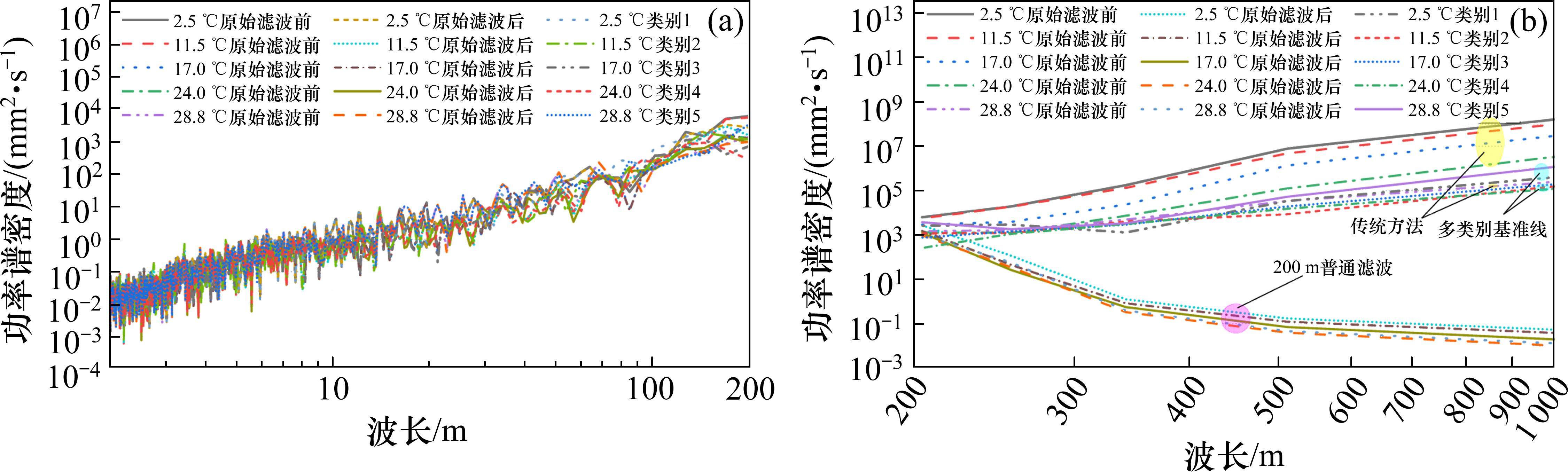
对原始滤波前后及5类别下的轨道偏差做功率谱密度,如图14所示。由图14可知,原始滤波后和多基准线下的轨道偏差均能降低200 m以上长波成分,高通滤波方法是较为直接滤除这部分成分,多基准线方法则是通过将绝大部分长波成分嫁接到基准线线形上,降低了轨道垂向偏差幅值。
3 精调方案模拟调整效果分析
3.1 多基准线精调方案
以2.5 ℃实测线形数据为例,分别以0~7 ℃温度区间基准线和2.5 ℃基准线为设计线形,计算实测线与2种基准线之间的垂向偏差,并制定精调方案。
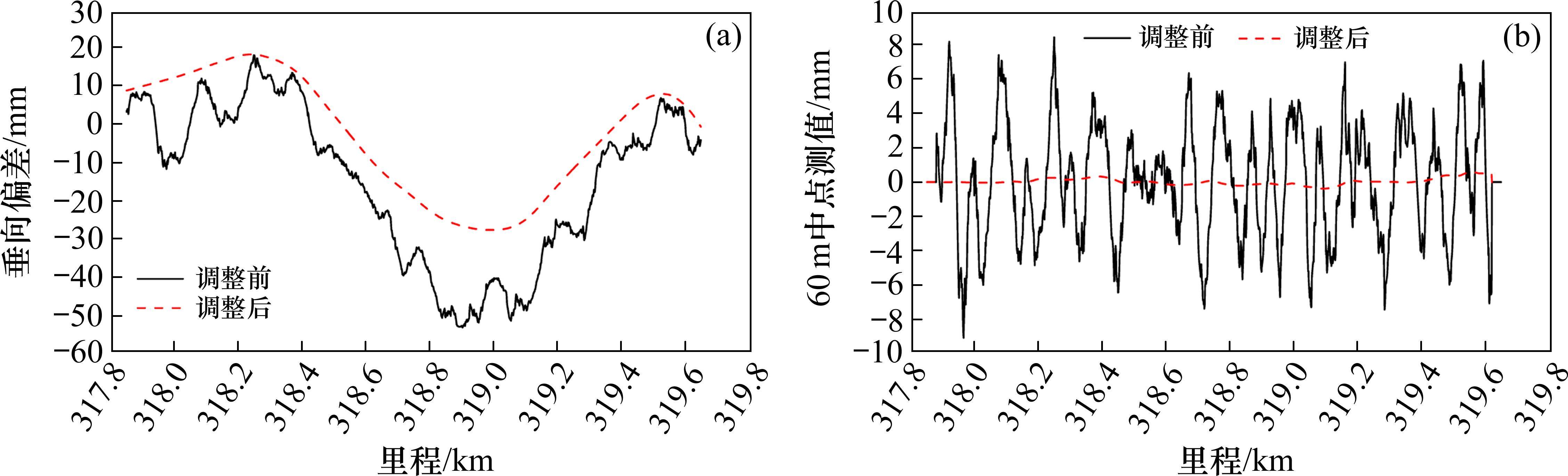
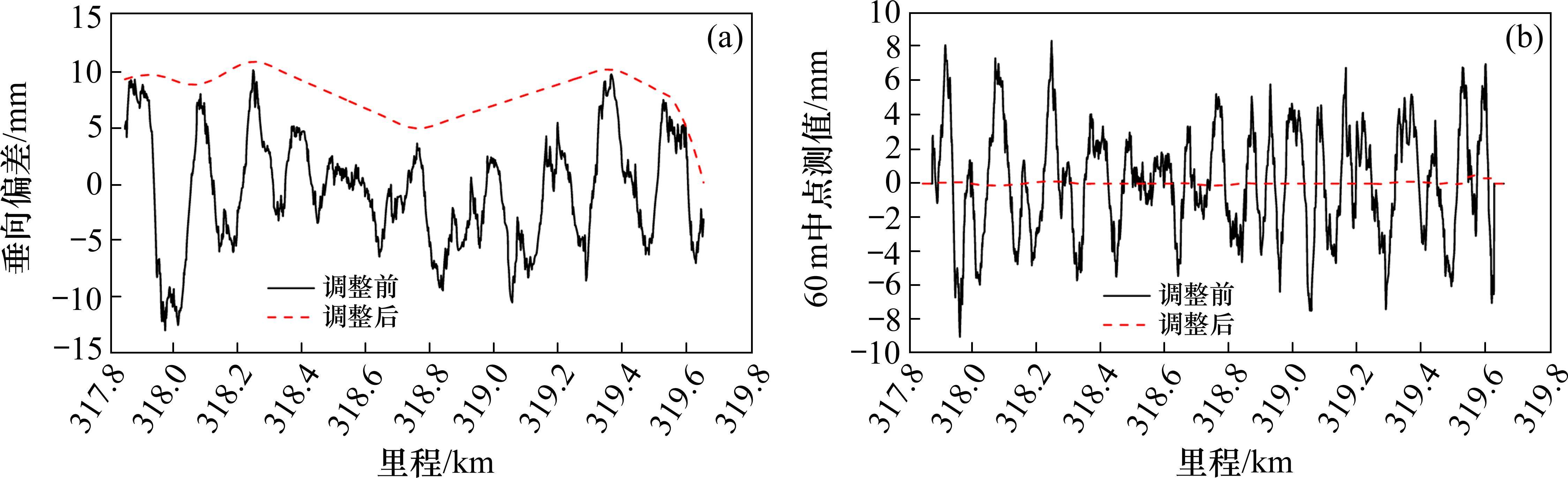
采用0~7 ℃温度区间基准线的模拟调整方案如图15所示,图中60 m中点弦测值由调整前、后线形与0~7 ℃温度区间基准线之间的垂向偏差计算得到。采用2.5 ℃基准线的模拟调整方案如图16所示。图中60 m中点弦测值由调整前、后线形与2.5 ℃基准线之间的垂向偏差计算得到。由图可知,调整后60 m中点弦测值得到了显著改善。
3.2 高通滤波精调方案
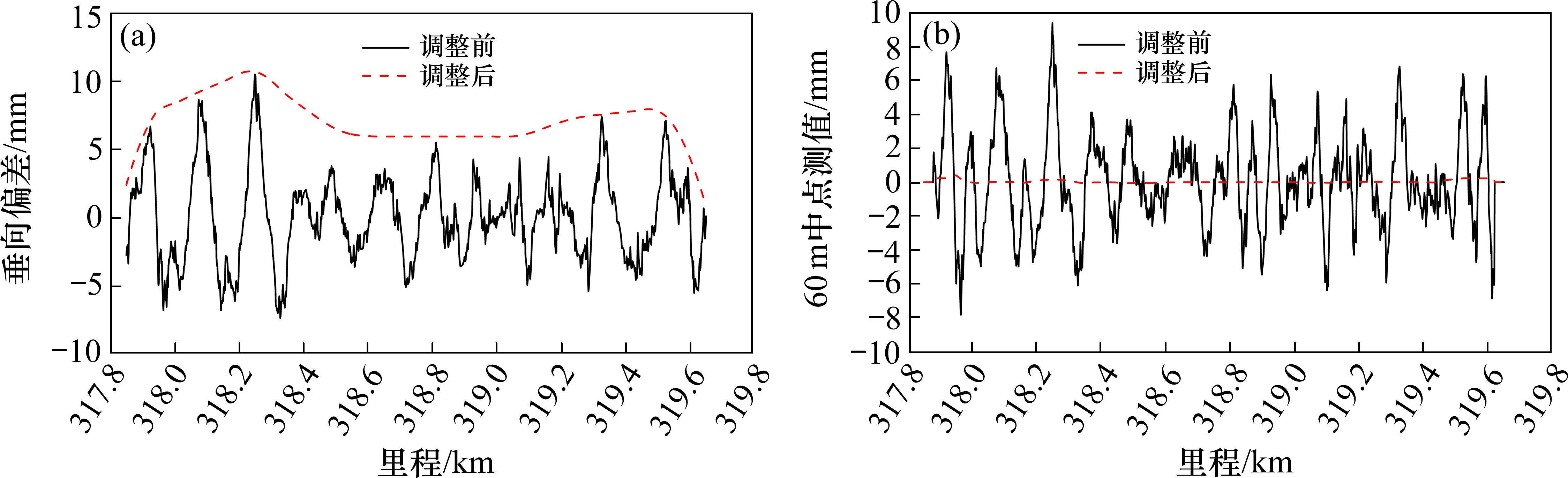
采用200 m滤波后实测线垂向偏差制定精调方案,模拟调整前后的垂向偏差如图17(a)所示。以上述精调目标线形为基础,计算调整前、后垂向偏差的60 m中点弦测值,如图17(b)所示。由图可知,调整后60 m中点弦测值得到显著改善。
3.3 模拟精调效果对比
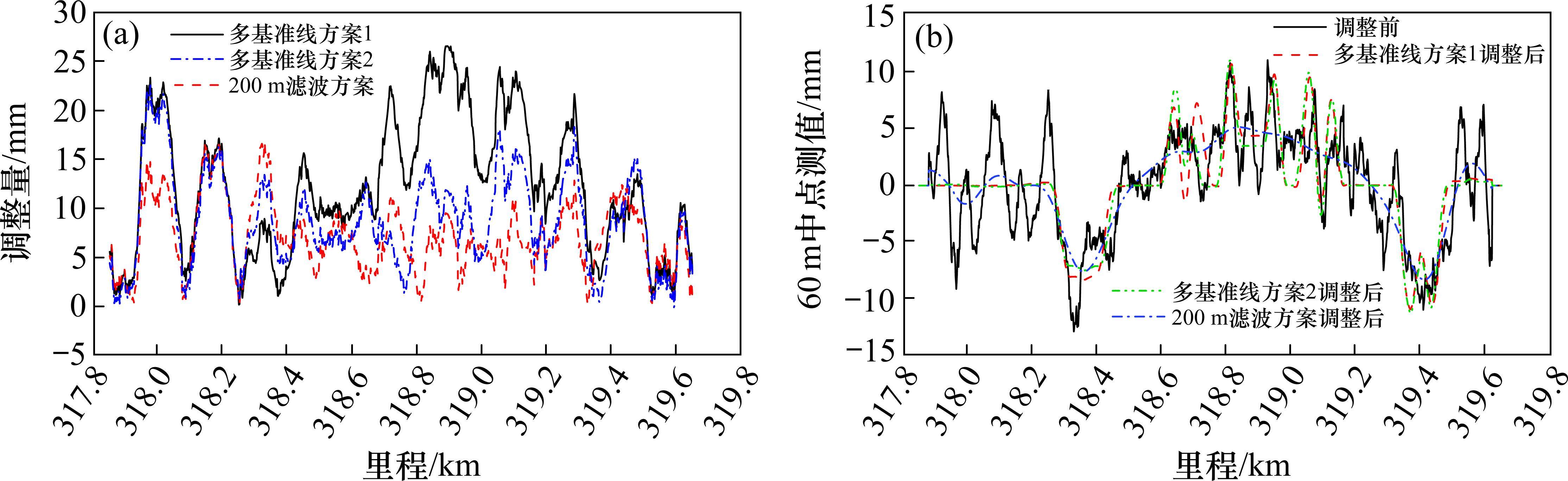
多基准线精调方案和高通滤波精调方案的调整量如图18(a)所示,图中“多基准线方案1”表示采用0~7 ℃温度区间基准线的精调方案;“多基准线方案2”表示采用2.5 ℃基准线的精调方案。计算3种方案调整后线形与原始设计线之间垂向偏差的60 m中点弦测值,如图18(b)所示。由图18可知,200 m滤波方案的起道量更小,且调整后平顺性更好,这是由于多基准线受竖曲线、夹直线等参数限制,拟合方案并不是一个足够圆顺的线形。而高通滤波无此限制条件,线形则较为圆顺。因此,尽管2种方案均以2 mm/60 m中点弦测值为平顺性约束目标,但将调整后线形与原始设计线对比,相当于分别叠加了一条带有趋势项的长波不平顺成分,而高通滤波法对应的长波成分平顺性更优,最终造成二者调整后平顺性不一致。
4 结论
1) 结合有限元仿真模型分析了多基准线法的制定原则,以五峰山长江大桥为例,通过考虑大桥温度变形、线路随机不平顺和线形拟合偏差的影响,提出温度每变化7 ℃设置一条基准线,覆盖的温度范围为±3.5 ℃。该方法操作简单,但对不同跨度、不同类型桥上轨道线形的通用性较差。为降低温度变化对高低不平顺的影响,也可对每一条实测线形进行拟合,制定基准线。需要说明的是,该做法的实质是设计线形不是事先给定的,而是依据实测线形拟合的。
2) 结合车线动力学模型分析了高通滤波法的滤波原则,以五峰山长江大桥为例,通过统计不同轨道不平顺滤波波长条件下高速列车车体垂向加速度的变化规律,发现210 m以下波长会显著影响行车响应,采用200 m作为滤波波长。该方法通用性强,但需依赖滤波软件完成运算。
3) 结合不同温度实测数据分析发现,多类别基准线和高通滤波方法均可有效剔除大跨桥温度变形引起的长波不平顺成分,消除60 m中点弦测值在大桥跨中和主塔位置的趋势项。2种方法均可用于评判高速铁路大跨度桥上轨道平顺性状态。
4) 应用多基准线法和高通滤波法分别制定了2个精调方案,将调整后线形与原始设计线对比可发现,高通滤波方案的调整量更小,且调整后平顺性更优。这是由于多基准线受轨道线形设计参数限制,其长波成分的平顺性相比滤波线形略差,造成二者调整后平顺性不同。若对每一条实测线形进行拟合,制定基准线,以此进行线形调整,则二者调整后线路平顺性一致。
国家铁路局关于发布铁道行业标准的公告
[2023]第4号(工程建设标准2023年第2批)[EB/OL]. [谭社会,张雨潇,周丽等.多基准线与高通滤波方法的大跨度桥上轨道精调方案论证[J].铁道科学与工程学报,2025,22(02):613-624.
TAN Shehui,ZHANG Yuxiao,ZHOU Li,et al.Demonstration of track precise adjustment scheme on long-span bridge with the methods of multiple baselines and high-pass filtering[J].Journal of Railway Science and Engineering,2025,22(02):613-624.

