无砟轨道是高速铁路基础设施的核心组成部分,服役期持续保持高平顺、高稳定是列车高速运行的先决条件。双块式无砟轨道因其较为经济的建造成本被广泛应用于中国高速铁路,应用里程超过2万km,占高速铁路总里程一半以上。当双块式无砟轨道应用于桥上时,为适应桥梁的伸缩变形,将应用于路基上的纵向连续方案进行单元化,采用混凝土底座并与桥面浇筑为一体,底座上设置2个凹槽,为后期浇筑的混凝土道床提供水平向限位。底座与混凝土道床间设置隔离层和弹性缓冲垫层,允许层间相对变形来释放上下层温度应力。服役期内,上层混凝土道床受太阳辐射、气温变化及降雨等影响,温度变化较为剧烈,下层混凝土温度变化则较为缓慢,因此会在垂向上产生明显的温度梯度。无砟轨道温度场早期的研究中,通过对多条高速铁路无砟轨道温度梯度进行现场监测,提出了轨道板沿竖向的分布特征[1-4],构建了气象参数与轨道板竖向温差之间的映射关系[5-7]。部分研究则是从解析的角度出发,将无砟轨道温度场视作半无限空间的一维传热问题,建立温度场理论解析式,分析无砟轨道温度沿垂向分布的规律[8-11],进而对无砟轨道垂向温度荷载取值提出了建议[12]。随着对无砟轨道温度场研究的深入,研究人员注意到温度是引起无砟轨道变形、损伤的主要因素之一[13],学者们开始关注轨道板内部温度分布特征[14]。近些年,有研究基于无砟轨道温度场模型试验,研究太阳照射方位[15-18]、约束条件的影响,得到轨道结构温度变化沿深度方向存在时滞效应[19-21],并提出温度沿垂向、纵向和横向均呈非线性分布[22-24]。同时,也有部分学者引入混合方法[25]或优化的机器学习[26],分析了自然环境下轨道内部温度的分布特征。基于动态轨道不平顺检测数据,研究发现单元式无砟轨道存在显著的周期性不平顺现象[27-28],并从平顺性管理的角度提出了短弦法。运营期内,轨道周期性不平顺易引起车辆激振,增加车辆脱轨风险,严重影响行车的舒适性和安全性[29-30]。周期性不平顺被发现后,受到了研究人员的广泛关注,并从模板、养护工艺以及轨道板存放等角度对轨道结构进行了改进[31],但收效甚微。尤其是预制的板式和现浇的双块式无砟轨道结构均能够检测出相似的周期性不平顺特征。近年来,温度梯度引起的单元式无砟轨道上层结构翘曲变形逐渐被发现,研究表明轨道结构层间黏结失效时,轨道板上下表面温度差10 ℃会产生约0.33 mm的翘曲变形[2]。随着无砟轨道温度场及温度变形研究的深入,赵国堂等[32]首次提出温度梯度导致轨道板翘曲变形,进而引发轨道产生周期性不平顺,并将研究热点转向翘曲变形下无砟轨道结构受力特征及其时变的层间接触方式。虽然已有大量研究采用模型试验、原位实测及理论仿真等方法对无砟轨道温度场分布特征进行了深入研究,然而既有温度场的相关研究相对独立,鲜有研究针对温度场与轨道结构变形之间的联系开展相关试验验证。因此,为弥补无砟轨道温度与道床板变形映射关系缺乏试验验证的不足,本文提出一种无砟轨道温度场及温度变形测试方法,以现场实测数据建立了温度荷载与道床板变形之间的相关关系。同时,构建了双块式无砟轨道多层结构空间接触关系有限元模型,并结合现场试验数据验证了可靠性,进而探究了温度梯度作用下双块式无砟轨道周期性不平顺特征。
1 双块式无砟轨道温度变形研究试验方案
1.1 试验测试内容
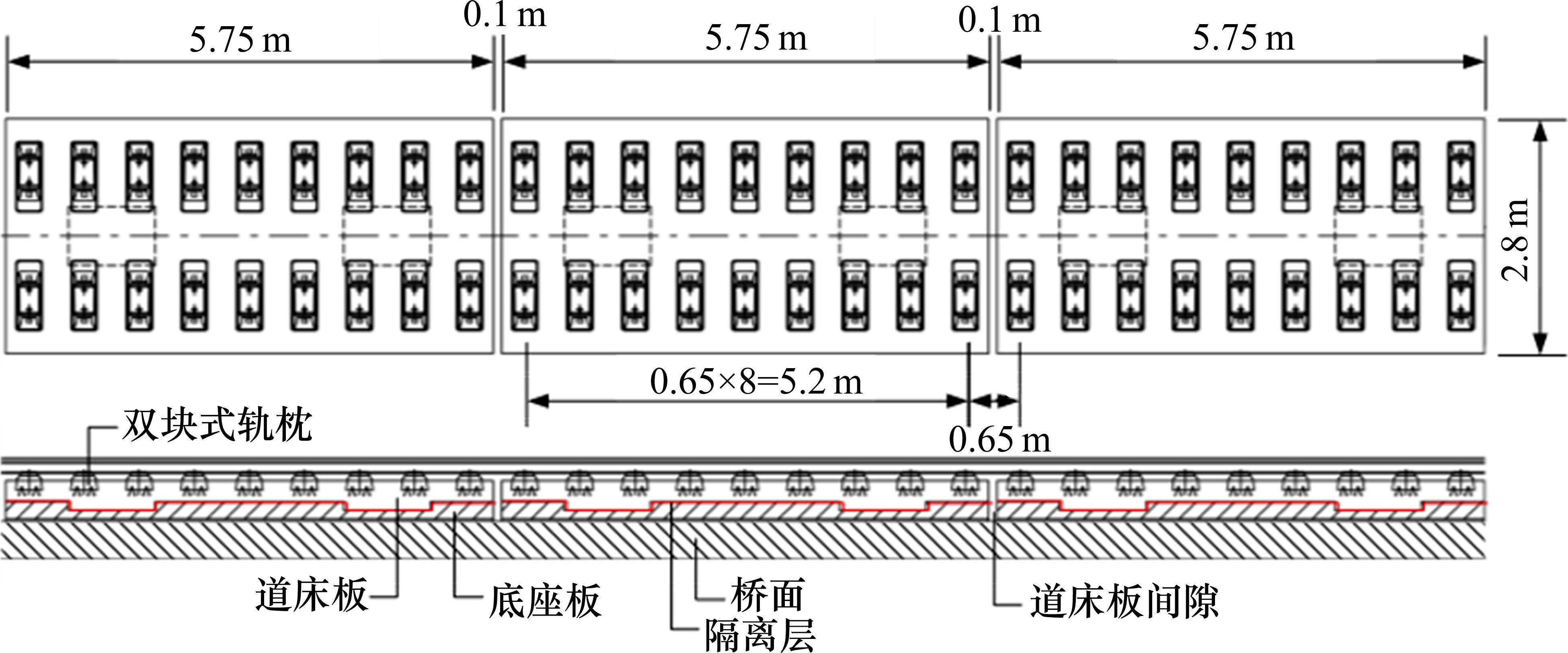
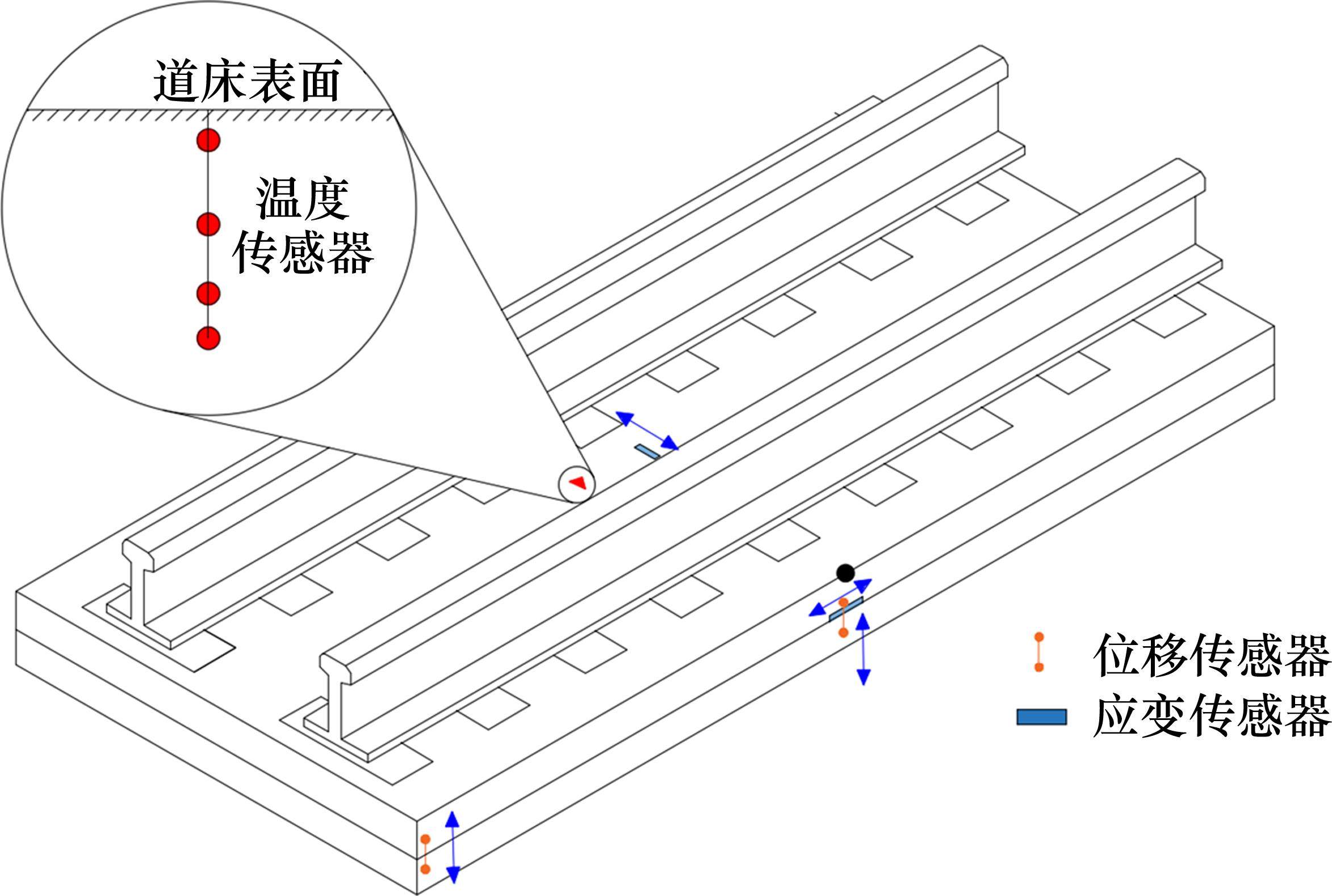
本文试验实施于中国南方某新建高铁线路上,线路轨道结构为双块式无砟轨道,下部基础类型为40 m的箱型简支梁。双块式无砟轨道结构自上而下依次为钢轨、扣件、双块式轨枕、现浇混凝土道床、隔离层、混凝土底座。其中,双块式无砟轨道采用单元体系,道床板宽2.8 m,长5.75 m,扣件间距为0.65 m,相邻道床板间间隔为0.1 m,如图1所示。为探究无砟轨道温度变化规律、温度梯度与道床板变形之间的映射关系,实时采集无砟轨道结构不同深度处温度以及道床板翘曲变形量。试验设计温度测点共1处,包括4个温度传感器,位移传感器和应变传感器各2处,无砟轨道总体传感器布置如图2所示。
1.2 试验测试方案
为实时监测试验过程中双块式无砟轨道结构的温度值,在道床板中心布置温度监测工点,包括4个温度传感器,分别布置于距离道床表面20、80、160和200 mm处,如图3所示。为建立无砟轨道温度与道床板变形之间的映射关系,在道床板角和板中分别布设了激光和振弦式位移传感器,如图4所示。激光传感器布置在道床板底层,激光接受台布设在底座板顶层,从而用激光传感器采集道床板与底座板之间的竖向变形差;振弦式位移传感器一端布置在道床板底层,一端固定在底座板底层,两端通过振弦连接,收集道床板与底座板之间的竖向变形差。


2 试验结果分析
2.1 双块式无砟轨道温度场变化规律
双块式无砟轨道结构始终暴露于自然环境之中,其温度场受复杂多变的气象因素影响,为探究双块式无砟轨道温度场时变规律,试验对2块道床板深度0.2 m范围内各深度处温度进行了长期观测。双块式无砟轨道温度观测数据如图5所示。
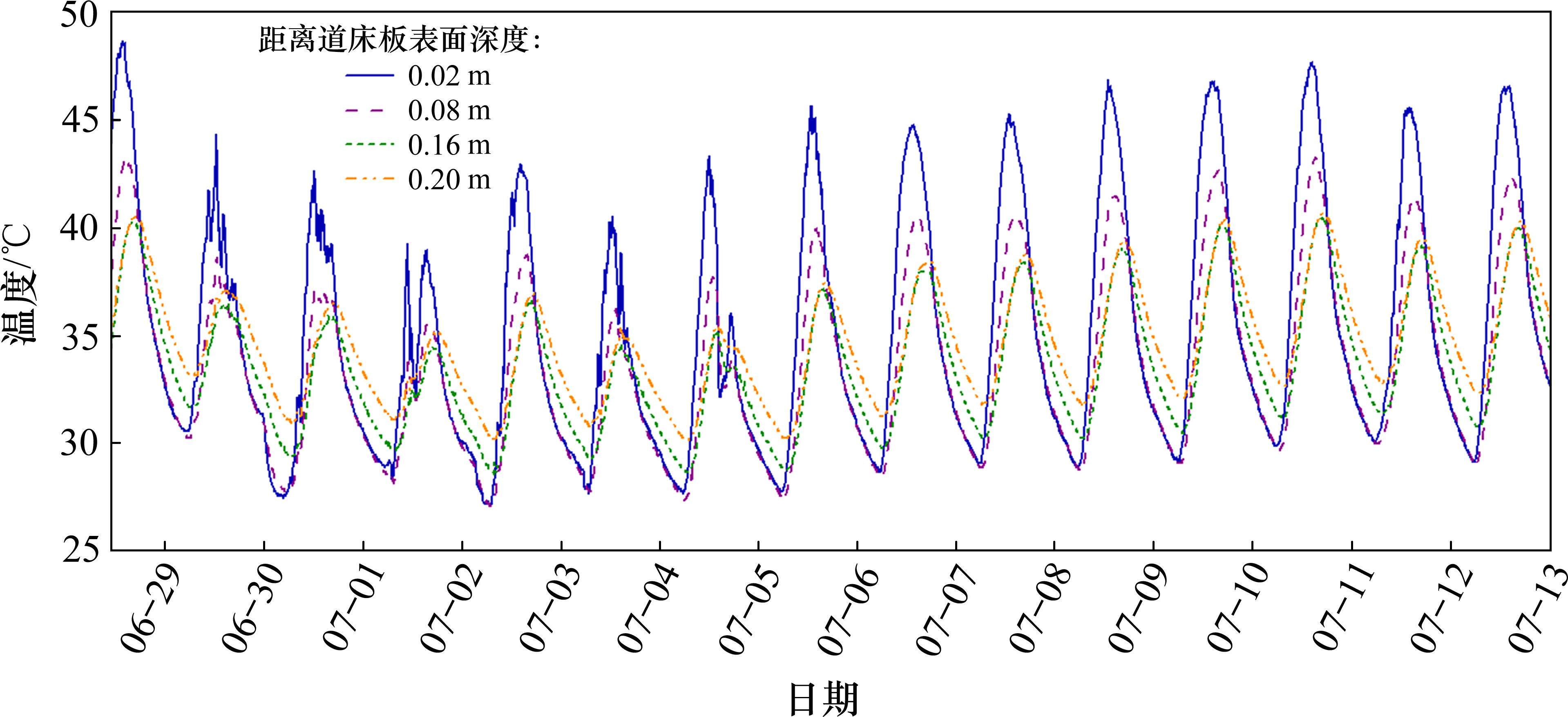
图5展示了6月28—7月13日内道床板各深度处温度的时变规律。不难发现,双块式无砟轨道各层温度具有显著的日周期性时变规律,距离道床板表面越近温度越高,温度日变化幅度也越大。距离道床板表面深度0.02 m处,在6月28日14点温度达到峰值48.6 ℃,且当日日振幅最大,达到18 ℃。道床板在保持日周期性时变特征不变的前提下,存在不同程度的短时突变,且这种短时突变导致的温度变幅和出现次数都随着深度增加而降低。这是由于双块式无砟轨道结构接收和释放热量主要从道床板表层向结构内部传递,因此道床板表层受环境因素影响明显,短时突变在表层温度变幅最大,出现次数最多,当距离道床板表层深度超过0.16 m时,道床板温度基本不受环境短时突变的影响。
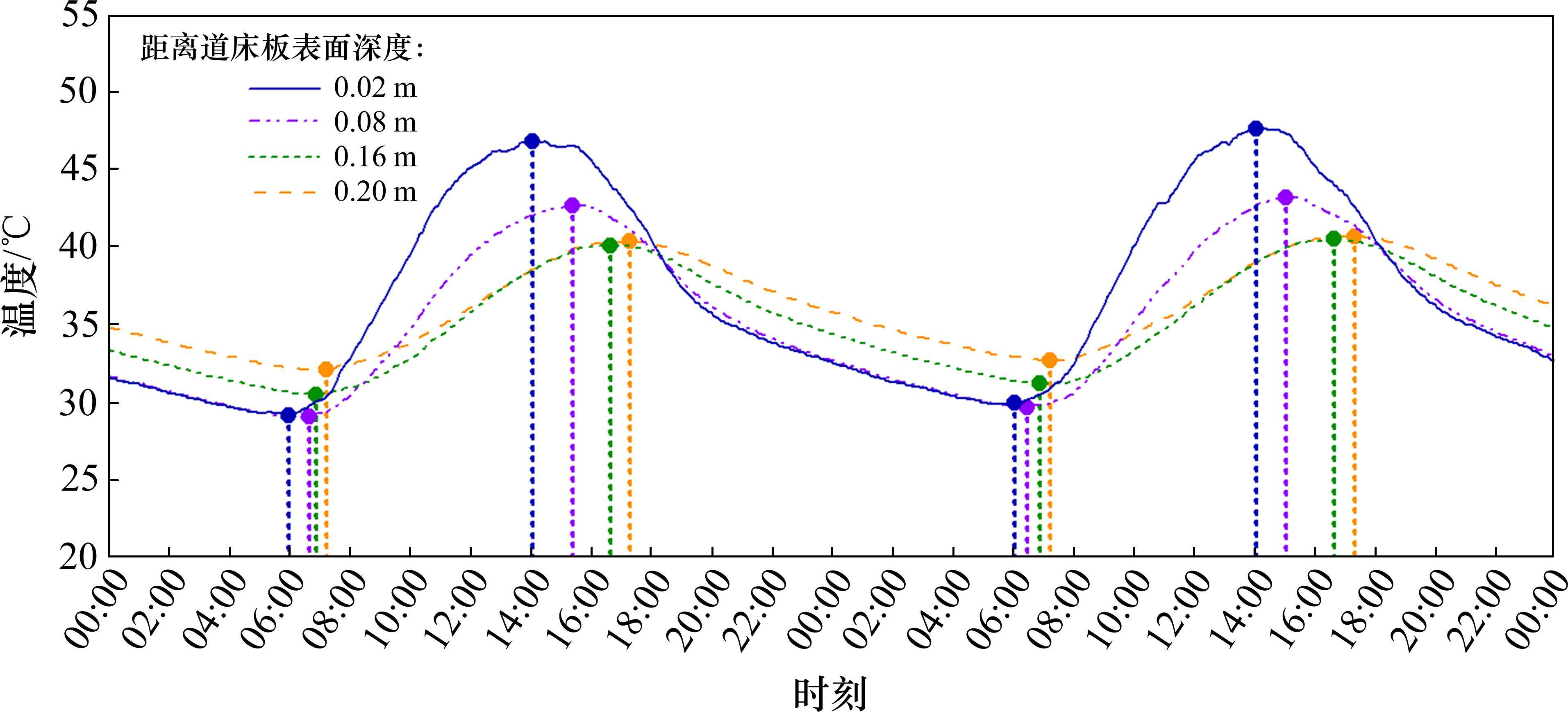
为研究双块式无砟轨道道床板温度场日演变规律,图6展示了7月9日—10日2天内道床板各深度温度时变曲线。如图所示,双块式无砟轨道各深度温度均呈日周期性升-降。夜间时段(0:00—6:00),道床板各深度处温度在对流换热作用下逐渐降低。6:00以后,道床板表层温度率先开始迅速攀升,这是由于日出之后太阳辐射作为道床板温度场的主控因素使得温度快速升高。道床板所接收的热量由道床板表层向内部传递,故而使得中层(0.08 m)温度攀升时间滞后于表层约1 h,深层2处(0.16 m和0.2 m)又滞后于中层约1 h。在太阳辐射和环境温度共同作用下,道床板表层温度在14:00左右达到峰值,此后持续降低。相似地,道床板中层达到峰值时间也滞后于表层约1 h,道床板深层又滞后于中层约1 h。双块式无砟轨道道床板温度降低过程中,道床板表层温度下降速率显著大于中层和深层,在18:00后表层温度低于深层温度且将持续至次日凌晨6:00。
依据上述对双块式无砟轨道温度场时变规律的分析可知,同一时刻道床板各深度处温度差异明显,且温度差异也具有日周期性变化特征。因此,为探究双块式无砟轨道道床板温度沿深度方向分布规律,及其随时间的演变特征,图7展示了连续2天(7月9—10日)内典型时刻下无砟轨道温度沿深度方向的分布曲线,图中用虚线代表夜间时段(0:00—6:00和20:00—22:00),实线则代表日间时段(8:00—18:00)。
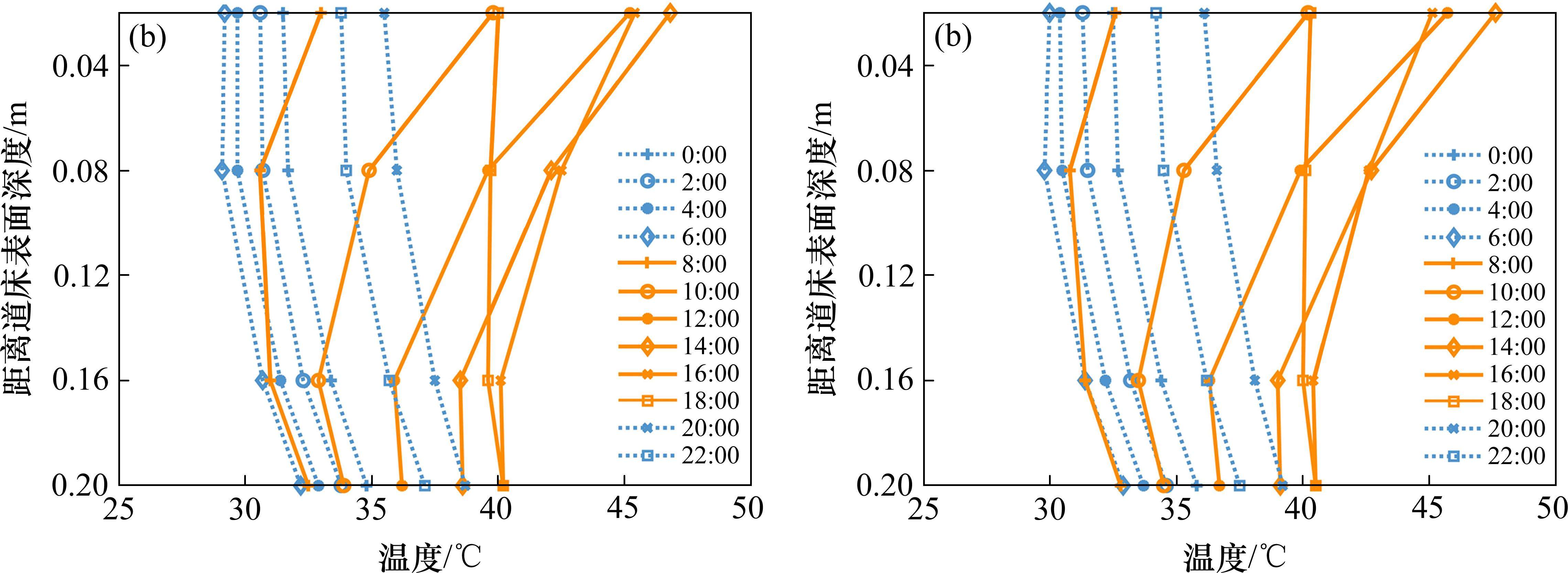
如图7(a)所示,夜间时段(0:00—6:00和20:00—22:00),无砟轨道温度沿深度方向逐渐升高,在对流换热作用下,温度随着时间整体降低,但沿深度方向的分布规律保持不变。日间时段(8:00—18:00),在太阳辐射作用下,道床板表层温度率先升高,并在14:00达到峰值46.8 ℃;无砟轨道温度先随深度增加而降低,且深度越深,温度降低速率越缓慢,当深度超过0.16 m后,温度变化趋势转变为随深度增加而增加。观察同一深度处各典型时刻温度可知,距离道床板表面越近,不同时刻温度的离散程度越高,当深度处于0.02 m处,各典型时刻温度极差达到17.6 ℃,深度0.2 m处温度极差降低至8.0 ℃,降幅达到54.55%,这表明双块式无砟轨道温度距离结构表面越近,变化越剧烈。由图7(a)可知,距离无砟轨道表面0.16 m深度范围以内,温度变化较为活跃,且该范围内线性度较好,可选用0.02 m和0.16 m处温度差拟合道床板线性温度梯度;当距离无砟轨道表面大于0.16 m后,温度相对稳定且沿深度方向分布形式差异不大。
图7(b)为典型时刻下无砟轨道温度沿深度方向的分布曲线,与图7(a)具有相同的分布特征和演变规律。同时,由于无砟轨道各深度处温度随时间呈日周期性升-降,对比分析图7(a)和7(b)可发现,相同时刻下沿深度方向具有相同的分布规律。
2.2 双块式无砟轨道温度变形特征
根据无砟轨道温度场沿深度方向的分布特征可知,热量在双块式无砟轨道传递过程中存在明显时滞效应,导致距离道床板表面越近,温度变化越活跃。为有效量化双块式无砟轨道道床板温度梯度,实测道床板温度梯度通过道床板表层(0.02 m)温度减去道床板深层(0.16 m)温度并除以测点间距0.14 m拟合得到,6月28日—7月13日间温度梯度变化如图8所示。由图可知,双块式无砟轨道道床板温度梯度同样具有日周期性的时变规律,且正、负温度梯度昼夜交替出现,夜间(0:00—6:00和20:00—22:00)以负温度梯度为主,昼间(8:00—18:00)以正温度梯度为主。6月28日—7月13日内,正温度梯度在6月28日最大,达58.9 ℃/m,负温度梯度在6月30日最大,达-25.6 ℃/m,均在设计温度梯度-45~90 ℃/m取值区间内。
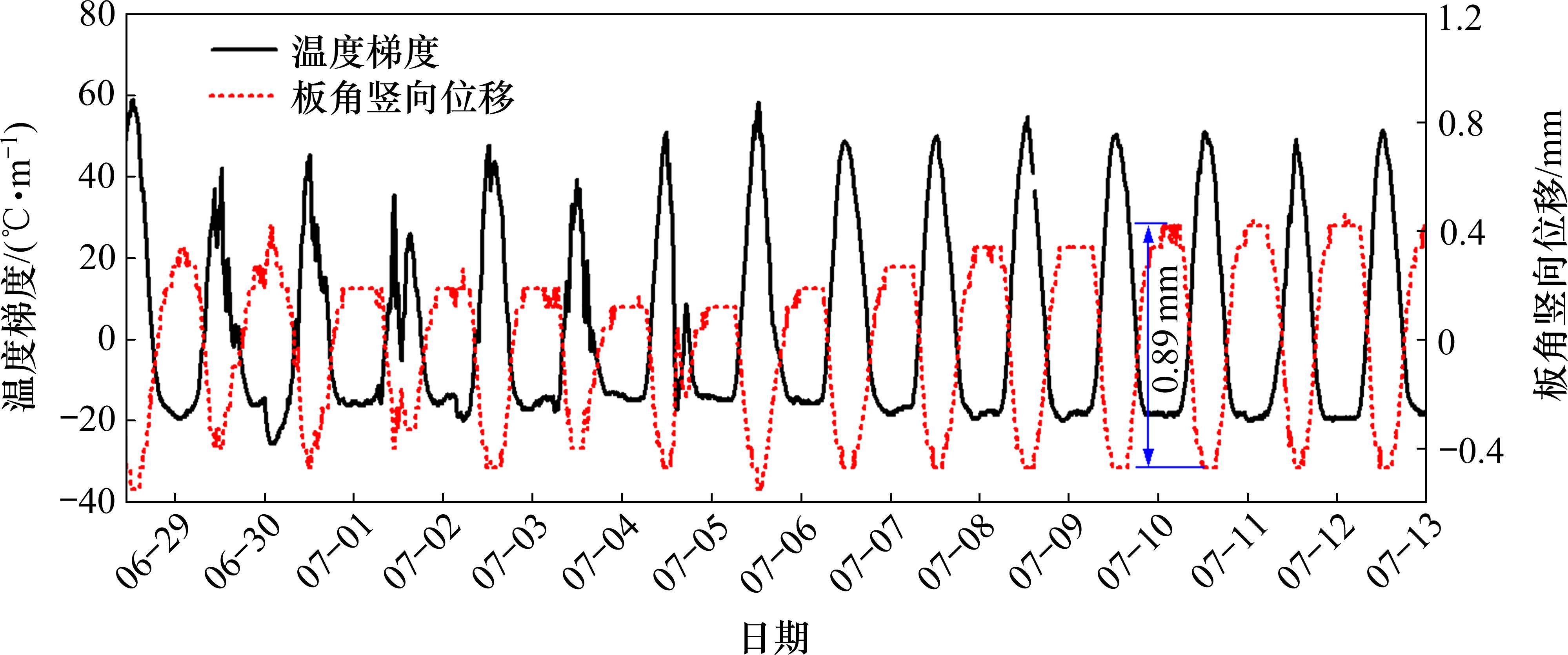
温度梯度作为双块式无砟轨道重要的温度荷载,在温度梯度作用下道床板发生翘曲变形。由于在测试道床板翘曲变形时,无法确认传感器设置时刻的初始竖向变形量。因此,在对道床板竖向位移测试数据进行处理时,假定温度梯度为0时对应的板中和板角竖向位移为0,其中6月28日—7月13日内板角竖向位移如图8所示。试验结果表明,温度梯度作用下板角竖向位移同样具备日周期性变化,日平均变化幅度在0.8 mm左右,最大日竖向位移量达到0.89 mm。
为探究温度梯度与板角、板中竖向位移变化之间的相关关系,选取7月15日—7月20日试验测试数据进行对比分析,如图9和图10所示。由图9可知,温度梯度值与板角竖向位移量呈正相关关系,正温度梯度值越大,板角竖向位移越大,随着负温度梯度值增大,板角向上位移也不断增大。
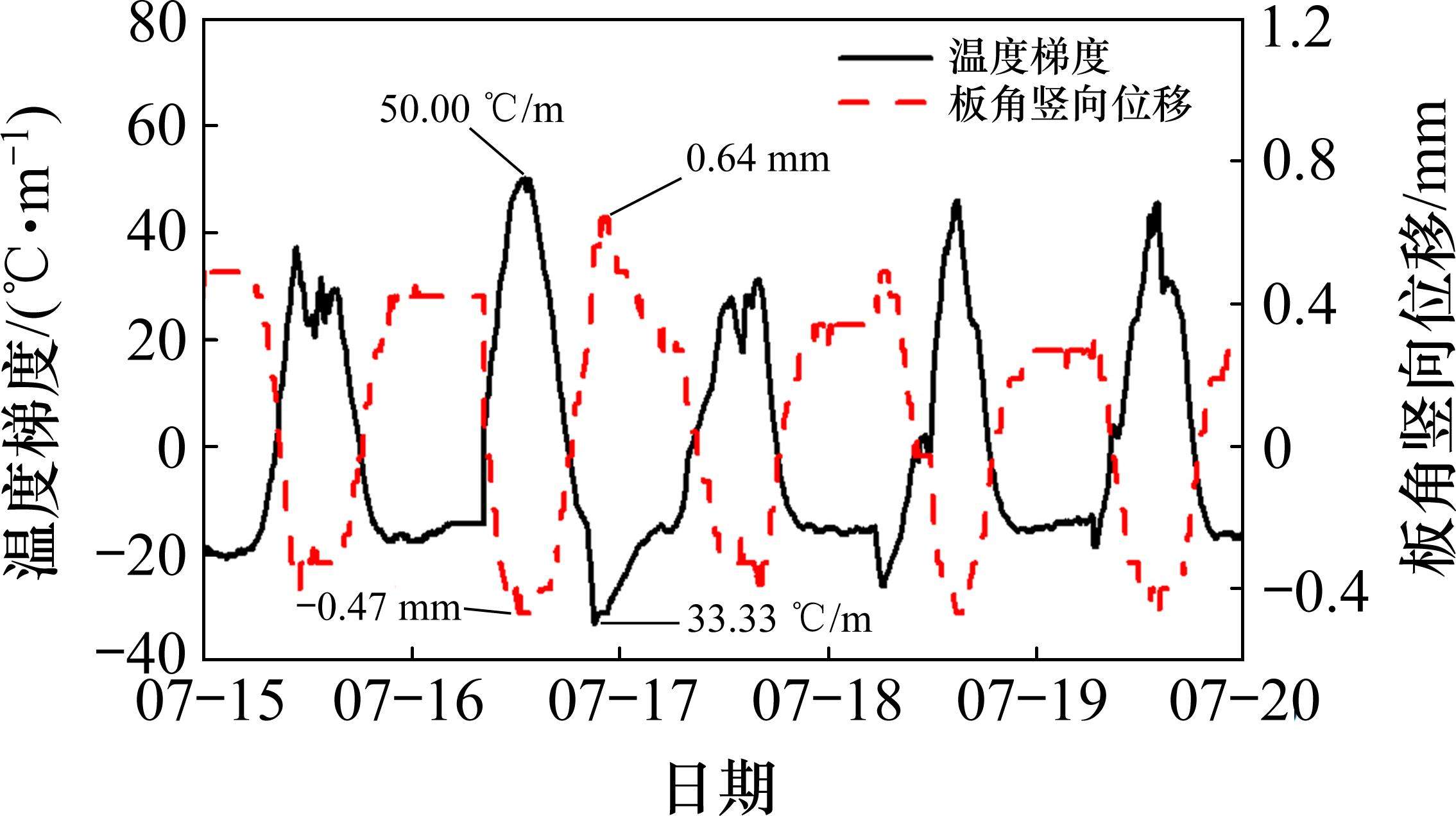
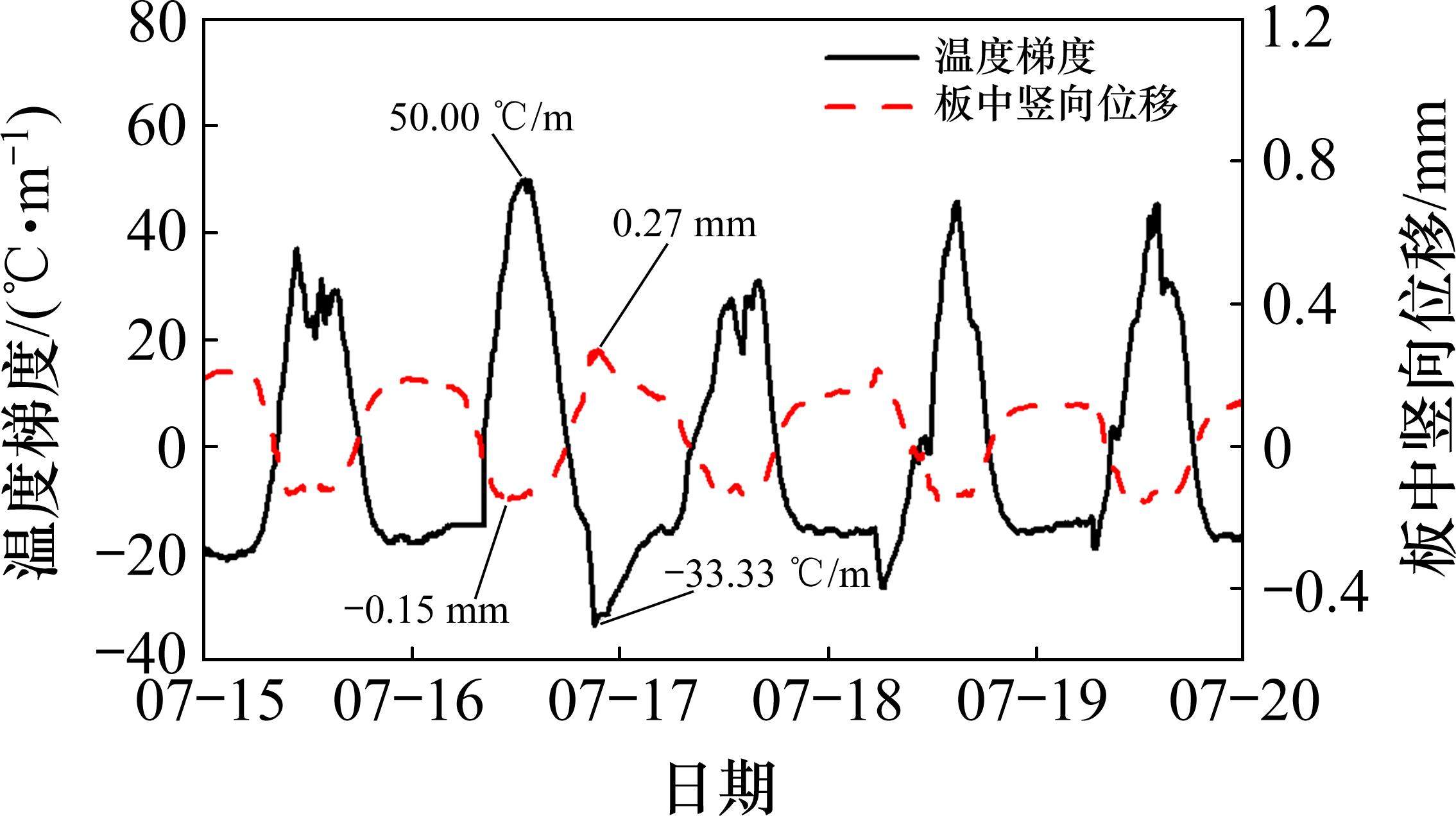
图10展示了7月15日—7月20日间道床板板中竖向位移与温度梯度之间的相关关系。与板角竖向位移变化趋势一致,板中竖向位移值与温度梯度值呈正相关关系,板中竖向位移值随正温度梯度值增加而向下增大。所选时间段内,正温度梯度在7月16日最大,达50 ℃/m,板角/板中竖向位移分别为-0.47/-0.15 mm,板中竖向位移量较板角小约68.1%;负温度梯度在7月17日最大,达-33.33 ℃/m,板角/板中竖向位移分别为0.64/0.27 mm,板中竖向位移量较板角少约57.8%。由此得出,在温度梯度作用下,双块式无砟轨道道床板板角与板中竖向位移量差异明显,发生了显著的翘曲变形。
3 温度梯度对双块式无砟轨道周期性变形的影响
3.1 构建有限元分析模型
双块式无砟轨道主要由钢轨、扣件、双块式轨枕、道床板、隔离层、底座等构成。根据双块式无砟轨道结构特点,钢轨、道床板、双块式轨枕及底座均采用8节点六面体实体单元进行模拟。模型中钢轨为CHN60标准轨,钢轨按扣件间距划分网格,每个扣件间距划分3个单元。扣件类型为WJ-8型扣件,扣件间距为0.65 m,为考虑扣件对轨道板温度变形的限制,扣件由弹簧-阻尼单元模拟,每组扣件提供的最大纵向阻力为9.0 kN,横向静刚度为50 kN/mm,垂向静刚度为35 kN/mm。道床板材料为C40混凝土,长宽高分别为5.75 m×2.8 m×0.26 m,控制最大单元长度为0.25 m;底座材料为C30,长宽高分别为5.75 m×2.8 m×0.3 m,底座上设置2个凹槽,为后浇道床板提供水平向限位,底座网格平面上与道床板一致,垂向上划分为3层。底座与道床间设置隔离层,刚度为0.4 N/mm3。底座与桥梁之间共节点,桥梁为C60混凝土,桥梁截面为典型40 m简支箱梁截面。所构建的桥上单元双块式无砟轨道有限元分析模型如图11所示。
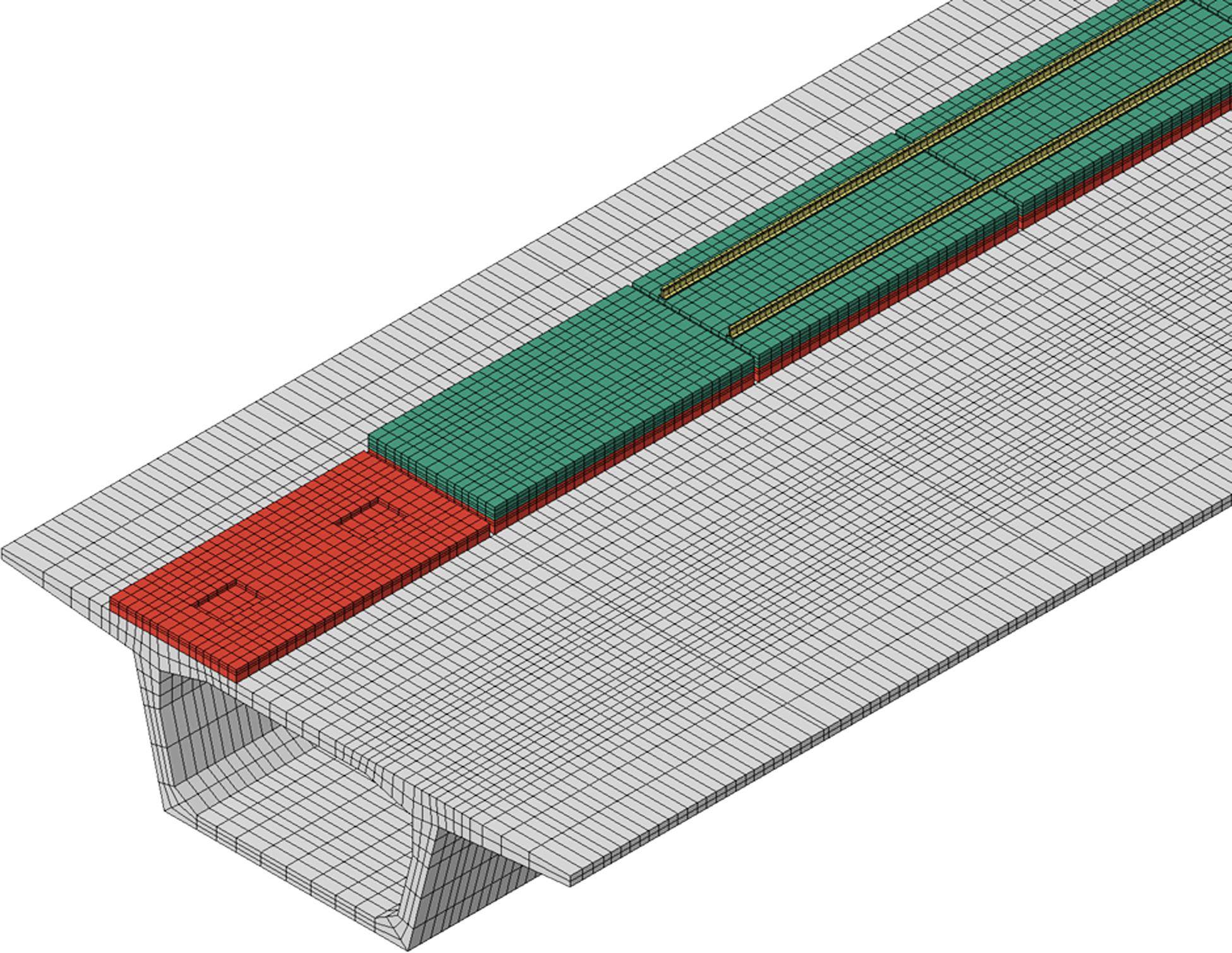
3.2 模型验证
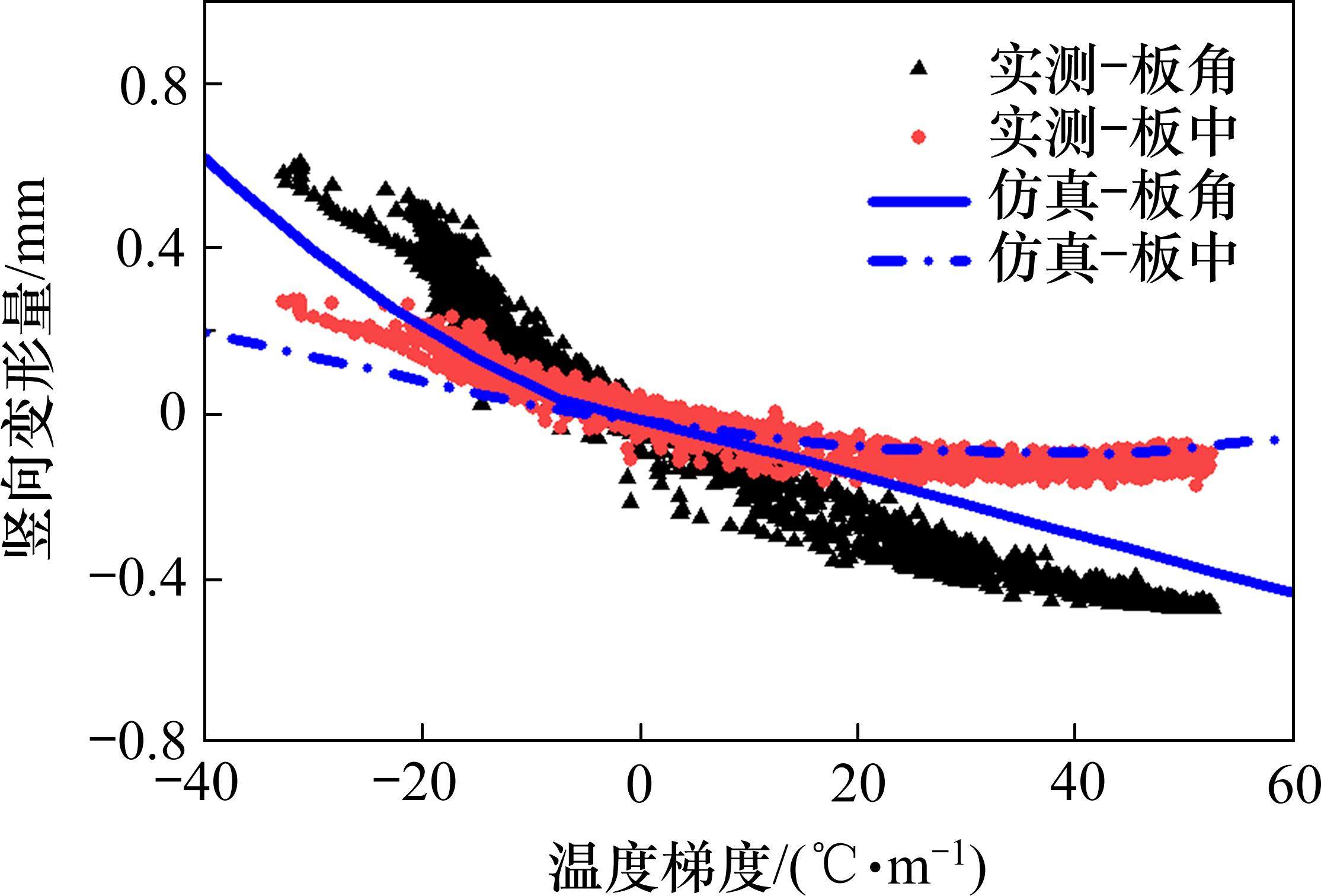
图12展示了温度梯度与道床板板角和板中竖向位移量的对应关系,其中实测结果表明,道床板竖向位移量与温度梯度值呈明显的正相关关系,即温度梯度值越大,竖向位移量越大,且侧边板中位移量变幅要小于板角。为验证双块式无砟轨道理论分析模型的可靠性,提取了不同温度梯度作用下有限元模型中道床板板角和板中的竖向位移,并与现场实测板角和板中竖向位移数据进行对比。结果显示,理论模型板角竖向位移与实测数据走势一致,均随温度梯度增加而降低,板中竖向位移同样也与实测数据较为吻合。模拟道床板板角竖向位移与实测板角位移的均方根误差为0.142 mm,模拟道床板板中与实测值竖向位移的均方根误差为0.072 mm。产生偏差的主要原因为:仿真分析模型中竖向温度梯度加载简化为线性温度梯度,而实际温度在道床内沿竖向分布存在一定的非线性。
3.3 温度梯度对双块式无砟轨道变形的影响规律
3.3.1 正温度梯度作用下轨道结构变形规律
图13和图14结果表明,在正温度梯度下,钢轨和道床板会形成板中高、板端低的典型周期性变形趋势,竖向变形差随着正温度梯度增加呈逐渐增加趋势,最大90 ℃/m正温度梯度下,轨道板侧边垂向变形差达1.01 mm,钢轨垂向变形差达0.58 mm。
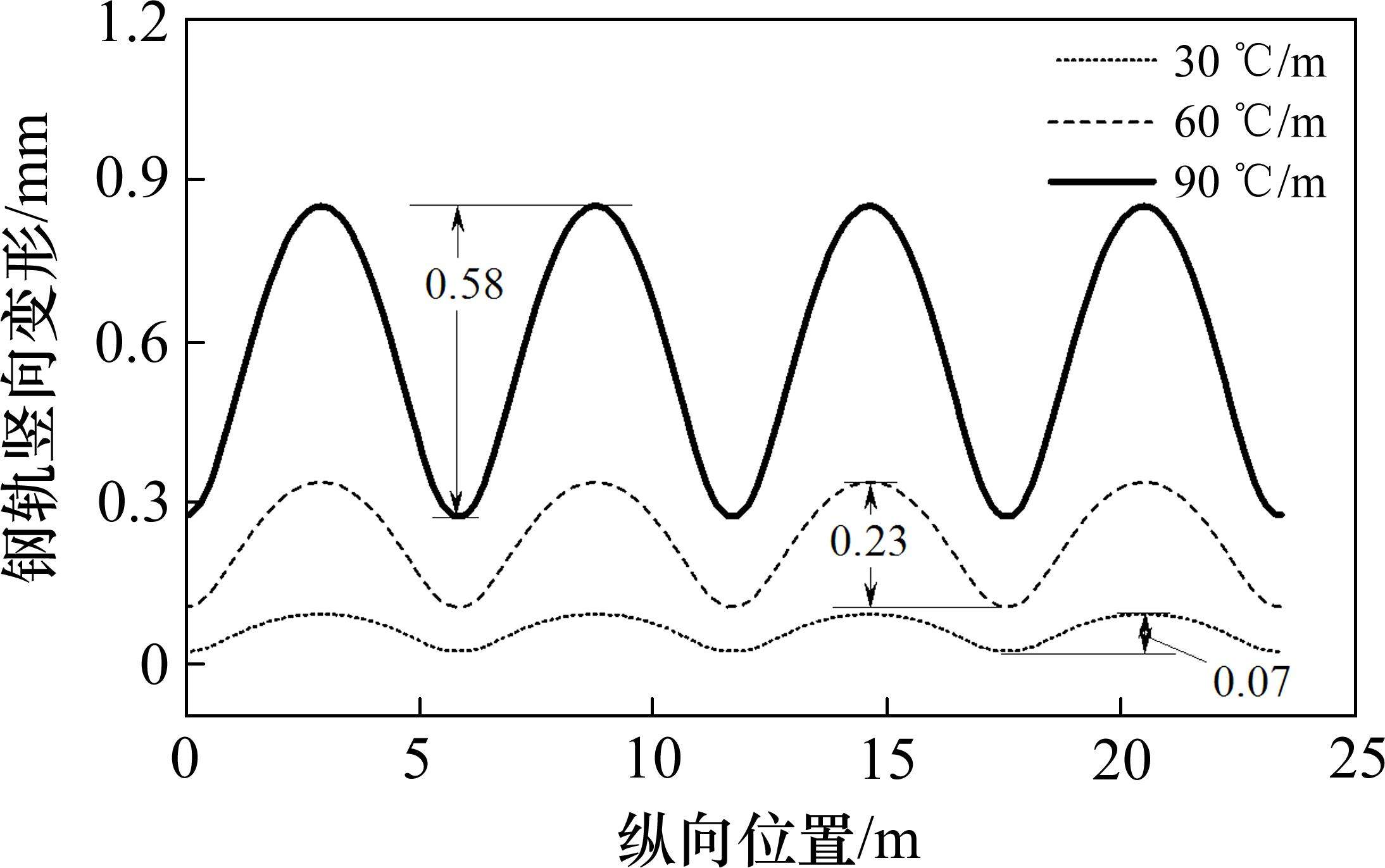
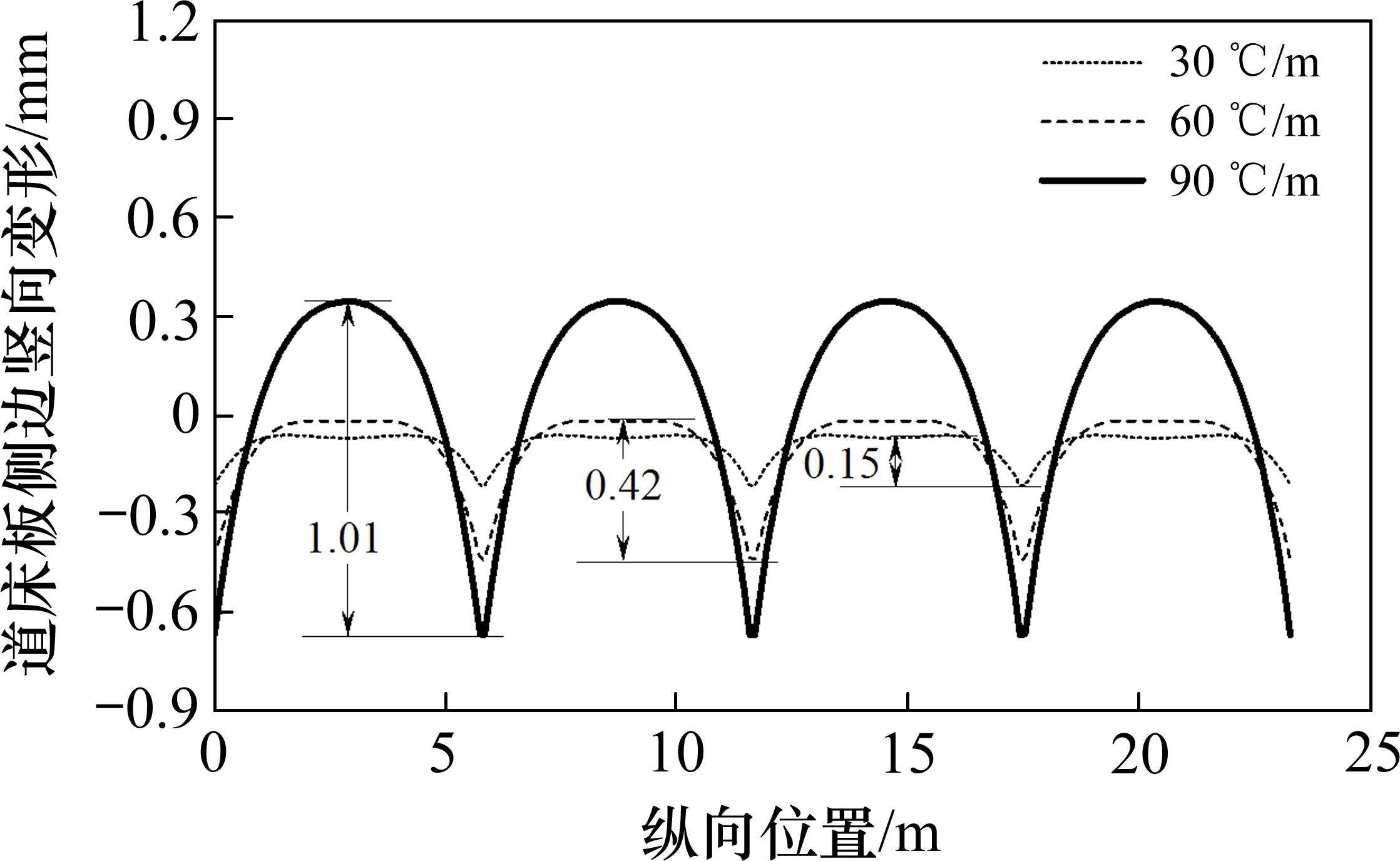
钢轨和道床板侧边竖向变形差u随正温度梯度Tg增大而增加,如图15所示。图15可以看出,钢轨和道床板侧边位置处的竖向变形差呈抛物线型增长趋势。定义传递比ξ(单位:mm∙(℃∙m-1)-1)为单位温度梯度增加量(单位:℃/m)导致的竖向变形差增加量(单位:mm),传递比ξ直接表达了道床板温度梯度与翘曲变形量之间的对应关系。
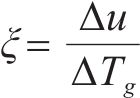
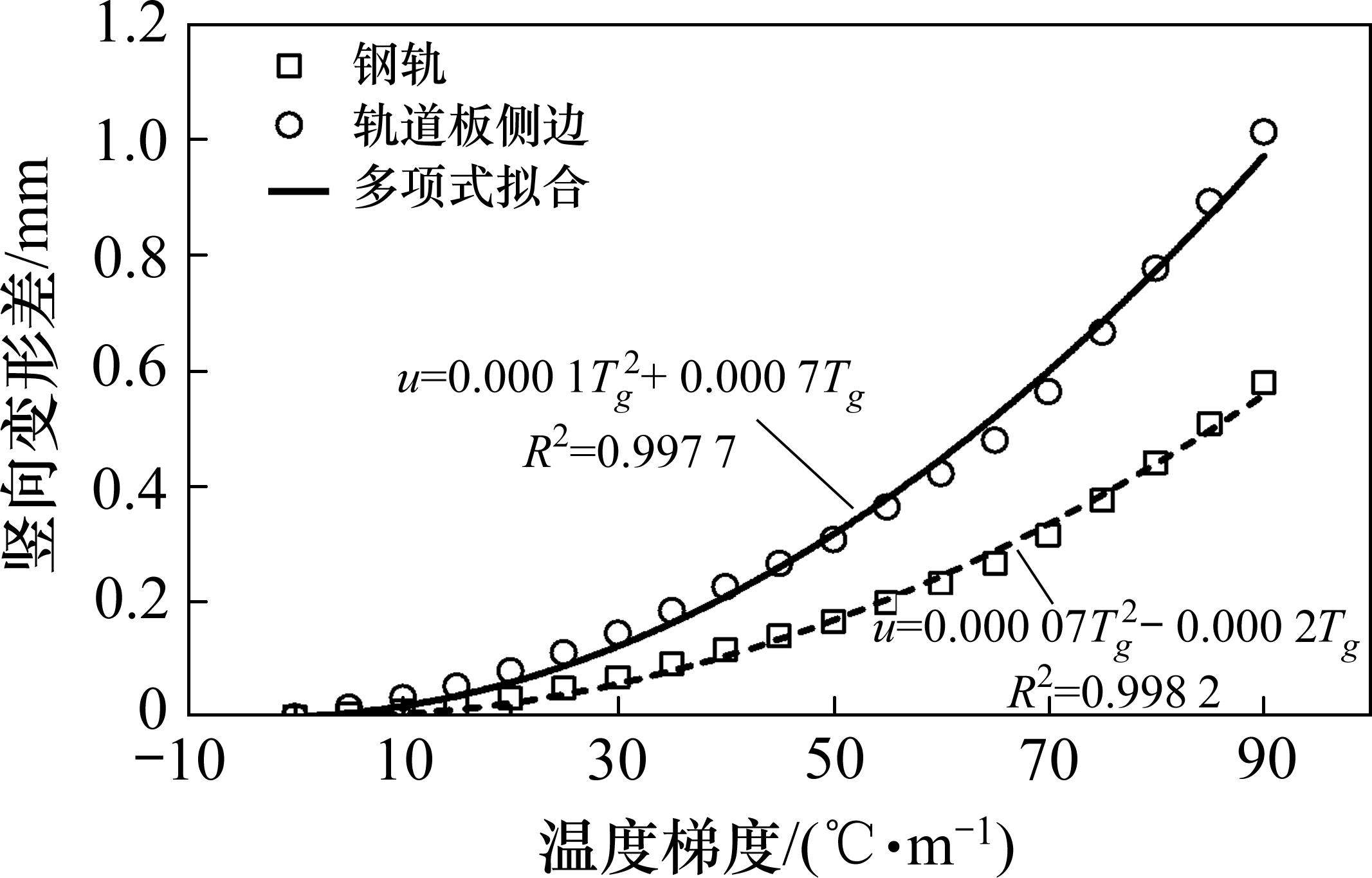
可以得出:
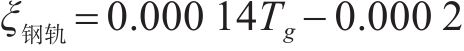
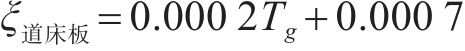
正温度梯度越大,ξ越大,当Tg=45 ℃/m时,ξ钢轨=0.006 1 mm∙(℃∙m-1)-1,ξ轨道板=0.009 7 mm∙(℃∙m-1)-1;当Tg=90 ℃/m时,ξ钢轨=0.012 4 mm∙(℃∙m-1)-1,ξ轨道板=0.018 7 mm∙(℃∙m-1)-1,传递比均增加了近2倍。
3.3.2 负温度梯度作用下轨道结构变形规律
图16和图17结果表明,在负温度梯度下,钢轨和道床板会形成板中低、板端高的典型周期性变形趋势,竖向变形差随着负温度梯度增加呈逐渐增加趋势,最大-45 ℃/m负温度梯度下,道床板侧边垂向变形差达0.55 mm,钢轨垂向变形差0.26 mm。
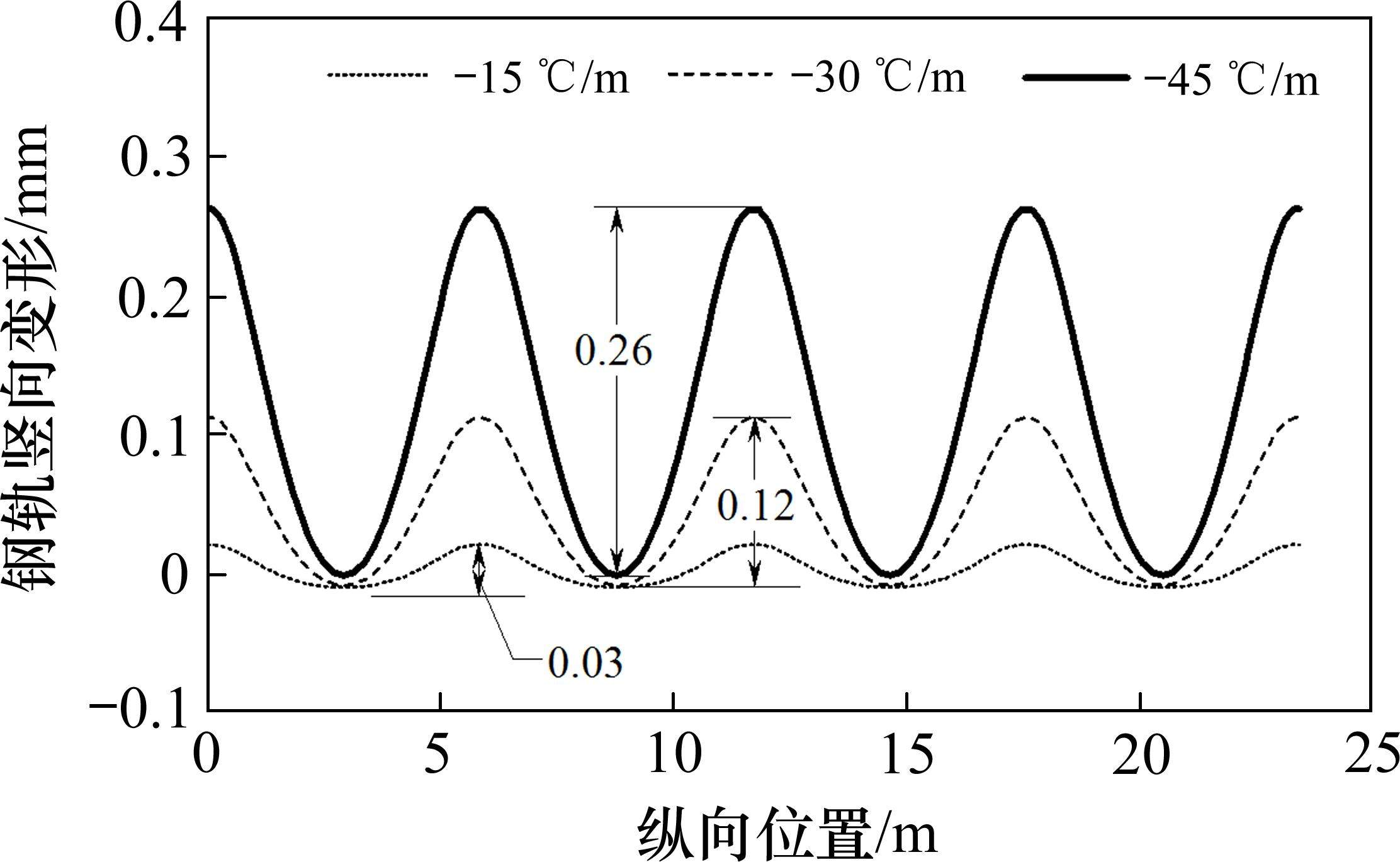
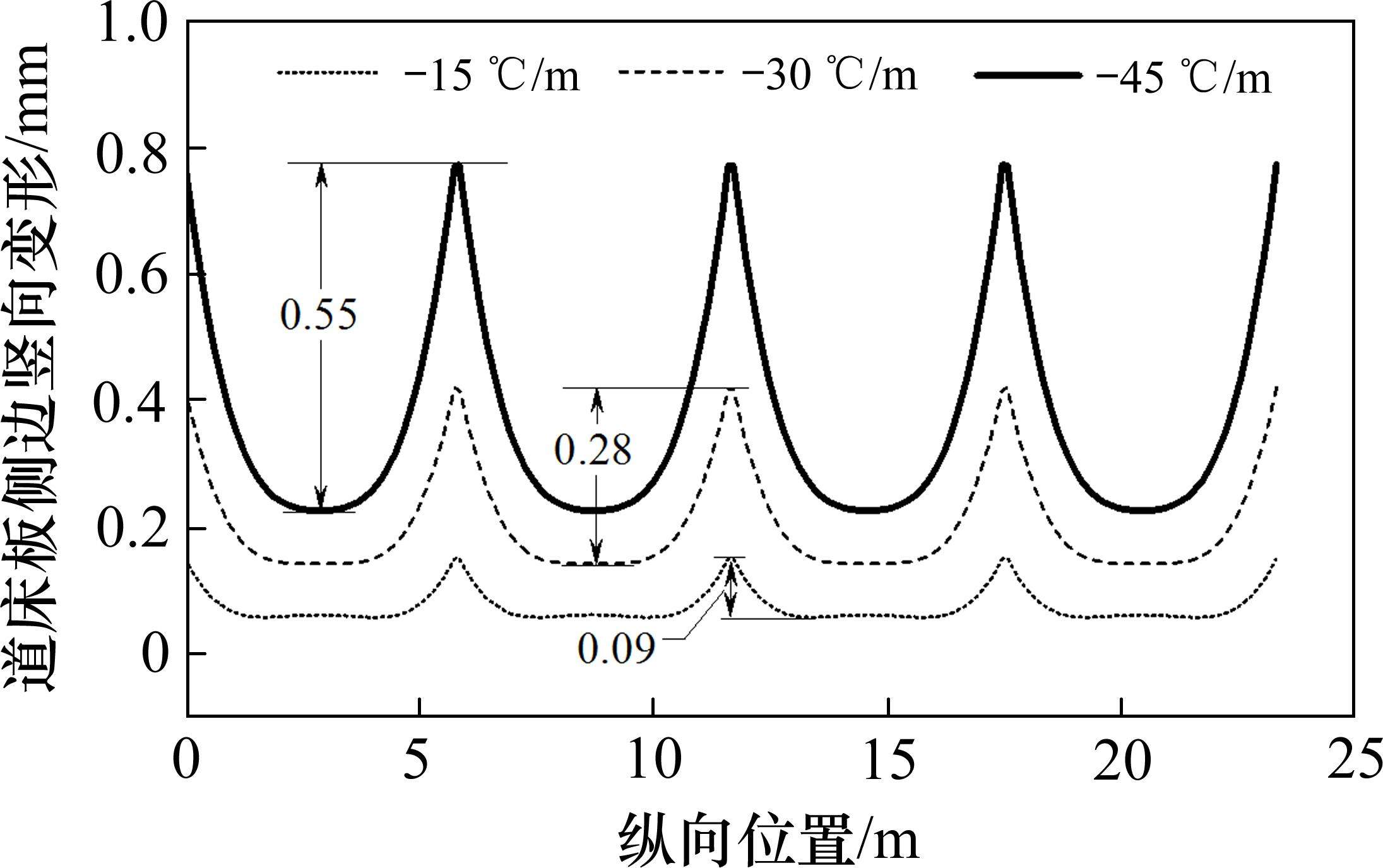
从图18中可以看出,钢轨和轨道板侧边位置处的竖向变形差呈抛物线型增长趋势。负温度梯度下钢轨与轨道板侧边处传递比计算如下所示。
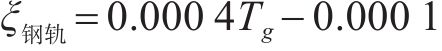
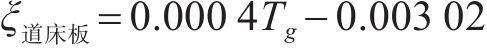
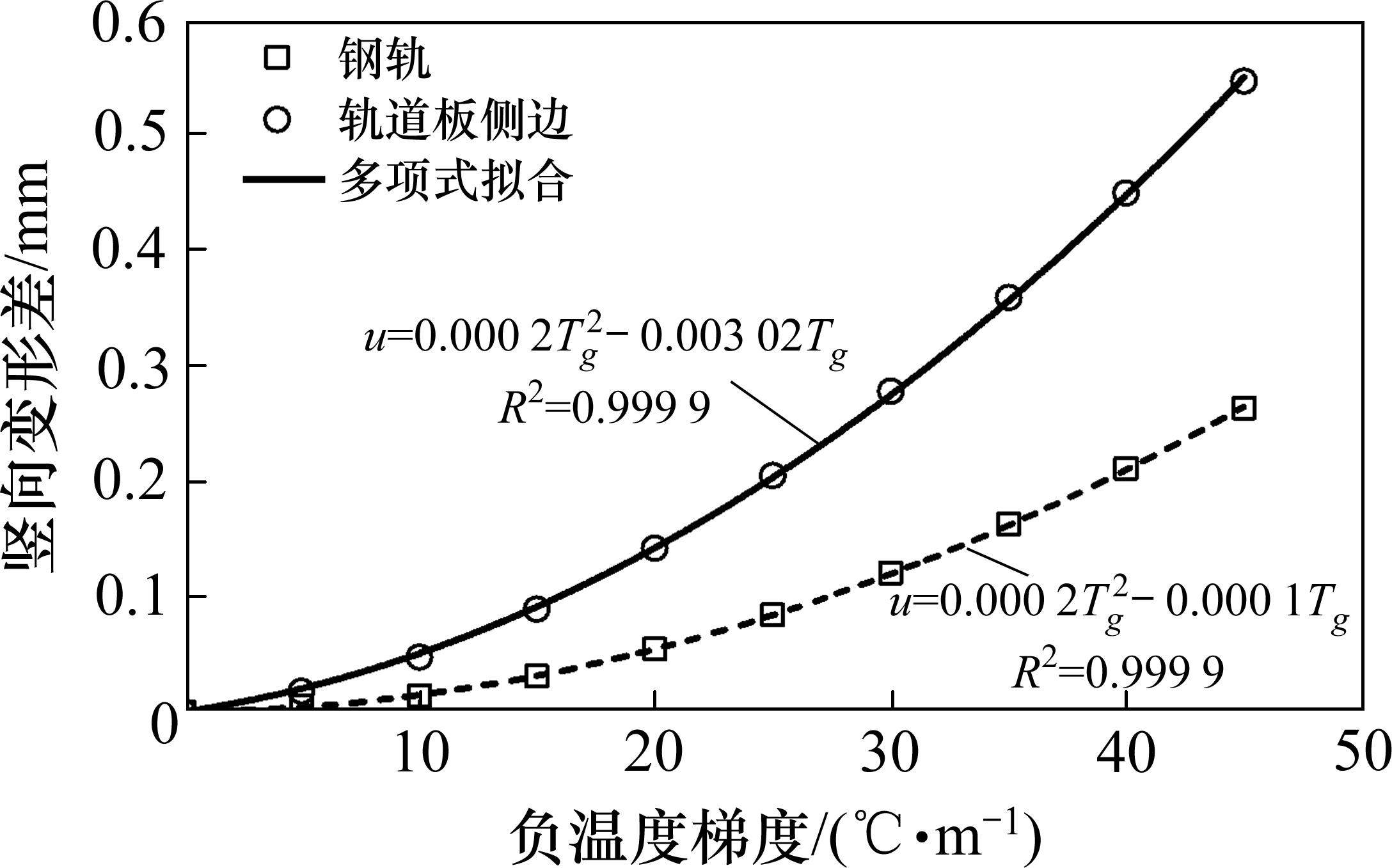
负温度梯度越大,ξ越大,当Tg=-45 ℃/m时,ξ钢轨=0.018 1 mm/(℃∙m-1),ξ轨道板=0.021 02 mm/(℃∙m-1)。与同量值正温度梯度相比,负温度梯度下传递比更大,钢轨传递比约为正温度梯度的2.9倍,道床板传递比约为正温度梯度的2.1倍。
4 结论
1) 试验结果表明,双块式无砟轨道温度场具有日周期性变化规律,道床板温度时变规律随深度增加存在显著的滞后现象;表层温度在每日6:00左右达到最低值,在每日14:00左右达到峰值,然而道床板中层温度极值均滞后表层1 h达到,深层则滞后2 h达到。
2) 双块式无砟轨道在距离道床板表面0.16 m深度范围温度变化活跃。夜间时段,各典型时刻道床板温度沿深度方向分布形式一致,温度随深度增加而逐渐升高,道床板呈负温度梯度;昼间时段,道床板温度随深度增加而降低,且降低速率随深度增加而减缓,道床板呈正温度梯度。
3) 受双块式无砟轨道温度场时变规律影响,道床板板角和板中竖向位移也具有日周期性变化规律。道床板角和板中竖向位移量与温度梯度值呈正相关关系,温度梯度值越大,竖向位移量越大。同时,温度梯度作用下,板角与板中竖向位移差异显著,道床板产生翘曲变形。现场测试结果表明,正温度梯度50 ℃/m作用下,板角/板中竖向位移分别为-0.47 mm/-0.15 mm,板中竖向位移量较板角少约68.1%;负温度梯度-33.33 ℃/m时,板角/板中竖向位移分别为0.64 mm/0.27 mm,板中竖向位移量较板角少约57.8%。
4) 仿真结果表明,正温度梯度作用下,钢轨与道床板会形成板中高、板端低的典型周期性变形趋势,最大90 ℃/m正温度梯度下,钢轨竖向变形差为0.58 mm,道床板侧边竖向变形差为1.01 mm;负温度梯度下,钢轨和道床板会形成板中低、板端高的典型周期性变形趋势,最大-45 ℃/m负温度梯度下,钢轨竖向变形差为0.26 mm,道床板侧边竖向变形差为0.55 mm。
5) 为减小运营期单元双块式无砟轨道周期性变形,应合理掌握轨道精调时机和方法。一方面,建设期应避免在道床板存在负温度梯度时进行轨道精调测量,另一方面在精调测量时可根据本文变形曲线合理预设初始不平顺,修正测量数据,以部分抵消运营期周期性不平顺。
赵磊,蒋典佑,施成.单元双块式无砟轨道翘曲变形特征的试验研究[J].铁道科学与工程学报,2024,21(10):4053-4064.
ZHAO Lei,JIANG Dianyou,SHI Cheng.Experimental study on warping deformation characteristics of unit bi-block ballastless track[J].Journal of Railway Science and Engineering,2024,21(10):4053-4064.

