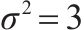薄膜电容器在列车变流系统直流环节中起到稳定电压、滤波、储能等关键作用。但是,由于受到温度、充放电频率、谐波等因素影响,薄膜电容器容易老化失效,进而影响变流系统安全[1-3]。因此,薄膜电容器状态监测对于保障列车安全运行显得尤为重要。目前,电容器的状态辨识受到国内外学者的广泛关注。注入小信号是一种侵入式的电容器状态辨识方法。AGARWAL等[4]向系统中注入不同奇次谐波频率的电流,评估各频率下的直流支撑电容器阻抗,并利用最小均方算法估计ESR与电容值。LI等[5]向直流电压中注入低频信号,采用滑动离散傅里叶变换进行电容估计。但是,这类方法可能会因注入电流或电压给电路带来潜在故障,不易于拓展到实际应用。LC谐振法也可以用于电容器状态辨识。XIANG等[6]基于直流电容开关环的阻尼特性,利用高频谐振等效电路建立了阻尼特性与ESR间的解析关系,使用半功率带宽算法估算ESR,该方法需加装非接触式高频电流传感器。LI等[7]在系统停止时引入LC谐振,采用大幅度信号测量和基于时间的多参数识别算法,来实现电容量辨识。当逆变器与直流支撑电容器断开时,电容量可以利用简化电路的纹波电压计算出来[8]。但是,这类方法通常需要获取高频电压或电流信号,对设备要求较高。物理建模是另一种常用的参数辨识方法。AHMAD等[9]提出了一种基于电气模型的在线非侵入技术,通过2个相邻过零点之间的电容电流和电压计算电容量。SUNDARARAJAN等[10]结合电气模型与Goertzel算法,引入自校准算法,同样可以得到准确的电容器参数辨识结果。RSNA算法也可以用于电容器参数辨识,但需要较高电压采样频率和较多迭代步数[11]。此外,赵洋等[12]通过系统辨识方法建立超级电容器模型,利用输出误差准则推导出非线性目标函数,应用粒子群优化算法模型求解该函数得到电容器参数的正确状态辨识。虽然文献[12]与本文皆使用了粒子群算法,但其所采用的电气模型只关注了电容器本身结构,而忽视了外部电路特点,故不适用于直流支撑电容器状态辨识。需要注意,对于同一元器件的不同特性往往可以建立多个模型,因此在运用中需要结合实际场景具体分析。信号处理方法也常用于电容器状态辨识。罗丹等[3]利用Haar小波变换重构开关序列来采集充电时段的电压变化时序,结合桥臂实测电流信号实现电容器容值在线反演计算。RIGAMONTI等[13]提出一种基于粒子滤波的预测模型,通过引入一种独立于温度变化的指标,可以避免温度影响,从而正确地对电容器电容量和ESR进行辨识。LAADJAL等[2]利用短时傅里叶变换技术,同样对电容器参数辨识取得了良好的效果。ZHAO等[14]提出了一种基于灰盒法的非侵入式暂态等效电路模型,选择变换器大信号瞬态轨迹的阻尼因子α(与电容有关)作为电容器健康的新指标,实现对直流电容的评估。XIAO等[15]选择基频(FF)电容电压平方的一半作为输入变量,选择功率积分计算出的FF电容能量作为反馈分量,通过合理设计估计律,可以在降低噪声干扰的情况下实现闭环电容监测。基于灰箱或黑箱的数据训练方法是一个热门的发展方向。AMARAL等[16]提出一种基于决策树回归量(DTR)的模型,使用短时间最小二乘法(STLSP)对DTR模型训练,以此估算电容值。WU等[17]在预充电模型的基础上使用三段迭代算法估算电容。此外,人工神经网络(ANN)算法[18-20]、自适应神经模糊推理系统(ANFIS)[21]、遗传算法[22]、物理信息神经网络[23]均被证实是可行的。然而,在铁路领域应用中,直流支撑电容器状态辨识仍有一些问题尚未得到很好解决。现有的状态辨识方法通常基于纹波分量的检测,但是这些纹波在有些情况下可能因噪声干扰过大无法测量。例如,地铁接触网直流电压达到1 500 V,此时电压传感器的噪声波动可能近似于纹波电压幅值。在这种情况下,为了获得精确的结果,就必须在电路中加装高精度的电压传感器,这又会增加铁路运营的成本。针对上述问题,本文提出基于预充电模型与改进粒子群算法的直流支撑电容器状态辨识方法。在不改变电路结构的前提下建立等效预充电模型,采集预充电过程的电压信号,利用改进粒子群算法在参数变化区间内搜索损失值最小的参数值,实现对电容值的辨识,进而避免了噪声的干扰。这种方法精度较高,计算量小,同时具有较好的抗干扰能力。
1 直流支撑电容器与建模
图1为某变流器中间直流环节拓扑结构。直流环节主要包括接触器开关K1与K2、测量电压u1(t)和u2(t)的电压传感器(精度为1%以内)、限流电阻R1、均压电阻R2、放电电阻R3以及直流支撑电容器C。
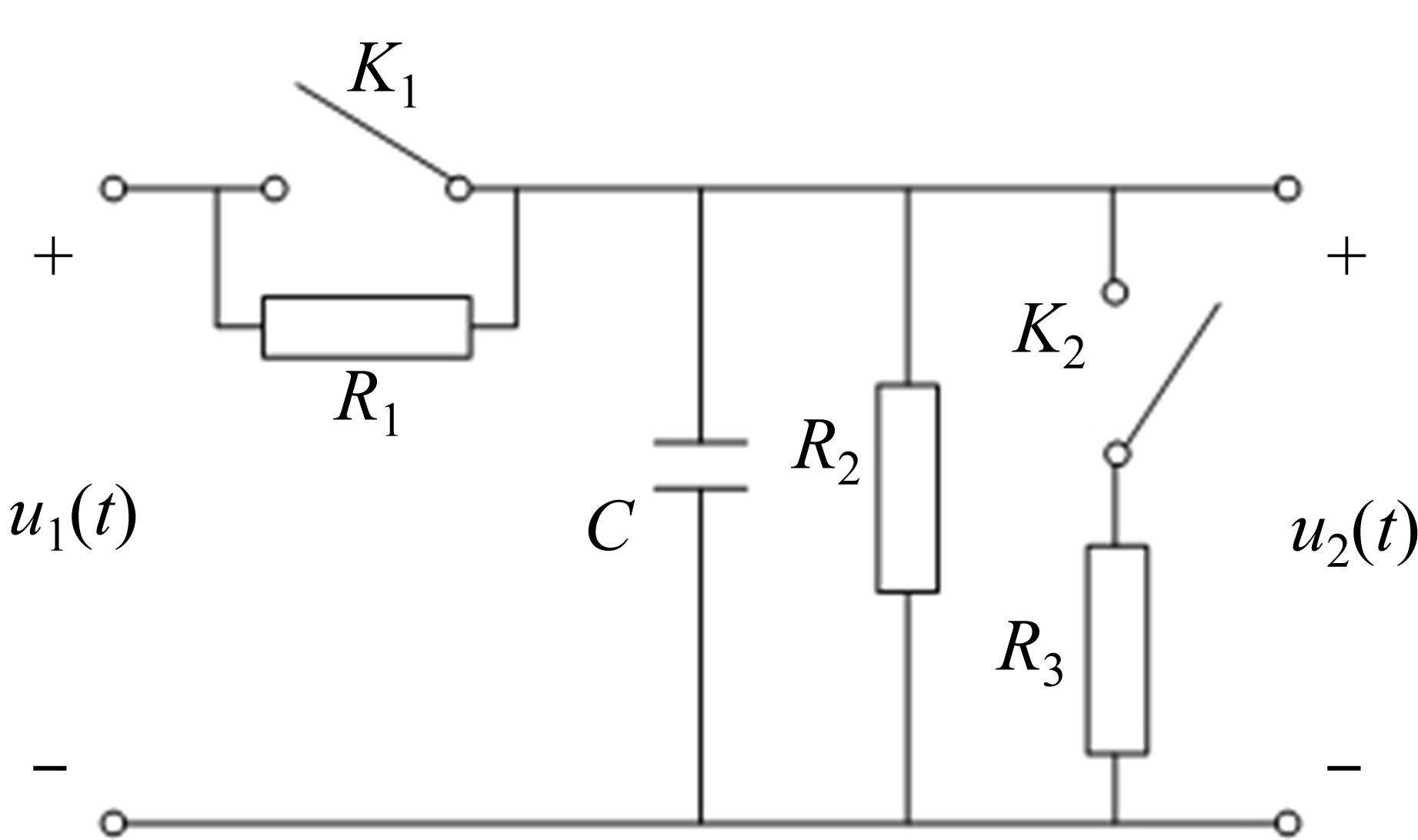
直流支撑电容器多采用金属薄膜电容器。该电容器在聚丙烯薄膜上蒸镀金属电极,并将薄膜卷绕在芯轴上,最后在芯轴两端喷金。在这样的制造工艺下,薄膜电容器元件的串联等效电阻(ESR)可分为接触电阻与金属电阻2部分,其中接触电阻主要由于金属层与喷金层的相互接触产生,其值取决于喷金的工艺水平,而金属电阻则主要为聚丙烯薄膜的金属层电阻,与蒸镀金属本身的材料性质有关。薄膜电容器的串联等效电阻大小即为接触电阻与金属电阻的代数和。为了简化电路,可以将薄膜电容器等效为理想电容与电阻的串联,如图2所示。
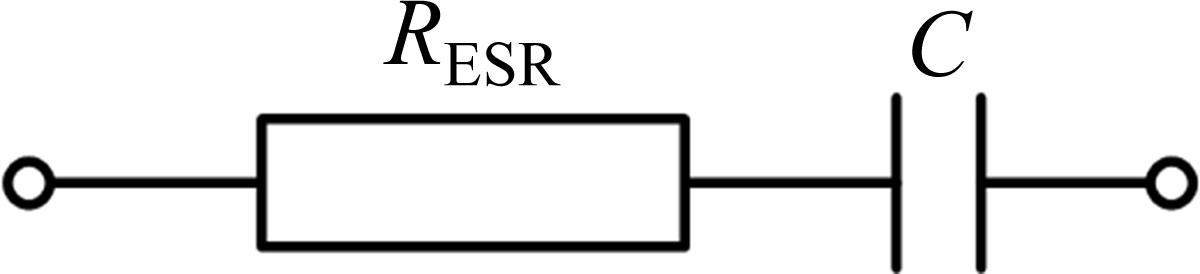
为了保护电路的安全,需要进行预充电。预充电过程中,接触器开关K1与K2均处于断开状态,限流电阻R1接入电路工作,放电电阻R3与直流环节断开。预充电过程在u1(t)和u2(t)差值小于50 V时结束,逆变器开始工作。整个预充电过程可以等效为图3所示电路,RESR为电容器的等效串联电阻。
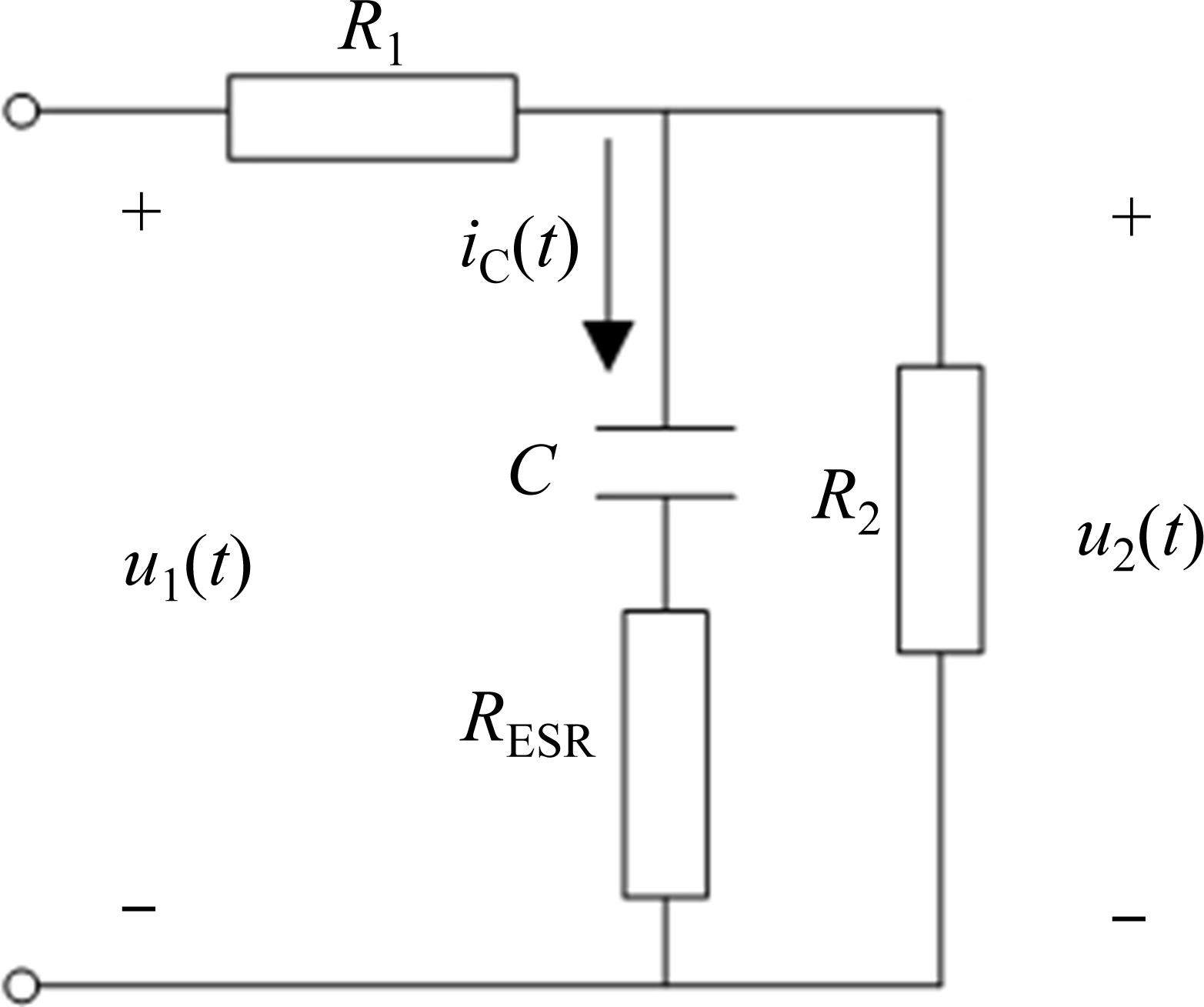
根据基尔霍夫定律,可得电容器电流:
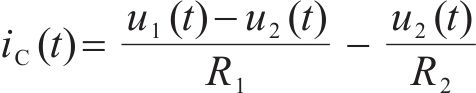
因此,在复频域分析中有
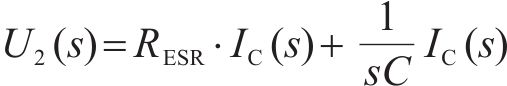
令采样周期为T,使用双线性变换
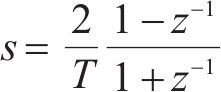
可以将式(2)转化为以下离散形式
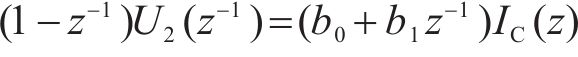
其中,
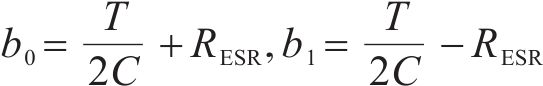
故通过对b0和b1的参数估计便可以间接求得电容C:
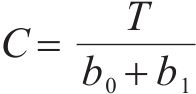
由于薄膜电容器的RESR非常小(毫欧级),一般不作为电容器寿命衡量的重要指标,因此本文只进行电容量的辨识。
2 基于粒子群算法的状态辨识方法
电容的状态辨识对参数计算的精度要求较高,而粒子群算法具有较强的随机性和全局探索能力,不容易陷入局部最优解,因而具有较高的准确性,适用于此类问题。因此,本文采集电容器在预充电模型过程中的电压数据,并使用递推平均滤波算法进行滤波,随后使用改进粒子群算法求得电容器电容的结果。
2.1 递推平均滤波
由于传感器存在噪声干扰,因此采集的电压信号是带有微小波动的非平滑信号。为了减小不平滑分量对实验结果所造成的影响,使用平均滤波递推算法进行滤波。将一系列连续的采样值按照一定的权重进行平均化处理,从而使信号变得更加平滑。将信号传感器采集到的信号记为数组X:
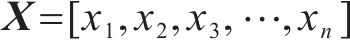
使用平均滤波法:
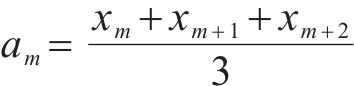
滤波得到数组A:
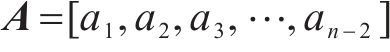
其中: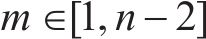
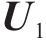
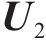
2.2 电容器容值辨识
对于电容值C的辨识采用改进的粒子群算法。粒子群算法的原理为通过模拟鸟类觅食行为估算最优解。每个离散粒子代表一只鸟,目标解代表食物点。粒子在随机搜寻目标解的过程中,受到自身速度、个体经验、群体经验的影响,进而通过有限次迭代找到限定范围内的最优解。本算法在粒子群算法的基础上改进了粒子迭代的系数,使其具有更强的全局搜索能力和更快的收敛速度。以下为算法实现具体过程。
随机生成n个粒子的初始位置x=(b0,b1),分别初始化每个粒子的速度v=(v0,v1),其中b0和b1为位置向量的2个参数,v0和v1为2个参数方向上的速度分量,如图4所示。
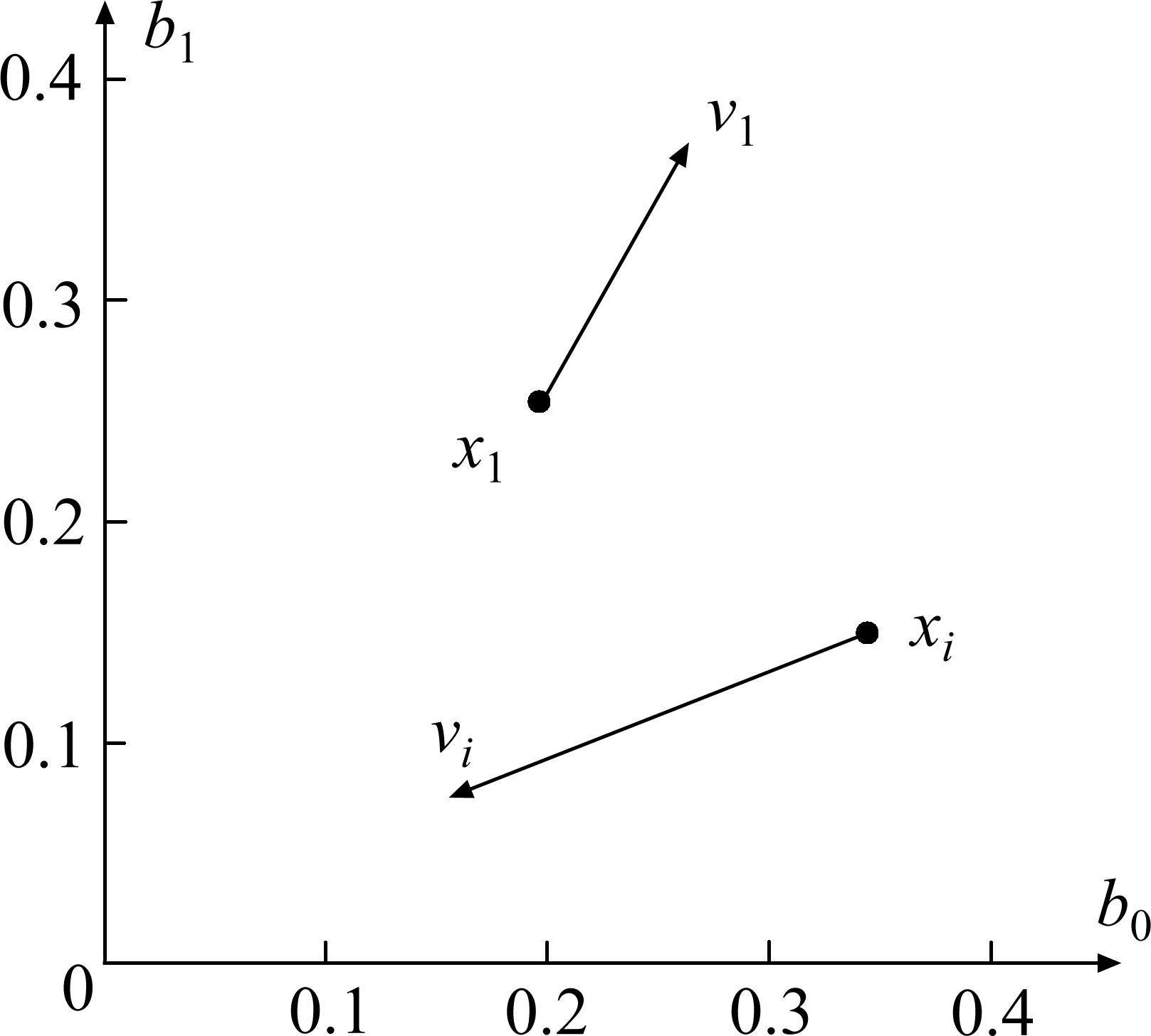
其中x1和v1分别表示第1个粒子初始的位置和速度,xi和vi分别表示第i个粒子初始的位置和速度。
接下来计算第i个粒子的损失值e(i)。根据式(4),有
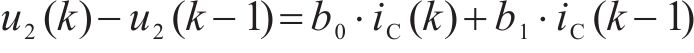
则损失函数可表示为
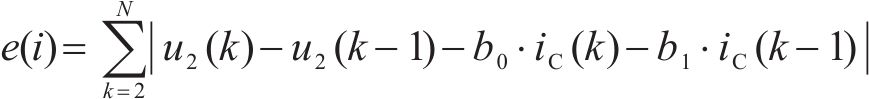
粒子的损失函数值越小,则表示粒子越接近最优解,称其位置越优。每次迭代分别计算每个粒子的损失值,记录历次迭代的群体最优位置和每个粒子的个体最优位置。
迭代过程中,粒子的速度更新公式和位置更新公式分别为
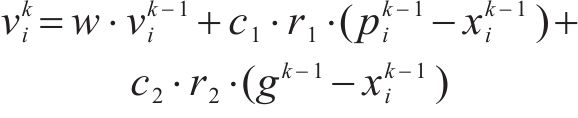
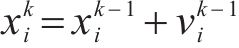
其中,w为惯性权重,表示粒子对自身速度的记忆;c1,c2为学习因子,分别表示粒子对自身经验和群体经验的学习;r1,r2为[0,1]内的随机数;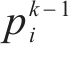
在普通粒子群算法中,惯性权重ω随迭代次数增加线性减少,而本算法采用非线性随机递增的惯性权重ω,并在其中引入混沌映射[24]。混沌Sine映射作为一种经典的混沌映射,具有良好的遍历性,在满足快速收敛的同时也保证了后期不错的全局搜索能力,减少在搜索中陷入局部最优解的可能。改进后的惯性权重ω表达式如下:
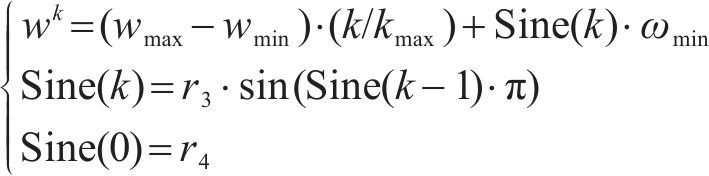
其中,ωmax和ωmin分别为惯性权重的上界和下界;k和kmax分别为当前迭代次数和最大迭代次数;r3,r4为[0,1]内的随机数。
对于学习因子c1和c2,当c1较大、c2较小时,算法具有较强的全局搜索能力,反之则具有较强的局部搜索能力。为了加强算法前期的局部搜索能力和后期的全局搜索能力,降低陷入局部最优解的概率,引入正余弦函数构造非线性异步学习因子[25]:
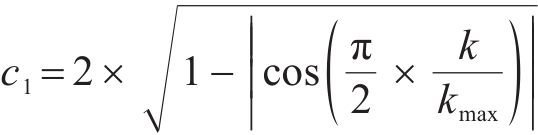
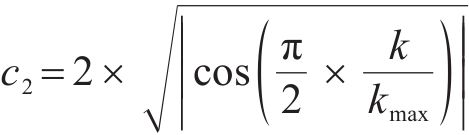
按上述方法进行多次迭代之后通过式(6)得到最终电容C。
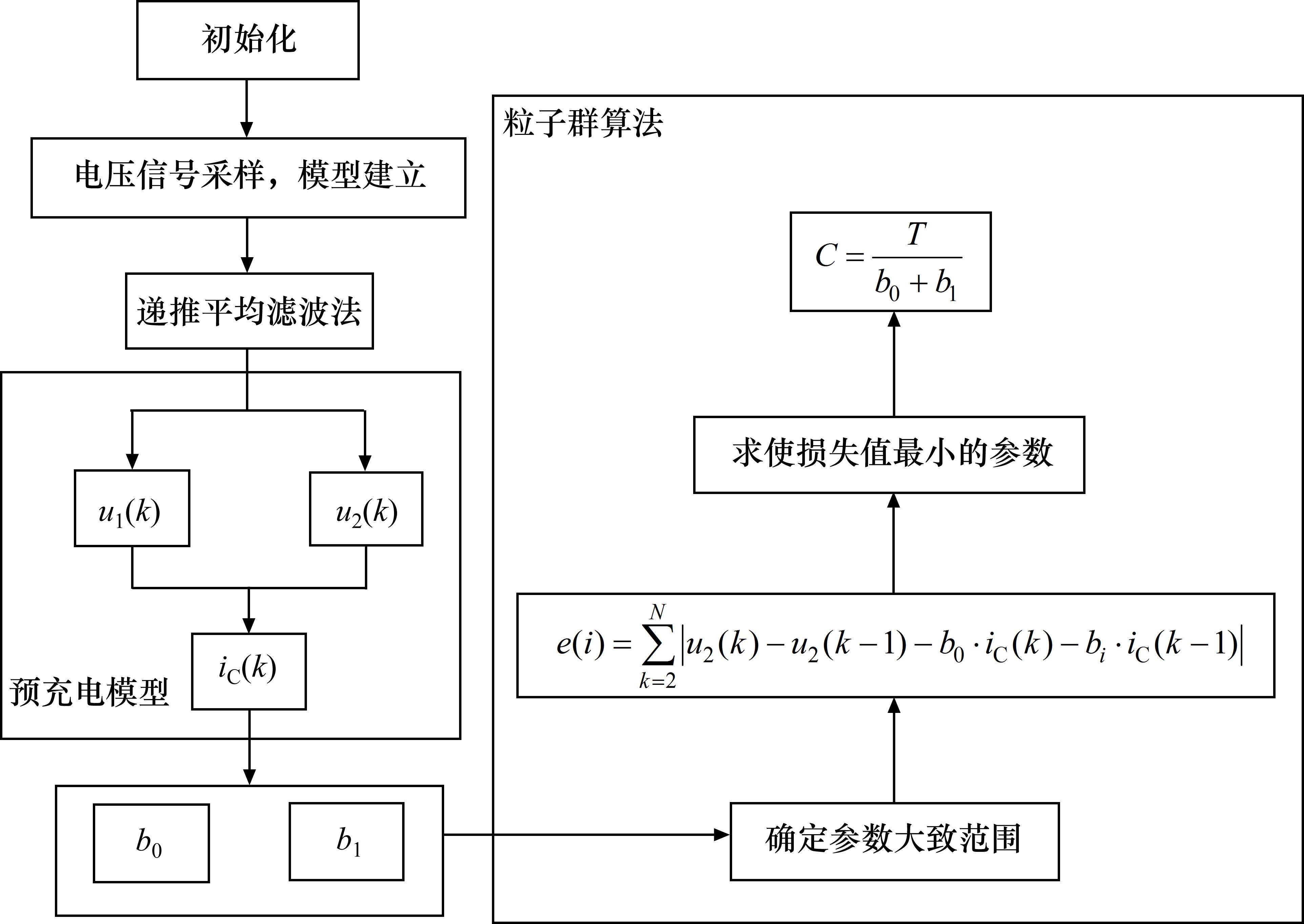
直流支撑电容器状态辨识流程如图5所示。
3 方法验证
3.1 有效性分析
通过Matlab/Simulink平台构造图3所示直流预充电模型仿真电路,在此仿真电路的基础上进行实验,采样出u1和u2的数据,并导入到Matlab工作区进行计算。为了模拟现实场景中的噪声对于电压测量的影响,在电压源、电压传感器中均添加了方差σ2=0.5的有限带宽的白噪音模型。
分别采用表1给出的参数进行2组仿真实验。为了在模拟实际情况的基础上分析电压采样频率对辨识有效性的影响,选取电压u1、u2的采样频率分别为10、20、50和100 Hz。粒子个数为100,迭代步数为100步,粒子搜索范围为(0,20)。每组分别重复实验4次,得到的结果如表2和表3所示。
| 参数 | A组值 | B组值 |
|---|---|---|
| u1/V | 1 500 | 600 |
| R1/Ω | 230 | 200 |
| R2/kΩ | 10 | 66 |
| C/mF | 6.8 | 6.8 |
| 采样频率/Hz | 序号 | b0 | b1 | 损失值 | C/mF | 误差/% |
|---|---|---|---|---|---|---|
| 100 | 1 | 0.000 17 | 2.322 19 | 216.96 | 4.306 | 0.14 |
| 2 | 1.668 89 | 0.660 90 | 218.22 | 4.292 | 0.18 | |
| 3 | 0.812 00 | 1.512 83 | 217.56 | 4.301 | 0.03 | |
| 4 | 0.000 01 | 2.322 35 | 216.96 | 4.306 | 0.14 | |
| 50 | 1 | 0.853 92 | 3.773 84 | 104.55 | 4.322 | 0.51 |
| 2 | 3.648 19 | 1.037 17 | 106.18 | 4.269 | 0.73 | |
| 3 | 0.163 33 | 4.448 61 | 104.19 | 4.337 | 0.85 | |
| 4 | 3.280 94 | 1.396 18 | 105.96 | 4.276 | 0.56 | |
| 20 | 1 | 2.105 22 | 9.322 51 | 43.29 | 4.375 | 1.75 |
| 2 | 4.783 78 | 6.779 99 | 43.77 | 4.324 | 0.55 | |
| 3 | 2.753 63 | 8.708 95 | 43.41 | 4.362 | 1.44 | |
| 4 | 3.923 34 | 7.600 87 | 43.64 | 4.339 | 0.90 | |
| 10 | 1 | 7.434 03 | 15.436 11 | 17.77 | 4.373 | 1.69 |
| 2 | 11.338 93 | 11.899 33 | 18.10 | 4.303 | 0.08 | |
| 3 | 6.883 21 | 15.930 94 | 17.75 | 4.383 | 1.94 | |
| 4 | 16.073 16 | 7.641 29 | 18.30 | 4.217 | 1.93 |
| 采样频率/Hz | 序号 | b0 | b1 | 损失值 | C/mF | 误差/% |
|---|---|---|---|---|---|---|
| 100 | 1 | 0.000 01 | 1.452 99 | 180.14 | 6.882 | 1.21 |
| 2 | 0.000 10 | 1.452 87 | 180.14 | 6.882 | 1.21 | |
| 3 | 0.096 03 | 1.357 97 | 180.21 | 6.878 | 1.14 | |
| 4 | 0.873 43 | 0.591 67 | 180.80 | 6.825 | 0.37 | |
| 50 | 1 | 0.436 10 | 2.485 78 | 85.22 | 6.845 | 0.66 |
| 2 | 0.220 74 | 2.698 18 | 85.10 | 6.852 | 0.76 | |
| 3 | 0.222 20 | 2.697 77 | 85.10 | 6.849 | 0.73 | |
| 4 | 2.075 22 | 0.871 20 | 86.19 | 6.788 | 0.18 | |
| 20 | 1 | 2.936 04 | 4.339 37 | 31.29 | 6.872 | 1.07 |
| 2 | 3.457 47 | 3.835 81 | 31.37 | 6.856 | 0.82 | |
| 3 | 2.579 32 | 4.685 49 | 31.23 | 6.882 | 1.21 | |
| 4 | 0.000 00 | 7.169 35 | 30.86 | 6.974 | 2.56 | |
| 10 | 1 | 5.019 68 | 9.532 03 | 13.78 | 6.872 | 1.06 |
| 2 | 2.602 81 | 11.781 96 | 13.69 | 6.952 | 2.23 | |
| 3 | 3.778 90 | 10.687 59 | 13.73 | 6.913 | 1.65 | |
| 4 | 2.181 46 | 12.174 05 | 13.67 | 6.966 | 2.44 |
由表2和表3可知,对于A组参数,电压采样频率在100 Hz和50 Hz时,辨识结果的误差可以在100步以内稳定于1%以内。当采样频率减小到20 Hz和10 Hz时,误差略有上升,但仍稳定在2%以内。该结果说明电压采样频率对辨识准确性有一定影响,但采样频率相差不大时,其影响可忽略。B组参数辨识结果与A组相似,在不同的电压采样频率下,辨识误差的最大值为2.65%,较为精确。因此,该算法适用于较低电压采样频率的电容量测量。
3.2 收敛性分析
绘制以上实验迭代过程中损失函数值随迭代次数变化的图像,如图6所示。相同条件下的重复实验绘制在同一图像中,图例中的实验1至实验4分别对应表2和表3中序号1至4的实验。
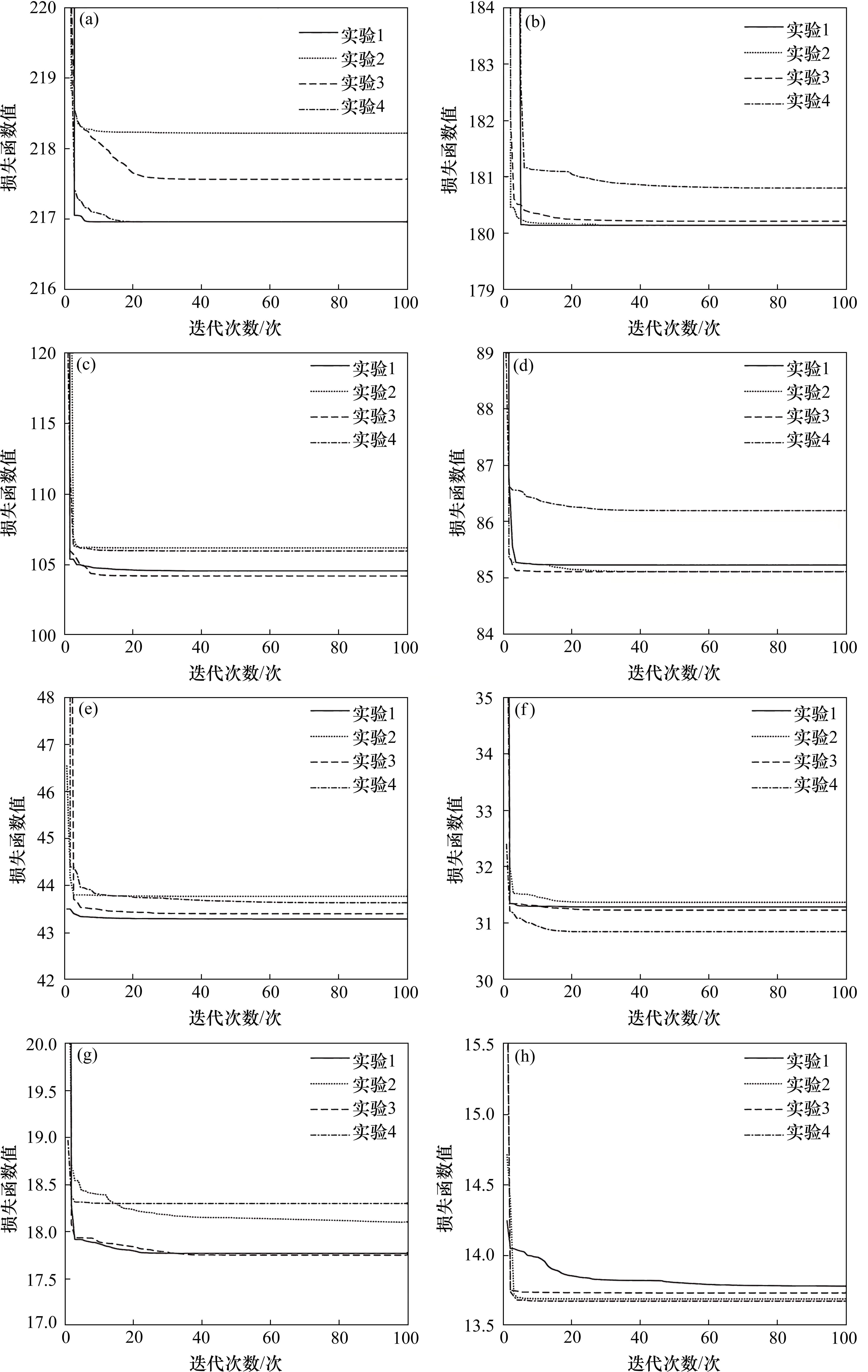
由图6可知,粒子群算法计算过程中,损失函数值随迭代次数先迅速下降,后基本保持不变,表示该算法找到使损失值最小的目标解。由于噪声的影响,迭代完成时损失值不能减少到0,而是稳定在一个非零值附近。由此可知,在电容器状态辨识场景下粒子群算法具有较快的收敛速度。
3.3 抗噪性分析
为了验证算法的抗噪能力,在Simulink仿真平台中加入方差σ2=2、σ2=3的高斯噪声,分别进行仿真实验。针对每个采样频率和噪声方差,分别选取连续5次实验的相对误差记录在表4中。
| 序号 | 10 Hz | 20 Hz | 50 Hz | 100 Hz | ||||
|---|---|---|---|---|---|---|---|---|
| σ2=2 | σ2=3 | σ2=2 | σ2=3 | σ2=2 | σ2=3 | σ2=2 | σ2=3 | |
| 1 | 4.70% | 2.12% | 2.36% | 2.43% | 0.95% | 1.15% | 0.96% | 0.41% |
| 2 | 0.84% | 4.97% | 2.38% | 2.43% | 0.41% | 0.88% | 0.10% | 0.91% |
| 3 | 1.03% | 0.73% | 2.58% | 2.72% | 0.48% | 1.68% | 0.93% | 1.08% |
| 4 | 4.30% | 3.69% | 2.45% | 2.48% | 0.60% | 0.52% | 0.13% | 0.40% |
| 5 | 1.37% | 2.64% | 2.40% | 2.49% | 1.09% | 0.87% | 0.22% | 0.73% |
根据表4可知,整体来看电容辨识误差随噪声方差增大而增大。当电压采样频率为100 Hz和50 Hz时,辨识误差为1%左右;当电压采样频率减小到20 Hz时,误差少于3%;当电压采样频率为10 Hz时,辨识略微增加,但仍误差少于5%。说明该算法在频率较低的情况下仍然有较好的抗干扰能力。
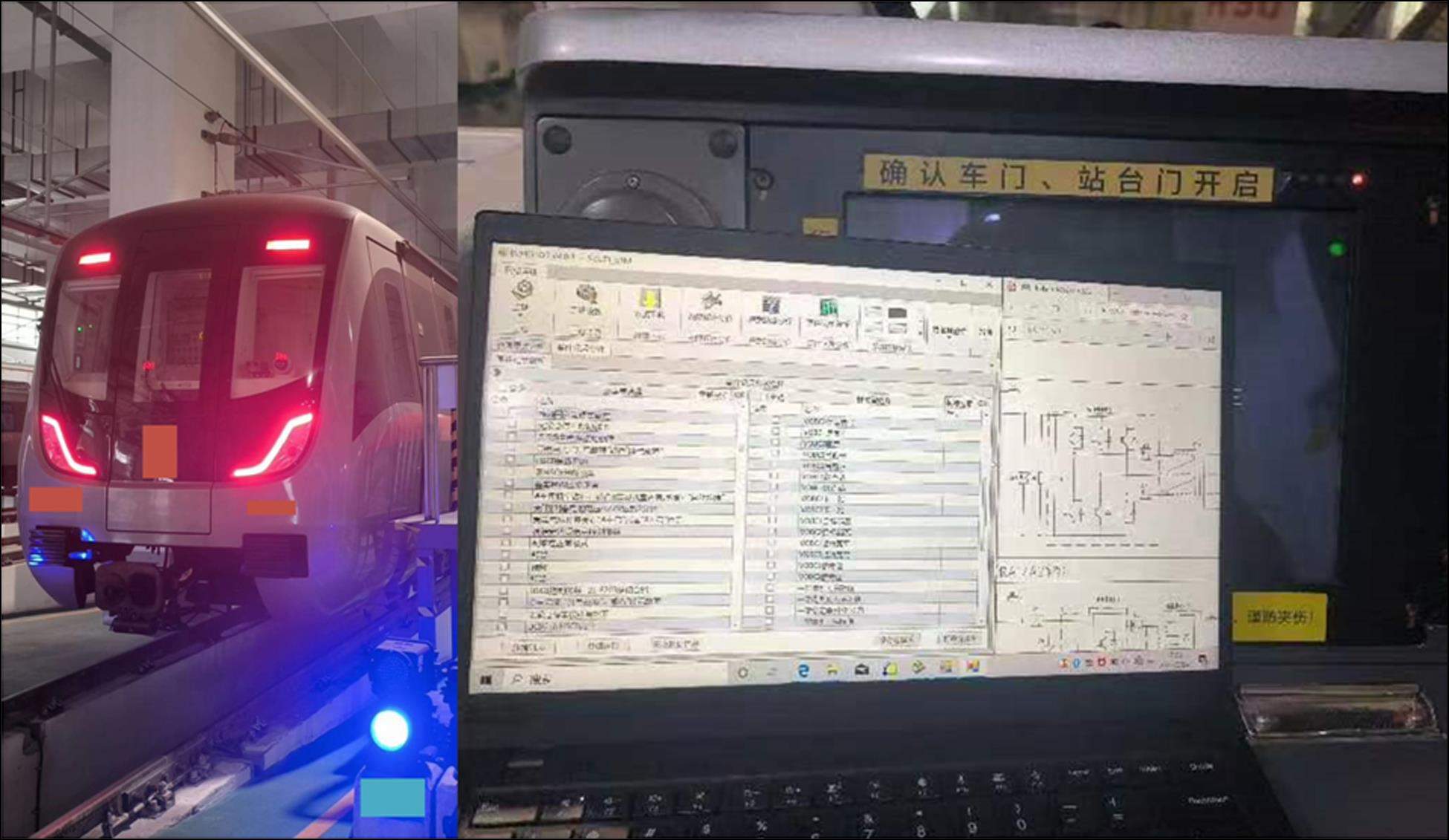
3.4 实车验证
为了验证本文提出算法的有效性,进行了实车验证。测试平台如图7所示,在变流器预充电过程中,监测u1和u2的电压变化并采样,采样间隔为100 ms。根据预充电测量数据对方法进行验证,主要参数如表5所示。
| 参数 | 值 |
|---|---|
| 电阻R1/Ω | 230 |
| 电阻R2/kΩ | 10 |
| 待辨识电容C/mF | 4.258 |
| 电压采样频率/Hz | 10 |
对于3组数据,分别重复进行2次实验,在表6中记录其辨识结果。
| 数据 | 序号 | b0 | b1 | 损失值 | C/mF | 误差/% |
|---|---|---|---|---|---|---|
| 第1组 | 1 | 3.740 58 | 19.365 46 | 198.14 | 4.328 | 1.64 |
| 2 | 8.512 14 | 15.077 55 | 202.06 | 4.239 | 0.44 | |
| 第2组 | 1 | 8.056 02 | 15.512 13 | 160.18 | 4.243 | 0.35 |
| 2 | 6.485 02 | 16.923 85 | 159.26 | 4.272 | 0.33 | |
| 第3组 | 1 | 9.630 51 | 14.034 50 | 239.24 | 4.226 | 0.76 |
| 2 | 12.292 96 | 11.623 51 | 241.69 | 4.181 | 1.80 |
绘制以上辨识过程的损失函数值随迭代次数变化的图像,如图8所示,实验1和实验2分别对应表6中序号1和序号2。
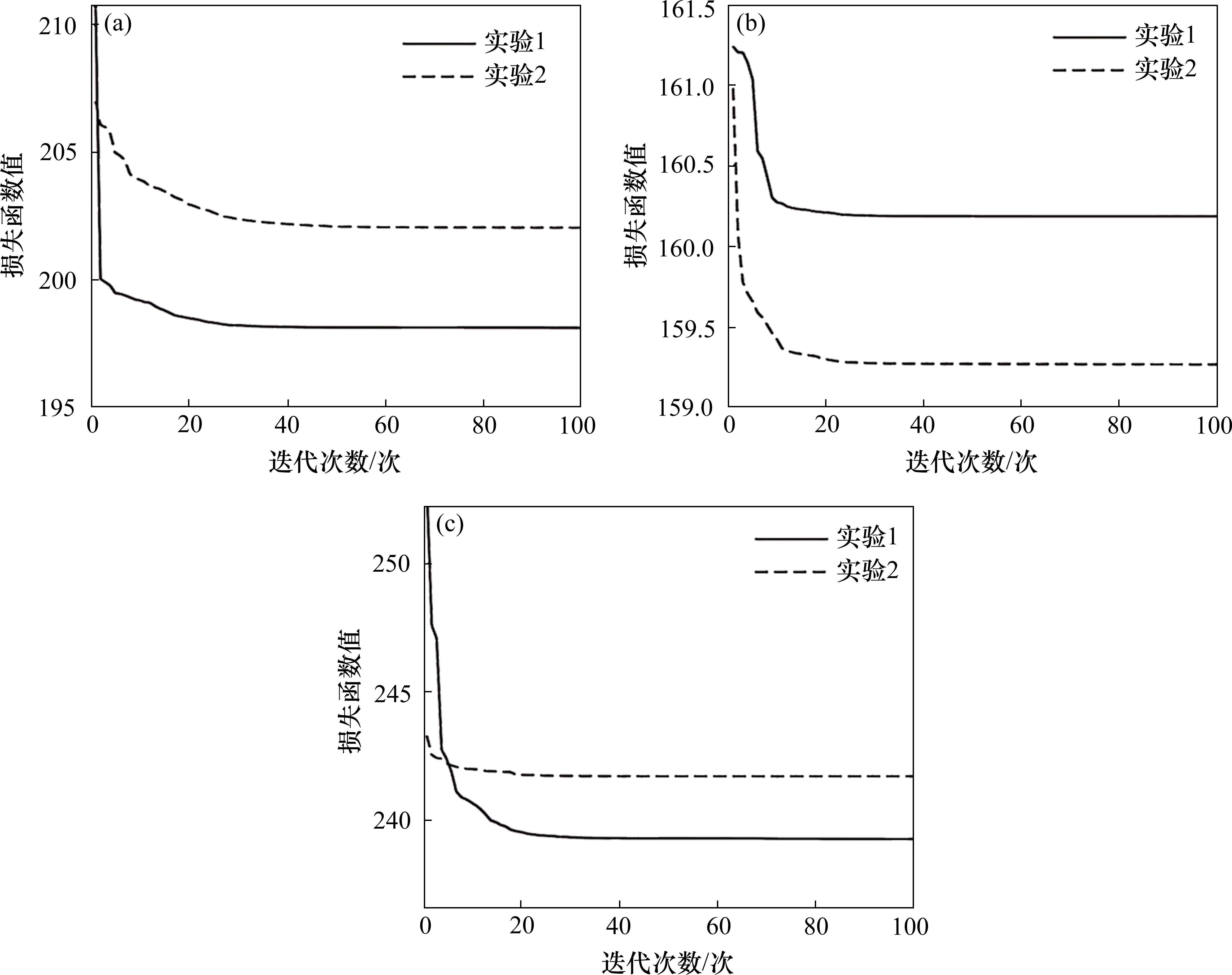
3组数据的验证均显示,结果在进行100步迭代后,电容值稳定在4.258 mF左右,且误差少于1.8%,实车验证与仿真结果一致。说明该方法具有较好的准确性和收敛性,在实际应用中可以抵抗噪声的干扰,有良好的鲁棒性。因此,认为本文提出的方法适合在较低频率下应用于实车直流支撑电容器状态辨识。
3.5 与现有方法的对比
将本文所提方法与现有电容器状态辨识方法进行对比,见表7。基于注入电流的电容器辨识方法[5]精度较低,并且可能因向电路中注入电流引起潜在故障,不易应用于实践。基于纹波的辨识方法[8]需要对电压纹波进行高精度与高频率监测,而在地铁场景中,传感器的噪声波动近似于纹波电压幅值,因此该方法同样难以应用。基于物理神经网络的辨识方法[23]辨识精度较高,但具有收敛速度慢、需要特定的训练集的缺点,对计算机运算能力要求较高。与上述方法对比,文献[11]的方法和本文所提方法不改变系统原有结构,避免了噪声对纹波检测的影响,同时原理更为简单,有效解决了上述问题。同时,本文所提方法在文献[11]方法的基础上具有更高的辨识精度、更快的收敛速度和更低的信号采样频率,因此更适用于铁路领域的直流支撑电容器状态辨识。
4 结论
1) 针对直流支撑电容器状态辨识易受噪声干扰的问题,提出一种基于预充电模型与改进粒子群算法的辨识方法。该方法以预充电过程中的电压为检测量,建立电容器状态辨识模型,并利用改进粒子群算法对电容量进行计算,可以有效降低噪声对测量的干扰,实现对电容器状态的正确辨识。
2) 验证结果表明,该方法对不同电压采样频率下的电容值辨识具有较高的辨识精度,辨识误差少于3%。并且其具有良好的抗噪能力,噪声方差σ2=3时,辨识误差少于5%。使用实车数据验证误差少于1.8%。
3) 与现有的方法相比,该方法原理简单,计算量小,避免了噪声对纹波电压的干扰,并且在恶劣工况下有较好的抗干扰能力。
Capacitance estimation algorithm for condition monitoring of electrolytic DC-link capacitors using artificial neural network in front-end diode rectifier three-phase motor drive systems
[C]//基于物理信息神经网络的牵引变流器直流支撑电容参数辨识方法
[J/OL]. 电工技术学报: 1-15[基于混沌映射和高斯扰动的改进粒子群算法MPPT控制策略研究
[J/OL]. 电源学报: 1-13[孙潞,吴宜霖,伍珣.基于预充电模型与改进粒子群算法的直流支撑电容器参数辨识方法[J].铁道科学与工程学报,2025,22(03):1243-1253.
SUN Lu,WU Yilin,WU Xun.Capacitance estimation method for DC-link capacitors based on pre-charging model and improved PSO algorithm[J].Journal of Railway Science and Engineering,2025,22(03):1243-1253.