金属化薄膜电容器是轨道交通动车组牵引变流系统中重要元件之一,而在牵引变流器的故障之中,电容器故障占到所有变流器故障的30%以上,因此对电容的剩余寿命预测对动车组的安全运行至关重要[1]。电容的退化形式包括自愈,热降解,金属层氧化等,其中电容的主要损伤模式为电容自愈,其造成的电极损伤可占到总损伤的80%[2],而热降解主要出现在高温条件下,金属层氧化则主要出现在高温高湿或者交流电压条件下,这与实际应用工况不符。当电容内部绝缘介质发生击穿时,其产生的能量会蒸发附近金属层,从而恢复绝缘,这一过程叫做自愈。这种自愈行为是一种有损伤的自我修复过程,它会导致金属层的有效面积不断降低,从而使得电容量下降,当电容容量下降5%时,通常认为电容寿命达到终结。因此,对电容的自愈行为的分析,建立相应的损伤机理模型显得十分重要。目前针对电容自愈的研究主要是通过模拟自愈来探究压力[3-4]、方阻[5]、含氢量[6]、温度[7]和化学成分[8]等对电容自愈性能的影响。对于电容自愈的研究多作为电容薄膜性能评判,利用电容自愈性能对电容退化进行估计的研究较少。LIU等[9]通过声电混合的方式定性分析了电容在脉冲电压下自愈频率随着老化逐渐增加的趋势。ZHU等[10]发现电容寿命接近尽头时,自愈波形可能会出现失真,且自愈频率和幅度都会增加。李志元等[11]采用图像识别统计电容自愈点数的方式对直流电压下电容的寿命进行预测,于成龙等[12]基于分析电容自愈性能与内部空间畸变机理,对电容在脉冲电压下的寿命预测公式进行了修正。但是这些研究未能定量地利用自愈参数对电容的寿命进行很好的预测,或者需要拆解后才能对寿命进行预测,实用性较差。本文构建了一套适用于薄膜电容容值退化评估理论,对自愈中的能量与频次参数进行分析,建立自愈能量的分布模型以及自愈发生次数和时间的关系,并构建自愈参数与电容退化之间的模型,最终提出一套基于自愈性能的电容寿命预测方法。
1 电容自愈机理分析
电容的生产过程之中,薄膜内部不可避免地存在空气隙、缺陷杂质、物理缺陷和结晶形态等杂质,同时,在电容使用过程之中,电介质也会不可避免地产生缺陷,这些先天或者后天的缺陷一般统称为电弱点。在电容受到外界电场的作用时,会使得电弱点处产生累积的空间电荷,从而导致内部电场发生畸变。而绝缘材料的这些电弱点处的击穿场强会远低于周围地区,因此会在畸变电场和外部电场共同作用下电弱点会发生击穿,导致两边电极相互接触,形成一条放电通道,电容出现绝缘失效。电荷通过绝缘通道形成大电流并产生焦耳热,由于附近金属层比较薄,金属电极会在焦耳热的影响下受热蒸发并向外扩散,金属蒸汽被电离成等离子体。随着蒸发面积的扩散,其绝缘失效的面积越来越少,直至放电电弧熄灭,电容器恢复绝缘,其过程如图1所示,这一过程叫做自愈。由于放电自愈过程中产生的焦耳热和电弧,缺陷周围的介质和介质表面的绝缘隔离区不可避免地受到热损伤和电损伤,从而发生化学分解、气化和碳化,甚至发生机械损伤。因此,自愈会使得电容薄膜的有效面积减少,从而降低容量,直至寿命终结。在自愈的过程之中,自愈的能量影响单次自愈蒸发金属层区域的面积,而自愈的次数会影响蒸发的金属层区域数量,均会影响电容的容值及其他特征参数。因此,自愈与电容寿命的状态息息相关,通过对自愈现象的观察,有望实现电容状态的识别。
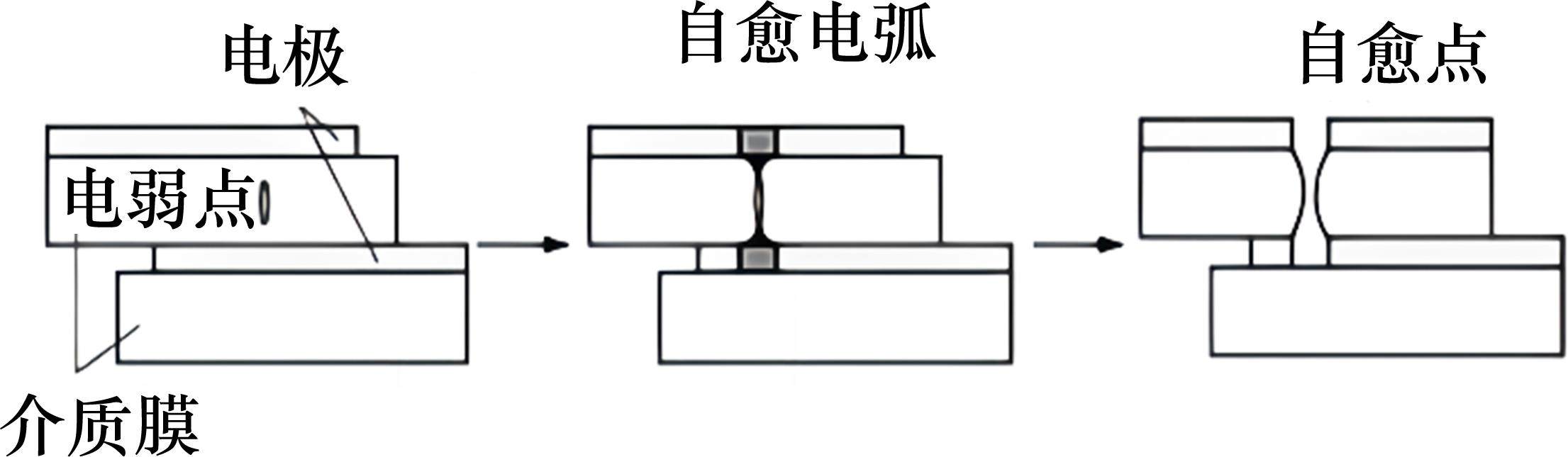
由于车载薄膜电容主要工作在脉冲电压作用下,除了因为电压过高而导致电弱点的击穿而发生自愈外,因为电压快速上升或者下降也会造成介质膜内局部放电,从而产生自愈。在脉冲放电过程之中,自愈损伤主要发生在工作电压阶段,在充电阶段的自愈损伤较少[10],其自愈损伤主要跟工作电压下的工作时间有关,因此,为了简化模型,本文采用直流电压的加载方式对电容寿命进行分析。
2 电容自愈现象分析及寿命建模
2.1 基于霍尔特指数平滑法的电容计数过程拟合
由于在老化的过程中,电容的自愈次数会随着老化的进行而逐渐增加,具有指数增长的趋势,为了合理地对自愈退化过程进行评估,需要针对给定时间序列的历史数据拟合出一条满足曲线增长趋势的方法,这里选用霍尔特指数平滑法对增长趋势进行分析。霍尔特指数平滑法主要有加性方程和乘性方程2种,这里选用乘法模型进行预测。其预测方程表示为[13]
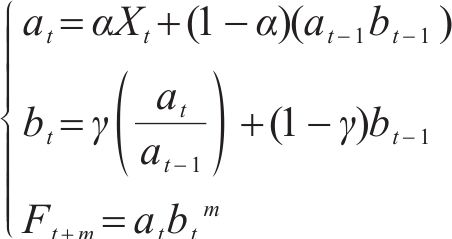
其中,Ft+m为第t+m个小时的自愈累积次数预测值;m为预测的时长;at为第t个区间的平滑值;bt为第t个区间的增长率;Xt为第t个区间的实际自愈累积次数;ɑ,γ为平滑相关参数。使用霍尔特趋势预测法的基本步骤如下。
1) 确定初始值a0,b0,这里取a0为第1小时内的自愈次数,b0为0;
2) 确定参数ɑ,γ的初值,这里假定初始“水平部分”为第1个实际需求值,初始“趋势部分”为第2个实际需求值减去或者除以第1个实际需求值;
3) 根据初始值和霍尔特指数平滑参数取值,计算第t个时间段内的平滑值St和趋势值bt。
通过霍尔特趋势预测法,对过去时间段的累积自愈次数曲线的趋势进行分析,并利用过去时间段的趋势对未来时间内的累积自愈次数进行预测。
2.2 电容计数拟合过程中的参数估计
霍尔特指数平滑系数是霍尔特指数平滑法的重要参数,其估计结果决定了预测结果的准确性,这里选择使用改进的粒子群算法(improved particle swarm optimization,IPSO)来进行估计,该方法相较于经典的线性递减权重优化和固定权重能够更加准确地求出最优平滑系数[14]。其更新公式可表示为
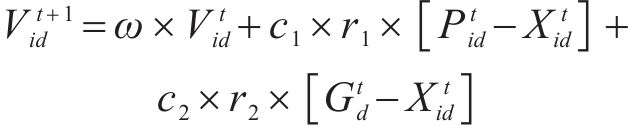
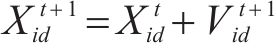
式中:X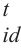
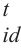
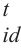
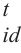
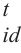
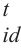
在传统的粒子群算法之中,一般采用固定权重的方法来寻求最优解,为了提高粒子群的搜寻能力,这里采用非线性变化权重对粒子群算法进行优化,其权重w的优化公式为
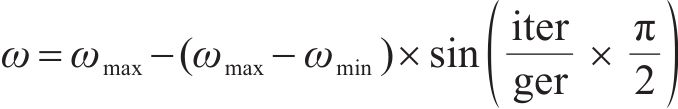
参数估计的过程如图2所示,根据霍尔特指数平滑法预测各个小时的自愈频次,计算粒子适应度,要求预测结果的平均相对误差的绝对值最小,因此适应度函数表示为
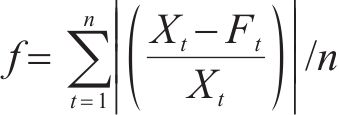
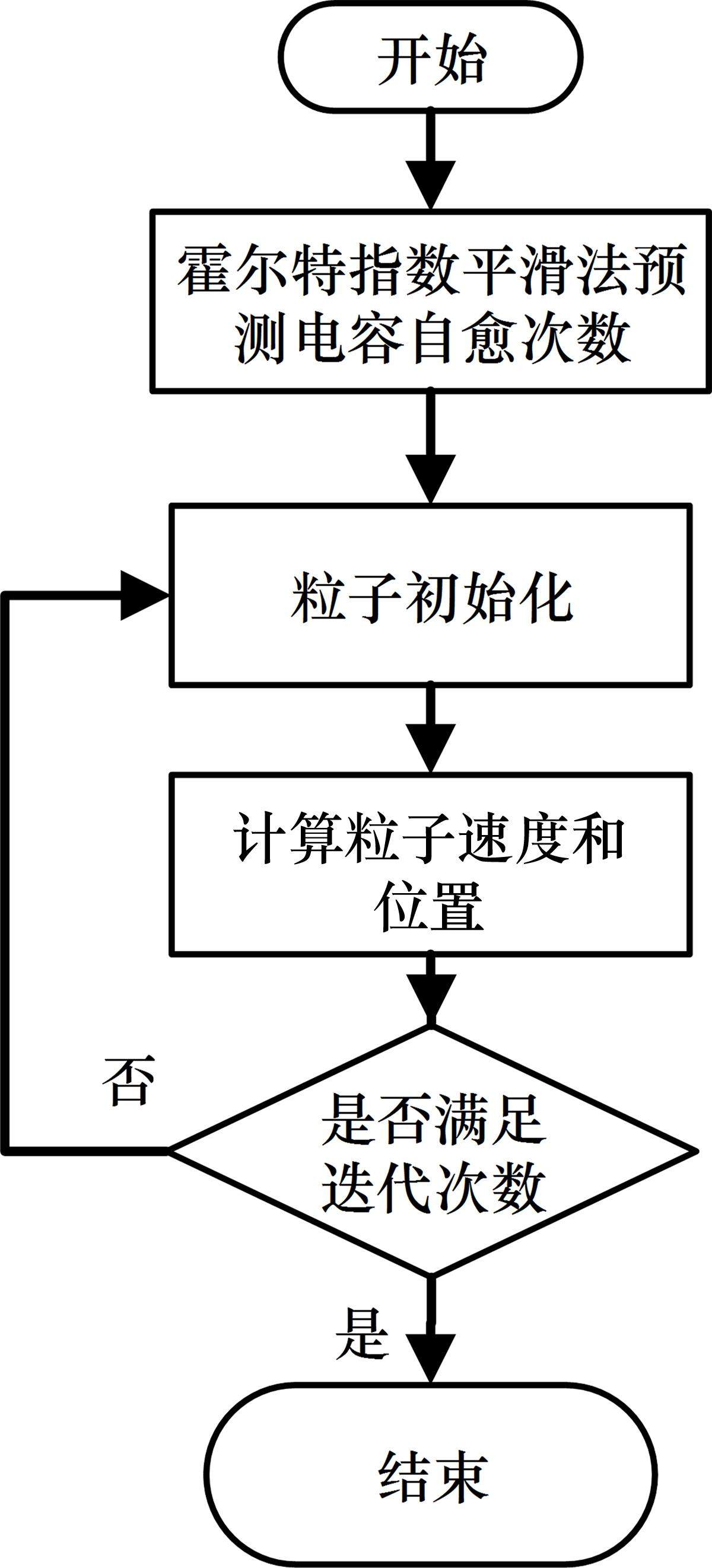
并将计算的粒子适应度进行比较以寻找当前最优粒子适应度及其位置,判断是否满足迭代结束条件,若满足则算法结束。通过优化粒子群算法,能够较为准确地对霍尔特参数进行估计,从而更加精确地对电容自愈次数进行估计。
2.3 自愈累积损伤模型建立
在电容的退化中,可以将自愈看成随机冲击对电容的损伤[15],其累积损伤过程可表示为poisson过程[16],其在t时间内的自愈造成的累积损伤可表示为
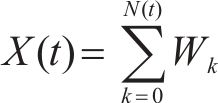
其中,Wk表示第k次自愈时的能量;N(t)表示到t时刻为止的累积自愈次数,也称为计数过程;Wk表示第k次自愈时其自愈能量,由于自愈发生时具有独立增量性,则可将自愈造成的损伤看成一个poisson过程,则在t时间内发生k次冲击的概率为
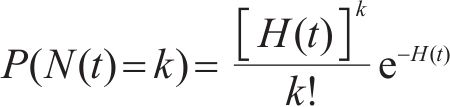
式中:H(t)为累积自愈次数N(t)的均值,则在t时刻,自愈造成的累积损伤满足非齐次复合poisson过程(Non-Homogeneous Compound Poisson Process,NHCPP),其累积损伤的累积概率分布可表示为
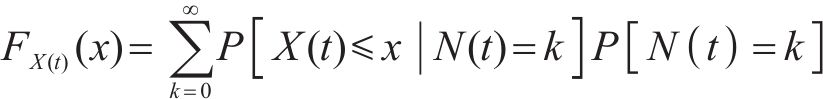
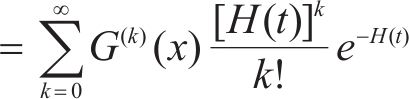
其中,G(k)(x)表示自愈能量分布G(x)的斯蒂杰斯卷积,其表示k次累积自愈所产生的累积能量的分布。设失效阈值为l,则在退化过程严格正则的条件下,失效时间分布函数可表示为
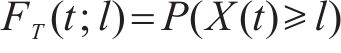
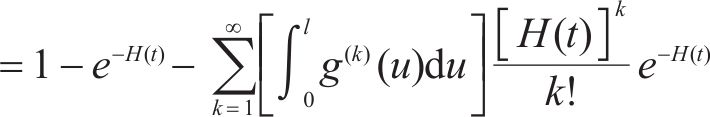
则失效时间可表示为
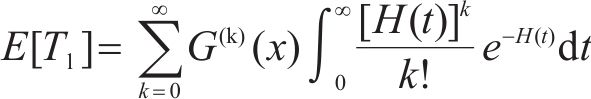
通过非齐次复合poisson过程,可将累积自愈次数和单次自愈能量转化为电容累积自愈能量,由此得到失效阈值能量下的失效时间分布。
3 电容寿命实验及检测结果分析
3.1 电容检测方案
电容在发生自愈时,两端电压会出现电压下降,但是相较电容本身电压而言非常小,下降幅度难以检测[17],因此本文选用电荷补偿的方式对自愈进行检测。电容自愈发生后,与电容并联的储能电容会向被测电容补充电荷,使得回路出现电流脉冲,通过对串联的检测电阻上的电流脉冲进行检测,就可以合理地对电容的自愈性能进行检测。自愈电路如图3所示,DC为直流电源,Cs为测试电容,R1为充电电阻,一般阻值为1 MΩ,C1为储能电容,起着稳定电压的作用,同时在Cs发生自愈时为Cs提供电荷,R2为限流电阻,同时也是电流取样电阻,限制Cs上所流过的电流,防止电容两端出现较大电流导致自愈失败。
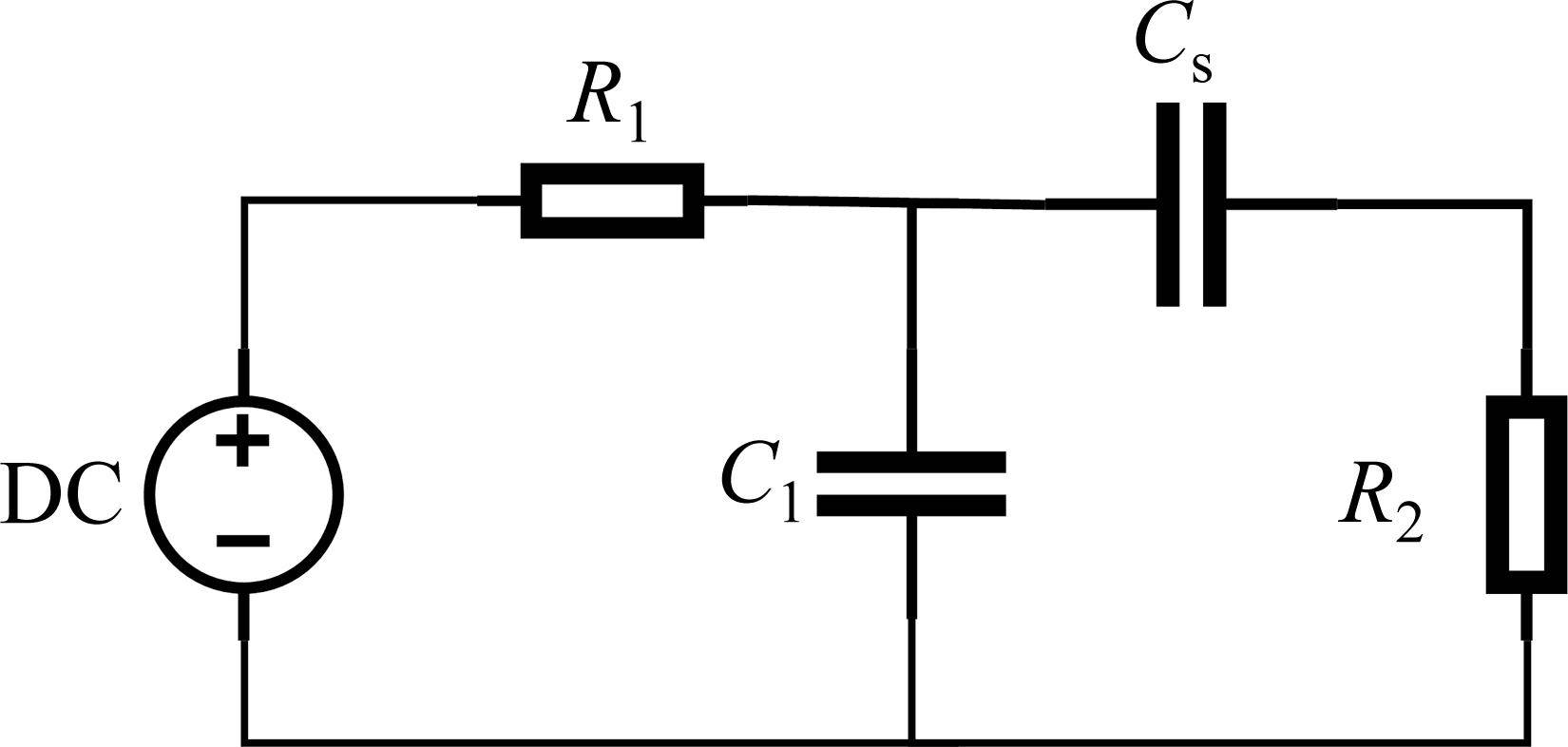
在电容自愈的检测中,常用的检测参数包括自愈时间、自愈电压、自愈能量和自愈频次等。由于电容自愈导致的容值退化与自愈烧毁的面积相关,而这部分面积又与自愈能量相关,因此,选择自愈能量和自愈频次作为电容自愈检测参数。
在测试之中,由于自愈电流较小,电阻上消耗的热量可以忽略不计,此时可认为电路所损失的能量为电容自愈损失的能量,其表达式为
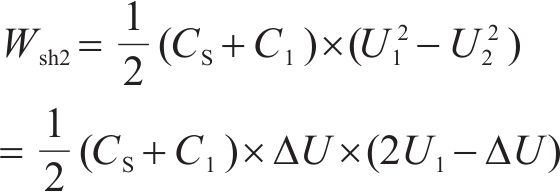
其中,U1,U2分别为自愈发生前后待测电容Cs两端的电压;ΔU为自愈前后电容两端电压差。当自愈能量过小时,难以对电容两端的压降进行检查,可以使用电荷补偿的方式对串联电阻的电压波形进行计算,即
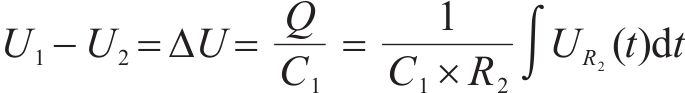
本文选用动车组牵引变流器中常用的金属化薄膜电容为研究对象。选取2倍额定电压作为实验条件,为了防止其他老化形式的干扰,这里设置实验温度为常温25 ℃,每隔1 h记录一次累积自愈频次,并使用LCR测试仪进行一次容值测量。
3.2 自愈能量特征分析
为了得到自愈发生时其冲击能量的分布G(x),需要对其自愈能量进行分布拟合。在电容自愈的过程之中,虽然以低能量自愈为主导,实际上高能量自愈在电容退化中起到的作用较大,不可忽视,因此需要使用重尾分布来对电容的自愈能量进行拟合,更能体现高能量自愈的作用。常见的重尾分布及其表达式如表1所示。选取以上3种分布对自愈能量分布进行拟合,得到其概率密度图像如图4所示。
| 分布名称 | 概率密度 |
|---|---|
| 广义帕累托 | 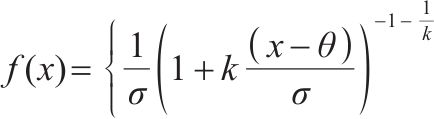 |
| 对数正态 | 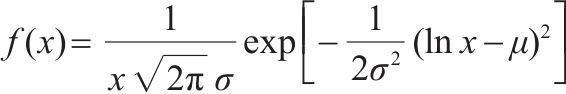 |
| 威布尔 | 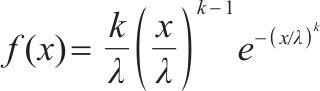 |
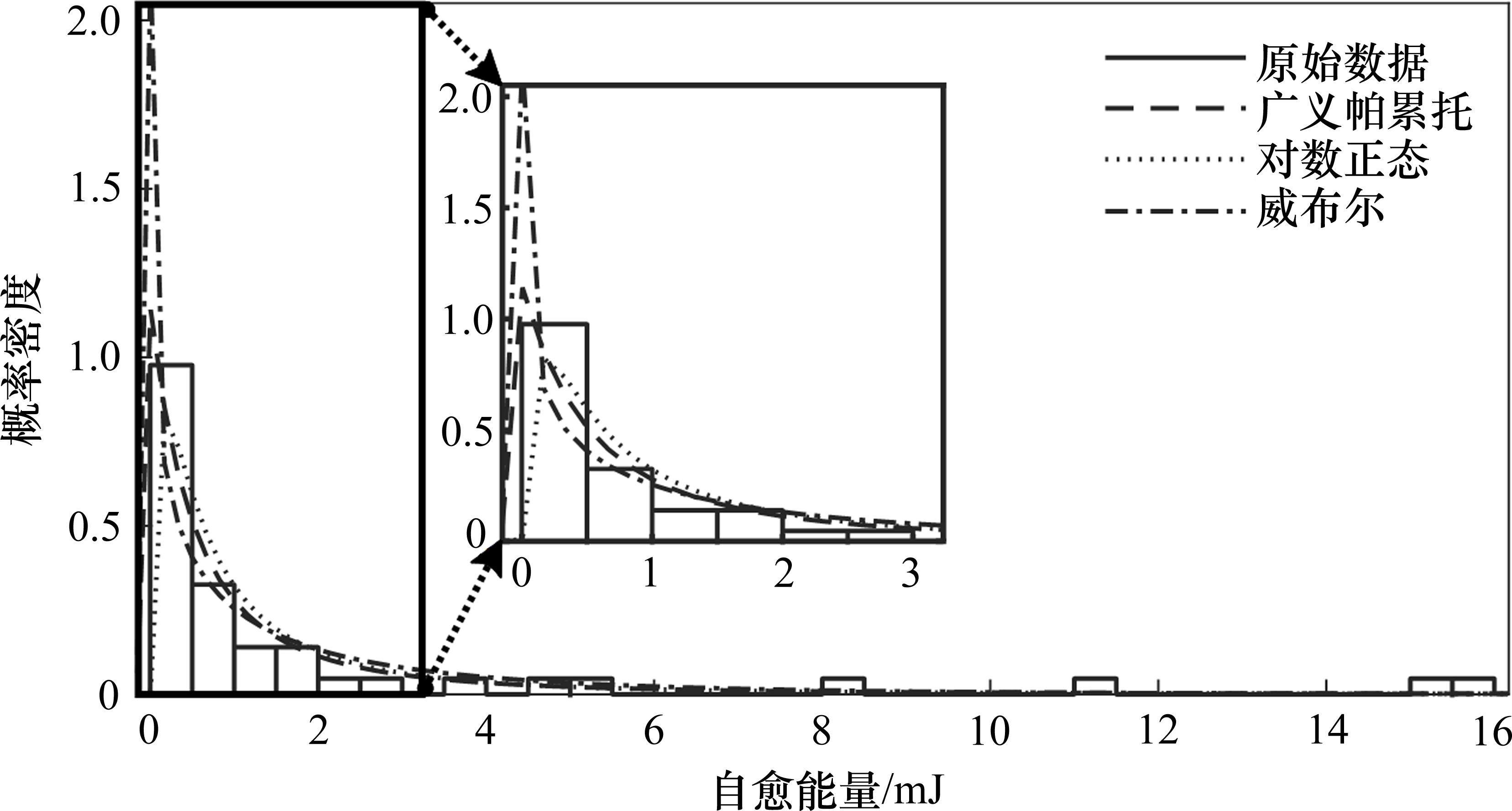
利用KS检验法[18](Kolmogorov-Smirnov)在显著性水平为5%的条件下对分布进行检验,其检验统计量为
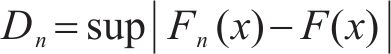
其中,Fn(x)为实际分布累积概率;F(x)为拟合后分布累积概率,其检验结果如表2所示。根据表2可知,自愈能量分布基本满足对数正态分布。
| 分布 | 对数正态 | 威布尔 | 广义帕累托 |
|---|---|---|---|
| p | 0.178 1 | 0.027 9 | 0.026 6 |
| Dn | 0.158 5 | 0.211 3 | 0.212 5 |
| 结果 | 不拒绝 | 拒绝 | 拒绝 |
3.3 自愈累积频次特征分析
取老化前30 h的数据作为训练数据,运用霍尔特指数平滑法对各时间段内的累积自愈能量进行估计,设定粒子群规模为30,迭代次数为100次。计算得到参数α=0.967 6,γ=0.762 3,得到的平均相对误差为0.140 7。利用优化粒子群算法计算的霍尔特参数,做出电容自愈退化计数过程曲线,如图5所示,将未来的预测曲线与实际曲线相比其平均相对误差为0.009 5。
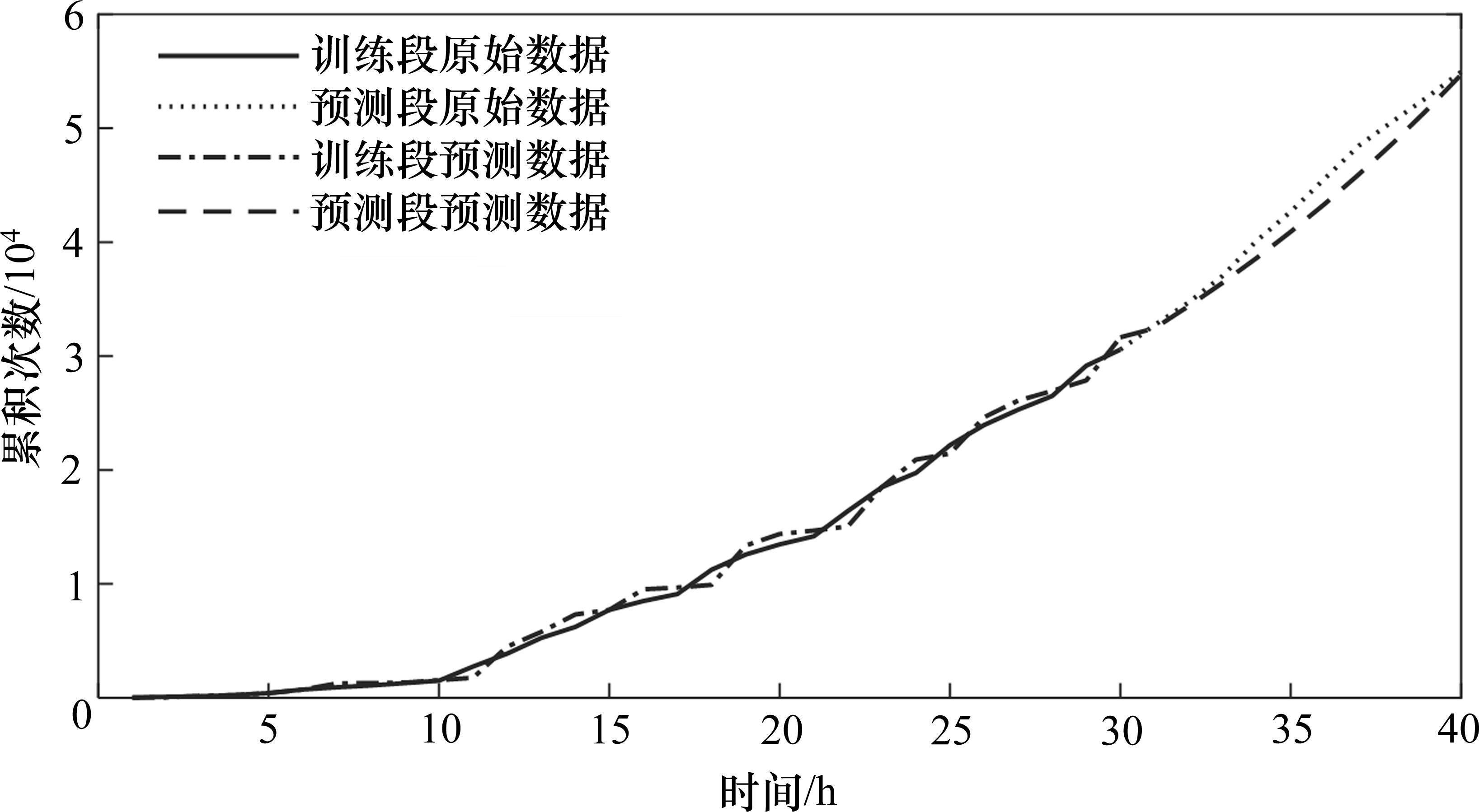
3.4 自愈损伤阈值分析
电容在自愈的过程中,其自愈能量与击穿面积正相关[19],而击穿面积又跟容值损伤正相关[20],因此可以用累积自愈能量来表示容量的损失。由于单次自愈造成的能量损失较小,这里选取电容短期内的多次自愈的累积自愈能量与自愈前后容值退化的结构,如图6所示。可见,容值与累积自愈能量呈线性关系,从而将电容自愈能量阈值与电容参数退化阈值关联。
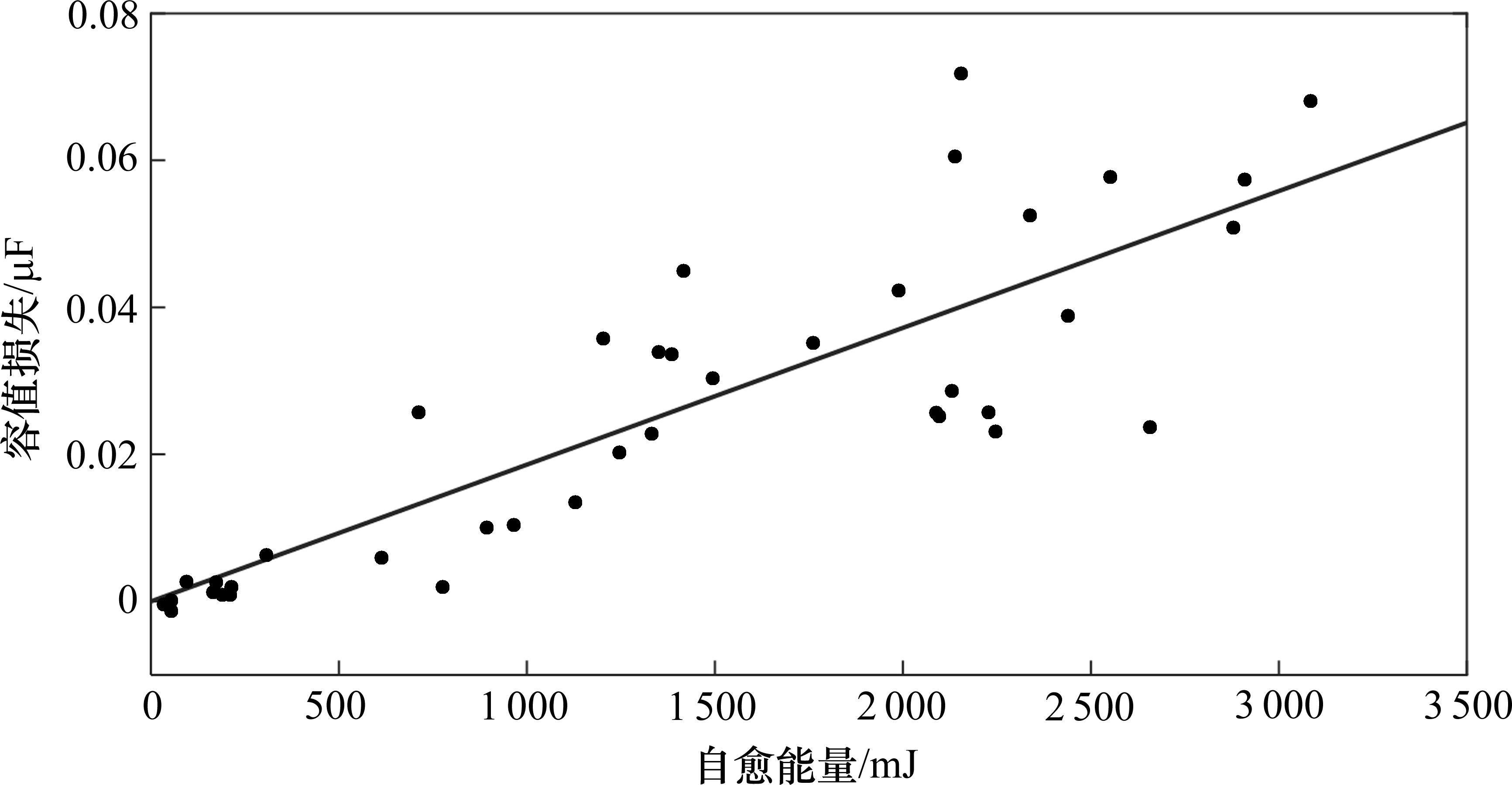
可见,容值退化与自愈能量基本呈现线性关系,其斜率k=5.347×10-6。以电容容值退化5%为电容失效的评判标准,则电容累积自愈能量阈值与电容失效阈值的关系可表示为:
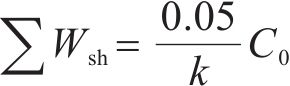
3.5 电容寿命预测
利用poisson过程计算并分析得到电容的退化曲线,做出其预测曲线与90%预测边界,如图7所示。随着电容的退化不断进行,其自愈能量的增长速度也在不断增长。可以看出,随着电容的使用时间的增长,其累积损伤自愈次数呈现指数式的增长,随着电容的使用时间越长,其自愈频次也会随之增加,反应到电参数上则表现为电容退化速度增加,其短时间失效的风险也会逐渐增加,同时其自愈失效的风险也就越大,容易在短时间内完全烧毁直至短路。
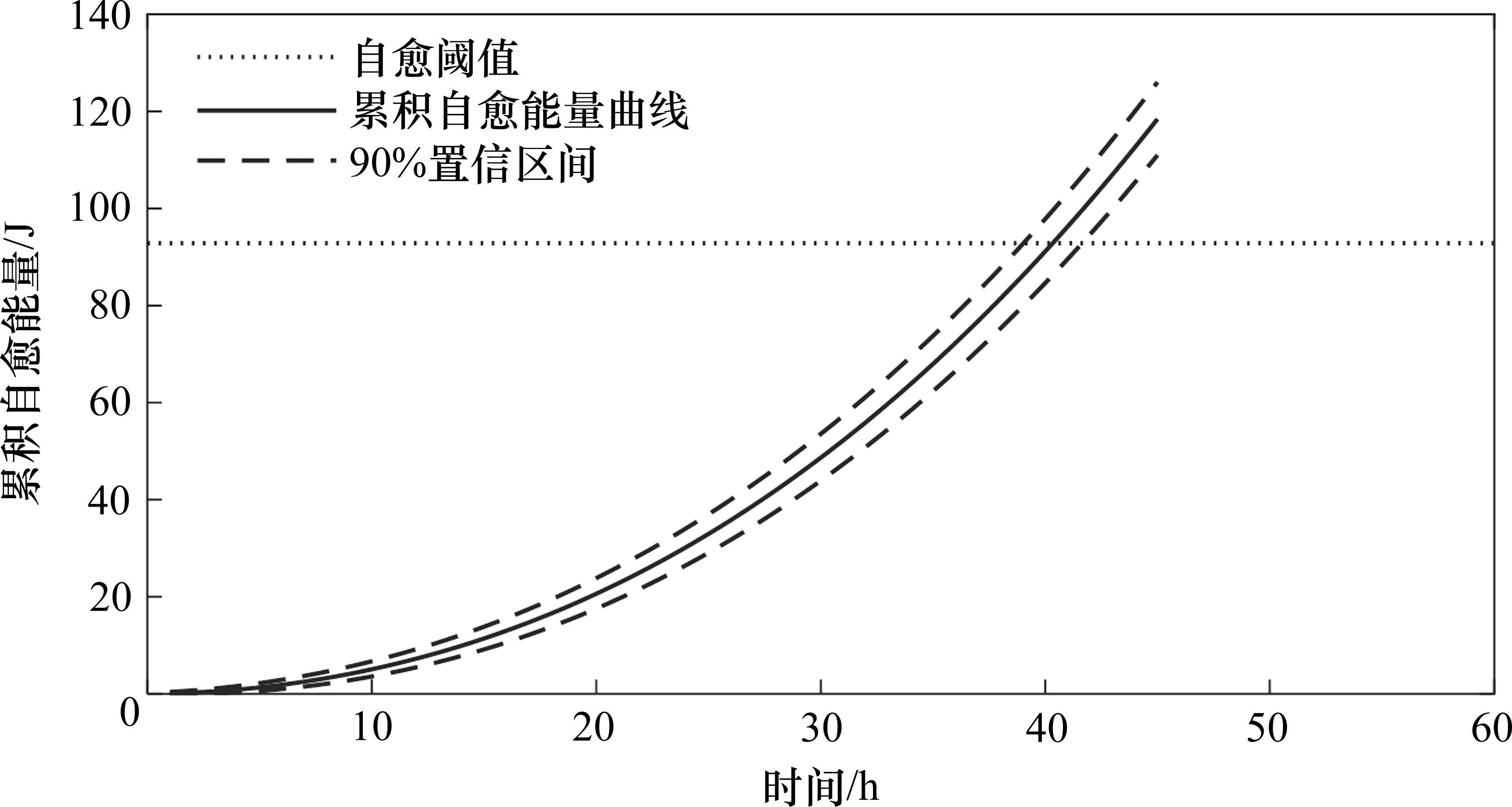
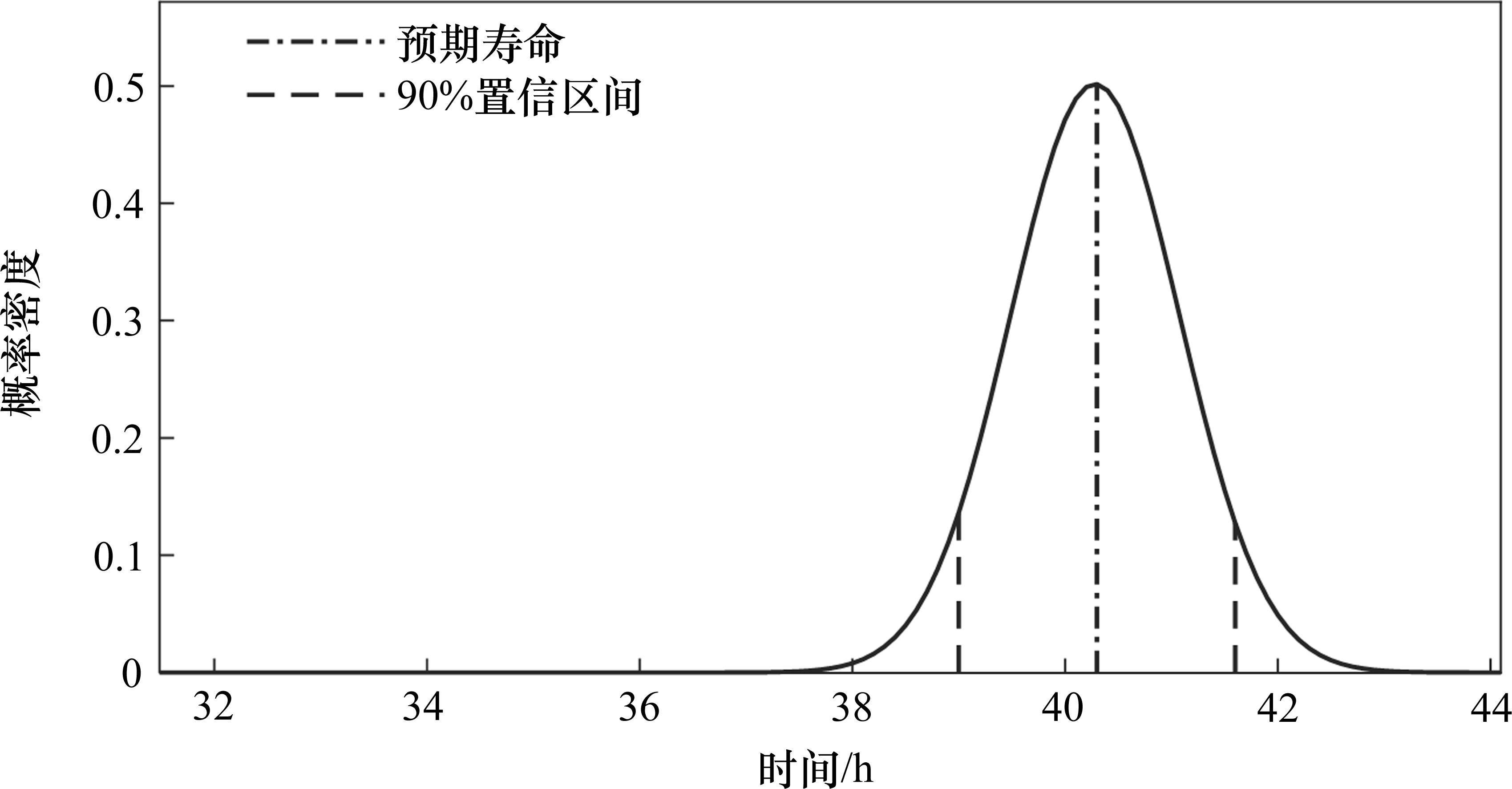
根据式(14),得到所测电容的失效阈值为92 855.80 mJ,得出其累积自愈能量下的概率密度分布图像如图8所示。可见,经过非齐次复合poisson过程预测的电容寿命为39.4 h,其90%置信区间为38.1~40.7 h。
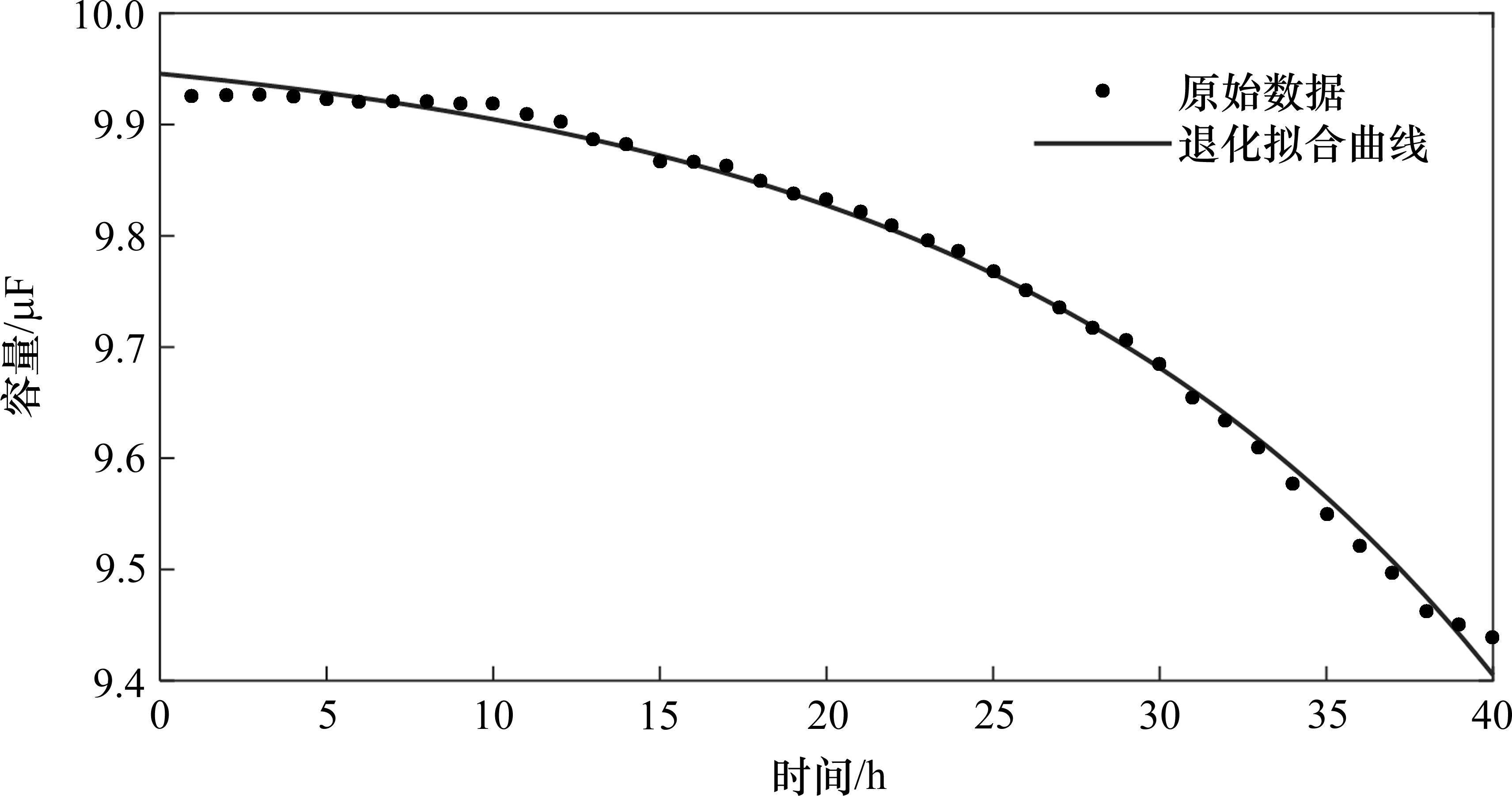
由于电容的容值随时间的退化趋势近似满足指数退化模型,我们将通过指数退化模型拟合得到的寿命认为真实寿命,如图9所示,通过对电容容值的指数退化拟合可知,得到其实际寿命为40.43 h。使用NHCPP模型的方式与实际经验模型拟合的寿命相比,其相对误差约为2.55%。
4 结论
1) 针对电容自愈所带来的老化问题,结合电容老化过程的特性,制定了一套基于电容损伤的评判方案。
2) 利用霍尔特参数预测法对电容自愈过程进行拟合,并用粒子群算法对霍尔特参数进行估计,得到的相对误差较小。
3) 通过将电容自愈带来的冲击转化为非齐次复合poisson过程,并基于此模型对电容器的寿命进行预测,与根据容值所得的寿命比较相差较小。
本文所用研究方法针对电容自愈这一主要失效模式,建立电容累积损伤退化模型,该方法能够很好地对电容自愈退化过程进行拟合分析,并描述自愈退化过程及其退化机理。由于本实验仅考虑恒定工况的电容退化过程,在未来的研究中,可以考虑在复杂时变工况下对电容自愈行为进行研究,以提高自愈研究的可靠性。同时,本实验为了尽量减少其他老化形式的干扰,采用了常温常湿的加载方式,在未来的研究中,也可以考虑对高温高湿等极端条件下的多退化形式竞争失效进行研究。
Experimental study of self-healing characteristics and insulation resistance of metallized polypropylene film under various inter-layer pressure
[C]//Efficiency evaluation of the self-healing process of metallized film capacitors for polymer films with various chemical composition
[C]//成庶,邹阳.基于自愈特性的电容剩余寿命预测[J].铁道科学与工程学报,2025,22(02):900-908.
CHENG Shu,ZOU Yang.Prediction of capacitor remaining useful life based on self-healing characteristics[J].Journal of Railway Science and Engineering,2025,22(02):900-908.

