连续倒塌是指在突发荷载作用下,墙体、柱子等重要构件失效导致局部倒塌,蔓延至邻近构件造成连锁反应,最终导致整个结构的大范围倒塌[1]。建筑结构发生连续倒塌后的致命率高达62%[2],需要进行抗连续倒塌研究来保护生命财产安全,对此,许多学者针对不同结构体系进行研究,包括混凝土框架结构[3]、钢-混凝土组合框架结构[4]、装配式框架结构[5]、预应力混凝土结构[6]和钢框架结构[7]等。对各结构体系的研究发现,节点延性对结构抗连续倒塌性能有重要作用,使塑性铰偏离节点区可改善节点延性,例如,在梁端设置转动铰[8]、对梁翼缘和腹板进行削弱[9]等方法将塑性铰外移。其中,美国规范针对焊接钢框架提出的梁翼缘削弱截面(RBS)节点[10],使塑性铰偏离节点焊缝区,避免极端荷载作用下的节点脆性破坏,最早被运用于抗震研究领域[11-12]。焊接钢框架结构发生大变形时,RBS节点的削弱区可能会出现局部屈曲[13]、失稳[14]和断裂[15]等局部破坏,导致梁端失效并引起框架结构的连续倒塌[16]。为提高RBS节点在极端荷载下的冗余度,可在削弱位置采取措施,保证钢框架结构具有良好的抗倒塌性能。在节点区域增加附属受力构件被广泛用于改善小变形下的受力性能,LU等[17]在耗能角钢位置设置加劲肋以提高节点的强度和耗能能力;TIAN等[18]在网壳结构中设置内嵌构件以提高结构的稳定性;QIAN等[19]在钢框架节点设置角钢和穿心螺栓以提高节点转动能力。还可以在节点区域增加二次防御构件提高大变形下的悬链线效应,FENG等[20]和YU等[21]在钢筋混凝土结构设置起波钢筋和交叉钢筋发挥大变形阶段的承载能力;MENG等[22]在节点设置滑动内芯以提高焊接钢框架的悬链线效应。2类措施均可以提高节点在极端荷载下的冗余度,由于第1类措施通过加固梁柱节点提高结构的刚度和承载能力,在小变形下便起作用,有时会抵消RBS节点的塑性铰外移功能,第2类措施与RBS节点配合,既满足节点转动能力,又为发生大变形的节点提供第2道防线,故选择第2类措施。本文提出一种在RBS节点设置加强板的节点冗余度改善措施。首先对焊接节点进行梁翼缘削弱,再将加强板通过焊接方式布置在梁翼缘削弱截面内侧,防止其占用焊接框架结构层空间。通过对子结构进行静力加载试验,重点分析子结构的变形能力、内力分布及荷载-位移响应等关键特性,再通过验证后的数值模型,进一步研究加强板弯曲高度、翼缘削弱长度和深度等参数对子结构抗连续倒塌性能的影响。
1 试验概况
1.1 试件设计
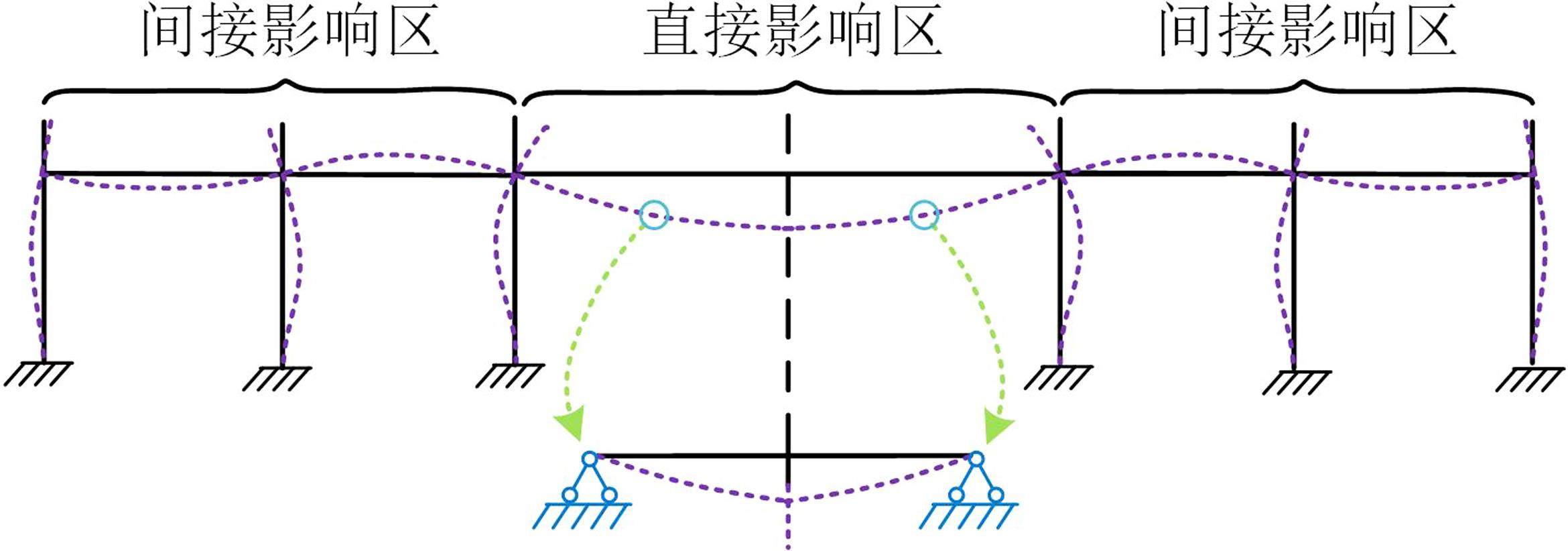
假设框架结构的底层中柱失效,失效柱所在跨变形较大,被称为直接影响区,其余跨变形较小,被称为间接影响区,为直接影响区提供边界约束。直接影响区的内力在中间节点和端部节点近似呈反对称分布。图1对移除中柱后剩余结构的挠度分析发现,直接影响区的挠度拐点位于两侧失效跨的中间位置。由此,从剩余结构中提取2个半跨梁及中间节点作为子结构模型,并将拐点位置视为铰支座进行简化分析。需要注意的是,失效跨的拐点在大变形时可能会偏离跨中,将拐点作为铰接边界在大变形时存在一定误差,精确计算时需要结合整体框架分析修正结果[19]。
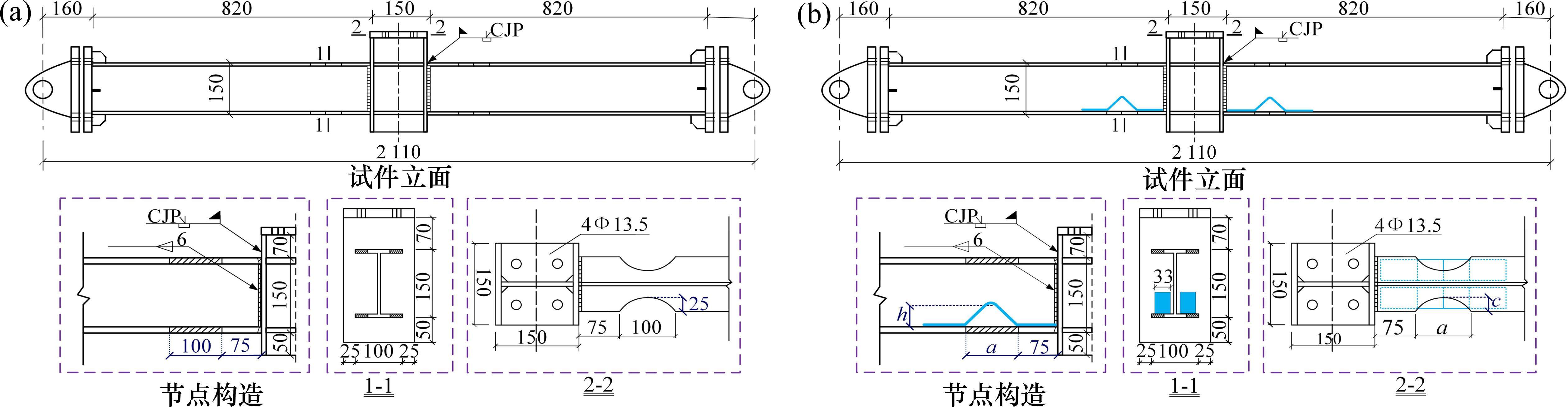
SONG等[23]于2007年对俄亥俄州综合大楼进行拆除试验,以该大楼底层作为原型,并考虑到实验室场地限制,设计2组缩尺试验试件,试件包含1个仅削弱梁翼缘的RBS试件(图2(a)),2个带不同高度加强板的翼缘削弱试件RBS-h30和RBS-h40(图2(b)),加强板高度h分别为30 mm和40 mm。各试件的梁柱采用相同尺寸,其中钢梁截面尺寸为H150×100×6×8 mm,钢柱截面尺寸为H150×150×8×10 mm,梁跨度L为2 110 mm,失效柱高H为290 mm。梁翼缘削弱长度a=100 mm,削弱深度c=25 mm。加强板与削弱翼缘的协同工作,考虑腹板和焊缝的宽度,取加强板的宽度略小于梁翼缘宽度一半。钢梁与钢柱通过完全焊透坡口焊接进行连接。
1.2 加载装置和加载制度
加载装置如图3所示,首先将反力墩通过地脚螺栓与地梁连接,将反力架的4根立柱固定到地梁上,使反力架形成自平衡体系;液压伺服作动器的顶部与反力架相连,单向加载头通过转接件与柱顶部连接,防止试件发生面外失稳。试件两端通过高强度螺栓与铰支座连接,铰支座则进一步通过高强度螺栓固定于反力墩的轴承上,为试件提供稳定的轴向拉力,并保证试件两端在平面内能够自由转动。

采用作动器对柱顶施加向下的竖向力,先对试件进行预加载,以测试加载设备和采集设备的运行情况,再对试件进行正式加载。屈服前试验采用力控制模式进行加载,加载速率设定为4 kN/min;屈服后切换为位移控制模式,加载速率调整为6 mm/min。当试件完全断裂或出现异常的面外变形时,试验即刻终止。
1.3 测点布置
在试件加载点和约束点附近选择测点布置的关键截面,其中,截面W1和E1位于梁的拐点附近,距离梁端100 mm,在整个加载过程中基本处于弹性状态;截面W2和E2位于翼缘削弱和加强板区域,距离柱面125 mm,处于复杂应力状态。关键截面的位移计与应变片布置如图4所示。
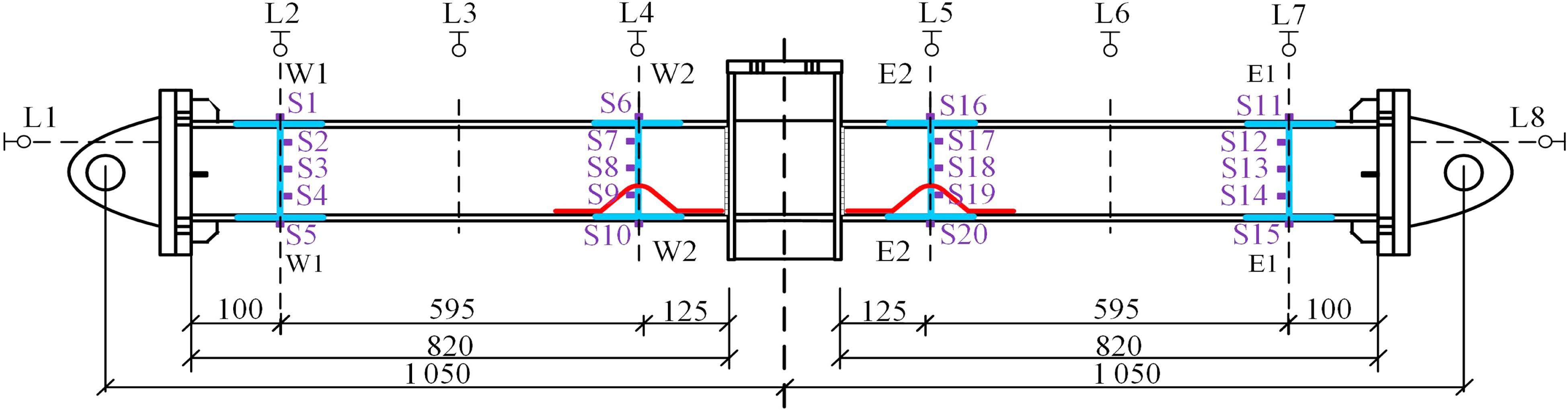
根据关键截面的挠度值选择相应量程的位移计,以满足测量精度和测量范围的需求。在截面W2和E2布置量程为300 mm的位移计L4和L5;在梁中部截面布置量程为200 mm的位移计L3和L6;在截面W1和E1布置量程为100 mm的位移计L2和L7。此外,考虑到梁端铰接点在大变形阶段会产生一定的水平位移,在梁端部布置2个水平位移计L1和L8。为测量关键截面应变,在截面W2和E2分别布置5个应变片(S6至S10和S16至S20),用于捕捉在复杂应力条件下的应变响应;在截面W1和E1也分别布置5个应变片(S1至S5和S11至S15),结合对应截面挠度测量值,为关键截面的内力计算提供可靠数据。
2 试验结果
2.1 破坏现象
在试验过程中,各试件表现出相似的变形特征,图5为代表性试件的变形,上翼缘屈服前试件两侧对称变形,达到极限荷载后,试件在梁翼缘削弱处发生断裂,两侧梁变形呈不均匀发展,导致荷载-位移曲线骤降。然而,各试件断裂发展路径存在一定差异,试件RBS的裂缝发展路径呈直线形,试件RBS-h30在下翼缘断裂后,加强板刚被拉直,裂缝发展路径呈斜线形,而试件RBS-h40在翼缘开裂后,裂缝的发展路径呈现出先直线后斜线的特征。图6~图8给出各试件的具体试验结果,包括载荷-位移曲线和关键点的试验现象。

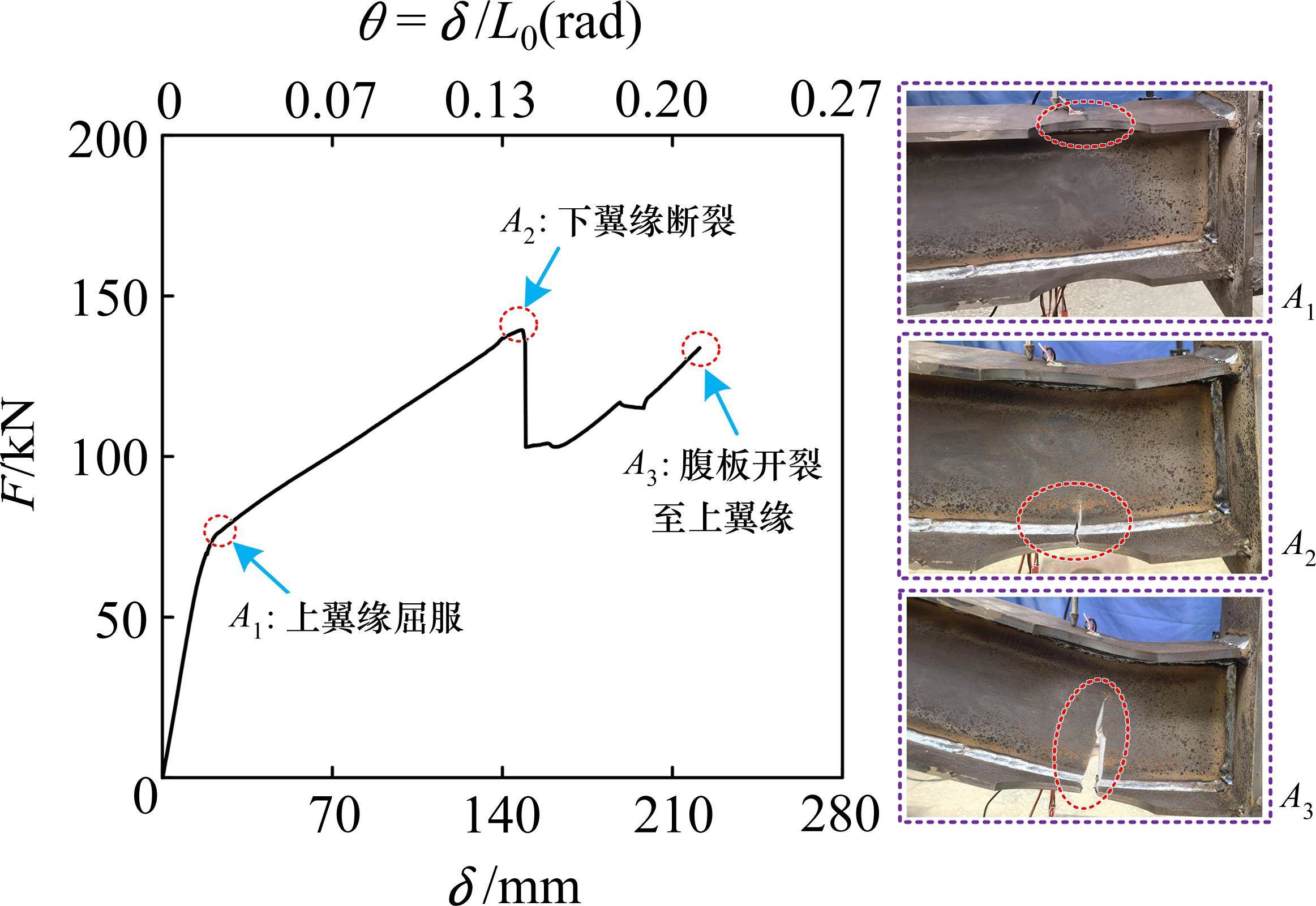
对于图6试件RBS,荷载-位移曲线在弹性阶段呈线性增长,直到上翼缘屈服(点A1),屈服点位移δ=20 mm,对应于梁转角θ=0.019 rad;继续加载,当竖向位移为δ=148 mm时,梁下翼缘削弱位置出现初始断裂(对应点A2),引起竖向荷载由139.2 kN降至102.9 kN;裂缝沿梁腹板继续向上延伸,发展路径呈直线形,随着竖向位移增加到δ=221 mm,裂缝即将延伸至上翼缘(对应点A3)。
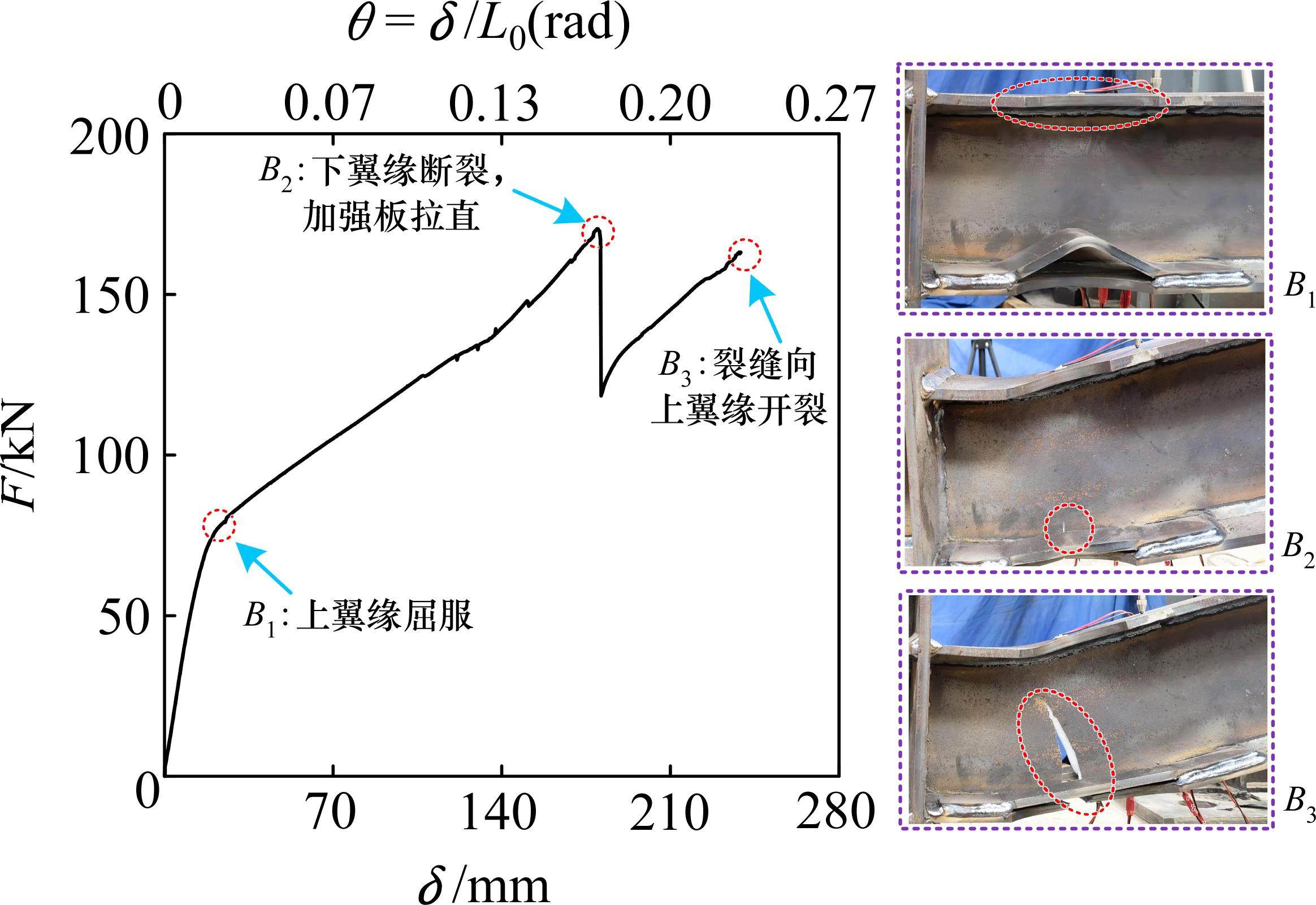
试件RBS-h30的荷载-位移曲线及破坏现象如图7所示,弹性阶段无明显变形,当竖向位移δ=21 mm,梁转角θ=0.02 rad时,能够观察到上翼缘发生屈曲(对应于点B1);随着竖向位移的继续增加,荷载-位移曲线进入非线性阶段,当δ=180 mm时,下翼缘削弱处发生断裂(对应于点B2),竖向荷载由169.7 kN下降至110.2 kN,此时加强板刚被拉直,代替下翼缘参与轴向受力;随着加载继续,裂缝沿梁腹板向上翼缘延伸,加强板的拉结作用使裂缝发展呈斜线形剪切破坏。
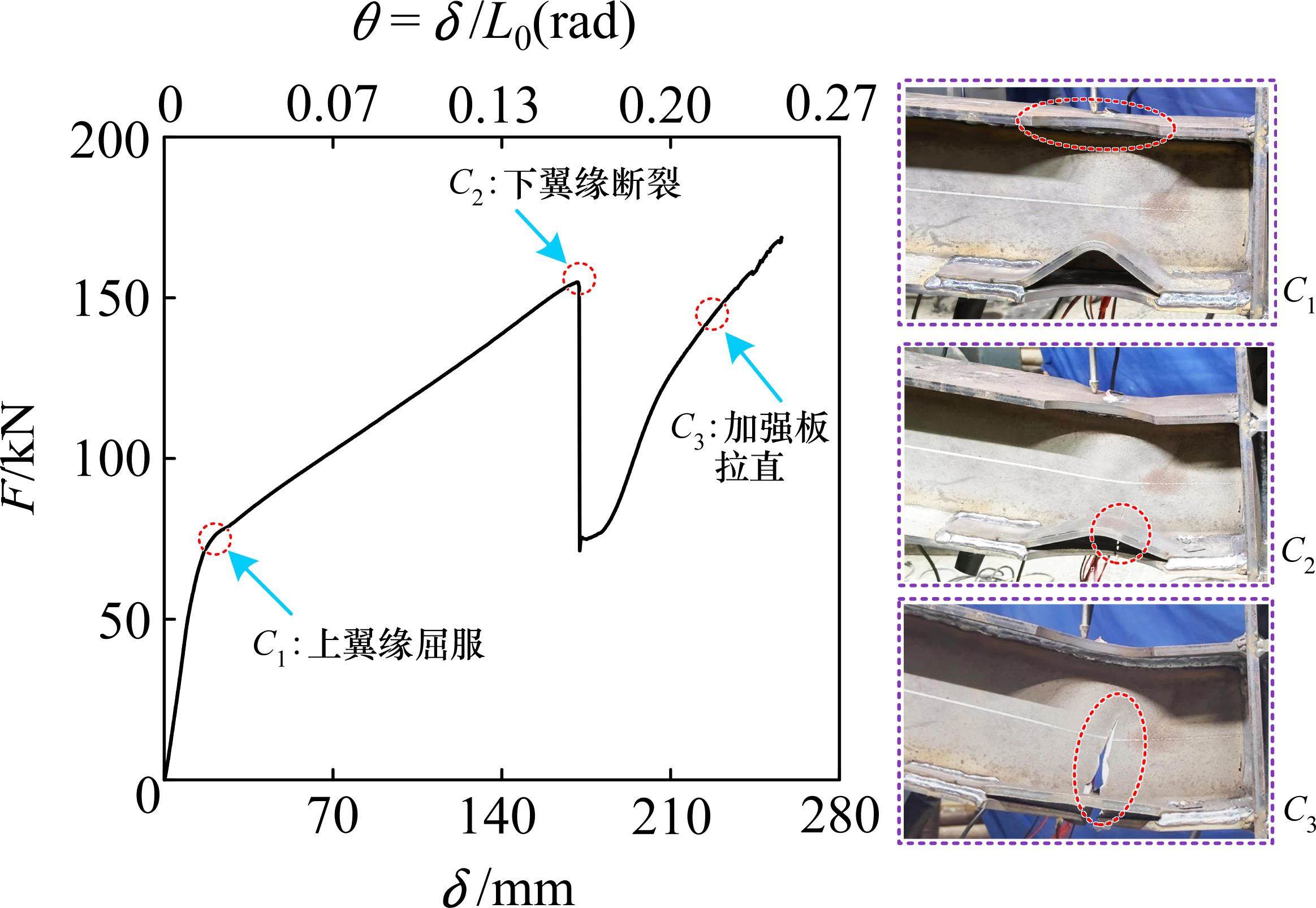
而试件RBS-h40(图8),在竖向位移δ=19 mm时,标志试件弹性阶段结束开始进入塑性阶段(对应于点C1);当δ=171 mm时,下翼缘发生断裂(对应于点C2),此时加强板并未拉直,板中拉力较小,对裂缝发展控制有限;随着竖向位移持续增加,裂缝沿腹板向上翼缘持续发展,断裂侧的加强板逐渐被拉直与梁的共同承受轴向拉力(对应于点C3);当δ=255 mm时,作动器轴线的倾角过大,停止加载。
2.2 荷载-位移曲线对比
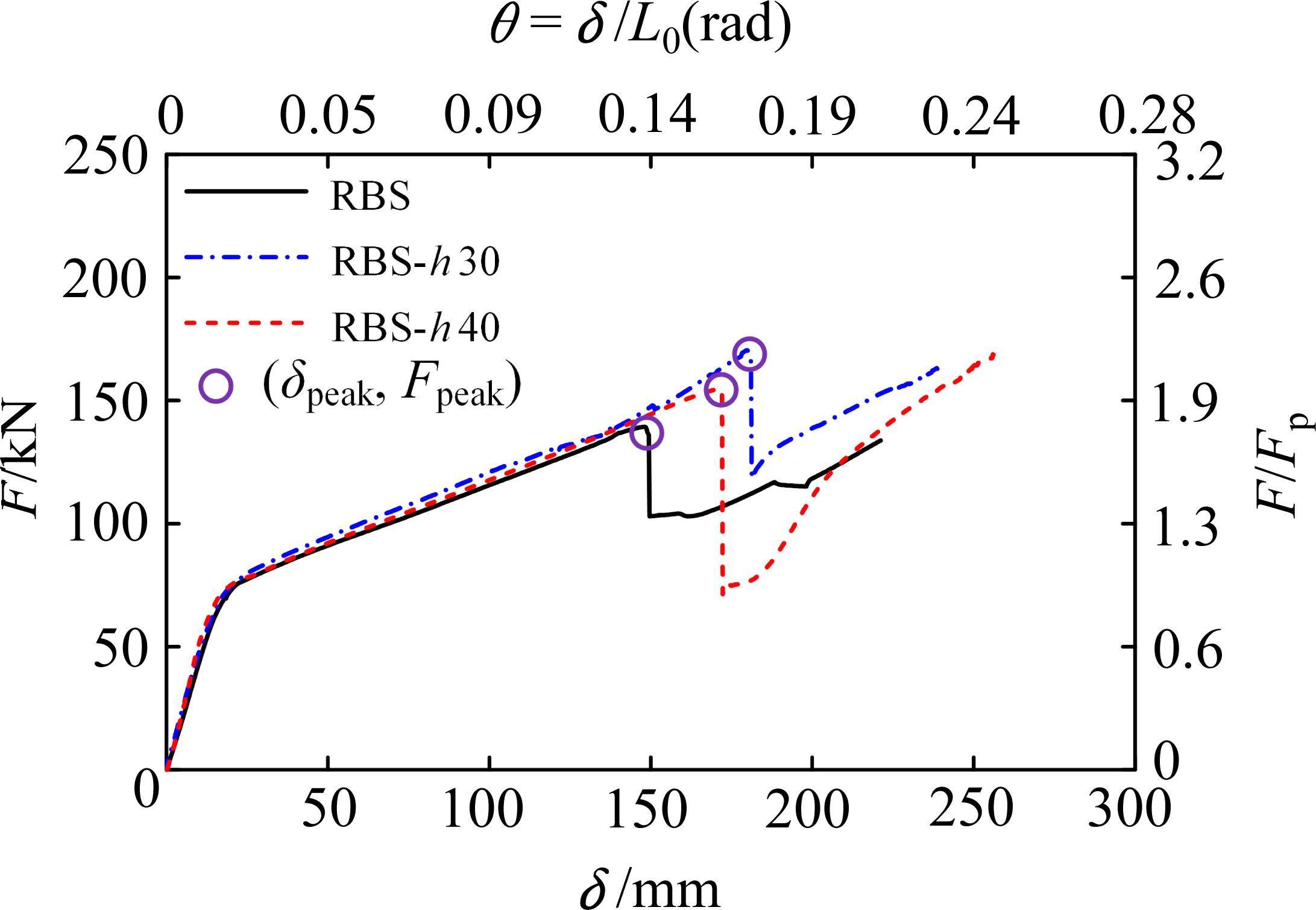
对比分析3个试件的荷载-位移曲线(图9),可以看出各曲线在翼缘屈服前相近,加强板形状也无明显变化,试件RBS-h30和RBS-h40的承载能力比基础试件RBS分别提高4.5%和1.8%,说明加强板在小变形下的作用有限。试件RBS-h30在加强板拉直的过程中,作为替代路径协助钢梁承受荷载,伸直的加强板代替刚断裂的下翼缘承受荷载,变形能力和承载能力比基础试件RBS分别提升21.7%和21.8%。而试件RBS-h40的变形能力和承载能力仅比RBS提升15.3%和11.0%,因为加强板在拉直的过程中,裂缝已经从梁下翼缘发展到腹板中性轴,加强板弯曲高度过大延迟了其与翼缘的协同工作,导致加强板提供的荷载替代路径传递效率下降。
2.3 试件变形
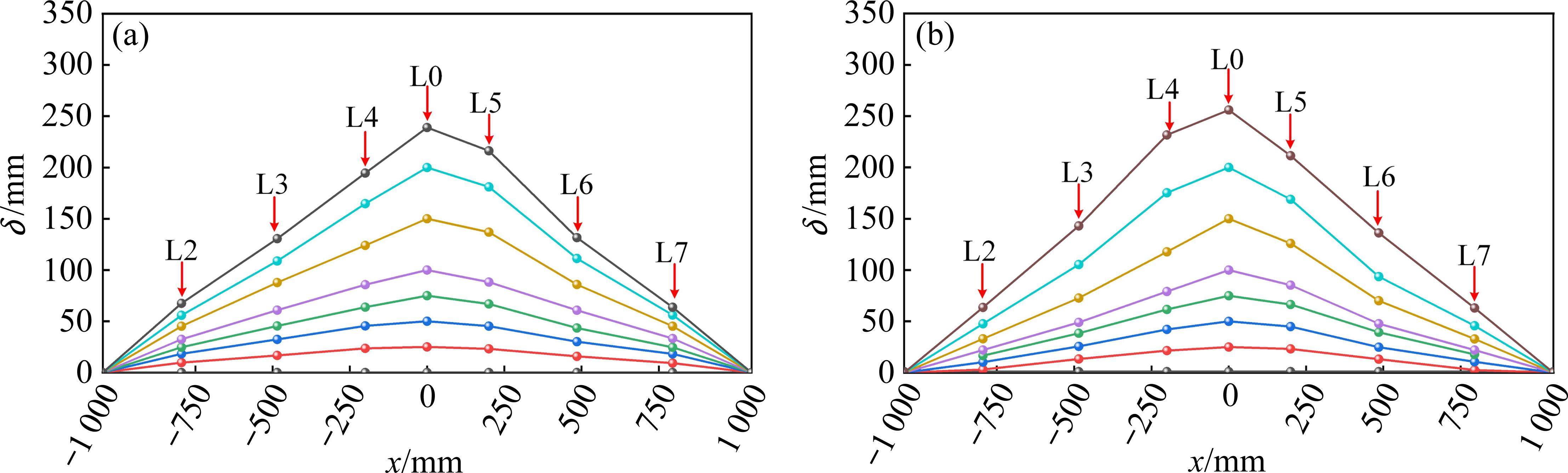
图10分析了带加强板试件RBS-h30和RBS-h40的竖向变形,其中,L0为液压伺服作动器施加的竖向位移,L2至L7为梁上各位移计的测量值,铰接点的水平位移较小,在图中未予标注。在小变形阶段(δ<50 mm),各试件两侧的变形表现出较好的对称性。在大变形阶段,特别是梁翼缘削弱处发生断裂后,两侧梁的变形呈不均匀发展。对于图10(a)的试件RBS-h30,当δ=180 mm时,右侧下翼缘削弱处发生断裂,接着裂缝向腹板扩展导致腹板局部变形过大,两侧梁对称性变形遭到破坏,在δ=239 mm时,试验加载终止。对于图10(b)的试件RBS-h40,当δ=171 mm时,左侧下翼缘削弱处发生断裂,导致腹板局部变形增加,两侧的变形开始出现差异,断裂侧的竖向变形明显高于另一侧,在δ=256 mm时,加载终止。
3 子结构抗倒塌机制分析
3.1 截面应变
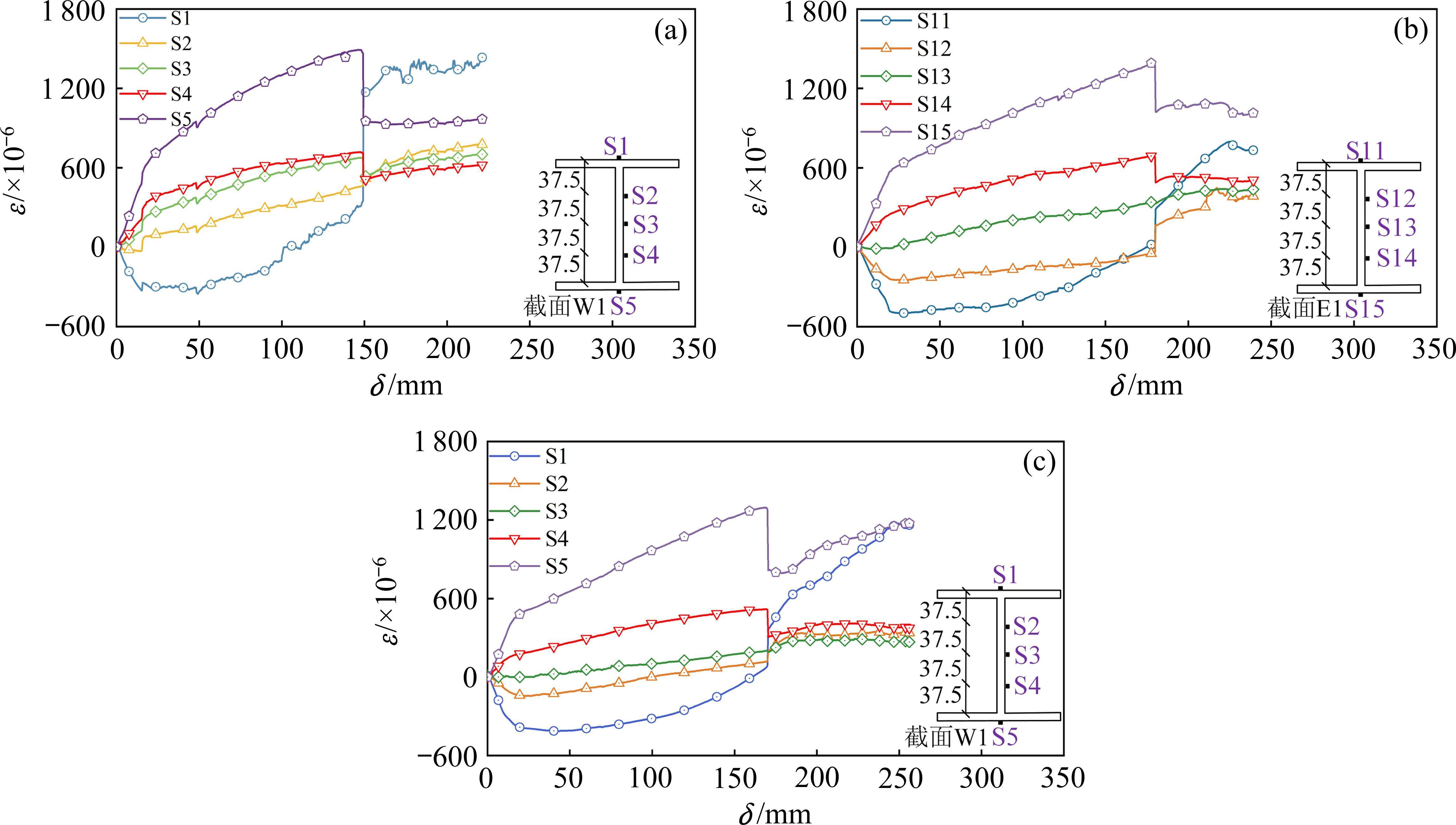
各试件断裂侧的梁端应变为研究裂缝和内力发展提供重要依据,选取试件RBS-h30右侧截面E1和试件RBS-h40左侧截面W1的应变曲线,并与基础试件RBS的应变对比,如图11所示。两侧梁的中性轴下部受拉、上部受压,所以S1和S11的应变值为负值,S5和S15的应变值为正值。基础试件RBS与加强板改进的试件相比,S2的应变值为正值,而对应加强板改进试件的S2或S12的应变值为负值,加强板弯折在加载初期影响梁腹板受力。试件RBS-h30和试件RBS-h40相比,前者加强板的弯曲高度小于后者,其加强板能够更早发挥作用,使RBS-h30下翼缘应变曲线高于RBS-h40;两试件的加强板对上翼缘作用较小,S1和S11应变曲线较为接近,直到在下翼缘开裂后,均从受压逐渐转为受拉。翼缘断裂后,裂缝沿腹板延伸,试件主要依靠上翼缘和加强板来承受竖向荷载,腹板上的应变片退出工作。
3.2 内力发展
靠近支座的截面W1和E1在整个加载过程中保持弹性,可由图11对应截面的应变数据,并依据力学基本原理计算截面轴力N1、弯矩M1和剪力V1,如下:
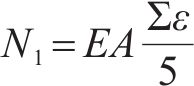
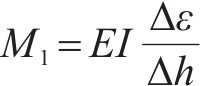
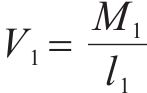
式中:E为钢材弹性模量;A为截面面积;I为截面绕强轴惯性矩;Σε为对应截面5个应变值的代数和;Δε/Δh为计算截面的曲率;l1为截面距拐点的长度。
对试件RBS、RBS-h30和RBS-h40的内力进行讨论,图12为梁的轴力和弯矩曲线,其中横轴表示试件竖向位移,纵轴表示内力值,图中δy、δp和δpeak分别为曲线的屈服位移、塑性位移和断裂位移。
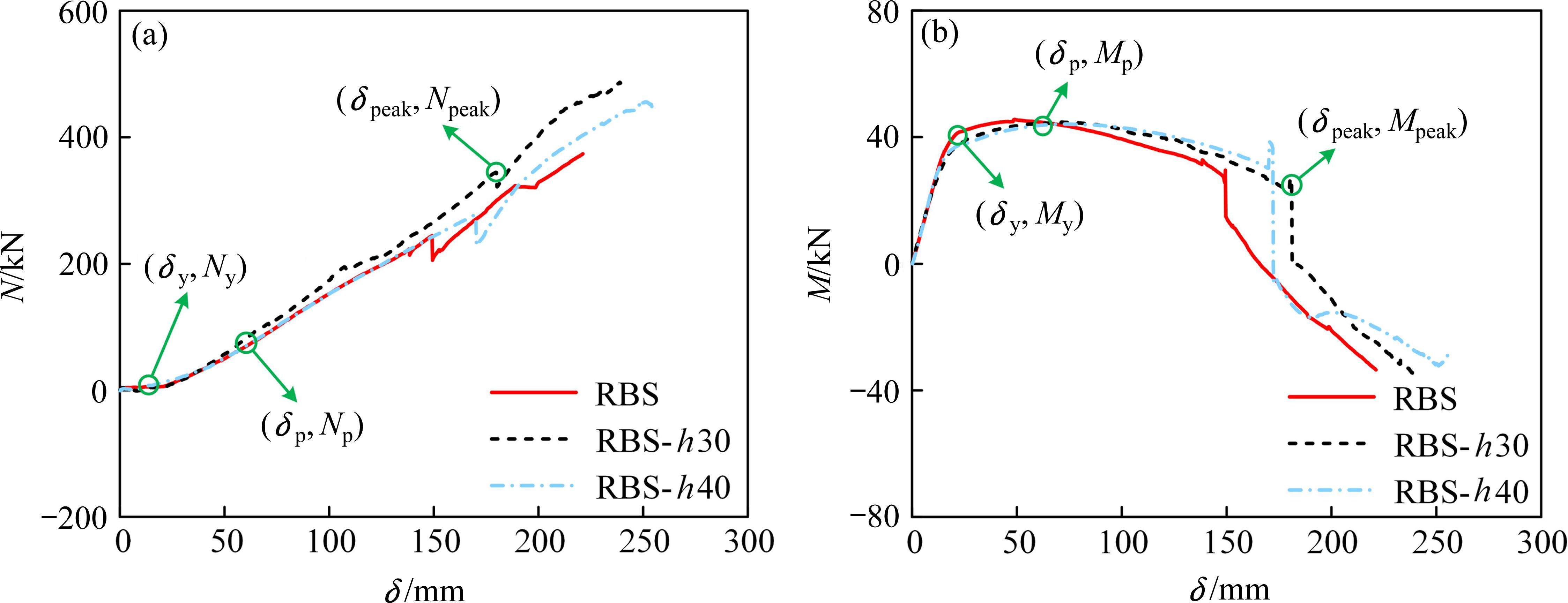
在δ<δy的情况下,3个试件的弯矩曲线M快速增长,而轴力曲线N并未上升,轴力值接近于0,表明在此阶段试件主要由弯曲效应主导。
当δy≤δ<δp时,各试件在竖向位移δp约为60 mm时形成塑性铰,对应塑性弯矩Mp约为45 kN∙m,说明加强板在弯折状态下对试件的截面弯矩影响有限。
在δp≤δ<δpeak时,N快速升高,悬链线效应成为试件内力发展的主要影响因素,特别是布置加强板的RBS-h30和RBS-h40试件,断裂轴力Npeak约为398 kN和336 kN,是基础试件RBS的1.41倍和1.19倍,表明加强板中的拉力有利于悬链线效应。
在δ>δpeak的情况下,弯矩曲线降至0或负数,弯曲效应失效;而拉直状态的加强板使轴力曲线保持增长,促进悬链线效应充分发展。
3.3 抗力发展
基于梁柱子结构简化模型,研究中柱失效后抗力机制的演变,如图13所示,VW和VE代表支座竖向反力,HW和HE代表支座水平反力,Vi、Mi和Ni分别代表截面i处的剪力、弯矩和轴力。由于试验过程采用拟静力加载,支座反力与截面i的内力(Vi、Mi、Ni)可通过以下静力平衡关系来描述:
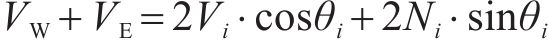
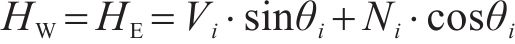
式中:li为i截面到铰支座的距离;θi为截面i的转角,由tanθi=δi/li计算。
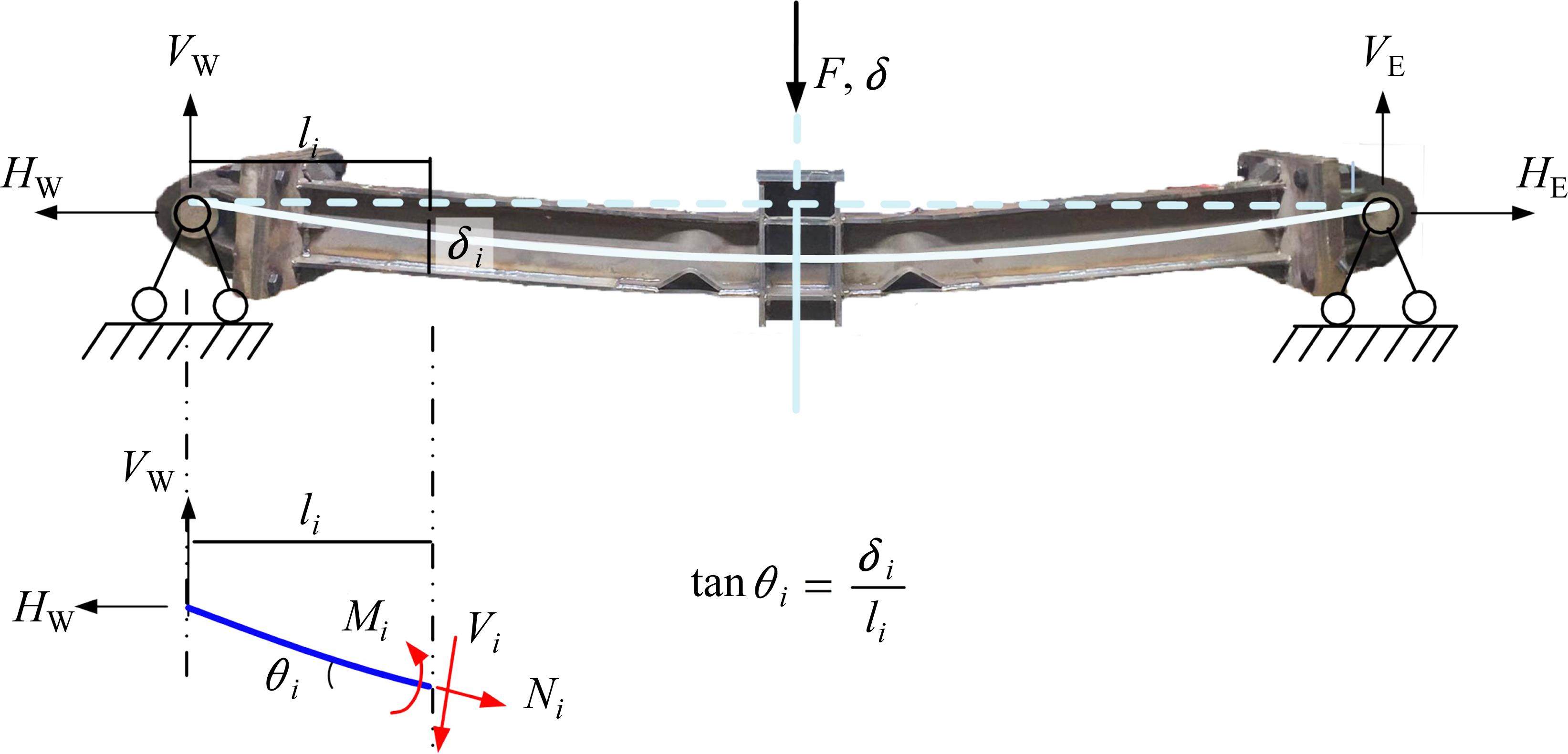
方程(4)右侧的第1项由弯矩起主导作用的弯曲效应控制,记为弯曲抗力FF;右侧第2项由轴力起主导作用的悬链效应控制,记为悬链抗力FC,重新表述如下:
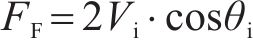
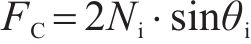
对试件RBS、RBS-h30和RBS-h40分别进行抗力机制分析,给出弯曲抗力FF、悬链抗力FC和总抗力F随竖向位移δ的发展曲线,如图14所示。为量化分析,对FF引入贡献系数βF,对FC引入贡献系数βC,如下:
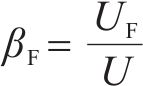
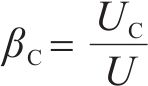
式中:UF、UC和U分别表示试件的弯曲抗力、悬链线抗力和总抗力的内能,分别等于对应曲线包围的面积。

计算下翼缘断裂时刻各试件的内能与贡献系数,列于图14和表1。试件RBS-h30的悬链线贡献系数为39.4%,是基础试件RBS的1.84倍,说明悬链线效应不仅由钢梁提供,还由逐渐拉直的加强板提供。试件RBS-h40也有相同的趋势,加强板的设置有助于提高悬链线效应的贡献,甚至导致悬链线抗力FC超过总抗力F的情况。
| 试件编号 | UF/(kN∙m) | UC/(kN∙m) | U/(kN∙m) | βF/% | βC/% |
|---|---|---|---|---|---|
| RBS | 11.55 | 3.07 | 14.62 | 78.6 | 21.4 |
| RBS-h30 | 12.34 | 8.02 | 20.36 | 60.6 | 39.4 |
| RBS-h40 | 13.07 | 5.46 | 18.53 | 70.5 | 29.5 |
4 有限元的建立及验证
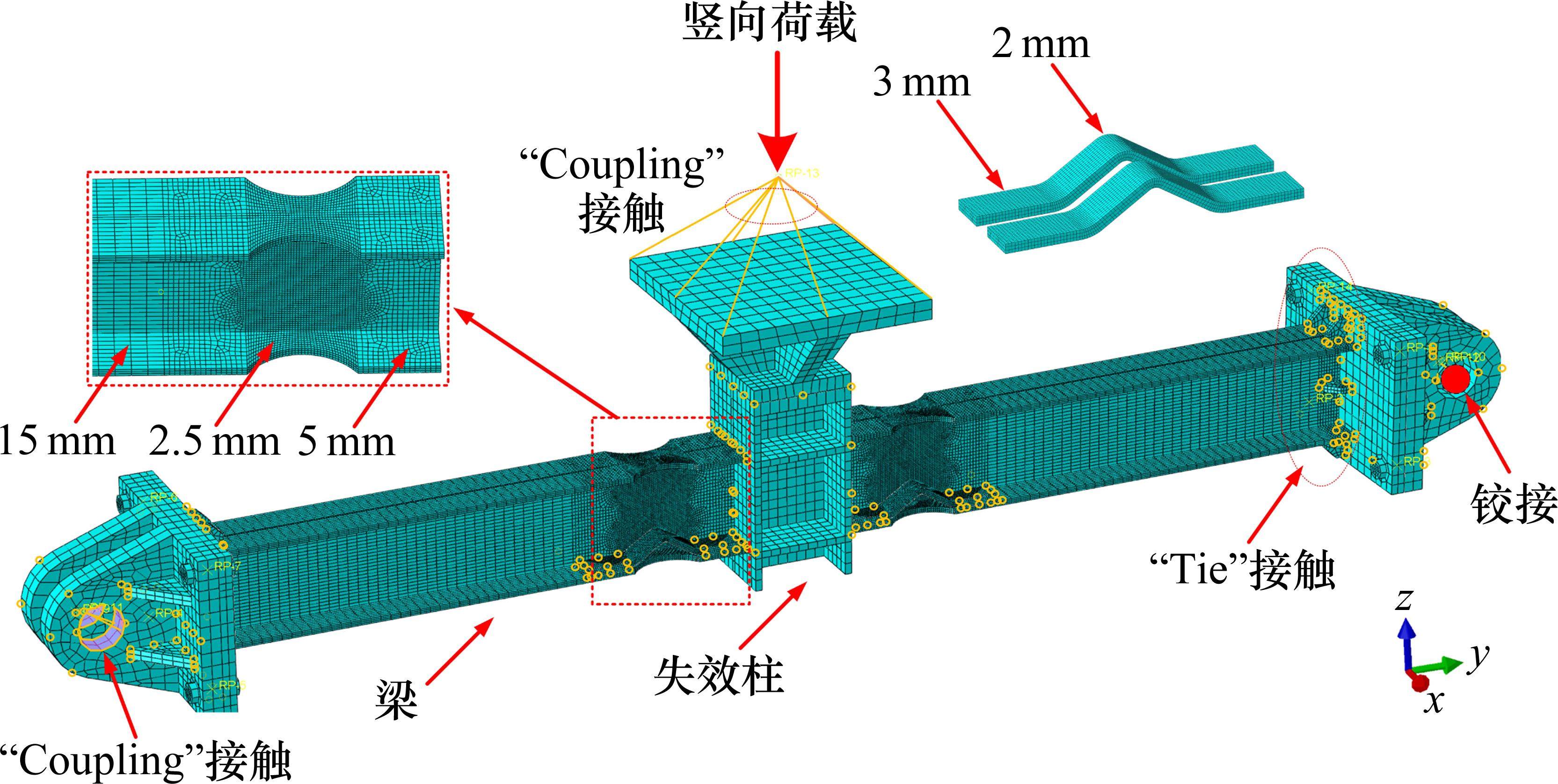
4.1 模型建立
使用ABAQUS软件对子结构进行准静态分析,如图15所示。试件中的所有部件均使用C3D8R实体单元建模,根据位置的不同选择不同尺寸的网格,将翼缘削弱区域加密至2.5 mm,加强板弯折部分进一步细化至2 mm,而梁的整体网格设为15 mm。模拟过程采用单元删除模拟钢梁断裂,忽略焊接残余应力和材料缺陷的作用,钢材焊接连接部位通过“Tie”命令绑定。为与试验过程相符,模型边界采用铰接约束,中柱采用位移加载控制,分析步的设置采用显式动力,该算法能够解决各部件之间的接触、模型的收敛及断裂问题。起始断裂应变ε0是断裂问题的关键[24],与应力三轴度η的关系为:
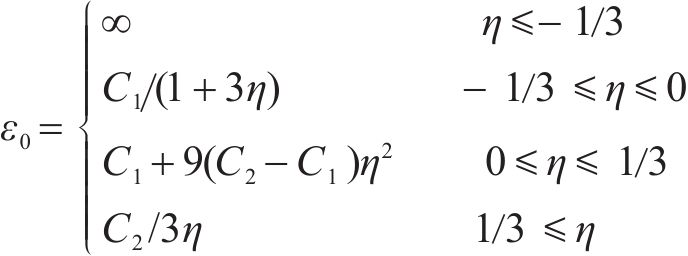
式中:C1和C2分别为纯剪切和单轴拉伸下的起始断裂应变,与材料的断面收缩率、真实应力(fy,T,fu,T)和真实应变(εy,T,εu,T)相关。模型中用到的材料特性列于表2。
| 类别 | E/GPa | fy,T/MPa | fu,T /MPa | εy,T | εu,T | C1 | C2 |
|---|---|---|---|---|---|---|---|
| 梁翼缘 | 197 | 294 | 544 | 0.001 49 | 0.097 6 | 0.088 7 | 0.235 7 |
| 梁腹板 | 199 | 334 | 527 | 0.001 67 | 0.075 6 | 0.077 36 | 0.261 3 |
| 柱 | 203 | 322 | 612 | 0.001 58 | 0.107 86 | — | — |
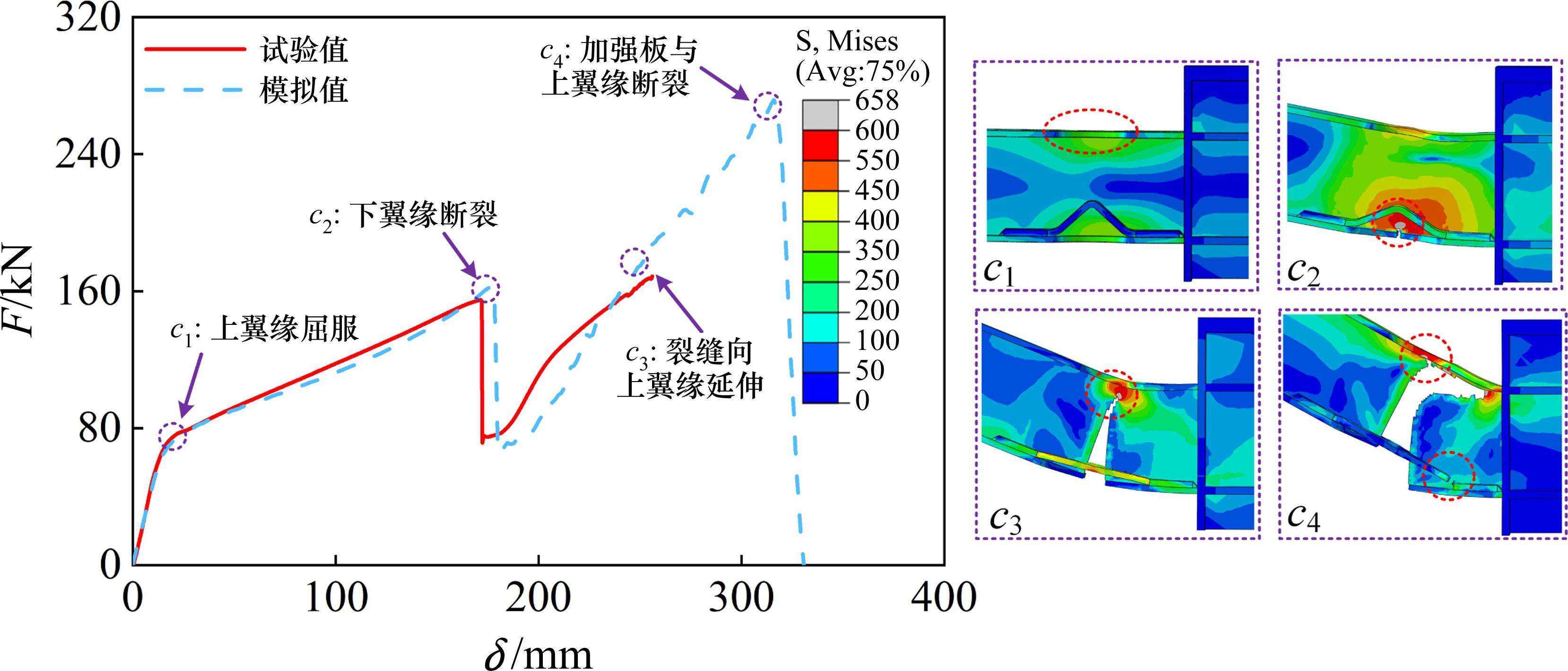
4.2 模型验证
试件RBS-h30与RBS-h40的数值模拟结果如图16和图17所示,其模拟结果分别对应于图7和图8中的试验结果。观察到模拟曲线在弹性段与试验曲线重合,塑性段也吻合良好。例如,模型RBS-h30的屈服荷载误差低于2%,断裂荷载误差为6.9%。下翼缘断裂后,采用单元删除法模拟断裂会引起曲线波动,但波动发展趋势仍与试验曲线一致。图16和图17还给出模型的应力演化过程,从弹性状态到上翼缘屈服,再到下翼缘断裂,模型变形及其破坏现象与试验结果相符。此外,试验加载终止时,裂缝发展仅穿过腹板中性轴,而数值模型补充了裂缝穿过整个腹板后,上翼缘和加强板协同受力的变形细节。对比表明,模拟结果可以反映试验结果的主要特征,模型可用于后续的参数分析。

5 参数分析
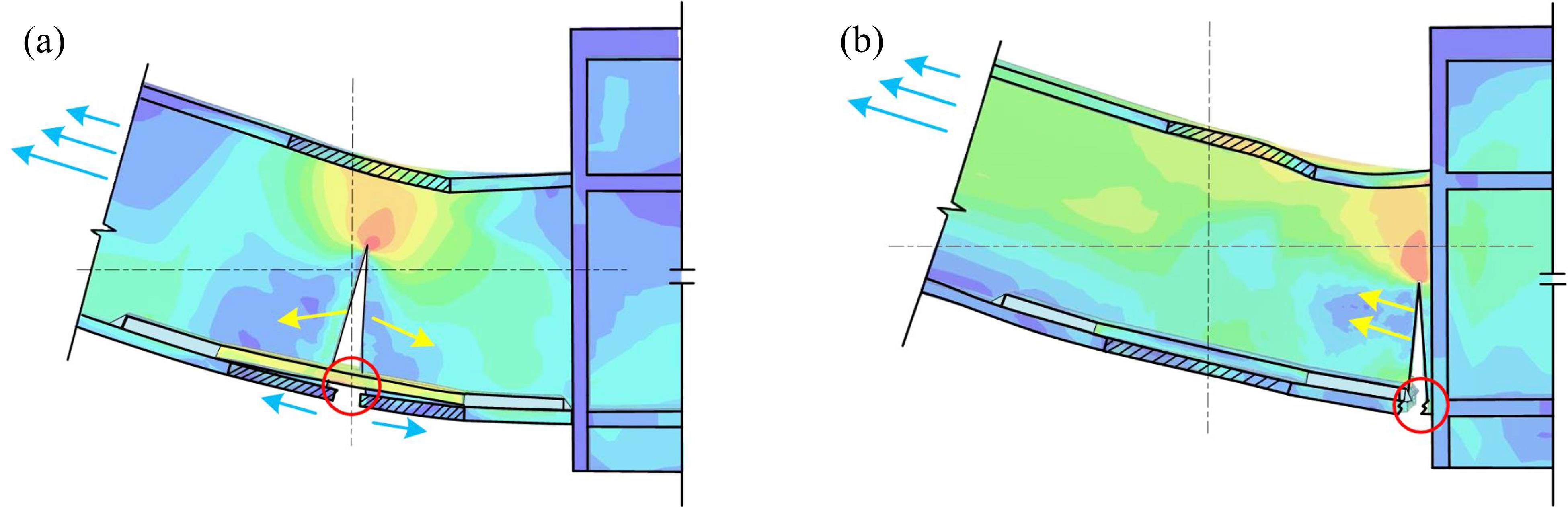
为分析不同参数对钢框架结构抵抗连续倒塌性能的影响,本节建立36个模型进行参数分析,模型编号基于翼缘削弱深度c和加强板弯曲高度h,比如削弱深度c为25 mm和弯曲高度h为30 mm的模型RBS-h30,可重新编号为模型RBS-c25-h30。首先分析不同翼缘削弱深度c和加强板弯曲高度h对模型承载能力和破坏模式的影响,根据分析结果,将模型的破坏模式归纳为2种类型:1) ModeⅠ,模型首先在翼缘削弱位置发生断裂,随后裂缝沿腹板向上发展(图18(a));2) ModeⅡ,模型首先在梁柱焊缝附近发生破坏,随后裂缝沿腹板竖直向上扩展(图18(b))。最后,针对2类破坏模式,叠加分析翼缘削弱长度a对模型承载能力的影响。
5.1 加强板弯曲高度
以模型RBS-c25-h30为基础,取加强板弯曲高度h=10~45 mm进行参数分析。此外,规范建议削弱深度c为梁翼缘宽度的0.20~0.25倍[11],补充分析削弱深度取下限值c=21 mm情况下,模型承载能力受弯曲高度h的影响,图19为各模型的荷载-位移曲线。
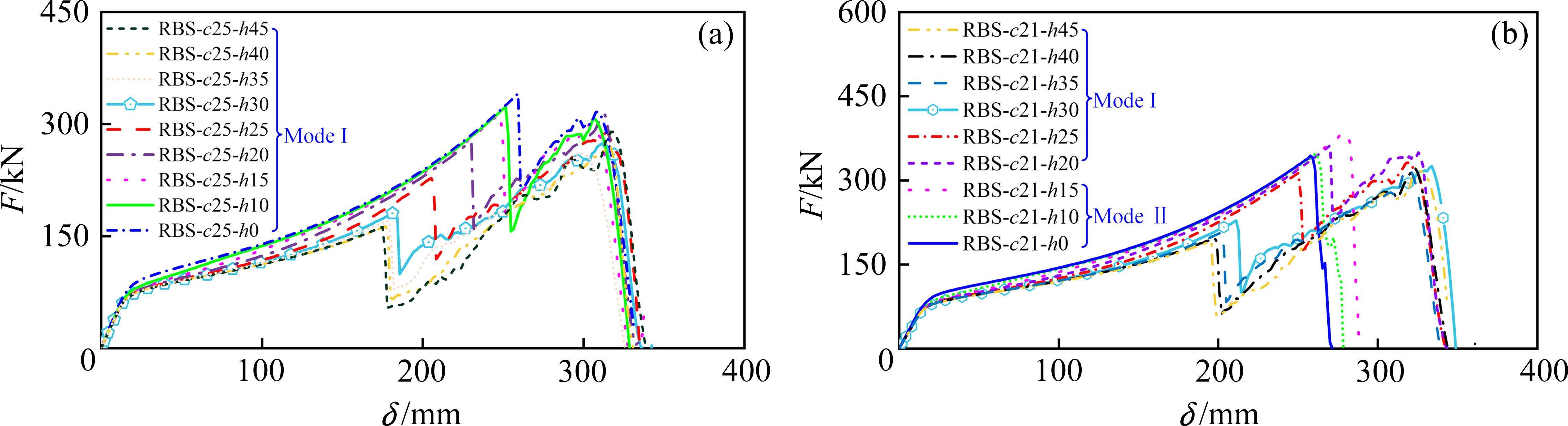
通过对图19(a)中曲线分析发现,当削弱深度c=25 mm时,模型的破坏模式没有受加强板高度h的影响,均为ModeⅠ,甚至采用高度h=0 mm的加强板也未改变模型破坏模式,说明采用规范建议的削弱深度上限值时,翼缘削弱在受力过程中占主导作用,而加强板对模型承载能力也起一定作用,荷载峰值随加强板高度h的降低而提高。值得注意的是,模型RBS-c25-h40和RBS-c25-h45在开裂前基本重合,加强板高度超过40 mm后作用有限。
当削弱深度c=21 mm时(图19(b)),模型的破坏模式随h的变化分为2类:h≥20 mm时,破坏模式为Mode Ⅰ,模型的峰值荷载随着h的降低而增加;h<20 mm时,破坏模式为Mode Ⅱ,峰值荷载随着h的降低而减小,但h超过40 mm后作用不明显。模型RBS-c21-h15的峰值荷载最高,但最终破坏模式为ModeⅡ,使模型在梁柱焊接处发生脆性破坏,没有二次承载能力,对结构的抗连续倒塌贡献有限。而模型RBS-c21-h20的峰值荷载仅比模型RBS-c21-h15的值低5%,最终破坏模式为ModeⅠ,在翼缘断裂后能够继续承受荷载,具有抗连续倒塌的二次防御能力。因此,加强板弯曲高度与翼缘削弱深度共同影响承载能力和破坏模式。
5.2 梁翼缘削弱深度
在RBS-c25-h30的基础上研究梁翼缘削弱深度c对试件承载能力的影响,取c=0~25 mm。为增加样本,结合图19(a)中破坏模式分界点的模型RBS-c21-h20,分析h=20 mm时模型受参数c的影响,图20为各模型的F-δ曲线与破坏模式。
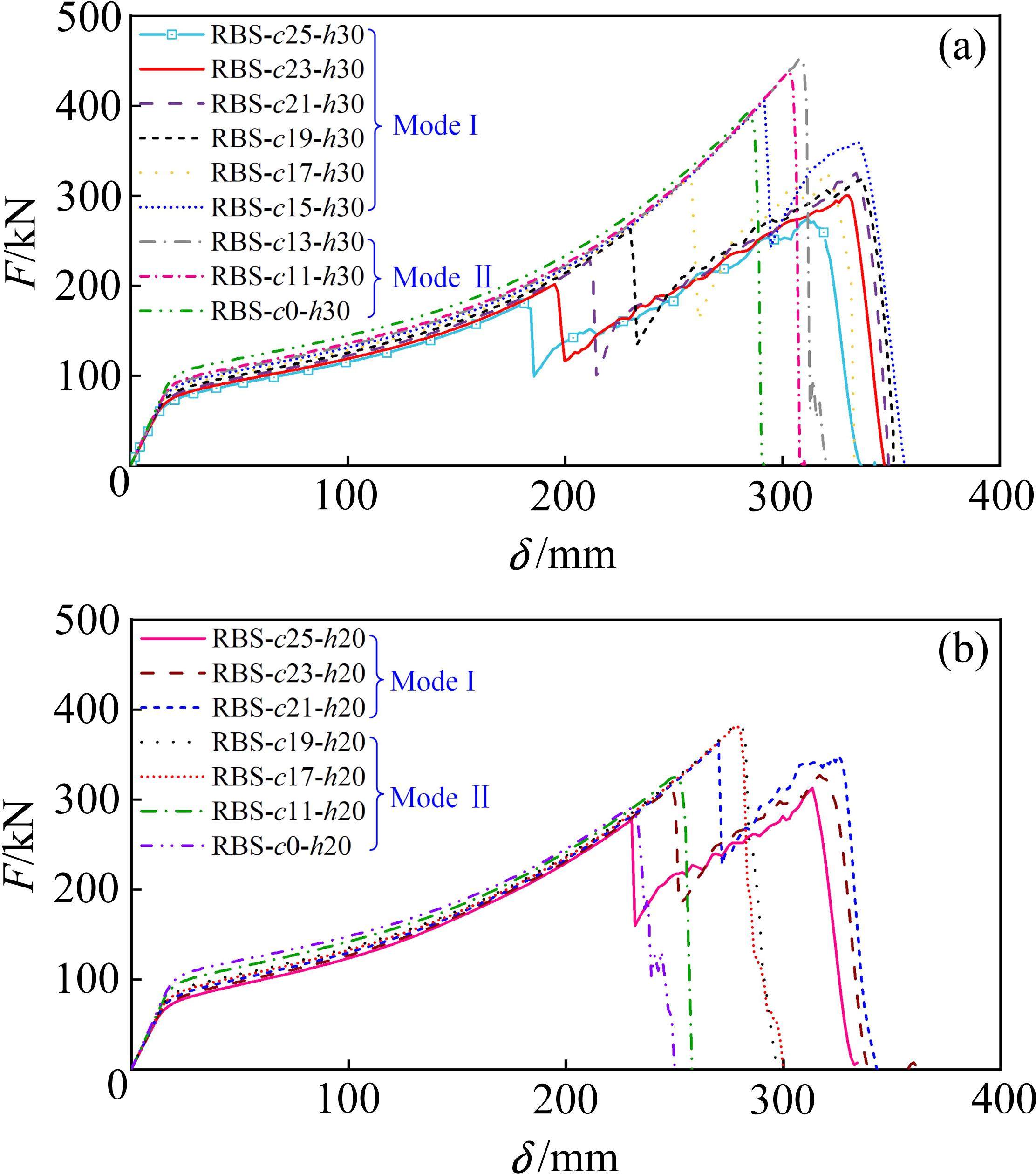
通过对图20中曲线分析发现,当加强板弯曲高度h=30 mm时,模型的峰值荷载随着削弱深度c的减少呈现先升高后降低的趋势,并在c=13 mm时达到最大值453.4 kN。同时,c=13 mm也是破坏模式的分界点,c>13 mm时破坏模式表现为ModeⅠ,c≤13 mm时破坏模式表现为ModeⅡ。模型RBS-c15-h30的峰值荷载为405.7 kN,略低于模型RBS-c13-h30,但其初始开裂发生在下翼缘削弱位置,随后伸直的加强板与剩余截面协同承受荷载,可以提供二次承载能力,这种受力模式有利于结构的抗连续倒塌。
当加强板弯曲高度h=20 mm时,模型的峰值荷载随着削弱深度c的增加也呈现先升高后降低的趋势,并在c=19 mm时达到最大值383.4 kN。破坏模式的变化规律为:c>19 mm时为ModeⅠ;c≤19 mm时为ModeⅡ。同时,对比模型RBS-c21-h20和RBS-c19-h20,虽然两者的峰值荷载接近,但前者在下翼缘削弱位置断裂后仍能继续承受荷载,对结构抗连续倒塌能力的提高有显著优势。
5.3 梁翼缘削弱长度
选取2个不同破坏模式的代表性模型,其中,模型RBS-c25-h30的破坏模式为ModeⅠ,模型RBS-c19-h20的破坏模式为ModeⅡ,翼缘削弱长度均为100 mm。规范建议削弱长度a为梁高度的0.65~0.85[11],因此以代表性模型为例,补充削弱长度a=110、120和130 mm的模型,进一步分析翼缘削弱长度a对承载能力的影响。图21为各模型的荷载-位移曲线。
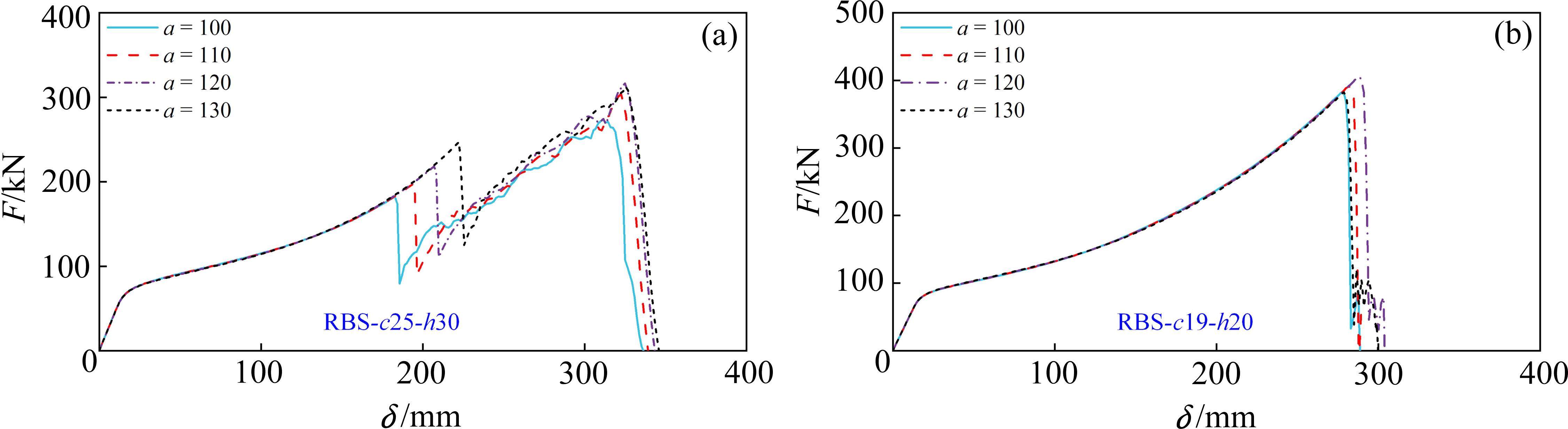
通过对图21(a)中各曲线对比分析发现,模型RBS-c25-h30的荷载峰值随削弱长度a增加而提高,这是由于当破坏发生在翼缘削弱位置时,增大模型削弱长度,可以使削弱截面和未削弱截面之间的过渡更加平缓,减小削弱截面附近的应力集中,有利于大变形时发挥悬链线效应。对于图21(b)中模型RBS-c19-h20,削弱长度a为100、110、120和130 mm对应的模型峰值荷载分别为382.4、407.1、390.9和383.8 kN,峰值荷载差异少于5%,表明当破坏发生在梁端时,削弱长度a变化对模型的承载能力影响有限,更没有改变ModeⅡ破坏模式。
6 结论
1) 加强板在小变形阶段作用有限,但随着变形增大,加强板逐渐拉直作为替代路径,协助钢梁承受荷载,使试件的变形能力和承载能力分别提高了21.7%和21.8%。若加强板弯曲高度过大,会延迟其与梁翼缘的协同工作,使加强板提供的荷载传递效率下降。
2) 引入悬链线贡献系数和弯曲贡献系数,进一步量化弯曲抗力和悬链线抗力对总抗力的贡献。加强板改进翼缘削弱节点的悬链线效应不仅由钢梁提供,还由逐渐拉直的加强板提供,且悬链线贡献系数是基础试件的1.84倍。
3) 翼缘削弱深度和加强板弯曲高度影响试件的破坏模式,根据钢梁的破坏位置分为ModeⅠ和ModeⅡ2种类型:ModeⅠ的裂缝始于翼缘削弱处,ModeⅡ的裂缝始于梁柱焊缝附近。破坏模式为ModeⅠ时,荷载峰值随削弱长度增加而提高;破坏模式为ModeⅡ时,削弱长度变化对承载能力影响有限。
4)试件峰值荷载随着削弱深度的增加,呈现先升后降的变化规律。削弱深度取规范建议上限值时,破坏模式为ModeⅠ,峰值荷载随加强板弯曲高度降低而增加,采用规范建议的下限值时,承载能力随加强板弯曲高度先升高后降低。
乔惠云,林誉,韦建刚等.翼缘削弱改进型节点的抗连续倒塌分析[J].铁道科学与工程学报,2025,22(03):1229-1242.
QIAO Huiyun,LIN Yu,WEI Jiangang,et al.Progressive collapse resistance of improved joints with reduced beam sections[J].Journal of Railway Science and Engineering,2025,22(03):1229-1242.

