高速列车在通过曲线段遭遇大风时,空气动力学效应异常复杂且极具挑战性,复杂气动环境下的安全运营问题日益凸显[1]。强侧风环境不仅考验列车的抗风稳定设计,还直接关系到乘客安全与铁路系统运营效率。在高速与大风双重因素交织的场景下,列车横向动态响应加剧,极易发生失稳,严重时甚至导致倾覆与脱轨,对铁路运输安全构成重大威胁。我国独特的地理特征决定了某些线路区域(如兰新线著名的百里风区、南疆线的前百公里路段)经常遭受极端风力影响[2],历史上这些区域频繁发生的行车安全事故,不仅造成了人员伤亡和财产损失,也严重干扰了铁路运输秩序。因此,如何在强风条件下确保高速列车运行的安全稳定,成为亟待解决的紧迫课题[3-5]。针对侧风环境下高速列车通过安全性,国内外学者进行了大量的研究工作。BAKER[6]基于APT-P列车模型进行了大量的风洞台架试验,结果表明侧风下该列车速度增加5%,倾覆增加12%。田红旗[7]通过不同类型风洞试验测量列车气动阻力、升力、横向力以及相应力矩、列车压力分布、列车尾部流场,并建立了一系列理论关系式。刘伟等[8]建立了高架线和路堤2种不同路况下侧风作用于列车的空气动力学模型并进行数值计算,结果表明有侧风作用时,两侧车轮的轮轨力变化明显,迎风侧减载,背风侧增载,背风侧车轮受到很大的轮轨横向力。孙丽霞等[9]通过空气动力学和车辆动力学方法对横风作用下的高速列车空气动力学模型进行分析,结果表明无风工况下车辆易发生二次蛇行,风载作用下车辆易发生一次蛇行。周素霞等[10]对不同风向角下的某型动车组的车辆运行安全性进行仿真模拟分析,结果表明风速20 m/s、车速300 km/h下的105°风向角的风载对列车运行安全性影响最大。增强铁路运输竞争力的一个关键策略是提升列车运行速度,但提速往往伴随着异常振动和运行安全性问题的发生,因此采取先进的车体振动控制技术成为必要措施,将二系横向悬挂作为主动作动器对车辆系统施加主动控制力是目前使用较多的方法[11-13]。杨建伟等[14]对高速铁道车辆横向二系半主动悬挂系统提出了加速度阻尼控制方法,其具有对传感器和测量系统误差不敏感的优点。刘沿修等[15]建立整车横向简化7自由度非线性动力学模型,将二系横向减振器的理想主动力表示为车体或转向架横向位移和速度的三次多项式函数,证明了合理设计天棚/地棚阻尼和刚度控制律及参数能够有效调控车辆系统分岔速度及极限环幅值。李德仓[16]基于二系主动悬挂的列车横向振动模型,研究对侧风环境下高速列车运行姿态和速度主动控制策略,仿真表明在不同风速和车速情况下,自适应PID预测控制能够有效地抑制侧风激励导致的列车车体横向振动加速度响应,提高列车运行的安全性。DI GIALLEONARDO等[17]提出了横向和侧滚联合控制方法,采用基于液压互联作动器的主动防侧倾装置和基于液压主动横向悬架对列车进行主动控制。GAO等[18]基于库伯理论和谐波叠加法,计算了随机侧风作用下的非定常气动载荷,针对侧风波动和随机轨迹谱引起的垂直振动,分别采用天棚阻尼和磁流变模糊半主动控制策略抑制振动幅值,提高了运行安全性。综上所述,目前侧风作用下高速列车的研究大多局限于被动工况下运行安全稳定性分析与列车运行安全域的判定,对于在侧风下运用主动悬挂技术改善车辆动力学性能的研究较少,且未兼顾车体姿态的控制。因此,本文针对高速列车在实际运行过程中受横风影响下的横向振动问题,分析不同风载作用下的车辆动力学行为规律,通过以调整车体姿态为目标的横向振动模态分析,设计了天棚阻尼控制律、加速度反馈PID控制律和滑模控制律,对比分析了3种控制律对车体横向振动和倾覆安全性的改善效果。针对不同类型风载荷、风向角和风速下车辆运行工况,从时域上研究所提控制方法对车辆运行安全性和运行平稳性的控制效果。
1 车辆系统动力学模型及风载模型
1.1 车辆动力学模型
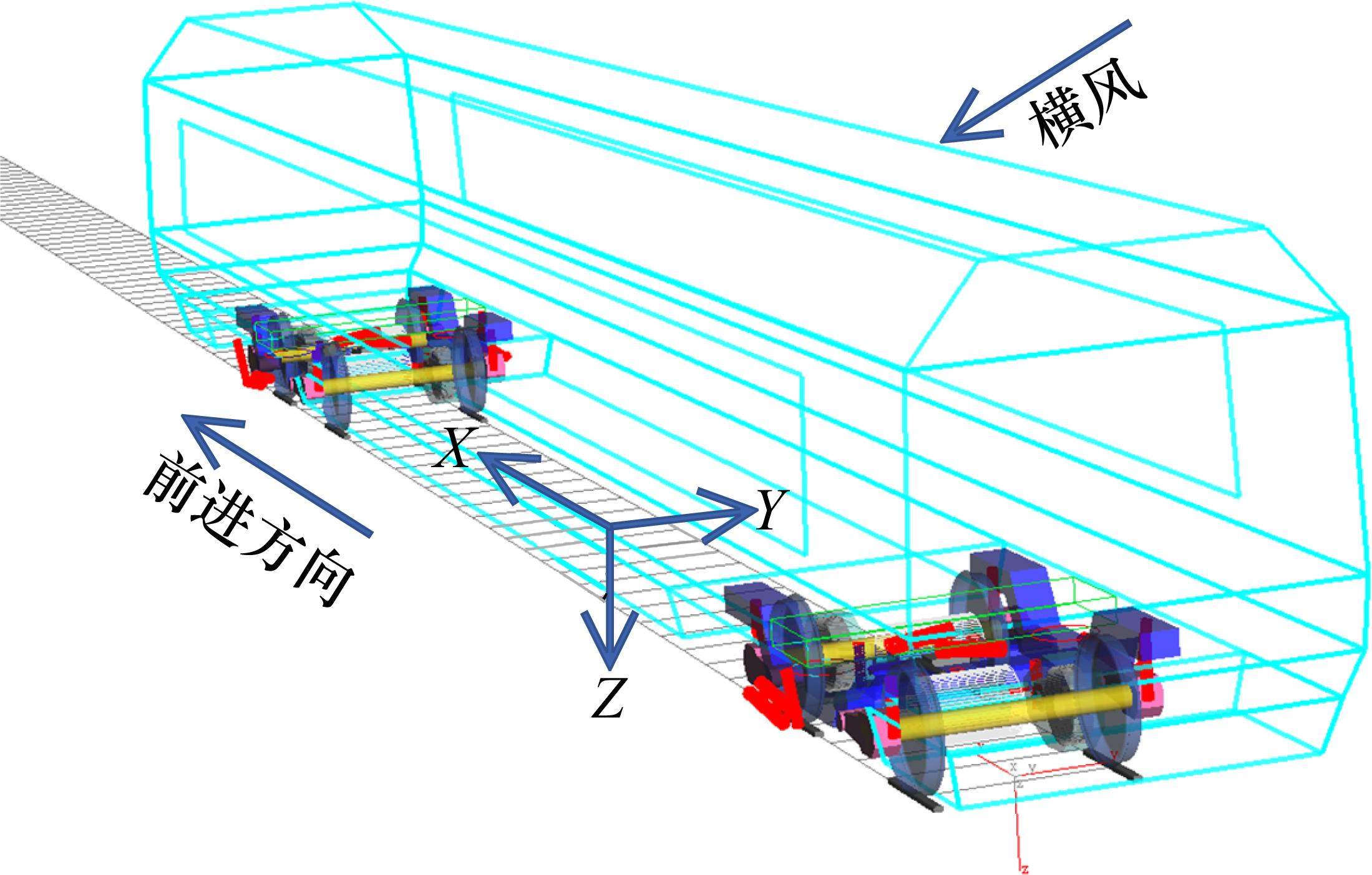
以某型号高速车辆为研究对象,使用通用多体动力学软件Simpack建立车辆系统非线性动力学模型,如图1所示。车辆系统考虑为经典多刚体弹簧-阻尼振动系统;对于车体、构架、轮对和电机,每个刚体考虑纵向、垂向、横向、侧滚、点头和摇头6个自由度,转臂和齿轮箱仅考虑点头自由度,共66个自由度;悬挂元件和轮轨关系考虑为非线性。车辆模型相关参数见文献[1]和文献[19]。根据风载模型计算得到风载荷结果,将其等效施加到车体质心位置。
横风作用下的车辆系统动力学方程可描述为:
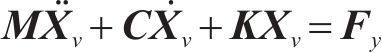
式中:M、C、K分别为车辆的质量、阻尼、刚度矩阵;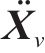
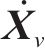
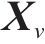
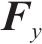
1.2 典型风载激励特征及模拟
基于瞬态中国帽子风模型和非定常随机风载荷模型计算风载荷,并直接作用到车体上。
瞬态帽子风模型是《风载评估实验要求标准》[20]提出的一种考虑到瞬态效应的风载荷模型,其风速的时间历程非常类似于中国的一种帽子,故名“中国帽子风”,其载荷时间历程见图2。
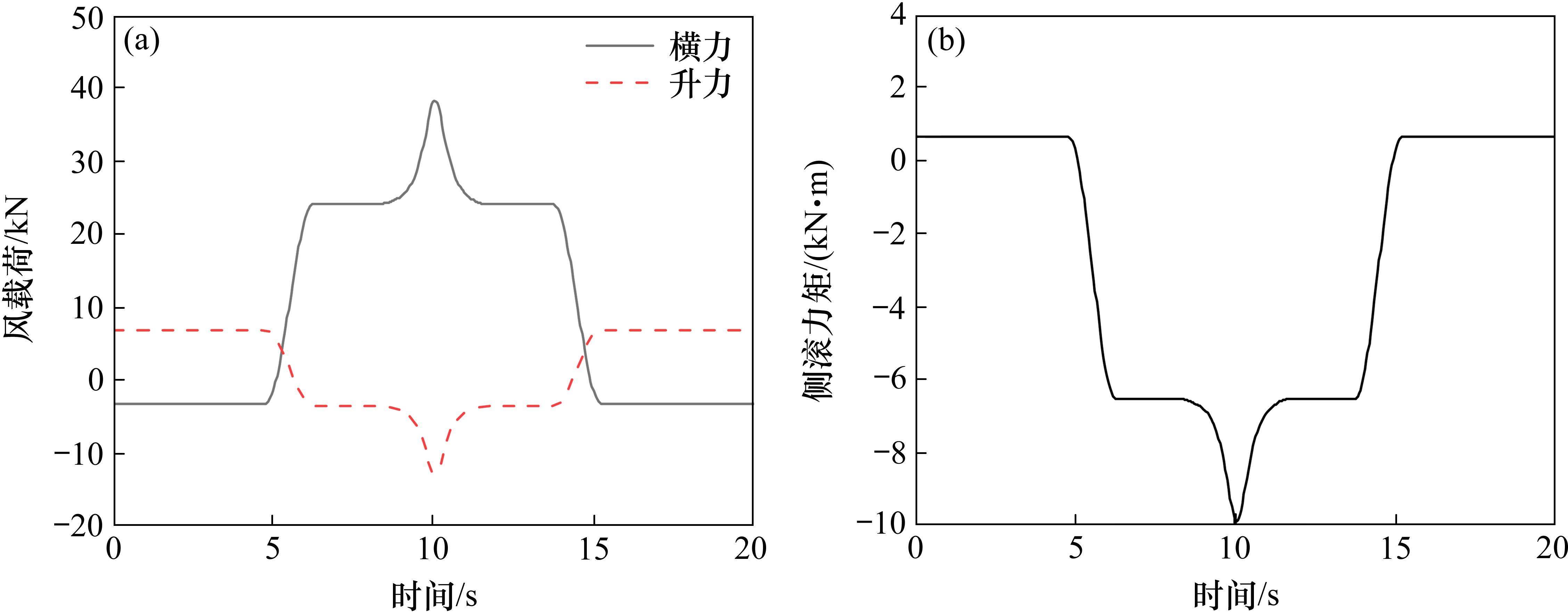
对于非定常随机风载荷模型[21]采用经典可靠的Simiu谱进行模拟,通过Simiu谱可以计算出AR[21]模型,进而通过傅里叶变换实现功率谱与自相关函数之间的相互变换,使用Levinson递归算法[21]接触AR模型参数便可得到风随机信号,根据力与力矩平衡原理可得到相关风力,如图3所示。
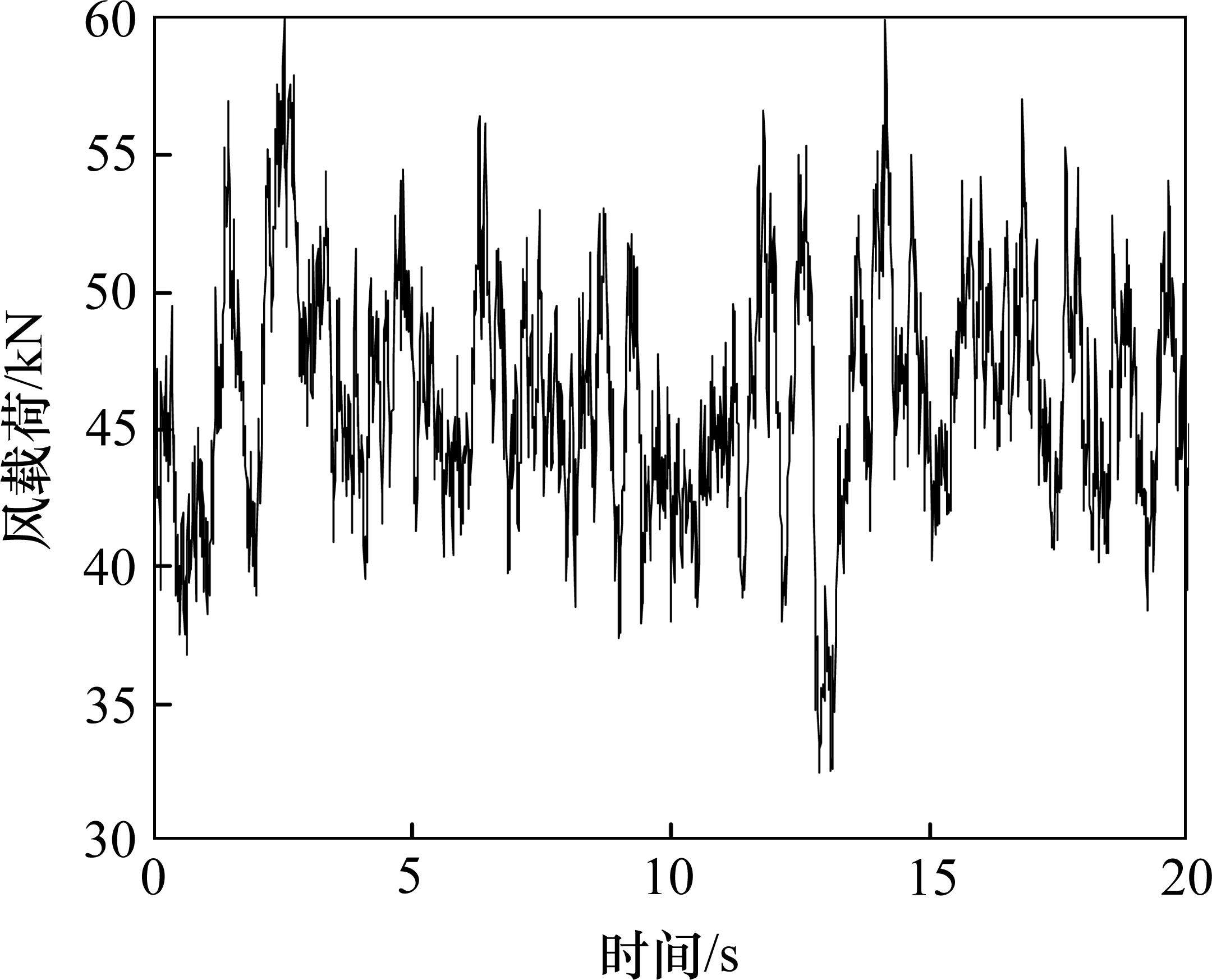
1.3 联合仿真模型
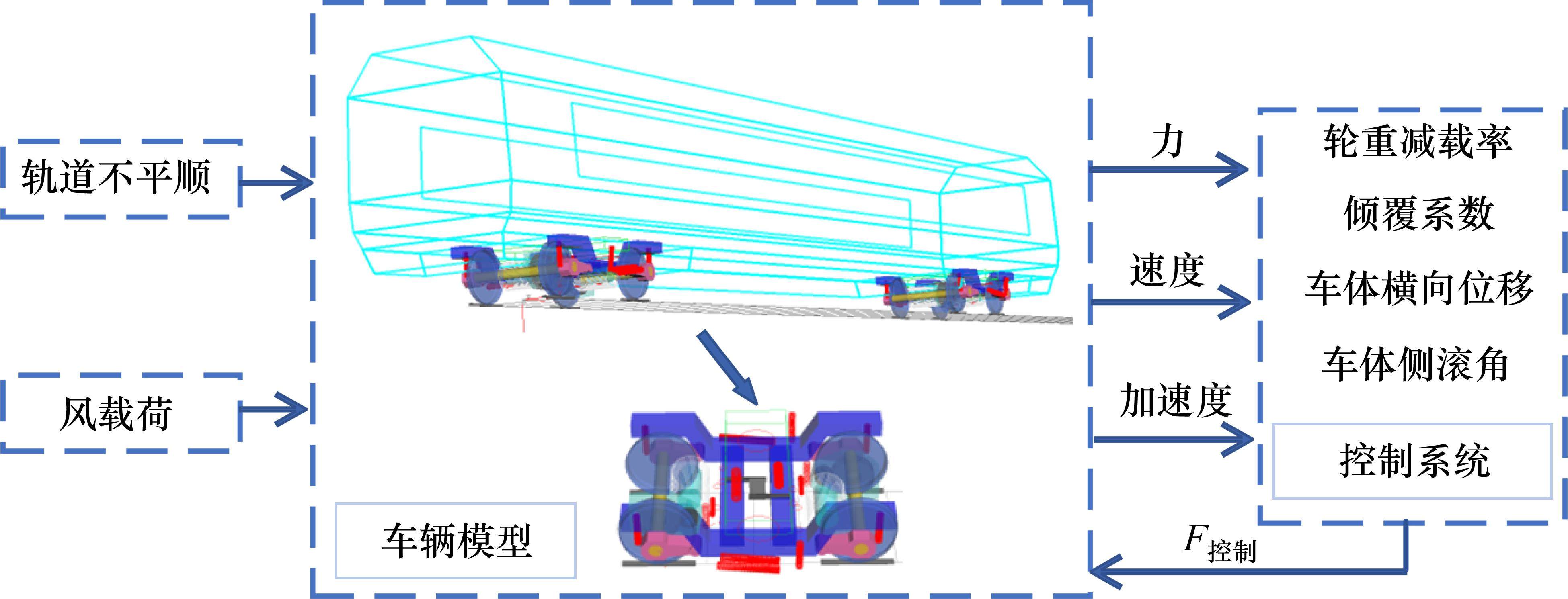
将整车三维非线性动力学模型通过simat接口与Simulink多域仿真控制模块结合,以实现车辆悬架主动控制,见图4。在整车三维模型中,施加风载荷和轨道谱激励,并将车辆系统力、速度和加速度等实时状态量传送到主动悬挂控制器中,主动控制器根据接收的状态信号量计算得到主动控制力,并反馈给车辆系统,从而实现车辆系统的主动控制功能。
2 车辆主动横向悬挂及其控制方法
车辆系统模型中共有4根二系横向减振器,本文将距车体中心最远端的2根减振器替换为主动作动器以实现主被动并联控制。
2.1 天棚阻尼半主动控制
天棚阻尼(Sky-Hook Control,SH)法[22-23]是目前较为适用的悬挂控制方法,其出发点是以一个虚拟的“天棚减振器”连接在车体与一堵虚拟墙之间(天棚),其中虚拟墙保持绝对静止,利用假想的与天棚固连的阻尼器来达到车体减振的目的。本文采用连续型天棚阻尼控制,其阻尼系数可以连续变化,提供更多的阻尼耗散功,控制力表达式为:
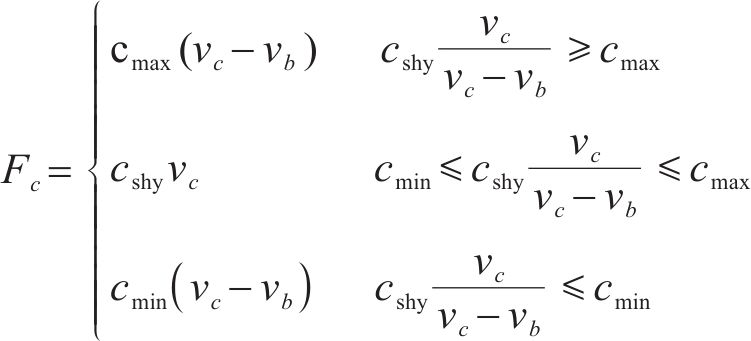
式中:cshy为理想天棚阻尼系数;cmax为最大阻尼系数;cmin为最小阻尼系数,文中分别取150、100和3 (kN∙s)/m。
2.2 加速度反馈PID半主动控制
PID是一种常见的反馈控制算法[24-25],含有比例(Proportion)、积分(Integration)、微分(Differentiation)这3个参数,其控制原理是一种基于系统输出与输入之间偏差的调节方式。在PID控制系统中,控制器的输出值由系统设定值与实际输出值之间的偏差、偏差的积分以及偏差微分的线性加权组合所决定。通过调整比例、积分和微分参数的值,能够有效地控制系统的稳定性和响应速度。
本文采用开关型PID控制策略,其结合了PID算法和天棚阻尼策略的开关判断思想,表达式为:
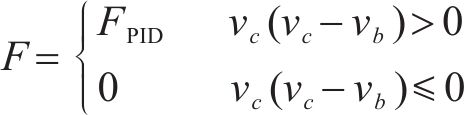
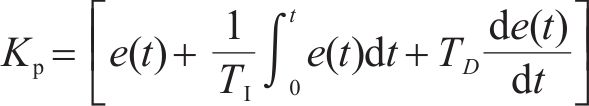
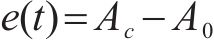
式中:F为半主动控制力;FPID为主动控制力;KP比例系数取3 800;TI积分系数取300;TD微分系数取1;e(t)为系统偏差;Ac为车体横向加速度;A0理想加速度取0 m/s2。
通过模拟系统在不同PID参数下的动态响应,比较响应时间、超调量和振荡程度,进而确定相关参数。
2.3 滑模控制
滑模控制[26](Sliding Mode Control)是一种在动态系统控制中广泛应用的非线性控制策略。其核心思想是通过引入一个“滑模面”[27-30],使系统状态在该面上快速滑动,从而实现对系统的稳定控制。
由于上文提及二系横向减振器布置方法为主被动并联控制,所以本文滑模控制方法设定车体横向位移和摇头角度作为滑模面:
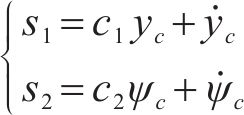
滑模变量导数形式为:
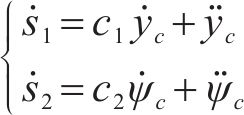
式中:si为滑模变量;ci为增益系数,i=1,2;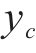
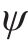
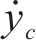
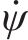
为计算作动器理想控制力,需计算车辆系统运动微分方程,使滑模变量导数方程中的车体横移、摇头模态振动加速度以力的形式表现,进而得出包含车体所有主动力和被动力的微分方程:
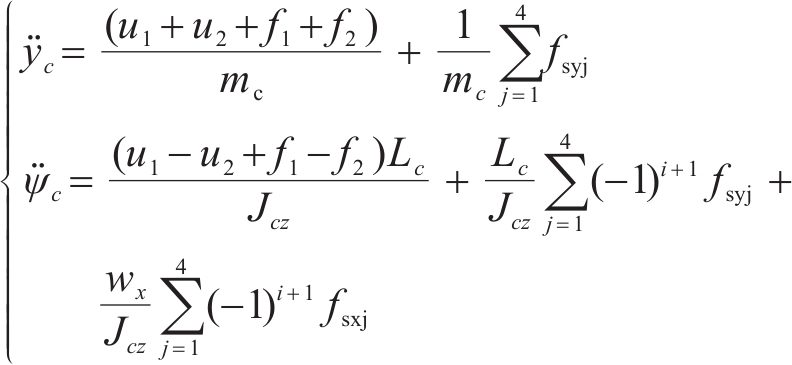
式中:u1、u2分别为车体前端左侧、后端右侧二系横向减振器主动控制力;f1、f2分别为车体前端右侧、后端左侧二系横向减振器被动控制力;mc为车体质量;fsyj、fsxj分别为二系空气弹簧产生的横向力和纵向力,j=1,2,3,4;Lc为前后二系横向减振器纵向跨距之半;Jcz为车体摇头转动惯量;wx为左右二系空气弹簧跨距之半。
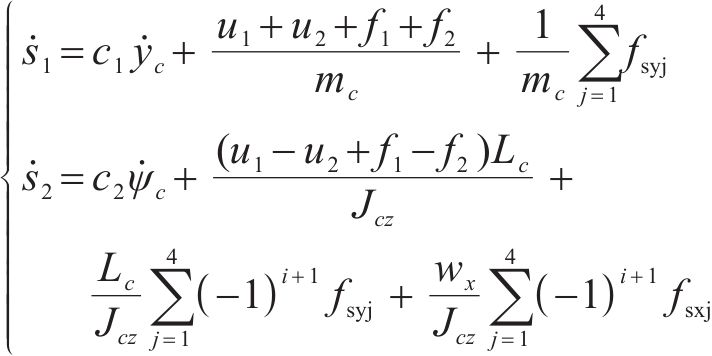
将式(9)简化为:
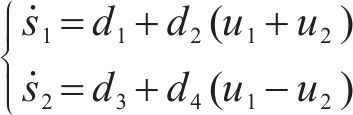
其中:
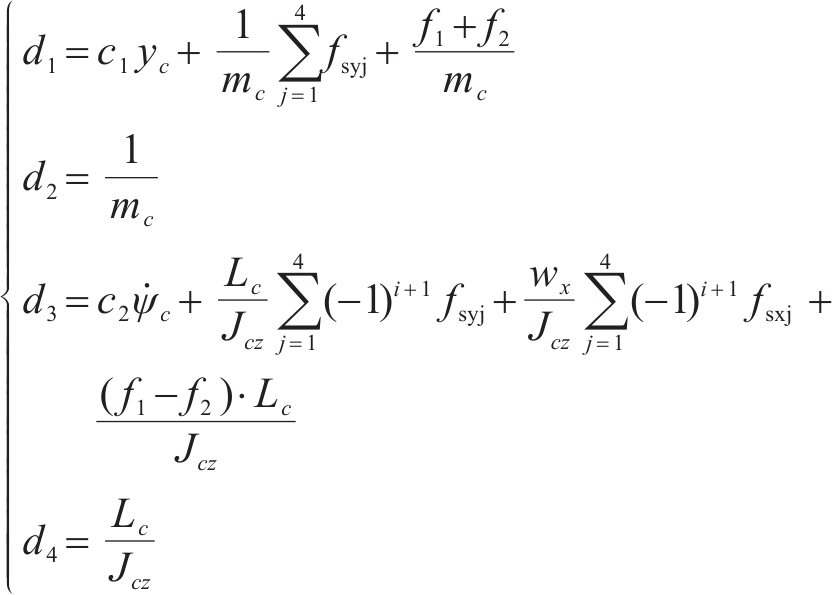
进而可得出理想控制力:
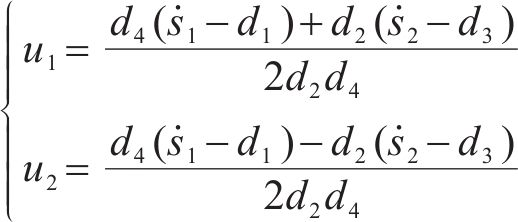
3 不同风载条件对被动车辆动力学性能影响分析
3.1 帽子风切变时间的影响
在车辆通过曲线时,设置如表1所示的运行工况,仅考虑帽子风切变时间[20]对于车辆动力学性能的影响。
| 项目 | 缓+圆+缓/m | 曲线半径/m | 车速/(km∙h-1) | 风速/(m∙s-1) | 风向角/(°) | 设计超高/mm |
|---|---|---|---|---|---|---|
| 数值 | 500+300+500 | 4 000 | 300 | 20 | 90 | 110 |
根据《机车车辆动力学性能评定及试验鉴定规范》[31]规定,轮轴横向力应符合条件H<15+P0/3,本文中轮轴横向力限值为62 kN;轮轨垂向力规定限值为P≤170 kN;脱轨系数Y/Q规定限值为0.8;轮重减载率
使用不同风切变时间[20](0.5、1、2、3、4 s)获得帽子风模型得到相关动力学指标,见表2。可见,在侧风影响下,车辆系统产生了一定的强迫振动,其中,横向振动与垂向振动问题均存在,但垂向振动响应较为微弱,更应重点关注横向振动问题。
风切变 时间/s | 轮轴横向力/kN | 轮轨垂向力/kN | 脱轨 系数 | 轮重减 载率 |
|---|---|---|---|---|
| 0.5 | 34.85 | 114.07 | 0.33 | 0.57 |
| 1 | 32.82 | 100.37 | 0.32 | 0.55 |
| 2 | 30.66 | 90.14 | 0.29 | 0.54 |
| 3 | 29.07 | 89.44 | 0.23 | 0.51 |
| 4 | 28.45 | 89.15 | 0.20 | 0.51 |
随着风切变时间增加,脱轨系数、轮重减载率、轮轴横向力和轮轨垂向力都呈下降趋势,其中在风切变时间为0.5 s和3 s时,轮轨垂向力减小了25 kN。风切变时间超过3 s后,动力学性能指标之间无明显差异,表明风切变时间超过3 s对动力学性能无明显影响。
3.2 风向角的影响
设定车辆在300 km/h速度下直线运行,仅施加帽子风载荷,不考虑轨道谱激励影响,选定风向角范围为0°~180°,与车辆前进方向相同为0°,设定风向角梯度为10°,结果见图5。可以得知,风向角为锐角时会引起车辆更大的响应;在风向角从0°~90°变化时,倾覆系数呈上升趋势,在90°之后呈对称的下降趋势,在90°风向角时出现最大值为0.35;轮重减载率呈现出了同样的增减趋势,在90°风向角时取得最大值为0.31。可见,垂直于车体的侧风引起的振动响应更为明显,后文应以90°风向角作为研究工况。
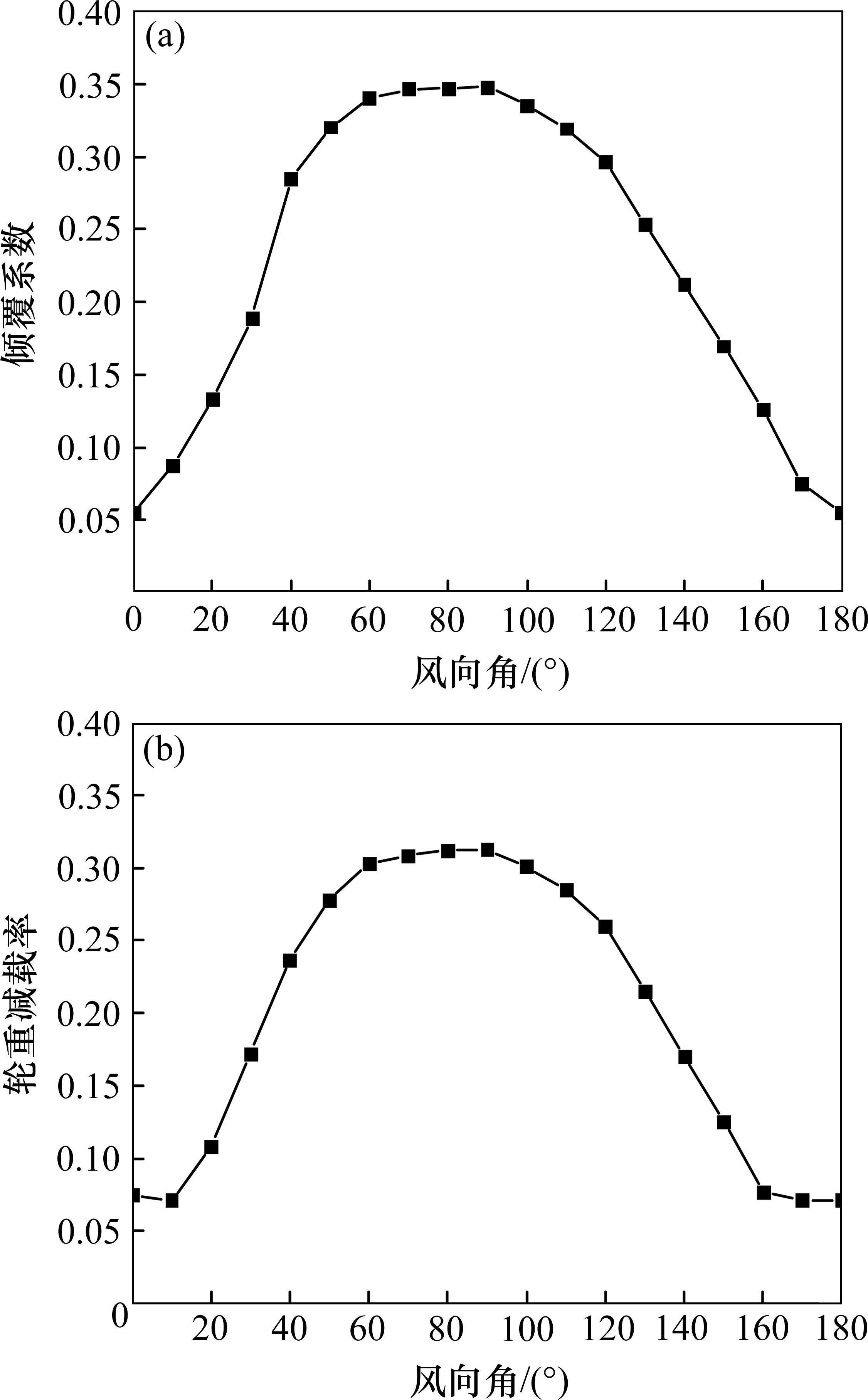
在随机风载荷与轨道谱激励共同作用下,得到了车体横向加速度(最大值)以及横向、垂向平稳性指标,见图6。在50°~130°风向角范围内,3项指标均显著增大,在80°风向角时,横向平稳性和垂向平稳性指标达到最大值,其中横向平稳性指标接近限值3.0,而车体横向加速度在90°风向角时达到最大值。
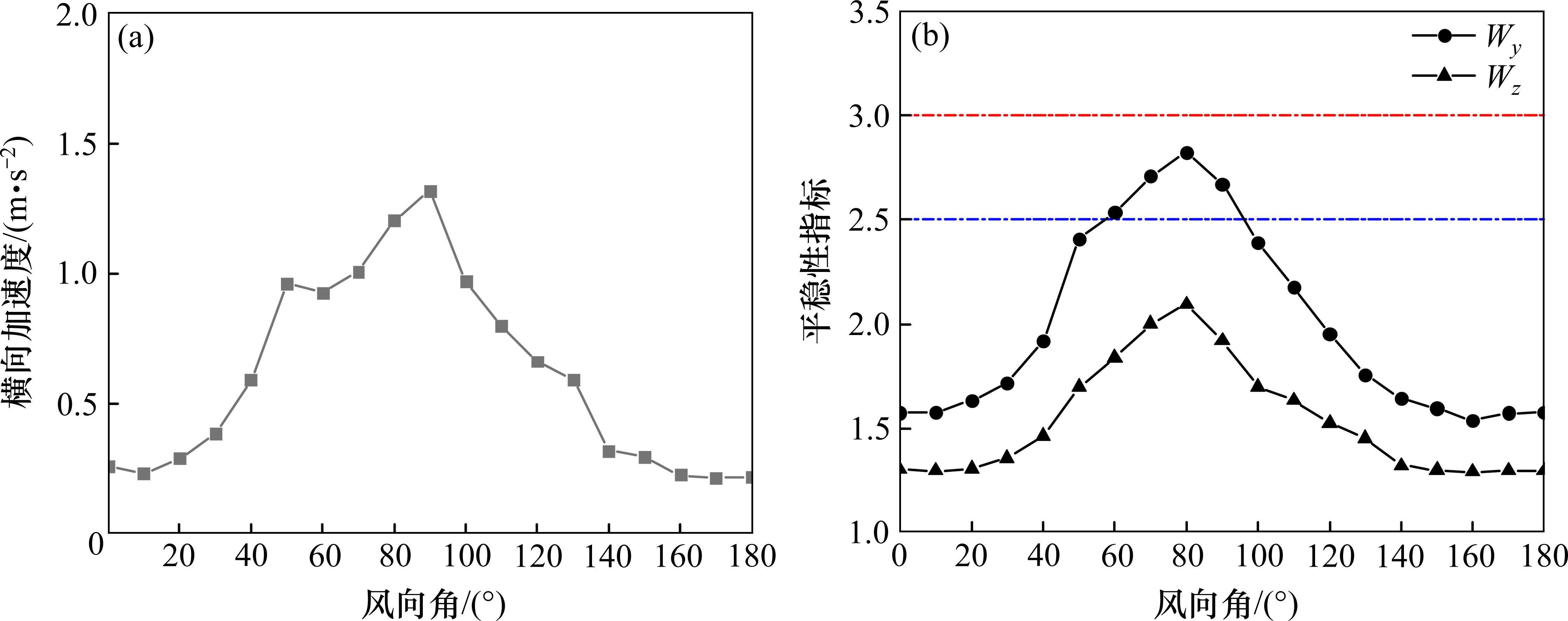
3.3 车辆运行安全域
根据《机车车辆动力学性能评定及试验鉴定规范》[31]对各项安全性指标限值规定,可以通过插值计算方法得到在某一车速下,高速车辆安全运行时所允许的最大风速。在帽子风载荷下车辆系统部分动力学性能指标见图7。
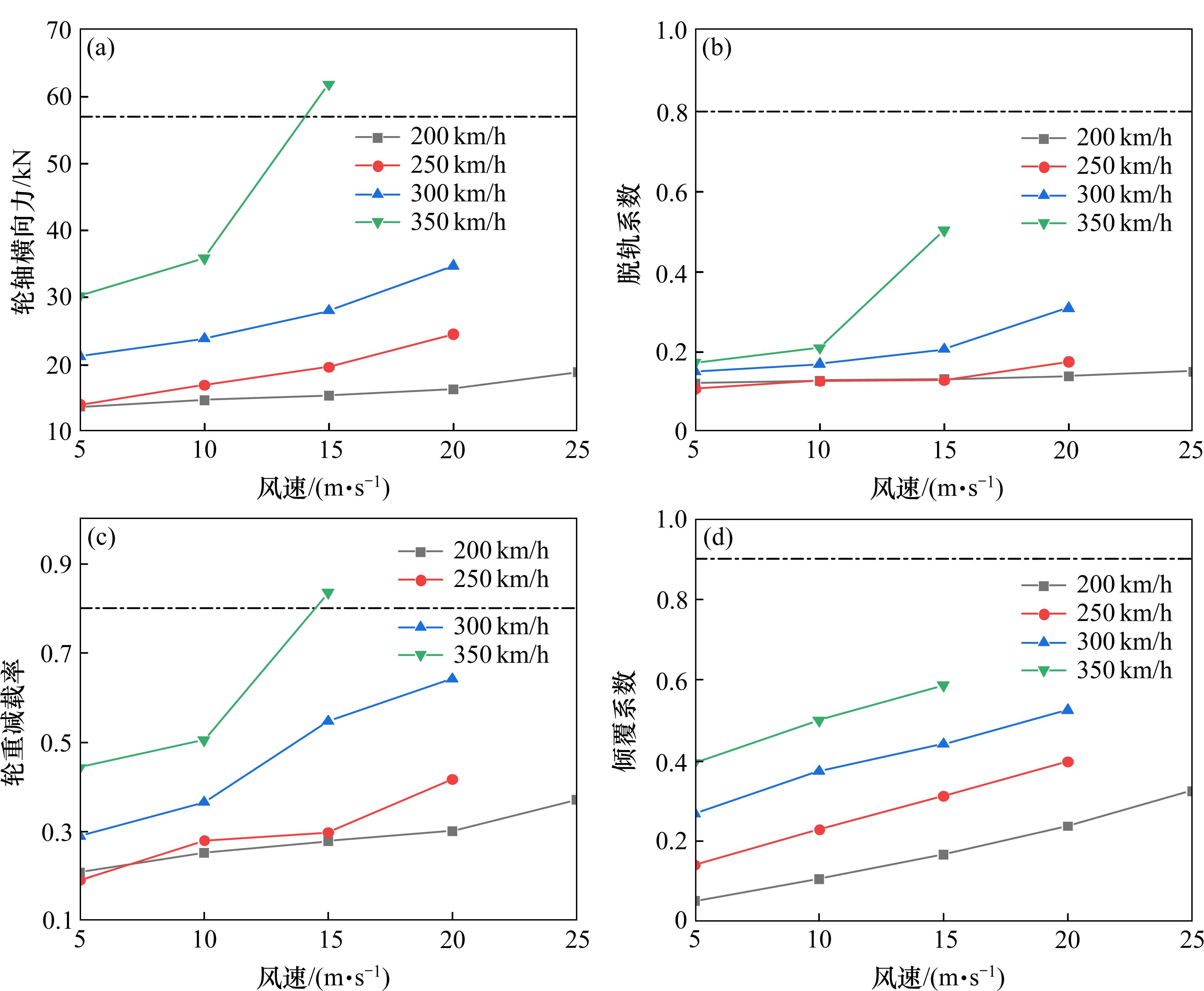
仿真所得脱轨系数和倾覆系数均远小于试验规范规定限值。轮轴横向力和轮重减载率仅在车速350 km/h、风速15 m/s的工况下超出规定限值。当车速超过300 km/h时,以轮轴横向力和轮重减载率为安全判据计算得到的最高风速最小,在车速不超过250 km/h时,以倾覆系数作为安全评估指标计算所得最高允许风速最小。当车辆运行速度为350 km/h、风切变时间为2 s时,安全运行所允许的最大风速为14.47 m/s。
4 主动横向悬挂控制效果分析
4.1 不同风载激励下控制效果
在高速车辆行驶过程中受到侧风影响下,会出现二系横向减振器行程过大而碰触止挡的情况,由于止挡刚度过大,会对列车运行安全产生恶劣的影响,因此下文将二系横向悬挂横向行程作为验证控制有效性的指标之一,车辆系统安全性指标及最大位移响应见图8。
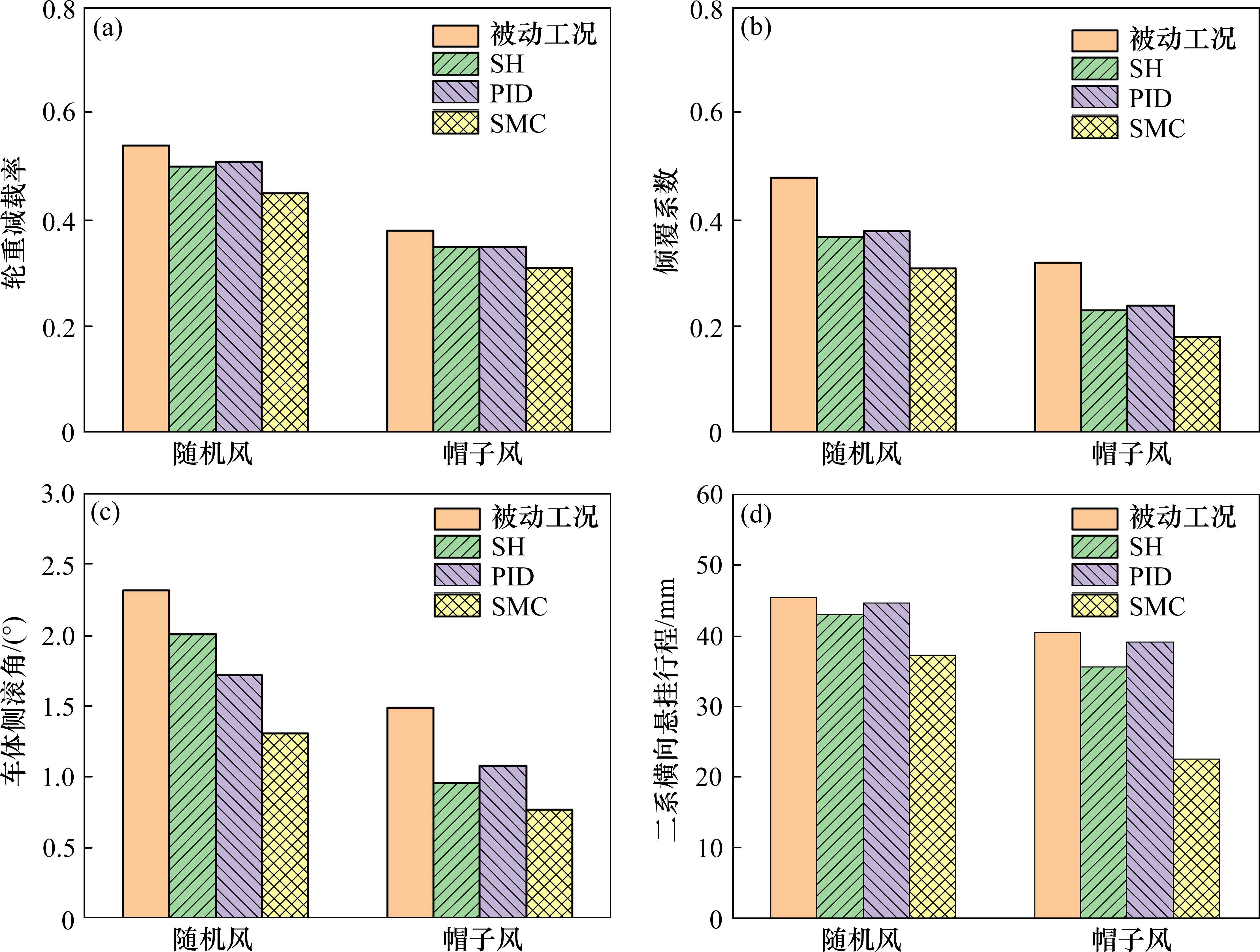
在随机风影响下,车辆系统产生了幅值更大的响应。不同风载下轮重减载率与倾覆系数相近,其中主动悬挂工况对应的倾覆系数更优。随机风引起的车体侧滚角显著大于帽子风载荷,随机风作用下滑模控制对车体侧滚角优化效果显著,而帽子风作用下各控制方法则表现接近且优化幅度较小。二系横向悬挂行程在不同风载荷影响下变化相近,天棚阻尼控制与PID控制改善效果不佳,而滑模控制对于帽子风作用下二系横向悬挂行程的优化效果良好。
较于运行安全性性能,不同风载引起的车辆平稳性性能差异更为显著,其中随机风作用引起的车辆横向加速度最大值显著大于帽子风,见图9。在随机风作用下,PID控制对于加速度最大值与横向平稳性指标优化效果均表现不佳,但在帽子风作用下对加速度最大值表现出较好控制效果,加速度最大值由0.81 m/s2降低至0.28 m/s2;滑模控制在不同风载下对二者都起到了显著的改善效果,其中在随机风作用下使加速度最大值由1.48 m/s2降低至0.54 m/s2。
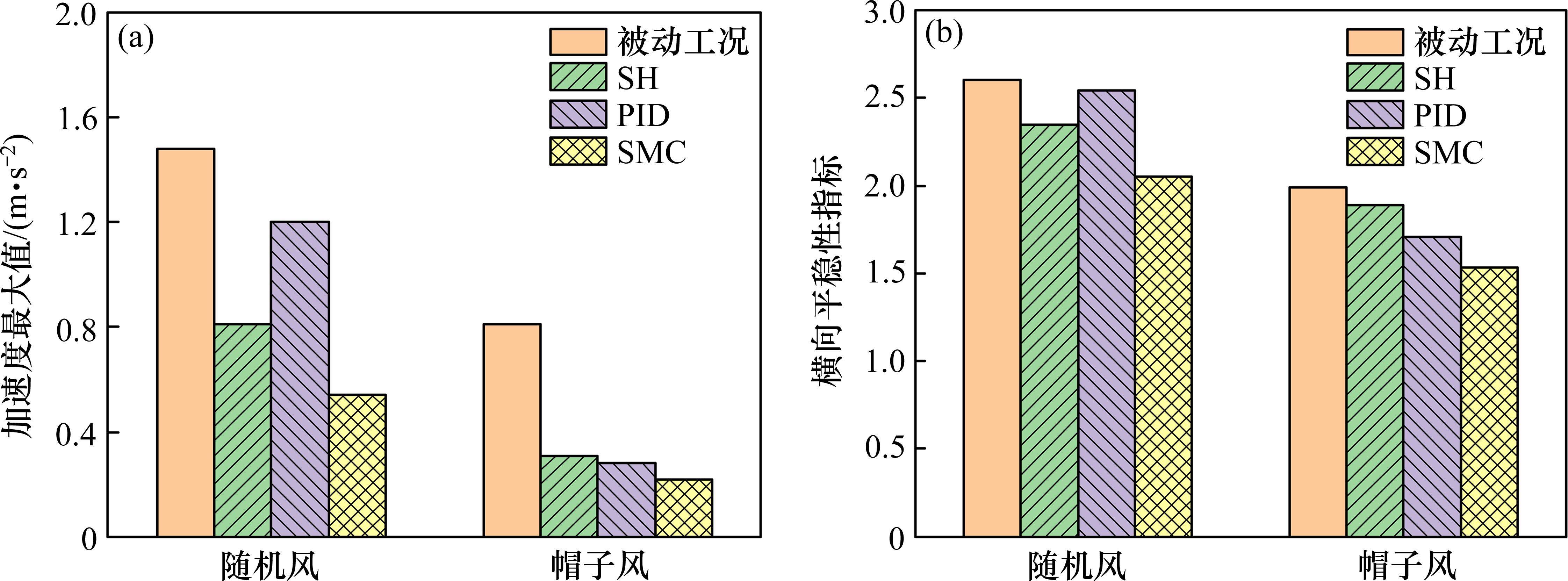
综上可知,在车辆运行过程中,随机风载荷对车辆动力学性能显著大于帽子风载荷的影响。天棚阻尼控制与PID控制对2种风载下车辆安全性和平稳性性能均有一定控制效果,其中PID控制对于帽子风下车辆平稳性控制效果更优;滑模控制方法在2种风载下均有着比前两者更为明显的改善效果。
4.2 控制方法对风速的适应性
车辆在5、10和15 m/s速度横风下行驶,各项安全性指标随风速提高而上升,主动控制效果见图10。各控制方法均对轮重减载率改善效果微弱;对倾覆系数的改善效果随风速的增加而变得更为显著,15 m/s风速下滑模控制方法可使倾覆系数降低至0.31;车体侧滚角改善效果略优于倾覆系数,控制效果随风速增加而上升;二系横向悬挂行程则在低风速时优化效果良好,改善效果随风速的上升而逐渐减弱。
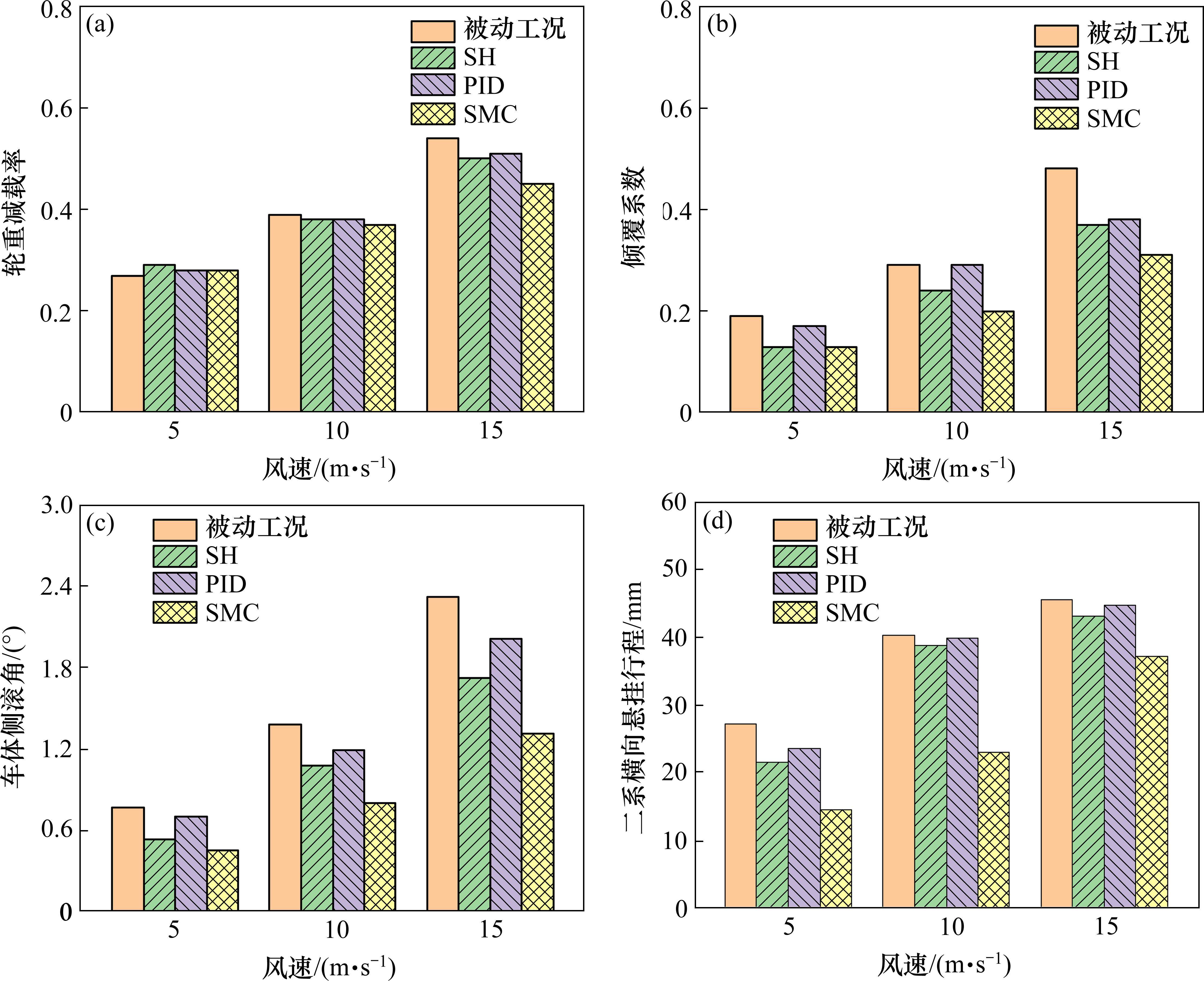
不同风速下施加不同控制得到车辆平稳性指标,见图11。随风速提高,各项平稳性指标随之增大。考虑3种风速工况,在3种控制方法下,横向加速度最大值与横向平稳性指标均有一定改善效果,其中PID控制在3种风速下控制效果接近,天棚阻尼控制与滑模控制在15 m/s风速下控制效果优异,其中又以滑模控制效果最佳,使加速度最大值降低至0.54 m/s2。综上可知,在不同风速下,3种控制方法对于车辆运行安全性与平稳性均具有一定改善效果,其中在风速适应性方面,滑模控制表现出了较强的鲁棒性和效果稳定性。
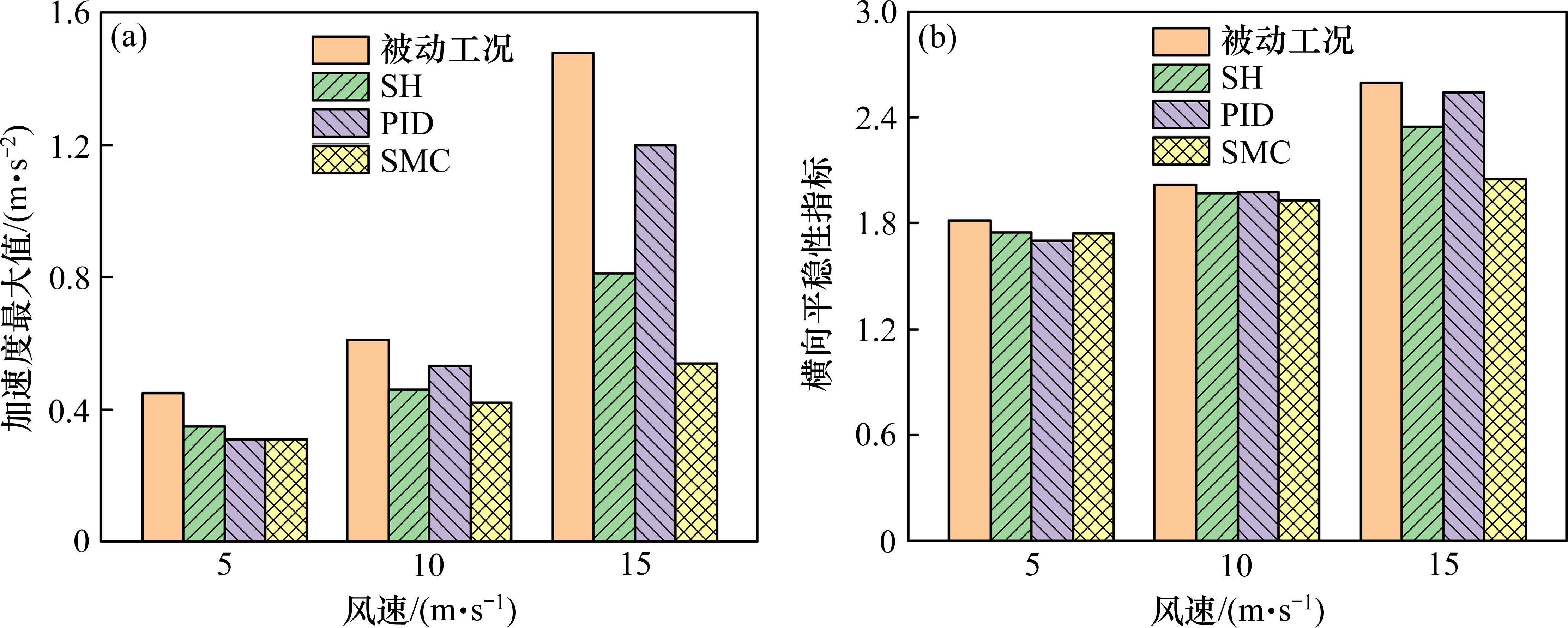
4.3 控制方法对车速的适应性
车辆分别以200、250、300和350 km/h速度行驶,各项安全性指标随车速提高而增大,主动控制效果见图12。
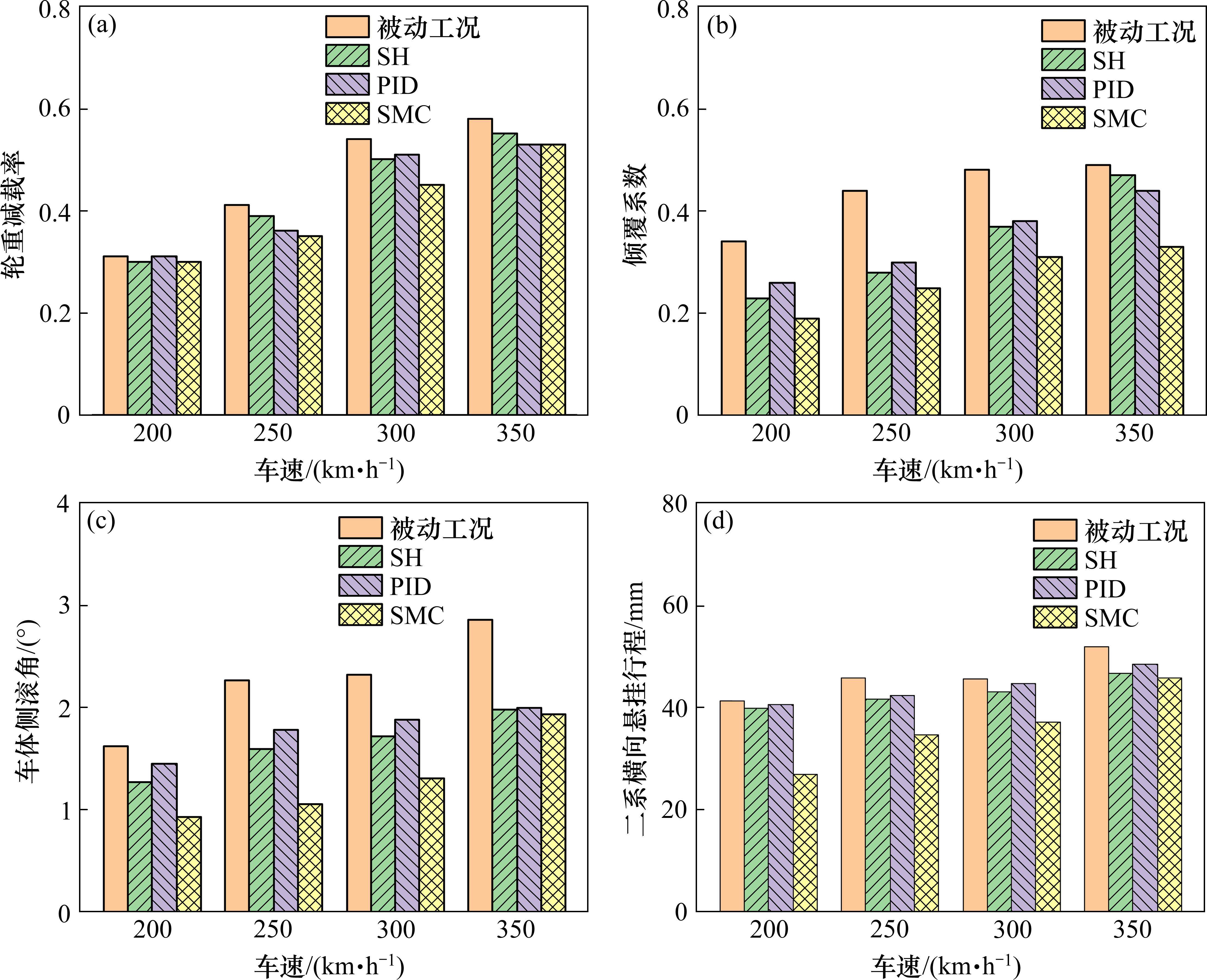
图12中,3种控制方法对轮重减载率的改善效果均较为微弱,优化幅度在0.1以下;而对倾覆系数改善效果则较为明显,天棚阻尼控制和PID控制在200、250和300 km/h下都表现出良好的改善效果,而滑模控制在各车速下均具有良好控制效果。各车速下滑模控制对车体侧滚角改善效果均优于天棚阻尼控制和PID控制,其中在中低速下的改善效果更为显著。滑模控制在200 km/h车速下将二系横向悬挂行程自41.32 mm降至26.98 mm,其控制效果随车速增加逐渐下降。
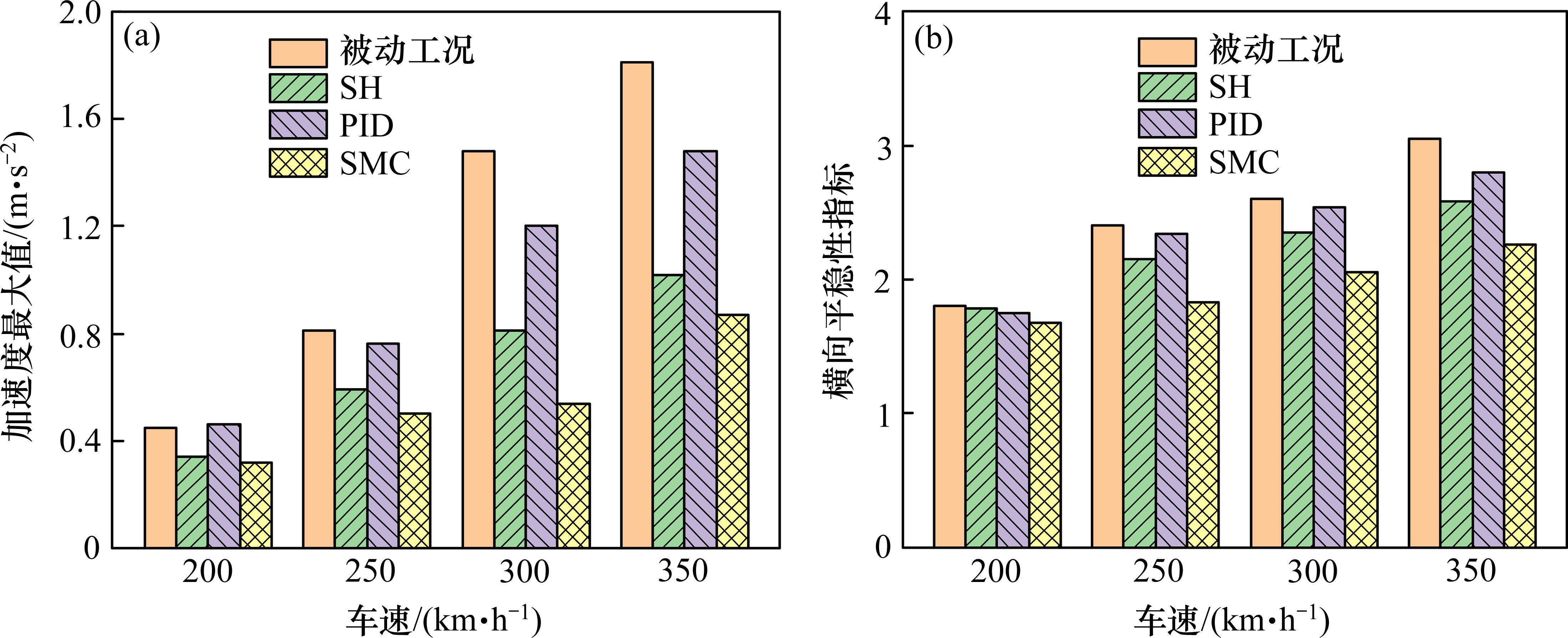
在不同车速下得到车辆系统部分平稳性指标,见图13。考虑4种车速工况,3种控制方法均对车体横向加速度最大值和均方根值具有一定改善效果,其中天棚阻尼控制和滑模控制效果优异,而滑模控制又优于天棚阻尼控制,尤其在高速行驶下,控制效果更为明显。滑模控制对平稳性指标改善效果随车速的增加而上升,在350 km/h速度下可降至2.25。
5 结论
1) 在被动悬挂工况下,风向角、风速和车速均对车辆动力学性能有明显影响,其中风向角的影响最为显著。风向角为90°时,倾覆系数达到最大值0.35,轮重减载率达到0.31,整体呈现关于90°风向角对称的钟形曲线规律。
2) 在车速达到300 km/h及以上时,轮轴横向力、轮重减载率等指标对车速变化较为敏感;在车速不超过250 km/h时,倾覆系数变化较为敏感;当车辆运行速度为350 km/h、风切变时间为2 s时,安全运行所允许的最大风速为14.47 m/s。
3) 随机风载荷大于帽子风载荷对车辆动力学性能的影响,其中运行平稳性指标差异显著,天棚阻尼控制与PID控制对2种风载模型下车辆安全性和平稳性性能均有一定控制效果;PID控制方法更适合改善帽子风载荷下的车辆平稳性性能;滑模控制方法在2种风载下均有着比前两者更为显著的改善效果。
4) 当车辆运行速度为350 km/h、风速15 m/s时,滑模控制可使横向振动加速度最大值降低63.5%,加速度均方根值降低58.5%,倾覆系数降低35.4%,车体侧滚角降低42.8%,对车速、风速表现出了良好的适应性。
高速车辆低频晃动的主动控制方法及适应性研究
[J/OL]. 机械工程学报, (陈璨,石怀龙,刘佳宁等.强侧风环境下动车组运行安全主动控制方法[J].铁道科学与工程学报,2025,22(04):1444-1456.
CHEN Can,SHI Huailong,LIU Jianing,et al.Active control method for train operation safety under strong side wind environment[J].Journal of Railway Science and Engineering,2025,22(04):1444-1456.

