接触应力过大是导致钢轨出现伤损的重要因素之一[1-3],轮轨间接触状态的匹配直接关系到轮轨接触应力[4]。钢轨打磨作业可以将钢轨廓形打磨成特定形状,是减小轮轨间接触应力的最佳手段,而钢轨打磨廓形设计是打磨作业的基础[5]。
针对轮轨间廓形的优化设计,国内外学者从众多角度进行了大量研究。POLACH等[6]开发了非线性参数,用于评估轮轨接触几何的等效锥度,并探讨了这些几何参数与车辆动力学行为之间的关系,确认了轮轨接触几何形状与轮轨磨损之间的对应性。EKBERG等[7]应用Hertz接触理论和Boussinesq积分技术,探讨了车轮与轨道之间的纵横向蠕滑率,并对接触应力场进行了分析。SHEVTSOV[8]探论了磨损指数与疲劳指数的关联,并选取合适的RDD曲线作为优化目标,利用数值优化技术,对钢轨廓形进行了改进。我国钢轨廓形优化设计随着轨道建设的发展得到迅猛发展。刘云涛等[9]利用弹塑性接触理论创建了三维瞬态轮轨接触的有限元分析模型,通过模拟不同轨底坡度下的接触情况,实现了通过调整轨底坡度来优化轮轨接触的方法。林凤涛等[10]将车辆-轨道耦合动力学与轮轨接触分析相结合,为优化曲线和恒定半径曲线上的磨损钢轨打磨廓形制定了多目标优化函数,以此来优化曲线段钢轨的廓形。雷腾[11]针对Hertz载荷分布,研究了其中的3种假设(半椭球分布、半椭圆柱分布和矩形平均分布),通过计算得到了轮轨接触的最大剪应力。沈钢等[12]提出了一种基于接触角曲线反推钢轨廓形的方法,其利用了接触角曲线,通过最小距离搜索法来定位车轮踏面,进而通过数值关系确定接触点和接触角。最后,通过积分方法调整接触曲线,以达到预期的轮廓目标。黄佳乐[13]基于轮轨接触应力,用APDL语言建立了轮轨接触有限元模型,分别对重载线路标准钢轨型面和磨耗型面进行设计,使接触应力水平显著降低,但单次优化设计时间长、效率低。CHEN等[14]根据轮轨接触的分布特性,采用一种基于轮径差函数的设计策略,使轮轨接触点分布更加均匀,并提升了车辆系统的动力学性能,但没有将接触应力作为直接的优化目标。然而,基于钢轨曲率半径及轮轨接触应力的关系反推钢轨廓形优化的研究相对较少,且轮轨间接触应力较大的主要原因是车轮和钢轨廓形的曲率半径不匹配,因此,通过降低轮轨间最大接触应力来优化钢轨廓形有助于减少钢轨磨耗量,优化轮轨接触,提升轨道车辆动力学性能,具有一定的研究价值。
轮轨间的接触应力直接影响轮轨磨耗、滚动接触疲劳的萌生和发展,优化设计钢轨廓形是减小轮轨间的接触应力和钢轨伤损的最佳手段[15]。本研究基于Hertz接触应力理论,建立钢轨廓形半径与接触应力的联系,通过改变轮轨接触点处钢轨曲率半径的方式,将当前轮轨间最大接触应力降至理想值,通过该方式反推钢轨优化廓形。将优化后的钢轨廓形进行轮轨几何匹配计算,根据计算结果进行闭环的反馈计算,直至所有峰值点都优化完毕,最后输出优化后的钢轨廓形。对优化后的钢轨廓形进行磨耗预测仿真及车辆动力学仿真,通过对比优化廓形前后钢轨的磨耗情况及对车辆形式品质的影响验证该设计方法的效果。
1 钢轨廓形设计模型
1.1 数学模型
根据Hertz接触理论可知,车轮和钢轨型面曲率半径的变化直接影响轮轨间法向接触应力,本文主要针对直线工况或大曲线半径的钢轨进行研究分析,因此,能减少极端工况下所得接触应力偏大的情况。基于Hertz接触理论,建立钢轨廓形的半径与接触应力之间的联系,并依据目标半径反推设计钢轨廓形。
钢轨廓形优化设计变量示意图如图1所示。图1中,Y为钢轨廓形横坐标,Z为钢轨廓形纵坐标。选取钢轨廓形最高点为坐标零点,并将钢轨廓形离散点分为可动点和固定点(加粗的点为可动点,其余为固定点)。固定点为优化设计前、后的横坐标纵坐标均不变的点;而在钢轨优化设过程中,可动点的横坐标和纵坐标可以改变。经过廓形优化后,将可动点与固定点整合,过渡区采用平滑处理(图1中的可动点区间为假设区间,用于示范,并非实际优化区间)。
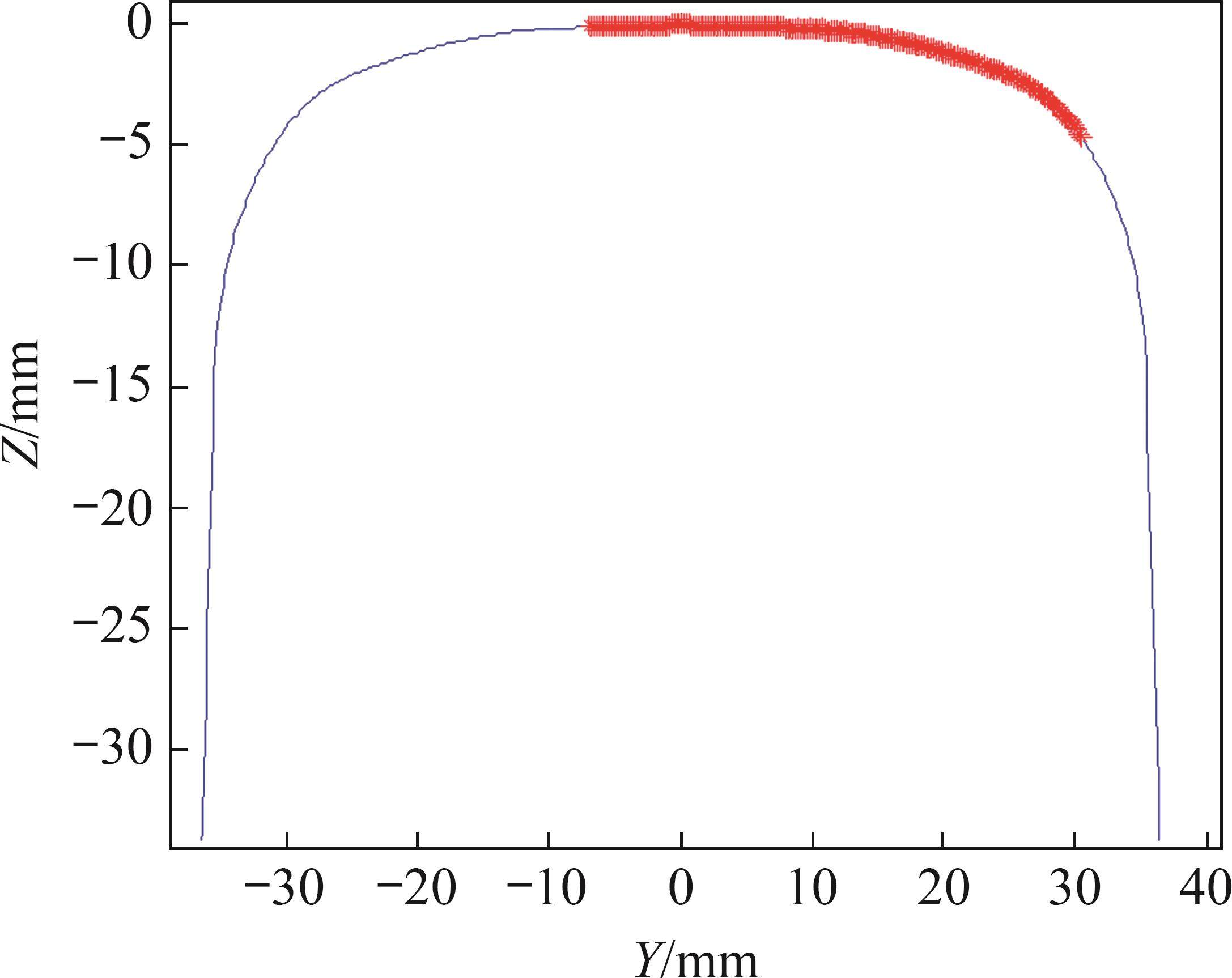
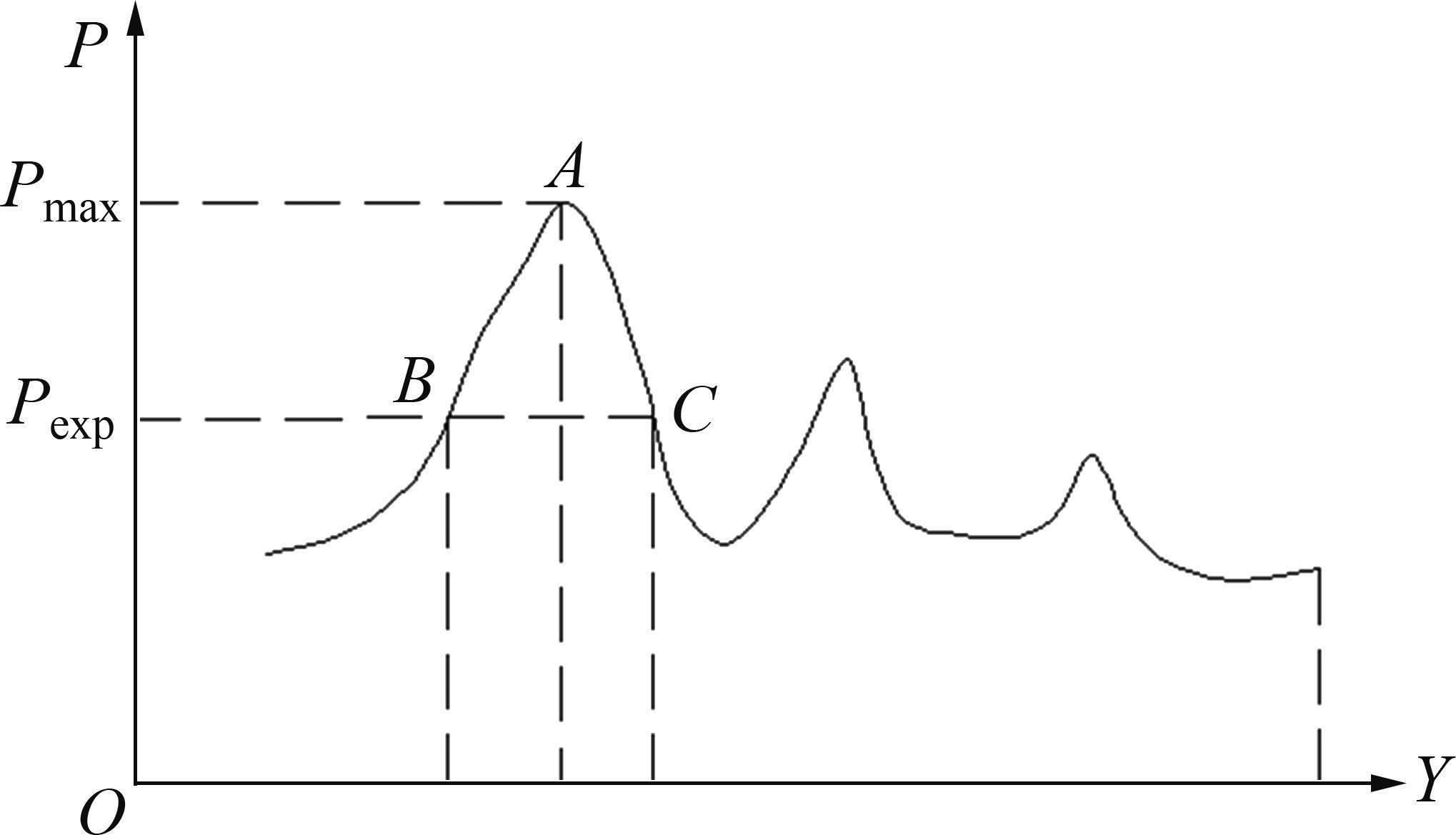
图1中加粗点所表示的钢轨廓形优化范围,在不降低其他动力学性能的前提下,最大程度地减小轮轨间的接触应力,将优化目标函数定为在钢轨廓形优化范围内轮轨间总的接触应力最小。在静态接触下,轮轨接触应力P分布示意图如图2所示。
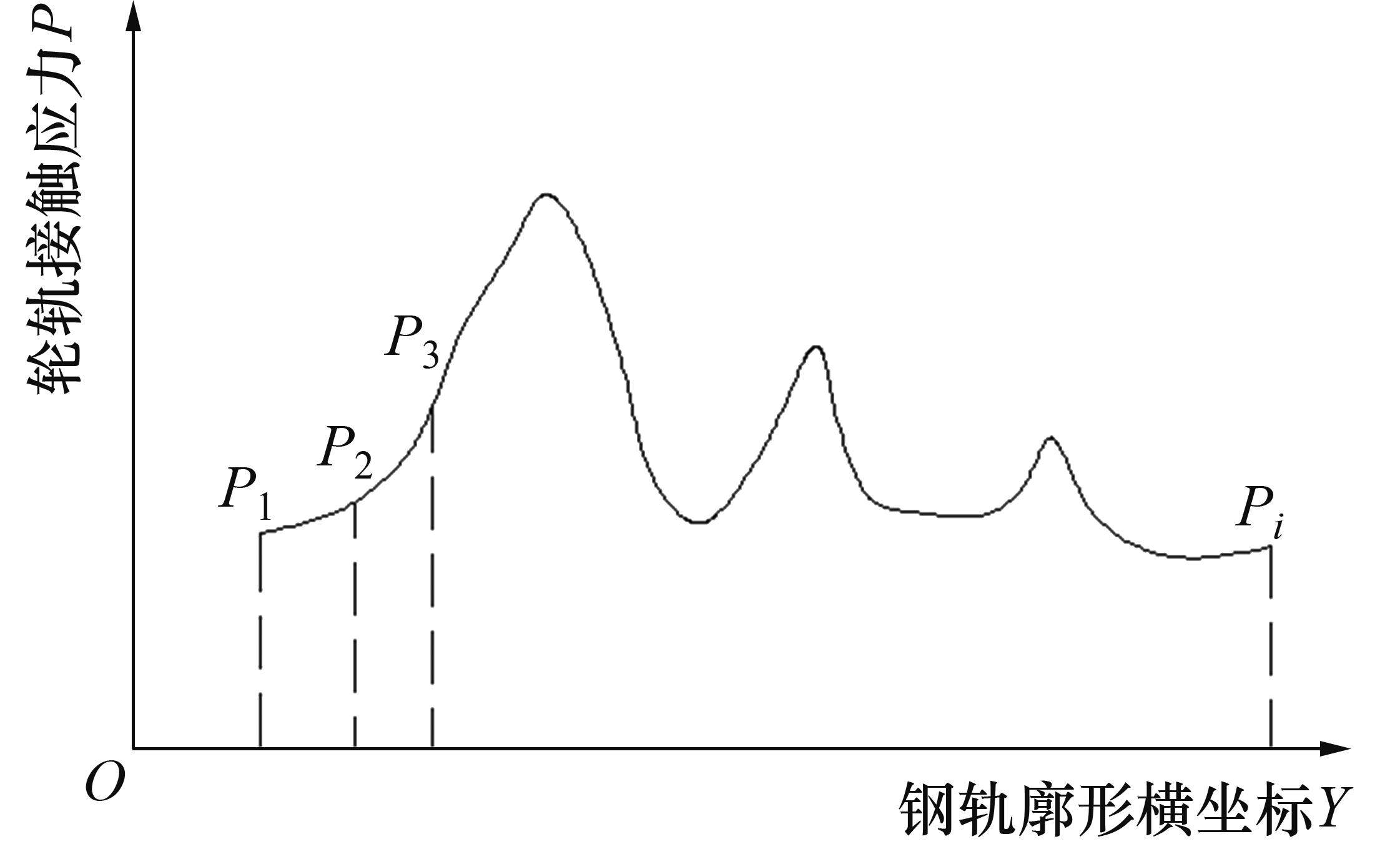
将轮轨间最大接触应力的总和作为优化目标函数,有
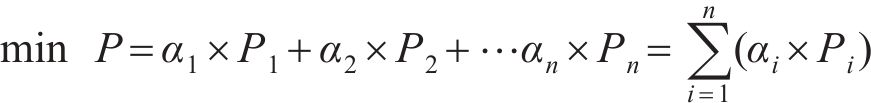
式中:Pi(i=1,2,3,…,n)为轮轨间最大的接触应力;αi为权重系数,权重系数由接触点接触频率来确定;n为优化范围内最大接触应力点的个数。
1.2 期望接触应力
基于轮轨间初始接触应力图像,确定局部最大接触应力,设置期望接触应力。其中,期望接触应力由局部最大接触应力及优化范围内平均接触应力决定,期望接触应力值计算公式为:
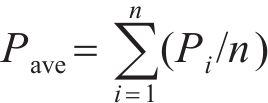
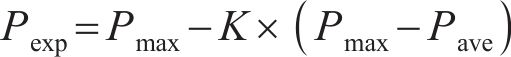
式中:Pmax为优化范围内接触应力最大值;Pave为优化范围内平均接触应力;Pexp为期望的接触应力;K为期望的接触应力的调整系数(0<K<1)。若出现接触应力-钢轨曲率半径曲线往外插值导致程序中断的情况,则调整系数K将自动减小,直至K为0。
1.3 优化算法
在廓形待优化区间内,根据钢轨曲率半径,逆向设计出钢轨廓形。已知起点坐标,将起点坐标处的曲率半径近似为圆弧半径,根据圆弧半径直接求出下一点的坐标,如图3所示。
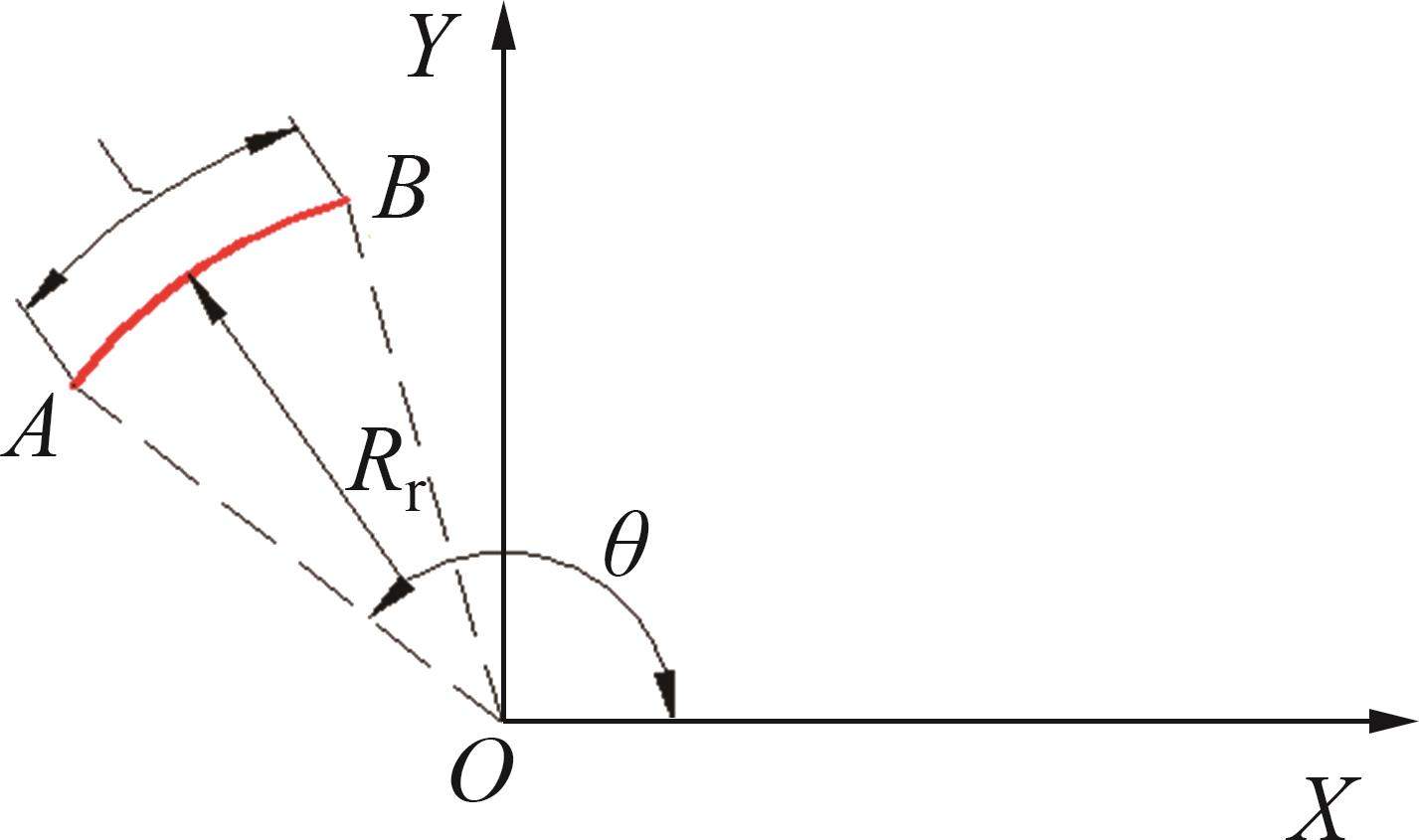
假设已知A点坐标(yi,zi),曲线段AB的弧度l,弧长AB的半径为Rr,点A的角度θ,则可以求出B点的坐标(yi+1,zi+1),即
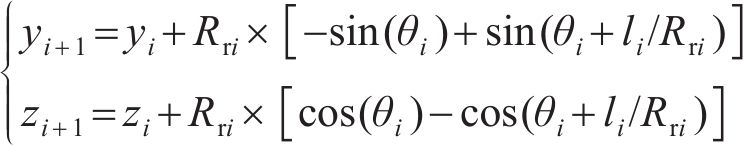
式中:(yi,zi)和(yi+1,zi+1)分别为钢轨上第i和i+1个点的坐标;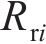
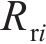
为了确保优化后廓形的接触应力最小,需要对目标函数进行检验,有
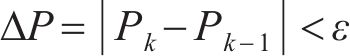
式中:Pk和Pk-1分别为相邻两次轮轨间总的接触应力;ε为收敛容差。若在优化设计中,出现Pk>Pk-1的情况,则认为此次优化后的型面无效,继续进行下一次迭代。
钢轨型面在几何形状上是严格的凸曲线(除基本轨与尖轨非工作边形成的凹陷区域之外,由于此区域不发生轮轨接触,因此,对该区域不进行优化设计),有
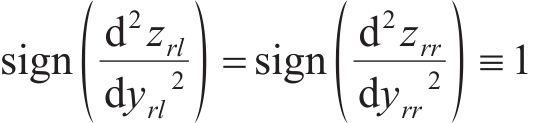
式中: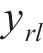
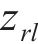
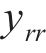
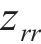
为避免优化后的廓形出现往复点,优化区域的横坐标尽量保持单调,有
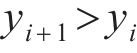
优化设计的打磨廓形不应该超过原始廓形,有
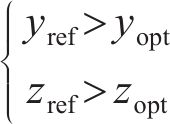
式中:(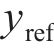
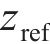
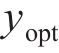
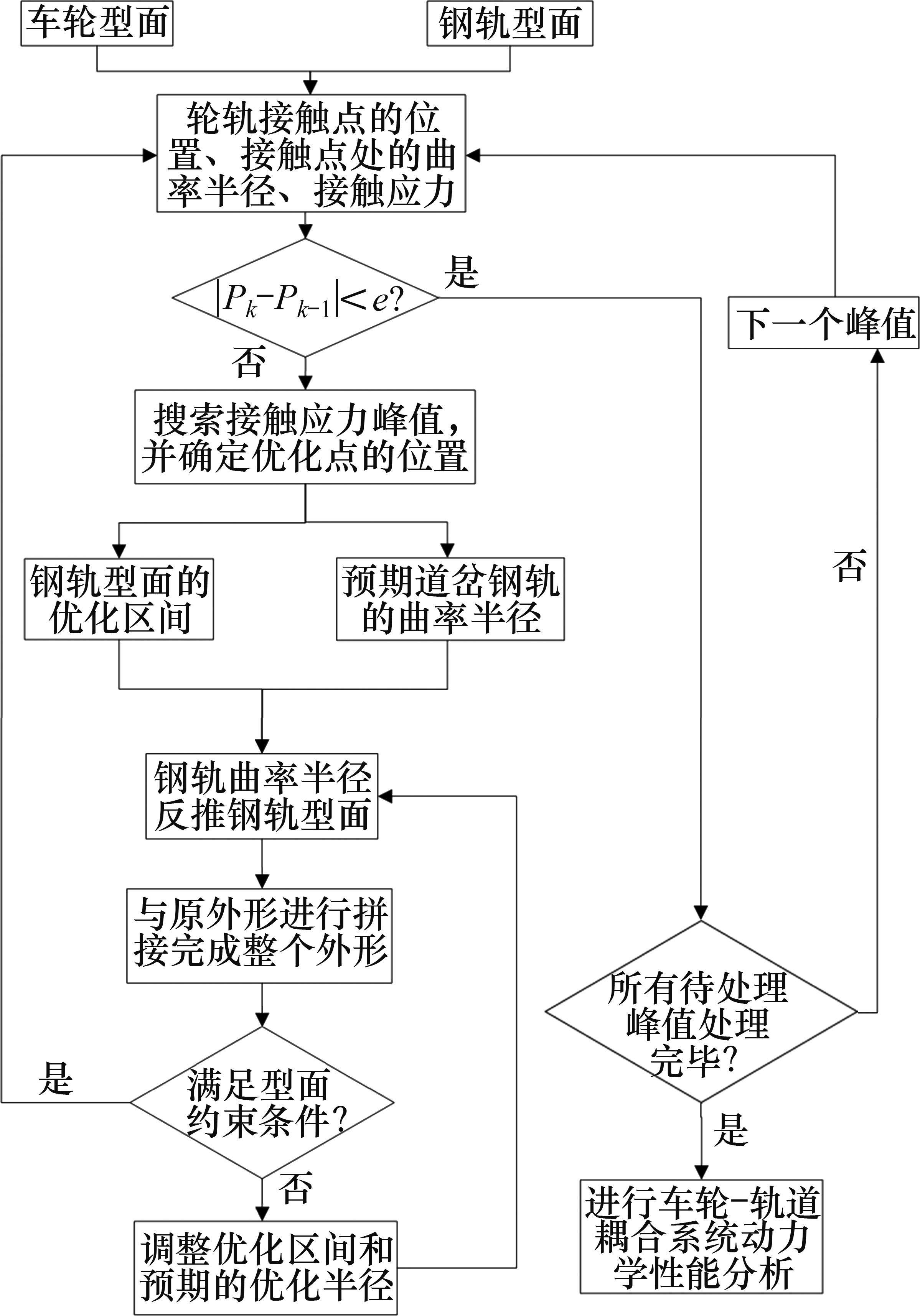
1.4 总体设计流程
1) 首先给定车轮踏面外形、待优化的钢轨廓形以及相关的轮轨接触参数,根据轮轨几何匹配计算,利用Hertz接触理论求出轮对不同横移量下轮轨间最大接触应力,把车轮与钢轨之间的最大接触应力作为直接的优化对象[16]。
2) 根据最大接触应力Pmax来确定钢轨廓形和车轮外形的接触点位置[17],并求出钢轨和车轮接触点的曲率半径,基于接触应力最大值Pmax设定接触应力的期望值Pexp,根据期望的接触应力确定钢轨型面的优化区间,如图4所示。
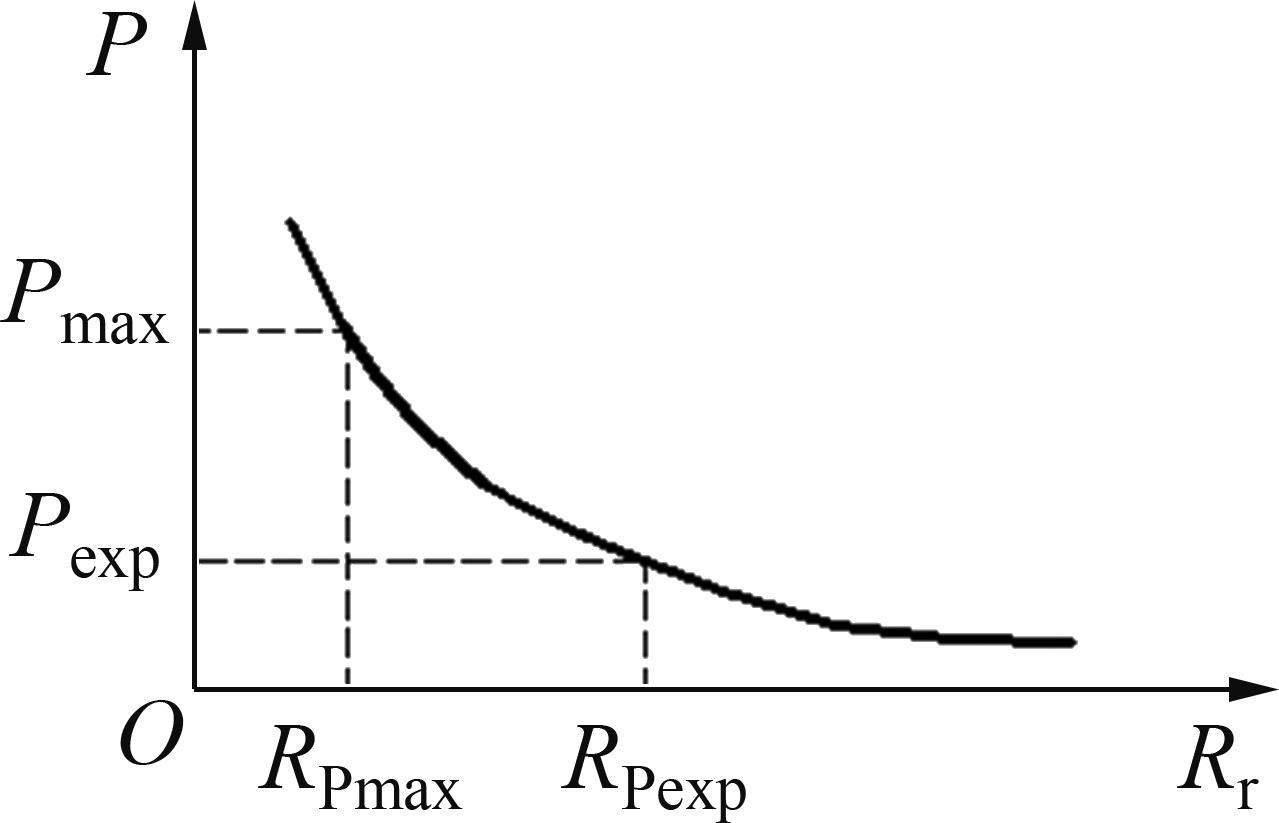
3) 假设车轮上接触点的位置不发生改变。改变钢轨接触点处的曲率半径,利用Hertz接触理论可以得到不同钢轨曲率半径下的接触应力最大值曲线(P=Hertz(Rr))[18]。根据步骤2)中期望的接触应力Pexp和P=Hertz(Rr),可以求得钢轨接触点处的期望曲率半径RPexp,如图5所示,RPmax为最大接触曲率半径。
4) 根据步骤2),假设从优化区间的起点B到点A之间的钢轨曲率呈线性变化,则优化区间BA之间的曲率和优化区间AC之间的曲率为:
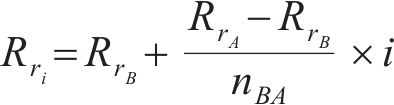
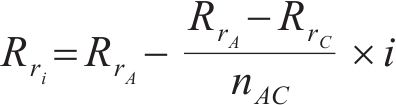
式中:nBA和nAC分别代表优化区间BA和优化区间AC之间点的总个数;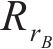
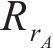
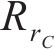
5) 对设计好的钢轨廓形进行轮轨几何匹配计算,求出实际轮轨接触应力的最大值,再与原始最大值进行比较,若实际设计最大接触应力比原始最大值小,但比收敛容差e大,则调整预期的最大接触应力以及优化区间,再执行步骤2);若实际设计最大接触应力比原始接触应力大,则也需要调整预期的最大接触应力以及优化区间,再执行步骤2);若实际设计最大接触应力比原始最大值小,并且比收敛容差小,则对下一个峰值点进行优化设计,执行步骤1)。直到所有峰值点都优化完毕,程序结束,输出优化后的钢轨廓形。
钢轨廓形的设计应构成一个闭环设计,如图6所示。
2 钢轨廓形半径的计算及算法验证
Hertz接触应力主要依据车轮踏面半径和钢轨廓形半径计算得到,车轮和钢轨曲率半径的计算结果对轮轨接触应力影响很大。虽然标准车轮和钢轨外形每个位置的曲率半径都是给定的,但钢轨和车轮上线运行一段时间之后,由于存在磨耗等,车轮和钢轨的曲率半径均发生了改变,不再适合于根据标准车轮和钢轨的位置来插值得到曲率半径[19-20]。本研究采用最小二乘拟合圆的曲率半径。
2.1 最小二乘拟合圆的曲率半径
最小二乘法是寻找一种最佳的函数匹配,使得计算求得的数据与实际数据之间误差的平方最小。工程中常用最小二乘算法对曲线或者直线进行拟合。
假设存在某离散数据点(yi,zi)(i=1,2,3,…,n),并且这些数据点基本落在某圆上,如图7所示。
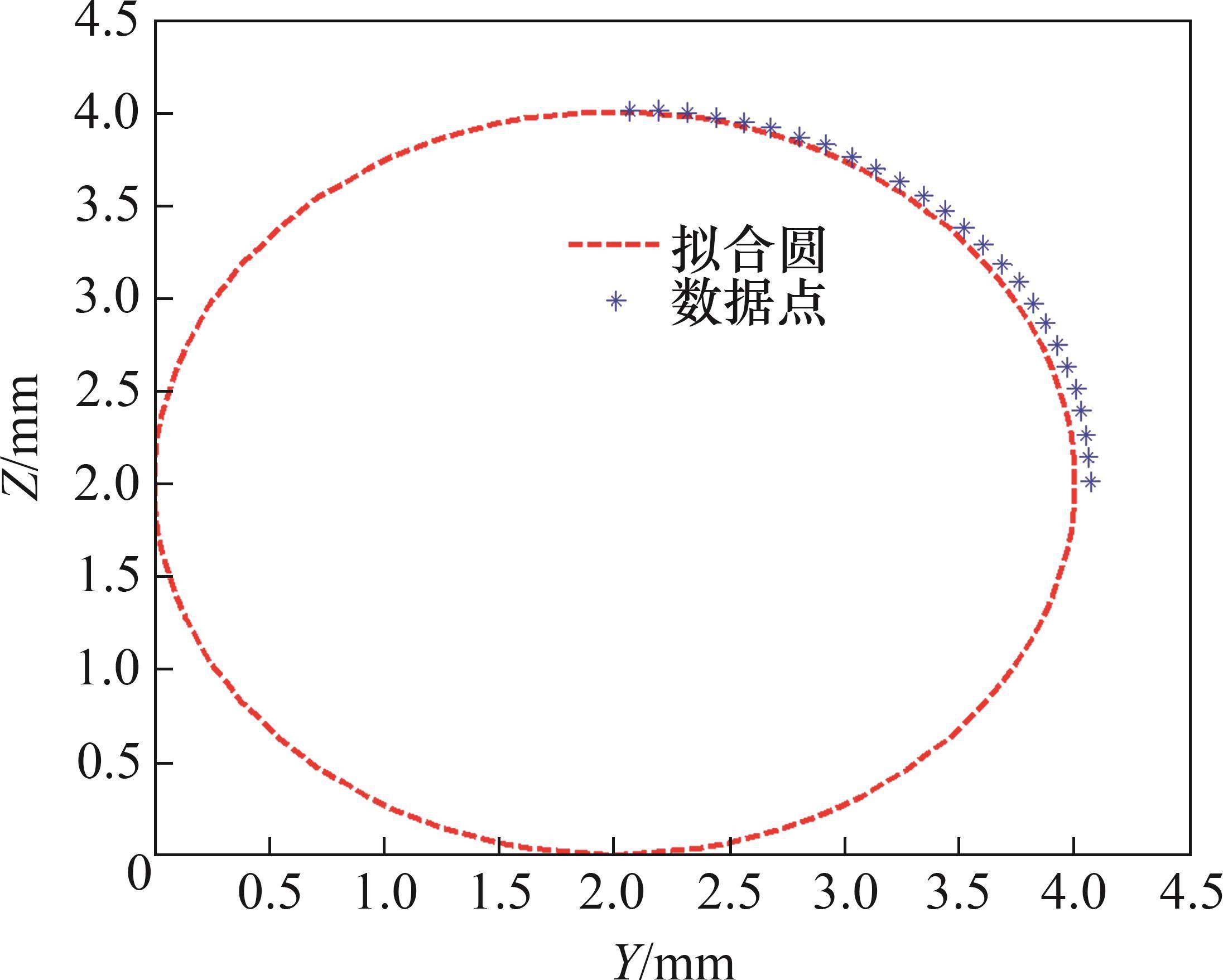
给定圆心坐标为(y0,z0),半径为R,圆的标准方程为
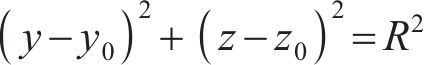
令
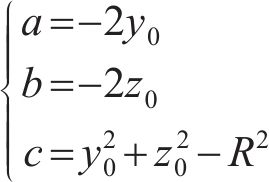
离散点(yi,zi)到圆心(y0,z0)的距离的平方与半径方差的差值为
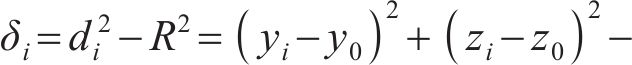
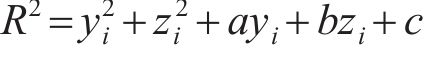
借用最小二乘法,令g(a,b,c)为δi的平方和,即
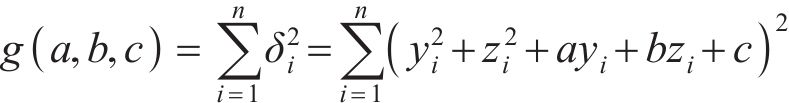
从式(13)可知,g(a,b,c)大于等于0,且存在极小值。将g(a,b,c)对a、b、c求偏导,得到极值点。g(a,b,c)取极值时的条件有:
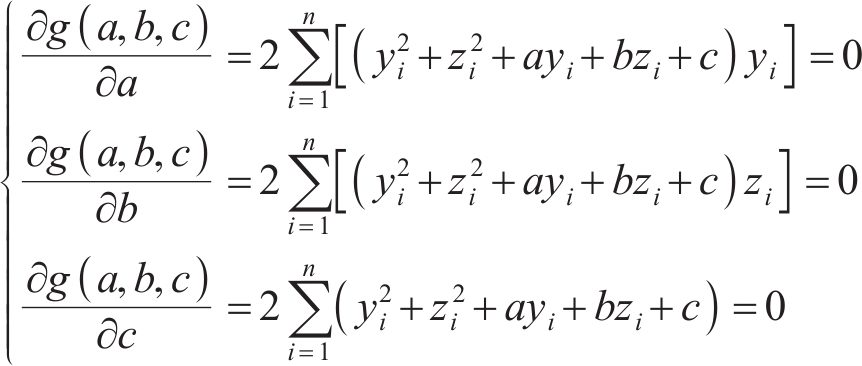
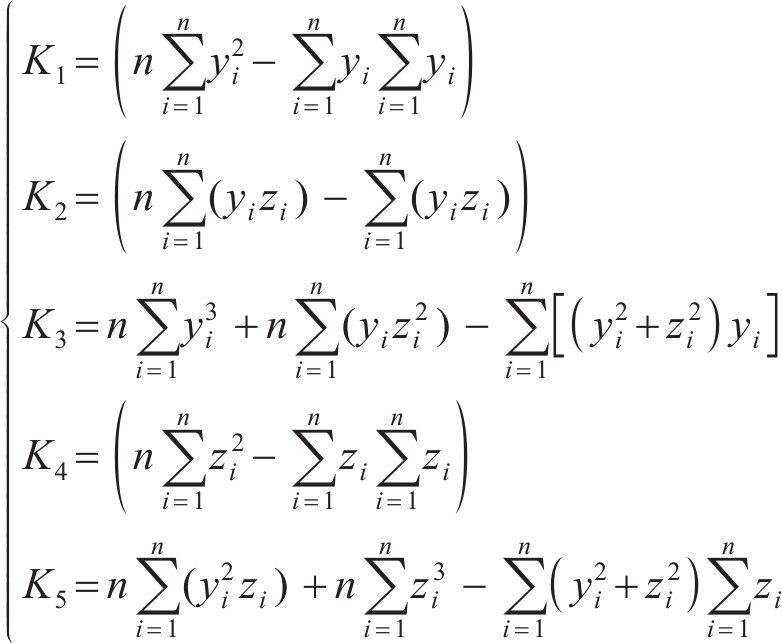
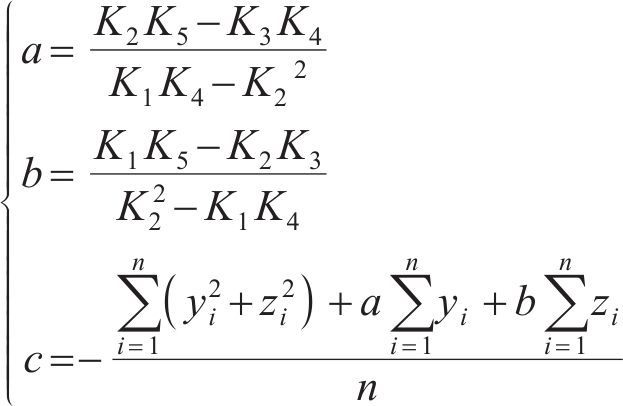
2.2 算法验证
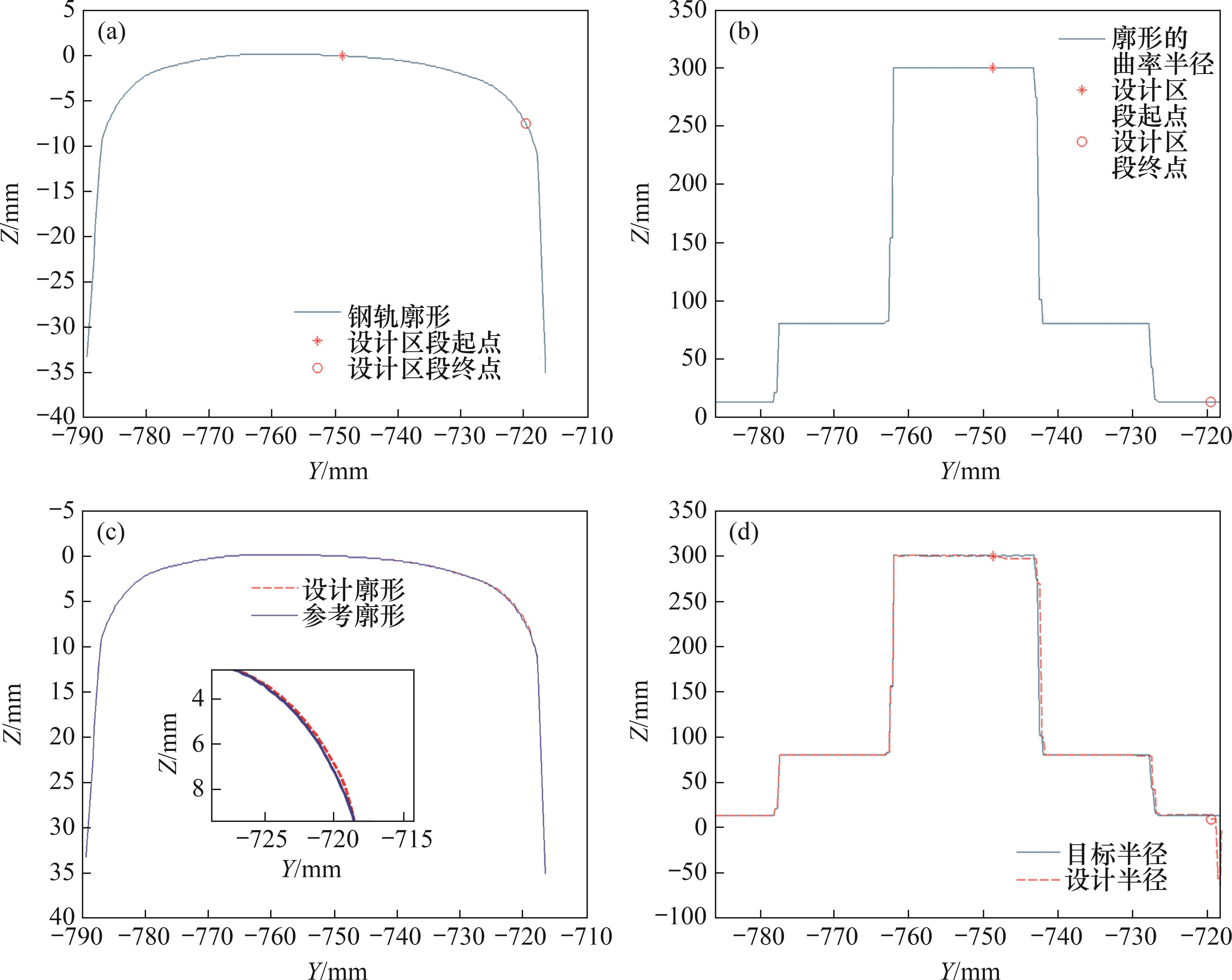
以标准60轨廓形为例,给定优化设计区段,根据是否能根据已知离散点曲率半径反推钢轨区段来判断设计方法的正确性[21],结果如图8所示。从图8(c)可知:反推算法设计廓形与原始廓形基本一致。对设计的廓形重新计算曲率半径,并与已知的曲率半径进行对比发现:设计后的半径与原始半径基本一致,只有最后几个离散点的误差较大,原因是:最后几个点已经偏离了原始廓形,拼接就是将最后几个点与原始廓形进行光顺,就会导致这几个点处的曲率发生变化[22]。总体来说,据该算法能按照要求设计出合理的廓形。
3 结果分析
3.1 廓形对比及静态轮轨几何接触关系
根据图7所示流程图对设计方法进行编程求解,得到闭环的设计程序。选取与LM车轮踏面匹配的标准60轨对钢轨廓形进行优化设计,轮对横移量选取-12 mm到12 mm,间隔为0.5 mm。计算参数如表1所示。
| 参数 | 数值 |
|---|---|
| 屈服强度/MPa | 880 |
| 冲角/(°) | 0 |
| 车轮廓形 | LM型 |
| 钢轨廓形/(kg·m-1) | 60 |
| 轴重/t | 17 |
| 泊松比 | 0.3 |
| 弹性模量/GPa | 210 |
| 密度/(kg·m-3) | 7 800 |
| 权重系数 | 1 |
优化前后钢轨廓形如图9所示。
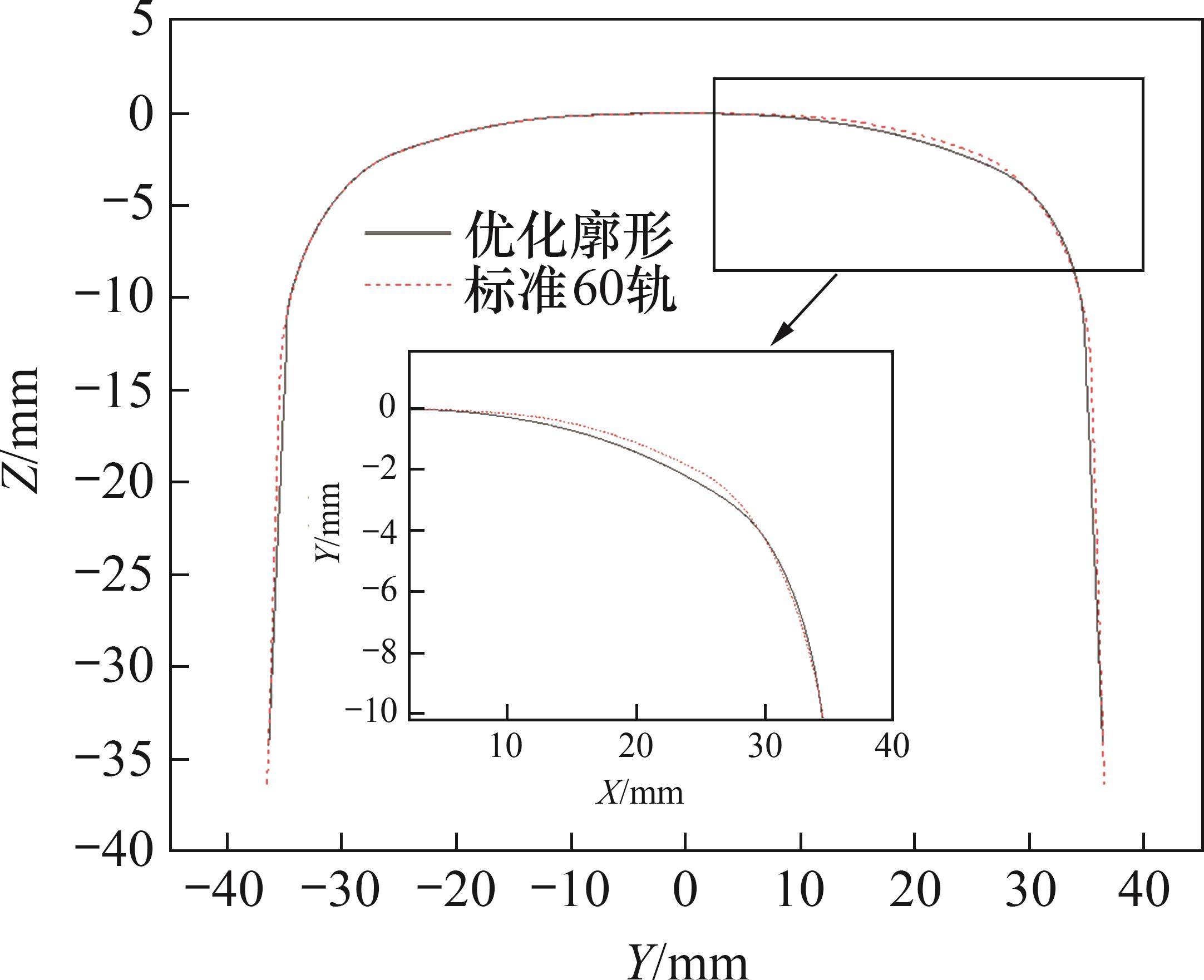
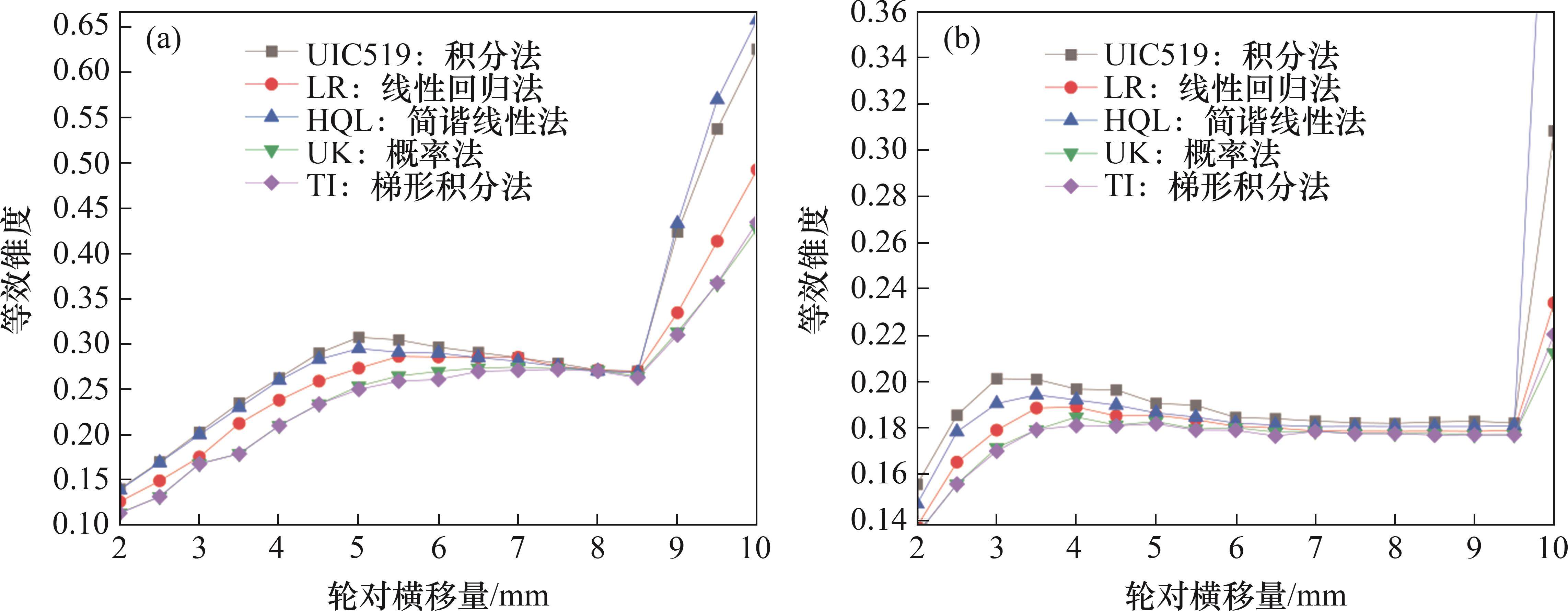
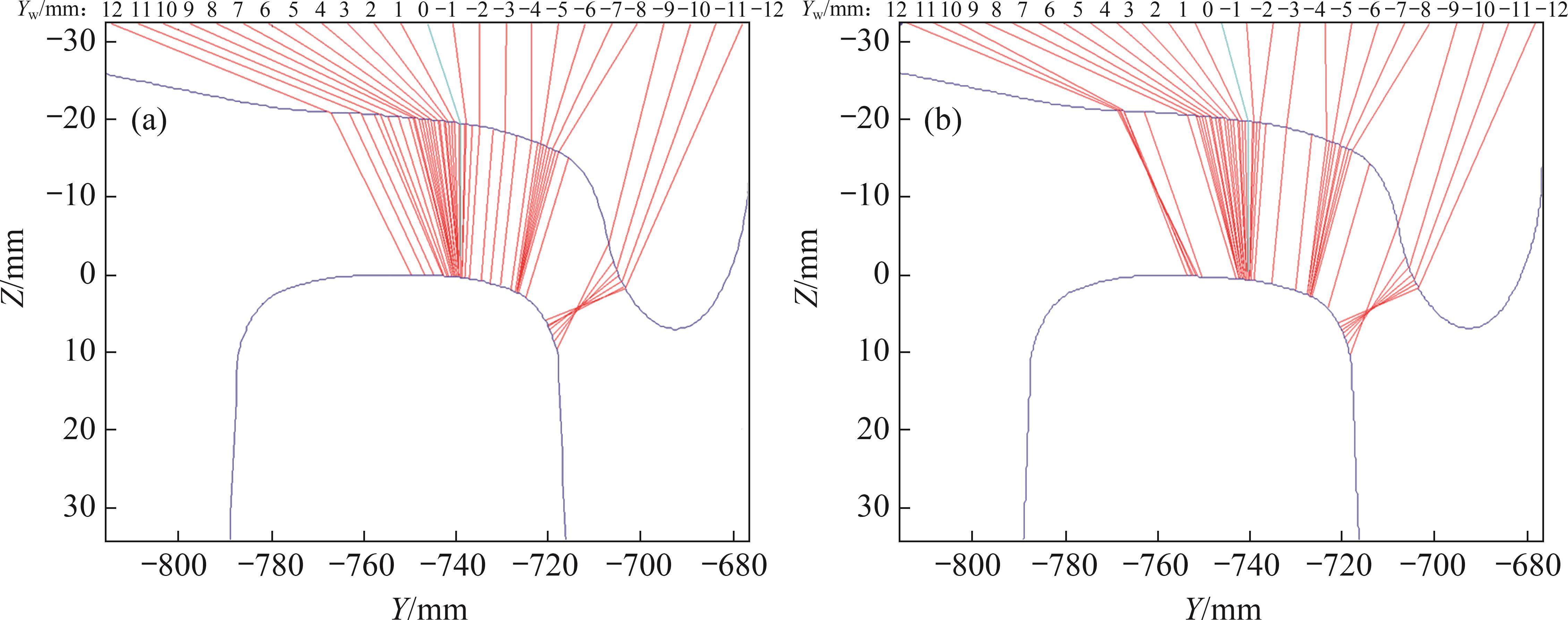
等效锥度是反映轮对恢复对中性能、曲线通过能力和蛇行失稳的关键参数之一,钢轨廓形优化前后等效锥度结果对比如图10所示。从图10可以看出:优化后的钢轨廓形等效锥度下降约30%,有利于提高轨道车辆运行稳定性[23]。基于等效锥度进一步对优化钢轨廓形对轮轨接触点的分布和接触应力的影响进行讨论,以左侧钢轨廓形为例,钢轨廓形优化前后轮轨接触点的分布对比如图11所示,其中Yw为横移量。从图11可知:优化后钢轨廓形轮轨接触点的分布更加均匀,接触点的跳变现象得到了有效抑制,轮轨有效接触面积扩大;同时,由于优化后钢轨廓形等效锥度更小,在相同的法向轮轨力作用下,轮轨接触面积更大,接触应力更小[24],有助于减小钢轨磨耗。
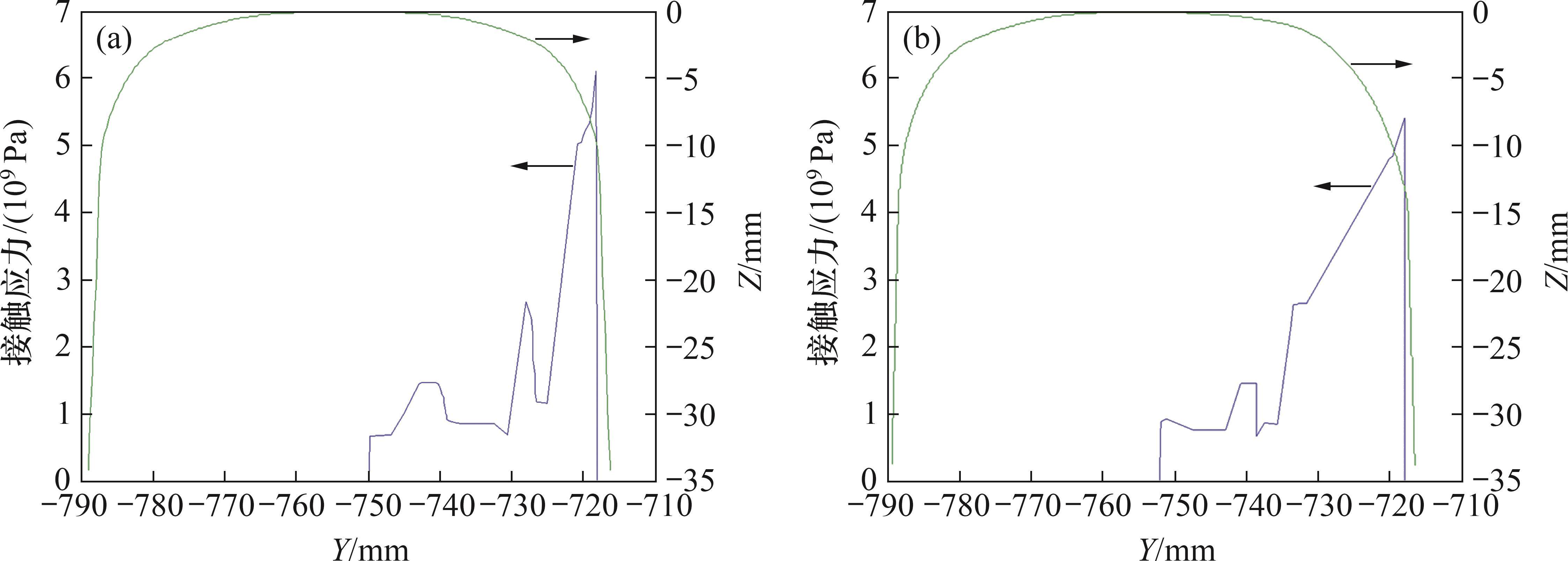
以左侧钢轨廓形为例,钢轨廓形优化前后接触应力对比如图12所示,可见最大接触应力由 6 300 MPa下降到5 300 MPa,下降了15.8%。结合图10及图11分析可知:廓形优化后,接触点分布位置得到优化,接触点跳变现象得到缓解[25]。
3.2 钢轨廓形优化前后钢轨磨耗性能对比
采用多体动力学软件UM将优化后的钢轨廓形与标准60轨在直线工况下进行磨耗预测仿真。相关仿真参数如表2所示。
| 参数 | 数值 |
|---|---|
| 磨耗指数/(m3⋅J-1) | 1.2×10-12 |
| 轨底坡/rad | 0.12 |
| 行驶速度/(km⋅h-1) | 250 |
| 单次迭代通过轴重/t | 0.25×106 |
| 轨顶摩擦因数 | 0.25 |
| 磨耗预测迭代次数 | 400 |
| 磨损阶数 | 2 000 |
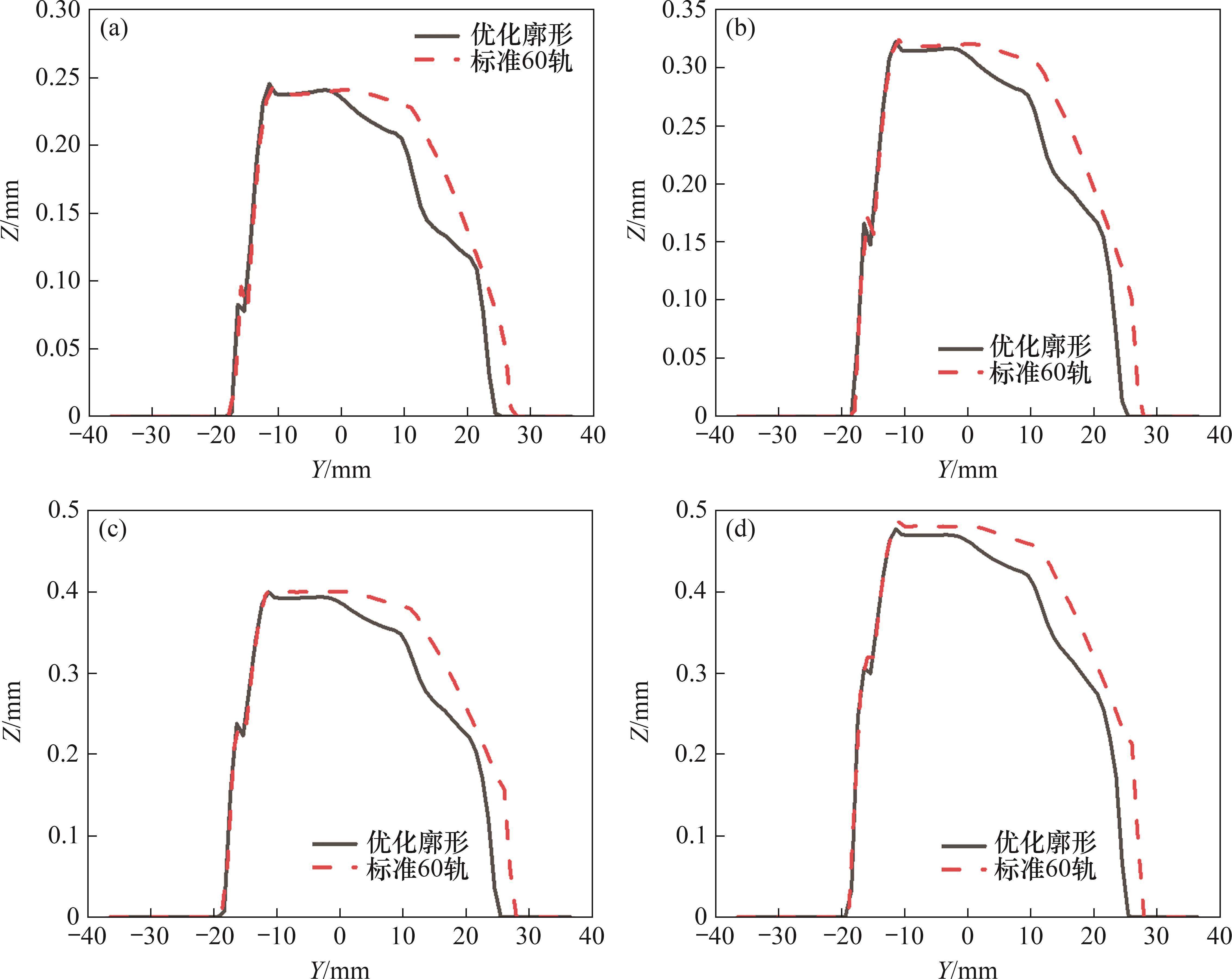
将通过相同轮重的2种钢轨模型的磨耗深度进行对比,以行驶方向左侧钢轨为例,钢轨磨耗预测仿真结果如图13所示。由图13可知:优化后的钢轨廓形顶面位置与标准60轨相比有一定程度降低,当通过轴重为19×106 t时,优化后的钢轨廓形顶面位置平均磨耗深度为0.45 mm,相较于标准60轨减少4%;优化后的钢轨廓形轨距角位置磨耗相较于标准60轨明显减少。以通过轴重为19×106 t时为例,轨侧边工作边位置,优化廓形后钢轨平均磨耗深度为0.26 mm,标准60轨平均磨耗深度为0.34 mm,减少24%。结合图10与图12分析可知,钢轨廓形优化后,轮轨间接触点分布更加均匀,同时伴随钢轨轨距角处的最大应力降低[26],这与图13所示结果基本吻合。
3.3 钢轨廓形优化前后动力学性能分析
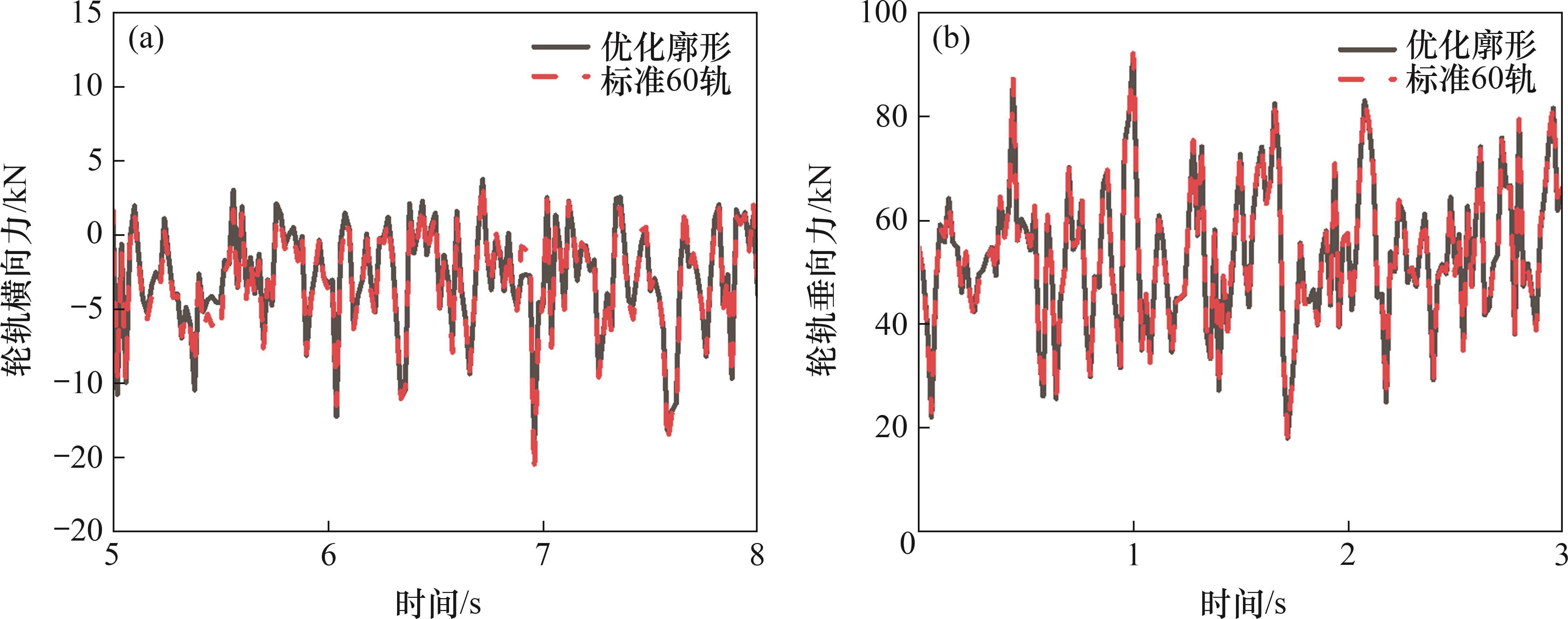
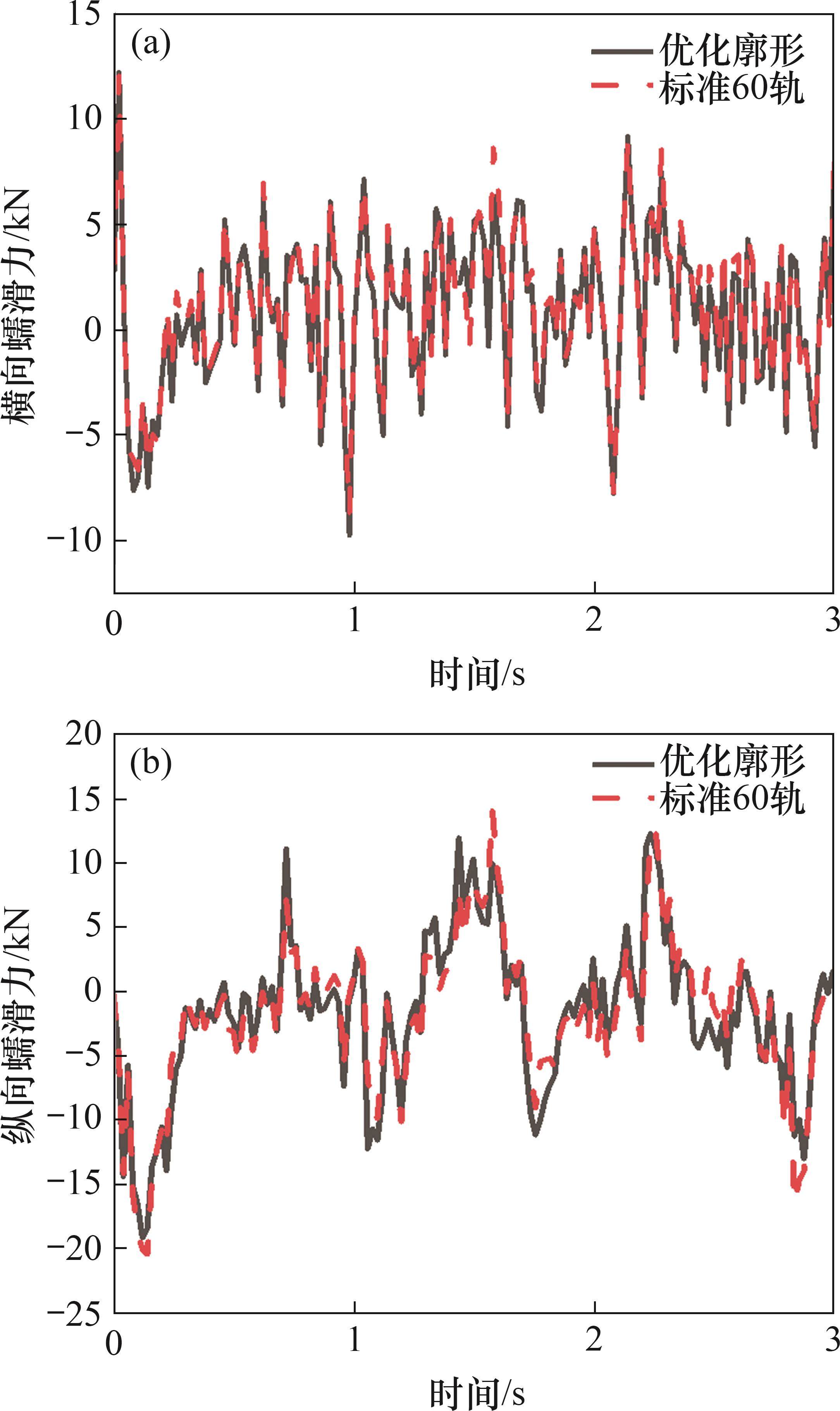
使用多体动力学软件UM搭建轨道车辆动力学模型,模型参数如表3所示。将优化后的钢轨廓形与标准60轨进行对比仿真。导入美国不平顺五级谱作为轨道不平顺激励,仿真车辆车轮采用LM廓形,以200 km/h的速度对直线工况行驶时的轮轨横垂向力及切向蠕滑力进行仿真对比,仿真结果如图14和图15所示。由图14和图15可知:在采用优化钢轨廓形的工况下,轮轨间的横向力和垂向力最大值分别为18.7 kN和91.6 kN,在标准60轨工况下,轮轨间的横向作用力和垂向力最大值分别为18.3 kN和92.1 kN;当钢轨使用优化后的钢轨廓形时,其横向蠕滑力和纵向蠕滑力的最大值分别为13.4 kN和18.3 kN,钢轨使用标准60轨廓形时,横向蠕滑力和纵向蠕滑力的最大值分别为 14.7 kN和22.0 kN;廓形优化后的钢轨廓形相较于标准60轨横纵向蠕滑力均有减小,减小幅度分别为8.8%、16.8%,纵向蠕滑力基本一致,有利于减缓滚动疲劳接触,并有效降低钢轨磨耗速率,有助于提高列车行驶平稳性[27]。
| 部件 | 数值 |
|---|---|
| 车体质量/t | 30 |
| 构架质量(单个)/t | 2.5 |
| 空气弹簧横向刚度(每台转向架)/(kN·m-1) | 300 |
| 二系横向减振器阻尼(每台转向架)/(kN·s·m-1) | 20 |
| 空气弹簧横向刚度(每台转向架)/(kN·m-1) | 360 |
| 二系横向减振器阻尼(每台转向架)/(kN·s·m-1) | 16 |
| 二系抗蛇行减振器阻尼(每台转向架)/(kN·s·m-1) | 150 |
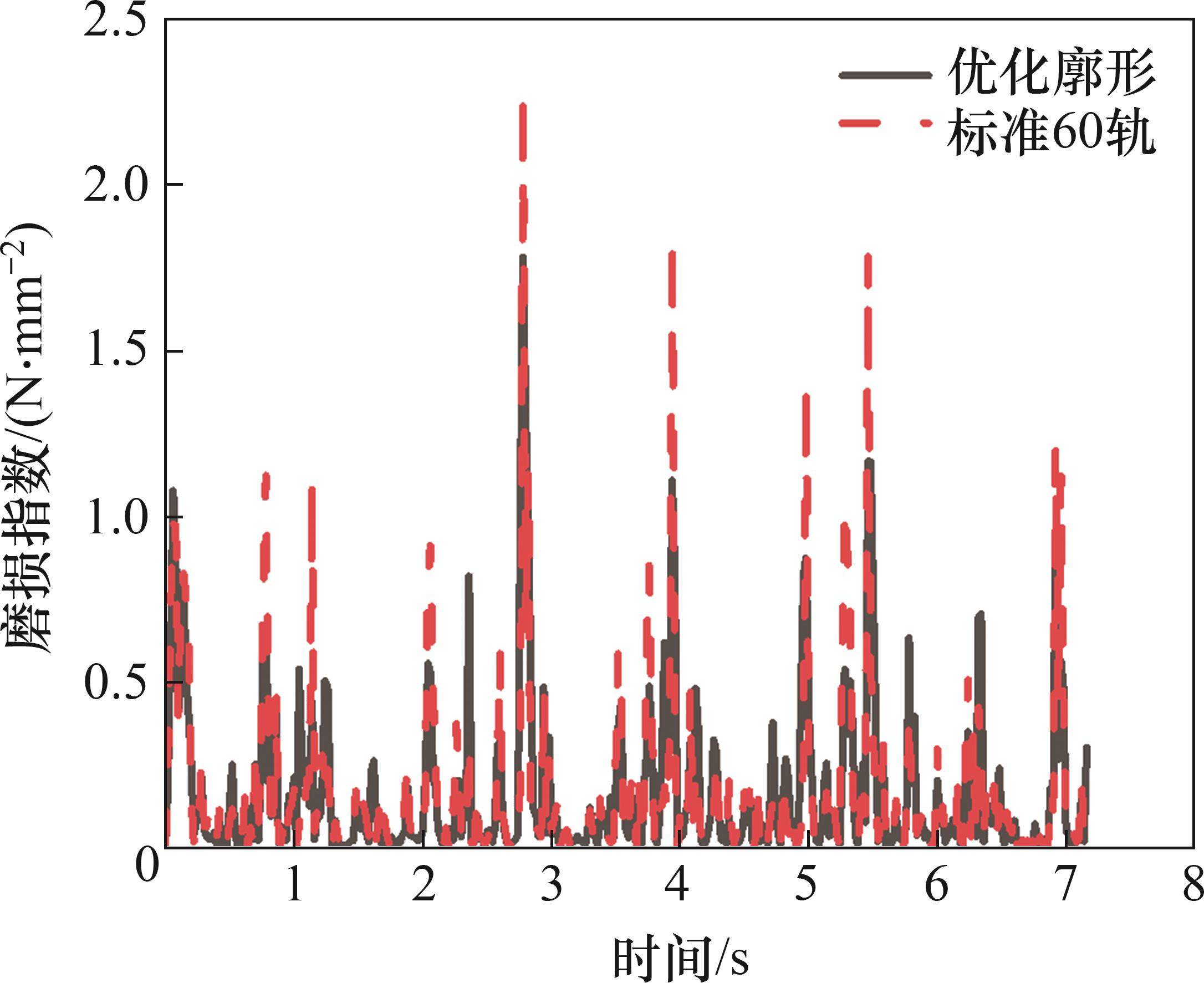
在直线工况下,当列车以200 km/h的速度行驶在优化后的钢轨和标准60轨上时,钢轨廓形优化前、后的磨耗指数对比如图16所示。由图16可见:优化后的钢轨磨损指数最大值为1.78,标准60轨的磨损指数最大值为2.28。优化后的钢轨廓形的磨损指数最大值相较于标准60轨的磨损指数减小21.9%。磨损指数得到优化的原因是,优化后钢轨廓形使轮轨间蠕滑力减小,轮轨相对滑动情况得到了有效抑制,有助于减少滚动疲劳接触,减缓钢轨磨耗速率[28-29]。
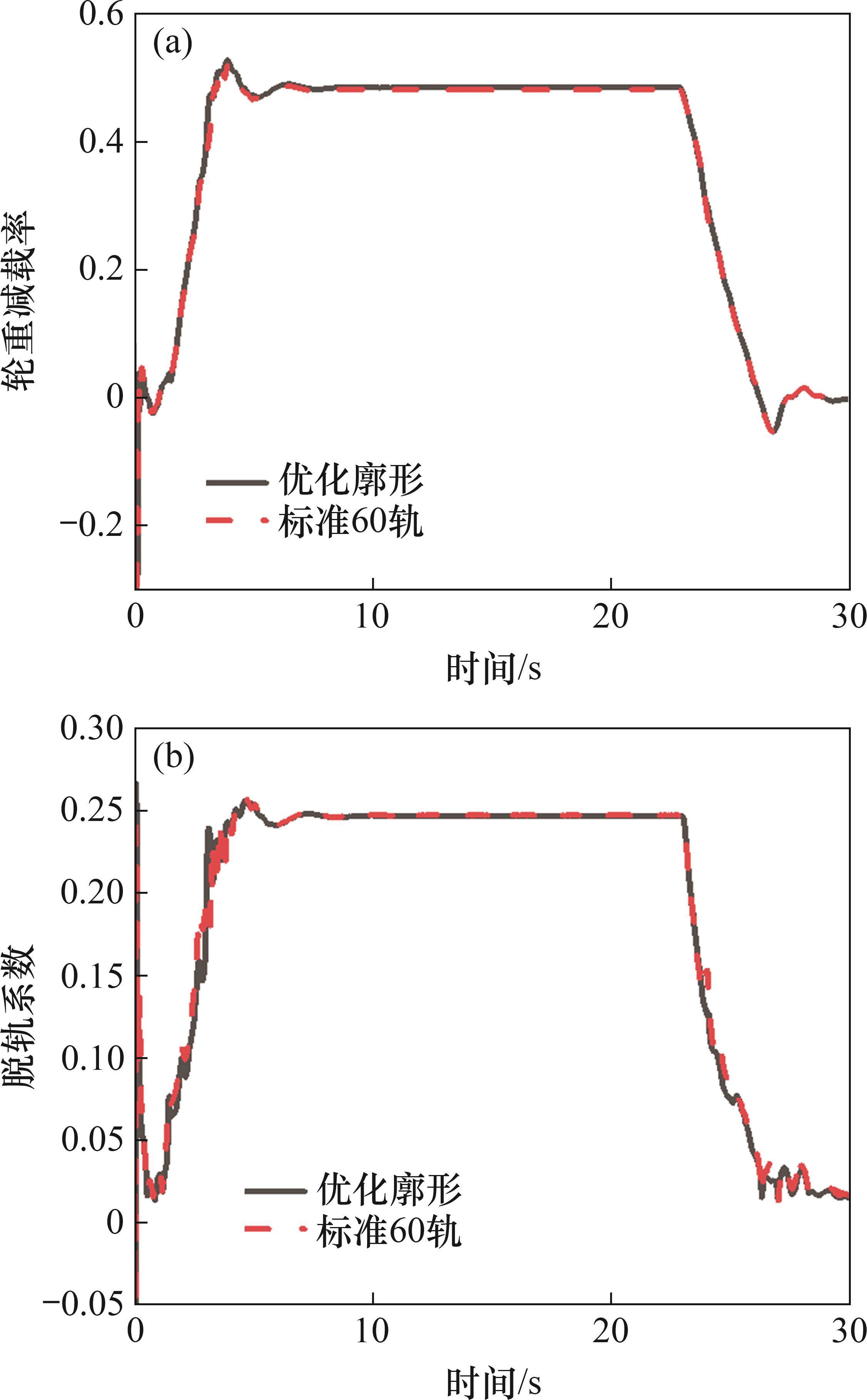
在同样的工况及在曲线半径为1 000 m的圆曲线段下,从车辆的轮重减载率和脱轨系数的角度分析优化后的钢轨廓形对车辆曲线通过性产生的影响[30],结果如图17所示。由图17可见:廓形优化后的钢轨相较于标准60轨,对车辆曲线通过性基本没有影响。
4 结论
1) 基于Hertz应力接触理论,通过设定理想接触应力,根据轮轨间接触最大应力和接触点曲率半径反推出优化钢轨廓形的办法,由该方法计算得到的优化钢轨廓形在轮轨接触点分布方面相较于标准60轨更加均匀,等效锥度下降约30%,出现在轨距角处的轮轨间最大接触应力下降15.8%。基于Hertz接触应力的钢轨打磨廓形设计方法能提高列车的行驶的稳定性和减低钢轨的磨耗。
2) 在钢轨磨耗预测仿真中,当通过轴重为19×106 t时,标准60轨优化后的钢轨廓形顶面位置平均磨耗深度减小4%,优化后的钢轨廓形轨距角位置平均磨耗深度减小24%。相较于标准60轨,优化后的钢轨廓形能有效减小钢轨顶面及轨距角区域的磨耗量,说明基于Hertz接触应力的钢轨打磨廓形设计方法在预防钢轨磨耗方面具有优越性。
3) 采用优化后钢轨廓形,轮轨横向力和垂向力,轮轨横、纵向蠕滑力的最大值分别为18.7、91.6、13.4和18.3 kN,均比标准60轨工况的值小,有利于减少滚动疲劳接触,其磨损指数最大值为1.78,相较于标准钢轨最大磨损指数2.28下降了21.9%。总体来说,基于Hertz接触应力的钢轨打磨廓形设计方法具有较好的适用性。
陈迪来, 孙庚辰, 陆晨旭, 等. 基于Hertz接触应力的钢轨打磨廓形设计方法[J]. 中南大学学报(自然科学版), 2025, 56(2): 782-794.
CHEN Dilai, SUN Gengchen, LU Chenxu, et al. Design method of rail grinding profile based on Hertz contact stress[J]. Journal of Central South University(Science and Technology), 2025, 56(2): 782-794.
http://dx.doi.org/10.11817/j.issn.1672-7207.2025.02.031

