随着我国城市轨道交通的迅猛发展,车轮磨耗问题日益显著,给地铁车辆日常运营和维护带来了不可忽视的挑战[1]。而且,随着客流量、轴重以及小半径线路的增加,同一车轮常伴随多种磨耗形式,直接影响车辆的运行质量,严重时甚至危及乘客的生命安全[2]。因此,深入探究车轮不同磨耗形式间的相互作用以及对车辆动态响应的影响规律,对于确保车辆的可靠运行具有重要价值。车轮磨耗主要表现为横向和纵向2种形式,即车轮型面磨耗和车轮多边形[3]。型面磨耗容易导致车辆发生低频晃动,影响轮轨之间的相互作用。侯茂锐等[4]进行了轮轨型面的现场测试和等效锥度分析。研究结果表明,与磨耗范围较大的车轮型面相比,磨耗范围较小者对等效锥度的影响更为显著,这种现象与踏面发生凹磨有直接关系。作为踏面磨耗的一种特殊形式,凹磨的出现将显著影响车辆的运行安全性[5]。针对这一问题,WANG等[6]分析了踏面凹磨对车辆动力学性能的影响。研究发现,凹磨程度加剧导致轮轨等效锥度增大,降低车辆运行的稳定性,严重情况下可能导致构架发生失稳并触发危险报警。轮缘磨耗作为另外一种常见的横向磨耗,在曲线占比较高的线路上时常发生[7]。KOU等[8]通过轮轨三维稳态滚动接触模型分析了型面磨耗状态对曲线路段上车轮磨耗的影响规律。研究发现,轮轨多点接触时,轮缘位置存在较高的接触压力和滑移速度,加剧了轮缘的磨耗速率。由此可知,轮缘磨耗的发生势必会影响轮对的使用寿命,降低车辆运行的经济性[9-11]。车轮纵向磨耗,即车轮多边形,容易在列车轨道系统中引发强烈的振动及啸叫现象,严重影响车辆的运行安全性及乘坐舒适性[12-14]。铁路运输现场广泛存在车轮多边形现象,相关研究主要聚焦于车辆动力学响应和形成机理的分析[15-17]。YANG等[18]采用现场实验与数值模拟相结合的方法,研究了重型机车车轮多边形磨耗对车辆动态响应以及轮轨相互作用的影响规律。研究发现,严重的车轮多边形磨损不仅会影响轮轨系统的垂向性能,还显著影响其纵向性能。此外,车轮高阶多边形对机车系统部件的纵向、横向和垂向振动都产生显著影响。SPENGENBERG等[19]在南非的一辆货运机车上验证了车辆结构部件发生剧烈振动和疲劳故障与车轮多边形之间的关系。研究显示,交流牵引系统机车的结构故障是由20阶车轮多边形造成,而20阶多边形是由5fg~7fm谐波与42 km/h的耦合共振导致。为了从根本上解决车轮多边形问题,相关学者对多边形磨耗机理开展了大量的研究工作[20-23]。结果表明,车轮多边形形成机理主要与轮对模态共振、P2共振、轮轨黏滑自激振动以及钢轨共振等有关。然而,上述研究主要侧重于分析和比较车轮横向或纵向磨耗对车辆性能响应的影响规律和形成机理,未能有效考虑车轮磨耗的复杂形式,即车轮横向和纵向磨耗在车辆实际运行过程中的耦合作用。因此,本研究针对国内某地铁车辆进行了长期的跟踪测试,采集了不同磨耗阶段的车轮型面和车轮多边形。旨在深入探究车轮型面磨耗与多边形之间的耦合作用,特别关注这种复杂磨耗形式对车辆动态响应的影响规律,从而为车辆维护和运营提供更为准确的指导。
1 车轮磨耗数据采集与分析
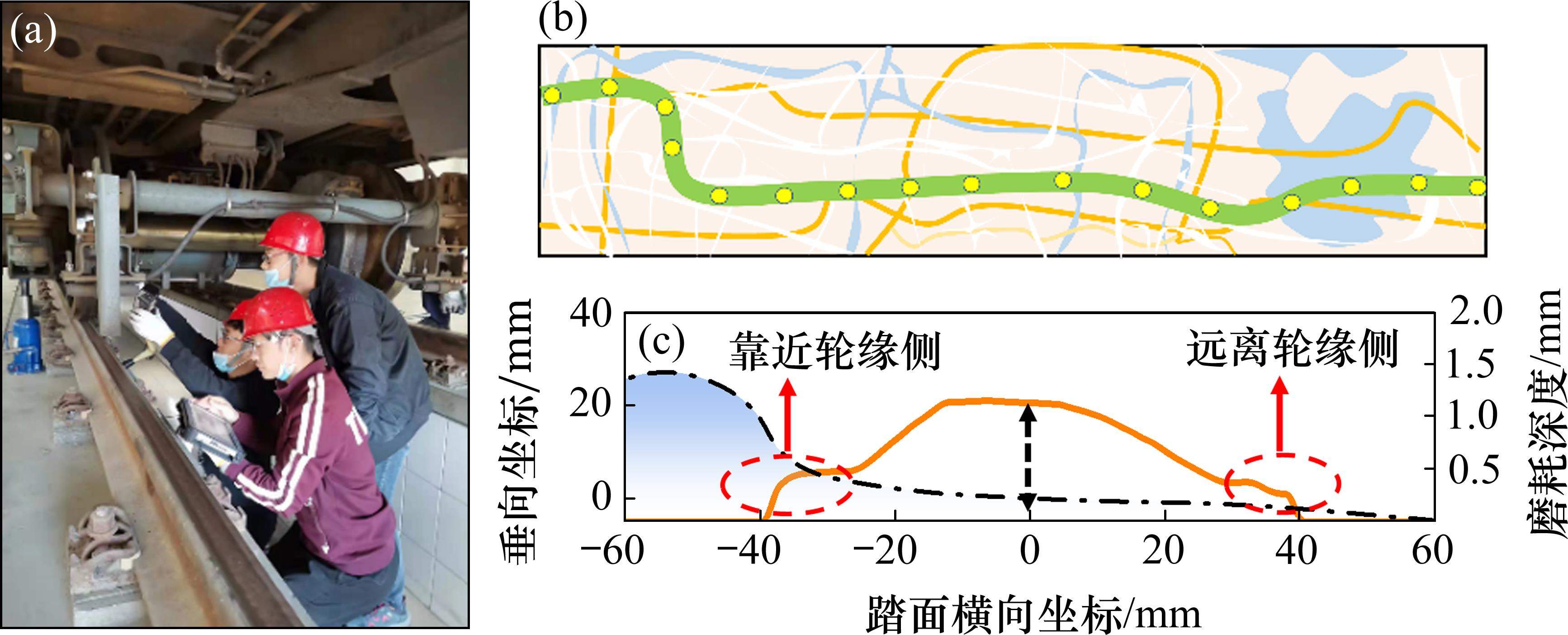
采用CALIPRI非接触式测量仪对车轮型面磨耗和车轮多边形分别进行了5次现场测试,每次测试间隔3个月。对于测试车辆,车轮和钢轨分别采用LM和CHN60型面。跟踪测试期间,车轮未进行镟修,钢轨未进行打磨。车轮多边形测试时,需要使用千斤顶将轴箱抬升3~5 mm,以确保测试车轮可以自由旋转,测试现场见图1(a)。为便于本文的后续分析,依据测试次数将车轮磨耗(型面磨耗和多边形)划分为磨耗初期(第1次)、磨耗中期(第3次)和磨耗后期(第5次),3轮测试时地铁车辆的运营里程分别为3.85×104 km、8.78×104 km和14.81×104 km。
1.1 车轮型面磨耗
由图1(b)可以看出,测试车辆的运营线路中直线路段占比较高。这种线路特征使得车轮踏面相比于轮缘位置出现了更为显著的磨耗,且最大磨耗深度出现在名义滚动圆(横向坐标为0 mm)附近,如图1(c)所示。
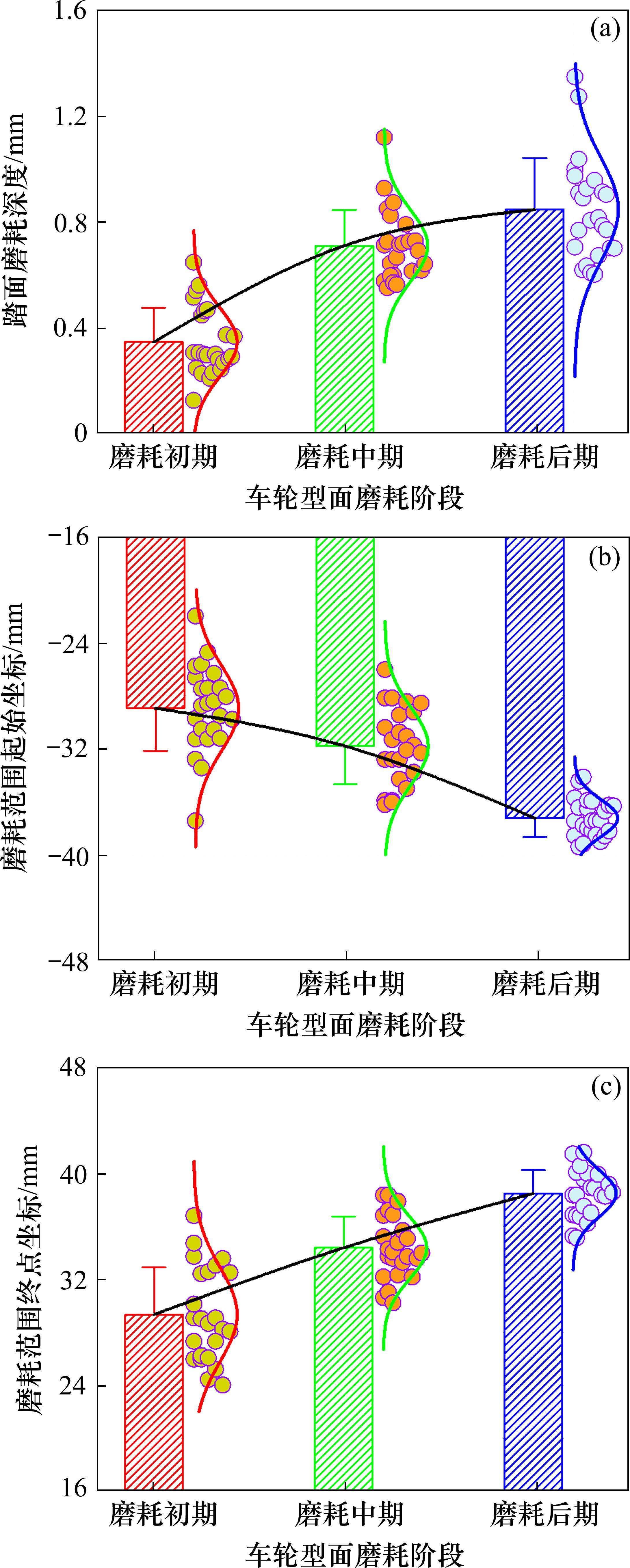
图2采用箱型图展示了测试车辆3节拖车共24个车轮的最大磨耗深度和磨耗范围。由图2(a)可知,磨耗深度随着运行里程的增加而增加,3种磨耗阶段的平均磨耗深度分别为0.44,0.82和0.99 mm。图2(b)和图2(c)分别显示了型面磨耗的起始坐标(靠近轮缘侧)和终点坐标(远离轮缘侧)。数据表明,随着运行里程的增加,车轮型面的磨耗范围持续扩大,3种磨耗阶段的平均磨耗范围分别为-28.95~29.34,-31.81~34.37和-37.24~38.48 mm。
1.2 车轮多边形磨耗
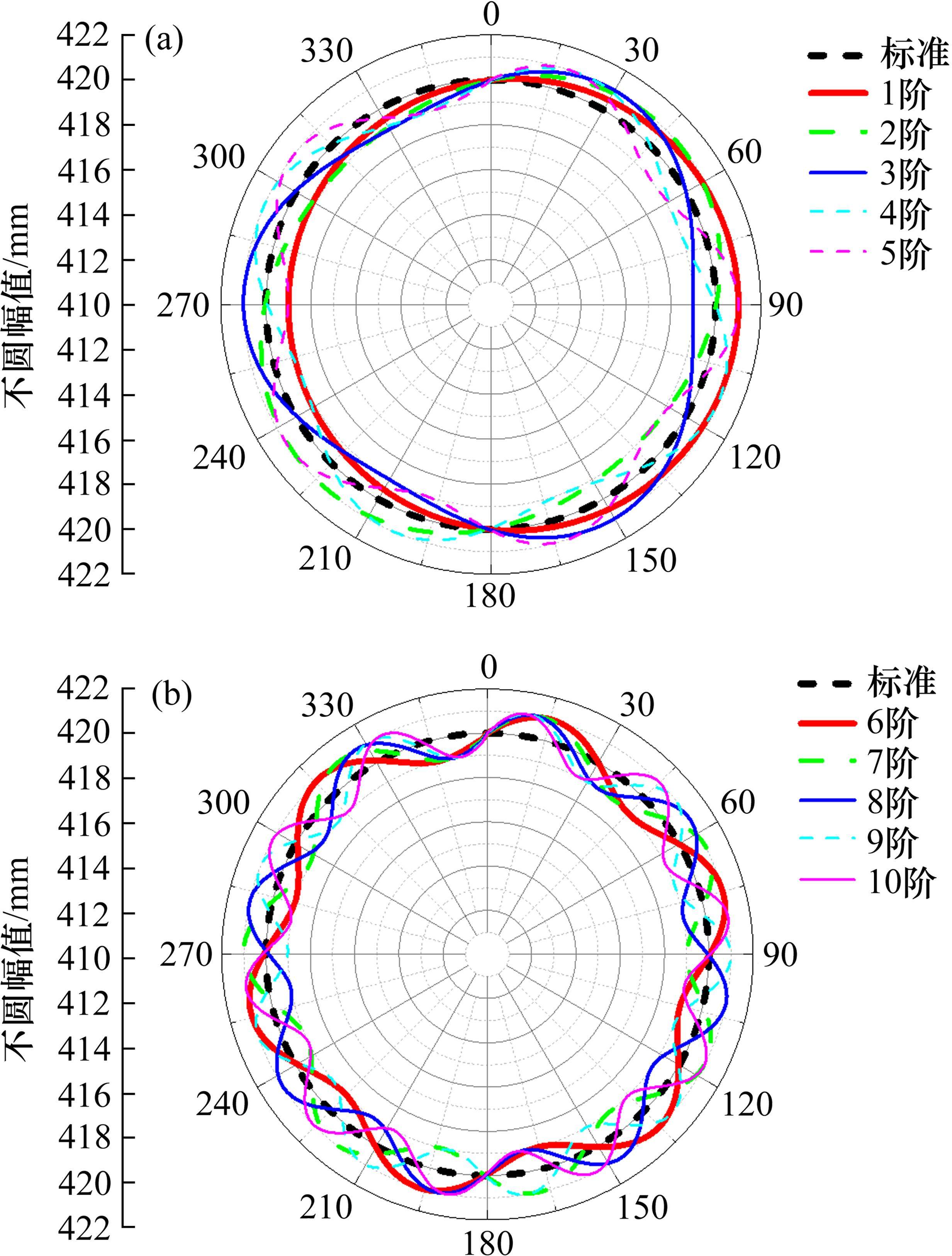
车轮多边形测试时,测点设定在车轮型面的名义滚动圆处,即距离轮缘内侧70 mm的位置。车轮多边形测试结果见图3。
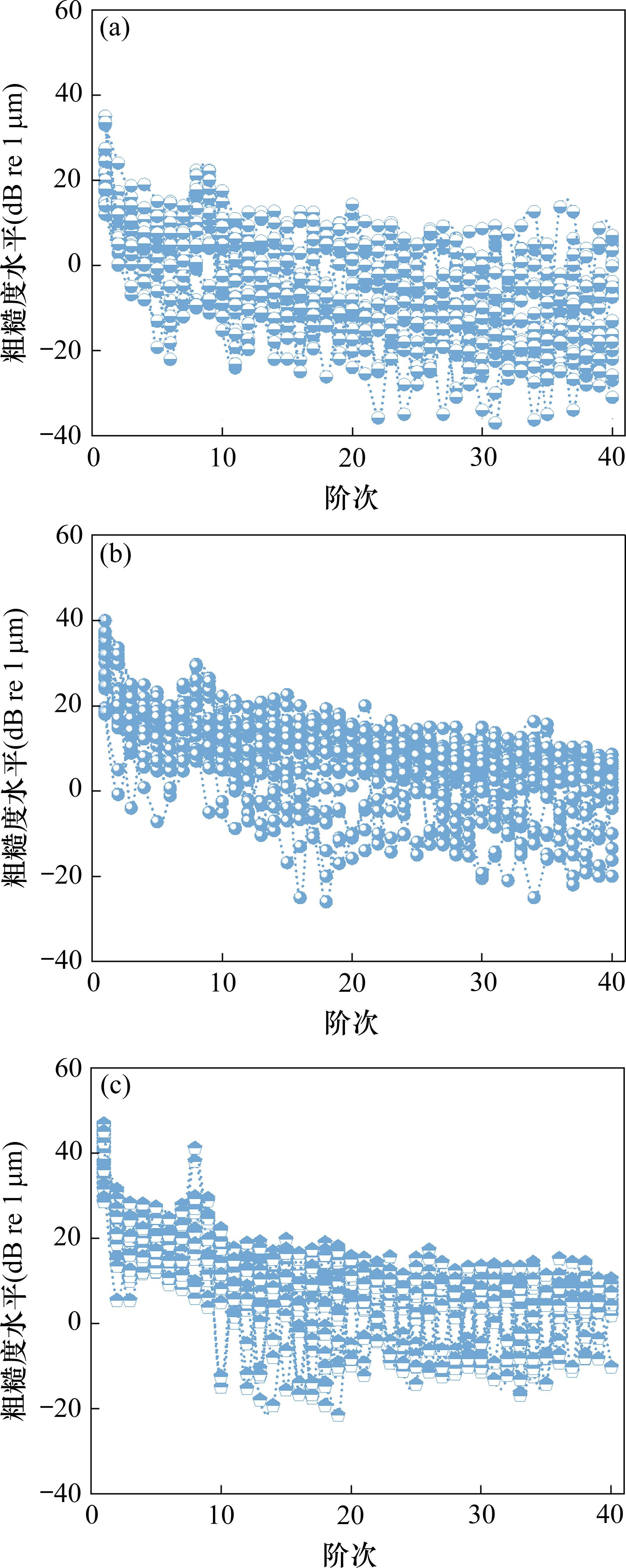
由图3可知,在3种磨耗阶段,多边形的主导阶次均为1阶偏心。随着车轮磨耗程度的加剧,10阶范围内的多边形粗糙度水平逐渐上升。结合文献[24-25]的研究结果可知,当车轮表面粗糙度大于18 dB时,表明车轮多边形现象显著。通过分析实测数据后发现,磨耗初期时,1~10阶多边形粗糙度幅值超过18 dB的占比7.9%;磨耗中期时占比上升至37.9%;而在磨耗后期时占比达到52.9%。对于地铁车辆而言,这种明显的多边形现象和较高的车轮粗糙度水平将显著加剧车辆振动和车内噪声,进而影响车辆的乘坐舒适性,甚至可能对车辆的运行安全性产生潜在影响。
1.3 车轮横向和纵向磨耗综合分析
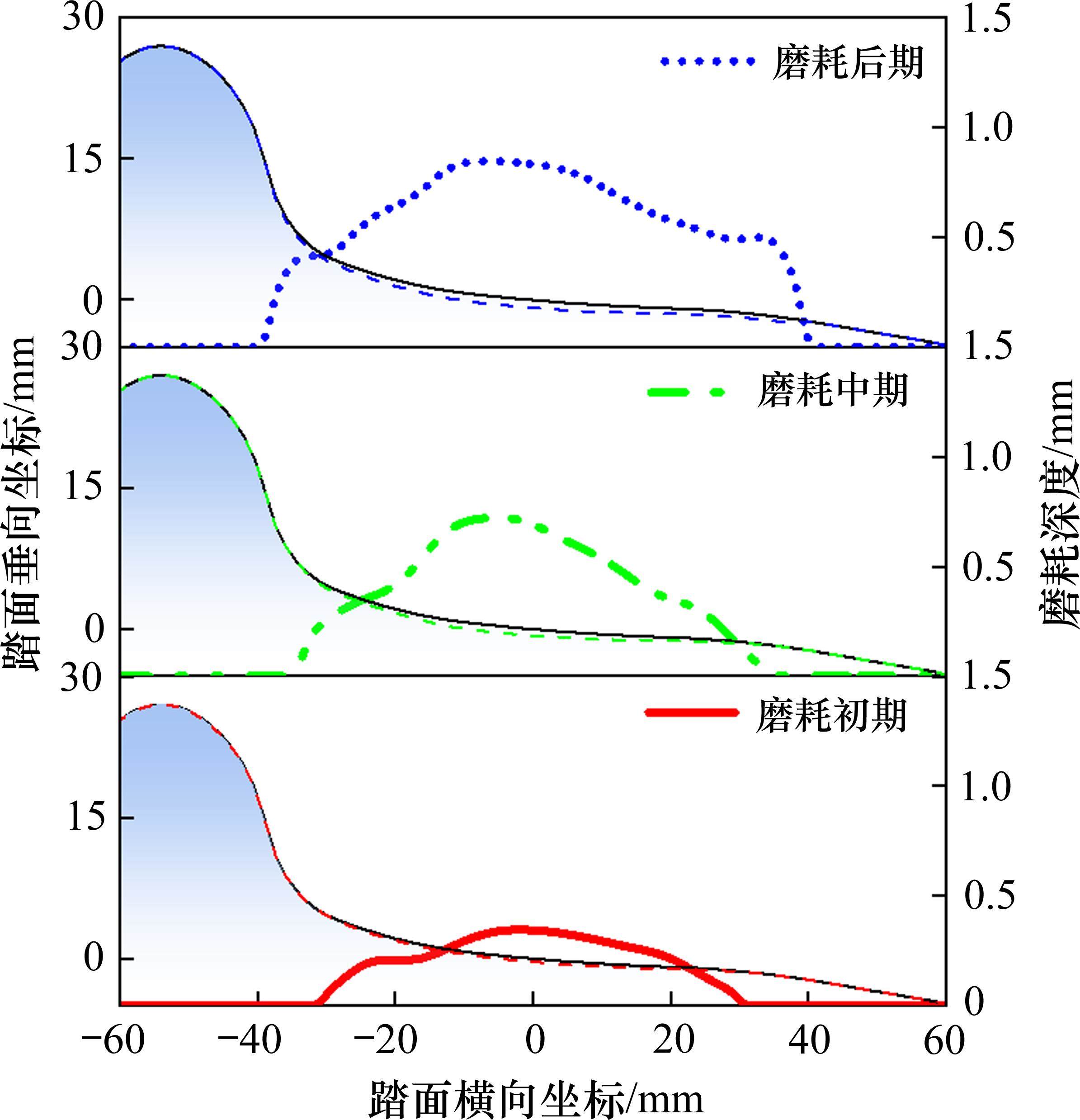
为全面考虑2种车轮磨耗形式及所有车轮的磨损情况,基于实测数据求取所有车轮磨损型面的平均值,即采用3个磨损阶段的平均型面进行后续分析。如图4所示,3种磨耗阶段下,车轮磨耗主要发生在踏面位置,且磨耗中期时呈现明显的凹磨特征。对于车轮多边形,3个磨损阶段中,1至10阶多边形的粗糙度水平均相对较高,故选取前10阶多边形用于进一步的计算和分析,如图5(a)和图5(b)所示。
2 模型搭建
2.1 车辆系统动力学模型
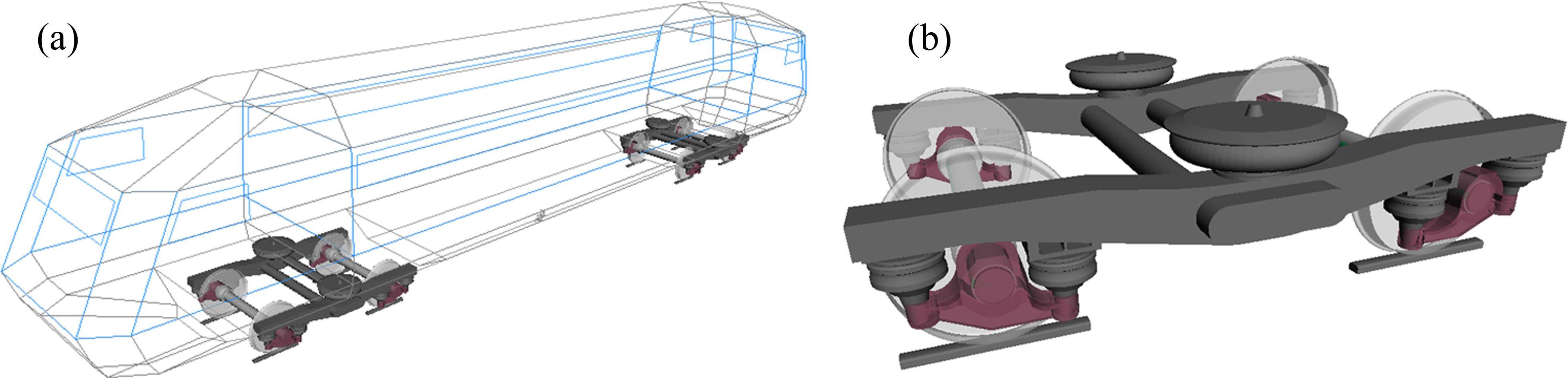
基于测试车辆的结构与质量参数,在SIMPACK中搭建车辆系统动力学模型。模型主要包括1个车体、2个构架、4条轮对、8个轴箱以及一系和二系悬挂系统,相关参数见表1。另外,车体、构架和轮对考虑6自由度,轴箱考虑相对轮对点头方向的自由度,整车共计50个自由度。车辆模型如图6所示。
| 参数名称 | 参数 |
|---|---|
| 车体质量/t | 33.86 |
| 构架质量/t | 2.1 |
| 轮对质量/t | 1.02 |
| 轴箱质量/t | 0.11 |
| 转向架轴距/m | 2.3 |
| 车辆定距/m | 12.6 |
| 滚动圆横向跨距/m | 1.493 |
| 一系弹簧垂向刚度/(MN∙m-1) | 1.3 |
| 一系弹簧垂向阻尼/(N∙s∙m-1) | 1 800 |
| 一系弹簧横向跨距之半/m | 0.97 |
| 二系空气弹簧垂向阻尼/(kN∙s∙m-1) | 25 |
| 二系空气弹簧横向阻尼/(kN∙s∙m-1) | 58 |
2.2 车轮磨耗型面与车轮多边形的耦合模型
结合图4确定的车轮型面磨耗数据,通过SIMPACK中的Wheel Profiles模块调用Database数据库,完成车轮4种型面模型的搭建,包括标准型面及3种磨耗型面。同时,结合图5中的车轮多边形数据,通过Untrueness模块调用Harmonic function设定多边形阶次(1~10阶)及波深(0.05~0.2 mm),完成车轮多边形模型搭建。
最后,基于车辆系统动力学模型,将4种磨耗阶段的车轮型面模型与不同阶次及波深的多边形模型分别耦合,完成车轮三维磨耗模型的搭建。
2.3 模型验证
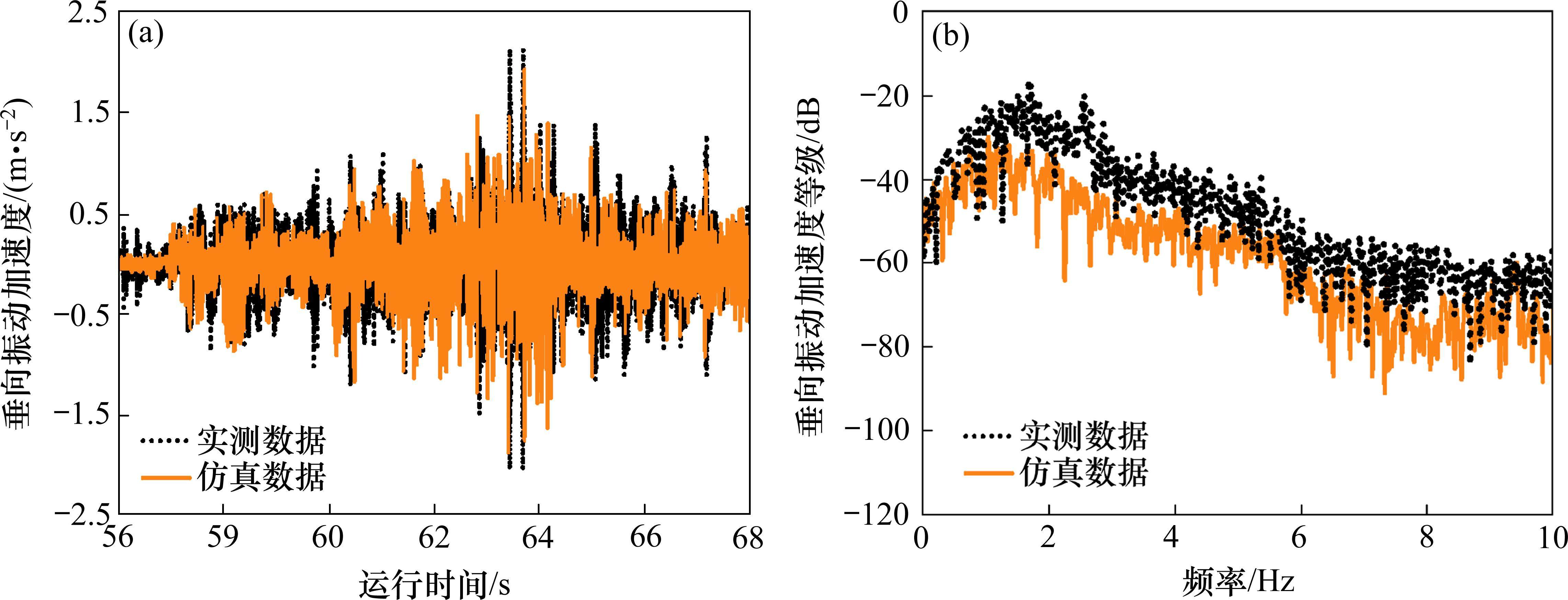
为了确保所建立的模型能够准确反映车辆动力学性能,选用车体垂向振动加速度的实测数据验证模型的准确性。现场测试时,传感器放置在前转向架中心线左侧1 m处,用于采集振动加速度数据。为保证工况一致性,仿真实验时传感器被加装在相同位置,且采用实测轨道不平顺作为轨道激励。
由图7可知,仿真实验计算的振动加速度时域和频域结果与现场实测具有较好的一致性。因此,本文所建立的模型可以有效用于后续的车辆动力学性能计算。
3 车轮型面磨耗耦合车轮多边形对车辆动态响应的影响规律
通过建立的车辆系统动力学模型,并基于图4和图5中确定的车轮磨耗型面和车轮多边形,研究车轮型面磨耗耦合车轮多边形对车辆动态响应的影响规律。模型考虑了车轮型面在磨耗初期、磨耗中期和磨耗后期3个阶段的变化特征,涵盖了车轮多边形的阶次和波深2个方面因素,旨在深入理解车轮不同磨耗形式之间的关联及其对车辆直线运行性能和曲线通过性能的影响。另外,计算过程中,采用该运营线路实测轨道不平顺作为轨道激励。
3.1 车轮型面磨耗耦合车轮多边形对车辆直线运行稳定性的影响
采用临界速度作为车辆运行稳定性的评价指标。由图8(a)可知,在不考虑车轮多边形的情况下,车轮型面不同磨耗阶段的临界速度分别为192,177,157和163 km/h,磨耗中期时取得最小值。这是因为车轮型面在磨耗中期时呈现明显的凹磨特征(见图4),使得轮轨之间的有效接触面积减小,降低了附着力,从而导致车辆运行稳定性较差。
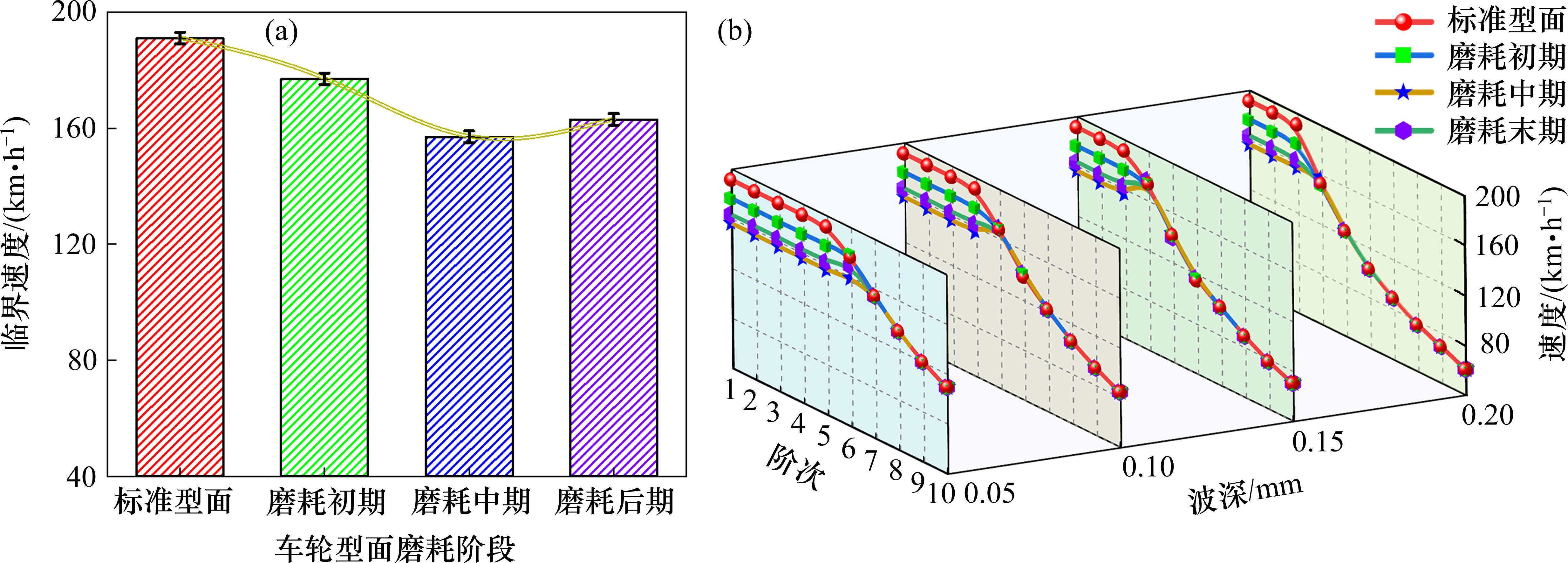
由图8(b)可知,型面磨耗耦合车轮多边形后,低阶多边形对临界速度影响较小,其阶次范围与波深幅值有关。具体而言,当波深为0.05 mm时,5阶及以下的多边形对临界速度影响有限。类似地,在波深为0.1,0.15和0.2 mm时,分别对应的多边形阶次为4、3和3。此时,车轮型面磨耗对临界速度起主导作用。然而,随着阶次增大,车轮多边形与型面磨耗产生不良耦合效应,临界速度逐渐下降,且下降幅度与波深成正比。这是因为阶次升高和波深增大导致轮轨系统的动力学阻尼减小,车辆振动能量积聚,使得车辆在运行过程中更容易受到外界扰动,降低了临界速度。需要特别注意的是,阶次大于7后,0.1 mm及以上波深对临界速度的影响尤为显著。例如,波深为0.1 mm,阶次为9~10时,临界速度降至100 km/h以下。更为严重的是,波深为0.2 mm,阶次为7~10时,临界速度已降至90 km/h以下,最小值仅为61 km/h,这将显著影响车辆的运行稳定性。
3.2 车轮型面磨耗耦合车轮多边形对车辆直线运行平稳性的影响
图9和图10采用平稳性指标分别评价了车辆垂向和横向的运行平稳性。其中,图9(a)和图10(a)分别呈现了车轮型面磨耗对平稳性指标的影响规律。由图9(a)和图10(a)可知,随着车轮型面磨耗程度的加剧,垂向和横向平稳性指标均呈现先增后减的变化趋势,在磨耗中期时取得最大值。这种现象同样与踏面在磨耗中期时出现凹形磨耗密切相关,使得轮轨接触表面产生非线性变化,导致轮轨摩擦与轮轨相互作用力分布不均匀。此外,依据《铁道车辆动力学性能评定和试验鉴定规范》,在5~10 Hz滤波后,平稳性指标W<2.5为优。由图9(a)和图10(a)可知,2个方向的平稳性指标均未超过该限值。
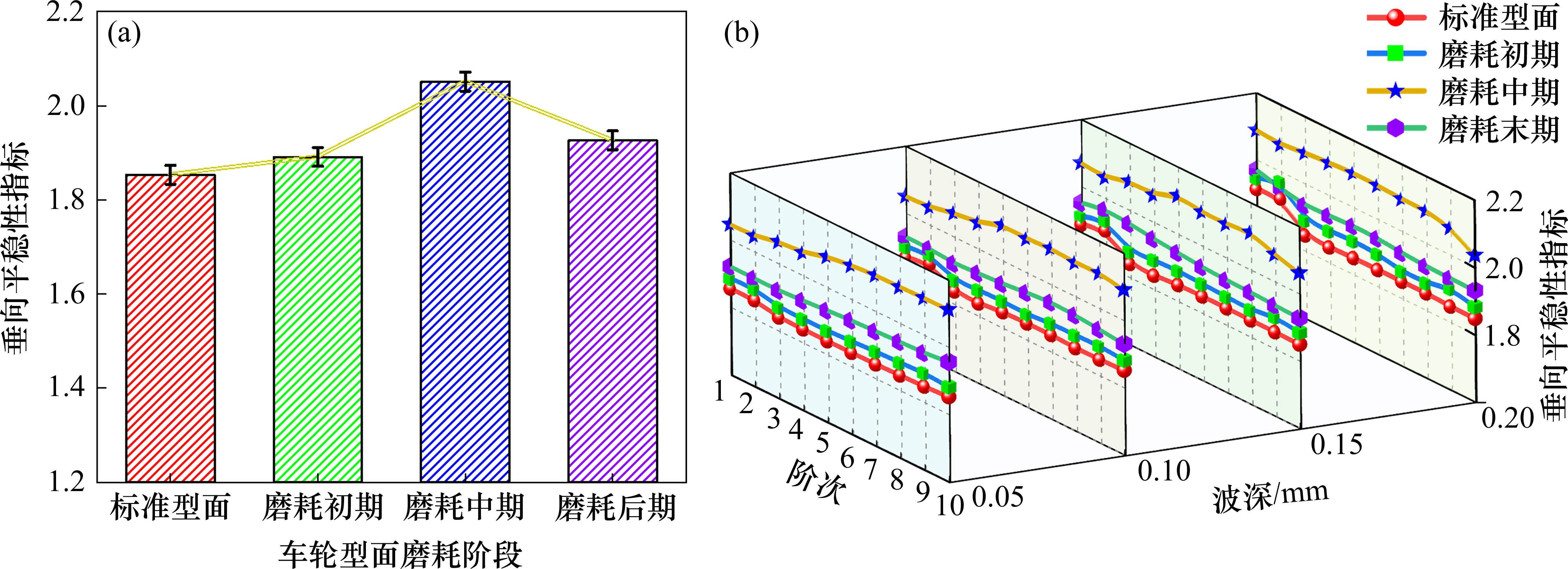
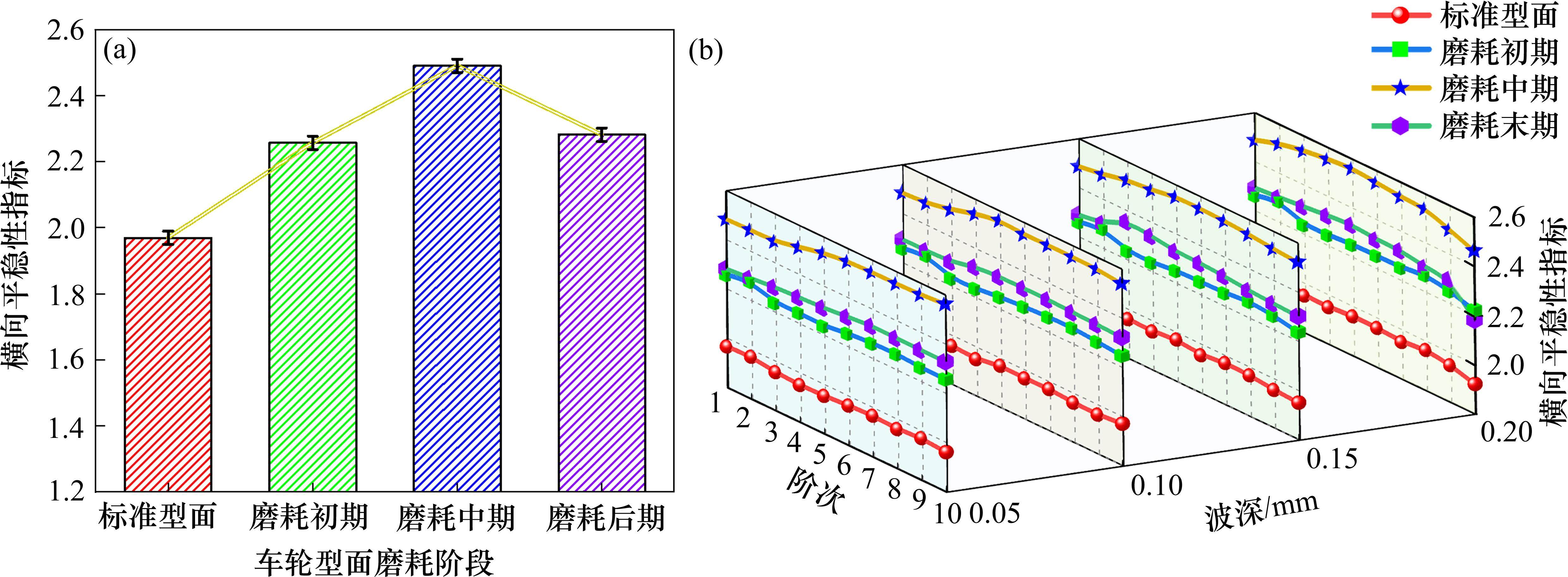
由图9(b)和图10(b)可知,车轮型面磨耗耦合车轮多边形后,阶次和波深增大并未引起平稳性指标的明显变化,说明车轮多边形对车辆运行平稳性影响较小。进一步分析表明,这是因为车轮多边形引起的振动频率超出了平稳性的频率敏感范围。
3.3 车轮型面磨耗耦合车轮多边形对车辆曲线通过性能的影响
对于车辆曲线通过性能而言,本项研究重点关注运营线路中小半径曲线段的整体性能表现。因此,选择了半径为300 m,由直线(245 m)-缓和曲线(55 m)-圆曲线(400 m)-缓和曲线(55 m)-直线(245 m)5部分组成的曲线路段进行深入研究。计算过程中,曲线超高为120 mm,轨底坡为1/40,轨距为1 435 mm,轮对内侧距为1 353 mm,车辆运行速度为60 km/h。研究内容主要围绕轮轨相互作用力、曲线通过安全性以及磨耗指数3个方面。其中,轮轨相互作用力和曲线通过安全性关注外侧车轮的性能响应,而磨耗指数则关注内外两侧的响应差异。
3.3.1 轮轨相互作用力
图11和图12分别为轮轨垂向力和轮轨横向力,其中包括车轮型面磨耗以及型面磨耗耦合车轮多边形对两者的影响规律。由图11(a)可知,对于轮轨垂向力,不考虑车轮多边形时,轮轨垂向力随着车轮型面磨耗程度的加剧呈现先增后减的变化趋势,但整体变化幅度较小,表明型面磨耗对轮轨垂向力的影响较小。
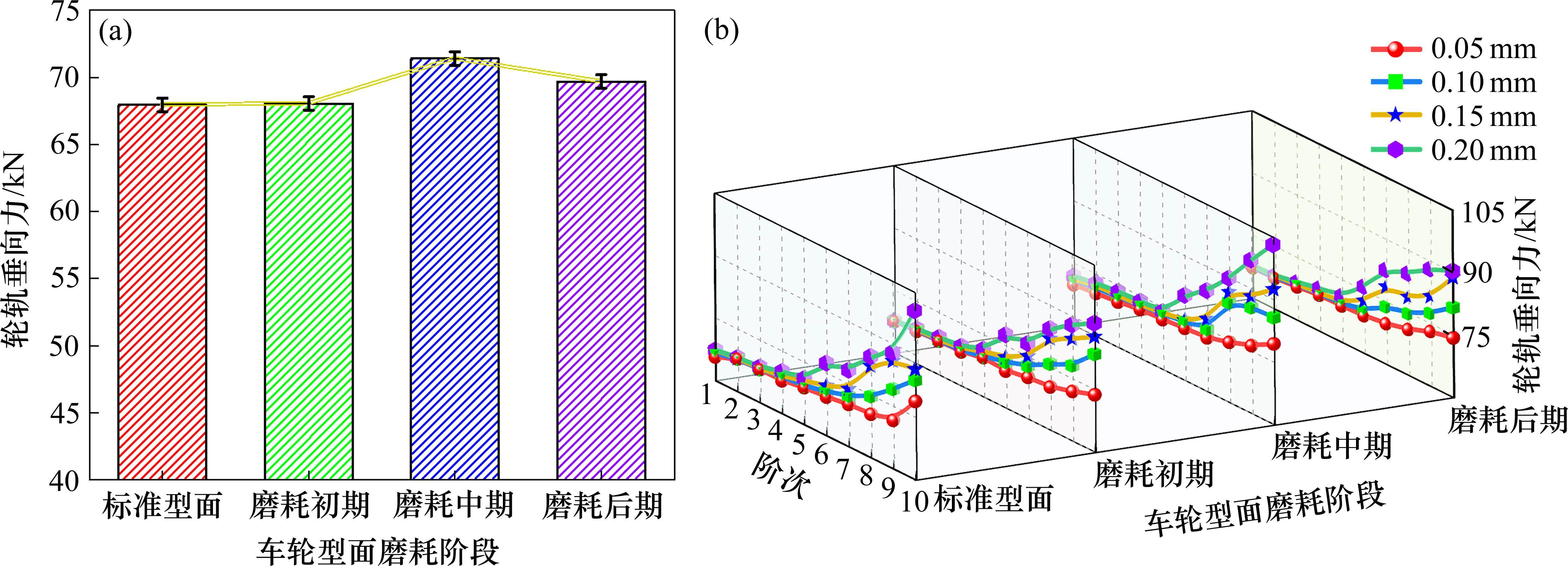
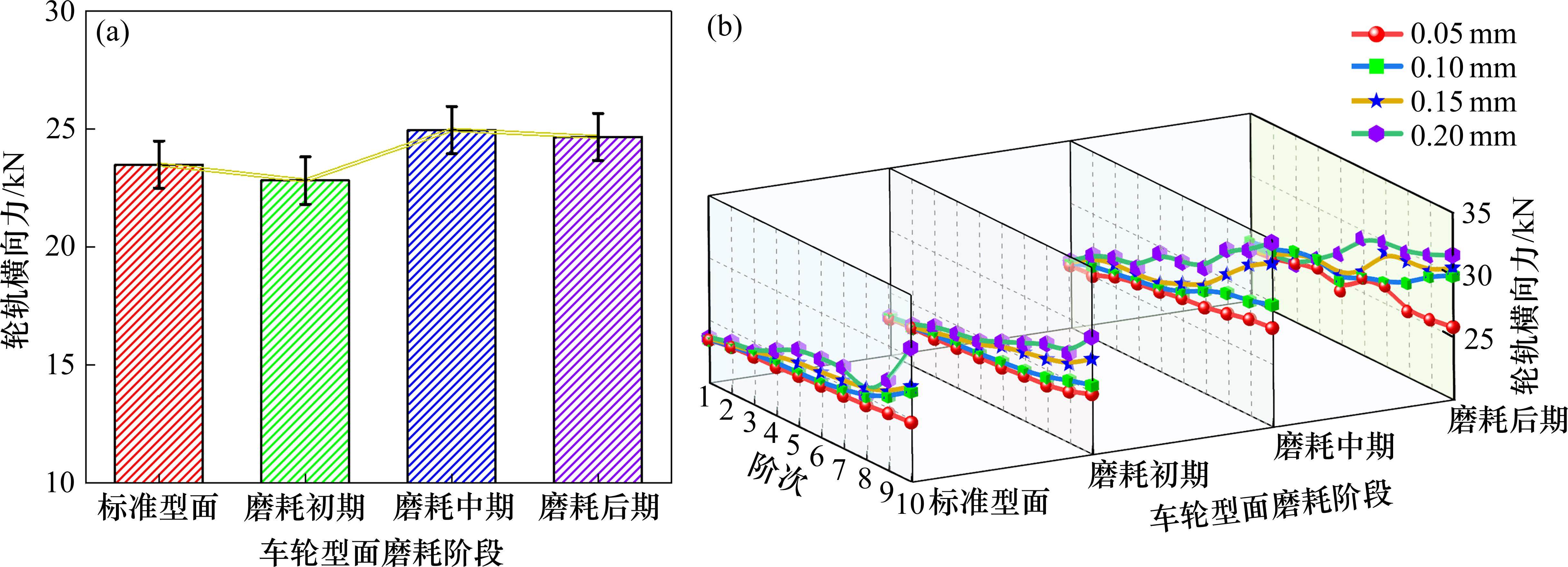
图11(b)显示了型面磨耗耦合车轮多边形对轮轨垂向力的影响。由图可知,多边形阶次小于5时,轮轨垂向力变化幅度较小,且4种型面工况下均是如此。然而,当多边形阶次超过5时,轮轨垂向力会随着阶次的升高而逐渐上升。而且,上升幅度与波深和型面磨耗程度有着直接相关性。波深越大,轮轨垂向力上升幅度越显著,即多边形波深为0.2 mm时,轮轨垂向力在4种磨耗阶段取得较大值。另外,相比于标准型面,车轮型面位于磨耗中期时,轮轨垂向力幅值进一步上升,说明磨耗中期的车轮型面会加剧车轮多边形的不良影响。与之相反,磨耗初期和磨耗后期的车轮型面使得轮轨垂向力幅值降低且上升幅度减缓。结合图4中3种磨耗阶段的车轮型面可知,当车轮型面位于磨耗中期时,名义滚动圆附近的型面磨耗具有显著的深度差异,呈现明显的凹磨特征。由此说明,型面发生凹磨现象将与5阶以上的车轮多边形发生不良耦合效应,加剧轮轨之间的垂向冲击。相比于磨耗中期的车轮型面,磨耗初期和磨耗后期的车轮型面在名义滚动圆附近的磨耗深度差异较小,型面局部变化相对均匀,一定程度上抑制了车轮多边形对轮轨垂向力的不良影响。
由图12可知,轮轨横向力变化规律与轮轨垂向力基本一致。但需要强调的是,车轮型面位于磨耗中期时,随着波深的增大,轮轨横向力上升非常显著。例如,波深和阶次分别为0.2 mm和10阶时,轮轨横向力高达34.81 kN,严重影响车辆的行驶稳定性和轨道设施的使用寿命。另外,当波深为0.2 mm时,多边形大于4阶便开始引起轮对横向力的上升,这比轮轨垂向力提前了一个阶次。
3.3.2 安全性指标
为避免车辆发生脱轨以及倾覆等安全问题,脱轨系数通常作为评定安全性问题的重要参数。由图13(a)可知,未考虑车轮多边形时,型面磨耗程度的加剧使得脱轨系数呈现先减后增的变化规律,磨耗初期的车轮型面取得脱轨系数最小值。
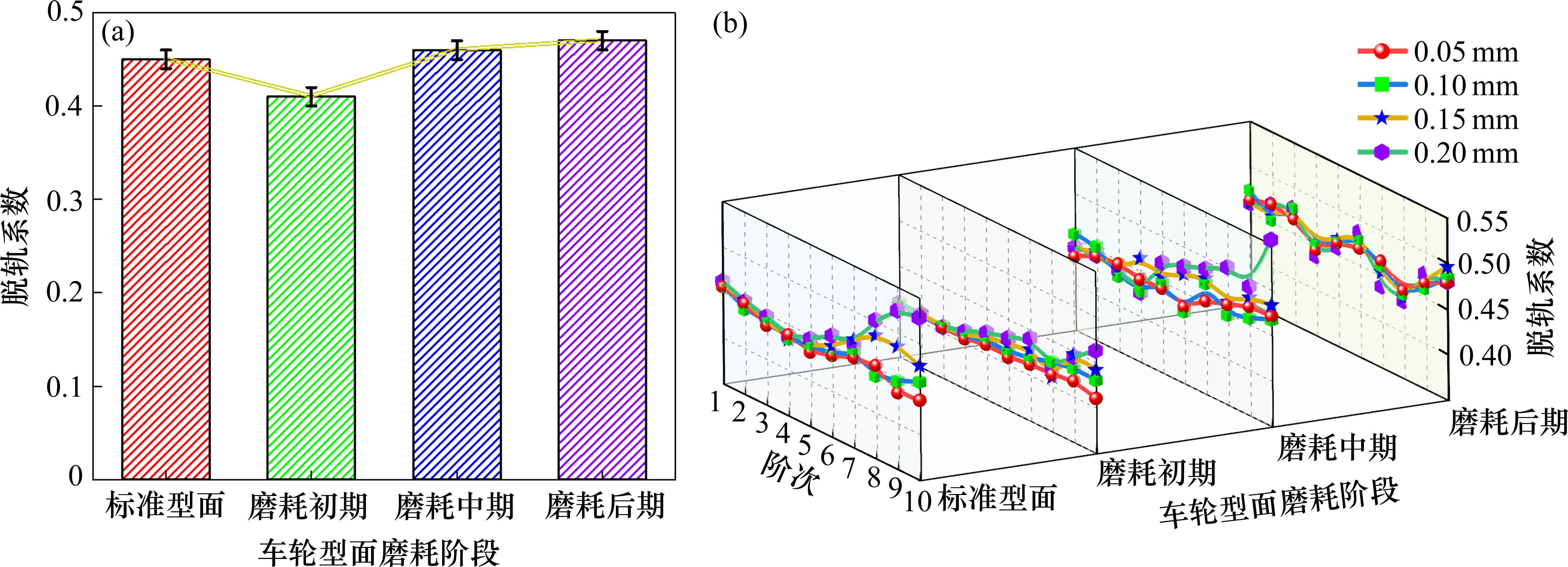
然而,耦合车轮多边形后(见图13(b)),波深和阶次均会引起脱轨系数幅值波动。而且,磨耗阶段不同,2种参数对脱轨系数的作用规律存在明显差异。例如,标准型面工况下,多边形阶次大于7时,波深增大对脱轨系数的影响更为明显。磨耗初期时,波深和阶次变化均未引起脱轨系数的显著波动,且整体幅值相对较小。由此说明,该阶段的车轮型面趋于稳定,有利于降低车轮多边形对脱轨系数带来的不良影响。与之相反,磨耗中期时的车轮型面发生凹磨,导致轮轨系统垂向和横向载荷分布不均匀,加剧了车轮多边形产生的不良影响(见图11(b)和图12(b))。脱轨系数为轮轨横向力和轮轨垂向力的比值,且轮轨横向力增幅更为显著。因此,型面凹磨进一步加剧了车轮多边形对脱轨系数的不良影响,增加了车辆的脱轨风险。当车轮型面位于磨耗后期时,相较于波深,多边形阶次对脱轨系数的影响更为显著。
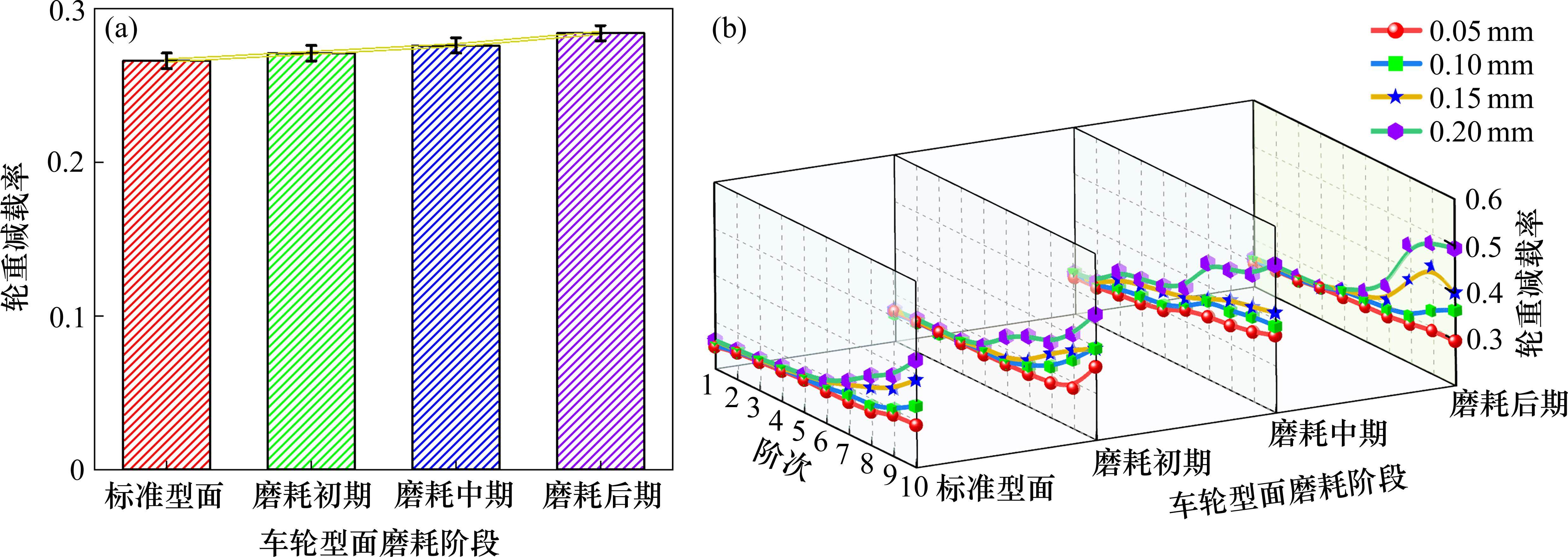
另外,车辆实际运行过程中车轮若发生严重减载也会增加车辆脱轨的危险性。因此,在分析脱轨系数的基础上,还需考虑轮重减载率的变化规律。由图14(a)可知,车轮型面磨耗程度加剧使得轮重减载率逐渐上升,但上升幅度较小。型面磨耗耦合车轮多边形后(见图14(b)),7~10阶多边形往往会引起轮重减载率的上升。而且,轮重减载率增幅与波深成正比。另外,相比于标准型面,车轮多边形在磨耗型面工况下对应的轮重减载率幅值较高。由此说明,车轮多边形与车轮型面磨耗发生耦合作用,从而影响轮重减载率幅值。
3.3.3 磨耗指数
轮轨间的磨耗与轮轨接触斑内所消耗的能量相关,轮轨接触斑内的磨耗量可由轮对磨耗功率来近似表示。其中,Elkins磨耗指数是用来描述轮轨接触斑处蠕滑力与蠕滑率标量积之和的一项指标。磨耗指数考虑了车轮蠕滑率,能够有效地代表轮轨间的磨耗情况,适合研究轮轨间的磨耗问题。
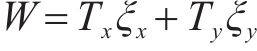
式中:W为磨耗指数;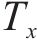
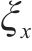
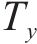
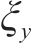
图15显示,未考虑车轮多边形的情况下,磨耗指数与型面磨耗程度呈现明显的线性关系。由此说明,车轮廓形改变会加剧轮轨间的摩擦,导致能量损失,进而引起额外的磨损。这种现象在长期运行中会对车辆的可靠性和安全性产生负面影响。
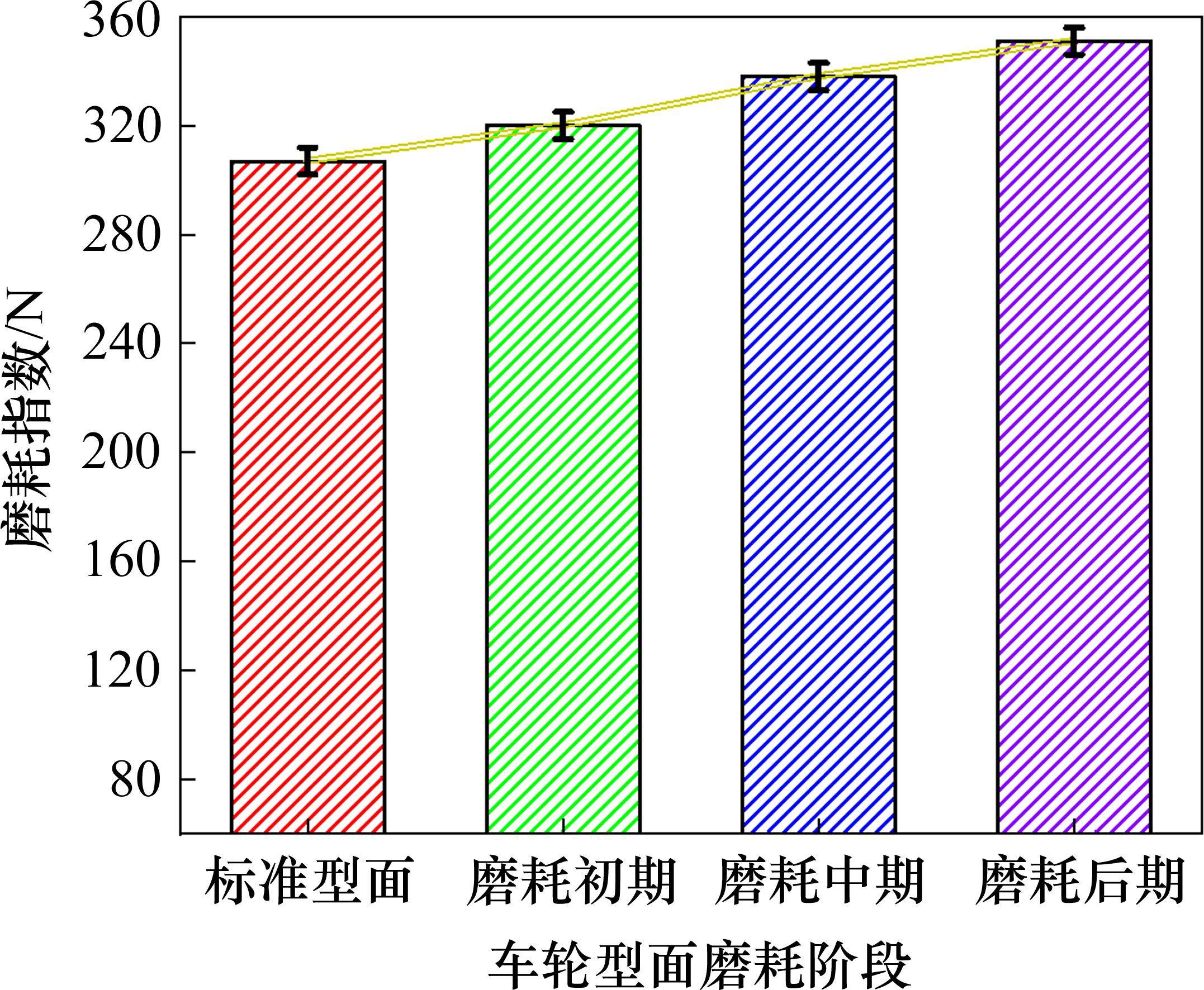
图16展示了车轮型面磨耗耦合车轮多边形对磨耗指数的影响。由图16可知,耦合车轮多边形后,内侧轮轨的磨耗指数出现轻微波动,幅值相对稳定,说明多边形的出现对内侧轮轨磨耗的影响较轻。然而,外侧轮轨的磨耗指数随着波深及阶次的增大逐渐升高。而且,相比于阶次,波深增大对磨耗指数的影响更为显著。
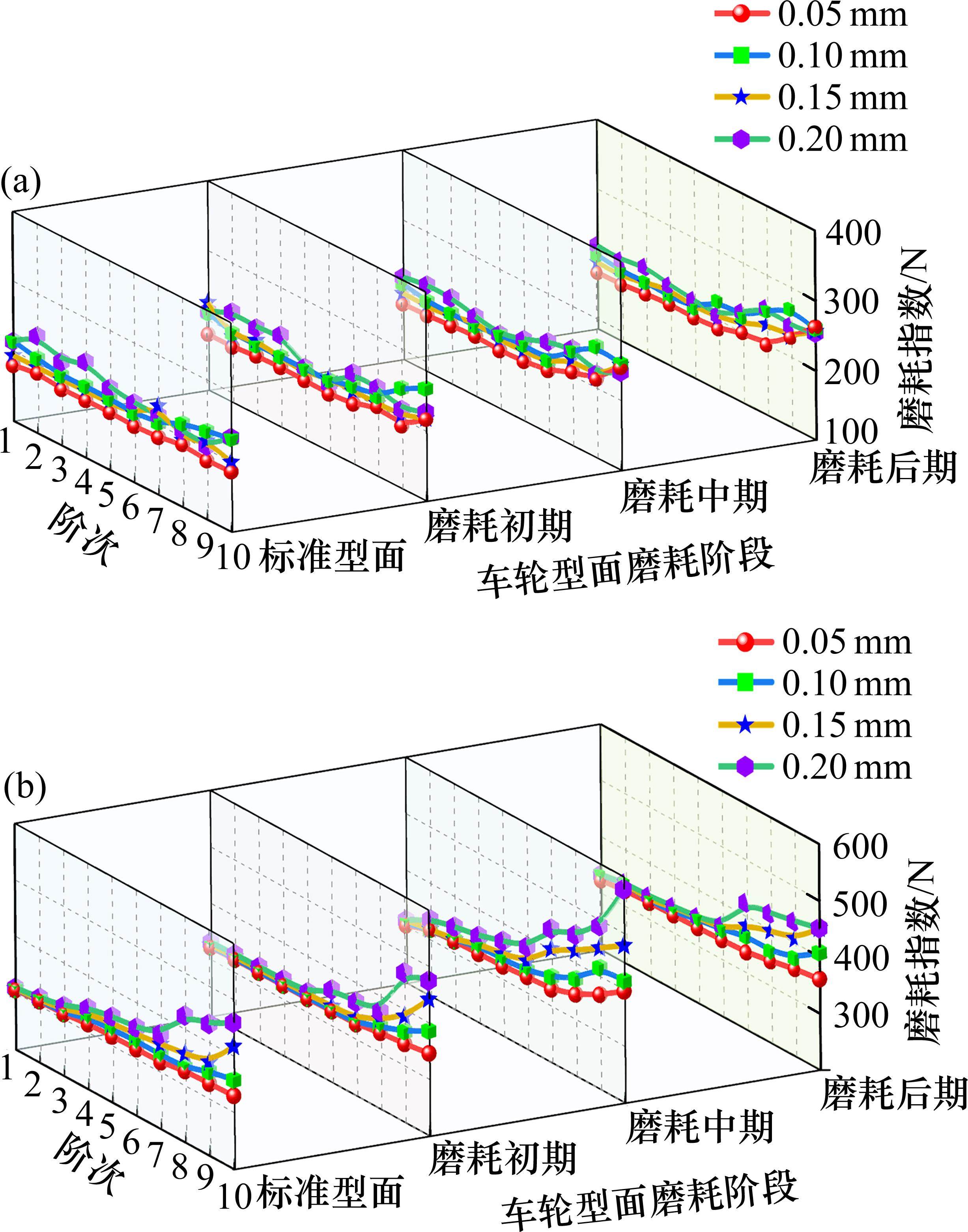
另外,对于外侧轮轨的磨耗指数而言,型面磨耗程度不同,阶次及波深增大对磨耗指数的影响程度也不同。标准型面和磨耗初期工况下,多边形阶次大于8,波深增大才会引起磨耗指数上升。然而,型面位于磨耗中期时,多边形阶次大于5,波深增大便可引起磨耗指数的显著提高。这是因为踏面凹磨使得局部应力较高,导致车轮更容易发生疲劳和磨损。耦合车轮多边形后,凹磨形成的不规则表面导致多边形效应更为突出,进一步增大了磨耗指数。值得注意的是,该工况下,波深为0.2 mm时,磨耗指数高达578.54 N,这将显著加剧轮轨磨耗,同时也说明型面磨耗和车轮多边形产生了不良耦合作用,严重影响车辆的运行经济性。当车轮型面位于磨耗后期时,6阶以上的车轮多边形会引起磨耗指数上升,但上升幅度较小,处于相对稳定阶段。
4 结论
1) 车轮型面磨耗会降低车辆的运行平稳性,但耦合车轮多边形对平稳性指标的影响较小。另外,若车轮型面发生凹磨且最大磨耗深度位于0.8 mm附近,将会显著提高车辆的平稳性指标。
2) 车辆运行稳定性同样易受车轮型面磨耗的影响,且型面发生凹磨时临界速度显著降低。耦合车轮多边形后,临界速度随着多边形阶次增大而逐渐下降,且下降幅度与波深成正比。值得强调的是,当多边形阶次为10阶且波深为0.2 mm时,临界速度仅为61 km/h,严重影响车辆的运行稳定性。
3) 对于曲线通过性能,综合分析轮轨相互作用力、安全性指标以及磨耗指数后发现,4种型面磨耗工况下,性能指标一般在多边形阶次高于5时逐渐上升,且上升幅度与波深成正比。另外,若车轮型面发生凹磨现象,将会显著加剧车轮多边形对轮轨横向力以及磨耗指数的不良影响。该工况下,若车轮多边形的波深和阶次上升至0.2 mm和10,外侧轮轨横向力和磨耗指数高达34.81 kN和578.54 kN。与之相反,若车轮型面在名义滚动圆附近的磨耗深度差异较小,即型面局部变化相对均匀,将会一定程度上抑制车轮多边形产生的不良影响,减缓轮轨横向力和磨耗指数的增长幅度。
因此,在对地铁车辆进行车轮磨耗检测时,不仅要依据相关标准对单一磨耗形式进行定量检测,还需关注不同磨耗形式间的耦合作用。避免出现单一磨耗形式未超过限值,但因为不同磨耗形式间的耦合效应而影响车辆安全运行的危险工况,从而进一步保证车辆的服役性能。
李洪晓,李莉,张云飞等.车轮型面磨耗耦合车轮多边形对车辆动态响应的影响研究[J].铁道科学与工程学报,2024,21(10):4240-4252.
LI Hongxiao,LI Li,ZHANG Yunfei,et al.Research on the influence of wheel profile wear coupled with wheel polygon on the dynamic response of vehicles[J].Journal of Railway Science and Engineering,2024,21(10):4240-4252.

