随着轨道交通不断深入国民日常生活,轨道结构的平顺状态越来越受到铁路运营管理及研究人员的关注[1]。对于无砟轨道而言,轨道子系统的耦合性较强,下部基础(土体、桥梁等)变形将不可避免地造成轨道结构的整体附加几何变形。在车致振动作用下,将持续对轨道结构产生伤损破坏作用,影响列车运行平稳性、安全性。显然,开展轨道结构与下部基础的协同变形及线路几何状态改变下的车致振动研究,对保证列车运行平稳性与安全性,控制轨道结构平顺状态起着关键作用。目前国内外学者分别采用解析或数值的方法进行了大量轨道结构变形与下部基础的映射关系研究。陈兆玮等[2-4]基于多层叠合梁微分方程,从理论上推导了高速铁路桥墩沉降、板底脱空等行为与钢轨变形间的映射关系,给出了钢轨变形的解析表达式。郭宇等[5-6]利用有限元法研究了板式无砟轨道轨面变形与路基沉降的映射关系。ZHENG等[7-8]考虑路基约束的影响,利用最小势能原理推导出梁变形与钢轨变形之间的映射关系,基于上述映射关系,对车线桥耦合系统进行了动态仿真分析。GROSSONI等[9]建立有砟轨道半解析模型并与车辆-轨道相互作用分析相结合,计算不同初始轨道刚度、车辆类型和速度下的永久沉降发展速率。GOU等[10]通过建立列车-轨道-桥梁耦合有限元模型以确定动力响应(加速度与轮轨力)与桥墩沉降、梁端扭转、梁拱度引起的轨道变形之间的映射关系。JIANG等[11]建立了考虑不同层间接触的无砟轨道3-D模型,模拟不同的沉降情况得出轨道结构变形与路基的映射关系并计算了轨道附加拉应力与接触应力。然而现有的研究方法存在以下不足:解析法[2-3, 7-8, 12]依靠梁、杆静力变形理论将复杂的轨道结构进行了简单处理,难以模拟复杂工况;而传统的数值模型[5-6, 10-11, 13-16]采用商业软件建模,在解决复杂的基础变形问题时难以保证全过程的计算效率。基于此认识,为了更加准确地模拟轨道结构与基础结构之间的映射关系,为车辆-轨道-基础结构动力相互作用的研究提供精确的几何激励来源,本文以无砟轨道地表土体变形为例,分别建立了轨道结构-土体空间变形映射分析模型与车辆-轨道-土体动力相互作用模型。其中轨道结构-土体空间变形映射分析模型考虑了复杂的轨道结构层间关系与地表变形场,通过引入解决层间接触非线性的增量法和迭代法,实现了地表土体任意变形下的轨道-基础土体空间变形映射关系分析。在动力相互作用模型中,以土体变形诱发的轨道附加不平顺作为车辆-轨道-土体动力相互作用模型的几何激励,研究了地表变形对车致振动规律的影响。具体的仿真模型信息、数值处理方法,以及计算结果讨论见下文描述。
1 车辆-轨道-土体动力相互作用模型基本模型框架
1.1 动力相互作用模型基本组成及模拟方法
图1为本文建立的车辆-轨道-土体动力相互作用模型示意图。其中:车辆模拟为具有一、二系悬挂的多刚体系统,拥有7个部件,即1个车体、2个转向架和4个轮对。车体和转向架各有6个自由度(纵向、横向、垂向、摇头、侧滚和点头),轮对有5个自由度(纵向、横向、垂直、摇头和侧滚)。无砟轨道结构包括钢轨、扣件、轨道板、充填层、底座或基座,其中钢轨采用Euler-Bernoulli梁单元模拟;轨道板的弯曲振动采用Mindlin板单元模拟,横向振动采用Euler-Bernoulli梁单元模拟;混凝土底座的弯曲振动采用双向梁单元模拟,横向振动则采用Euler-Bernoulli梁单元模拟;下部土体采用8节点实体单元模拟;扣件和其他层间相互作用系统均为弹簧-阻尼单元。
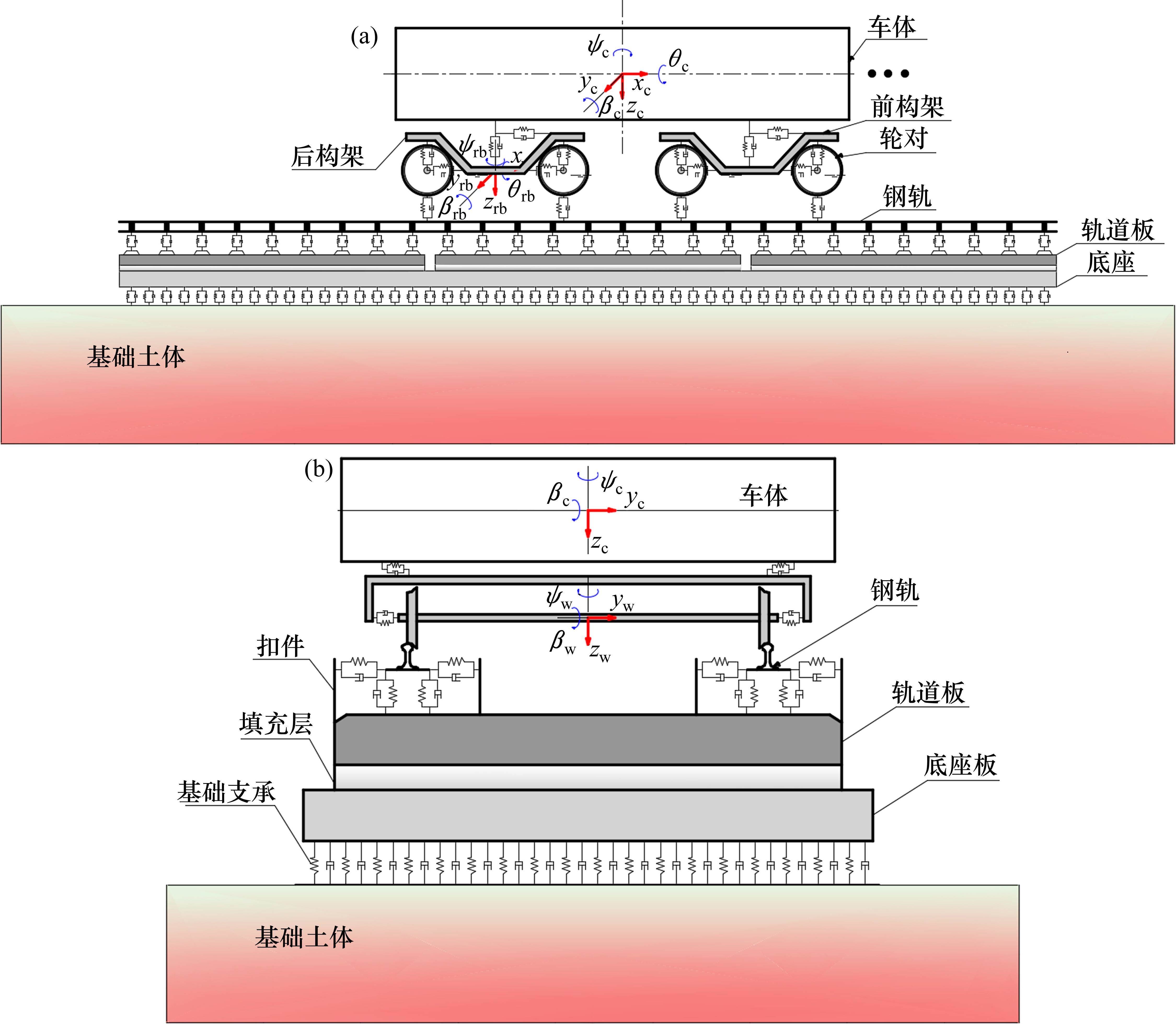
对于车辆和轨道(钢轨)的耦合,本文采用经典且通用的简化轮-轨接触模型来建立,即采用Hertz接触理论和Kalker蠕滑理论来模拟轮-轨的法向和切向接触行为。对于车辆-轨道-土体动力相互作用模型的建立,如上述的Euler-Bernoulli梁单元,Mindlin板单元,以及轮-轨接触模型等子模型具体的建模方法与公式表达已汇总在文献[17-19]中,本文不再详细阐述。
1.2 动力相互作用系统运动方程
传统的车辆-轨道-土体动力相互作用模型可以表达为以下矩阵形式的动力学运动方程:
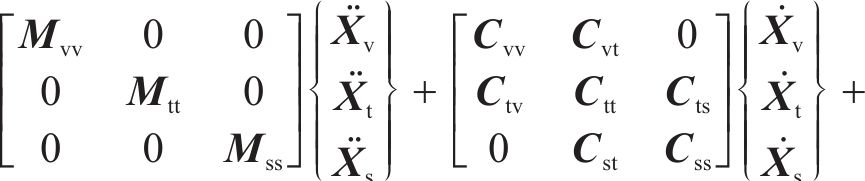
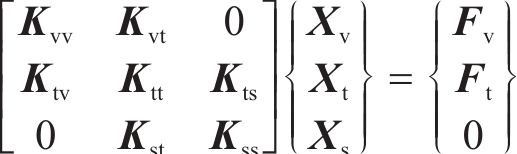
式中:

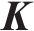
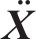
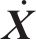
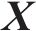
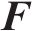
1.3 动力相互作用系统外界激励
对于铁路车辆和轨道的相互作用而言,轨道不平顺是其最重要且最直接的几何激励[7],故本文建立的车辆-轨道-土体动力相互作用系统将轨道的不平顺视为系统的最原始激励。此外,由地表变形诱发的轨道结构附加变形也被视为相互作用系统的几何激励。因此,本文将地表变形导致的轨道结构附加不平顺与原始的轨道不平顺叠加,在初始不平顺的基础上额外考虑了由地表变形诱发的轨道结构附加不平顺作为系统的外部激励。
1.4 计算参数
本文模拟的车辆为城市轨道交通地铁B型车辆,其动力学计算参数可见文献[17]。本文建立的无砟轨道和土体的动力学模型参数见表1和表2。
| 参数 | 取值 | 参数 | 取值 |
|---|---|---|---|
| 钢轨弹性模量/Pa | 2.059×1011 | 扣件垂向阻尼/(N∙s∙m-1) | 3.0×104 |
| 钢轨扭转惯量/m4 | 5.24×10-5 | 道床板尺寸/(m×m×m) | 6.0×2.5×0.35 |
| 钢轨绕y轴惯性矩/m4 | 3.217×10-5 | 道床板弹性模量/Pa | 3.45×1010 |
| 钢轨绕z轴惯性矩/m4 | 5.24×10-6 | 道床板泊松比 | 0.2 |
| 钢轨单位长度质量/(kg∙m-1) | 60.64 | 道床板密度/(kg∙m-3) | 2 400 |
| 扣件间距/m | 0.6 | 填充层厚度/m | 0.09 |
| 扣件纵向刚度/(N∙m-1) | 6.7×107 | 填充层弹性模量/Pa | 3.25×1010 |
| 扣件横向刚度/(N∙m-1) | 5.0×107 | 底座尺寸/(m∙m) | 3.1×0.49 |
| 扣件垂向刚度/(N∙m-1) | 5.0×107 | 底座混凝土弹性模量/Pa | 3.45×1010 |
| 扣件纵向阻尼/(N∙s∙m-1) | 3.0×104 | 底座混凝土泊松比 | 0.2 |
| 扣件横向阻尼/(N∙s∙m-1) | 3.0×104 | 底座混凝土密度/(kg∙m-3) | 2 400 |
| 参数 | 取值 |
|---|---|
| 土体弹性模量/Pa | 3.08×108 |
| 土体泊松比 | 0.33 |
| 土体密度/(kg∙m-3) | 2 010 |
| 阻尼比 | 0.038 |
2 轨道-土体空间变形映射分析模型
2.1 层间脱空与接触处理方法
为进行映射关系分析,在程序中设置自动识别分析区段的加窗函数,将分析区段的层间相互作用删除,并分别考虑地表的沉降和上拱。处于沉降区段的单元继续保持层间脱空的状态,而在上拱区段则考虑层间接触密贴,补齐接触部分的层间相互作用并对边界施加强制位移。具体的模拟方法在本节给出。
2.1.1 层间脱空/接触模拟
通过删除分析区段的层间相互作刚度和阻尼矩阵,以此模拟地表土体支承缺失产生的底座板下脱空,公式如下:
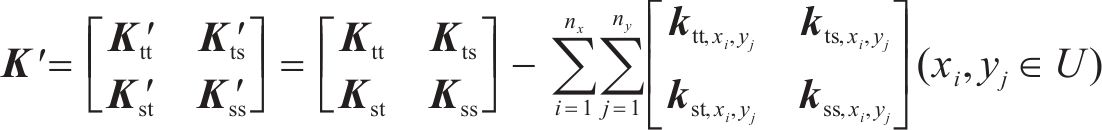
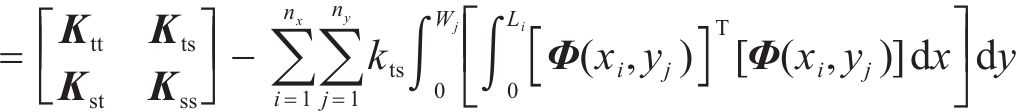
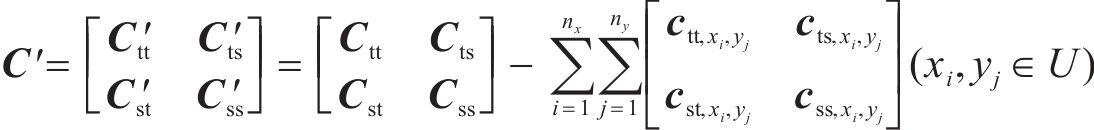
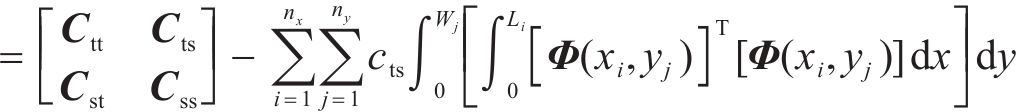
式中: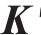

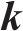
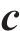
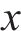
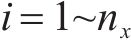
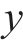
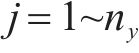
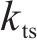
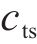
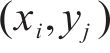
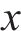
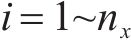
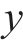
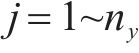
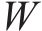
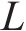
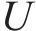

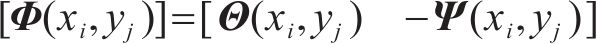
式中:

若分析区段存在上拱区域,则视为层间接触密贴,此时该区域内不再存在刚度和阻尼缺失并且必须给边界施加强制的位移边界条件。对于一般连续的上拱区域,该区域的动力矩阵与式(2)有着相同的表达:
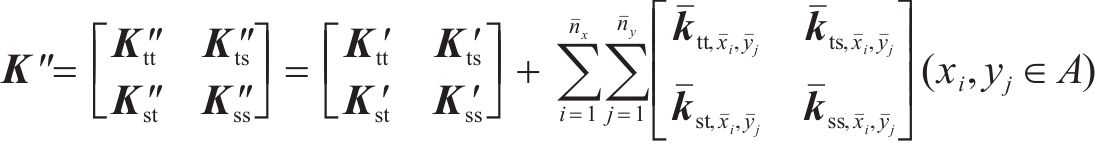
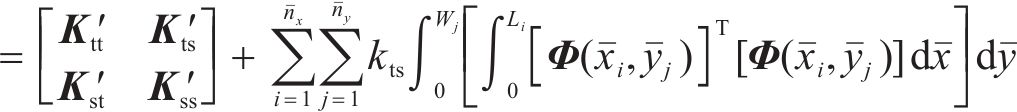
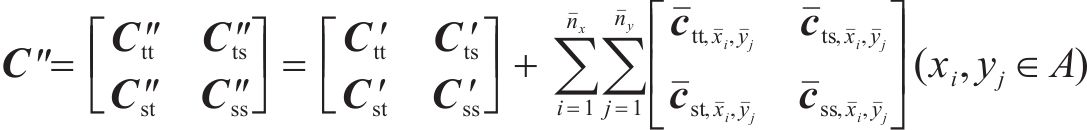
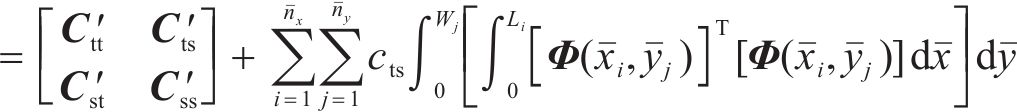
式中: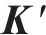

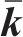
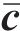
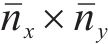
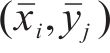
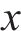
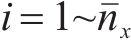
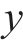
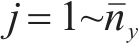
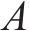
2.1.2 地表土体上拱模拟方法
对于上拱区域,还应该对边界施加强制位移边界条件,作为映射关系分析的位移初始条件。在有限元中,针对需要施加强制位移边界的自由度,施加边界条件可采用置大数法,对于刚度矩阵:
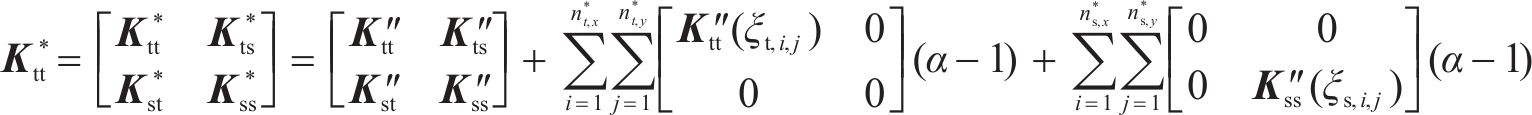
式中: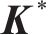
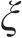
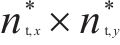
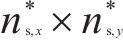
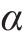
对于边界的节点荷载,可采用相同方式处理:
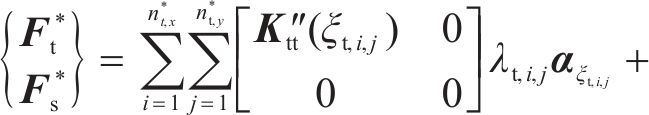
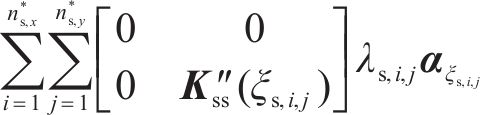
其中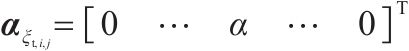

式中:
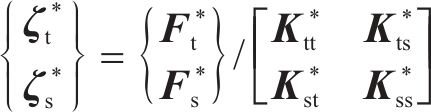
式中: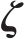
2.2 映射关系分析的增量法和迭代法
轨道-土体空间变形映射可模拟为轨道结构与土体在静力变形中的层间接触密贴和脱离的非线性协调过程,在层间接触或者脱离时,更新相互作用单元矩阵以达到最终的静力平衡状态。针对层间接触密贴的非线性过程可采取增量和迭代2种处理方式,具体方法及细节将于本小节阐述。
2.2.1 解决层间接触/分离的增量法
增量法是非线性处理中的常见方法,取合适的尺度因子把总荷载转为多个分荷载,每一次分荷载加载完成后进行一次刚度修正,直到所有荷载加载完成。
在映射关系分析中,假设土体的应力已处于平衡状态,此时系统的荷载仅为自重,此时增量法处理非线性的过程可以表征如下。
1) 计算总荷载列阵:
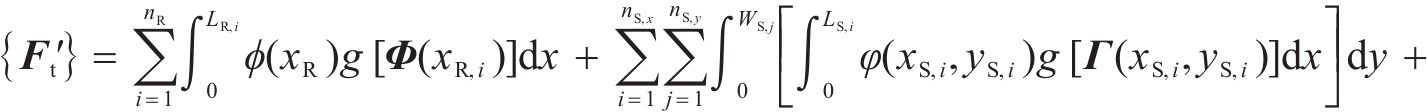
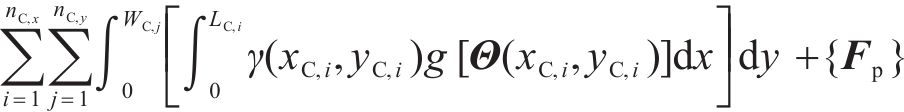
式中: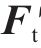

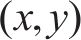
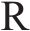
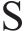

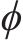

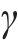
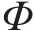


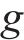
2) 若存在地表的上拱,则将位移边界条件作为初始条件,与层间离缝的空间距离叠加,得到实际的层间离缝值:
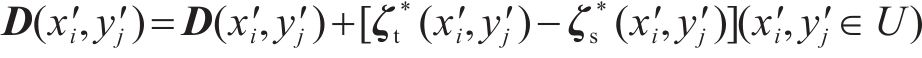
式中: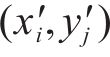
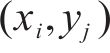
3) 利用第2节所述方法处理后得到刚度矩阵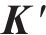
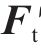
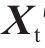
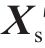
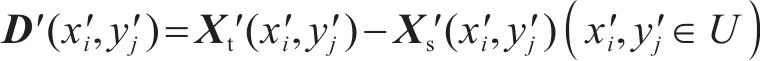
4) 结合步骤2与步骤3的结果,判定最先接触的点的坐标。先计算层间空间距离与相对位移之间的比值:
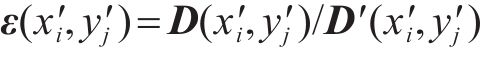
若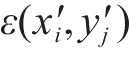
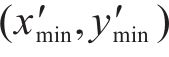
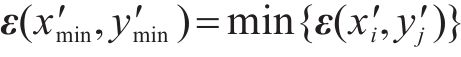
5) 接触单元相互作用生成:利用式(5)和式(6)同样的方式将判定点处的相互作用单元整合到全局矩阵,并且记录此时荷载的荷载增量,即尺度因子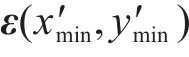
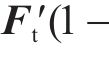
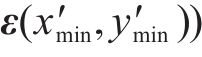
6) 重复步骤3至步骤5直到荷载残余量为0,计算终止,可得基础土体变形条件下的轨道结构空间变形。
2.2.2 解决层间接触/分离的迭代法
相较于增量法,在处理非线性问题时,迭代法具有更高的效率,尤其是在处理层间接触非线性问题方面。根据每次迭代后得到的残余力进行反向加载,可计算系统最终的协调变形,具体步骤如下:
1) 根据式(10)计算初始荷载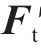
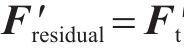
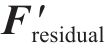
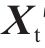
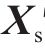
2) 根据位移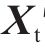
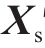
3) 接触单元相互作用生成:由式(2)~(6)将判定点处的相互作用单元删除或整合到全局矩阵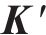
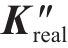
4) 计算此时系统的真实荷载:
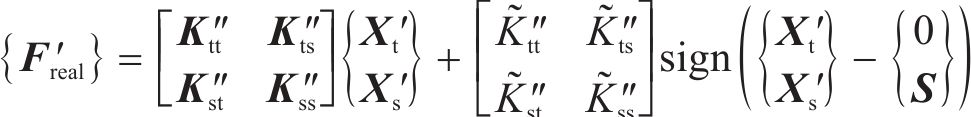
其中
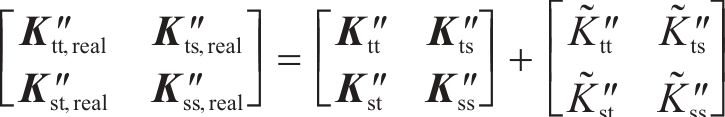
式中: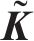
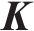
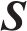
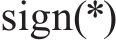
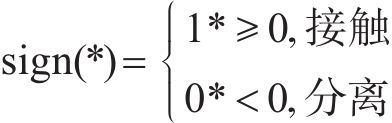
5) 计算此时系统的残余力:
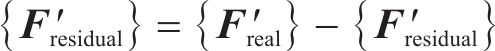
6)计算残余力作用下的系统位移,并与原系统位移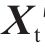
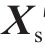
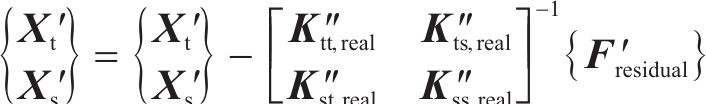
7) 重复步骤2至步骤6,直到残余力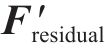
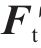
2.3 模型验证
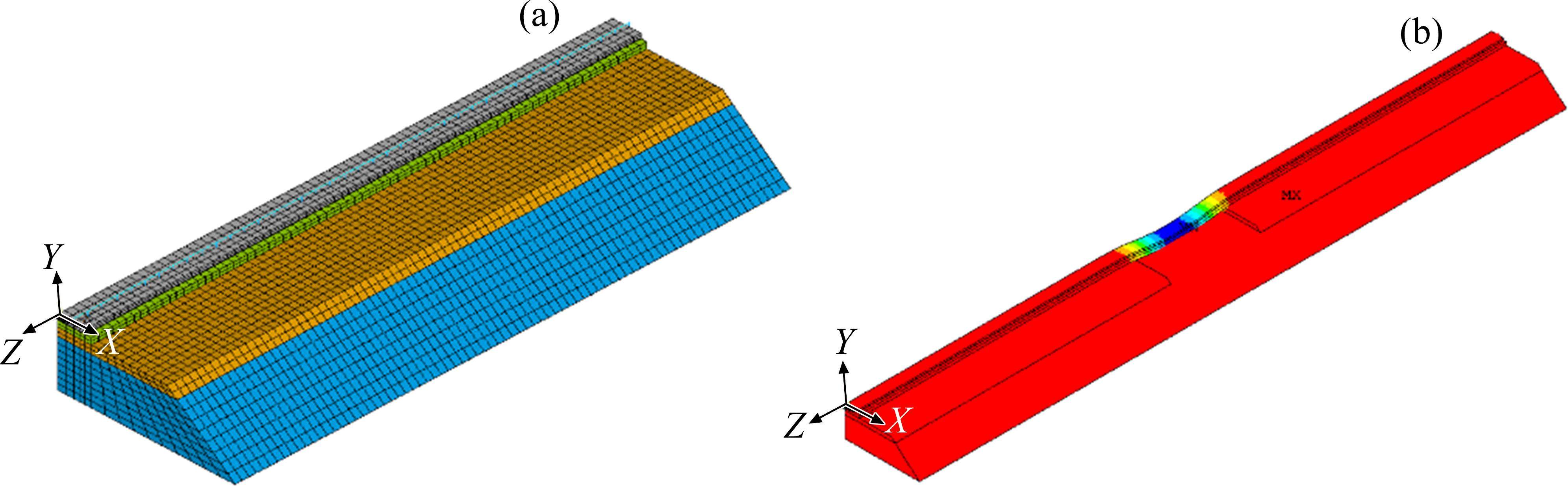
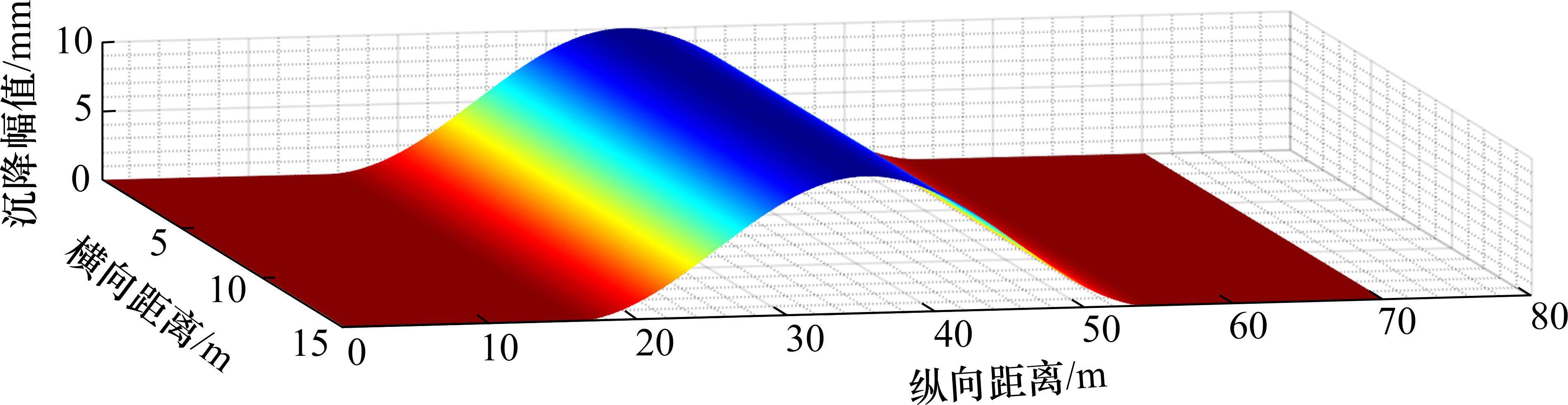
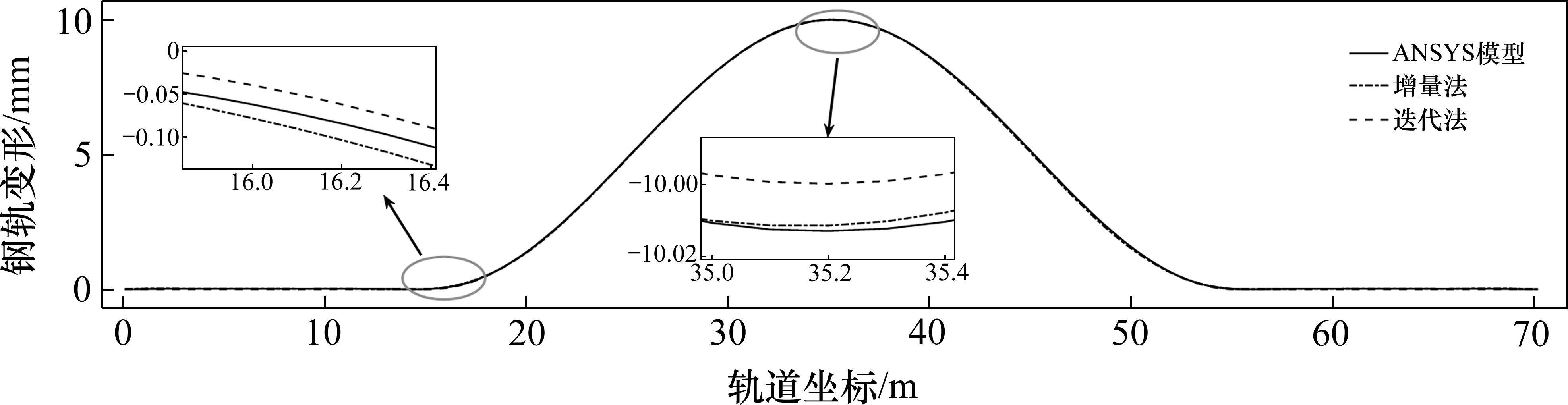
为了验证所提出的“映射关系分析模型”的准确性,采用商业软件ANSYS建立了同参数的半尺寸模型,见图2。在验证工况中,地表融沉区域为纵向40 m,融沉曲线为余弦,幅值为10 mm,横向视为均匀,如图3所示。ANSYS模型中,底座与路基之间的接触采用“接触单元”进行模拟,路基底部采用固定约束。在自编程模型中,路基底部的约束采用强刚度模拟(1013 N/m3)。在模型中,对轨道结构施加自重(轨道板与底座),得到上部钢轨的映射变形,如图4所示。由计算结果可知,由本文建立的增量法与迭代法计算的钢轨映射变形与ANSYS计算结果十分吻合,说明了本文建立的模型具有较强的可靠性。
3 数值算例
3.1 工况与地表变形边界条件设置
本节以广州某城际铁路的融沉问题进行算例分析。该线路采用双块式道床板,2个相邻车站区间的融沉监测范围为右线隧道976~1 001环(1环长度2 m)范围内,测站里程为右线隧道YDK32+819~YDK32+869,在整体轨道模型中的位置为50~100 m,测点设置在每个隧道环对应的道床板左侧与右侧底部,取第539周期的竖向位移监测值,如图5(a)所示。在土体融沉数据已知的情况下,可将其作为映射关系分析模型的边界条件,即为式(12)增量法和式(15)中的地表变形,从而计算轨道由于自重产生的跟随性变形,并视为动力相互作用模型的额外几何激励。作为系统原始几何激励的轨道不平顺同样采用现场实测值,如图5(b)、图5(c)和图5(d)所示。
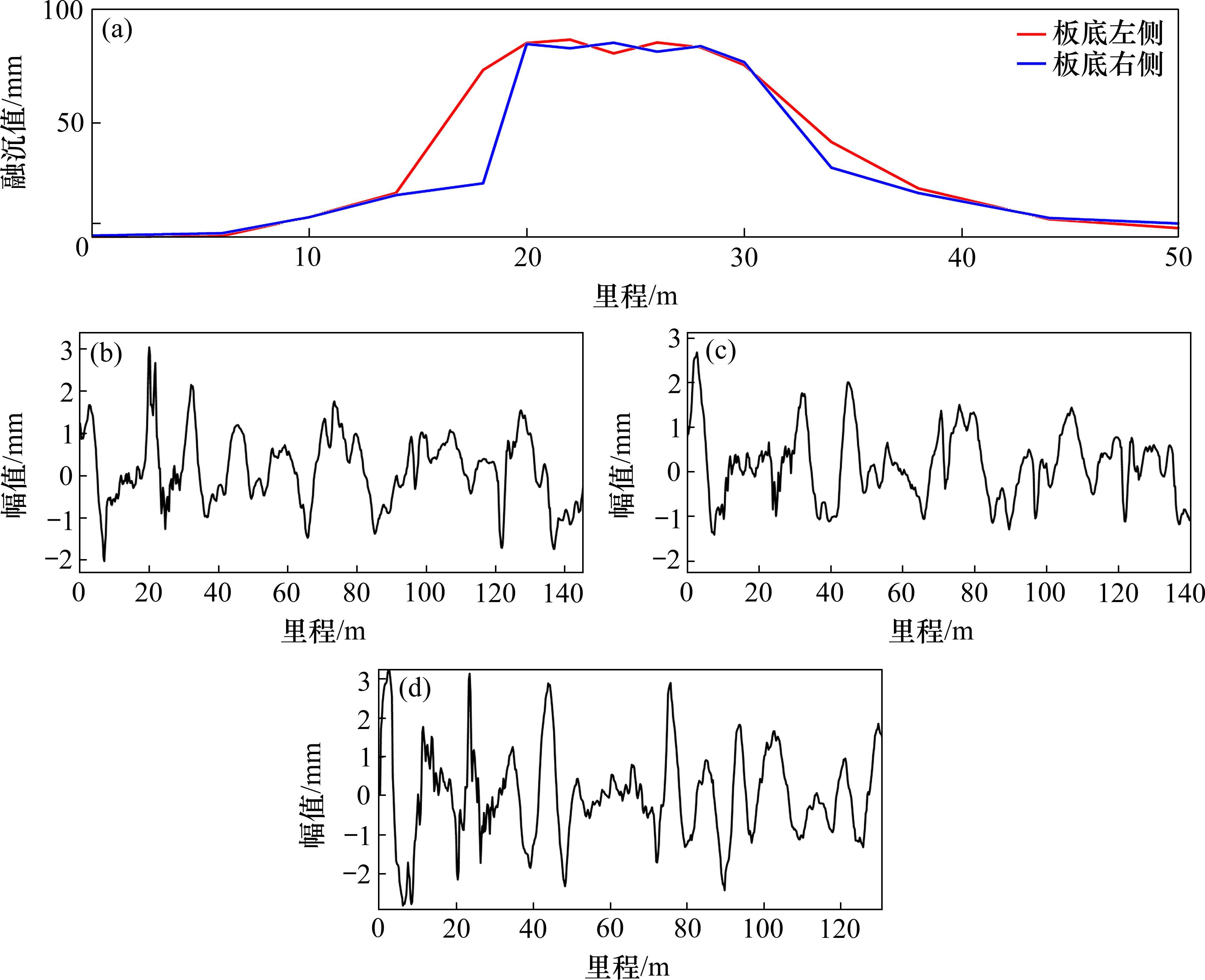
3.2 仿真结果
基于图5(a)的实测数据,将非测点的地表融沉用三次插值进行模拟,得到该区段地表融沉曲线。不考虑外荷载的情况下,仅考虑轨道结构的重力作用,分别采用增量法和迭代法计算出道床板底部的静力变形,其中接触判断点取1/4个单元维度进行等间隔均匀划分,迭代法的收敛因子(残余力与外力的比值)取0.01%。由增量法和迭代法分别计算的道床板映射变形如图6所示。
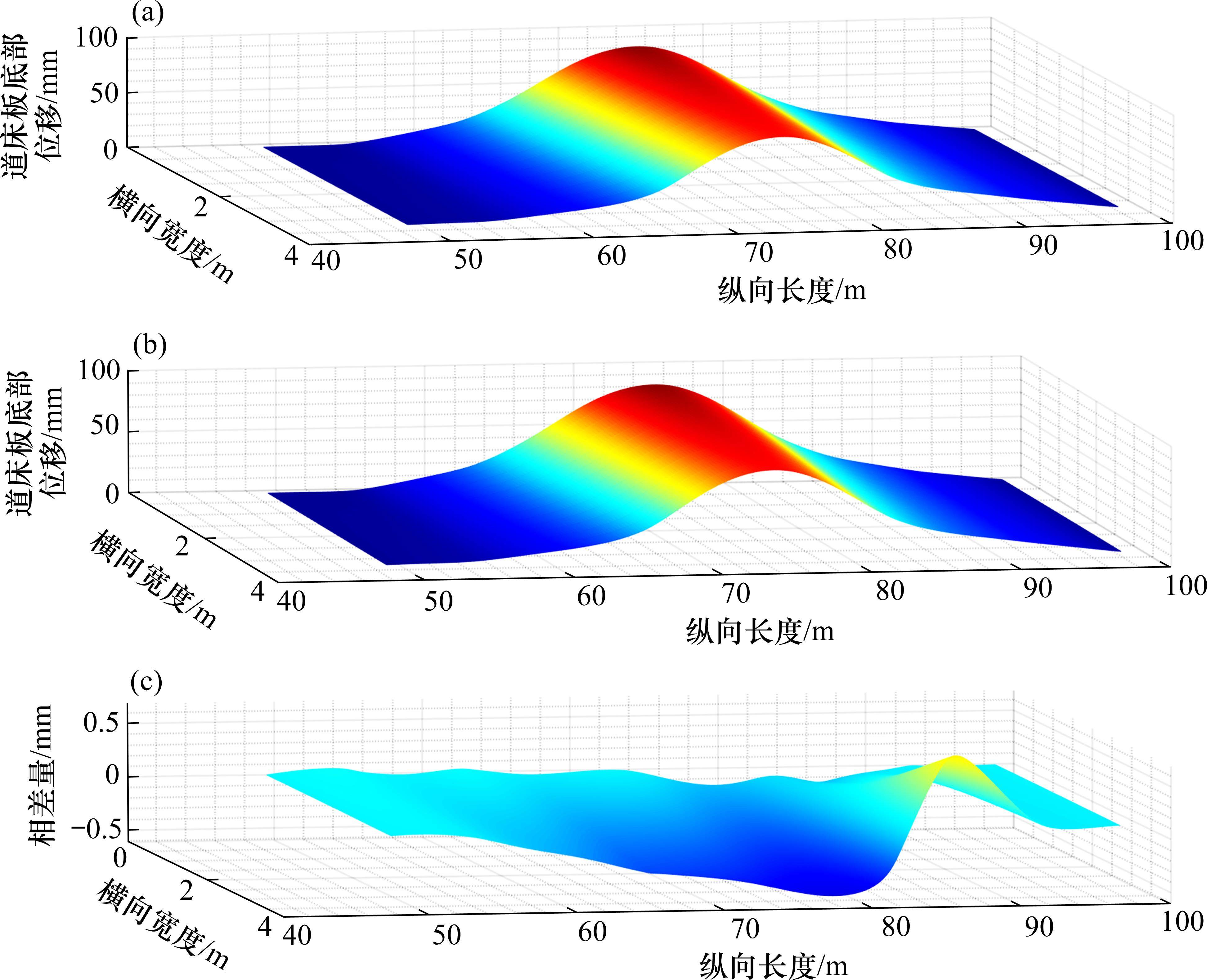
由图6可知,增量法和迭代法的计算结果基本吻合,在道床板底部的变形幅值分布基本与地表融沉分布一致,说明轨道结构在空间变形上与地表的融沉具有映射关系。精度方面,迭代法与增量法的相差量主要分布在70~85 m范围内,最大值为0.688 3 mm,占增量法结果的比例为2.825%,说明在收敛因子为0.000 1的条件下,迭代法的计算精度满足要求。在计算用时方面:在计算机CPU硬件为Intel Core i7-9700的运算环境下,增量法的增量步共383步,用时382.1 s;迭代法的迭代次数共19次,用时32.3 s。仿真结果表明,迭代法在处理层间接触非线性的问题时,可以在保证不损失较大精度的条件下得到较为理想的数值结果。
增量法和迭代法计算的道床板底部与土体的层间接触关系如图7所示,其中白色部分为层间的接触区域,黑色部分为层间未接触区域。根据计算结果可知,在纵向80~90 m范围内的接触关系存在细微差别,这是由于迭代法求解的系统未能使内力和外力达到平衡。同时,由图6(c)可清晰观察到,轨道结构映射变形的计算结果在该区域内的差别也最为明显,说明残余力在该区域内未能有效耗散,迭代产生的误差在该区域内较大。
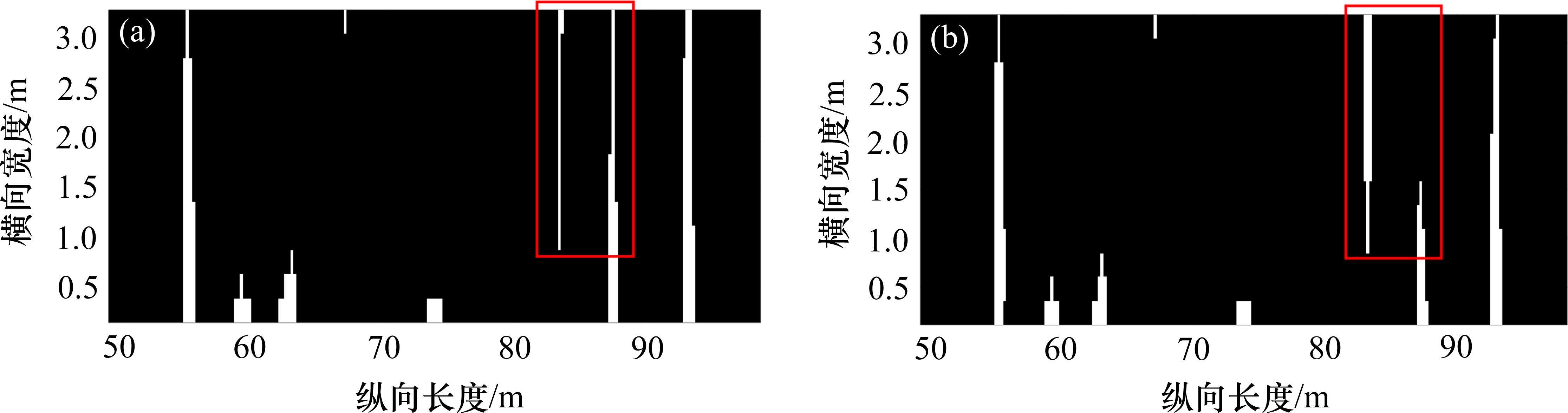
通过映射关系分析增量法和迭代法均可得到地表融沉区域内的土体-轨道层间脱空值,如图8所示。对比图7和图8可知,在轨道-土体变形协调(映射)后,轨道底部和地表并未处于完全接触的状态。在分析区段主要有3个区域有着较大的层间间距,分别为55~60 m,63~73 m和90~100 m。
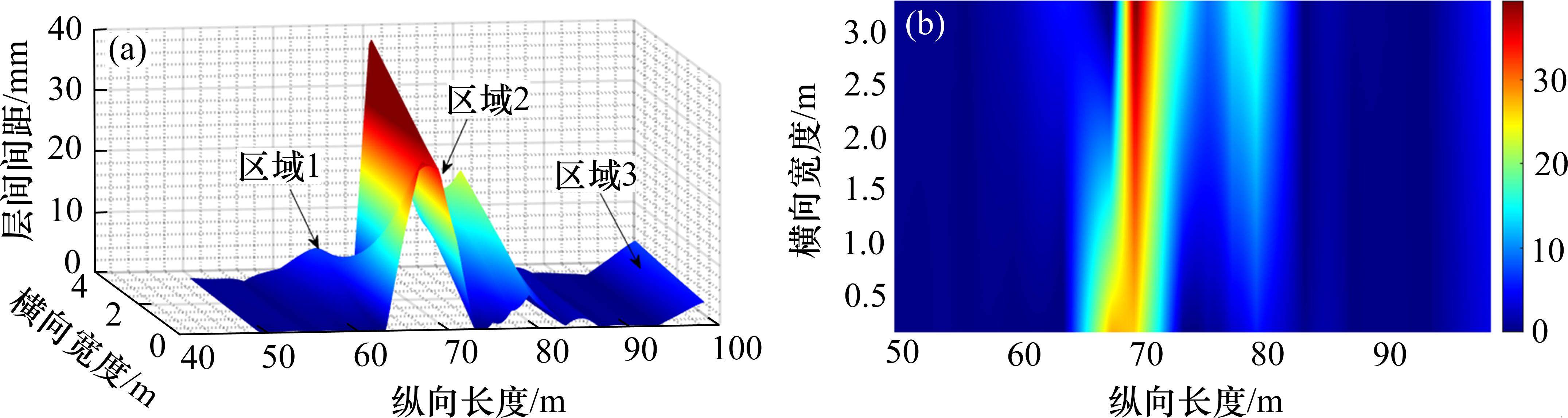
图9为车辆-轨道结构的动力响应,其中图9(a)为第1轮对下道床板底部中心在不同车速下的动位移;图9(b)和图9(c)分别为车体垂向加速度和Sperling指标;图9(d)和图9(e)分别为第1轮对轮轨垂向力和脱轨系数最大值;图9(f)为35(非融沉区域内),60,65和70 m处的道床板底部应力。
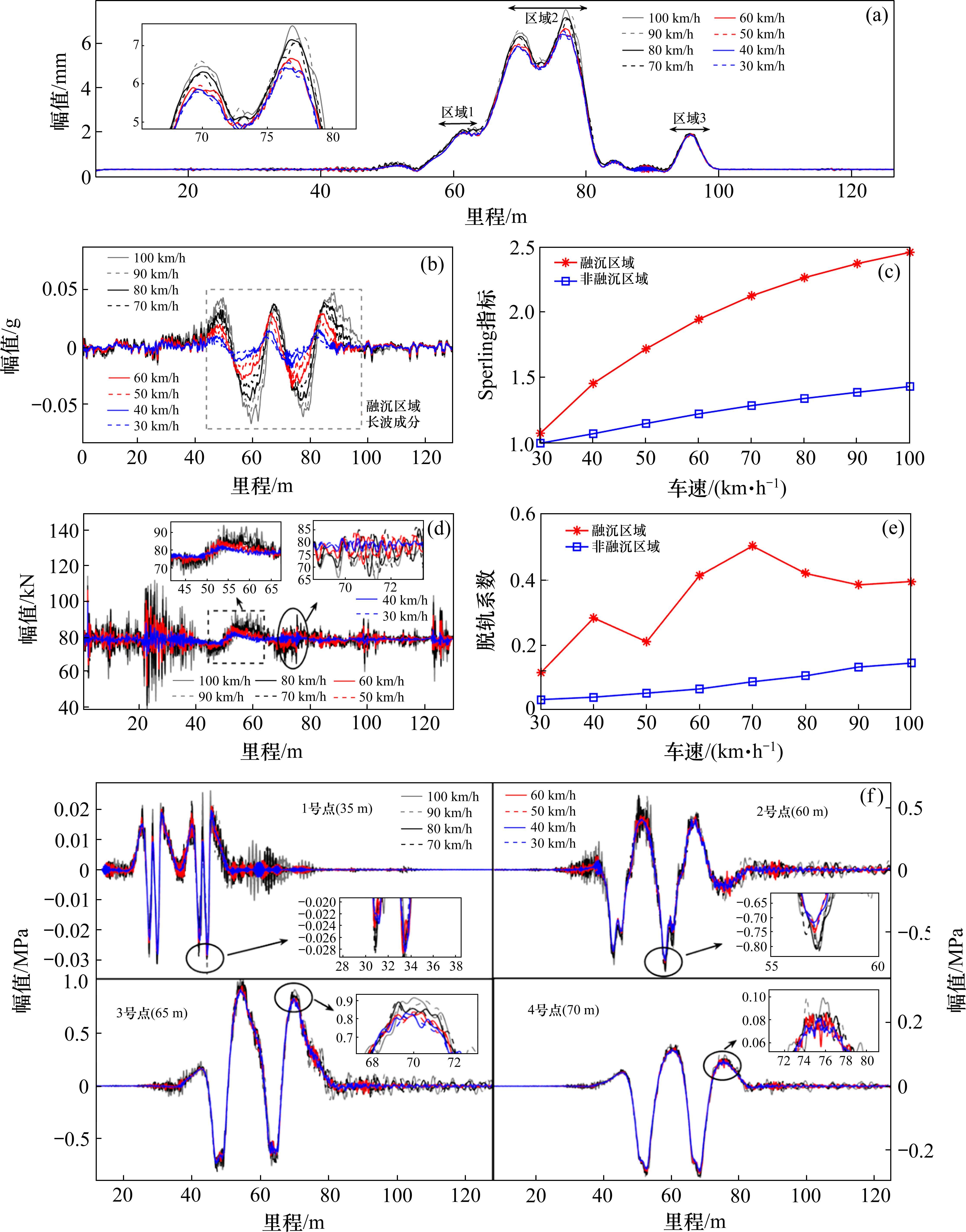
由图9(a)可知,随着车辆运行速度的增大,道床板底部动位移和车体垂向加速度也相应地增大。图8(a)所示的3个层间分离区域存在层间刚度的缺失,造成该区域的位移出现了峰值,且道床板底部可能与地表接触,造成刚度的突变。
由图9(b)和图9(c)可知,车辆在经过融沉区域时,车体振动有明显的加剧,在融沉区域出现长波成分,且在融沉区域内有不同程度的波动,说明在轨道长波附加变形激励下,车体振动被较大程度激发,从而影响行车的平稳性。计算的Sperling平稳性指标显示,当车辆行驶在非融沉区域时,不同车速的平稳性均小于2.5,车辆运行平稳性评估为优;而当车辆行驶到融沉区域时,当车速为30 km/h时,平稳性指标为1.07,平稳性评价为优;当车辆提速后,100 km/h的Sperling指标为2.45,增加了1.29倍,且已接近评价指标为良好的2.5,说明车辆运行平稳性受到融沉的影响较大。
由图9(d)和图9(e)可知,融沉区域内由于层间存在一定的空间间距(脱空),响应呈现与融沉区域相似的长波成分,且车速越大,幅值越大。同时,由于车速不同,层间的动态接触与脱离的效应不同,当车速为70 km/h时,轮对的脱轨系数最大,高于80,90和100 km/h的脱轨系数。
由图9(f)可知,处于融沉区域的2、3和4号点的应力幅值较处于非融沉区域的1号点更大,且2号点的最大拉应力达到0.81 MPa(压应力为正,拉应力为负),接近C50混凝土设计强度1.89 MPa的一半,融沉区域可能对轨道结构产生较大的损伤。当车辆运行在融沉区域时,应力曲线依然出现长波成分。处于融沉区域的2、3和4号点,当车辆运行过后依然存在较大的短波成分,说明在车辆经过后,层间虽然处于未接触状态,但冲击效应依然存在,且随着车速的增大,该冲击效应也相应地增大,并一直保持拉-压反复变换的状态。
4 结论
1) 通过与ANSYS模型的对比,说明提出的数值模型可较好地预测地表土体变形条件下轨道结构与土体变形之间的映射关系。
2) 在处理层间接触非线性问题时,迭代法比增量法有着更高的计算效率,可在不损失较大精度的同时得到较为理想的数值结果。
3) 层间脱空区域的刚度缺失造成了位移在该区域出现峰值,动力响应在脱空区域产生明显的长波成分。
4) 融沉区域内道床板的最大拉应力接近设计抗拉强度的一半,且处于反复的拉-压变换状态,极易造成道床板结构的损伤,在实际中应避免大面积的融沉造成轨道与土体之间的层间脱空。
李正,徐磊,王卫东.考虑地表变形的轨道-土体空间映射关系分析与车致振动评估[J].铁道科学与工程学报,2024,21(12):5005-5017.
LI Zheng,XU Lei,WANG Weidong.Analysis of track-soil spatial mapping relationship and evaluation of vehicle-induced vibrations considering deformation of ground[J].Journal of Railway Science and Engineering,2024,21(12):5005-5017.

