现代有轨电车具有投资小、曲线通过及爬坡能力强等优点,是缓解城市交通拥堵的一种新型公共交通方式[1]。为满足城市建设需要,有轨电车线路常采用高架桥梁跨越城市主干道等重要城市设施,同时受城市复杂地形及道路条件限制等因素影响,需要设置小半径曲线通过某些特殊地段,并采用连续梁桥以提高梁体小半径曲线段抗倾覆能力[2-3]。现代有轨电车车辆采用独立轮对,在曲线轨距不加宽的情况下可通过曲线半径为15~30 m的超小半径曲线线路[4]。现代有轨电车技术自20世纪80年代逐步发展[5],国内外学者针对现代有轨电车小半径曲线无缝线路受力特征开展了广泛研究。谢铠泽等[6]以实际钢-混组合梁桥为背景,建立有限元模型并研究了有轨电车小半径曲线桥上线路平顺性与桥墩横向刚度的相互作用规律。吴青松等[7]建立钢轨-道床三维有限元模型,研究了曲线半径及长度对无缝线路受力变形特征的影响规律。RUGE等[8]提出了考虑先期变形的非线性梁轨相互作用下的钢轨应力求解方法,并考虑多种荷载工况与传统方法获得的钢轨应力进行比较。徐庆元等[9]建立了考虑钢轨、轨枕及梁体相互作用的连续梁桥无缝线路相互作用模型,分析了连续梁桥上无缝线路附加力分布规律。SZABÓ[10]分析了无缝线路在小半径曲线等薄弱部位易产生横向屈曲病害,提出采用道砟黏结、安全帽和Y型钢轨等技术措施提高无缝线路横向稳定性,并通过现场试验进行验证。罗信伟等[11]采用有限元法研究了温度作用下小半径曲线无缝线路的横向鼓曲失稳问题,获得了不同工况下钢轨横向位移随温度变化的影响规律。魏贤奎等[12]针对小半径曲线桥上无缝线路稳定性问题,提出一种基于护轨横撑的轨道加强方案,并通过建立有限元模型对加强方案进行验证计算。罗锟等[13]以实际城市轨道交通线路为背景建立有限元模型,研究了连续桩板结构上无缝线路纵向力随桥梁跨数、结构纵向刚度等因素下的变化规律。于向东等[14]以实际线路为工程背景研究了小半径曲线桥梁梁轨相互作用规律,探究了不同曲线半径以及考虑加载历史效应下的曲线桥梁梁轨相互作用变化规律。ALI等[15]提出一种简化的数值模型研究温度荷载作用下梁轨相互作用对无缝线路稳定性的影响,探讨了受梁轨相互作用显著影响的无缝线路参数指标。冯青松等[16-17]为研究桥上嵌入式轨道的关键因素及最优参数组合,建立嵌入式轨道桥上无缝线路有限元计算模型,综合蒙特卡洛法和响应面法评估了简支梁桥上嵌入式轨道无缝线路可靠性,通过正交试验分析了钢轨类型、桥墩纵向刚度、桥梁跨数等因素的最优参数组合。狄怡霏等[18]为研究有轨电车桥上无缝线路小半径曲线稳定性,建立了小半径连续梁桥上无缝线路梁轨相互作用有限元模型,提出有轨电车小半径曲线桥上无缝线路扣件及钢轨伸缩调节器的选用建议。ENSHAEIAN等[19]综述了近30年来无缝线路钢轨纵向力和静动力荷载作用下的钢轨稳定性计算模型,并概述了无缝线路钢轨应力的无损检测方法。HASAN[20]分析了温度作用下有砟轨道保持稳定的阈值半径,并推导了阈值半径所对应的温度界限的计算公式,为线路养护维修提供指导。LOU等[21]建立考虑桥梁温度变化的连续梁桥上无缝线路有限元模型,研究了钢轨伸缩附加力达到最小时,钢轨伸缩调节器布置位置与连续梁桥固定支座位置的相互关系,并提出了两者的合理匹配关系。国内外学者的研究对象大多是单一曲线,而实际工程中常出现多段衔接的曲线线路。为适应城市复杂多变的地形环境,曲线梁桥以其线形布置较为灵活的特点而得到广泛应用。现代有轨电车线路由于其规划滞后性,易受城市街道、建筑物的阻碍,相比于直线梁,小半径曲线梁乃至小半径S型曲线梁得到大量应用,受桥梁跨度及倾覆稳定性影响,S型曲线桥梁以连续梁为主。综合以上应用背景,考虑温度、车辆动载等复杂环境作用,对于复杂线路类型下的有轨电车桥梁无缝线路相互作用研究愈加重要。本文以广州某实际有轨电车S型小半径曲线桥梁无缝线路为工程背景,利用ABAQUS有限元软件建立曲线连续梁桥无缝线路数值仿真模型,研究桥梁温度、扣件纵向阻力、钢轨伸缩调节器、扣件横向刚度及车辆横向摇摆力等因素对梁轨相互作用的影响规律。
1 工程背景
广州某有轨电车区段线路3跨连续梁桥位于S型小半径曲线地段,前2跨与第3跨处于反向曲线上,半径为120 m。轨道采用60R2槽型钢轨,轨距1 435 mm且不考虑加宽,YGI-2型扣件,混凝土整体道床,轨道结构高度为530 mm。S型小半径曲线及前后为连续梁及简支梁桥,如图1所示,桥梁类型及跨度见表1。

墩台 编号 | 墩高/m | 梁体 编号 | 梁型 | 跨度/ m | 梁两端支 座类型 | 墩台 编号 | 墩高/m | 梁体 编号 | 梁型 | 跨度/m | 梁两端支 座类型 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 01号 | 2 | 1 | 简支梁 | 30 | 固定—活动 | 13号 | 8 | 13 | 连续梁 | 80 | 固定—固定 |
| 02号 | 3.5 | 2 | 简支梁 | 30 | 固定—活动 | 14号 | 8 | 14 | 连续梁 | 65 | 活动—活动 |
| 03号 | 5 | 3 | 简支梁 | 20 | 固定—活动 | 15号 | 10.5 | 15 | 简支梁 | 30 | 固定—活动 |
| 04号 | 6 | 4 | 简支梁 | 20 | 固定—活动 | 16号 | 9.5 | 16 | 简支梁 | 30 | 固定—活动 |
| 05号 | 7 | 5 | 简支梁 | 20 | 固定—活动 | 17号 | 8.5 | 17 | 简支梁 | 30 | 固定—活动 |
| 06号 | 8 | 6 | 简支梁 | 30 | 固定—活动 | 18号 | 7.5 | 18 | 简支梁 | 30 | 固定—活动 |
| 07号 | 9 | 7 | 简支梁 | 30 | 固定—活动 | 19号 | 6.5 | 19 | 简支梁 | 35 | 固定—活动 |
| 08号 | 10.5 | 8 | 简支梁 | 30 | 固定—活动 | 20号 | 5.5 | 20 | 简支梁 | 35 | 固定—活动 |
| 09号 | 11.5 | 9 | 简支梁 | 30 | 固定—活动 | 21号 | 7.5 | 21 | 简支梁 | 35 | 固定—活动 |
| 10号 | 12 | 10 | 简支梁 | 30 | 固定—活动 | 22号 | 6.5 | 22 | 简支梁 | 35 | 固定—活动 |
| 11号 | 12 | 11 | 简支梁 | 30 | 固定—活动 | 23号 | 2 | ||||
| 12号 | 11.5 | 12 | 连续梁 | 65 | 活动—活动 |
2 数值模型及计算参数
2.1 轨道桥梁有限元模型及计算参数
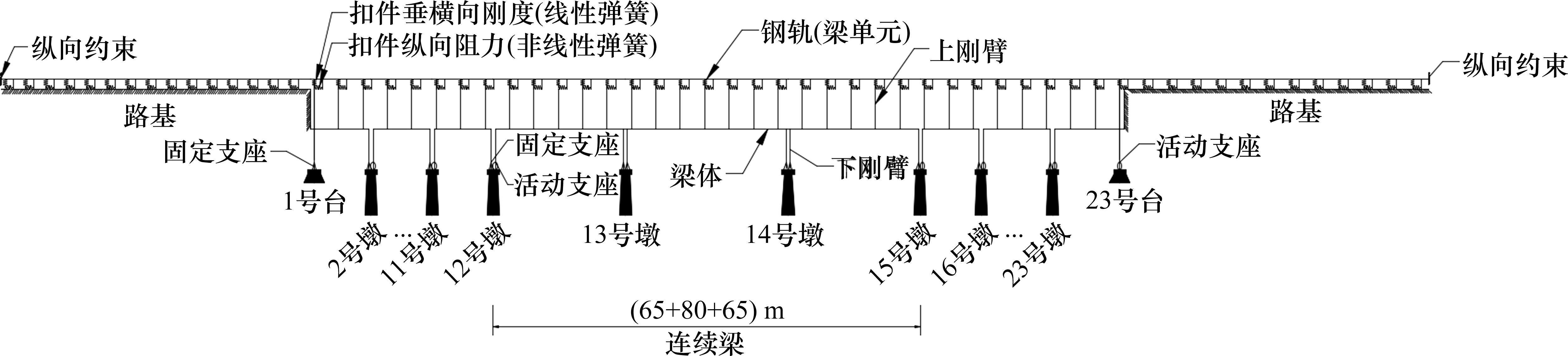
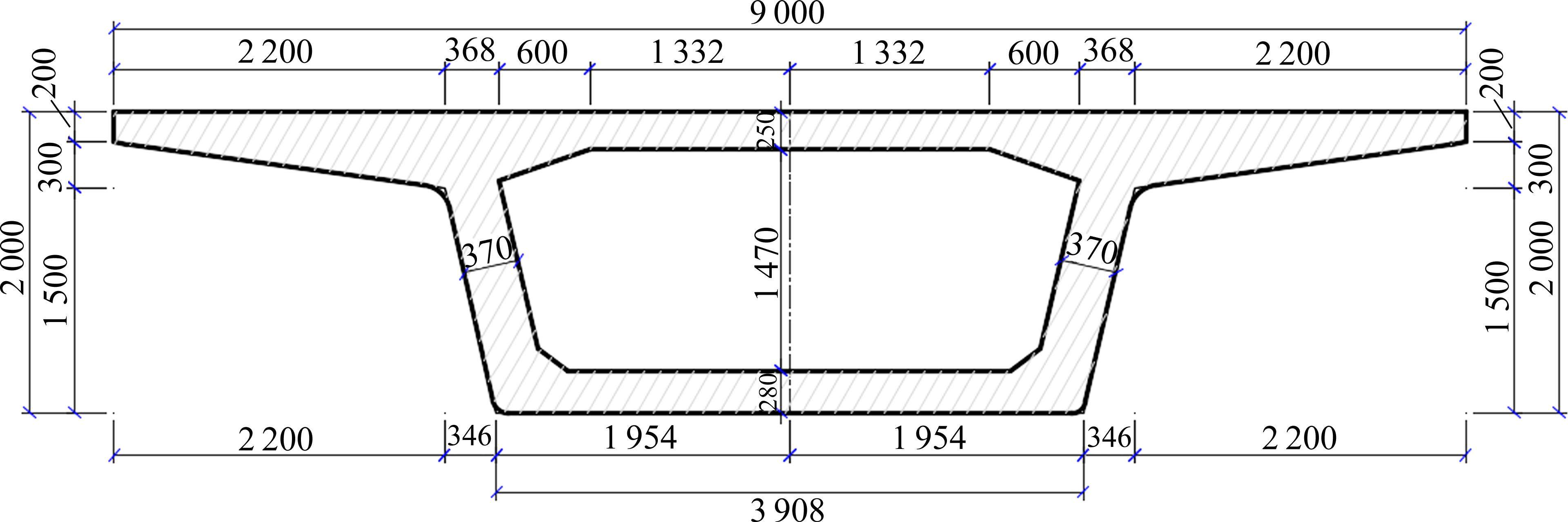
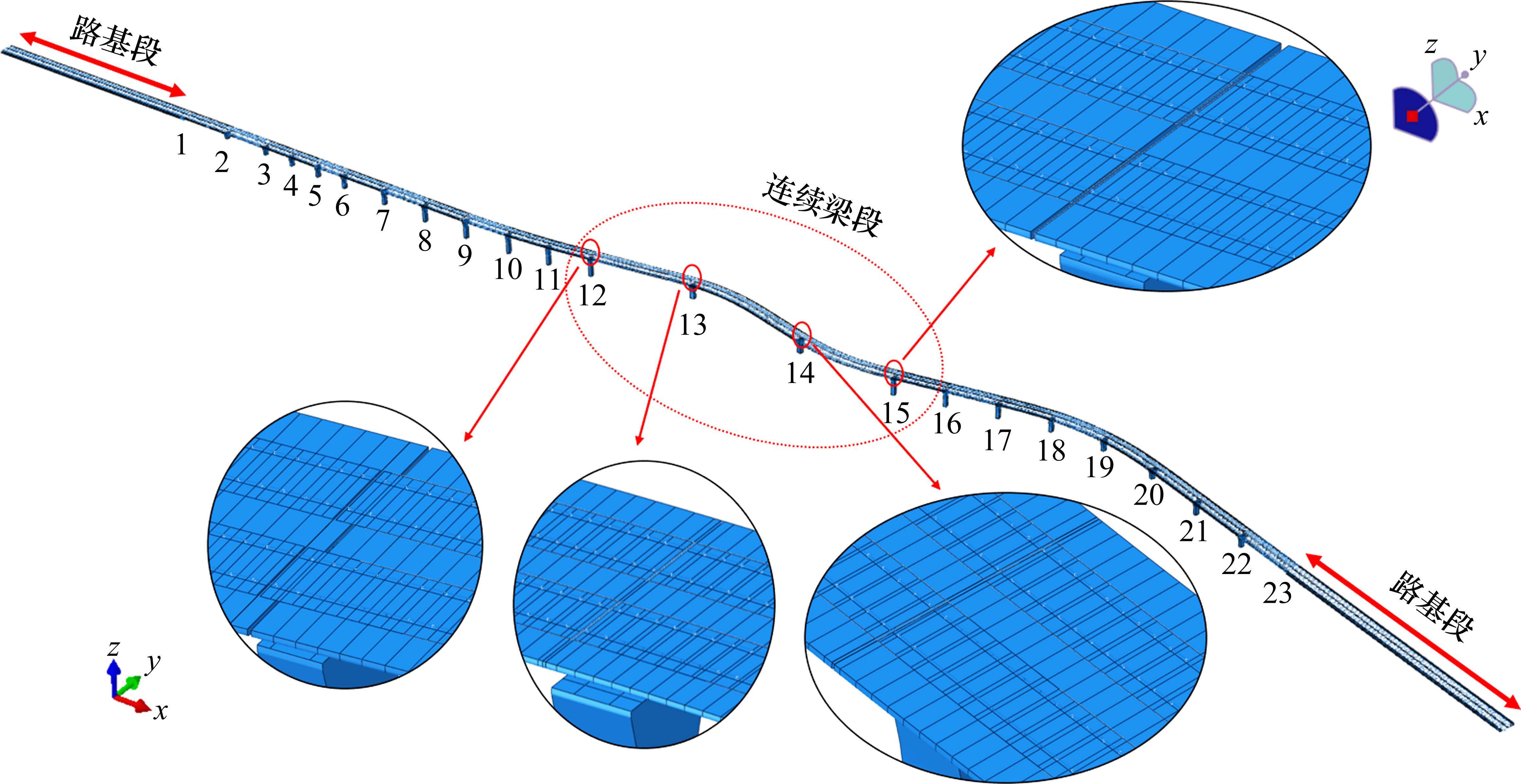
有轨电车桥上轨道采用混凝土长枕埋入式整体道床结构,整体道床通过预埋钢筋与桥面相连,钢轨纵向阻力仅由扣件提供,建立梁轨纵向相互作用力学模型,如图2所示,梁体跨中截面如图3所示。利用ABAQUS软件建立S型小半径曲线及其前后桥梁无缝线路相互作用数值模型,如图4所示,B31梁单元模拟60R2槽型钢轨,S4R壳单元模拟道床板,C3D8实体单元模拟梁体和桥墩,非线性弹簧-阻尼单元模拟扣件纵向阻力,线性弹簧-阻尼单元模拟扣件垂向、横向及桥梁支座阻力,整体道床绑定约束于桥面,桥梁墩底固结,钢轨两侧设置纵向约束,桥梁两侧考虑长度为150 m的路基段。本文有限元模型桥梁段长度800 m,考虑桥梁两端路基段,有限元模型总长1 100 m。轨道及桥梁计算参数见表2。
| 结构部件 | 参数 | 量值 |
|---|---|---|
| 60R2槽型钢轨 | 质量/(kg∙m-1) | 58.14 |
| 密度/(kg∙m-3) | 7 850 | |
| 弹性模量/GPa | 206 | |
| 泊松比 | 0.30 | |
| 扣件 | 垂向刚度/(kN∙mm-1) | 30 |
| 横向刚度/(kN∙mm-1) | 35 | |
| 纵向阻力/(kN∙组-1) | 5.6 | |
| 扣件间距/m | 直线段:0.625,曲线段:0.595 | |
| 道床板 | 弹性模量/GPa | 32.5 |
| 混凝土强度等级 | C40 | |
| 泊松比 | 0.20 | |
| 桥梁 | 弹性模量/GPa | 34.5 |
| 混凝土强度等级 | C50 | |
| 泊松比 | 0.20 |
2.2 有轨电车计算参数
采用四模块100%低地板有轨电车,在车辆中部下方设置1个转向架,有轨电车模型如图5所示,计算参数见表3。

| 参数 | 量值 |
|---|---|
| 轴重/t | 12.5 |
| 车辆定距/m | 8 |
| 轴距/m | 1.8 |
| 车轮名义直径/m | 0.6 |
2.3 模型验证
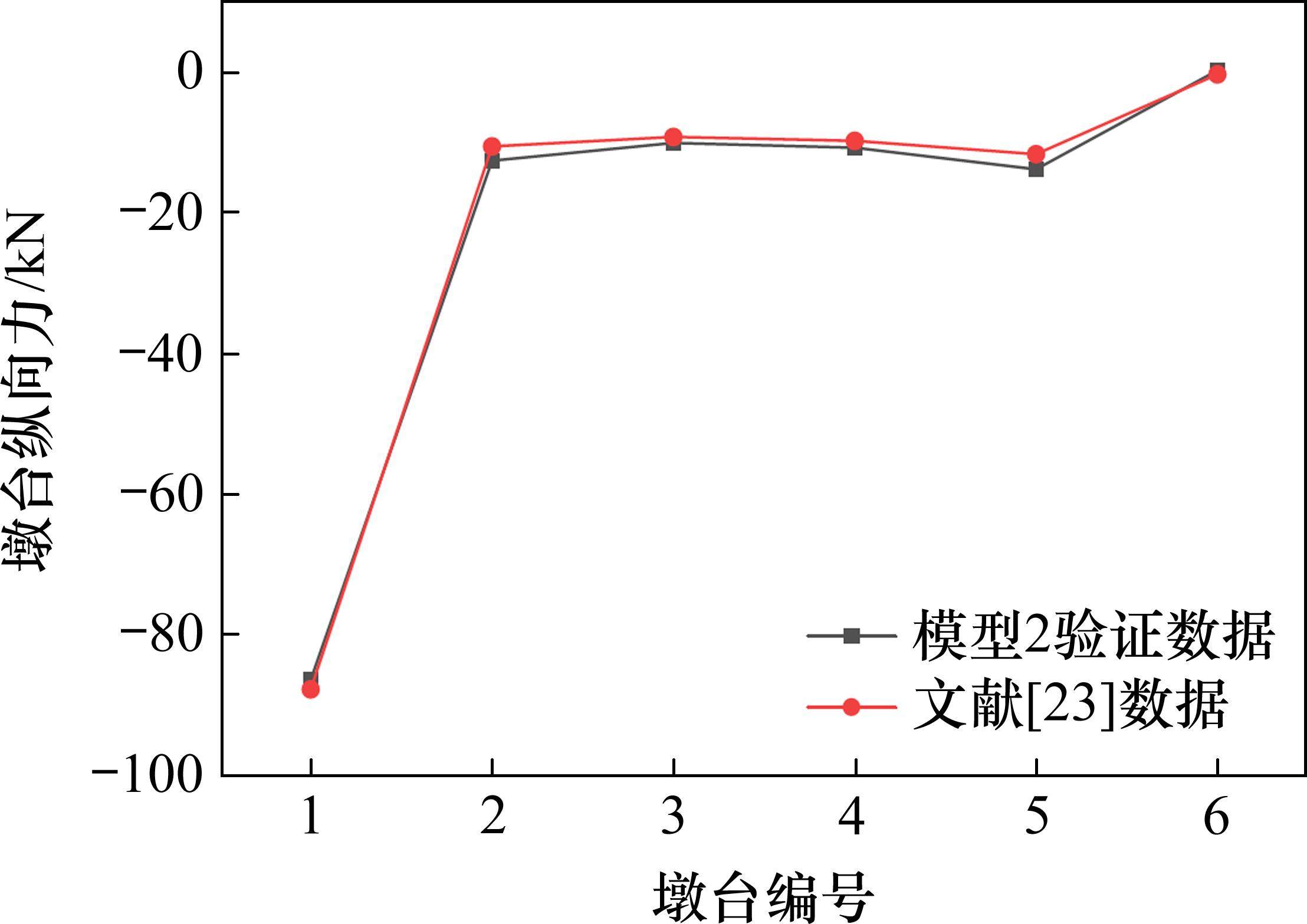
为验证本文所建立模型的可靠性,退化为简支梁桥-无缝线路模型,建立模型1,考虑10跨32 m简支梁桥,在桥梁两端各设置长度为150 m的路基段,桥梁温度变化15 ℃,有关计算参数取自文献[22]。另建立模型2,考虑5跨32 m简支梁-无缝线路模型,设置桥梁两侧路基段长度为100 m,桥梁温度变化15 ℃,有关计算参数选自文献[23],墩台纵向力对比如图6所示。表4列出了本文模型及文献[22-23]的计算结果。
钢轨受 力特征 | 所建模型 计算结果 | 文献计 算结果 | 相对误差/% |
|---|---|---|---|
钢轨最大纵向 压应力(N∙m-2) | 1.524×107 | 1.521×107 | 0.19 |
钢轨最大纵向 拉应力(N∙m-2) | 1.665×107 | 1.570×107 | 6.0 |
钢轨最大纵 向位移/mm | 2.605 | 2.551 | 5.4 |
墩台最大纵 向力/kN | 86.4 | 87.3 | 1.0 |
3 S型小半径曲线段梁轨相互作用分析
3.1 桥梁温度变化对梁轨纵向相互作用的影响
桥梁温度发生变化,梁跨结构将产生较大的伸缩位移,由于桥梁与无缝线路的相互作用,钢轨会产生伸缩附加力。为探明桥梁温度变化对S型小半径曲线桥梁无缝线路纵向相互作用的影响规律,考虑桥梁温度降低3种工况,即降温10 ℃、20 ℃和30 ℃,钢轨的伸缩附加力及梁轨纵向相对位移如图7所示。
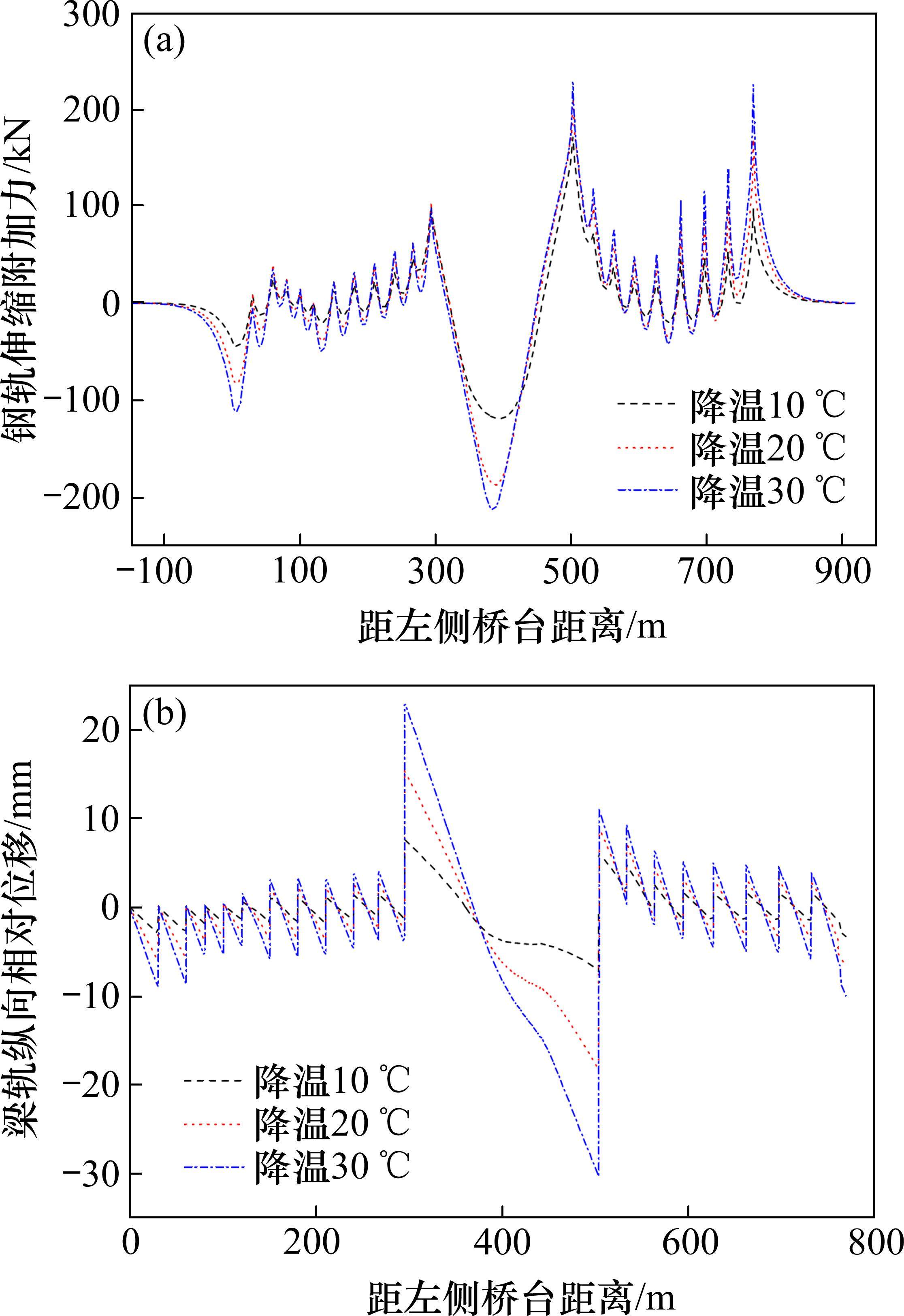
由图7可知,钢轨伸缩附加力和梁轨纵向相对位移均随温降幅度增大而增大,不同温降工况下钢轨伸缩附加力及梁轨纵向相对位移均在13号墩后跨连续梁右端达到最大。各温降工况下,钢轨伸缩附加力最值和梁轨相对位移最值对比见表5。
桥梁温度 降低工况 | 钢轨伸缩附加 力最值/kN | 梁轨纵向相对 位移最值/mm |
|---|---|---|
| 降温10 ℃ | 218.414 | 8.11 |
| 降温20 ℃ | 285.601 | 18.57 |
| 降温30 ℃ | 315.169 | 30.09 |
由表5可知,当桥梁由降温10 ℃至降温20 ℃时,钢轨伸缩附加力最值由284.414 kN增长至285.601 kN,增长幅度为30.76%;梁轨纵向相对位移最值由8.11 mm增长至18.57 mm,增长幅度为128.9%。当桥梁由降温20 ℃至降温30 ℃时,钢轨伸缩附加力最值由285.601 kN增长至315.169 kN,增长幅度为10.3%;梁轨纵向相对位移最值由18.57 mm增长至30.09 mm,增长幅度为62.04%。由此可知,桥梁温度变化对钢轨伸缩附加力和梁轨纵向相对位移的影响不可忽视,且由降温10 ℃工况至降温20 ℃工况,钢轨伸缩附加力及梁轨纵向相对位移在此温度区间内增长速率较大,由降温20 ℃工况至降温30 ℃工况,增长速率逐渐放缓。主要原因是钢轨受到扣件及轨下结构的约束,使得钢轨纵向伸缩位移随温度降低变化较缓,即在较低的降温区间内,钢轨纵向伸缩位移比梁跨结构纵向伸缩位移小得多,在较高的降温区间内,钢轨纵向伸缩位移克服部分纵向阻力,使钢轨纵向伸缩位移与梁跨结构纵向伸缩位移的差距减小。
3.2 桥梁温度变化对钢轨横向位移的影响
图8给出了桥梁降温30℃工况下,4股钢轨横向位移变化情况,钢轨横向正位移在13号墩连续梁右端达到极大值,钢轨横向负位移在14号墩连续梁右端达到极大值,且反向曲线上的钢轨横向位移方向相反,横向位移最值出现在S型曲线的衔接区域,即14号墩附近。钢轨横向位移的正负规定见图1,按桥墩墩号由小至大方向,4股钢轨从左到右分别编为1~4号。
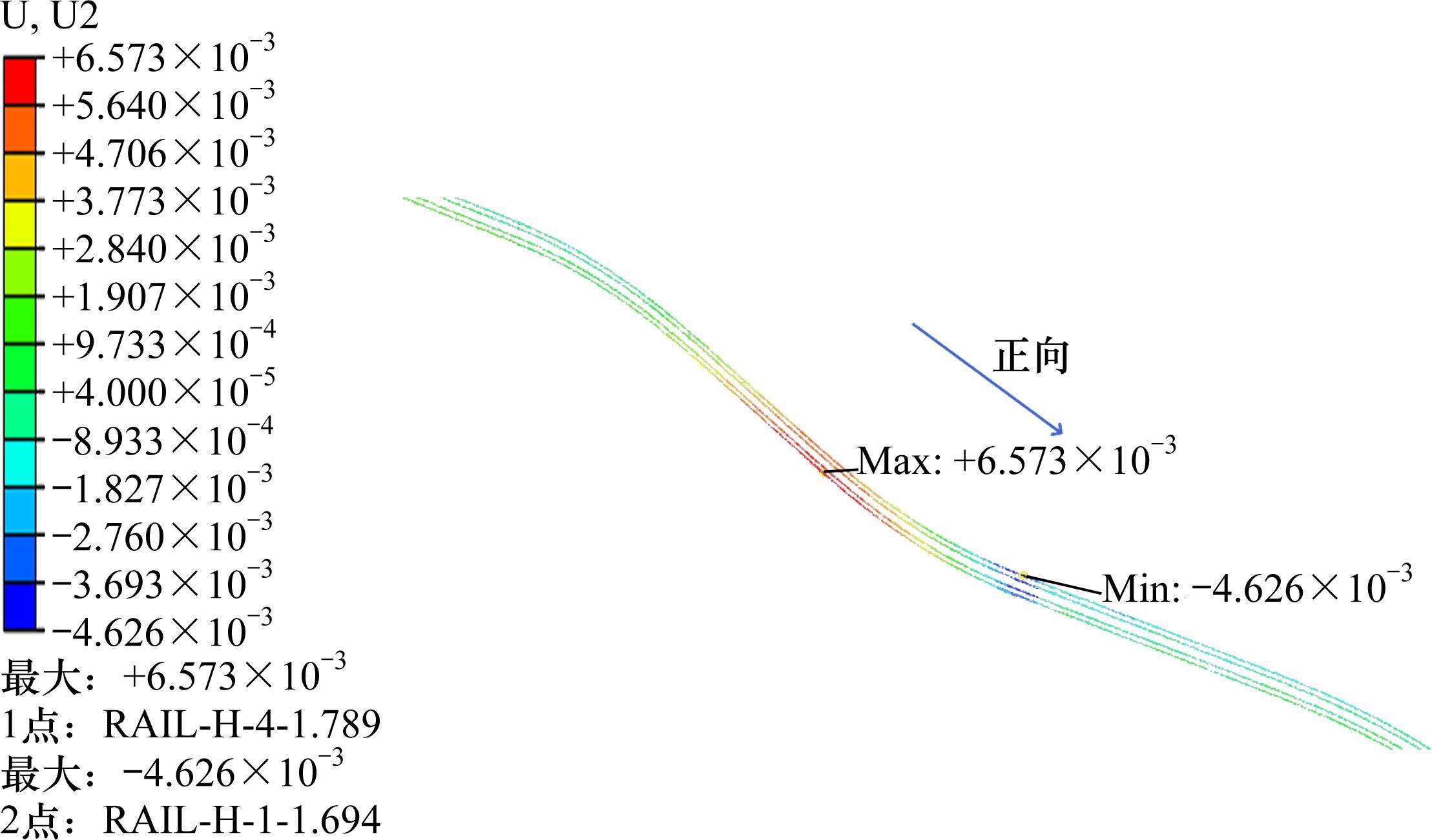
桥梁不同温降工况下,4股钢轨横向位移极值如图9所示。由图9可知,每股钢轨的横向位移极值均随桥梁降温幅度增大而增大。以1号钢轨为例,当桥梁由降温10 ℃至降温20 ℃时,钢轨横向正位移极值由1.656 mm增长至3.303 mm,增长幅度为99.46%,钢轨横向负位移极值由1.420 mm增长至3.001 mm,增长幅度为111.34%;当由降温20 ℃至降温30 ℃时,钢轨横向正位移极值由3.303 mm增长至5.004 mm,增长幅度为51.50%,钢轨横向负位移极值由3.001 mm增长至4.626 mm,增长幅度为54.15%。
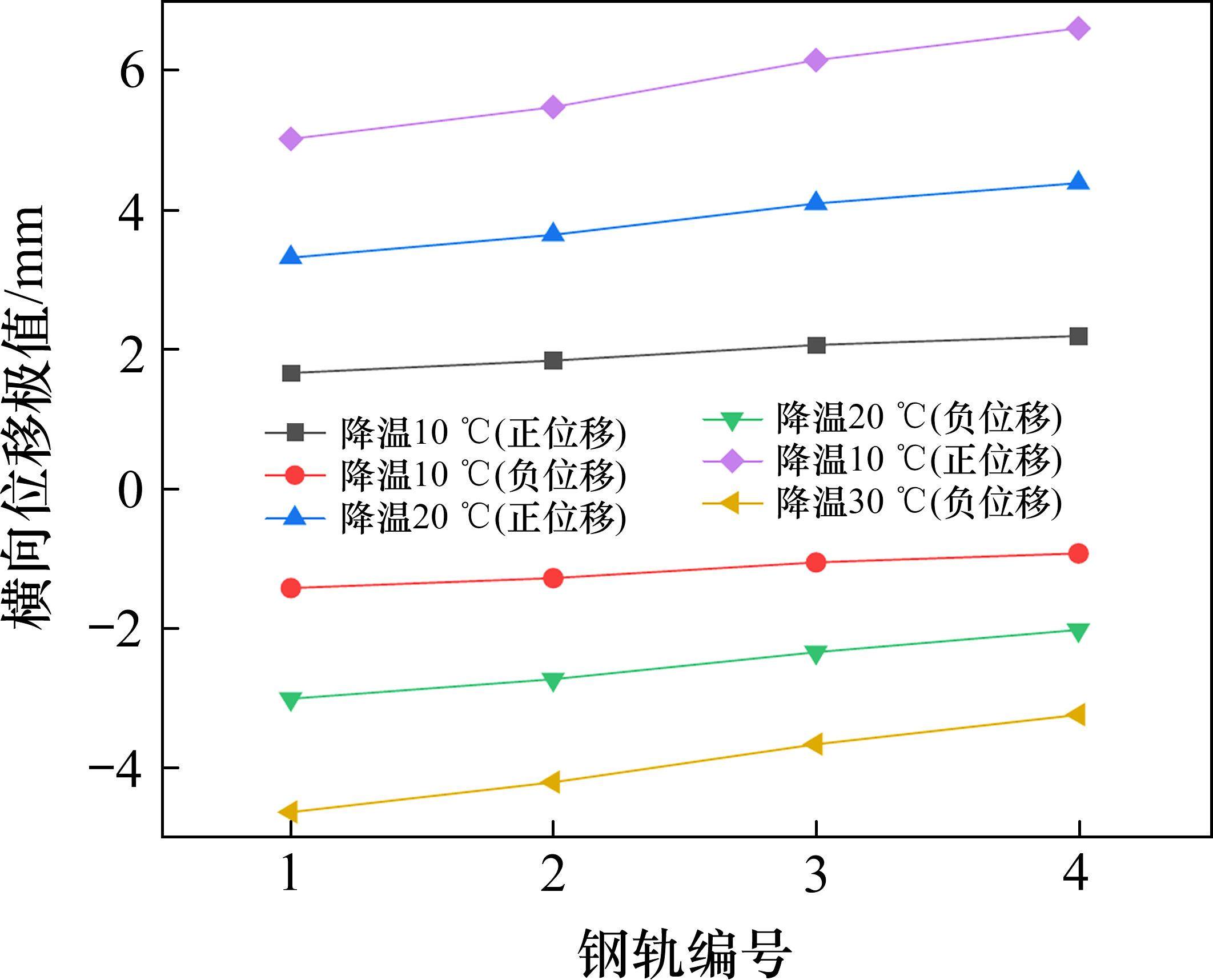
对比各股钢轨,可以发现钢轨横向正位移极值随着钢轨编号的增大而增大,而钢轨横向负位移极值随钢轨编号的增大而减小,且随着桥梁降温幅度而增大,各股钢轨的横向正位移极值的增长幅度快于横向负位移的减小幅度,主要原因是12号墩连续梁与13号墩后跨连续梁均位于第1曲线上,14号墩连续梁位于第2曲线上,第1曲线桥梁跨度大、钢轨长度长,钢轨横向稳定性差,在桥梁温降幅度增大时,第1曲线上的钢轨横向位移变化值大于第2曲线上的钢轨横向位移变化值。
3.3 扣件纵向阻力对S型小半径曲线段梁轨相互作用的影响
扣件纵向阻力对桥上无缝线路梁轨相互作用有重要影响,合理的扣件纵向阻力可以较好地减小梁轨相互作用。桥上无缝线路常采用WJ-8型常阻力扣件(15 kN/m/组),而在本文所述的有轨电车S型曲线连续梁桥上,无缝线路采用YGI-2型扣件,由《YGI-2扣件供货技术条件》可知YGI-2型扣件每组扣件钢轨防爬阻力为3.5~5.6 kN/m/组。本节在桥梁降温30 ℃的基础上,考虑WJ-8型常阻力扣件(15 kN/m/组)、YGI-2型常阻力扣件(5.6 kN/m/组)及YGI-2型小阻力扣件(3.5 kN/m/组)3种扣件以不同布置工况探究对有轨电车S型曲线桥梁无缝线路相互作用的影响,3种扣件纵向阻力如图10所示,布置工况见表6。由于只改变扣件纵向阻力值,对钢轨横向位移并无明显影响,故不作钢轨横向位移对比,不同扣件纵向阻力下钢轨伸缩附加力及梁轨纵向相对位移分布如图11所示。
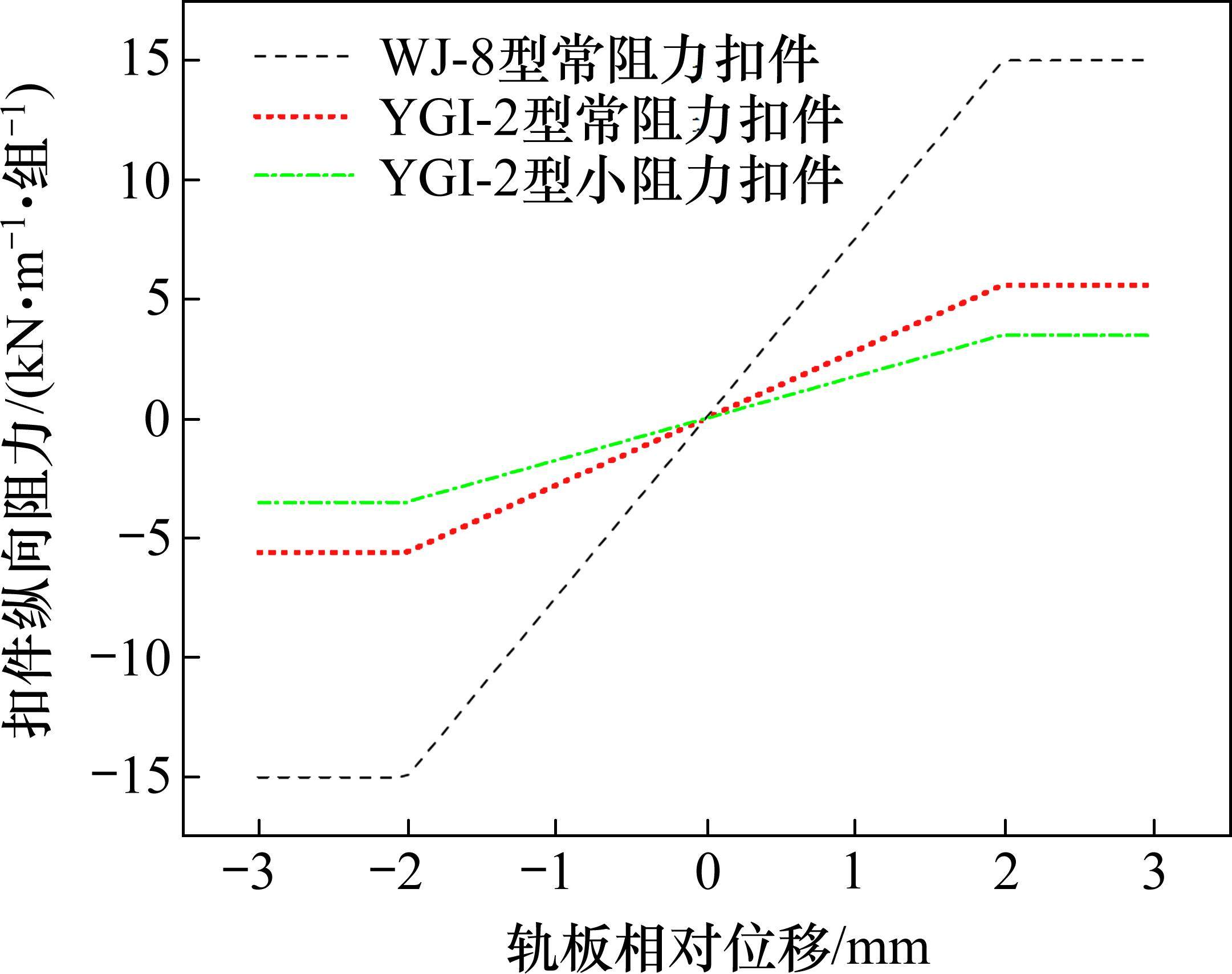
| 工况 | 布置方式 |
|---|---|
| 1 | 全桥采用WJ-8型常阻力扣件 |
| 2 | 连续梁桥上采用YGI-2型常阻力扣件,其余桥段采用WJ-8型常阻力扣件 |
| 3 | 全桥采用YGI-2型常阻力扣件 |
| 4 | 连续梁桥上采用YGI-2型小阻力扣件,其余桥段采用YGI-2型常阻力扣件 |
| 5 | 全桥采用YGI-2型小阻力扣件 |
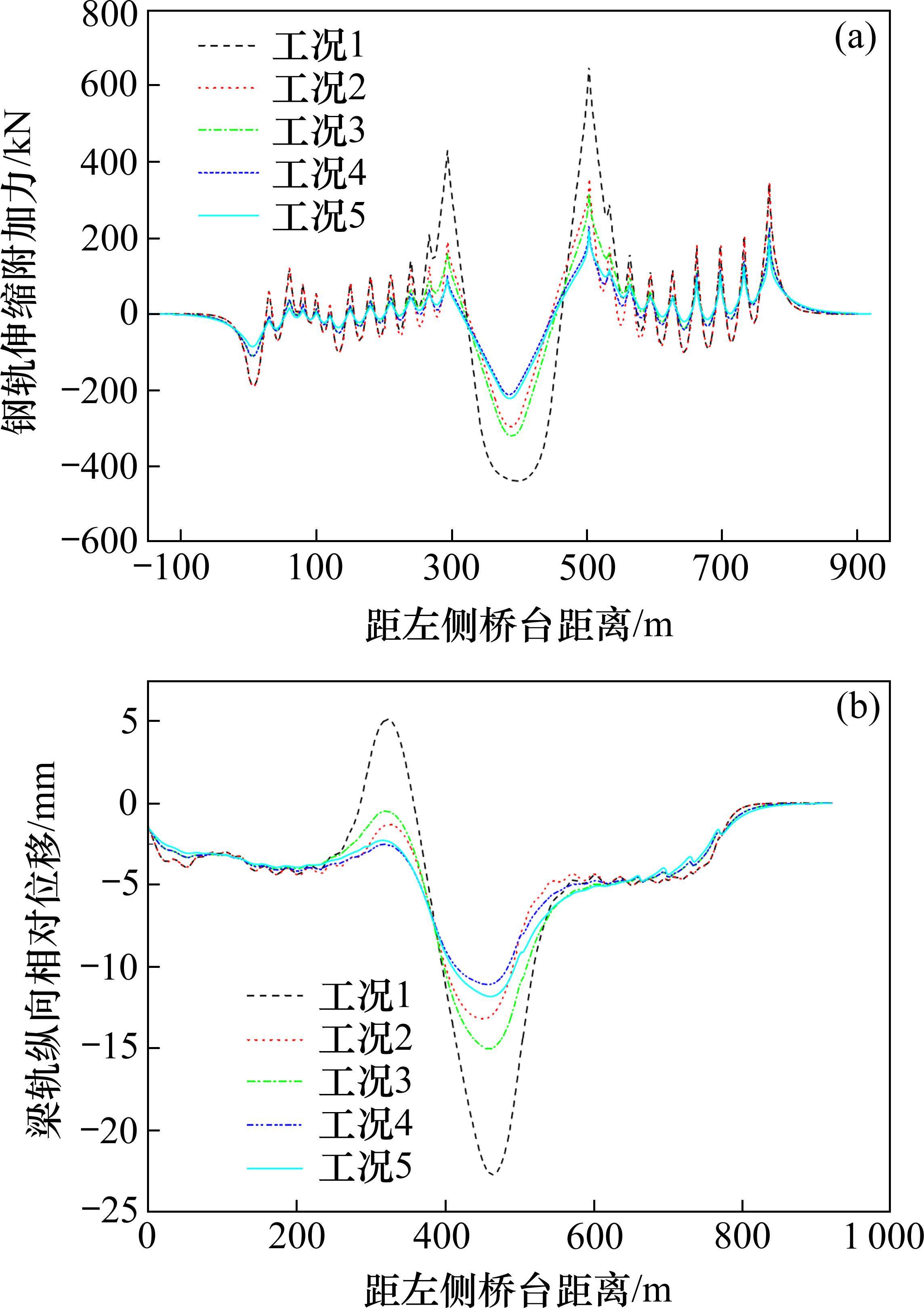
由图11可知,在设置的5种扣件纵向阻力工况中,钢轨伸缩附加力最值与钢轨纵向位移最值均发生在13号墩连续梁右端区域。钢轨伸缩附加力在全桥采用WJ-8常阻力扣件时达到最大,即钢轨伸缩附加力在工况1下达到最大,而钢轨伸缩附加力最值在工况2和工况3下较小,在工况4和工况5下最小,且两者的值相近,由此说明在连续梁上使用纵向阻力较小的扣件有利于减小钢轨伸缩附加力。钢轨纵向位移在全桥采用WJ-8常阻力扣件时达到最大,即钢轨纵向位移在工况1下达到最大,而钢轨纵向位移最值在工况3、工况2、工况5、工况4下依次减小。
上述结果表明,为降低钢轨伸缩附加力和梁轨纵向相对位移,宜采用工况4的扣件布置方式,即在S型小半径曲线连续梁段无砟轨道上布置YGI-2型小阻力扣件,其余梁段布置YGI-2型常阻力扣件。采用工况4的扣件布置方式,钢轨伸缩附加力最值为229.38 kN,相比于工况1下钢轨伸缩附加力最值650.413 kN降低了64.73%。采用工况4的扣件布置方式,梁轨纵向相对位移最值为11.12 mm,相比于工况1下梁轨纵向相对位移最值22.75 mm降低了51.13%。
3.4 钢轨伸缩调节器布置方式对S型小半径曲线段梁轨相互作用的影响
对于大跨度桥梁,合理布置钢轨伸缩调节器可有效减小梁轨相互作用。根据TB 10015—2012《铁路无缝线路设计规范》中桥上无缝线路中不宜设置过多的钢轨伸缩调节器这一原则,本文在工况4的基础上,即在连续梁桥段采用YGI-2型小阻力扣件,其余桥段采用YGI-2型常阻力扣件的扣件布置工况下,在钢轨伸缩附加力峰值处设置钢轨伸缩调节器,考虑桥梁温降30 ℃工况。钢轨伸缩调节器设置工况如表7所示,钢轨伸缩附加力和钢轨纵向位移分别如图12和13所示。
| 工况 | 布置方式 |
|---|---|
| 6 | 全桥不设置钢轨伸缩调节器 |
| 7 | 连续梁桥左端设置一个钢轨伸缩器,连续梁桥右端不设置钢轨伸缩器 |
| 8 | 连续梁桥左端不设置钢轨伸缩器,连续梁桥右端设置一个钢轨伸缩器 |
| 9 | 连续梁桥左右两端均设置一个钢轨伸缩器 |
| 10 | 连续梁桥左右两端均不设置钢轨伸缩器,连续梁中部设置一个钢轨伸缩器 |
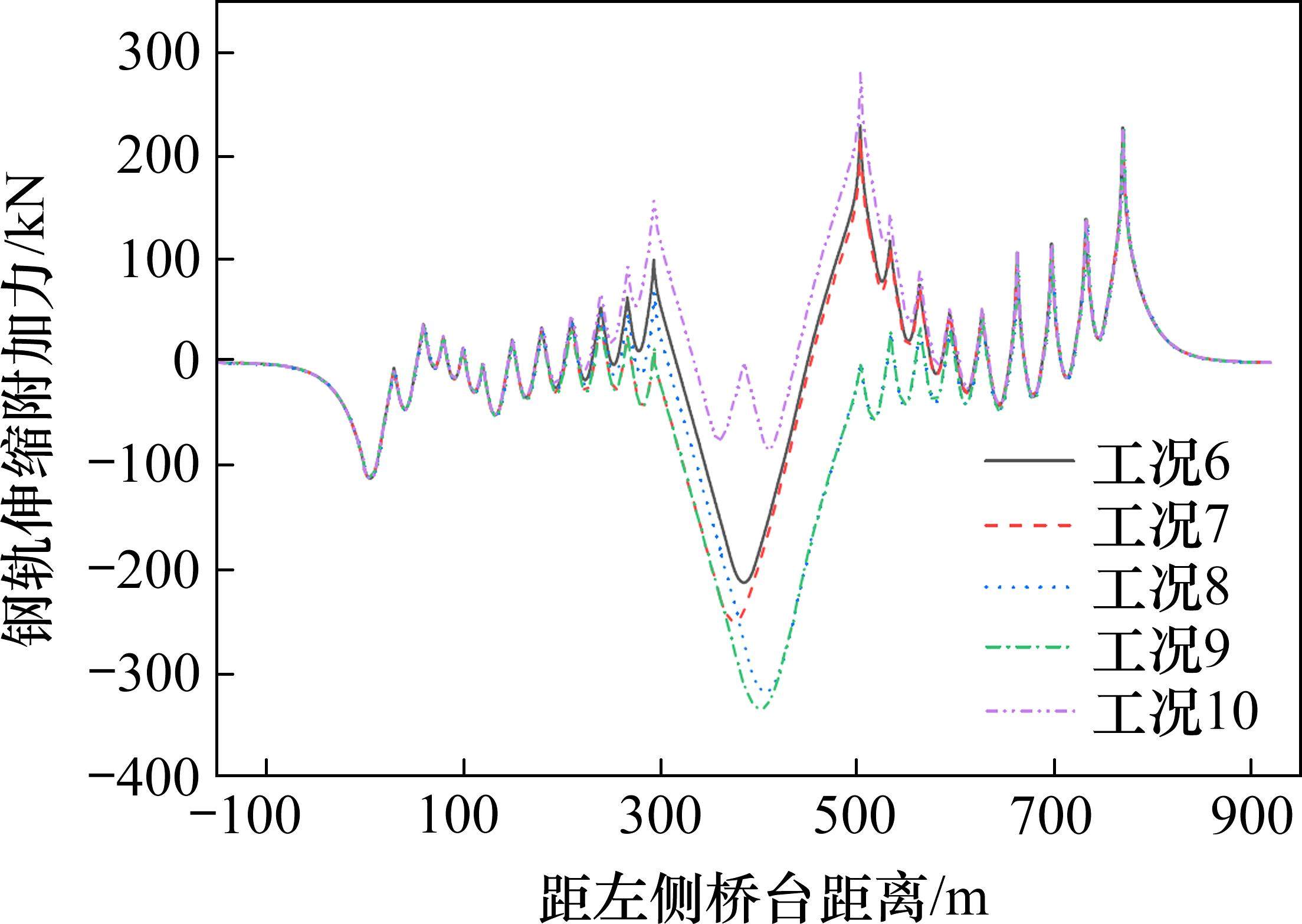
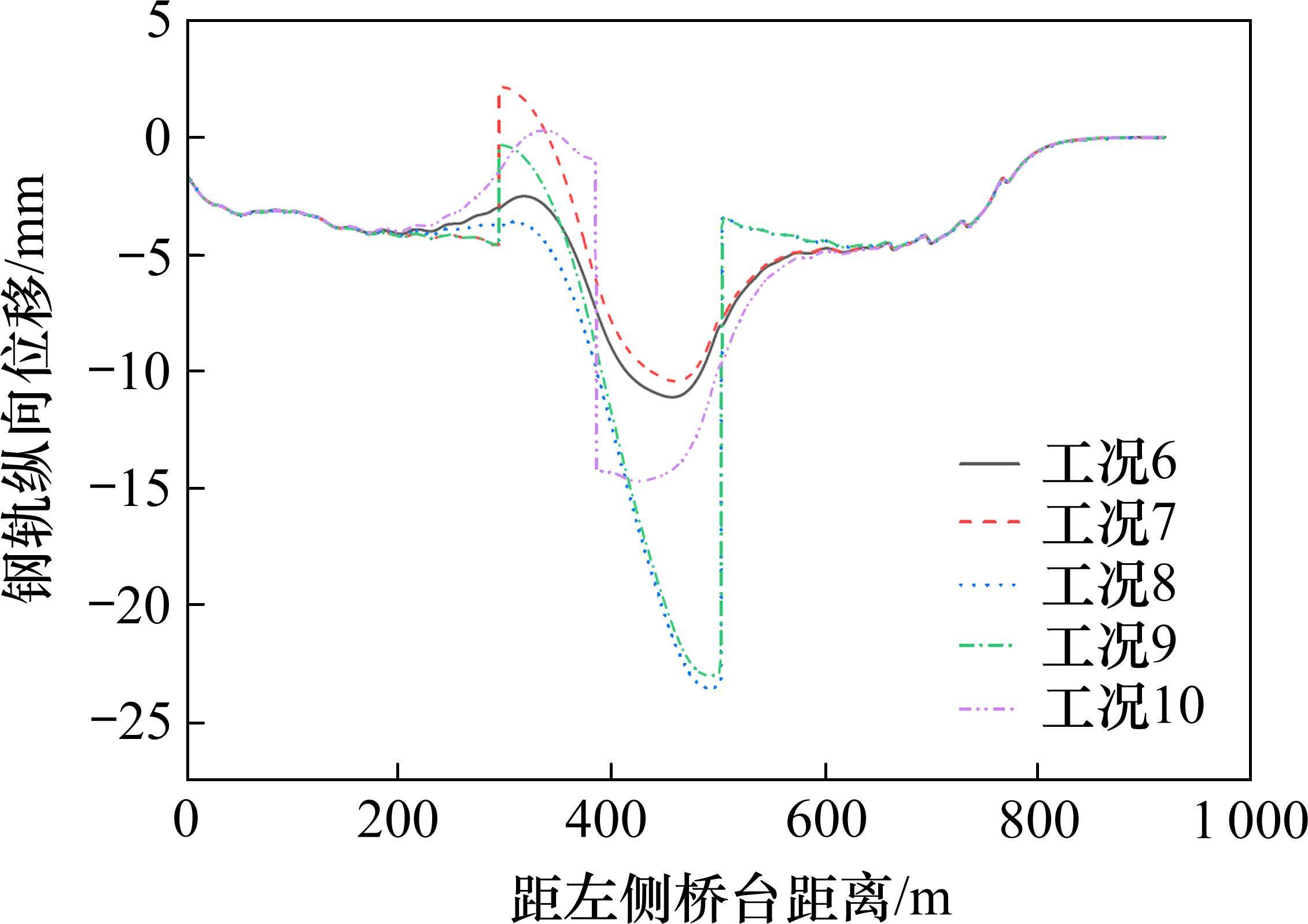
由图12~13可知,连续梁桥段一端设置一个钢轨伸缩调节器能够有效降低该处的钢轨伸缩附加力,但会增大连续梁桥段中部的钢轨伸缩力,且相应的钢轨纵向位移值大幅度增大。采用工况9的钢轨伸缩调节器设置方式,虽然降低了连续梁桥段两端的钢轨伸缩附加力,但连续梁桥段中部的钢轨伸缩附加力达到-334.796 kN,相比于工况6中不设置钢轨伸缩调节器时的连续梁桥段中部的钢轨伸缩附加力-212.679 kN,增大了57.42%。对比工况7、工况8,当在连续梁桥段两端设置钢轨伸缩调节器时,能有效减少设有伸缩器的连续梁端部的钢轨伸缩附加力,但会显著增大相应位置的钢轨纵向位移。采用工况10的钢轨伸缩调节器设置方式,即仅在连续梁桥段中部设置一个钢轨伸缩调节器,能够有效减小连续梁桥段中部的钢轨伸缩附加力,但会增大梁端钢轨纵向位移,达到-14.70 mm,相比于工况6不设置钢轨伸缩调节器的钢轨纵向位移最值-11.12 mm增大了32.19%,但相比其他工况,工况10的钢轨伸缩器布置方式可在保证钢轨纵向位移的前提下,有效减小连续梁中部的钢轨伸缩附加力,达到-82.689 kN,相比工况6的连续梁中部钢轨伸缩附加力最值-211.679 kN减少了60.93%。
钢轨伸缩调节器的布置方式对钢轨伸缩调节器和钢轨纵向位移影响较大,主要原因是温度荷载作用下钢轨伸缩附加力和钢轨纵向位移呈现负相关趋势,而设置钢轨伸缩调节器会破坏轨道结构尤其是无缝线路的整体性,使原本储存在轨道结构中的温度力释放出来,即降低了钢轨伸缩附加力,增大了钢轨纵向位移。虽然在连续梁桥段设置钢轨伸缩调节器可以有效削弱钢轨伸缩附加力,但同时会大幅度增大相应位置的钢轨纵向位移,综合考虑下,在实际有轨电车桥上无缝线路上应当以不设或少设钢轨伸缩调节器为原则。
3.5 扣件横向刚度及车辆横向摇摆力对S型小半径曲线段梁轨相互作用影响
有轨电车在通过S型小半径曲线桥上无砟轨道时会产生较大的横向摇摆力,影响无缝线路的横向稳定性。为探究扣件横向刚度对S型小半径曲线连续梁上梁轨相互作用的影响,本文在桥梁降温30 ℃,不设置钢轨伸缩调节器,连续梁桥段布置YGI-2型小阻力扣件,其余桥段布置YGI-2型常阻力扣件的基础上设置不同的扣件横向刚度,分别为15,35,55,75和95 kN/mm,计算分析S型小半径曲线连续梁桥上钢轨横向位移和支座横向力的变化规律。
根据Q/440112/JT-001-2019《黄埔区有轨电车设计规范-广州开发区城投企业标准》10.2.7条规定,有轨电车横向摇摆力按相邻2节车体轴重的15%计,以横桥向集中力形式取最不利位置作用于轨顶面,多线桥只计算任一线上的横向摇摆力。选取车辆轴重为12.5 t,即集中力大小为73.5 kN。考虑的横向摇摆力4种不同施加位置方案如表8所示,不同施加位置方案下计算的钢轨横向位移及支座横向力最大值分别如图11和图12所示。
| 方案 | 施加位置 |
|---|---|
| 1 | 车辆横向摇摆力施加于S型曲线连续梁左端 |
| 2 | 车辆横向摇摆力施加于第1曲线中部 |
| 3 | 车辆横向摇摆力施加于第2曲线中部 |
| 4 | 车辆横向摇摆力施加于S型曲线连续梁右端 |
由图14可知,扣件横向刚度相同时,钢轨最大横向位移与横向摇摆力施加位置无关;横向摇摆力施加方案相同时,钢轨的最大横向位移随扣件横向刚度的增大而逐渐减小,当扣件横向刚度由15 kN/mm增至95 kN/mm时,钢轨最大横向位移值减少约59%。钢轨横向最大位移与扣件横向刚度呈现明显的负相关关系,与有轨电车横向摇摆力的施加位置基本无关。主要原因是相比于温度荷载,车辆横向摇摆力是造成钢轨横向位移的次要因素而非主要因素,且S型小半径曲线连续梁桥段轨道结构整体性较好,轨道结构共同分担了车辆横向摇摆力的集中作用;扣件横向刚度与钢轨横向位移直接相关,扣件横向刚度的增大意味着钢轨所受横向约束加强,钢轨横向稳定性增强,抵抗横向变形的能力增强。
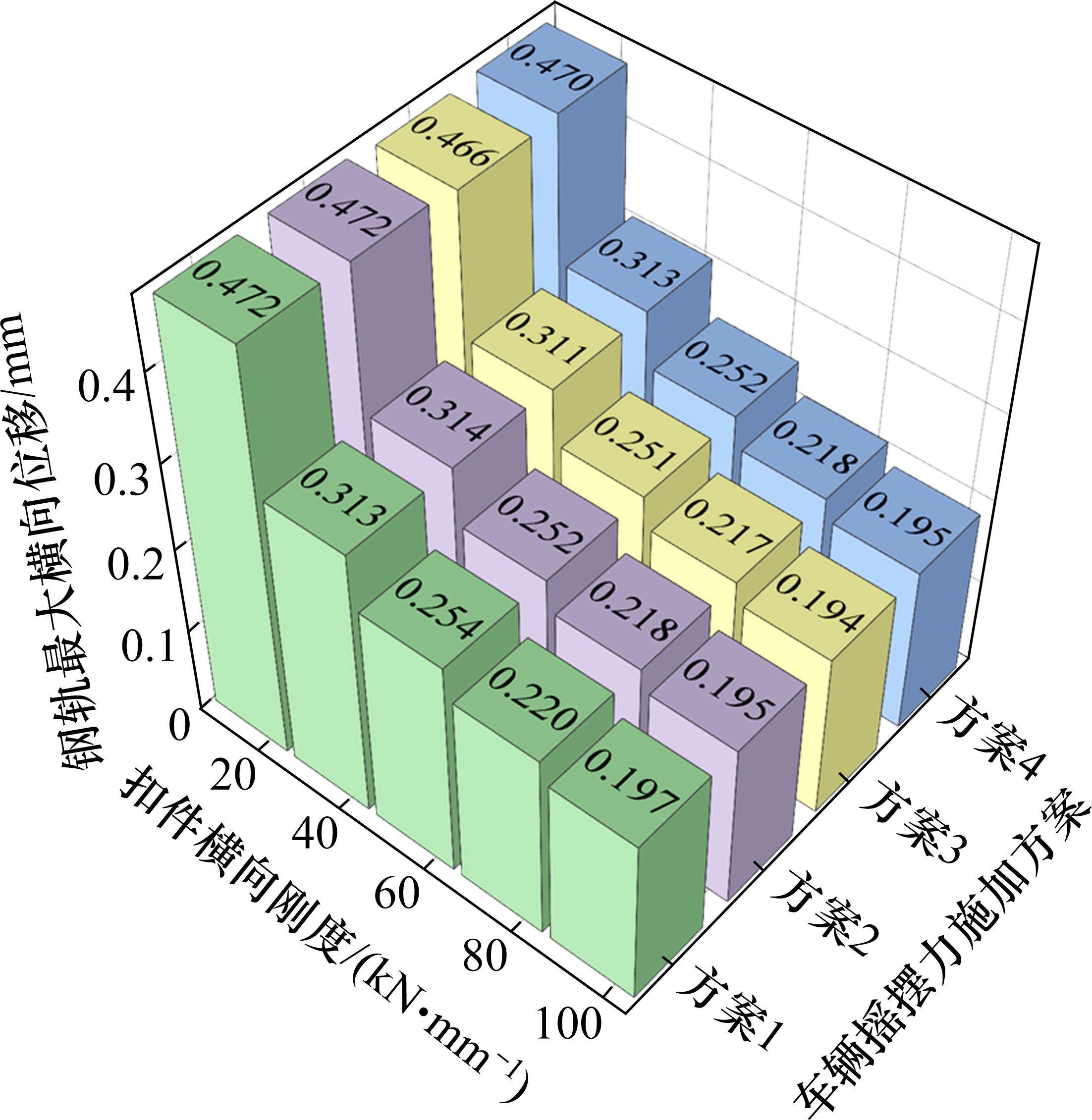
由图15可知,扣件横向刚度相同时,横向摇摆力施加位置对桥墩支座最大横向力影响不大;不同扣件横向刚度条件下,桥墩支座最大横向力均在方案2达到最值,即在车辆横向摇摆力施加于第1曲线中部时达到最大值。横向摇摆力施加方案相同时,桥墩支座横向摇摆力随扣件横向刚度增大而缓慢增大,例如,对于方案1,扣件横向刚度由15 kN/mm增至95 kN/mm,相应的桥墩支座横向力由63.89 kN增至67.47 kN,增幅仅5.6%。由此可知,扣件横向刚度对桥墩支座最大横向力的影响较小,主要原因是横向摇摆力作用需要经过钢轨、扣件联接系统、轨枕、道床、梁跨结构等多层结构才能传递至桥墩支座,单一的改变扣件横向刚度不能明显影响桥墩支座最大横向力。
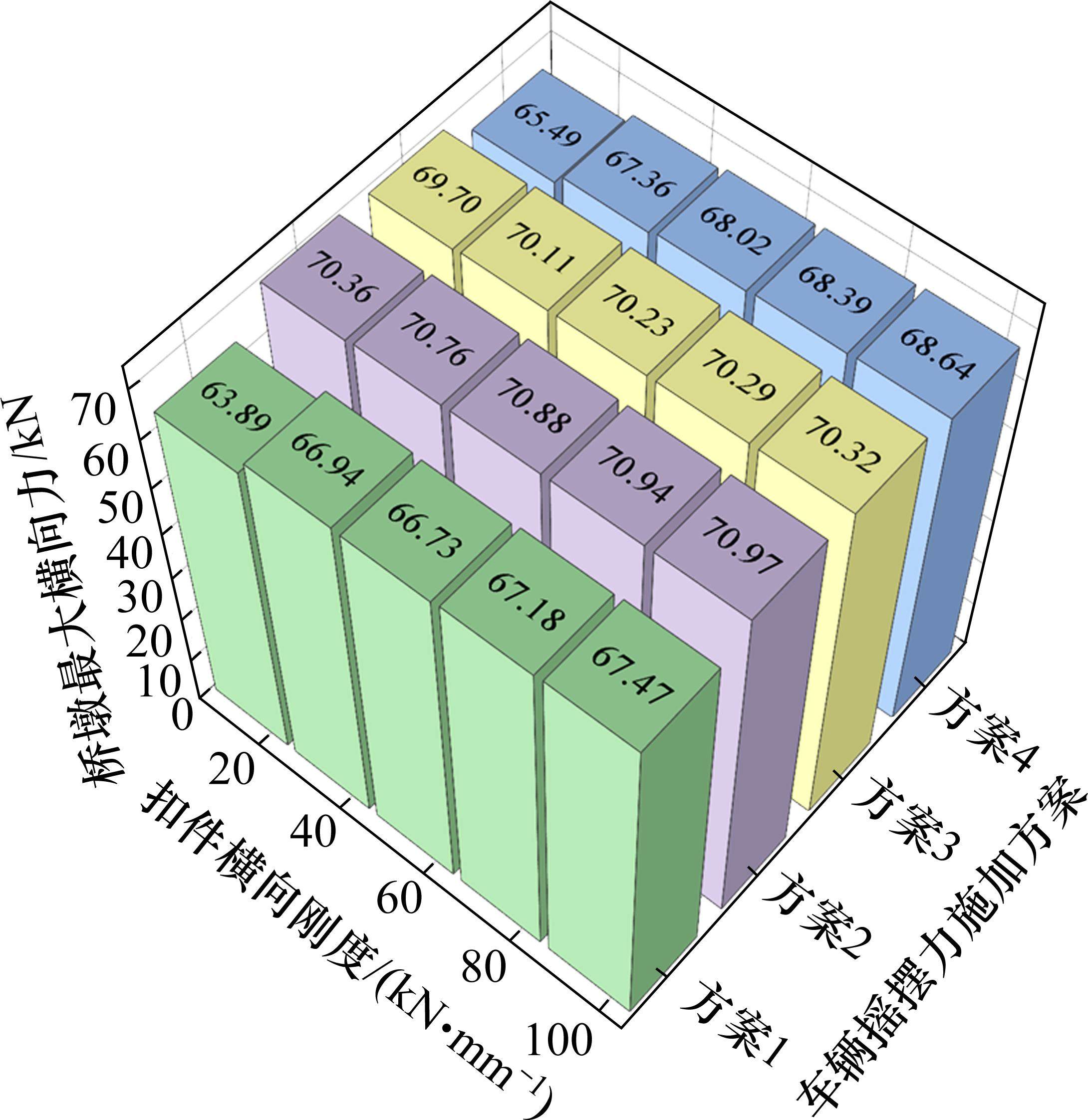
由上述分析可知,采用不同的扣件横向刚度可以显著地控制桥上无缝线路钢轨的横向变形,但单一的改变扣件横向刚度对桥墩支座横向力的影响有限。有轨电车横向摇摆力在S型小半径曲线连续梁桥上钢轨的施加位置对钢轨横向变形的影响基本无关,对桥墩支座横向力的影响也较小。
4 结论
1) 随着桥梁降温幅度的增大,钢轨伸缩附加力和梁轨纵向相对位移均随之增大。由于桥梁跨度及弯曲方向的不同,S型小半径曲线连续梁处钢轨横向正位移随着桥梁降温幅度的增大而增大,而钢轨横向负位移则随之减小,桥梁温降由10 ℃增长至20 ℃,连续梁处钢轨横向正、负位移极值均增长约1倍。
2) 在连续梁上采用较小的钢轨纵向阻力有利于减小钢轨伸缩附加力和钢轨纵向位移,S型小半径曲线桥上无砟轨道宜采用的扣件布置方式为:连续梁桥处采用YGI-2型小阻力扣件,其他采用YGI-2型常阻力扣件。此种扣件布置方式相比全桥设常阻力扣件钢轨伸缩力最值降低约60%,梁轨相对位移最值降低约50%。
3) 设置钢轨伸缩器虽然能有效减小钢轨伸缩附加力,但会显著增加相应的钢轨纵向位移。在连续梁中部设置一个钢轨伸缩器相比不设置钢轨伸缩器,可在钢轨纵向位移增大32.19%的前提下,相应减少钢轨伸缩力达60.93%。综合考虑,小半径曲线桥上有轨电车无缝线路应根据实际情况不设或少设钢轨伸缩调节器。
4) 钢轨横向位移随着扣件横向刚度的增大而减小,单一改变扣件横向刚度对桥墩支座横向力的影响可忽略不计。
5) 车辆横向摇摆力的施加位置对钢轨横向位移和桥墩支座横向力的影响很小,可忽略不计。
Finite element analysis of the thermal interaction of continuously welded rails with simply supported bridges considering nonlinear stiffness
[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2020, 234(10): 1358-1367.祝朋玮,张硕,娄徐瑞利等.有轨电车S型小半径曲线桥梁无缝线路相互作用分析[J].铁道科学与工程学报,2024,21(12):4993-5004.
ZHU Pengwei,ZHANG Shuo,LOU Xuruili,et al.Analysis of interaction between continuously welded rail track and bridge on S-shaped curve line with small radius for trams[J].Journal of Railway Science and Engineering,2024,21(12):4993-5004.

