轨道车辆在行驶过程中会途径多曲线路段,小弯道半径、过高通过速度和不平衡超高等因素使得轮对接触发生横移,在横移影响下,轮轨接触斑的形状及黏着-滑移区域均发生变化,导致接触斑内部的法向和切向接触力分布等特性发生显著变化[1],轮对-齿轮传动系统作为轨道车辆的核心子系统,会受到振动和冲击,从而直接影响整车运行的稳定性与可靠性。因此,研究轮对横移黏着接触特性对传动系统的动力学影响对于提高传动系统的可靠性和延长其使用寿命具有重要意义。
轮对-齿轮传动系统本身处于一个较为复杂多变的内外部激励环境,内部激励主要包括齿轮的时变啮合刚度、轴承非线性接触力、传递误差等[2-4];外部激励主要包括轨道不平顺、轮对失圆、电机的谐波转矩、轮轨之间的非线性黏着力矩等[5-7]。国内外学者研究了多种内外部激励对轨道车辆齿轮传动系统动态特性的影响。KONOWROCKI等[8]建立了包含牵引电机和齿轮箱的轨道车辆机电耦合动力学系统,并分析了电磁转矩对齿轮箱扭转振动的影响。KOSTRZEWSKI等[9]研究了小半径曲线工况下传动系统动态特性,并分析了不同传动方式对轮轨接触特性的影响。CHEN等[10]建立了包含齿轮传动系统的轨道-车辆耦合动力学模型,并分析了不同工况下轮轨黏着特性对系统动态特性的影响。XU等[11]基于等效模型建立了高速列车的传动系统动力学模型,并分析了不同黏着特性下的轮对动力学响应。HUANG等[12]建立了考虑齿轮时变啮合刚度、非线性齿侧间隙、静态传递误差的高速列车齿轮传动系统二自由度动力学模型,得出载荷和黏滑状态对齿轮的非线性动力学有重要影响。黄冠华等[13]将黏滑振动引起的负载波动作为外部激励,建立了考虑齿轮啮合的高速列车动力车整车动力学模型,结果表明黏滑振动会严重影响齿轮系统的稳定性。杨柳等[14]考虑不平衡质量、齿轮啮合刚度、轴承支撑刚度和轮轨接触的影响,建立了机车传动系统有限元单元动态模型,分析了传动系统齿轮单元幅频响应变化。王燕等[15]基于轮轨黏着特性的双线性模型,推导了黏着阻尼的表达式,建立了考虑时变啮合刚度、齿侧间隙的机车齿轮纯扭转动力学模型,并研究了黏着阶段和滑动阶段对齿轮非线性振动的影响。综上所述,目前研究多关注于直线行驶路段轮轨黏着对轮对-齿轮传动系统的影响,而对于曲线行驶路段轮对横移黏着的接触特性及其对传动系统动态特性影响的研究较少,而且基于赫兹理论和简化的轮轨黏着特性曲线来研究轮轨黏着接触特性与实际情况不相符;此外,在传动系统动力学建模中均将轮对作为整体,忽略了左右车轮与轮轴间的相互作用;并且仅建立齿轮-轮对纯扭转振动模型,忽略了齿轮传动的平移运动和轴承的内部激励,弱化了齿轮传动和轮轨之间的耦合效应。
针对上述问题,本文通过对轨道车辆曲线区段行驶过程中轮轨横移受力和空间接触进行几何分析,结合改进的Kik-Piotrowski理论和FaStrip算法,提出曲线段轮轨横移动态黏着接触模型,并综合考虑轮轨黏着力激励、齿轮时变啮合刚度、轮轴扭转、轴承内部接触力等因素,建立考虑轮轨非线性黏着特性的轮对-齿轮传动系统动力学模型,并研究不同曲线段横移量下轮轨黏着接触特性以及不同曲线半径和运行速度下轮对-齿轮传动系统的动态特性。
1 曲线段轮对横移下轮轨动态黏着接触分析
1.1 曲线段轨道车辆轮对横向滑移分析
轨道车辆在通过小半径曲线弯道时,由于离心力和外轨超高产生的向心力不平衡,轮对发生横移;并且轮轨关系是动态变化的,轮轨接触界面特性会随车辆横移量的改变而发生相应变化[16]。对曲线段下的单节动力车辆(包含4组轮对)进行受力分析,为展示轮轨力的作用形式和方向,仅用单个轮对来表示整车的受力状态,如图1(a)所示。图1(a)中,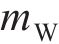
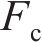
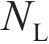
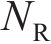
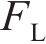
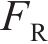
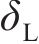
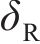
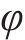
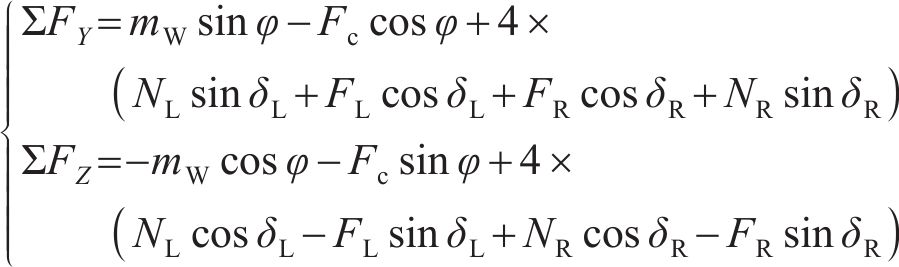
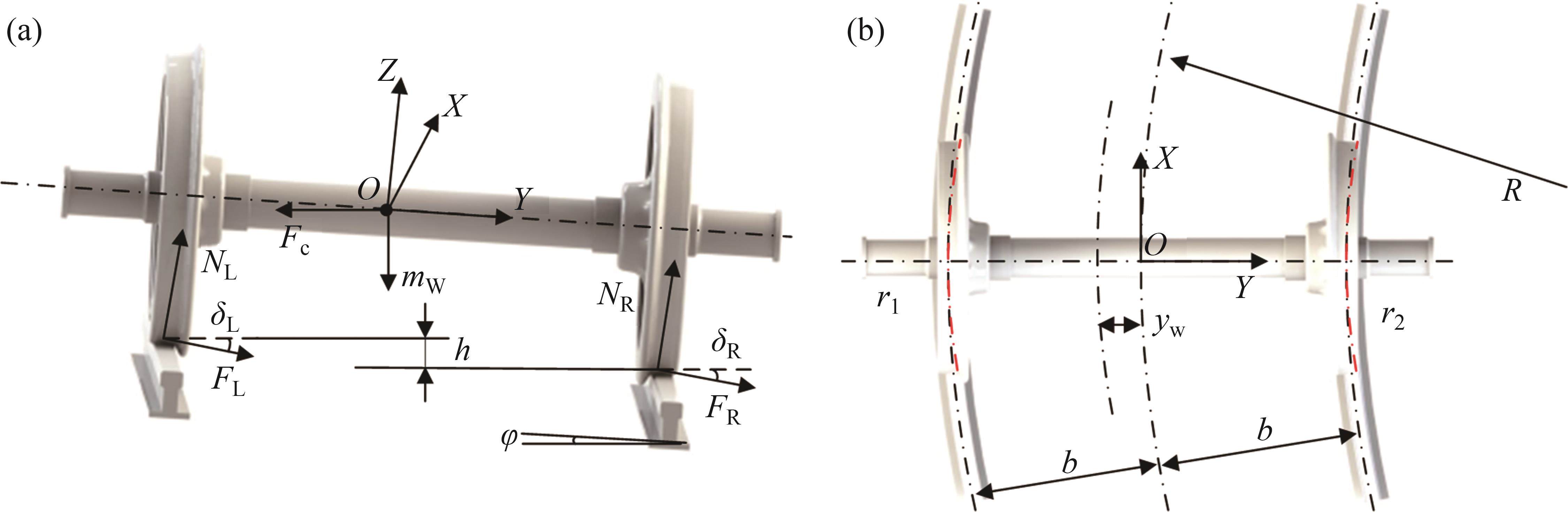
当平衡方程(1)不为0时,车辆发生横向滑移,如图1(b)所示,本文将整个动力车辆的横移量等同于轮对的横移量。根据文献[17]提出的非线性稳态曲线通过时的轮对横移量计算方法,可知横移量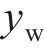
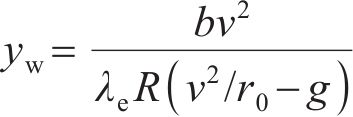
式中:R为曲线半径;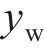
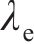
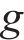
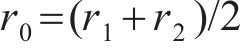
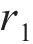
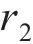
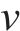
1.2 轮对横移下轮轨空间接触几何分析
本文以前进方向的左侧车轮为例,根据文献[18]提出的空间迹线法,构建轮对横移下轮轨空间接触几何分析模型,如图2所示。图2中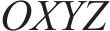
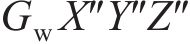
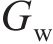

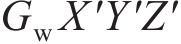
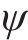
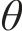
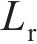
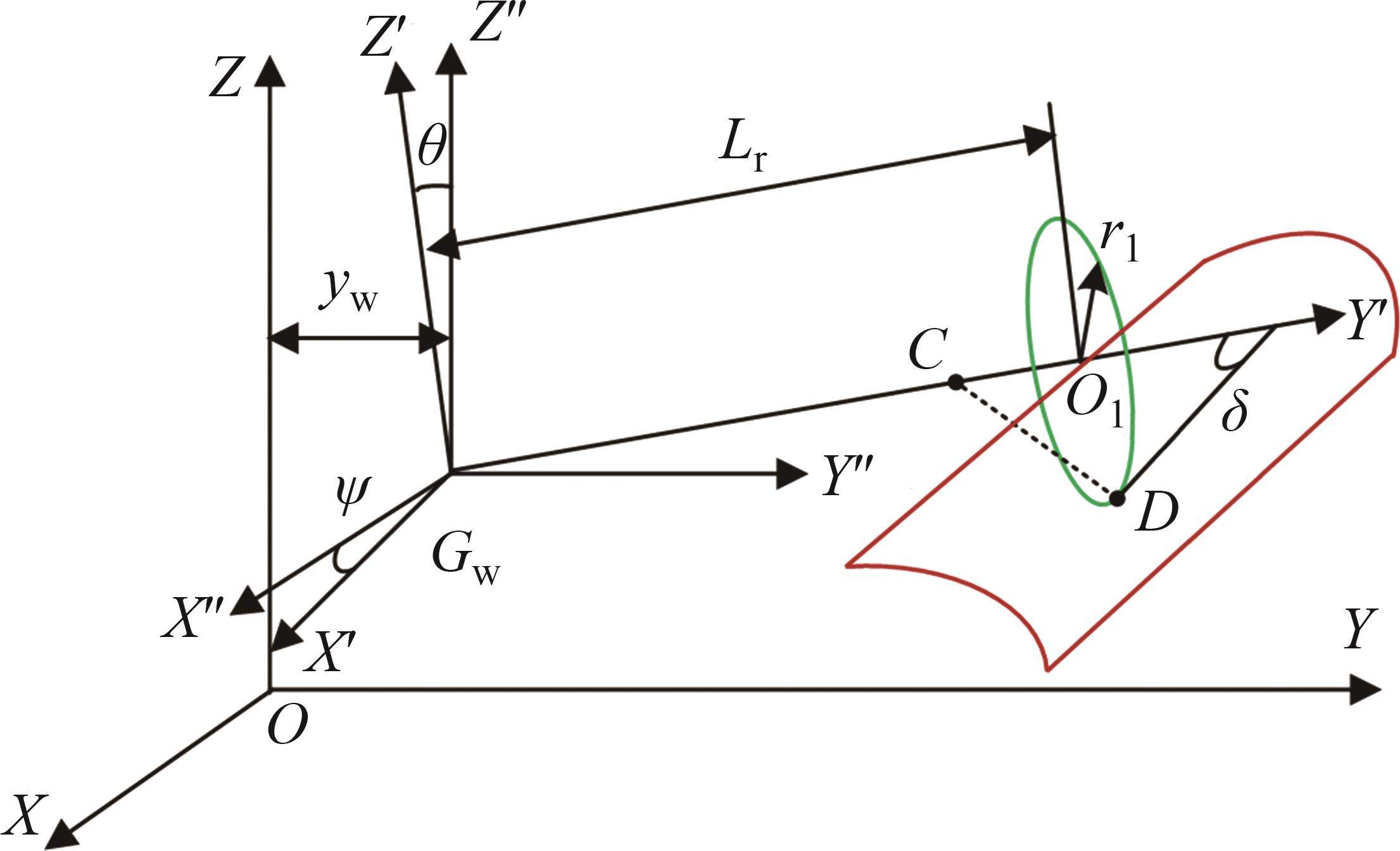
设轮轨接触点D在坐标系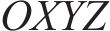
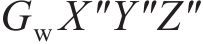
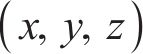
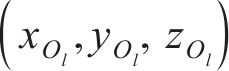
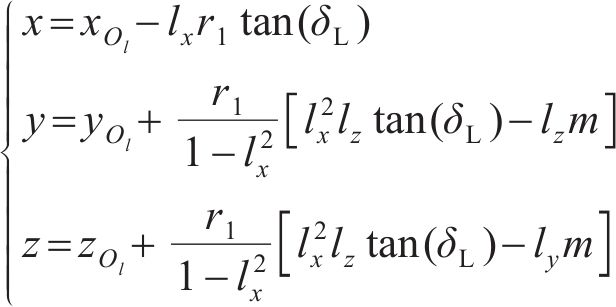
式中: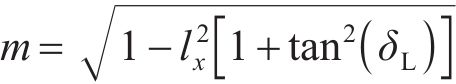
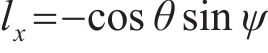
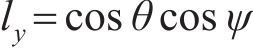
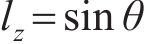
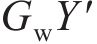
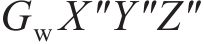
过接触点D作公法线交轮对中心线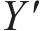
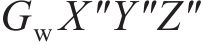
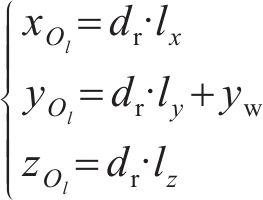
式中: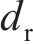
通过改变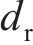
1.3 轮对横移作用下轮轨动态黏着接触模型
当车辆在轨道上运行时,轮轨法向压缩量随着轮轨相对运动的变化而变化,不同横移量下的法向压缩量也是不同的,要正确计算轮轨法向力,就必须准确求出每一时刻轮轨接触处的法向弹性压缩量。由1.2节中轮对横移下轮轨空间接触几何关系,可得到t时刻左、右轮轨垂向相对位移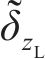
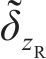
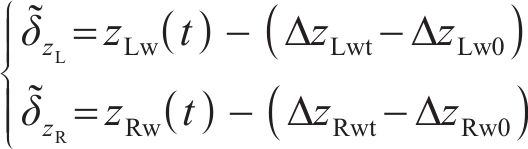
式中: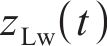
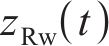
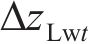
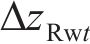
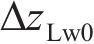
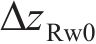
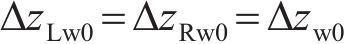
根据文献[19]提出的轮轨动态相互作用原理,左、右侧轮轨间法向压缩量可以表达为:
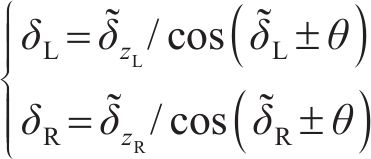
轮轨接触区域上轮轨外形的曲率半径往往不是常数,使得轮轨法向的接触斑表现为非椭圆形状的非Hertz接触。本文采用文献[20]提出的MKP方法(modified Kik-Piotrowski method)求解轮轨间的法向接触,假设接触斑的形状可以由轮轨型面和压入量直接决定,接触模型如图3所示。
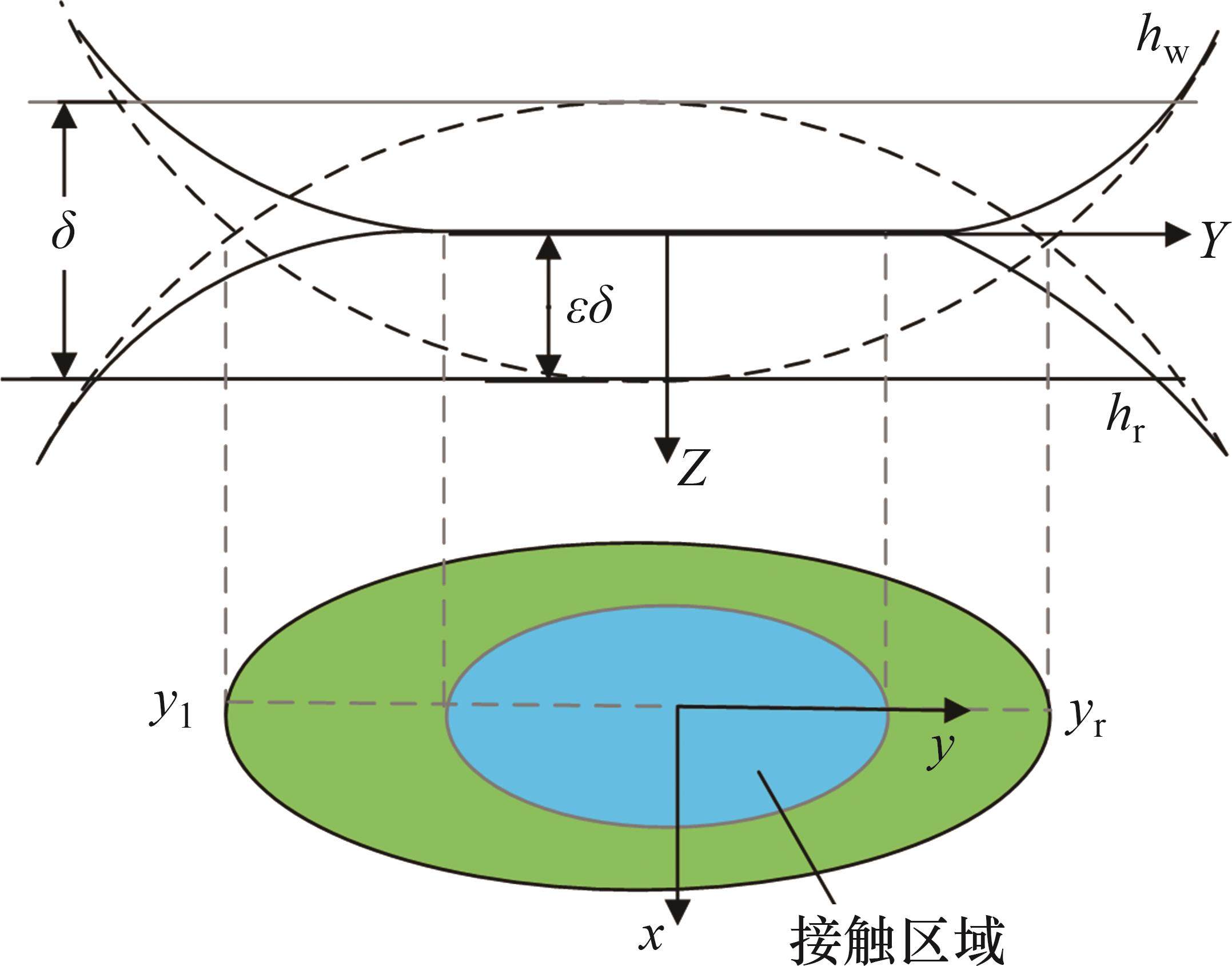
根据虚拟渗透量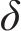
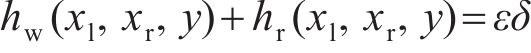
式中: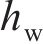
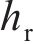
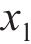
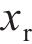
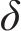
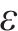
接触斑沿滚动方向的前后边界可表示为
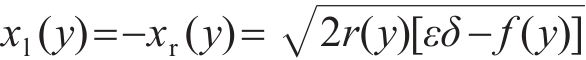
式中: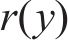
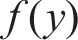
接触斑上的压力分布可表示为:
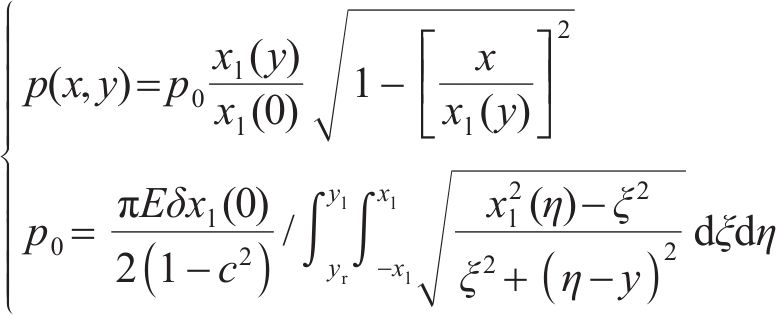
式中: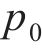
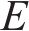
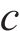
对接触压力在整个接触斑内进行积分,可得横移作用下轮轨法向接触力为
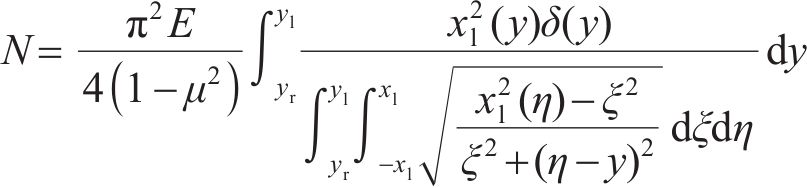
轮轨切向蠕滑求解是分析轮轨动力相互作用、轮轨黏着行为以及整车动力学分析的基础。根据条带理论对于切向应力分布的假设,将接触斑划分成黏着区和滑动区,分别计算这两个区域内的切向应力分布[7],示意图如图4所示。
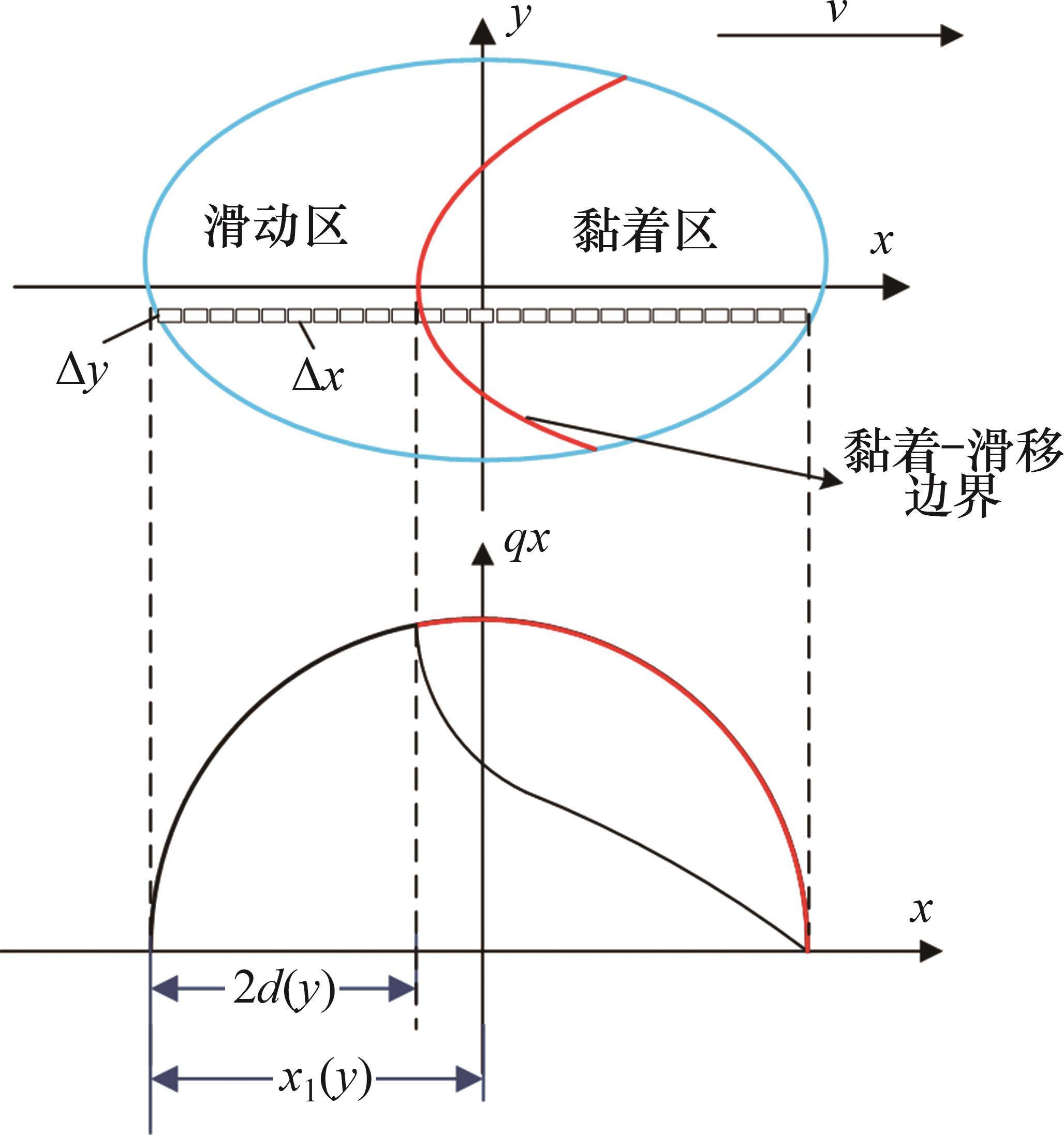
在黏着区域的纵向和横向切应力分布可以表示为:
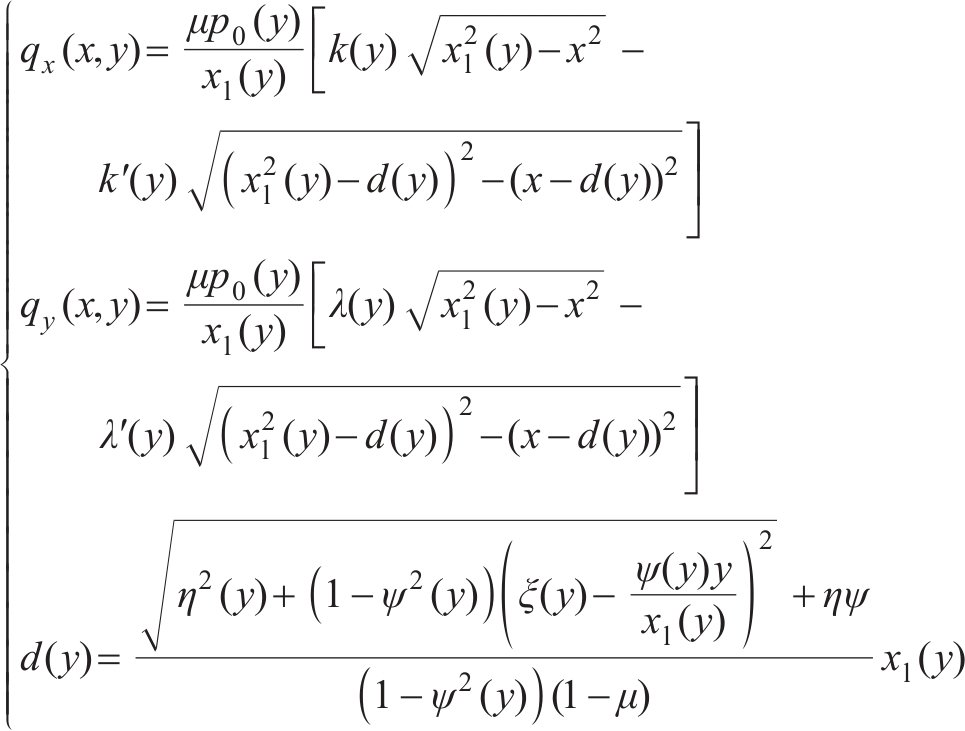
式中: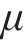
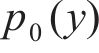
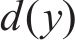
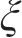
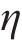
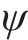
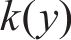
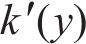
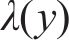
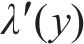
在滑动区,根据FaStrip轮轨蠕滑模型求解所得滑动区内的纵、横向轮轨切应力,计算式为:
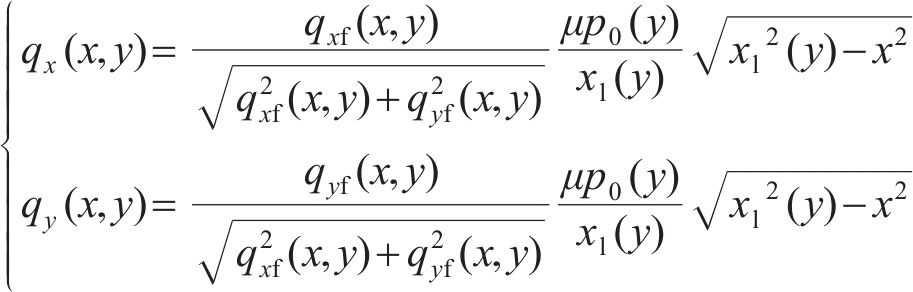
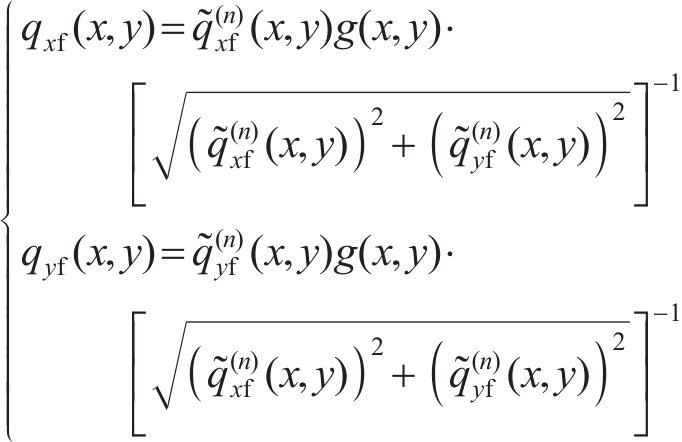
式中: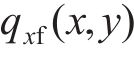
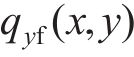
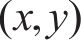
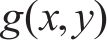
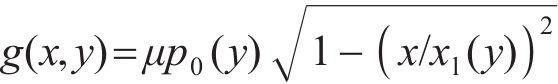
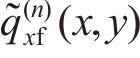
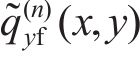
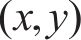
综上可得轮轨黏滑区域分布以及区域内的切向接触应力。轮轨纵、横向蠕滑力和自旋力矩可表示为:
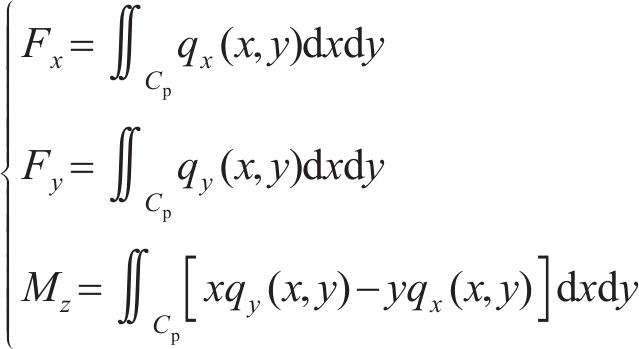
2 考虑轮轨横移黏着的轮对-齿轮传动系统动力学建模
忽略传动轴质量和齿面摩擦,不考虑摇头和侧滚角位移,研究横移作用下的轮轨黏着对系统动态特性影响。主动齿轮、从动齿轮和左、右轮的当量质量分别为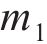
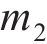
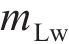
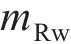
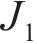
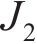
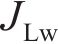

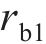
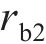
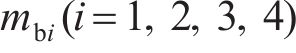
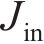

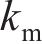
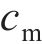
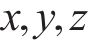
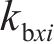
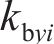
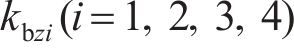
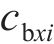
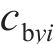
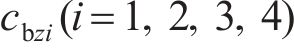
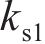
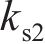
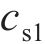
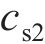
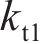
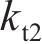
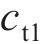
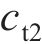
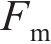
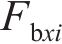
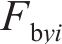
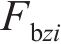
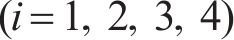
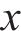
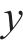
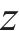
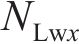
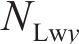
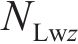
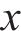
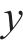
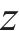
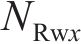
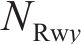
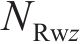
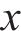
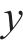
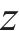
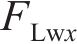
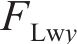
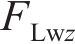
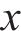
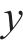
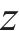
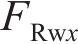
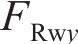
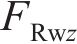
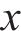
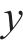
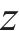
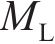
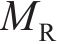
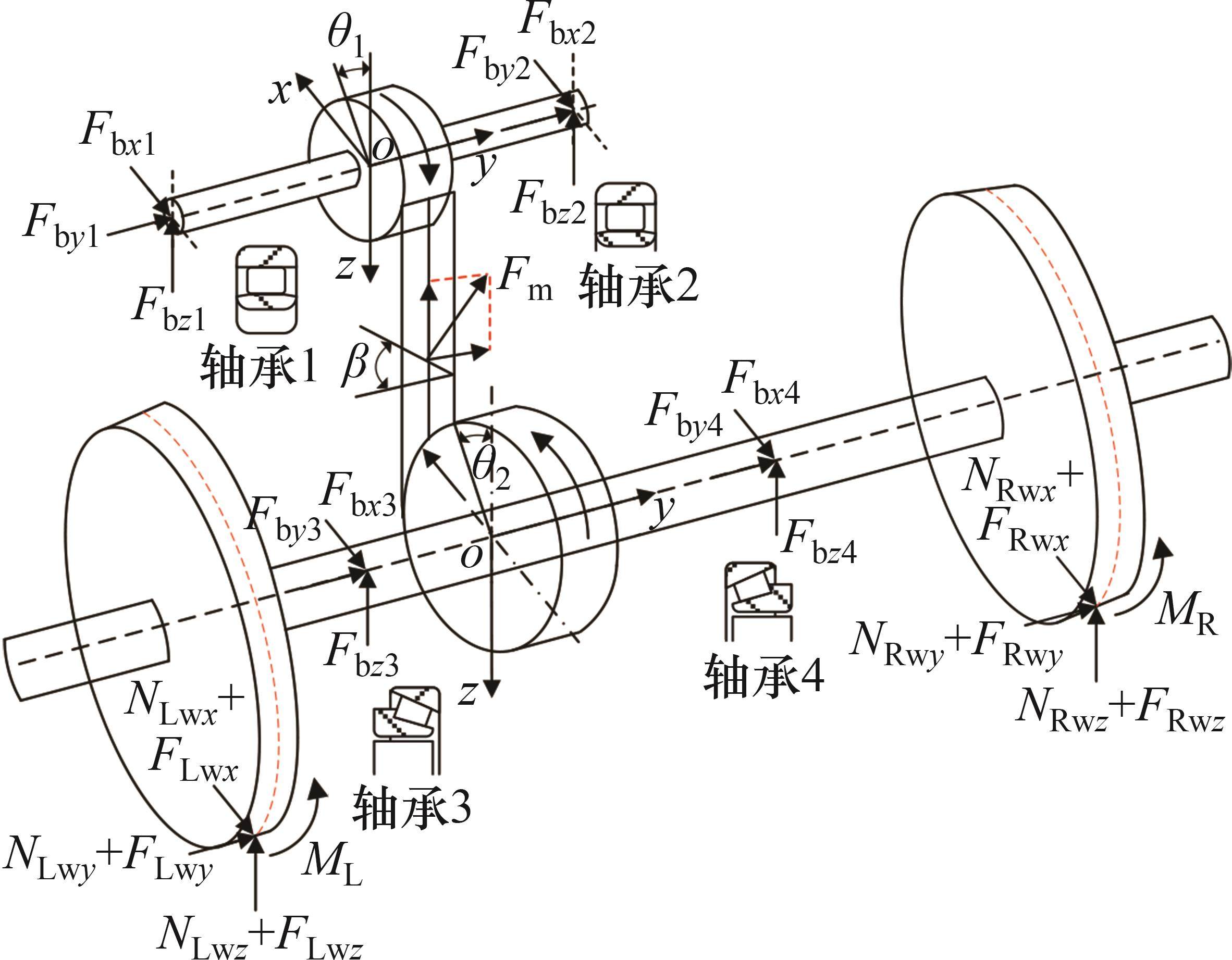
系统广义坐标列阵可表示为:
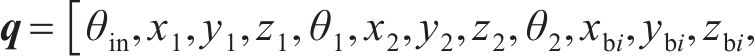
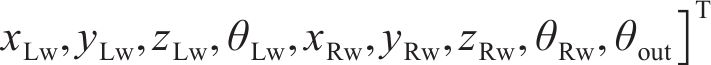
式中: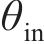
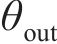
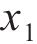
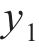
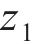
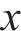
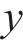
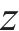
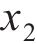
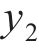
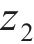
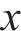
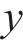
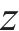
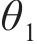
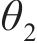
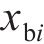
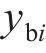
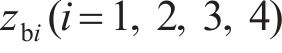
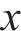
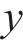
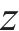
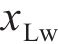
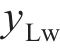
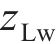
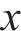
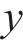
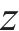
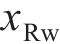
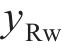
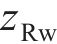
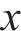
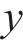
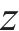
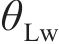
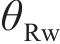
综上分析,根据拉格朗日普遍方程,可得轮对-齿轮传动系统的动力学微分方程如式(16)~(21)所示。
主动齿轮的动力学微分方程为:
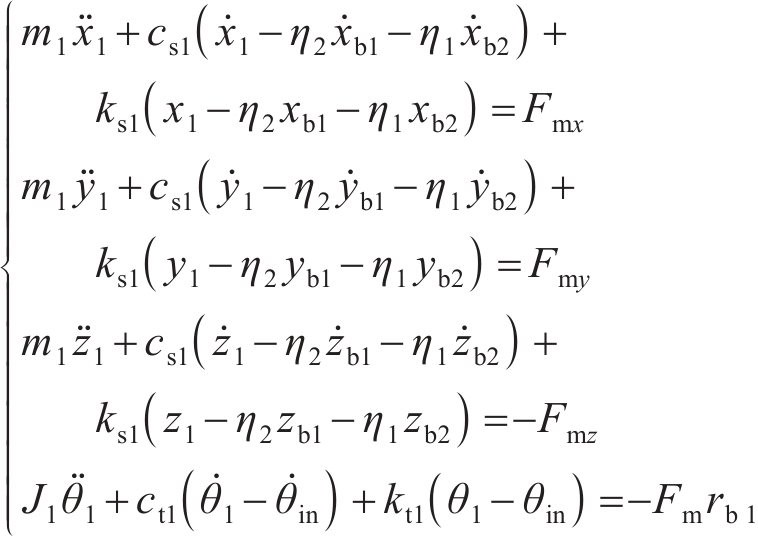
式中: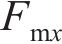
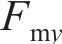
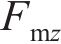
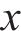
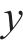
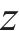
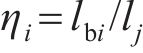
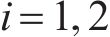
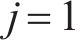
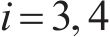
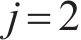
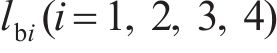
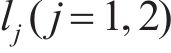
从动齿轮的动力学微分方程为:
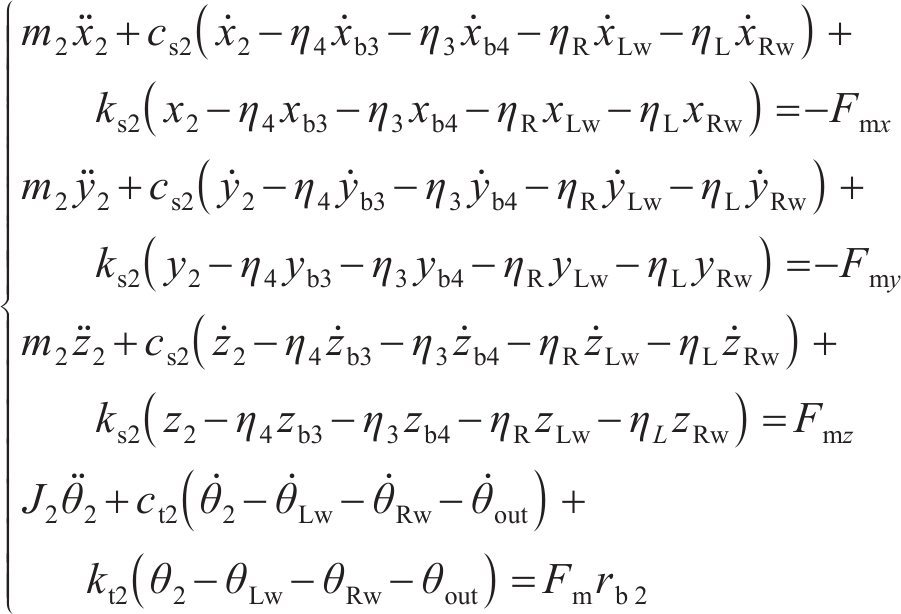
式中: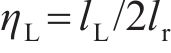
左、右车轮的动力学微分方程为:
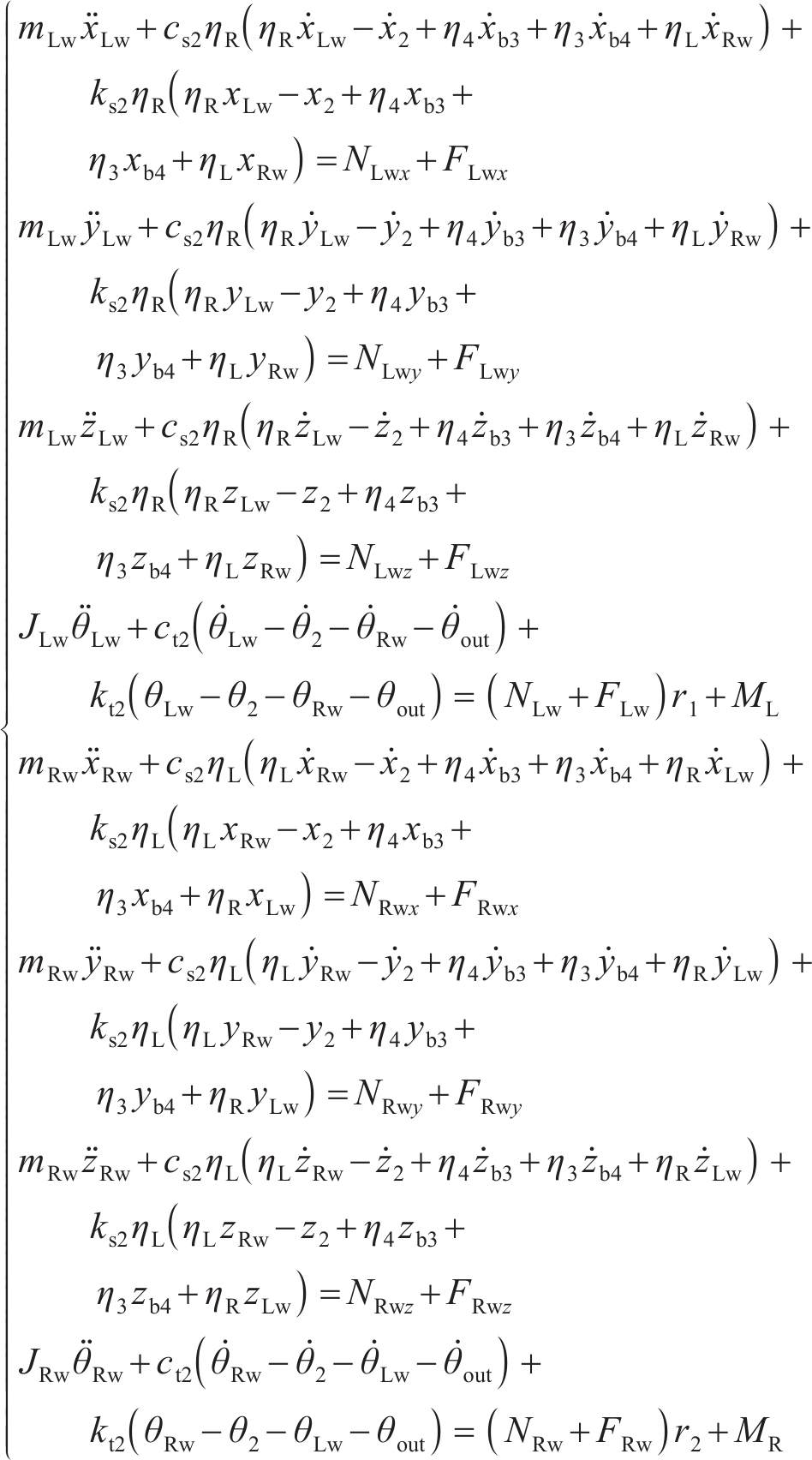
支撑轴承1和2的动力学微分方程为:
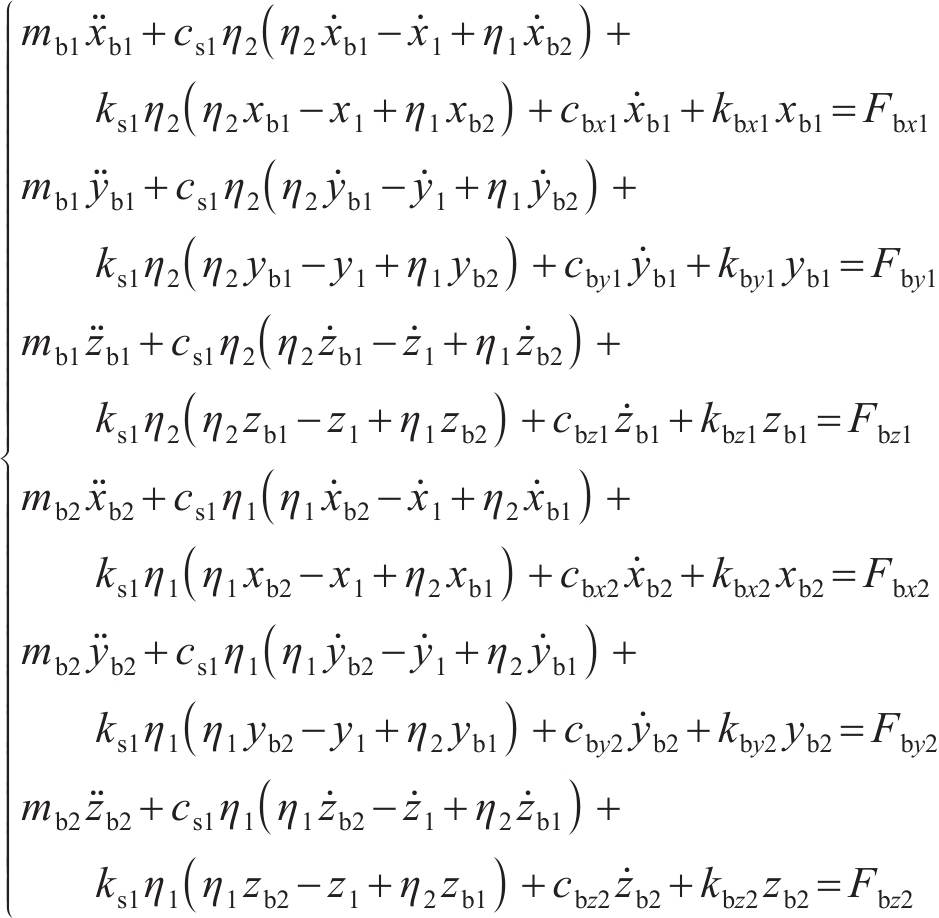
支撑轴承3和4的动力学微分方程为:

输入、输出轴的动力学微分方程为:
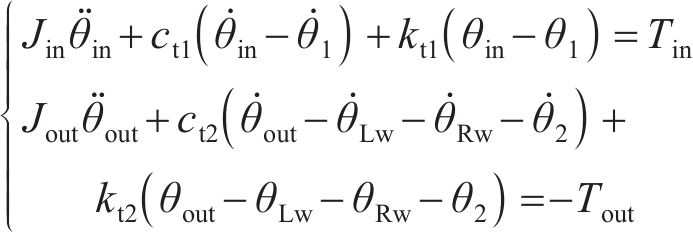
3 结果分析
轮对-齿轮传动系统包含轮轨接触非线性、时变啮合刚度和非线性支撑力等因素,为了简捷快速地求解,本研究采用ZHAI[21]提出的快速显式积分方法来求解轮对-齿轮系统的动力学方程,并以文献[22]中的轨道车辆为研究对象。该轨道车辆的车轮踏面为LM型踏面,钢轨外形为CN60,弹性模量E=205.9 GPa,泊松比c=0.3,齿轮箱为NPT216型号地铁齿轮箱,具体参数如表1所示。
| 参数 | 数值 |
|---|---|
主动齿轮齿数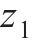 | 36 |
从动齿轮齿数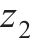 | 90 |
| 螺旋角β/(°) | 15 |
| 压力角α/(°) | 20 |
| 模数 | 5.5 |
| 齿宽B/mm | 80 |
| 齿厚s/mm | 15 |
| 轮对质量/kg | 1 365 |
支撑轴承1质量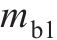 | 1.76 |
支撑轴承2质量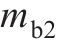 | 1.76 |
支撑轴承3质量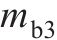 | 8.86 |
支撑轴承4质量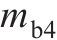 | 8.86 |
主动齿轮转动惯量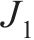 | 0.021 |
从动齿轮转动惯量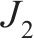 | 0.935 |
输入轴转动惯量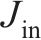 | 1.56 |
输出轴转动惯量 | 0.58 |
左车轮转动惯量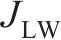 | 36.8 |
右车轮转动惯量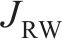 | 36.8 |
3.1 曲线段轮对横移下轮轨黏着接触特性分析
假设车轮处于正常情况,且在切向接触对法向接触不产生影响的条件下,研究曲线段轮对横移量对接触斑形状、接触斑面积和接触应力的影响。根据1.1节中曲线段轨道车辆轮对横向滑移分析,可得到当车辆运行速度为50 km/h时,通过不同曲线半径的弯道对应的横移量(左移)如表2所示。
| 曲线半径R/m | 运行速度/ (km‧h-1) | 超高/mm | 横移量 (左移)/mm |
|---|---|---|---|
| 300 | 50 | 100 | 6.3 |
| 500 | 50 | 100 | 4.4 |
| 0 | 50 | 0 | 0 |
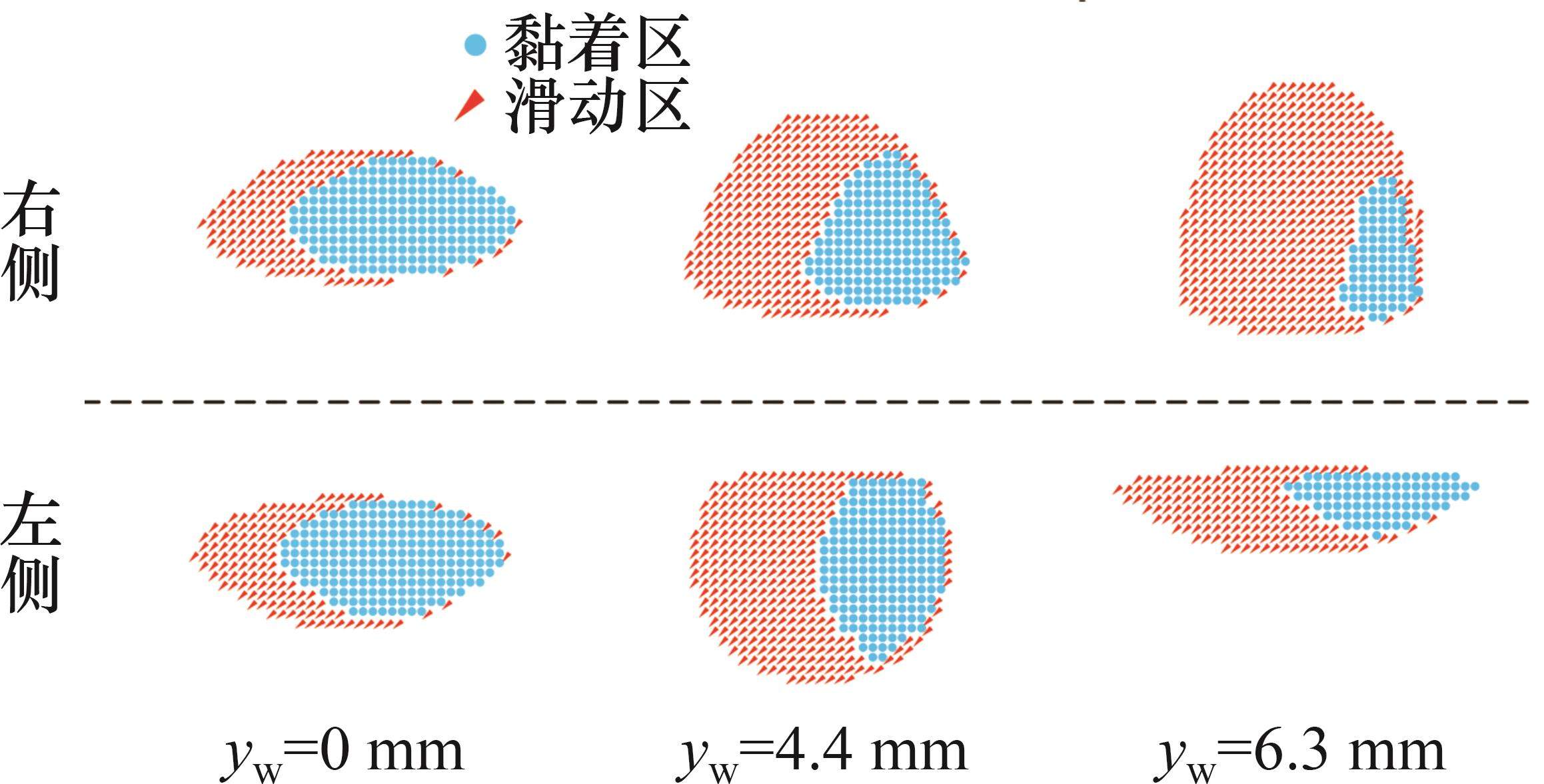
选取横移量为6.3、4.4、0 mm对轮轨黏着接触特性进行研究,表3所示为某时刻3个横移量下左、右轮轨法向接触应力和切向接触应力的分布结果。从表3可以看出:基于非赫兹接触算法计算的接触斑均呈非椭圆形状,当横移量为0 mm时,左、右轮轨的接触斑对称且面积相等,轮轨两侧最大法向接触应力均为155.1 MPa,位置处于接触斑正中心,最大切向接触应力均为40.2 MPa,且均位于接触斑左侧滑移区;当横移量为4.4 mm时,左、右轮轨接触斑变化明显,左侧接触斑整体呈圆形且有多点接触现象,右侧接触斑表现出上端尖、下端宽的形态,两侧最大法向接触应力分别为113.4 MPa和128.5 MPa,且分别位于两侧接触斑的顶端和底端,两侧最大切向接触应力分别为32.5 MPa和38.6 MPa,分布位置相比于直线行驶向右偏移;当横移量为6.3 mm时,左侧车轮发生轮缘接触,接触斑沿滚动方向(x轴)变长,在横移作用下,右侧接触斑明显沿y轴正向发生偏移,左右两侧最大法向接触应力分别为301.3 MPa和103.3 MPa,最大切向接触应力分别为88.7 MPa和33.5 MPa。图6所示为3个横移量下接触斑黏-滑区域分布结果。根据图6计算接触斑面积可知:当yw=0 mm时,左右侧接触斑面积均为76.8 mm2,滑动区面积占比为36%;当yw=4.4 mm时,左、右侧接触斑面积分别为91.2、100.8 mm2,滑动区面积占比分别为57%和58%;当yw=6.3 mm时,左、右侧接触斑面积分别为60.5、108 mm2,滑动区面积占比分别为76%和70%。综上可知,随着正向横移量的增大,左侧接触斑面积先增后减,右侧接触斑面积逐渐增大,左侧法向和切向接触应力幅值先减后增,右侧法向和切向接触应力幅值逐渐减小,且两侧的应力差值不断增大,应力幅值分布位置向轮对中心偏移,且接触斑滑动区面积占比逐渐增大,轮轨黏着接触性能逐渐变差。
| 横移量yw/mm | 接触应力类型 | |||
|---|---|---|---|---|
| 左侧法向接触应力 | 右侧法向接触应力 | 左侧切向接触应力 | 右侧切向接触应力 | |
| 0 | ||||
| 4.4 | ||||
| 6.3 | ||||
3.2 轮轨横移黏着作用下轮对-齿轮传动系统动态特性分析
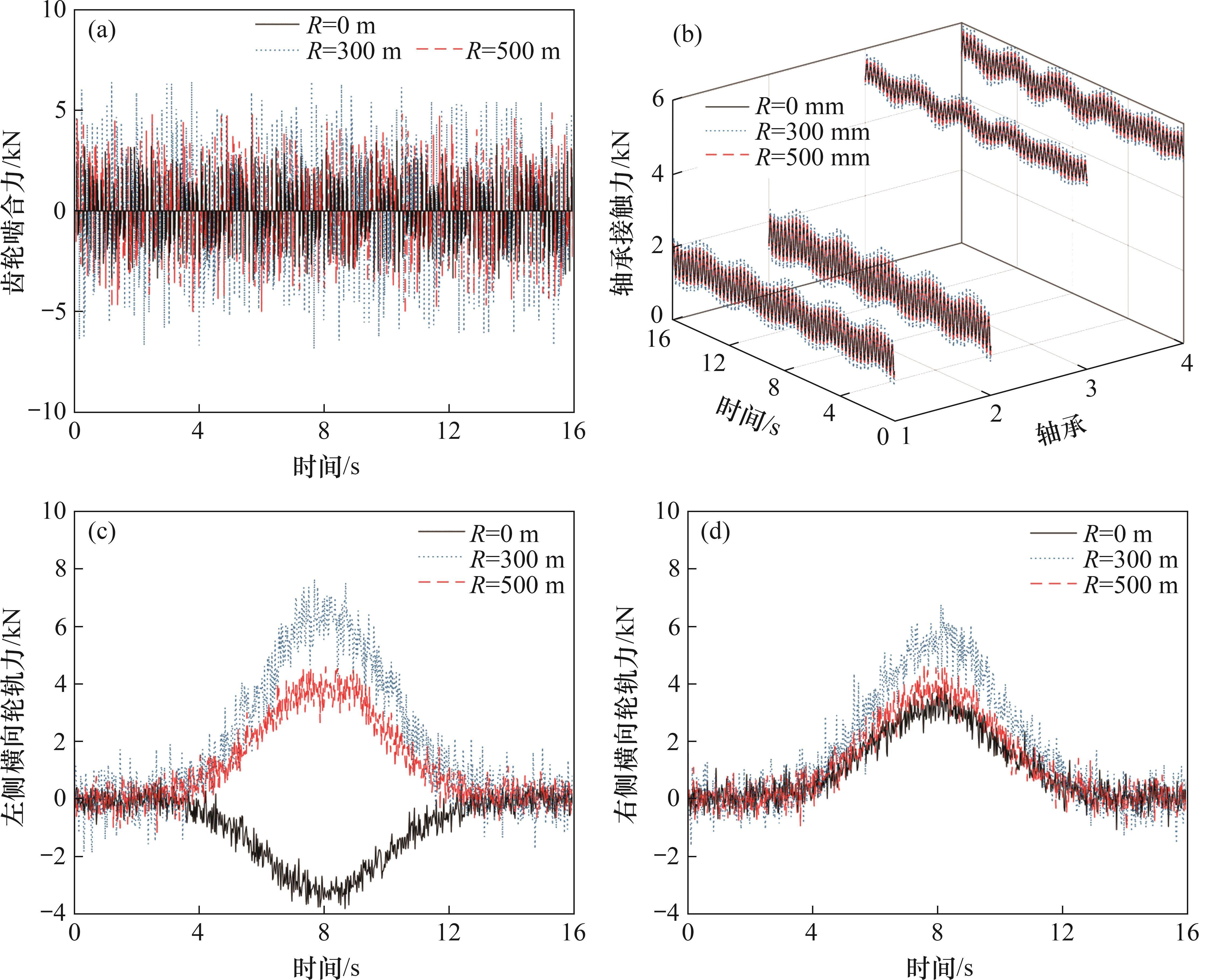
为分析轮轨横移黏着对轮对-齿轮传动系统动态特性的影响,选取车辆运行速度为50 km/h,通过弯道曲线半径R分别为0、300、500 m的工况进行对比研究。图7(a)所示为3种曲线半径下齿轮副时变啮合力的计算结果。从图7(a)可知:在R=300 m时,啮合力振幅最大,幅值为6.2 kN,这是由于在横移黏着作用下轮轨之间的黏着力矩不足以驱动车辆前进而发生打滑,加剧齿轮箱振动;而当R=0 m时,啮合力振幅最小,幅值为3.3 kN,这是因为此时黏着力较大,黏着力提供的阻尼作用降低了齿轮系统的振动。图7(b)所示为3种曲线半径下4个轴承接触力的计算结果。从图7(b)可见:在曲线段轮对横移作用下,4个轴承的接触力均发生显著变化,其中主动齿轮两侧轴承的接触力明显小于从动齿轮两侧轴承的接触力,并且左侧轴承(1、3号)的接触力始终大于右侧轴承(2、4号)的接触力,这是由于齿轮轴向啮合分力和横向轮轨力使齿轮箱向左侧偏移。图7(c)和(d)所示为3种曲线半径下左、右两侧横向轮轨力的计算结果,整体呈先增后减的趋势,直线工况时,左、右侧横向轮轨力大小相等、方向相反,均指向轨道中心线,曲线工况下左右侧横向轮轨力均增大;R=300 m时,轮轨力最大,分别为7.8 kN和6.4 kN,并且由于处于欠超高状态,地铁车辆向外侧(左侧)偏移,发生轮缘接触,导致左侧轮轨力比右侧的大。
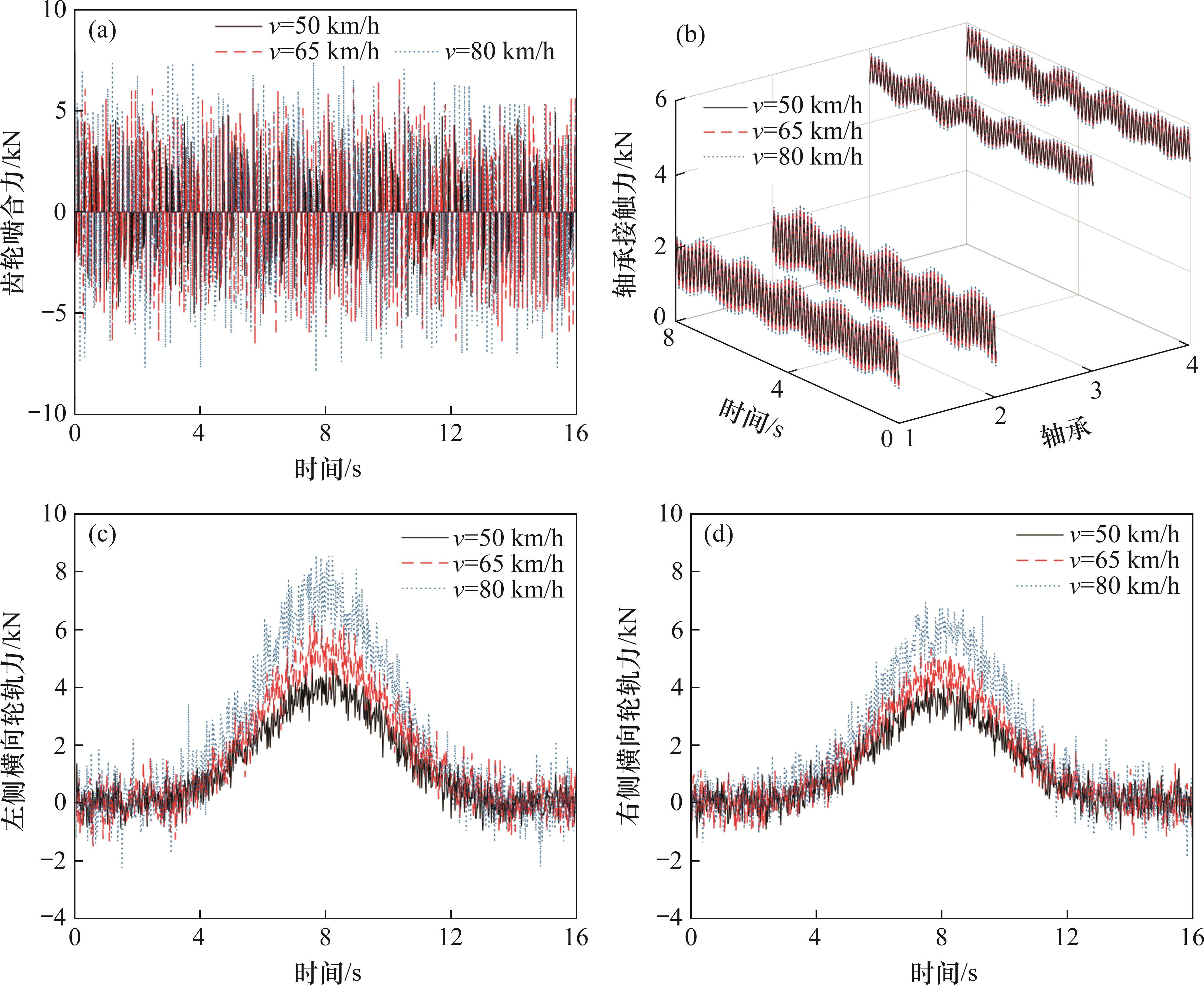
轨道车辆在不同运行速度下轮轨横移黏着接触特性也不同,因此,选取曲线半径为500 m,车辆运行速度分别为50、65、80 km/h,对这3种工况下传动系统的动态特性进行研究。图8(a)所示为3种运行速度下齿轮副时变啮合力的计算结果。从图8(a)可见:在v为65、80 km/h时,啮合力幅值分别为6.4、7.5 kN,比v为50 km/h时,啮合力幅值分别增加了30.6%和53.1%,说明曲线段轮轨横移黏着对啮合副时变啮合力有显著影响,并且速度越大影响越明显。图8(b)所示为3种运行速度下4个轴承接触力的计算结果。从图8(b)可见:随着运行速度的增大,4个轴承的接触力也逐渐增大,且在内外激励的耦合作用下,左侧轴承(1、3号)的接触力始终比右侧(2、4号)的大。图8(c)和(d)所示为3种运行速度下左、右轮横向轮轨力的计算结果。从图8(c)和(d)可见:由于轮轨具有横移黏着的动态接触特性,轮轨力整体呈先增后减趋势,并随着速度增大,横移作用也逐渐增强,左右侧横向轮轨力均增大,且左侧的轮轨力始终大于右侧的轮轨力。
4 结论
1) 本文通过曲线段轮对横移滑移和空间接触几何分析,提出了轮轨横移动态黏着接触模型,并在此基础上构建了考虑轮轨动态黏着激励、齿轮时变啮合刚度、非线性轴承接触力等因素的轨道车辆轮对-齿轮传动系统动力学模型,为研究曲线段轮轨动态黏着接触特性及轮轨横移黏着作用下轮对-齿轮传动系统动态特性提供了更符合实际的理论模型。
2) 轮对的横移作用导致轮轨接触特性发生显著改变。当横移量为0 mm时,左、右轮轨接触斑对称且面积相等,两侧最大法向接触应力均为155.1 MPa,位置处于接触斑正中心,最大切向接触应力均为40.2 MPa,且均位于接触斑左侧滑移区;随着正向横移量的增大,左侧接触斑面积先增大后减小,右侧接触斑面积逐渐增大,左侧法向和切向接触应力幅值先减小后增大,右侧法向和切向接触应力幅值逐渐减小,且两侧的应力差值不断增大,应力幅值分布位置向轮对中心偏移,并且接触斑滑动区占比逐渐增大,轮轨黏着接触性能逐渐变差。
3) 曲线半径和运行速度对传动系统动态特性影响显著,随着曲线半径的减小和运行速度的增加,黏着力矩不足以驱动车辆前进而发生打滑,使得齿轮副啮合力、轴承接触力和左右侧横向轮轨力都随之增大,传动系统振动加剧,并且由于轮轨具有横移黏着的动态接触特性,轮轨力整体呈先增大后减小趋势,并在横移黏着作用影响下,左侧的轴承接触力和横向轮轨力均比右侧的大。
樊林放, 徐向阳, 田富文, 等. 轮轨横移黏着作用下轨道车辆轮对-齿轮传动系统动力学研究[J]. 中南大学学报(自然科学版), 2025, 56(2): 795-806.
FAN Linfang, XU Xiangyang, TIAN Fuwen, et al. Study on dynamics of wheelset-gear transmission system of rail vehicle in wheel-rail lateral adhesion[J]. Journal of Central South University(Science and Technology), 2025, 56(2): 795-806.

